Short-Term Wind Power Prediction Based on a Variational Mode Decomposition–BiTCN–Psformer Hybrid Model

Abstract

Precise wind power forecasting is essential for the successful integration of wind power into the power grid and for mitigating the potential effects of wind power on the power system. To enhance the precision of predictions, a hybrid VMD-BiTCN-Psformer model was devised. Firstly, VMD divided the original sequence into several data components with varying time scales. Furthermore, the BiTCN network was utilized to extract the sequence features. These features, along with the climate features, were then input into the positional encoding and ProbSparse self-attention improved Transformer model. The outputs of these models were combined to obtain the ultimate wind power prediction results. For the prediction of the wind power in Fujian Province on April 26, four additional models were developed for comparison with the VMD-BiTCN-Psformer model. The VMD-BiTCN-Psformer model demonstrated the greatest level of forecast accuracy among all the models. The R² increased by 22.27%, 12.38%, 8.93%, and 2.59%, respectively.

1. Introduction

In 2020, China put forward the goal of “reaching peak carbon by 2030 and achieving carbon neutrality by 2060” [1]. Global carbon dioxide emissions from energy combustion hit a historic peak of 36.8 billion tons in 2022. Hence, wind energy, which embodies the latest advancements in energy generation, has emerged as a pivotal area of investigation in multiple nations [2]. Nevertheless, meteorological factors in the atmosphere change rapidly, causing transient or short-term fluctuations in wind power generation. This poses a challenge to the optimum scheduling and safe operation of the power system [3,4]. By improving the accuracy of wind power prediction, the grid scheduling department can rationally arrange the power generation plan and improve the economy of grid operation.

With the development of Artificial Intelligence (AI) [5], machine learning models [6] and deep learning models have been widely used in wind power prediction and are gradually replacing previous methods. Reference [7] presents a distinctive hybrid forecasting model that integrates Long Short-Term Memory (LSTM) with Gauss, Moret, Ricker, and Shannon for power forecasting. This integration enhances the utilization of deep learning by tackling issues like gradient vanishing and nonlinear mapping through the use of wavelet transforms, thus enhancing the precision of wind power prediction. Reference [8] introduces a novel framework designed to improve the accuracy of predicting wind power generation in 5 min intervals. The system incorporates signal decomposition and heuristic techniques, known as CEMOLS, to optimize the parameters of neural networks. Reference [9] introduces the AMC-LSTM model designed for wind power forecasting. It includes an Attention Mechanism to dynamically assign weights to physical attribute data, utilizes Convolutional Neural Networks (CNN) to extract short-term features, and applies LSTM to capture long-term trends. In reference [10], Three types of Deep Neural Networks (DNNs) were used for the experiment and the best result was achieved with the Gated Recurrent Unit (GRU) network. Reference [11] introduces a novel spatiotemporal directed graph convolution neural network and verify the superiority of the proposed model in spatiotemporal correlation representation. Reference [12] combines point prediction and probability density prediction, and the results show accurate prediction in extreme weather. The literature outlined above demonstrates that the accuracy of the prediction model can be significantly enhanced by the utilization of various model combinations.

The Transformer is a highly effective deep learning model architecture that demonstrates strong performance when applied to continuous data. It is becoming increasingly popular in the field of wind power prediction. Reference [13] utilizes transformer neural networks that incorporate a multi-head attention mechanism to effectively capture successive dependencies, irrespective of their distance. The reference [14] investigates the application of Transformer-based architectures: Informer, LogSparse Transformer, and Autoformer for the first time. The study carried out in [15] introduces a novel deep neural network structure based on transformers that incorporates wavelet transform to predict wind speed and wind energy generation up to 6 h ahead. The author of [16] introduces a wind power forecasting model that integrates LSTM to capture the temporal dynamics of weather data and a Vision Transformer (ViT) to construct connections between extracted characteristics and desired outputs using multi-headed self-attention methods. However, the conventional Transformer model encounters the issue of significant time complexity when handling long sequential data, which can be resolved by using Probsparse self-attention. The ProbSparse self-attention mechanism achieves a time complexity and memory consumption of O (LlogL), which presents a significant enhancement compared to the self-attention mechanism in the conventional Transformer model [17]. We utilized the Probsparse self-attention to enhance the original self-attention mechanism of the Transformer, which we refer to as the Psformer.

The Temporal Convolutional Network (TCN) utilizes convolutional operations to extract and acquire features from time series data. It has demonstrated a strong performance in many applications, including time series prediction and classification. Reference [18] employs a deep clustering model based on the Categorical Generative Adversarial Network (CGAN) for precise classification. Additionally, they enhance the TCN by integrating a gating mechanism within its activation function. In reference [19], an enhanced Temporal Convolutional Network (MITCN) is devised for predicting multi-step time series. They have incorporated the quadratic spline quantile function (QSQF) to facilitate probabilistic forecasting. Recently we have found that bi-directional neural networks are gaining popularity due to the fact that they can capture contextual information about both past and future states, which makes it possible to accurately model and predict sequences with long-term dependencies. To address the issue of offshore wind power generation being affected by extreme weather conditions, reference [20] introduces a new prediction method that merges convolution and attention mechanisms. The approach integrates a bidirectional long short-term memory (BiLSTM) network with an attention mechanism (AM). It is proved that the mean square error of this model is much lower than that of LSTM without bidirectional structure. In [21], BiLSTM’s bidirectional capability was also used to extract deep correlation in data to analyze wind power data. Reference [22] proposed a model based on the XGBoost algorithm combining financial technical indicators, The model has high prediction accuracy and speed. Reference [23] presents a hybrid model that combines BiTCN and BiLSTM with an attention mechanism; the attention mechanism improves the model’s capacity to concentrate on significant characteristics. From the recent literature, it can be seen that neural networks with forward and reverse processes are becoming more widely used than traditional neural networks.

Data decomposition is a highly successful technique for extracting the underlying patterns in data, thereby lowering the complexity of training prediction models and improving their accuracy. The Wavelet Packet Transform (WPT) [24] uses a collection of orthogonal and rapidly decaying wavelet function bases to accurately fit signals. Ensemble Empirical Mode Decomposition (EEMD) [25] is an enhanced version of Empirical Mode Decomposition (EMD) [26]. EEMD improves EMD by introducing white noise into the signal to fill in missing scales. This technique has demonstrated excellent performance in signal decomposition. Variational Mode Decomposition (VMD) [27] is an algorithm that iteratively searches for the optimal solution of a variational model to identify the center frequency and bandwidth of each component. This algorithm is a completely non-recursive model. The experimental findings from reference [28] demonstrate that the decomposition impact of VMD is more pronounced in power prediction compared to EMD.

According to the aforementioned research, the majority of studies focus solely on enhancing prediction accuracy through the integration of one or two models. There is a scarcity of research that combines signal decomposition, BiTCN extraction features, and the Transformer model. Therefore, we propose a novel hybrid prediction model named VMD-BiTCN-Psformer, which offers the following key contributions:

• Through VMD, the original signal is decomposed as a whole into other component signals. The decomposition process is carried out on the features of specific significance and can yield a greater amount of comprehensive information and structure within the signal.
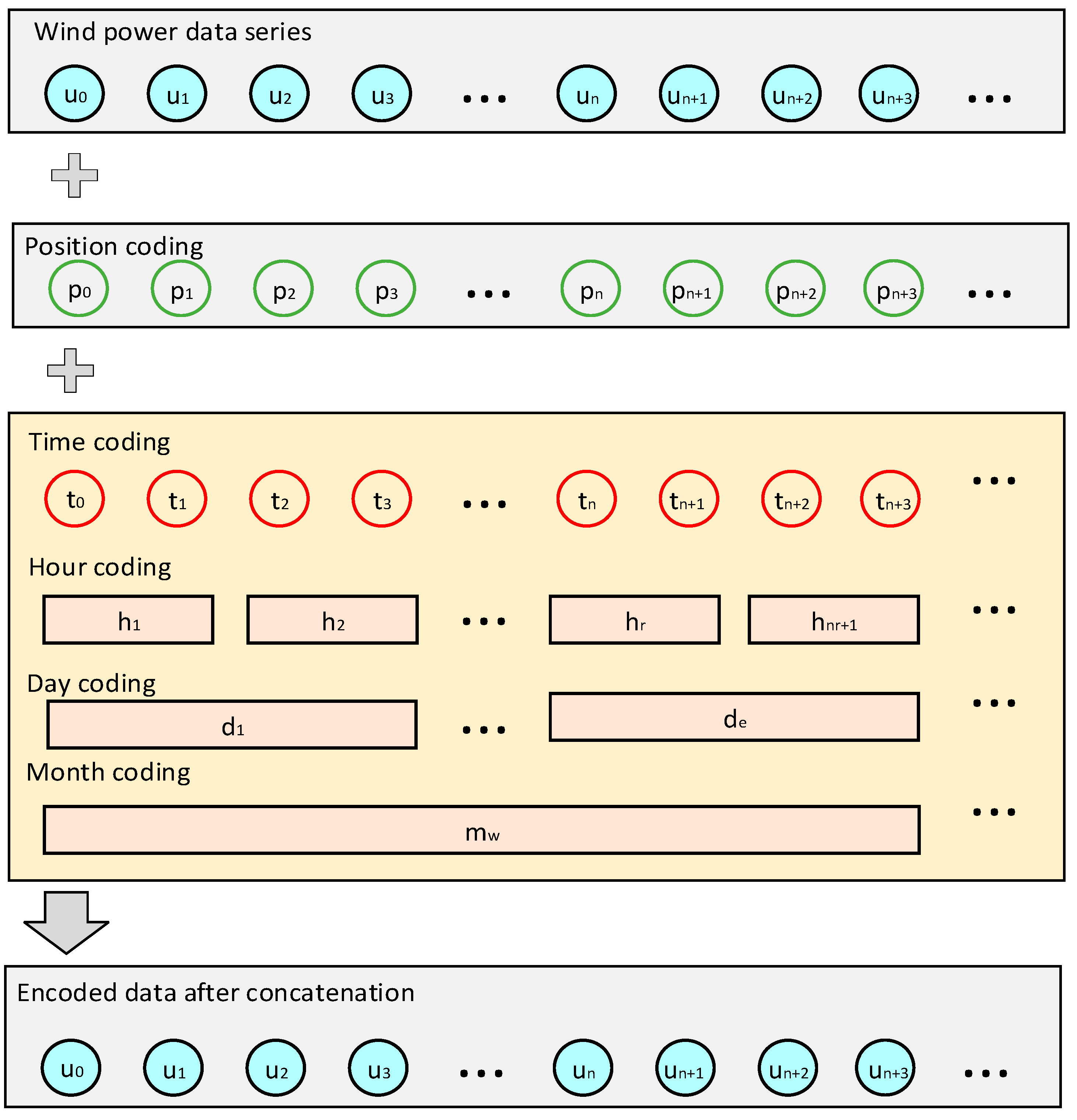
• The concept of position encoding is utilized to extract the hidden aspects of multi-scale temporal seasonal information, which are then merged with position encoding.
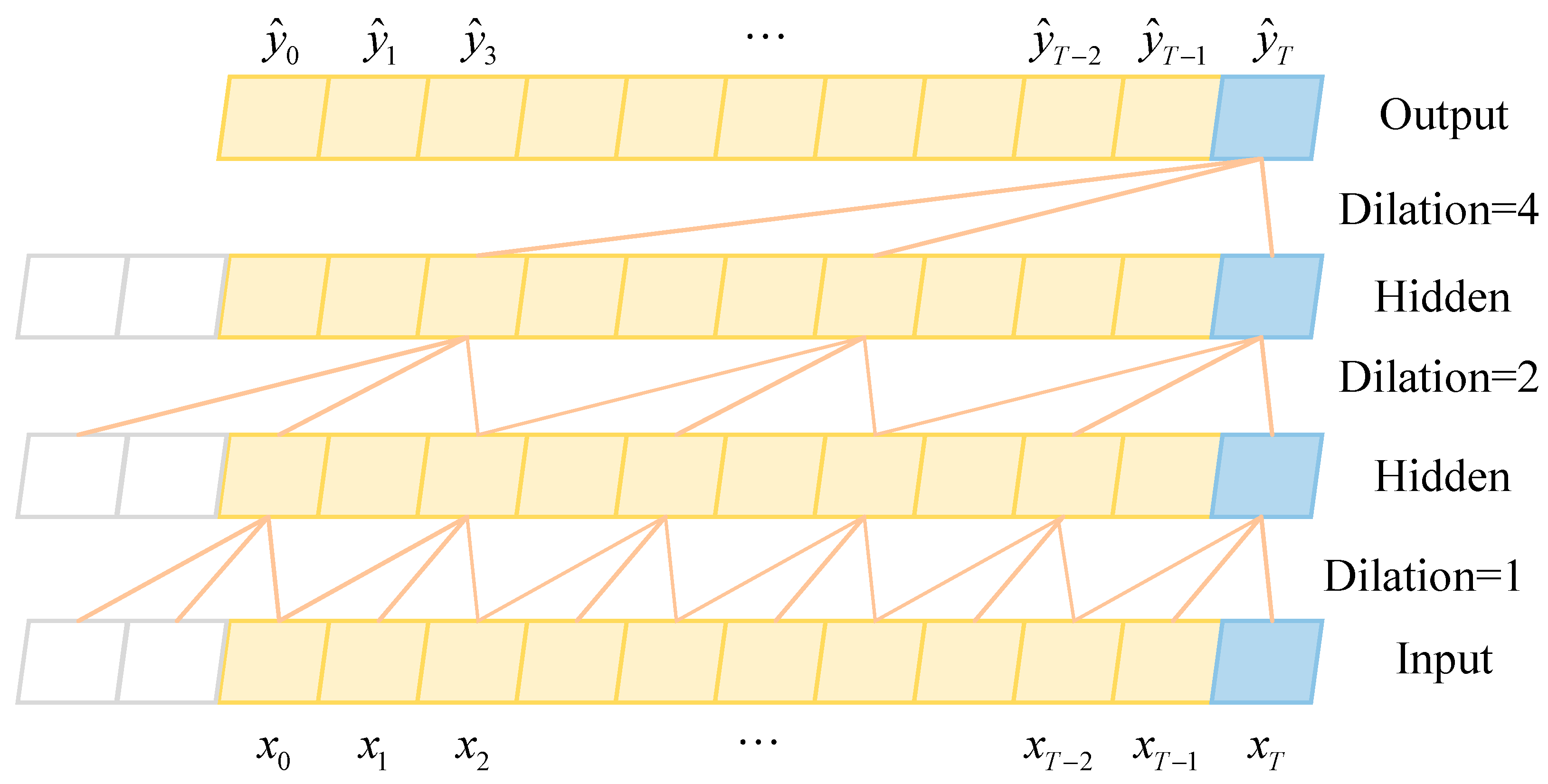
• BiTCN was introduced to extract features of near-time segments of observation points, expand the scope from which the model may acquire information and generate predictions, and adjust the connection structure of the self-attention mechanism and BiTCN output data.
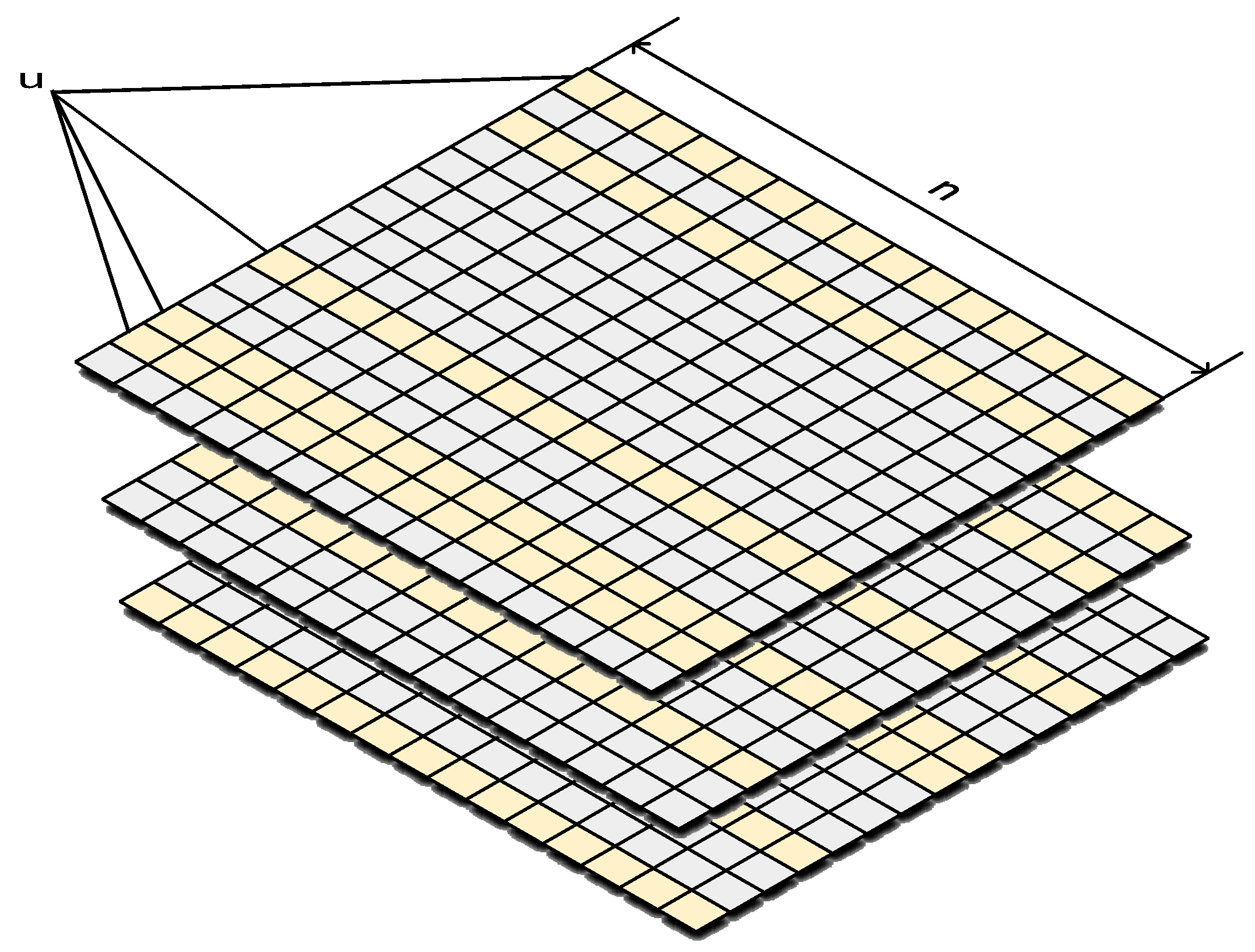
• The ProbSparse self-attention is introduced, and the Psformer model is designed to integrate the characteristics of significant time points into the self-attention mechanism, resulting in enhanced forecast accuracy of wind power and reduced computational complexity.

2. Materials and Methods

2.1. Decomposition of Wind Power Using VMD

To address the unpredictable, variable, and ever-changing characteristics of wind power time series, decomposition techniques are often employed to reveal their inherent features and enhance the precision of wind power forecasting. Variational Mode Decomposition (VMD) was proposed by Dragomiretskiy et al. in 2014 [29]. The model uses a collection of modes and their respective center frequencies in order to accurately reproduce the input signal as a whole. Furthermore, each mode is smoothly demodulated to the baseband. The alternate direction multiplier approach is employed to optimize the variational model effectively, thereby enhancing the model’s robustness to sampling noise.

The goal is to minimize the total bandwidth of each modal component while ensuring that the sum of all modal functions after decomposition is identical to the original signal before decomposition. Equation (1) is a problem with constraints. To solve this problem, we converted it into an unconstrained variational problem, as depicted in Equation (2), by incorporating Lagrange multipliers and second-order penalty factors.

$$\left\{\begin{array}{l}\underset{\left\{{\nu }_k\right\},\left\{{\omega }_k\right\}}{\min }\left\{{{\displaystyle \sum _k‖{\mathsf{\partial }}_t\left[\left(\delta \left(t\right)+\frac{\mathrm{j}}{\pi t}\right)\ast {\nu }_k(t)\right]e^{-\mathrm{j}{\omega }_{k}t}‖}}^2\right\}\\ s.t.{\displaystyle \sum _k{\nu }_k=s(t)}\end{array}\right.$$

(1)

$$\mathrm{L}\left(\left\{{\nu }_k\right\},\left\{{\omega }_k\right\},\tau \right)=\alpha {{\displaystyle \sum _k‖{\mathsf{\partial }}_t\left[\left(\delta \left(t\right)+\frac{\mathrm{j}}{\pi t}\right)\ast {\nu }_k(t)\right]e^{-\mathrm{j}{\omega }_{k}t}‖}}^2+{‖s\left(t\right)-{\displaystyle \sum _k{\nu }_k\left(t\right)}‖}^2+〈\tau \left(t\right),s\left(t\right)-{\displaystyle \sum _k{\nu }_k\left(t\right)}〉$$

(2)

where $\delta \left(t\right)$ is the Dirac function, ${\nu }_k\left(t\right)$ is the k-th modal component, ${\omega }_k(t)$ is the k-th center frequency, $s(t)$ is the original wind power, ∗ denotes convolution.

The saddle point of Equation (1) is solved by iteratively updating the solution, employing the alternating direction multiplier method described in Equations (3)–(5).

$${\widehat{\nu }}_k^{n+1}\left(\omega \right)={\displaystyle \frac{\widehat{s}\left(\omega \right)-{\displaystyle \sum _{i\ne k}{\widehat{\nu }}_i\left(\omega \right)+\widehat{\tau }\left(\omega \right)/2}}{1+2\alpha {\left(\omega -{\omega }_k\right)}^2}}$$

(3)

$${\omega }_k^{n+1}={\displaystyle \frac{{\displaystyle {\int }_0^{\infty }\omega {\left|{\nu }_k^{n+1}\left(\omega \right)\right|}^{2}d\omega }}{{\displaystyle {\int }_0^{\infty }{\left|{\nu }_k^{n+1}\left(\omega \right)\right|}^{2}d\omega }}}$$

(4)

$${\widehat{\tau }}^{n+1}\left(\omega \right)={\widehat{\tau }}^n\left(\omega \right)+\tau \left(\widehat{s}\left(\omega \right)-{\widehat{\nu }}_k^{n+1}\left(\omega \right)\right)$$

(5)

where $\widehat{s}\left(\omega \right)$, ${\widehat{\nu }}_k\left(\omega \right)$, and $\widehat{\tau }\left(\omega \right)$ are the Fourier transformed form of $s(t)$, ${\nu }_k\left(t\right)$, and ${\omega }_k(t)$, n is the number of iterations.

The algorithm stops when Equation (6) is satisfied, otherwise, it continues updating the values.

$${{\displaystyle \sum _k‖{\widehat{\nu }}_k^{n+1}-{\widehat{\nu }}_k^n‖}}_2^2/{‖{\widehat{\nu }}_k^n‖}_2^2<\epsilon (\epsilon >0)$$

(6)

2.2. Original Transformer’s Multi-Head Self-Attention

The Transformer self-attention equation is:

$$A(Q,K,V)=\mathrm{Softmax}({\displaystyle \frac{Q{K}^T}{\sqrt{d}}})V$$

(7)

where A (.) represents the function of attention, Q, K, V represents the query, key, and value matrix, respectively. Softmax represents the fixed normalized exponential function, and d is the dimension.

The utilization of the multi-head self-attention mechanism enhances the capacity of the model to convey information effectively. Equation (8) illustrates the functional structure of the d-th self-attention in the multi-head self-attention mechanism.

$$M(Q,K,V)=\mathrm{Concat}(H_1,H_2,\cdots ,H_d)W^o$$

(8)

$$H_g=\mathrm{A}(Q{W}_g^Q,K{W}_g^K,V{W}_g^V)$$

(9)

where M (.) represents multi-head self-attention function, Concat(.) represents the concatenation function, $H_g$ represents the g-th self-attention function, $W^o$ represents linear mapping matrix of the mechanism, $Q{W}_g^Q,K{W}_g^K$, and $V{W}_g^V$ represent the linear mapping matrix of Q, K, and V, W represents the weight matrix.

2.3. Original Transformer’s Positional Encoding

Transformer adopts a parallel structural framework that is unable to capture temporal and positional features. To compensate for this shortcoming, Transformer neural networks usually use absolute position encoding to obtain positional information from the data, as seen in Equations (10) and (11).

$$P(l,2k)=\sin ({\displaystyle \frac{l}{{1000}^{\frac{2k}{d_{\mathrm{model}}}}}})$$

(10)

$$P(l,2k+1)=\cos ({\displaystyle \frac{l}{{1000}^{\frac{2k}{d_{\mathrm{model}}}}}})$$

(11)

where P shows the bit encoding, l is the sequential position corresponding to the encoded data, $d_{\mathrm{model}}$ is the dimension, and k is an integer value between 0~0.5 $d_{\mathrm{model}}$ − 1.

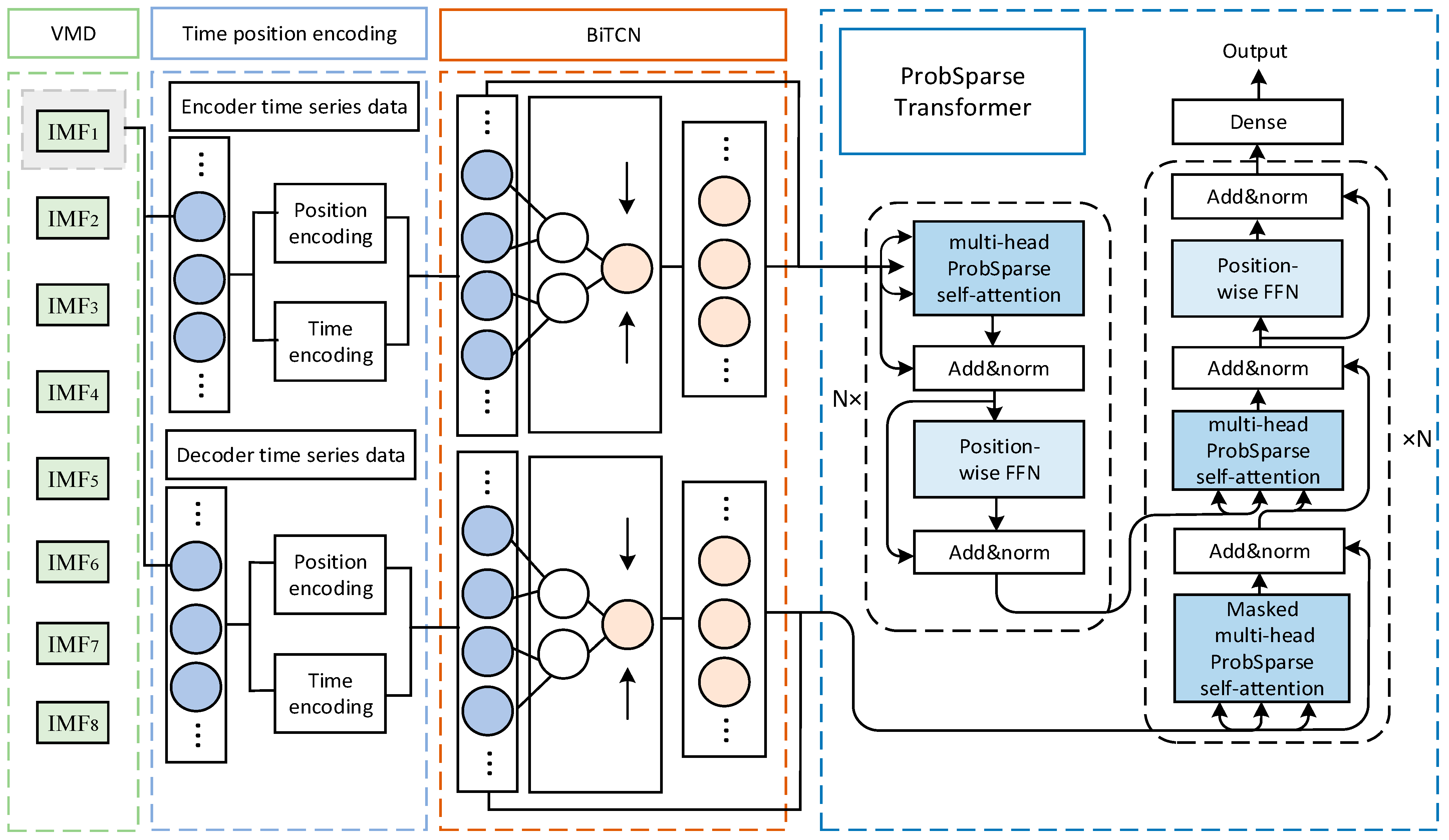
3. Model of VMD-BiTCN-Psformer

3.1. Improvement of Transformer’s Positional Encoding

For time-series data, time-hidden features are essential in addition to location information. Therefore, we improved the original location coding of Transformer by incorporating temporal and seasonal information encoding. Based on the concept of positional encoding, time features are processed to extract global time features from different timestamps. The dimensions of time encoding, hourly encoding, daily encoding, and monthly encoding are normalized and then merged.

In Figure 1, u_n is the projection of wind farm data series, p_n is absolute positional encoding, t_n, h_r, d_e, and m_w represents temporal and seasonal information encoding data in different time dimensions.

After splicing the three parts, c_n is obtained, and the equation for this is:

$$c_i^t=\alpha {\mu }_i^t+P_i^t+{\displaystyle \sum _z{E}_{i,z}^t}$$

(12)

where $c_i^t$ represents the i-th column data for the t-th sequence input, $u_i^t$ is the normalized vector of the i-th column data for the t-th sequence input, $P_i^t$ is the absolute positional encoding of the i-th column data for the t-th sequence input vector quantity, $E_{i,z}^t$ is the encoding vector for the i-th column data input for the t-th sequence normalized according to the z time dimension, ${\displaystyle \sum _z{E}_{i,z}^t}$ represents the data after normalization processing of time, hour, day and month encoding, and z is the number of time dimensions.

3.2. BiTCN

TCN is a model that combines the benefits of causal convolution and expansive convolution, building upon the CNN paradigm. Figure 2 shows the structural diagram of TCN.

Prioritizing the prevention of information leakage is crucial for long-term data prediction challenges. In contrast to convolution in a CNN, causal convolution is a unidirectional structure in which the features extracted at time t are solely influenced by the values of the current and previous moments, and the original data after time t cannot be used. By utilizing dilated convolution in TCN, the model can attain a larger receptive field with a reduced number of layers. This is possible because the input can be sampled at intervals during convolution, leading to an exponential increase in the size of the receptive field as more layers are added. Thus, TCN can effectively capture long-range dependencies and temporal patterns in the input data while reducing computational complexity. The equation for TCN causal unfolding convolution is:

$$H(t)={\displaystyle \sum _{i=0}^{k-1}h(s)}{x}_{t-d_{m}s}$$

(13)

where $H(t)$ represents the t-th output of TCN, k is the kernel size, $h(s)$ is the s element in the convolution kernel, $x_{t-d_{m}s}$ is the input, dm is the expansion factor.

TCN exclusively focuses on the forward convolutional computation of the input sequence and ignores the backward information of the prediction results. BiTCN can capture the hidden features of the wind power sequences by considering both forward and backward information to better capture the long-term dependencies. BiTCN processes the input data through multiple convolutional layers, each of which extracts the features through different filters and activation functions. Meanwhile, dilated convolution is used to increase the receptive field, i.e., to expand the coverage of the model on the input data without increasing the parameters. The structure of BiTCN is shown in Figure 3.

Wind power time series models will change over time due to the occurrence of extreme weather, day and night, and seasonal changes. Therefore, whether the current wind power is an anomaly, a change point, or part of a state pattern, it is highly dependent on the surrounding environment. BiTCN can extend the receptive field of the model by increasing the number of layers and then extracting the features of the time segments.

BiTCN is also introduced to improve the inherent defects of the Transformer model. Q, K, and V in Transformer are different vectors obtained by multiplying the encoded and spliced initial vector with three weight matrices: W_Q, W_K, and W_V. In this case, the dot product of the query and value is computed as the correlation of time point data, without considering the time segment features near the observation point. As shown in Figure 4, the introduction of BiTCN will change the connection structure of the self-attention mechanism, taking the time series data containing the feature information of different time segments as the input of the query vector and the key vector, while still using the original time series data as the input of the value vector. The correlation calculation with the query vector and key vector generated by BiTCN can effectively establish the relationship between time segments of time series data and highlight the feature information of key historical time segments.

3.3. Improvement of Multi-Head Self-Attention Mechanism

The wind power sequences undergo processing by BiTCN and are input into the Psformer model. When handling long-time sequences, the multi-head attention mechanism of the Transformer model often suffers from a high computational complexity and slow computation speed. Therefore, this paper proposes a multi-head ProbSparse self-attention mechanism. The structure is shown in Figure 5.

During the calculation of self-attention, there is not a strong connection between all the data at every time point. Only a small number of dot products significantly contribute to the main attention, while the impact of other dot products is weak and can be ignored. Therefore, the ProbSparse self-attention mechanism model prioritizes the query vectors based on their relevance and then performs dot product computation on the selected vectors. The ProbSparse self-attention matrix is obtained by restricting each key vector to attend to only primary query vectors. The query vectors that have a relatively high relevance are kept as the primary elements of the ProbSparse matrix, while the query vectors with a relatively low importance are discarded. This process results in the formation of the ProbSparse self-attention matrix.

In ProbSparse self-attention, each key can focus on only u major queries. The ProbSparse self-attention calculation process is shown in Algorithm 1. The improved mechanism function is:

$$A(Q,K,V)=\mathrm{Softmax}({\displaystyle \frac{\overline{Q}{K}^T}{\sqrt{d}}})V$$

(14)

$$\overline{M}(q_i,K)=\max ({\displaystyle \frac{q_i{k}_j^T}{\sqrt{d}}})-{\displaystyle \frac{1}{L_K}}{\displaystyle \sum _{j=1}^{L_K}\frac{q_i{k}_j^T}{\sqrt{d}}}$$

(15)

where $\overline{Q}$ represents the part of the ProbSparse self-attention matrix, $q_i$, $k_i$ represent the i-th row of Q, and K respectively, $L_K$ represents the length of the key. The time and space complexity of attention calculated by ProbSparse method are $O(L\ln L)$.

Algorithm 1. ProbSparse Self-Attention Calculation Process

$\mathrm{Input}: Q\in R^{m\ast d}$$, K\in R^{n\ast d}$$, V\in R^{n\ast d}$

Initialize: hyperparameter c, u = clnm, U = mlnn

1. Choose $U$ dot product pairs randomly from $K$ to $\overline{K}$

2. $\mathrm{Set} \mathrm{sample} \mathrm{score} \overline{S}=Q{\overline{K}}^T$

3. $\mathrm{Calculate} M=\max (\overline{S})-\mathrm{mean}(\overline{S})$

4. Choose the first u-th $M$ as $\overline{Q}$

5. $\mathrm{Calculate} S_1=\mathrm{softmax}(\overline{Q}{K}^T/\sqrt{d})V$

6. $\mathrm{Calculate} S_0=\mathrm{mean}(V)$

7. $\mathrm{Calculated} \mathrm{from} \mathrm{raw} \mathrm{row} \mathrm{data} S=\left\{S_1,S_0\right\}$

Output: feature $S$

3.4. VMD-BiTCN-Psformer Wind Power Prediction Model

The short-term wind power prediction based on the VMD-BiTCN-Psformer is shown in Figure 6.

Step 1: The VMD technique is employed to decompose the wind power data into several sub-series that exhibit generally stable behavior at different frequencies. This process effectively decreases the complexity and nonlinearity of the sequence.

Step 2: Each sub-mode of the decomposed wind farm original data is mapped to form a time series matrix, and the time features are transformed into dimensions through a one-dimensional convolution layer and then spliced with the improved positional encoding matrix and time series matrix.

Step 3: BiTCN is employed to extract the characteristics of the spliced matrices and capture the enduring connections between them.

Step 4: The output matrix of BiTCN is transformed into query vector and key vector by weight matrix W_Q and W_K, respectively. The concatenation matrix is transformed into value vector by weight matrix W_V. Q, K, V are obtained as matrices by the attention mechanism function, and finally processed to obtain the intermediate feature matrices, which are used in the decoding layer.

Step 5: The output matrix of BiTCN, along with the mask concatenation matrix goes to the decoding layer of Psformer to obtain the query vector. The key vector, the value vector, and the query vector together go to the next sub-layer of the Psformer decoder. The wind power predictions for each sub-mode are derived through the fully connected layer, and then these predictions are aggregated to obtain the final wind power prediction.

4. Results and Discussion

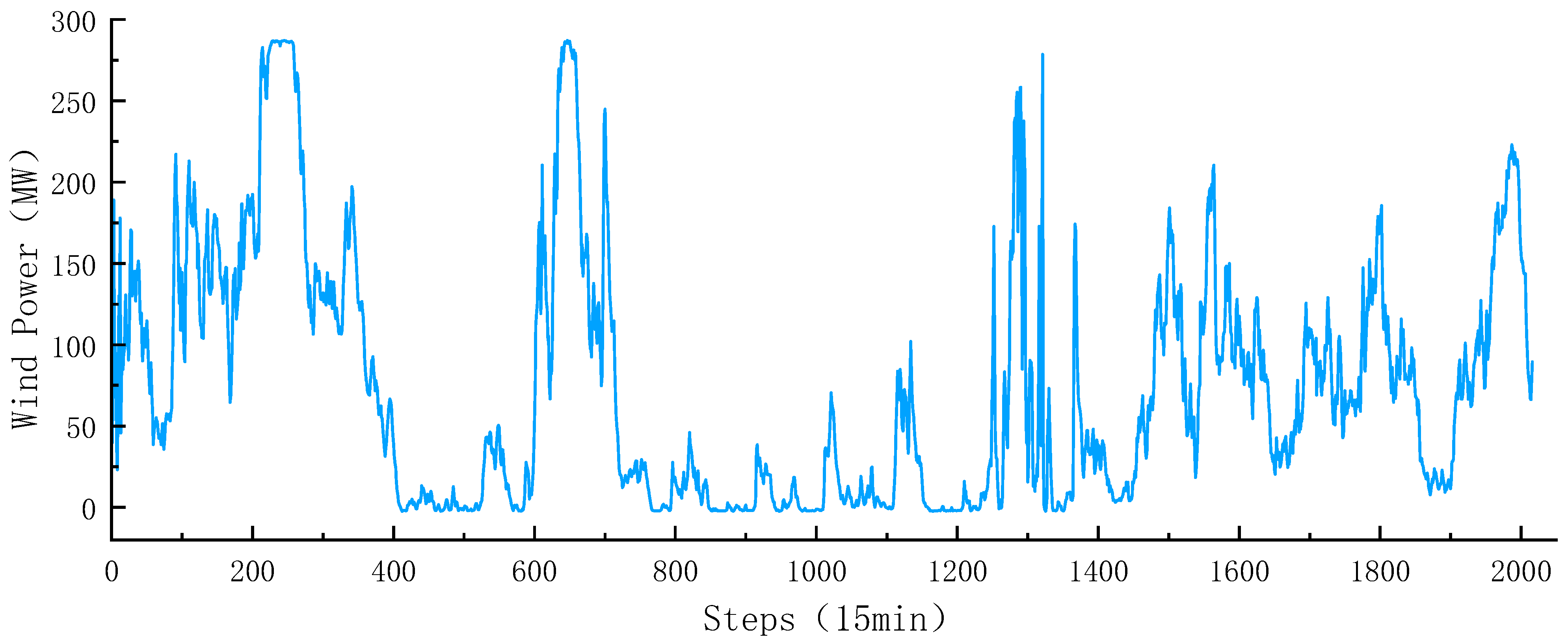
4.1. Data and Evaluation Metrics

The hardware platform used was Intel(R) Core (TM) i7-13, 620H [email protected] GHz and NVIDIA GeForce RTX 4060 Laptop GPU, and CUDA12.3 was used for acceleration. The software platform used was Python3.6 and MATLAB 2022a.

The example data are derived from historical wind power and local meteorological data collected from a wind farm located in Fujian, China. These data includes wind and meteorological data collected from the wind farm between April 6 and April 26, 2023, with measurements taken every 15 min. There are 2016 sets of data in total. The first 20 days’ data are used as the training set to forecast the data for the 21st day. The data contain rich information on variables such as barometric pressure, relative humidity, cloud cover, 10 m wind speed, 100 m wind speed, and temperature. The original wind power data is shown in Figure 7.

Due to the different units of data such as wind turbine output power and wind speed, which are not comparable in their respective dimensions. In order to improve the generalization ability of the model, we trained the hybrid network after normalizing the data sets decomposed by VMD from the original wind power series data; other meteorological data were also normalized into the hybrid model. The normalization is shown in Equation (16).

$$x^{\prime }={\displaystyle \frac{x-x_{\min }}{x_{\max }-x_{\min }}}$$

(16)

where x_min represents the minimum value, x_max represents the maximum value. The data were mapped between [0, 1].

For the normalization of the wind power of the target predicted value, the maximum, and minimum values of the data are saved in an array, which is used for the denormalization of the data after the network forecasting. Finally, the results are restored to the original power interval. The evaluation effect of the model is also based on the results after denormalization. The denormalization is shown in Equation (17).

$$x=x^{\prime }(x_{\max }-x_{\min })+x_{\min }$$

(17)

To reasonably detect the performance of the model, we compared MAE, RMSE, $R^2$, and RRMSE using the following equations:

$$MAE={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N\left|{\widehat{x}}_i-x_i\right|}$$

(18)

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{({\widehat{x}}_i-x_i)}^2}}$$

(19)

$$R^2=1-{\displaystyle \frac{{\displaystyle \sum _i{({\widehat{x}}_i-x_i)}^2}}{{\displaystyle \sum _i{({\overline{x}}_i-x_i)}^2}}}$$

(20)

$$\mathrm{RRMSE}=\sqrt{{\displaystyle \frac{1}{\mathrm{N}}}{\displaystyle \sum _{i=1}^{\mathrm{N}}{(\frac{{\widehat{x}}_i-x_i}{x_i})}^2}}$$

(21)

where $x_i$ represents the actual value, ${\widehat{x}}_i$ represents the predicted value, ${\overline{x}}_i$ represents the average value, and N represents the number.

Among them, smaller MAE, RMSE, and RRMSE indicate the better prediction effect, and the closer $R^2$ to 1, indicates a smaller error.

4.2. Model Parameter Setting

The main parameter settings of the Transformer are shown in

Table 1. Comparison of prediction models.

Parameter	Set Value	Parameter	Set Value
seq_len	192	batch_size	64
enc_in	6	train_epochs	50
dec_in	6	dropout	0.05
sampling factor u	5	learning_rate	0.001
n_head	8	activation	Gelu

.

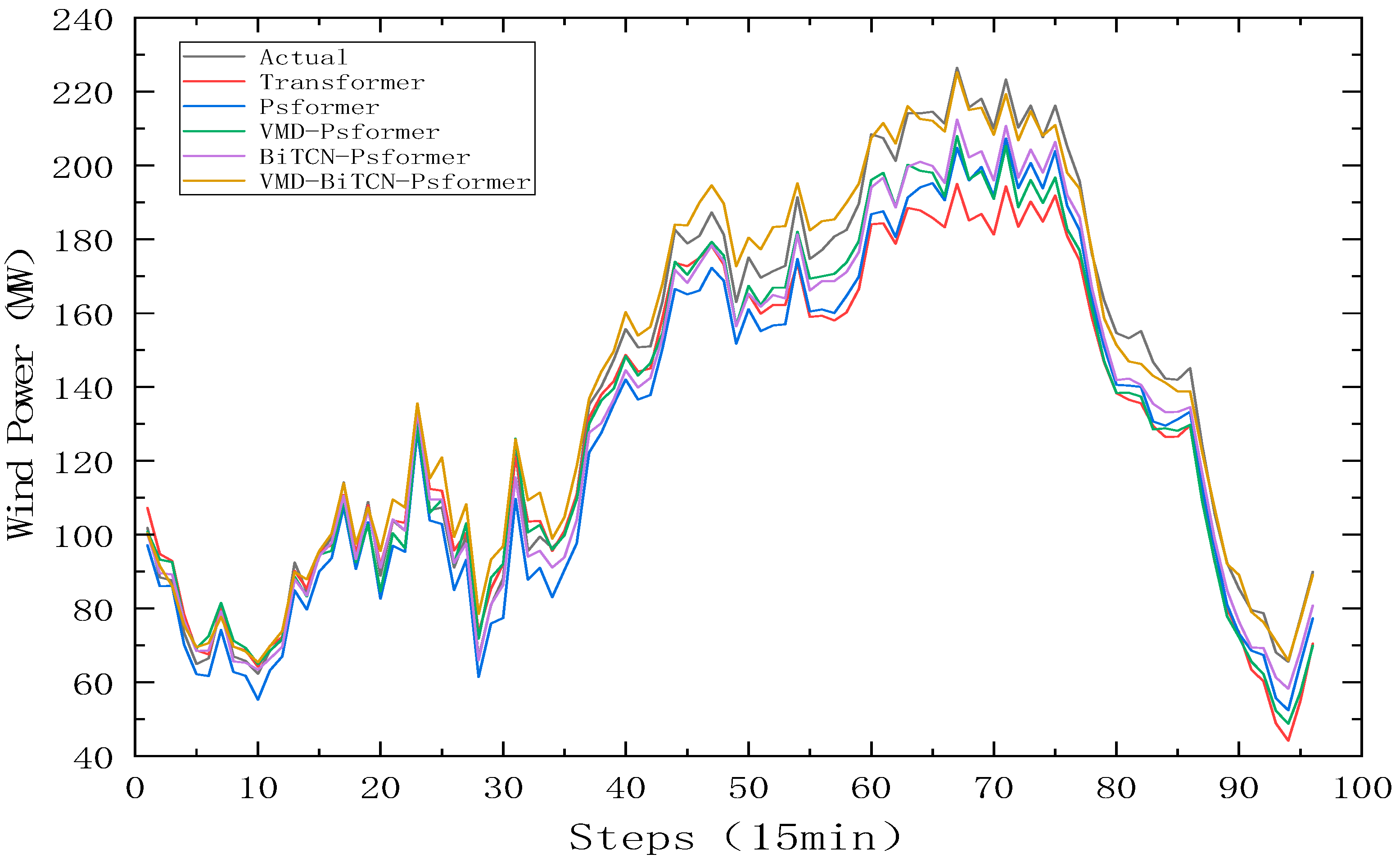
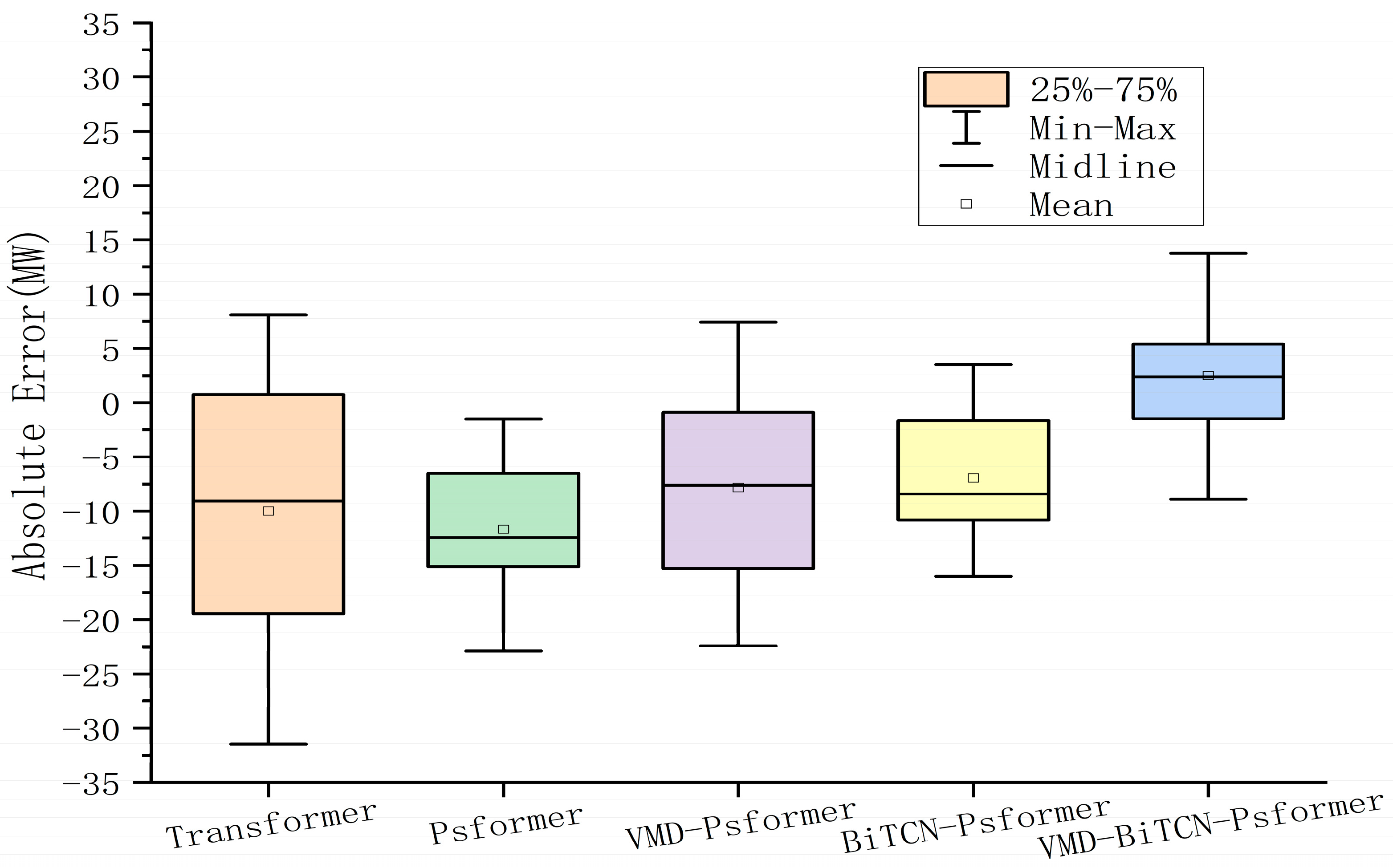
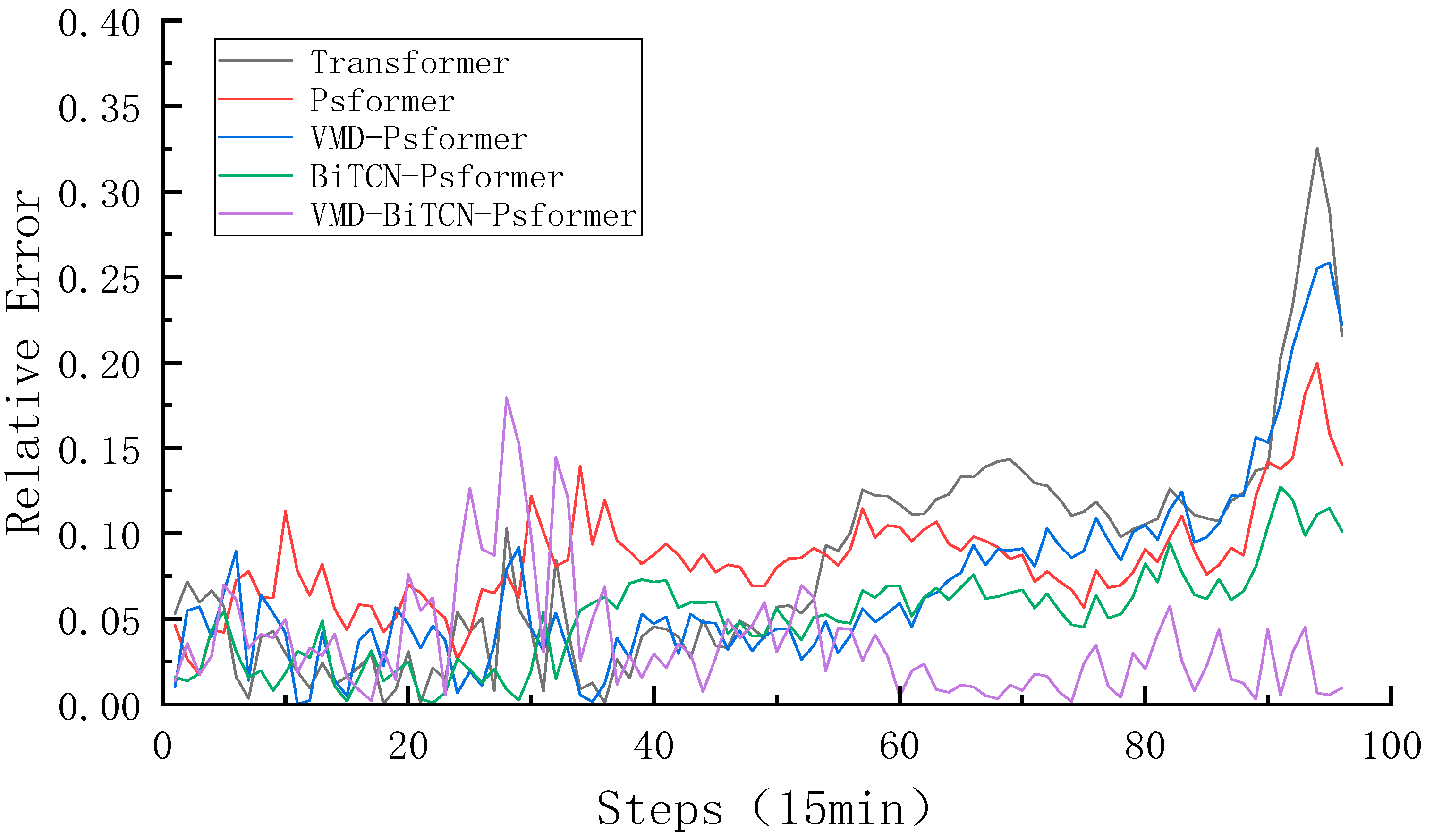
4.3. Validation of Model Effectiveness

4.3.1. Comparative Analysis of the Forecasting

To verify the performance of each module, four sets of comparison tests were constructed, as shown in

Table 2. Comparison of different modules.

Model	VMD	BiTCN	Psformer
Transformer	×	×	×
Psformer	×	×	√
VMD-Psformer	√	×	√
BiTCN-Psformer	×	√	√
VMD-BiTCN-Psformer	√	√	√

. “√” indicates that the module was included in the corresponding model. To control the variables, all models used improved positional encoding.

To verify the validity of the module combination, we designed the five models shown in Table 2. Their performance is shown in

Table 3. Comparison of module performance of Transformer, Psformer, VMD-Psformer, BiTCN-Psformer, and VMD-BiTCN-Psformer.

Model	Evaluation Metrics
	MAE	RMSE	${\mathit{R}}^2$	RRMSE
Transformer	11.8262	15.1559	0.9120	0.1030
Psformer	11.6762	12.8298	0.9369	0.0872
VMD-Psformer	9.2985	11.3005	0.9511	0.0768
BiTCN-Psformer	7.3939	8.6925	0.9710	0.0591
VMD-BiTCN-Psformer	5.5979	6.6849	0.9829	0.0454

. The wind power results are shown in Figure 8. Among all models, the VMD-BiTCN-Psformer model has the best prediction effect.

(1)

Comparing VMD-Psformer with Psformer, and VMD-BITCN-Psformer with BiTCN-Psformer, the MAE of each model decreased by 25.58% and 32.08%, respectively, and the R² of each model increased by 1.52% and 1.23%, respectively. We found that the prediction effect of the model with VMD is better than that of the model without VMD. The VMD is able to decompose the unstable and highly fluctuating wind power signal into more stable sub-sequences, which greatly improves the accuracy of the model prediction.

(2)

To verify the effectiveness of the improved ProbSparse module, the Psformer model is compared with the Transformer model. We found that Psformer, which discards key values of relatively low importance, performs better in terms of prediction accuracy. The MAE, RMSE, and RRMSE of Psformer are reduced by 1.28%, 18.13%, and 18.12%, respectively, and R² is increased by 2.73%.

(3)

Compared with Psformer and BiTCN-Psformer, the MAE, RMSE, and RRMSE decreased by 57.92%, 47.60%, and 47.55%, respectively, while R² increased by 3.64%. BiTCN-Psformer uses BiTCN to adequately capture bi-directional information in time series data, improving the model’s modeling and forecasting performance on sequence data. This means that BiTCN provides a better performance in complex time series tasks.

The box plot of the four models’ prediction errors is shown in Figure 9, where it can be seen that the error proposed in this paper is minimized. It can be clearly seen from the relative error shown in Figure 10 that the predicted result of the original transformer has a large deviation from the actual value. The purple part of the figure indicates that the relative error of the model in this paper is at the bottom, and the error is the smallest.

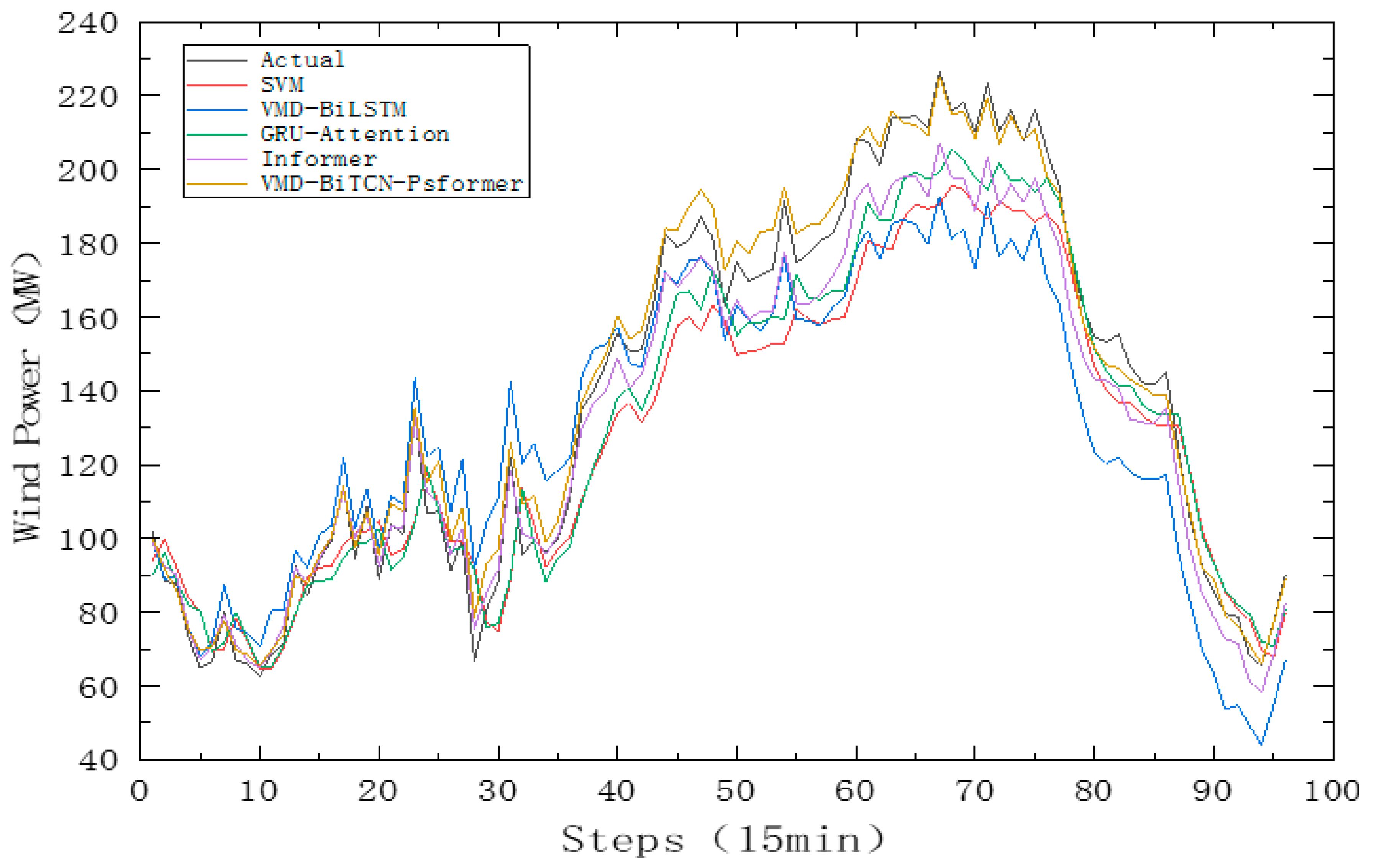
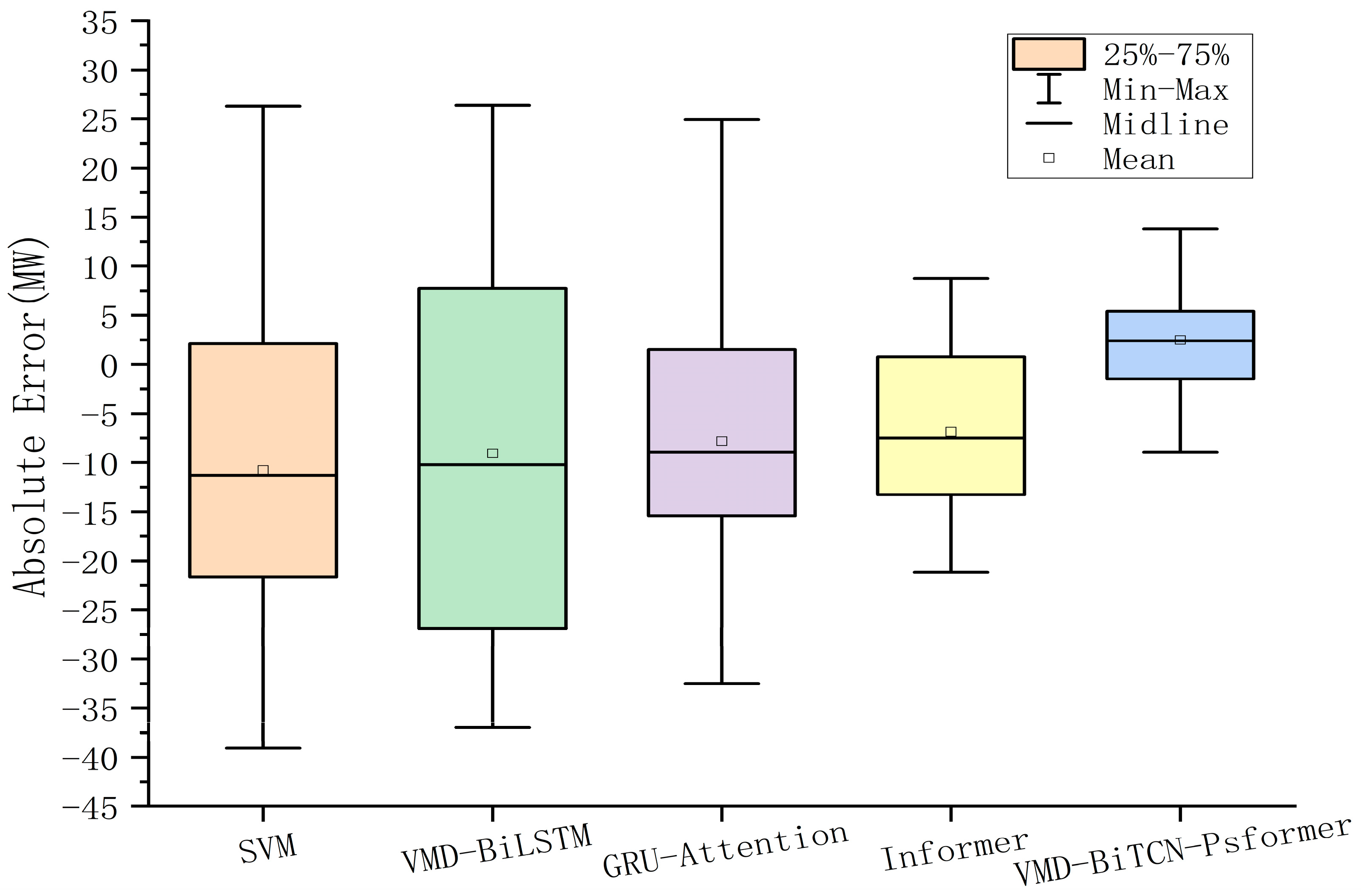
4.3.2. Comparative Analysis with Other Models

To demonstrate the superior performance of the VMD-BiTCN-Psformer model, we compared it with several other traditional models. We designed four models (SVM, VMD-BiLSTM, GRU-Attention, and Informer) to forecast wind power in a region of Fujian on 26 April 2023. As you can see from Figure 11, the proposed model is closest to the raw power data. The box plot of the different models’ prediction errors is shown in Figure 12. The error values in Figure 12 are larger than the prediction errors in Figure 9.

In

Table 4. Performance comparison of SVM, VMD-BiLSTM, GRU-Attention, Informer, and VMD-BiTCN-Psformer.

Model	Evaluation Metrics
	MAE	RMSE	${\mathit{R}}^2$	RRMSE
SVM	15.0076	17.7801	0.8039	0.1333
VMD-BiLSTM	15.6544	18.0880	0.8746	0.1230
GRU-Attention	11.7395	13.7568	0.9023	0.1001
Informer	8.6425	10.4532	0.9581	0.0711
VMD-BiTCN-Psformer	5.5979	6.6849	0.9829	0.0454

, we compared SVM, VMD-BiLSTM, GRU-Attention, Informer, and VMD-BiTCN-Psformer, in which the error of the VMD-BiTCN-Psformer model is the smallest among all traditional models. Compared with SVM, VMD-BiLSTM, GRU-Attention, and Informer models, the R² of VMD-BiTCN-Psformer has increased by 22.27%, 12.38%, 8.93%, and 2.59%, respectively. It has been observed that the VMD-BiTCN-Psformer model proposed in this paper possesses the highest accuracy and a better prediction effect.

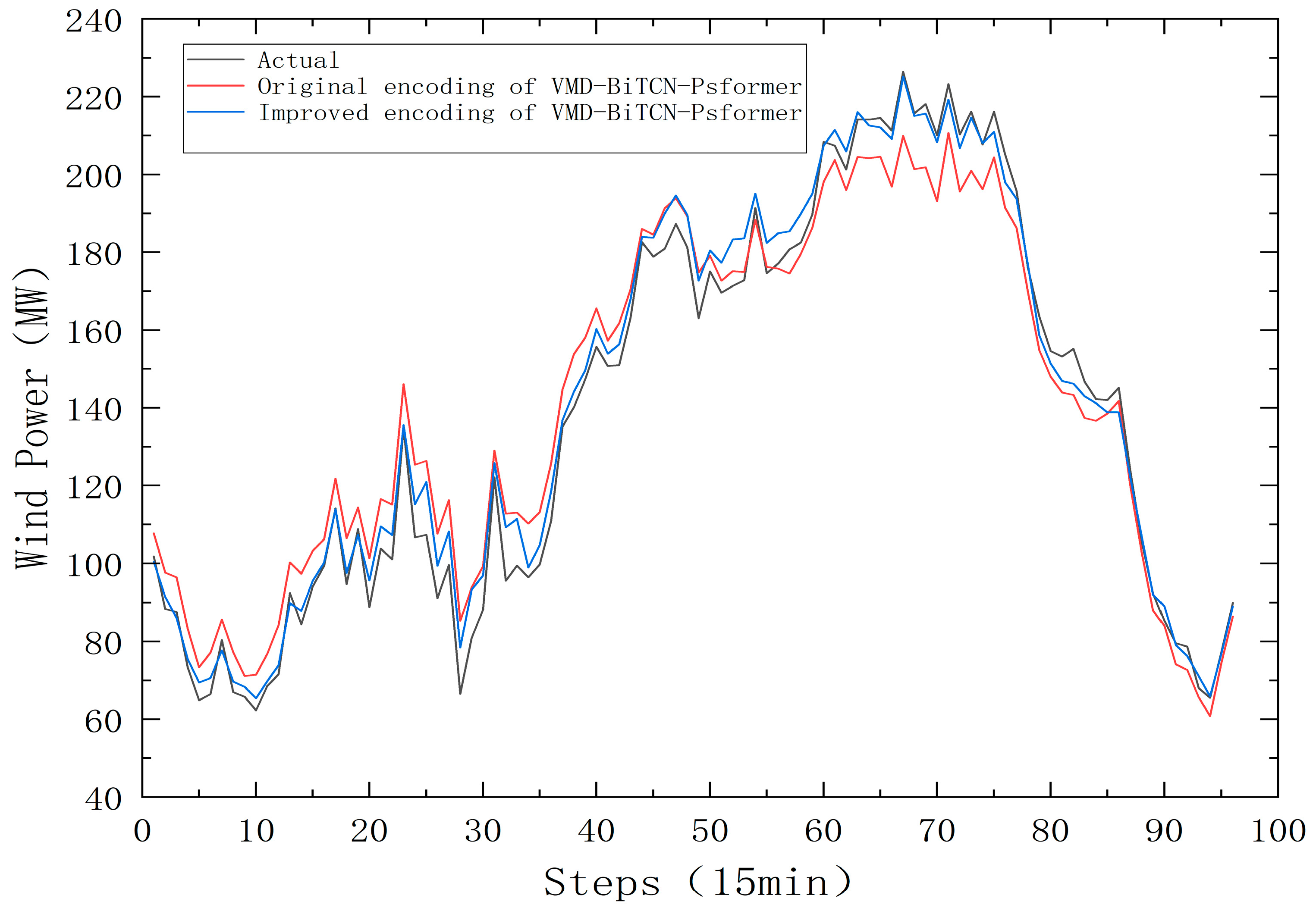
4.3.3. Forecasting Performance of Improved Positional Encoding

As shown in Figure 13, we also compared the effects before and after the improved position encoding. The data in

Table 5. Performance of improved positional encoding.

Model	Evaluation Metrics
	MAE	RMSE	R2	RRMSE
Original encoding of VMD-BiTCN-Psformer	9.0976	10.1782	0.9603	0.0692
Improved encoding of VMD-BiTCN-Psformer	5.5979	6.6849	0.9829	0.0454

show that the improved positional encoding improves the accuracy of wind power to some extent, and the R² of the improved position encoding model is higher than that of the original model. The experiments proved that after adding more detailed encoding information, the model was more applicable and the prediction was more accurate.

5. Conclusions

We propose a VMD-BiTCN-Psformer model based on temporal and positional encoding, which aims to improve the accuracy of forecasting wind power.

Combined with the measured wind power data and the meteorological data from a wind farm in Fujian, the proposed VMD-BiTCN-Psformer prediction model was studied:

(1)

The combination model of VMD-BiTCN-Psformer is superior to relatively single combination models, and the application of VMD, BiTCN, and Transformer all contributes to improving the accuracy of predictions.

(2)

Table 4 shows that the MAE, RMSE, RRMSE, and R² of the wind power prediction results of the proposed model are better than those of other models. The prediction of the designed model is closest to the actual values, so it has a more accurate prediction effect.

(3)

We compared the models before and after improving the positional encoding and found that the prediction accuracy improved after the improvement, demonstrating the effectiveness of the improved encoding.

Our proposed model still has some limitations, which we will continue to study in future work. In the process of VMD, we determined the number of decomposed modes as a fixed value, and it is more effective to optimize VMD parameters by using swarm intelligence algorithm or determine the number of sub-modes according to entropy. At the same time, for power data close to 0, the predicted values of the network model tend to be much higher than the true values, which is an issue that we need to address in our next study.