Effects and Mechanisms of Dilute-Foam Dispersion System on Enhanced Oil Recovery from Pore-Scale to Core-Scale
Abstract
1. Introduction
2. Simulation of Jamin Effect in Water–Gas Dispersion System
2.1. Simulation of Jamin Effect in Simplified Channels
2.1.1. Level-Set Function and Fluid Control Equation
- (1)
- Level-Set Function
- (2)
- Fluid Control Equation
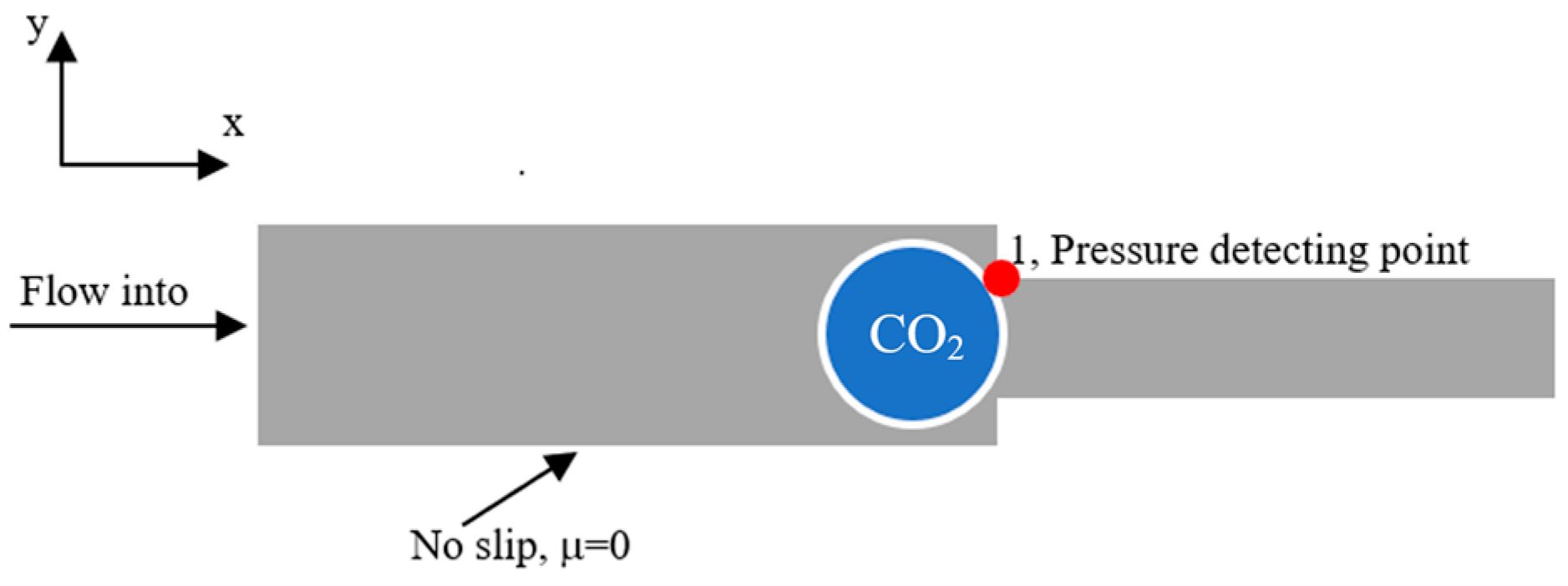
2.1.2. Establishment of Geometric Model
2.1.3. Setting Initial Values and Boundary Conditions
- (1)
- Initial value
- (2)
- Setting of boundary conditions
- ①
- Inlet boundary conditions: The water–vapor dispersion system flows into the left inlet at a certain flow rate through the narrow throat, using the inlet boundary condition with a level-set function of 1.
- ②
- Outlet boundary condition: The pressure of the water–gas dispersion system fluid flowing out of the fixed outlet is constant, and the outlet pressure is 0.
- ③
- Wetting wall boundary conditions: the contact angle of the wetting degree of the wall is expressed as θ, and the slip length of the wetting wall is certain. The model and boundary conditions of the Jamin effect in the water–gas dispersion system are shown in Figure 1.
2.1.4. Mesh Division and Model Solving
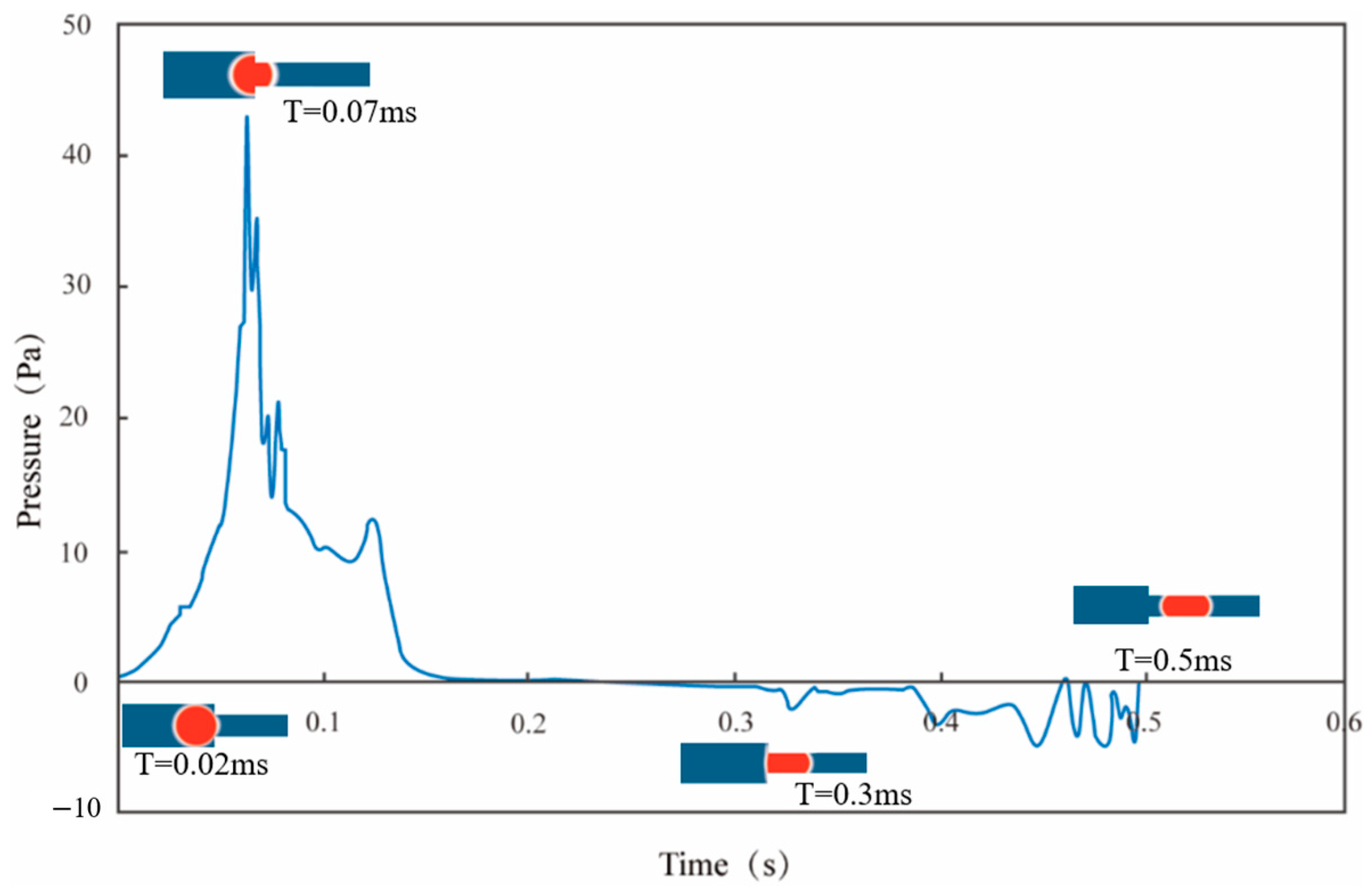
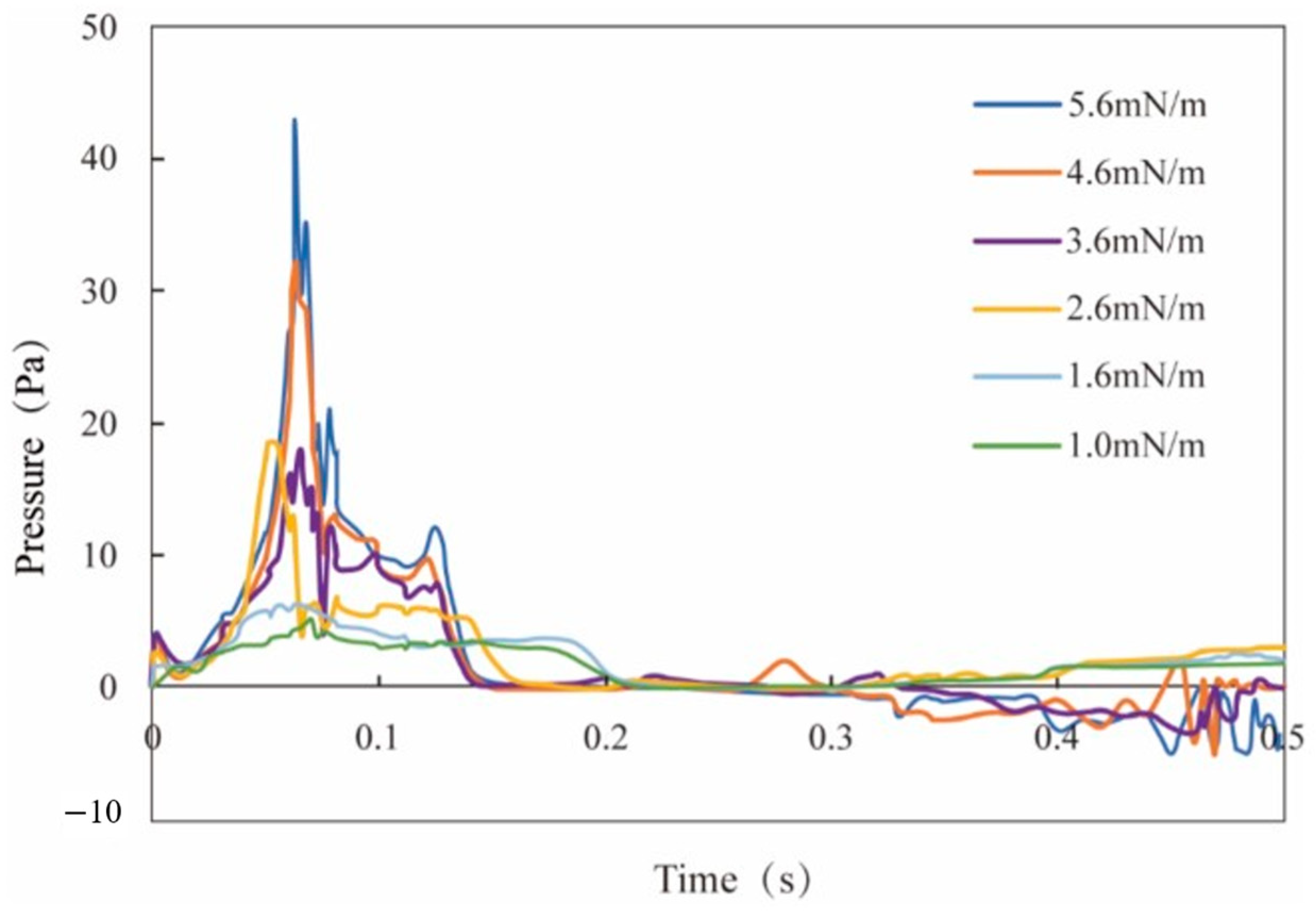
2.2. Simulation Results
3. Experimental Description
3.1. Experimental Materials and Instruments
3.2. Foamability and Foam Stability Experimental Methods
- (1)
- Weigh a certain amount of surfactant and dissolve it in 100 mL of distilled water in a beaker. Pour the solution into a high-speed mixer and stir at 10,000 rpm for 1 min.
- (2)
- Quickly pour the generated foam into a 1000 mL graduated cylinder and start timing. The initial foam volume V (mL), measured at 0 s, indicates the foaming volume.
- (3)
- Record the time t (s) to drain 50 mL of liquid from the foam, representing the foam’s half-life for drainage and indicating foam stability.
3.3. Pore-Scale Investigation with Online NMR CO2 Huff-n-Puff Experiments
- (1)
- Put the core in a 50 °C high-temperature and high-pressure gripper and vacuum for 48 h. Close the back pressure valve, and then inject the prepared simulated oil. When the system pressure reaches 20 MPa, stop the pump and stabilize it for a long enough time.
- (2)
- Close the inlet end and outlet end of the core holder and connect the return pressure valve to the inlet end.
- (3)
- Dilute-foam dispersive system (DFDS for short)-assisted CO2 huff-n-puff: inject 0.05 PV dilute foam alternately at a pressure of 25 MPa to strengthen the dispersion system and 0.05 PV CO2. When the system pressure reaches 25 MPa, stop the pump and wait for 5 h.
- (4)
- Then, carry out throughput until the pressure at the gas injection end drops to 15 MPa, and measure and record the oil production; proceed to the next injection huff. Repeat steps (2)–(3) three or more times until no oil is produced and the final huff pressure is reduced to atmospheric pressure. Test the NMR T2 spectra after each round of huff-n-puff and perform NMR imaging analysis after huff-n-puff. The experimental parameters are shown in Table 3.
3.4. Core-Scale Investigation with Core-Flooding Experimental Methods
- (1)
- After the core is vacuumed, saturate it with formation water, measure its wet weight, and calculate the effective pore volume. Measure the gas permeability and use crude oil to displace the water until no water is produced, calculating the oil saturation.
- (2)
- Age the core in a 50 °C electric thermostat for 12 h.
- (3)
- Water flooding: maintain the thermo-tank at 50 °C, set the back pressure to 10 MPa, and displace the core at a constant flow rate.
- (4)
- Parallel double-pipe core displacement: after water flooding, inject the DFDS (0.1 PV CO2 + 0.1 PV foaming solution + 0.1 PV CO2) into cores 3# and 4#, and then inject water again until the combined water cut at the outlet is 98%.
4. Experimental Results and Analysis
4.1. Selection of Foaming Agent and Stabilizer
4.1.1. Selection of Type and Concentration of Foaming Agent
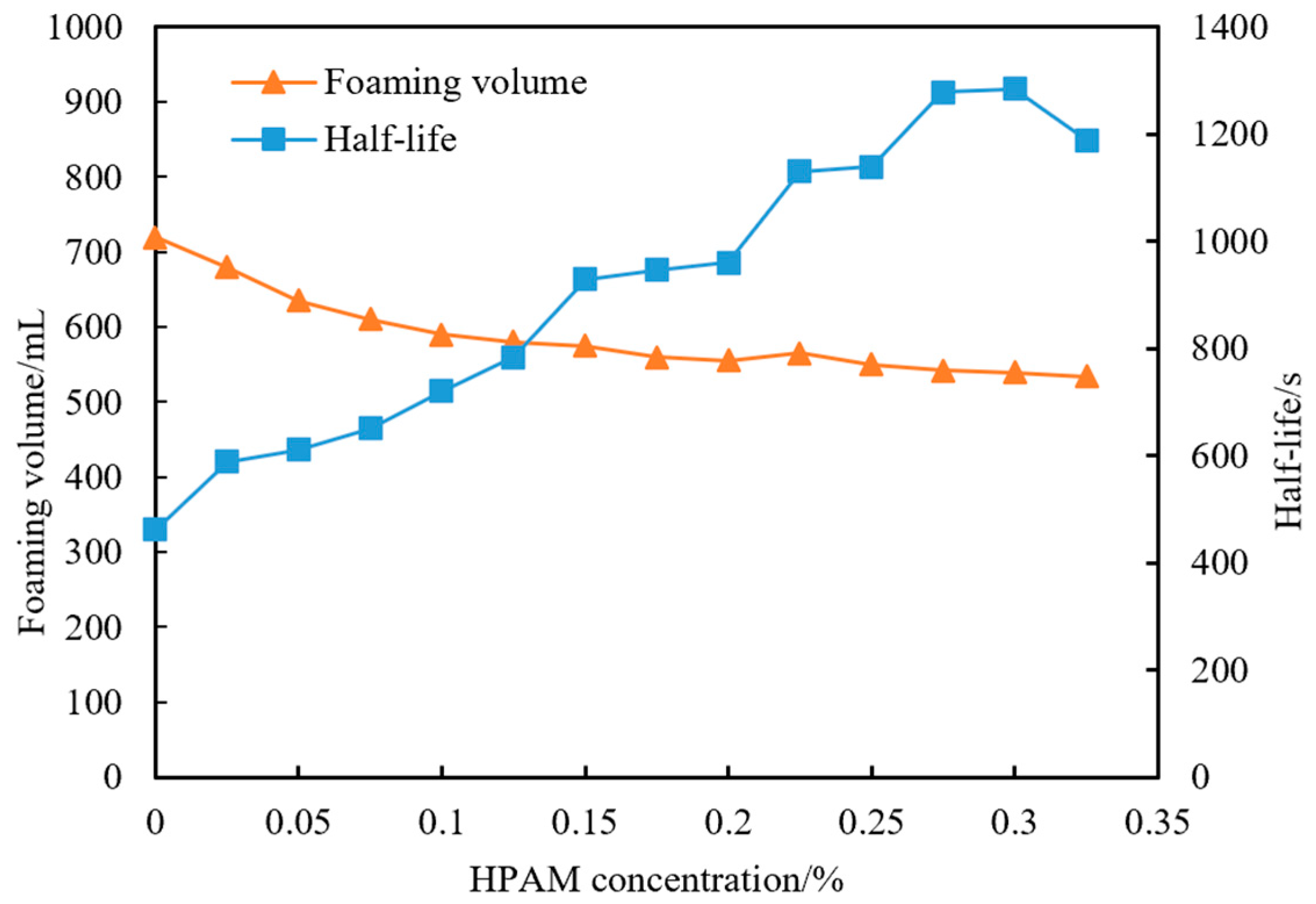
4.1.2. Selection of Foam Stabilizer Concentration
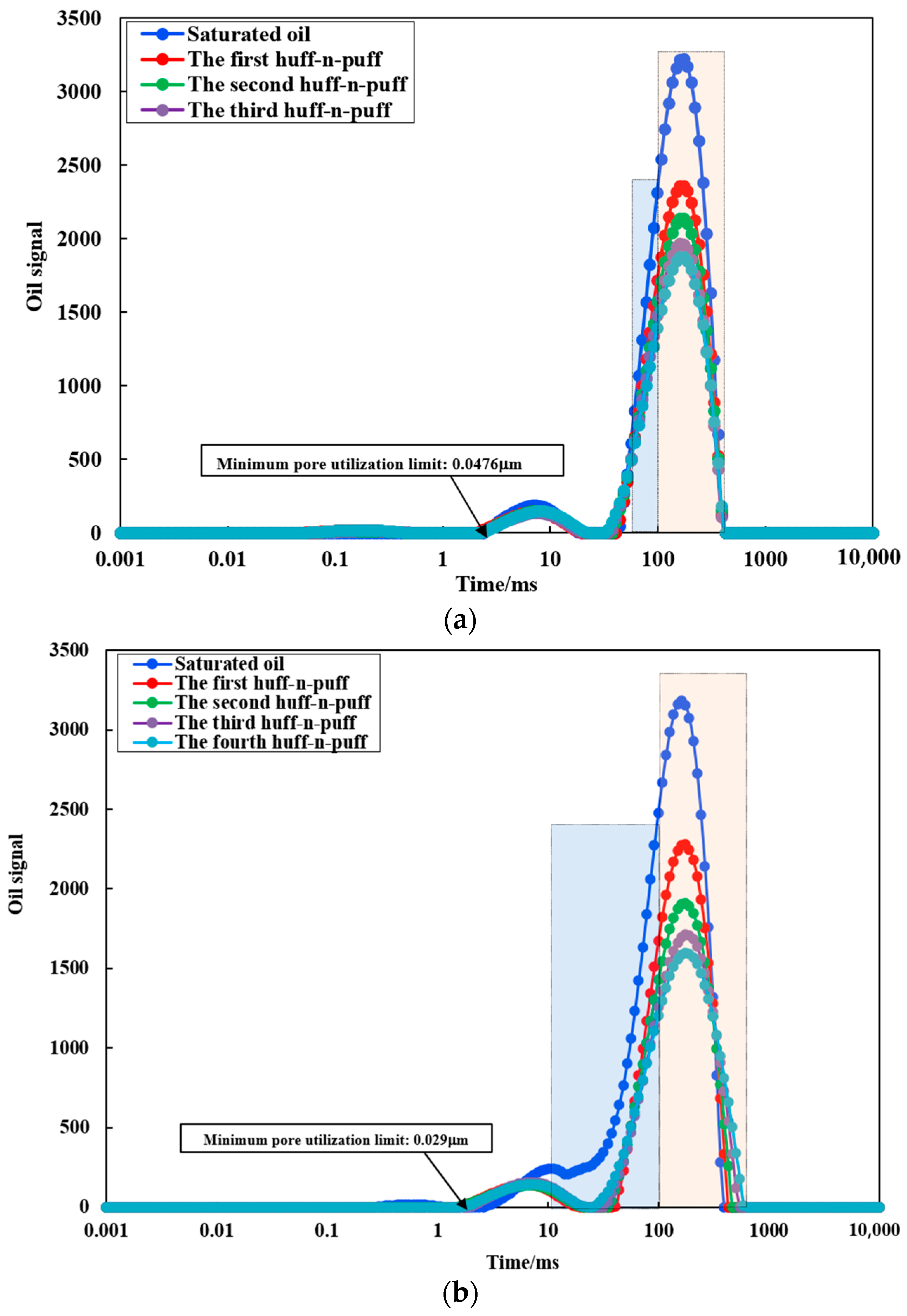
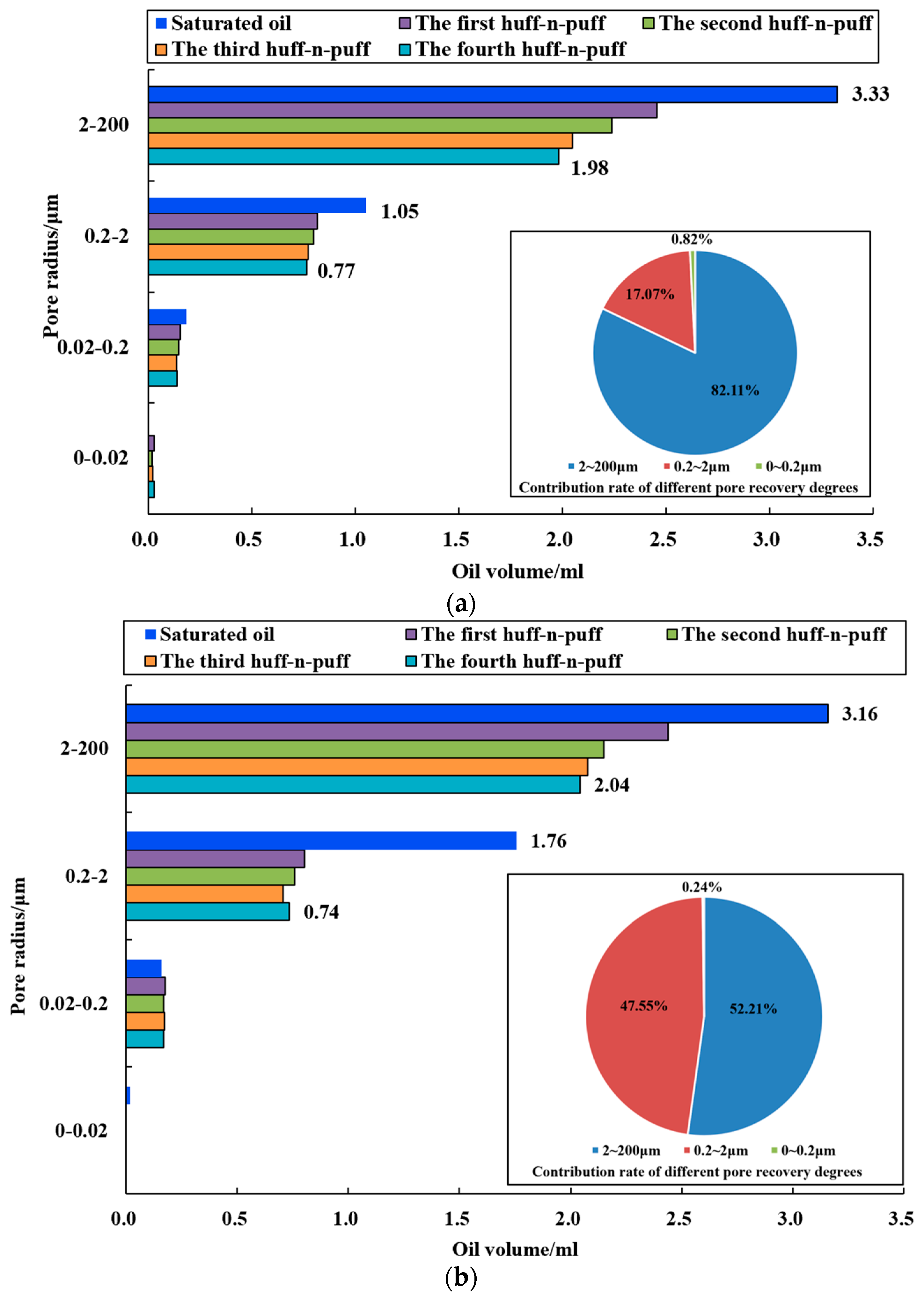
4.2. Mechanisms of Enhanced Oil Recovery by DFDS from Pore-Scale
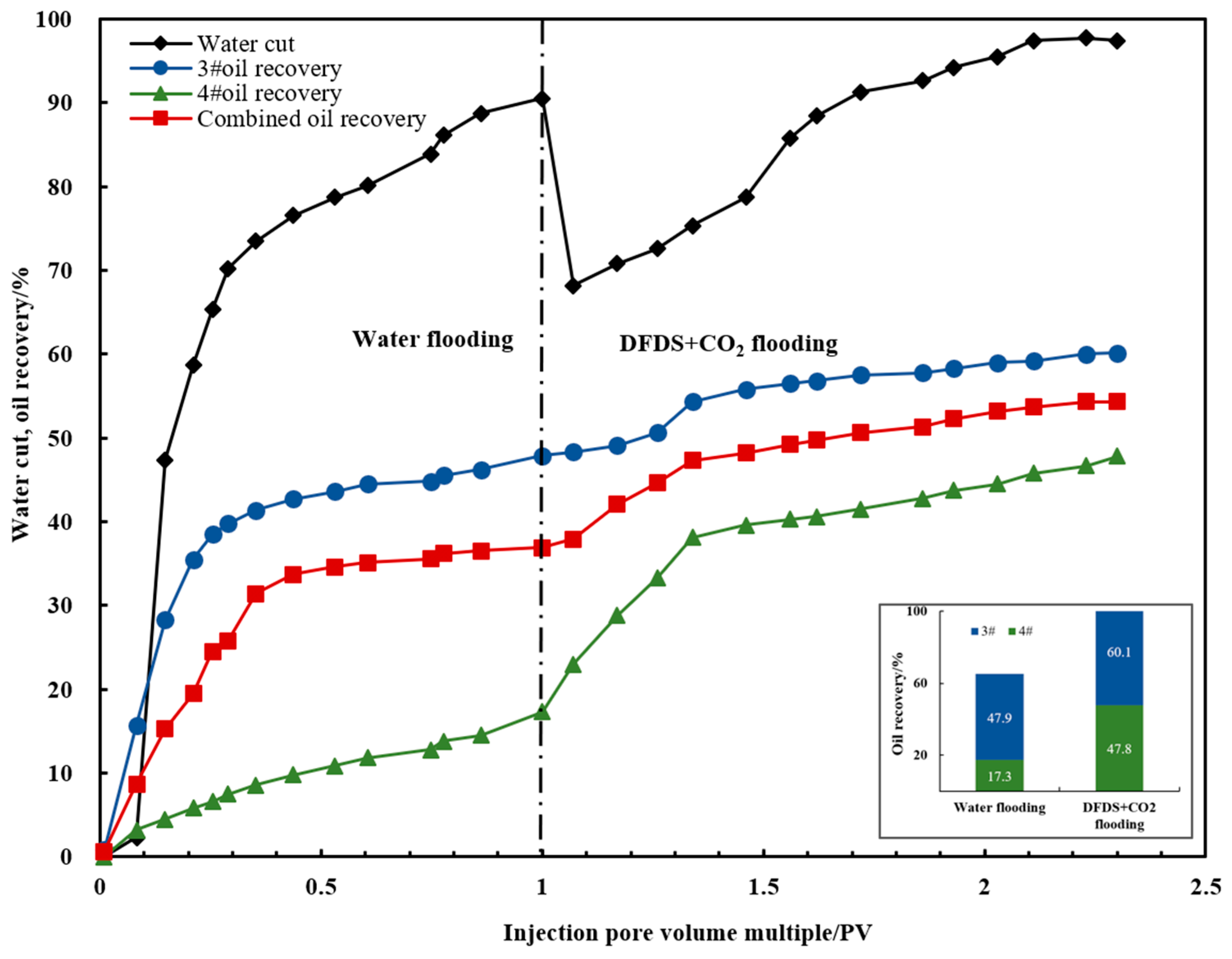
4.3. Mechanisms of Enhanced Oil Recovery by DFDS from Core-Scale
5. Conclusions
- (1)
- Foam stability evaluation: The static stability of the foam was evaluated using the high-speed stirring method, comparing three typical surfactants: sodium dodecyl sulfate (SDS), betaine surfactant (BS-12), and alpha-olefin sulfonate (AOS). The concentrations of foam stabilizers were also screened, with the optimal system being 0.6% AOS foaming agent + 0.3% HPAM.
- (2)
- DFDS-assisted CO2 huff-n-puff can improve the degree of recovery in 0.2~2 µm pores. Compared with CO2 huff-n-puff, DFDS-assisted CO2 huff-n-puff reduced the lower limit of available pores from 0.0476 µm to 0.029 µm and increased the effective working distance from 1.7 cm to 2.05 cm on a 5 cm long core scale, increasing the contribution rate of 0.2–2 µm pores to the total recovery degree by 30.48%. This shows that DFDS can increase the swept volume and, thus, improve the recovery factor of CO2 huff-n-puff.
- (3)
- The DFDS showed good oil recovery enhancement capability in the parallel double-pipe core-flooding experiment. The dispersion system can block dominant channels and increase the swept volume of low-permeability cores, acting as a temporary plug and diversion agent. The results showed that the subsequent injection of the system after water flooding increased the low-permeability core’s oil recovery factor by 30.5% and ultimately increased the combined oil recovery factor by 17.4%, indicating a significant enhancement in oil recovery.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, N. Research on Dynamic Mechanism and Application of Gas Displacement in Porous Media. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2020. [Google Scholar]
- Chen, X.; Wu, J.; Han, H.; Liu, L. Formation of gas bubble-water dispersion system using ultrasonic vibration method and research on its impact on ultimate oil recovery. Nat. Gas Oil 2021, 39, 48–52. [Google Scholar]
- Xing, X. Microscopic oil displacement mechanism and oil displacement effect of foam flooding. Pet. Geol. Recovery Effic. 2020, 27, 7. [Google Scholar]
- Sun, Z.; Wu, X.; Kang, X.; Lu, X.; Li, Q.; Jiang, W.; Zhang, J. Comparison of oil displacement mechanisms and performances between continuous and dispersed phase flooding agents. Pet. Explor. Dev. 2019, 46, 9. [Google Scholar] [CrossRef]
- Li, Z. Application of Foam Fluid in Oil and Gas Exploitation; Petroleum Industry Press: Beijing, China, 2010; pp. 5–15. [Google Scholar]
- Duan, X. The Method and Theoretical Research on EOR of Water-Gas Dispersion System with Adjustable Resistance. Ph.D. Thesis, China University of Petroleum, Beijing, China, 2015. [Google Scholar]
- Yu, H.; Ma, D.; Li, S.; Ji, Z.; Chen, X.; Zhang, K. Experimental study on enhanced oil recovery by water-gas dispersion flooding system. Sci. Technol. Eng. 2013, 13, 9946–9949. [Google Scholar]
- Frled, A.N. The Foam-Drive Process for Increasing the Recovery of Oil; Department of the Interior, Bureau of Mines: Washington, DC, USA, 1961; pp. 1–63.
- Romero Zern, L.; Kantzans, A. Pore Level Displacement Mechanisms during Foam Flooding. In Proceedings of the Canadian International Petroleum Conference, Calgary, AB, Canada, 10–12 June 2003. [Google Scholar]
- He, G.; Li, H.; Guo, C.; Liao, J.; Deng, J.; Liu, S.; Dong, H. Stable foam systems for improving oil recovery under high-temperature and high-salt reservoir conditions. J. Pet. Sci. Eng. 2022, 211, 110145. [Google Scholar] [CrossRef]
- Hanssen, J.E. Foam as a gas-blocking agent in petroleum reservoirs I: Empirical observations and parametric study. J. Pet. Sci. Eng. 1993, 10, 117–133. [Google Scholar] [CrossRef]
- Kong, D.; Li, Y.; Yuan, H.; Asimu, A.; Sun, L.; Xu, S.; Chen, J. Study on migration characteristics and displacement effect of polymer reinforced foam in porous media. Chin. J. Chem. Eng. 2018, 32, 1027–1033. [Google Scholar]
- Norouzi, H.; Madhi, M.; Seyyedi, M.; Rezaee, M. Foam propagation and oil recovery potential at large distances from an injection well. Chem. Eng. Res. Des. 2018, 135, 67–77. [Google Scholar] [CrossRef]
- Wu, F.; Cao, H.; Cai, W.; Zhu, M. Review of petroleum additives and their applications. Energy Conserv. Technol. 2010, 28, 6. [Google Scholar]
- Wang, F. Study on Micro-Migration Mechanism and Oil Displacement Effect of Water-Gas Dispersion System in Porous Media. Master’s Thesis, China University of Petroleum, Beijing, China, 2023. [Google Scholar]
- Hu, G.; Dong, X.; Qiu, J.; Zhang, S.; Ren, T. Study on foam properties of sulfonates with different structure in pesticide saturated solution. Shanghai Chem. Ind. 2019, 45, 12–15. [Google Scholar]
- Lu, C.; Zhang, B.; Li, B.; Zheng, Z.; Wang, H.; Fan, H.; Kang, W. Study on Synergistic enhancement of foaming performance by amphoteric/anionic surfactants. J. Petrochem. Univ. 2015, 28, 55–59. [Google Scholar]



| Item | Continuous Phase (Water) | Dispersed Phase (CO2) |
|---|---|---|
| Density/kg·m−3 | 1000 | 1.225 |
| Viscosity/Pa·s | 0.00298 | 1.789 × 10−3 |
| Surface tension/N·m | 5.6 × 10−2 | |
| Contact angle/° | 90 | 90 |
| Slip length/m | 1 | 1 |
| Type | Representative Material | Specific Example |
|---|---|---|
| Anionic surfactant | Sulfonates | Sodium dodecyl sulfonate |
| Sulfate salts | Sodium lauryl sulfate | |
| Phosphate ester salts | Potassium cetyl phosphate | |
| Cationic surfactant | Alkyl pyridine salts | Stearate TEA salt |
| Alkyl amine salts | Tetacylpyridine salt | |
| Amphoteric surfactant | Amino acid salts | Sodium lauryl glutamate (LG-95P) |
| betaine | Dodecyl dimethyl betaine (BS-12) | |
| Imidazoline type | Sodium cocamyl amphoacetate (CAMC) | |
| Nonionic surfactant | Polyoxyethylene type | Polysorbate |
| Polyol type | Glycerin stearate ester |
| Core Number | Diameter /cm | Porosity /% | Length /cm | Permeability /(10−3 μm2) | Experimental Scheme | Experimental Content |
|---|---|---|---|---|---|---|
| 1# | 2.51 | 19.55 | 5.00 | 50.42 | Online NMR huff-n-puff | CO2 huff-n-puff |
| 2# | 2.51 | 22.13 | 5.00 | 50.36 | DFDS-assisted CO2 huff-n-puff | |
| 3# | 2.50 | 37.73 | 29.90 | 49.59 | Parallel core displacement | Water flooding + DFDS flooding + water flooding |
| 4# | 2.50 | 12.10 | 30.35 | 9.61 |
| Core Number | Permeability /(10−3 μm2) | Water Flooding Oil Recovery/% | DFDS Oil Recovery/% | Enhanced Oil Recovery/% |
|---|---|---|---|---|
| 3# | 49.59 | 47.9 | 60.1 | 12.2 |
| 4# | 9.61 | 17.3 | 47.8 | 30.5 |
| Combined oil recovery | 36.9 | 54.3 | 17.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Shen, R.; Gao, Y.; Xiong, S.; Zhao, C. Effects and Mechanisms of Dilute-Foam Dispersion System on Enhanced Oil Recovery from Pore-Scale to Core-Scale. Energies 2024, 17, 4050. https://doi.org/10.3390/en17164050
Wang X, Shen R, Gao Y, Xiong S, Zhao C. Effects and Mechanisms of Dilute-Foam Dispersion System on Enhanced Oil Recovery from Pore-Scale to Core-Scale. Energies. 2024; 17(16):4050. https://doi.org/10.3390/en17164050
Chicago/Turabian StyleWang, Xiuyu, Rui Shen, Yuanyuan Gao, Shengchun Xiong, and Chuanfeng Zhao. 2024. "Effects and Mechanisms of Dilute-Foam Dispersion System on Enhanced Oil Recovery from Pore-Scale to Core-Scale" Energies 17, no. 16: 4050. https://doi.org/10.3390/en17164050
APA StyleWang, X., Shen, R., Gao, Y., Xiong, S., & Zhao, C. (2024). Effects and Mechanisms of Dilute-Foam Dispersion System on Enhanced Oil Recovery from Pore-Scale to Core-Scale. Energies, 17(16), 4050. https://doi.org/10.3390/en17164050






