Abstract
Electric mobility is a sustainable alternative for mitigating carbon emissions by replacing the conventional fleet. However, the low availability of data from charging stations makes planning energy systems for the integration of electric vehicles (EVs) difficult. Given this, this work focuses on developing an adaptive computational tool for charging simulation, considering many EVs and mobility patterns. Technical specifications data from many EVs are considered for charging simulation, such as battery capacity, driving range, charging time, charging standard for each EV, and mobility patterns. Different simulations of charging many EVs and analyses of weekly charging load profiles are carried out, portraying the characteristics of the different load profiles and the challenges that system planners expect. The research results denote the importance of considering different manufacturers and models of EVs in the composition of the aggregate charging load profile and mobility patterns of the region. The developed model can be adapted to any system, expanded with new EVs, and scaled to many EVs, supporting different research areas.
1. Introduction
Electric mobility has been encouraged in recent years, motivated by the need to reduce atmospheric pollution and promote sustainable development. In the year 2021, the transport sector and the electricity and heat sector comprised more than 2/3 of total global carbon emissions [1]. Thus, the insertion of battery electric vehicles (BEVs) and plug-in hybrid electric vehicles (PHEVs), replacing the conventional fleet, originally powered by fossil fuels, is one of the alternatives for reducing carbon emissions [2]. Electric vehicles (EVs) significantly reduce carbon emissions by eliminating direct exhaust emissions, incentivize the use of renewable energy sources, achieve greater energy efficiency, improve air quality, and foster technological innovation [3,4,5,6].
Numerous studies have confirmed that EVs are more environmentally friendly than internal combustion engine vehicles (ICEVs), particularly when considering the entire lifecycle and the use of renewable energy sources. For instance, in [7] it was demonstrated that using photovoltaic panels can significantly reduce the environmental impact of EVs by 50% despite the challenges of lithium battery production and disposal. In [8], it was highlighted that under high-recycling scenarios, BEVs can significantly reduce lifecycle emissions compared to ICEVs. Similarly, ref. [9] shows that advancements in technology and energy sources are continually improving the emission reduction rates of EVs over ICEVs. These studies collectively support the notion that EVs, especially when paired with renewable energy and effective recycling practices, represent a more sustainable option in the long run.
Encouraged by widespread jurisdictional benefits, including tax incentives and subsidies aimed at facilitating EV acquisition, the production and commercialization of such vehicles have significantly escalated worldwide [10]. Although these are promising initiatives that should be encouraged, a series of challenges arise in this new panorama and must be considered when planning energy systems with the integration of EVs. To ensure neutrality in carbon emissions, the energy generation to supply EV charging must be low or zero carbon. Furthermore, the large-scale insertion of EVs leads to an increase in load in the system, which makes it more difficult due to the fact that EV load demand occurs in a non-linear manner, where there is a random charge, in a random charging station, and at a random time. In this context, electric utilities will play a crucial role in accommodating the variable load of EVs. Given this, several factors must be evaluated, such as the capacity of the distribution grid [11], load and grid management [12], energy generation to meet this new load demand [11,13], the increase in aggregate energy demand for EVs charging [10,14], future EV charging load scenarios [15], load peaks [14,16,17], voltage drop, and power factor [18].
The availability of charging station infrastructure and a suitable location are other essential factors for meeting the energy needs of EVs and the success of electric mobility [12,19,20]. Charging control strategies [21], availability of different charging standard options [22], and an accurate estimation of the types of charging stations [23] are essential means to improve grid impact analyses and the mass adoption of EVs. However, the scarcity of data on EV charging stations and, consequently, the low availability of real data on charging profiles make it difficult to advance studies on planning energy systems for large-scale insertion. By definition, a charging profile represents the power demand over time for charging EVs, reflecting variations in charging standards and intensity. Properly modeling EV charging profiles is one of the fundamental principles to assist and mitigate these problems and to aid the large-scale dissemination of EVs.
To overcome this problem of data unavailability, different strategies are observed in the literature. In [24], EV charging load profiles were modeled considering standard driving cycles, battery state of charge (SoC) conditions, and energy demand of various vehicles to study the variable effect of charging/discharging. In [11], daily EV charging load profiles were created considering the annual cycle of 8760 h of real data from charging stations, with aggregated residential charging data from 100 homes, commercial stations with slow charging, and commercial stations with public fast charging. In [10], an integrated model was developed from data to investigate energy use patterns and reveal the aggregate fast and slow charging load profiles of private, taxi, rental, and commercial EVs at an urban scale. The data used in this research were the operational states of the vehicles, locations, fleet types, ambient temperatures, and vehicle specifications, in addition to considering the operation of a fleet of 230,000 light vehicles.
In the study by [13] an intelligent EV charging/discharging model was developed, where the aggregate charging load demand is calculated considering typical variations in EV charging. To model the load profiles, it was simulated based on the charging/discharging schedule observing time criteria established about the initial SoC and based on the connection and disconnection times of EVs. Also considered was a battery capacity of 36 kWh, charge/discharge rate of 3.6 kW, and charging efficiency of 80%, common information for 80 EVs.
Furthermore, the use of mathematical models is common in applications for the purpose of simulating EVs’ charging load profiles. In [25] the Monte Carlo (MC) method was used to simulate EV charging based on urban mobility patterns of Brazilian drivers, such as estimating trip frequency, distance traveled, connection and disconnection times, and information characteristic of different models of EVs, similar to the study carried out in [26]. Likewise, in [18] the MC method was used to simulate charging and discharging profiles of EVs, based on theoretical data, considering three urban charging strategies, uncontrolled, economical, and V2G mode. In [27], a simulation model of the daily load profile was developed using the MC method based on data on charging preferences, energy consumption rates, travel patterns, and demographic and social attributes of drivers. Already in [28], to determine load profiles based on urban mobility studies, the non-homogeneous Poisson process was used to determine new charging strategies.
A country’s mobility characteristics directly impact energy consumption for charging EVs, which highlights the importance of characterizing this variable in estimating future load. In this sense, real data from three electric mobility studies in the southwest region of Germany were used in the study by [29] to analyze the load profiles and develop a model to generate synthetic load profiles. In [30] a set of methodologies was developed to transform EV charging data from Norwegian residential buildings into an EV charging dataset. In [12], to investigate the impact of EV charging on the load profile, mobility patterns of Portuguese drivers and EV consumption rates were considered. In the study by [31], research was carried out with Pakistani car owners, where information was collected on daily driving practices, distance traveled, and vehicle charging preferences, in addition to making use of technical data from three different EVs for simulating load profiles using MC simulation.
Furthermore, technical specifications data on EVs prove to be fundamental for the charging simulation, as the intrinsic characteristics of each EV significantly interfere with load demand. Thus, EV charging times, which vary in function for the charging option and the final SoC, are fundamental information to determine the energy demand estimate and, consequently, obtain the charging load profile, as well as evaluate grid limitations [32]. Other variables are essential for determining the load profiles, such as the time at which the EV starts and finishes charging [16,33], the amount of energy requested for charging [34,35], the available energy, and the time for discharge [34,35,36], as well as battery capacity [34,35], charging power, and efficiency [30].
Based on the literature, it appears that the mobility patterns of each country differ from each other and, consequently, directly impact the EV charging load profiles, in the same way as the technical data of EVs and their close relationship with load demand. Although some studies present technical data and other real charging data, many of the studies analyzed do not declare the technical specifications data of EVs, such as battery capacity, driving range, charging time, and charging standard, information that is important for obtaining EV charging load profiles.
In this sense, this work focuses on the development of an adaptive computational tool to obtain charging load profiles of many EVs, considering technical specifications data and mobility patterns. The technical specifications data of the EVs used in the model include battery capacity, driving range, charging time, and different charging standards, considering many vehicles of the BEV and PHEV type. The mobility patterns used in this research were the average driving distance of the Brazilian population and the start charging probability rate. By inputting the variability of different manufacturers and models of EVs, with technical specifications data and mobility patterns, realistic charging load profiles are generated. Therefore, this tool aims to support several research areas and overcome the low availability of data. Given this, the main contributions of this paper are the following:
- The charging simulation model makes use of technical data from different EVs, which results in charging load profiles with greater realism.
- The proposed methodology has the capacity to scale many EVs and the possibility of expanding new EVs.
- The developed model is adaptable to any energy system, provided existing EVs are considered and the mobility parameters of the region under study are adjusted.
The remainder of the paper is presented as follows. Section 2 presents the methodology developed in this work, highlighting the details of the charging simulation model and its parameterization. In Section 3, the individual simulation results of EVs selected for model testing are presented as a way of validating the developed tool. In Section 4, the charging load profiles obtained from the processing of the complete model are presented, where different simulations were carried out for sensitivity analysis. Finally, in Section 5 the work is concluded.
2. Electric Vehicle Charging Simulation Model
For this study, an EV charging simulation model was developed. The model considered the technical specifications data of many EVs, including battery capacity, driving range, and charging time conditions for slow charging (Level 1), semi-fast charging (Level 2), and fast charging (DCFC). Based on this, constraints were developed for conditioning EV charging. The model has an hourly resolution and a period of two weeks.
The model was developed in the Python programming language, implemented by the Spyder 4 software from the ANACONDA package, version 3.8.5, and processed in a workstation with an Intel(R) Xeon(R) Silver 4108 processor at 1.8 GHz (2 Processors), 64 GB of memory RAM, and a Microsoft Windows Server 2016 operating system. The libraries used for this model were Pandas [37] and NumPy [38], respectively in versions 1.5.3 and 1.23.5. The definitions and equations of the EV charging simulation model are presented in the next section.
Model Development
To develop the EV charging model, it was first necessary to define a random selector to select the vehicle model. This selector, defined by the variable , where is a positive integer with , will indicate the selected EV. The technical specifications data of the EVs used in this study are established in [39,40,41] and can be seen in Table 1.

Table 1.
Technical specifications of commercially available EVs.
From the selected EV, the recharge type it will perform is determined. Therefore, it was necessary to evaluate the different charging standards for each EV. The different charging standards are Level 1, Level 2, and DCFC. The functions of Equations (1)–(3) were then developed, considering charging times and technical data, such as the driving range and battery capacity of each EV. As stated in [39], the charging times in Table 1 are rough estimates for the vehicle charging to SoC of 0–80% at different charging standards. The SoC range of 0–80% is commonly used as a benchmark in electric vehicle charging studies because the charging rate tends to slow down significantly after 80% to prevent battery damage and optimize battery life. Additionally, Level 1 corresponds to a charging voltage of 110–120 Volts, Level 2 from 220–240 Volts, and DCFC from 200–800 Volts [39].
Given the different charging standards, a random selector was necessary, which is indicated by the variable , where is a positive integer with , which will determine the type of EV charging.
where:
- is the charging time for the selected charging standard (hours);
- is the energy demand average for charging the EV (kWh/h);
- is the battery capacity (kWh);
- is the maximum load constant, established in 80% ( = 0.8);
- is the battery discharge time (hours);
- is the total of hours in a day ( = 24 h);
- is the battery driving range (km);
- is the daily average driving distance by a car, established at 40 km ( = 40).
Thus, each charging standard has a different charging time, which directly affects the discharge time of the battery. However, some EVs do not have all three charging standards. Therefore, if a charging standard is selected that does not exist in the selected EV, the variables , , and , respectively from Equations (1), (2), and (3), will result in a value equal to zero (“0”).
After selecting the EV charging standard, the energy consumption for charging is expressed by Equation (4). To present greater realism for the EV charging load profiles, a charging efficiency indicator was defined by , where is a positive rational number with , selected randomly for each new recharge. This indicator limits the percentage of energy consumed, the charging time, the waiting time for the next recharge, and the driving range of the EV.
where represents the energy consumption in kWh for EV charging.
Given this, constraints were defined for the possible charging start of the selected EV. These constraints were defined based on the charging probability rate (δ), following Brazilian mobility patterns based on empirical knowledge, as presented in Table 2 and Table 3.

Table 2.
Charging probability rate for working days.

Table 3.
Charging probability rate for Saturdays, Sundays, and holidays.
Table 2 and Table 3 present the EV charging probability rates within each time range. For clarification, an EV in slow charging conditions, Level 1, on a working day, will have a 40% chance of starting charging in the time range (, with the start time and the end time). This definition of limits for the time range applies to all times reported in Table 2 and Table 3. By definition, varies from 0 to 335 h, which is equivalent to the range of two full weeks.
To use the probability rates relating to time ranges, a random selector is necessary, called , where is a positive integer with . Therefore, if observing the range containing , the EV will be able to recharge. However, other charging start constraints were established, such as the waiting time criteria for the next recharge. In this case, from the moment the EV starts charging, a time is counted as defined in Equation (5).
where is the minimum waiting time until the next recharge, and is the time at which the EV starts charging.
Therefore, this EV will perform a new charging after a time , where it will again go through the selecting process, the charging standard, and the charging constraints imposed in Table 2 and Table 3. Once the EV and the charging standard are selected, and after meeting the constraints, the charging process begins. At the same time, a new counter will be started, which is represented by Equation (6)
where is the end charging time of the EV.
Then, three constraints are listed in Equation (7) to dilute the EV charging load and condition the waiting time for the next recharge.
where represents the load for the entire charging time of the selected EV, is the EV hourly load, and is the hourly load of each new charging. is considered an empty vector whenever a new charging begins, and is an empty vector whenever a new EV is selected. In addition to Equation (7), the constraint in (i) defines the conditions for the charging load equal to . The constraint in (ii) aims to determine the residual charging load, which will be a value greater than 0 and less than . The constraint in (iii) is intended to define the value as 0 for the EV charging load when the other restrictions are not met.
Finally, with the definition of the criteria and constraints, the EV charging simulation model is complete and can be replicated times, where represents the total number of EVs desired to obtain the data of the charging load profiles. To complement the description of the methodology of the EV charging simulation model, a flowchart of the processes developed is presented, which can be viewed in the macro diagram in Figure 1.
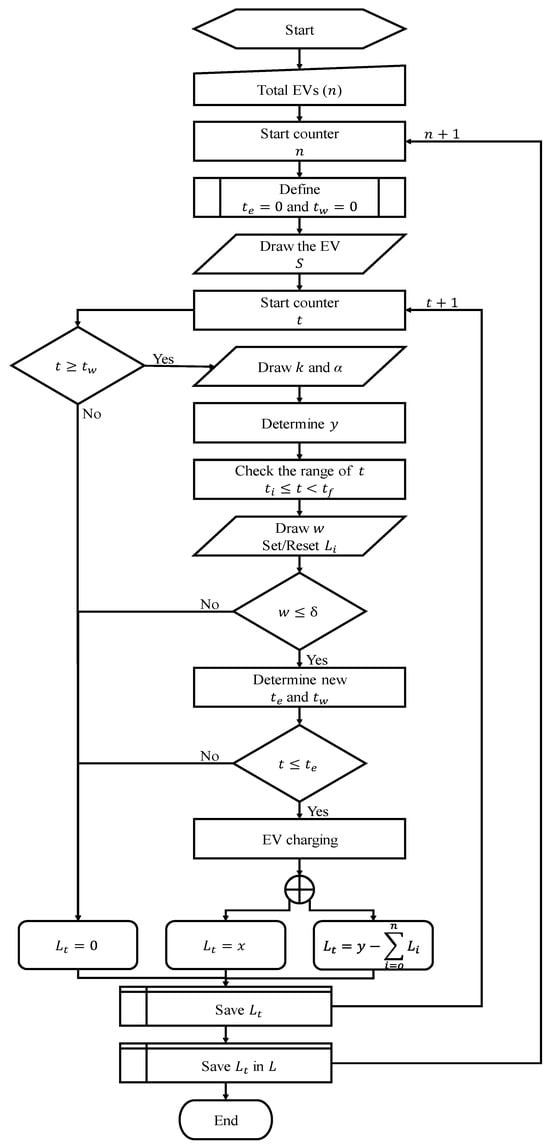
Figure 1.
Representative flowchart of the EV charging simulation model.
Thus, with the EV charging load profiles resulting from the developed model, it is possible to develop planning, operation, and energy management studies to meet the additional load requested by EVs, highlighting the research carried out in this study. Notably, the methodology developed can be adapted to any study as long as the parameters in Table 1 and Table 2 are adjusted and the daily average driving distance by a car for the region under study is considered.
3. Validation of the Electric Vehicle Charging Simulation Model
To validate and evaluate the effectiveness of the model developed, charging simulations of different types of vehicles were carried out. For this purpose, EVs numbered 1, 2, 9, and 24 in Table 1 were considered for the tests, with the manufacturer and model of the vehicles being Nissan Leaf, Chevrolet Volt, Tesla Model 3, and Audi e-tron S Sportback, respectively. For a better interpretation of the test results, the efficiency indicator was set to 0.5. Considering that the maximum load constant is equal to 80%, when setting at 0.5, the EV recharges carried out during the tests will be 40%. Table 4 presents the parameters and results of the equations used to obtain the EV charging load profiles selected for the tests, considering the condition of = 0.5.

Table 4.
Charging parameters of different EVs for the condition of the = 0.5.
To facilitate the interpretation of the results and ensure greater readability, the parameters of all EVs were calculated for the condition of = 1 (80%), which can be found in Appendix A of this paper. The individual analyses of the simulation tests carried out are presented below.
Charging Simulation of the Electric Vehicles Selected for Model Testing
The first vehicle selected for the charging simulation test was the Nissan Leaf, a BEV model with a driving range of 243 km and a 40 kWh battery. This EV is characterized as a vehicle with intermediary performance and capacity in relation to technical issues compared to the other EVs considered in this study. It presents charging standards covering the three different recharge types. Figure 2 shows the charging load profile of the Nissan Leaf EV over a period of 336 h, covering two full weeks.
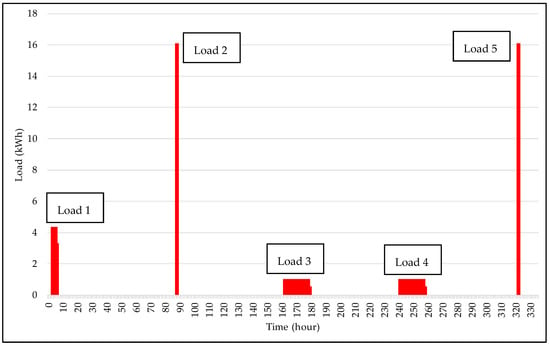
Figure 2.
Charging Load Profile of the Nissan Leaf EV.
In analyzing Figure 2, the first load of the Nissan Leaf EV was a Level 2 charging, with an average demand of 4.267 kWh/h and energy consumption of 16 kWh, with a charging time of 3.75 h and a discharging time of 62.07 h, respectively , , , and , as described in Table 4. Based on these time ranges, and as indicated in Table 5, load 1 began at hour 3, charging until hour 6.75, expressed by , and minimum waiting time until the next recharge at hour 65.07, declared by . Thus, the subsequent charging will only occur after a time range bigger than , where, from the first full hour and bigger than or equal to , new draws are carried out following the constraints established in the methodology.

Table 5.
Start and end time of charging the Nissan Leaf EV.
Given this, the next recharge, represented by load 2 in Table 5, began at hour 88, with a DCFC recharge type. This charging condition is more harmful as it requires a more significant response from the system, as can be seen in Figure 2, where in this case, the charging occurred in a range of equal to 0.25 h, with equal to 64 kWh/h, and equal to 16 kWh. Note that the of the previous recharge must be lower than the start time of the forward recharge, which is intended to be obeyed for all the charging. Thus, respecting the charging and discharging range and observing the time range of load 2, the draw for the new recharge was enabled, which began at hour 162 with a Level 1 charging condition called load 3. This charging standard is softer than the others, usually available at residential charging stations, where in this case, the range of is equal to 17.5 h, with equal to 0.914 kWh/h, and also with equal to 16 kWh due to being considered constant in this analysis. Another two recharges of the Nissan Leaf EV were carried out in load 4 and load 5 of Table 5, which will not be detailed so as not to make the explanations of the methodology repetitive.
The second vehicle for the charging simulation test was the Chevrolet Volt, a PHEV with three different charging standards. In real operating conditions, this EV could run using battery energy and other fuels. However, for simplification purposes, for this and the other PHEV type EVs reported in Table 1, the battery driving range only was considered. Figure 3 illustrates how the charging load profile of the Chevrolet Volt EV behaved during the charging simulation test.
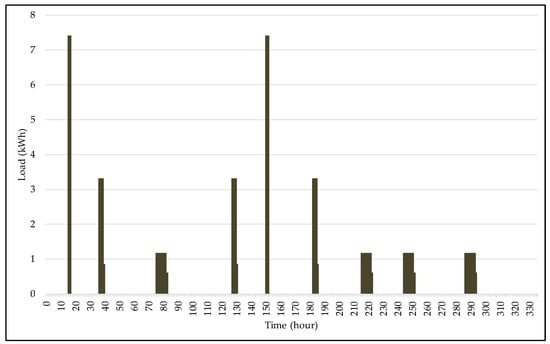
Figure 3.
Charging load profile of the Chevrolet Volt EV.
As it has a battery with a lower storage capacity (18.4 kWh) and consequently a shorter driving range (85 km), charging and discharging times are shorter, as seen in Figure 3 and Table 4. However, this implies a greater need for charging at shorter ranges, which resulted in nine loads within a range of 336 h, and information can be found in Table 6. Although the Chevrolet Volt EV has this battery and driving range limitation, the three different charging standards are not very significant in terms of energy consumption. For the condition of = 0.5, the energy consumption is 7.36 kWh, with an average demand of 44.606 kWh/h for the DCFC recharge type, and 1.132 kWh/h and 3.271 kWh/h, respectively, for the Level 1 and Level 2 charging standards.

Table 6.
Start and end times of charging the Chevrolet Volt EV.
The next vehicle selected for the charging simulation test was the Tesla Model 3 EV, which has a battery with a storage capacity of 50 kWh and a driving range of 354 km. This EV is a BEV with the unique feature of having charging standards only in Level 2 and DCFC. Given this, Figure 4 represents the charging load profile of the Tesla Model 3 EV for charging simulation under the condition of = 0.5.
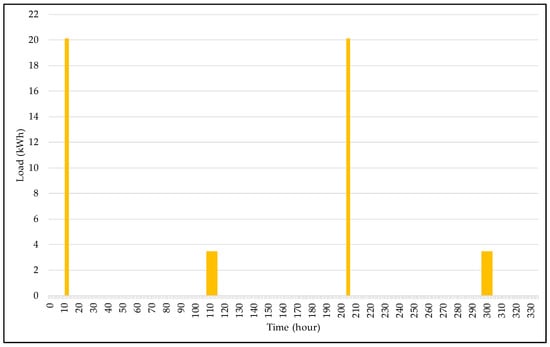
Figure 4.
Charging load profile of the Tesla Model 3 EV.
The Tesla Model 3 EV charging simulation resulted in four loads for the period under analysis, as seen in Figure 4 and Table 7. As presented in Table 4, the average demand for the two different charging standards was 3.333 kWh/h and 46.153 kWh/h, respectively, for Level 2 and DCFC, to meet an energy demand of 20 kWh. As this EV has a relatively considerable driving range, the times between recharges are more extended, in the range of close to 100 h.

Table 7.
Start and end time of charging the Tesla Model 3 EV.
Finally, the last vehicle selected for the simulation tests was the Audi e-tron S Sportback EV, with a 95 kWh battery and a driving range of 335 km, with three different charging standards. This EV is a BEV, being the vehicle with the largest-capacity battery among the EVs selected for testing and one of the largest among all the EVs used in this study. The energy demand observed in the charging load profile of the Audi e-tron S Sportback EV was 38 kWh for each of the four loads resulting from the simulation, with the highest energy peak in load 2, as illustrated in Figure 5.
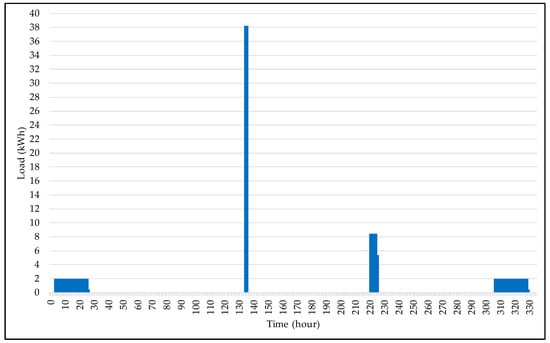
Figure 5.
Charging load profile of the Audi e-tron S Sportback EV.
This high energy peak represents an average demand of 152 kWh/h for the DCFC recharge type, denoted in Table 4. When analyzing this charging standard, it is the one that requires the most power from the system, and if it is neglected in the planning and operation, it can put the integrity of the system at risk. Additionally, Level 2 charging has an average demand of 8.216 kWh/h and it is 1.718 kWh/h for Level 1 charging, which are lighter and do not impose such severity on the system.
The Audi e-tron S Sportback VE, like the Tesla Model 3 VE, also has a high driving range, which is the reason why it has longer times between recharges, observed in Table 8, with time ranges close to or greater than 100 h. However, as it has a higher-capacity battery, the charging time of this EV can be longer than 24 h. In the case under analysis, considering = 0.5, the time was 22.125 h for the Level 1 charging standard, information which can be seen in Table 4.

Table 8.
Start and end times of charging the Audi e-tron S Sportback EV.
In this way, the EV charging simulation tests exemplified how the developed methodology proceeds given the technical specifications of each EV and of the charging standards. Then, through the simulations carried out to validate and prove the effectiveness of the developed model, the methodology was processed considering all EVs and their specifications established in Table 1. The results obtained considering the complete model are presented below.
4. Charging Simulation of Many Electric Vehicles
To analyze the results of the EV charging simulation model, 1 million EVs were considered for each charging load profile. As all selected EVs start from the initial time ready to charge if the EV meets the constraints, there is a load peak in the first hours of the simulation. Given this, the analyses were carried out using only the second half of the EV recharge data, which is equivalent to a period of one week. Thus, the charging load profile of many EVs, called the pattern charging load profile, was evaluated, analyzing the behavior of the aggregate load profile over a period of one week. Then, for the same EVs selected for the pattern charging simulation, the charging load profiles were estimated considering, in each situation, only one charging standard. Finally, new charging load profiles were processed for comparative analysis against the pattern charging load profile. The results and discussions of the simulation model for charging many EVs are presented below.
4.1. Simulation of the Pattern Charging Load Profile Considering Different Charging Standards
For the simulation of the pattern charging load profile, the processing of the complete model was considered, simulating the charging of a total of 1 million randomly selected EVs and considering the different charging standards, that is, Level 1, Level 2, and DCFC, as long as the selected EV has this charging condition. The processing time of the charging simulation model, considering 1 million EVs, was 3 h, 10 min, and 18 s. Given this, Figure 6 presents the pattern charging load profile considering the aggregate charging loads of 1 million EVs.
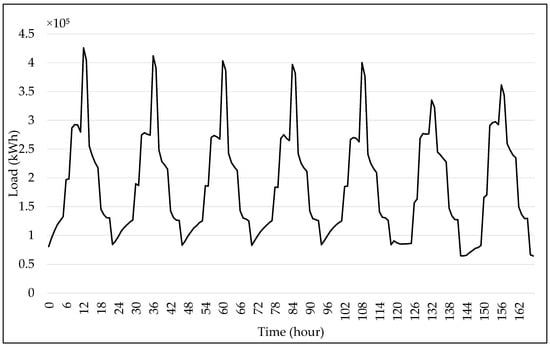
Figure 6.
Pattern charging load profile for 1 million EVs.
As shown in Figure 6, the aggregate charging load profile for one week has well-defined peaks and valleys, with a similar load profile on weekdays and a decline in consumption on weekends (Saturday and Sunday), and the same is observed in the study by [42]. Daily load peaks occurred in all cases at hour 12 due to the high percentage of adherence to fast charging considered at noon. The point of lowest consumption is at hour 22, with a gradual increase until hour 6 of the following day.
The choice of charging standard has a significant impact on the daily charging load profile of EVs, as mentioned in [31], such that the accentuated influence between peaks and valleys can be seen in Figure 6. It is observed that energy consumption throughout the day starts at values below 20%, with a steep load ramp until reaching 100%, characteristics also identified in [43]. Furthermore, the mobility patterns of one country differ from the others, as shown when analyzing the studies by [12,29,32], in which peaks and valleys may not coincide at precisely the same times. However, due to the flexibility of the developed model in this paper, adjustments can be made to the parameters in Table 1 and Table 2 about the charging probability rate and time ranges, as well as the daily average driving distance estimate, to adapt to the purpose of the study to be carried out the face of the mobility patterns of the region under analysis. These adjustments guarantee the generalization of the developed model.
4.2. Assessment of Charging Load Profiles for Fixed Charging Standards
To demonstrate the influence of different charging standards on the EV charging load profile, EV recharges with fixed charging standards were simulated for the same EVs selected during the pattern charging simulation. This implies that the EVs that made up the pattern charging load profile in this simulation will only perform one charging standard throughout the entire period as long as the EV has this charging condition. Given this, Figure 7 shows the charging load profiles for Level 1, Level 2, and DCFC load conditions, in addition to the pattern load profile.
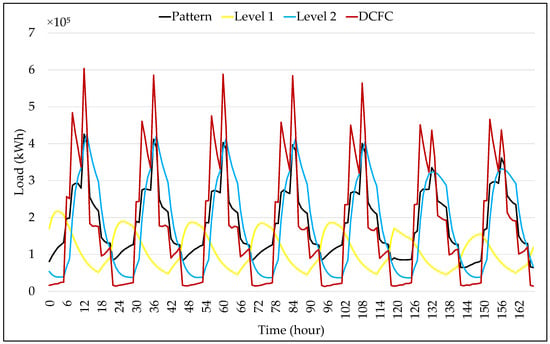
Figure 7.
Charging load profile considering fixed charging standard.
In analyzing the charging load profiles in Figure 7, it is observed that they are different from each other since each charging standard results in a typical load profile. This is in accordance with studies by [11,16,32], which reference the importance of the EV charging start time and of the different recharge types, where EV charging time varies depending on the charging condition and the final SoC and, consequently, will result in different load profiles.
Evaluating the load profiles with a fixed charging standard in comparison to the pattern load profile, the load by Level 1 type, slow recharge, has its maximum demand during the first hours and the end of the day, in the same way as observed in the results obtained from the study by [30], analyzing slow charging load profiles. This is explained by the adoption of this recharge type at residential charging stations. Furthermore, the Level 1 charging load profile is substantially lower than the pattern load profile, representing approximately 60.79% of the load, since charging times for this charging standard can exceed periods of 24 h, as mentioned in the study by [11], resulting in a delay in the next recharge.
The Level 2 charging load profile is the one that most resembles the pattern load profile, with maximum energy demand at hour 13 every day and load smoothing on weekends. However, it presents a lower load in the first hours of the day, lower than the pattern load, and a constant load ramp until reaching the maximum energy demand. Compared to the accumulated load from the pattern charging load profile, this recharge type resulted in 96% of the load.
Finally, the DCFC charging load profile, which represents fast charging, as illustrated in Figure 7, presents the lowest and highest global energy demands. This characteristic is due to the request for energy in short time ranges, which generally occurs at times when EV users are active. However, this implies high daily load peaks, which in the study developed at hour 8 with a local peak and at hour 12 with the global daily peak, except on weekends, when these peaks are reversed. The accumulated load for the fast charging resulted in 98.38% of the load compared with the pattern load profile. Although this charging condition is closer to the refueling time of conventional vehicles [44], it is worth highlighting that the impact of fast charging on the electrical grid is one of the main challenges for system planners. Fast charging stations being implemented without adequate planning can cause severe problems for the grid [12].
4.3. Comparative Analysis between Charging Load Profiles of Many Electric Vehicles
To analyze the variability between different load profiles when considering the randomness of EVs, ten new charging load profiles were simulated. These were evaluated in relation to the pattern charging load profile. To improve the interpretation of the analysis performed, all data from the new charging load profiles were normalized by the hourly load of the pattern load profile, which was considered unitary in all periods. This normalization ensures that comparisons between the profiles are on a consistent scale, helping to identify relative differences in load variations rather than absolute values. Figure 8 presents the charging load profiles from the new simulations alongside the pattern load profile. The EVs comprising each charging load profile in Figure 8 can be viewed in Appendix B, Table A2.
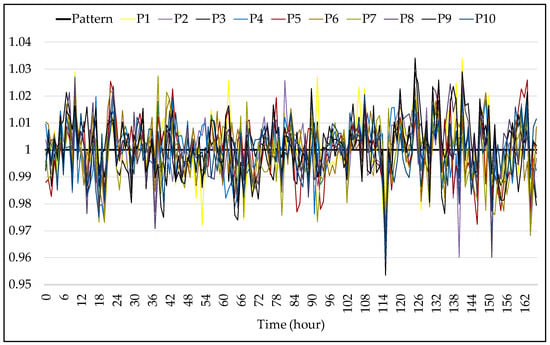
Figure 8.
Simulation of many charging load profiles.
When analyzing the charging load profiles in Figure 8, it can be observed that the different load profiles diverge, despite all having a total of 1 million EVs, differing minimally in the EVs that make up each curve, as seen in Table A2 of Appendix B. However, since the model randomly selects the vehicle, the charging start probability rate, the charging standard, and the efficiency, it was expected that the charging load profiles would result in different peaks and valleys. The randomness in selecting which EVs recharge at which times introduces variability, which collectively contributes to the differences observed in the load profiles. These factors are crucial in modeling realistic scenarios, as they reflect the unpredictable nature of human behavior and EV usage patterns.
Compared with the pattern charging load profile, the new simulations resulted in load peaks with a maximum increase of approximately 3.41% and valleys with a load decrease of up to 4.65%. This indicates that while the overall number of EVs remains constant, the timing and efficiency variations cause significant fluctuations in load demand. These fluctuations can stress the grid if not adequately managed, underscoring the need for effective load balancing strategies. Understanding the potential range of load fluctuations can help design more resilient and adaptive systems. It also highlights the importance of incorporating randomness in simulations to estimate real-world scenarios. Grid operators and planners can use this information to develop strategies that mitigate the impact of peak loads and fill in valleys, ensuring a more stable and reliable power supply.
Additionally, to exemplify the importance of considering the different types of EVs present in an energy system, a new charging load profile was simulated considering only the four EVs selected for the charging simulation in Section 3, that is, the vehicles of the manufacturer and model Nissan Leaf, Chevrolet Volt, Tesla Model 3, and the Audi e-tron S Sportback, each totaling 250,000 vehicles. Thus, Figure 9 presents the load profiles for comparative analysis between the charging load profile resulting from this simulation and the pattern charging load profile. To show these results more clearly, all hourly loads in Figure 9 were normalized by pattern load profile, as in Figure 8.
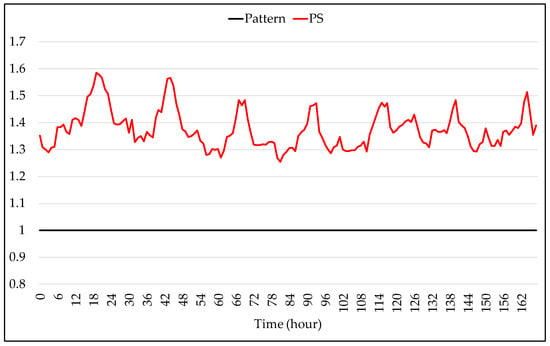
Figure 9.
Simulation of the charging load profile with set EVs.
The results of the analysis between the charging load profiles in Figure 9 denote a significant increase in the hourly load of the PS load profile in relation to the pattern load profile for the entire simulation period. The maximum and minimum loads of the PS load profile represent an increase in the hourly load of around 58.46% and 25.37%, respectively. Although this simulation represents the hypothetical load profile of only four EVs under Brazilian mobility characteristics, the differences between the load profiles in Figure 9 demonstrate the importance of considering different EVs in synthetic charging load profile simulations. Likewise, for a more realistic estimate of load profiles, mobility patterns in the region, the total number of EVs of each manufacturer and model, and the charging standards must be considered because of the impact on aggregate charging load profiles.
5. Conclusions
The integration of EVs into energy systems to reduce carbon emissions is a subject of research worldwide. However, the unavailability of data from charging stations makes energy system planning difficult, impacting infrastructure availability and, consequently, the low adoption of EVs by the population. In this sense, this study aimed to develop an adaptive computational tool for EV charging simulation to obtain aggregated charging load profiles of many EVs, considering different EVs and mobility patterns.
Results analysis of the charging simulation model demonstrates the complexity and variability of load profiles resulting from different charging standards and user behaviors. The results showed that the choice of charging standard significantly impacts daily load profiles since each recharge type influences energy demand and load peaks on the electrical grid differently. Likewise, the load profiles obtained when processing the complete model many times showed variations between peaks and valleys, and when considering a few EVs, there were increases in load demand concerning the pattern charging load profile. These results confirm the importance of considering the diversity of EV types and mobility patterns in modeling.
In conclusion, the importance of characterizing the input information for EV charging load simulation is highlighted, as if omitted, it may result in inaccuracy in the estimates of the simulated load profiles. Additionally, a calibrated model can help EVs integrate into energy systems and support several research areas. Given this, the developed model presents itself as a robust and scalable tool for simulating EV charging load profiles and overcoming low data availability. Future research on the subject can be described by system expansion planning, energy management, demand response, and EV charging strategies as a solution for recharge control.
Author Contributions
Conceptualization, B.K.H., C.U.-V., J.P.S., M.B.C. and A.d.R.A.; methodology, B.K.H. and A.d.R.A.; software, B.K.H., J.P.S., M.B.C. and C.H.B.; validation B.K.H., C.U.-V. and A.d.R.A.; formal analysis, B.K.H., A.R.A., M.D.T., C.H.B. and A.d.R.A.; investigation, B.K.H., J.P.S. and M.B.C.; resources, B.K.H. and A.d.R.A.; data curation, B.K.H.; writing—original draft preparation, B.K.H.; writing—review and editing, C.U.-V., A.R.A. and A.d.R.A.; visualization, M.D.T. and C.H.B.; supervision, C.U.-V. and A.d.R.A.; project administration, A.d.R.A.; funding acquisition, B.K.H. and A.d.R.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the technical and financial support from the National Council for Scientific and Technological Development (CNPq—no. 23/2551-0000108-0), and Research Support Foundation of the State of Rio Grande do South (FAPERGS—no. 23/2551-0000108-0), Brazilian Institutions.
Data Availability Statement
The data presented in this study might be available on request from the corresponding author.
Acknowledgments
The authors express their gratitude for the technical and financial support from the National Council for Scientific and Technological Development—CNPq, Research Support Foundation of the State of Rio Grande do South—FAPERGS, Federal University of Santa Maria—UFSM, and Federal University of Parana—UFPR, Brazilian Institutions.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Charging parameters of different EVs for the condition of α = 1.
Table A1.
Charging parameters of different EVs for the condition of α = 1.
| Vehicle Model | Manufacturer | Model Year | Type | Charging Standard | (h) | (kWh) | (km) | (kWh/h) | (kWh) | (h) | (h) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Prius Prime | Toyota | 2018 | PHEV | Level 1 | 5.5 | 8.8 | 40 | 1.28 | 7.04 | 5.5 | 24.7 |
| Level 2 | 2.1 | 3.352 | 2.1 | 21.3 | |||||||
| DCFC | - | - | - | - | - | ||||||
| Leaf | Nissan | 2018 | BEV | Level 1 | 35 | 40 | 243 | 0.914 | 32 | 35 | 151.64 |
| Level 2 | 7.5 | 4.267 | 7.5 | 124.14 | |||||||
| DCFC | 0.5 | 64 | 0.5 | 117.14 | |||||||
| Volt | Chevrolet | 2018 | PHEV | Level 1 | 13 | 18.4 | 85 | 1.132 | 14.72 | 13 | 53.8 |
| Level 2 | 4.5 | 3.271 | 4.5 | 45.3 | |||||||
| DCFC | 0.33 | 44.606 | 0.33 | 41.13 | |||||||
| Bolt | Chevrolet | 2019 | BEV | Level 1 | - | 60 | 383 | - | - | - | - |
| Level 2 | 9.3 | 5.161 | 48 | 9.3 | 193.14 | ||||||
| DCFC | 1.33 | 36.09 | 1.33 | 185.17 | |||||||
| Spark | Chevrolet | 2016 | BEV | Level 1 | - | 19 | 132 | - | - | - | - |
| Level 2 | 7 | 2.171 | 15.2 | 7 | 70.36 | ||||||
| DCFC | 0.75 | 20.267 | 0.75 | 64.11 | |||||||
| Fit | Honda | 2014 | BEV | Level 1 | 15 | 20 | 132 | 1.067 | 16 | 15 | 78.36 |
| Level 2 | 3 | 5.333 | 3 | 66.36 | |||||||
| DCFC | - | - | - | - | - | ||||||
| Clarity | Honda | 2018 | PHEV | Level 1 | 12 | 25.5 | 75 | 1.7 | 20.4 | 12 | 48 |
| Level 2 | 2.5 | 8.16 | 20.4 | 2.5 | 38.5 | ||||||
| DCFC | - | - | - | - | - | ||||||
| Model S | Tesla | 2018 | BEV | Level 1 | 96.7 | 100 | 506 | 0.827 | 80 | 96.7 | 339.58 |
| Level 2 | 10.7 | 7.477 | 10.7 | 253.58 | |||||||
| DCFC | 1.33 | 60.15 | 1.33 | 244.21 | |||||||
| Model X | Tesla | 2018 | BEV | Level 1 | 89 | 100 | 465 | 0.899 | 80 | 89 | 312.2 |
| Level 2 | 9.5 | 8.421 | 9.5 | 232.7 | |||||||
| DCFC | 1.33 | 60.150 | 1.33 | 224.53 | |||||||
| Model 3 | Tesla | 2017 | BEV | Level 1 | - | 50 | 354 | - | - | - | - |
| Level 2 | 12 | 3.333 | 40 | 12 | 181.92 | ||||||
| DCFC | 52/60 | 46.154 | 52/60 | 170.787 | |||||||
| Kia Soul | Kia | 2018 | BEV | Level 1 | 24 | 30 | 177 | 1 | 24 | 24 | 108.96 |
| Level 2 | 4.8 | 5 | 4.8 | 89.76 | |||||||
| DCFC | 0.75 | 32 | 0.75 | 85.71 | |||||||
| Focus | Ford | 2016 | BEV | Level 1 | 20 | 23 | 161 | 0.92 | 18.4 | 20 | 97.28 |
| Level 2 | 3.5 | 5.257 | 3.5 | 80.78 | |||||||
| DCFC | 0.5 | 36.8 | 0.5 | 77.78 | |||||||
| i-MiEV | Mitsubishi | 2017 | BEV | Level 1 | 22 | 16 | 180 | 0.582 | 12.8 | 22 | 108.4 |
| Level 2 | 6 | 2.133 | 6 | 92.4 | |||||||
| DCFC | 0.5 | 25.6 | 0.5 | 86.9 | |||||||
| e-Golf | Volkswagen | 2017 | BEV | Level 1 | - | 35.8 | 201 | - | - | - | - |
| Level 2 | 6 | 4.773 | 28.64 | 6 | 102.48 | ||||||
| DCFC | 1 | 28.64 | 1 | 97.48 | |||||||
| E-Up | Volkswagen | 2018 | BEV | Level 1 | - | 20 | 159 | - | - | - | - |
| Level 2 | 9 | 1.778 | 16 | 9 | 85.32 | ||||||
| DCFC | 0.5 | 32 | 0.5 | 76.82 | |||||||
| Zoe | Renault | 2017 | BEV | Level 1 | 16 | 41 | 400 | 2.05 | 32.8 | 16 | 208 |
| Level 2 | 4.5 | 7.289 | 4.5 | 196.5 | |||||||
| DCFC | 2.67 | 12.284 | 2.67 | 194.67 | |||||||
| Twizy | Renault | 2017 | BEV | Level 1 | - | 6.1 | 100 | - | - | - | - |
| Level 2 | 3 | 1.627 | 4.88 | 3 | 51 | ||||||
| DCFC | - | - | - | - | - | ||||||
| i3 | BMW | 2018 | BEV and PHEV | Level 1 | 13 | 33 | 183 | 2.031 | 26.4 | 13 | 100.84 |
| Level 2 | 5 | 5.28 | 5 | 92.84 | |||||||
| DCFC | 0.5 | 52.8 | 0.5 | 88.34 | |||||||
| Nixon | TATA | 2020 | BEV | Level 1 | - | 30.2 | 312 | - | - | - | - |
| Level 2 | 8 | 3.02 | 24.16 | 8 | 157.76 | ||||||
| DCFC | 1 | 24.16 | 1 | 150.76 | |||||||
| Tigor | TATA | 2020 | BEV | Level 1 | 11.2 | 16.2 | 142 | 1.157 | 12.96 | 11.2 | 79.36 |
| Level 2 | 6 | 2.16 | 6 | 74.16 | |||||||
| DCFC | - | - | - | - | - | ||||||
| Kona | Hyundai | 2019 | BEV | Level 1 | - | 64 | 455 | - | - | - | - |
| Level 2 | 37/6 | 8.303 | 51.2 | 37/6 | 224.567 | ||||||
| DCFC | 0.9 | 56.889 | 0.9 | 219.3 | |||||||
| Kona | Hyundai | 2019 | BEV | Level 1 | - | 39.2 | 288 | - | - | - | - |
| Level 2 | 9.5 | 3.301 | 31.36 | 9.5 | 147.74 | ||||||
| DCFC | 0.9 | 34.844 | 0.9 | 139.14 | |||||||
| e-Verito | Mahindra | 2017 | BEV | Level 1 | - | 21.2 | 181 | - | - | - | - |
| Level 2 | 6 | 2.827 | 16.96 | 6 | 92.88 | ||||||
| DCFC | 2.1 | 8.076 | 2.1 | 88.98 | |||||||
| e2o plus | Mahindra | 2016 | BEV | Level 1 | - | 16 | 140 | - | - | - | - |
| Level 2 | 5 | 2.56 | 12.8 | 5 | 72.2 | ||||||
| DCFC | 1.5 | 8.533 | 12.8 | 1.5 | 68.7 | ||||||
| e-tron S Sportback | Audi | 2022 | BEV | Level 1 | 44.25 | 95 | 335 | 1.718 | 76 | 44.25 | 205.05 |
| Level 2 | 9.25 | 8.216 | 76 | 9.25 | 170.05 | ||||||
| DCFC | 0.5 | 152 | 76 | 0.5 | 161.3 |
Appendix B

Table A2.
Total number of vehicles in each charging load profile.
Table A2.
Total number of vehicles in each charging load profile.
| Vehicle Model | Manufacturer | Total Number of Vehicles | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pattern | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 | ||
| Prius Prime | Toyota | 39,918 | 39,813 | 39,982 | 40,175 | 39,945 | 39,900 | 39,668 | 39,956 | 40,159 | 39,860 | 39,962 |
| Leaf | Nissan | 39,770 | 40,256 | 40,028 | 39,968 | 40,515 | 39,892 | 39,820 | 40,094 | 39,964 | 40,000 | 40,113 |
| Volt | Chevrolet | 39,975 | 39,895 | 39,968 | 40,018 | 40,122 | 39,748 | 40,404 | 39,877 | 40,090 | 40,348 | 40,438 |
| Bolt | Chevrolet | 40,215 | 39,751 | 39,797 | 40,188 | 40,036 | 40,026 | 40,270 | 39,803 | 39,966 | 39,809 | 39,677 |
| Spark | Chevrolet | 39,897 | 39,979 | 40,280 | 39,994 | 40,160 | 39,801 | 39,874 | 40,013 | 40,038 | 39,939 | 39,968 |
| Fit | Honda | 40,407 | 39,907 | 39,963 | 39,902 | 39,979 | 39,837 | 39,817 | 39,567 | 40,015 | 39,949 | 40,004 |
| Clarity | Honda | 39,982 | 39,986 | 40,054 | 39,821 | 40,273 | 39,766 | 40,251 | 39,858 | 39,741 | 39,921 | 40,091 |
| Model S | Tesla | 39,966 | 39,634 | 40,034 | 40,188 | 40,080 | 39,547 | 39,752 | 40,119 | 40,103 | 39,966 | 40,060 |
| Model X | Tesla | 39,808 | 40,066 | 39,761 | 39,832 | 39,935 | 40,098 | 40,112 | 39,882 | 40,252 | 39,899 | 40,077 |
| Model 3 | Tesla | 40,265 | 40,166 | 39,791 | 40,046 | 39,766 | 40,151 | 40,180 | 40,002 | 39,700 | 40,200 | 39,597 |
| Kia Soul | Kia | 39,855 | 40,087 | 40,251 | 39,552 | 39,974 | 39,933 | 39,706 | 39,776 | 39,847 | 40,104 | 39,963 |
| Focus | Ford | 39,716 | 40,040 | 40,127 | 39,875 | 39,423 | 40,277 | 39,817 | 40,126 | 40,133 | 39,727 | 39,972 |
| i-MiEV | Mitsubishi | 39,950 | 39,986 | 40,290 | 40,191 | 39,990 | 39,889 | 40,058 | 39,997 | 39,890 | 39,928 | 39,763 |
| e-Golf | Volkswagen | 39,797 | 39,833 | 39,864 | 40,234 | 39,874 | 40,041 | 40,077 | 39,705 | 39,905 | 39,935 | 40,397 |
| E-Up | Volkswagen | 40,098 | 40,310 | 39,899 | 39,865 | 39,728 | 40,242 | 39,820 | 39,956 | 40,113 | 40,211 | 40,084 |
| Zoe | Renault | 40,070 | 40,165 | 40,196 | 39,755 | 40,145 | 39,999 | 40,141 | 39,992 | 40,035 | 40,243 | 39,945 |
| Twizy | Renault | 40,033 | 39,958 | 40,125 | 39,852 | 40,038 | 39,646 | 39,975 | 40,255 | 39,907 | 39,878 | 39,889 |
| i3 | BMW | 40,256 | 40,014 | 40,085 | 39,957 | 40,090 | 39,883 | 39,811 | 39,983 | 40,346 | 40,053 | 39,967 |
| Nixon | TATA | 40,024 | 39,774 | 39,623 | 40,160 | 39,958 | 40,049 | 40,275 | 40,354 | 39,833 | 40,054 | 39,963 |
| Tigor | TATA | 39,727 | 40,146 | 40,060 | 40,208 | 40,146 | 40,538 | 40,033 | 39,887 | 40,238 | 39,809 | 40,136 |
| Kona | Hyundai | 39,896 | 40,248 | 40,025 | 40,022 | 39,902 | 40,240 | 39,796 | 40,220 | 40,171 | 40,278 | 39,908 |
| Kona | Hyundai | 40,054 | 39,983 | 40,151 | 39,694 | 40,061 | 39,925 | 39,905 | 40,573 | 39,701 | 40,171 | 40,182 |
| e-Verito | Mahindra | 39,948 | 39,729 | 39,685 | 40,279 | 39,989 | 39,978 | 39,938 | 40,072 | 40,279 | 39,850 | 39,731 |
| e2o plus | Mahindra | 40,045 | 39,984 | 40,106 | 40,211 | 39,779 | 40,204 | 40,058 | 40,046 | 39,588 | 39,711 | 40,151 |
| e-tron S Sportback | Audi | 40,328 | 40,290 | 39,855 | 40,013 | 40,092 | 40,390 | 40,442 | 39,887 | 39,986 | 40,157 | 39,962 |
References
- IEA. Greenhouse Gas Emissions from Energy Data Explorer; International Energy Agency: Paris, France, 2023. [Google Scholar]
- Fakhrooeian, P.; Pitz, V. Scheduling the Charging and Discharging Events of Electric Vehicles for Quasi Dynamic Load Flow Calculations of a Low-Voltage Distribution Grid with Regard to Stochastic Behavior and Grid Requirements. Electr. Power Syst. Res. 2023, 216, 109021. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Mohamed, A. A Review of Lithium-Ion Battery State of Charge Estimation and Management System in Electric Vehicle Applications: Challenges and Recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Da Silva, S.F.; Eckert, J.J.; Silva, F.L.; Silva, L.C.A.; Dedini, F.G. Multi-Objective Optimization Design and Control of Plug-in Hybrid Electric Vehicle Powertrain for Minimization of Energy Consumption, Exhaust Emissions and Battery Degradation. Energy Convers. Manag. 2021, 234, 113909. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, H.; Li, Y.; Gao, J.; Dave, K.; Chen, J.; Li, T.; Tu, R. Exhaust and Non-Exhaust Emissions from Conventional and Electric Vehicles: A Comparison of Monetary Impact Values. J. Clean. Prod. 2022, 331, 129965. [Google Scholar] [CrossRef]
- Fernandes, P.; Macedo, E.; Tomás, R.; Coelho, M.C. Hybrid Electric Vehicle Data-Driven Insights on Hot-Stabilized Exhaust Emissions and Driving Volatility. Int. J. Sustain. Transp. 2024, 18, 84–102. [Google Scholar] [CrossRef]
- Oliveri, L.M.; D’Urso, D.; Trapani, N.; Chiacchio, F. Electrifying Green Logistics: A Comparative Life Cycle Assessment of Electric and Internal Combustion Engine Vehicles. Energies 2023, 16, 7688. [Google Scholar] [CrossRef]
- Safarian, S. Environmental and Energy Impacts of Battery Electric and Conventional Vehicles: A Study in Sweden under Recycling Scenarios. Fuel Commun. 2023, 14, 100083. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, F.; Hao, H.; Liu, Z. Comparative Analysis of Life Cycle Greenhouse Gas Emission of Passenger Cars: A Case Study in China. Energy 2023, 265, 126282. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiang, Z.; Chen, X.; Liu, P.; Peng, T.; Shu, Z. Toward Environmental Sustainability: Data-Driven Analysis of Energy Use Patterns and Load Profiles for Urban Electric Vehicle Fleets. Energy 2023, 285, 129465. [Google Scholar] [CrossRef]
- Hasan, K.N.; Muttaqi, K.M.; Borboa, P.; Scira, J.; Zhang, Z.; Leishman, M. Distribution Network Voltage Analysis with Data-Driven Electric Vehicle Load Profiles. Sustain. Energy Grids Netw. 2023, 36, 101216. [Google Scholar] [CrossRef]
- Meintjes, T.; Castro, R.; Pires, A.J. Impact of Vehicle Charging on Portugal’s National Electricity Load Profile in 2030. Util. Policy 2021, 73, 101310. [Google Scholar] [CrossRef]
- Mathew, M.S.; Kolhe, M.L.; Kandukuri, S.T.; Omlin, C.W. Data Driven Approach for the Management of Wind and Solar Energy Integrated Electrical Distribution Network with High Penetration of Electric Vehicles. J. Clean. Prod. 2023, 421, 138467. [Google Scholar] [CrossRef]
- Zhao, Z.; Lee, C.K.M.; Ren, J. A Two-Level Charging Scheduling Method for Public Electric Vehicle Charging Stations Considering Heterogeneous Demand and Nonlinear Charging Profile. Appl. Energy 2024, 355, 122278. [Google Scholar] [CrossRef]
- Gschwendtner, C.; Knoeri, C.; Stephan, A. The Impact of Plug-in Behavior on the Spatial–Temporal Flexibility of Electric Vehicle Charging Load. Sustain. Cities Soc. 2023, 88, 104263. [Google Scholar] [CrossRef]
- Blasius, E.; Wang, Z. Effects of Charging Battery Electric Vehicles on Local Grid Regarding Standardized Load Profile in Administration Sector. Appl. Energy 2018, 224, 330–339. [Google Scholar] [CrossRef]
- Williams, B.; Bishop, D.; Hooper, G.; Chase, J.G.; Carlo, M. Driving Change: Electric Vehicle Charging Behavior and Peak Loading. Renew. Sustain. Energy Rev. 2024, 189, 113953. [Google Scholar] [CrossRef]
- Hu, Q.; Li, H.; Bu, S. The Prediction of Electric Vehicles Load Profiles Considering Stochastic Charging and Discharging Behavior and Their Impact Assessment on a Real UK Distribution Network. Energy Procedia 2019, 158, 6458–6465. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, Z.; Wang, Z.; Li, X.; Sun, F. An Urban Charging Load Forecasting Model Based on Trip Chain Model for Private Passenger Electric Vehicles Cased Study in Beijing. Energy 2024, 299, 130844. [Google Scholar] [CrossRef]
- Çelik, S.; Ok, Ş. Electric Vehicle Charging Stations: Model, Algorithm, Simulation, Location, and Capacity Planning. Heliyon 2024, 10, e29153. [Google Scholar] [CrossRef]
- Gschwendtner, C.; Knoeri, C.; Stephan, A. Mind the Goal: Trade-Offs between Flexibility Goals for Controlled Electric Vehicle Charging Strategies. iScience 2023, 26, 105937. [Google Scholar] [CrossRef]
- Powell, S.; Cezar, G.V.; Min, L.; Azevedo, I.M.L.; Rajagopal, R. Charging Infrastructure Access and Operation to Reduce the Grid Impacts of Deep Electric Vehicle Adoption. Nat. Energy 2022, 7, 932–945. [Google Scholar] [CrossRef]
- Farhadi, F.; Wang, S.; Palacin, R.; Blythe, P. Data-Driven Multi-Objective Optimization for Electric Vehicle Charging Infrastructure. iScience 2023, 26, 107737. [Google Scholar] [CrossRef]
- Nisha, K.S.; Gaonkar, D.N.; Jayalakshmi, N.S. Operation and Control of Multiple Electric Vehicle Load Profiles in Bipolar Microgrid with Photovoltaic and Battery Energy Systems. J. Energy Storage 2023, 57, 106261. [Google Scholar] [CrossRef]
- Sausen, J.P.; da Rosa Abaide, A. Residential Charging Scheduling of Electric Vehicles in Brazilian Context. IEEE Lat. Am. Trans. 2021, 19, 1624–1631. [Google Scholar] [CrossRef]
- Sausen, J.P.; Abaide, A.R.; Adeyanju, O.M.; Paixao, J.L. EV Demand Forecasting Model Based on Travel Survey: A Brazilian Case Study. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Conference—Latin America (ISGT Latin America), Gramado, Brazil, 15–18 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Zhang, J.; Yan, J.; Liu, Y.; Zhang, H.; Lv, G.; Key, S.; Electrical, A.; System, P.; Sources, E.; Energy, R.; et al. Daily Electric Vehicle Charging Load Profiles Considering Demographics of Vehicle Users. Appl. Energy 2020, 274, 115063. [Google Scholar] [CrossRef]
- Knak Neto, N.; Piotrowski, L. Methodology for Analysis of the Impact of Residential Charging of Electric Vehicles. IEEE Lat. Am. Trans. 2019, 17, 953–961. [Google Scholar] [CrossRef]
- Schäuble, J.; Kaschub, T.; Ensslen, A.; Jochem, P.; Fichtner, W. Generating Electric Vehicle Load Profiles from Empirical Data of Three EV Fleets in Southwest Germany. J. Clean. Prod. 2017, 150, 253–266. [Google Scholar] [CrossRef]
- Sørensen, Å.L.; Sartori, I.; Lindberg, K.B.; Andresen, I. A Method for Generating Complete EV Charging Datasets and Analysis of Residential Charging Behaviour in a Large Norwegian Case Study. Sustain. Energy Grids Netw. 2023, 36, 101195. [Google Scholar] [CrossRef]
- Mouhy-Ud-Din, M.A.; Azeem, F.; Memon, Z.; Arshad, J. Comparative Techno-Economic Assessment of Electric Vehicle Charging Preferences: A Quantitative Study for Sustainable EV Policy in Pakistan. Energy Sustain. Dev. 2024, 78, 101355. [Google Scholar] [CrossRef]
- Sausen, J.P.; Abaide, A.R.; Vasquez, J.C.; Guerrero, J.M. Battery-Conscious, Economic, and Prioritization-Based Electric Vehicle Residential Scheduling. Energies 2022, 15, 3714. [Google Scholar] [CrossRef]
- Ge, X.; Shi, L.; Fu, Y.; Muyeen, S.M.; Zhang, Z.; He, H. Data-Driven Spatial-Temporal Prediction of Electric Vehicle Load pro Fi Le Considering Charging Behavior. Electr. Power Syst. Res. 2020, 187, 106469. [Google Scholar] [CrossRef]
- Tariq, A.; Ali, S.; Kazmi, A.; Ali, G.; Hussain, A.; Bhatti, U. Multivariate Stochastic Modeling of Plugin Electric Vehicles Charging Profile and Grid Impact Analysis. Sustain. Energy Grids Netw. 2023, 36, 101155. [Google Scholar] [CrossRef]
- Lin, G.; Qi, B.; Ma, C.; Rostam, F. Intelligent Electric Vehicle Charging Optimization and Horse Herd-Inspired Power Generation for Enhanced Energy Management. Energy 2024, 291, 130395. [Google Scholar] [CrossRef]
- Dong, G.; Feng, Y.; Wang, Y.; Wei, J. Probabilistic Dischargeable Time Forecasting of Power Batteries via Statistical Characterization of Future Loading Profiles. J. Energy Storage 2023, 59, 106488. [Google Scholar] [CrossRef]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; Scientific Research Publishing: Wuhan, China, 2010; Volume 1, pp. 56–61. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array Programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Das, H.S.; Rahman, M.M.; Li, S.; Tan, C.W. Electric Vehicles Standards, Charging Infrastructure, and Impact on Grid Integration: A Technological Review. Renew. Sustain. Energy Rev. 2020, 120, 109618. [Google Scholar] [CrossRef]
- Kumar, L.; Ravi, N.A. Electric Vehicle Charging Method and Impact of Charging and Discharging on Distribution System: A Review. Int. J. Electr. Hybrid Veh. 2022, 14, 87. [Google Scholar] [CrossRef]
- Audi. Audi E-Tron S Sportback. Available online: https://www.audi.com/en.html (accessed on 10 March 2024).
- Vertgewall, C.M.; Trageser, M.; Kurth, M.; Ulbig, A. Modeling Probabilistic Driving and Charging Profiles of Commercial Electric Vehicles. Electr. Power Syst. Res. 2022, 212, 108538. [Google Scholar] [CrossRef]
- Hathaway, Z.; Polis, H.; Loomis, J.; Boroski, J.; Milano, A.; Ouyang, J. A Utility Roadmap for Expanding Customer Adoption of Electric Vehicles. World Electr. Veh. J. 2021, 12, 81. [Google Scholar] [CrossRef]
- Annamalai, M.C.; Amutha Prabha, N. A Comprehensive Review on Isolated and Non-Isolated Converter Configuration and Fast Charging Technology: For Battery and Plug in Hybrid Electric Vehicle. Heliyon 2023, 9, e18808. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).