Abstract
Energy models require accurate calibration to deliver reliable predictions. This study offers statistical guidance for a systematic treatment of uncertainty before and during model calibration. Statistical emulation and history matching are introduced. An energy model of a domestic property and a full year of observed data are used as a case study. Emulators, Bayesian surrogates of the energy model, are employed to provide statistical approximations of the energy model outputs and explore the input parameter space efficiently. The emulator’s predictions, alongside quantified uncertainties, are then used to rule out parameter configurations that cannot lead to a match with the observed data. The process is automated within an iterative procedure known as history matching (HM), in which simulated gas consumption and temperature data are simultaneously matched with observed values. The results show that only a small percentage of parameter configurations (0.3% when only gas consumption is matched, and 0.01% when both gas and temperature are matched) yielded outputs matching the observed data. This demonstrates HM’s effectiveness in pinpointing the precise region where model outputs align with observations. The proposed method is intended to offer analysts a robust solution to rapidly explore a model’s response across the entire input space, rule out regions where a match with observed data cannot be achieved, and account for uncertainty, enhancing the confidence in energy models and their viability as a decision support tool.
1. Introduction
Energy consumption in buildings represents a major source of primary energy use globally. This explains the recent attention given to optimal retrofit and investment decisions by policy makers, in efforts to comply with global decarbonization pledges. In this context, accurate modeling of building energy consumption has become a key tool to support decision making. In turn, this has recently driven an accelerated trend in model uncertainty research and performance gap analysis.
According to [1], a large proportion of the building modeling community lacks essential knowledge on what the most fundamental parameter inputs for buildings are and how these impact model predictions. This knowledge gap has major consequences, as retrofit strategies are mostly based on some form of building energy models and low-fidelity models produce techno-economic results that can be misleading. The concept of smart buildings has raised the expectation that buildings will respond to the wider energy system (e.g., power grid, EVs, district energy systems) [2]. This will require building models to be aggregated to generate district- and potentially city-level insights. Building-level inaccuracies can therefore propagate to district and city levels, making uncertainty treatment of models an invaluable tool to improve the robustness of model-based decisions against a wider spectrum of uncertain outcomes.
For a model used in decision support, the model’s prediction accuracy is of special interest to stakeholders. While it is not possible to know in advance the accuracy of a future prediction, it is instead possible—and in fact crucial—to ensure that the model is able to replicate past observations. This is usually achieved through model calibration. Calibration is classically performed by running the model multiple times (at different configurations of model parameter values), evaluating the discrepancy between model outputs and observed data each time, with the aim of identifying a combination of parameter values that yields sufficiently low discrepancy. In the context of building energy consumption, ASHRAE guidelines [3] are often followed to identify thresholds below which the discrepancy is considered acceptable [4,5].
Implementing the above approach requires performing a high number of simulations, in order to explore the model’s parameter space thoroughly. This number grows exponentially with increasing parameter counts, posing extensive computational challenges even in medium-low dimensions. These computational requirements have prompted the rise of an area of Bayesian statistics devoted to the creation of fast statistical models that can be used as surrogates of the original model (also known as a simulator). This area is known as emulation [6,7,8] and is part of the wider field of the uncertainty quantification of computer models.
An emulator approximates the simulator output at values of model parameters where the simulator has never been evaluated. Moreover, it quantifies the uncertainty of the approximation, laying the basis for an uncertainty analysis of the computer model [9]. The main advantages of emulators are their speed and low computational requirements: an emulator can be trained and validated on a personal device, allowing for a near instantaneous prediction of the model results at a very large number of inputs.
Emulation is developed under Bayesian principles, which provide a natural framework to handle uncertainties. In the context of model calibration, key sources of uncertainties that come into play include (i) the intrinsic ability of the model to simulate the target process (model discrepancy); (ii) the accuracy of the observations used to calibrate the model (observational error). The inability of a schedule-driven occupancy template to represent the stochastic behavior of occupants is an example of model discrepancy, while temperature sensor errors are an example of observational error. To deal coherently with these and other sources of uncertainty before and during model calibration, we discuss and advocate here for the use of an iterative procedure, known as history matching. History matching (HM) is used in conjunction with emulation to quickly evaluate the simulator’s response across the full region of model parameter configurations, and discard those input configurations that—in light of quantified uncertainties—cannot match the observed data. The procedure is performed iteratively, sequentially refocusing on smaller regions of parameter configurations that have not yet been ruled out.
Due to their inherent ability to handle multiple uncertainties, both emulation and HM have been employed to tackle complex problems in a variety of fields. Notable examples can be found in the sixth assessment report by the Intergovernmental Panel on Climate Change [10], whose future scenario projections were substantially based on the use of emulators [11,12]. Emulation in conjunction with history matching has also been employed to constraint uncertainties in the reconstruction of past climates [13], particularly in relation to ice losses and associated sea-level changes [14,15], and to coherently integrate different sources of uncertainty within complex problems in a variety of other scientific contexts. A non-exhaustive list of these includes disease spreading [16], cardiac functionality [17,18], gene–hormone interaction [19], galaxy formation [20], and hydrocarbon reservoirs [21].
Despite the widespread use of these tools across different fields, their uptake within the energy community remains limited, if at all present. This work is thus offered as a tutorial, which may help bridge the current gap. We illustrate the principles behind Bayesian emulation and HM, outline their advantages and disadvantages, and provide a practical illustration of their application to a case study. Here, eight model parameters of a single dwelling’s energy model are selected, each with an initial uncertainty range, and plausible values for them are identified through HM, by making simultaneous use of the dwelling’s energy and environmental records. An R package is referenced to allow analysts to implement the proposed methodology.
This article is organized as follows. Section 2 discusses key sources of uncertainty in computer-model-based inference and specifically in the context of building energy models, outlining some limitations of the current approaches. Section 3 outlines the proposed methodology and relevant tools. Section 4 gives details of the building energy model and field data used in our case study. Section 5 illustrates the results, also discussing approaches to scenarios that may be encountered in other case studies. Section 6 concludes the article with discussions and future works.
2. Uncertainty Sources in Building Energy Models
2.1. Accounting for Uncertainty during Model Calibration
The problem of calibration (identifying values of a model’s parameters so that model outputs match observed data) can be formulated mathematically as follows. The model or simulator is represented as a function f. An input to f is a vector containing a specific configuration of values of model parameters: the component of identifies the value of the kth model parameter. Given real-world observations z of the simulated process, we aim to identify the input(s) for which is “close enough” to the observed data z.
Proximity between simulations and observations z should be assessed in light of all sources of uncertainty that affect the system. While an exhaustive list of such sources is problem-dependent and challenging to specify in its entirety [6], two sources of uncertainty usually play a prominent role in energy system modeling and beyond:
- Model Discrepancy (MD). Due to modeling assumptions and numerical approximations, the model output will be different from the real-world value that would be observed in the target process under the same physical conditions that represents. This difference is referred to as model discrepancy.
- Observational Error (OE). This error is intrinsic to any measurement. Its magnitude depends on the precision of the measuring device.
Accounting for these two uncertainty sources is crucial to assess whether a model has been successfully calibrated against observed data, and to make sure that robust inference can be drawn from subsequent model predictions.
2.2. Model Discrepancy in Building Energy Systems
This section highlights sources of model discrepancy in building energy systems, with a particular focus on thermal properties of envelope, microclimate, and oversimplification of human behavior.
2.2.1. Building Thermal Properties
A major source of model discrepancy concerns fabric thermophysical properties, for instance fabric conditions (e.g., its non-homogeneity, moisture content, etc.), as well as surface properties (radiative or convective characteristics). Most notably, the hypothesis of uni-dimensional heat flow—which is fundamental to thermal resistance (U-value) calculations in ISO 6946:2007 [22], ISO 9869-1:2014 [23], CIBSE [24] and ASHRAE [3]—remains a major simplification. In solid bodies, heat travels in a diffused and three-dimensional manner, which energy modeling platforms are not able to replicate.
In addition, differences in thermal properties can exist in seemingly uniform building envelopes [25,26,27,28]. This is not represented in U-value calculations that assume surface thermal uniformity [26]. As such, disagreements between measured and calculated figures have been reported to be up to 393% [25]. Traditional solid masonry walls [29,30] and floors [31] have been found to perform better than model calculations suggest, while modern composite walls are reported to perform worse. In [32], CIBSE U-value calculation were found to overpredict performance by 30.3%, 15.5%, and 9.9% for brick walls, ceilings, and doors, respectively. A study of 57 properties found that, while variations between similar wall types (and even within the same dwelling’s walls) existed, 44% of walls performed better than CIBSE calculations, 42% were within acceptable bounds, and only 14% of sampled walls performed worse than calculations [33]. However, the measured and calculated floor U-values were found to be in good agreement.
In summary, difficulties in identifying the composition and thickness of building fabrics, their density and surface properties, and fabric non-homogeneity result in fabric value uncertainty. The cumbersome nature of performing an in situ fabric study means that analysts often base existing building models on inaccurate assumptions.
2.2.2. Weather and Occupant Activity
The topology around each building determines the wind speed and direction, solar irradiance, local temperature, local humidity, and ground albedo, which result in a micro-climate unique to each building. This unique micro-climate is rarely acknowledged in a building’s energy model, since the employed weather files are normally extracted from historical data and are in some cases collected from the open fields of airports miles away from the building, e.g., using methods such as Finkelstein–Schafer. This is a major source of energy simulation uncertainty for the following reasons: (i) building energy performance is affected by future rather than past weather; (ii) a single weather file can hardly represent all meteorological conditions; (iii) using nearby records leads to inadequate representation of urban heat island and sheltering effects [34].
Occupant behavior is another area of uncertainty, due to oversimplification. Nearly all building energy models represent the variations in occupant-related activities in a homogeneous and deterministic manner. In a review paper, stochastic space-based (or person-based) models were found to offer better capabilities when compared to deterministic space-based models [35]. The review highlighted the ability of stochastic agent-based occupant models to improve urban building energy models. In this regard, pervasive sensing and data collection continue to enable better understanding of occupant presence and movements, and have informed behavioral models of the occupant’s interaction with their surroundings [36]. These solutions continue to be deployed by the scientific community but have not yet found widespread adoption by building energy modeling practitioners.
2.3. Limitations of Current Calibration Approaches
The approximations and assumptions discussed in Section 2.2 do not undermine the validity of a model. However, awareness of their presence is key to quantify the discrepancies induced when comparing model outputs and real-world observations.
In the context of building energy models, ASHRAE guidelines [3] are often followed to assess whether a model has been successfully calibrated against observed data [4,5]. These guidelines make use of the two following discrepancy measures between a sequence of N simulated outputs , and a corresponding sequence of N measurements :
The model is considered calibrated if the relevant condition of the following two is met:
- (a)
- Hourly measurements: and .
- (b)
- Monthly measurements: and .
While the above criteria are easy to check, their use to assess model calibration presents some limitations. Firstly, acceptance thresholds are independent of (i) the level of accuracy to which measurements are available, (ii) the level of discrepancy between model and reality. In addition, both expressions compare bias and root mean square error to the average measurement. As such, they are meaningful for intrinsically positive quantities, such as energy consumption, but they are not so for other quantities for which model outputs and observations may also be available, such as temperature. In such a case, using different units leads to seemingly different results. If Kelvin degrees are used to ensure positivity, the above two criteria will be fulfilled in most circumstances, due to the presence of a large denominator in expressions (1) and (2).
In Section 3, we propose a statistical framework which overcomes these limitations. The framework makes it easy to account for recognized uncertainties when model and data are compared and it is applicable to any quantity of interest (and, in fact, to several quantities simultaneously). Furthermore, the use of emulators allows us to efficiently explore the model response for many millions of input choices, in a fraction of the time required for physics-based models to generate the corresponding outputs.
3. Methodology
3.1. Overview
This section discusses statistical procedures to quantify different sources of uncertainty and account for them before and during model calibration. The overall process we illustrate is referred to as history matching (HM). The name is commonly used in the oil industry to describe the attempt to “replicate history”, i.e., to produce model outputs that match historical data, in the context of hydrocarbon reservoirs; for an early discussion of the statistical principles underlying history matching in this context, see [21]. Since then, its statistical principles and methods have been successfully applied to a variety of disciplines [13,14,15,16,17,18,19,20]. However, to the best of the authors’ knowledge, there has been little to no application to energy systems.
The HM procedure sequentially rules out regions of the model’s parameter space (input space) where, in light of quantified uncertainties, model outputs cannot match observed data. Emulators and implausibility measures are the two key tools used to accomplish this task.
- Emulators allow predicting the model output for configurations of model parameters in which the model has never been run. The prediction is accompanied by a measure of its uncertainty. Given their speed, emulators can be used to thoroughly explore the model parameter space, even in high dimensions.
- Implausibility measures quantify the distance between model outputs and observations, in light of different sources of uncertainty.
The overall procedure is illustrated in the infographic in Figure 1. Results of the physics-based model (simulator) are initially used to create emulators of the model. Predictions from the emulators, alongside quantified uncertainties, enable the quick evaluation of implausibility measures: these assess the compatibility between observed and simulated data, for any choices of model parameter configurations. Finally, implausibility measures are used within history matching to rule out parameter configurations that are not compatible with the observed data. The combined procedure of model sampling, emulation, and implausibility assessment is iteratively repeated within the collection of parameter choices that have not been ruled out in the previous stages.
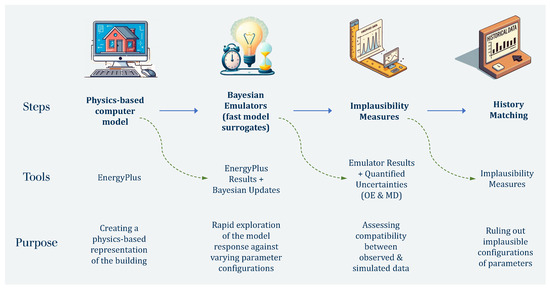
Figure 1.
Key steps of the methodology illustrated in this work. Given a computer model, the aim is to identify values of the model parameters that yield outputs compatible with observed data, while accounting for uncertainties. The process starts from the original computer model, whose results enable the construction of emulators (fast statistical surrogates of the model). Emulator predictions are used to compute implausibility measures, which quantify the distance between simulations and observations. Implausibility measures are employed within history matching to reach the overall goal.
The following four subsections expand upon each of the above steps. The concluding Section 3.6 reviews the robustness of the overall procedure in handling uncertainties.
3.2. Bayes Linear Emulators as Fast Model Surrogates
An emulator is a statistical, fast-to-run surrogate of the original model. It can be used to perform a thorough exploration of the model response across its entire input space, while keeping time and computational costs at a minimum.
In order to build an emulator, statistical assumptions need to be made about the behavior of the original model, or simulator, across its input space. These assumptions are updated given a small, carefully chosen, set of runs of the simulator (design runs) and are used to make a prediction of the simulator’s response at any new input. Each prediction is accompanied by a quantification of its accuracy, which lays the basis for the model uncertainty analysis. The emulator is checked through diagnostic comparison of the simulator prediction against the actual simulator response for a new set of model evaluations.
Different assumptions about the simulator’s behavior lead to different kinds of emulators. In this work we build emulators based on Bayes linear principles: that is, we only assume a prior mean and a prior covariance of the simulator, and subsequently adjust them to the simulated outputs on the design runs. Other types of emulators have also been developed [8] that make full distributional (Gaussian) assumptions on the simulator and update them using Bayes’ rule. Both approaches are valuable. The structure of Bayes linear emulators (BLEs) is arguably simpler than that of “full Bayes” emulators and is particularly suited to performing HM, as in this work. Full Bayes emulators may however be more suited to other cases, e.g., if a whole posterior distribution is needed to sample entire emulated trajectories.
For brevity purposes, we limit our treatment of emulators here to an overview of their structure and of the main choices that need to be made to train them. The reader is referred to Appendix A for additional details and for the mathematical meaning of those parameters whose value will be set within the case study of this work.
The output of the simulator at an input is modeled as the sum of two terms:
The first term is a regression component, where a linear combination of known functions is used to model the global behavior of f across the input space. The coefficients can be estimated through linear regression, starting from the known outputs of the simulator in the design runs. The second term, , instead captures the local residual fluctuations of f. The choice of a specific statistical model for the process u determines the form of the final emulator of f.
In a Bayes linear framework, is modeled as a stochastic process with zero mean and a specific covariance function. The mean and covariance are then adjusted to the known regression residuals via a Bayes linear approach—please refer to Appendix A for more details. At the end of the process, a mean prediction and an associated standard deviation are obtained for the unknown value at a new input . Software tools to automate emulator fitting are available, e.g., the hmer package in the R 4.1.0 (or any more recent version) software [37].
In this work, the squared exponential kernel (Equation (A4)) is used as prior covariance of the process . The correlation lengths in the covariance function represent a hyperparameter to set. Other choices to make concern the model parameters to account for in the covariance function (active parameters) and the prior variance in the regression residuals. We make all these choices by comparing the performance of different emulators on a validation set, i.e., on a set of runs not used during the emulators’ training.
Note that the heaviest computational step in training an emulator usually consists in running the simulator on the initial experimental design. After that, all computations involve relatively simple matrix algebra and the computation of the nonlinear covariance function, which allows the emulator to capture non-linearities.
3.3. Model Discrepancy and Observational Error
The concepts of model discrepancy (MD) and observational error (OE) are relevant to any uncertainty analysis linking simulations to real-world observations. This section formalizes the two concepts using a general framework. An example illustrating the meaning of the different quantities in the context of building energy models may be the following. : building energy consumption simulated under a set of model parameters ; y: actual building consumption; z: (imperfect) meter reading of the consumption.
Following [38], we assume that an appropriate input configuration exists that best represents the values of the system’s parameters. We link the corresponding simulator output to the real-world value y of the quantity being simulated, via the relationship
In Equation (4), the MD term accounts for the difference between the real and the simulated process. The value y of the real system is usually unobservable, but it can be estimated via a measurement z. Hence, we write
where the term accounts for the observational error in the measurement.
The additive formulation in Equations (4) and (5) is a simple but efficient way to model MD and OE, which also makes statistical inference tractable. The two errors are assumed to be independent of each other and information on them is sought in statistical form, (i.e., their variances), rather than quantified as single numbers.
Manufacturer guidelines are usually available to estimate the OE magnitude (e.g., up to of the measured value). Estimates of the MD magnitude may be more challenging to obtain. Assuming independence between the MD term and the simulated value is a simple choice, which may already allow the researcher to operate within a robust uncertainty framework in most applications. This assumption leads to modeling the variance of as a constant. In this work, we use a slightly more complex model for , by assuming it is proportional to the emulated value (more details in Section 5.3). More involved estimations of the MD term are also possible, see [38] for further details, particularly for the further distinction between internal and external MD.
In all cases, however, the modeler’s knowledge of the assumptions/approximations used within the simulator, alongside literature research, usually provide guidance on the effects that these have on the simulated process and can therefore lead to an approximate estimate of the MD magnitude.
3.4. Implausibility Measures
Implausibility measures (IMs) are used to quantify the agreement between simulation results and observed data, in light of quantified sources of uncertainties. IMs represent the key tool used within HM to rule out regions of the model parameter space that cannot lead to a match with observed data. Here, we discuss the meaning and analytical expression of IMs. Appendix B provides additional mathematical insights into the derivation of the expression and the rationale behind the choice of IM thresholds.
In a general history matching framework, several measurements are available to history match the model. We thus consider the case where the model simulates the dynamics of m quantities , for which corresponding observations are available. At an input , different sources of uncertainty should be considered when comparing the simulated value to the measured value . MD and OE affect the precision of both terms and should therefore be accounted for. Moreover, the simulated value is rarely readily available. The availability of an emulator allows obtaining an instantaneous approximation that can be used in place of the unknown . This, however, introduces an additional source of uncertainty, quantified by the emulator variance .
The following expression may then be used to relate the difference between the emulated value and the observed value to the three above sources of uncertainty:
is called the implausibility measure (IM) of input , with respect to quantity j. Values of greater than a predetermined threshold T suggest that, all uncertainties considered, the input is implausible to lead to a match with observation . On the grounds of Pukelsheim’s rule [39], the threshold is often chosen to be (see Appendix B).
After defining , an overall measure of implausibility at each input is needed, with respect to all outputs simultaneously. In this work, we define this as follows:
A high value of implies that at least one is high and therefore that a match between and is implausible for that j. Vice versa, a low value of implies that the quantified uncertainties (MD, OE, emulation) make it possible for the input to yield outputs matching all observations simultaneously: in this case, we call non-implausible.
3.5. History Matching: The Algorithm
History matching (HM) proceeds in waves. At each wave, new emulators are built and the associated implausibility measure is used to rule out currently implausible inputs. The procedure repeats until a final region is identified where the model outputs and observations match. The steps of the procedure are expanded upon below and summarized thereafter in a schematic algorithm.
In the first wave, some or all of the model outputs for which observations are available are emulated. The IM (7) is computed across the space, and all inputs for which exceeds a given threshold T are discarded as implausible. The remaining region, comprising the currently “non-implausible” inputs, is referred to as the not-ruled-out-yet (NROY) region.
The process is repeated in consecutive waves. Crucially, at any new wave, additional simulations are run within the current NROY region. These allow new emulators to be trained and validated on the region, so that an additional fraction of the region can be discarded as implausible. Emulator validation takes place by comparing the emulator predictions against a small subset of the new runs that have been held out during emulator training. The overall procedure terminates whenever one of the following conditions is met: (i) the new NROY region shows no significant change from the previous one, or (ii) all inputs have been ruled out as implausible (empty NROY region), or (iii) limited time/computational budget make additional waves too costly. The Algorithm 1 below summarizes the steps.
| Algorithm 1. History Matching Algorithm |
Choose a positive threshold T. Define a sequence of NROY regions as follows:
|
The flowchart in Figure 2 illustrates the overall methodology. In R, the hmer package [37] can be used to automate the whole procedure. The package guides the researcher into multiple waves, by automatically suggesting a new design at each wave.
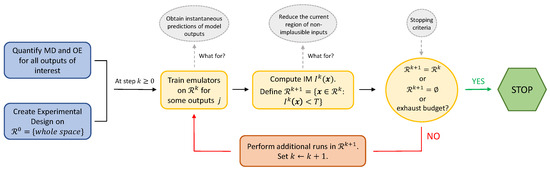
Figure 2.
Flow chart illustrating the history matching (HM) algorithm. The initial steps (blue) consist in quantifying the main sources of uncertainty and designing a first set of runs over the whole space. The central part of the diagram (yellow) describes the steps of a typical HM wave, which aim to reduce the volume of the region comprising currently non-implausible inputs. Waves are repeated, until one of the stopping criteria is met.
3.6. Comments on the Procedure and Its Strengths
We comment here on some of the choices needed to perform HM and on the overall strengths of the procedure, particularly in handling uncertainties. A list of these and of possible shortcomings of HM compared to classical model-based approaches can be found in Table 1.

Table 1.
Summary of the main advantages and disadvantages of HM over entirely model-based approaches to calibration.
The choice of the threshold T reflects how large an implausibility we are prepared to accept before ruling out an input as implausible. In light of Pukelsheim’s rule [39], is a common choice (see Appendix B). However, a larger threshold may be chosen if several quantities are being history-matched simultaneously. Indeed, mainly due to emulation error, for each output j, there is a small probability that , even for a “good” input . This probability increases if we consider the event that at least one j leads to , which is indeed the event . A larger threshold T keeps this probability of error low.
As highlighted by point (2a) of the algorithm, at each wave, only some of the model outputs are used to compute . This is a key feature of HM. Especially in early waves, some of the outputs may be difficult to emulate over large parts of the space, typically because the model’s behavior varies significantly across different input regions. As the search of non-implausible inputs is narrowed down to much smaller regions, outputs that were difficult to emulate may behave more uniformly within the region of interest. They can therefore be emulated precisely and included in the definition of , to rule out as implausible further regions of the input space.
Particularly in early waves, not ruling out an input (i.e., ) does not suggest that the input will lead to a match. Indeed, the implausibility of may be low as a consequence of large emulator uncertainty (term in Equation (6)), rather than because of actual proximity between the emulated prediction and the observation. However, emulator uncertainty is typically reduced between waves, because the new emulators are trained on smaller regions and on more design points. Reducing emulator uncertainty leads to larger implausibilities and, therefore, to more inputs being discarded as implausible. This is why HM proceeds in sequential waves.
We note an additional property of the IMs defined in (6). Since they only involve differences (numerator) and measures of variability (denominator), they can be computed for any quantity for which measurements are available, even if these are measured on non-positive scales. This marks a crucial difference with respect to Formulas (1) and (2), and allows also robustly performing HM on physical quantities such as temperature.
Moreover, if additional sources of uncertainty are recognized and quantified, these can be easily included in the denominator of , expression (6). We note additionally that the definition of the overall IM in Equation (7) can be easily customized. For example, may be defined as the second- or third-highest value of all , to avoid classifying as implausible an input that matches all but one or two observations: a similar approach is followed in the initial HM waves in [20].
We conclude this section with a consideration. By designing model runs only where needed, HM allows the researcher to focus sequentially on the region of interest, while keeping the overall number of runs low. This is crucial in medium and high dimensions. In these cases, the region where a match is possible may only represent a tiny fraction of the space originally explored. An approach where compatibility with observations is checked on a fixed (even large) number on runs across the original space, would almost surely miss the region. The refocusing HM procedure instead allows identifying the region, even in high dimensions.
The event where, at some wave, all inputs have been discarded as implausible is possible and in fact very informative. Causes for a mismatch between model and data may be multiple: (i) original parameter ranges are incorrect, (ii) there is a problem with the data, (iii) uncertainties are higher than estimated, (iv) the model dynamics have a flaw. It is of course the researcher’s task to step back and analyze what caused the mismatch, intervening in the model or in the assessment of uncertainties if necessary.
4. Case Study
This section describes the case study building used to illustrate the methodology in Section 3, and its computer model. Longitudinal energy consumption and temperature data were collected to history-match the model.
4.1. The Building and Its Energy Usage
The building is a detached two-story masonry construction, built in 1994. Two occupants are the only residents of the dwelling and were asked to archive their gas cooker and shower usage each day across an annual cycle. Given a very predictable pattern of occupancy (both occupants had 8 a.m.–5 p.m. working commitments), it was possible to limit the stochastic nature of occupant activity as far as practically manageable and to use deterministic schedules to represent occupant interventions with the building and its energy system. The building (with a gross area of m2 and m2 of unheated space) is located in a UK built-up urban area and is only partly shaded on its west elevation by an adjacent property (shading represented in the model).
Across the monitoring year (2016), the property had observed annual gas (15,381 kWh) and electricity (2991 kWh) consumptions that respectively correspond to high and medium UK domestic consumption values. The occupants utilized shower facilities at a measured flow rate of L/min and recorded on average eight 20 min showers per week corresponding to an average of 50 L/person/day (occupants used cold water over wash basin and dishwasher supplied with cold feed only). These recorded values are below UK average domestic hot water usage (reported as 142 L/person/day [40] and 122 L/person/day [41]), but primarily reflected the occupants’ heavy use of gym washing facilities. Gas cookers (containing 3 kW and 5 kW hubs) were used on average 4 times a week for 1 hour per cooking session.
4.2. The Model: Co-Dependency of Energy and Temperature Predictions
A model for energy consumption in the building was created using EnergyPlus (E+) 9.3.0 software. The basic principles of the software are described below, while greater details of E+ operating principles are documented here [42].
E+ is a collection of dynamic modules simulating different environmental, climatic, and operational conditions that define both the flow and the stored quantity of energy within building internal zones. The core of the program is a heat-balance equation (equation (2.4) in [42]) that is solved for all zones in the model. Once a simulation is launched, the software deploys all relevant modules, to perform (i) a simultaneous calculation of radiative and convective heat and mass transfer processes; (ii) adsorption and desorption of moisture in building elements; and (iii) iterative interactions of plant, building fabric, and zone air.
The interactions between E+ modules (with multiple equations solved simultaneously and/or iteratively) therefore makes it difficult to pin down a single set of expressions where most model prediction uncertainties lie. It is reasonable, however, to regard zone air temperature as the interconnection where conductive, radiative, and convective heat balance and mass transfers are realized. This underpins our model validation approach, in which both energy and temperature data are examined.
4.3. Data Collection
A proprietary set of environmental and energy sensors were deployed to record electricity consumption and zone temperatures (Figure 3). Temperature was compiled in two rooms: the south-facing master bedroom and the north-facing kitchen. To reduce measurement uncertainty, each of the two zones was equipped with two separate air temperature sensors, whose average was considered. The sensors were positioned at 1.3 m above floor level and set to log data at 30 s intervals.

Figure 3.
(Left panel): power monitor used to characterize household appliances. (Right panel): AC sensor, monitoring transmitters, and temperature sensors deployed in the case study building.
Gas consumption data were manually recorded on a monthly basis using a mains gas meter. Electricity consumption was logged at 10 s intervals using two mains-powered clip-on current sensors on the incoming live cable. The average of the two (practically identical) readings formed the measured power usage. These data streams and the associated equipment used are summarized in Table 2.

Table 2.
Data collection equipment type and accuracy, as well as deployment details and purpose.
In order to parameterize the energy model more accurately, a plugin power monitor was also used to characterize instantaneous and time-averaged consumption of the main electrical devices (TV, washing machine, ICT).
4.4. Model Inputs, Associated Ranges, and Outputs
By consulting the manufacturer’s specification and the house builder’s literature, a set of eight uncertain parameters for the model were compiled. Lower and upper bands for these were derived from the scientific literature and used to dictate the ranges explored in the design runs (Table 3).

Table 3.
The eight model parameters history-matched in this work, and their explored ranges in the design runs used to train the emulators. The V8 parameter represents the fraction of consumed gas employed for cooking.
As far as the opaque fabric of a building is concerned, variations in internal and external air velocities are less pronounced in ground floors, but more significant for walls and roofs. Therefore, smaller floor uncertainty margins are reported in the literature. Estimation of building infiltration rates would instead require convoluted air permeability tests. Table 4.16 of CIBSE guide A [24] outlines a range of 0.25 to 0.95 air change per hour (ACH) for various 2-story buildings below 500 m2. Therefore, this was the range we explored in our simulations. Domestic hot water (DHW) consumption followed a tailored schedule in the model, running only for part of the day. The range reported in Table 3 refers to the full-day equivalent DHW consumption.
With respect to glazed fabric, the manufacturer’s literature for glazing (installed in 2009) stated respective G- and U-values of 0.69 and 1.79 W/m2K. Error bands of and for G- and U-values respectively altered the simulated gas consumption by only kWh (). Given the negligible nature of this change, the fixed values provided by the manufacturer for the G- and U-values were used in the simulations. Finally, local weather files compiled at a weather station approximately 3 miles away from the site were used to support the model development.
We explore the model response at different values of the eight parameters in Table 3. For any given parameter configuration, the model simulated monthly energy consumption (gas and electricity) in the building and hourly temperature in two rooms (master bedroom and kitchen). We employed actual gas consumption and temperature records to history-match the eight parameters.
5. Results
This section illustrates the results of applying the statistical principles and methods in Section 3 to the example study of Section 4. We initially history-match the model parameters in Table 3 to the energy consumption in the building: for the sake of illustration, we just use gas consumption. Later, we add the constraints from temperature, thus identifying a region of parameter configurations matching both energy and environmental constraints at the same time.
5.1. Running the Simulator
5.1.1. Experimental Design
As described in Section 3.2, the first step to build an emulator is to create the experimental design, i.e., the set of inputs at which the simulator is run. We accomplished this task via Latin hypercube sampling, easily performed in R via the “lhs” package.
A rule of thumb [45] suggests using a number of design runs equal to at least 10 times the number of dimensions of the explored space: in our case, this translated into 80 or more runs. Our simulator was, however, moderately fast to evaluate. This allowed us to create a design of runs and perform the corresponding simulations in E+ in about 16 h. We stress, nonetheless, that a much smaller design is generally sufficient to perform emulation and HM successfully. We discuss this in more detail in Section 5.6.
5.1.2. Simulated Gas Consumption
Figure 4 shows simulated values of monthly gas consumption in the design runs, alongside the observed consumption for each month. A difference between summer and non-summer months can be noticed: in June, July, and August, all model runs considerably underestimated the observed consumption. This, in principle, does not rule out the possibility that other inputs within the explored space (an eight-dimensional hypercube with side ranges as in Table 3) may lead to a match. In our case, however, particularly in June and July, the distance between simulations and observation was too large when compared to the variability shown by the simulations, and this cannot lead to a match under the levels of MD and OE we consider later. A simple linear regression model of the output also confirms this.
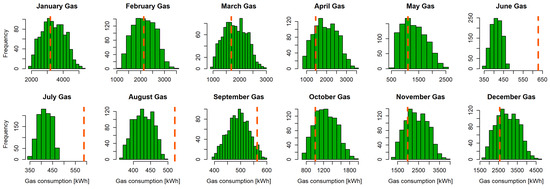
Figure 4.
Distribution of simulated monthly gas consumption for the experimental design used in this study ( inputs). The dashed vertical line in a plot denotes the observed consumption for that month.
As an illustration of the proposed methodology, in the following, we look for inputs that match all nine non-summer monthly gas consumptions simultaneously, excluding the three summer conditions from the match. It is important to note that, in a real case study, the model’s underestimation of summer consumptions should be identified and acted upon, prior to calibration/HM. While the most likely reason for the deviation was the inability of deterministic schedules to capture stochastic aspects of energy governance in the household (i.e., additional use of hot water/cooking in these months), any intervention in the model to reflect historical occupant behavior for which we had little certainty would have been speculative. However, greater insight into variations in seasonal energy use would have allowed one or more parameters to be added as additional variables to be history-matched.
5.2. Emulation of Monthly Gas Consumption
For each of the nine non-summer months, the design runs provided a dataset of pairs , where represents one configuration of the 8 input parameters and the associated simulated gas consumption. This dataset was used to build an emulator of that month’s gas consumption, after linearly rescaling each of the eight parameters into the range .
Several choices (of covariates, correlation lengths, prior variances) have to be made when building an emulator, see Section 3.2. To validate these choices, we split the dataset as follows:
- Training set (700 runs): used to train the emulators.
- Validation set (150 runs): used to decide on the values of the emulator hyperparameters, by comparing the emulator’s performance on this set to the known simulator’s outputs.
- Test set (150 runs): used to test the previously built emulators on a completely new set of runs not used for training and validation.
We note again that such large training and validation/test sets are used here for illustration purposes, but are not needed in general, see the comments in Section 5.6.
As discussed in Section 3.2, the prediction of the simulated consumption at an input is computed as the sum of (i) a linear regression part, (ii) a prediction of the residuals.
5.2.1. Linear Regression
The only choice to be made in building a regression model concerns the predictors to use. For all months of interest, a preliminary exploration revealed that the response y (gas consumption) was very well explained as a quadratic function of the eight input parameters, denoted in Table 3. Thus, we proceeded as follows.
Let be the set of all mutually orthogonal linear, quadratic, and interaction terms of (for 8 parameters, there is a total 44 linear, quadratic, and interaction terms. In R, these are be obtained via the command poly(X, deg = 2), where X is the matrix whose rows are the training inputs). For a given integer k, we consider the linear model with highest adjusted coefficient of determination (adj. ) among all models with exactly k of the predictors in . In our case, the “best” 10 predictors yield models with notably high adj. (about ) across all months. Hence, to keep the approach uniform, for each month we consider the linear model with the best 10 predictors for that month, summarized in Table 4. However, a different number of predictors for each output may be considered in other case studies.

Table 4.
Properties of the gas consumption emulators. For each month, from left to right: covariates used to build the linear regression model; adjusted of the linear model; variance of the regression residuals; active parameters used in the covariance function; value of the correlation lengths (same for all active parameters). In the predictor’s column, the ∗ symbol denotes the combination of all linear and interaction terms: = {}.
In general, such a high should raise concerns about overfitting. In our case, this concern can be ruled out by observing that only 10 predictors were used to explain the variability of 700 observations. The high coefficient of determination mirrors the intrinsically near-quadratic model dynamics.
5.2.2. Emulators of the Residuals
To build an emulator of the regression residuals of each month’s consumption, choices about the following quantities had to be made: active parameters , correlation lengths , prior emulator variance , and noise variance , see Equation (A4) in Appendix A and comments thereafter. We proceed as follows:
- Active parameters : To identify these, we look for the most significant second- and third-order terms in a linear model of the regression residuals. Parameters appearing by themselves with a high t-value () are included as active. The inclusion of parameters appearing alone with a lower t-value, or in interaction with other parameters, is instead considered on a case by case basis, according to the emulator performance on the validation set—see Section 5.2.3.
- Correlation lengths : In a given month, the same correlation length d is used for all active parameters. The value of d for each month is chosen by assessing the emulator’s performance on the validation set and is reported in Table 4. To attain a similar level of correlation across the space, higher correlation lengths are used when a higher number of active parameters is present.
- Prior variances and : Let denote the variance of the regression residuals being fitted. We then set and .
Table 4 provides details of all choices made to build each of the nine emulators, including choices concerning the regression line. We discuss validation of the emulators in the next section.
5.2.3. Emulator Validation and Performance
The active parameters and correlation lengths d in Table 4 were chosen based on the emulator’s performance on the validation set. The latter consists of 150 pairs not used during the emulator’s training, where each is the simulated output at input . At each such , the emulator provides a prediction of and a standard deviation quantifying the uncertainty of the prediction.
We then consider the number of standard deviations that separate the emulator prediction from the true simulated output:
and use to assess the emulator’s performance at . As we make no distributional assumption about the emulator, we can once again appeal to Pukelsheim’s rule [39] to constrain expected values of : for a reliable emulator, at least of the should lie between −3 and 3.
We validate this by considering, for each of the nine months, the plot of versus the predictions , and check that the points in the plot are (randomly) scattered around the line , and with about of the less than 3. We assess these properties visually for different choices of active parameters and correlation lengths and choose the ones that return plots with the desired properties. We tend to be slightly conservative in this phase, by choosing correlation lengths which generally yield more than of . This is to prevent making choices tailored to the specific points used for validation.
Once the parameters and d are chosen, we compute the standardized errors in Equation (8) on the 150 elements of the test set, and confirm that no anomalies show up on a set of points not used during training or validation.
5.3. Observational Error and Model Discrepancy
In order to perform HM, with the aim of identifying parameter configurations that yield a match between predicted and observed consumptions, we need to quantify the OE and MD that are used to define the IMs in Section 3.4. We proceed as follows.
- The OE is set to of the observed value z, in agreement with the manufacturer’s largest accuracy band.
- For illustrative purposes, we set MD to either or of the emulated consumption and compare results in the two cases.
The last point is implemented by setting the term in Equation (6) to be the variance of a uniform random variable with range equal to ().
Note that, as discussed at the end of Section 3.3, accurate estimation of MD requires careful statistical analyses and possibly additional model runs. However, an order of magnitude between and 20% of the simulated values is likely to represent a good estimate in most energy applications. If there are reasons to believe that MD is significantly higher, the possibility of revisiting the model should be considered, by possibly including in the model additional key factors affecting the simulated dynamics.
5.4. History Matching
History matching can now be performed. Recall that the procedure sequentially removes inputs with implausibility larger than a threshold T: here, represents the implausibility of month j. In the following, we choose . As discussed in Section 3.6, the choice of such a threshold ensures that the probability of incorrectly rejecting an input as implausible is kept small, whenever several observations are being matched simultaneously (nine in our case).
With the above choices, a single wave of HM rules out of the parameter space as implausible when MD is used, leaving only as non-implausible. With MD, one wave of HM instead rules out of the original space, leaving of it as non-implausible. These percentages were computed on a sample of random inputs, generated as a Sobol sequence [46] in the eight-dimensional cube with side ranges given in Table 3. The absolute error on the estimates using such a large sample (approximately equal to ) thus leads to a relative error which is order of and in the two cases, respectively. This makes both estimates very accurate.
In this case, we do not need to proceed to further waves. For all months, the emulator uncertainty, reported in Table 5, is 1–2 orders of magnitude lower than the combined one from MD and OE. Additional waves therefore leave the IM essentially unchanged. We comment further on this in Section 6.

Table 5.
For each month: variance of the regression residuals to which the emulator is fitted (first row) and empirical confidence interval of the emulator variance (second row), computed on the 150 test points. Unit: (kWh)2. A notable reduction between the original regression residuals and the emulated residuals can be observed.
5.4.1. Visualization of the Non-Implausible Region
The non-implausible region lives in an eight-dimensional space, one dimension per input parameter. To identify parameters that play a role in constraining the region, we inspect several two-dimensional scatter plots of the non-implausible inputs: specifically, for each pair of the eight parameters, we look at how the non-implausible inputs scatter along the selected two dimensions. For brevity, we do not report all scatter plots here. The visual inspection reveals that the parameters infiltration rate () and percentage of gas used for cooking () are particularly significant. To a lower extent, heating setpoint () also plays a role in classifying inputs as non-implausible. We thus inspect in more detail the effect of these three parameters and their interdependence.
There are three pairs of the above parameters (–, –, –). Each column in Figure 5 contains the minimum-implausibility plot (MIP, top row) and the optical-depth plot (ODP, bottom row) for one of the three pairs. The MIP shows the minimum value assumed by the implausibility measure , when the two concerned parameters are fixed to some value and the remaining six are free to vary. Thus, values greater than in a MIP identify pairs of values of the two parameters in question that always lead to an implausible input, irrespective of the value taken by the remaining six parameters. On the contrary, values lower than in a MIP reveal the presence of non-implausible inputs (i.e., inputs that can lead to a match with observed data). The percentage of these inputs, across the remaining six dimensions, is shown in the ODP. Information provided by each pair of MIP and associated ODP is thus complementary.
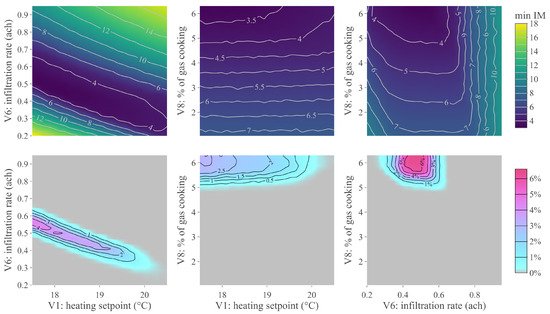
Figure 5.
Two-dimensional views of the non-implausible region, when model discrepancy is used. Each plot concerns one pair of the three model parameters , , (same pair along a given column). Minimum implausibility plots (top panels): the color at the point of coordinates shows the minimum value taken by the IM when the two concerned parameters take the value and the remaining six parameters are free to vary. Optical depth plots (bottom panels): the color at the point shows the percentage likelihood that a match can be found with observed data, when the two concerned parameters take value and the remaining six are free to vary.
The panels in the middle and right columns of Figure 5 reveal that only values of higher than are able to yield a match with the observed consumptions. Moreover, such values should be paired with values of approximately between 0.25 and 0.65 ACH (rightmost panels). Note that the two variables seem to be relatively independent. A stronger dependence can instead be seen between non-implausible values of and (leftmost panels): for example, higher non-implausible values of can only be paired with low values of .
The left subplots in Figure 5 also suggest that non-implausible values of may also be found to the left of the range originally explored. A similar consideration is valid for values higher than (the maximum value explored in the design runs). Similar findings are not uncommon, particularly during the first wave of HM. In such a case, it is advisable to step back and expand the ranges in question, running additional simulations in the new region before proceeding with HM. In this example study, however, in accordance with the methodological and illustrative aim of the work, we progress our illustration and discussion, focusing on the ranges specified by Table 3.
5.4.2. Sensitivity to Model Discrepancy Magnitude
Figure 6 shows ODPs for the same three parameters considered in Figure 5, but in the case where MD is set to . Roughly similar patterns emerge, but spread over larger regions: due to a lower confidence in the model, we rule out fewer inputs as implausible. The percentage of non-implausible inputs has risen to , from only in the MD case.
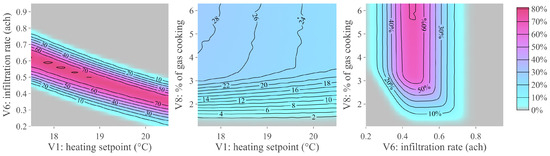
Figure 6.
Optical depth plots, in the case of MD—same three variables as Figure 5.
This comparison highlights the potential sensitivity of HM results to the choice of MD. Note that the precision of the emulator(s) also plays a role. In our case, as Table 5 shows, we have remarkably precise emulators. This implies that essentially all the uncertainty accounted for in comparing emulator predictions and observations comes from MD and, to a lesser extent, OE. Doubling the MD will thus make inputs significantly more likely to be deemed non-implausible.
5.4.3. Role of Different Constraints and Correlation among Outputs
Emulation allows us to explore a wide range of questions, for which it would otherwise be impossible to draw sound inference. We briefly discuss one such example here: the compatibility between the pair of observed consumptions in any two different months, and the correlation of model outputs across months. Note, in fact, that a strong correlation between two model outputs restricts the pairs of observed consumptions that can lead to a match. This relationship is explored in Figure 7: the figure agglomerates different pieces of information, which we explain and comment on below.
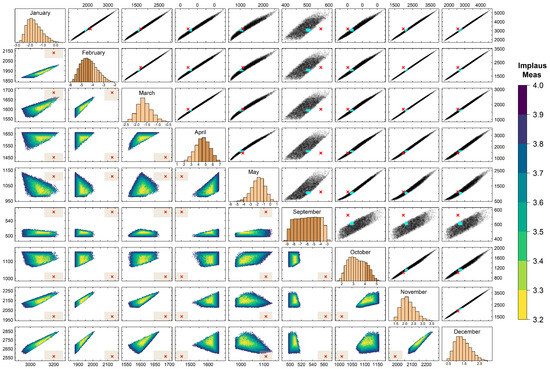
Figure 7.
Information on model outputs, observations, and each month’s contribution to reducing the non-implausible region. Upper-diagonal panels: scatter plot of emulated gas consumption for each pair of months (randomly selected 10,000 inputs). The red cross locates the observation to be matched, the turquoise stain locates the non-implausible outputs. Lower-diagonal panels: zoom of the non-implausible region, colored by implausibility measure (IM). Shaded rectangle around the cross identifies observational error. Diagonal panels: distribution of each month’s IM, on the space deemed non-implausible when only constraints from the remaining months are considered. The darker color denotes values outside the interval , i.e., identifies inputs that transition from being non-implausible to being implausible when that month’s constraint is added.
Each of the upper-diagonal panels of Figure 7 shows a scatter plot of emulated gas consumption for a pair of months, on a random sample of 10,000 inputs. The observed consumption to be matched is identified by a red cross. Whilst the latter is often outside the region of outputs, the presence of MD (10%) and OE (5%) still allows identifying a region of non-implausible outputs: this is highlighted in turquoise in each upper-diagonal plot. Note: this is a subregion of the output space, not of the input space as in Figure 5 and Figure 6. The lower-diagonal panels display a zoom of this region, with points colored according to the value of the overall IM (7). In these panels, each rectangle around the observed consumption identifies the OE.
The histograms along the diagonal of Figure 7 instead show the distribution of the IM of a given month (expression (6)), on the points that would be classified as non-implausible if all months, except that one, were included in the HM procedure. The IM is reported with its original sign: positive (negative) values denote an emulated consumption higher (lower) than the observed one. Values outside the range are highlighted by a darker color. They correspond to gas consumptions (and associated parameter configurations of the model) that match the observed consumption of all months, except the specific month considered.
Months such as January, March, November, and December, where all values are between and 4, did not contribute to reducing the space once the other eight months’ constraints were included. On the other hand, a month such as September ruled out around of the space that would be considered non-implausible without the September constraint itself.
As the upper-diagonal panels reveal, some of the simulated monthly consumptions were highly correlated, e.g., January’s and February’s. In similar cases, matching one month’s observed consumption will impose limits on which consumptions of the other month can be simultaneously matched.
In the case of January and February, the cross aligns well with the line of simulated consumptions, hence both observations can be easily matched simultaneously. However, despite their high correlation, the two months do not play an interchangeable role. The January histogram reveals that the January constraint is redundant if the February constraint is accounted for. On the other side, instead, including the February constraint ruled out more than of the space that was considered non-implausible without it (in particular, when January was also accounted for). A similar reasoning holds true for other pairs of strongly correlated outputs, e.g., Feb-Mar, Feb-Nov, and Oct-Nov to a lesser extent.
5.5. Adding Temperature Constraints
History matching can be performed with any model output for which observations are available, a feature that marks a difference with measures such as MBE and CV(RMSE), as discussed in Section 2.3. For illustrative purposes, in addition to gas consumption, in this section, we history-match temperature records in the kitchen and master bedroom, for which hourly time series are available both as observations and as model outputs.
Accounting for uncertainty when comparing simulations and observations is more challenging for time series than it is for scalar quantities. The correlation across time should be considered, for which dimension-reduction techniques or multidimensional IMs may be employed. It is beyond the scope of this work to go into these details, some of which are active areas of research. However, scalar quantities can be extracted from a time series and history-matched through the same methodology discussed in Section 3. We provide an illustration below.
In order to include summer constraints, we consider the following quantity: the average temperature difference in July between day (8 a.m.–11 p.m.) and night (00 a.m.–7 a.m.). For each of the two rooms, we compute the above quantity for the 1000 design runs, build an emulator of it as a function of the eight input parameters, and history-match the parameters. We consider the same levels of MD () and OE () as in Section 5.4.1.
Accounting separately for each of the two temperature constraints classifies (kitchen) and (master) of the space as non-implausible, respectively (we use the threshold here, since only one condition is considered in each of the two cases). A total of of the space is instead classified as non-implausible with respect to both constraints at the same time. Unsurprisingly, a strong dependence between the constraints coming from the two rooms emerges ( is indeed much greater than ).
Accounting simultaneously for both energy (gas) and environmental (temperature) constraints classifies only of the original eight-dimensional cube as non-implausible. This is about four-times less than would be expected if the two constraints were independent. The interplay between energy and environmental constraints is highlighted in Figure 8, in the case of the three parameters , , and . For each of them, the plot shows the distribution of non-implausible values for that parameter, when the constraints from either gas, or temperature, or both are considered. As an illustration, we comment on the left plot of Figure 8, concerning the heating setpoint (.
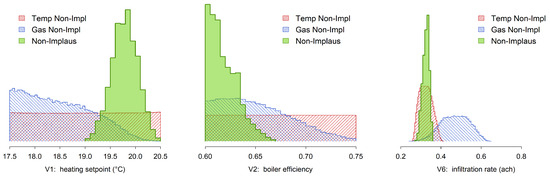
Figure 8.
Marginal distribution of three input variables on non-implausible points. The shaded histograms mirror non-implausibility with respect to gas or temperature constraints only, the filled histogram with respect to both.
On the one hand, if we only account for the July temperature constraint, the distribution of values across the non-implausible inputs is uniform (red shade): this is expected, as heating is switched off in summer and does not, therefore, affect room temperature. On the other hand, imposing only the gas constraint (blue shade) yields a skewed distribution favoring lower values of . However, when both gas and temperature constraints are considered, only higher values turn out to be non-implausible (solid green). The explanation for this is as follows: third parameters are present whose values are in fact constrained by temperature, and which are correlated with . Forcing these parameters to have temperature-compatible values rules out low values of .
A related phenomenon can be observed for the boiler efficiency parameter, the middle plot of Figure 8. Finally, the infiltration rate, which plays an important role in limiting temperature variations in the building, is indeed mainly driven by the temperature constraint (red shade, rightmost plot in Figure 8). The additional imposition of the gas constraint only slightly reduces its non-implausible range (solid green).
5.6. Results with a Smaller Experimental Design
As remarked previously, the size of the experimental design used in this work () is much larger than typically needed. In the presence of eight parameters, it is advisable to start with 80–100 design runs, but a smaller design can also be used if the simulator is particularly slow to run.
Indeed, the main advantage of a large design is that precise emulators are obtained from the first HM wave, hence a large portion of the parameter space may be ruled out as implausible in early stages. However, even in the presence of a small design, the same results will generally be achieved at the expense of one or two more waves.
In additional research that we do not detail here for brevity, we randomly subselected 100 of the design runs and used these to train (80 runs) and validate (20 runs) the new emulators. The quadratic simulator dynamics were however easily captured by the smaller design and, once again after just one wave of HM, the results were practically identical to the ones shown in Section 5.
6. Conclusions and Extensions of the Work
This work presented a statistically robust way of accounting for uncertainty in pre-calibration and calibration of building energy models. The methodology was illustrated on an actual dwelling and its energy model, with the aim of simultaneously matching observations of different nature: energy (gas use) and environmental (temperature in two zones) data.
Typical sources of uncertainty (model discrepancy and observational error) and their magnitude are accounted for in the proposed history matching (HM) framework. The procedure quantifies the proximity between simulation results and observations in light of the above uncertainties, ruling out regions of the input space where a match cannot be achieved. The refocusing nature of HM allows locating the region where simulations and observations can match, even when the latter only represents a very small portion of the space originally explored. This feature marks a key difference with alternative approaches where only the original model is used.
The value of the proposed HM framework is indeed in enabling an energy assessor to explore a model’s response across the entire input space, at low computational cost. This is achieved by Bayesian statistical models (emulators) that can run near instantaneously on a personal laptop to estimate the response of the original model at a new range of input configurations. The hmer R package [37] can be used to implement emulation and HM on a personal device.
In the case study discussed in this work, the input region where gas simulations and observations can match was identified using only one HM wave. This was due to the fact that remarkably precise emulators could be built from the outset of work, to rapidly assess the simulator’s response on the whole input space. Where more than one wave is performed, the sequential procedure allows the researcher to add constraints as waves proceed. A quantity that is difficult to emulate in an early wave often behaves more smoothly within the more constrained NROY region of a later wave, and it can therefore be emulated with greater precision at that stage.
We also note that, while HM classically employs emulators to approximate the model, less precise statistical surrogates may also be used, especially during the first exploratory stages of research. Using linear regression in conjunction with implausibility measures [47] would still allow the researcher to rule out large parts of the input space as implausible, while keeping time and computational costs to a minimum.
The principal value of this approach is the computational efficiency of emulation over the original simulator. All emulation and HM computations carried out in this work were performed on a personal laptop with 16 GB RAM and 1.9 GHz processor. Without any parallelization, the gas computations (emulation and HM at input configurations, on nine months) were carried out in less than 28 hours. This duration is several orders of magnitude faster than the E+ running times, and yet relatively slow for emulation standards due to the large number of training points used (700). As a comparison, inference on the same inputs (on the nine months) using only 80 training points was performed in 2 h and 5 min. If we were to use the original E+ simulator directly, performing simulations would have required about 18 years.
This method can be extended to combine a simple, fast version and a more complex, slow version of the simulator. This is referred to as multi-level emulation [48], which combines information from the two and builds reliable emulators of the complex version. In doing so, the practical applicability of the proposed methodology starts from calibration of a single building fabric or energy model, with the possibility of building multi-level emulators to assist with calibration of much more complex systems, such as a cluster of buildings or even urban level energy models (where increasing the physical resolution of the model imposes a significantly higher computational duty). Emulation case studies of complex systems such as an urban energy model are still missing and as such can form the basis of future works.
Author Contributions
Conceptualization, M.R., H.D., S.W. and M.G.; methodology, D.D.; software, D.D., M.R. and A.B.; validation, D.D.; formal analysis, D.D.; investigation, D.D.; data curation, D.D. and M.R.; writing—original draft preparation, D.D. and M.R.; writing—review and editing, D.D., M.R., H.D. and M.G.; visualization, D.D.; supervision, M.G.; project administration, MG; funding acquisition, S.W., M.G. and H.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was delivered through the National Centre for Energy Systems Integration (CESI), funded by the UK Engineering and Physical Sciences Research Council [EP/P001173/1]. Additional support for HD was also provided by the EPSRC-funded Virtual Power Plant with Artificial Intelligence for Resilience and Decarbonisation (EP/Y005376/1).
Data Availability Statement
The original data presented in the study are openly available in the Collections data repository [49], at https://collections.durham.ac.uk/files/r105741r794 (accessed on 9 August 2024).
Conflicts of Interest
Author Mohammad Royapoor was employed by the company RED Engineering Design Ltd. Author Aaron Boranian was employed by the company Big Ladder Software. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AC | Alternating Current |
| ACH | Air Change per Hour |
| BLE | Bayes Linear Emulator |
| CT | Current Transformers |
| DHW | Domestic Hot Water |
| E+ | EnergyPlus |
| HM | History Matching |
| ICT | Information and Communication Technologies |
| IM | Implausibility Measure |
| MD | Model Discrepancy |
| MIP | Minimum Implausibility Plot |
| NROY | Not Ruled-Out Yet |
| ODP | Optical Depth Plot |
| OE | Observational Error |
Notation (Emulation and History-Matching)
The following notation is used in this manuscript:
| f | Simulator (computer model) |
| General input to the simulator (vector of model parameter values) | |
| Experimental design used to train the emulator | |
| Simulated output at input | |
| Emulated output at input | |
| Standard deviation associated with | |
| Standard deviation of regression residuals | |
| Correlation length of ith model parameter | |
| Model input best representing the true system parameters | |
| y | True value of the system |
| z | Measured value of the system |
| Model discrepancy term | |
| Observational error term | |
| Implausibility measure at input , for output j | |
| Overall implausibility measure at input | |
| T | Threshold to identify an input as implausible () |
| NROY region after wave k of HM |
Appendix A. Emulators
This section provides details on the structure of a Bayes linear emulator (BLE) and the choices that need to be made to train one. Following [38] and as anticipated in Section 3.2, we model the output of the simulator at an input as the sum of two terms:
The first term is a regression term with predictors : this term models the global behavior of f across the whole input space. The second term instead captures the local residual fluctuations of f.
In order to choose values of the coefficients and a statistical model of the term , the simulator is run n times at a sequence of n different inputs, which we denote here by . These form the so-called experimental design and the associated runs are named design runs. A good experimental design must fill the input space well and have no two points too close to each other [50]. In this work, we use Latin hypercube sampling [51] to accomplish the goal.
Once the simulator has been run on the n elements of the experimental design and the outputs become known, then
- The first term in Equation (A1) can be obtained by fitting a linear regression model with predictors to the known pairs .
- Values of the residual process u at each design point will then be known: . These values will oscillate around 0, with local patterns that the regression term has not been able to detect. Starting from the known values , values of for general will be predicted via a BLE.
A BLE for u is built in two steps, by modeling u as a stochastic process for which are known. First, a prior mean and prior covariance of the process u are assumed, at all inputs , (choices detailed below). Hence, for any new input , these are adjusted to the values that the process u is known to take at the n inputs , by using the two Bayes linear formulae below [52]:
Here, is the vector of known values of the process at inputs . The quantities and are termed adjusted mean and adjusted variance of given U, respectively. They represent the best prediction and associated uncertainties of , given the known values . Formulas (A2) and (A3) also hold if is replaced by a vector V of unknown values of at an arbitrary set of new inputs.
Concerning the prior mean and covariance of , we make the following choices. The prior mean of is set to zero at all inputs , since this is the mean we expect the regression residuals to have. The prior covariance function of u is instead modeled via a stationary kernel, i.e., a kernel for which the covariance between and only depends on the difference . Common choices in emulation are discussed in ([53] [§4.2.1]). In this work, we use the squared exponential kernel:
The subscript k in and denotes the kth component of the two inputs, i.e., the kth model parameter. The positive coefficient (correlation length or length scale) measures the strength of correlation in output when the kth parameter is varied. Finally, the coefficient denotes the common prior variance of at all inputs .
Expression (A4) has been written in terms of all components of the input vector . In practice, only a subset of the components (model parameters) often prove relevant to explain most of the variability in u. We call these active parameters, and only use them in expression (A4). This step reduces the dimension of the input space and has the significant advantage of simplifying the search during HM. The small variability left in u, due to the inactive parameters, is modeled as uncorrelated noise with constant variance .
Technically, the above procedure builds an emulator of the residual process u. However, once the regression component in Equation (3) is added, an emulator of f is obtained. At an input , this provides a prediction of the unknown value , and a standard deviation quantifying the uncertainty of such prediction (square root of the adjusted variance in Equation (A3)).
Appendix B. Implausibility Measures
This section provides additional insight into the derivation of , expression (6), and mathematical grounds for the choice of associated threshold values to be used in HM. The index j is fixed here, hence we will remove it from the notation of this section for simplicity. We will thus assume to have a simulator f of a physical system and one observation z of the system. The latter is an imperfect measurement of the real system value y.
As introduced in Section 3.3, we suppose that there exists an unknown configuration of model parameters that represents the true system’s parameters. In order to evaluate whether an input corresponds to the system’s parameters , the following two quantities should be compared:
- (i)
- The value that the real system would take under conditions ;
- (ii)
- The actual value that the real system takes (y)
By definition of , the above two quantities coincide when . None of the two quantities is however available for general . Nonetheless,
- (I)
- The quantity in (i) can be approximated by (approximation affected by MD);
- (II)
- The quantity in (ii) can be approximated by z (approximation affected by OE).
Moreover, if an emulator of f is available, can in turn be approximated by .
The difference may then be considered as a proxy for the difference of the unknown quantities in (i) and (ii). Mathematically, it is worth noticing that the former can be decomposed into three components, each reflecting one of the above approximations:
The first term is by definition the OE term , cf. Equation (5). The second term, when , is the MD term , cf. Equation (4). The third term is the difference between the emulated and simulated output at , which we denote here for convenience by .
When , we then have
Therefore, under the reasonable assumption of independence among the three error terms in Equation (A6), the expression of , recalled below for convenience in (A7), represents the absolute ratio between a random variable and its standard deviation
Typical values of such a variable can be identified by appealing to Pukelsheim’s rule [39]: the result states that, under the only assumption of unimodality, at least of the probability mass of any random variable lies within 3 standard deviations of the mean. This implies that most values of should be smaller than 3 when the input coincides with the “best” input . Equivalently, if an input is such that , then can be deemed implausible to represent the true system’s features .
References
- Imam, S.; Coley, D.A.; Walker, I. The building performance gap: Are modellers literate? Build. Serv. Eng. Res. Technol. 2017, 38, 351–375. [Google Scholar] [CrossRef]
- Royapoor, M.; Antony, A.; Roskilly, T. A review of building climate and plant controls, and a survey of industry perspectives. Energy Build. 2018, 158, 453–465. [Google Scholar] [CrossRef]
- American Society of Heating, Refrigerating and Air-Conditioning Engineers. ASHRAE Handbook: Fundamentals; ASHRAE: Atlanta, GA, USA, 2017. [Google Scholar]
- Royapoor, M.; Roskilly, T. Building model calibration using energy and environmental data. Energy Build. 2015, 94, 109–120. [Google Scholar] [CrossRef]
- Hou, D.; Hassan, I.; Wang, L. Review on building energy model calibration by Bayesian inference. Renew. Sustain. Energy Rev. 2021, 143, 110930. [Google Scholar] [CrossRef]
- Kennedy, M.C.; O’Hagan, A. Bayesian Calibration of Computer Models. J. R. Stat. Soc. Ser. B 2001, 63, 425–464. [Google Scholar] [CrossRef]
- Craig, P.S.; Goldstein, M.; Rougier, J.C.; Seheult, A.H. Bayesian Forecasting for Complex Systems Using Computer Simulators. J. Am. Stat. Assoc. 2001, 96, 717–729. [Google Scholar] [CrossRef]
- O’Hagan, A. Bayesian analysis of computer code outputs: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 1290–1300. [Google Scholar] [CrossRef]
- McFarland, J.; Mahadevan, S.; Romero, V.; Swiler, L. Calibration and Uncertainty Analysis for Computer Simulations with Multivariate Output. AIAA J. 2008, 46, 1253–1265. [Google Scholar] [CrossRef]
- Climate Change 2021: The Physical Science Basis. Working Group I Contribution to the IPCC Sixth Assessment Report. 9 August 2021. Available online: https://www.ipcc.ch/report/ar6/wg1/ (accessed on 9 August 2024).
- Jackson, L.; Forster, P. The Role of Climate Model Emulators in the IPCC 6th Assessment Report. Workshop Report. 29 October 2021. Available online: https://www.constrain-eu.org/wp-content/uploads/2021/10/The_Role_of_Climate_Model_Emulators_in_IPCC_AR6_D4.3.pdf (accessed on 9 August 2024).
- Smith, C. The Role ‘Emulator’ Models Play in Climate Change Projections. 29 September 2021. Available online: https://www.carbonbrief.org/guest-post-the-role-emulator-models-play-in-climate-change-projections/ (accessed on 10 June 2024).
- Lord, N.S.; Crucifix, M.; Lunt, D.J.; Thorne, M.C.; Bounceur, N.; Dowsett, H.; O’Brien, C.L.; Ridgwell, A. Emulation of long-term changes in global climate: Application to the late Pliocene and future. Clim. Past 2017, 13, 1539–1571. [Google Scholar] [CrossRef]
- Domingo, D.; Malmierca-Vallet, I.; Sime, L.; Voss, J.; Capron, E. Using ice cores and Gaussian process emulation to recover changes in the Greenland ice sheet during the last interglacial. J. Geophys. Res. Earth Surf. 2020, 125, e2019JF005237. [Google Scholar] [CrossRef]
- Edwards, T.L.; Brandon, M.A.; Durand, G.; Edwards, N.R.; Golledge, N.R.; Holden, P.B.; Nias, I.J.; Payne, A.J.; Ritz, C.; Wernecke, A. Revisiting Antarctic ice loss due to marine ice-cliff instability. Nature 2019, 566, 58–64. [Google Scholar] [CrossRef] [PubMed]
- Andrianakis, I.; Vernon, I.R.; McCreesh, N.; McKinley, T.J.; Oakley, J.E.; Nsubuga, R.N.; Goldstein, M.; White, R.G. Bayesian history matching of complex infectious disease models using emulation: A tutorial and a case study on HIV in Uganda. PLoS Comput. Biol. 2015, 11, e1003968. [Google Scholar] [CrossRef] [PubMed]
- Coveney, S.; Clayton, R.H. Fitting two human atrial cell models to experimental data using Bayesian history matching. Prog. Biophys. Mol. Biol. 2018, 139, 43–58. [Google Scholar] [CrossRef]
- Strocchi, M.; Longobardi, S.; Augustin, C.M.; Gsell, M.A.F.; Petras, A.; Rinaldi, C.A.; Vigmond, E.J.; Plank, G.; Oates, C.J.; Wilkinson, R.D.; et al. Cell to whole organ global sensitivity analysis on a four-chamber heart electromechanics model using Gaussian processes emulators. PLoS Comput. Biol. 2023, 19, e1011257. [Google Scholar] [CrossRef] [PubMed]
- Vernon, I.; Liu, J.; Goldstein, M.; Rowe, J.; Topping, J.; Lindsey, K. Bayesian uncertainty analysis for complex systems biology models: Emulation, global parameter searches and evaluation of gene functions. BMC Syst. Biol. 2018, 12, 12. [Google Scholar] [CrossRef] [PubMed]
- Vernon, I.; Goldstein, M.; Bower, R.G. Galaxy formation: A Bayesian uncertainty analysis. Bayesian Anal. 2010, 5, 619–669. [Google Scholar] [CrossRef]
- Craig, P.S.; Goldstein, M.; Seheult, A.H.; Smith, J.A. Pressure matching for hydrocarbon reservoirs: A case study in the use of Bayes linear strategies for large computer experiments. In Case Studies in Bayesian Statistics; Lecture Notes in Statistics; Springer: New York, NY, USA, 1997; Volume 121, pp. 37–93. [Google Scholar] [CrossRef]
- ISO 6946:2017; Building Components and Building Elements—Thermal Resistance and Thermal Transmittance—Calculation Methods. International Organization for Standardization: Geneva, Switzerland, 2017.
- ISO 9869-1:2014; Thermal Insulation—Building Elements—In-Situ Measurement of Thermal Resistance and Thermal Transmittance. International Organization for Standardization: Geneva, Switzerland, 2014.
- The Chartered Institution of Building Services Engineers. CIBSE Guide A: Environmental Design; CIBSE: London, UK, 2021. [Google Scholar]
- Rasooli, A.; Itard, L.; Ferreira, C.I. A response factor-based method for the rapid in-situ determination of wall’s thermal resistance in existing buildings. Energy Build. 2016, 119, 51–61. [Google Scholar] [CrossRef]
- Deconinck, A.H.; Roels, S. Comparison of characterisation methods determining the thermal resistance of building components from onsite measurements. Energy Build. 2016, 130, 309–320. [Google Scholar] [CrossRef]
- Meng, X.; Yan, B.; Gao, Y.; Wang, J.; Zhang, W.; Long, E. Factors affecting the in situ measurement accuracy of the wall heat transfer coefficient using the heat flow meter method. Energy Build. 2015, 86, 754–765. [Google Scholar] [CrossRef]
- Ficco, G.; Iannetta, F.; Ianniello, E.; Alfano, F.R.d.; Dell’Isola, M. U-value in situ measurement for energy diagnosis of existing buildings. Energy Build. 2015, 104, 108–121. [Google Scholar] [CrossRef]
- Gaspar, K.; Casals, M.; Gangolells, M. A comparison of standardized calculation methods for in situ measurements of façades U-value. Energy Build. 2016, 130, 592–599. [Google Scholar] [CrossRef]
- Desogus, G.; Mura, S.; Ricciu, R. Comparing different approaches to in situ measurement of building components thermal resistance. Energy Build. 2011, 43, 2613–2620. [Google Scholar] [CrossRef]
- Hoffmann, C.; Geissler, A. The prebound-effect in detail: Real indoor temperatures in basements and measured versus calculated U-values. Energy Procedia 2017, 122, 32–37. [Google Scholar] [CrossRef]
- Marshall, A.; Fitton, R.; Swan, W.; Farmer, D.; Johnston, D.; Benjaber, M.; Ji, Y. Domestic building fabric performance: Closing the gap between the in situ measured and modelled performance. Energy Build. 2017, 150, 307–317. [Google Scholar] [CrossRef]
- Baker, P. U-Values and Traditional Buildings; Historic Scotland Conservation Group: Glasgow, UK, 2011. [Google Scholar]
- Yassaghi, H.; Mostafavi, N.; Hoque, S. Evaluation of current and future hourly weather data intended for building designs: A Philadelphia case study. Energy Build. 2019, 199, 491–511. [Google Scholar] [CrossRef]
- Happle, G.; Fonseca, J.A.; Schlueter, A. A review on occupant behavior in urban building energy models. Energy Build. 2018, 174, 276–292. [Google Scholar] [CrossRef]
- Hong, T.; Taylor-Lange, S.C.; D’Oca, S.; Yan, D.; Corgnati, S.P. Advances in research and applications of energy-related occupant behavior in buildings. Energy Build. 2016, 116, 694–702. [Google Scholar] [CrossRef]
- Iskauskas, A. hmer: History Matching and Emulation Package. 2022. Available online: https://CRAN.R-project.org/package=hmer (accessed on 9 August 2024).
- Goldstein, M.; Huntley, N. Bayes Linear Emulation, History Matching, and Forecasting for Complex Computer Simulators. In Handbook of Uncertainty Quantification; Ghanem, R., Higdon, D., Owhadi, H., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 9–32. [Google Scholar] [CrossRef]
- Pukelsheim, F. The three sigma rule. Am. Stat. 1994, 48, 88–91. [Google Scholar] [CrossRef]
- Energy Saving Trust. At Home with Water. Technical Report, London. 2013. Available online: https://www.energysavingtrust.org.uk/sites/default/files/reports/AtHomewithWater%287%29.pdf (accessed on 9 August 2024).
- Energy Saving Trust. Measurement of Domestic Hot Water Consumption in Dwellings. Technical Report, Department for Energy and Climate Change. 2011. Available online: https://www.gov.uk/government/publications/measurement-of-domestic-hot-water-consumption-in-dwellings (accessed on 9 August 2024).
- EnergyPlus Version 22.1.0 Documentation. U.S. Department of Energy. 2022. Available online: https://energyplus.net/assets/nrel_custom/pdfs/pdfs_v22.1.0/EngineeringReference.pdf (accessed on 9 August 2024).
- SI684 (1983); The Gas (Meters) Regulations. UK Secretary of State: London, UK, 1983.
- IEC 62053-21 (2020); Electricity Metering Equipment—Particular Requirements—Part 21: Static Meters for AC Active Energy. International Electrotechnical Commission: Geneva, Switzerland, 2020.
- Loeppky, J.L.; Sacks, J.; Welch, W.J. Choosing the Sample Size of a Computer Experiment: A Practical Guide. Technometrics 2009, 51, 366–376. [Google Scholar] [CrossRef]
- Sobol, I. Uniformly distributed sequences with an additional uniform property. USSR Comput. Math. Math. Phys. 1976, 16, 236–242. [Google Scholar] [CrossRef]
- Salter, J.M.; Williamson, D. A comparison of statistical emulation methodologies for multi-wave calibration of environmental models. Environmetrics 2016, 27, 507–523. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.C.; Henderson, D.A.; Wilson, K.J. Multilevel emulation for stochastic computer models with application to large offshore wind farms. J. R. Stat. Soc. Ser. C Appl. Stat. 2023, 72, 608–627. [Google Scholar] [CrossRef]
- Domingo, D.; Royapoor, M. Calibration under Uncertainty of a Building Energy Model: Simulated and Observed Records [Dataset]; Collections; Durham University: Durham, UK, 2024. [Google Scholar] [CrossRef]
- Mckay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output From a Computer Code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Helton, J.; Davis, F. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- Goldstein, M.; Wooff, D. Bayes Linear Statistics: Theory and Methods; Wiley Series in Probability and Statistics; John Wiley & Sons: Chichester, UK, 2007. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).