Enhancement of Low Voltage Ride Through (LVRT) Capability of DFIG-Based Wind Turbines with Enhanced Demagnetization Control Model
Abstract
1. Introduction
- (1)
- In DFIG, a demagnetization control model has been developed to limit parameter changes within a certain trajectory in stability situations. Moreover, the rotor electromotive force model has been developed mathematically to dampen the oscillations in the system more quickly.
- (2)
- Small time steps are required for numerical operations in the simulation study because of the integration of incremental calculation results. Therefore, the stator electromotive force model was developed mathematically to facilitate calculations.
- (3)
- The electromotive force models developed in both stator and rotor circuits are adapted to work in a coordinated manner to provide the best system control in balanced and unbalanced faults.
- (4)
- This study aims to support the demagnetization control model by developing a forced flux model in order to better control the dynamic process in providing LVRT capability in DFIG according to grid code requirements.
2. Stator Dynamic Model in DFIG
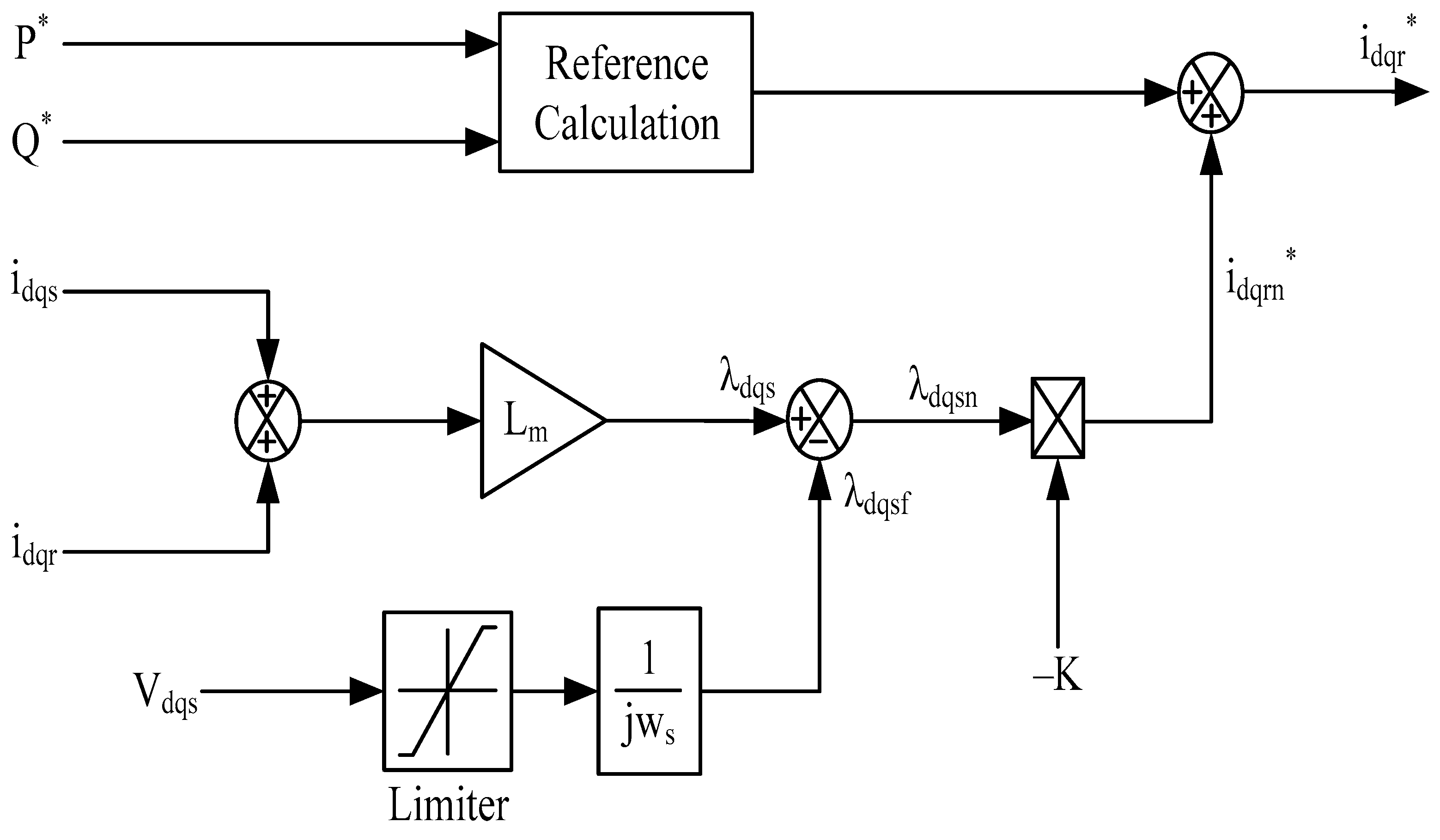
3. Enhanced Demagnetization Control (EDC) Model in DFIG
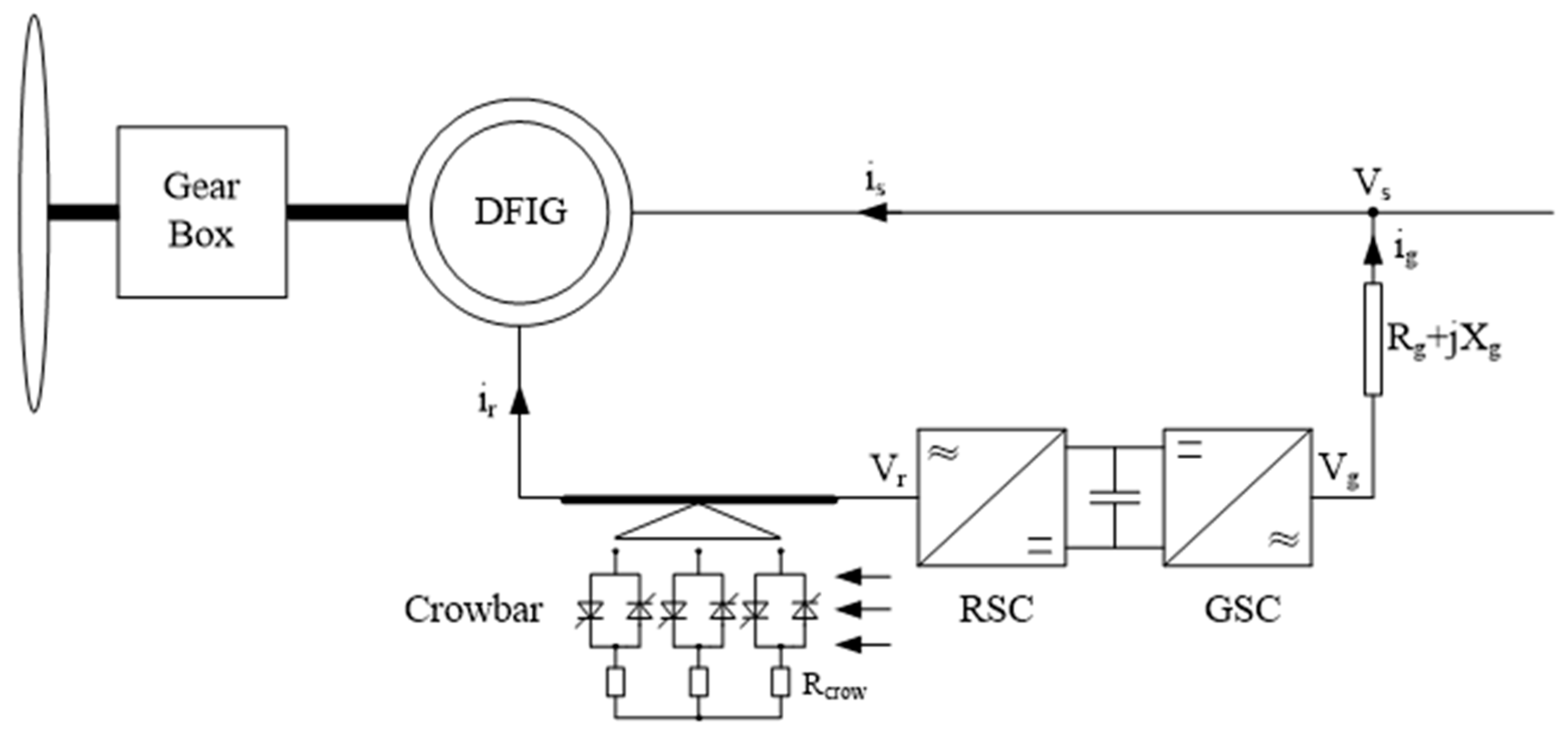
4. Simulation Study
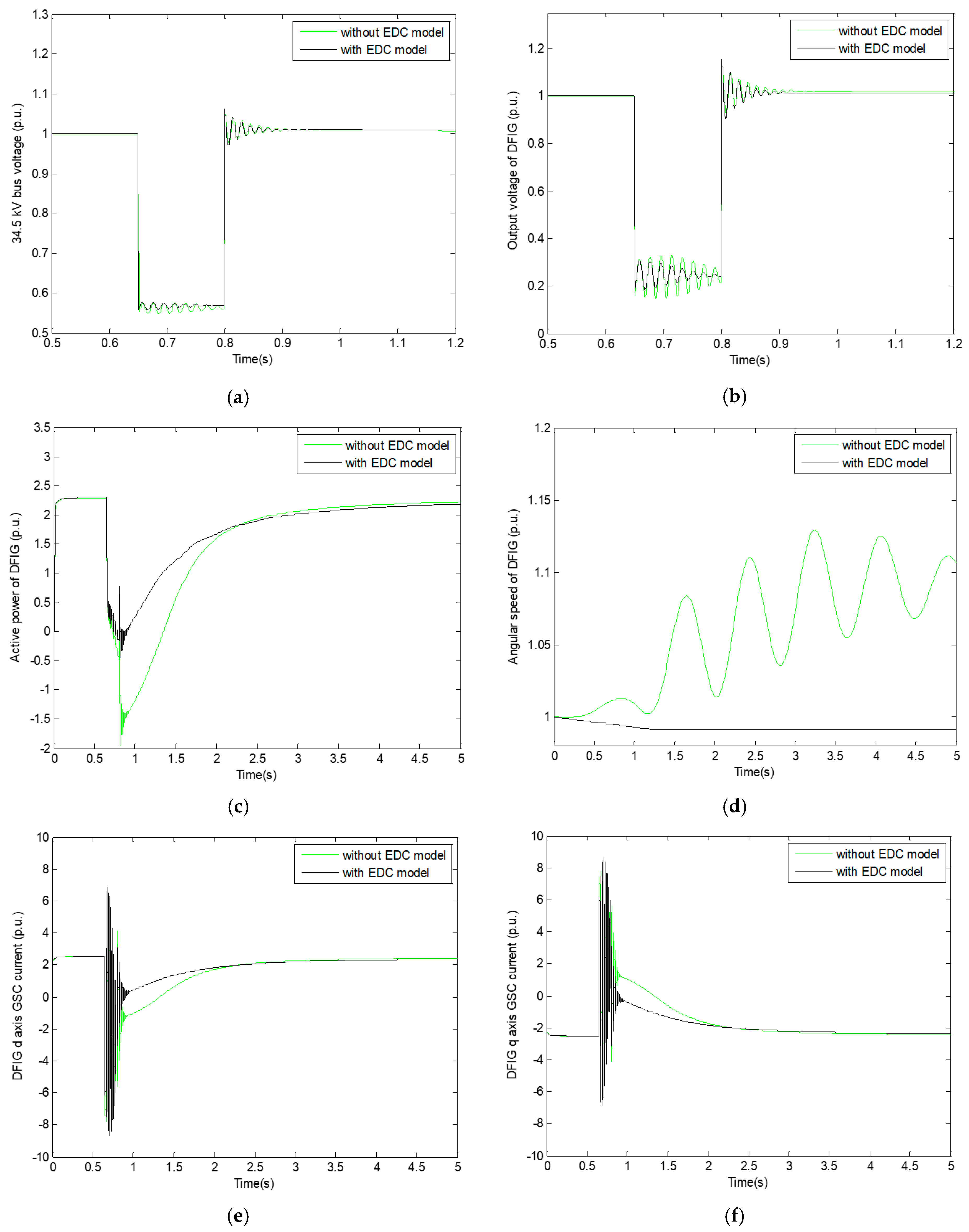
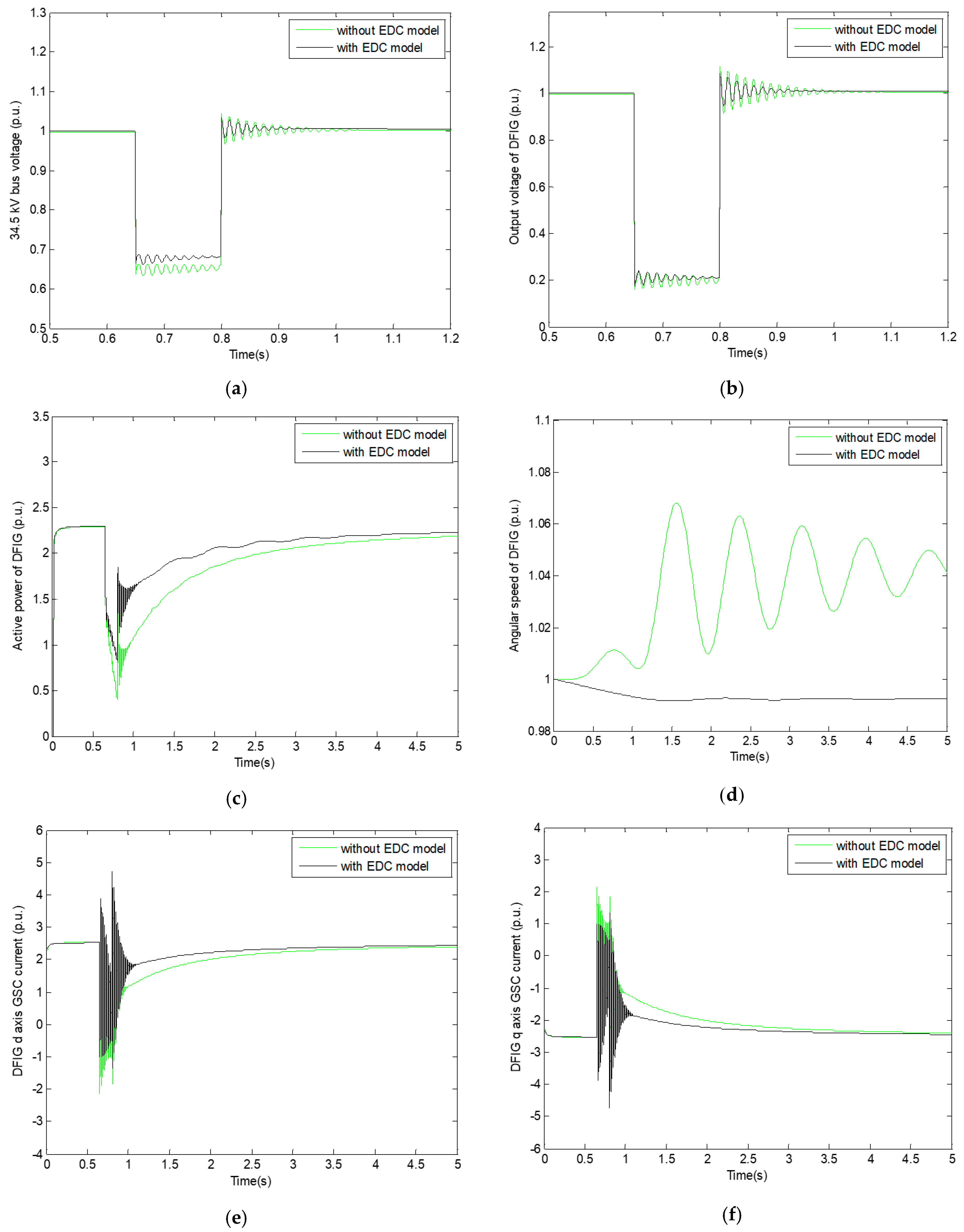
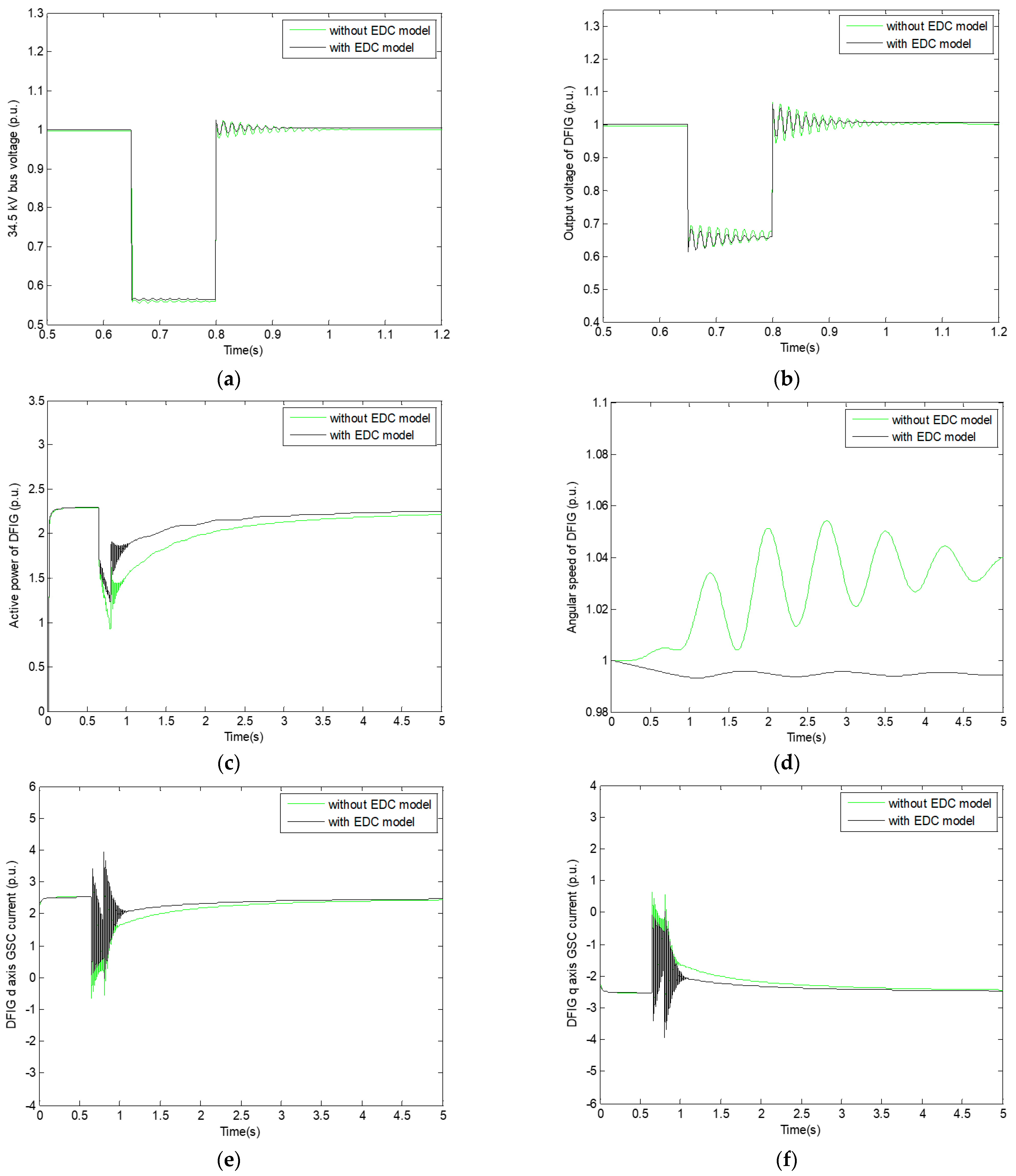
5. Results from the Simulation Study
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rodríguez, J.M.; Fernández, J.L.; Beato, D.; Iturbe, R.; Usaola, J.; Ledesma, P.; Wilhelmi, J.R. Incidence on power system dynamics of high penetration of fixed speed and doubly fed wind energy systems: Study of the Spanish case. IEEE Trans. Power Syst. 2002, 17, 1089–1095. [Google Scholar] [CrossRef]
- Zhu, D.; Zou, X.; Dong, W.; Jiang, C.; Kang, Y. Disturbance feedforward control for type-3 wind turbines to achieve accurate implementation of transient control targets during LVRT. Int. J. Electr. Power Energy Syst. 2020, 119, 105954. [Google Scholar] [CrossRef]
- Liang, J.; Howard, D.F.; Restrepo, J.A.; Harley, R.G. Feedforward transient compensation control for DFIG wind turbines during both balanced and unbalanced grid disturbances. IEEE Trans. Ind. Appl. 2013, 49, 1452–1463. [Google Scholar] [CrossRef]
- Zhu, D.; Zou, X.; Zhou, S.; Dong, W.; Kang, Y.; Hu, J. Feedforward current references control for DFIG-based wind turbine to improve transient control performance during grid faults. IEEE Trans. Energy Convers. 2017, 33, 670–681. [Google Scholar] [CrossRef]
- Chang, Y.; Kocar, I.; Hu, J.; Berger, M. Comparison of internal voltage vectors of DFIG-based wind turbine generator and synchronous generator during asymmetrical fault. Electr. Power Syst. Res. 2023, 223, 109628. [Google Scholar] [CrossRef]
- Alsmadi, Y.M.; Xu, L.; Blaabjerg, F.; Ortega, A.J.P.; Abdelaziz, A.Y.; Wang, A.; Albataineh, Z. Detailed investigation and performance improvement of the dynamic behavior of grid-connected DFIG-based wind turbines under LVRT conditions. IEEE Trans. Ind. Appl. 2018, 54, 4795–4812. [Google Scholar] [CrossRef]
- Taveiros, F.E.V.; Barros, L.S.; Costa, F.B. Heightened state-feedback predictive control for DFIG-based wind turbines to enhance its LVRT performance. Int. J. Electr. Power Energy Syst. 2019, 104, 943–956. [Google Scholar] [CrossRef]
- Shahriari, S.A.A.; Mohammadi, M.; Raoofat, M. A new method based on state-estimation technique to enhance low-voltage ride-through capability of doubly-fed induction generator wind turbines. Int. J. Electr. Power Energy Syst. 2018, 95, 118–127. [Google Scholar] [CrossRef]
- Ardjoun, S.A.E.M.; Denai, M.; Abid, M. A robust power control strategy to enhance LVRT capability of grid-connected DFIG-based wind energy systems. Wind Energy 2019, 22, 834–847. [Google Scholar] [CrossRef]
- Uddin, M.N.; Arifin, M.S.; Rezaei, N. A novel neuro-fuzzy based direct power control of a DFIG based wind farm incorporated with distance protection scheme and LVRT capability. IEEE Trans. Ind. Appl. 2023, 59, 5792–5803. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, L.; Sang, S.; Xue, X.; Zhang, X.; Sun, T.; Gao, N. Optimized series dynamic braking resistor for LVRT of doubly-fed induction generator with uncertain fault scenarios. IEEE Access 2022, 10, 22533–22546. [Google Scholar] [CrossRef]
- Dong, H.; Wu, H.; Pan, J.; Chen, Y.; Xu, B. Research on double-fed induction generator low voltage ride through based on double braking resistors using fuzzy control. Energies 2018, 11, 1155. [Google Scholar] [CrossRef]
- Ghorbani, M.; Firouzi, M.; Mozafari, B.; Golshan, F. Power flow management and LVRT enhancement by using multi-functional capacitive bridge-type fault current limiter in DFIG system. Int. J. Electr. Power Energy Syst. 2023, 148, 108810. [Google Scholar] [CrossRef]
- Chakraborty, A.; Maity, T. Integrated control algorithm for fast and accurate detection of the voltage sag with low voltage ride-through (LVRT) enhancement for doubly-fed induction generator (DFIG) based wind turbines. Control Eng. Pract. 2023, 131, 105393. [Google Scholar] [CrossRef]
- Shanmugam, R.; Sakthivel, D.K.; Ramaiah, A.N.; Ramalingam, S. Nonlinear Control Strategy for DC-Link Voltage Control in a DFIG of WECS During 3φ Grid Faults. IEEE Trans. Ind. Electron. 2024, 71, 12468–12475. [Google Scholar] [CrossRef]
- Döşoğlu, M.K. Hybrid control approach for low-voltage ride-through capability in doubly-fed induction generator-based wind turbines. Comput. Electr. Eng. 2021, 90, 106972. [Google Scholar] [CrossRef]
- Hiremath, R.; Moger, T. Modified Super Twisting algorithm based sliding mode control for LVRT enhancement of DFIG driven wind system. Energy Rep. 2022, 8, 3600–3613. [Google Scholar] [CrossRef]
- Chowdhury, M.A.; Shafiullah, G.M.; Ferdous, S.M. Low voltage ride-through augmentation of DFIG wind turbines by simultaneous control of back-to-back converter using partial feedback linearization technique. Int. J. Electr. Power Energy Syst. 2023, 153, 109394. [Google Scholar] [CrossRef]
- Delavari, H.; Veisi, A. A new robust nonlinear controller for fractional model of wind turbine based DFIG with a novel disturbance observer. Energy Syst. 2024, 15, 827–861. [Google Scholar] [CrossRef]
- Beltran-Pulido, A.; Cortes-Romero, J.; Coral-Enriquez, H. Robust active disturbance rejection control for LVRT capability enhancement of DFIG-based wind turbines. Control Eng. Pract. 2018, 77, 174–189. [Google Scholar] [CrossRef]
- Huang, C.; Zhao, H. Error-based active disturbance rejection control for wind turbine output power regulation. IEEE Trans. Sustain. Energy 2023, 14, 1692–1701. [Google Scholar] [CrossRef]
- López, J.; Gubía, E.; Olea, E.; Ruiz, J.; Marroyo, L. Ride through of wind turbines with doubly fed induction generator under symmetrical voltage dips. IEEE Trans. Ind. Electron. 2009, 56, 4246–4254. [Google Scholar] [CrossRef]
- Mendes, V.F.; de Sousa, C.V.; Silva, S.; Rabelo, B.C.; Hofmann, W. Modeling and ride-through control of doubly fed induction generators during symmetrical voltage sags. IEEE Trans. Energy Convers. 2011, 26, 1161–1171. [Google Scholar] [CrossRef]
- Krause, P.C. Analysis of Electric Machinery, 2nd ed.; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Kundur, P. Power System Stability and Control; Tata McGraw-Hill Education: New York, NY, USA, 1994. [Google Scholar]
- Ekanayake, J.B.; Holdsworth, L.; Jenkins, N. Comparison of 5th order and 3rd order machine models for double fed induction generators (DFIG) wind turbines. Electr. Power Syst. Res. 2003, 67, 207–215. [Google Scholar] [CrossRef]
- Patel, K.; Das, S.P. Improved Traditional Demagnetization Control of DFIG Under Balanced Grid Faults. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 16–19 December 2020. [Google Scholar]
- Döşoğlu, M.K.; Özkaraca, O.; Güvenç, U. Novel active–passive compensator–supercapacitor modeling for low-voltage ride-through capability in DFIG-based wind turbines. Electr. Eng. 2019, 101, 1119–1132. [Google Scholar] [CrossRef]

| Literature | Method | Developed LVRT Capability Strategy | Purpose | Result |
|---|---|---|---|---|
| Ref. [4] | Feed-forward control | Positive and negative sequence flux models | Reducing overvoltages and overcurrents in the RSC circuit | It gives effective results. However, the work done is costly. |
| Ref. [6] | Dynamic model | Positive, negative and natural sequence flux models | Protecting the RSC circuit against transient instability | It gives effective results. However, the oscillations have been relatively dampened. |
| Ref. [22] | Crowbar model | Positive, negative and natural sequence flux models | Reducing maximum rotor current | It gives effective results. However, a large current capacity problem arises in the rotor converter. |
| Ref. [23] | Magnetizing current control | Positive, negative, natural and forced sequence flux models | Improving system stability during faults | It gives effective results. However, it takes time for the oscillations to dampen. |
| In this study | Enhanced demagnetization control model | Positive, negative, natural, forced sequence flux models and stator dynamic models | Damping oscillations, overcurrent and voltage reduction, and stabilizing the system in a short amount of time, ease of calculation in simulation work | It is effective against various transient stability states. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Döşoğlu, M.K.; Doğan, M.U. Enhancement of Low Voltage Ride Through (LVRT) Capability of DFIG-Based Wind Turbines with Enhanced Demagnetization Control Model. Energies 2024, 17, 4015. https://doi.org/10.3390/en17164015
Döşoğlu MK, Doğan MU. Enhancement of Low Voltage Ride Through (LVRT) Capability of DFIG-Based Wind Turbines with Enhanced Demagnetization Control Model. Energies. 2024; 17(16):4015. https://doi.org/10.3390/en17164015
Chicago/Turabian StyleDöşoğlu, M. Kenan, and Muhsin Uğur Doğan. 2024. "Enhancement of Low Voltage Ride Through (LVRT) Capability of DFIG-Based Wind Turbines with Enhanced Demagnetization Control Model" Energies 17, no. 16: 4015. https://doi.org/10.3390/en17164015
APA StyleDöşoğlu, M. K., & Doğan, M. U. (2024). Enhancement of Low Voltage Ride Through (LVRT) Capability of DFIG-Based Wind Turbines with Enhanced Demagnetization Control Model. Energies, 17(16), 4015. https://doi.org/10.3390/en17164015






