1. Introduction
The recent advancements in electric vehicles and renewable energy storage applications have developed a significant demand for lithium-ion batteries (LIBs). LIBs are essential to many applications, including electric vehicles, aerospace systems, and portable devices. Due to the increasing demand for renewable energy sources, the demand for advanced predictive maintenance strategies for batteries is increasing since they are vital for safe operation [
1]. As these batteries age, their material mechanisms interact with one another due to surface cracking, material dissolution, and the growth of a solid electrolyte inter-phase layer. Therefore, the LIB’s performance decreases, potentially causing safety and reliability issues [
2]. The precise prediction of the RUL is particularly important for ensuring their reliability and safety during operation. An accurate prediction of a battery’s RUL can help with planning for predictive maintenance, preventing an unpredicted failure, and extending the useful life of the battery [
3].
The conventional RUL prognosis techniques have primarily depended on physical modeling and basic statistical techniques, which often fail to capture the complex degradation procedures of the latest battery technologies. The conventional RUL prognosis methods usually include empirical models and statistical techniques by using Kalman filters, particle filters, and Bayesian approaches. These conventional methods typically require significant domain knowledge and are limited by their incapacity to operate according to the nonlinear and dynamic nature of battery aging [
4]. The research work in [
5] used a particle-filter-based framework for the modeling of LIBs’ capacity depletion and showed the ability of this technique in handling uncertainties in a battery degradation process.
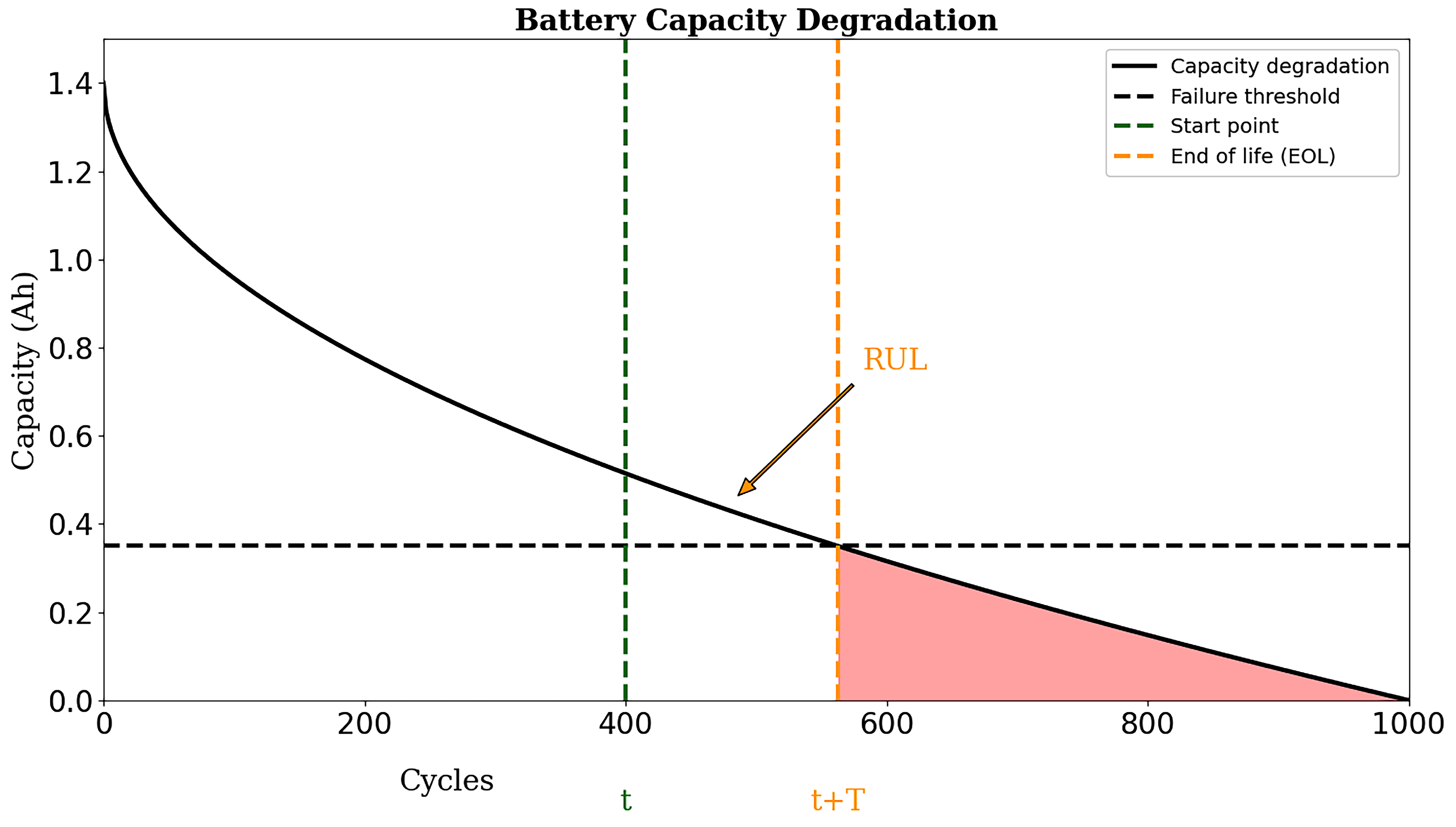
Figure 1 demonstrates the battery capacity degradation over multiple cycles to predict the RUL. The battery’s full capacity was 1.4 ampere hours (Ah); the failure threshold was 75 percent, which was at 0.35 Ah; and observation starting point was at 400 cycles. The capacity degradation curve crossed the threshold line at 562.5 cycles, which was the end of life (EOL) point, and thus, the RUL was the difference between the observation starting point to the EOL, which was 162 cycles. The shaded area from cycle 562.5 to 1000 suggests replacing the battery or improving its capacity through maintenance.
As long as batteries work under various operating conditions, the degradation patterns can be extremely nonlinear and affected by multiple factors, such as the temperature, discharge rates, and used cycles. This has led to the research of machine learning (ML) techniques that can learn these complex patterns from data.
The research work in [
6] examined various methods that utilize ML and statistical-based models to forecast the RUL using historical recorded data. These methods include support vector machines (SVMs), random forests, gradient boosting machines, artificial neural networks (ANNs), convolution neural networks (CNNs), long short-term memory (LSTM), recurrent neural networks (RNNs), gated recurrent units (GRUs), attention-based models, and auto-encoders. However, these models often struggle with the complexity and nonlinearity of battery degradation processes. Contemporary research has developed many hybrid models that combine the traditional ML method with deep learning (DL) to improve the RUL prediction accuracy. The authors of [
7] investigated and compared how well various DL-based hybrid models work. These include CNNs with wavelet packet decomposition and RNNs with nonlinear auto-regressive exogenous models. SVMs have been extensively utilized for fault classification [
8] and RUL prediction due to their strong ability to handle high-dimensional data. However, the research work in [
9], which compared an SVM with LSTM and GRU models, indicates that SVMs may not be as effective as DL models in capturing the complex, nonlinear relationships inherent in battery degradation data. ANNs were the first AI-based techniques to be used for RUL prognosis. The working principle of neural architecture is like a human brain’s ability to understand data and detect patterns. These methods are useful in applications in which the connection between the input data and the target cell is difficult and nonlinear. If not properly regularized, it can lead to over-fitting and requires significant computational resources for model training [
10].
CNNs have achieved popularity for their strong ability to automatically capture features from unprocessed data for RUL prediction. A technique based on a deep dilated CNN (D-CNN) was proposed in [
11] to enhance the receptive field and improve the prediction accuracy. This model presented good performance on the C-MAPSS dataset and required less training time compared with conventional methods. However, it required high computing power and skill to avoid over-fitting problems. Additionally, it had a lower prediction accuracy than the RNN and LSTM. RNNs are a type of neural network that can effectively model sequence data. RNNs developed from feed-forward networks behave like human brains. An RNN outperforms other algorithms at predicting sequential data [
12]. LSTM networks are a variant of an RNN that can capture long-term dependencies in historical data of battery degradation for RUL prediction. It controls data flow in recurrent computations with gates. LSTM networks can hold long-term memories. Depending on the data, the network may or may not retain memory. The network’s gating mechanisms preserve long-term dependencies. The network may store or release memory through gating [
13]. In the research work of [
9], the LSTM-RNN method of RUL prediction was developed using six different cells from the NCR18650PF battery datasets. The RMS prop method was used to train on a combination of online and offline data for an LSTM-RNN model. The dropout technique was used to reduce over-fitting. The results indicate that the LSTM-RNN outperformed the SVM and a simple RNN. However, this model’s accuracy still needs to be improved and other batteries also need to test the model in the future.
An advanced framework for the RUL prediction of LIBs is presented in [
14], where online real-world data and a NASA battery dataset were used. This method consists of three stages. First, using the state of charge equation, the value of the state of health (SOH) is predicted for each separate vehicle. In the second stage, the Lasso regression model was developed on aggregated data for all vehicles. Then, the internal and real battery parameters were predicted by using a Monte Carlo simulation method. In the last stage, the RUL was predicted through a probability distribution of SOH values using the Lasso model. This method works for both the short-term and long-term demands of electric-by-electric vehicles. However, the prediction error still needs to be reduced. In [
15], a GRU-RNN model is proposed by using the adaptive gradient descent approach to enhance the RUL prediction accuracy and reduce the computing costs. The GRU-RNN model shows reliable performance through the experiments as compared with LSTM and an SVM, while having an average RMS error of around 2%. Another technique for RUL prediction is presented in [
16], where it combines the Monte Carlo dropout and GRU to compensate for uncertainty in estimation results and prevent over-fitting. This technique provided probabilistic distribution-based RUL results that need to be improved. Attention mechanisms focus more on relevant features [
17] and were recently incorporated into multiple DL-based models to enhance the prediction accuracy.
Attention techniques have enhanced IoT networks by increasing the network speed and security especially in unmanned aerial vehicle (UAV)-enabled networks. The research work in [
18] presents an innovative UAV trajectory planning method that blends risk factor optimization with energy consumption and uses attention mechanisms to enhance the UAV’s real-time decision making in risky environments. Attention mechanisms filter and prioritize sensor data to focus on mission-critical information. UAVs can quickly make intelligent decisions based on the most relevant and current data because of their selective attention. By incorporating TinyML, the attention mechanisms deliver more decision-making privileges to the UAVs to independently conduct extensive computations and amendments. The research work [
19] introduces a deep policy gradient action quantization (DPGAQ) technique that utilizes attention with deep reinforcement learning (DRL) to effectively manage the high-dimensional actions of vehicle networks. This work used attention processes that enable the DRL model to make quick decisions by focusing on the most important environmental features. This selectivity effectively controls the intelligent vehicle network’s high-dimensional data input issues. Attention techniques help the model control, and thus, minimize the number of unnecessary computations and enhance the rate of decisions and accuracy of actions to be taken. In [
20], the authors developed a hybrid model by integrating a TCN, GRU, and deep neural network (DNN) by incorporating attention mechanisms. Initially, a TCN with a feature attention mechanism was used to capture the degradation patterns. Then, a combined TCN-GRU was used as a decoder to obtain a better understanding of data patterns using features, and finally, a DNN was used to predict the RUL through a multi-layer operation. The experimental work used the CALCE and NASA battery datasets to train and evaluate the model. However, this method needs high computational power and skill, and also needs to check the model on online data.
Transformer models are considered superior for predicting the RUL of LIBs due to their advanced capabilities. They apply self-attention mechanisms to effectively manage noisy data, capture complex dependencies, and also integrate denoising and prediction operations into a unified structure [
21]. Transformers simultaneously process entire input sequences, leading to faster training and inference time compared with sequential models. Transformers are more efficient and effective than ANN, CNN, LSTM, RNN, GRU, and hybrid models. This is because the transformer benefits from transfer learning from the pre-trained model, which leads to better performance with less labeled data and a short training time [
22]. To improve the prediction accuracy of the RUL for LIBs, the research work in [
23] presents a transformer-based method that uses the capacity regeneration (CR) phenomenon. The increased value of CR leads to inaccuracies in RUL estimation. The first step is to pre-train the LSTM with the transformer-learning model without the CR of the NASA battery dataset. After pre-training, the weights of the first two layers are frozen. In the second step, the data are updated for training through the CR algorithm and the model is fine tuned with unfrozen layers. The results show that the mean relative error was 9%, which still needs to be improved. However, this model’s results fully depend on the efficiency of the CR algorithm.
The denoising encoder with a transformer-based framework developed in [
24] by using the NASA battery datasets was further normalized and denoised by utilizing one-dimensional convolution layers to decrease the noise. The data patterns are captured using a transformer encoder. A multi-head self-attention mechanism and feed-forward network enhances the RUL prediction. This model can face difficulties for longer sequences of data because its flattening of the feature edges may not effectively capture sharp peaks or sudden data changes, which leads to inaccuracies. Furthermore, results need to be improved and validated across different batteries. Therefore, after critical analysis, it was found that DL-based methods struggle to effectively manage the complex and nonlinear degradation processes of LIB datasets, and their reliability under different operational conditions is challenging [
25]. DL-based methods require significant computational power and skills and face over-fitting issues [
26]. Current transformer-based methods involve flattening the feature edges since they cannot capture sharp peaks and they have computational complexity [
27].
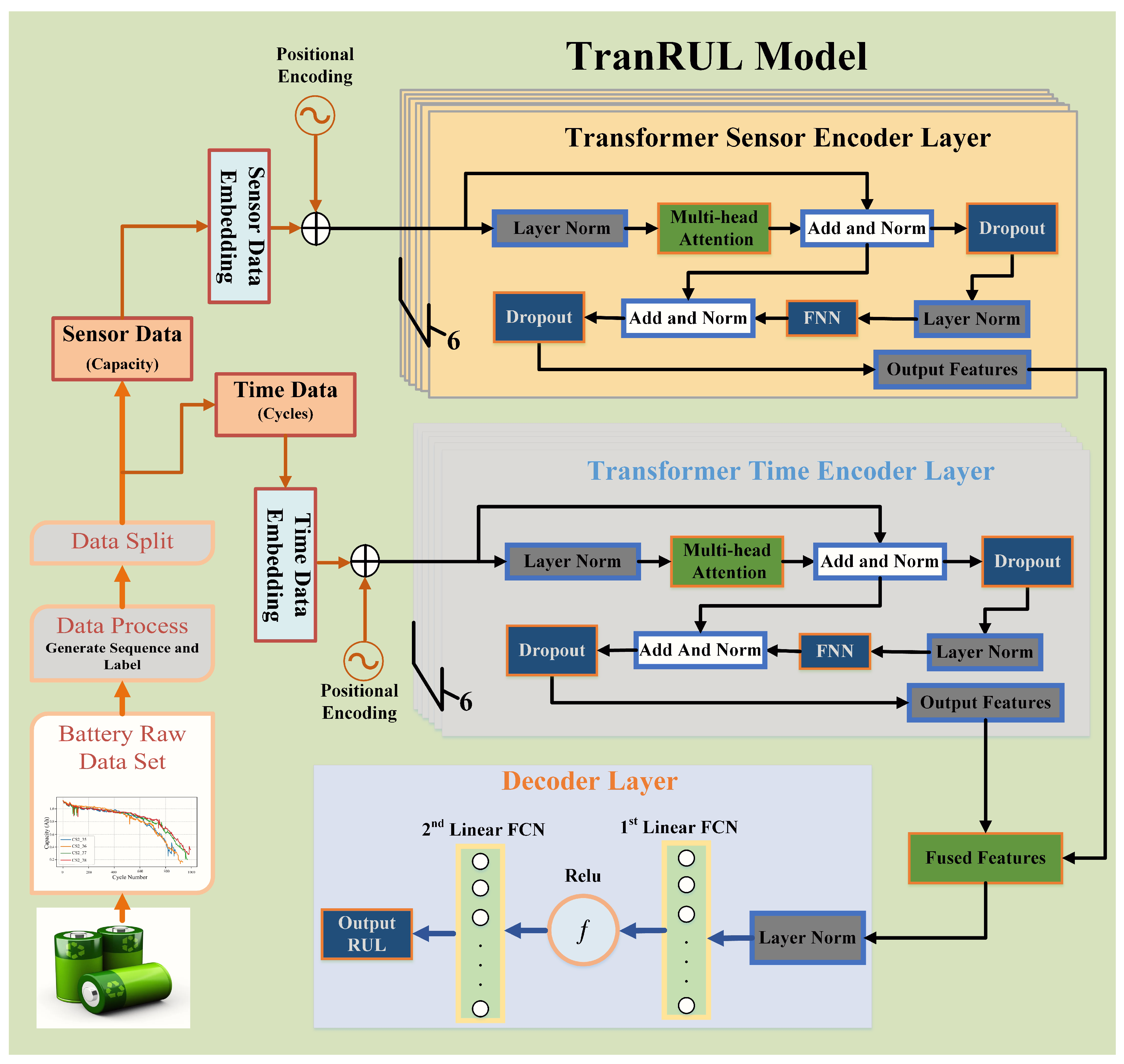
To address all the issues mentioned in this section, this research work proposes a TransRUL framework for the RUL prediction of LIBs, which was especially designed for time series data to enhance the capture of temporal dependencies. The TransRUL model uses a dual encoder and a self-attention mechanism to handle complex patterns of LIB datasets and integrates the embedding layers to convert data to a higher-dimensional vector space. It incorporates positional encoding for understanding the complex sequence’s temporal and multi-head attention to focus the input sequence simultaneously and enhance the overall model ability to capture complex dependencies, dropout layers to prevent over-fitting, and a transformer decoder layer to make accurate RUL predictions. This proposed TransRUL model will provide a robust framework for assessing a battery RUL, thus contributing valuable insights to the field of battery management systems. The principal contributions of this research are outlined as follows:
The proposed TransRUL model integrates the positional encoding and multi-head attention mechanisms with a dual encoder for capturing complex temporal dependencies in LIB datasets.
The model incorporates an advanced attention mechanism that selectively focuses on important features through temporal sequences, hence improving the RUL prediction accuracy.
The sliding-window-based technique is utilized in the TransRUL model to effectively capture temporal patterns in LIB data for generating feature–label pairs.
The inclusion of positional encoding and transformer encoder layers in the model strengthens the feature extraction without increasing the computing complexity.
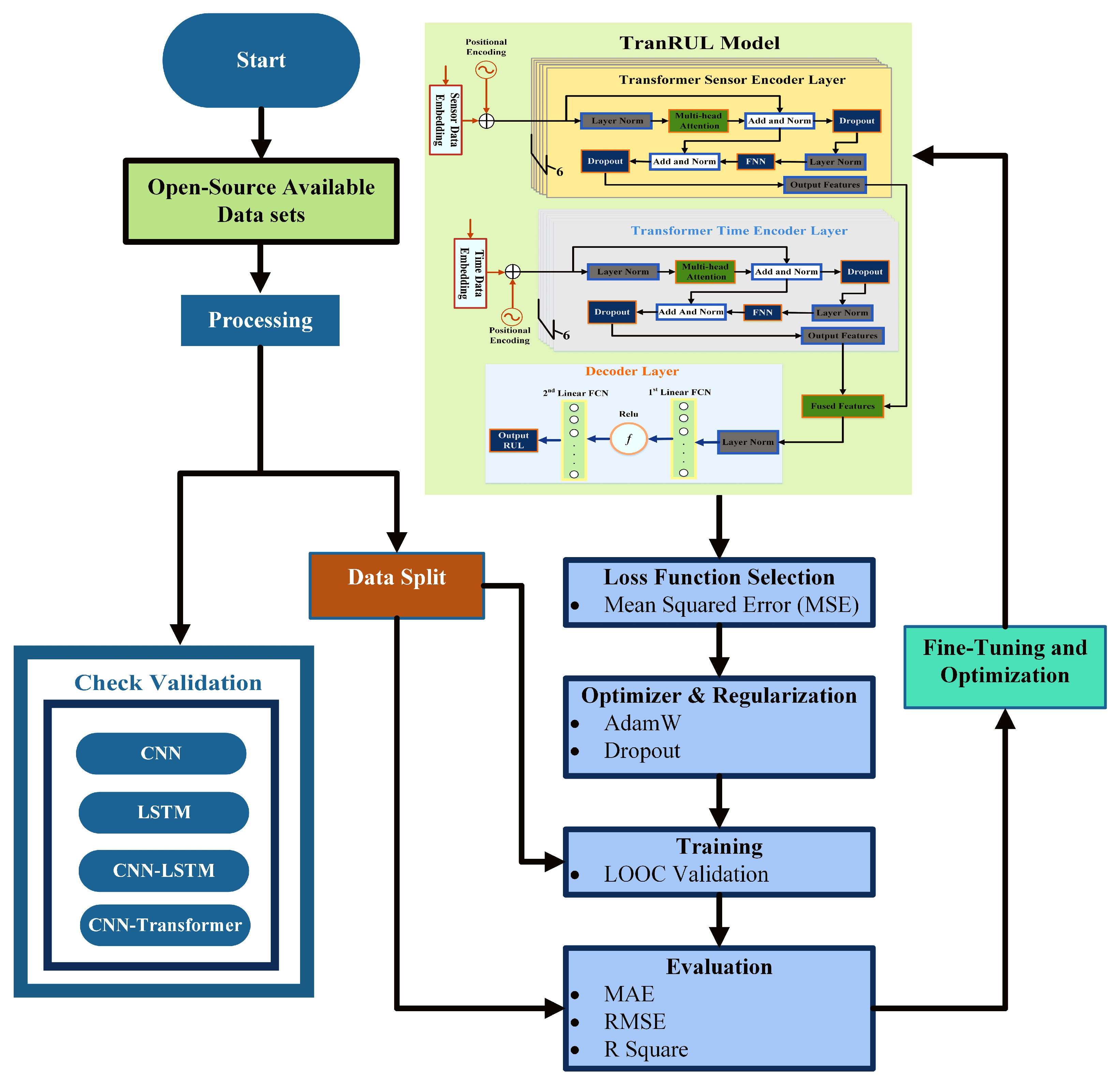
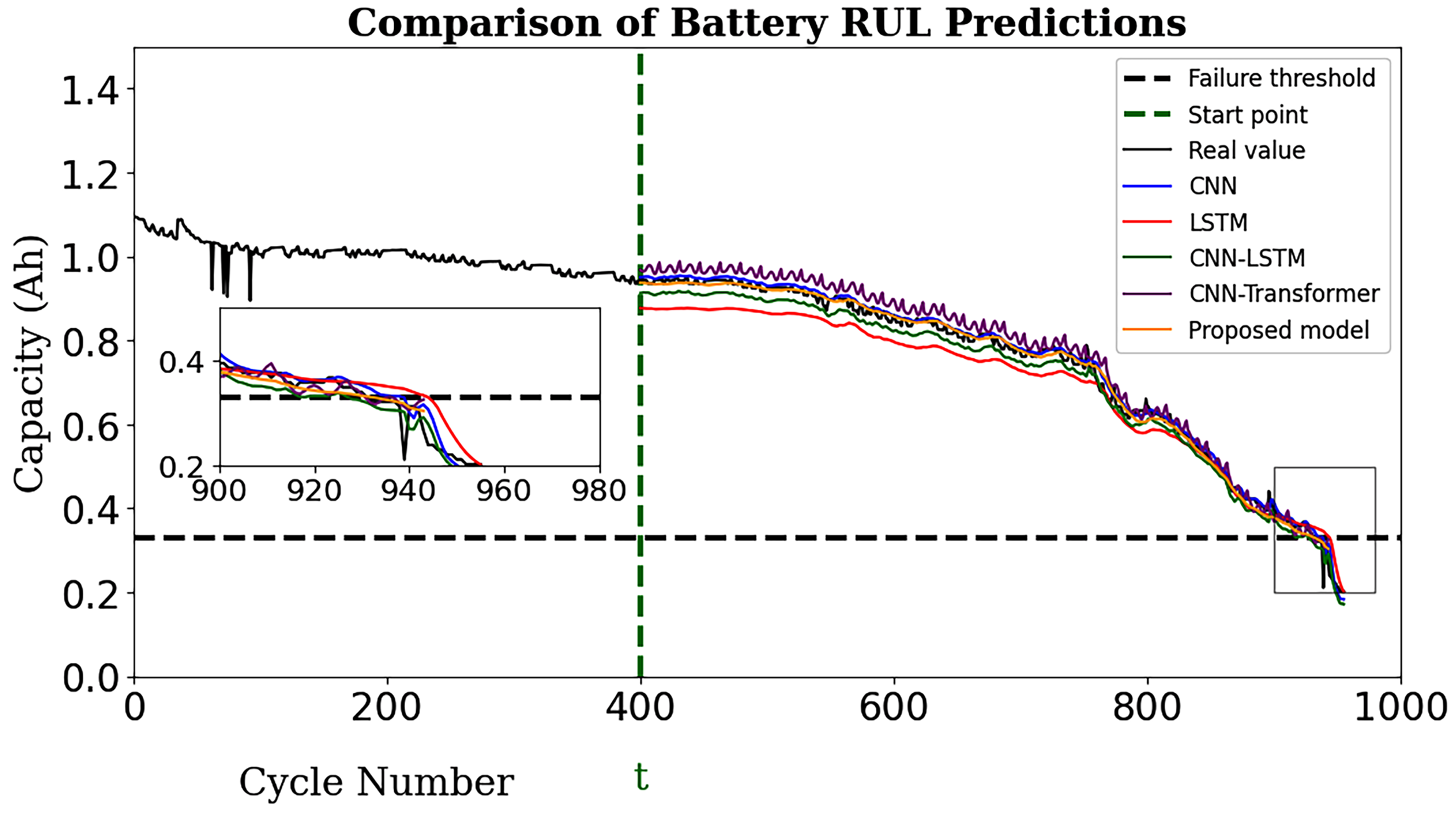
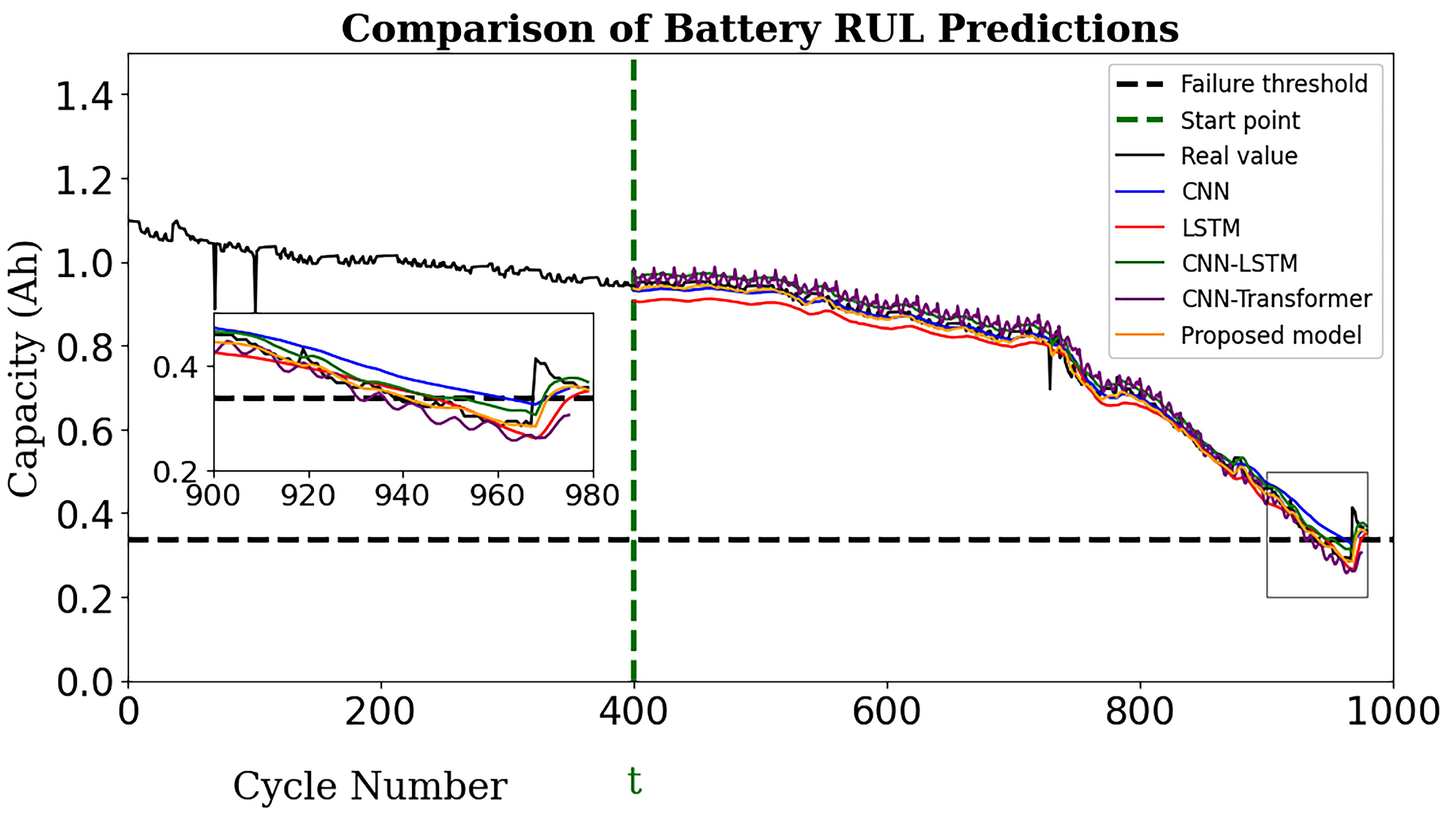
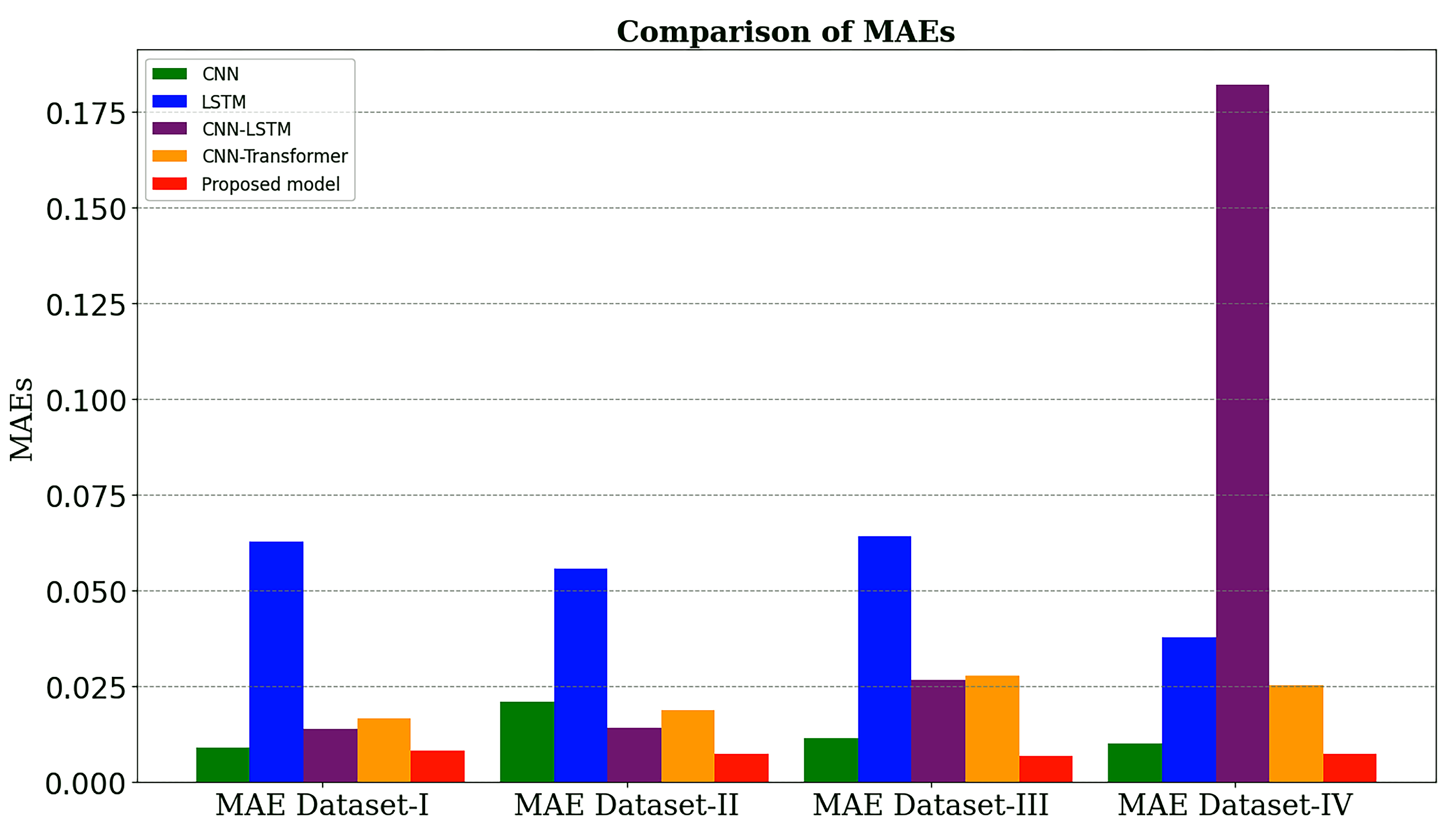
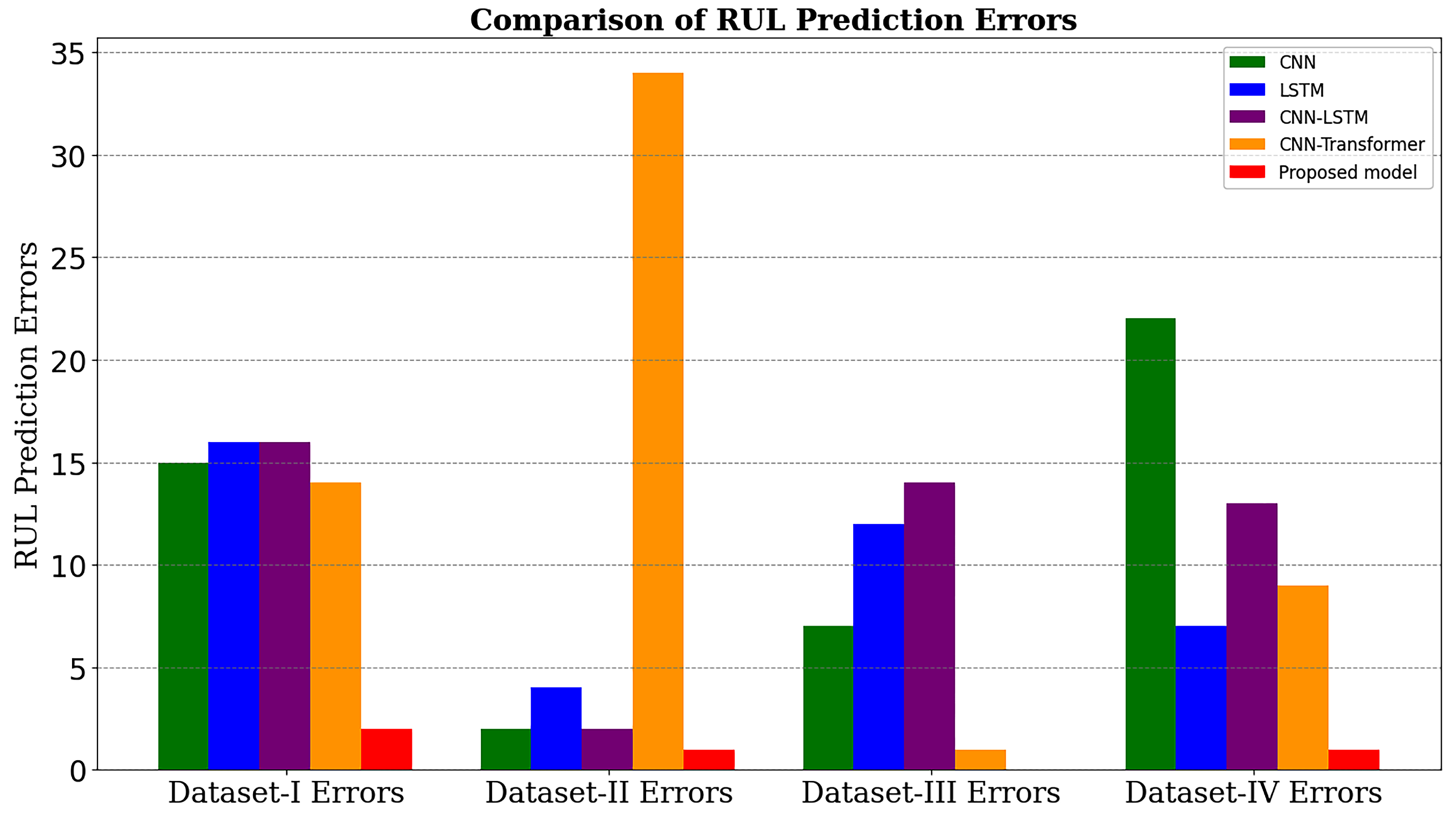
A comprehensive set of evaluation metrics, including MAE, RMSE, and R2, were used to evaluate the overall performance of the proposed model with existing models, like CNN, LSTM, CNN-LSTM, CNN-Transformer, and latest research work.
5. Conclusions
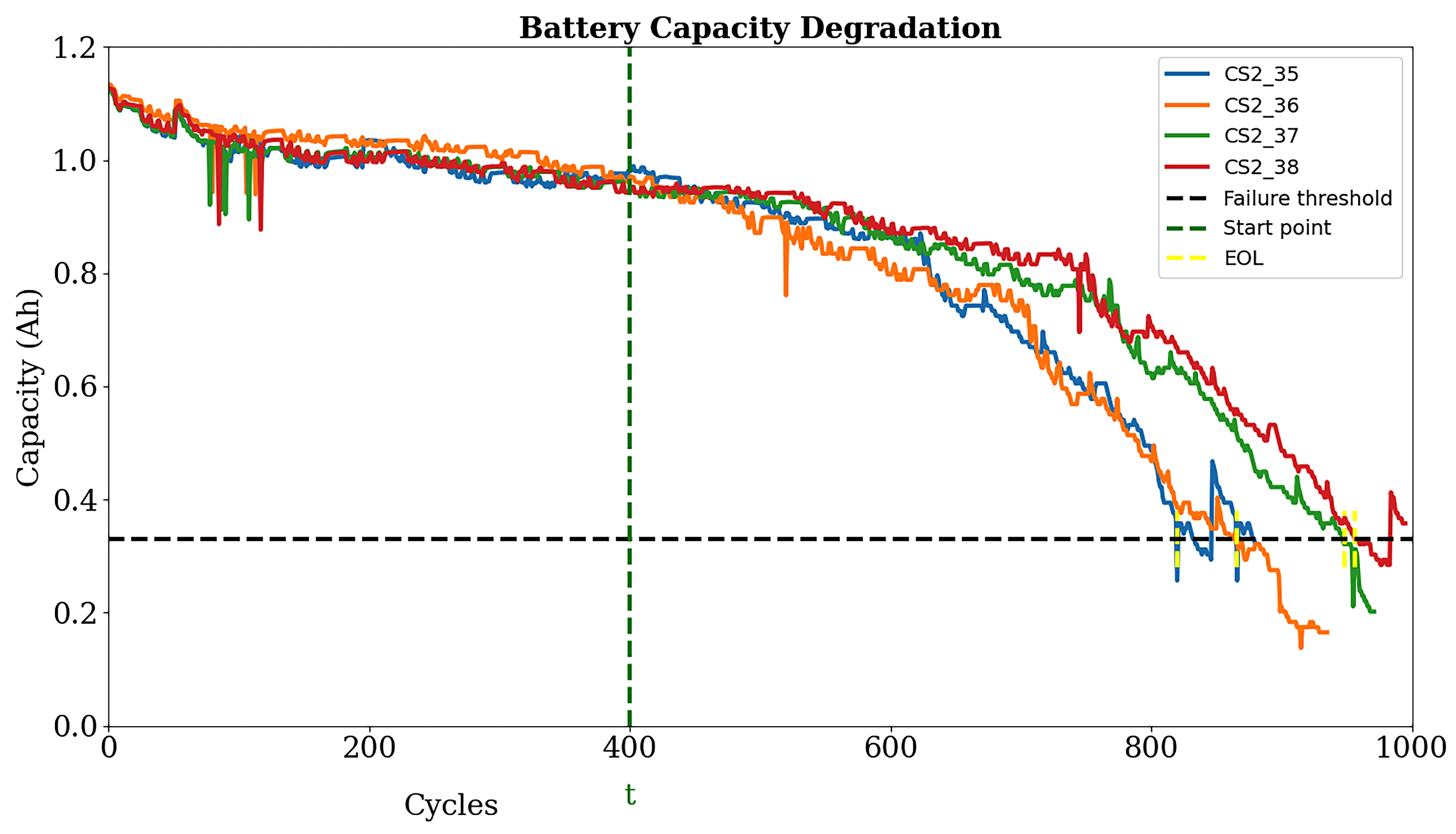
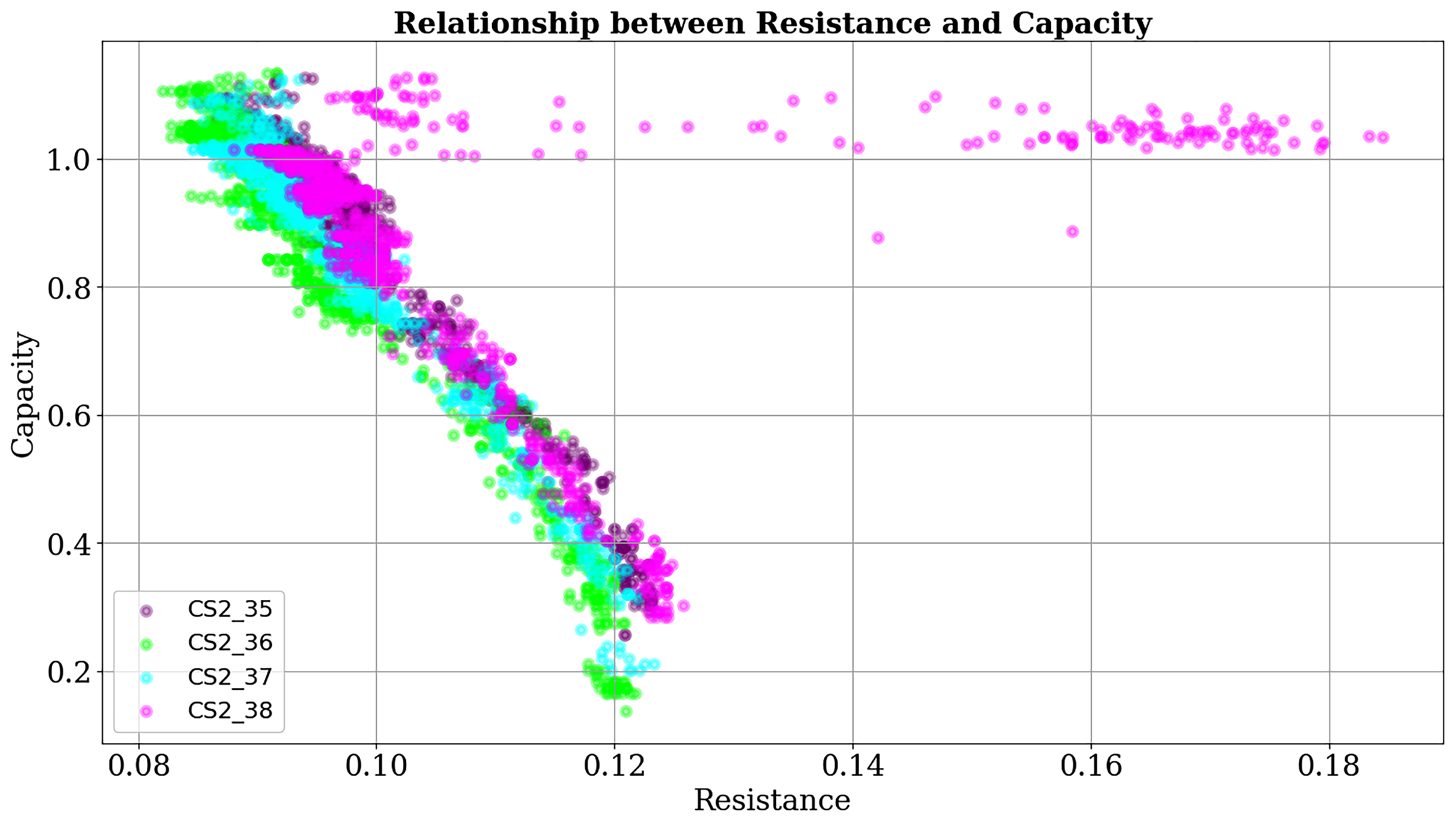
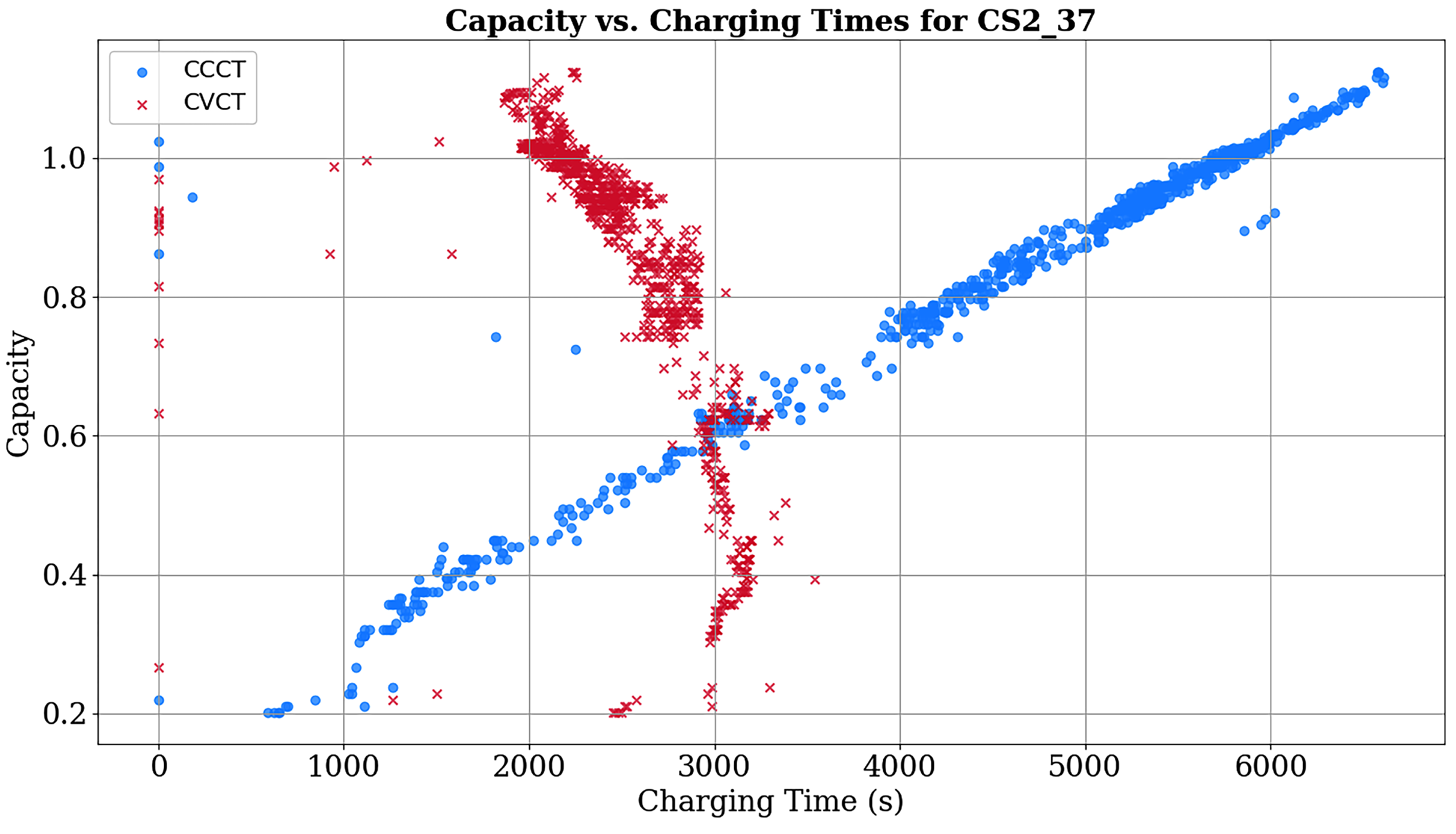
Accurate RUL prediction is essential for the safe and reliable operation of battery-based systems. To achieve an accurate RUL prediction, this work presents a time series transformer with a dual encoder and multi-head attention based TransRUL model, where a CALCE capacity dataset of four groups was used. The TransRUL model takes raw data as the input; the sliding window technique is used to generate the sequence, labeling, and splitting into time and capacity data. Then, the positional encoding and embedding was applied to both the datasets to prepare them for the encoder input. The TransRUL model uses a dual encoder, with six sub-layers of both, and each layer of them consisted of layer normalization, multi-head attention mechanisms, and FNNs. Both the encoders use the dropout technique to prevent over-fitting. The output features from both the sensor and time encoder are fused using the mean pool method and given as the input to the model decoder. The decoder produces the final output, which is the predicted RUL that uses two FCN layers and the ReLU activation function.
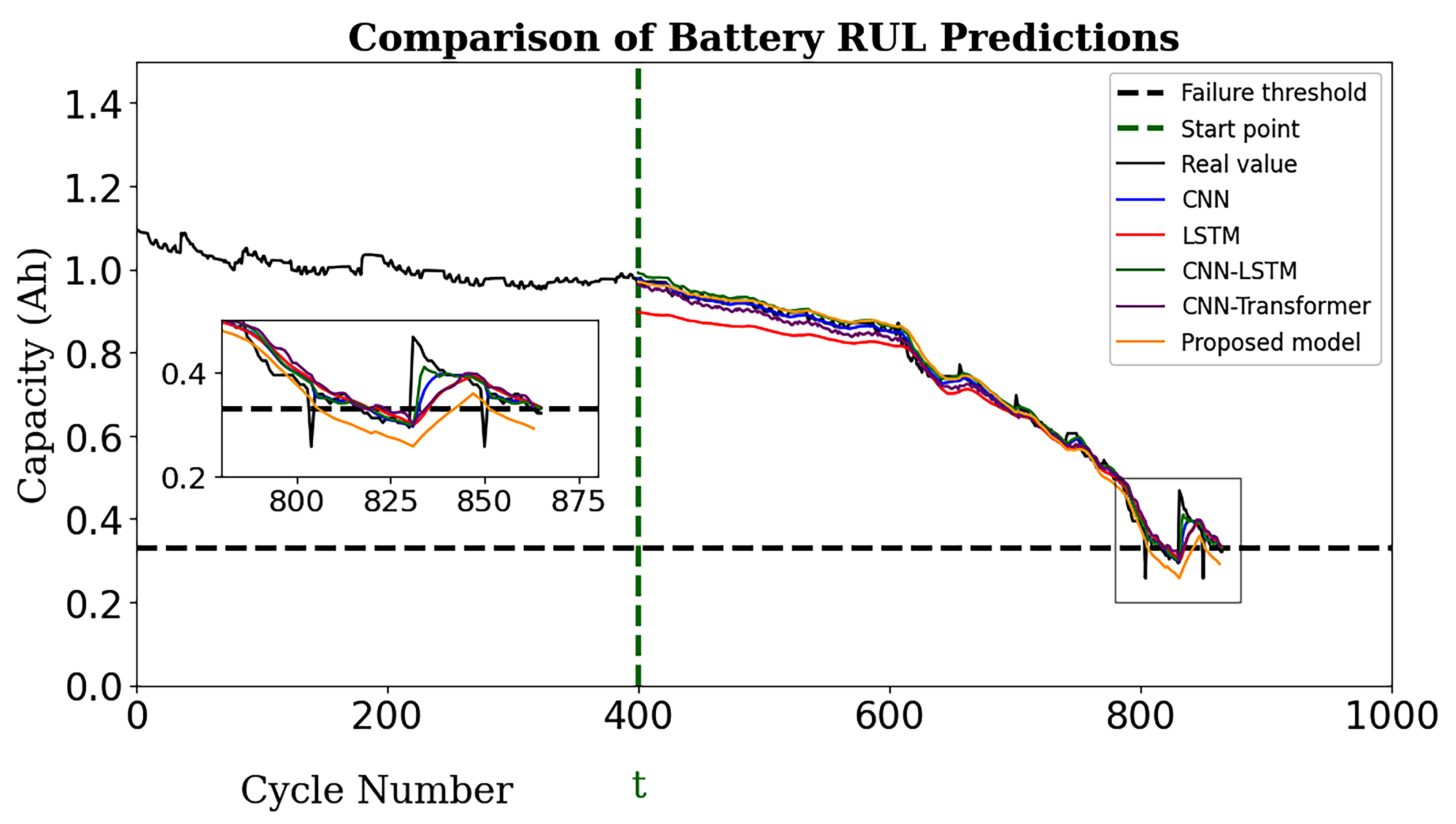
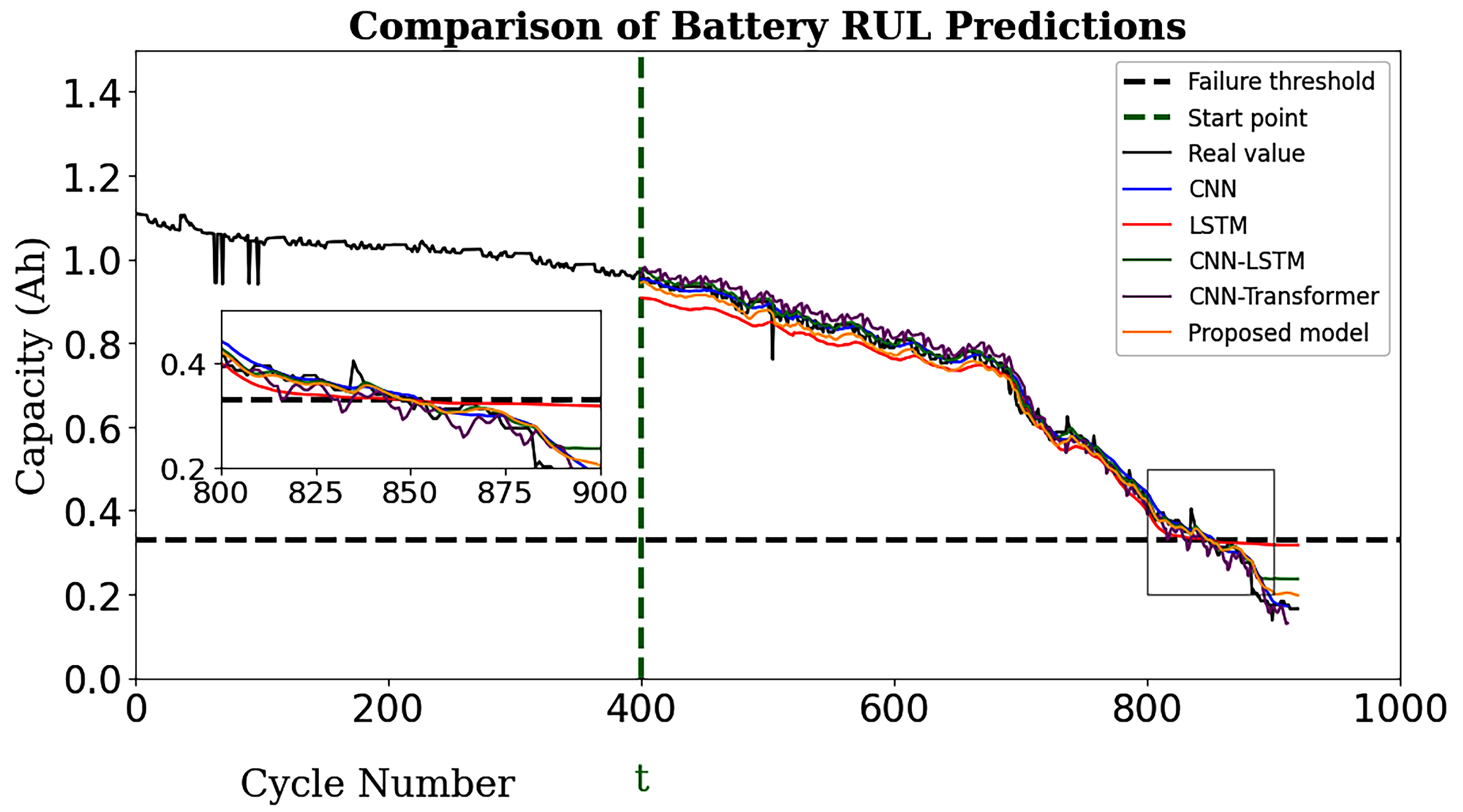
To train and test the proposed model, the LOOC validation method was used in this work. To validate the performance of the TransRUL model, a rigorous experimental assessment was conducted through the CALCE dataset for four different groups. The results highlight that the TransRUL model had a higher capability to predict the RUL with a high accuracy. The proposed model consistently demonstrated low MAE and RMSE values and a higher score compared with the following benchmark DL-based methods: CNN, LSTM, CNN-LSTM, and CNN-Transformer. The proposed method’s superiority in accurately predicting the RUL compared with the recent research is also noteworthy. Despite its good performance, the proposed TransRUL model has some limitations. First, the model has complexity that can lead to a higher computational load and skill for real-time deployment. Second, the model was trained and validated only on the CS_2 battery type using four groups from the CALCE dataset, which might limit its ability on other battery types or may require additional training. Third, the reliance on large datasets for training could pose challenges in scenarios where data are scarce or expensive to obtain.
In the future, this work can be extended to a wider range of battery types and develop less computationally expensive versions for deployment with online battery management systems for proactive maintenance. This research work presents a significant advancement in the field of battery energy storage systems.