Comparative Study for DC-DC Converter Output Bank’s Reliability Evaluation Using Prediction Standards MIL-HDBK-217F vs. Telcordia SR-332
Abstract
1. Introduction
- Mission-critical systems: DC-DC converters are integral to critical applications such as aerospace, medical devices, and telecommunications. Ensuring their reliability is essential to prevent system failures that could have severe consequences.
- Efficiency and cost optimization: reliable converters minimize downtime and maintenance costs. The calculation of the predicted reliability helps to optimize component selection, leading finally to efficient designs.
- Long service life: many systems require converters to function reliably for extended periods of time.
- Harsh environments: converters operate in different conditions, like elevated temperatures, humidity, and vibration.
2. Brief Math Presentation of the Reliability Concept
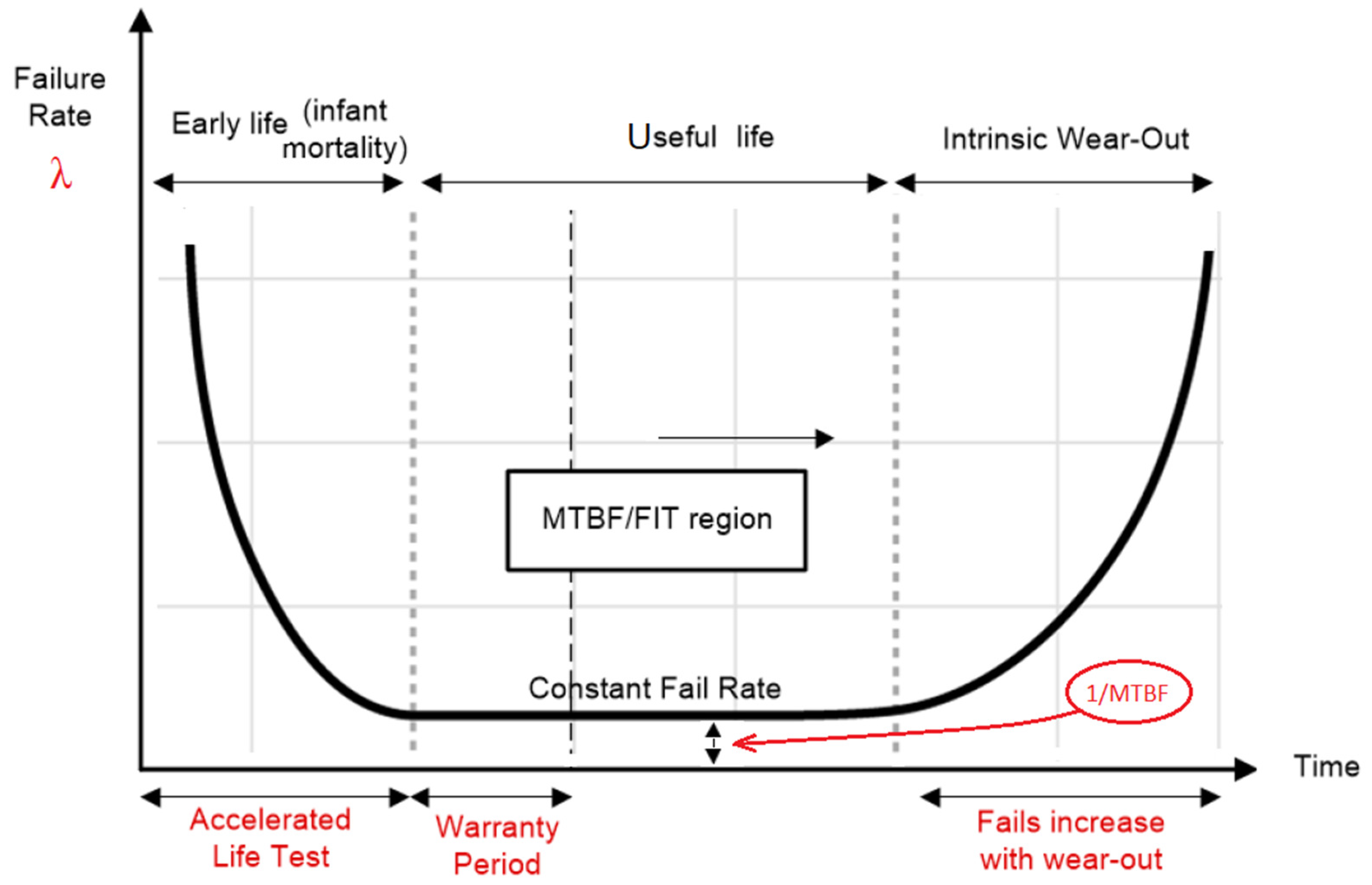
- Early life failures—characterized by a relatively higher initial failure rate, which reduces rapidly. Early life failures are primarily caused by manufacturing defects that are not effectively screened. Defects will always occur.
- Useful (normal) life failures—the region of the bathtub curve where the failure rate is relatively low and constant. This failure rate is quantified in units of failures in time (FIT) which is an estimate of the number of failures that could occur in a billion (i.e., 109) cumulative hours of the product’s operation.
- Intrinsic wear-out—a period of the product’s lifecycle when intrinsic wear-out dominates and failures increase exponentially. The end of a product’s useful lifetime is specified as the time of onset of wear-out. These types of failures are caused by well-known factors such as channel-hot-carrier effects, electromigration, time-dependent dielectric breakdown and negative bias temperature instability [11]. Usually there are two units of measure for its expression:
- ○
- [F/106 h], which stands for failures per one million component-hours.
- ○
- [FIT], which stands for failures in time (*) (that is, one failure per one billion component-hours).
3. Reliability Investigation—Experimental Part
- Point of load voltage regulation, such as distributed power systems where the individual components (GPUs, FPGAs, CPUs) require precise and low-voltage power supplies (e.g., Vout = 1.2 V).
- Battery-powered devices, such as portable electronic devices which often operate at low voltages (buck converters efficiently step-down battery voltage to power these devices).
- Also, the 1.2 V output is suitable for powering digital circuits, sensors, and display panels.
- Automotive applications. Buck converters are used in automotive electronics for various purposes. Here, a 1.2 V output can be useful for specific sensors or low-power components.
- LED drivers. LEDs require precise current control which is suitable with buck converters which maintain constant current and efficiency.
- Telecommunications equipment. In networking devices, routers, and switches buck converters regulate voltage for various components, such as ASICs and memory. Also, they can power specific integrated circuits in this field.
- Topology—the buck converter is a very popular choice due to its simplicity, reliability and low cost. It is suitable for most DC-DC applications.
- Operating conditions—it is necessary to ensure that the converter operates within its specified voltage and current limits. It is compulsory to consider input voltage range, load conditions, and switching frequency.
- Component selection—choosing cutting edge high-quality components especially for capacitors and MOSFETs to ensure reliable operation.
- Efficiency—it needs to be evaluated (as it impacts reliability) knowing that all converters generate less heat and experience less stress when they are more efficient.
- Output impedance—needs to be investigated to understand load regulation and transient behavior.
- Simulation—using tools like SPICE to simulate the buck converter behavior and evaluate thermal regime and performances.
- Real-time testing—conduct real-time experiments to verify the converter’s behavior under various load conditions.
- Comparison—compare different reliability prediction approaches.
| Convertor’s Parameters | Value |
|---|---|
| Rated output active power, Po | Max. 0.06 Ω × (25 A)2 = 37.5 W |
| Load current | Iout = max. 25 A, (5A @ transition step) |
| Input voltage, Vin | 12 V DC with 5% tolerance |
| Output voltage, Vout | 1.2 V DC ± 50 mV |
| Switching frequency, fsw | 500 kHz @ Duty cycle = 7.65% |
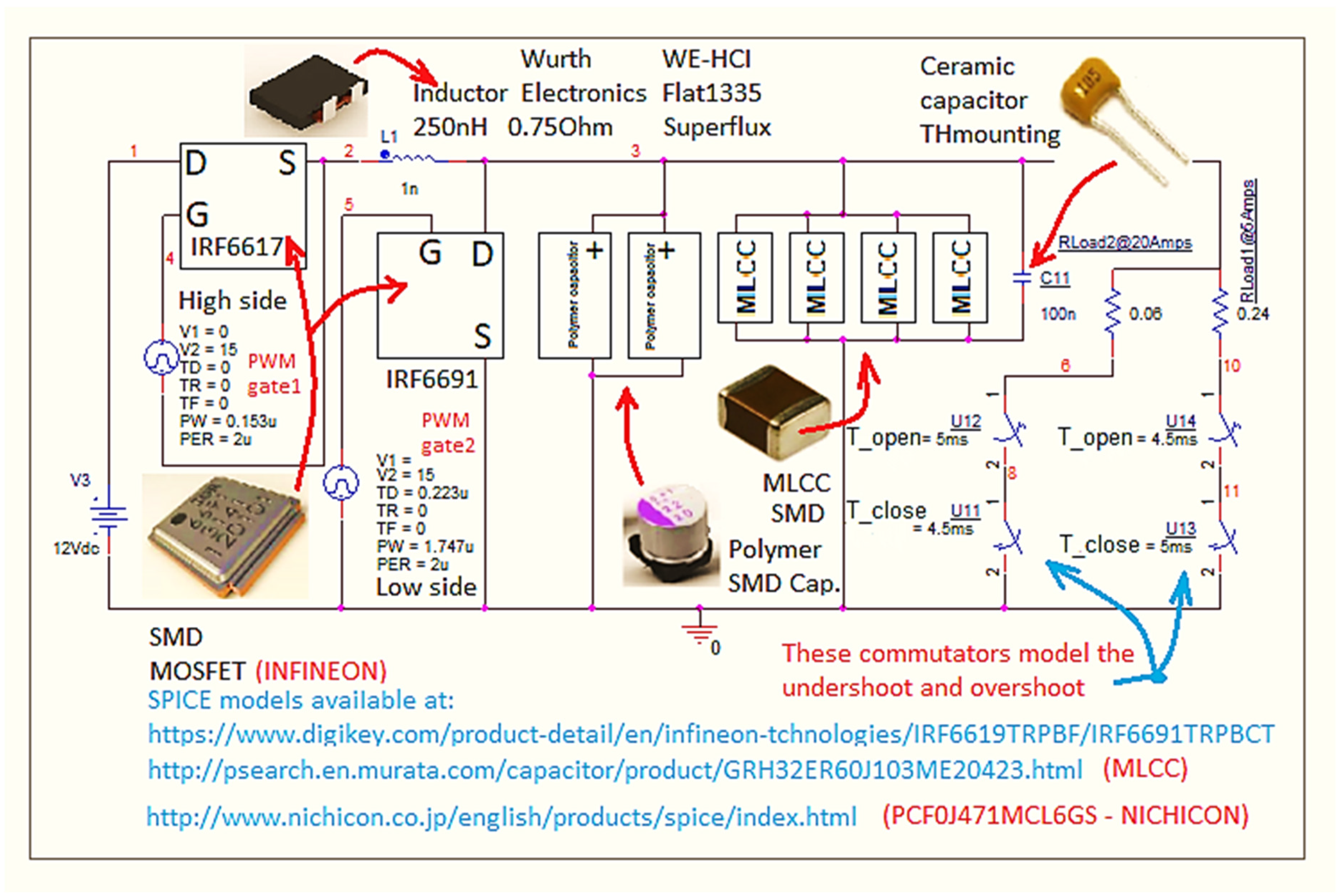
| Output capacitor bank, C | Polymer electrolytic [18]: 2 pcs. × 470 μF MLCCs [19]: 4 pcs. × 100 μF HF through hole ceramic: 1 pcs. × 100 nF |
| Inductor, L | 250 nH, 0.75 Ω, flat 1335, superflux |
| Switching transistors (MOSFETs) | IRF6617 (drive) and IRF6691 (sync) [16,18] |
| Transient load step | Current range variation: Idown = 5 A, Iup = 25 A |
4. PSPICE Simulation for Determining the Capacitor’s Temperature
5. MIL-HDBK-217F Prediction Standard—Brief Presentation, Discussion, and Reliability Calculation according to It
5.1. How MIL-HDBK-217 Standard Describes the Reliability Calculation
- operating phase;
- failure criterion;
- mode of operation (continuous or intermittent);
- mechanical stresses;
- electrical stresses;
- climatic stresses.
- technology of packaging;
- different manufacturers;
- manufacturing process;
- complexity.
5.2. Reliability Calculation for the Converter under Test
(for 2 parts in parallel we have 0.015334 or 15.334 [FIT])
(for 4 parts in parallel we have 0.5259 [F/106 h] or 525.9 [FIT])
(for only 1 part)
or 548.9 [FIT], (2 × polymer-SMD + 4 × MLCC-SMD + one ceramic HF)
6. Telcordia SR-332 Prediction Standard—Brief Presentation and Reliability Calculation according to It
- quality;
- stress;
- temperature.
- the term λGi represents the generic steady-state failure rate for the device i (according to Section 8 within the standard);
- the term σGi represents the standard deviation of the generic steady-state failure rate for device i (according to Section 8 within the standard);
- the term πQi represents the quality factor for device i (according to Section 9.3 within the standard);
- the term πSi represents the electrical stress factor for device i (according to Section 9.2 within the standard) and is based on the percentage of electrical stress. If stress is unknown, we use 1, which assumes 50% electrical stress;
- the term πTi represents the temperature factor that corresponds to device i (according to Section 9.1 within the standard) and is based on normal operating temperature during the steady state.
- λSSi = λBBi;
- σSSi = σBBi.
- Electrical stress percentage for capacitors in this standard is based on voltage, i.e., electrical stress (%) = (applied DC voltage + AC peak voltage)/rated voltage. So, we have for both MLCCs and for polymer: (1.2 + 0.2 V)/6.3 V = 22.2%, and for ceramic TH mounted capacitor: (1.2 + 0.2 V)/25 V = 5.6%.
- The πS factor for capacitor stress is taken from Table 9-2 (from the standard) and for polymer capacitors πS = 0.32 (using curve 3), for MLCCs πS = 0.52 (using curve 7), and for ceramic TH capacitors πS = 0.2.
- From the standard’s Table 8-1: λG-polymer = 0.19, λG-MLCC = 1, σ G-polymer = 0.13, σ G-MLCC = 4.4, and the temperature factors: πT-polymer = 1.48, πT-MLCC = 0.7, πT-ceramic TH = 0.9.
52.416 [FIT]
42.294 [FIT]
0.53628 [F/106 h] = 536.28 [FIT]
7. Comparative Results
8. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| a. List of abbreviations | |
| AC | Alternate current |
| DC | Direct current |
| ESL | Equivalent series inductance |
| ESR | Equivalent series resistance |
| F | Failure |
| FIT | Failures in time |
| HF | High frequency |
| MIL-HDBK | Military Handbook |
| MOSFET | Metal oxide semiconductor field effect transistor |
| MTBF | Mean time between failures |
| MTTF | Mean time to failure |
| MLCC | Multilayer ceramic capacitor |
| LED | Light-emitting diode |
| PoL | Point of load |
| PWM | Pulse width modulation |
| R | Reliability |
| RMS | Root mean square |
| SMD | Surface-mounted device |
| SPICE | Simulation Program with Integrated Circuit Emphasis |
| TH | Through hole |
| TD | Time delay |
| TR | Time rise |
| TF | Time fall |
| PW | Pulse width |
| PER | Period |
| b. List of symbols and their unit of measure | |
| λbase | [F/106 h] (failures per million hours) or [FIT] (failure per 109 h) |
| λref | [F/106 h], [FIT] |
| λsystem | [F/106 h], [FIT] |
| πT | [dimensionless] |
| πQ | [dimensionless] |
| πV | [dimensionless] |
| πSR | [dimensionless] |
| πE | [dimensionless] |
| πC | [dimensionless] |
References
- UN DESA Policy Brief No. 141: A Just Green Transition: Concepts and Practice So Far. Available online: https://www.un.org/development/desa/dpad/publication/un-desa-policy-brief-no-141-a-just-green-transition-concepts-and-practice-so-far (accessed on 31 July 2024).
- Vega Customer Applications Manual. Available online: https://www.emea.lambda.tdk.com/uk/KB/Vega-MTBF-to-MIL-217F-Application-Note.pdf (accessed on 31 July 2024).
- AFBR-57D7AMZ. Reliability Data Sheet. Available online: https://www.mouser.com/datasheet/2/678/av02-3362en-1828315.pdf (accessed on 31 July 2024).
- Darla, R.B.; Chitra, A. A Blackbox Failure Rate Prediction Method for Power Electronic Converters. In Proceedings of the 2021 IEEE Madras Section Conference (MASCON), Chennai, India, 27–28 August 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Catelani, M.; Ciani, L.; Bartolini, A.; Guidi, G.; Patrizi, G. Standby Redundancy for Reliability Improvement of Wireless Sensor Network. In Proceedings of the 2019 IEEE 5th International Forum on Research and Technology for Society and Industry (RTSI), Florence, Italy, 9–12 September 2019; pp. 364–369. [Google Scholar] [CrossRef]
- Zhang, Y.; Xia, J.; Zhang, X.; Chen, Z.; Li, B.; Luo, Q.; He, Y. Modeling and Prediction of the Reliability Analysis of an 18-Pulse Rectifier Power Supply for Aircraft Based Applications. IEEE Access 2020, 8, 47063–47071. [Google Scholar] [CrossRef]
- IEC 60601-1; Medical Electrical Equipment. IEC: Geneva, Switzerland, 2024. Available online: https://www.tuv.com/world/en/iec-60601-1-electrical-medical-equipment.html (accessed on 31 July 2024).
- ISO 26262; Road Vehicles—Functional Safety. ISO: Geneva, Switzerland, 2011. Available online: https://www.synopsys.com/glossary/what-is-iso-26262.html (accessed on 31 July 2024).
- Pecht, M.G.; Nash, F.R. Predicting the reliability of electronic equipment. Proc. IEEE 1994, 82, 992–1004. [Google Scholar] [CrossRef]
- Chong, A.B. Automated CHIP MTBF Calculator. In Proceedings of the 2022 11th International Conference on Communications, Circuits and Systems (ICCCAS), Singapore, 13–15 May 2022; pp. 59–63. [Google Scholar] [CrossRef]
- Kanert, W. Product reliability at low failure rates: Wrong expectations and real limitations. In Proceedings of the 2012 IEEE International Reliability Physics Symposium (IRPS), Anaheim, CA, USA, 15–19 April 2012; pp. 5C.4.1–5C.4.5. [Google Scholar] [CrossRef]
- Krasich, M. How to estimate and use MTTF/MTBF would the real MTBF please stand up? In Proceedings of the 2009 Annual Reliability and Maintainability Symposium, Fort Worth, TX, USA, 26–29 January 2009; pp. 353–359. [Google Scholar] [CrossRef]
- Zhou, D.; Song, Y.; Liu, Y.; Blaabjerg, F. Mission profile-based reliability evaluation of capacitor banks in wind power converters. IEEE Trans. Power Electron. 2019, 34, 4665–4677. [Google Scholar] [CrossRef]
- Griffith, W.S. Representation of Distributions Having Monotone or Bathtub-Shaped Failure Rates. IEEE Trans. Reliab. 1982, R–31, 95–96. [Google Scholar] [CrossRef]
- Understanding Functional Safety FIT Base Failure Rate Estimates per IEC 62380 and SN 29500. Available online: https://www.ti.com/lit/pdf/SLOA294 (accessed on 31 July 2024).
- IRF6617. 30V Single N-Channel Power MOSFET in a DirectFET™ ST Package. Available online: https://www.infineon.com/cms/en/product/power/mosfet/n-channel/irf6617/ (accessed on 31 July 2024).
- IRF6691TR1PBF. DigiKey. Available online: https://www.digikey.in/en/products/detail/infineon-technologies/IRF6691TR1PBF/1189804 (accessed on 31 July 2024).
- Technical Support Tools for SPICE MODEL Download. Available online: https://www.nichicon.co.jp/english/products/spice/index.html (accessed on 12 July 2024).
- Murata. Available online: https://www.murata.com/en-us/products/productdetail?partno=GRM32ER60J107ME20%23 (accessed on 31 July 2024).
- Butnicu, D.; Neacsu, D.O. Using SPICE for reliability based design of capacitor bank for telecom power supplies. In Proceedings of the 2017 IEEE 23rd International Symposium for Design and Technology in Electronic Packaging (SIITME), Constanta, Romania, 26–29 October 2017; pp. 423–426. [Google Scholar]
- Butnicu, D.; Neacsu, D.O. Using SPICE for multiple-constraint choice of capacitor bank for telecom power supplies. In Proceedings of the 2017 IEEE 23rd International Symposium for Design and Technology in Electronic Packaging (SIITME), Constanta, Romania, 26–29 October 2017. [Google Scholar]
- Military Handbook—Reliability Prediction of Electronic Equipment, MIL-HDBK-217F, Notice 2, 28 February 1995. Available online: http://everyspec.com/MIL-HDBK/MIL-HDBK-0200-0299/MIL-HDBK-217F_NOTICE-2_14590/ (accessed on 31 July 2024).
- Reliability Prediction Procedure for Electronic Equipment. Available online: https://telecom-info.njdepot.ericsson.net/site-cgi/ido/docs.cgi?ID=SEARCH&DOCUMENT=SR-332 (accessed on 31 July 2024).
- Neacsu, D.O.; Butnicu, D. A review and ultimate solution for output filters for high-power low-voltage DC/DC converters. In Proceedings of the 2017 International Symposium on Signals, Circuits and Systems (ISSCS), Iasi, Romania, 13–14 July 2017. [Google Scholar]
- RaghavendraRao, N.S.; Chitra, A.; Krishnachaitanya, D.; Anusha, M.K.; Srinath, M.S.; Raziasultana, W. Reliability Analysis of PMSM Drives Processor for Commercial Electric Vehicle Utility. In Proceedings of the 2024 Second International Conference on Emerging Trends in Information Technology and Engineering (ICETITE), Vellore, India, 22–23 February 2024; pp. 1–8. [Google Scholar] [CrossRef]
- Zhou, D.; Wang, H.; Blaabjerg, F. Mission Profile Based System-Level Reliability Analysis of DC/DC Converters for a Backup Power Application. IEEE Trans. Power Electron. 2018, 33, 8030–8039. [Google Scholar] [CrossRef]
- Zhou, L.; Cao, R.; Qi, C.; Shi, R. Reliability prediction for smart meter based on Bellcore standards. In Proceedings of the 2012 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, Chengdu, China, 15–18 June 2012; pp. 631–634. [Google Scholar] [CrossRef]

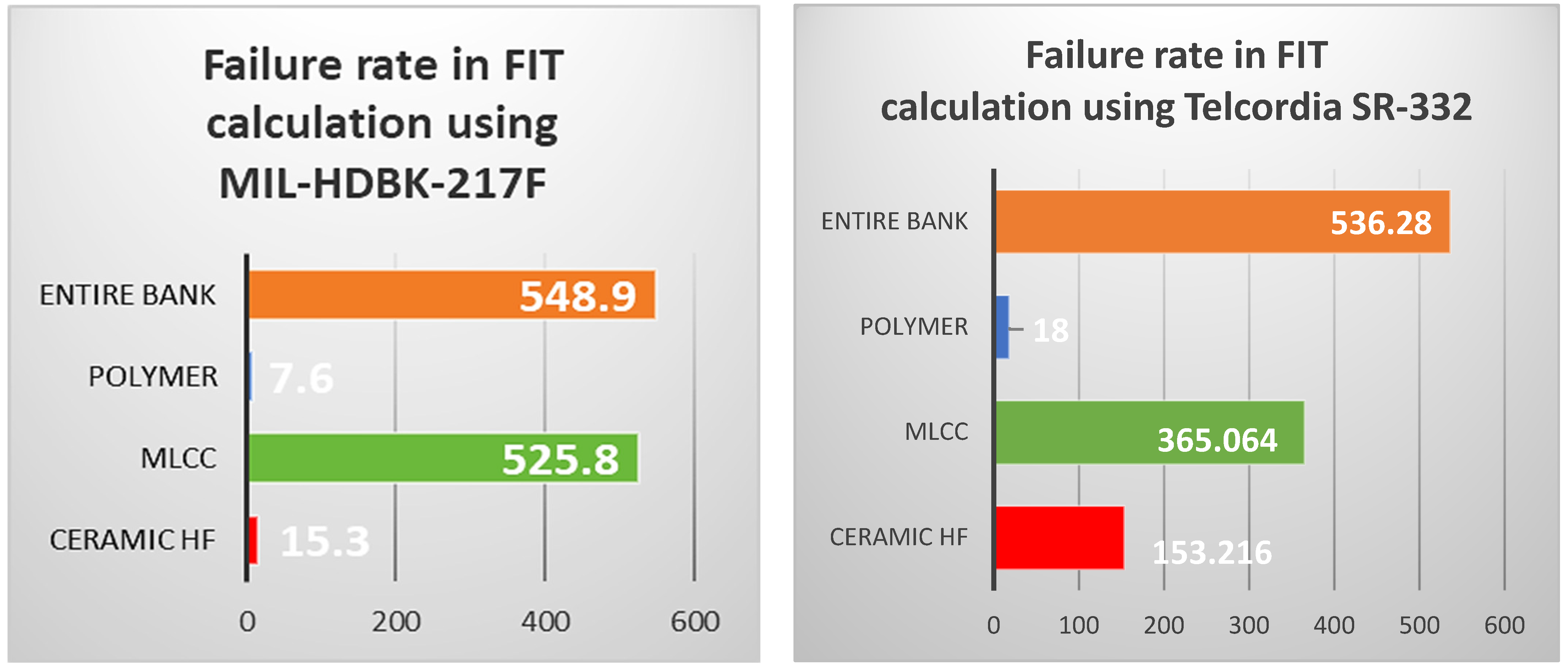
| Capacitor’s Technology | Failure Rate [FIT] and MTBF [h] (Values Calculated for 27 °C Ambient Temperature) | |
|---|---|---|
| λ MIL-HDBK-217 MTBF MIL-HDBK-217 | λ Telcordia SR-332 MTBF Telcordia SR-332 | |
| Two polymer electrolytic capacitors (SMD); each capacitor has T = 59 °C | 15.3 [FIT] 65,359,477 h | 153.216 [FIT] 6,526,733 h |
| Four MLCCs (SMD); each capacitor has T = 32 °C | 525.8 [FIT] 1,901,863 h | 365.064 [FIT] 2,739,245 h |
| One HF ceramic capacitor (through hole); T = 28 °C (due to small amount of current through it) | 7.6 [FIT] 131,578,947 h | 18 [FIT] 55,555,555 h |
| Entire capacitor bank | 548.9 [FIT] 1,821,825 h | 536.28 [FIT] 1,864,697 h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Butnicu, D. Comparative Study for DC-DC Converter Output Bank’s Reliability Evaluation Using Prediction Standards MIL-HDBK-217F vs. Telcordia SR-332. Energies 2024, 17, 3957. https://doi.org/10.3390/en17163957
Butnicu D. Comparative Study for DC-DC Converter Output Bank’s Reliability Evaluation Using Prediction Standards MIL-HDBK-217F vs. Telcordia SR-332. Energies. 2024; 17(16):3957. https://doi.org/10.3390/en17163957
Chicago/Turabian StyleButnicu, Dan. 2024. "Comparative Study for DC-DC Converter Output Bank’s Reliability Evaluation Using Prediction Standards MIL-HDBK-217F vs. Telcordia SR-332" Energies 17, no. 16: 3957. https://doi.org/10.3390/en17163957
APA StyleButnicu, D. (2024). Comparative Study for DC-DC Converter Output Bank’s Reliability Evaluation Using Prediction Standards MIL-HDBK-217F vs. Telcordia SR-332. Energies, 17(16), 3957. https://doi.org/10.3390/en17163957







