Comparative PSO Optimisation of Microgrid Management Models in Island Operation to Minimise Cost
Abstract
1. Introduction
- Objective 1: Analysis, systematisation and selection of optimal centralised microgrid management in islanded operation. This paper presents a comprehensive analysis of existing microgrid management models, focusing on their optimisation methods. Different approaches, including classical methods, metaheuristic techniques and artificial intelligence-based management, are analysed. Metaheuristic Particle Swarm Optimisation (PSO) is used due to its adaptability to problems with different types of constraints and objective functions and its iterative process of searching the solution space, improving the results through multiple iterations [34,35].
- Objective 2: Simulation model of centralised microgrid management considering microgrid components. In this paper, a detailed simulation model for centralised microgrid management is developed considering all relevant components such as photovoltaic panels, battery storage systems, diesel generators and bidirectional converters. This model was created using MATLAB R2022a Simulink and the Simscape Power Systems Toolbox and provides a robust environment for analysing and optimising the performance of microgrids under different conditions and configurations.
- Objective 3: Evaluation of the microgrid simulation model. The effectiveness of the proposed simulation model is evaluated through extensive simulations. Comparative analyses will be conducted to measure the performance of different management strategies, focusing on cost minimisation, reliability and resource utilisation. The results highlight the benefits of integrating advanced optimisation techniques such as PSO for optimal microgrid management.
2. Methodology and Mathematical Modelling
2.1. Selection of Optimal Management
- Preparation of the microgrid model: A microgrid model with discrete data is created to simulate the real operating conditions. MATLAB R2022a Simulink with the Simscape Power Systems Toolbox, which enables the modelling and analysis of energy systems, is used for the simulation. The model includes PV modules, a battery, a diesel generator, a bidirectional converter and loads. Parameters and constraints are also defined for each element of the MG.
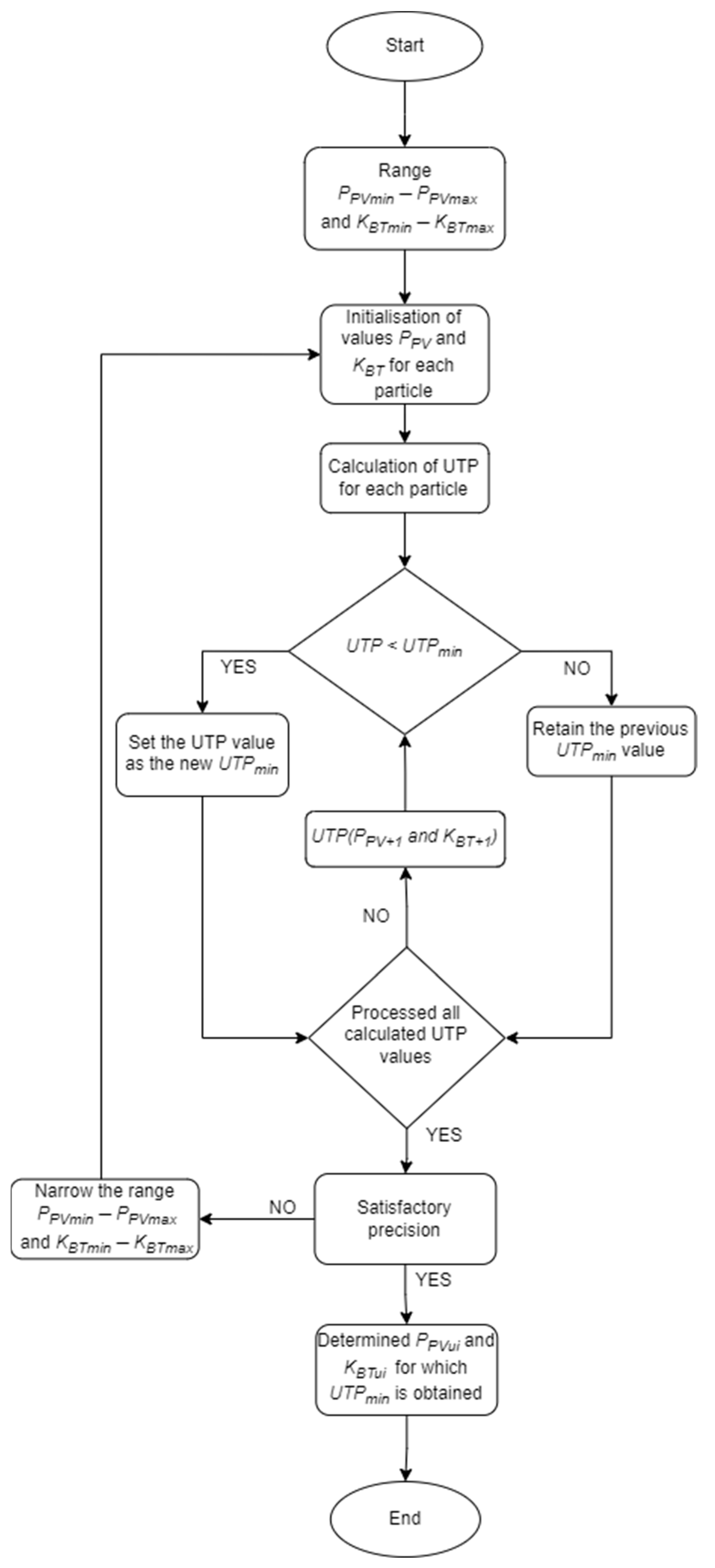
- Implementation of the PSO algorithm (Figure 3): The PSO algorithm is used to optimise the management of the MG. This process includes initialising a population of particles, evaluating the objective function, updating the velocity and position of the particles, checking convergence and selecting the optimal management model.
- Simulation of the proposed management algorithms: The proposed management algorithms are simulated in MATLAB R2022a Simulink using the Simscape Power Systems Toolbox. This setup enables the modelling and analysis of power systems. Parallel processing is used to speed up the execution of the algorithms and achieve efficient results.
- Analysis and comparison of the results: The results of the two algorithms for the management of the microgrid in islanded mode are analysed and compared. The production costs, including the fuel costs for the diesel generator, the maintenance costs and the costs of replacing batteries and inverters, are taken into account to minimise the objective function (UTP). The effects of various parameters on the optimisation process and the quality of the solution are also analysed.
2.2. Economic Indicators for Microgrid Optimisation
- o
- All system costs over the lifetime minus all revenues.
- o
- The value of the costs is reduced to present value by discounting.
- o
- Included costs: capital costs, replacement of system components, operation and maintenance costs, fuel, electricity purchased from the grid.
- o
- Revenues include sale of electricity to the grid, residual value of the system at the end of the project.
2.3. Defining the Input Data for the Microgrid Model
2.4. Location and Meteorological Data
2.5. Electricity Consumption Requirements at the Site
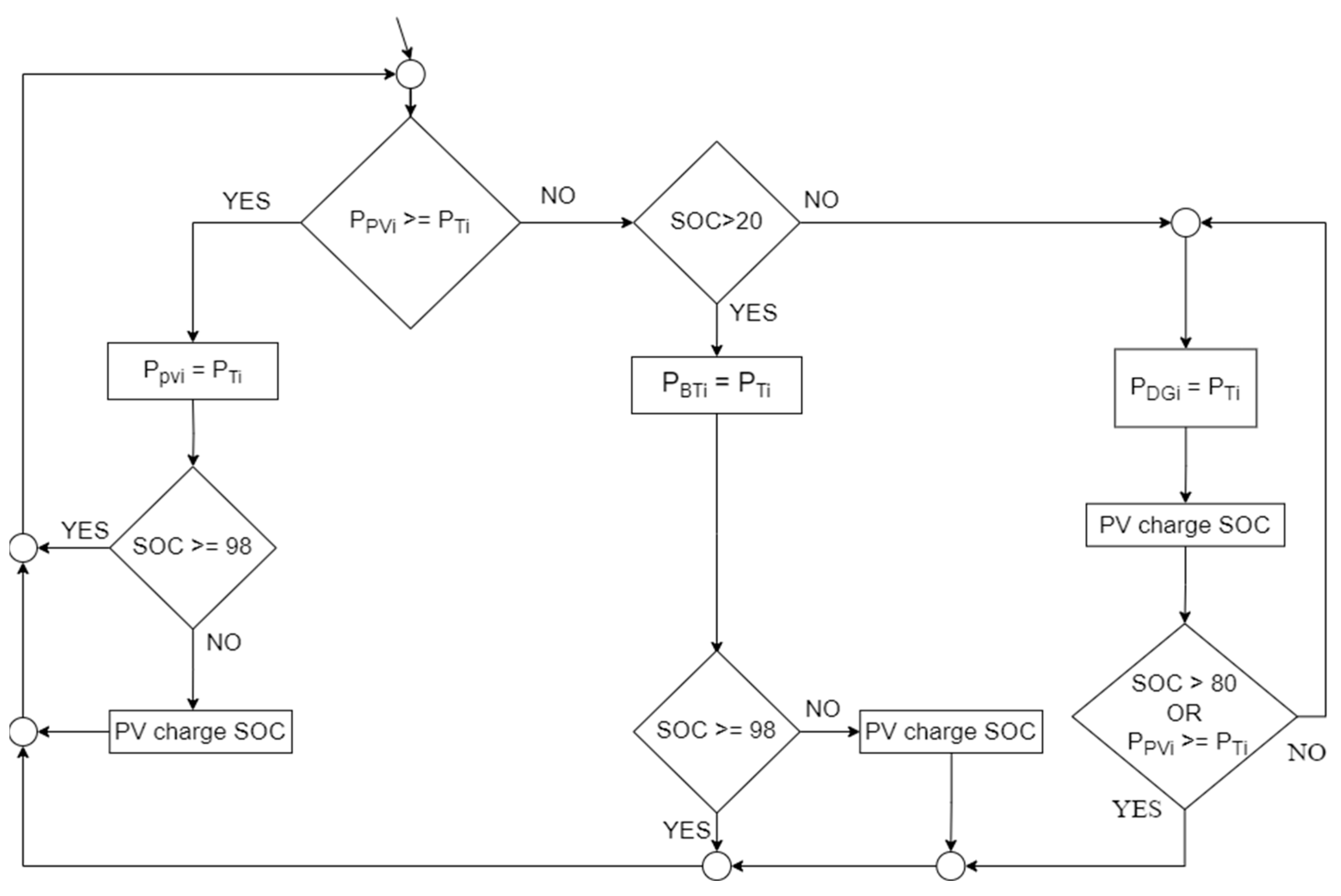
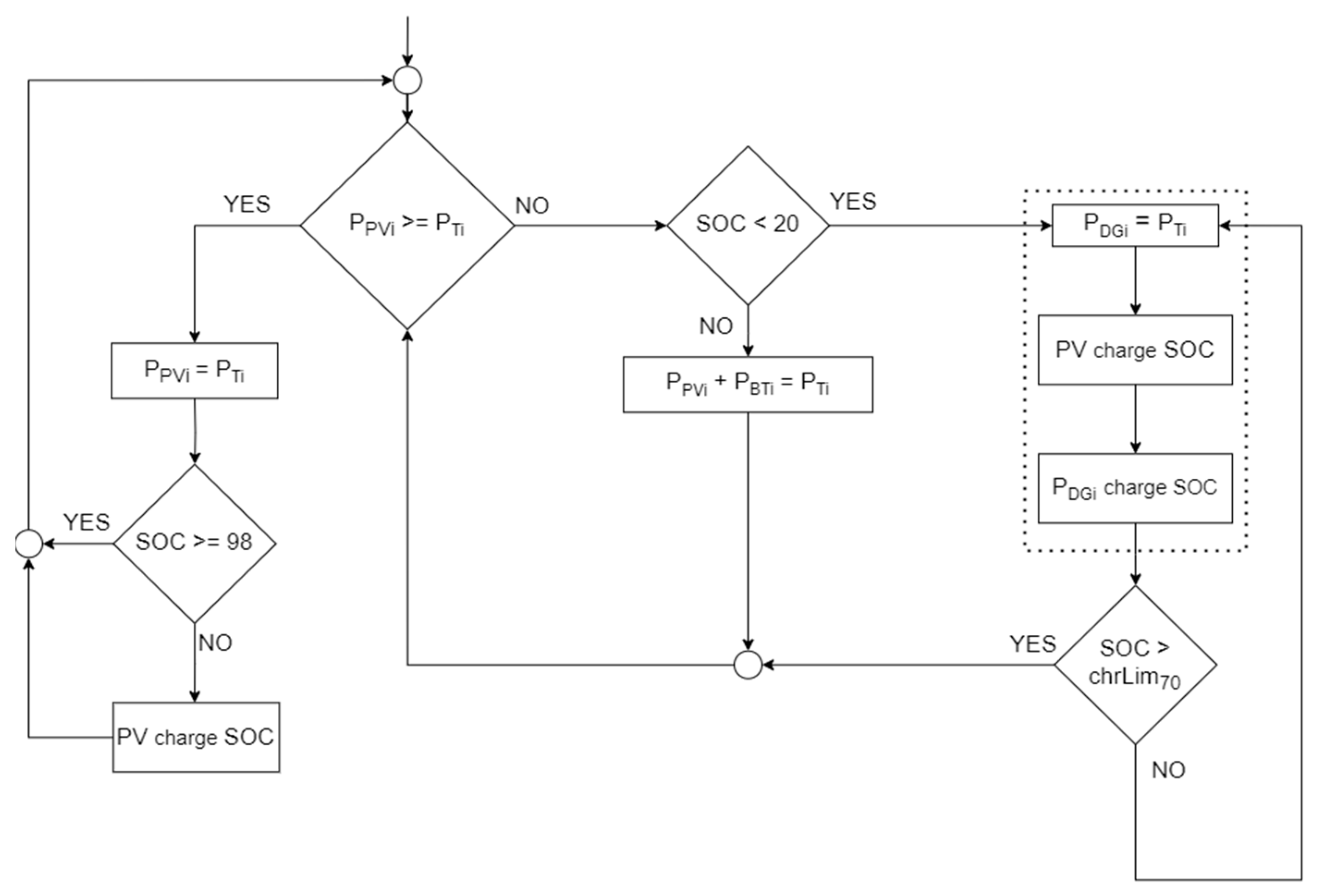
2.6. Selection of Optimal Microgrid Management in Island Operation
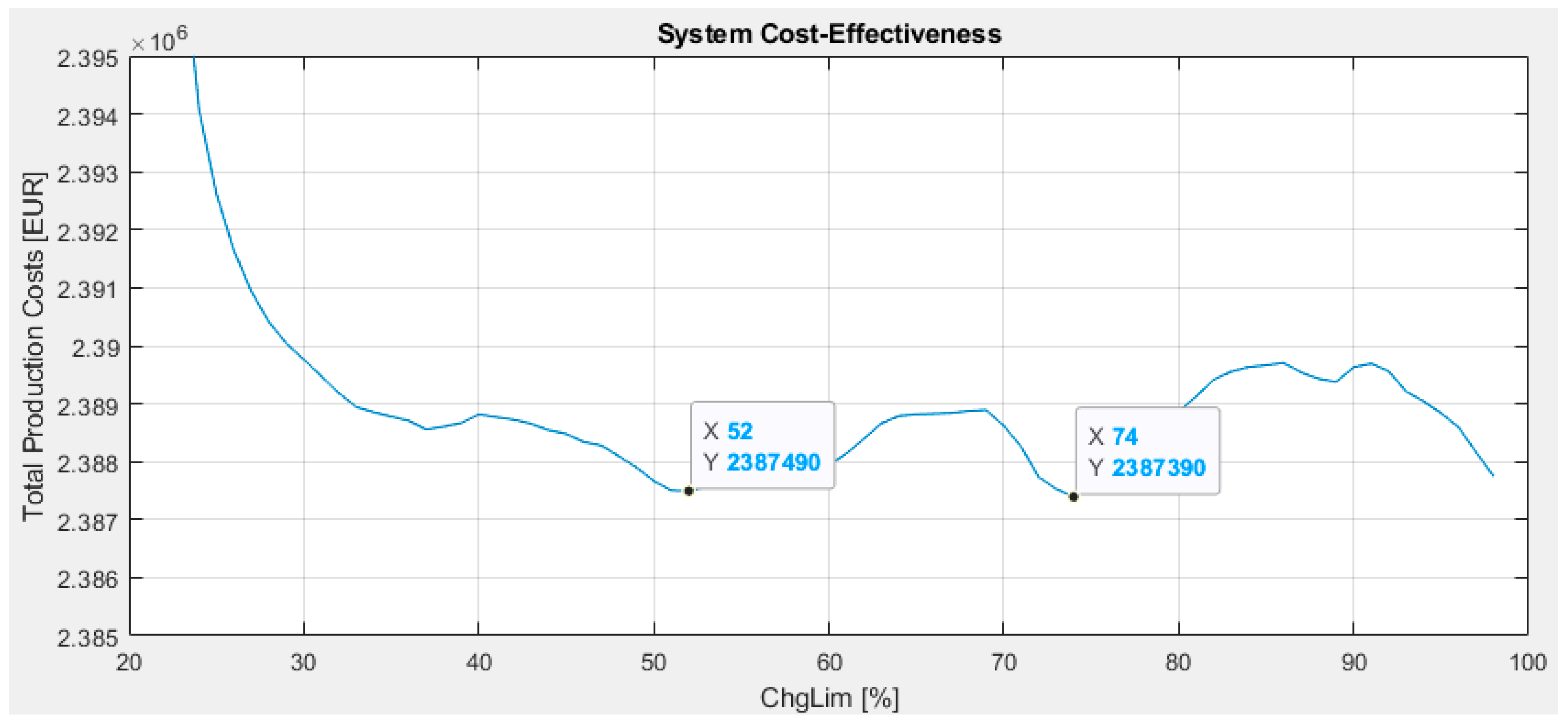
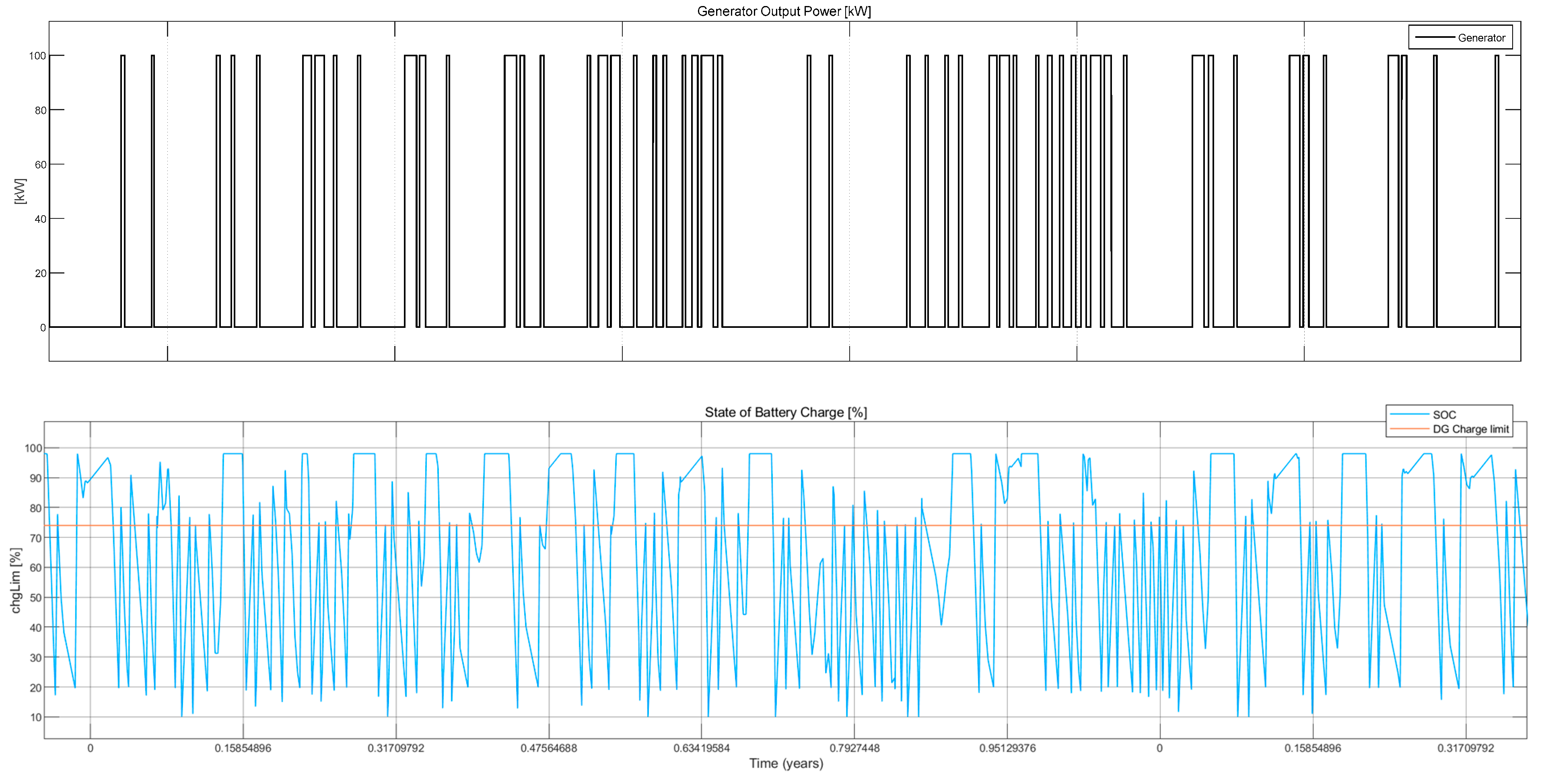
3. Evaluation Results and a Comparative Analysis
4. Discussion
- Objective 1: Analysis, systematisation and selection of optimal centralised microgrid management in islanded operation. The analysis and systematisation of optimisation methods, especially the PSO method, provided a comprehensive understanding of their performance and led to the selection of the M70 algorithm as the optimal model for centralised microgrid management in islanded operation, based on the minimisation of production costs.
- Objective 2: Simulation model for centralised microgrid management considering microgrid components. The development and implementation of detailed simulation models in MATLAB R2022a Simulink for both algorithms enabled an accurate evaluation of their performance under different conditions and revealed the strengths and weaknesses of each approach.
- Objective 3: Evaluation of the simulation model for the microgrid. The comprehensive evaluation of the simulation results highlighted the economic and operational benefits of the M70 algorithm and confirmed its superiority over the P algorithm in terms of cost efficiency and system reliability.
5. Conclusions
- The M70 algorithm achieved a total project cost (UTP) of EUR 2,312,823, which is significantly lower than the EUR 2,666,491 of the P model.
- The M70 model had lower maintenance and fuel costs due to the efficient operation of the diesel generator and the optimised balance of PV and battery capacities.
- The use of the PSO method to dynamically adjust the chrLim parameter in the M70 model proved to be highly effective in minimising costs and improving the overall efficiency of the system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- AlDavood, M.S.; Mehbodniya, A.; Webber, J.L.; Ensaf, M.; Azimian, M. Robust Optimization-Based Optimal Operation of Islanded Microgrid Considering Demand Response. Sustainability 2022, 14, 14194. [Google Scholar] [CrossRef]
- Parhizi, S.; Lotfi, H.; Khodaei, A.; Bahramirad, S. State of the art in research on microgrids: A review. IEEE Access 2015, 3, 890–925. [Google Scholar] [CrossRef]
- Shi, L.; Luo, Y.; Tu, G.Y. Bidding strategy of microgrid with consideration of uncertainty for participating in power market. Int. J. Electr. Power Energy Syst. 2014, 59, 1–13. [Google Scholar] [CrossRef]
- Liu, G.; Xu, Y.; Tomsovic, K. Bidding strategy for microgrid in day-ahead market based on hybrid stochastic/robust optimization. IEEE Trans. Smart Grid 2016, 7, 227–237. [Google Scholar] [CrossRef]
- Conti, S.; Nicolosi, R.; Rizzo, S.A.; Zeineldin, H.H. Optimal dispatching of distributed generators and storage systems for MV islanded microgrids. IEEE Trans. Power Deliv. 2012, 27, 1243–1251. [Google Scholar] [CrossRef]
- Ranjbar, H.; Safdarian, A. A Robust Model for Daily Operation of Grid-connected Microgrids During Normal Conditions. Sci. Iran. 2021, 28, 3480–3491. [Google Scholar] [CrossRef]
- Farzin, H.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M. Stochastic Energy Management of Microgrids during Unscheduled Islanding Period. IEEE Trans. Industr. Inform. 2017, 13, 1079–1087. [Google Scholar] [CrossRef]
- Ignat, A.; Lazar, E.; Petreus, D. Energy Management for an Islanded Microgrid Based on Particle Swarm Optimization. In Proceedings of the 2018 IEEE 24th International Symposium for Design and Technology in Electronic Packaging, SIITME 2018—Proceedings, Iasi, Romania, 25–28 October 2018; pp. 213–216. [Google Scholar] [CrossRef]
- Borowy, B.S.; Salameh, Z.M. Methodology for optimally sizing the combination of a battery bank and PV array in a Wind/PV hybrid system. IEEE Trans. Energy Convers. 1996, 11, 367–373. [Google Scholar] [CrossRef]
- Ai, B.; Yang, H.; Shen, H.; Liao, X. Computer-aided design of PV/wind hybrid system. Renew. Energy 2003, 28, 1491–1512. [Google Scholar] [CrossRef]
- Markvart, T. Sizing of hybrid photovoltaic-wind energy systems. Sol. Energy 1996, 57, 277–281. [Google Scholar] [CrossRef]
- Karaki, S.H.; Chedid, R.B.; Ramadan, R. Probabilistic performance assessment of autonomous solar-wind energy conversion systems. IEEE Trans. Energy Convers. 1999, 14, 766–772. [Google Scholar] [CrossRef]
- Tina, G.; Gagliano, S.; Raiti, S. Hybrid solar/wind power system probabilistic modelling for long-term performance assessment. Sol. Energy 2006, 80, 578–588. [Google Scholar] [CrossRef]
- Kellogg, W.D.; Nehrir, M.H.; Venkataramanan, G.; Gerez, V. Generation unit sizing and cost analysis for stand-alone wind, photovoltaic, and hybrid wind/PV systems. IEEE Trans. Energy Convers. 1998, 13, 70–75. [Google Scholar] [CrossRef]
- Yang, H.; Lu, L.; Zhou, W. A novel optimization sizing model for hybrid solar-wind power generation system. Sol. Energy 2007, 81, 76–84. [Google Scholar] [CrossRef]
- Heymann, B.; Bonnans, J.F.; Martinon, P.; Silva, F.J.; Lanas, F.; Jiménez-Estévez, G. Continuous optimal control approaches to microgrid energy management. Energy Syst. 2018, 9, 59–77. [Google Scholar] [CrossRef]
- Luu, N.A.; Tran, Q.T. Optimal energy management for grid connected microgrid by using dynamic programming method. In Proceedings of the IEEE Power and Energy Society General Meeting 2015, Denver, CO, USA, 26–30 July 2015. [Google Scholar] [CrossRef]
- Střelec, M.; Berka, J. Microgrid energy management based on approximate dynamic programming. In Proceedings of the 2013 4th IEEE/PES Innovative Smart Grid Technologies Europe, ISGT Europe 2013, Lyngby, Denmark, 6–9 October 2013. [Google Scholar] [CrossRef]
- Chalise, S.; Sternhagen, J.; Hansen, T.M.; Tonkoski, R. Energy management of remote microgrids considering battery lifetime. Electr. J. 2016, 29, 1–10. [Google Scholar] [CrossRef]
- Merabet, A.; Ahmed, K.T.; Ibrahim, H.; Beguenane, R.; Ghias, A.M.Y.M. Energy Management and Control System for Laboratory Scale Microgrid Based Wind-PV-Battery. IEEE Trans. Sustain. Energy 2017, 8, 145–154. [Google Scholar] [CrossRef]
- Choudar, A.; Boukhetala, D.; Barkat, S.; Brucker, J.-M. A local energy management of a hybrid PV-storage based distributed generation for microgrids. Energy Convers. Manag. 2014, 90, 21–33. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Optimization of solar systems using artificial neural-networks and genetic algorithms. Appl. Energy 2004, 77, 383–405. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, W.; Lu, L.; Fang, Z. Optimal sizing method for stand-alone hybrid solar-wind system with LPSP technology by using genetic algorithm. Sol. Energy 2008, 82, 354–367. [Google Scholar] [CrossRef]
- Koutroulis, E.; Kolokotsa, D.; Potirakis, A.; Kalaitzakis, K. Methodology for optimal sizing of stand-alone photovoltaic/wind-generator systems using genetic algorithms. Sol. Energy 2006, 80, 1072–1088. [Google Scholar] [CrossRef]
- Hong, Y.Y.; Lian, R.C. Optimal sizing of hybrid wind/PV/diesel generation in a stand-alone power system using markov-based genetic algorithm. IEEE Trans. Power Deliv. 2012, 27, 640–647. [Google Scholar] [CrossRef]
- Mostofi, F.; Shayeghi, H. Feasibility and optimal reliable design of renewable hybrid energy system for rural electrification in Iran. Int. J. Renew. Energy Res. 2012, 2, 574–582. [Google Scholar]
- Coello, C.A.C.; Lamont, G.B.; Van Veldhuizen, D.A.; Goldberg, D.E.; Koza, J.R. Evolutionary Algorithms for Solving Multi-Objective Problems; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Ramírez-Rosado, I.J.; Bernal-Agustín, J.L. Reliability and costs optimization for distribution networks expansion using an evolutionary algorithm. IEEE Trans. Power Syst. 2001, 16, 111–118. [Google Scholar] [CrossRef]
- Tsoi, E.; Wong, K.P.; Fung, C.C. Hybrid GA/SA algorithms for evaluating trade-off between economic cost and environmental impact in generation dispatch. In Proceedings of the IEEE Conference on Evolutionary Computation, Perth, Australia, 29 November–1 December 1995; Volume 1, pp. 132–137. [Google Scholar] [CrossRef]
- Corso, G.; Di Silvestre, M.L.; Ippolito, M.G.; Sanseverino, E.R.; Zizzo, G. Multi-objective long term optimal dispatch of distributed energy resources in micro-grids. In Proceedings of the Universities Power Engineering Conference, Cardiff, UK, 31 August–3 September 2010. [Google Scholar]
- Kitamura, S.; Mori, K.; Shindo, S.; Izui, Y.; Ozaki, Y. Multi-objective energy management system using modified MOPSO. In Proceedings of the 2005 IEEE International Conference on Systems, Man and Cybernetics, Waikoloa, HI, USA, 12 October 2005; Volume 4, pp. 3497–3503. [Google Scholar] [CrossRef]
- Pourmousavi, S.A.; Nehrir, M.H.; Colson, C.M.; Wang, C. Real-time energy management of a stand-alone hybrid wind-microturbine energy system using particle swarm optimization. IEEE Trans. Sustain. Energy 2010, 1, 193–201. [Google Scholar] [CrossRef]
- Mohammed, O.H.; Amirat, Y.; Benbouzid, M. Particle Swarm Optimization of a Hybrid Wind/Tidal/PV/Battery Energy System. Application To a Remote Area In Bretagne, France. Energy Procedia 2019, 162, 87–96. [Google Scholar] [CrossRef]
- Liu, E.J.; Hung, Y.H.; Hong, C.W. Improved Metaheuristic Optimization Algorithm Applied to Hydrogen Fuel Cell and Photovoltaic Cell Parameter Extraction. Energies 2021, 14, 619. [Google Scholar] [CrossRef]
- Faria, J.; Marques, C.; Pombo, J.; Mariano, S.; Calado, M.D.R. Optimal Sizing of Renewable Energy Communities: A Multiple Swarms Multi-Objective Particle Swarm Optimization Approach. Energies 2023, 16, 7227. [Google Scholar] [CrossRef]
- Pascual, J.; Arcos-Aviles, D.; Ursúa, A.; Sanchis, P.; Marroyo, L. Energy management for an electro-thermal renewable–based residential microgrid with energy balance forecasting and demand side management. Appl. Energy 2021, 295, 117062. [Google Scholar] [CrossRef]
- Zhou, W.; Lou, C.; Li, Z.; Lu, L.; Yang, H. Current status of research on optimum sizing of stand-alone hybrid solar-wind power generation systems. Appl. Energy 2010, 87, 380–389. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Mathiesen, B.V.; Leahy, M. A review of computer tools for analysing the integration of renewable energy into various energy systems. Appl. Energy 2010, 87, 1059–1082. [Google Scholar] [CrossRef]
- Mocanu, E.; Mocanu, D.C.; Nguyen, P.H.; Liotta, A.; Webber, M.E.; Gibescu, M.; Slootweg, J.G. On-Line Building Energy Optimization Using Deep Reinforcement Learning. IEEE Trans. Smart Grid 2019, 10, 3698–3708. [Google Scholar] [CrossRef]
- Mbuwir, B.; Ruelens, F.; Spiessens, F.; Deconinck, G. Reinforcement learning-based battery energy management in a solar microgrid. Energy-Open 2017, 2, 36. [Google Scholar]
- Maletsie, N.M.; Krishnamurthy, S. Review of Planning and Optimization of the Renewable-Energy-Based Micro-Grid for Rural Electrification. In Proceedings of the 32nd Southern African Universities Power Engineering Conference, SAUPEC 2024, Stellenbosch, South Africa, 24–25 January 2024; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2024. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC 2002, Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1051–1056. [Google Scholar] [CrossRef]
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Microgrids energy management systems: A critical review on methods, solutions, and prospects. Appl. Energy 2018, 222, 1033–1055. [Google Scholar] [CrossRef]
- Katche, M.L.; Makokha, A.B.; Zachary, S.O.; Adaramola, M.S. Techno-Economic Assessment of Solar–Grid–Battery Hybrid Energy Systems for Grid-Connected University Campuses in Kenya. Electricity 2024, 5, 61–74. [Google Scholar] [CrossRef]
- Miao, C.; Teng, K.; Wang, Y.; Jiang, L. Technoeconomic Analysis on a Hybrid Power System for the UK Household Using Renewable Energy: A Case Study. Energies 2020, 13, 3231. [Google Scholar] [CrossRef]
- Mongird, K.; Viswanathan, V.; Balducci, P.; Alam, J.; Fotedar, V.; Koritarov, V.; Hadjerioua, B. An Evaluation of Energy Storage Cost and Performance Characteristics. Energies 2020, 13, 3307. [Google Scholar] [CrossRef]
- Yimen, N.; Tchotang, T.; Kanmogne, A.; Abdelkhalikh Idriss, I.; Musa, B.; Aliyu, A.; Okonkwo, E.C.; Abba, S.I.; Tata, D.; Meva’a, L.; et al. Optimal Sizing and Techno-Economic Analysis of Hybrid Renewable Energy Systems—A Case Study of a Photovoltaic/Wind/Battery/Diesel System in Fanisau, Northern Nigeria. Processes 2020, 8, 1381. [Google Scholar] [CrossRef]
- Lakhina, U.; Elamvazuthi, I.; Badruddin, N.; Jangra, A.; Truong, B.H.; Guerrero, J.M. A Cost-Effective Multi-Verse Optimization Algorithm for Efficient Power Generation in a Microgrid. Sustainability 2023, 15, 6358. [Google Scholar] [CrossRef]
- Hu, X.; Eberhart, R.C.; Shi, Y. Particle swarm with extended memory for multiobjective optimization. In Proceedings of the 2003 IEEE Swarm Intelligence Symposium, SIS 2003—Proceedings, Indianapolis, IN, USA, 26 April 2003; pp. 193–197. [Google Scholar] [CrossRef]
- Alarcon-Rodriguez, A.; Ault, G.; Galloway, S. Multi-objective planning of distributed energy resources: A review of the state-of-the-art. Renew. Sustain. Energy Rev. 2010, 14, 1353–1366. [Google Scholar] [CrossRef]
| Ref. | Year | Proposed Optimisation Method | Advantages | Disadvantages |
|---|---|---|---|---|
| [8] | 2018 | PSO | Cost-effective, shorter calculation time compared to other methods | Requires detailed meteorological and load data |
| [16] | 2018 | Dynamic programming | Achieves global optimal solutions quickly, accurate modelling, handles switching costs effectively | Computer complexity and high resource requirements for large problems |
| [42] | 2018 | Multi-Objective Particle Swarm Optimisation (MOPSO) | Efficient handling of multiple objectives using Pareto dominance, maintains diversity through a global repository. | Complexity in implementation, requires careful tuning of parameters for effective performance |
| [43] | 2018 | Various methods, including PSO, GA, MILP and rule-based approaches | A wide range of methods ensures flexibility and robustness in optimisation, suitable for various microgrid scenarios | High computational complexity, need for extensive data and parameter tuning |
| [33] | 2019 | PSO | High reliability, optimised cost of energy (COE) and total net present cost (TNPC), efficient management of constraints | Requires considerable computing resources, the quality of the solution depends on the parameters and initial conditions |
| [39] | 2019 | Deep Reinforcement Learning (DRL) | Real-time optimisation, processing of high-dimensional data, adaptability to changing environments | High computing requirements, complexity in implementation and tuning |
| [44] | 2020 | Simulation using HOMER Pro 3.14.5 software | Significant reduction in annual electricity costs (83.94%), high proportion of renewable energy (67.1%), environmentally friendly design | Without diesel generators, increasing dependence on photovoltaics and grid stability |
| [45] | 2020 | Simulation using HOMER Pro 3.14.5 software | Optimum configuration with low net present cost (NPC) and levelised cost of energy (LCOE) identified | High initial investment, complexity of system integration |
| [46] | 2020 | PSO | High efficiency in exploring the search space, good compromise between different goals | Risk of premature convergence to local optimum |
| [47] | 2020 | Genetic Algorithm (GA) for optimisation using MATLAB R2022a | Achieves minimum total annual costs (TAC) and a high proportion of renewable energy (98.72%) | High computational requirements, complex implementation |
| [6] | 2021 | Robust Optimisation (RO) using Bi-level Max-Min Optimisation | Takes into account uncertainties in renewable energy production, demand and market prices, leading to more reliable and robust solutions | Computationally intensive, requires iterative process and complex implementation |
| [34] | 2021 | Three types of PSO (Inertia Weight PSO, Constriction PSO, Momentum PSO) | High efficiency in parameter extraction, improved accuracy, fast convergence | Potential risk of premature convergence, computationally intensive |
| [36] | 2021 | Combined use of Central Moving Average (CMA) approach | Reduces battery size by 25%, achieves a better grid current profile, minimises current peaks and fluctuations | Computer complexity, requires accurate prediction of performance profiles |
| [1] | 2022 | Hybrid Genetic Algorithm (GA) and Mixed-Integer Linear Programming (MILP) | Minimises the total cost of ownership of microgrids, manages worst-case uncertainties, improves reliability and robustness | High computational complexity, requires extensive computing resources |
| [35] | 2023 | Multi-Objective Particle Swarm Optimisation (MOPSO) | Improves solution diversity, ensures a broad spectrum of non-dominant solutions, mitigates premature convergence | Complex implementation, requires high computing resources |
| [48] | 2023 | Cost-effective Multi-Verse Optimisation Algorithm (CMVO) | Efficient energy planning, lower generation costs, better convergence speed | Complexity in implementation, requires careful parameter tuning |
| [41] | 2024 | PSO | Flexibility, fast convergence time, high performance | High computing requirements, complexity of implementation |
| 2024 | This paper—PSO | Adaptability to various constraints and objectives, improved cost efficiency and system reliability | Requires detailed tuning of the parameters and can be computationally intensive for extensive applications |
| Optimal Values | 1. PSO Algorithm P | 2. PSO Algorithm M70 | ||
|---|---|---|---|---|
| PPVmin–PPVmax | KBTmin–KBTmax | PPVmin–PPVmax | KBTmin–KBTmax | |
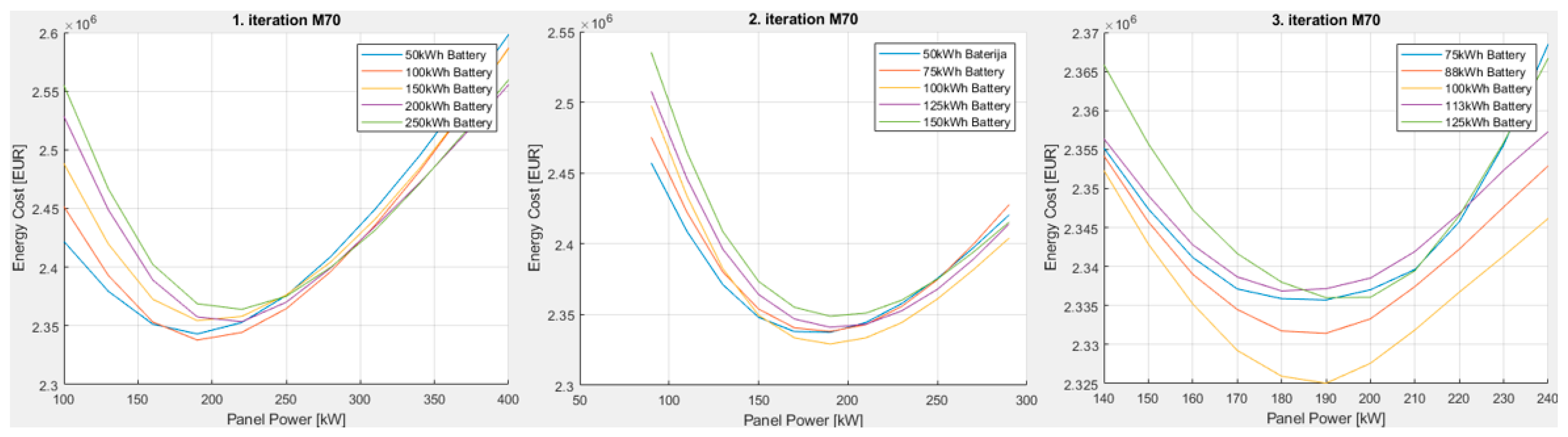
| 1. iteration | 100–400 | 50–500 | 100–400 | 50–250 |
| 2. iteration | 240–440 | 275–500 | 90–290 | 50–150 |
| 3. iteration | 290–390 | 388–500 | 140–240 | 75–125 |
| PPV i KBT | 330 kW | 419 kWh | 190 kW | 100 kWh |
| UTP | EUR 2,666,491 | EUR 2,312,823 | ||
| COE | EUR 0.397 | EUR 0.343 | ||
| NPC | EUR 2,065,129 | EUR 1,690,412 | ||
| LCOE | EUR 0.307 | EUR 0.251 | ||
| Model | PV (kW) | Converter (kW) | Battery (kWh) | DG (kW) | PV Energy (kWh) | DG Energy (kWh) | Average Power DG (kW) | Fuel (L) 0.335 L/kWh | Consumption (kWh) |
|---|---|---|---|---|---|---|---|---|---|
| P | 330 | 313.5 | 419 | 100 | 222,189 | 66,882 | 30 | 28,370 | 269,431 |
| M70 | 190 | 180.5 | 100 | 100 | 143,454 | 138,728 | 100 | 38,671 | 269,431 |
| Economic Indicators | Management Algorithm | ||
|---|---|---|---|
| Optimal Point of Algorithm P | M70 | P | |
| Initial Investment | EUR 751,411 | EUR 751,411 | |
| Annual Maintenance and Fuel Costs | EUR 52,532 | EUR 58,870 | |
| Total Project Cost (UTP) | EUR 2,508,051 | EUR 2,666,491 | |
| Cost of Energy per kWh (COE) | EUR 0.372 | EUR 0.396 | |
| Average Annual Cost | EUR 100,322 | EUR 106,660 | |
| Net Present Cost (NPC) | EUR 1,950,789 | EUR 2,058,490 | |
| Levelised Cost of Energy per kWh (LCOE) | EUR 0.290 | EUR 0.306 | |
| Economic Indicators | Management Algorithm | ||
|---|---|---|---|
| Optimal Point of Algorithm M70 | M70 | P | |
| Initial Investment | EUR 363,022 | EUR 363,022 | |
| Annual Maintenance and Fuel Costs | EUR 72,641 | EUR 103,287 | |
| Total Project Cost (UTP) | EUR 2,312,823 | EUR 3,078,970 | |
| Cost of Energy per kWh (COE) | EUR 0.343 | EUR 0.457 | |
| Average Annual Cost | EUR 92,513 | EUR 123,159 | |
| Net Present Cost (NPC) | EUR 1,690,412 | EUR 2,211,205 | |
| Levelised Cost of Energy per kWh (LCOE) | EUR 0.251 | EUR 0.328 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Žigman, D.; Tvorić, S.; Lonić, M. Comparative PSO Optimisation of Microgrid Management Models in Island Operation to Minimise Cost. Energies 2024, 17, 3901. https://doi.org/10.3390/en17163901
Žigman D, Tvorić S, Lonić M. Comparative PSO Optimisation of Microgrid Management Models in Island Operation to Minimise Cost. Energies. 2024; 17(16):3901. https://doi.org/10.3390/en17163901
Chicago/Turabian StyleŽigman, Dubravko, Stjepan Tvorić, and Manuel Lonić. 2024. "Comparative PSO Optimisation of Microgrid Management Models in Island Operation to Minimise Cost" Energies 17, no. 16: 3901. https://doi.org/10.3390/en17163901
APA StyleŽigman, D., Tvorić, S., & Lonić, M. (2024). Comparative PSO Optimisation of Microgrid Management Models in Island Operation to Minimise Cost. Energies, 17(16), 3901. https://doi.org/10.3390/en17163901







