Leveraging Gaussian Processes in Remote Sensing
Abstract
1. Introduction
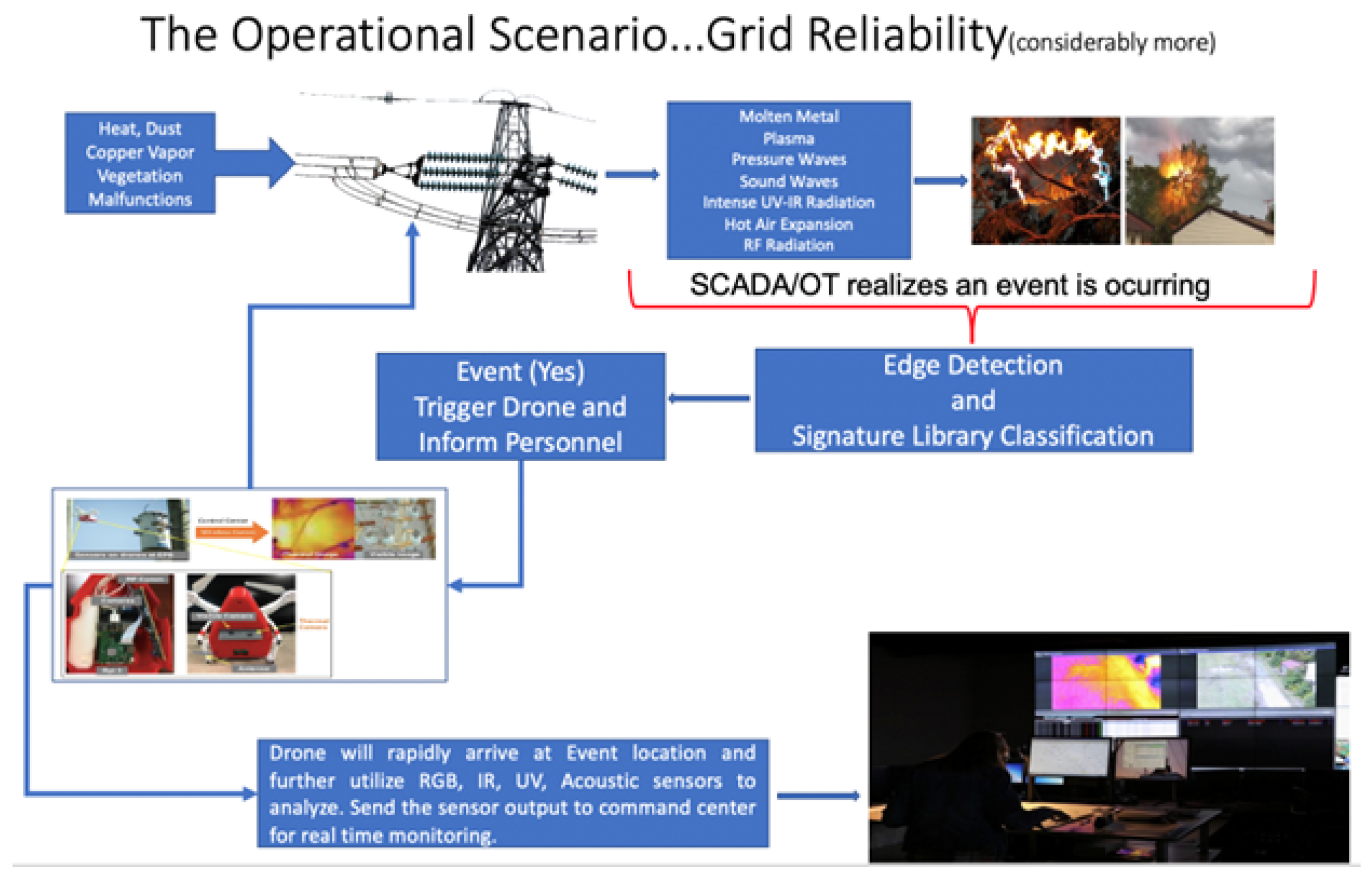
1.1. Remote Sensing
- Efficiency: Drones can quickly and autonomously cover large areas, making it feasible to monitor extensive power infrastructure efficiently. They can capture data from challenging or inaccessible locations, such as remote areas or areas with difficult terrain, more easily and cost-effectively than traditional manual inspections.
- Safety: By using drones, human inspectors can avoid hazardous or risky situations, such as working at heights or navigating dangerous environments. Drones can reach areas that may be unsafe for personnel, minimizing the potential risks associated with manual inspections.
- Data accuracy and detail: Drones equipped with advanced sensors can capture high-resolution imagery and collect precise measurements, providing detailed data on the condition of power infrastructure. This allows for better assessment and understanding of the grid’s health and can aid in detecting early signs of potential issues.
- Real-time monitoring: Drones can be deployed for regular or periodic monitoring, providing real-time or near-real-time data on the grid’s status. This enables proactive maintenance and prompt response to changing conditions.
- Cost-effectiveness: Adopting drone technology for power grid monitoring can lead to cost savings compared to traditional inspection methods. Drones can cover larger areas in less time, reduce the need for manual inspections, and improve the efficiency of maintenance operations.
1.2. Gaussian Processes
1.2.1. Definition
1.2.2. Advantages
1.2.3. Computational Complexity
- Hierarchical low-rank approximation: This method uses low-rank approximations in hierarchies. Breaking the approximation up in this way transforms the multi-dimensional calculation into a linear solution [12].
- Nearest-neighbor GP: This method uses a simple hierarchical nearest-neighbor algorithm to create subsets that approximate the covariance matrix [13].
- Spatial meta-kriging: This method uses the geometric median to pool subsets that are representative of the full data distribution, as opposed to other methods, where each subset may have a starkly different distribution [14].
- Vecchia approximation: This method leverages the statistical property according to which the joint density can be written as the product of conditional densities and uses various variable ordering and conditioning schemes to reduce complexity [7].
- Permutation and grouping: This method also uses ordering to reduce computational cost but focuses on a permutation algorithm that automatically chooses the most efficient grouping [15].
- Fourier feature transform:
- Sparse approximation: Inducing sparsity into datasets is another way to create manageable subsets to reduce computational cost [18].
- Online processes: Online processes can reduce computational cost because data are processed sequentially in a constant stream rather than training on the entire dataset [19].
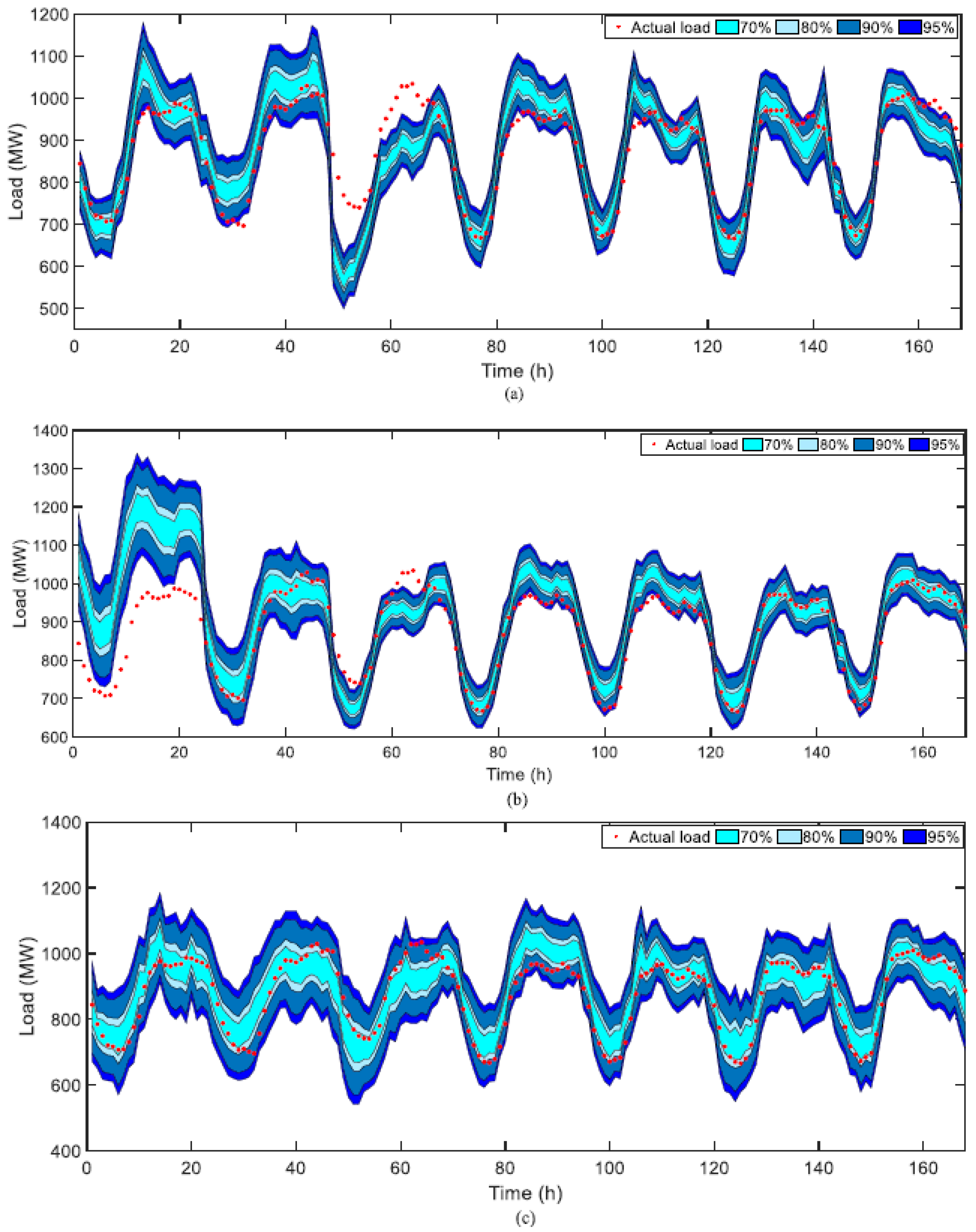
2. Power Flow and Load Forecasting
3. Incorporating Weather
3.1. Wind Speed Forecasting
3.2. Temperature Detection from Remotely Sensed Images
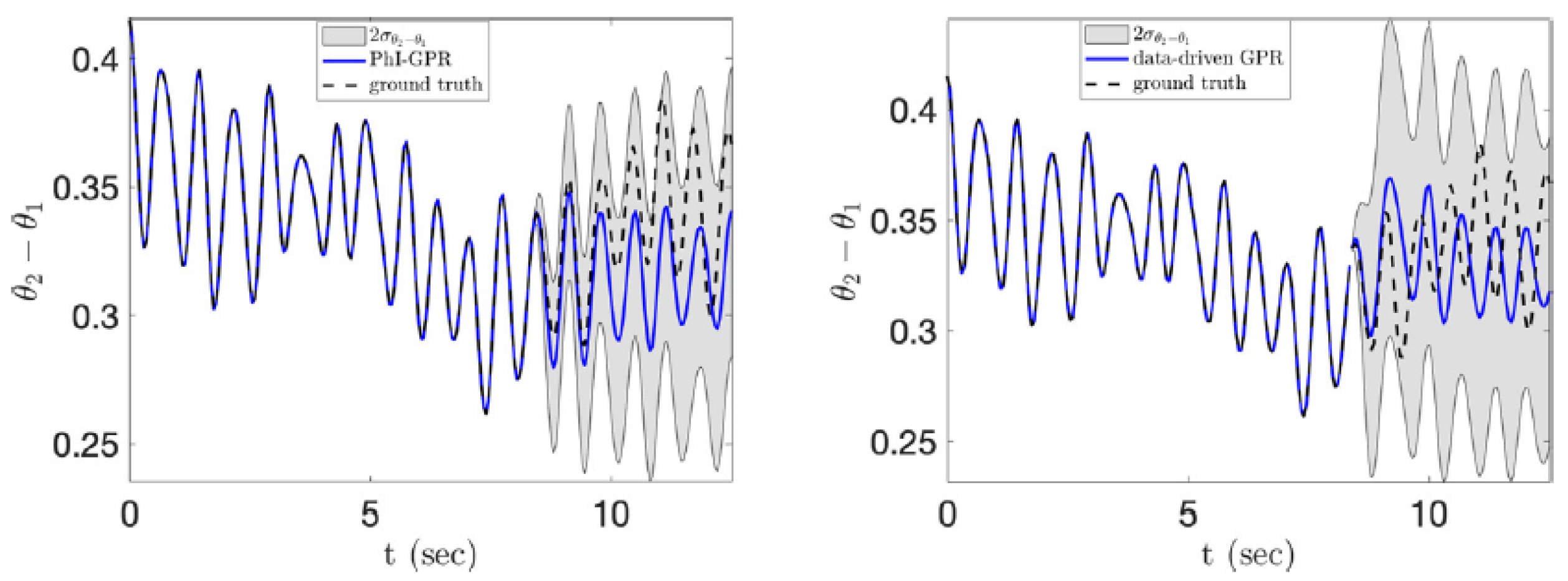
4. Physics-Based Modeling
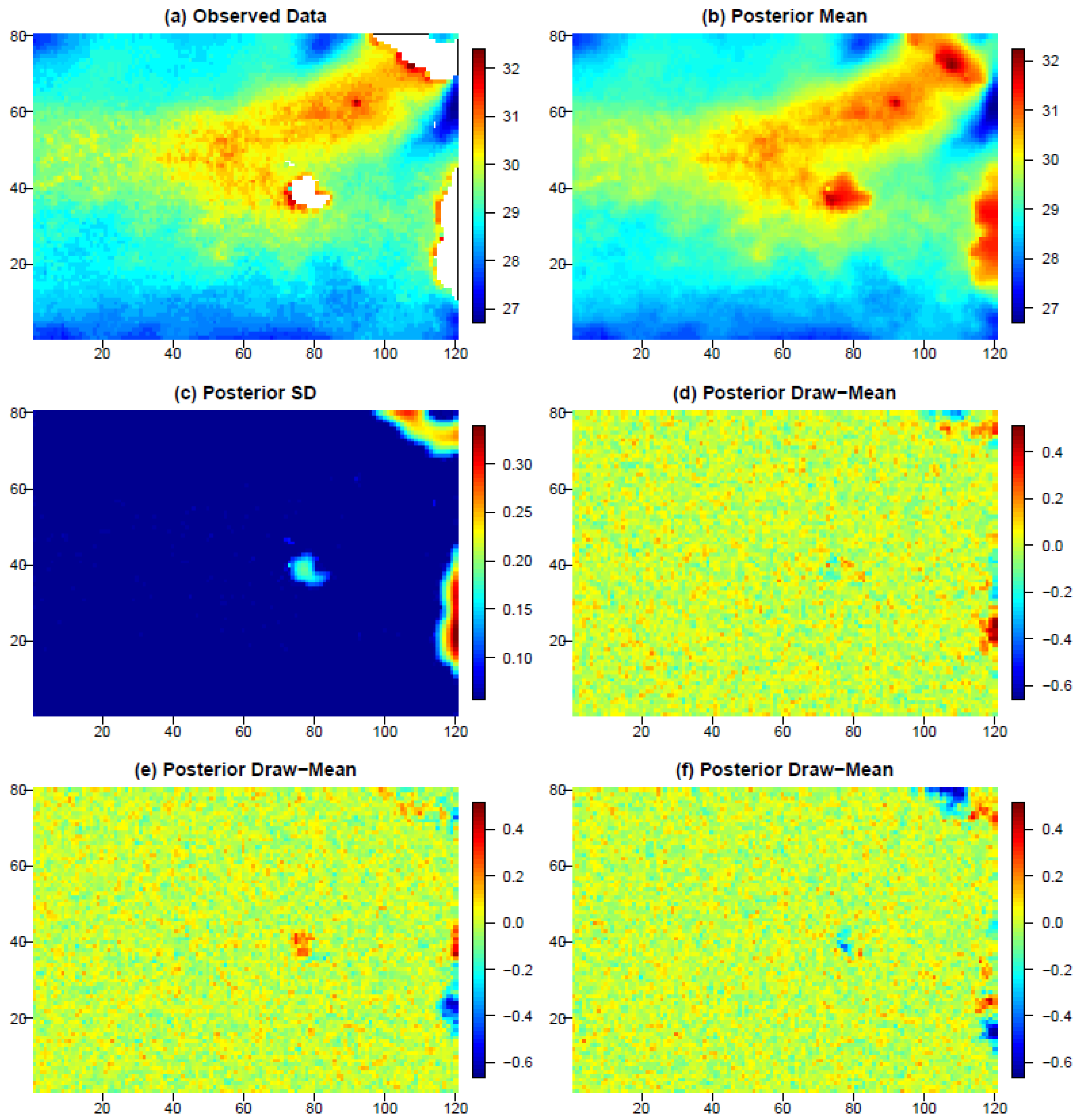
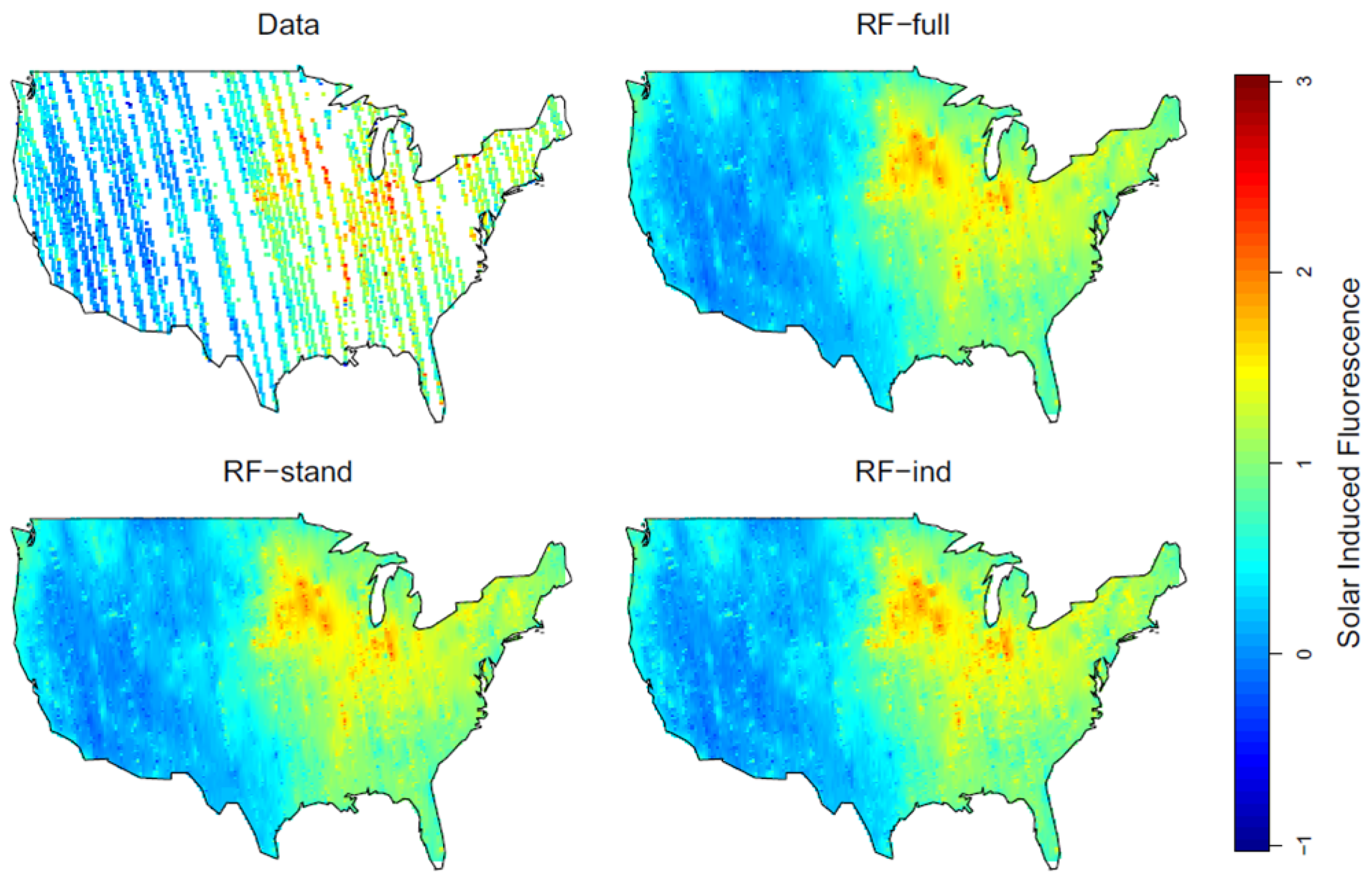
4.1. Spatial Statistics
4.2. Low-Rank and Sparse Approximation
4.3. Spectral Applications
4.4. Gaussian Process Emulators
5. Additional Gaussian Applications
6. Drone Functionality
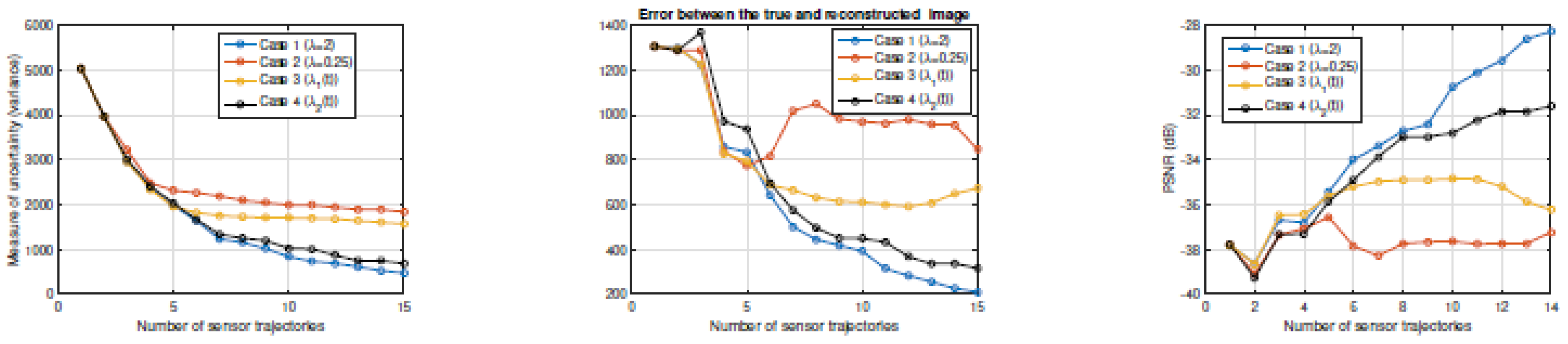
6.1. Exploration
6.2. Energy Harvesting
7. Conclusions
Funding
Conflicts of Interest
References
- Weiss, M.; Weiss, M. An assessment of threats to the American power grid. Energy Sustain. Soc. 2019, 9, 18. [Google Scholar] [CrossRef]
- International Energy Agency. Energy Efficiency 2023; Licence: CC BY 4.0.; IEA: Paris, France, 2023. [Google Scholar]
- Department of Energy. Electric Emergency and Disturbance (OE-417) Events. 2023. Available online: https://www.oe.netl.doe.gov/OE417_annual_summary.aspx (accessed on 21 July 2024).
- Touati, R.; Mignotte, M.; Dahmane, M. Multimodal Change Detection in Remote Sensing Images Using an Unsupervised Pixel Pairwise-Based Markov Random Field Model. IEEE Trans. Image Process. 2020, 29, 757–767. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Piramanayagam, S.; Monteiro, S.T.; Saber, E. Semantic segmentation of remote sensing data using Gaussian processes and higher-order CRFS. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5454–5457. [Google Scholar] [CrossRef]
- Svendsen, D.H.; Martino, L.; Camps-Valls, G. Active emulation of computer codes with Gaussian processes—Application to remote sensing. Pattern Recognit. 2019, 100, 107103. [Google Scholar] [CrossRef]
- Katzfuss, M.; Guinness, J.; Gong, W.; Zilber, D. Vecchia Approximations of Gaussian-Process Predictions. J. Agric. Biol. Environ. Stat. 2020, 25, 383–414. [Google Scholar] [CrossRef]
- Svendsen, D.H.; Morales-Álvarez, P.; Molina, R.; Camps-Valls, G. Deep Gaussian Processes for Geophysical Parameter Retrieval. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 6175–6178. [Google Scholar] [CrossRef]
- Zhang, A.; Lipton, Z.C.; Li, M.; Smola, A.J. Dive into Deep Learning; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Jain, A.; Nghiem, T.; Morari, M.; Mangharam, R. Learning and Control Using Gaussian Processes. In Proceedings of the 2018 ACM/IEEE 9th International Conference on Cyber-Physical Systems (ICCPS), Porto, Portugal, 11–13 April 2018; pp. 140–149. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; Massachusetts Institute of Technology: Cambridge, MA, USA, 2006. [Google Scholar]
- Huang, H.; Sun, Y. Hierarchical Low Rank Approximation of Likelihoods for Large Spatial Datasets. J. Comput. Graph. Stat. 2018, 27, 110–118. [Google Scholar] [CrossRef]
- Finley, A.O.; Datta, A.; Cook, B.D.; Morton, D.C.; Andersen, H.E.; Banerjee, S. Efficient Algorithms for Bayesian Nearest Neighbor Gaussian Processes. J. Comput. Graph. Stat. 2019, 28, 401–414. [Google Scholar] [CrossRef] [PubMed]
- Guhaniyogi, R.; Banerjee, S. Meta-Kriging: Scalable Bayesian Modeling and Inference for Massive Spatial Datasets. Technometrics 2018, 60, 430–444. [Google Scholar] [CrossRef] [PubMed]
- Guinness, J. Permutation and Grouping Methods for Sharpening Gaussian Process Approximations. Technometrics 2018, 60, 415–429. [Google Scholar] [CrossRef] [PubMed]
- Ton, J.F.; Flaxman, S.; Sejdinovic, D.; Bhatt, S. Spatial mapping with Gaussian processes and nonstationary Fourier features. Spat. Stat. 2018, 28, 59–78. [Google Scholar] [CrossRef]
- Stroud, J.R.; Stein, M.L.; Lysen, S. Bayesian and Maximum Likelihood Estimation for Gaussian Processes on an Incomplete Lattice. J. Comput. Graph. Stat. 2017, 26, 108–120. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Mao, J. Sparse Gaussian process regression for multi-step ahead forecasting of wind gusts combining numerical weather predictions and on-site measurements. J. Wind. Eng. Ind. Aerodyn. 2022, 220, 104873. [Google Scholar] [CrossRef]
- Kou, P.; Gao, F.; Guan, X. Sparse online warped Gaussian process for wind power probabilistic forecasting. Appl. Energy 2013, 108, 410–428. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Ma, T.; Barajas-Solano, D.A.; Tipireddy, R. Physics-informed Gaussian process regression for states estimation and forecasting in power grids. Int. J. Forecast. 2023, 39, 967–980. [Google Scholar] [CrossRef]
- Ghasempour, A.; Martínez-Ramón, M. Short-Term Electric Load Prediction in Smart Grid using Multi-Output Gaussian Processes Regression. In Proceedings of the 2023 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 27–28 April 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Mitrovic, M.; Kundacina, O.; Lukashevich, A.; Budennyy, S.; Vorobev, P.; Terzija, V.; Maximov, Y.; Deka, D. GP CC-OPF: Gaussian Process based optimization tool for Chance-Constrained Optimal Power Flow. Softw. Impacts 2023, 16, 100489. [Google Scholar] [CrossRef]
- Mitrovic, M.; Lukashevich, A.; Vorobev, P.; Terzija, V.; Budennyy, S.; Maximov, Y.; Deka, D. Data-driven stochastic AC-OPF using Gaussian process regression. Int. J. Electr. Power Energy Syst. 2023, 152, 109249. [Google Scholar] [CrossRef]
- Yadav, A.; Bareth, R.; Kochar, M.; Pazoki, M.; Sehiemy, R.A.E. Gaussian process regression-based load forecasting model. IET Gener. Transm. Distrib. 2024, 18, 899–910. [Google Scholar] [CrossRef]
- Pareek, P.; Nguyen, H.D. A Framework for Analytical Power Flow Solution Using Gaussian Process Learning. IEEE Trans. Sustain. Energy 2022, 13, 452–463. [Google Scholar] [CrossRef]
- Cao, D.; Zhao, J.; Hu, W.; Zhang, Y.; Liao, Q.; Chen, Z.; Blaabjerg, F. Robust Deep Gaussian Process-Based Probabilistic Electrical Load Forecasting against Anomalous Events. IEEE Trans. Ind. Inform. 2022, 18, 1142–1153. [Google Scholar] [CrossRef]
- Chin, J.X.; Hug, G. Formation of ad hoc microgrids for prompt critical load pickup during blackouts by leveraging stochastic distributed energy resources. J. Eng. 2021, 2021, 705–714. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, Q.; Zhang, Z.; Xu, T.; Yang, Y.; Liu, Y. A Medium/Long-Term Electrical Power and Electrical Energy Balance Method for Power System Considering Extreme Weather. In Proceedings of the 2023 5th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 23–26 March 2023; pp. 749–752. [Google Scholar] [CrossRef]
- Guo, Y.; Baker, K.; Dall’Anese, E.; Hu, Z.; Summers, T.H. Data-Based Distributionally Robust Stochastic Optimal Power Flow—Part I: Methodologies. IEEE Trans. Power Syst. 2019, 34, 1483–1492. [Google Scholar] [CrossRef]
- Guo, Y.; Baker, K.; Dall’Anese, E.; Hu, Z.; Summers, T.H. Data-Based Distributionally Robust Stochastic Optimal Power Flow—Part II: Case Studies. IEEE Trans. Power Syst. 2019, 34, 1493–1503. [Google Scholar] [CrossRef]
- Pobočíkováa, I.; Sedliačkováa, Z.; Michalkováa, M. Application of Four Probability Distributions for Wind Speed Modeling. Procedia Eng. 2017, 192, 713–718. [Google Scholar] [CrossRef]
- Hoolohan, V.; Tomlin, A.S.; Cockerill, T. Improved near surface wind speed predictions using Gaussian process regression combined with numerical weather predictions and observed meteorological data. Renew. Energy 2018, 126, 1043–1054. [Google Scholar] [CrossRef]
- Zhu, S.; Yuan, X.; Xu, Z.; Luo, X.; Zhang, H. Gaussian mixture model coupled recurrent neural networks for wind speed interval forecast. Energy Convers. Manag. 2019, 198, 111772. [Google Scholar] [CrossRef]
- Kim, J.; Kim, S. Temperature Estimation Adaptive to Variables over Distance Using Infrared—LiDAR. Appl. Sci. 2021, 11, 4063. [Google Scholar] [CrossRef]
- Kay, J.; Handcock, R.; Gillespie, A.; Konrad, C.; Burges, S.; Naveh, N.; Booth, D. Stream-temperature estimation from thermal infrared images. In Proceedings of the IGARSS 2001, Scanning the Present and Resolving the Future, IEEE 2001 International Geoscience and Remote Sensing Symposium (Cat. No.01CH37217), Sydney, NSW, Australia, 9–13 July 2001; Volume 1, pp. 112–114. [Google Scholar] [CrossRef]
- Jalil, B.; Pascali, M.A.; Leone, G.R.; Martinelli, M.; Moroni, D.; Salvetti, O. To Identify Hot Spots in Power Lines Using Infrared and Visible Sensors. In Proceedings of the Multimedia and Network Information Systems; Springer International Publishing: Berling/Heidelberg, Germany, 2019; pp. 313–321. [Google Scholar]
- Pipia, L.; Muñoz-Marí, J.; Amin, E.; Belda, S.; Camps-Valls, G.; Verrelst, J. Fusing optical and SAR time series for LAI gap filling with multioutput Gaussian processes. Remote Sens. Environ. 2019, 235, 111452. [Google Scholar] [CrossRef]
- Liu, Z.; Tang, B.; He, X.; Qiu, Q.; Liu, F. Class-Specific Random Forest with Cross-Correlation Constraints for Spectral–Spatial Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 257–261. [Google Scholar] [CrossRef]
- Cheng, H.; Liu, Z.; Yang, J. Learning feature transforms for object detection from panoramic images. In Proceedings of the 2010 IEEE International Conference on Multimedia and Expo, Singapore, 19–23 July 2010; pp. 643–648. [Google Scholar] [CrossRef]
- Alaca, O.; Ekti, A.R.; Wilson, A.; Holliman, J.; Piersall, E.; Yarkan, S.; Stenvig, N. Detection of Grid-Signal Distortions Using the Spectral Correlation Function. IEEE Trans. Smart Grid 2023, 14, 4980–4983. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Martino, L.; Svendsen, D.H.; Campos-Taberner, M.; Muñoz-Marí, J.; Laparra, V.; Luengo, D.; García-Haro, F.J. Physics-aware Gaussian processes in remote sensing. Appl. Soft Comput. 2018, 68, 69–82. [Google Scholar] [CrossRef]
- Mateo-Sanchis, A.; Muñoz-Marí, J.; Pérez-Suay, A.; Camps-Valls, G. Warped Gaussian Processes in Remote Sensing Parameter Estimation and Causal Inference. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1647–1651. [Google Scholar] [CrossRef]
- Shekaramiz, M.; Moon, T.K.; Gunther, J.H. Exploration and data refinement via multiple mobile sensors based on gaussian processes. In Proceedings of the Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 29 October–1 November 2017; pp. 885–889. [Google Scholar] [CrossRef]
- Ma, K.C.; Liu, L.; Sukhatme, G.S. Informative planning and online learning with sparse Gaussian processes. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4292–4298. [Google Scholar] [CrossRef]
- Sanislav, T.; Mois, G.D.; Zeadally, S.; Folea, S.C. Energy Harvesting Techniques for Internet of Things (IoT). IEEE Access 2021, 9, 39530–39549. [Google Scholar] [CrossRef]
- Zeng, X.; Yang, Z.; Wu, P.; Cao, L.; Luo, Y. Power Source Based on Electric Field Energy Harvesting for Monitoring Devices of High-Voltage Transmission Line. IEEE Trans. Ind. Electron. 2021, 68, 7083–7092. [Google Scholar] [CrossRef]
- Stamatakis, G.; Pappas, N.; Traganitis, A. Control of Status Updates for Energy Harvesting Devices That Monitor Processes with Alarms. In Proceedings of the 2019 IEEE Globecom Workshops (GC Wkshps), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Foley, E. Leveraging Gaussian Processes in Remote Sensing. Energies 2024, 17, 3895. https://doi.org/10.3390/en17163895
Foley E. Leveraging Gaussian Processes in Remote Sensing. Energies. 2024; 17(16):3895. https://doi.org/10.3390/en17163895
Chicago/Turabian StyleFoley, Emma. 2024. "Leveraging Gaussian Processes in Remote Sensing" Energies 17, no. 16: 3895. https://doi.org/10.3390/en17163895
APA StyleFoley, E. (2024). Leveraging Gaussian Processes in Remote Sensing. Energies, 17(16), 3895. https://doi.org/10.3390/en17163895





