A Fast State-of-Charge (SOC) Balancing and Current Sharing Control Strategy for Distributed Energy Storage Units in a DC Microgrid
Abstract
1. Introduction
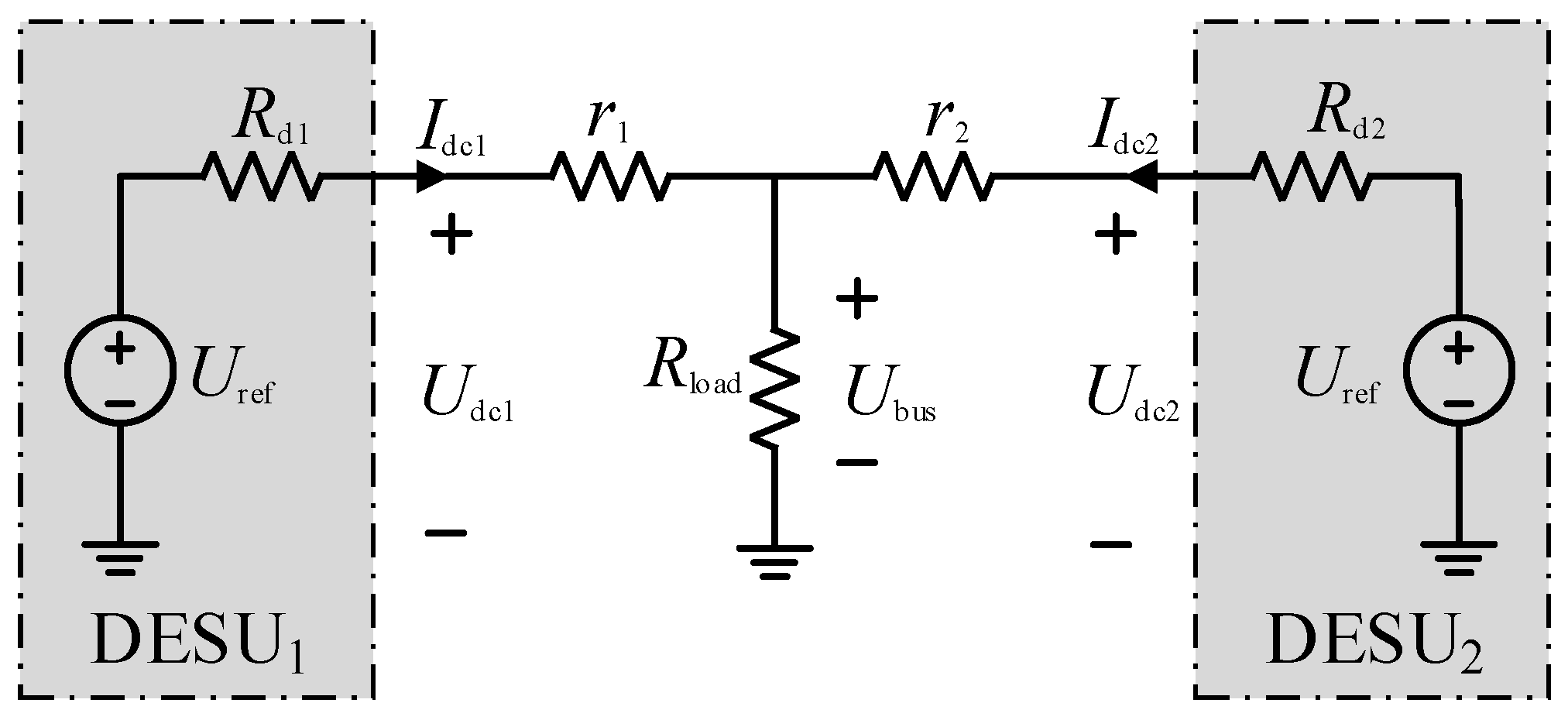
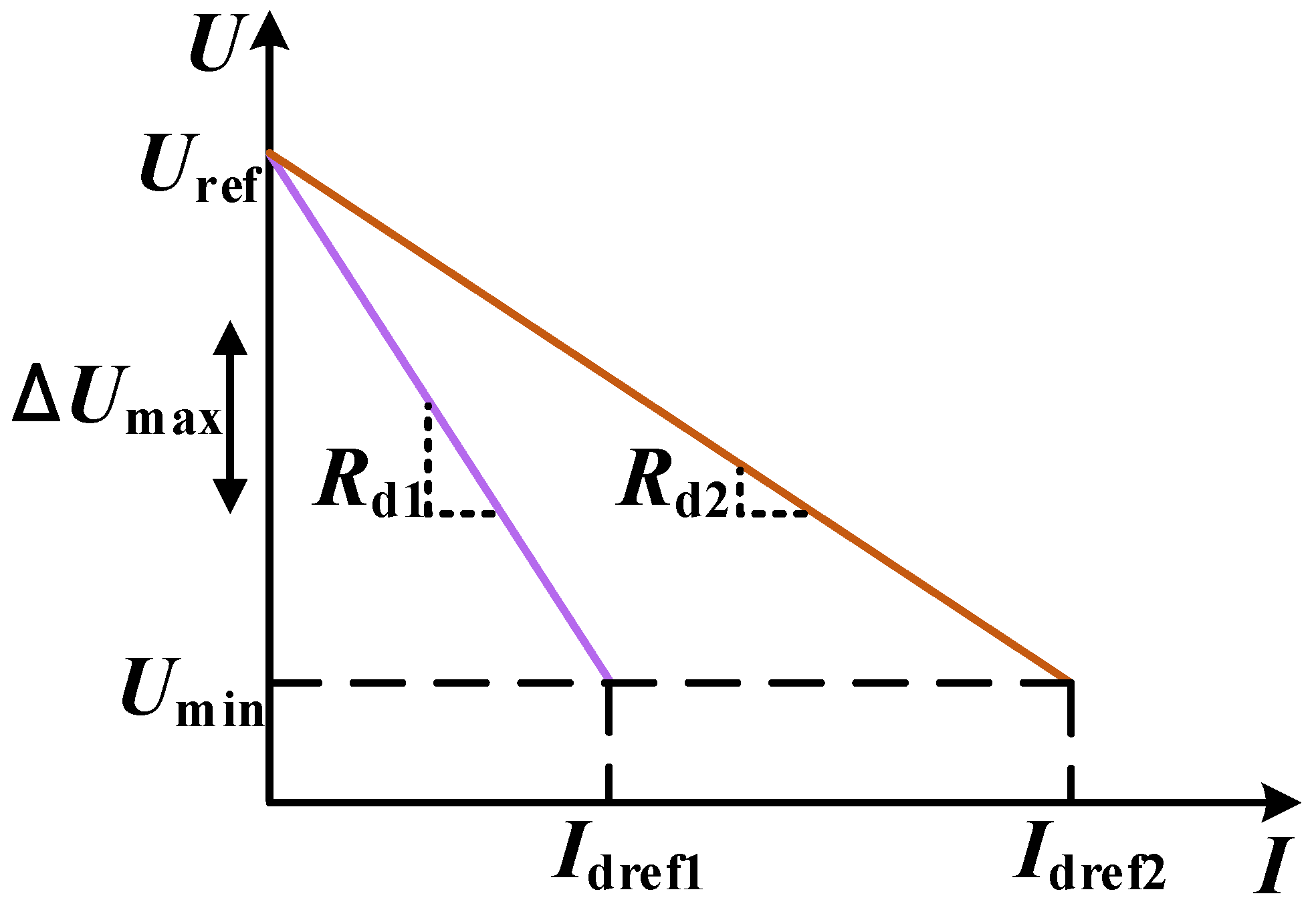
2. Isolated DC Microgrid Structures and the Analysis of Conventional Droop Control
3. Improved Droop Control Strategy
3.1. Dynamic Consistency Algorithm
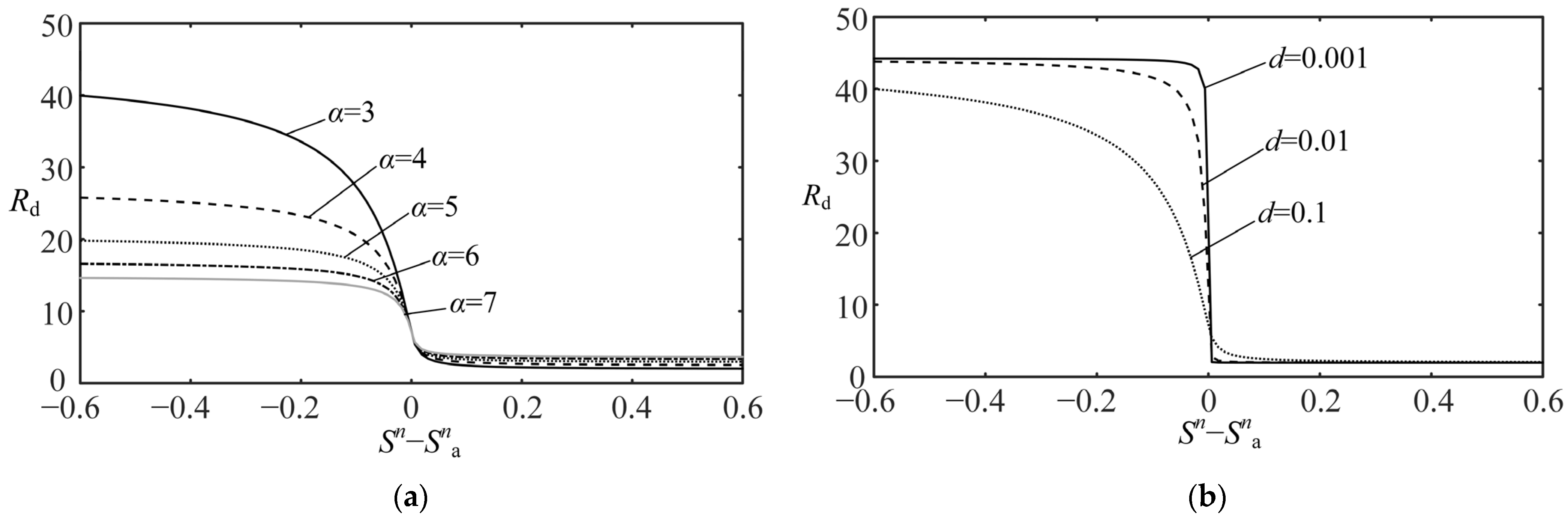
3.2. SOC Balancing Control Strategy with an Adaptive Acceleration Factor
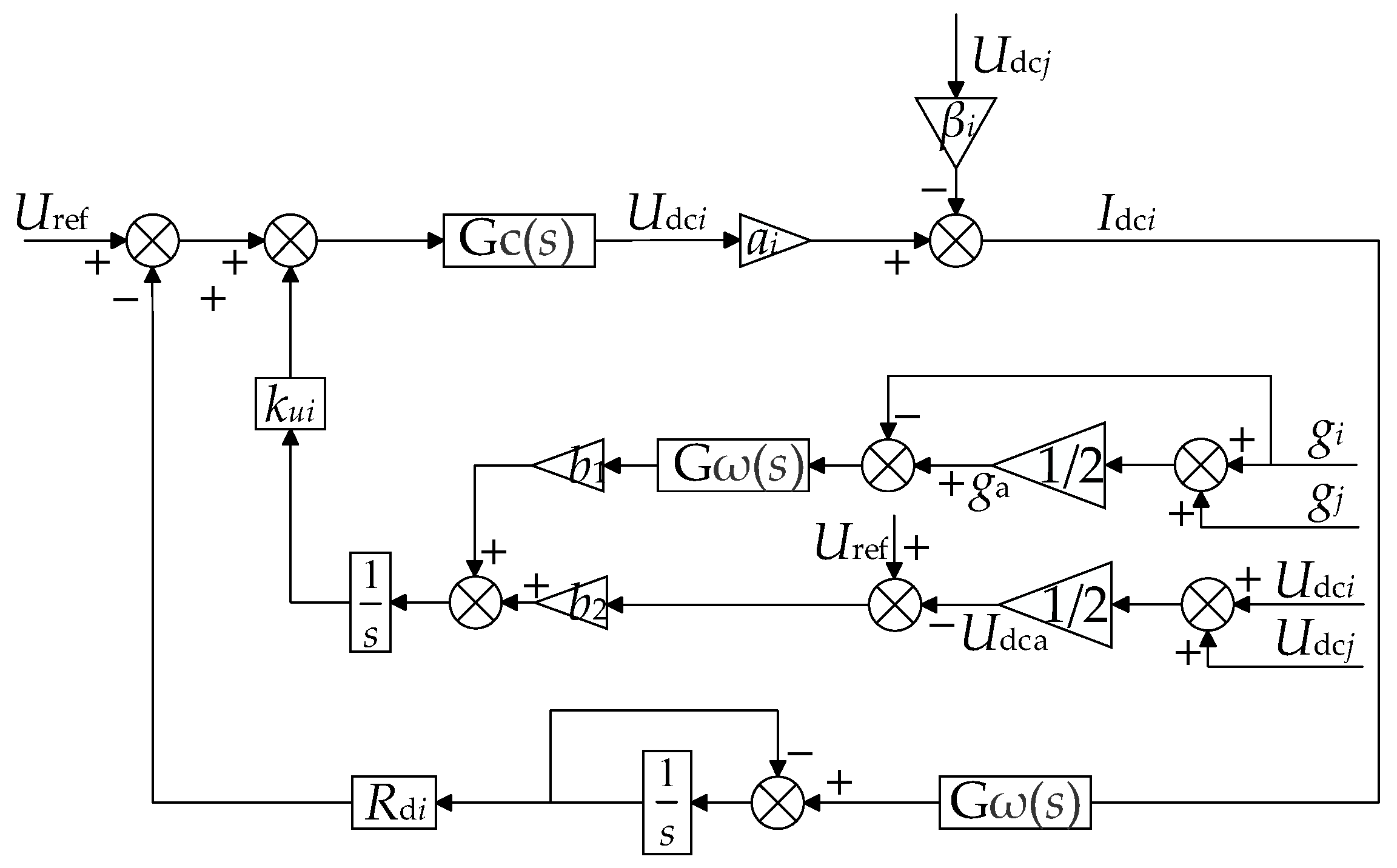
3.3. Global Optimisation Controller
4. Stability Analysis
5. Simulation Results
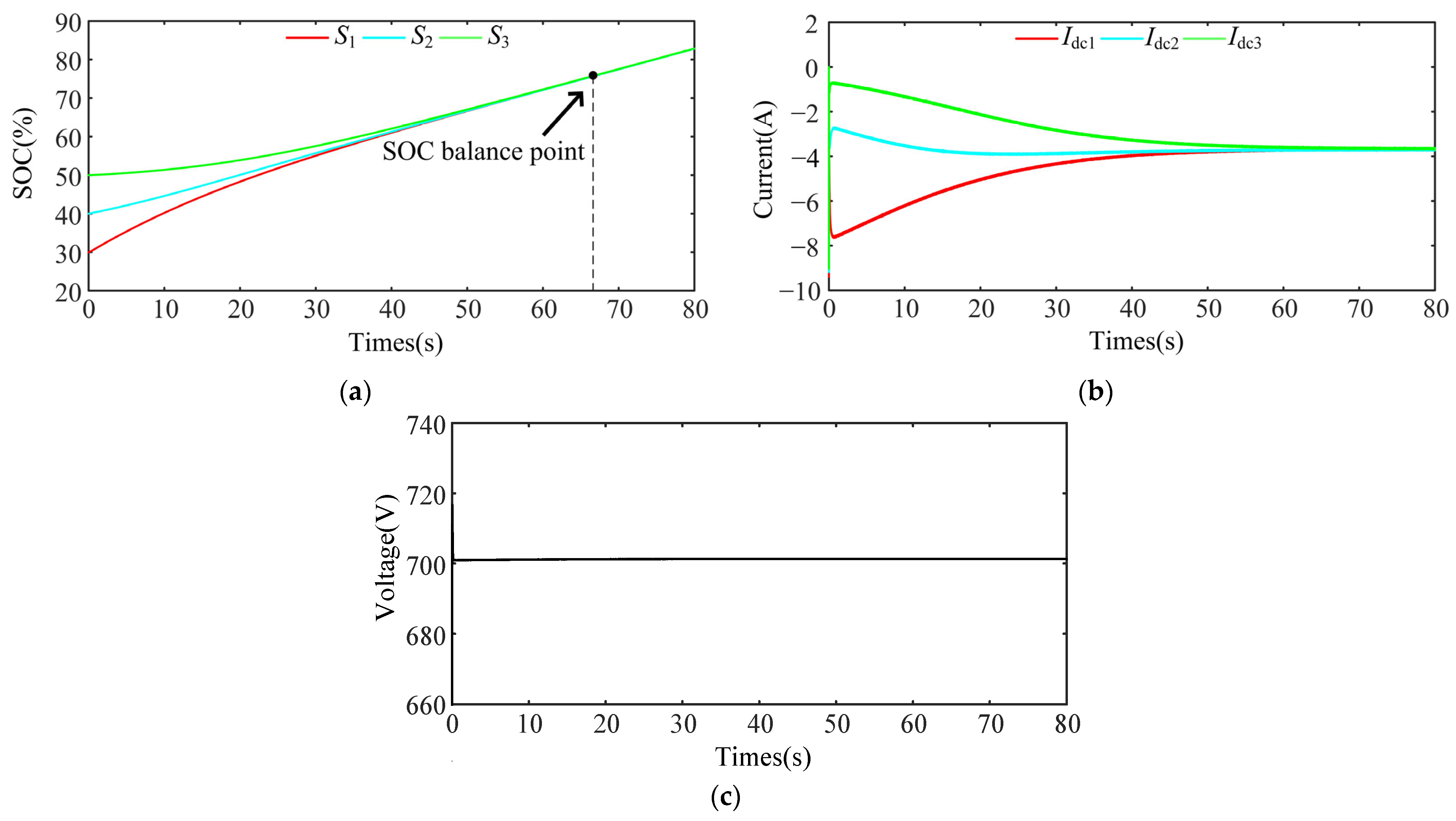
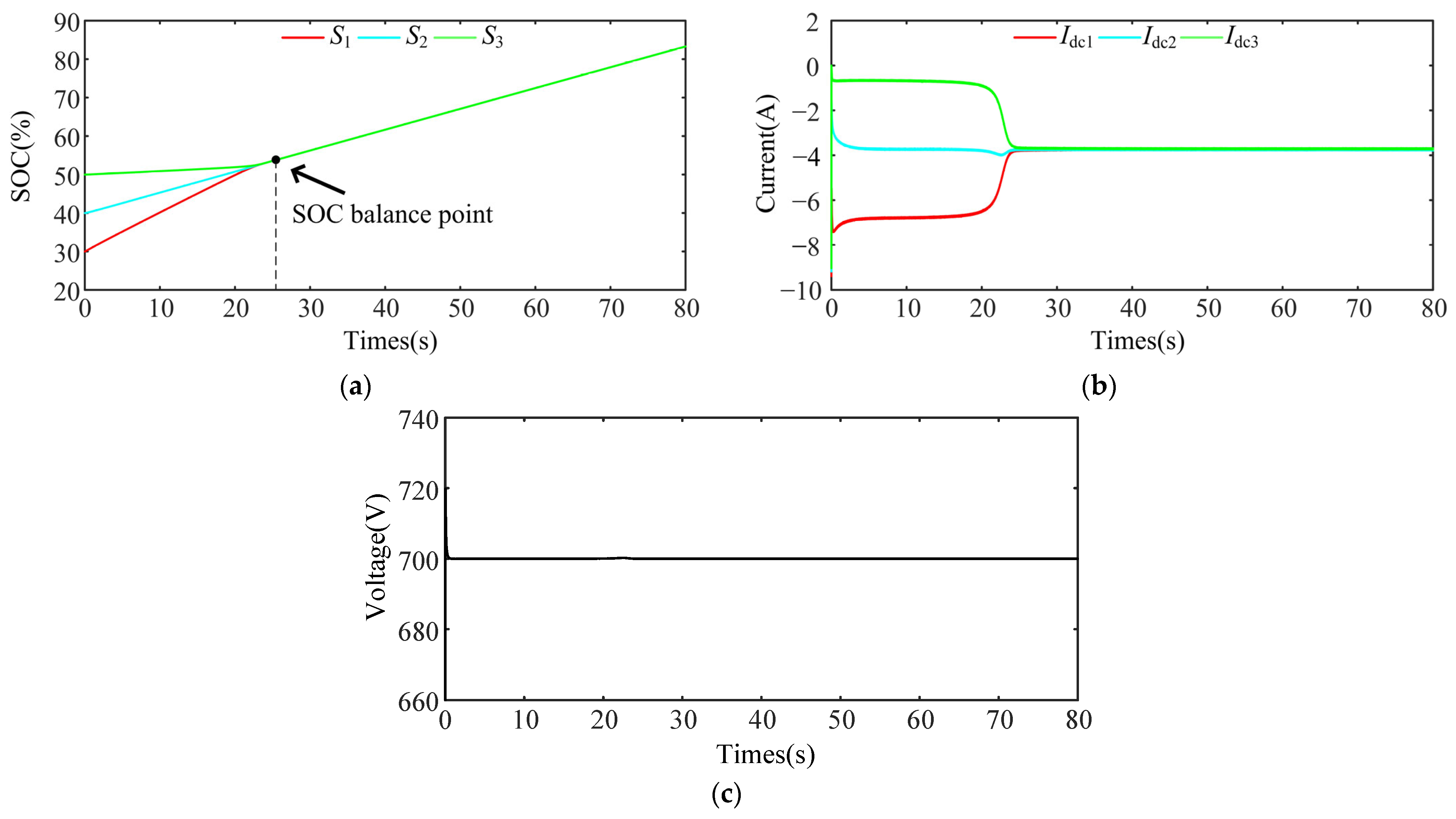
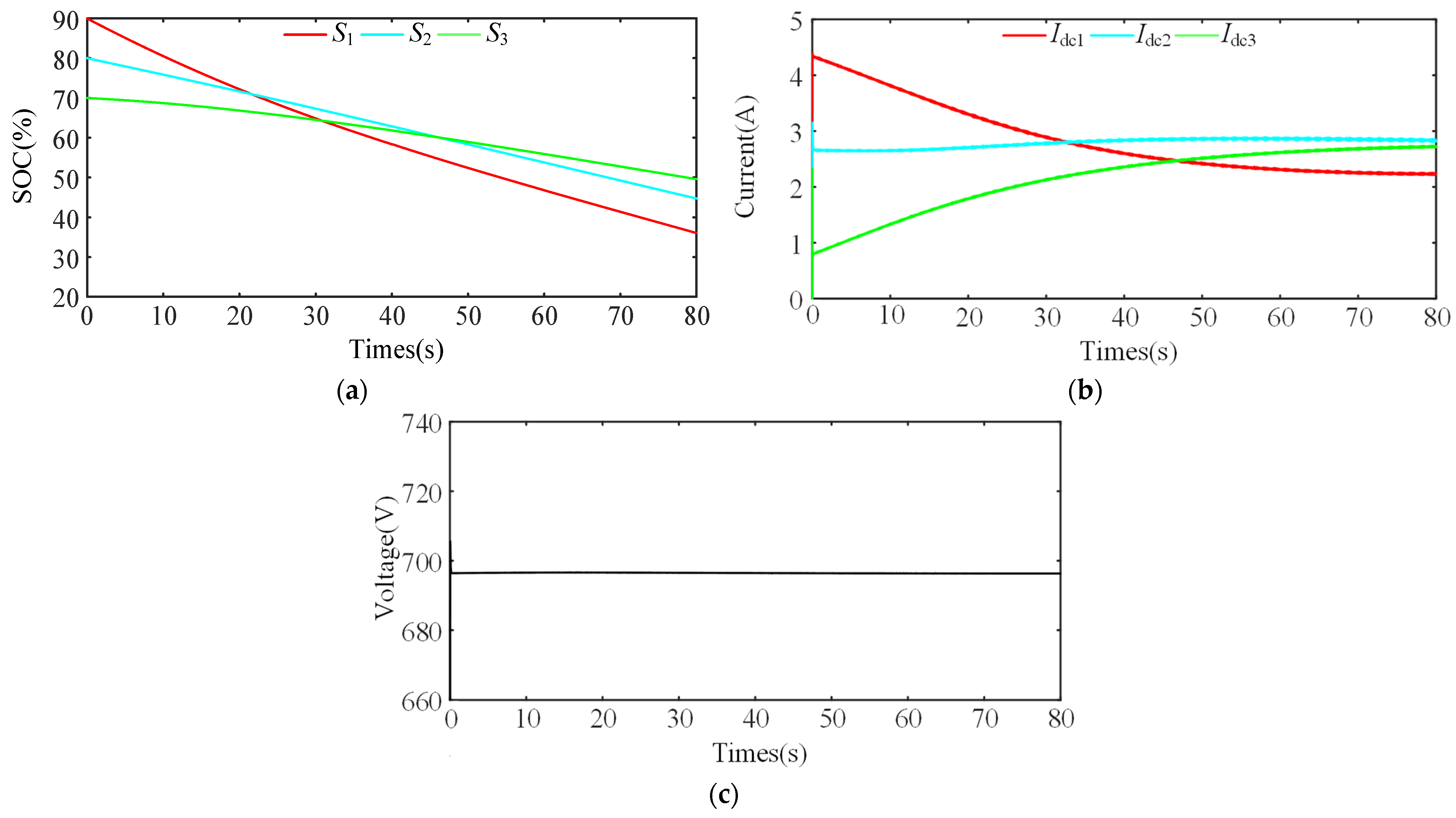
5.1. Case 1: Normal Charging Ignoring Line Resistance
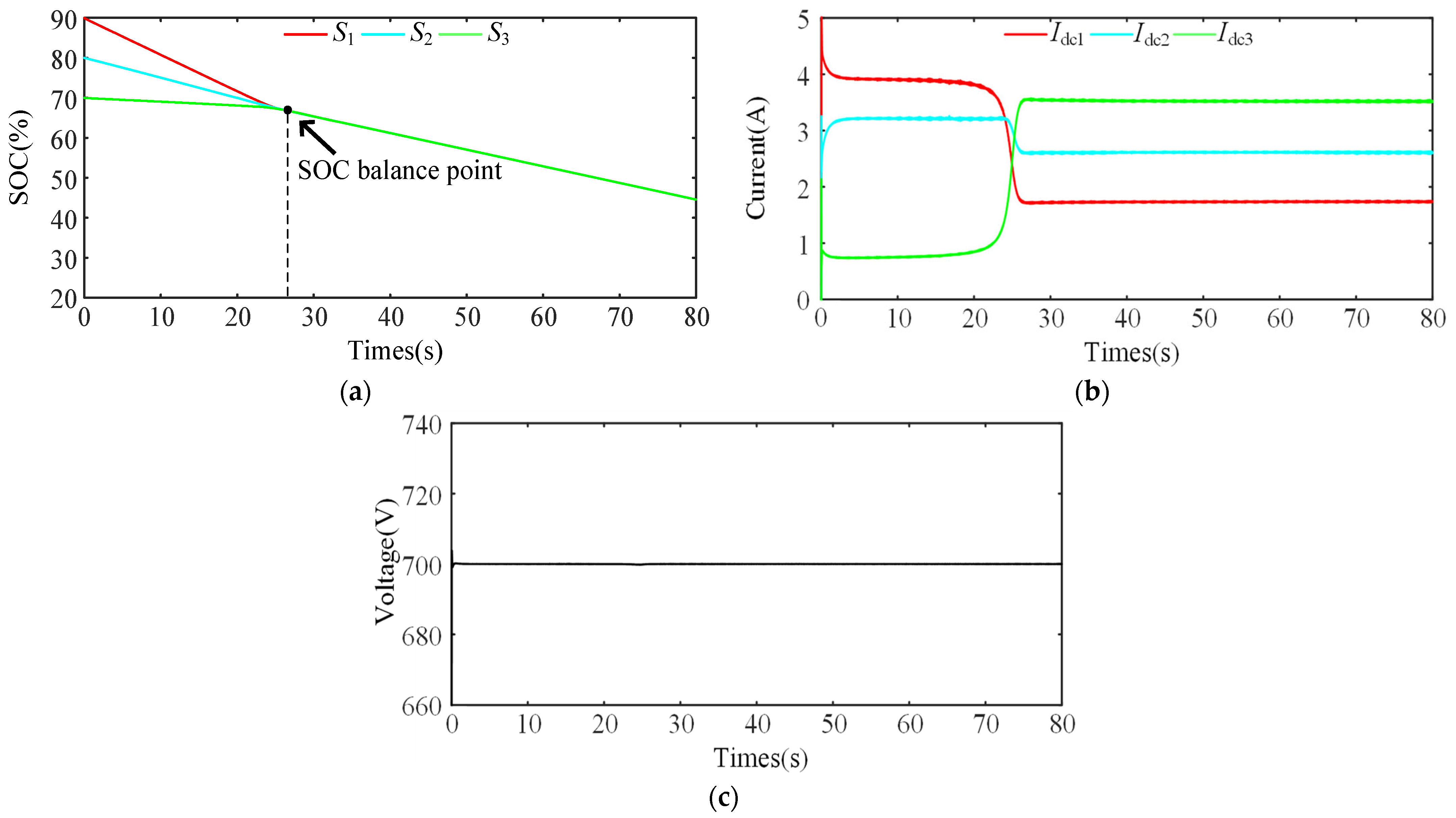
5.2. Case 2: Normal Discharge with Line Resistance Mismatch
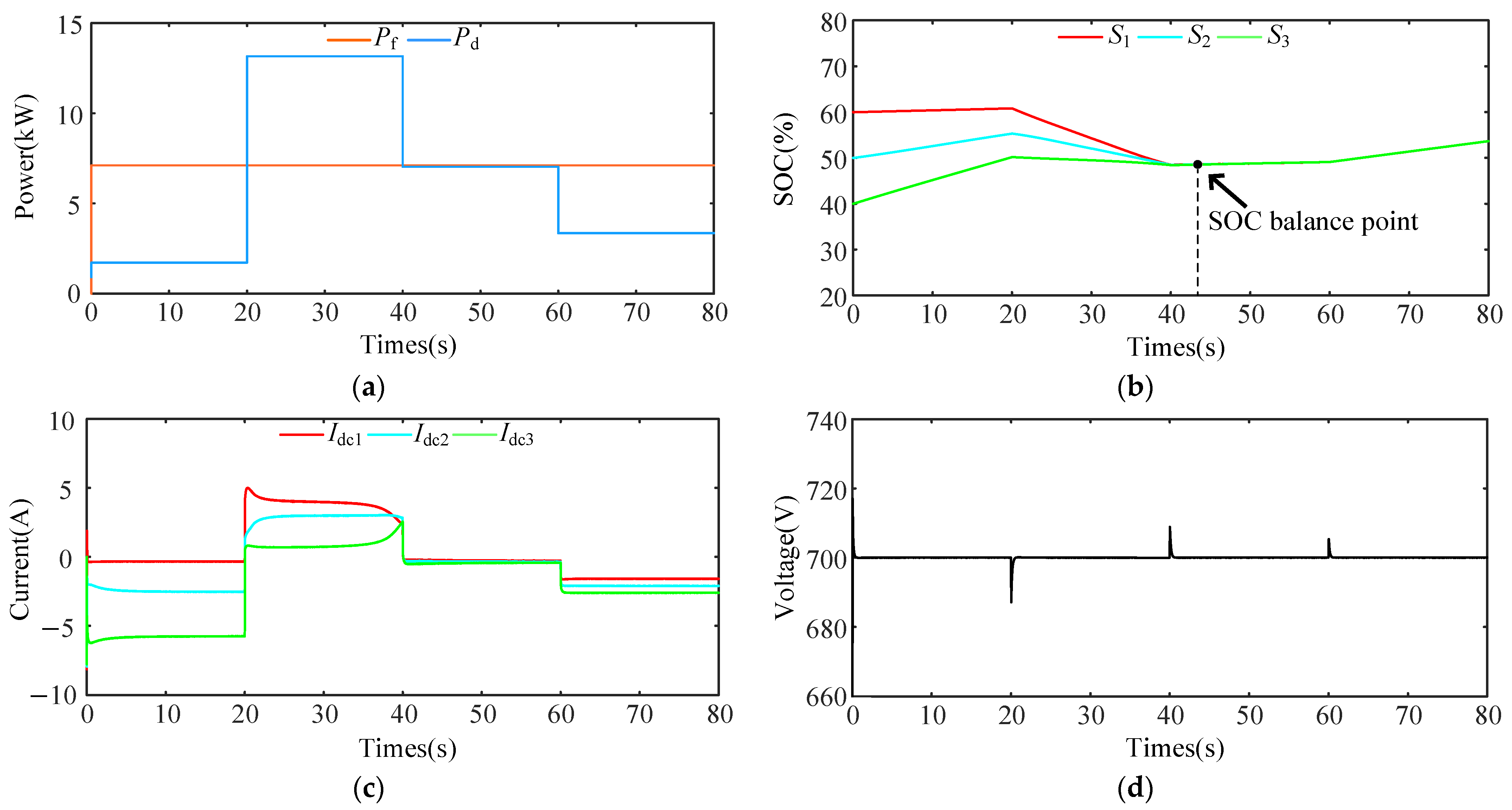
5.3. Case 3: Load Change
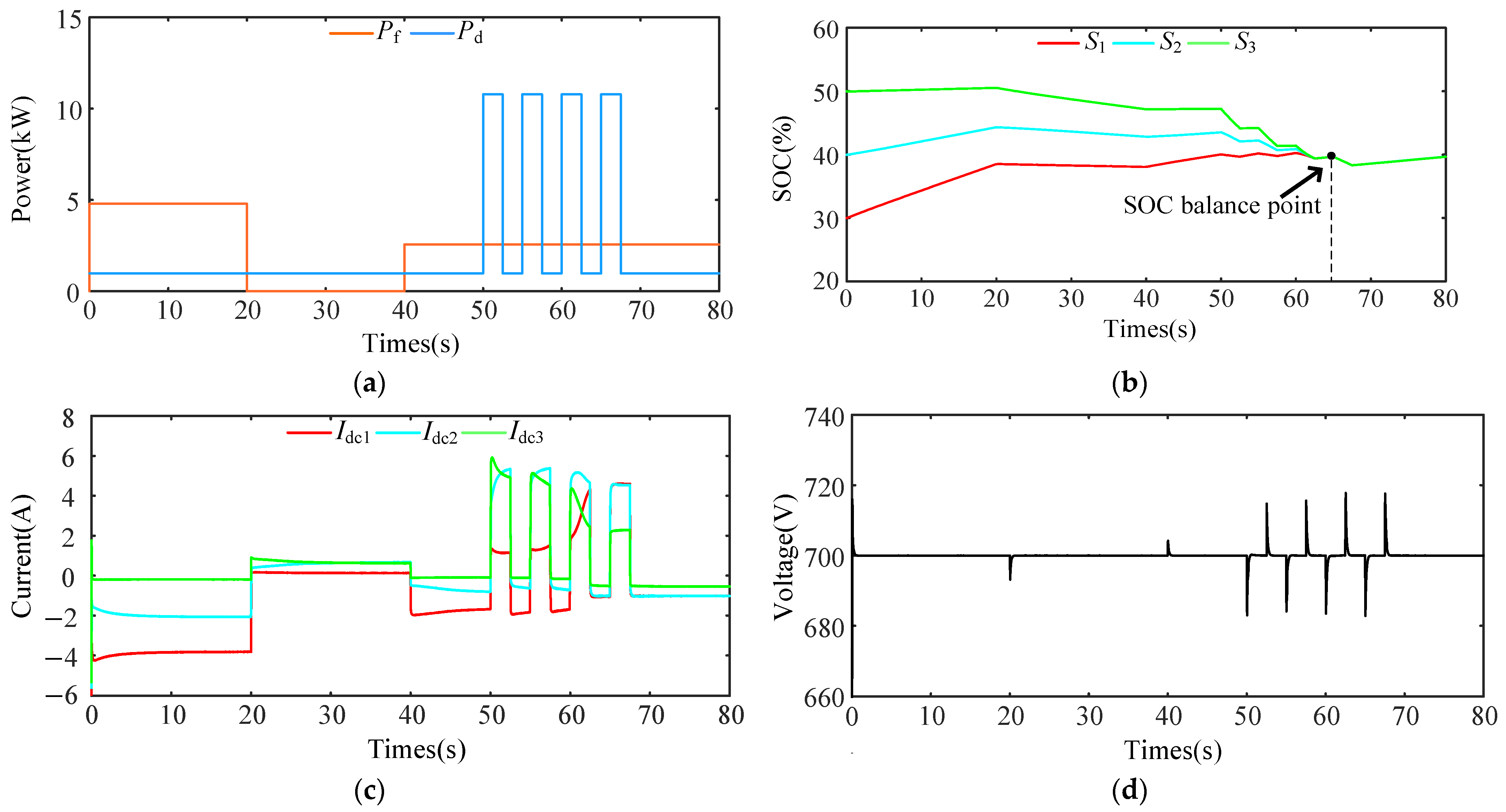
5.4. Case 4: Failure of PV-Generating Units and Frequent Load Switching
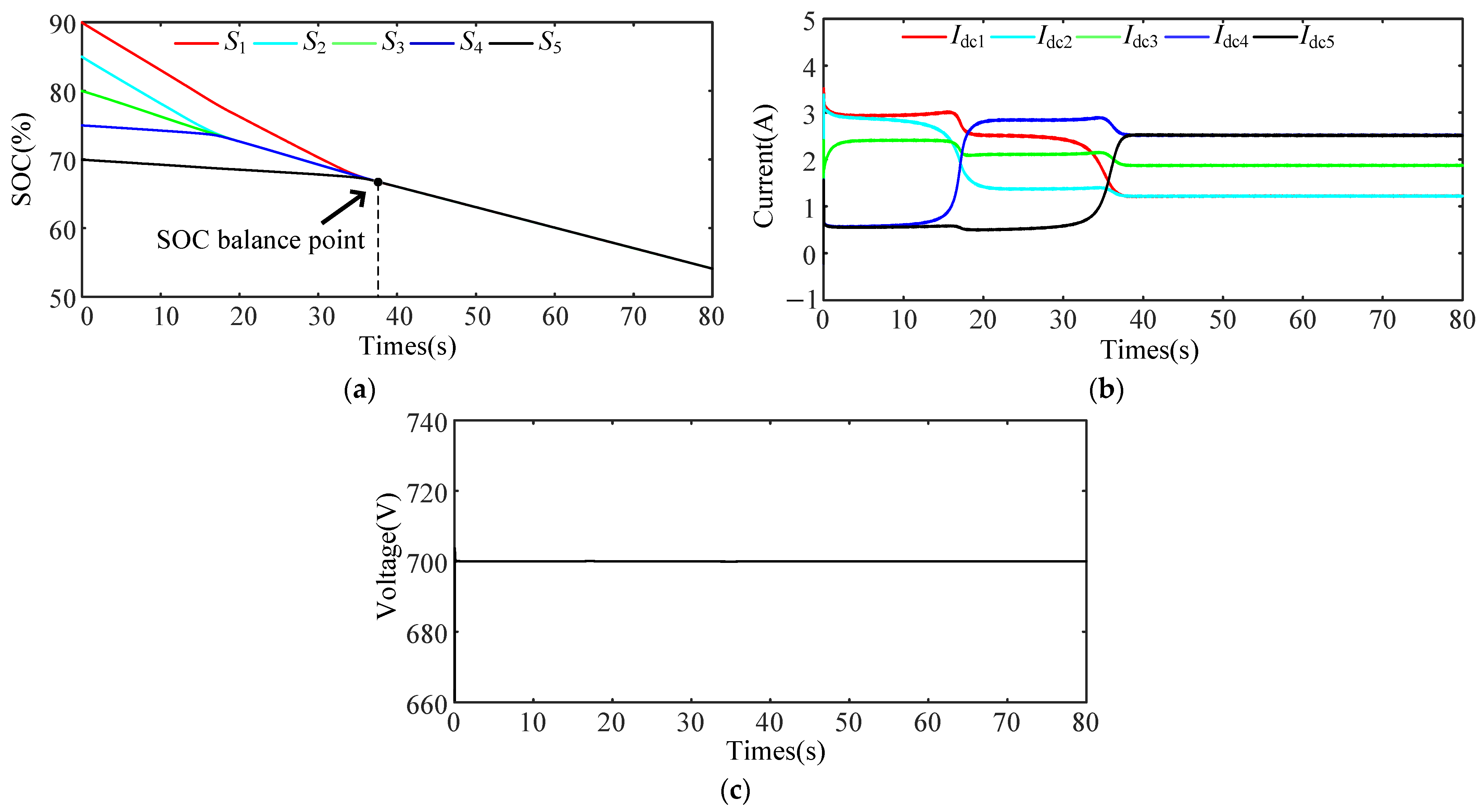
5.5. Case 5: Validation of System Scalability
6. Conclusions
- (1)
- By designing a new SOC balancing function, the SOC is closely associated with combining exponential function and power function, and two convergence factors and an adaptive acceleration factor are introduced. It effectively improves the problem of slow SOC balancing in the late stage of system operation, significantly accelerates SOC balancing, and improves the energy utilization efficiency of the DESUs.
- (2)
- To design a global optimization controller that combines bus voltage compensation and output current correction to achieve bus voltage stabilization and accurate load current distribution with only a simple integrator, it effectively reduces the communication burden of the system, reduces the control links, and improves the stability and reliability of the system operation.
- (3)
- The control strategy uses an improved consistency algorithm to obtain the global average state information and optimizes the communication topology combination of DESUs by establishing a sparse communication network, which dramatically reduces the system’s communication pressure and makes the method more adaptable to various complex working conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, B.; Zheng, S.; Wang, R.; Wang, H.; Xiao, J.; Wang, P. Distributed optimal control of DC microgrid considering balancing of charge state. IEEE Trans. Energy Convers. 2022, 37, 2162–2174. [Google Scholar]
- Peng, L.; Luo, L.; Yang, J.; Li, W. A Wind Power Fluctuation Smoothing Control Strategy for Energy Storage Systems Considering the State of Charge. Energies 2024, 17, 3132. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, F.; Chen, K.; Lu, Q. Research on Adaptive Droop Control Strategy for a Solar-Storage DC Microgrid. Energies 2024, 17, 1454. [Google Scholar] [CrossRef]
- Li, B.; Yu, C.; Lu, X.; Wang, F. A novel adaptive droop control strategy for SoC balancing in PV-based DC microgrids. ISA Trans. 2023, 141, 351–364. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Hu, H.; Wang, M.; Ge, Y.; Wang, K.; Huang, Y.; Yang, K.; He, Z.; Xu, Z.; Li, Y. Power flow control-based regenerative braking energy utilization in AC electrified railways: Review and future trends. IEEE Trans. Intell. Transp. Syst. 2024, 25, 6345–6365. [Google Scholar] [CrossRef]
- Huang, Z.; Li, Y.; Cheng, X.; Ke, M. A voltage-shifting-based state-of-charge balancing control for distributed energy storage systems in islanded DC microgrids. J. Energy Storage 2023, 69, 107861. [Google Scholar] [CrossRef]
- Lv, J.; Wang, X.; Wang, G.; Song, Y. Research on control strategy of isolated DC microgrid based on SOC of energy storage system. Electronics 2021, 10, 834. [Google Scholar] [CrossRef]
- Tian, G.; Zheng, Y.; Liu, G.; Zhang, J. SOC Balancing and Coordinated Control Based on Adaptive Droop Coefficient Algorithm for Energy Storage Units in DC Microgrid. Energies 2022, 15, 2943. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, C.; Han, J.; Yang, F.; Shen, Y.; Min, H.; Hu, W.; Song, H. Analysis of voltage control strategies for DC microgrid with multiple types of energy storage systems. Electronics 2023, 12, 1661. [Google Scholar] [CrossRef]
- Kumar, R.; Pathak, M.K. Distributed droop control of dc microgrid for improved voltage regulation and current sharing. IET Renew. Power Gener. 2020, 14, 2499–2506. [Google Scholar] [CrossRef]
- Gorijeevaram Reddy, P.K.; Dasarathan, S.; Krishnasamy, V. Investigation of adaptive droop control applied to low-voltage DC microgrid. Energies 2021, 14, 5356. [Google Scholar] [CrossRef]
- Oliveira, T.R.; Silva, W.W.A.G.; Donoso-Garcia, P.F. Distributed secondary level control for energy storage management in DC microgrids. IEEE Trans. Smart Grid 2016, 8, 2597–2607. [Google Scholar] [CrossRef]
- Zhang, C.; Li, P.; Guo, Y. Bidirectional DC/DC and SOC drooping control for DC microgrid application. Electronics 2020, 9, 225. [Google Scholar] [CrossRef]
- Lu, X.; Sun, K.; Guerrero, J.M.; Vasquez, J.C.; Huang, L. State-of-charge balancing using adaptive droop control for distributed energy storage systems in DC microgrid applications. IEEE Trans. Ind. Electron. 2013, 61, 2804–2815. [Google Scholar] [CrossRef]
- Lu, X.; Sun, K.; Guerrero, J.M.; Vasquez, J.C.; Huang, L. Double-quadrant state-of-charge-based droop control method for distributed energy storage systems in autonomous DC microgrids. IEEE Trans. Smart Grid 2014, 6, 147–157. [Google Scholar] [CrossRef]
- Belal, E.K.; Yehia, D.M.; Azmy, A.M. Adaptive droop control for balancing SOC of distributed batteries in DC microgrids. IET Gener. Transm. Distrib. 2019, 13, 4667–4676. [Google Scholar] [CrossRef]
- Diaz, N.L.; Dragičević, T.; Vasquez, J.C.; Guerrero, J.M. Intelligent distributed generation and storage units for DC microgrids—A new concept on cooperative control without communications beyond droop control. IEEE Trans. Smart Grid 2014, 5, 2476–2485. [Google Scholar] [CrossRef]
- Zhang, L.; Li, T. SoC dynamic balancing strategy based on adaptive droop control with variable regulating factor. In Proceedings of the 2021 3rd Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 26–29 March 2021; pp. 638–643. [Google Scholar]
- Mi, Y.; Guo, J.; Fu, Y.; Wang, C.; Wang, P. Accurate power allocation of multienergy storage island DC microgrid based on virtual power rating. IEEE Trans. Power Electron. 2022, 38, 261–270. [Google Scholar] [CrossRef]
- Silva, W.W.A.; Oliveira, T.R.; Donoso-Garcia, P.F. An improved voltage-shifting strategy to attain concomitant accurate power sharing and voltage restoration in droop-controlled DC microgrids. IEEE Trans. Power Electron. 2020, 36, 2396–2406. [Google Scholar] [CrossRef]
- Zhang, Q.; Zeng, Y.; Liu, Y.; Zhuang, X.; Zhang, H.; Hu, W.; Guo, H. An improved distributed cooperative control strategy for multiple energy storages parallel in islanded DC microgrid. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 455–468. [Google Scholar] [CrossRef]
- Hoang, K.D.; Lee, H.-H. Accurate power sharing with balancingd battery state of charge in distributed DC microgrid. IEEE Trans. Ind. Electron. 2018, 66, 1883–1893. [Google Scholar] [CrossRef]
- Andrade, P.; Alcaso, A.N.; Bento, F.; Marques Cardoso, A.J. Buck-Boost DC-DC Converters for Fuel Cell Applications in DC Microgrids—State-of-the-Art. Electronics 2022, 11, 3941. [Google Scholar] [CrossRef]
- Pang, C.; Wu, H.; Jia, B. A multi-mode coordinated operation control strategy for optical storage DC microgrid. Energy Rep. 2023, 9, 230–235. [Google Scholar] [CrossRef]
- Roy, T.K.; Oo, A.M.T.; Ghosh, S.K. Designing a High-Order Sliding Mode Controller for Photovoltaic-and Battery Energy Storage System-Based DC Microgrids with ANN-MPPT. Energies 2024, 17, 532. [Google Scholar] [CrossRef]
- Chen, X.; Tian, R.; Wang, Y.; Xu, S.; Jiang, W.; Hashimoto, S. A Novel Voltage-Current Dual-Drop Control Method for Shipboard DC Micro-Grid with Energy Storage Systems. IEEE Access 2024, 12, 62912–62925. [Google Scholar] [CrossRef]
- Tu, H.; Yu, H.; Lukic, S. Dynamic Nonlinear Droop Control (DNDC): A Novel Primary Control Method for DC Microgrids. IEEE Trans. Power Electron. 2024, 39, 10934–10949. [Google Scholar] [CrossRef]
- Yang, M.; Xin, C.; Liang, J. Accurate current sharing of distributed energy storage units in DC microgrid based on virtual rated current. Power System Technol. 2020, 44, 823–835. [Google Scholar]




| Comparison of Strategies | SOC Balancing Speed | Capacity Difference | Overcoming Line Impedance Mismatch | Bus Voltage Restoration |
|---|---|---|---|---|
| [12] | Slow | × | × | × |
| [13] | Slow | × | × | × |
| [14] | Slow | × | × | × |
| [15] | Slow | × | × | × |
| [16] | Slow | √ | × | × |
| [17] | Slow | × | × | × |
| [18] | Slow | × | × | √ |
| [19] | Fast | √ | √ | √ |
| [20] | — | — | √ | √ |
| [21] | Fast | √ | √ | √ |
| [22] | Fast | × | √ | √ |
| This paper | Fast | √ | √ | √ |
| Parameter | Symbol | Value |
|---|---|---|
| Input-Side Capacitance of DC/DC Converter | C1 | 0.2 mF |
| Output-Side Capacitance of DC/DC Converter | C2 | 0.5 mF |
| Filter Inductance | L | 0.9 mF |
| Line Impedance | r1 | 0.8 Ω |
| r2 | 1.0 Ω | |
| r3 | 1.2 Ω | |
| Rated Bus Voltage | Uref | 700 V |
| Rated Battery Voltage | U1 | 400 V |
| U2 | 400 V | |
| U3 | 400 V | |
| Maximum Bus Voltage Deviation | ΔUmax | 35 V |
| Maximum Output Current | Idcmax | 100 A |
| Initial Virtual Impedance | Rd0 | 0.35 |
| Maximum Power of PV | Pfmax | 20 kW |
| Maximum Power of DESU | Pdmax | 20 kW |
| SOC Balancing Controller Factor | m | 5 |
| p | 6 | |
| n | 2 | |
| α | 4 | |
| d | 0.01 | |
| μ | 0.1 | |
| Global Optimization Controller Factor | Kui | 15 |
| b1 | 11 | |
| b2 | 1 | |
| Switching Frequency | fs | 15 kHz |
| Cut-Off Frequency | ωc | 60 rad/s |
| PI Controller Current Loop | KPI + KII/s | 0.5 + 30/s |
| PI Controller Voltage Loop | KPV + KIV/s | 1.5 + 60/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Q.; Wang, J.; Huang, X.; Li, S. A Fast State-of-Charge (SOC) Balancing and Current Sharing Control Strategy for Distributed Energy Storage Units in a DC Microgrid. Energies 2024, 17, 3885. https://doi.org/10.3390/en17163885
Luo Q, Wang J, Huang X, Li S. A Fast State-of-Charge (SOC) Balancing and Current Sharing Control Strategy for Distributed Energy Storage Units in a DC Microgrid. Energies. 2024; 17(16):3885. https://doi.org/10.3390/en17163885
Chicago/Turabian StyleLuo, Qin, Jiamei Wang, Xuan Huang, and Shunliang Li. 2024. "A Fast State-of-Charge (SOC) Balancing and Current Sharing Control Strategy for Distributed Energy Storage Units in a DC Microgrid" Energies 17, no. 16: 3885. https://doi.org/10.3390/en17163885
APA StyleLuo, Q., Wang, J., Huang, X., & Li, S. (2024). A Fast State-of-Charge (SOC) Balancing and Current Sharing Control Strategy for Distributed Energy Storage Units in a DC Microgrid. Energies, 17(16), 3885. https://doi.org/10.3390/en17163885






