Study on Geological Deformation of Supercritical CO2 Sequestration in Oil Shale after In Situ Pyrolysis
Abstract
1. Introduction
2. Geological Background
3. Model Building
3.1. Basic Assumptions
- The oil shale formation is located below 200 m underground, and the CO2 injection pressure is relatively large. During the injection process, the pore pressure of the oil shale layer exceeds the critical CO2 pressure value, so the injected fluid is regarded as a supercritical CO2 fluid.
- After the injection of supercritical CO2 into oil shale after pyrolysis, its seepage channels are mainly concentrated in the cracks generated by the pyrolysis and are considered to be in a state of high pressure, saturated by fluids.
- The gradients of fluid pressure and percolation velocity in oil shale follow Darcy’s law.
- The oil shale layer is in a water-saturated state after pyrolysis, and the relationship between injected supercritical CO2 and pore water follows the Brooks–Corey capillary pressure model.
- A CO2–water–rock reaction occurs between supercritical CO2 and the water-saturated rock mass, which affects the mechanical properties of oil shale. The equilibrium state of the CO2–water–rock reaction is proportional to the concentration of CO2.
- Oil shale is a sedimentary structure and is regarded as a transverse isotropic material, and the mechanical properties of oil shale after pyrolysis are greatly reduced. The mechanical damage caused by the coupling of the pore stress-state change and the chemical damage caused by the CO2–water–rock reaction are mainly considered in the process of supercritical CO2 injection.
3.2. Control Equation of Mixed-Fluid Seepage
3.3. Transversely Isotropic Static Equilibrium Equation
3.4. Establishment of Damage Evolution Equation
3.4.1. CO2–Water–Rock Chemical Damage
3.4.2. Stress Damage
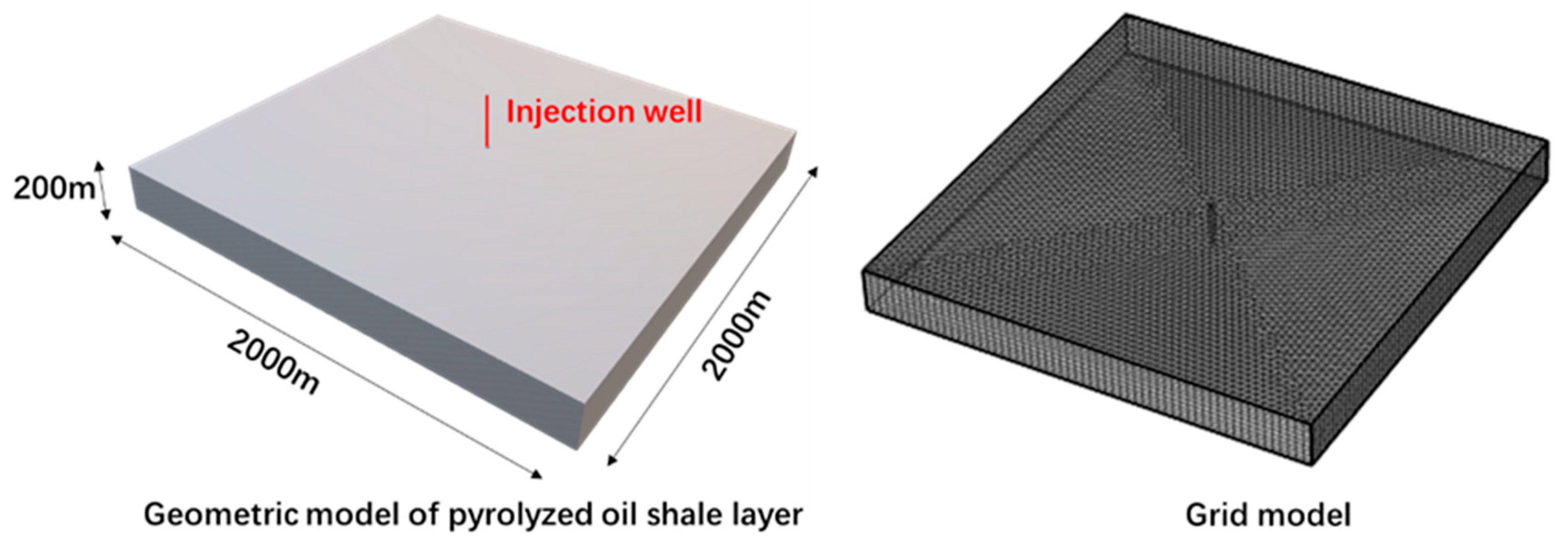
4. Geometric Model and Calculation Parameters
4.1. Simplification of Calculation Model
4.2. Simplification of Calculation Model
4.3. Parameter Selection for Transverse Isotropic Mechanical Simulation
4.4. Selection of Other Simulation Parameters
5. Simulation Results and Analysis
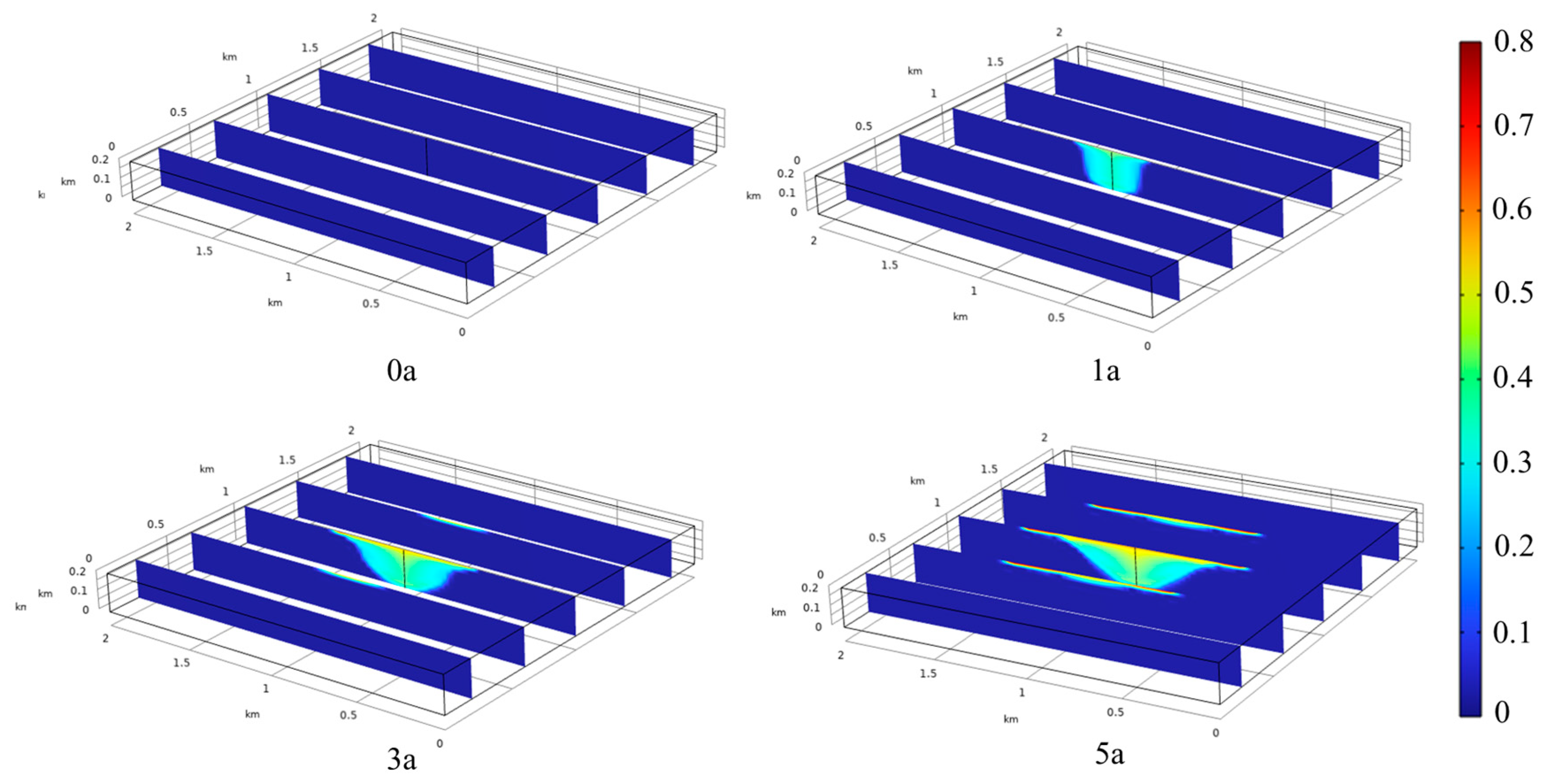
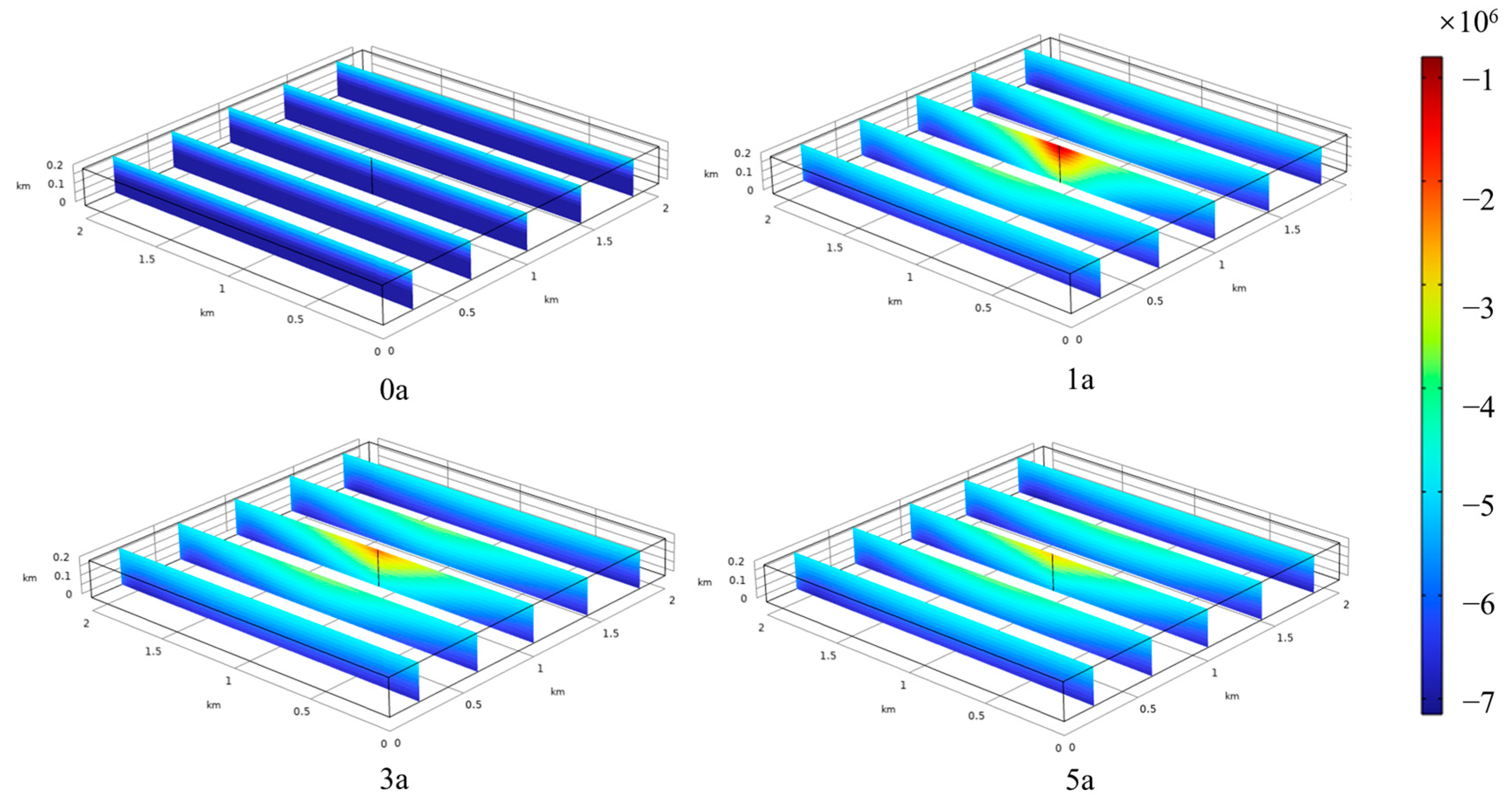
5.1. Distribution of CO2 Volume Fraction
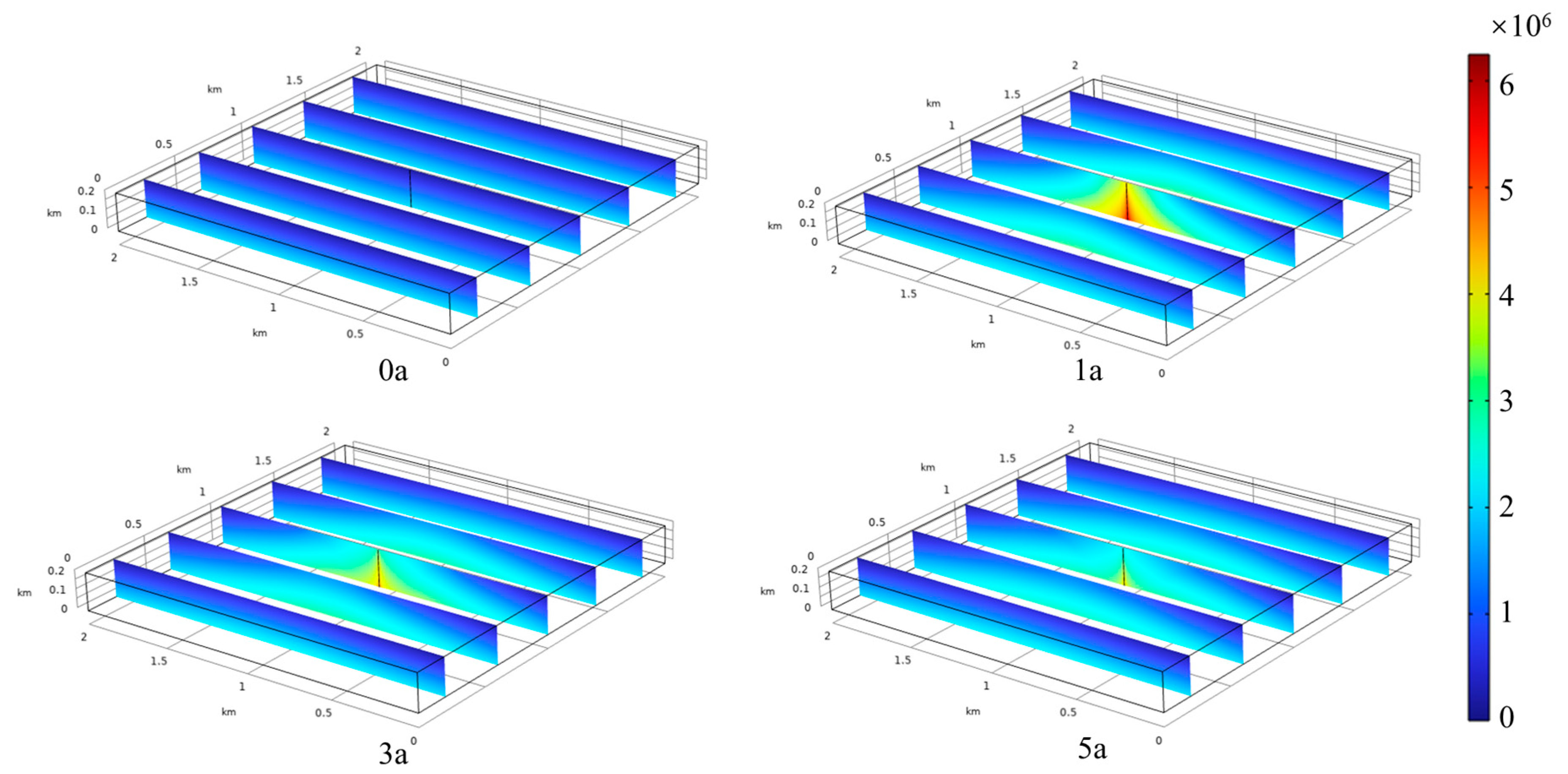
5.2. Pore Pressure Distribution
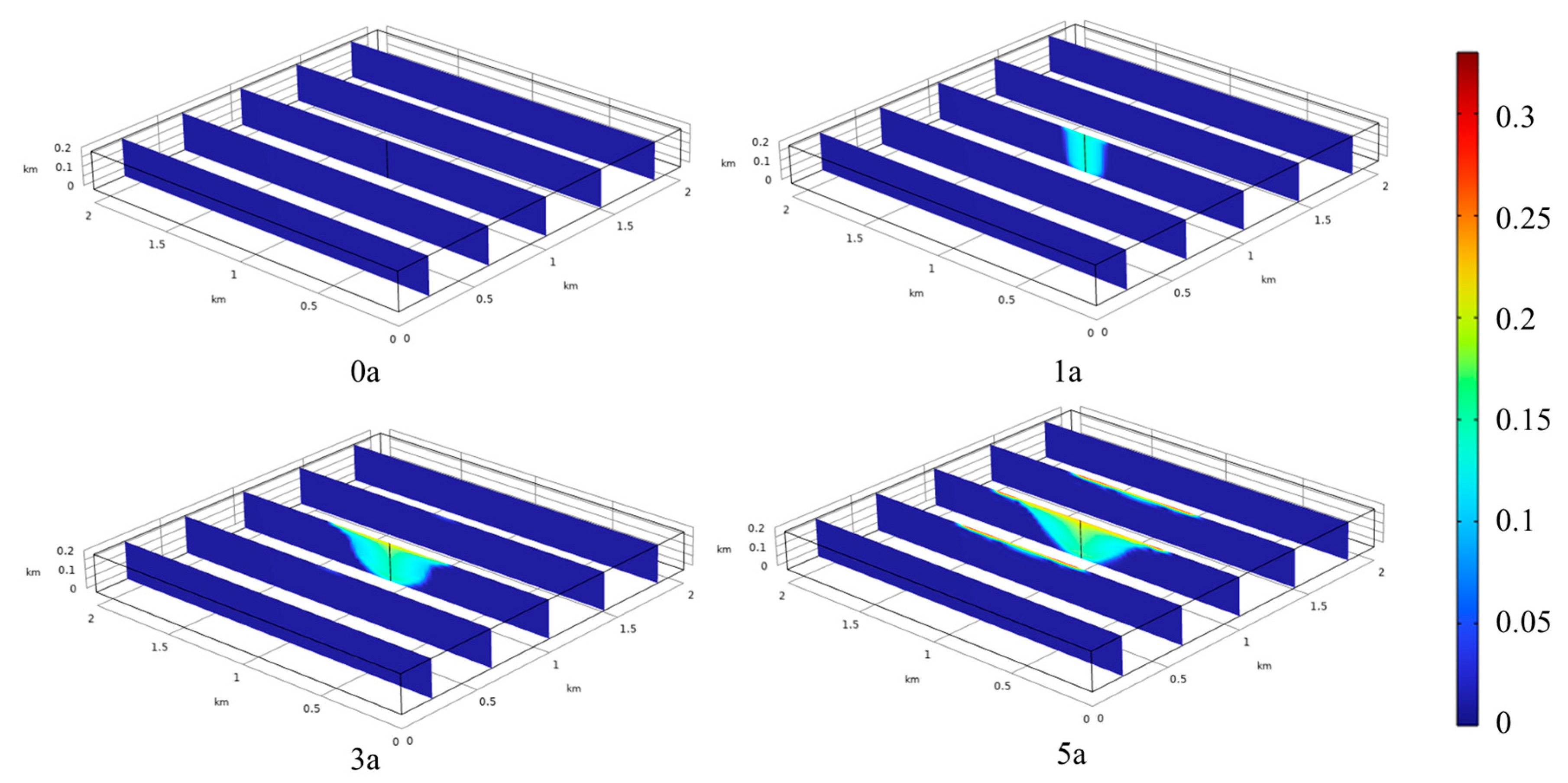
5.3. Stress-State Distribution
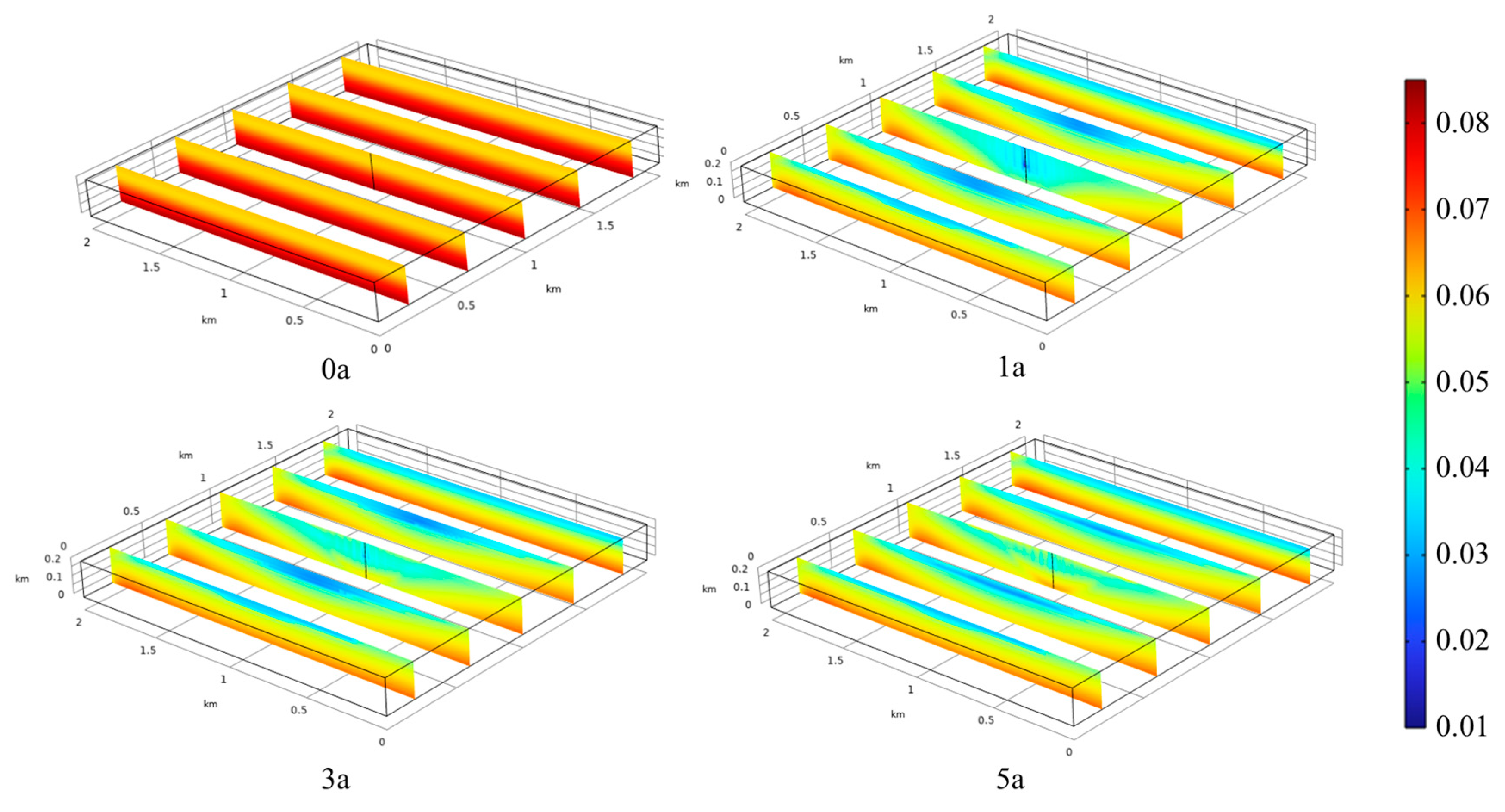
5.4. Damage Parameters
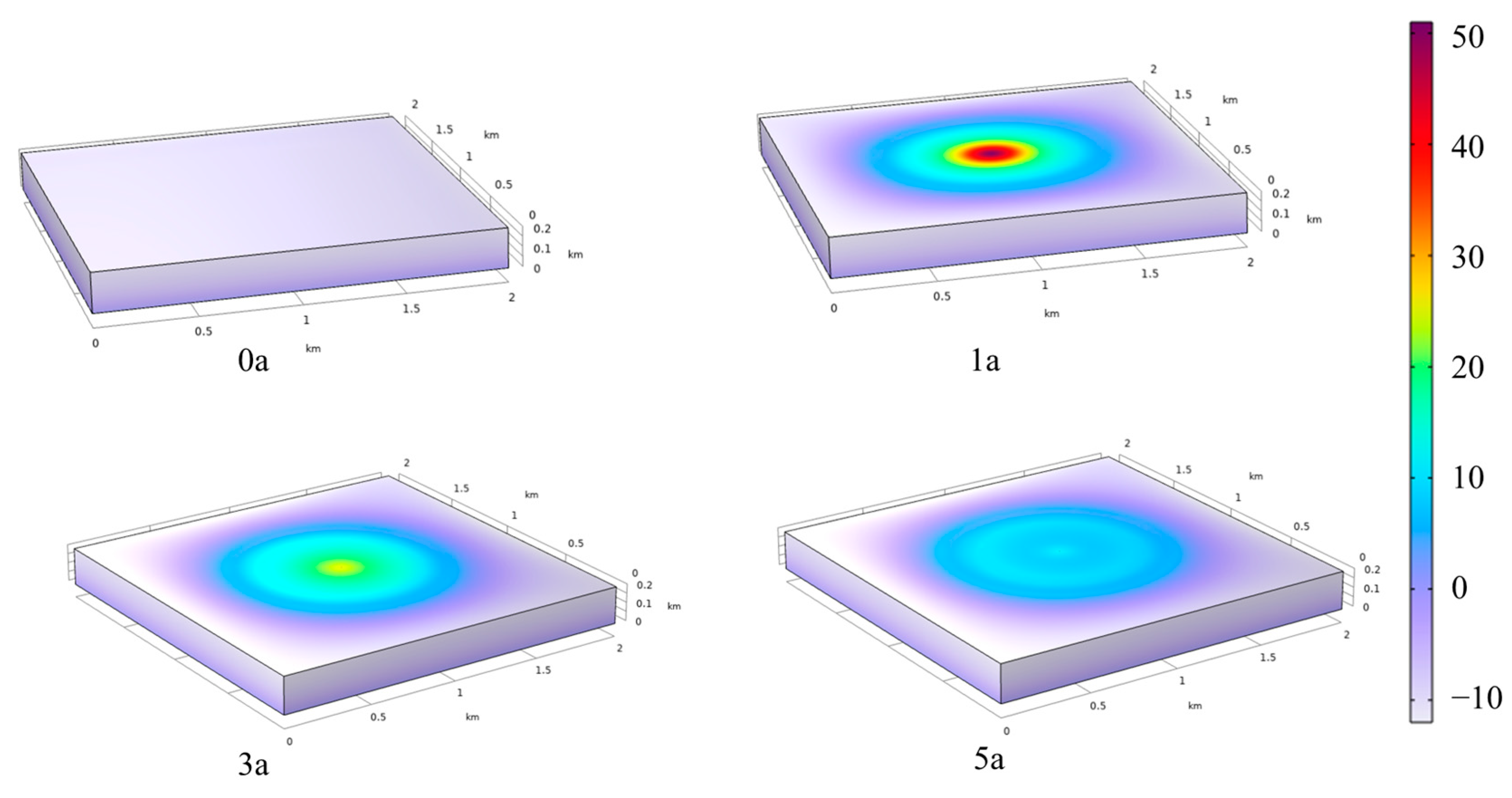
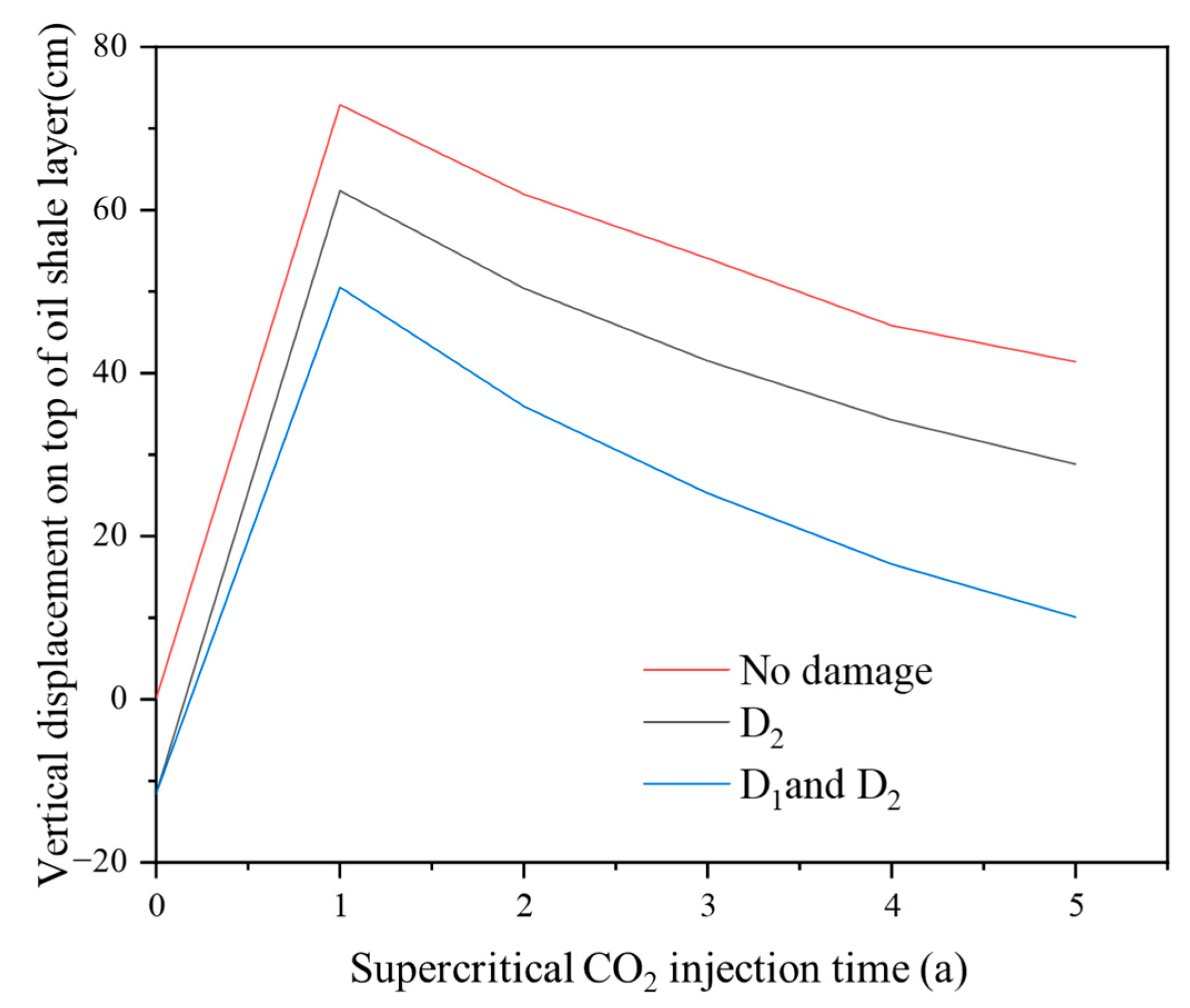
5.5. Deformation Field Distribution
6. Conclusions
- After the injection of supercritical CO2 into the oil shale, as the density of CO2 is lower than that of water, supercritical CO2 gradually diffused to the top of the oil shale and eventually formed an inverted conical distribution area with a radius of 600 m and a height of 200 m. Due to the transport mode of supercritical CO2, the pore pressure in the formation reached its maximum at the bottom of the injection well and gradually decreased at the top and surrounding the formation.
- After the injection of supercritical CO2 into oil shale, the effective stress in the rock mass decreased due to the increase in pore pressure. Since the pore pressure at the bottom of the rock layer was the largest, the expansion at the bottom was large, and then the displacement of the rock mass at the bottom played a stretching role in the top rock mass, resulting in the greatest reduction in pressure occurring at the top of the oil shale layer. The most significant reduction in effective stress occurred in the first year, with horizontal and vertical stresses at the top of the injection well decreasing to 1.5 and 0.8 MPa, respectively, and then rising slowly to 3.37 and 2.75 MPa over the next four years.
- The settlement caused by the decrease in the mechanical properties of oil shale after pyrolysis offset the ground uplift and other geological effects caused by CO2 injection to a certain extent. Under the combined action of CO2 chemical damage and stress damage, the formation uplift was only 10 cm.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chaffartzik, A.; Fischer-Kowalski, M. Latecomers to the Fossil Energy Transition, Frontrunners for Change? The Relevance of the Energy ‘Underdogs’ for Sustainability Transformations. Sustainability 2018, 10, 2650. [Google Scholar] [CrossRef]
- Middleton, R.S.; Gupta, R.; Hyman, J.D.; Viswanathan, H.S. The shale gas revolution: Barriers, sustainability, and emerging opportunities. Appl. Energy 2017, 199, 88–95. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, X.M.; Han, X.X.; Tong, J. Investigation of Chinese oil shale resources comprehensive utilization performance. Energy 2012, 42, 224–232. [Google Scholar] [CrossRef]
- Kwinta, A.; Gradka, R. Analysis of the damage influence range generated by underground mining. Int. J. Rock Mech. Min. Sci. 2020, 128, 104263. [Google Scholar] [CrossRef]
- Wu, X.; Jiang, X.W.; Chen, Y.F.; Tian, H.; Xu, N.X. The influences of mining subsidence on the ecological environment and public infrastructure: A case study at the Haolaigou Iron Ore Mine in Baotou, China. Environ. Earth Sci. 2009, 59, 803–810. [Google Scholar] [CrossRef]
- Khan, I.; Zakari, A.; Dagar, V.; Singh, S. World energy trilemma and transformative energy developments as determinants of economic growth amid environmental sustainability. Energy Econ. 2022, 108, 105884. [Google Scholar] [CrossRef]
- China’s carbon dioxide capture use and storage (CCUS) annual report (2023). Polyvinyl Chloride 2023, 51, 42.
- Li, Y.; Ma, H.; Li, H.; Ganzer, L.; Tang, Z.; Li, K.; Luo, H. Dissolution of supercritical CO2 on carbonate reservoirs. Pet. Reserv. Eval. Dev. 2023, 13, 288–295+357. [Google Scholar]
- Lei, H.W.; Jin, G.R.; Shi, Y.; Li, J.Q.; Wang, F.; Xu, T. Numerical simulation of subsurface coupled thermo-hydro-mechanical (THM) processes: Application to CO2 geological sequestration. Rock Soil Mech. 2014, 35, 2415–2425. [Google Scholar]
- Yang, L.; Yang, D.; Zhao, J.; Liu, Z.; Kang, Z. Changes of oil shale pore structure and permeability at different temperatures. Oil Shale 2016, 33, 101–110. [Google Scholar] [CrossRef]
- Wang, G.; Yang, D.; Liu, S.; Fu, M.; Wang, L. Experimental Study on the Anisotropic Mechanical Properties of Oil Shales Under Real-Time High-Temperature Conditions. Rock Mech. Rock Eng. 2021, 54, 6565–6583. [Google Scholar] [CrossRef]
- Jin, Z.F.; Li, W.; Jin, C.; Hambleton, J.; Cusatis, G. Anisotropic elastic, strength, and fracture properties of Marcellus shale. Int. J. Rock Mech. Min. Sci. 2018, 109, 124–137. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, K.; Zhong, X.; Wang, Y.; Chen, C.; Zhang, H.; Pan, D.; Zhai, L.; Gao, S. Experimental Investigation on the Anisotropic Behaviors Induced by Bedding Planes in Mechanical Properties of Ma’quan Oil Shale. Arab. J. Sci. Eng. 2022, 47, 11385–11403. [Google Scholar] [CrossRef]
- Bai, Y.L.; Xia, M.F.; Ke, F.J.; Li, H.L. Closed trans-scale statistical microdamage mechanics. Acta Mech. Sin. 2002, 18, 1–17. [Google Scholar]
- Hui, X.; Ma, F.S.; Xu, J.M.; Guo, J. Study on statistical damage constitutive model for rocks considering length and occurrence distribution of joint fissures. Chin. J. Rock Mech. Eng. 2017, 36, 3233–3238. [Google Scholar]
- Zhao, G.; Chen, C.; Yan, H. A Thermal Damage Constitutive Model for Oil Shale Based on Weibull Statistical Theory. Math. Probl. Eng. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Song, J.; Zhang, D. Comprehensive Review of Caprock-Sealing Mechanisms for Geologic Carbon Sequestration. Environ. Sci. Technol. 2013, 47, 9–22. [Google Scholar] [CrossRef] [PubMed]
- Ling, R. Study on thermodynamic chemical effect coupling model of CO2 geological storage process. Adhesion 2022, 49, 93–97. [Google Scholar]
- Ji, Y.J.; Wang, X.Y.; Zhou, T.Y.; Wang, Z.G.; Jiang, G.B. Effect of CO2 geological sequestration on reservoir mechanicaiproperties and gas migration and diffusion under multi field coupling. Huanjinggongcheng 2023, 41, 442–446. [Google Scholar]
- Gong, G.; Li, Y.; Tang, D.; Yu, H.; Jiang, Z. Research on optimization of CO2 injection scheme under thm couplings in CO2 geological storage. J. Eng. Geol. 2023, 31, 1084–1096. [Google Scholar]
- Wang, G.Y.; Yang, D.; Kang, Z.Q.; Lv, Y.Q. Numerical Study on In-situ Injecting Superheated Steam Thermal Recovery of Transversely Isotropic Oil Shale Reservoir. J. Taiyuan Univ. Technol. 2020, 51, 81–90. [Google Scholar]
- Khan, S.; Khulief, Y.; Al-Shuhail, A. Reservoir Geomechanical Modeling and Ground Uplift during CO2 Injection into Khuff Reservoir. In Proceedings of the ASME-JSME-KSME Joint Fluids Engineering Conference (AJK-FED 2019), San Francisco, CA, USA, 28 July–1 August 2019. [Google Scholar]
- Xu, R.; Luo, S.; Jiang, P. Pore scale numerical simulation of supercritical CO2 injecting into porous media containing water. In Proceedings of the 10th International Conference on Greenhouse Gas Control Technologies, Amsterdam, The Netherlands, 19–23 September 2010. [Google Scholar]
- Huang, B.; Li, L.; Tan, Y.; Hu, R.; Li, X. Investigating the Meso-Mechanical Anisotropy and Fracture Surface Roughness of Continental Shale. J. Geophys. Res.-Solid Earth 2020, 125, e2019JB017828. [Google Scholar] [CrossRef]
- Lin, S.; Li, H.; Luo, X.; Zhang, Y.; Zhang, L. An experimental investigation into the elastic and thermal properties of oil shales: Yanchang formation, Ordos basin. Mar. Pet. Geol. 2023, 158, 106530. [Google Scholar] [CrossRef]
- Lekhnitskii, S.G.; Fern, P.; Brandstatter, J.J.; Dill, E.H. Theory of Elasticity of an Anisotropic Elastic Body. Phys. Today 1964, 17, 84. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Zhang, W.Q. 3D FEM analysis for layered rock considering anisotropy of shear strength. J. Cent. South Univ. Technol. 2010, 17, 1357–1363. [Google Scholar] [CrossRef]
- Ma, W. Study on the Evolution Laws of Structural and Mechanical Characteristics of Oil Shale during Temperature Rise and the Application of Numerical Simulation. Ph.D. Thesis, Jilin University, Changchun, China, 2023. [Google Scholar]
- Huang, Y.H. Effect of Supercritical CO2 on Dynamic and Static Mechanical Properties of Shale. Ph.D. Thesis, China University of Petroleum, Beijing, China, 2023. [Google Scholar]

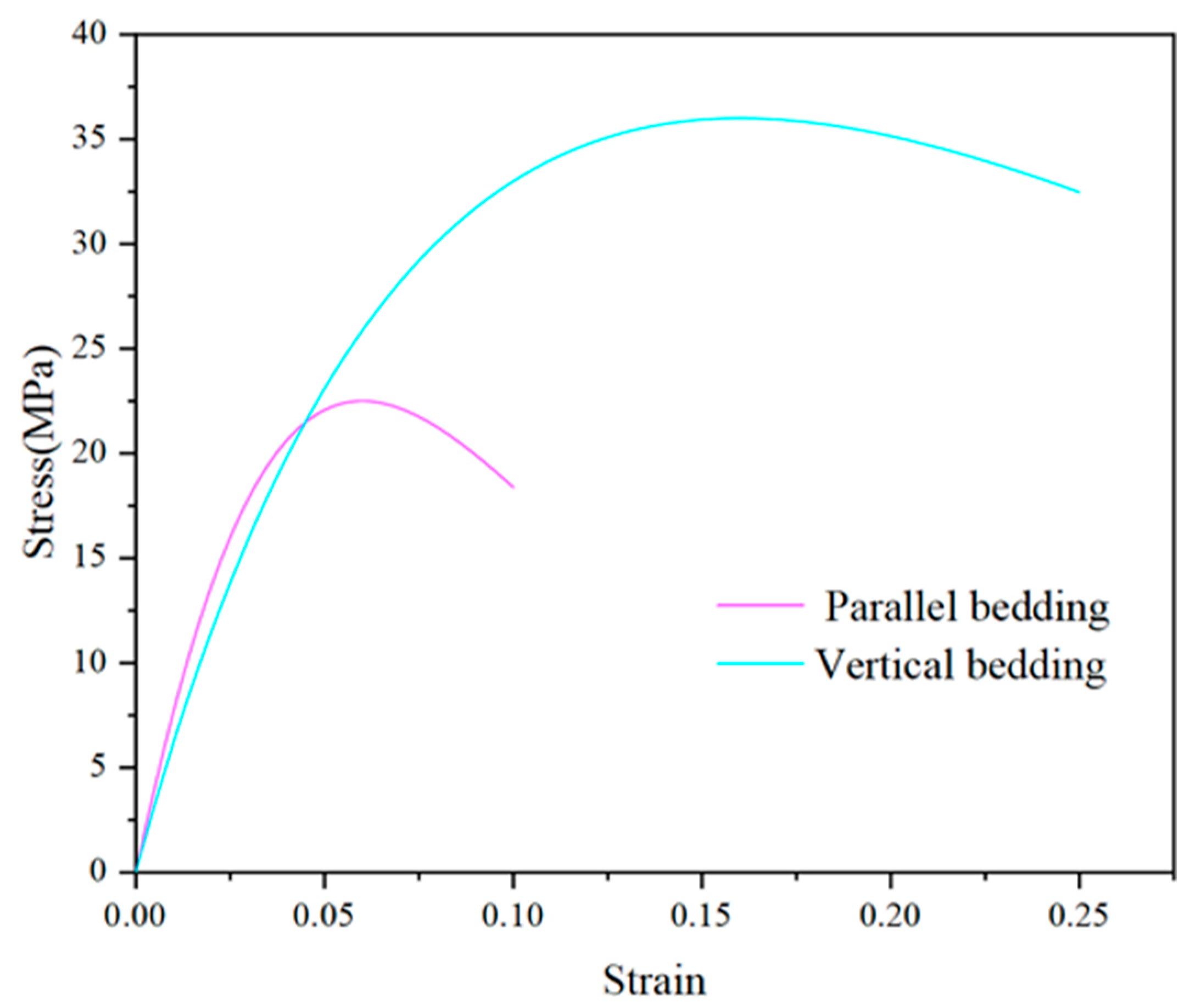

| Unpyrolyzed | Failure Strain | Failure Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|---|
| Parallel bedding | 0.03 | 68 | 2.5 |
| Vertical bedding | 0.08 | 108 | 2 |
| Pyrolyzed | Failure Strain | Failure Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|---|
| Parallel bedding | 0.06 | 22.5 | 0.84 |
| Vertical bedding | 0.16 | 36 | 0.68 |
| Pyrolyzed | m | F |
|---|---|---|
| Parallel bedding | 1.24 | 44.8 |
| Vertical bedding | 0.904 | 72.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, H.; Wu, X.; Li, Q.; Fang, Y.; Zhang, S. Study on Geological Deformation of Supercritical CO2 Sequestration in Oil Shale after In Situ Pyrolysis. Energies 2024, 17, 3849. https://doi.org/10.3390/en17153849
Yan H, Wu X, Li Q, Fang Y, Zhang S. Study on Geological Deformation of Supercritical CO2 Sequestration in Oil Shale after In Situ Pyrolysis. Energies. 2024; 17(15):3849. https://doi.org/10.3390/en17153849
Chicago/Turabian StyleYan, Heping, Xiurong Wu, Qiang Li, Yinghui Fang, and Shuo Zhang. 2024. "Study on Geological Deformation of Supercritical CO2 Sequestration in Oil Shale after In Situ Pyrolysis" Energies 17, no. 15: 3849. https://doi.org/10.3390/en17153849
APA StyleYan, H., Wu, X., Li, Q., Fang, Y., & Zhang, S. (2024). Study on Geological Deformation of Supercritical CO2 Sequestration in Oil Shale after In Situ Pyrolysis. Energies, 17(15), 3849. https://doi.org/10.3390/en17153849






