1. Introduction
The present study aims to address the following two issues in one solution: on one hand, our coastal infrastructure and property as well as precious beaches are put at risk by the projected sea-level rise and change in coastal wave conditions caused by climate change; on the other hand, our effort to combat climate change by reducing greenhouse emissions calls for a greater use of renewable energy, including wave energy. Breakwaters and seawalls are among the marine structures frequently used to protect shorelines. A dual function design of a breakwater integrated with wave-energy converters has the potential to address the two problems in one solution [
1]. In addition, the availability of power from the breakwater can be used for local port operations or naval facilities.
There are many types of transitional breakwaters for shore protection and the construction of harbors [
2]. Traditional gravity-type breakwaters such as rubble mounds may cause concerns such as water stagnation [
3]. Newer designs such as Bragg-type breakwaters [
4,
5,
6,
7], which reduce the harbor-side wave heights by inducing Bragg resonance, are effective only for a narrow frequency range. Additionally, such breakwaters require multiple structures in an array, leading to a high construction cost. Slotted breakwaters are relatively new concepts which allow the exchange of seawater between the sea side and the shore side of the breakwaters. The gaps in slotted barriers can be designed to allow fish to pass through and thus reduce potential adverse impacts of traditional breakwaters on local coastal ecosystems. The construction cost for this type of breakwaters can be lower than that for the traditional rubble mound breakwaters in relatively deep waters. A review on the wave interaction with slotted/perforated marine structures can be found in Huang et al. [
8].
Ocean waves contain tremendous energy that has not been utilized [
9]. Many technologies for using wave-energy converters (WECs) to generate electricity have been proposed [
10,
11]. Among existing WEC concepts, Oscillating-Water-Column (OWCs)-type WECs are one of the most studied and tested [
10,
12]. A Oscillating-Water-Column (OWC)-type WEC is chosen in this study for the integration with a slotted breakwater due mainly to prior extensive studies of pile breakwaters [
1,
13] and its simplistic working principle and design [
14].
A typical OWC consists of a partially submerged, bottomless, pneumatic air chamber and out of water turbine [
12]. Multi-chamber OWCs have also been proposed [
15]. Typical slotted breakwaters/barriers consists of a thin plate with vertical or horizontal slots, which are usually affixed to the sea floor [
16,
17,
18]. The dual function design to be examined in this study has an OWC supported by a bottom-sitting slotted barrier.
The use of numerical tools have been recently applied to further understand OWC structures, such as computational fluid dynamics (CFD) [
19,
20] and smoothed particle hydrodynamics (SPH) [
21,
22]. However, these numerical models are computationally expensive to run and still require validation using laboratory experiments prior to trusting the results. Thus, this study shall provide means of validation for such models, which is needed to optimize the design for the given site conditions. This work is also mainly focused on providing a new design of a slotted breakwater which integrates an OWC-type wave energy converter. This manuscript evaluates the performance of such a design in terms of wave transmission, wave energy extraction, and wave loading under various wave conditions, focusing on the effects of the porosity of the slotted barrier and tide level changes.
2. Methods
This section shall provide detail on the OWC–breakwater model and the experimental setup and tests, including the derivation of non-dimensional parameters to be used in the succeeding sections.
2.1. OWC–Breakwater Model
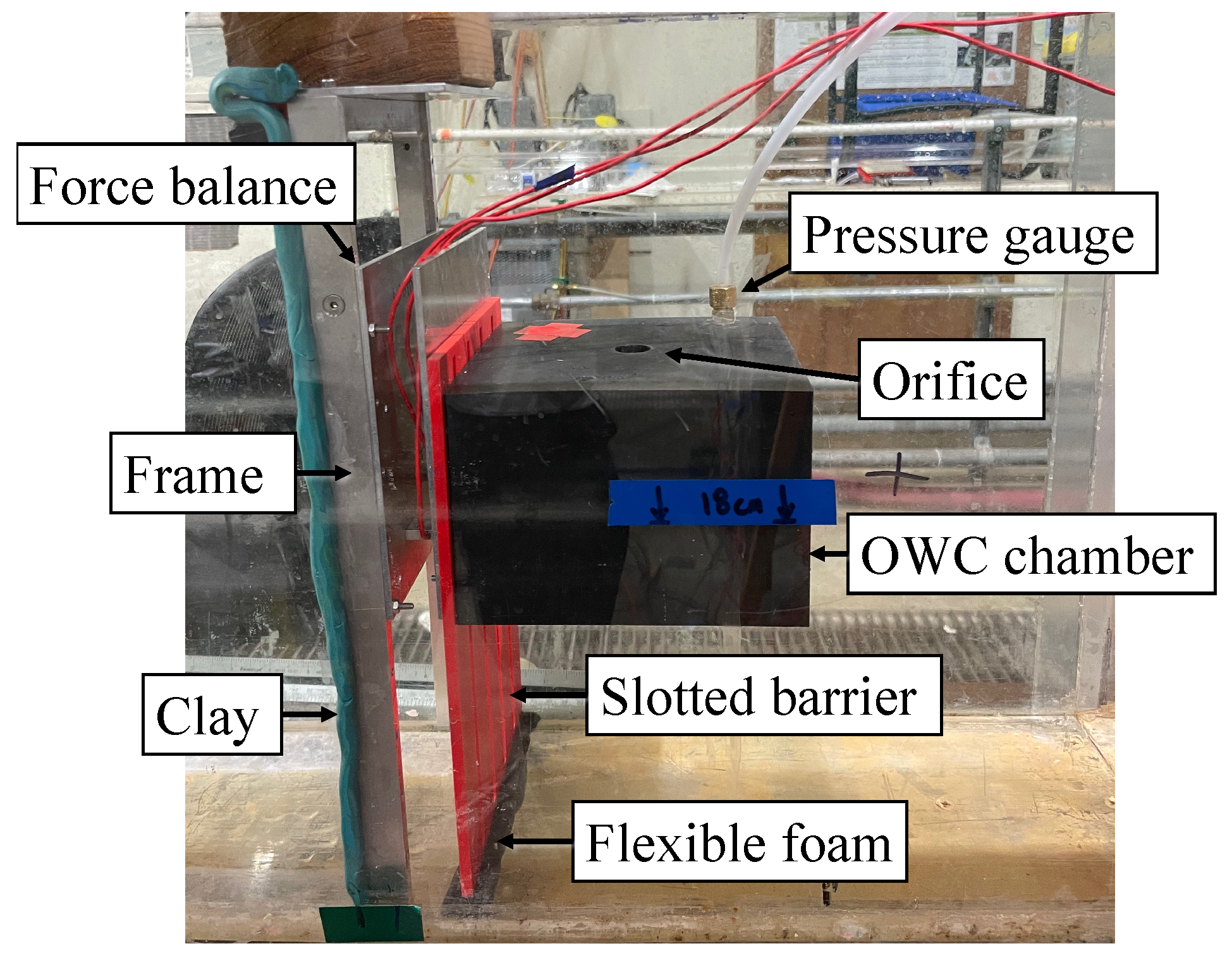
The OWC slotted barrier model affixed in the wave flume consists of a slotted barrier, an air chamber and an orifice in the top plate. A differential pressure sensor was mounted on the top, and a force balance was used to connect the model to a frame which was fixed to the flume, with the gaps being sealed to the flume walls with clay, as shown in
Figure 1. The model is installed orthogonally to the bottom surface and the sidewalls of the flume. The structure was affixed at the rear to a single-axis force balance, which consists of 3 single-axis submbersible Futek load cells oriented in a triangular fashion in between two metal plates (see
Figure 1). The force balance was precisely manufactured such that individual load cells are perpendicular to the plates so that no internal forces are generated by their orientation or installation. Special care was taken to make sure that the structure was not touching the wave flume. To seal the small gap between the flume bottom and the lower end of the slotted barrier, a thin flexible strip of foam was placed at the gap to avoid any unnecessary increase in the porosity of the slotted barrier. The foam material is very soft so that it will not affect the force readings.
The OWC air chamber and slotted barrier is 3D printed out of PLA. The Setra Model 239 differential pressure sensor has a high accuracy 0.073% FS and fast response time of <10 ms [
23].
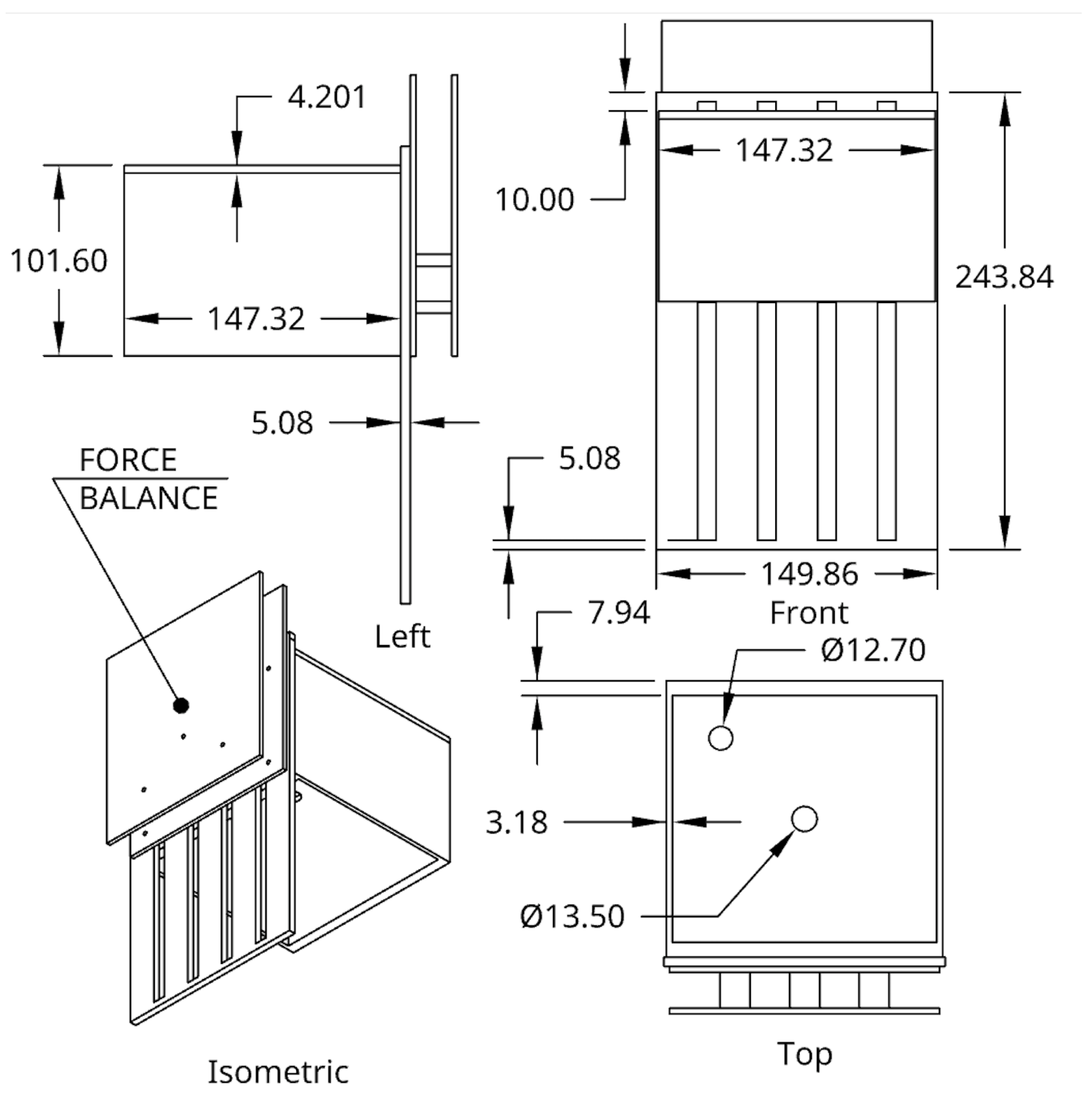
The dimensions of the OWC slotted barrier and air chamber are shown in
Figure 2. The porosity of the slotted barrier is calculated for a fixed depth of
mm, height of
mm, width of
mm, and top and bottom borders of
mm, such that four equal slot widths varying for porosity are evenly distributed among the slotted barrier width. The OWC air chamber is 147.32 × 147.32 × 101.60 mm with a void volume of 1.80 ×
mm
3. The orifice and pressure sensor circular openings at the top of the air chamber are
mm
2 and
mm
2, respectively. The orifice opening ratio is
%. The opening for the pressure sensor is sealed with screw thread tape and clay.
2.2. Experimental Setup
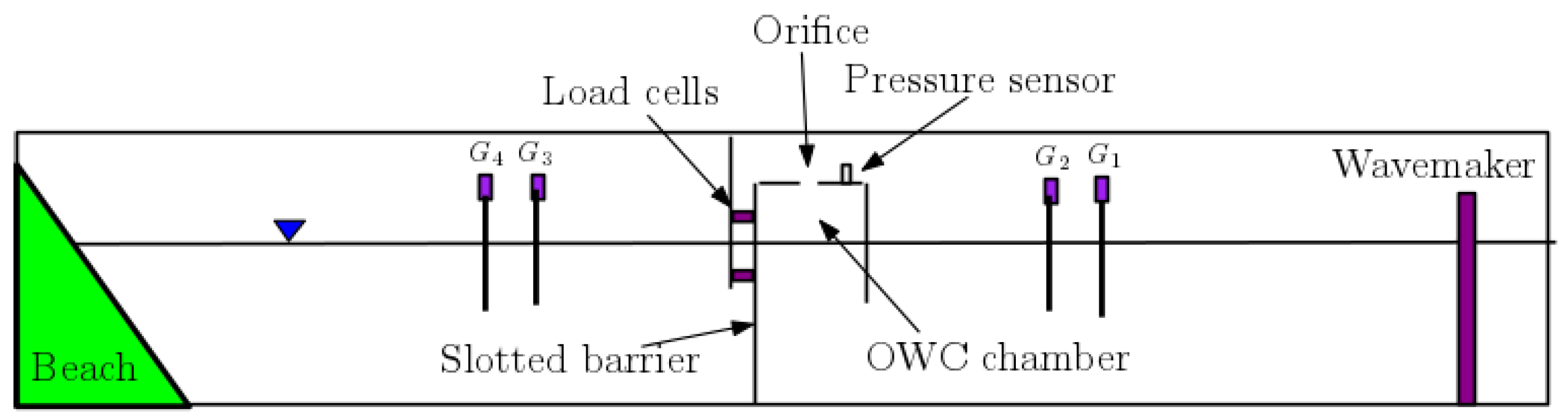
Figure 3 shows the experimental setup used for this study. The wave flume used in this study is
m long,
m deep and
m wide. It is equipped with a piston-type wave-maker on one end and a wave-absorbing beach on the other end. The wave-absorbing beach is
m long and has a 1/10 slope. To further reduce the wave reflection, the slope was covered with an array of plastic cylinders, each with a diameter of about 1 mm. The OWC–breakwater model was installed in the middle section of the wave flume. Four capacitance-type wave gauges (
) are installed in the flume in two pairs on either side of the OWC slotted barrier model, as shown in
Figure 3. The wave gauge pairs are spaced around 25 cm apart, while the distance between the wave gauge pairs and the structure (center to center) are about 2.15 m and 1.03 m for the seaward wave gauge pair and shoreward wave gauge pair, respectively.
These distances between the wave gauges were selected to avoid the influence of evanescent waves radiating from the structure. A pressure sensor was used to measure the air pressure inside the OWC air chamber, and a force balance built with three single-axis load cells was used to measure the wave force normal to the structure.
Note that the reason for using only two wave gauges for each location is limited by the data acquisition (DAQ) device used in the experiment having only eight differential channels. Wherein the pressure sensor uses one channel, and the force balance uses three channels, and this leaves four channels left for the wave gauges.
With regard to scaling, the structure dimensions are at an order of a 15 cm chamber width, while we can expect a full-scale breakwater with a width of about 7 m when testing at a 1:49 scale under Froude scaling. Note that this small scale makes it difficult to work with actual PTO systems, and thus, the use of an orifice as the PTO enables us to estimate the extracted power of the OWC at such a small scale. The underlying assumptions involved in using an orifice as a PTO are described in the succeeding subsection.
2.3. Calculations of Pneumatic Power and Extraction Efficiency
Since an orifice is used to model a nonlinear PTO in this small-scale experimental study, the difference of the air pressures inside and outside the air chamber,
, can be parameterized by a quadratic loss coefficient
[
24]
where
is the density of the air, and
is the spatially averaged velocity of the air flow in the air chamber. For in-compressible air, this is equivalent to the spatially averaged velocity of the air–water interface inside the OWC chamber. Strictly speaking, the quadratic loss coefficient
needs to be determined experimentally. In this study, since the surface elevation inside the OWC chamber cannot be measured due to the small size of the model, the following empirical formula [
24,
25] is used with the assumption of a sharp-edged orifice,
where
is the opening ratio and
is the empirical coefficient of contraction given by
Using the experimental data available in the literature on OWC and orifice studies, Ulm et al. [
26] argued that for the orifices used in the OWC studied, the dependence of
on the Reynold’s number should be weak, and thus,
could be regarded as a function of the opening ratio
only.
The power of the incident waves in the wave flume,
, can be calculated by
where
E is the wave energy flux,
is the group velocity,
W is the width of the wave flume,
is the water density,
g is the gravitational acceleration, and
is the incident wave amplitude.
The pneumatic power generated by the OWC,
, is the work performed by the up-and-down motion of the air–water interface. Since the air pressure is nearly uniform inside the air chamber,
can be calculated by
where
, with
B being the distance between the front and back walls of the OWC chamber, while W is the cross-sectional area of the air chamber, and the overline represents a phase average (i.e., a time average over one wave period). He and Huang [
25] have shown that the pneumatic power that can be extracted by the OWC,
, can be calculated by the measured air pressure inside the air chamber
alone using Equation (
6),
The performance of the (pneumatic) energy extraction by the model can be measured by the pneumatic efficiency
, which is defined by
which is in the range of 0 and 1. For brevity, it must be noted that the efficiency mentioned from hereon is the pneumatic efficiency and does not include mechanical losses due an actual PTO system.
2.4. Determination of Measured Reflection and Transmission Coefficients
The two-point wave separation method of Goda and Suzuki [
27] is used to determine these three amplitudes in this study.
,
and
are the amplitudes of incident, reflected, and transmitted first harmonic waves. Wave reflection and transmission coefficients are two important design parameters for breakwaters. In this study, only regular waves are considered, and the reflection coefficient
and the transmission coefficient
are defined by
To improve the accuracy of the measured reflection and transmission coefficients, a correction was applied as shown below.
2.5. Wave Spatial Decay and Its Correction to Reflection and Transmission Coefficients
The reflection and transmission coefficients should be calculated using the amplitudes of the incident, reflected and transmitted waves measured at the OWC–breakwater. Due to the presence of evanescent waves and large eddies near the OWC–breakwater, the wave probes in the experiment cannot be placed close to the OWC–breakwater, which makes it difficult to obtain the wave amplitudes needed to accurately calculate the reflection and transmission coefficients. In practice, the wave probes are placed at a certain distance away from the OWC–breakwater; this distance is usually about several times the water depth. As a result, the reflection and transmission coefficients may carry systematic errors due to the spatial decay of the wave amplitude. This spatial attenuation can be caused by the wave boundary layers adjacent to solid boundaries [
28], surface contamination [
29,
30], and the capillary hysteresis associated with the meniscus formed at the contact line [
30].
Following Ippen [
31] or Stiassnie et al. [
32], the spatial decay of wave amplitude from
to
can be expressed as
where the spatial decay rate is denoted by
. Hunt [
28] presented a theoretical expression for the spatial decay rate due to the solid boundaries of a rectangular channel. In this theory, the spatial decay rate
increases with decreasing channel width
B and wave frequency
as shown in Equation (
10)
where
k is the wave number,
h is the water depth and
is the kinematic viscosity of water. For a given wave period
and flume width
B, Equation (
10) suggests a larger
value for a smaller
h.
For the spatial decay rate due to surface contamination, Dorn [
29] presented the following theoretical expression by assuming a horizontally immobilized surface,
The total spatial decay rate due to viscous damping should be the sum of the values given by Equations (
10) and (
11). However, these theoretical predictions do not agree with measurements well [
29]. As a result, the spatial decay rate
is usually determined by performing empty wave-flume tests.
To correct the measured reflection and transmission coefficients with a given spatial decay rate
, we adopt the approach used by Stiassnie et al. [
32]. We denote the amplitudes of the incident, reflected and transmitted waves at the OWC–breakwater as
,
and
. According to Equation (
9), we have
where
is the distance between the OWC–breakwater structure and the wave gauges placed in front of the structure, and
is the distance between the OWC–breakwater structure and the wave gauges placed after the structure. A constant spatial decay rate is assumed for incident, reflected and transmitted waves. Combining Equations (
8) and (
12) gives
Therefore, the actual reflection and transmission coefficients,
and
, are larger than those determined by Equation (
8).
2.6. Determination of Viscous Loss Coefficient
The conservation of wave power says that the incident wave power is equal to the sum of the wave power in the reflected waves, the wave power in the transmitted waves, the pneumatic power extracted by the OWC and the wave power dissipated by viscous effects (i.e., vortex shedding). This can be expressed mathematically as
where
represents the wave power dissipated by viscous effects. It then follows that the energy dissipation coefficient
can be calculated by
where both
and
are corrected using Equation (
13) by a constant spatial decay rate for all test conditions.
2.7. Drag Coefficient
For engineering applications, we are mainly interested in the maximum wave force acting on the structure. Since weak nonlinearity is observed in the generated waves, wherein the crest is slightly larger than the trough, the analysis is focused on the maximum compressive force induced by the waves. Thus, the maximum compressive (positive) force measured under each wave was obtained and averaged over five wave periods. The force induced by the fluctuating water surface is then non-dimensionalized with the hydrodynamic pressure. Since we are only interested in the maximum force, we shall use the incident wave amplitude, which is assumed to be constant, to calculate the hydrodynamic pressure. This value is then assumed to be acting on the whole structure wherein the representative area is defined by the product of the still water depth and structure width. The non-dimensionalized force is given as
where
is the average of the maximum values of the wave force
in five stable waves,
W is the width of the structure, and
h is the still water depth.
2.8. Test Conditions and Procedure
Various wave conditions for small amplitude, long-crested, linear, and shallow water waves were tested to show the effects of porosity and tide levels on the extraction efficiency, wave energy, and wave loading for the OWC slotted barrier model. Four different slotted barrier porosities (10%, 15%, 20%, and 25%) were affixed at the same location to the OWC air chamber. Each slotted barrier model was tested at different water depths (16 cm, 17 cm, and 18 cm) representing tidal changes. For each water depth, 11 unique wave conditions were performed with one repeating test. The wave conditions, summarized in
Table 1,
Table 2,
Table 3 and
Table 4, include a fixed wave amplitude at
cm with a varying period from 0.7 to 1.4 s with an interval of
s (Cases 1–8); and a fixed wave period
s with varying wave amplitudes of 0.5; 1.0; 1.5; and 2.0 cm (Cases 9–12). A fixed wave period of 1.0 s was used since it is the design wave period in this study. The wave conditions used can be mainly classified as 2nd-order Stokes waves except for wave Case 12, which is classified under 3rd-order Stokes, based on the classification of Zhao et al. [
33].
The same test conditions were used for each porosity. Wave amplitudes were obtained by performing a wave separation analysis using the measured surface elevations. The data from the wave gauges, pressure sensor, and force balance were obtained by one DAQ at 100 Hz. Each test for a given wave condition yielded a 3 min time series, which consisted of about one minute of still water, one minute of waves, and one minute of still water.
2.9. Dimensional Analysis
To find out a set of dimensionless parameters to present the results, we present the following dimensionless analysis. The dimensionless parameters , , , and are functions of the following parameters
Wave length (L), wave amplitude () and water depth h.
The geometry of the OWC–breakwater. For geometrically similar models, the geometry of the OWC–breakwater model can be represented by the width of the OWC–breakwater B, which is the distance between the front and back walls of the OWC chamber.
The porosity of the slotted barrier and the opening ratio of the orifice .
Density of the air , density of water , and gravitational acceleration g.
A dimensional analysis can lead to the following dimensionless relationships
In the experiment, both and are fixed. Therefore, the results for , , , and can be presented as functions of the following dimensionless parameters: dimensionless chamber width (), dimensionless water depth (), porosity of the slotted barrier () and the dimensionless wave amplitude (). Note that for a linear problem, the results should be independent of .
4. Discussion
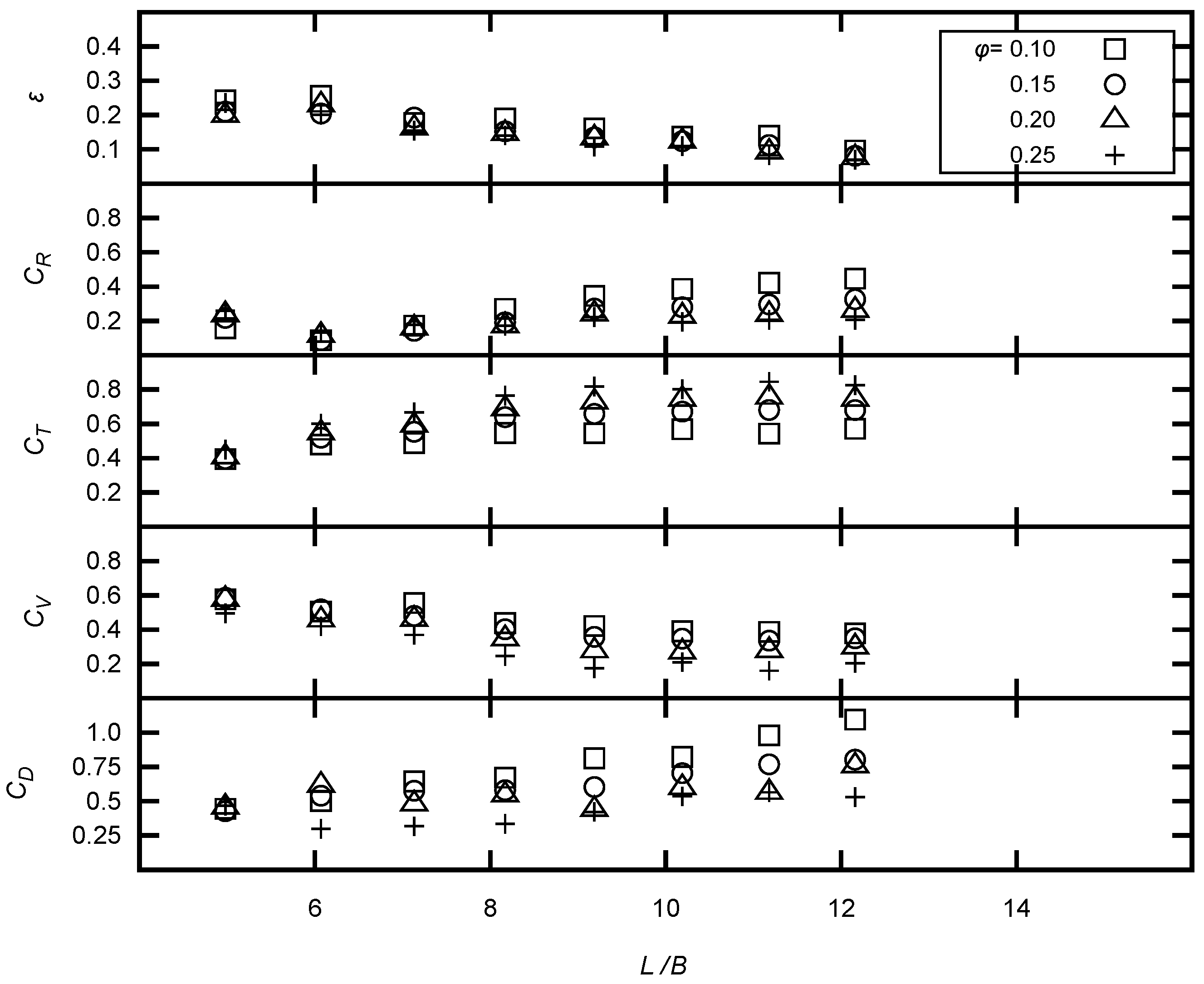
We have observed the effects of varying wave height, wave length, water depth, and slotted barrier porosity on each of the relevant non-dimensional parameters. In this section, we shall attempt to further elaborate and theorize the reasons behind the observed results in the previous section.
The nonlinear decrease of the reflection coefficient under varying wavelengths is observed, which occurs at around L/B = 6.0. This can be explained by the effect of multiple reflections between the front face of the OWC chamber and the slotted barrier. Waves reflect between both vertical walls at a distance apart, producing a partial standing wave inside the chamber, leading to a reduced reflection coefficient. Thus, it should occur theoretically when the width of the chamber is 1/4 of the wave length, which of course may be affected by the viscous effects. Our results show that the effect of multiple reflections may have occurred when the width of the chamber is about 1/6 of the wavelength. Similar studies have also been performed for an OWC with a rear vertical wall [
35], wherein the reduction of the reflection coefficient occurs at around 1/5 of the wavelength.
The transmission coefficient,
, is observed to be fairly constant under the lowest porosity case (10%), which applies to the tested
values from 5 to 12. This range decreases during higher tide levels (
Figure 7) and higher porosities (
Figure 9). This constant property of the
value for a wide range of wavelengths is an interesting finding since this is unconventional for typical breakwaters. The constant wave transmission coefficient may be useful to harbor planners, since it shows that the design is effective for a wide range of wave periods. The possible cause of this phenomena for an OWC–breakwater shall be discussed in the succeeding subsection. Moreover, it must be noted that in the field, these results cannot be applied at the gaps or the heads of the breakwater. This is mainly due to wave diffraction and the fact that the results are limited to 1D flume experiments.
The constant reflection coefficient means that the reflected wave amplitude is linear with the incoming wave amplitude. This shows that the wave reflection is constant in amplitude for weakly nonlinear waves. On the other hand, all other parameters are variable under small changes of the wave amplitude. This shows the nonlinearity of the wave amplitude with respect to the other parameters. This is expected, since the wave energy is directly proportional to the square of the wave amplitude (or wave height). Also, note that the scale of the wave amplitude with respect to B, in contrast to is much smaller, which is an order of .
From varying the amplitude of the wave, we observe an increase in the energy efficiency of the OWC and the dissipation through the slotted barrier, which leads to a decrease in the wave transmission. This observation for the transmission coefficient is not typical for traditional breakwaters, and so this result is thought to be mainly due to the presence of the OWC and the slotted barrier. The efficiency is related to the power extracted, which is related to the square of the velocity,
. We also know that the energy dissipated by viscous damping through the slotted barrier is related to
[
36]. From this, we can see that an increase in the velocities, which is driven by the increase in the wave height, creates higher flow speeds at the chamber orifice and slots of the slotted barrier. This leads to an increased power extracted from the OWC (as well as extraction efficiency) and dissipation due to the slotted barrier.
We can see that the orifice at the top of the chamber, which acts as a power take-off (PTO), seems to have a similar effect as the slots of the slotted barrier, both of which have been modeled as a damper which applies viscous damping to the flow simply by introducing turbulence to the flow. This direct relationship of the velocity and wave amplitude with the energy extracted or dissipated by flow-damping orifices or slots is also the reason why for constant wave amplitudes and varying wave periods, the transmission coefficient is kept at a consistent value.
We note from Equation (
5) that the power output,
, is directly related to the cube of the wave steepness,
Since the incident wave power is proportional to
, the extraction efficiency as defined by Equation (
7) can be formally written as
The change of the pneumatic efficiency with wave amplitude shown in
Figure 8 confirms Equation (
19).
The results show that increasing
or decreasing
can slightly increase the value of
when all other dimensionless parameters are fixed. The results also show
decreases almost linearly with increasing
when all other dimensionless parameters are fixed. If we write
with
and both
a and
b are positive functions of
and
, we have
We remark that
and
are not independent for ocean waves, and there might be a statistical relationship between wave height and period [
37,
38]; therefore, increasing
does not necessarily decrease the efficiency
for ocean waves.
The effects of water-level change due to tides have been observed to be small and negligible for and . This is possibly due to the relative scale of the tidal range with respect to the water depths being small, which is of an order of 0.1. On the other hand, the effect of decreasing the porosity leading to a higher reflection coefficient and lower transmission coefficient is intuitive and can be seen as similar to that of the extreme case of an impermeable vertical wall with a porosity of 0.0, which can induce maximum reflection and minimum transmission—or the case with no wall at all (a porosity of 1.0), which allows for maximum transmission and minimum reflection.
The force coefficient values obtained are around the range of 0.0 to 1.1. This is a good indication, since this coefficient can also serve as a safety factor that can easily be applied to engineering design. The range of values being close to 1.0 is a good indication, since this allows us to easily apply safety factors to the force coefficient, which is typically performed in engineering design. Do note that these results are limited to wave conditions, from 0.05 to 0.2 and from 9 to 18. Engineers might also be interested in the actual scale values of the extractable power by the OWC. Based on the experimental results, the power extracted when scaled up to a 10 m wide chamber, with a 10% porous slotted wall, at 11 m water depth when subjected to 0.8 m high waves at 8 s is in the order of 7.5 kW. Note that this value is the power generated per unit length of chamber, and that power is based on pneumatic power, which does not involve mechanical losses. In addition, effects of air compressibility at full scale may slightly reduce the energy efficiency of the OWC. Related experiments have found that this reduction is around 5%.
The particles acted upon by waves move in a circular-like motion, and due to the presence of the OWC chamber, they will naturally absorb a significant vertical loading and transfer it to the structure foundation, which can also contribute to the moment induced at the base of the structure. Thus, future tests must include measurements of the vertical load on the structure.
Note that we are testing at a scale of 1:49 under Froude scaling, and that most of the assumptions involve neglecting the effect of varying Reynolds number. However, when scaling up, we must eventually consider a possible change in the effects of the Reynolds number. This may possibly impact our assumptions for a sharp-edged orifice. Thus, actual measurements of the velocity of the water surface inside the chamber would be necessary. Another means of measurement would be the use of an actual PTO system. The findings from this study are limited to the range of wave conditions presented in the Results section, which in the form of the dimensionless parameters presented are values from 0.05 to 0.2 and values from 9 to 18. For a 10 m wide chamber, this corresponds to incident wave amplitudes, , from 0.05 to 0.2 m and wave periods, T, from 7 to 14 s.