1. Introduction
With the improvement of technology and social demand, the heights of buildings or spatial structures are constantly increasing. The technical regulation for concrete high-rise buildings [
1] stipulates that reinforced concrete structures with ten floors or more or a height of more than 28 m are called high-rise building structures. However, because of the significant heights of high-rise buildings, the impact of wind loads is more pronounced and considered a critical factor. Various problems frequently occur on tall buildings and seriously affect the development of tall buildings. These problems can be attributed to particular wind flow phenomena in the environment, like down-drought wind, vortices, downwind effects, and the resulting abnormal wind loads. Especially for areas affected by seasonal gale or typhoon weather, the problems can be expected to worsen. Therefore, the research on wind resistance safety in tall buildings has become essential for architects and town planners who need guidelines or standard design tools to consider the effects of wind on their buildings. It is worth emphasizing that the research by Estrado et al. [
2] demonstrated that the current methods for calculating the structural wind response in the Eurocode do not provide methods for unconventional building shapes.
It is known that the turbulent flow over the bluff body exerts significant wind loads on the object’s surfaces. In other words, the aerodynamic shape of high-rise buildings greatly influences the wind resistance of the structure. Architectural design often involves different planar shapes, most commonly including the setting of concavity on the planar configuration [
3]. The complexity of structural design for the wind resistance of buildings requires a detailed wind tunnel/CFD (Computational Fluid Dynamics) study as the guidelines. Wind-induced responses are the primary function of the outer geometry of the building, which means that the aerodynamics of the tall buildings can be adjusted by modifying the outer geometry. More and more studies have shifted from the conventional concept of prismatic shape along the height to the influence of the specific shape configuration of the bluff body, such as height ratio [
4,
5], opening [
6,
7,
8], corner modification [
9,
10,
11,
12,
13], and concavity [
14], emphasizing the parameters that determine better aerodynamic properties referring to wind-resistance effects. Some of the recent progress based on the numerical technique has been reviewed as follows. Yang [
15] used the agent model combined with the optimization method of NSGA-2 to study the wind effect of the convexity and concavity of building sections on the wind-induced response. He found that the convexity of the building makes the building shape more streamlined and suppresses the intensity of vortex shedding. Montazeri et al. [
16] compared the wind-induced pressure coefficients on buildings with and without balconies by CFD simulations; it was found that the facade details, such as balconies, drastically change the flow pattern and the overall pressure distribution on the facade. The results show that the presence of the fourth row of balconies leads to a substantial decrease in the surface-average wind pressure coefficient of approximately 30%. Alminhana et al. [
9] carried out a numerical study to optimize the aerodynamic performance of a building by modifying its corner shapes; the results showed that the use of corner modifications can significantly reduce the aerodynamic forces on building structures. In the research, the lifting force shows a maximum reduction of 31% and the flow conditions near the building locations improved, which may have an essential influence on aeroelastic effects. Shahab et al. [
17] performed a series of numerical simulations to compare the aerodynamic loads on tall prismatic buildings with different sections, such as square, pentagonal, and hexagonal, with their twisted forms; the results show that the hexagonal models have the lowest values of drag coefficient and mean moment coefficient followed by pentagonal models and square models. Liao [
18] evaluated the aerodynamic performance of tall buildings with different sections using CFD numerical simulation; the results found that the concave angle can reduce the torque coefficient.
The above research studies demonstrate that much progress has been made based on numerical simulation for the study of wind resistance of buildings. However, the research focus is still heavily dependent on experimental testing. Wind tunnel technology has been proven to be the most commonly used and effective method for determining wind loads and effects in construction structures based on airflow phenomena. At the early stage, Kwok et al. [
19] conducted wind tunnel model tests to investigate the effect of edge configuration on the wind-induced response of a tall building with a rectangular cross-section. It was found that slotted corners and chamfered corners, and combinations of these, caused significant reductions in both the along-wind and crosswind responses. In 2009, Quan et al. [
20] conducted the wind tunnel test of a rigid high-rise building model and analyzed the influence of local shape characteristics on the wind load of the envelope on the facades. The results show that the most unfavorable negative wind pressure coefficient is related to wake separation and is greatly influenced by the local shape characteristics of the building. Xie et al. [
21] tested the cross-wind effect on the tapered super-tall building models with the modification of a corner cut; the results show that the peak base bending moment can be reduced with a maximum reduction of 31.13%. Ke et al. [
22,
23] studied the influence of facade accessories of high-rise buildings on local peak wind pressure through a series of wind tunnel tests. A total of 21 configurations of different appurtenances were tested. They found that the correlation between the response of the building model and the appendages at different positions was higher than that of the building model with smooth surfaces, and the discontinuous appendages could reduce the crosswind force to some extent. Ke et al. [
13] conducted a wind tunnel test to verify the aerodynamic effect on high-rise buildings. The work shows that the corner modification has a considerable benefit in reducing the cross-wind loads and responses.
Through the analysis of the research above, it can be concluded that high-rise buildings’ different shape features significantly impact the distribution characteristics of wind loads. To optimize the structural design of conventional buildings for better aerodynamic performance, a series of studies have been performed on the modified shape of high-rise buildings. However, it can be found that most of the studies only focus on the concave corners of the buildings, and little thought was given to the design of concavity on other facades of the building. Moreover, most of the existing studies focus on the force characteristics of the building as a whole, while the wind pressure characteristics of each facade of the building with various planar configurations still need to be analyzed with more awareness. Finally, there is also a lack of research on the aerodynamic performance of whole-wind azimuths for buildings with different cross-sections [
18].
Based on the summary of research cases and methods, it also shows that studies on designed experiments to study the distribution characteristics of wind loads are still insufficient in terms of persuasion to some extent, and it is meaningful to improve the understanding of building wind resistance. Therefore, the wind tunnel experiment, referring to three high-rise building models with different planar configurations, has been designed to study the influence on the wind load distribution of buildings.
2. Experimental Models
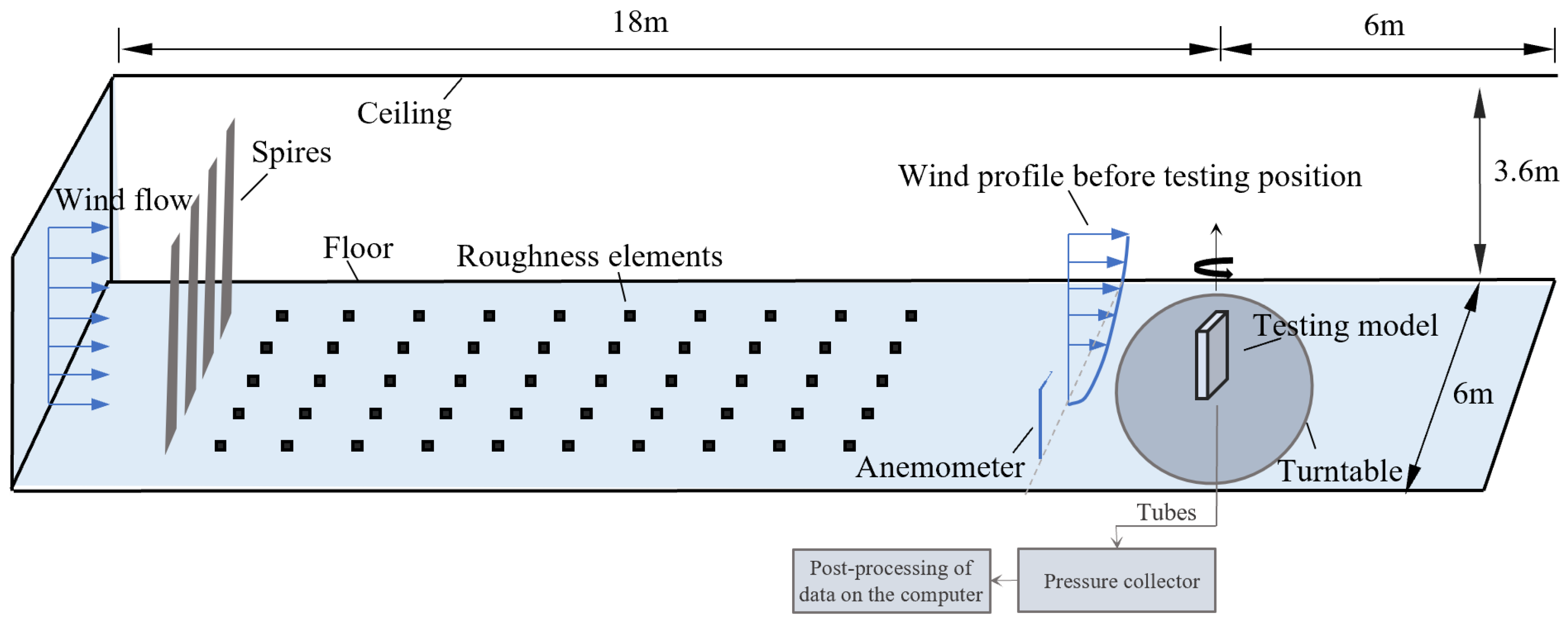
The designed experiment was conducted in the Wind Tunnel Laboratory of Xiamen University of Technology (WT for short). The schematic diagram of the test site is shown in
Figure 1. The dimensions of the test section are 24 m long, 6 m wide, and 3.6 m high. In
Figure 1, the setting of roughness elements and upstream spires can be seen, which are adopted for atmosphere turbulent boundary layer simulation in the WT and achieving the designed wind profiles before the testing position.
In this experiment, three building models with different shape characteristics were set up for comparison tests. Firstly, the CAARC (Commonwealth Advisory Aeronautical Research Council) standard high-rise model [
24] was adopted as the background model (BG model for short), which was first proposed to test the results of various wind tunnel tests when simulating natural winds. The full-scale prototype sizes of the CAARC are 45.72 m long, 30.48 m wide, and 182.88 m high. Considering the test blocking ratio requirement in the test, the model scale ratio was determined as 1:200; specifically, the CAARC test model is manufactured as 228 mm long, 152 mm wide, and 914 mm high. Secondly, the planar configurations of the buildings were adjusted while keeping the height constant, and then two groups of comparative models were obtained (named the T1 model and the T2 model, as seen in
Figure 2a,b). The T1 building has concave corners around the model and the T2 building has concave corners in the middle of the long side of the model. In
Figure 2b, the definition of column numbers can also be noted.
Regarding model manufacture, acrylic plates with a thickness of 3.7 mm were adopted with smooth surfaces, sufficient stiffness, and sealing. During the production process, a minimum gap of 10 mm should be left between the measuring points and the outer contours to facilitate model bonding. In
Figure 2, the tiny dots on the model’s facades and roofs represent the deployment of the collection points for the wind pressure.
3. Experimental Arrangement
3.1. Test Cases
To investigate the effects of wind loads on the three high-rise models shown in
Figure 2, three models were tested with a wind speed of 10 m/s, based on China’s building load code [
25]. The static pressure value measured is 101,324.7 Pa. Due to the symmetry of the testing model, the wind azimuths were changed from 0° to 180° with an interval of 15° during the test. The definition of wind azimuth is shown in
Figure 2a1, and the detailed test conditions are shown in
Table 1.
3.2. Testing Equipment
In this experiment, an anemometer (Croba Probe) manufactured by TFI was used in the wind tunnel to calibrate the static pressure and wind speed of the incoming flow field at the model’s height. The wind pressures on the building models were collected using the DTC Initium electronic pressure scanning valve manufactured by PSI. During the data collection process, the pressure signal’s sampling frequency was 330 Hz and the sampling duration was 60 s. A total of 19,800 wind pressure data were recorded at each measuring point at every wind azimuth.
The reference wind pressure in this paper is based on the incoming wind pressure at the height of the model, and the calculation formula of the wind pressure coefficient is as follows:
where p
i(
θ) and C
pi(
θ) represent the wind pressure and wind pressure coefficient at measuring point
i when the wind azimuth is
θ;
ρ is the density of air, 1.225 kg/m
3; and U is the incoming wind speed at the model height.
The most unfavorable wind pressure of the three building models is the most unfavorable wind pressure of each measuring point at all wind angles. The most unfavorable wind pressure coefficient is calculated as follows:
where
and
represent the most unfavorable positive and negative wind pressure coefficients at measuring point
i, respectively.
is the variation range of wind azimuths, as shown in
Table 1.
4. Results
4.1. The Average Wind Pressure Coefficients along the Height of the Building Models
The variations in average wind pressure coefficients along the height under whole wind azimuths are shown in
Figure 3,
Figure 4 and
Figure 5.
4.1.1. The Columns at the Building Corners
Figure 3 shows the variations in the average wind pressure coefficients of Col.1 (marked in red on the models) of the three building models with heights under different wind azimuths. Parameters H and Cp represent the height of the models and the average wind pressure coefficient, separately. The most unfavorable wind pressures (positive/negative) are summarized in
Table 2.
BG model: Among the wind azimuths of 0°~60°, the points of Col.1 are controlled by positive wind pressure, and the positive wind pressure coefficients gradually increase when the azimuth varies from 0° to 45°. When the wind azimuth turns to 60°, the wind pressure coefficient values are positive but close to zero and it changes to negative pressure at the highest testing point. Later, when the wind azimuth further increases, the column gradually reaches the crosswind side and then the left side, which is dominated by negative wind pressures. To be specific, for Col.1, the gauging points obtain the maximum positive wind pressure coefficient ( = 0.73 at h/H = 0.71) at θ = 45°, as well as the maximum negative wind pressure coefficient ( = −0.81 at h/H = 0.99 near the top) at θ = 90°.
T1 model: The gauging points of Col.1 are located on the windward side at a wind direction of 0° but are affected by negative pressure, indicating that the adjustment of the section shape at the corners causes apparent changes in the airflow characteristics around the building. The maximum positive wind pressure coefficient ( = 0.73 at h/H = 0.93) at 45° and the maximum negative wind pressure coefficient was obtained at 105° ( = −1.21 at h/H = 0.38).
T2 model: The change in the sectional shape of this model is mainly reflected in the middle area of the building, so the wind pressure coefficient distribution of the Col.1 represents only a slight difference from that of the BG model. The maximum positive wind pressure coefficient ( = 0.73 at h/H = 0.93) was obtained at θ = 30°.
4.1.2. The Columns in the Middle of the Windward Sides When θ = 0°
Figure 4 shows the variations of the average wind pressure coefficients of the middle columns (marked in red on the model) with height under different wind azimuths. In
Figure 4, the three models are mainly subjected to positive pressure in the range of 0°~60° wind azimuths. The analysis of the most unfavorable wind pressure data at 30°~90° is summarized in
Table 3.
As can be seen from
Figure 4 and
Table 3, the most unfavorable wind pressure value is mainly reflected in the middle and upper floors of buildings (
h/H ≥ 0.71). Under the same wind azimuth, the extreme value of wind pressure of the T1 model is lower than that of the other two models. To be detailed, in the conditions of 30°, the maximum adverse positive wind pressure coefficient of the T1 model decreased by 32.8% compared with the BG model. At 60°, the decrease in the T1 model is 60%, whereas the T2 model further aggravates the adverse wind pressure value, increasing by 135%. The change in model shape also significantly impacts the maximum adverse negative wind pressure coefficient. When the wind azimuth is 90°, the measuring points in this column are in the crosswind side position and controlled by negative pressures. Compared with the BG model, the value of the T1 model decreases by 72.1%, while that of the T2 model decreases by 4.8%.
4.1.3. The Columns in the Middle of the Windward Sides when θ = 90°
Figure 5 shows the variations in the average wind pressure coefficients of the middle columns (marked in red on the models) of the 90° windward face with height under different wind azimuths. The analysis of the most unfavorable wind pressure data at 30°~90° is summarized in
Table 4.
It can also be found that adverse wind pressures appear in the middle and upper regions of buildings. The of the models occurs in the T2 model, but there is no obvious discrepancy among them. The of the models occurs in the T1 model at θ = 15° when the analyzed column is located on the crosswind side.
4.2. The Average Wind Pressure Coefficients around the Perimeters of the Building Models
For further analysis of the distribution characteristics of the wind pressure coefficients along the circumference of the models, three horizontal layers (
h/H = 0.27, 0.60, and 0.98) were selected, as shown in
Figure 6 and
Figure 7.
4.2.1. The Cp around the Perimeters of the Building Models at Wind Azimuth 0°
As shown in
Figure 6, when the wind azimuth is 0° (the wind direction is facing the windward side), the pressure coefficients decrease from the middle of the windward side to both sides. The Cp values of the three models at the center position of the windward side are the same on the whole, but the speeds of attenuation from the center to both sides vary. The regression rate of the T1 model is the fastest, while that of the T2 model is the slowest. Moreover, at the corner, the Cps of BG and T2 models present positive pressures, but the value of the T1 model is already under the control of negative pressure. It can be interpreted that the T1 model is modified to conform more to the streamlined shape, and then a swirl of air occurs around the corner of the building, creating negative pressures.
In addition, from the comparisons of the three horizontal layers in
Figure 6, on the windward surface, taking points from Col.5 for example (marked in dashed circles), it is found that along the height, the positive pressure value increases first and then decreases. According to the continuity equation of the fluid, the maximum pressure on the building surface occurs when the speed is reduced to the lowest value, so there is a stagnation point in the height direction where the airflow blowing windward is diverted.
4.2.2. The Cp around the Perimeters of the Building Models at Wind Azimuth 90°
The variations in the wind pressure coefficients of the three models with the circumference at 90° wind azimuth were analyzed in
Figure 7. As shown in the diagram, in the condition of a 90° wind direction, the testing points of the T1 model present negative pressures in the concave regions of the left and right end sides of the windward facade (namely, Col. No.1/2/20/21). Through our analysis, we found that the concave pattern of the building causes the surrounding wind field flow to separate and then bypass the concave area where the vortex is generated, causing more tremendous negative pressure. To be specific, on the bottom layer (
h/H = 0.27) of the T1 building model,
is −1.07; as the height increases,
is −1.42 at
h/H = 0.98. Furthermore, the generation of negative pressure on the windward side directly affects the downwind load response of buildings, and the wind resistance design cannot fully copy the case provided by the code, so wind tunnel tests are needed to accurately evaluate the wind load effect caused by these detailed structures.
4.3. The Average Wind Pressure Coefficients on the Roof of Building Models
In this section, the variations in the Cp on the roof were studied to evaluate the effect of planar modifications on the wind load characteristics, as shown in
Figure 8. Four representative wind azimuths (0°/30°/60°/90°) were selected and are displayed in the figure.
Through the comparisons, it can be seen that, in the same incoming wind field, the change in the external geometric characteristics of the building has a significant impact on the wind load of the building roof. At the condition of 0° wind azimuth, the average wind pressure coefficients of the roof of the three models are all negative, and the contour maps are symmetrical on the whole. For the BG model, the area with severe negative pressure is mainly concentrated in the middle zone on both the left and right sides, where the is −0.95. On the other hand, the areas with high negative pressure in the T1 and T2 models are mainly concentrated near the windward sides. Among them, of the T1 model is −0.80 and that of the T2 model is −0.71.
In the conditions of a 30° wind azimuth, it can be seen that the roofs of these models at a 30° wind azimuth are still under the control of negative wind pressure, and the even reaches −1.4 in the BG model, while the value of the T1 model is −1.3 and −1.2 for the T2 model. When the wind azimuth was further changed to 60°, it can be observed that the average wind pressure coefficients of the roofs of the three models are still negative. Furthermore, the reaches −1.5 in the BG model, while the of the T1 and T2 models is −1.2 and −1.1, respectively.
Referring to the case of a 90° wind azimuth in
Figure 8, the wind flows from the left side of the sections, the contour maps of average wind pressures display symmetric features, and the areas with more serious negative pressure in the three models are concentrated close to the windward sides. Through comparisons, it is found that although the average wind pressure coefficient of the T1 model is −1.2, the area occupied by severe negative pressure is relatively small. In the T2 model, although
is −0.77, nearly half of the area is occupied by significant negative pressures (Cp > 0.70), obviously impacting the roof loads.
In addition, the wind loads on the roofs of the three building models were further studied, and the comparison diagram of the stresses on the roof per unit area was drawn, as shown in
Figure 9. It can be seen from
Figure 9 that all roofs are subjected to upward wind force. Compared with the BG model, the T1 and T2 models significantly reduce the stress on the unit area of the roof. When the wind azimuth is 0°, the uplift force on the unit area of the T1 model roof is reduced by 17.5% and the uplift force on the unit area of the T2 model roof is reduced by 24.5%. The most significant difference occurs at the 90° wind azimuth; the stress reduction in the T1 model roof is 47.2% and the T2 model has a 19.8% reduction, compared with the BG model.
5. Discussions
In the paper, three types of building models with different exterior features that are widely used in practical engineering were selected for wind tunnel pressure tests to improve the understanding of the law of the shape influence on the wind-resistance design of tall buildings.
(1) The wind load distribution on the building surface is the representation of the flow features around the blunt body in the wind field. When the wind direction is perpendicular to the building surface, the surface is predominantly controlled by positive wind pressure. When the angle between the incoming flow direction and the normal direction of the facade is less than or equal to 15°, the most unfavorable positive wind pressure coefficient occurs. That is, the incoming flow is approximately blowing directly to the measuring points. However, when the angle between the wind direction of the incoming flow and the normal direction of the facade is between 75° and 105°, the most unfavorable negative wind pressure coefficient occurs. That is, the incoming flow is approximately orthogonal to the normal line of the facade.
(2) The T1 building model has concave shapes at the corners of the model, and the T2 building model has concave shapes in the middle of the long side of the model. Based on the analysis of the distribution law of wind pressure coefficients, it can be seen that, compared with the BG model, the appearance adjustment of the T1 model makes the flow field around the building more streamlined, hence reducing the influencing range and value of negative pressures to a certain extent.
It is also important to consider that the T1 model presents negative pressures in the concave regions of the windward facade. The reason can be explained as follows. The existence of concavities around the T1 model causes the wind flow to accelerate around the concave area, resulting in flow separation and other possible flow phenomena such as vortices, leading to a large negative pressure within a small range, as shown in
Figure 7, in which the value reaches −1.21 (
= −1.21 at
h/H = 0.38 when
θ = 105°). This is consistent with the findings in the literature [
14], which also shows a relatively obvious increase in negative pressure at the concave corner of the building.
On the other hand, the concavity in the middle area of the building (T2 model) has less influence on the negative pressure area than that of the T1 model but its positive-pressure extreme value increases compared with that of the BG model. Moreover, the most significant growth rate of pressure is 135.0% compared with that of the BG model (as shown in
Table 3). This significant wind pressure increment brought by the long-side concavity shape of buildings has not been mentioned in previous research as they have mainly focused on the influence of different concave corner shapes of buildings [
13,
26,
27].
(3) From the analysis of the forces on the roof per unit area, it can be seen that both T1 and T2 models are more favorable to the uplift force. In particular, when the wind azimuth is 90 degrees, the T1 model can effectively reduce the wind pressure load on the roof, lowering the probability of wind damage to the roof and ensuring the safety of the structure.
(4) In this study, the high-precision instruments used in the experiment ensured the reliability and accuracy of the test data to the greatest extent and provided a good basis for the further parameterization analysis of different concave configurations. However, the uncertainties need to be further discussed in follow-up work.
6. Conclusions
The wind effect is a crucial factor in the wind-resistance design of high-rise buildings. For aesthetic or functional requirements, architects sometimes consider designing different areas of concavity on the planar shape of high-rise buildings, which makes the wind pressure distribution more complicated. The reference value of the wind load on the building cannot be directly given by relevant standards but needs to be determined by a wind tunnel test. In this study, wind tunnel pressure measurement tests were carried out for three rigid building models with different planar designs. The distribution law of the average wind pressure coefficients of the building facades and roofs was analyzed and discussed. The following conclusions were drawn:
(1) It can be observed that the change in exterior configuration plays a certain role in wind pressure distribution. On the facade of high-rise buildings, the wind load on the windward side is generally dominated by positive pressure. It can be found that the absolute magnitude of the maximum negative pressure coefficient is greater than the value of the maximum positive pressure coefficient. When the angle between the wind direction and the surface normal direction is around 75°~105°, the most unfavorable negative wind pressure coefficient usually occurs; furthermore, the value varies with the local geometry characteristics of the building where the measuring point is located.
(2) The most unfavorable positive wind pressure coefficient on the three high-rise building models with different sectional shapes appears in the T2 model, but there is no significant increase (a 4.7% increment compared with the BG model). On the other hand, the most unfavorable negative wind pressure coefficient appears at the concave corner of the T1 model, which has a more obvious increment than the magnitudes of the other two models (a 25% increment compared with the BG model). The explanation is that when the direction of incoming flow changes, the airflow may accelerate at the concave corner around the T1 building model. When the air flows around the concave area, flow phenomena such as air separation may occur, resulting in significant adverse wind pressure.
(3) In general, although the T1 building model has extreme wind pressure, its planar feature makes the flow field around the building more streamlined, and the wind pressure distribution of each facade and roof of the building reflects more favorable characteristics. The extreme negative wind pressure only appears at a certain gauging point of the concavity, indicating that the subsequent research on the specific types of concave shapes around the building can be further explored to achieve more favorable wind pressure characteristics on high-rise buildings.
To summarize, this work quantitatively discusses the influence of planar configuration on wind load distribution characteristics of high-rise buildings with whole wind azimuths. In addition, to better correlate the wind pressure distribution characteristics of the building with the wind flow field around, three-dimensional aerodynamic simulations should be carried out in the subsequent research.