1. Introduction
Burnup calculation is an indispensable part of the numerical simulation of reactor physics. By solving the point depletion equation of each burnup region, the time-dependent atom number density is provided for neutron transport calculation. Accurately predicting the material composition changes in fuel assemblies during irradiation is crucial for nuclear fuel management and reactor design. Gadolinium oxide (Gd
2O
3), an important neutron absorber, plays a role in adjusting reactivity in nuclear fuel and is widely used in light water reactors (LWRs), including pressurized water reactors (PWRs) and boiling water reactors (BWRs) [
1]. In LWRs, Gd
2O
3 is blended with uranium dioxide (UO
2) fuel to extend the operational life of the reactor and flatten the power distribution. Owing to their high neutron absorption cross-section, gadolinium isotopes Gd-155 and Gd-157 are employed to offset the initial surplus of positive reactivity in the reactor core. As these isotopes undergo burnup concurrently with the fuel, the positive reactivity is progressively liberated. The burnup dynamics of Gd
2O
3 exhibit a notable complexity, thus they require refined computational models to accurately capture and describe their behavior. In the depletion calculations of fuel assemblies containing Gd
2O
3, a gadolinia-bearing fuel pellet is annularly divided into regions ranging in number from several to more than a dozen [
2]. In asymmetric problems, further subdivision in the circumferential quadrants may be required. However, this is still not sufficient; due to the strong absorption effects of Gd-155 and Gd-157, their reaction rates change too rapidly, and even with the traditional predictor—corrector (PC) method [
3,
4,
5,
6] extremely fine time steps are needed.
To enhance the efficiency of assembly burnup calculations, a series of burnup calculation methods for Gd
2O
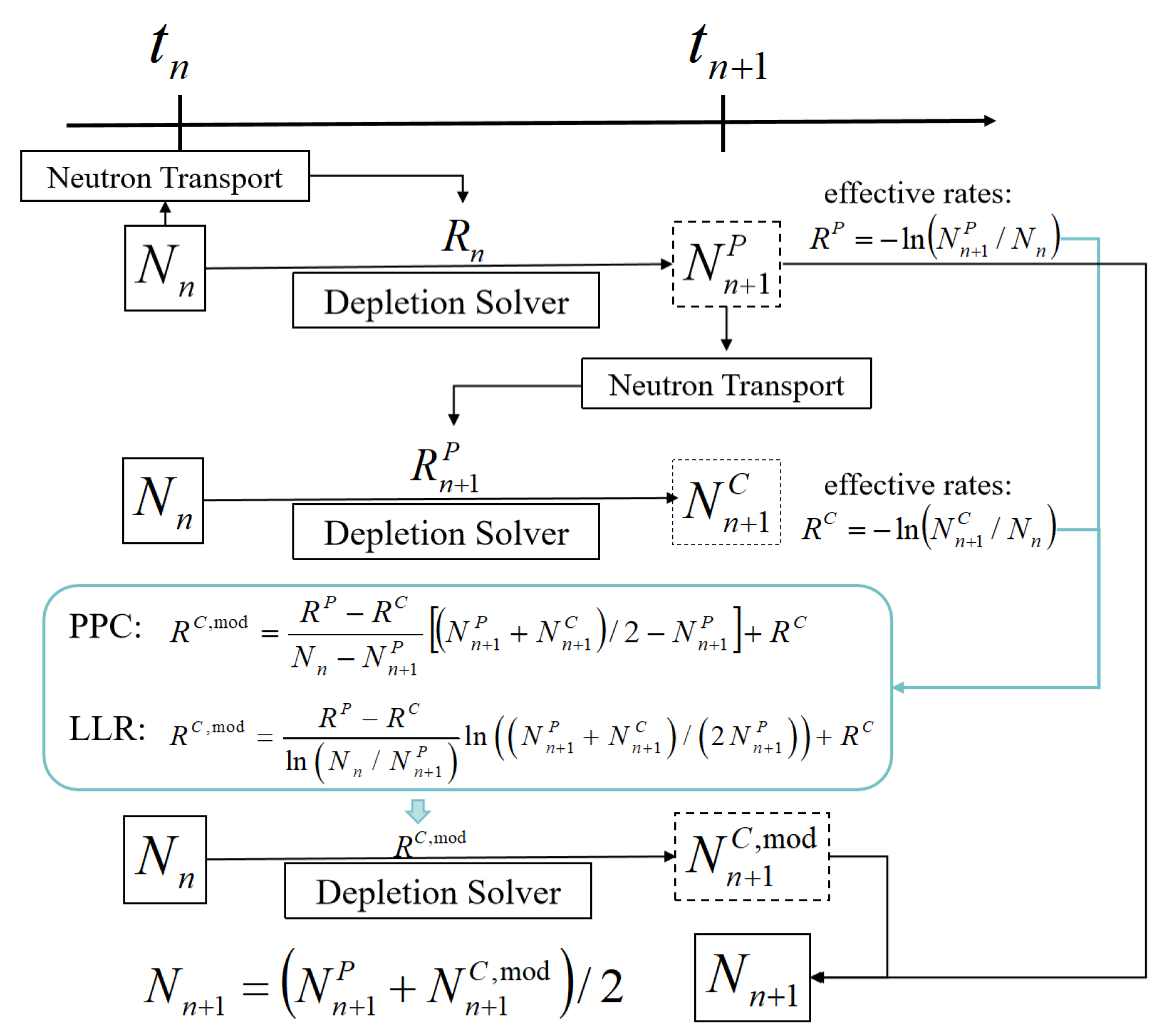
3 have been developed in recent years. In traditional predictor–corrector methods, it is assumed that the reaction rates in the burnup equation remain constant over a time step, while many improved methods have challenged this assumption, taking into account the variation of reaction rates within a time step. Yamamoto proposed the projected predictor–corrector (PPC) [
7] method for PWR assembly burnup calculations in 2009. The PPC method takes advantage of the correlation between the number density of fissionable materials and reaction rates, improving the accuracy of microscopic reaction rates in the corrector step by estimating the “projected” reaction rates. The PPC method has been implemented in the AEGIS [
8] code and has demonstrated better performance in reducing temporal discretization errors in calculations of PWR assembly problems. Its accuracy is comparable to that of the conventional PC method, which uses a time step half the length of the PPC method’s. Subsequently, the log-linear rate (LLR) [
9] method was introduced in the joint development project of MC21 (2010). This method assumes that the microscopic reaction rates of strongly absorbing nuclides are linearly related to the natural logarithm of the nuclide’s atom number density. The LLR method has a significant advantage over the PPC method in predicting the concentrations of Gd-155 and Gd-157. The CASMO-5 code employs the quadratic gadolinium depletion model [
8], which posits that the microscopic reaction rates of Gadolinium isotopes are quadratic functions of the Gd-155 atom number density. Numerical results indicate that the quadratic model can achieve satisfactory accuracy using four times the traditional PC step length. Isotalo [
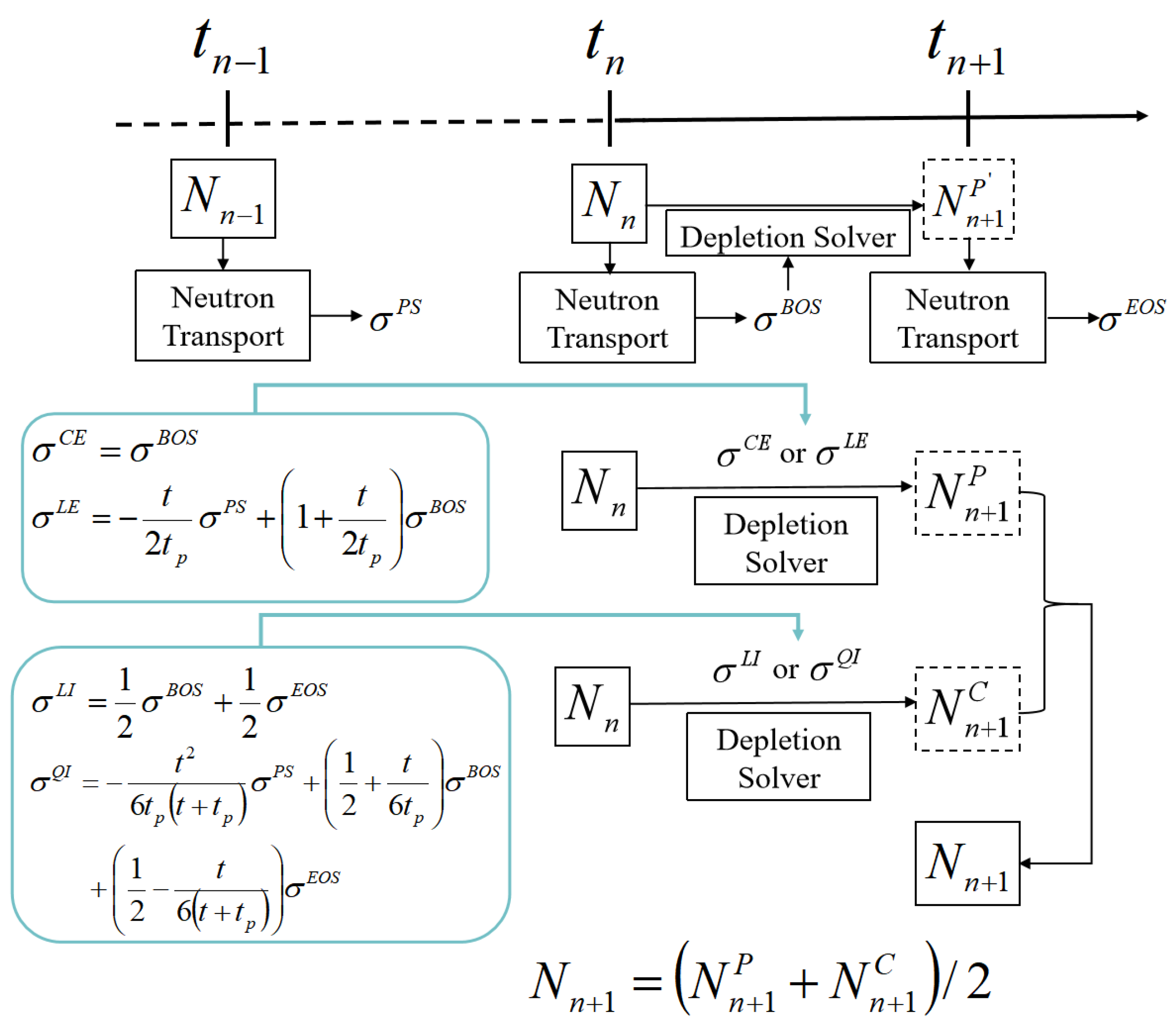
10] systematically proposed higher-order coupling methods for burnup—transport in 2011. Based on the traditional predictor–corrector (PC) method, linear extrapolation instead of constant extrapolation as the prediction step and quadratic interpolation instead of linear interpolation as the correction step are proposed. These high-order methods were implemented in Serpent [
11]. The results showed that under thermal spectrum conditions, the performance of using linear extrapolation in the prediction step was superior to that of constant extrapolation, while the effect of quadratic interpolation in the correction step was not as good as linear interpolation. Subsequently, Isotalo [
12] conducted a more in-depth comparison of the performance of various higher-order methods in 2015. The test cases included PWR, BWR, SFR (sodium-cooled fast reactor), and a PWR constant flux density case, revealing that the LE/QI (linear extrapolation with quadratic interpolation) method performed the best in most situations.
Previous research on various burnup–transmutation coupling strategies for Gd
2O
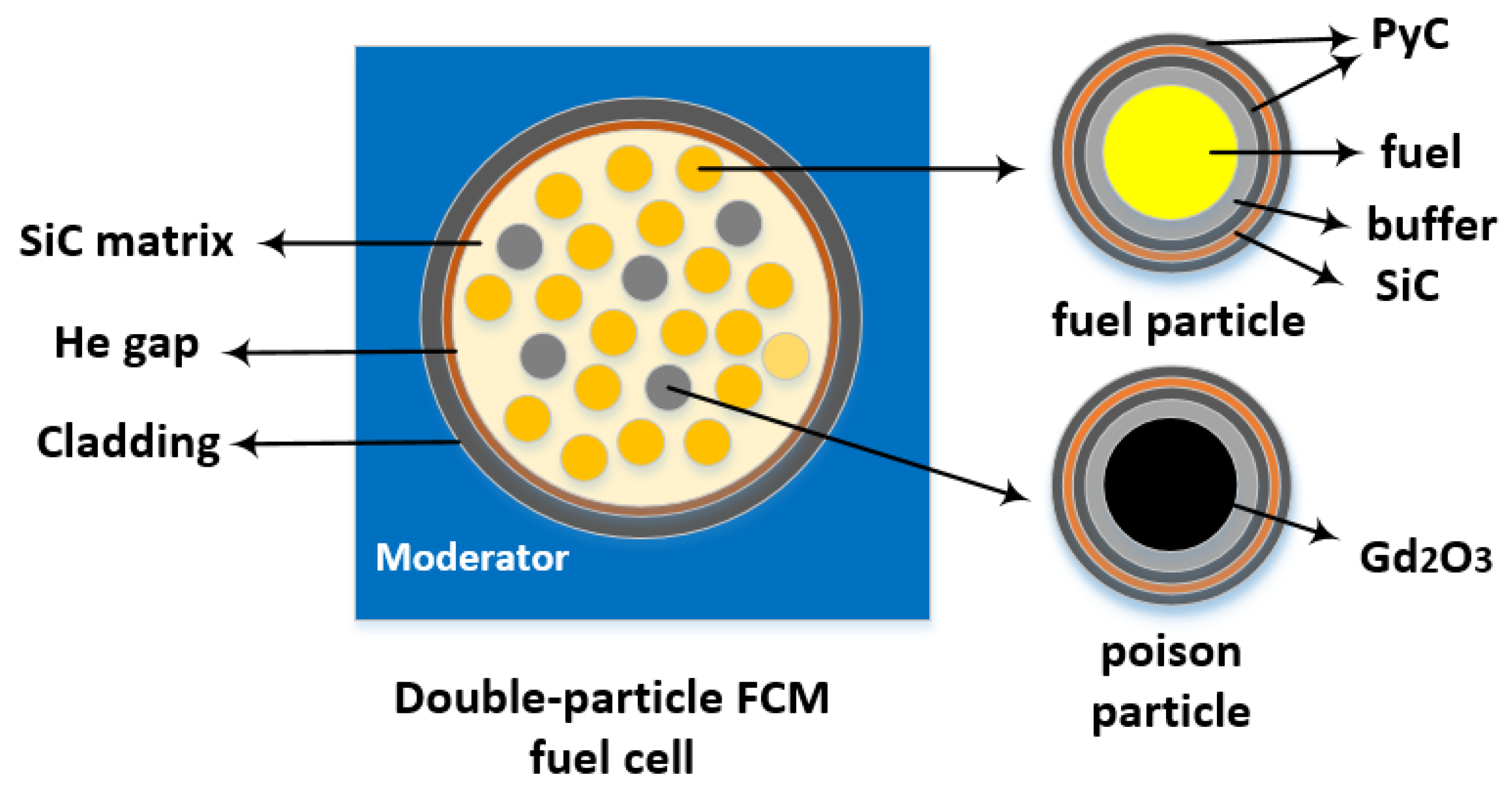
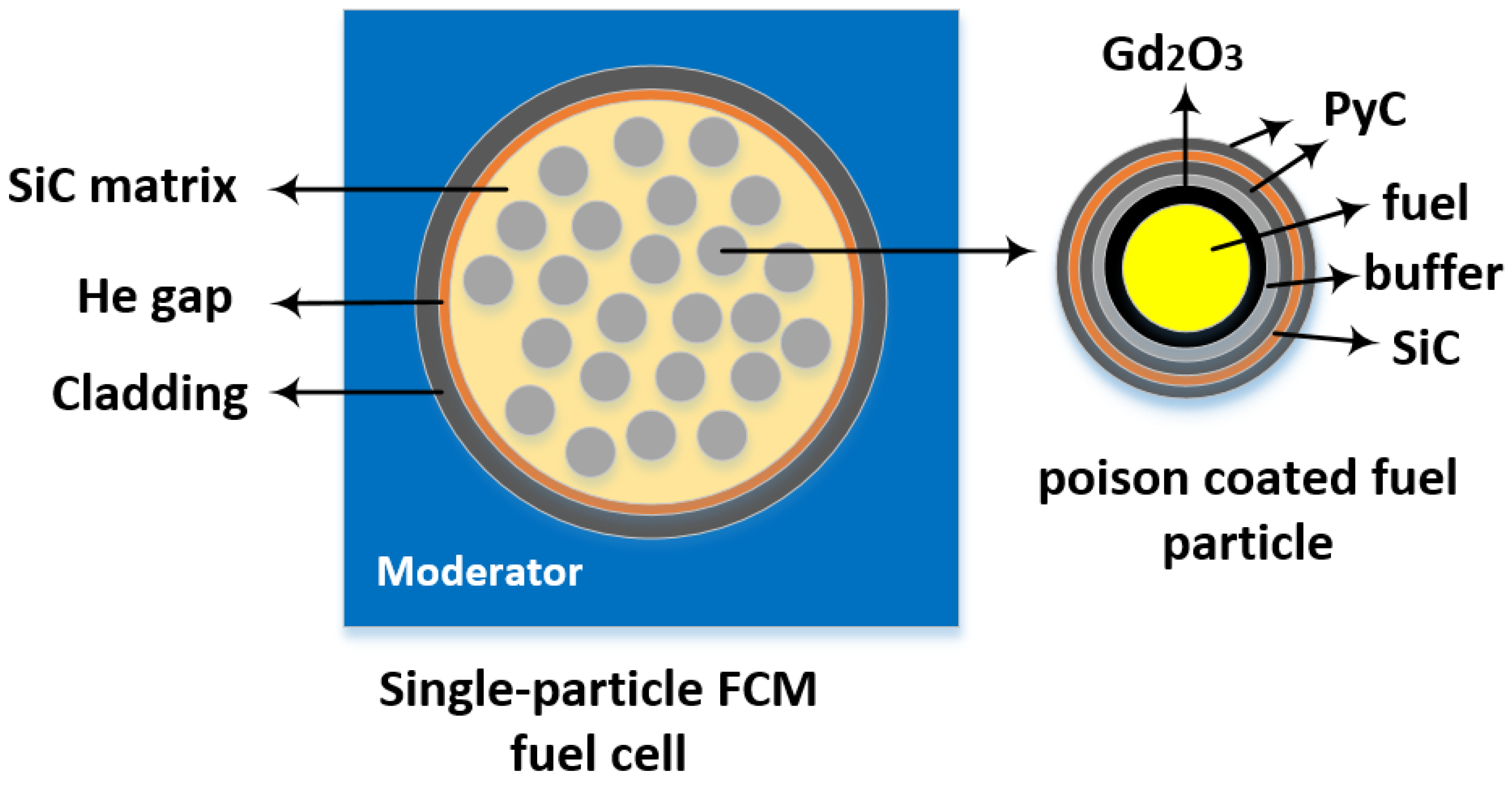
3 was primarily focused on conventional light water reactor (LWR) fuels. As a type of accident tolerant fuel, the fully ceramic micro-encapsulated (FCM) [
13] fuel offers better fuel utilization, thermal conductivity, and fission product containment compared to traditional fuels, making it a promising new type of nuclear fuel in recent years. FCM fuel exhibits a double heterogeneity (DH) not found in conventional LWR fuels, which is characterized by the fuel pellets and the moderator, the tristructural isotropic (TRISO) particles, and the surrounding matrix. It should be noted that the double heterogeneity mentioned in this article refers specifically to the FCM fuel in LWRs, not the fuel pebbles of high-temperature reactors (HTRs) [
14,
15]. Among the many designs for LWRs using FCM fuel, the dispersed particle poison design often employs Gd
2O
3 [
16,
17,
18]. Currently, there has been no research on the burnup calculation methods for Gd
2O
3 under the double heterogeneity conditions of FCM fuel. In the design of the FCM fuel element, when using pure gadolinium Oxide (Gd
2O
3) in the form of particles or coatings as a burnable poison, the requirements for burnup step sizes are more refined due to the higher initial concentrations of Gd-155 and Gd-157. Therefore, building upon the previously developed computational code ALPHA [
19] for FCM fuel assembly, this paper has developed a variety of accelerated calculation methods for the strong absorber Gd
2O
3, including PPC, LLR, and four high-order burnup methods: CE/LI, CE/QI, LE/LI, and LE/QI. Additionally, this research analyzes the performance of various algorithms when Gd
2O
3 is present in the form of a particle core and as a coating.
The organization of this paper is as follows.
Section 2 briefly describes the double heterogeneity (DH) burnup calculation capability of ALPHA and various transport–burnup coupling strategies developed in the program for poison.
Section 3 presents the analysis results of various coupling strategies. Conclusions are drawn in
Section 4.
4. Conclusions
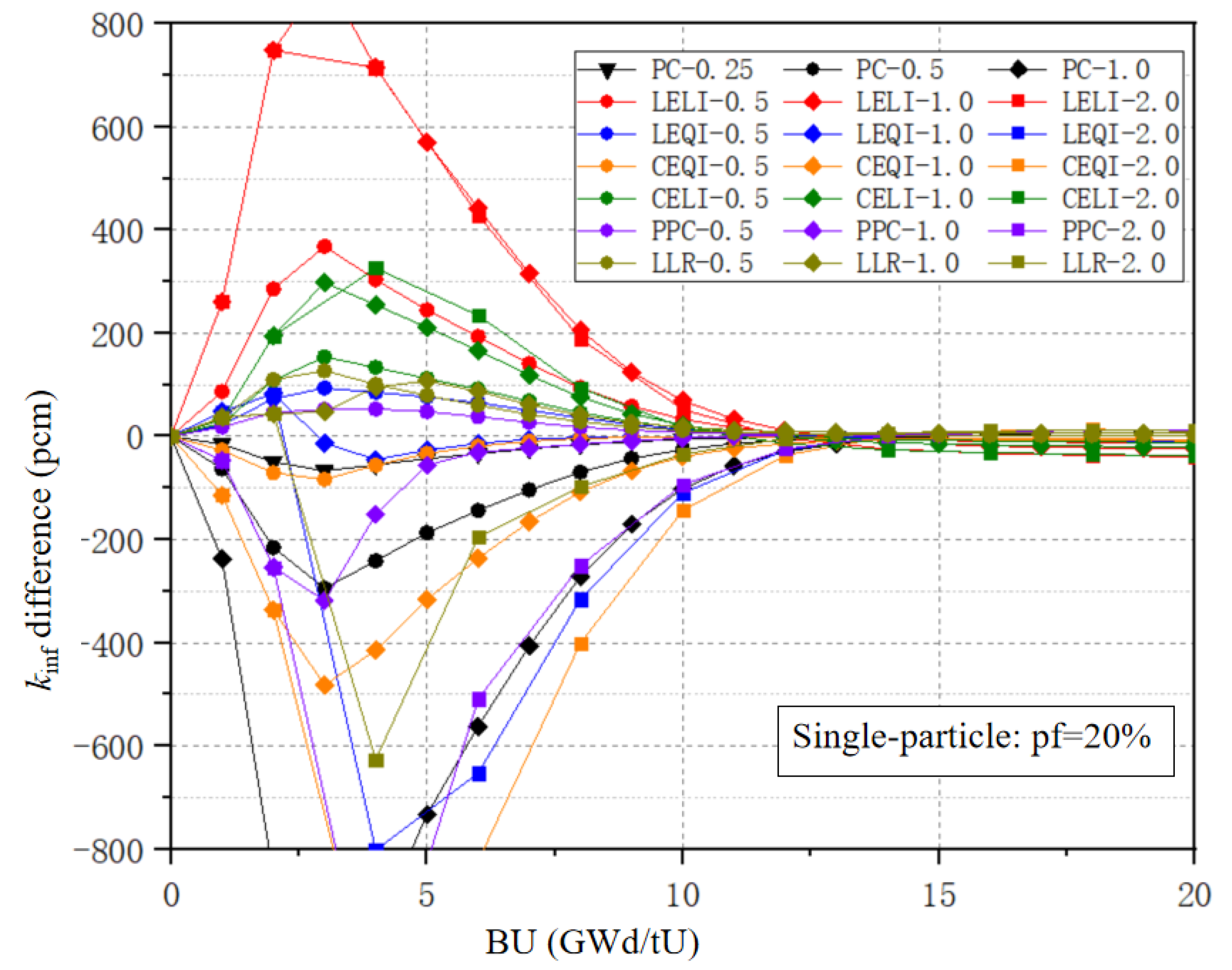
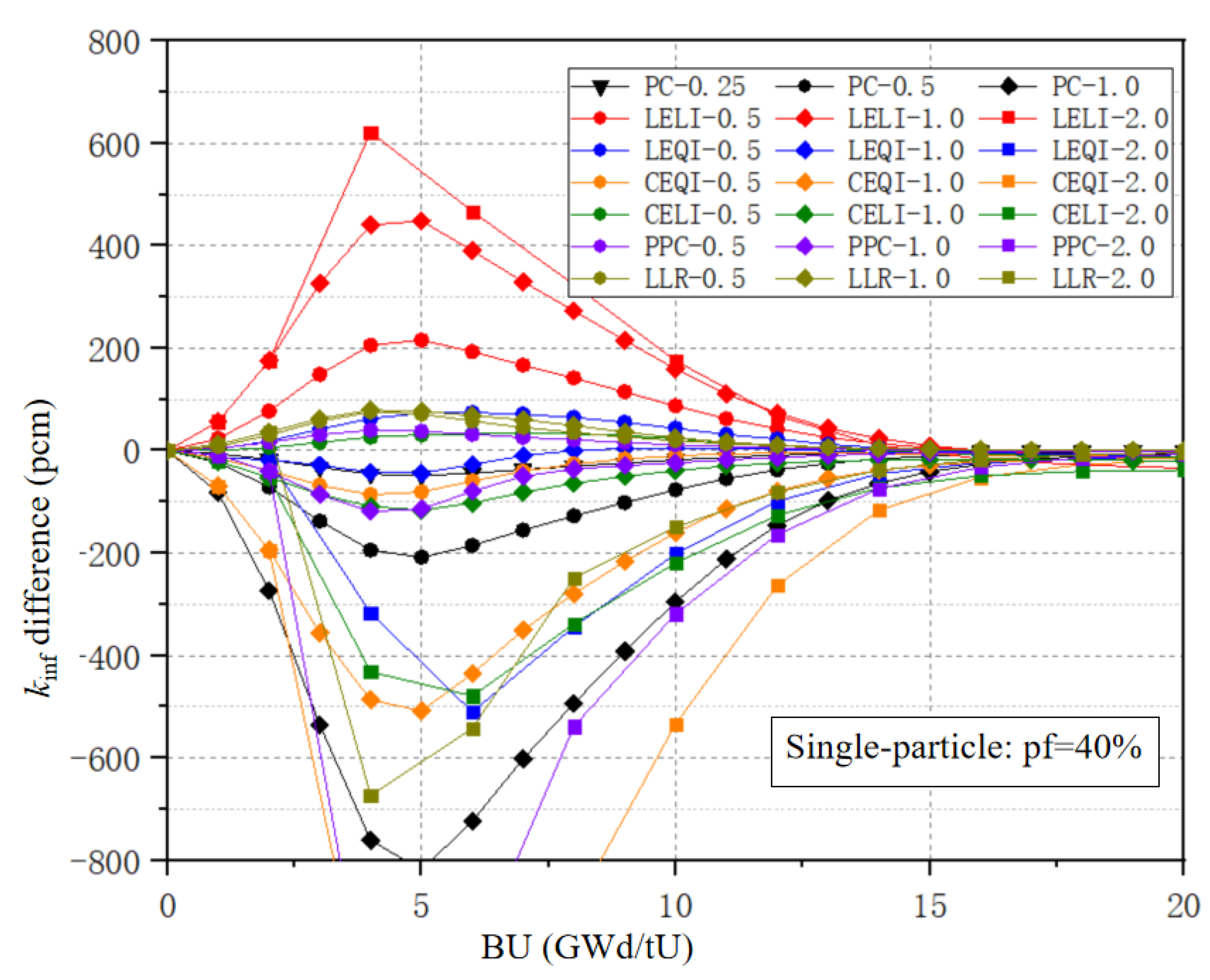
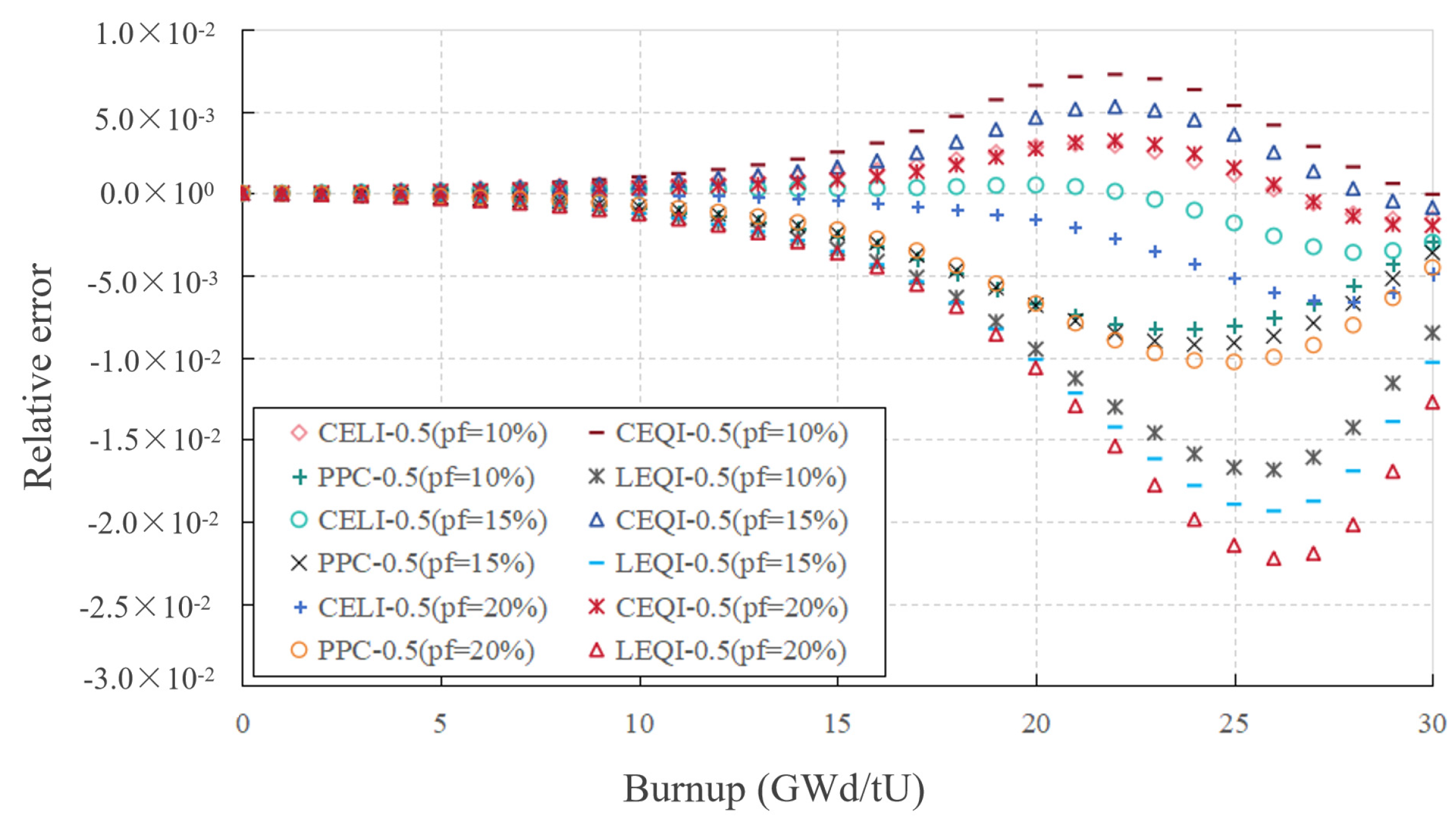
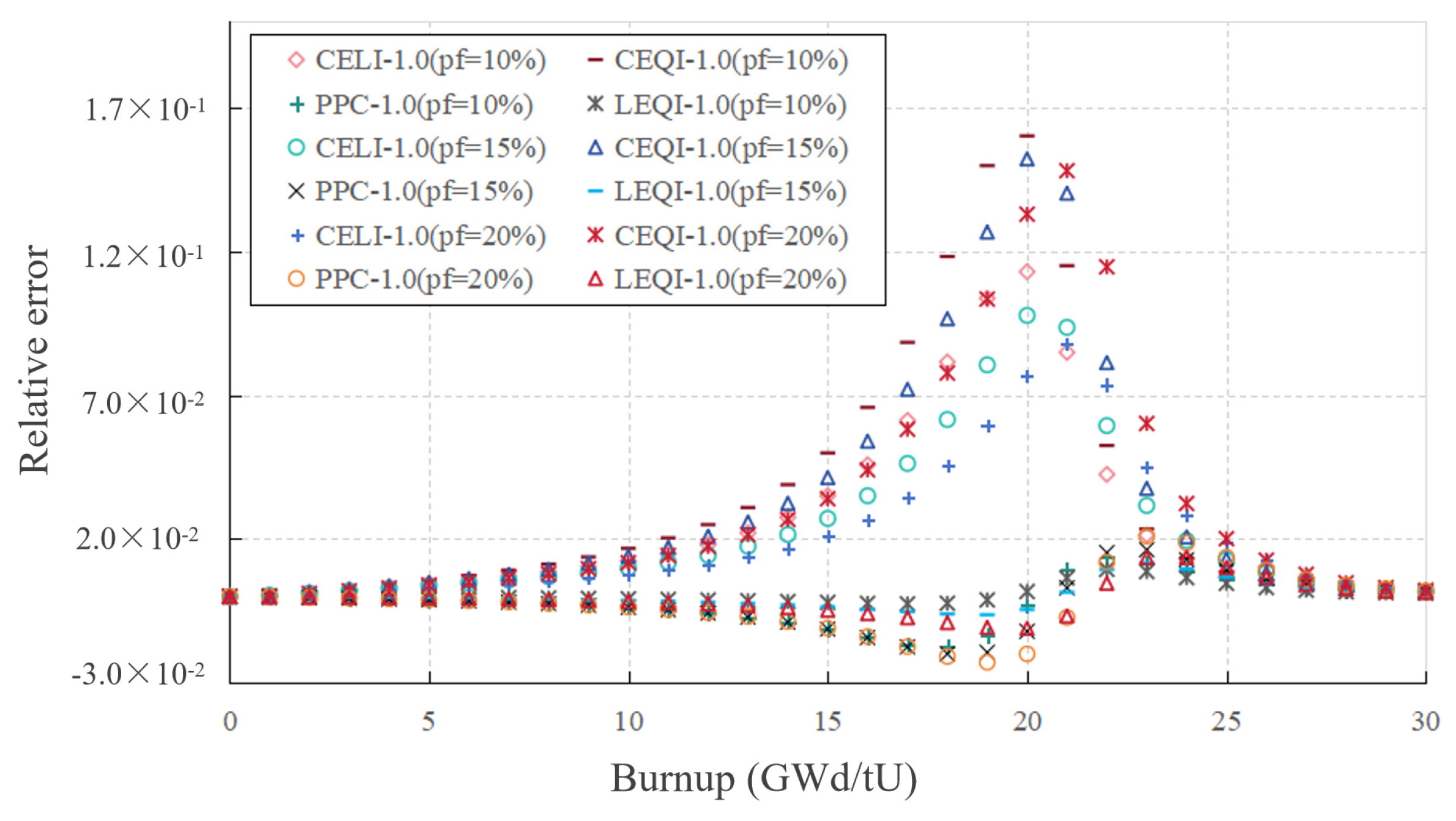
The transport–burnup coupling strategies for Gd2O3 have been developed in the ALPHA code, including six coupling methods: PPC, LLR, CE/LI, CE/QI, LE/LI, and LE/QI. These six methods have made different corrections to the reaction rates of Gd-155 and Gd-157. This study conducted a comprehensive analysis of these methods using two types of FCM fuel cell types: a single-particle cell and a double-particle cell. Overall, the LE/QI method has the highest accuracy, showing good performance in terms of the overall kinf of burnup and the atomic number density of Gd-155 and Gd-157. This method can use a step size four times that of the traditional estimation correction method in most cases, while maintaining satisfactory accuracy. The CE/QI, CE/LI, and PPC methods have the next levels of accuracy and, in most cases, a step size twice that of the PC method can achieve good accuracy. The LLR method has poor stability in the double-particle type of lattice cell calculations, showing an abnormal phenomenon where the accuracy of large steps is better than that of small steps. This study provides a reference for the selection of coupling strategies for Gd2O3-bearing fuel under double heterogeneity conditions.
Constrained by computational resources, the current analysis of various coupling strategies is limited to FCM pin cell problems, without being tested on lattice or core problems. Therefore, it is also impossible to quantify their impact on more macroscopic physical parameters, such as lattice power distribution and core reactivity coefficients, etc. Future work will focus on studying the evolution of reaction rates for Gd-155 and Gd-157 under double heterogeneous conditions and developing coupling strategies based on feature extraction techniques to significantly reduce the time consumption of burnup calculations.