Improved Model-Free Predictive Control of a Three-Phase Inverter
Abstract
1. Introduction
- The proposed approach uses a continuous control set-based MFPC to control a three-phase inverter with an LC filter in the presence of the system constraints. The CCS approach eliminates the problem of variable switching frequency and provides sinusoidal voltages of low THD.
- The model-free approach uses an auto-regressive structure with exogenous input (ARX) to estimate the system dynamics. ARX is a linear parametric model that reduces the complexity of the proposed approach. Moreover, a well-established method of recursive least squares (RLS) is available to be used to estimate ARX parameters.
- The system constraints of the maximum permissible filter current and duty cycle constraints are part of the control.
- A computationally efficient optimization algorithm based on an active set method (ASM). The computations of ASM depend on the number of constraints. The system constraints are reduced by combining the constraints of the maximum permissible filter current and duty cycle due to their dependence on each other.
- A detailed stability analysis of the proposed MFPC has been presented using the Lyapunov theory.
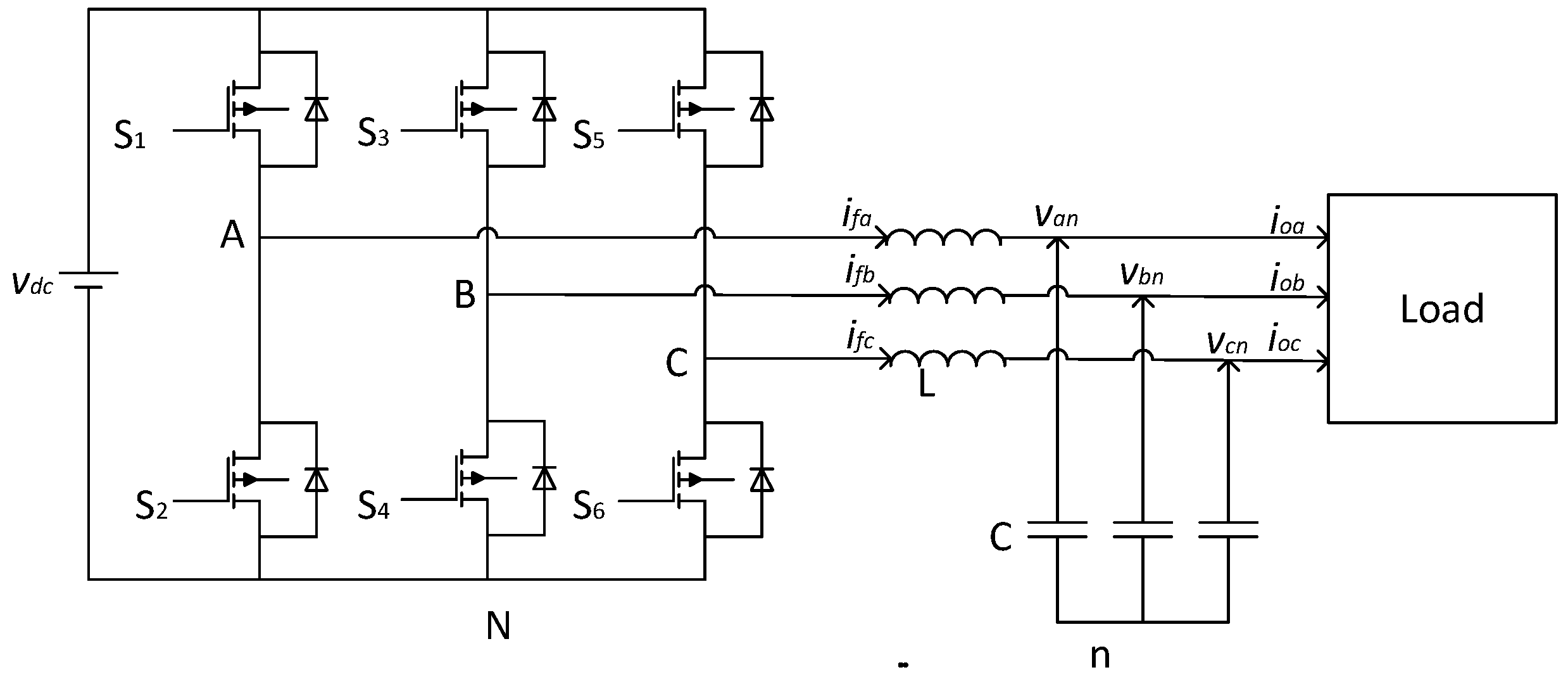
2. System Modeling
2.1. Continuous-Time State-Space Model
2.2. Discrete-Time State-Space Model
3. Autoregressive Representation of the System
3.1. Parameter Estimation Algorithm
3.2. Future Values
4. Problem Formulation
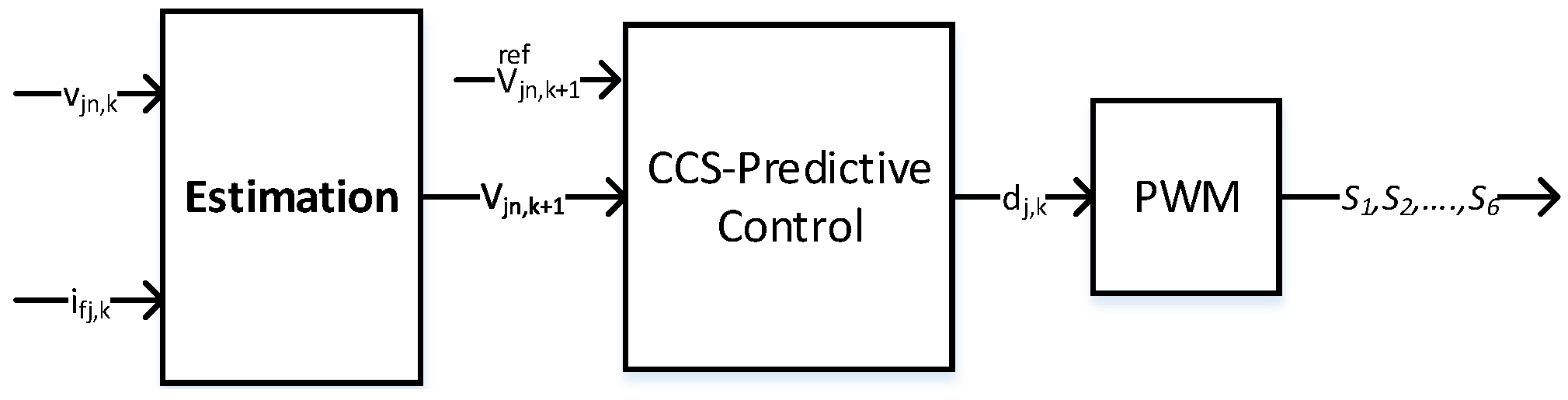
5. Controller Formulation
| Algorithm 1: Proposed model-free predictive control |
 |
6. Stability Analysis
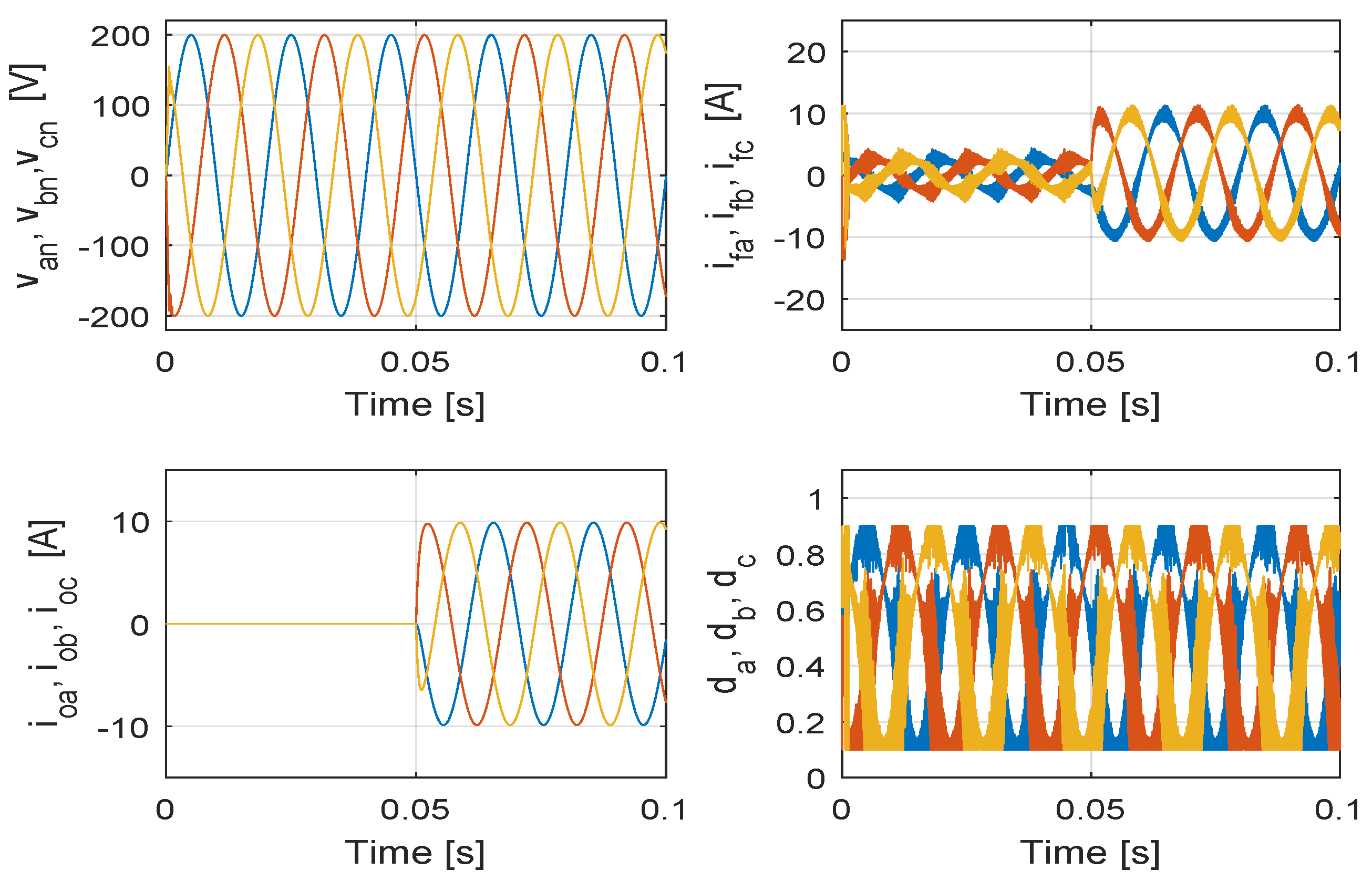
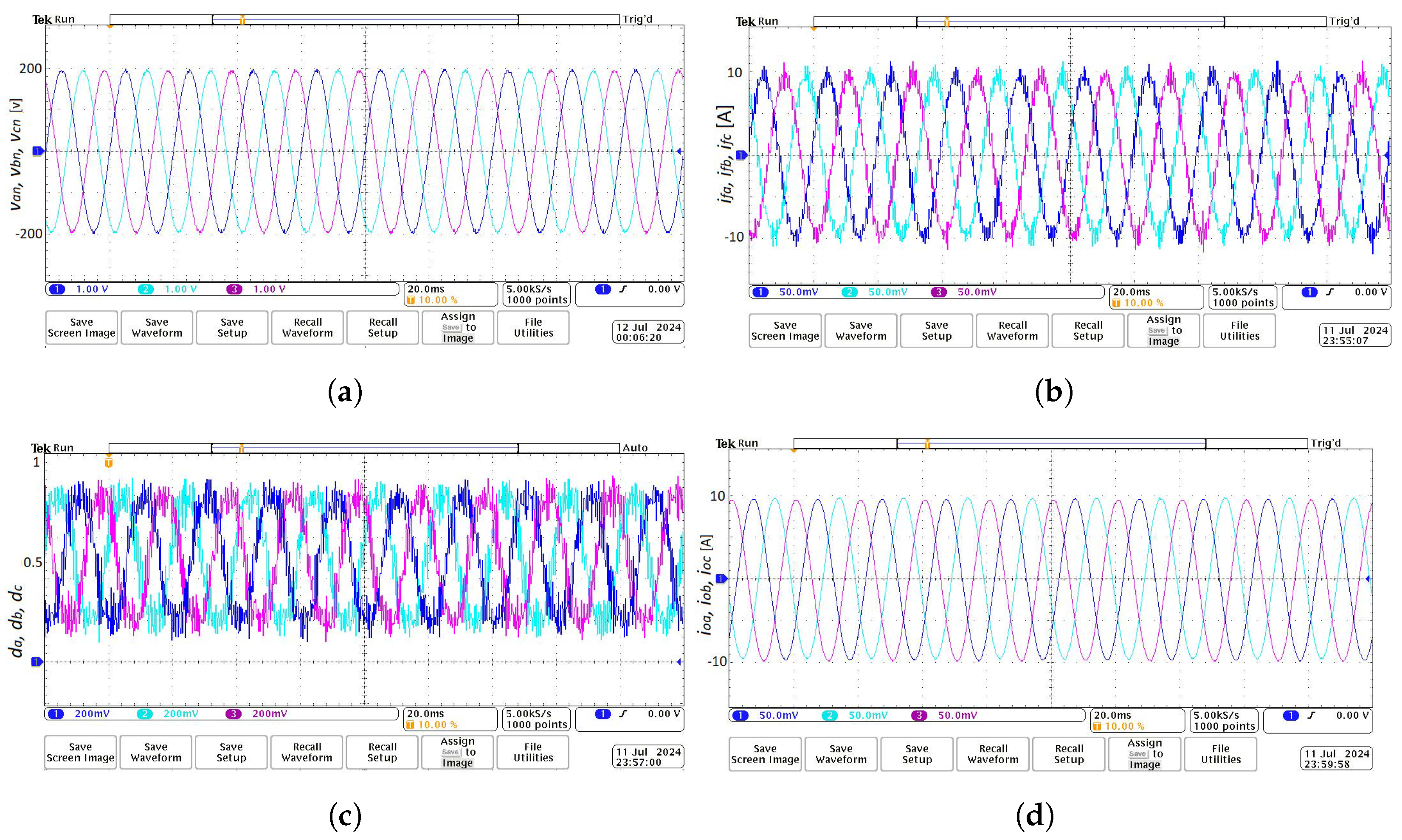
7. Results
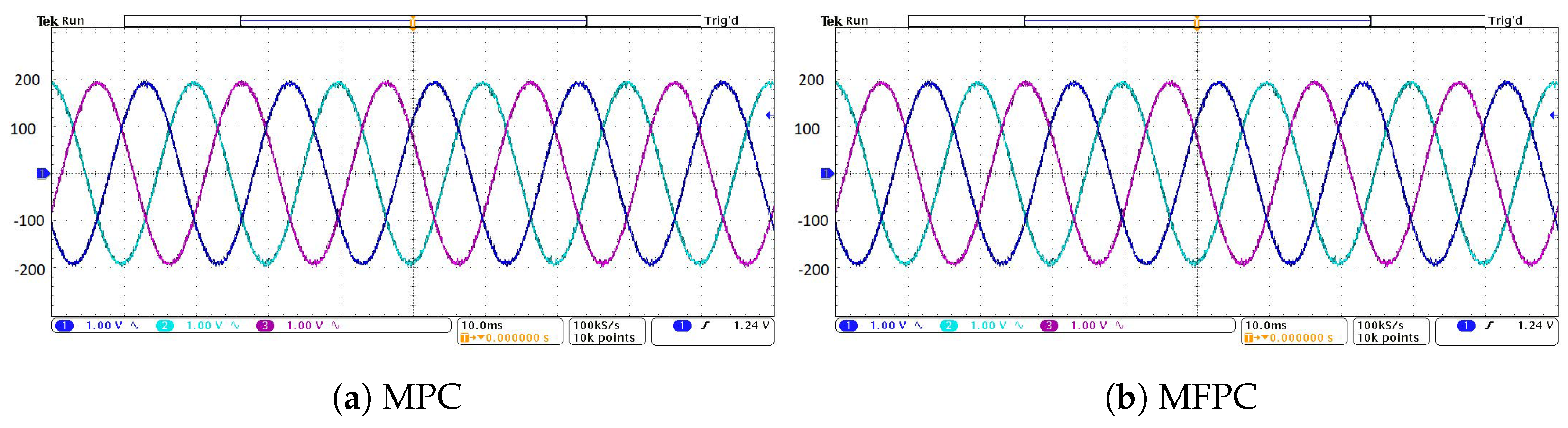
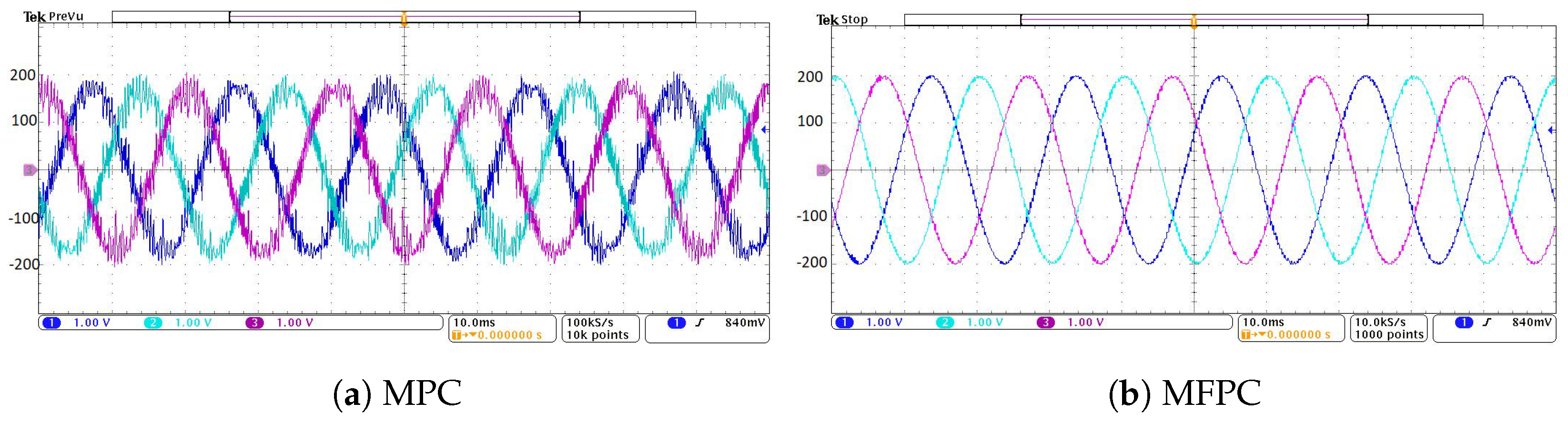
7.1. Steady State Performance
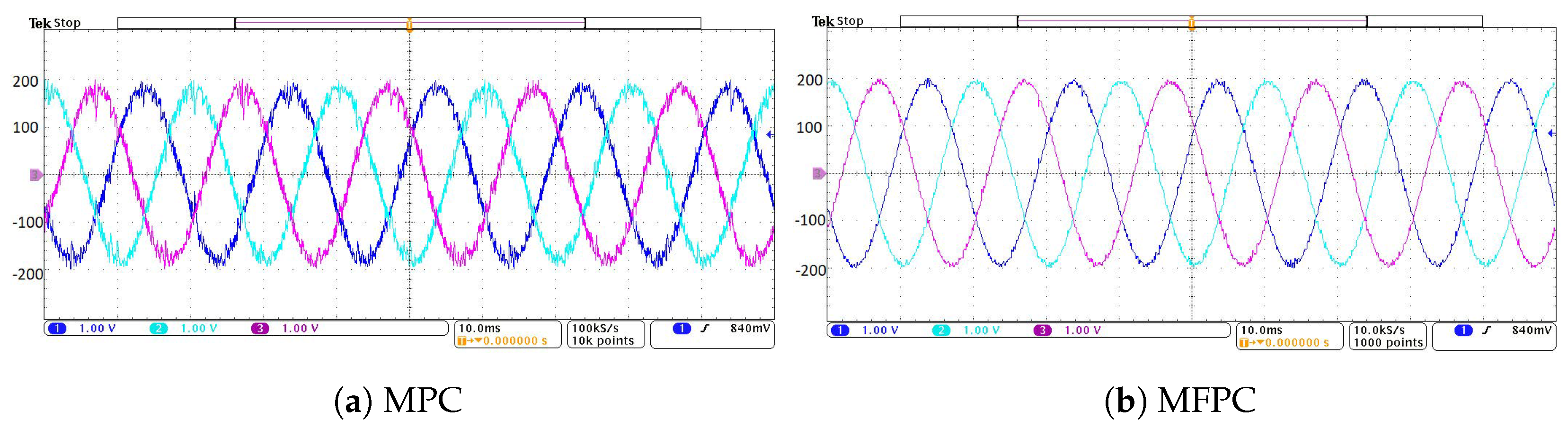
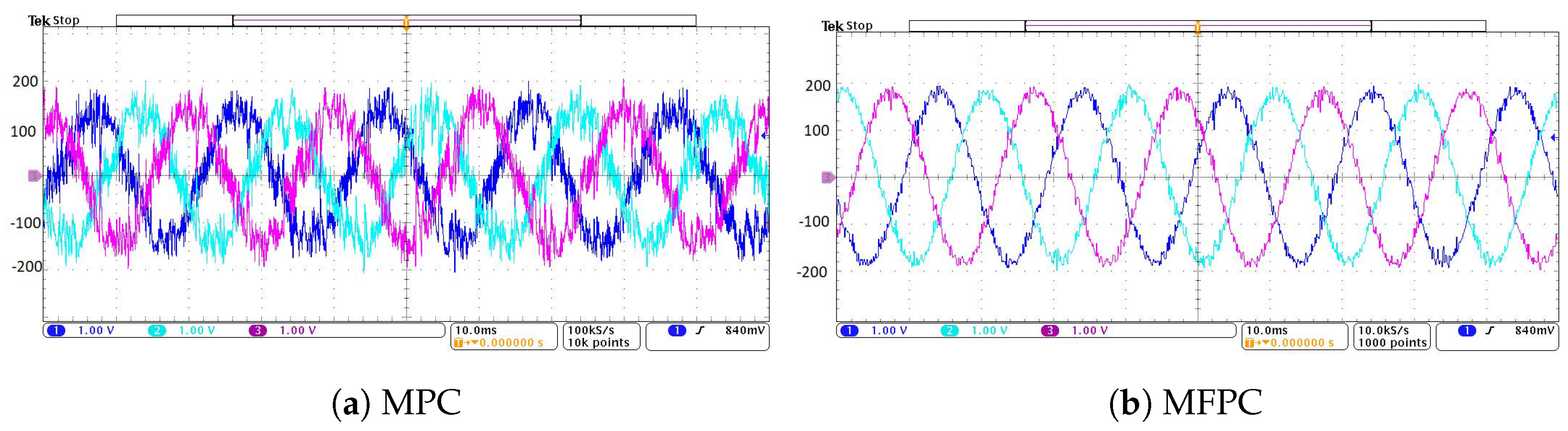
7.2. Model Mismatch Performance
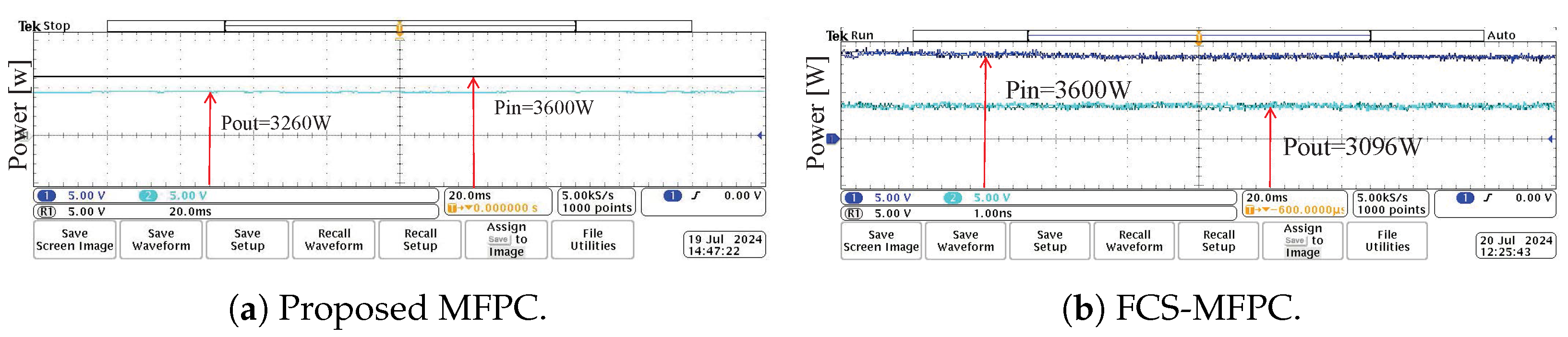
8. Converter Efficiency
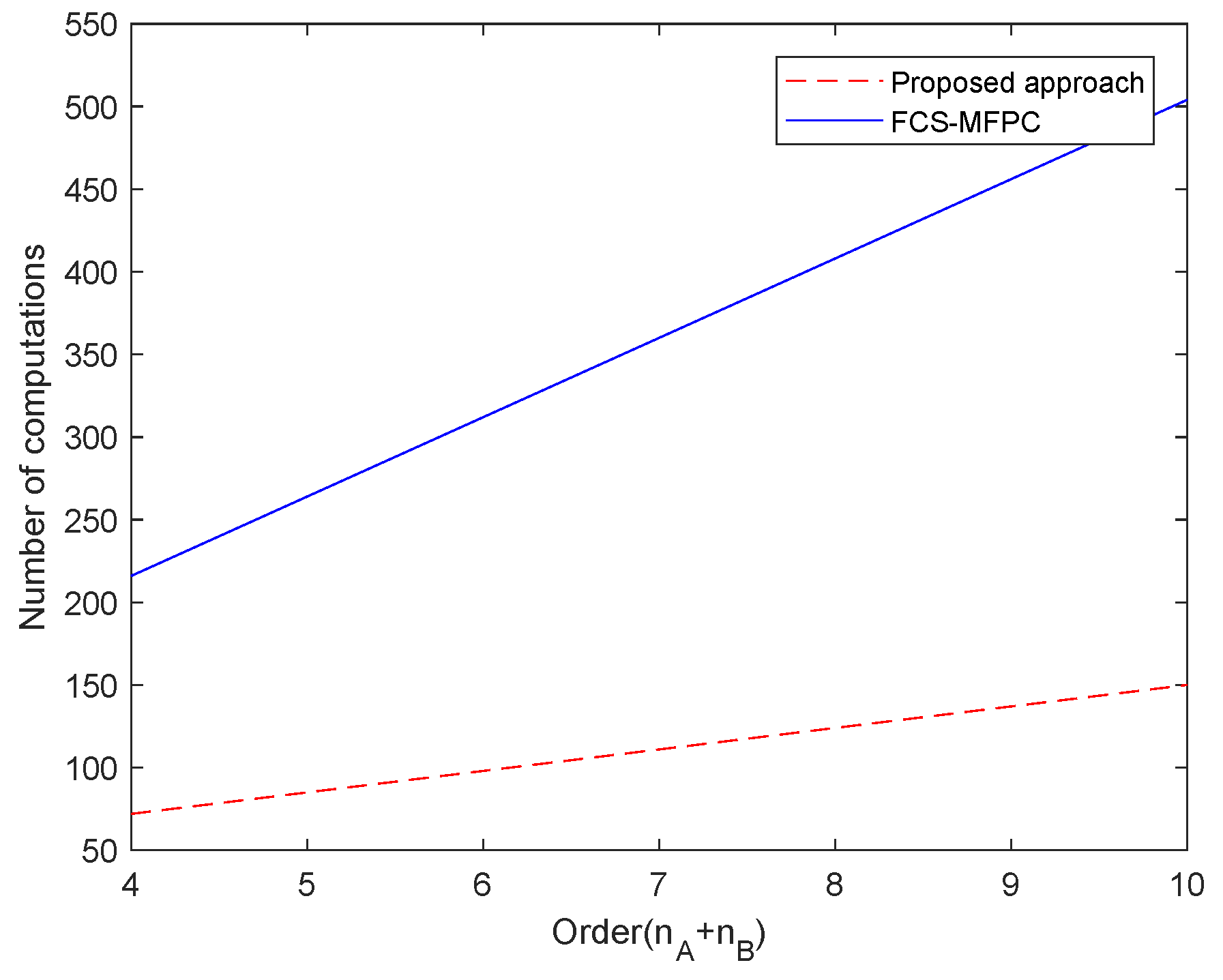
9. Computational Efficiency
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Xiao, Y.; Fan, M.; Wang, K.; Zhang, X.; Hu, J.; Fang, G.; Zeng, W.; Vazquez, S.; Rodriguez, J. A novel continuous control set model predictive control for LC-filtered three-phase four-wire three-level voltage-source inverter. IEEE Trans. Power Electron. 2023, 38, 4572–4584. [Google Scholar] [CrossRef]
- Pirsto, V.; Kukkola, J.; Hinkkanen, M. Multifunctional cascade control of voltage-source converters equipped with an LC filter. IEEE Trans. Ind. Electron. 2021, 69, 2610–2620. [Google Scholar] [CrossRef]
- Xue, C.; Zhou, D.; Li, Y. Finite-control-set model predictive control for three-level NPC inverter-fed PMSM drives with LC filter. IEEE Trans. Ind. Electron. 2020, 68, 11980–11991. [Google Scholar] [CrossRef]
- Safamehr, H.; Najafabadi, T.A.; Salmasi, F.R. Adaptive control of grid-connected inverters with nonlinear LC filters. IEEE Trans. Power Electron. 2022, 38, 1562–1570. [Google Scholar] [CrossRef]
- Nauman, M.; Hasan, A. Efficient implicit model-predictive control of a three-phase inverter with an output LC filter. IEEE Trans. Power Electron. 2016, 31, 6075–6078. [Google Scholar] [CrossRef]
- Karamanakos, P.; Liegmann, E.; Geyer, T.; Kennel, R. Model predictive control of power electronic systems: Methods, results, and challenges. IEEE Open J. Ind. Appl. 2020, 1, 95–114. [Google Scholar] [CrossRef]
- Toso, F.; Favato, A.; Torchio, R.; Alotto, P.; Bolognani, S. Continuous control set model predictive current control of a microgrid-connected pwm inverter. IEEE Trans. Power Syst. 2020, 36, 415–425. [Google Scholar] [CrossRef]
- Bemporad, A. Explicit model predictive control. In Encyclopedia of Systems and Control; Springer: Cham, Switzerland, 2021; pp. 744–751. [Google Scholar]
- Nauman, M.; Shireen, W.; Hussain, A. Model-Free Predictive Control and Its Applications. Energies 2022, 15, 5131. [Google Scholar] [CrossRef]
- Saeed, J.; Wang, L.; Fernando, N. Model predictive control of phase shift full-bridge DC–DC converter using Laguerre functions. IEEE Trans. Control Syst. Technol. 2021, 30, 819–826. [Google Scholar] [CrossRef]
- Berberich, J.; Köhler, J.; Müller, M.A.; Allgöwer, F. Data-driven model predictive control with stability and robustness guarantees. IEEE Trans. Autom. Control 2020, 66, 1702–1717. [Google Scholar] [CrossRef]
- Ipoum-Ngome, P.G.; Mon-Nzongo, D.L.; Flesch, R.C.C.; Song-Manguelle, J.; Wang, M.; Jin, T. Model-free predictive current control for multilevel voltage source inverters. IEEE Trans. Ind. Electron. 2020, 68, 9984–9997. [Google Scholar] [CrossRef]
- Khalilzadeh, M.; Vaez-Zadeh, S.; Rodriguez, J.; Heydari, R. Model-free predictive control of motor drives and power converters: A review. IEEE Access 2021, 9, 105733–105747. [Google Scholar] [CrossRef]
- Rodriguez, J.; Heydari, R.; Rafiee, Z.; Young, H.A.; Flores-Bahamonde, F.; Shahparasti, M. Model-free predictive current control of a voltage source inverter. IEEE Access 2020, 8, 211104–211114. [Google Scholar] [CrossRef]
- Heydari, R.; Young, H.; Flores-Bahamonde, F.; Vaez-Zadeh, S.; Gonzalez-Castano, C.; Sabzevari, S.; Rodriguez, J. Model-free predictive control of grid-forming inverters with LCL filters. IEEE Trans. Power Electron. 2022, 37, 9200–9211. [Google Scholar]
- Wei, Y.; Young, H.; Wang, F.; Rodríguez, J. Generalized data-driven model-free predictive control for electrical drive systems. IEEE Trans. Ind. Electron. 2022, 70, 7642–7652. [Google Scholar] [CrossRef]
- Cheng, C.; Xie, S.; Qian, Q.; Xu, J.; Zeng, B.; Lv, J. On Stability of Time-Invariant Current Controlled Weak-Grid-Tied Inverters Considering Sinusoidal Pulsewidth Modulation Saturation and Parameter Uncertainties. IEEE Trans. Ind. Electron. 2022, 69, 11359–11369. [Google Scholar] [CrossRef]
- Van Waarde, H.J.; Eising, J.; Trentelman, H.L.; Camlibel, M.K. Data informativity: A new perspective on data-driven analysis and control. IEEE Trans. Autom. Control 2020, 65, 4753–4768. [Google Scholar] [CrossRef]
- Li, Y.R.; Peng, C.C.; Juang, J.N. An integral method for parameter identification of a nonlinear robot subject to quantization error. Nonlinear Dyn. 2023, 111, 22419–22441. [Google Scholar] [CrossRef]
- Schoukens, J.; Dobrowiecki, T.; Pintelon, R. Parametric and nonparametric identification of linear systems in the presence of nonlinear distortions-a frequency domain approach. IEEE Trans. Autom. Control 1998, 43, 176–190. [Google Scholar] [CrossRef]
- Kang, T.; Peng, H.; Xu, W.; Sun, Y.; Peng, X. Deep Learning-Based State-Dependent ARX Modeling and Predictive Control of Nonlinear Systems. IEEE Access 2023, 11, 32579–32594. [Google Scholar] [CrossRef]
- Brosch, A.; Hanke, S.; Wallscheid, O.; Böcker, J. Data-driven recursive least squares estimation for model predictive current control of permanent magnet synchronous motors. IEEE Trans. Power Electron. 2020, 36, 2179–2190. [Google Scholar] [CrossRef]
- Jiang, Shunhua and Natura, Bento and Weinstein, Omri, A faster interior-point method for sum-of-squares optimization. Algorithmica 2023, 85, 2843–2884. [CrossRef]
- Cimini, Gionata and Bemporad, Alberto Exact complexity certification of active-set methods for quadratic programming. IEEE Trans. Autom. Control. 2017, 62, 6094–6109. [CrossRef]
- Mariéthoz, S.; Morari, M. Explicit model-predictive control of a PWM inverter with an LCL filter. IEEE Trans. Ind. Electron. 2008, 56, 389–399. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Inductance of LC filter | 1 [mH] |
| Capacitance of LC filter | 40 [μF] |
| Sampling time Ts | 20 [μsec] |
| Inverter input DC voltage | 520 [V] |
| Reference voltage | 200 [V] |
| Inductive load inductance | 10 [mH] |
| Inductive load resistance | 20 |
| Maximum filter current | 12 [A] |
| Minimum filter current | −12 [A] |
| lambda () | 0.9 |
| Algorithm | +/− | |
|---|---|---|
| Proposed MFPC | ||
| FCS-MFPC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nauman, M.; Shireen, W. Improved Model-Free Predictive Control of a Three-Phase Inverter. Energies 2024, 17, 3761. https://doi.org/10.3390/en17153761
Nauman M, Shireen W. Improved Model-Free Predictive Control of a Three-Phase Inverter. Energies. 2024; 17(15):3761. https://doi.org/10.3390/en17153761
Chicago/Turabian StyleNauman, Muhammad, and Wajiha Shireen. 2024. "Improved Model-Free Predictive Control of a Three-Phase Inverter" Energies 17, no. 15: 3761. https://doi.org/10.3390/en17153761
APA StyleNauman, M., & Shireen, W. (2024). Improved Model-Free Predictive Control of a Three-Phase Inverter. Energies, 17(15), 3761. https://doi.org/10.3390/en17153761






