Abstract
This paper reviews the use of game theory tools to study the operation and design of modern power grids. The contribution of this work is to summarize the literature to highlight the versatile solution capability of game theory by focusing on the interconnected objectives of energy trading and energy management. This review was conducted with a focus on various applications in energy systems, including general energy markets, micro grids (MGs), virtual power plants (VPP), electric vehicles (EVs), and smart homes, and explores how game theory can summarize the solutions for pricing, bidding, demand side management, and resource optimization. A key finding is the suitability of game theory for modeling decentralized energy systems where strategic incentives can lead to outcomes that benefit both individuals and society. It also discusses the limitations, challenges, and potential benefits of game theory in complex power systems. This study provides researchers and policy makers with a comprehensive overview of current research and insights into the potential of game theory to shape the future of energy systems.
1. Introduction
The modernization of electrical grids is undergoing a dizzying transformation as new technologies penetrate power systems and lead to a shift from a vertical to a horizontal control structure. However, these changes have also brought about a number of problems that have complicated the decision-making process [1]. Consequently, there are greater challenges in dealing with matters concerning the reliability, operation, control, and management of power systems [2,3]. To address these challenges, there is a growing interest in applying game theory approaches to the study of next-generation electrical grids, particularly to find solutions to decision-making and control processes [4,5].
Game theory is an academic field that examines conflicts arising from the decisions made by multiple interacting participants, extending the principles of decision theory to situations involving multiple players or decision-makers [6,7]. Therefore, game theory serves as a valuable tool for studying the strategic actions of rational decision-makers under the assumption that all participants act rationally and that their decisions are influenced by the choices made by others. It finds extensive applications across various disciplines, encompassing the analysis of strategic behavior and rationality in decision-making processes [8]. Game theory can be employed to study a wide range of interactions involving humans and computers, thereby contributing to the development of a systematic approach to logical decision-making. It encompasses the analysis of various scenarios where humans and computers interact, aiming to enhance our understanding of rational decision-making processes.
With the increasing complexity of power systems, there is an imperative to fundamentally transform the approach taken by electricity utilities and governments in the planning and operation of the power grid. This transformation involves the accurate prediction and effective management of the actions and conduct of various entities that operate within the system. This entails a shift in how we anticipate and regulate the behavior of multiple entities functioning within the power system. Most studies focus on improving power systems by solving optimization problems from the perspective of a single entity, which is insufficient and unrealistic for real applications. For example, for the free energy market, it is a great challenge to predict its development taking into account the different goals of many players. Instead, game theory is preferred to study the interaction between rational players in the energy market. In this approach, every piece of equipment in the power system is considered a player, including grid operators, consumers, energy sources, and storage systems. Recent studies indicate that the interplay among these participants holds equal significance to the individual actions they take, resulting in an increasing inclination toward the application of game theory in the context of power systems. The initial utilization of game theory in power systems dates back to the 1970s, and ever since, there has been a notable rise in employing game theory to examine power systems, particularly with the advent of energy market liberalization.
As mentioned above, modern electricity grids involve multiple stakeholders, such as producers, consumers, and ESS operators. Game theory is a suitable optimization method due to its mathematical infrastructure, which aims to maximize the profits of each of the players and stakeholders in order to analyze how these stakeholders will interact with each other and optimize their strategic decisions. Modern electrical systems are dynamic systems, and game theory is suitable for developing adaptive strategies to these changing conditions. In particular, the inherent uncertainty and volatility of renewable energy sources can be resolved using game theory. It can be used to develop dynamic pricing strategies to incentivize electricity consumption and optimize the grid.
This paper [9] systematically reviews cooperative game theory applications in power system expansion planning, highlighting its potential to facilitate mutually beneficial collaboration and equitable benefit distribution among stakeholders. Similarly, the paper in [10] only focused on cooperative game work for smart grids. This article [11] has discussed game theory applications of transactive energy systems for energy trading.
A relatively more comprehensive study in terms of energy systems and game theory is presented in. In their study, the authors classified energy systems into four main headings and presented analyses of technical articles related to game theory. Similarly, in , the technical analysis of game theory applications to power systems problems is presented with a game-based classification. Limited research has been conducted on the potential uses of game theory in the context of power systems. Paper [12] investigated the utilization of game theory and related methodologies in the areas of MG systems, demand-side management, and smart grid communications. In another study [13], game theory was examined in the context of energy trading, energy balancing, grid planning, and reliability in power systems. However, the study did not specifically discuss the distinctions between grid planning and reliability in relation to the other topics investigated. The authors categorized their studies based on the genre of the game in [10]. A study on cooperative game theory [9] presented solution techniques and a straightforward case study that showcased the benefits and effectiveness of these methods in resolving cost allocation problems. However, this study was limited to MGs. Similarly, the paper in [14] also focused on collaborative work among MGs. Game theory has extensively investigated the subject of energy trading and has been extensively discussed in existing literature. For example, ref. [15] presented an extensive examination of game theory methodologies applied to power demand response (DR) within the dynamic and expanding electricity market (EM), classifying them into non-cooperative, cooperative, and evolutionary game categories. Another study examining Stackelberg game articles looked at energy trading specifically in the context of EVs [16]. Unfortunately, there is currently only one review study on VPPs and game theory [17], which grouped its findings based on the types of games analyzed (cooperative, non-cooperative, and Stackelberg).
The contributions of this study are as follows.
- Contrary to the above-mentioned comprehensive review papers, the focus of this review is on different types of game theory and analysis applications in power systems in terms of energy management and energy trading.
- This study reviews existing studies that highlight the interrelated objectives of energy trading and management and the diverse solutions that game theory offers to these collective objectives.
- This analysis goes beyond the traditional scope to provide a broader perspective on the use of game theory in various areas within energy systems, such as general energy markets, MGs, VPPs, EVs, and smart homes.
With the growth of distributed generation facilities, prosuming consumers, and flexible loads, energy management has developed various objectives. The sole aim of energy management has evolved beyond just minimizing costs to include pricing. Energy trading has begun to encompass decision-making processes related to pricing and the quantity of energy. Along with changing energy structures, these two issues have become intertwined. Concerning this subject, dynamic pricing models that consider demand response, bidding strategies, planning, and questions such as from which source and during what hours the energy will be supplied, now encompass both issues. The mathematical algorithm of game theory provides a suitable topology for these targets, and there are publications in the literature that initially focus on energy trading while also dealing with energy management or whose primary objective was energy management but also worked on energy pricing and costs. This study analyzes modern power systems across different application fields and offers an in-depth review of technical articles through the lens of game theory in energy management and trading. The literature review conducted until 8 June 2023 covers terms such as ‘bidding’, ‘pricing’, ‘management’, ‘demand-side management’, ‘demand-response management’, ‘MG’, ‘EV’, ‘HOMES’, ‘VPP’, and ‘power system’. Searches conducted on Scopus are represented in percentage slices over the years, as shown in Figure 1. As can be understood from the charts, research in these fields is on the rise, and the topic continues its academic trajectory. Particularly, the year 2023 saw an increase in auctions and demand-side management topics, while pricing and planning reached their highest rates in 2022.
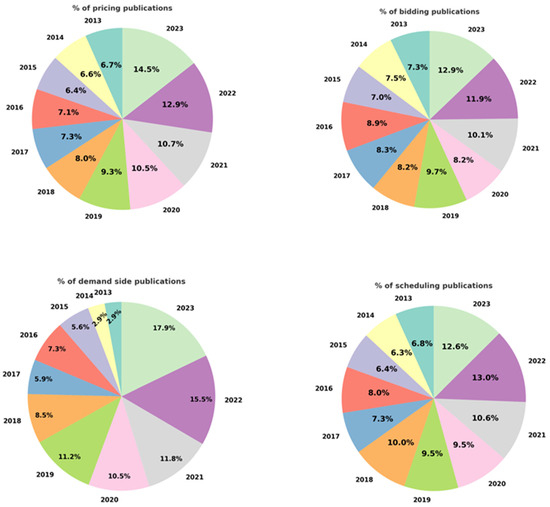
Figure 1.
Percentage Distribution of Game-Related Academic Publications from 2013 to 2023.
Section 2 delivers an elaborate exposition of game theory, followed by its categorization in Section 3, while Section 4 outlines the pros and cons associated with game theoretical approaches. Section 5 discusses the shared objectives of energy trading and management. Detailed examples of game theory applications in energy system implementations are expounded in Section 6. Section 7 presents instances of the limitations, challenges, and benefits of game theory, culminating in a conclusion and discussion in Section 8.
2. Definition of Game Theory
The game theory approach finds its natural application in economic theory, where the economic system is viewed as a complex game involving interactions between producers and consumers facilitated by a market intermediary. In 1928, John von Neumann introduced game theory to the scientific community, utilizing the mathematical concept of Brouwer’s fixed point theorem, which guarantees the existence of a fixed point in a function. This seminal work laid the groundwork for the study of two-person zero-sum games. In 1944, John von Neumann and Oskar Morgenstern collaborated on the publication of the influential book “Theory of Games and Economic Behavior”, which further solidified the application of game theory in economics [18]. The significant impact of game theory is reflected in the recognition it has received, with 11 Nobel prizes awarded for research contributions in various fields applying game theory principles [19,20].
Game theory is a mathematical approach to decision-making that analyzes systems in which rational individuals or decision-makers strive to attain predefined objectives. Game theory is a discipline that focuses on the process of making decisions and the outcomes that result from interactions between rational actors. It is concerned with understanding the strategic behavior of individuals or entities and how their choices are influenced by the actions of others. Decision-making plays a central role in game theory as it explores various strategies, tactics, and outcomes in different scenarios. It is a mathematical model of competition or cooperation between rational decision-makers or parties. What is meant by the concept of rationality is actually rational behavior. Game theory aims to maximize benefits and minimum losses for all players involved in the process, not just a single player. Its prominent feature is that it takes into account the interests of each player.
The elements and premises of a game are outlined as follows:
Player: The rational side that participates in a game and tries to maximize its payoffs;
Strategy: The whole of the decisions that the players will make in the game;
Payoff: The payoff that the player receives as a result of each strategy; it can be positive to negative and zero.
Order of Play: Players can play simultaneously or in turns.
In order for game theory to be applicable, certain assumptions must be made:
- There must be at least two players, and the number of players must be finite;
- Every player has a set of strategies to play, and the players’ strategies are also finite;
- Players’ earnings are not solely dependent on their own decisions; the decisions made by other players in the game also affect the wins or losses;
- All players know the strategies of their own and all other players in the game;
- Each player’s decision-making process is driven by rationality, as they strive to maximize their financial gains while considering their personal interests. The gains or losses resulting from players’ decisions must be numerical or quantifiable data.
There are two ways of representing games: normal form and common form, also known in the literature as the game tree. The normal form presents the strategies chosen by the players and the corresponding outcomes or payoffs they will obtain, all summarized in a single table. This simplifies the analysis and comprehension of intricate events or situations. The normal form is a common representation used in game theory to analyze strategic interactions. It is depicted as a table that shows the outcomes of each strategy combination and the corresponding payoffs or losses for the players. On the other hand, the common form represents the players’ strategies and decisions in a time-based tree structure. It provides a detailed representation of a game where players sequentially make decisions. Each node in the tree represents the available choices for the players, and the structure of the tree illustrates the strategic interactions among them. This representation is particularly useful for analyzing the dynamic nature of games and examining the players’ decision-making mechanisms. (i: i-th player).
- : number of players;
- : the set of strategies available to the i-th player;
- : the i-th strategy () in the strategy set;
- : the union of strategies from the first player’s strategy to the n-th player’s strategy;
- : the payoff of the i-the player.
3. Classification of Game Theory
3.1. Cooperative Games
Games can be classified based on the behavior of the players, and within game theory, there are two main branches: cooperative games and non-cooperative games. Cooperative games refer to situations where players can form alliances and collaborate to achieve mutual benefits. On the other hand, non-cooperative games involve independent decision-making by each player, with a focus on maximizing individual outcomes. In cooperative games, players act individually, forming coalitions of independent decision-makers to increase their winnings. These players can make agreements among themselves, which can affect the strategic choices and benefits. Within the category of cooperative games, there are two main branches: bargaining theory and coalition games. Bargaining theory focuses on the negotiation and agreement process among players to establish cooperative terms. On the other hand, coalition games examine the formation of groups or coalitions among players, which can enhance their positions and outcomes in the game. Figure 2 shows the classification of game theory.
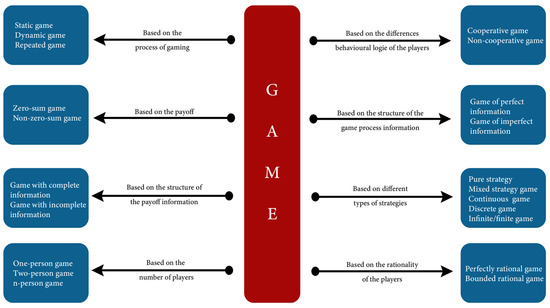
Figure 2.
Classification of Game Theory Schema.
3.2. Non-Cooperative Games
Non-cooperative game theory focuses on the analysis of decision-making processes among independent organizations with conflicting interests. It provides a framework for studying competitive decision-making involving multiple players. This theory is particularly useful in understanding interactions and decision-making processes where players have conflicting interests in the outcomes influenced by their actions. Non-cooperative games can be observed in various domains, such as economics, political science, and sociology. They are further divided into static and dynamic games. Static games refer to situations where time and information do not affect players’ choices, and there is a single move by each player that is independent of time and order. On the other hand, dynamic games involve multiple moves, with players being aware of each other’s moves and time playing a crucial role in decision-making.
3.2.1. Static Game with Incomplete Information (Bayesian Game)
A competitive game is characterized by players who are aware of their own payoffs but have no information about the other players. In the literature, a static game with incomplete information is called a Bayesian game. In such a game, when a player lacks information about their opponent, they represent the opponent with different types denoted by ω.
A Bayesian game consists of the following components. Each player receives a signal about their type and forms beliefs about the types of other players based on the common prior distribution. Players choose their strategies to maximize their expected payoffs, taking into account their beliefs about the types and strategies of other players. The type of player, denoted as , can represent their private information, preferences, or any other characteristic that affects their decision-making process. Strategies are chosen from the sets available to each player, and the overall strategy profile is denoted as . Players calculate their expected payoffs by considering the probability distribution over the types of other players and their corresponding strategies. The goal of each player is to choose a strategy that maximizes their expected payoff given their type and their beliefs about the other players’ types and strategies [21].
Players and Strategies:
- : number of players;
- : the set of strategies available to the i-th player;
- : the i-th strategy () in the strategy set;
- : The profile of strategies chosen by all players.
Types and Signals:
- : The set of possible types for the i-th player;
- : The actual type of the i-th player ();
- = : The set of all possible type profiles;
- : The common prior probability distribution over the type profiles .
Payoffs:
: The payoff function for the i-th player, which depends on their strategy , the strategies of other players and their type .
Expected Payoff:
The expected payoff for player i is calculated as:
where represents the types of all players except i, and represents the strategies of all players except i given their types.
3.2.2. Static Game with Full Information
One of the main categories of non-cooperative games is the full information static game. Players make a single move simultaneously and independently. In this type of game, players are aware of all possible moves. Each player knows the entire structure of the game, including the payoff functions and the strategy sets of all players. Players choose their strategies simultaneously and independently to maximize their own payoffs. The game reaches an equilibrium when no player can improve their payoff by unilaterally changing their strategy [22].
A static game with full information includes the following components:
Payoffs:
: The payoff function for the i-th player, which depends on the strategies chosen by all players.
In a static game with full information, each player aims to maximize their payoff by choosing the best strategy, considering the strategies chosen by other players. Formally, the objective of player i is to solve the following optimization problem:
where represents the strategies of all players except player i.
In equilibrium, each player’s strategy is the best response to the strategies of the other players. A common solution concept for static games with full information is the Nash equilibrium. A strategy profile is a Nash equilibrium if for every player i,
3.2.3. Dynamic Game with Full Information
Dynamic games are also referred to as comprehensive games in the literature. Such games involve players participating sequentially over time. In full information dynamic games, players know the moves chosen by other players but are unsure of their next moves and attempt to anticipate them. An example of this is the Stackelberg game, where the leader first makes a decision, and then the other players take turns making their moves. Each player knows the entire structure of the game, including the payoff functions, the strategy sets of all players, and the history of the game. Players choose their strategies at each stage to maximize their own payoffs, taking into account the past actions of all players. The game reaches an equilibrium when no player can improve their payoff by unilaterally changing their strategy at any stage of the game [22].
Timing and Moves:
- The game is played over a series of stages or periods;
- At each stage, players may have different sets of available actions depending on the history of the game up to that point;
- The history up to any stage t is denoted by , which includes all previous actions taken by all players.
Payoffs:
: The payoff function for the i-th player, which depends on the strategies chosen by all players and the entire history of the game.
3.2.4. Dynamic Game with Incomplete Information
A competitive game is characterized by players who have knowledge of their own payoffs but lack complete information about the payoffs and strategies of other players. In the literature, such a game is referred to as a dynamic game with incomplete information or a Bayesian dynamic game. In such a game, when a player lacks information about their opponent, they represent them as different types denoted as ω. Each player knows the entire structure of the game, including the payoff functions, the strategy sets of all players, and the history of the game, but has incomplete information about the types of other players. Players choose their strategies at each stage to maximize their expected payoffs, taking into account the past actions of all players and their beliefs about the types of other players. The game reaches an equilibrium when no player can improve their expected payoff by unilaterally changing their strategy at any stage of the game [23].
Types and Signals:
- : The set of possible types for the i-th player;
- : The actual type of the i-th player ();
- = : The set of all possible type profiles;
- : The common prior probability distribution over the type profiles .
Timing and Moves:
- The game is played over a series of stages or periods;
- At each stage, players may have different sets of available actions depending on the history of the game and their types up to that point;
- The history up to any stage t is denoted by , which includes all previous actions taken by all players.
Payoffs:
: The payoff function for the i-th player, which depends on their strategy , the strategies of other players , and their type .
Expected Payoff:
The expected payoff for player i is calculated as:
where represents the types of all players except i, and represents the strategies of all players except i given their types.
3.3. Evolutionary Games
Evolutionary game theory was created as a mathematical framework to examine the dynamics of interaction among rational biological agents within a population. Basically, evolutionary games consider the behavior of populations in non-cooperative themed games. Just like Nash equilibrium (NE) static games, the evolutionary equilibrium in this game occurs when the population strives to maintain a state that maximizes their overall returns. The population gradually converges towards this point, and the equilibrium represents the solution to the game.
In the evolutionary game, the game is played repeatedly by players selected from a large population. The evolutionary process comprises two main parts: mutation and selection. Mutation occurs when a player changes their characteristics, and players with new characteristics are included in the population. Through the selection mechanism, individuals with high compatibility are favored and selected, while those with lower compatibility are eliminated. In static evolutionary games, this is described by the concept of evolutionary stable strategies (ESS), which defines the mutation mechanism. In dynamic evolutionary games, the selection mechanism is defined by replicator dynamics. Multiplier dynamics is a significant concept that demonstrates the selection dynamics of a population represented as a system of ordinary differential equations within the evolutionary game.
3.4. Auction Theory and Mechanism Design
An auction is a market mechanism where participants submit bids to exchange an object, service, or set of objects. It follows specific rules that govern the sale or purchase of the object, with the highest bidder typically winning. The theoretical auction game model is a mathematical representation that includes players, their available actions or strategies, and corresponding payoff vectors. In this model, the players can be buyers or sellers, and their actions consist of bid functions or reservation prices. These bid functions map the player’s value (for buyers) or cost (for sellers) to a bid price. The payoff for each player is determined by their expected utility or expected profit based on the chosen strategy combination. A game designer aims to examine various game scenarios and select the one that has the greatest impact on the choices of other players. Mechanism design is employed to establish the game rules in order to achieve a desired outcome. This differs from game analysis, where the rules of the game are already established, and the focus is on studying the resulting outcomes. Moreover, the game designer must take into account situations in which players may provide false information. However, the disclosure principle suggests that it is sufficient to consider games in which players accurately disclose their private information.
4. Game Theory Advantages and Disadvantages
The selection of game theory over other tools for addressing energy transactions and designing energy markets has been primarily motivated by its proven effectiveness in analyzing decision-making behaviors. Game theory, mathematically, enables us to accurately justify the strategic interactions of multiple independent players in highly competitive environments and assists in predicting the outcomes of these interactions.
In the context of future power demand, game theory provides a robust framework to address the inherent complexity and uncertainties of energy markets. Future energy demand is expected to be influenced by various factors such as population growth, economic development, technological advancements, and the integration of renewable energy sources. By 2050, demand for electricity will rise from its current level by over 80% in the Stated Policies Scenario (STEPS), 120% in the Announced Pledges Scenario (APS), and 150% in the Net Zero Emissions (NZE) Scenario [24]. These factors contribute to increased variability and unpredictability in energy consumption patterns, necessitating more sophisticated and adaptive modeling approaches. Different types of game theory can be utilized to optimize future power demand, each offering unique advantages and disadvantages.
The various game methods listed in Table 1, such as cooperative, non-cooperative, auction theory, and evolutionary games, can be beneficial in different scenarios within the context of future power demand. Firstly, the cooperative game approach eliminates the need for centralized control and optimizes societal benefits. However, it may face challenges in maintaining financial equilibrium and devising fair distribution strategies. Factors like the increasing energy demand and the integration of renewable energy sources can exacerbate these challenges.

Table 1.
Comparative Analysis of Game Theory Methods: Advantages and Disadvantages.
On the other hand, the non-cooperative game approach provides significant autonomy to participants and aligns with personal gains. However, it may encounter difficulties in achieving equilibrium and entail extensive computational requirements. Given the variability and unpredictability of energy consumption models, this approach may necessitate more complex modeling and analysis techniques.
Auction theory facilitates price discovery and efficient resource allocation but may also involve risks such as strategic bidding and collusion. Managing these risks in future energy markets may require the development of effective pricing and transparency mechanisms.
Lastly, evolutionary game models address dynamic strategies and adaptation over time. However, they may require complex simulations and struggle to identify stable strategies or equilibria in dynamic environments. This complexity can be heightened by factors such as technological advancements and the evolving nature of energy sources.
Considering the potential and disadvantages of these methods, each may be necessary in specific situations. Effectively applying these different game theory approaches to cope with future energy demand can enable adaptation to the dynamic nature of energy markets and optimize strategic decision-making processes. These explanations are detailed in Table 1.
5. Background of Energy Trading and Energy Management
As the world’s energy demand continues to surge, finding effective ways to meet this increasing need is paramount for maintaining economic progress and environmental sustainability. This challenge underscores the pivotal role of energy efficiency and the strategic management of energy resources. The integration of distributed generation and storage technologies is key, offering not only a way to meet energy demands more sustainably but also providing significant economic incentives for both consumers and suppliers [25]. This dual benefit maintains the relevance of energy management and trading in academic and industry discussions.
For consumers, the drive toward energy management and trading is largely influenced by the potential for cost savings and the opportunity to generate revenue through smart energy practices. Energy providers, on the other hand, see economic value in a more efficient and flexible grid system that responds adaptively to demand patterns. For policymakers and governments, the appeal lies in achieving greater energy efficiency and sustainability, aligning with global objectives to reduce carbon footprints and mitigate climate change impacts.
The core goals of focusing on energy trading and management include the following:
Improving System Efficiency: The adoption of distributed generation and storage enhances the overall efficiency of the power grid [26]. It allows for a reduction in reliance on centralized, high-capacity power plants and mitigates transmission congestion and losses. This strategic approach not only defers the necessity for extensive grid upgrades but also bolsters the reliability and resilience of energy infrastructure.
Minimizing Operational Costs: Real-time adjustments to energy production and consumption, facilitated by energy trading, help flatten peak demand curves and reduce the operational costs associated with meeting high-demand periods. This dynamic management of energy resources optimizes the use of low-cost, renewable energy sources during peak times, contributing to a more cost-effective energy market [27].
Reducing Greenhouse Gas Emissions: A strategic focus on renewable energy integration and distributed generation through energy management practices plays a crucial role in decreasing greenhouse gas emissions. By promoting local energy trading and enhancing the efficiency of energy usage, the power sector can significantly contribute to global efforts to combat climate change. Smart grid technologies further support this goal by enabling more precise control over energy distribution and usage, leading to lower emissions.
Advancing Energy Profiling and Optimization: The implementation of intelligent energy systems, such as smart MGs, facilitates better energy profiling and optimization [28]. These technologies ensure that energy production closely matches consumer demand, reducing wastage and improving the overall balance between supply and demand. Networking MGs allow for the integration of renewable sources at the community level, enhancing the sustainability of energy systems and enabling consumers to play an active role in energy management.
6. Application of Game Theory to Energy Systems
6.1. General Energy Market Applications
In this subsection, we explore a range of recent literature that applies game theory to analyze practices in contemporary energy markets. Figure 3 shows the structure of the general energy market. The studies are organized according to the modeled game type: non-cooperative, cooperative, and Stackelberg.
Figure 3.
Game Theory Applications in General Energy Market Structure.
Studies [29,30] have addressed examples of cooperative game types in the context of the general electricity market in the literature. Ref. [29] analyzes the negotiation process for contracts between a generation company and a load-serving entity (LSE) in wholesale electricity markets, using Nash bargaining theory to highlight how negotiation outcomes change based on participants’ risk and price preferences, considering risk management and strategic behavior. Ref. [30] emphasizes collaboration between the distribution company and flexible demand collectors in electricity pricing, aiming to lower peak demand and reduce costs, offering various pricing options instead of a uniform payment.
Refs. [31,32] addressed examples of non-cooperative game types in the context of the general electricity market in the literature. In [31], a pricing model for the day-ahead electricity market involving prosumers and a local utility company was developed, with market prices determined using game-theoretic algorithms and success demonstrated through simulations. Refs. [33,34] focus on demand management strategies encouraging individual consumers to minimize energy costs, while refs. [35,36] analyze pricing mechanisms and competition in energy trade between utility companies and consumers. In [37], a game to explore strategic interactions among suppliers in deregulated markets is proposed, researching optimal strategies through co-evolutionary algorithms. Ref. [38] addresses economic and operational improvements in a network with demand response and smart customers. Refs. [39,40] offer flexible pricing and multi-agent systems for demand management. Ref. [41] simulates a model including household appliances, energy storage, and production systems on the IEEE-33 bus system, while [42] develops a model for optimizing energy consumption to maximize user preferences. Refs. [32,43] present innovative studies on the impact of smart homes on the penetration of photovoltaic systems and managing wind power intermittency in isolated MGs, respectively.
Studies [44,45] addressed examples of Stackelberg game types in the context of the general electricity market in the literature. In [44], a real-time pricing model for demand response management was developed using a Stackelberg game approach between an energy producer and multiple energy center operators, employing a new distributed algorithm to determine the game equilibrium in energy trade and auction theory for pricing considerations. Refs. [46,47] focus on Stackelberg games where the power station acts as the leader and prosumers as followers, emphasizing the prosumers’ responsibility to decide on the quantity of energy they wish to sell and strategies for energy companies facing uncertainties in profits due to price volatility. Refs. [48,49] examine the dynamics of dynamic pricing and supply–demand balance in the energy market, analyzing the interaction between retailers (leaders) and consumers (followers) through a two-level game model and presenting a Stackelberg game formulation to model the interaction between a utility company and its users. Ref. [45] explores demand side management involving users with energy storage devices and a Stackelberg game between the utility and consumers, focusing on strategies for minimizing energy costs and maximizing profits.
Recent studies have focused on smart grids and renewable energy sources, highlighting the potential and effectiveness of P2P energy trading systems developed using blockchain and game theory approaches.
Studies [50,51] investigate P2P systems facilitating energy trade between residential homes within the smart grid, utilizing models based on double auction and iterative double auction mechanisms. These studies demonstrate how these systems can be empowered by blockchain technology and ensure the privacy of participants while proving the feasibility of real-time trading through simulation results. Research [52,53] focuses on the interactions between prosumers and MGs. Using a game theory model based on Practical Byzantine Fault Tolerance-based Consortium Blockchain (PBFT-CB) and a continuous double auction mechanism built on blockchain, they discuss how P2P electricity trading can contribute to the development of the electricity market and protect consumer interests. These models aim to enhance transaction transparency and efficiency through strategies that adapt to market changes and secure digital certificate exchanges.
Refs. [54,55], on the other hand, offer innovative solutions for electricity trading systems for EVs, protecting privacy in V2V and V2G transactions and encouraging active user participation in the electricity market through blockchain-based architectures and auction-based pricing mechanisms. These works showcase the transformative potential of blockchain in electricity trading by significantly improving social welfare and cost performance.
Summary
Literature reviews on general electricity markets comprehensively address the applications of game theory across various aspects, such as energy management, trading, pricing, bidding strategies, and demand-side management.
Non-Cooperative Games: The studies [31,32] demonstrate that considering the competitive structure of the market, non-cooperative games emerge as a prominent method for developing strategies aligned with the dynamics of the energy market. These types of games effectively model scenarios where market participants act independently and strive to maximize their own interests.
Cooperative Games: The studies [29,30] reveal that cooperative games are featured in more narrowly focused studies within general electricity markets, aiming at specific objectives. However, due to the competitive and complex nature of the general electricity market, cooperative games have been less preferred compared to other game types.
Stackelberg Games: The studies [44,45] indicate that games have become the preferred method in situations that demand more stable and predictable market control and decision-making processes. This game type, which involves leader–follower dynamics, is especially suitable for energy market studies that consider multiple objectives, such as cost optimization alongside energy efficiency enhancement. The summary of studies focusing on general market applications using game theory is provided in Table 2.

Table 2.
Summary of Key Papers on General Market Applications with Game Theory.
6.2. Microgrid Applications
In this subsection, we delve into various recent studies that utilize game theory to examine energy trading and management involving MGs. Figure 4 shows the structure of the MG. These studies are categorized according to the type of game modeled: non-cooperative, cooperative, and Stackelberg.
Figure 4.
Game Theory Applications in MG Structure.
The studies [57,58] addressed examples of non-cooperative game types in the context of MG application in the literature. The authors of [57] introduced a practical application of a multi-agent-based game theory reverse auction model for energy trading in MGs. The model encompassed both conventional and renewable energy sources. The study employed a multi-agent-based approach to monitor, control, and execute the reverse auction process for distributed energy resources (DER). The prices in the auction were determined based on the situation observed one hour earlier, aiming to foster competition among participants. The research highlighted the real-time implementation of game theory in facilitating efficient energy trading within MGs. Similarly, in [59], competing MGs can be energy providers or consumers according to the energy demand for each hour. In [60] proposes a multi-agent modeling and game theory-based control strategy for managing energy in hybrid systems comprising engine-generator, battery, and ultracapacitor, optimizing energy distribution via NE to enhance system performance and reduce costs. The paper [58] introduces a stochastic energy management algorithm for smart MGs with intermittent resources like wind and PV units, aiming to optimize their market participation and minimize total operational costs using the Copula method and game theory. Ref. [61] optimizes electricity exchange and revenue distribution among multiple MGs using a hybrid game theory-based P2P trading paradigm and a traditional time-of-use strategy, incorporating electric vehicles and flexible loads as energy assets.
Refs. [62,63] addressed examples of cooperative game types in the context of the MG application in the literature. In this study [62], a coalition game theory approach is applied to achieve a power–demand balance among multiple MGs. A consensus algorithm is utilized in the demand management system to facilitate cooperation and coordination. The transfer of excess energy between MGs is determined using the principles of Shapley value theory. To handle the large amounts of data and information involved in multi-agent smart MGs, the compute and storage units are relocated to the Fog layer, enabling efficient processing and storage capabilities. In [64], an incentive model is proposed to encourage the development of MGs in regulated electricity markets by supporting cooperation between a utility company and consumers. The analysis presented explores the impact of this model on prices and costs for all participants under various assumptions related to MG development. In [65], they proposed a coalition scheme based on hierarchical priority. Reaching the equilibrium state for all micro-networks and coalitions was determined as the goal, and a cooperative game theory model was created with a greedy-based strategy. In [63], a cooperative game model was introduced, utilizing Nash bargaining theory, with the aim of facilitating proactive energy trading and ensuring equitable distribution of benefits among interconnected MGs. This study [66] aims to achieve peer-to-peer power sharing and cooperative optimization among multiple low-carbon microgrids (LCMG) using an optimization model based on Nash bargaining theory.
Studies [67,68] addressed examples of Stackelberg game types in the context of MG application in the literature. Various models of Stackelberg games have been applied to optimize energy management within MGs and distributed energy systems, highlighting the strategic interaction between different entities like utility companies, MG operators, and consumers. For instance, refs. [67,69] both present two-level Stackelberg games for energy pricing and management, demonstrating the existence of unique Nash equilibriums (NEs) and proposing hierarchical game strategies where utility companies and MGs act as leaders at different levels, with users as followers. Similarly, ref. [70] explores a multi-leader, multi-follower Stackelberg game among interconnected MGs, allowing for independent decision-making by each MG based on local demands and productions and enabling sellers to offer prices independently. Further, ref. [71] focuses on energy management within MGs composed of combined heat and power (CHP) systems and PV consumers, offering a strategic framework for managing energy supply and demand with the MG operator as the leading consumer. On the other hand, ref. [72] introduces a decentralized pool system integrating MGs with a distribution company, where the distribution company leads and MGs follow, employing behavioral strategies for decision-making. Ref. [73] models a system where users with photovoltaic energy generation share excess energy, using a Pareto algorithm and decentralized control to determine the next day’s energy trade amounts. Lastly, ref. [68] proposes a coordinated energy management strategy for hybrid AC/DC systems with MGs, employing game theory and robust optimization to address renewable energy uncertainty and reduce operational costs within a Stackelberg game framework. Ref. [74] presents an energy-sharing management strategy based on Stackelberg game theory, aiming to optimize MGs by incorporating a suitable billing scheme to enhance robustness against uncertainties.
Summary
Energy management and trading in MGs have been addressed using various models of game theory. Each type of game seeks to explore ways to optimize energy management, trading, and pricing strategies within MGs, aiming to enhance their capability to cope with uncertainties, integrate renewable sources, and manage demand effectively.
Non-Cooperative Games: The studies [57,58] developed models that facilitate independent energy trading, pricing, and allocation among MGs. In these models, each MG autonomously makes decisions with the aim of reaching optimal strategies through NE.
Cooperative Games: The studies [62,63] explore the balance of power demand among MGs using consensus algorithms and coalition formation. These approaches aim for a more effective distribution of energy using theories such as the Shapley value.
Stackelberg Games: The papers [67,68] take on energy management in MGs through a leader–follower dynamic structure. Typically, a leader, such as a utility company, sets the energy prices, and the followers, such as MGs, adjust their energy supply and demand accordingly.
Each game model analyzes the behavior and interactions of MGs in the energy market from different perspectives and offers solutions to challenges such as uncertainty, the integration of renewable energy sources, and demand-side management. These game theory approaches encourage active and effective participation in energy trading, cost reduction, and the creation of a competitive environment in the power market for MGs. The summary of studies focusing on MG applications using game theory is provided in Table 3.

Table 3.
Summary of Key Papers on Microgrid Applications with Game Theory.
6.3. VPP Applications
In this section, we review a range of contemporary literature that applies game theory to the exploration of energy trading and management within VPPs. Figure 5 shows the structure of the VPP. The studies are systematically categorized based on the game theory model employed: non-cooperative, cooperative, and Stackelberg.
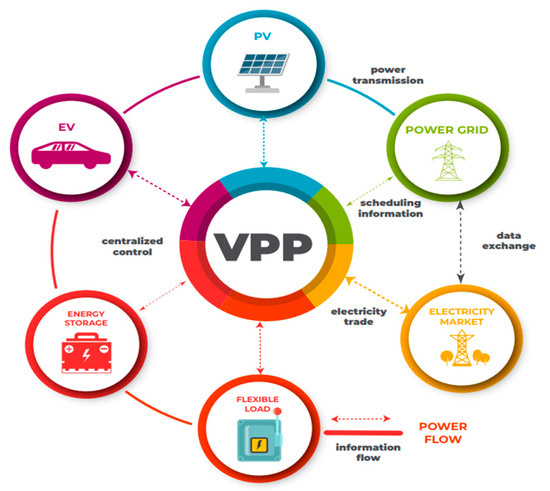
Figure 5.
Game Theory Applications in VPP Structure.
The studies [79,80] addressed examples of non-cooperative game types in the context of the VPP application in the literature. Studies [79,81] investigate how VPPs can be optimized using game theory, focusing on economic evaluation and benefits in multi-operator VPP systems and tender markets, respectively. In [79], a combination of non-cooperative and cooperative game theories is used to analyze competition among VPPs, who determine their power output and pricing based on supply and demand. The study suggests using particle swarm optimization and genetic algorithms to find the Nash equilibrium (NE) and introduces the particle Shapley value for fair profit sharing among VPPs. The effectiveness of this approach is demonstrated through case studies that link VPP profitability and market prices to the diversity of resources in the VPP. Ref. [81] explores how VPPs can increase their benefits by participating in tender markets, planning energy storage, demand response, and using renewable energy sources. This is done to optimize auctions for energy and reserve capacity, with the method tested on the Taiwan power system. Refs. [80,82] focus on VPPs as price setters and coordinators in the energy market. Ref. [82] looks at two VPPs in a distribution network, using a non-cooperative game to model their interactions and developing an iterative method to find the NE, where VPPs buy energy from DERs and sell it to the wholesale market. Ref. [80] introduces a method for VPP coordination control based on a non-cooperative game, aiming to reduce generation costs by managing various components like PV power supplies, energy storage, and DERs. Cost models are created to maximize the economic benefits for each VPP, allowing them to optimize their operations. Together, these studies present strategies for the operational and economic improvement of VPPs in the energy market, showing how game theory and optimization methods can be applied to improve the competitiveness and efficiency of VPPs.
The studies [83,84] addressed examples of cooperative game types in the context of VPP application in the literature. Studies [83,85] explore the impacts of Shared Energy Storage Systems (SES) and energy trading models on VPPs. Ref. [83] discusses how an SES leasing mechanism, considering electricity market prices and battery degradation, can enhance the market performance of VPPs. This study proposes a joint optimal market bidding model developed using SES to maximize VPPs’ expected daily profits and introduces a fair profit distribution method for SES-enabled VPPs based on the Shapley value method and minimum deviation algorithm. In [85] uses game theory to model the relationship among multiple VPPs within the SES, presenting an energy trading model that examines the effects of SES on multiple VPPs and simulates the VPPs’ bidding behavior. Refs. [86,87] focus on different profit-sharing frameworks for VPPs and DERs. Ref. [86] develops a profit distribution model that considers multiple objectives such as fair dividend distribution, stability of the cooperation alliance, and attractiveness for participating members, applying a multi-objective evolutionary optimization algorithm based on reference points to solve this multi-objective problem. Ref. [87] proposes a trading strategy and revenue distribution strategy for DERs, specifically EVs and wind turbines, taking into account factors like revenue from electricity sales, penalties for reducing wind abandonment, and electricity generation costs. Ref. [88] introduces a cooperative game model-based method for optimal profit distribution among DERs within a Combined Heat and Power (CHP)-VPP system, supported by simulations on a 4-node system and a modified IEEE 30-node + Heat 14-node system. Ref. [89] presents an approach for DERs to maximize their profits by forming coalitions in retail or VPP-based markets. Ref. [90] offers a two-level optimization scheduling approach to enhance the overall operating profit of multiple VPPs. This approach first implements a water-photovoltaic-storage complementary method to coordinate multiple power sources effectively and then introduces power-sharing and market game strategies among the VPPs. Ref. [91] proposes a peak balancing mechanism that combines the supply and demand sides to increase the system’s peak capacity. This study analyzes the key stakeholders’ interests using game theory and measures their contributions to the overall system using Pearson correlation coefficients. Finally, ref. [84] introduces a system where the Distribution System Operator (DSO) interacts with the VPP using distribution system constraints for voltage management. To facilitate collaborative operations between a DSO and a VPP, the VPP initiates the classification of DERs based on their locations. Following this, both Volt-Watt and Volt-Var control strategies are implemented, considering relevant constraints. This approach aims to improve the overall performance of the energy distribution network by enabling efficient collaboration between the DSO and VPP.
The studies between [92,93] have addressed examples of Stackelberg game types in the context of the VPP application in the literature. In studies [92,94], different pricing mechanisms for VPP retailers are explored. Ref. [92] proposes a special discount package pricing mechanism for consumers who produce energy, using a Stackelberg game to model the retailer’s pricing strategy and introducing a novel reinforcement learning algorithm for evolutionary game-based dynamic selection. Ref. [94] develops a VPP-specific utility with a critical peak discount strategy, using cumulative expectation theory for customized pricing and employing the Salp Swarm Algorithm to capture consumer behavior in extreme temperatures. Refs. [95,96] examine strategic exchanges and uncertainties in renewable energy generation and market prices within the energy sector. Ref. [95] describes a reciprocal strategic exchange between power sales companies and VPPs, using Stackelberg game applications for operational and planning decisions in China’s energy sector. Ref. [89] introduces a two-stage Stackelberg game model for VPPs participating in day-ahead and real-time markets, focusing on managing uncertainties in renewable energy generation and market prices, where a leading consumer sets internal prices and energy strategies. Ref. [93] proposes a three-stage energy management strategy for a VPP with energy cells, starting with a multi-agent system to frame group interactions, followed by demand response modeling for energy balance optimization, and concluding with an internal trade mechanism treated as a Stackelberg game.
These studies collectively highlight innovative solutions for pricing, strategic exchanges, and energy management in VPPs, demonstrating the application of game theory and algorithmic approaches like reinforcement learning, the Salp Swarm Algorithm, and Karush–Kuhn–Tucker (KKT) conditions for optimizing resources and energy trading in decentralized energy systems.
Summary
Energy management and trading in VPP applications have been studied using various game theory models. Each game model aims to explore ways to optimize energy management, trading, and pricing strategies in VPPs. Thus, it aims to increase their capacity to cope with uncertainties, integrate renewable resources, and manage demand effectively.
Non-Cooperative Games: The studies [79,80] frequently preferred non-cooperative games to model competition, management, and pricing in the energy market, reflecting the autonomous nature of VPPs in these aspects.
Cooperative Games: The papers [83,84] reveal the potential of VPPs to create synergy in resource-sharing and collective decision-making processes. Due to the primary goal of VPPs being energy providers, cooperative games have been the model of choice in these applications, facilitating collaboration and joint optimization.
Stackelberg Games: In studies [92,93], Stackelberg games have been favored, particularly for managing uncertainty and determining market strategies within VPPs. This model aligns with the hierarchical decision-making typical in VPP operations, where strategic leadership is crucial.
These game theory models enhance the strategic positioning of VPPs in the energy sector, addressing key challenges and capitalizing on the dynamic interplay of market forces. The summary of studies focusing on VPP applications using game theory is provided in Table 4.

Table 4.
Summary of Key Papers on VPP Applications with Game Theory.
6.4. EVs Applications
In this subsection, we conduct a review of recent scholarly work utilizing game theory to examine energy trading and management practices associated with EVs. Figure 6 shows the structure of the EV. The research is organized according to the type of game theory model applied: non-cooperative, cooperative, and Stackelberg.
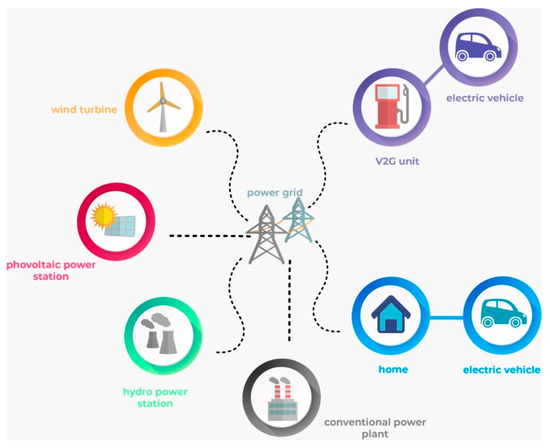
Figure 6.
Game Theory Applications in EV Structure.
The studies [104,105] addressed examples of non-cooperative game types in the context of the EV application in the literature. Studies [104,106] delve into decentralized energy management and competition among electric vehicle charging stations (EVCS), respectively. Ref. [104] aims to minimize the operating and charging costs within an MG incorporating plug-in EVs (PEVs), tested on the IEEE-33 bus, while [106] analyzes EVCS electricity pricing strategies under physical constraints like transmission capacity and charger availability, focusing on competitive pricing to optimize market dynamics. Ref. [107] presents an EV charging model in parking lots, tackling constraints such as total charge amount and transformer capacity, employing the Nikaido–Isoda algorithm for equilibrium calculation. This parallels [108]’s distributed EV charging mechanism that considers dynamic cost schemes to prevent power system overload, optimizing charging efficiency and resource utilization. Ref. [109] introduces a Mean Field Games-based strategy for coordinating charging in solar-powered lots, aiming for efficient energy management and SOC stability among battery EVs (BEVs), hinting at a shift towards energy trading by allowing BEV owners to participate in grid support. Similarly, ref. [110] explores EV charging navigation within a two-level game framework that accounts for the power and transportation systems’ interplay, emphasizing optimal charging and cost minimization. Ref. [111] proposes an aggregative game model for day-ahead EV charge planning, using real-world data to showcase its effectiveness. This approach indirectly relates to energy trading by considering electricity spot prices and EV demand impacts. In contrast, refs. [112,113] directly engage in energy trading, with [112] exploring decision-making for plug-in hybrid EVs (PHEVs) selling stored energy through auctions and [113] detailing a non-cooperative game among batteries in geographically dispersed storage units, focusing on PHEVs and auction-based pricing. Ref. [105] tackles the EV charge planning problem within the vehicle collector community using game theory and microeconomics to model charge start times and profiles, considering strategies of neighboring collectors, thus linking charge planning with broader energy management strategies.
The studies [114,115] addressed examples of Stackelberg game types in the context of EV application in the literature. In [114], a peer-to-peer (P2P) energy trading scheme using blockchain technology is proposed. The study focuses on balancing the energy gap between EVs and smart grids, as well as serving consumers. The authors develop a model based on Stackelberg game theory, where a second reverse auction is used to select a leader among all service providers (SPs). The leader announces a price, and EVs make decisions on energy consumption to minimize their energy bills. To maximize the leader’s profit, which is the SP, a genetic algorithm is proposed. In [115], a game model is presented where power regulation is performed between a fast charging station (FCS) as the leader and EVs as the followers. The FCS sets the energy reserve price, and the game is reformulated as a two-level optimization problem. The problem is then solved using mathematical programming with the method of equilibrium.
The study [116] addressed examples of cooperative game types in the context of EV application in the literature. In [116], the paper focuses on the optimal bidding strategy of DERs integrated within VPPs using a cooperative game model. To address the intermittency of renewable energies, the authors propose using EVs as energy storage facilities within the VPP. Considering the uncertainties associated with EVs and DERs, a stochastic optimization model is employed, incorporating the use of the Shapley value method for profit allocation. The study aims to optimize the bidding strategy and maximize the overall benefits of the VPP while accounting for the uncertainties in the system.
Summary
These studies explored energy management and trading in the context of EVs using various types of game theory.
Non-Cooperative games: The studies [104,105] have been specifically favored for identifying competitive pricing strategies and optimal charging timings of EV charging stations.
Cooperative games: Ref. [116] highlighted the potential for coordinating the energy storage capacities and charging processes of EVs.
Stackelberg games: The papers [114,115] focused on optimizing energy consumption decisions under the leadership of service providers with EVs acting as followers.
Each game type assesses the role and interactions of EVs in the energy market from different perspectives, offering innovative solutions to challenges in these domains. The summary of studies focusing on EV applications using game theory is provided in Table 5.

Table 5.
Summary of Key Papers on EV Applications with Game Theory.
6.5. Smart Home Applications
The studies [118,119] addressed examples of Stackelberg game types in the context of the smart home application in the literature. Figure 7 shows the structure of the smart home. In [118], a model addresses distributed home energy management with storage across multiple MGs. It sets a hierarchical structure where the MG leads by setting energy prices, and home systems follow, adjusting their energy storage needs. This model boosts network profits by up to 55% and customer gains by up to 30.79%, showcasing the benefits of collaboration. In [119] a smart community model, customers and aggregators collaboratively reduce bills and costs by smartly controlling home appliances and buying energy efficiently. This approach reduced the peak-to-average load ratio by 35.9% and cut bills by 34.3%.
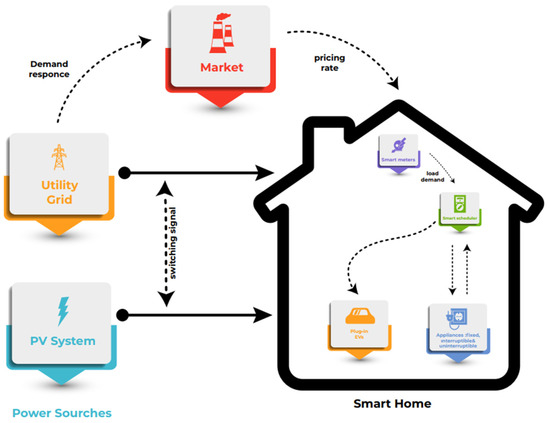
Figure 7.
Game Theory Applications in Smart Home Structure.
The studies [120,121] addressed examples of cooperative game types in the context of the smart home application in the literature. Ref. [120] proposes a game theory-based coalition system for energy management in smart homes, where each home acts as a player and surplus energy is equitably distributed among homes using the Shapley value according to demand. Utilizing smart meter infrastructure to forecast power demand and generation, the system facilitates the savings and distribution of 14.2 kW of extra power among homes at different times of the day. Ref. [121] presents a cooperative game theory model for demand-side management, using region-specific ToU tariffs and optimization algorithms to efficiently manage electrical device usage.
The studies [122,123] addressed examples of non-cooperative game types in the context of the smart home application in the literature. Ref. [122] proposes a two-level game model for multi-home MGs, showing a 169% profitability increase by simulating market and distribution operator interactions, emphasizing its financial benefits. In [123], a game theory model manages a smart home’s energy, focusing on nine devices coordinated by an energy management controller for efficient grid integration.
Summary
Energy management and trading within smart home applications have been explored through various game theory models.
Stackelberg Games: The studies [118,119] utilized Stackelberg games to model the leader–follower dynamics of energy management in smart homes. These works demonstrate how MGs and home energy management systems (HEMS) can effectively assume leadership roles in pricing energy and planning devices, facilitating community-wide energy savings and bill reductions.
Cooperative Games: The studies [120,121] indexed as [120] and have employed cooperative games to facilitate energy sharing and demand management among homes. These models aim to meet the energy demands of homes while enhancing overall system performance and consumer benefits.
Non-Cooperative Games: The works [122,123] also adopt cooperative game approaches to address energy management in smart homes. These research efforts offer innovative solutions for optimizing in-home device energy consumption and enhancing the financial outcomes for participants in MG markets, focusing on demand management and energy savings.
These varied game theory models strengthen the strategic positioning of smart homes and MGs in the energy sector, enabling them to tackle key challenges and leverage the dynamic interplay of market forces. The summary of studies focusing on smart home applications using game theory is provided in Table 6.

Table 6.
Summary of Key Papers on Smart Home Applications with Game Theory.
Additionally, studies [57,81,95,111,124,125] provide insights into practical applications of game theory and optimization models across various energy markets, highlighting the blend of theoretical frameworks with real-world case studies. Table 7 shows the type of game used and the country in which the study was conducted. Ref. [81] explores the optimization of VPPs by managing energy storage, demand response, and renewable sources for maximum profitability. It demonstrates a robust optimization model’s effectiveness with a case study on the Taiwan power system, focusing on uncertainties from renewables and demand response. Ref. [124] examines a dynamic pricing strategy for the Singapore electricity market, emphasizing real-time, time-of-use, and day/night pricing strategies for residential and commercial sectors. It finds that real-time pricing effectively reduces peak loads and increases profits, leading to more efficient energy consumption patterns. Ref. [95] presents an operational and transactional platform for China’s electricity market, employing a master–slave game optimization model to maximize power sales companies’ profits and minimize dispatching costs for VPPs. The platform enhances DERs and controllable loads’ integration and management. Ref. [111] offers a non-cooperative game model for day-ahead EV charging scheduling, incorporating real-world driving data from Danish National Travel Surveys. The model evaluates EV charging demand’s impact on electricity prices and optimizes charging schedules based on EV driving patterns. Ref. [125] introduces a process for participating in a high-profitability yet high-uncertainty reliability demand response program using a non-cooperative game model and surplus electricity trading through ESS. A case study with real data from the Korean DR market shows significant improvements in the benefit–cost ratio of small-scale ESSs. Ref. [57] introduces a game theory reverse auction model for MG operations tested at Florida International University, showing its integration potential into existing grids with new assets.

Table 7.
Practical Case with Game Theory.
7. Limitations, Challenges, and Benefits of the Game Theory
Although the development of game theory models aims to simulate the strategic behaviors and mutual interactions of participants, this process encounters challenges such as complexity, incomplete information, scalability, and regulatory limitations. Interactions in real-world systems are highly diverse and complex, which complicates the incorporation of these interactions into models, especially in scenarios involving multiple objectives, different risk tolerances, and varying levels of information. The lack of complete information introduces uncertainty in determining optimal strategies, potentially leading to incorrect decisions. The problem of incomplete information can result in the inability to fully predict participants’ strategies, and the accuracy of the obtained information can be questioned. To mitigate this issue, methods such as stochastic modeling, Bayesian approaches, and robust optimization can be employed. Additionally, the scalability of models becomes a significant challenge in large-scale systems, particularly in cases involving complex network structures and numerous decision variables, making real-time analysis difficult. Analyzing large-scale systems poses challenges in terms of computational power and time. Existing regulatory frameworks and policies may limit the applicability of game theory solutions, potentially restricting the implementation of theoretically optimal strategies. For instance, stringent regulations on energy trading in some countries may make it difficult to put theoretically optimal strategies into practice. Despite the complexity of modeling, game theory offers a robust tool for understanding the strategies and interactions of participants. By simulating real-world scenarios, it reveals the dynamics between various strategic options, thereby enabling decision-makers to make more informed choices. Concepts such as Bayesian approaches, stochastic modeling, and robust optimization can be utilized to navigate and mitigate uncertainty. Techniques like distributed computing and parallel processing enable game theory models to operate efficiently and swiftly on large datasets, facilitating better management of critical infrastructures like energy. High-performance computing infrastructure is necessary for real-time data analysis and decision-making processes. Game theory helps support large-scale decision-making processes by enabling optimal resource allocation and efficiency improvements across the system. Game theory models can be used to achieve real-time pricing and supply–demand balance in energy markets. For example, smart grids, with their real-time data collection and analysis capabilities, can optimize the balance between energy production and consumption.
8. Discussion
Studies on the management and control of power systems often model optimization problems as if there was a single authority with all the necessary information and control capacity. However, with the decentralization of energy markets and the increase in deregulation, this assumption is becoming less realistic. This situation complicates predicting the evolution of a power system considering the diverse objectives of numerous players. Research in the literature demonstrates that game-theoretic approaches are particularly suitable for analyzing the complex interactions between independent players. In this context, the type and accuracy of the model are crucial for developing effective and applicable control mechanisms and policy recommendations.
Studies often address non-cooperative games, examining the interactions between multiple players with conflicting goals. Formal analyses frequently reveal that the game has a unique equilibrium, allowing for the prediction of players’ behaviors and, accordingly, designing the system. In multiple equilibrium situations, identifying regulations that can direct players toward the most desired outcome is a common approach. Pricing mechanisms designed to encourage players to perform specific actions aim to achieve specific goals such as maximizing the profits of all players, balancing supply and demand, or regulating voltage. It is emphasized that the goals of all players must be considered for these mechanisms to be effective. For instance, strategies for demand management have been proposed, where energy provider companies develop pricing strategies to maximize their revenues or enhance system stability, and customers respond to these prices by trying to optimize their own objectives. In some studies, the main grid has been modeled as a player and included in the objective function to maximize its revenue, developing pricing strategies and incentive policies. Other studies have not included the public company or energy provider in the pricing mechanism, entering their data as constants, aiming for the system to create its own price and incentive policy. These policies have been applied in studies either together or separately with different options such as peak-load reduction, load shifting, or planning studies. Publications that develop bidding strategies along with pricing also exist, aiming to dynamically involve each player in the energy system.
Applications of cooperative game theory reveal that cooperation between different energy market players not only increases the benefits of participants but also enhances social welfare. Such cooperation is critically important, especially in finding the optimal combination of renewable energy sources and energy storage devices and in expansion planning problems. Some studies show that profits can be significantly increased if participants jointly lease the usage rights of SES and participate in energy and regulation markets through cooperation and bidding strategies. Studies examining the impact of SES device usage in multiple energy systems have found a place in the literature. Some studies have made cooperation considering profit sharing. Coordinated operation has enabled a profit greater than the sum of individual gains, later introducing pricing mechanisms to provide a profit-sharing scheme among stakeholders.
In conclusion, the increasing complexity and variability of energy markets necessitate a shift from centralized planning approaches to more flexible, dynamic, and participatory methods. Game theory plays a key role in this transformation, offering valuable insights into strategic interactions and decision-making processes. Non-cooperative and cooperative game theory models are essential tools for overcoming challenges in energy markets and developing effective policy recommendations. These models can help achieve goals such as market equilibrium, increased social welfare, and improved system efficiency. However, the success of game theory-based solutions depends on the realism of the model’s assumptions and scenario selection. Factors such as energy market regulations, legal limitations, and the business models of public utility companies significantly affect model outcomes. Moreover, the complexity of competitive energy markets in modern electrical grids may limit the applicability and effectiveness of game theory models. Therefore, the development and application of game theory-based models require a continuous research and innovation process for the management and optimization of energy systems. In summary, the increasing complexity of energy markets necessitates the re-evaluation of traditional management and control approaches. Game theory has the potential to offer flexible, dynamic, and inclusive solutions to these new challenges. Analyzing strategic interactions and decision-making processes in depth provides valuable insights for overcoming challenges faced by energy market participants and developing effective energy policies. In this context, further development and application of game-theoretic approaches are of great importance for the future management of energy systems.
9. Conclusions
This study highlights the interconnected objectives of energy trading and management in the contemporary energy market, demonstrating how game theory serves as a versatile optimization method to address various goals. By reviewing technical articles, it showcases applications in general energy markets, MGs, VPPs, EVs, and smart homes.
Traditional optimization assumes a single entity with unlimited information and control, a notion increasingly unrealistic due to market centralization and deregulation. Game theory, particularly in non-cooperative games, is effective in analyzing complex interactions among independent entities with different objectives. It predicts player behavior and system design, while cooperative games facilitate higher profit margins through mutual agreements and effective planning.
Game theory is also crucial in addressing cyber security in power systems, modeling interactions between attackers and defenders. The integration of blockchain technology offers innovative solutions for reliable and transparent energy transactions, enhancing market efficiency. Future applications include blockchain-based smart contracts to improve strategic decision-making in energy consumption, production, and distribution, as well as peer-to-peer energy trading and increased resilience against cyber-attacks. The intersection of machine learning and game theory promises more accurate and adaptable models by analyzing power system data.
In summary, game theory is an effective tool for modeling the current energy market, with academic interest and practical applications expected to grow. Its continued research and application will likely yield significant advances, improving the sustainability and efficiency of global energy markets.
Author Contributions
Conceptualization, N.Y. and Y.Y.; methodology, A.O.; validation, S.B. and J.J.; formal analysis, J.J.; investigation, S.B.; resources, N.Y. and Y.Y.; data curation, N.Y. and S.B.; writing—original draft preparation, N.Y.; writing—review and editing, J.J. and A.O.; visualization, S.B. and Y.Y.; supervision, Y.Y. and S.B.; project administration, N.Y.; funding acquisition, J.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the International Energy Joint R&D Program of the Korea Institute of Energy Technology Evaluation and Planning (KETEP), granted financial resources from the Ministry of Trade, Industry & Energy, Republic of Korea. (No. 20228530050030).
Conflicts of Interest
The funders had no role in the design of the study, in the collection, analyses, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
References
- Yoldaş, Y.; Önen, A.; Muyeen, S.M.; Vasilakos, A.V.; Alan, İ. Enhancing smart grid with microgrids: Challenges and opportunities. Renew. Sustain. Energy Rev. 2017, 72, 205–214. [Google Scholar] [CrossRef]
- Latran, M.B.; Teke, A.; Yoldaş, Y. Mitigation of power quality problems using distribution static synchronous compensator: A comprehensive review. IET Power Electron. 2015, 8, 1312–1328. [Google Scholar] [CrossRef]
- Sao, C.K.; Lehn, P.W. Control and power management of converter fed microgrids. IEEE Trans. Power Syst. 2008, 23, 1088–1098. [Google Scholar] [CrossRef]
- Mannini, R.; Eynard, J.; Grieu, S. A Survey of Recent Advances in the Smart Management of Microgrids and Networked Microgrids. Energies 2022, 15, 7009. [Google Scholar] [CrossRef]
- Slngh, H. Introduction to Game Theory and Evolutionary Games. In Adaptation and Evolution in Collective Systems; World Scientific Publishing: Singapore, 2006; pp. 31–64. [Google Scholar] [CrossRef]
- Gibbons, R. An Introduction to Applicable Game Theory. J. Econ. Perspect. 1997, 11, 127–149. [Google Scholar] [CrossRef]
- Osborne, M.J. An Introdcution to Game Theory. Psychiatr. Bull. 2000, 26, 476. [Google Scholar]
- Martinez-Ramos, J.L.; Marano-Marcolini, A.; Garcia-Lopez, F.P.; Almagro-Yravedra, F.; Onen, A.; Yoldas, Y.; Khiat, M.; Ghomri, L.; Fragale, N. Provision of ancillary services by a smart microgrid: An OPF approach. In Proceedings of the 2018 International Conference on Smart Energy Systems and Technologies (SEST), Seville, Spain, 10–12 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Churkin, A.; Bialek, J.; Pozo, D.; Sauma, E.; Korgin, N. Review of Cooperative Game Theory applications in power system expansion planning. Renew. Sustain. Energy Rev. 2021, 145, 111056. [Google Scholar] [CrossRef]
- Abapour, S.; Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Hagh, M.T. Game Theory Approaches for the Solution of Power System Problems: A Comprehensive Review. Arch. Comput. Methods Eng. 2020, 27, 81–103. [Google Scholar] [CrossRef]
- Zou, Y.; Xu, Y.; Feng, X.; Naayagi, R.T.; Soong, B.-H. Transactive Energy Systems in Active Distribution Networks: A Comprehensive Review. CSEE J. Power Energy Syst. 2022, 8, 1302–1317. [Google Scholar] [CrossRef]
- Saad, W.; Han, Z.; Poor, H.V.; Başar, T. Game-theoretic methods for the smart grid: An overview of microgrid systems, demand-side management, and smart grid communications. IEEE Signal Process. Mag. 2012, 29, 86–105. [Google Scholar] [CrossRef]
- Navon, A.; Ben Yosef, G.; Machlev, R.; Shapira, S.; Chowdhury, N.R.; Belikov, J.; Orda, A.; Levron, Y. Applications of game theory to design and operation of modern power systems: A comprehensive review. Energies 2020, 13, 3982. [Google Scholar] [CrossRef]
- Loni, A.; Parand, F.-A. A survey of game theory approach in smart grid with emphasis on cooperative games. In Proceedings of the 2017 IEEE International Conference on Smart Grid and Smart Cities (ICSGSC), Singapore, 23–26 July 2017; pp. 237–242. [Google Scholar] [CrossRef]
- Cheng, L.; Yu, T. Game-Theoretic Approaches Applied to Transactions in the Open and Ever-Growing Electricity Markets from the Perspective of Power Demand Response: An Overview. IEEE Access 2019, 7, 25727–25762. [Google Scholar] [CrossRef]
- Adil, M.; Mahmud, M.A.P.; Kouzani, A.Z.; Khoo, S.Y. Energy trading among electric vehicles based on Stackelberg approaches: A review. Sustain. Cities Soc. 2021, 75, 103199. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, D.; Jia, H.; Wang, W.; Yu, T.; Liu, J. Review of Game Theories Applied to Virtual Power Plants. In Proceedings of the 2021 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–8 November 2018; pp. 887–891. [Google Scholar] [CrossRef]
- Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1944. [Google Scholar]
- Game Theorists Who Have Received the Nobel Prize. Available online: https://gtl.csa.iisc.ac.in/gametheory/nobel.html (accessed on 1 June 2021).
- Bhuiyan, B.A. An Overview of Game Theory and Some Applications. Philos. Prog. 2018, 59, 111–128. [Google Scholar] [CrossRef]
- Fudenberg, D.; Jean, T. Game Theory; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Osborne, M.J.; Rubinstein, A. A Course in Game Theory; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Harsanyi, J.C. Games with Incomplete Information Played by “Bayesian” Players. Manag. Sci. 1967, 14, 159–182. [Google Scholar] [CrossRef]
- International Energy Agency. World Energy Outlook 2023; International Energy Agency: Paris, France, 2023. [Google Scholar]
- Seven, S.; Yoldas, Y.; Soran, A.; Alkan, G.Y.; Jung, J.; Ustun, T.S.; Onen, A. Energy Trading on a Peer-to-Peer Basis between Virtual Power Plants Using Decentralized Finance Instruments. Sustainability 2022, 14, 13286. [Google Scholar] [CrossRef]
- Falope, T.; Lao, L.; Hanak, D.; Huo, D. Hybrid energy system integration and management for solar energy: A review. Energy Convers. Manag. X 2024, 21, 100527. [Google Scholar] [CrossRef]
- Sati, S.E.; Abdelghany, M.B.; Hamad, B.; Al-Durra, A.; Zeineldin, H.; El-Fouly, T.H.; El-Saadany, E.F. Economic Power-Sharing and Stability Enhancement for Virtual Synchronous Generators in Islanded MG. IEEE Trans. Power Syst. 2024, 1–17. [Google Scholar] [CrossRef]
- Shah, M.I.A.; Wahid, A.; Barrett, E.; Mason, K. Multi-agent systems in Peer-to-Peer energy trading: A comprehensive survey. Eng. Appl. Artif. Intell. 2024, 132, 107847. [Google Scholar] [CrossRef]
- Yu, N.; Tesfatsion, L.; Liu, C.-C. Financial bilateral contract negotiation in wholesale electricity markets using Nash bargaining theory. IEEE Trans. Power Syst. 2012, 27, 251–267. [Google Scholar] [CrossRef]
- Fan, S.; Ai, Q.; Piao, L. Bargaining-based cooperative energy trading for distribution company and demand response. Appl. Energy 2018, 226, 469–482. [Google Scholar] [CrossRef]
- Su, W.; Huang, A.Q. A game theoretic framework for a next-generation retail electricity market with high penetration of distributed residential electricity suppliers. Appl. Energy 2014, 119, 341–350. [Google Scholar] [CrossRef]
- Wu, C.; Mohsenian-Rad, H.; Huang, J.; Wang, A.Y. Demand side management for Wind Power Integration in microgrid using dynamic potential game theory. In Proceedings of the 2011 IEEE GLOBECOM Workshops, Houston, TX, USA, 5–9 December 2011; pp. 1199–1204. [Google Scholar] [CrossRef]
- Chen, H.; Li, Y.; Louie, R.H.Y.; Vucetic, B. Autonomous demand side management based on energy consumption scheduling and instantaneous load billing: An aggregative game approach. IEEE Trans. Smart Grid 2014, 5, 1744–1754. [Google Scholar] [CrossRef]
- Marzband, M.; Javadi, M.; Domínguez-García, J.L.; Moghaddam, M.M. Non-cooperative game theory based energy management systems for energy district in the retail market considering DER uncertainties. IET Gener. Transm. Distrib. 2016, 10, 2999–3009. [Google Scholar] [CrossRef]
- Yang, P.; Tang, G.; Nehorai, A. A game-theoretic approach for optimal time-of-use electricity pricing. IEEE Trans. Power Syst. 2013, 28, 884–892. [Google Scholar] [CrossRef]
- Ma, K.; Wang, C.; Yang, J.; Hua, C.; Guan, X. Pricing mechanism with noncooperative game and revenue sharing contract in electricity market. IEEE Trans. Cybern. 2019, 49, 97–106. [Google Scholar] [CrossRef] [PubMed]
- Ladjici, A.; Tiguercha, A.; Boudour, M. Nash Equilibrium in a two-settlement electricity market using competitive coevolutionary algorithms. Int. J. Electr. Power Energy Syst. 2014, 57, 148–155. [Google Scholar] [CrossRef]
- Ghorbanian, M.; Dolatabadi, S.H.; Siano, P. Game Theory-Based Energy-Management Method Considering Autonomous Demand Response and Distributed Generation Interactions in Smart Distribution Systems. IEEE Syst. J. 2021, 15, 905–914. [Google Scholar] [CrossRef]
- Nguyen, H.K.; Bin Song, J.; Han, Z. Demand side management to reduce Peak-to-Average Ratio using game theory in smart grid. In Proceedings of the IEEE INFOCOM 2012—IEEE Conference on Computer Communications Workshops, Orlando, FL, USA, 25–30 March 2012; pp. 91–96. [Google Scholar] [CrossRef]
- Mohsenian-Rad, A.-H.; Wong, V.W.S.; Jatskevich, J.; Schober, R.; Leon-Garcia, A. Autonomous demand-side management based on game-theoretic energy consumption scheduling for the future smart grid. IEEE Trans. Smart Grid 2010, 1, 320–331. [Google Scholar] [CrossRef]
- Mishra, M.K.; Murari, K.; Parida, S.K. Demand-side management and its impact on utility and consumers through a game theoretic approach. Int. J. Electr. Power Energy Syst. 2022, 140, 107995. [Google Scholar] [CrossRef]
- Yaagoubi, N.; Mouftah, H.T. User-aware game theoretic approach for demand management. IEEE Trans. Smart Grid 2015, 6, 716–725. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Q.; Li, H.; McLellan, B.C.; Chen, S.; Li, Y.; Tian, Y. Study on the promotion impact of demand response on distributed PV penetration by using non-cooperative game theoretical analysis. Appl. Energy 2017, 185, 1869–1878. [Google Scholar] [CrossRef]
- Ma, T.; Wu, J.; Hao, L.; Yan, H.; Li, D. A real-time pricing scheme for energy management in integrated energy systems: A stackelberg game approach. Energies 2018, 11, 2858. [Google Scholar] [CrossRef]
- Soliman, H.M.; Leon-Garcia, A. Game-theoretic demand-side management with storage devices for the future smart grid. IEEE Trans. Smart Grid 2014, 5, 1475–1485. [Google Scholar] [CrossRef]
- Tushar, W.; Zhang, J.A.; Smith, D.B.; Poor, H.V.; Thiébaux, S. Prioritizing consumers in smart grid: A game theoretic approach. IEEE Trans. Smart Grid 2014, 5, 1429–1438. [Google Scholar] [CrossRef]
- El Rahi, G.; Etesami, S.R.; Saad, W.; Mandayam, N.B.; Poor, H.V. Managing Price Uncertainty in Prosumer-Centric Energy Trading: A Prospect-Theoretic Stackelberg Game Approach. IEEE Trans. Smart Grid 2019, 10, 702–713. [Google Scholar] [CrossRef]
- Zugno, M.; Morales, J.M.; Pinson, P.; Madsen, H. A bilevel model for electricity retailers’ participation in a demand response market environment. Energy Econ. 2013, 36, 182–197. [Google Scholar] [CrossRef]
- Yu, M.; Hong, S.H. Supply–demand balancing for power management in smart grid: A Stackelberg game approach. Appl. Energy 2016, 164, 702–710. [Google Scholar] [CrossRef]
- Doan, H.T.; Cho, J.; Kim, D. Peer-to-peer energy trading in smart grid through blockchain: A double auction-based game theoretic approach. IEEE Access 2021, 9, 49206–49218. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, T.; Wang, Y. Peer-to-Peer energy trading in a microgrid based on iterative double auction and blockchain. Sustain. Energy Grids Netw. 2021, 27, 100524. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhou, K.; Lu, X.; Yang, S. Electricity trading pricing among prosumers with game theory-based model in energy blockchain environment. Appl. Energy 2020, 271, 115239. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Q.; Zhou, N.; Chi, Y. A Novel electricity transaction mode of microgrids based on blockchain and continuous double auction. Energies 2017, 10, 1971. [Google Scholar] [CrossRef]
- Luo, L.; Feng, J.; Yu, H.; Sun, G. Blockchain-Enabled Two-Way Auction Mechanism for Electricity Trading in Internet of Electric Vehicles. IEEE Internet Things J. 2022, 9, 8105–8118. [Google Scholar] [CrossRef]
- Zhu, T.; Wei, Z.; Ning, B.; Niu, J.; Liu, J.; Li, S. Auction Based Distributed and Optimal Trading Mechanism in Electricity Markets under Blockchains. In Proceedings of the 2021 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Chengdu, China, 18–21 July 2021; pp. 39–43. [Google Scholar] [CrossRef]
- Chen, B.; Che, Y.; Zheng, Z.; Zhao, S. Multi-objective robust optimal bidding strategy for a data center operator based on bi-level optimization. Energy 2023, 269, 126761. [Google Scholar] [CrossRef]
- Cintuglu, M.H.; Martin, H.; Mohammed, O.A. Real-time implementation of multiagent-based game theory reverse auction model for microgrid market operation. IEEE Trans. Smart Grid 2015, 6, 1064–1072. [Google Scholar] [CrossRef]
- Hasankhani, A.; Hakimi, S.M. Stochastic energy management of smart microgrid with intermittent renewable energy resources in electricity market. Energy 2021, 219, 119668. [Google Scholar] [CrossRef]
- Park, S.; Lee, J.; Bae, S.; Hwang, G.; Choi, J.K. Contribution-Based Energy-Trading Mechanism in Microgrids for Future Smart Grid: A Game Theoretic Approach. IEEE Trans. Ind. Electron. 2016, 63, 4255–4265. [Google Scholar] [CrossRef]
- Yin, H.; Zhao, C.; Li, M.; Ma, C.; Chow, M.-Y. A Game Theory Approach to Energy Management of An Engine–Generator/Battery/Ultracapacitor Hybrid Energy System. IEEE Trans. Ind. Electron. 2016, 63, 4266–4277. [Google Scholar] [CrossRef]
- Liao, W.; Xiao, F.; Li, Y.; Peng, J. Comparative study on electricity transactions between multi-microgrid: A hybrid game theory-based peer-to-peer trading in heterogeneous building communities considering electric vehicles. Appl. Energy 2024, 367, 123459. [Google Scholar] [CrossRef]
- Alhasnawi, B.N.; Jasim, B.H.; Sedhom, B.E.; Guerrero, J.M. Consensus Algorithm-based Coalition Game Theory for Demand Management Scheme in Smart Microgrid. Sustain. Cities Soc. 2021, 74, 103248. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J. Incentivizing Energy Trading for Interconnected Microgrids. IEEE Trans. Smart Grid 2018, 9, 2647–2657. [Google Scholar] [CrossRef]
- Lo Prete, C.; Hobbs, B.F. A cooperative game theoretic analysis of incentives for microgrids in regulated electricity markets. Appl. Energy 2016, 169, 524–541. [Google Scholar] [CrossRef]
- Chakraborty, S.; Nakamura, S.; Okabe, T. Real-time energy exchange strategy of optimally cooperative microgrids for scale-flexible distribution system. Expert Syst. Appl. 2015, 42, 4643–4652. [Google Scholar] [CrossRef]
- Zhao, B.; Cao, X.; Duan, P. Cooperative operation of multiple low-carbon microgrids: An optimization study addressing gaming fraud and multiple uncertainties. Energy 2024, 297, 131257. [Google Scholar] [CrossRef]
- Naz, A.; Javaid, N.; Rasheed, M.B.; Haseeb, A.; Alhussein, M.; Aurangzeb, K. Game theoretical energy management with storage capacity optimization and Photo-Voltaic Cell generated power forecasting in Micro Grid. Sustainability 2019, 11, 2763. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, Z.; Li, Z.; Mi, Y. Energy Management for Hybrid AC/DC Distribution System with Microgrid Clusters Using Non-Cooperative Game Theory and Robust Optimization. IEEE Trans. Smart Grid 2020, 11, 1510–1525. [Google Scholar] [CrossRef]
- Dong, X.; Li, X.; Cheng, S. Energy management optimization of microgrid cluster based on multi-agent-system and hierarchical Stackelberg game theory. IEEE Access 2020, 8, 206183–206197. [Google Scholar] [CrossRef]
- Lee, J.; Guo, J.; Choi, J.K.; Zukerman, M. Distributed energy trading in microgrids: A game-theoretic model and its equilibrium analysis. IEEE Trans. Ind. Electron. 2015, 62, 3524–3533. [Google Scholar] [CrossRef]
- Ma, L.; Liu, N.; Zhang, J.; Tushar, W.; Yuen, C. Energy Management for Joint Operation of CHP and PV Prosumers Inside a Grid-Connected Microgrid: A Game Theoretic Approach. IEEE Trans. Ind. Informatics 2016, 12, 1930–1942. [Google Scholar] [CrossRef]
- Wu, Y.; Barati, M.; Lim, G.J. A Pool Strategy of Microgrid in Power Distribution Electricity Market. IEEE Trans. Power Syst. 2020, 35, 3–12. [Google Scholar] [CrossRef]
- Mediwaththe, C.P.; Stephens, E.R.; Smith, D.B.; Mahanti, A. A Dynamic Game for Electricity Load Management in Neighborhood Area Networks. IEEE Trans. Smart Grid 2016, 7, 1329–1336. [Google Scholar] [CrossRef]
- Erol, Ö.; Filik, Ü.B. A Stackelberg game-based dynamic pricing and robust optimization strategy for microgrid operations. Int. J. Electr. Power Energy Syst. 2024, 155, 109574. [Google Scholar] [CrossRef]
- Cai, W.; Kordabad, A.B.; Gros, S. Energy management in residential microgrid using model predictive control-based reinforcement learning and Shapley value. Eng. Appl. Artif. Intell. 2023, 119, 105793. [Google Scholar] [CrossRef]
- Liu, X.; Chen, X.; Jin, T.; Liu, Z.; Liu, Y.; Su, M.; Li, C.; Wu, Q. Network-Constrained Peer-to-Peer energy trading for multiple microgrids considering zoning pricing. Int. J. Electr. Power Energy Syst. 2023, 147, 108837. [Google Scholar] [CrossRef]
- Jani, A.; Jadid, S. Two-stage energy scheduling framework for multi-microgrid system in market environment. Appl. Energy 2023, 336, 120683. [Google Scholar] [CrossRef]
- Singh, A.; Sethi, B.K.; Kumar, A.; Singh, D.; Misra, R.K. Three-Level Hierarchical Management of Active Distribution System with Multimicrogrid. IEEE Syst. J. 2022, 17, 605–616. [Google Scholar] [CrossRef]
- Gougheri, S.S.; Dehghani, M.; Nikoofard, A.; Jahangir, H.; Golkar, M.A. Economic assessment of multi-operator virtual power plants in electricity market: A game theory-based approach. Sustain. Energy Technol. Assess. 2022, 53, 102733. [Google Scholar] [CrossRef]
- Da, T.; Zhang, D.; Ren, X.; Zhu, P.; Zhao, X.; Wu, N.; Liu, X. Non-Cooperative Game-based Coordination Control of Multiple Virtual Power Plants. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23–25 December 2021; pp. 1916–1921. [Google Scholar] [CrossRef]
- Tang, W.-J.; Yang, H.-T. Optimal Operation and Bidding Strategy of a Virtual Power Plant Integrated with Energy Storage Systems and Elasticity Demand Response. IEEE Access 2019, 7, 79798–79809. [Google Scholar] [CrossRef]
- Xu, Z.; Guo, Y.; Sun, H. Competitive Pricing Game of Virtual Power Plants: Models, Strategies, and Equilibria. IEEE Trans. Smart Grid 2022, 13, 4583–4595. [Google Scholar] [CrossRef]
- Zhang, T.; Qiu, W.; Zhang, Z.; Lin, Z.; Ding, Y.; Wang, Y.; Wang, L.; Yang, L. Optimal bidding strategy and profit allocation method for shared energy storage-assisted VPP in joint energy and regulation markets. Appl. Energy 2023, 329, 120158. [Google Scholar] [CrossRef]
- Park, S.-W.; Son, S.-Y. Interaction-based virtual power plant operation methodology for distribution system operator’s voltage management. Appl. Energy 2020, 271, 115222. [Google Scholar] [CrossRef]
- Chen, W.; Xiang, Y.; Liu, J. Optimal operation of virtual power plants with shared energy storage. IET Smart Grid 2022, 6, 147–157. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, M.; Ao, J.; Wang, Z.; Dong, H.; Zeng, M. Profit Allocation Strategy of Virtual Power Plant Based on Multi-Objective Optimization in Electricity Market. Sustainability 2022, 14, 6229. [Google Scholar] [CrossRef]
- Lu, Y.; Gao, G.; Yang, S.; Li, Y.; Wu, J. Research on Trading Strategy of Virtual Power Plant with Distributed Energy Aggregation Based on Cooperative Game. In Proceedings of the 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22–24 October 2021; pp. 2070–2075. [Google Scholar] [CrossRef]
- Fang, F.; Yu, S.; Liu, M. An improved Shapley value-based profit allocation method for CHP-VPP. Energy 2020, 213, 118805. [Google Scholar] [CrossRef]
- Rahmani-Dabbagh, S.; Sheikh-El-Eslami, M.K. A profit sharing scheme for distributed energy resources integrated into a virtual power plant. Appl. Energy 2016, 184, 313–328. [Google Scholar] [CrossRef]
- Ge, H.; Xia, Y.; Zou, W.; Hao, S.; Ma, G. Multi VPP bi-level optimization scheduling method based on complementary water-light-storage system. In Proceedings of the 2022 IEEE 3rd China International Youth Conference on Electrical Engineering (CIYCEE), Wuhan, China, 3–5 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, T.; Jiang, X.; Jin, Y.; Song, D.; Yang, M.; Zeng, Q. Peaking compensation mechanism for thermal units and virtual peaking plants union promoting curtailed wind power integration. Energies 2019, 12, 3299. [Google Scholar] [CrossRef]
- Chen, W.; Qiu, J.; Zhao, J.; Chai, Q.; Dong, Z.Y. Customized Rebate Pricing Mechanism for Virtual Power Plants Using a Hierarchical Game and Reinforcement Learning Approach. IEEE Trans. Smart Grid 2023, 14, 424–439. [Google Scholar] [CrossRef]
- Yin, S.; Ai, Q.; Li, J.; Li, Z.; Fan, S. Energy Pricing and Sharing Strategy Based on Hybrid Stochastic Robust Game Approach for a Virtual Energy Station with Energy Cells. IEEE Trans. Sustain. Energy 2021, 12, 772–784. [Google Scholar] [CrossRef]
- Chen, W.; Qiu, J.; Chai, Q. Customized Critical Peak Rebate Pricing Mechanism for Virtual Power Plants. IEEE Trans. Sustain. Energy 2021, 12, 2169–2183. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y.; Yan, R.; Abu-Siada, A.; Guo, Y.; Liu, J.; Huo, R. A Master-Slave Game Optimization Model for Electric Power Companies Considering Virtual Power Plant. IEEE Access 2022, 10, 21812–21820. [Google Scholar] [CrossRef]
- Yin, S.; Ai, Q.; Li, Z.; Zhang, Y.; Lu, T. Energy management for aggregate prosumers in a virtual power plant: A robust Stackelberg game approach. Int. J. Electr. Power Energy Syst. 2020, 117, 105605. [Google Scholar] [CrossRef]
- Bai, J.; Zhou, H.; Xu, Z.; Zhong, Y. Peer-to-Peer Energy Trading Method of Multi-Virtual Power Plants Based on Non-Cooperative Game. Energy Eng. J. Assoc. Energy Eng. 2023, 120, 1163–1183. [Google Scholar] [CrossRef]
- Li, X.; Li, C.; Liu, X.; Chen, G.; Dong, Z.Y. Two-stage Community Energy Trading under End-edge-cloud Orchestration. IEEE Internet Things J. 2022, 10, 1961–1972. [Google Scholar] [CrossRef]
- Li, J.; Zhu, Y.; Yong, M. Cooperative Operation and Profit Distribution of Virtual Power Plant. Electr. Power Components Syst. 2022, 51, 71–82. [Google Scholar] [CrossRef]
- Liu, X. Bi-layer game method for scheduling of virtual power plant with multiple regional integrated energy systems. Int. J. Electr. Power Energy Syst. 2023, 149, 109063. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Cao, Y.; Shahidehpour, M.; Jiang, L.; Long, Y.; Deng, Y.; Li, W. Optimal Operation Strategy for Multi-Energy Microgrid Participating in Auxiliary Service. IEEE Trans. Smart Grid 2023, 14, 3523–3534. [Google Scholar] [CrossRef]
- Nokandi, E.; Vahedipour-Dahraie, M.; Goldani, S.R.; Siano, P. A three-stage bi-level model for joint energy and reserve scheduling of VPP considering local intraday demand response exchange market. Sustain. Energy Grids Netw. 2023, 33, 100964. [Google Scholar] [CrossRef]
- Huang, H.; Li, Z.; Sampath, L.P.M.I.; Yang, J.; Nguyen, H.D.; Gooi, H.B.; Liang, R.; Gong, D. Blockchain-Enabled Carbon and Energy Trading for Network-Constrained Coal Mines with Uncertainties. IEEE Trans. Sustain. Energy 2023, 14, 1634–1647. [Google Scholar] [CrossRef]
- Rathor, S.; Saxena, D. Decentralized Energy Management System for LV Microgrid Using Stochastic Dynamic Programming with Game Theory Approach under Stochastic Environment. IEEE Trans. Ind. Appl. 2021, 57, 3990–4000. [Google Scholar] [CrossRef]
- Mediwaththe, C.P.; Smith, D.B. Game-theoretic electric vehicle charging management resilient to non-ideal user behavior. IEEE Trans. Intell. Transp. Syst. 2018, 19, 3486–3495. [Google Scholar] [CrossRef]
- Lee, W.; Xiang, L.; Member, S.; Schober, R.; Wong, V.W.S.; Member, S. Power Generators: A Game Theoretical Analysis. IEEE Trans. Smart Grid 2015, 6, 608–617. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Y. A Game-theoretic approach to optimal scheduling of parking-lot electric vehicle charging. IEEE Trans. Veh. Technol. 2016, 65, 4068–4078. [Google Scholar] [CrossRef]
- Kim, B.; Paik, M.; Kim, Y.; Ko, H.; Pack, S. Distributed Electric Vehicle Charging Mechanism: A Game-Theoretical Approach. IEEE Trans. Veh. Technol. 2022, 71, 8309–8317. [Google Scholar] [CrossRef]
- Muhindo, S.M.; Malhamé, R.P.; Joos, G. A Novel mean field game-based strategy for charging electric vehicles in solar powered parking lots. Energies 2021, 14, 8517. [Google Scholar] [CrossRef]
- Tan, J.; Wang, L. Real-time charging navigation of electric vehicles to fast charging stations: A hierarchical game approach. IEEE Trans. Smart Grid 2017, 8, 846–856. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, Q.; Huang, S.; Wang, L.; Shahidehpour, M.; Xue, Y. Optimal Day-Ahead Charging Scheduling of Electric Vehicles Through an Aggregative Game Model. IEEE Trans. Smart Grid 2018, 9, 5173–5184. [Google Scholar] [CrossRef]
- Saad, W.; Han, Z.; Poor, H.V.; Başar, T. A noncooperative game for double auction-based energy trading between PHEVs and distribution grids. In Proceedings of the 2011 IEEE Second International Conference on Smart Grid Communications (SmartGridComm), Brussels, Belgium, 17–20 October 2011; pp. 267–272. [Google Scholar] [CrossRef]
- Wang, Y.; Saad, W.; Han, Z.; Poor, H.V.; Başar, T. A game-theoretic approach to energy trading in the smart grid. IEEE Trans. Smart Grid 2014, 5, 1439–1450. [Google Scholar] [CrossRef]
- Aggarwal, S.; Kumar, N. PETS: P2P Energy Trading Scheduling Scheme for Electric Vehicles in Smart Grid Systems. IEEE Trans. Intell. Transp. Syst. 2022, 23, 14361–14374. [Google Scholar] [CrossRef]
- Zhao, T.; Li, Y.; Pan, X.; Wang, P.; Zhang, J. Real-Time Optimal Energy and Reserve Management of Electric Vehicle Fast Charging Station: Hierarchical Game Approach. IEEE Trans. Smart Grid 2018, 9, 5357–5370. [Google Scholar] [CrossRef]
- Ardakani, S.A.; Badri, A. Cooperative decision making of DERs in a joint energy and regulation market in presence of electric vehicles. Iran. J. Electr. Electron. Eng. 2017, 13, 374–384. [Google Scholar] [CrossRef]
- Hu, X.; Yang, Z.; Sun, J.; Zhang, Y. Optimal pricing strategy for electric vehicle battery swapping: Pay-per-swap or subscription? Transp. Res. Part E Logist. Transp. Rev. 2023, 171, 103030. [Google Scholar] [CrossRef]
- Mondal, A.; Misra, S.; Obaidat, M.S. Distributed home energy management system with storage in smart grid using game theory. IEEE Syst. J. 2017, 11, 1857–1866. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, S.; Huang, H.; Ranjan, R.; Zomaya, A.Y.; Wang, L. Game-Theoretic Market-Driven Smart Home Scheduling Considering Energy Balancing. IEEE Syst. J. 2017, 11, 910–921. [Google Scholar] [CrossRef]
- Khalid, A.; Javaid, N.; Mateen, A.; Rahim, M.H.; Ilahi, M. Smart homes coalition based on game theory. In Proceedings of the 2018 IEEE 32nd International Conference on Advanced Information Networking and Applications (AINA), Krakow, Poland, 16–18 May 2018; pp. 846–849. [Google Scholar] [CrossRef]
- Rahim, M.H.; Khalid, A.; Javaid, N.; Ashraf, M.; Aurangzeb, K.; Altamrah, A.S. Exploiting game theoretic based coordination among appliances in smart homes for efficient energy utilization. Energies 2018, 11, 1426. [Google Scholar] [CrossRef]
- Javadi, M.; Marzband, M.; Akorede, M.F.; Godina, R.; Al-Sumaiti, A.S.; Pouresmaeil, E. A centralized smart decision-making hierarchical interactive architecture for multiple home microgrids in retail electricity market. Energies 2018, 11, 3144. [Google Scholar] [CrossRef]
- Khalid, M.U.; Javaid, N.; Aslam, S. A game theoretic-based approach for appliances scheduling with real-time co-ordination in smart grid. In Proceedings of the 2018 5th International Multi-Topic ICT Conference (IMTIC), Jamshoro, Pakistan, 25–27 April 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Srinivasan, D.; Rajgarhia, S.; Radhakrishnan, B.M.; Sharma, A.; Khincha, H.P. Game-Theory based dynamic pricing strategies for demand side management in smart grids. Energy 2017, 126, 132–143. [Google Scholar] [CrossRef]
- Ryu, J.; Kim, J. A prospect-theoretic game approach to demand response market participation through energy sharing in energy storage systems under uncertainty. Energy Rep. 2023, 9, 1093–1103. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).