The Stabilization of a Nonlinear Permanent-Magnet- Synchronous-Generator-Based Wind Energy Conversion System via Coupling-Memory-Sampled Data Control with a Membership-Function-Dependent H∞ Approach
Abstract
1. Introduction
- We formulate the nonlinear PMSG-based WECS model as a collection of linear subsystems using Takagi–Sugeno (T-S) fuzzy logic with IF–THEN rules and membership functions.
- The membership function information is contained in the proposed performance index, with most commonly used performance is one example.
- Using a CMSDC approach which includes the SDC and MSDC, the stabilization issue of PMSG-based WECS is studied. The Bernoulli distribution order is involved in designing a CMSDC.
- The adequate requirements have been obtained as LMIs that guarantee the stability and stabilization of the expressed T–S fuzzy PMSG-based WECS.
1.1. Wind Turbine Aerodynamic Model
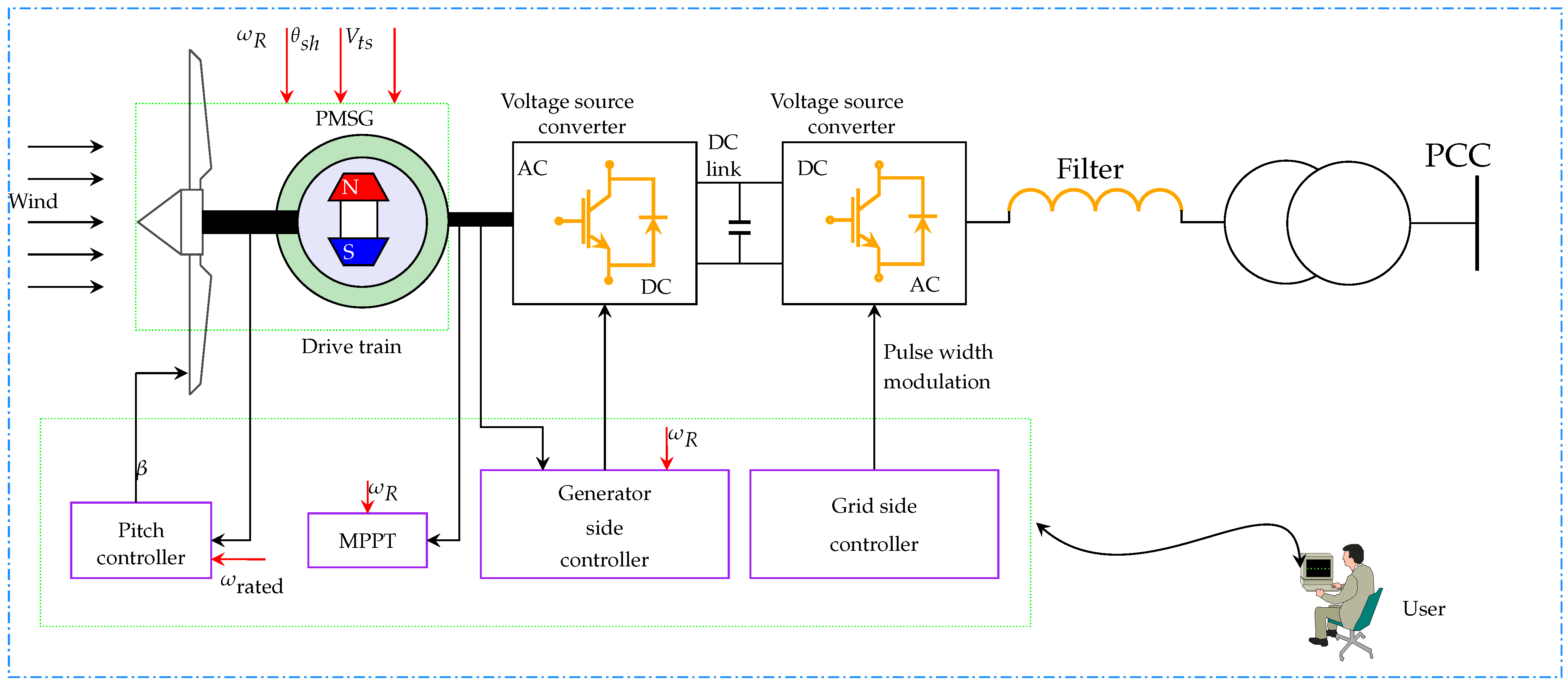
1.2. Modeling of PMSG-Based WECS
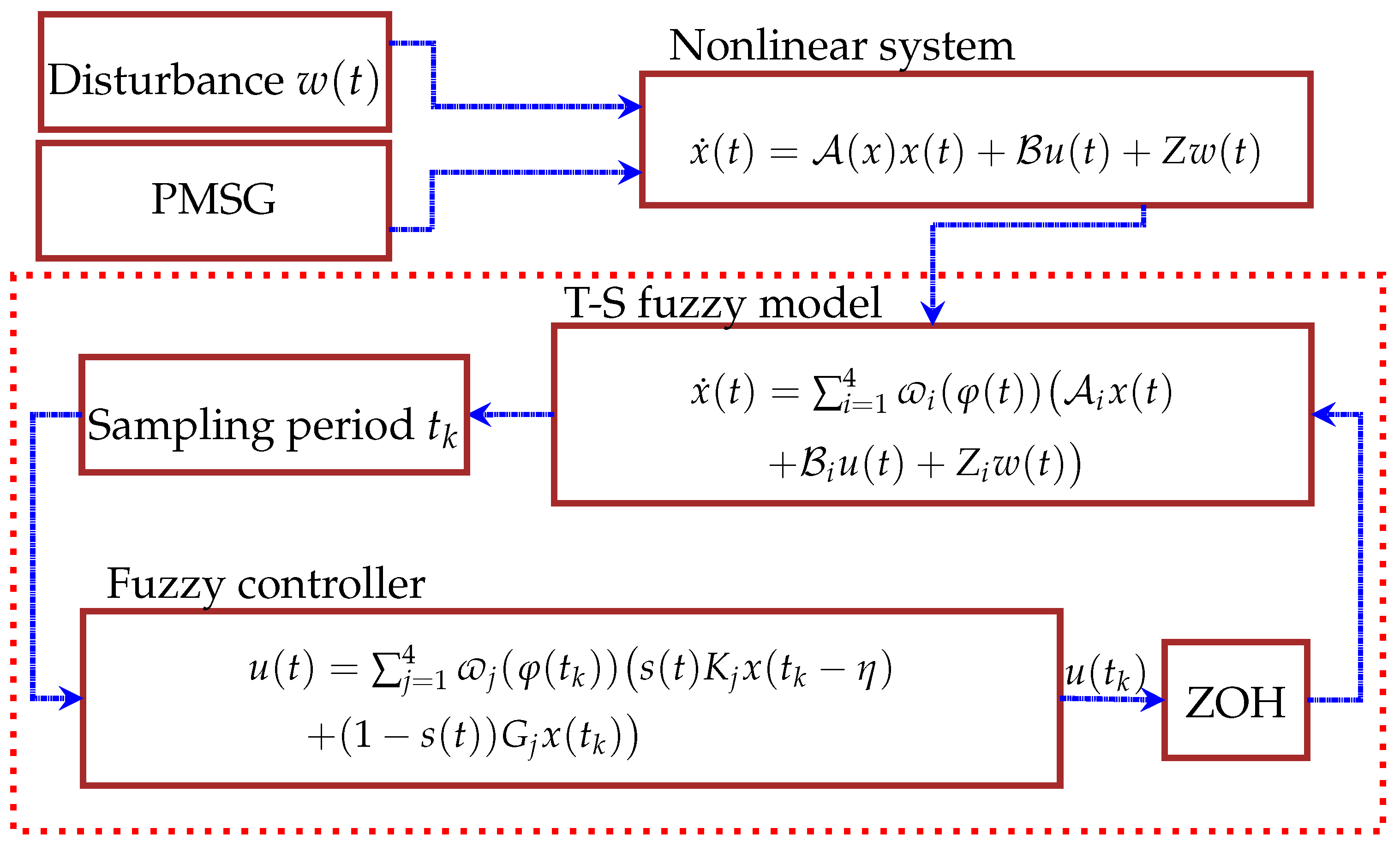
1.3. T-S Fuzzy Representation of the PMSG Model
1.4. CMSDC Design
2. Main Results
2.1. Stability of PMSG
2.2. Stabilization of PMSG
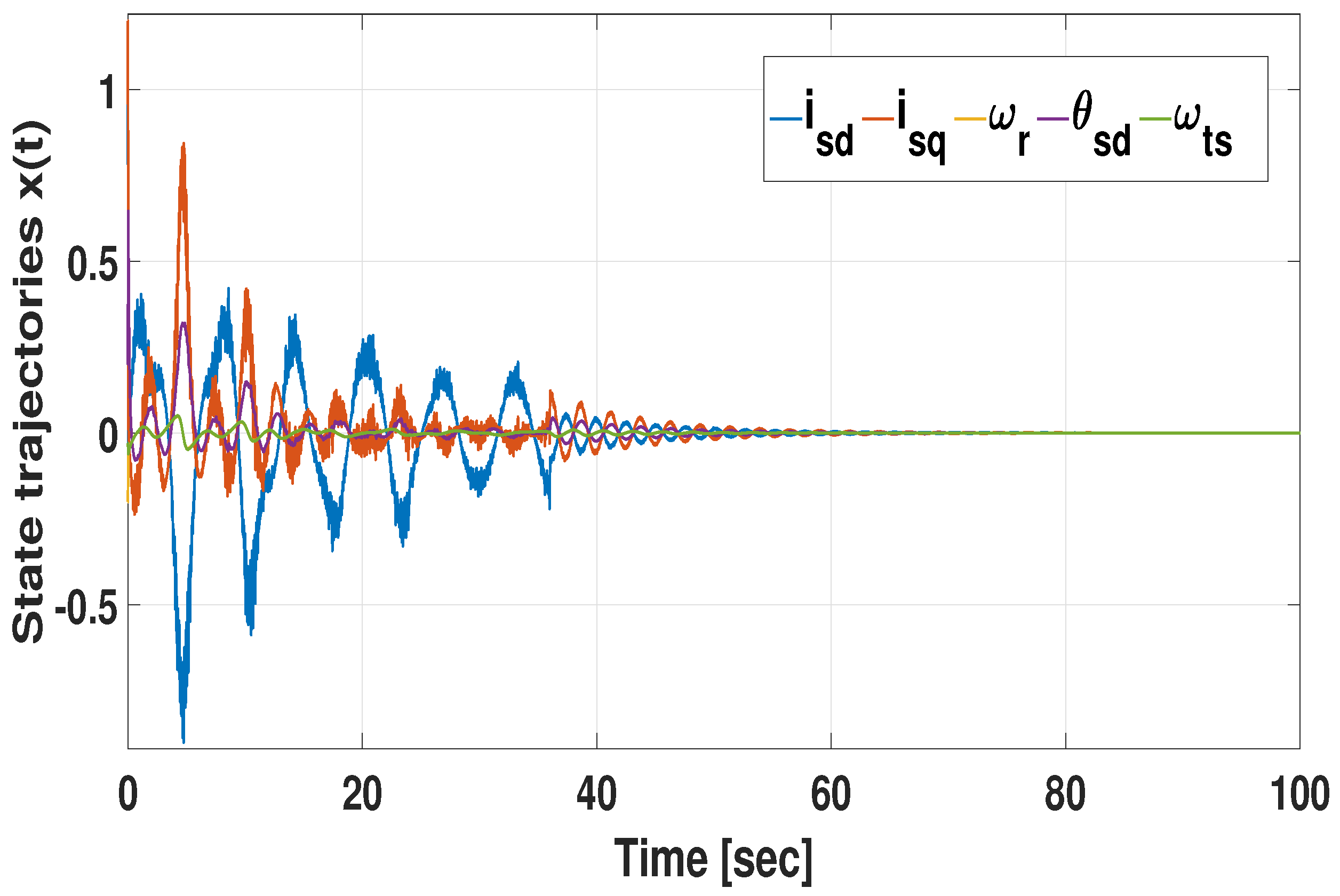
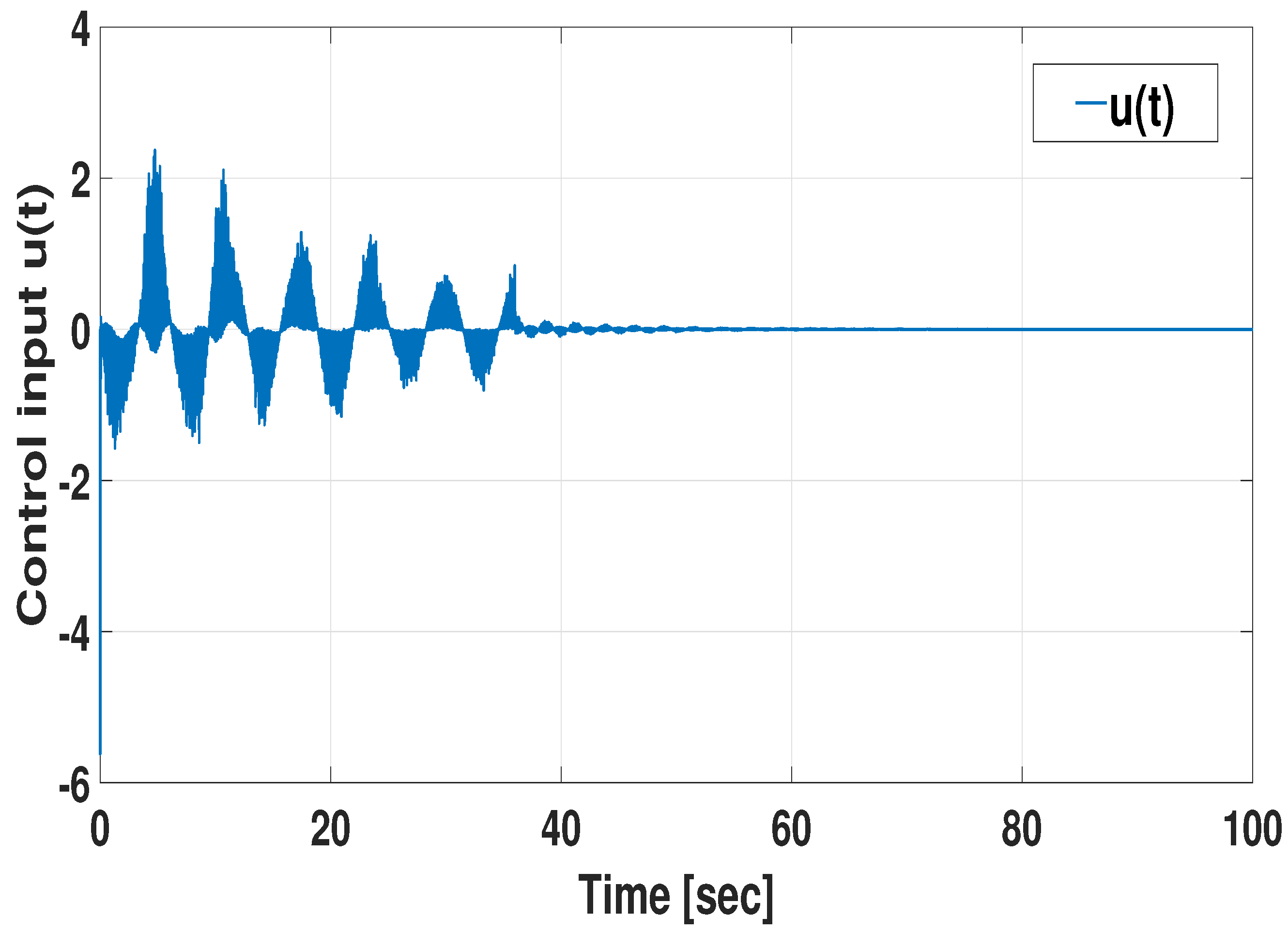
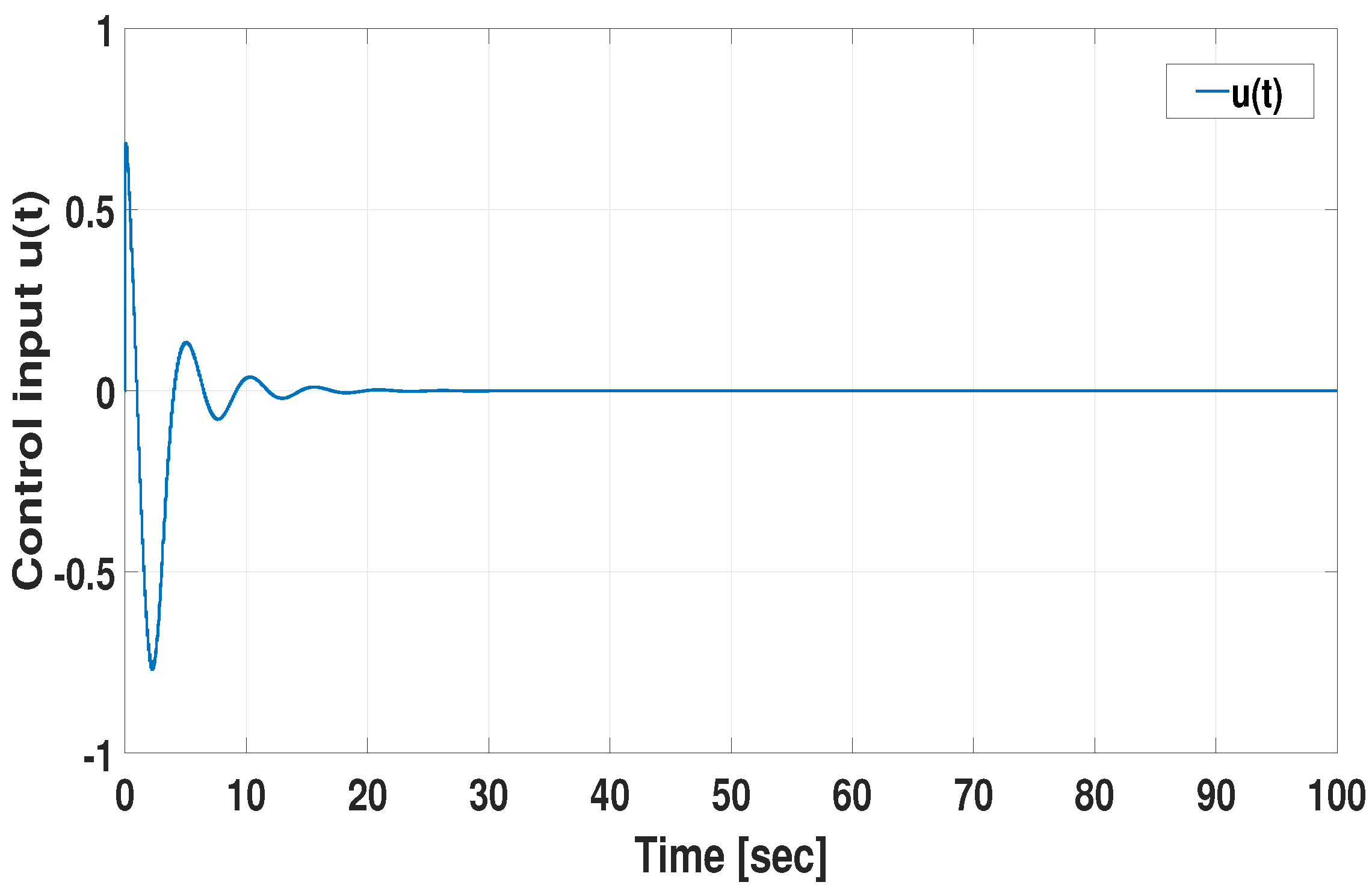
3. Numerical Validation
3.1. Design Example
| Algorithm 1 Calculating the control gain matrices and maximum allowable upper bound (MAUB) of . |
|
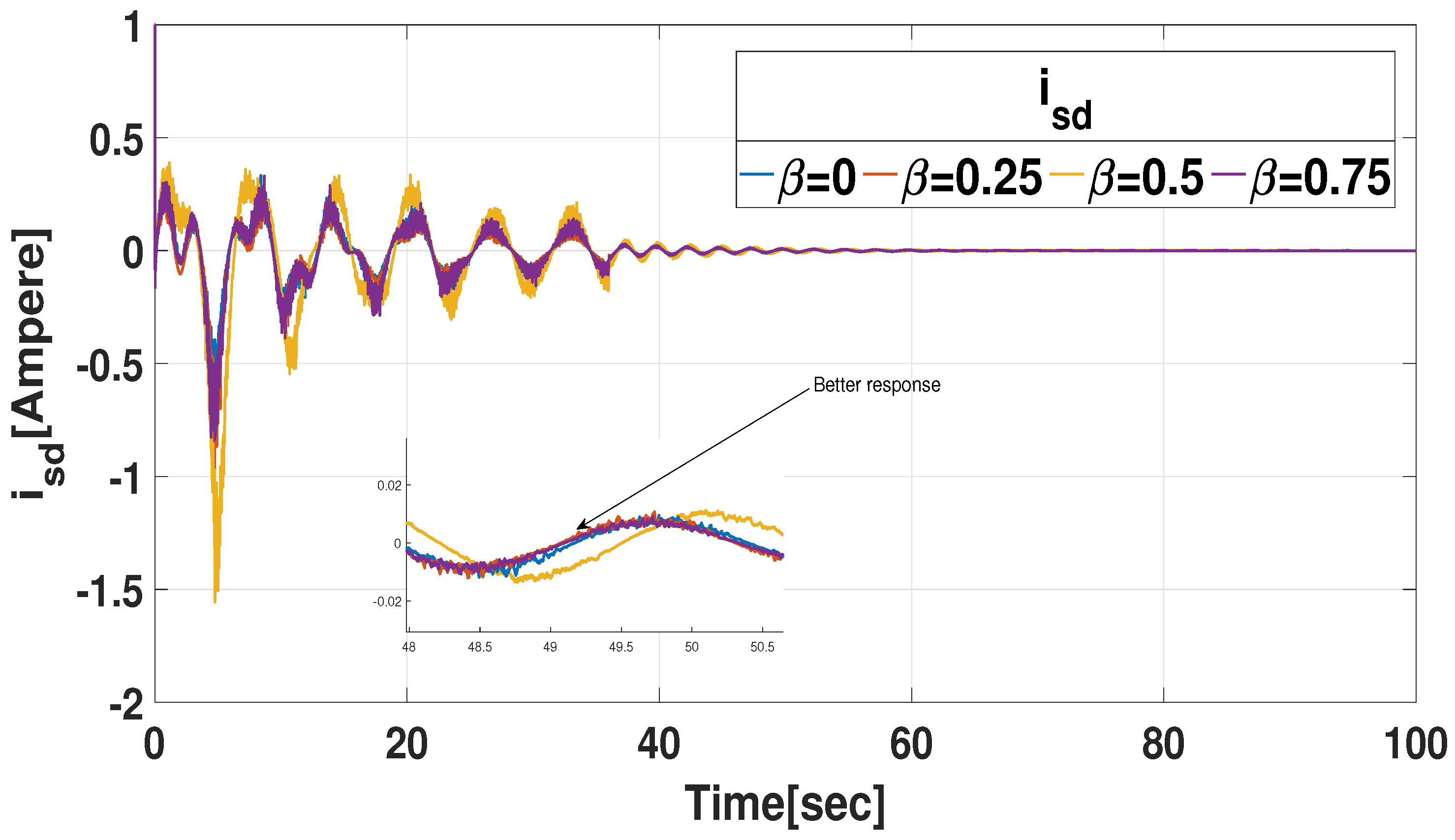
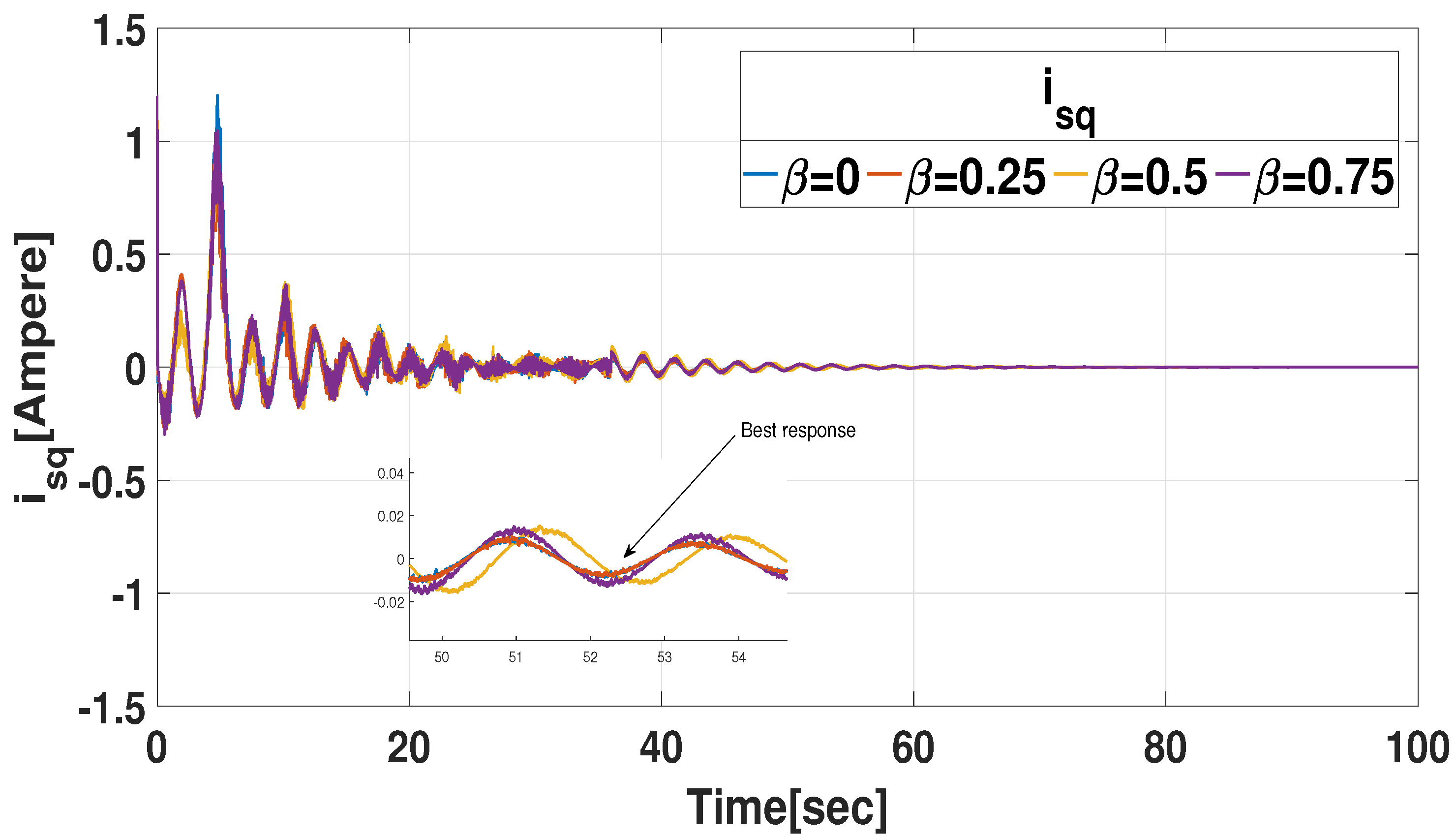
3.1.1. Simulation with Respect to Various Memory Parameter
3.1.2. Simulation Concerning Pitch Angles
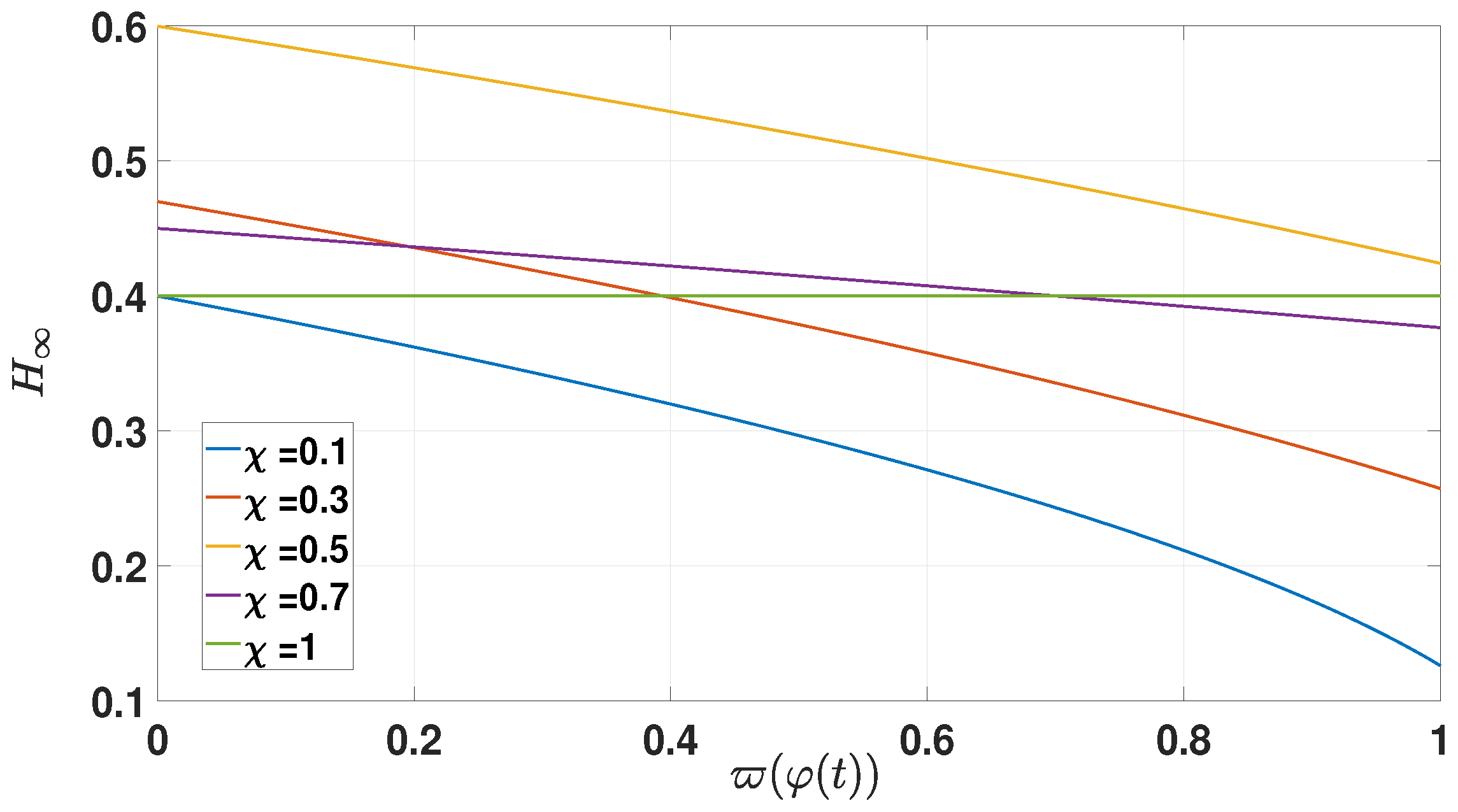
3.2. Evaluation of the MFD Performance Index
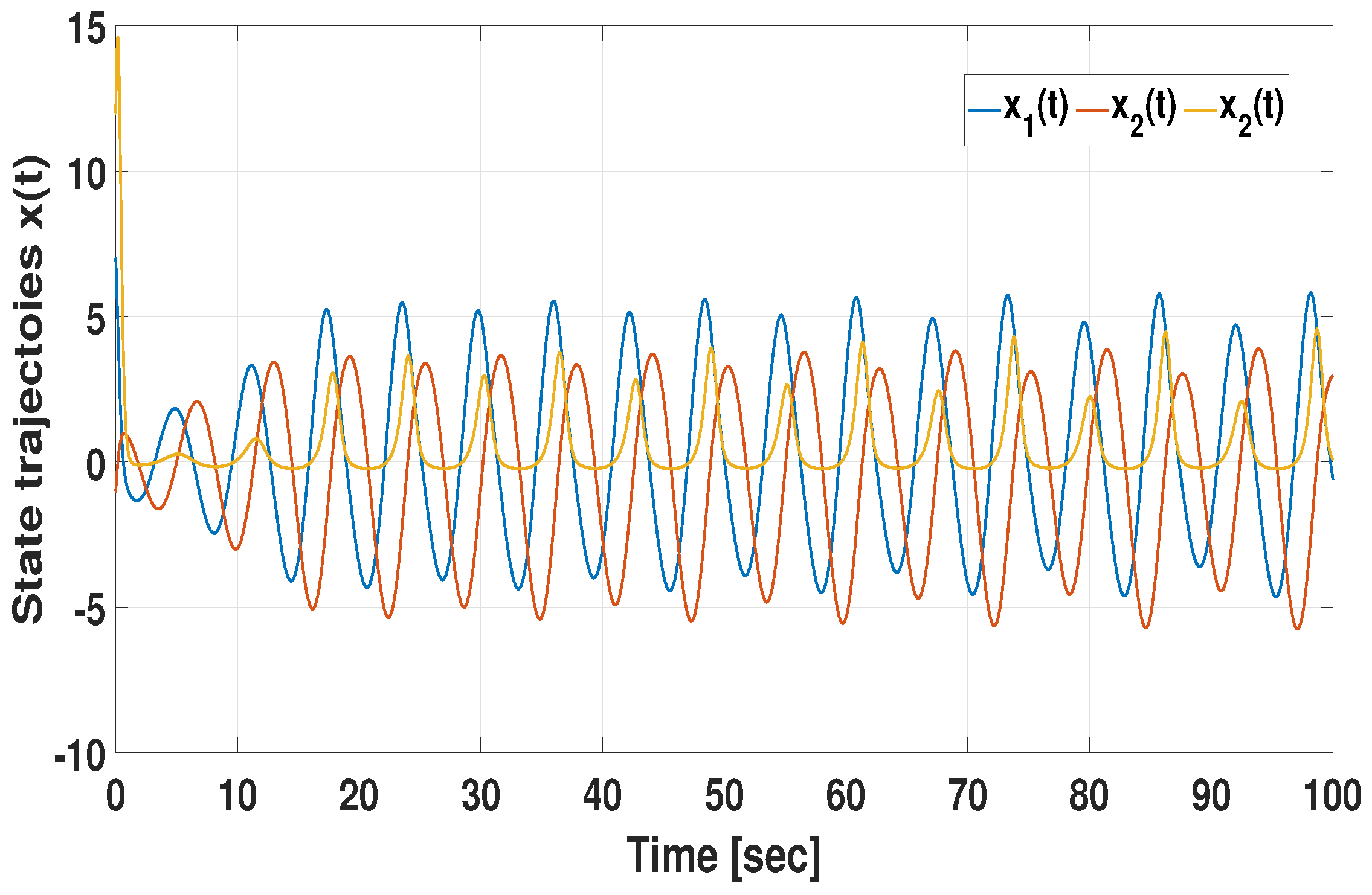
3.3. Comparative Example (Effectiveness of CMSDC Scheme)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gu, Y.; Huang, Y.; Wu, Q.; Li, C.; Zhao, H.; Zhan, Y. Isolation and protection of the motor-generator pair system for fault ride-through of renewable energy generation systems. IEEE Access 2020, 8, 13251–13258. [Google Scholar] [CrossRef]
- Mani, P.; Lee, J.H.; Kang, K.W.; Joo, Y.H. Digital controller design via LMIs for direct-driven surface mounted PMSG-based wind energy conversion system. IEEE Trans. Cybern. 2020, 50, 3056–3067. [Google Scholar] [CrossRef] [PubMed]
- Ghabraei, S.; Moradi, H.; Vossoughi, G. Investigation of the effect of the added mass fluctuation and lateral vibration absorbers on the vertical nonlinear vibrations of the offshore wind turbine. Nonlinear Dyn. 2021, 103, 1499–1515. [Google Scholar] [CrossRef]
- Mayilsamy, G.; Lee, S.R.; Joo, Y.H. An improved model predictive control of back-to-back three-level NPC converters with virtual space vectors for high power PMSG-based wind energy conversion systems. ISA Trans. 2023, 143, 503–524. [Google Scholar] [CrossRef] [PubMed]
- Apata, O.; Oyedokun, D.T.O. Novel reactive power compensation technique for fixed speed wind turbine generators. In Proceedings of the IEEE PES/IAS Power Africa, Cape Town, South Africa, 28–29 June 2018; pp. 628–633. [Google Scholar]
- Soufi, Y.; Kahla, S.; Bechouat, M. Particle swarm optimization based sliding mode control of variable speed wind energy conversion system. Int. J. Hydrogen Energy 2016, 41, 20956–20963. [Google Scholar] [CrossRef]
- Mousa, H.H.; Youssef, A.R.; Mohamed, E.E. Optimal power extraction control schemes for five-phase PMSG based wind generation systems. Eng. Sci. Technol. Int. J. 2020, 23, 144–155. [Google Scholar] [CrossRef]
- Marques, J.; Pinheiro, H.; Gründling, H.A.; Pinheiro, J.R.; Hey, H.L. A survey on variable-speed wind turbine system. Network 2003, 24, 26. [Google Scholar]
- Hou, L.; Wang, B.; Zhu, B. Energy extraction characteristic of the flapping wing type vertical axis turbine. IET Renew. Power Gener. 2020, 14, 2604–2611. [Google Scholar] [CrossRef]
- Bharathi, S.L.K.; Selvaperumal, S. MGWO-PI controller for enhanced power flow compensation using unified power quality conditioner in wind turbine squirrel cage induction generator. Microprocess. Microsystems 2020, 76, 103080. [Google Scholar] [CrossRef]
- Venkateswaran, R.; Joo, Y.H. Retarded sampled data control design for interconnected power system with DFIG-based wind farm: LMI approach. IEEE Trans. Cybern. 2022, 52, 5767–5777. [Google Scholar] [CrossRef]
- Mayilsamy, G.; Lee, S.R.; Joo, Y.H. Open-switch fault diagnosis in back-to-back NPC converters of PMSG-based WTS via zero range value of phase currents. IEEE Trans. Power Electron. 2023, 39, 4687–4703. [Google Scholar] [CrossRef]
- Jiao, N.; Liu, W.; Meng, T.; Sun, C.; Jiang, Y. Decoupling start control method for aircraft wound-rotor synchronous starter-generator based on main field current estimation. IET Electr. Power Appl. 2018, 13, 863–870. [Google Scholar] [CrossRef]
- Errami, Y.; Ouassaid, M.; Maaroufi, M. A performance comparison of a nonlinear and a linear control for grid connected PMSG wind energy conversion system. Int. J. Electr. Power Energy Syst. 2015, 68, 180–194. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, Y.; Qiao, W.; Qu, L. A discrete-time direct torque control for direct-drive PMSG-based wind energy conversion systems. IEEE Trans. Ind. Appl. 2015, 51, 3504–3514. [Google Scholar] [CrossRef]
- Kim, C.; Kim, W. Enhanced low-voltage ride-through coordinated control for PMSG wind turbines and energy storage systems considering pitch and inertia response. IEEE Access 2020, 8, 212557–212567. [Google Scholar] [CrossRef]
- Belkhier, Y.; Achour, A. Fuzzy passivity-based linear feedback current controller approach for PMSG-based tidal turbine. Ocean. Eng. 2020, 218, 108156. [Google Scholar] [CrossRef]
- K, S.; Joo, Y.H. Stabilization Criteria for T-S Fuzzy Systems With Multiplicative Sampled-Data Control Gain Uncertainties. IEEE Trans. Fuzzy Syst. 2021, 30, 4082–4092. [Google Scholar] [CrossRef]
- Chang, X.; Yang, G. Nonfragile H∞ filter design for T–S fuzzy systems in standard form. IEEE Trans. Ind. Electron. 2014, 61, 3448–3458. [Google Scholar] [CrossRef]
- Ge, C.; Park, J.H.; Hua, C.; Guan, X. Dissipativity analysis for T–S fuzzy system under memory sampled data control. IEEE Trans. Cybern. 2021, 51, 961–969. [Google Scholar] [CrossRef]
- Barkat, S.; Tlemcani, A.; Nouri, H. Noninteracting adaptive control of PMSM using interval type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 2011, 19, 925–936. [Google Scholar] [CrossRef]
- Pan, Y.; Du, P.; Xue, H.; Lam, H. Singularity-Free Fixed-Time Fuzzy Control for Robotic Systems with User-Defined Performance. IEEE Trans. Fuzzy Syst. 2020, 29, 2388–2398. [Google Scholar] [CrossRef]
- Hu, X.; Wu, L.; Hu, C.; Wang, Z.; Gao, H. Dynamic output feedback control of a flexible air-breathing hypersonic vehicle via T–S fuzzy approach. Int. J. Syst. Sci. 2014, 45, 1740–1756. [Google Scholar] [CrossRef]
- Jin, X.; Yu, Z.; Yin, G.; Wang, J. Improving vehicle handling stability based on combined AFS and DYC system via robust T-S fuzzy control. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2696–2707. [Google Scholar] [CrossRef]
- Santra, S.; Joby, M.; Sathishkumar, M.; Anthoni, S.M. LMI approach-based sampled data control for uncertain systems with actuator saturation: Application to multi-machine power system. Nonlinear Dyn. 2022, 107, 967–982. [Google Scholar] [CrossRef]
- Gandhi, V.; Joo, Y.H. T-S fuzzy sampled data control for nonlinear systems with actuator faults and its application to wind energy system. IEEE Trans. Fuzzy Syst. 2020, 30, 462–474. [Google Scholar] [CrossRef]
- Shanmugam, L.; Joo, Y.H. Stability and stabilization for T–S fuzzy large-scale interconnected power system with wind farm via sampled data control. IEEE Trans. Syst. Man, Cybern. Syst. 2021, 51, 2134–2144. [Google Scholar] [CrossRef]
- Sharmila, V.; Rakkiyappan, R.; Joo, Y.H. Fuzzy sampled data control for DFIG-based wind turbine with stochastic actuator failures. IEEE Trans. Syst. Man, Cybern. Syst. 2019, 51, 2199–2211. [Google Scholar] [CrossRef]
- Kim, H.S.; Park, J.B.; Joo, Y.H. Sampled-data control of fuzzy systems based on the intelligent digital redesign method via an improved fuzzy Lyapunov functional approach. IET Control Theory Appl. 2018, 12, 163–173. [Google Scholar] [CrossRef]
- Liu, Y.; Park, J.H.; Guo, B.; Shu, Y. Further results on stabilization of chaotic systems based on fuzzy memory sampled data control. IEEE Trans. Fuzzy Syst. 2018, 26, 1040–1045. [Google Scholar] [CrossRef]
- Mani, P.; Rajan, R.; Joo, Y.H. Design of Observer-Based Event-Triggered Fuzzy ISMC for T–S Fuzzy Model and its Application to PMSG. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2221–2231. [Google Scholar] [CrossRef]
- Dong, J.; Hou, Q.; Ren, M. Control Synthesis for Discrete-Time T–S Fuzzy Systems Based on membership-function-dependent H∞ Performance. IEEE Trans. Fuzzy Syst. 2020, 28, 3360–3366. [Google Scholar] [CrossRef]
- Ohtake, H.; Tanaka, K.; Wang, H.O. Fuzzy modeling via sector nonlinearity concept. Integr.-Comput. Aided Eng. 2003, 10, 333–341. [Google Scholar] [CrossRef]
- Ge, C.; Shi, Y.; Park, J.H.; Hua, C. Robust H∞ stabilization for TS fuzzy systems with time-varying delays and memory sampled data control. Appl. Math. Comput. 2019, 346, 500–512. [Google Scholar]
- Kwon, O.M.; Park, J.H.; Lee, S.M. An improved delay-dependent criterion for asymptotic stability of uncertain dynamic systems with time-varying delays. J. Optim. Theory Appl. 2010, 145, 343–353. [Google Scholar] [CrossRef]
- Shanmugam, L.; Joo, Y.H. Stabilization of Permanent Magnet Synchronous Generator-based Wind Turbine System via Fuzzy-based Sampled-data Control Approach. Inf. Sci. 2021, 559, 270–285. [Google Scholar] [CrossRef]
- Hwang, S.; Park, J.B.; Joo, Y.H. Disturbance observer-based integral fuzzy sliding-mode control and its application to wind turbine system. IET Control Theory Appl. 2019, 13, 1891–1900. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, J.; Su, C. T-S Fuzzy-Model-Based Robust H∞ Design for Networked Control Systems With Uncertainties. IEEE Trans. Ind. Inform. 2007, 3, 289–301. [Google Scholar] [CrossRef]
- Wang, Z.-P.; Wu, H.-N. On Fuzzy Sampled-Data Control of Chaotic Systems Via a Time-Dependent Lyapunov Functional Approach. IEEE Trans. Cybern. 2015, 45, 819–829. [Google Scholar] [CrossRef] [PubMed]
- Lam, H.K.; Narimani, M. Stability Analysis and Performance Design for Fuzzy-Model-Based Control System Under Imperfect Premise Matching. IEEE Trans. Fuzzy Syst. 2009, 17, 949–961. [Google Scholar] [CrossRef]
- Arino, C.; Sala, A. Extensions to “Stability Analysis of Fuzzy Control Systems Subject to Uncertain Grades of Membership”. IEEE Trans. Syst. Man Cybern. Part B (Cybernetics) 2008, 38, 558–563. [Google Scholar] [CrossRef]
- Zhang, R.; Zeng, D.; Park, J.H.; Liu, Y.; Zhong, S. A new approach to stabilization of chaotic systems with nonfragile fuzzy proportional retarded sampled data control. IEEE Trans. Cybern. 2019, 49, 3218–3229. [Google Scholar] [CrossRef] [PubMed]
- Hua, C.; Wu, S.; Guan, X. Stabilization of T-S fuzzy system with time delay under sampled data control using a new looped-functional. IEEE Trans. Fuzzy Syst. 2020, 28, 400–407. [Google Scholar] [CrossRef]
- Xia, Y.; Wang, J.; Meng, B.; Chen, X. Further results on fuzzy sampled data stabilization of chaotic nonlinear systems. Appl. Math. Comput. 2020, 379, 125225. [Google Scholar] [CrossRef]
- Yan, S.; Gu, Z.; Xie, X. Adaptive Critic Learning Control of Nonlinear Wind Turbine Systems via Integral Event-Triggered Scheme. IEEE Trans. Circuits Syst. II Express Briefs 2024, 1–5. [Google Scholar] [CrossRef]
- Yan, S.; Cai, Y. Integral-event-triggered H∞, Blood Glucose Control of Type 1 Diabetes via Artificial Pancreas. Int. J. Control Autom. Syst. 2024, 22, 1455–1460. [Google Scholar] [CrossRef]
- Subramaniam, S.; Lim, C.P.; Rajan, R.; Mani, P. Synchronization of Fractional Stochastic Neural Networks: An Event Triggered Control Approach. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 1113–1123. [Google Scholar] [CrossRef]



| Parameter | Description | Numerical Value |
|---|---|---|
| d and q axis mutual inductance | 0.05 mH | |
| Stator Resistance | 0.0027 | |
| Magnetic flux | 2 | |
| Number of poles | 2 | |
| Air density | 1.225 kg/m | |
| r | Blade Radius | 8 m |
| Wind speed | 12 m/s | |
| Pitch angle | 0.5 n/m.s | |
| Turbine Inertia | 4.29 kg/m | |
| Generator Inertia | 0.9 kg/m | |
| Base twist angle | 314 | |
| Viscous friction | 0.5 |
| Memory Parameter | Gain Matrix |
|---|---|
| = 0.01 | = [−0.8512 −0.7949 −0.3169 −0.1914 0.0028] = [−3.9244 −1.6717 0.2939 −0.0674 0.84076] |
| = 0.02 | = [−0.3755 −0.6057 −0.1964 −0.1619 0.0017] = [−3.7118 −1.5248 0.2043 −0.0574 0.8291] |
| = 0.05 | = [−0.1070 −0.4974 −0.0886 −0.2697 0.0007] = [−8.6157 −3.3236 0.0918 −0.1745 2.0742] |
| = 0.1 | = [−0.0148 −0.0904 −0.0142 −0.1131 0.0001] = [−2.7762 −1.5718 0.0605 −0.0277 0.6963] |
| Pitch | Power | Control Gains |
|---|---|---|
| = | 0.4151 | = [−0.5653−0.9582 −0.3037 −0.2654 0.0026] = [−7.4583 −2.5576 0.2975 −0.1639 1.7836] |
| = | 0.4098 | = [−0.5351 −0.8987 −0.2845 −0.2485 0.0025] = [−6.7517 −2.3801 0.2896 −0.1464 1.5872] |
| = | 0.4045 | = [−0.3755 −0.6057 −0.1964 −0.1619 0.0017] = [−3.7118 −1.5248 0.2043 −0.0574 0.8291] |
| = | 0.3992 | = [−0.5254 −0.8823 −0.2832 −0.2389 0.0026] = [−6.5118 −2.3396 0.2215 −0.1286 1.2341] |
| 0.1 | 0.3 | 0.5 | 0.7 | 1 | |
| 0.4 | 0.47 | 0.6 | 0.45 | 0.4 | |
| Performance Index | [0.3521,0.4] | [0.4269,0.47] | [0.4677,0.6] | [0.4328,0.45] | 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yesudhas, A.A.; Lee, S.R.; Jeong, J.H.; Govindasami, N.; Joo, Y.H. The Stabilization of a Nonlinear Permanent-Magnet- Synchronous-Generator-Based Wind Energy Conversion System via Coupling-Memory-Sampled Data Control with a Membership-Function-Dependent H∞ Approach. Energies 2024, 17, 3746. https://doi.org/10.3390/en17153746
Yesudhas AA, Lee SR, Jeong JH, Govindasami N, Joo YH. The Stabilization of a Nonlinear Permanent-Magnet- Synchronous-Generator-Based Wind Energy Conversion System via Coupling-Memory-Sampled Data Control with a Membership-Function-Dependent H∞ Approach. Energies. 2024; 17(15):3746. https://doi.org/10.3390/en17153746
Chicago/Turabian StyleYesudhas, Anto Anbarasu, Seong Ryong Lee, Jae Hoon Jeong, Narayanan Govindasami, and Young Hoon Joo. 2024. "The Stabilization of a Nonlinear Permanent-Magnet- Synchronous-Generator-Based Wind Energy Conversion System via Coupling-Memory-Sampled Data Control with a Membership-Function-Dependent H∞ Approach" Energies 17, no. 15: 3746. https://doi.org/10.3390/en17153746
APA StyleYesudhas, A. A., Lee, S. R., Jeong, J. H., Govindasami, N., & Joo, Y. H. (2024). The Stabilization of a Nonlinear Permanent-Magnet- Synchronous-Generator-Based Wind Energy Conversion System via Coupling-Memory-Sampled Data Control with a Membership-Function-Dependent H∞ Approach. Energies, 17(15), 3746. https://doi.org/10.3390/en17153746








