Abstract
This paper proposes a sophisticated, fault-tolerant, and centralized secondary controller that is designed for inverter-based, islanded microgrids. The proposed controller enhances system resilience to unexpected network partitions, which typically occur due to the tripping of protective devices under fault conditions. In typical radially configured MGs, a line fault can cause protective devices to isolate the faulted line, thereby splitting the MG into two electrically independent sub-microgrids (SMGs), while retaining the existing communication and control framework. In contrast to traditional centralized and distributed secondary controllers, which often fail to restore the frequency to the nominal value (50 Hz) in split SMGs, the proposed controller exhibits exceptional performance. Through simulation studies on 6-bus and 13-bus islanded MG setups, the controller has not only demonstrated its ability to swiftly restore the nominal frequency in both SMGs within a few seconds (specifically 5 s), but also to ensure fair power distribution among the distributed generators (DGs) supplying the SMGs. This rapid frequency stabilization underscores the controller’s effectiveness in maintaining stable frequency levels immediately following a fault. In contrast, the use of traditional centralized and consensus controllers typically results in a frequency deviation of about 3 Hz from the nominal value in one of the SMGs during the microgrid’s partition.
1. Introduction
Microgrids (MGs) are small-scale networks consisting of controllable components that can operate in grid-connected or islanded modes. During islanded operation, the control objectives of a MG are performed by a hierarchical control scheme consisting of three layers: primary, secondary, and tertiary [1]. The primary layer has the fastest reaction, and it is responsible for maintaining frequency stability and balance between power generation and consumption. The primary objective of the secondary layer is to eliminate the frequency and voltage deviations resulting from the primary layer. Secondary control strategies are categorized, depending on their communication infrastructure and control algorithms, into two major schemes: (a) centralized control [2,3], and (b) consensus (or distributed control) [4,5,6]. Last years, the traditional secondary control methods have been advanced via more sophisticated approaches that serve specific goals, as explained below. Finally, the tertiary control, with the slowest reaction time (in the order of several minutes or even hours), performs power and energy management, system optimization, economic dispatch [2], etc.
1.1. Review of Sophisticated Secondary Controllers
In the literature, there are several variations of the classical secondary control approaches mentioned above [2,3,4,5,6], each attempting to achieve a specific objective. These variants have more sophisticated characteristics. Specifically, Lu et al. [7] proposed a robust distributed controller, which effectively treats the disturbances and noises in the communication links between the DGs. The information exchange among DGs occurs in a discrete form, significantly reducing the communication requirements. Ahumada et al. [8] introduced a centralized predictive model and Smith predictor secondary controller, with improved performance under communication delays between the controller and DGs. Alhasnawi et al. [9] proposed a consensus-based secondary controller to mitigate frequency deviation, power-sharing imbalances between DGs, and voltage violations in islanded MGs. These were designed for use during fault conditions and before the action of protective devices. Shahab et al. [10] introduced a cooperative adaptive sliding mode consensus controller to explicitly address frequency and voltage restoration and provide stringent real power sharing in islanded MGs in the presence of actuation/propulsion faults and disturbances. Peng et al. [11] introduced a novel hierarchical control structure designed to suppress power oscillations in DGs under unbalanced conditions.
Zhou et al. [12] proposed a secondary control scheme for networked MGs to restore the communication among interconnected MGs in case the central controller or the master controllers of the interconnected MGs fail. Du et al. [13] introduced a distributed secondary controller for network MGs, also employing smart switches, aiming to reduce the transient voltages during MGs reconfiguration. Similar approaches to achieving the seamless reconfiguration of MGs were also proposed in [14,15], using single- and three-phase mathematical formulations, respectively.
Additionally, resilient and fault-tolerant control methods have been developed to mitigate the impact of false data injection (FDI) attacks on secondary controllers, thereby enhancing systems’ cyber resilience. Zhou et al. [16] analyzed the impacts of cyber-attacks on communication links, local controllers, and the master controller, as they can significantly disrupt the optimal operating conditions of MGs. In response, they propose a cyber-attack-resilient distributed control strategy that enables each participant detect and isolate corrupted links and controllers in timely and economical fashion. Their control strategy proves effective against time-varying attack signals and successive attacks, while preserving the operational merits of the MG. Researchers have also explored the consequences of denial-of-service (DoS) attacks on power systems and developed potential countermeasures. DoS attacks can severely disrupt operations by blocking data transmission among BESSs, compromising devices and jamming communication networks. Liu et al. [17] introduced a frequency control strategy for MGs that included an intrusion detector, enhancing the resilience of frequency control under DoS attacks. Ding et al. [18] addressed the challenge of implementing distributed resilient finite-time control for multiple heterogeneous battery energy storage systems within a microgrid, particularly for when they are subject to DoS attacks. To counteract these threats, they introduce a distributed secure control framework equipped with an acknowledgment (ACK)-based attack detection strategy and a communication recovery mechanism. This approach effectively mitigates the impact of DoS attacks by restoring the disrupted topology graphs to their original connected states. Wang et al. [19] developed a cyber-resilient control strategy for islanded MGs equipped with DGs and energy storage systems. This was designed to withstand hybrid cyber-attacks, including FDI and denial-of-service (DoS) attacks. This innovative approach leverages an adaptive method to mitigate the effects of bounded FDI attacks on secondary controllers while maintaining resilience to certain DoS attacks on communication links. The proposed control method effectively ensures frequency restoration, uniform power distribution, and an energy balance among DGs and ESSs, even during these complex hybrid attacks.
Despite their sophisticated contributions to several applications, none of the controllers in [7,8,9,10,11,12,13,14,15,16,17,18,19] handle the frequency problems occurring at the SMGs after unexpected network partitions in the event of faults. To the best of our knowledge, the consequences of unexpected MG partitions were studied for the first time by Rosero et al. in [20]. More specifically, Figure 6 of [20] clearly depicts the frequency and active power deviations in the split SMGs under unexpected electric and communication partitions of islanded MGs. A similar finding was confirmed by Zhou et al., in Figure 11 of [21]. However, these studies did not propose any measures with which to address these issues. Later, in [22], Rosero et al. developed a secondary controller that operates without droop control but seamlessly transitions to droop mode upon detecting a partition. Despite this advancement, as highlighted in Section V.D of [22], the controller effectively addresses only the instabilities caused by communication failures and does not solve the frequency deviations resulting from electrical partitions, which remains a critical unresolved challenge. Table 1 summarizes the main contributions of all cited references, including the proposed method.

Table 1.
Summary of literature advancements on secondary control.
1.2. Contribution of the Paper
This paper presents a robust centralized secondary controller designed to fill the gaps in existing research into secondary controllers, with respect to the frequency deviations caused in split SMGs after unexpected electrical MG partitions. In contrast to the existing literature, which presents frequency deviations in the range of several Hz, the proposed controller ensures rapid frequency restoration (in less than 5 s) and uniform power sharing among the DGs across all split SMGs. To clarify, with reference to the network depicted in Figure 1, after an electrical partition occurs, the proposed controller prompts DG 1 to restore the frequency of SMG 1 to 50 Hz, while doing the same for SMG 2 via the control of DG 2 and DG 3. Moreover, DG 2 and DG 3 maintain uniform power sharing throughout the electrical partition. Conversely, it is shown through simulation results that the traditional centralized and consensus-based secondary controllers present considerable frequency deviations from the nominal level in one of the two split SMGs. These features make the proposed controller an excellent tool for MGs experiencing frequent unexpected partitions, ensuring continuous and high-quality supply to all consumers. Beyond its primary benefit of maintaining the nominal frequency of all SMGs during unexpected electrical partitions, the proposed controller offers additional advantages, including:
- ✓
- Easy implementation to real microgrids. The controller is designed using straightforward digital equations, as detailed in Section 3, making it compatible with widely used commercial digital signal processors (DSPs). This compatibility ensures that the proposed control algorithm can be easily adapted and utilized within microgrid central controllers (MGCCs) in centralized infrastructure. Moreover, the simplicity of its design facilitates quick deployment and integration, minimizing potential disruptions and the need for extensive training or system modifications.
- ✓
- Low communication requirements. The proposed controller does not require any communication with the protective devices of the MG, thus reducing the complexity of the overall installation. The only communication infrastructure required is between the MGCC and the DGs of the microgrid.
- ✓
- Topology-independent implementation. The controller is designed to deliver consistent performance without the need for recalibration following network reconfigurations or load changes. It is initially set up based on the number of DGs and maintains its calibration permanently. This one-time setup ensures that the controller can seamlessly adapt to varying operational conditions without additional intervention, simplifying the management of the system.
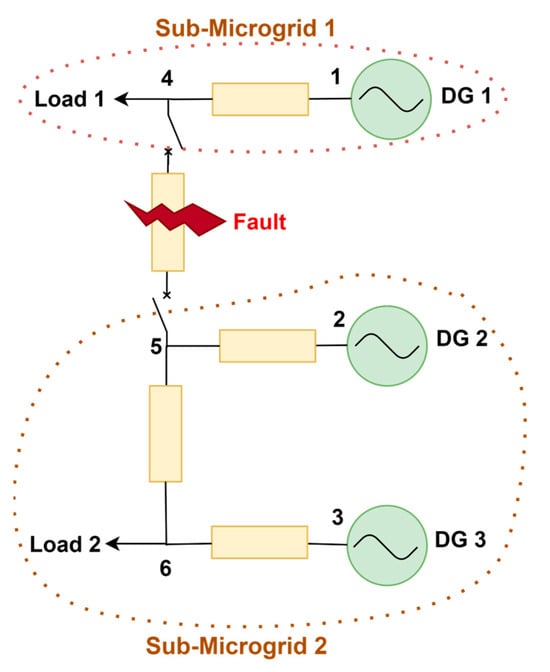
Figure 1.
Example 6—bus islanded MG with 3 DGs and 2 loads.
2. Review of Traditional Secondary Controllers
Practically, the scope of secondary control is to optimally calculate the terms and of the droop equations of the primary layer, given in (1)–(2), in order to restore the frequency and voltage of an MG.
Note that, in the equations above, , , , , , , and are the angular frequency measured by DG i, reference angular frequency of DG i, frequency droop gain, positive sequence active power output, positive sequence voltage magnitude, reference voltage, voltage droop gain, and positive sequence reactive power output of DG i, respectively.
Each secondary control scheme employs a different methodology to compute and , as explained below. To facilitate explanation, let us first assume utilization of the islanded MG of Figure 1. The communication structure of the two major schemes is shown in Figure 2.
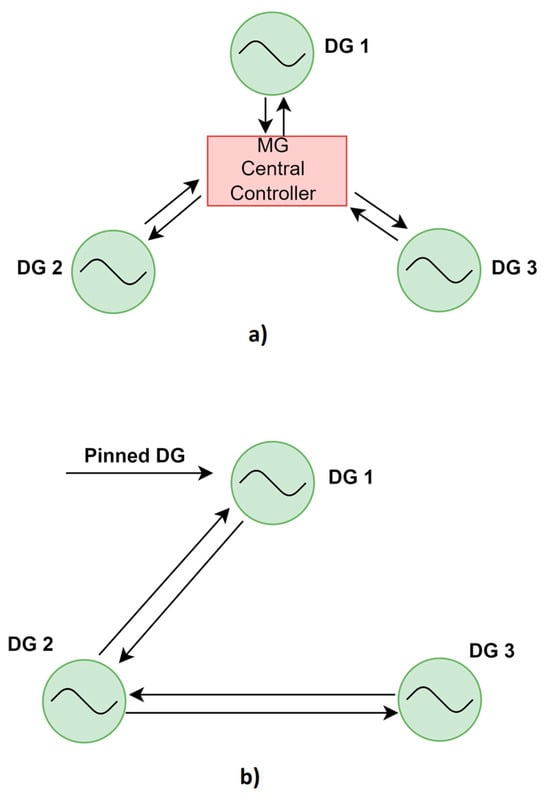
Figure 2.
Communication graphs of the 6-bus MG. From top to bottom (a): centralized control; (b): consensus (distributed) control.
The communication structure of a centralized controller, shown in Figure 2a [2,3], is based on a kind of one-to-all communication, where a microgrid central controller (MGCC) measures the voltage and frequency at a specific point of the network and restores them using simple PI controllers. The terms and , shown in (1) and (2), are calculated from the MGCC as follows ∀ i ∈ {1, 2, 3}:
where , and are the proportional and integral gains of the PI controllers, and are the angular frequency and voltage measured by the MGCC, and and are the desirable frequency and voltage values. It is shown in (3)–(4) that all DGs receive the same values from the MGCC, and thus they shift their droop equations equally, thus preserving the desired power sharing.
In the consensus control, DGs only communicate with some neighboring DGs [4,5], yielding a type of neighbor-to-neighbor communication. In consensus algorithms, the frequency controller performs, simultaneously, frequency restoration and active power sharing between the DGs, while the voltage controller executes voltage restoration or reactive power sharing. The mathematical expression of the frequency controller is quoted in (5) ∀ i ∈ {1, 2, 3}, where determines the access of DG i to the desired frequency () and depends on the connectivity between DG i and j. If DG i communicates directly with DG j, then ; otherwise, it is zero.
The mathematical formulation of the voltage controller is expressed by (6) ∀ i ∈ {1,2,3}, where the parameters and vary depending on whether the controller performs voltage regulation (, ) or optimal reactive power sharing (, ). For more details, please refer to ([5], Section IV.C).
Despite the benefits that each of the aforementioned controllers possesses, they all have an important drawback: they lose their ability to restore the frequency in split SMGs under unexpected electrical partitioning. For example, let us assume that a fault happens in line 4–5 of the MG of Figure 1. Τhe protective devices of the line are likely to switch the line off, thus unexpectedly forming two sub-microgrids (SMGs). The first consists of DG 1 and load 1, while the second includes DG 2, DG 3, and load 2. Since the controllers of either scheme cannot see the tripping of the line 4–5, they will continue to apply the same to all DGs, as dictated by (3), (5), even though the partitioning of the MG results in the newly formed SMGs supporting different load levels. This discrepancy leads to frequency deviations in one of the two SMGs.
3. Proposed Centralized Secondary Controller
For the sake of clarity, the proposed controller will be explained using the simple network in Figure 1; however, it is scalable and can be extended to larger MGs as well. Its communication graph is quoted in Figure 3, depicting all transmitting signals for the frequency restoration from and to the MGCC. Each DG i ∈ {1, 2, 3} operates in droop control (primary layer), represented by (1)–(2). The MGCC receives the frequency signals from DGs and updates the droop equations via output signals .
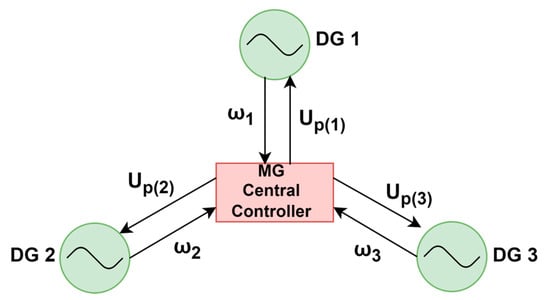
Figure 3.
Communication graph of the proposed centralized secondary controller.
The block diagram of the proposed controller (given in Z domain) is depicted in Figure 4. The controller is installed within the MGCC and has a centralized structure. The (namely, the secondary signal of DG 1) is computed in a similar manner to that employed the conventional centralized control, as shown in (7):
where denotes the at the present time instant t, at the previous time instant t − 1, is the desirable value of angular frequency (e.g., 2⋅π⋅50 rads/s), and is the gain. Equation (7) represents a typical digital PI controller.
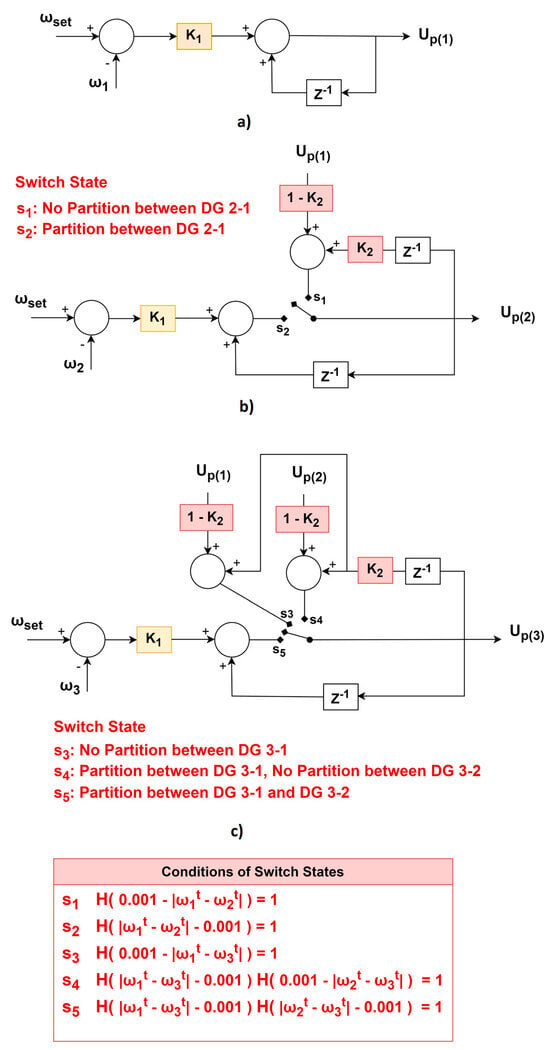
Figure 4.
Block diagram of proposed secondary controller. From top to bottom: calculation of (a) (b) , and (c) . State of switches (s1–s5) is determined based on frequencies of DGs, according to conditions of table.
The contribution of our paper lies in the novel approach to the calculation of and (namely, the secondary signal of DG 2 and 3). Specifically, and are obtained in the manner shown in (8) and (9), respectively.
It is noted that in (8)–(9) the function H denotes the Heaviside function, as follows,
while and are algorithm gains. The term , as applied in Equations (8)−(9), signifies a criterion for identifying a potential electrical partition between DG i and j. Specifically, the condition holds if DG i and j are electrically isolated. The threshold value of 0.001 is chosen arbitrarily. Practically, the detection of unexpected electrical partitions is realized by comparing the frequencies of DGs within the Heaviside functions H of Equations (8) and (9). If the difference between the frequencies of DG i and j surpasses a certain threshold (arbitrarily set to be equal to 0.001 in this paper), it means that the respective DGs are electrically split, potentially due to a fault. This occurs as the frequencies of the split MGs inherently deviate from each other due to their different load conditions. Subsequently, the proposed algorithm modifies the signals accordingly to restore the frequency of all sub-microgrids, while maintaining equal power sharing between the DGs within each sub-microgrids.
For example, with reference to Figure 1, due to the MG partition, , indicating the presence of an electrical partition between DG 2 and 1, since . Consequently, the control strategy for DG 2 transitions to yielding a decentralized (local) integral controller for this DG. At the same time, and indicate that there is an electric partition between DG 3 and 1 and no partition between DG 3 and 2, respectively. As a result, according to Equation (9), , resulting in DG 3 following the secondary signal of DG 2.
The block diagram illustrating the secondary control signals ∀ i ∈ {1, 2, 3} is quoted in Figure 4. The positions of these switches are determined by the frequencies of the DGs, as outlined in the conditions listed in the table at the bottom of Figure 4. Mathematically, these conditions are represented using Heaviside functions and are comprehensively integrated into Equations (8) and (9), as explained above. An interpretation of Figure 4 is quoted in Figure 5 in the form of a flowchart.
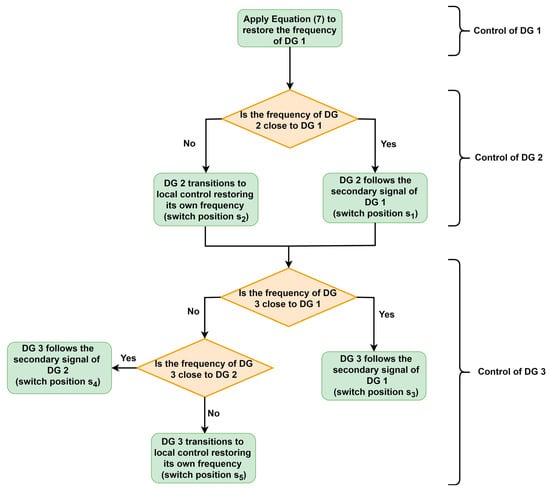
Figure 5.
Flowchart of the proposed secondary controller for the reference network.
4. Simulation Results
To validate the proposed controller, simulations were performed in MATLAB/Simulink 2019, using a 6-bus and 13-bus network. Moreover, a comparison against the state-of-the-art secondary controllers [2,3,4,5,6] is carried out through further simulations to highlight the superior characteristics of the proposed controller in restoring the frequency of all split SMGs under partitions.
4.1. Low-Voltage 6-Bus Network
The structure of the 6-bus network is illustrated in Figure 1, with the network parameters listed in Table 2. The following two Simulink test cases were studied:
- ▪
- Test 1: Load 2 is doubled at t = 20 s and returned to its initial value at t = 60 s, with no microgrid (MG) partition occurring.
- ▪
- Test 2: A fault is introduced at t = 20 s in the line between buses 4 and 5. The protective devices respond to clear the fault, resulting in the temporary formation of two sub-microgrids [23], as depicted in Figure 1. The fault is resolved at the t = 40 s, and the line is reconnected.

Table 2.
Parameters of the 6-bus network.
Table 2.
Parameters of the 6-bus network.
| Resistance of the lines | 0.25 Ω/km |
| Self-reactance of the lines | 0.6 mH/km [2] |
| Mutual-reactance of the lines | 0.1 mH/km [2] |
| Line lengths | 0.1 km [2] |
| Lines’ thermal limits | Neglected [2] |
| Loads (modeled as constant impedances) | Load 1: R//L = 0.1 Ω//0.001 H Load 2: R//L = 0.2 Ω//0.002 H |
| (i = 1, 3) | 1 × 10−6 (Hz/W) |
| (i = 2) | 0.5 × 10−6 (Hz/W) |
| (i = 1, 2, 3) | 2 × 10−4 (V/VAR) |
| Primary droop (i = 1, 2, 3) | 270 V |
| Primary droop (i = 1, 2, 3) | 50 Hz |
| Ground resistances | 25 Ω [2] |
The results of Test 1 are presented in Figure 6, Figure 7 and Figure 8. Specifically, Figure 6 displays the frequencies of the DGs using the proposed controller, demonstrating its capability to quickly restore frequency after each load change. Figure 7 illustrates the output signals of the controller, as calculated by Equations (7)–(9), which dynamically adapt to aid in frequency restoration. All DGs have the same secondary control signals. Finally, Figure 8 shows the output powers of the DGs. According to Table 2, the droop gain · for i= {1, 3}; thus, DG 2 contributes twice the power compared to DG 1 and DG 3.
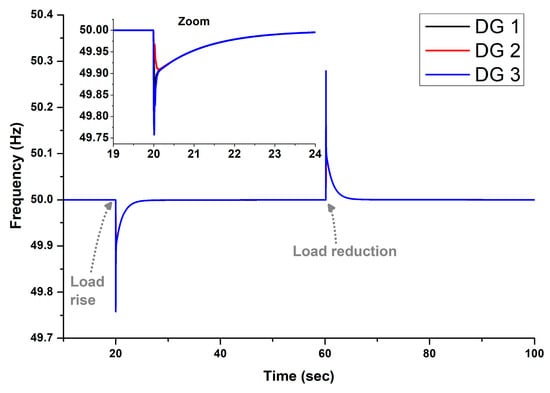
Figure 6.
DG frequencies for Test 1, determined using the proposed controller.
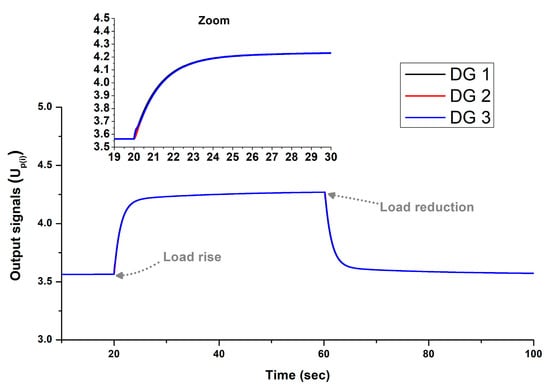
Figure 7.
Output signals of the proposed controller for Test 1.
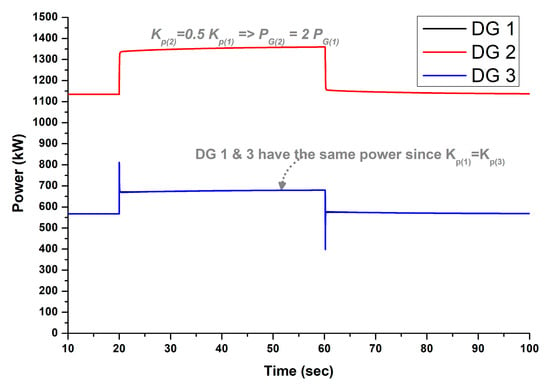
Figure 8.
Power of DGs for Test 1 using the proposed controller.
The results of Test 2 are quoted in Figure 9, Figure 10 and Figure 11. As shown in Figure 9, despite the partition of the MG into two sub-microgrids at t = 20 s, the frequency is restored in both SMGs in around 5 s. After the re-unification, the frequency is again restored to 50 Hz. The output signals of the controller for the second test are quoted in Figure 10. Due to the partition of the MG, the secondary control signal of DG 1 differs from those of DG 2 and 3. The reason for this is that, during the partition, DG 1 solely undertakes Load 1, forcing its frequency to be reduced. Consequently, a stronger secondary signal is required to restore the frequency in SMG 1. Lastly, Figure 11 displays the output powers of the DGs during the second test. Notably, DG 1 outputs the highest power during the partition as it solely supplies the entire Load 1. Following reunification, DG 2 exhibits the highest power output due to its lower droop gain
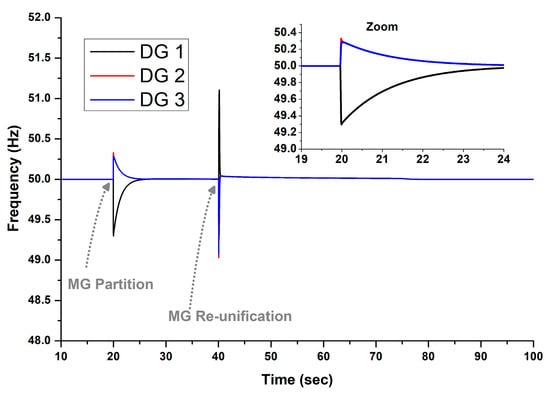
Figure 9.
DG frequencies for Test 2, determined using the proposed controller.
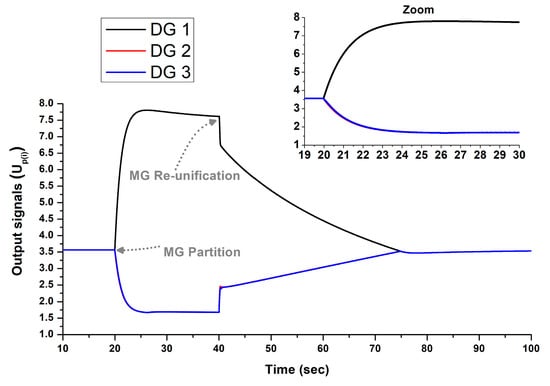
Figure 10.
Output signals of the proposed controller for Test 2.
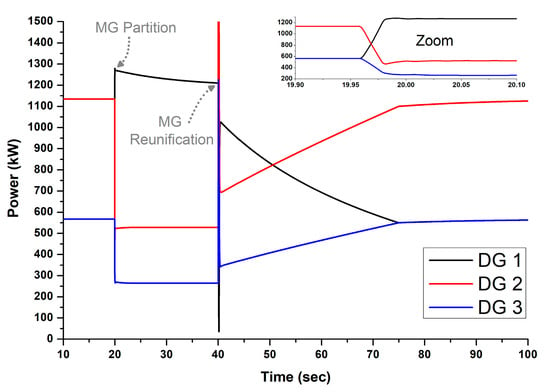
Figure 11.
Power of DGs for Test 2, determined using the proposed controller.
4.2. Medium-Voltage 13-nus Network
Test 3 employs the 12-bus medium-voltage MG shown in Figure 12, employing the network parameters detailed in Table 3. All DGs are assumed to be of the same size, having equal gains. A fault is presumed to occur between buses 4 and 9 at t = 20 s, leading to the activation of protective devices and splitting the MG into two sub-microgrids (SMGs): DGs 1, 2, and 3 and DGs 4 and 5, respectively. The fault is cleared at t = 40 s, resulting in the reunification of the MG. In this test, the performance of the proposed secondary controller is evaluated against the typical centralized controller [2,3], as described in Equations (3) and (4), and the consensus controller [4,5], specified in Equations (5) and (6).
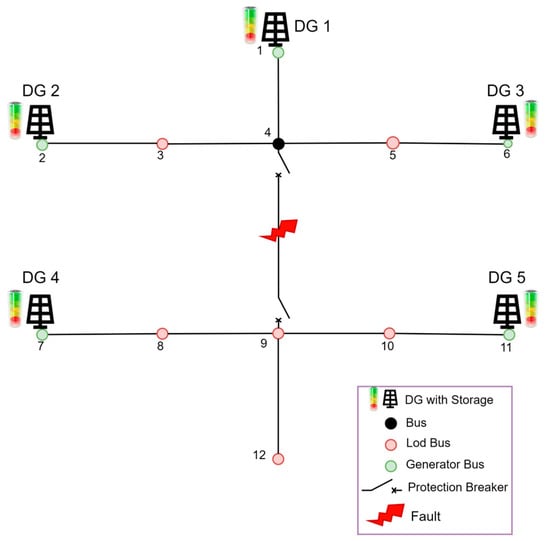
Figure 12.
Examined 12-bus medium-voltage islanded microgrid, consisting of 5 droop-controlled DGs.
The results of the proposed controller are presented in Figure 13, Figure 14 and Figure 15, in comparison to those of the typical centralized controller [2,3], shown in Figure 16, Figure 17 and Figure 18, and the consensus controller [4,5,6], shown in Figure 19, Figure 20 and Figure 21. Specifically, Figure 13 shows the frequency restoration of all DGs during the partition and after the reunification of the MG. Despite the partition, the frequency is successfully restored to 50 Hz during both phases, showcasing the proposed controller’s ability to detect the split and assign distinct secondary control signals to each DG. Figure 14 displays the output signals, highlighting the differential secondary control signals received by DGs 1–3 compared to DGs 4–5, reflecting their different load challenges. After reunification, all DGs receive the same secondary signals to equally distribute the overall load of the MG. Figure 15 illustrates the active power outputs of the DGs, showing that during the partition, DGs 1–3 maintain an equal loading that is lower than that of DGs 4–5.
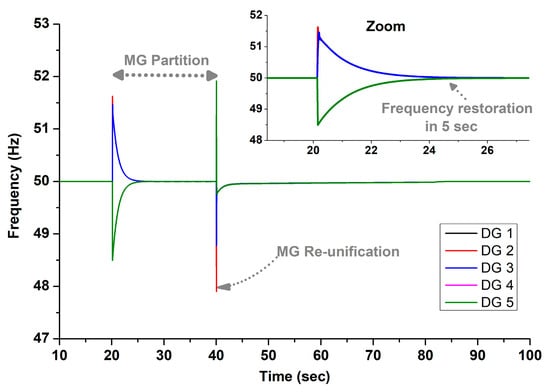
Figure 13.
DG frequencies for Test 3, determined using the proposed controller.
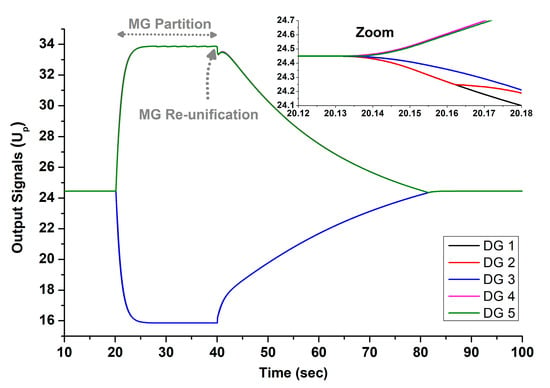
Figure 14.
Output signals of the proposed controller for Test 3.
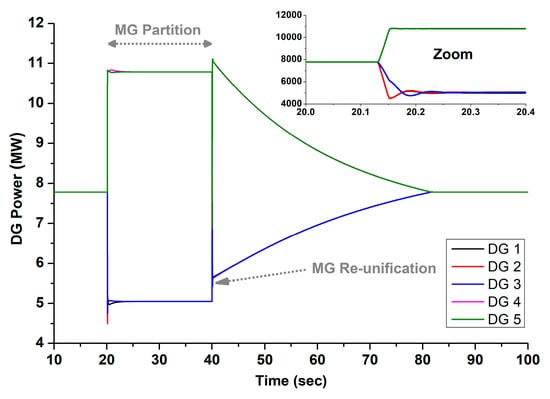
Figure 15.
Power of DGs for Test 3, determined using the proposed controller.
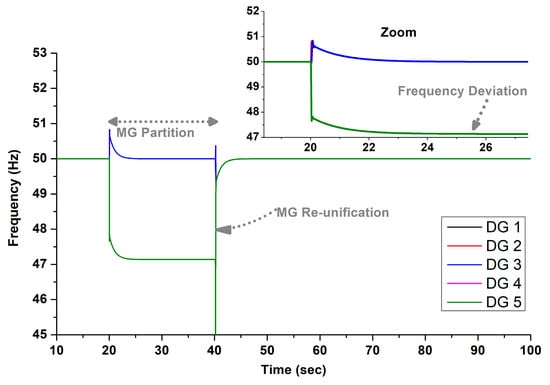
Figure 16.
DG frequencies for Test 3, determined using the typical centralized controller [2,3].
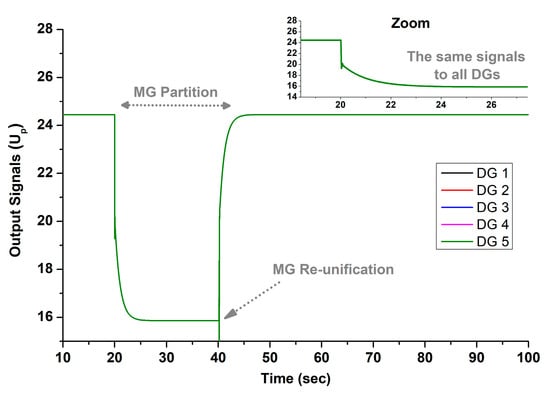
Figure 17.
Output signals of the typical centralized controller for Test 3 [2,3].
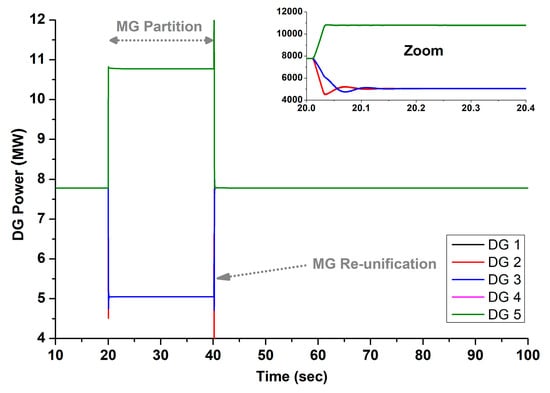
Figure 18.
Power of DGs for Test 3, determined using the typical centralized controller [2,3].
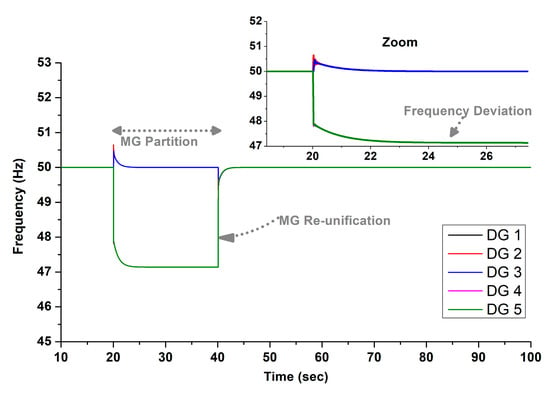
Figure 19.
DG frequencies for Test 3, determined using the typical consensus controller [4,5,6].
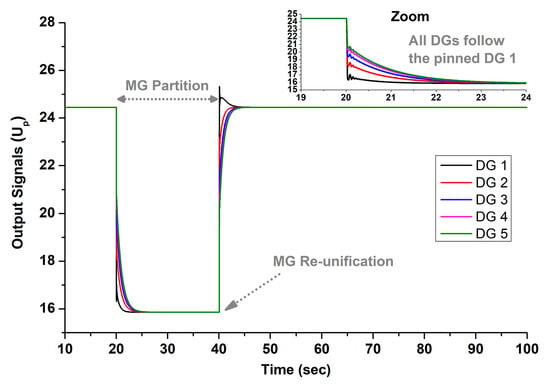
Figure 20.
Output signals of the typical consensus controller for Test 3 [4,5,6].
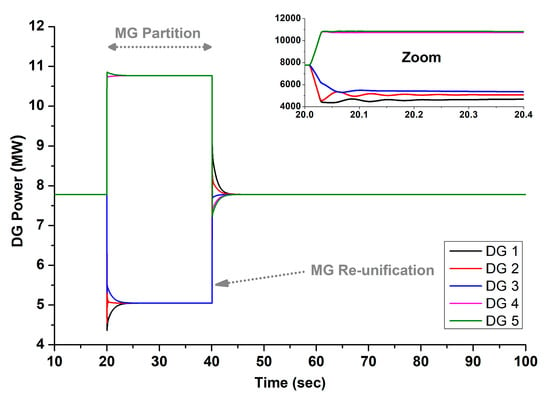
Figure 21.
Power of DGs for Test 3, determined using the typical consensus controller [4,5,6].
Figure 16 depicts the frequency behavior of the typical centralized controller, highlighting significant deviations in the second SMG during the partition. Specifically, the frequency drops as low as 47 Hz and fails to recover. Such a low frequency may trigger protective load shedding in the MG [24] or even cascading outages among the DGs, posing a risk to the overall network stability. This underfrequency event occurs because the standard secondary controller does not recognize MG partitions and continues to send uniform secondary control signals to all DGs, as shown in Figure 17, regardless of their individual loads. As a result, the group of DGs 4–5, which bear a higher load during the partition, experiences underfrequency issues.

Table 3.
Parameters of the 13-bus network [25].
Table 3.
Parameters of the 13-bus network [25].
| Resistance of the lines | 0.25 Ω /km |
| Self-reactance of the lines | 1 mH/km |
| Mutual-reactance of the lines | 0.1 mH/km |
| Line lengths | 10 km |
| Lines’ thermal limits | Neglected |
| Loads (modeled as constant impedances) | R//L = 20 Ω//0.25 H |
| (i = 1, 2, 3, 4, 5) | 5 × 10−7 (Hz/W) |
| (i = 1, 2, 3, 4, 5) | 2 × 10−5 (V/VAR) |
| (i = 1, 2, 3, 4, 5) | 7600 V |
| (i = 1, 2, 3, 4, 5) | 50 Hz |
| Ground resistances | 25 Ω |
Finally, Figure 19, Figure 20 and Figure 21 present the outcomes from the consensus controller. It is important to note that only DG 1 has access to the reference frequency value, acting as the pinned DG (e.g., ) [2]. As depicted in Figure 19, the group of DGs 4–5 experiences underfrequency conditions during the partition, similar to what is observed with the typical centralized controller. This occurs because, as specified in Equation (5), all DGs aim to align their secondary control signals with that of the pinned DG (), as clearly illustrated in Figure 20. As a result, during the partition, both groups of DGs display identical secondary control signals, even though DGs 4–5 are under higher loads, as evidenced in Figure 21. Consequently, the frequency drops as low as 47 Hz, jeopardizing overall MG stability.
Finally, Figure 22 illustrates the performance of the proposed controller after a topology change, specifically after the outage of DG 2. As shown, the proposed controller has the capability to restore the frequency in both split sub-microgrids, without any modification of the controller, even after the topology changes. This robust capability highlights a key advantage of the proposed system, which is designed to deliver consistent performances and does not require recalibration after network reconfigurations. This one-time initial setup guarantees that the controller can smoothly adjust to diverse operational conditions autonomously, thereby simplifying the management of the system.
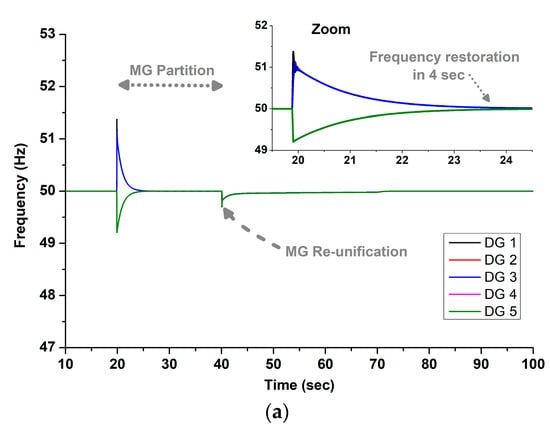
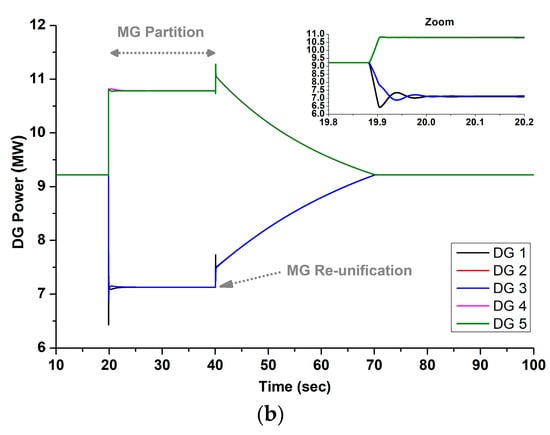
Figure 22.
Repetition of Test 3 for the proposed controller, assuming that DG 2 is out of service: (a) DG frequencies, (b) active power of DGs.
5. Conclusions
This paper introduces a fault-tolerant centralized secondary controller designed for inverter-based, islanded microgrids. This controller enhances system resilience to unexpected network partitions, which typically occur due to the tripping of protective devices under fault conditions. Typically, MGs have a radial configuration where a fault in any line prompts protective devices to isolate the affected line, consequently dividing the MG into two electrically independent sub-microgrids (SMGs) while preserving the existing communication and control framework. Unlike traditional secondary controllers, whether centralized or distributed, which fail to normalize frequency in one of the two SMGs following a sudden network split, the proposed controller demonstrates remarkable capabilities. Simulation studies conducted on 6-bus and 13-bus islanded MG setups reveal that, in contrast to conventional controllers, the controller not only swiftly re-establishes the nominal frequency in both SMGs within 5 s but also ensures uniform power distribution among the distributed generators (DGs) serving the SMGs. This quick frequency restoration validates the controller’s efficiency in maintaining stable frequency levels immediately after a fault.
Author Contributions
Conceptualization, E.E.P. and G.I.O.; Methodology, E.E.P.; Software, E.E.P.; Validation, E.E.P.; Formal analysis, E.E.P.; Investigation, E.E.P.; Resources, E.E.P.; Data curation, E.E.P.; Writing—original draft, E.E.P.; Writing—review & editing, G.I.O., K.Y. and E.S.K.; Project administration, G.I.O., K.Y. and E.S.K.; Funding acquisition, K.Y. and E.S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work received financial support from the project “Enhancing resilience of Cretan power system using distributed energy resources (CResDER)” (Proposal ID: 03698) financed by the Hellenic Foundation for Research and Innovation (H.F.R.I.) under the Action “2nd Call for H.F.R.I. Research Projects to support Faculty Members and Researchers”.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Angular frequency of DG i | |
| Reference frequency of DG i | |
| Frequency droop gain of DG i | |
| Active power of DG i | |
| Secondary control signal of the frequency control for DG i | |
| Positive-sequency voltage of DG i | |
| Reference voltage of DG i | |
| Voltage droop gain of DG i | |
| Reactive power of DG i | |
| Secondary control signal of the voltage control for DG i | |
| Proportional gain of secondary frequency controller | |
| Integral gain of secondary frequency controller | |
| Proportional gain of secondary voltage controller | |
| Integral gain of secondary voltage controller | |
| Angular frequency measured by the microgrid central controller (MGCC) | |
| Voltage measured by the MGCC | |
| Desirable angular frequency, i.e., 2⋅π⋅50 rads/sec | |
| Desirable voltage, i.e., 230 V | |
| Secondary control signal of the proposed method, for DG i, at time instant t | |
| Angular frequency of DG i at time instant t |
References
- Chopra, S.; Vanaprasad, G.M.; Tinajero, G.D.A.; Bazmohammadi, N.; Vasquez, J.C.; Guerrero, J.M. Power-flow-based energy management of hierarchically controlled islanded AC microgrids. Int. J. Electr. Power Energy Syst. 2022, 141, 108140. [Google Scholar] [CrossRef]
- Pompodakis, E.E.; Tinajero, G.D.A.; Karapidakis, E.S. Modelling the steady state of secondary control in islanded AC microgrids. Int. J. Electr. Power Energy Syst. 2023, 153, 109295. [Google Scholar] [CrossRef]
- Marti, P.; Velasco, M.; Martn, E.X.; de Vicua, L.G.; Miret, J.; Castilla, M. Performance evaluation of secondary control policies with respect to digital communications properties in inverter-based islanded microgrids. IEEE Trans. Smart Grid 2018, 9, 2192–2202. [Google Scholar] [CrossRef]
- Bidram, A.; Davoudi, A.; Lewis, F.L.; Qu, Z. Secondary control of microgrids based on distributed cooperative control of multi-agent systems. IET Gener. Transm. Distrib. 2013, 7, 822–831. [Google Scholar] [CrossRef]
- Simpson-Porco, J.W.; Shafiee, Q.; Dorfler, F.; Vasquez, J.C.; Guerrero, J.M.; Bullo, F. Secondary frequency and voltage control of islanded microgrids via distributed averaging. IEEE Trans. Ind. Electron. 2015, 62, 7025–7038. [Google Scholar] [CrossRef]
- Shafiee, Q.; Guerrero, J.M.; Vasquez, J.C. Distributed secondary control for islanded microgrids—A novel approach. IEEE Trans. Power Electron. 2014, 29, 1018–1031. [Google Scholar] [CrossRef]
- Lu, X.; Yu, X.; Lai, J.; Guerrero, J.M.; Zhou, H. Distributed Secondary Voltage and Frequency Control for Islanded Microgrids With Uncertain Communication Links. IEEE Trans. Ind. Inform. 2017, 13, 448–460. [Google Scholar] [CrossRef]
- Ahumada, C.; Cárdenas, R.; Sáez, D.; Guerrero, J.M. Secondary Control Strategies for Frequency Restoration in Islanded Microgrids with Consideration of Communication Delays. IEEE Trans. Smart Grid 2016, 7, 1430–1441. [Google Scholar] [CrossRef]
- Alhasnawi, B.N.; Jasim, B.H.; Sedhom, B.E. Distributed secondary consensus fault tolerant control method for voltage and frequency restoration and power sharing control in multi-agent microgrid. Int. J. Electr. Power Energy Syst. 2021, 133, 107251. [Google Scholar] [CrossRef]
- Shahab, M.A.; Mozafari, B.; Soleymani, S.; Dehkordi, N.M.; Shourkaei, H.M.; Guerrero, J.M. Distributed Consensus-Based Fault Tolerant Control of Islanded Microgrids. IEEE Trans. Smart Grid 2020, 11, 37–47. [Google Scholar] [CrossRef]
- Jin, P.; Li, Y.; Li, G.; Chen, Z.; Zhai, X. Optimized hierarchical power oscillations control for distributed generation under unbalanced conditions. Appl. Energy 2017, 194, 343–352. [Google Scholar] [CrossRef]
- Zhou, Q.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. Unification Scheme for Managing Master Controller Failures in Networked Microgrids. IEEE Trans. Power Syst. 2020, 35, 3004–3014. [Google Scholar] [CrossRef]
- Du, Y.; Lu, X.; Wang, J.; Lukic, S. Distributed Secondary Control Strategy for Microgrid Operation with Dynamic Boundaries. IEEE Trans. Smart Grid 2019, 10, 5269–5282. [Google Scholar] [CrossRef]
- Elsayed, W.T.; Farag, H.; Zeineldin, H.H.; El-Saadany, E.F. Dynamic Transitional Droops for Seamless Line-Switching in Islanded Microgrids. IEEE Trans. Power Syst. 2021, 36, 5590–5601. [Google Scholar] [CrossRef]
- Pompodakis, E.E.; Kryonidis, G.C.; Alexiadis, M.C.; Karapidakis, E.S. A Three-Phase Sensitivity-Based approach for smooth Line-Switching in islanded networks. Int. J. Electr. Power Energy Syst. 2023, 144, 108515. [Google Scholar] [CrossRef]
- Zhou, Q.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. A cyber-attack resilient distributed control strategy in islanded microgrids. IEEE Trans. Smart Grid 2020, 11, 3690–3701. [Google Scholar] [CrossRef]
- Liu, S.; Siano, P.; Wang, X. Intrusion-detector-dependent frequency regulation for microgrids under denial-of-service attacks. IEEE Syst. J. 2020, 14, 2593–2596. [Google Scholar] [CrossRef]
- Ding, L.; Han, Q.; Ning, B.; Yue, D. Distributed resilient finite-time secondary control for heterogeneous battery energy storage systems under denial-of-service attacks. IEEE Trans. Ind. Inf. 2020, 16, 4909–4919. [Google Scholar] [CrossRef]
- Wang, Y.; Deng, C.; Liu, Y.; Wei, Z. A cyber-resilient control approach for islanded microgrids under hybrid attacks. Int. J. Electr. Power Energy Syst. 2023, 147, 108889. [Google Scholar] [CrossRef]
- Rosero, C.X.; Velasco, M.; Martí, P.; Camacho, A.; Miret, J.; Castilla, M. Analysis of Consensus-Based Islanded Microgrids Subject to Unexpected Electrical and Communication Partitions. IEEE Trans. Smart Grid 2019, 10, 5125–5135. [Google Scholar] [CrossRef]
- Zhou, Q.; Tian, Z.; Shahidehpour, M.; Liu, X.; Alabdulwahab, A.; Abusorrah, A.M. Optimal Consensus-Based Distributed Control Strategy for Coordinated Operation of Networked Microgrids. IEEE Trans. Power Syst. 2020, 35, 2452–2462. [Google Scholar] [CrossRef]
- Rosero, C.X.; Velasco, M.; Martí, P.; Camacho, A.; Miret, J.; Castilla, M. Active Power Sharing and Frequency Regulation in Droop-Free Control for Islanded Microgrids Under Electrical and Communication Failures. IEEE Trans. Ind. Electron. 2020, 67, 6461–6472. [Google Scholar] [CrossRef]
- Debouza, M.; Al-Durra, A.; EL-Fouly, T.H.M.; Zeineldin, H.H. Survey on microgrids with flexible boundaries: Strategies, applications, and future trends. Electr. Power Syst. Res. 2022, 205, 107765. [Google Scholar] [CrossRef]
- Marzband, M.; Moghaddam, M.M.; Akorede, M.F.; Khomeyrani, G. Adaptive load shedding scheme for frequency stability enhancement in microgrids. Electr. Power Syst. Res. 2016, 140, 78–86. [Google Scholar] [CrossRef]
- Pompodakis, E.E.; Katsigiannis, Y.A.; Karapidakis, E.S. Optimizing Fault Ride-Through of DGs in Distribution Networks to Preserve Recloser-Fuse Coordination. IEEE Access 2024, 12, 31228–31242. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).