Optimization of Practicality for Modeling- and Machine Learning-Based Framework for Early Fault Detection of Induction Motors

Abstract

This paper addresses the further development and optimization of a modeling- and machine learning-based framework for early fault detection and diagnosis in induction motors. The goal behind the multi-level framework is to provide a pragmatic and practical approach for the autonomous monitoring of electrical machines in various industrial applications. The main contributions of this paper include the elimination of a fingerprint measurement in the processing of the framework and the development of a generalized model for fault detection and diagnosis. These aspects allow the training of neural networks with a simulated data set before even knowing the specific induction motor to be monitored. The pre-trained feed-forward neural networks enable the detection of several electrical and mechanical faults in a real induction motor with an overall accuracy of 99.56%. Another main contribution is the extension of the methodology to a larger operating range. As a result, various faults in a real induction motor can be detected under different load conditions with accuracies of over 92%. As a further part of the paper, a concept for a prototype is presented, which enables the autonomous and practice-friendly application of the framework.

1. Introduction

Industrial processes are essentially influenced by electrical machines. Induction motors in particular are used in production as operating equipment in processing machines, production lines and pumps. Reliable performance of the respective work step is crucial for a functioning process chain in the manufacturing industry. However, due to progressive aging or spontaneous damage to induction motors, the continuity of operations is inevitably compromised. Monitoring the functionality and detecting faults in electric drives therefore plays a major role in the industrial environment. Only with the help of early and reliable detection of faults in electrical machines is it possible to guarantee a robust and predictable production process. Predictive maintenance is also enabled on the basis of detailed fault information, which also saves time and costs in machine maintenance. The faster and more precise the fault detection works, the greater the savings in the maintenance of a production system.

The fault detection and diagnosis (FDD) of machines and systems is already well established in many companies and is not a new trend. Nevertheless, it is often only used for the largest and most critical systems, such as motors above the megawatt range. In addition to these special machines, however, a large number of electric drives are used in production overall. As a result, small and medium-sized electric motors also have a strong influence on manufacturing and transportation processes within companies due to their high quantity. Low-cost sensors and advancing digitalization are making it increasingly worthwhile to extend monitoring to these machines. The benefits of monitoring can thus be extended to the entire production facility and are no longer just focused on individual components. However, these current developments are also having an impact on the demands on motor monitoring. The reason for this is that the existing approaches to monitoring and fault detection are not suitable for application to a broad spectrum and a large fleet of induction motors. The available methods mostly require manual analysis of the respective motor. As a result, the effort multiplies with the number of systems to be monitored. Furthermore, such analyses demand a great deal of expertise in the field of electrical machines. A major goal for the future is therefore to enable monitoring and fault detection for a wide range of electrical machines. In order to guarantee the aspects described, the future focus should be on a high degree of autonomy and a universally transferable mode of operation for monitoring and fault detection.

There are already a large number of publications and extensive reviews in the research field of fault detection and diagnosis in induction motors and other machine types [1,2,3,4]. The selection of suitable measurement quantities is central to the implementation of monitoring. The three phase currents of the electrical machine are often used for further evaluation [5]. Alternatively, measured data on the mechanical vibrations can also be recorded and analyzed using a vibration or acceleration sensor [6,7]. These respective measurement quantities have their own advantages and disadvantages [8]. Other options for fault detection and diagnosis involve the use of a supplementary sensor to monitor the magnetic flux in the inner or outer area of the machine [9,10] and the use of infrared cameras for thermal monitoring [11,12] or microphones to record acoustic signals [13,14]. However, like the measurement of mechanical vibrations, these approaches require the installation of a special sensor, which is associated with additional effort and costs. Monitoring based on stator currents, on the other hand, has the advantage that the corresponding sensors are generally inexpensive, easy to install and easily scalable. Current sensors are often already integrated in existing motors and can therefore be used immediately.

There are generally different techniques for the fault detection and diagnosis of induction motors [2,15]. In model-based methods, detection is performed via the deviation between the real systems and the modeling used. Kalman filters, for instance, can be used for this purpose [16,17]. In addition, physical modeling in different variations such as simplified models [18,19], multiple coupled circuit models [20,21] or FEM models [22,23] are also widely applied. Another aspect is signal processing techniques, which work on the basis of an evaluation and analysis of measurements by extracting specific characteristics for individual fault cases from the recorded data. With the help of existing prior knowledge about the characteristics in the healthy and faulty states, it is then possible to evaluate the condition of the electrical machine. Frequency-based methods such as motor current signature analysis (MCSA) [24,25] or methods from the time–frequency domain such as discrete wavelet transform (DWT) [26,27], the Hilbert–Huang transformation (HHT) [28] or the Wigner–Ville distribution (WVD) [29] are frequently used for this purpose. Data-based approaches, on the other hand, only use data sets for fault detection and diagnosis. No additional prior knowledge of individual fault cases is required. Common approaches from the field of machine learning (ML) are the support vector machine (SVM) [30,31,32] or the k-Nearest Neighbors (kNN) [32,33] algorithm. The use of neural networks in a wide variety of designs is also very widespread. These include feed-forward neural networks (FFNNs) [34,35,36,37,38], recurrent neural networks (RNNs) [39,40], convolutional neural networks (CNNs) [41,42,43,44], deep belief networks (DBNs) [45], self-organizing maps (SOMs) [46] and autoencoders (AEs) [45,47,48]. A combination of both signal-based and data-based methods is also usual, with the signal-based approaches used for extracting known fault features [28,31,35]. The isolated features are in turn used by the algorithms to differentiate between conditions.

The various methods each have certain limitations and problems with regard to applicability and practical suitability. Extensive prior knowledge and manual analysis of the individual electrical machines are important prerequisites for the model-based approaches. In the case of data-based machine learning methods, despite the high degree of autonomy and transferability of these methods, the application of corresponding algorithms for fault detection and diagnosis requires large data sets with healthy and faulty status values. Such a data basis is generally not available in production-related situations. The combination of machine learning with analytical modeling, as used in [49], offers a solution to these problems. The major advantage is that individual data sets for healthy and faulty states of the respective electrical machine can be generated with the modeling and used for the training of neural networks. The difference between the healthy behavior and faulty states can subsequently be used to extract and recognize the characteristics of the individual fault cases. This method is implemented in the model- and machine learning-based framework from [50,51]. With this combined approach, it is possible to analyze very sensitively and the required autonomy and transferability can also be implemented in practical industrial environments. Nevertheless, the framework from [50,51] still has some disadvantages and weaknesses, which will be discussed in this paper and addressed with the help of appropriate solutions. For this purpose, Section 2 first introduces the theoretical background of the framework. This is followed in Section 3 by an analysis of the weaknesses and a presentation of the corresponding optimization approaches. With the help of the experimental setup presented in Section 4, the various improvements to the framework are then validated and evaluated in Section 5. To conclude the paper, a suitable prototype in the form of hardware for the practical application of the framework is presented in Section 6 and the most important conclusions are summarized in Section 7.

2. Theoretical Background

The basic idea behind the framework is presented in detail in publications [50,51]. The framework is based exclusively on the evaluation of stator currents. The most important arguments for this choice are the simplicity of modeling and the large variety of available models. The stator currents are also characterized by distinct fault characteristics, particularly in the frequency range. In addition, the transferability of the approach to various machines with different power ratings plays a decisive role in ensuring a high level of practical suitability. In this context, the stator currents are advantageous as they primarily indicate the internal behavior of the electrical machine. Mechanical vibrations and acoustic signals, on the other hand, are much more dependent on the environment and external influences. A further argument in favor of electrical currents lies in the measurement technology. Obtaining the stator currents only requires simple and affordable measurement equipment, which is either already available on the motor or can be easily retrofitted. In contrast to quantities such as vibrations, acoustic signals or magnetic flux, the sensor position is irrelevant. These numerous advantages are responsible for the selection of stator currents for the framework instead of alternative quantities.

Overall, the framework consists of several successive operations, which can be seen in Figure 1. In an initial process, the parameter values of a multiple coupled circuit model are determined using a specially developed methodology via an optimization algorithm. The parameter identification is conducted on the basis of an individual fingerprint measurement for the analyzed machine. The multiple coupled circuit modeling with the identified parameters is consequently able to simulate a data set for the stator currents in the healthy and faulty states. After applying special data pre-processing, the simulated data set is used to learn characteristic features of the faulty states using neural networks. This ultimately enables the detection of real faults in electrical machines on the basis of measured stator currents. The technological context of the individual components of the framework is explained in more detail in the following sections.

2.1. Modeling of Induction Motor

The core element of the framework for fault detection and diagnosis is a multiple coupled circuit model. This model is combined with the modified winding function method (MWFM), which is applied to calculate the inductances. The modeling simulates the stator currents in healthy and faulty conditions, which are later used as the basis for fault detection and diagnosis by the neural networks.

2.1.1. Healthy Motor

The multiple coupled circuit model is a suitable modeling approach for extensive and detailed fault detection and diagnosis [52,53]. This analytical model can represent the basic electrical and magnetic processes within the machine. In such a multiple coupled circuit model, the behavior of electrical machines is described by considering the individual windings in the system. For this purpose, the associated resistances R, leakage inductances L and inductances M are considered for both the windings in the stator and the windings in the rotor. Based on the electrical and magnetic properties of the individual windings, the voltage equation results in a system of equations that depicts the transient behavior of the voltages U and currents i of the individual windings. Accordingly, the indices S (stator) and R (rotor) indicate the assignment of the resistances R, the leakage inductances L and the inductances M to the respective components. For an induction motor with a squirrel cage rotor, Equation (1) results due to the short circuit in the rotor:

$$\begin{array}{cc}\hfill \left[\begin{array}{c}\left[U_{\mathrm{S}}\right]\\ 0\end{array}\right]& =\left[\begin{array}{cc}\left[R_{\mathrm{S}}\right]& 0\\ 0& \left[R_{\mathrm{R}}\right]\end{array}\right]\left[\begin{array}{c}\left[i_{\mathrm{S}}\right]\\ [i_{\mathrm{R}}]\end{array}\right]+\left[\begin{array}{cc}\left[L_{\mathrm{S}}\right]& 0\\ 0& \left[L_{\mathrm{R}}\right]\end{array}\right]{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left[\begin{array}{c}\left[i_{\mathrm{S}}\right]\\ [i_{\mathrm{R}}]\end{array}\right]\\ & +{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left(\left[\begin{array}{cc}\left[M_{\mathrm{SS}}\right]& \left[M_{\mathrm{SR}}\right]\\ [M_{\mathrm{RS}}]& \left[M_{\mathrm{RR}}\right]\end{array}\right]\left[\begin{array}{c}\left[i_{\mathrm{S}}\right]\\ [i_{\mathrm{R}}]\end{array}\right]\right)\hfill \end{array}$$

(1)

For the calculation of the self and mutual inductances, the winding function method is used [54]. The advantages of this analytical method are that it does not require symmetry in the winding arrangement in the slots and that it works under the assumption that the permeability of iron is infinite. Consequently, it can be used to calculate the coupling inductance between any two windings in an electrical machine [54]. In the case of a variable air gap, such as an eccentric rotor, the modified winding function method must be applied. The steps required to take a variable air gap into account are described in detail in [55].

The electrical behavior of an induction motor is described using the multiple coupled circuit model and the modified winding function method. Equation (1) is transformed into a solvable differential equation and extended by mechanical equations with the quantities of the torque of the load $T_{\mathrm{L}}$, the electrical machine $M_{\mathrm{el}}$, the moment of inertia J, the rotor speed $\omega$ and the rotation angle $\phi$. This results in a system with three differential equations for the dynamic consideration of the electrical and mechanical processes of the electrical machine:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left[\begin{array}{c}\left[i_{\mathrm{S}}\right]\\ [i_{\mathrm{R}}]\end{array}\right]=& \left(\left[\begin{array}{c}\left[U_{\mathrm{S}}\right]\\ 0\end{array}\right]-\left[\begin{array}{cc}\left[R_{\mathrm{S}}\right]& 0\\ 0& \left[R_{\mathrm{R}}\right]\end{array}\right]\left[\begin{array}{c}\left[i_{\mathrm{S}}\right]\\ [i_{\mathrm{R}}]\end{array}\right]-\omega ·{\displaystyle \frac{\partial }{\partial \phi }}\left(\left[\begin{array}{cc}\left[M_{\mathrm{SS}}\right]& \left[M_{\mathrm{SR}}\right]\\ [M_{\mathrm{RS}}]& \left[M_{\mathrm{RR}}\right]\end{array}\right]\left[\begin{array}{c}\left[i_{\mathrm{S}}\right]\\ i_{\mathrm{R}}]\end{array}\right]\right)\right)\hfill \\ & ·{\left[\begin{array}{cc}\left[M_{\mathrm{SS}}\right]+\left[L_{\mathrm{S}}\right]& \left[M_{\mathrm{SR}}\right]\\ [M_{\mathrm{RS}}]& \left[M_{\mathrm{RR}}\right]+\left[L_{\mathrm{R}}\right]\end{array}\right]}^{-1}\hfill \end{array}$$

(2)

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\omega ={\displaystyle \frac{1}{J}}(M_{\mathrm{el}}+T_{\mathrm{L}})$$

(3)

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\phi =\omega$$

(4)

The classic Runge–Kutta method is a common tool for solving initial value problems or ordinary differential equations. It is used for the numerical solution of differential Equations (2)–(4). The inductances $M\left(\phi \right)$ are calculated in advance by creating a look-up table of the inductances for different rotation angles $\phi$. As a result, the behavior of the electrical machine with the stator currents $i_{\mathrm{S}}$ and the rotor speed $\omega$ at a specific operating point can be calculated using the known stator voltages $U_{\mathrm{S}}$ and the specified load torque $T_{\mathrm{L}}$. The model inputs and outputs are summarized in Figure 2.

2.1.2. Faulty Motor

In addition to simulating the healthy behavior of the induction motor, the simulation of faults is essential for the monitoring. The multiple coupled circuit model is detailed enough to enable the calculation and reproduction of internal faults such as winding short circuits [20]. Depending on the respective fault case, various adjustments to the basic modeling are necessary for their simulation. For example, in the case of a short circuit in the stator, the existing matrices of resistances R and inductances M are expanded to take into account the changed winding distribution of the stator and rotor as well as the additional short-circuit path. The same procedure is used for broken rotor bars so that the effects on the respective winding distributions and current flows are considered. In the case of eccentricities, a variable air gap is included in the calculation of the self and mutual inductances so that the eccentric rotation of the squirrel cage rotor is replicated. An overview of the adjustments made within the modeling can be found in

Table 1. List of considered faults with their effects on the multiple coupled circuit model.

Fault	Effects on Model
Winding short circuit	Creation of short-circuit path and changes in winding distribution
Phase short circuit	Creation of short-circuit path and changes in winding distribution
High resistance stator	Increasing the stator resistances
Broken rotor bar	Changes in winding distribution
Mixed eccentricity	Variable air gap
Undervoltage	Change in input voltage
Overvoltage	Change in input voltage
Unsymmetrical voltage	Change in input voltage
Open stator phase	Changes in winding distribution

.

Different degrees of fault severity can be modeled depending on the fault. For instance, the quantity of short-circuited windings or the amount of broken cage bars can be adjusted. The percentage deviation from the original value can be modified accordingly for the different eccentricities and the faulty voltage supplies. This results in a large number of different states overall, which makes it easier to learn fault characteristics in a later step. With machine learning methods, increasing the size of the data set generally has a positive effects on the performance of the corresponding algorithm. In order to generate a comprehensive data set, there is therefore the additional option of mapping further states of the electrical machine by slightly changing the input variables in the multiple coupled circuit model. For example, randomized noise can be added to the voltages or the load torque.

2.2. Identification of Model Parameters

Knowledge of the parameter values is mandatory for the simulation of any squirrel cage induction motor with the multiple coupled circuit model. An important precondition for the model parameter identification suitable for use in fault detection and diagnosis is a high degree of practicability. For this reason, the basic idea is to use a time-resolved fingerprint measurement of the respective machine in the healthy state as the basis for parameter identification. The required parameter values of the modeling are adjusted using the differential evolution algorithm [56,57] over a large number of iterations until the simulated results of the multiple coupled circuit model match the measured data of the fingerprint as closely as possible.

The fingerprint measurement captures easy-to-acquire measurement data of the stator currents $i_{\mathrm{S}}$ and the applied voltages $U_{\mathrm{S}}$. This measurement covers the stationary operation of the electrical machine in a healthy state and is therefore designed for a constant load (see Figure 3a). The associated start-up process is also included in the measurement in order to take into account the dynamic processes of the electrical machine in the identification process. For further information, the data from the nameplate of the electrical machine are also recorded. The focus here is on the rated power $P_{\mathrm{N}}$, the rated voltage $U_{\mathrm{N}}$, the rated current in the stator $I_{\mathrm{N}}$, the power factor $\cos \phi$ and the efficiency $\eta$.

A fitness value is calculated as the goal function for the differential evolution algorithm, which describes the correlation between the modeling and the real behavior of the electrical machine. For this, the outputs of the multiple coupled circuit model are decisive. In general, a two-part approach is used to calculate the fitness value. It is first checked whether the deviation between the simulated rotor speed ${\omega }_{\mathrm{si}}$ and the measured rotor speed ${\omega }_{\mathrm{meas}}$ is less than 0.5% after reaching a stable operating point. Once this condition is true, the mean squared error (MSE) between the fast Fourier transform (FFT) of the simulated stator currents $i_{\mathrm{sim},\mathrm{FFT}}$ and the measured stator currents $i_{\mathrm{meas},\mathrm{FFT}}$ is utilized as the fitness value (see Figure 3b); otherwise, a penalty term is added. Further information on the calculation of the fitness function can be found in [50,51].

2.3. Artificial Neural Network

For fault monitoring of electrical machines based on measured or simulated data sets, artificial neural networks from the field of machine learning are particularly suitable due to their high flexibility and individual configurability, as they enable the independent learning of patterns and correlations from existing data sets [58].

In general, appropriate pre-processing of the data facilitates the further training process of the artificial neural networks. A fast Fourier transform is suitable for pre-processing the data in order to transfer the measurement data from the time domain to the frequency domain. This makes the characteristics of the individual fault cases in the frequency domain much more visible and any temporal offset between individual measurements is irrelevant. Limiting the frequency spectra to an area with the decisive fault characteristics (e.g., 0 to 1000 Hz) also places greater focus on differentiating between the fault cases. In addition, a normalization of the frequency spectrum based on the dominant base harmonics at 50 Hz is useful in order to compensate for deviating magnitudes in the amplitude and to create a standardized basis. As a further step, the difference from the frequency spectrum of the healthy state is calculated for the complete data set. With the help of this difference determination, the deviations of the fault cases from the healthy state are learned more sensitively. The entire pre-processing of the data is shown step by step for one phase of the stator currents in Figure 4.

With an appropriately pre-processed data set as a basis, artificial neural networks can be trained for the robust fault classification of electrical machines. The use of simply structured feed-forward neural networks is sufficient, as the different fault characteristics are already well extracted and isolated due to the extensive pre-processing of the data. The structure of feed-forward neural networks for fault detection and diagnosis consists of an input layer, several hidden layers and an output layer [59]. The number of neurons in the input layer corresponds to the number of data points in the frequency spectra (depending on the size of the individual samples) and the number of neurons in the output layer is equal to the number of healthy and faulty states. For the hidden layers, the ReLU activation function is used in each case, while for the output layer the softmax function is used to output probabilities for the individual labels or states. The standard Adam algorithm is applied as the optimizer for backpropagation [59]. Additionally, various regularization techniques are available for the purpose of generalization with early stopping [60], the addition of noise to the input neurons [61] and the dropout technique [62]. The described configuration provides the basic frame for training the feed-forward neural networks for functional fault monitoring.

3. Optimization of Framework

The model- and machine learning-based framework from [50] already offers a good opportunity for practice-oriented fault detection and diagnosis in induction motors with squirrel cage rotors. Using the approach for parameter identification, the values of the model parameters are determined automatically via a fingerprint measurement and the differential evolution algorithm. The parameterized multiple coupled circuit model reproduces the fault cases qualitatively well via simulations so that the neural networks can learn the differences between the individual states. Due to the sophisticated pre-processing of the stator current data and the regularization techniques for the training process, it is possible to transfer the simulated fault characteristics to the real fault cases. The resulting neural networks subsequently allow the robust fault detection of real faults with a high accuracy [50].

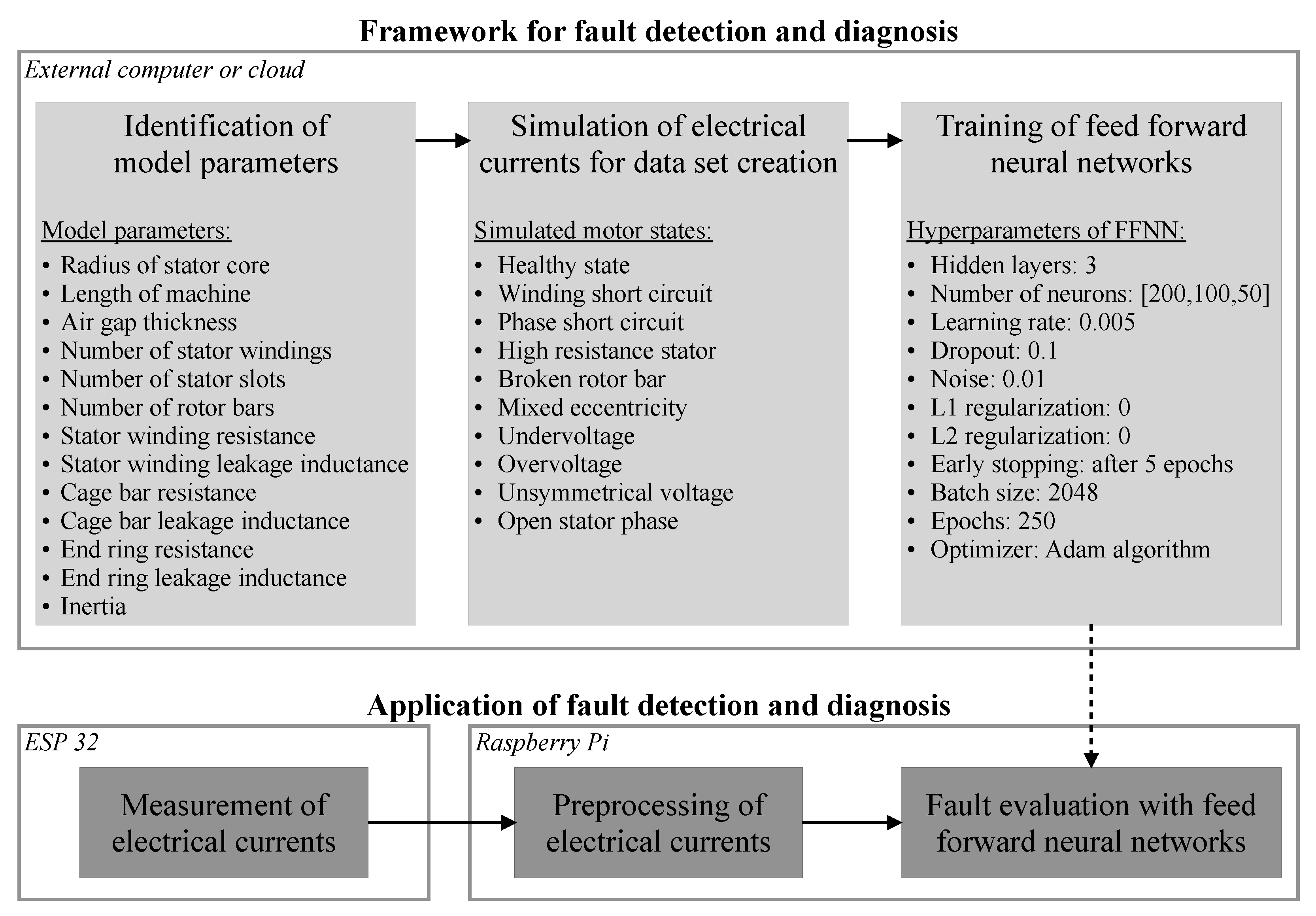
Despite the good results of the validation and the already strong focus on practical suitability, some aspects of the framework hinder a smooth and practice-friendly application. These various points will be discussed in detail in the following sections. The methodology developed in [50] serves as basis for the investigations in this paper. The three main steps and the fundamental procedure of the framework from Figure 1 remain unchanged. Only small details in the individual steps are modified in order to contribute to a further increase in the practicability of the framework and improvement in fault detection and diagnosis. This paper therefore offers an extension and optimization of the methodology presented in [50].

3.1. Parameter Identification without Voltage Measurement

The fault detection itself is based exclusively on the measured stator currents, but the stator voltages are also required alongside the currents for the identification of the model parameters in the framework. Only with this precondition are all inputs and outputs of the modeling (see Figure 2) known and the identification process with the differential evolution algorithm executable. However, this need for voltage measurement reduces the overall practical suitability of the method. The reason is that appropriate sensors and measurement technology must be installed. Otherwise, a great deal of effort is required for the installation, although the measurement is only needed to identify the model parameters.

As a solution to this problem, the voltages applied to the induction motor are specified analytically. For this purpose, the time characteristic of the mains voltage is modeled as a sinus curve with an amplitude of 400 V and a frequency of 50 Hz. The missing information about the phase shift between the current and voltage is taken into account as an additional parameter as part of the parameter identification and thus determined automatically. This allows the voltage measurement to be replaced by an analytical representation as a basis for the fingerprint and further simulations. However, this option is only available for electric drives that are operated directly via the mains voltage.

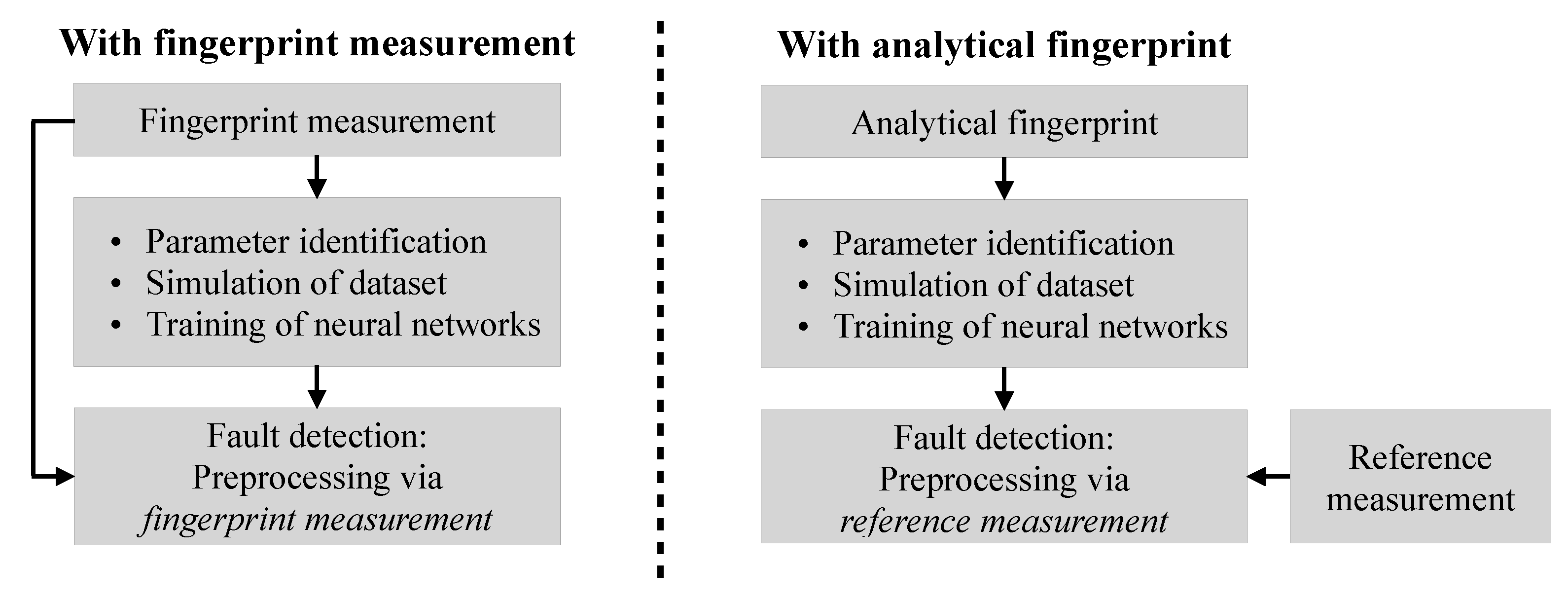
3.2. Parameter Identification with Analytical Fingerprint

The key strength of the flexible framework is also a certain weakness in terms of practicality. This is because the individual adaptation of the modeling to the respective electric drive requires a high time and computing effort of several hours. Therefore, the acquisition of the fingerprint measurement is followed by a longer process in which the parameter identification and generation of the simulation data for the induction motor take place. However, this intermediate step on the way to fault detection considerably reduces a practical application, as monitoring cannot be started immediately and the calculations have to be carried out on a suitable computing platform (e.g., cloud or simulation PC). In addition, in the case of identical machines, the application of the framework would have to be repeated in each case, which would also multiply the effort and computing time.

One conceivable solution to this problem is to completely neglect the fingerprint measurement for parameter identification. Instead, based on Section 3.1, the current measurement would now be analytically replicated in addition to the voltage measurement. For this purpose, the current characteristic of the corresponding induction motor is modeled using the quantities from the nameplate. The analytical fingerprint then no longer corresponds to a start-up process, but to operation in a stationary state. The analytical current characteristics are used for parameter identification to enable simulation of the data set with the identified parameters in the next step. This eliminates the preliminary fingerprint measurements for parameter identification and increases the practicality of the framework. An initial reference measurement of the stator currents in the healthy state at the start of fault detection is still required to enable a reference establishment during data pre-processing for precise analysis (see Figure 5). However, this approach allows the monitoring to start immediately without any further calculation steps.

3.3. Generalized Model for Fault Detection

The basic ideas from the previous sections will now be developed further. Instead of limiting the data set and fault detection to a single design of a specific induction motor, it is also conceivable to train the neural networks for a greater selection of induction motors. Such an approach leads away from an individually adapted solution to a generalized model for fault detection. This increases the practical suitability of the framework even further, as a generalized model can be used directly for an entire class of induction motors. In principle, the procedure is the same as described in Section 3.2. The parameter identification and simulation of the data sets is simply carried out for a number of induction motors with different power ratings. The neural networks are then trained with the composite data set so that a generalized fault detection can be achieved for a larger power range of induction motors.

3.4. Fault Detection for Larger Operating Range

Another limitation of the framework is the focus towards a single operating condition. The identified model parameters and the simulated data sets generally refer to the state at the rated load. However, the induction motor may also be operated at other loads, resulting in a deviation from the rated load. Stable detection of faults cannot be guaranteed in these deviating conditions.

In principle, the framework is already capable of detecting faults in several operating states. For this purpose, the simulations of the healthy state and the various faults are carried out under deviating load conditions. Due to the sophisticated pre-processing of the data and the qualitative differentiation of the fault cases via the neural networks, further changes within the framework are not necessary. Only an adapted reference establishment for the corresponding operating points is required. Consequently, reference measurements must be carried out in advance at the respective operating points in order to correctly pre-process the data of the measured stator currents. Under these circumstances, robust fault detection is also possible in deviating operating states.

4. Experimental Setup

The described adjustments in the framework are validated with the help of an experimental setup as already applied in [50,51]. The example machine used is a squirrel cage induction motor, which can be seen in Figure 6. The motor has two pole pairs and a mechanical power of 1.1 kW. Cooling is implemented via an integrated fan and the bearing arrangement with bearings of type 6205-ZZ/2Z-C3 in the bearing shields. The information from the nameplate of the induction motor is given in

Table 2. Nameplate data of the examined 1.1 kW squirrel cage induction motor for delta connection [50].

Parameter	Value
Rated power $P_{\mathrm{N}}$	1.1 kW
Rated voltage $U_{\mathrm{N}}$	400 V
Rated current $I_{\mathrm{N}}$	2.5 A
Rated rotor speed $n_{\mathrm{N}}$	1445 1/min
Frequency f	50 Hz
Power factor $\cos \phi$	0.75
Efficiency $\eta$	84.4%

.

Real fault cases in the exemplary induction motor with squirrel cage rotor serve as the basis for validating the framework. The individual faults are integrated into the example machine in different ways. A list of the fault cases with the corresponding manipulations can be found in

Table 3. List of the faults introduced on the investigated squirrel cage induction motor with the associated manipulations.

Fault of the Induction Motor	Type of Manipulation
Undervoltage	Voltage regulation via transformer
Unsymmetrical voltage	Voltage regulation via transformer
Open stator phase	Interruption of a phase
Broken rotor bar	Drill hole through bar
Winding short circuit	Contacting two windings
Mixed eccentricity	Installation of imbalance weight

.

The stator currents of the three phases and also the voltages of all three phases are required to perform and analyze the framework. Current transformers, which are shown on the right picture in Figure 6, are used to record the stator currents. These have a measuring range of ±150 A and an accuracy of ±1%. The voltages applied to the machine are converted to a lower voltage level using a transformer. The output signals of the individual sensors and the transformed voltages are linked to an analog-to-digital converter with an input range of ±10 V, which records the analog signals from the sensors in parallel at a sampling rate of 10 kHz.

For the fingerprint measurement, the stator currents and the applied voltages of all three phases are required for the healthy state of the electrical machine. These variables are measured over 10 s and include the transient startup process of the induction motor in delta connection with subsequent constant operation at rated torque.

To generate the data set for validation, measurements of the stator currents of all three phases in the healthy state and in the fault cases from Table 3 are carried out. The data are recorded for the operation of the electrical machine in delta connection at 60, 80, 100 and 120% rated torque, so that several stationary operating points are taken into account. The stator currents are recorded over a period of 10 s, with each measurement being taken three times in total. This results in a total of three independent measurement runs for each of the 10 states of the motor at each of the 4 stationary operating points. The measurements with a length of 10 s are divided into a total of 25 samples of 0.4 s each.

5. Experimental Results

The various optimizations from Section 3 are validated using the data set from the experimental setup in Section 4. For this purpose, the framework is applied according to Section 3. The starting point for this is the recording of a fingerprint measurement under rated load. Based on this measurement, the parameters are identified using the differential evolution algorithm with 50 iterations and a population of 25 individuals over a total of 10 runs. The five best parameter sets are then used to simulate 120 samples each for the healthy state and the different fault cases with the rated load and a additional random noise of ±4 V to the original voltage supply. This results in a total of 600 samples for each condition with a sampling rate of 10 kHz.

The simulated data set is subsequently used to train feed-forward neural networks. The learning process of the feed-forward neural networks is carried out using the Adam algorithm as an optimizer. The samples from the data set in the form of the three-phase stator currents with a length of 0.4 s serve as a source for the inputs to the neural networks. These currents are first transformed into the frequency domain as part of the pre-processing from Figure 4. The normalization and difference calculation to the healthy state are then carried out for the frequency range from 0 to 1000 Hz (see also Figure 4). This results in a vector with 1200 data points from the pre-processed frequency spectra of the three phases (400 data points per phase), which serves as actual input to the neural networks.

The number of neurons in the hidden layers and other hyperparameters are determined manually via parameter tuning. The aim of the tuning is to achieve the best possible trade-off between the classification performance of the neural networks and potential overfitting. The focus here is primarily on preventing overfitting so that the neural networks learn robust fault characteristics which can be transferred to the real measurement data for fault detection and diagnosis. As a result of the parameter tuning, the structure and hyperparameters of the neural networks are shown in

Table 4. Hyperparameters of the feed-forward neural networks for high generalization.

Hyperparameter	Values
Hidden layers	3
Number of neurons	[200, 100, 50]
Learning rate	0.005
Dropout	0.1
Noise	0.01
L1 regularization	0
L2 regularization	0
Early stopping	after 5 epochs
Batch size	2048
Epochs	250

. A total of 10 neural networks are trained separately and used jointly for fault detection with the help of ensemble learning.

The validation of the trained neural networks with the measured stator currents at the rated load results in a very high detection accuracy for the healthy state and the different real faults with a total value of 98.71%. The confusion matrix in Figure 7 shows that all fault cases are detected with an accuracy of nearly 100%. Only the broken rotor bar is detected with an accuracy of 92%, as this fault is quite similar to the mixed eccentricity.

Following on from this basic approach of the framework, the individual optimizations from Section 3 are now used and applied at the appropriate aspects within the methodology. The outcomes of these modifications are compared with the results of the original framework, which serve as a basic reference.

5.1. Parameter Identification without Voltage Measurement

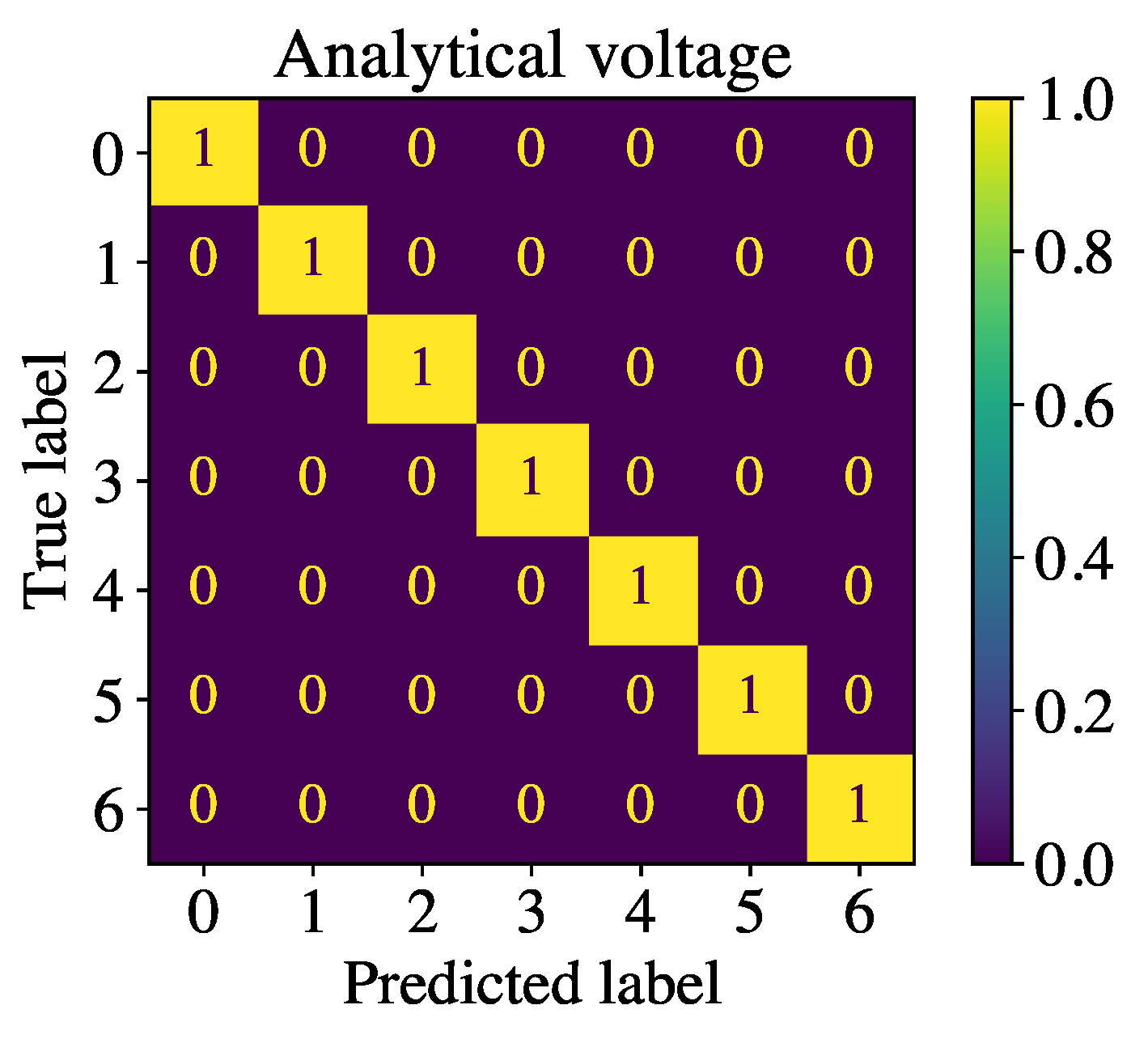
In the first optimization of the framework, an analytic voltage is used for the fingerprint instead of a voltage measurement. The phase shift between current and voltage is taken into account as an additional parameter in the parameter identification.

The result is an optimal detection accuracy of 100%. The outcomes for the individual fault cases are shown in the confusion matrix in Figure 8. It can be seen that the use of an analytical voltage provides even slightly better results in comparison to the original framework with voltage measurement. Consequently, the measurement of voltages for the identification process of the parameter values can be dispensed with in future. It should again be noted that this is only valid for electrical machines that are operated directly via the mains.

5.2. Parameter Identification with Analytical Fingerprint

In the following step, the stator current is modeled analytically in addition to the voltage in order to avoid the entire fingerprint measurement. For this purpose, the rated data from the nameplate in Table 2 are used, which specify a value of 2.5 A for the current $I_{\mathrm{N}}$ at the rated load. The phase shift between the current and voltage is again taken into account as an additional parameter in the parameter identification. Due to the lack of a fingerprint measurement, an additional reference measurement in the healthy state is necessary. This reference is required for data pre-processing in order to be able to analyze the deviations from the healthy state sensitively (see Section 3.2).

The result of this optimization is a lower detection accuracy of 82.86% compared to the original framework. The confusion matrix in Figure 9a shows that the undervoltage fault is no longer detected. This is explainable by the fact that the slot harmonics are not modeled appropriate due to the missing fingerprint measurement. However, the slot harmonics are essential for the undervoltage fault, as they contain information about the current speed of the motor. As this information is not contained in the simulated data, the undervoltage fault cannot be detected. In addition, the mixed eccentricity is only identified with an accuracy of 80% due to its similarity to the healthy state. However, the remaining conditions are still detected with an accuracy of 100%.

The previous analysis shows that taking the slot harmonics into account in the fault detection without fingerprint measurement has no additional benefit. The undervoltage and overvoltage faults cannot be identified without a fingerprint measurement. As a result, fault detection is carried out with a reduced frequency spectrum from 0 to 250 Hz and without the undervoltage and overvoltage faults in the data set. With these adjustments, the validation with the real measurement data results in a comparable accuracy of 78.14% with less information required overall (91.17% with neglecting undervoltage). The confusion matrix in Figure 9b shows that the undervoltage is now recognized as a healthy state. In addition, the mixed eccentricity with a value of 47% is still not identified without doubt.

Overall, it is possible to completely eliminate the fingerprint measurement by neglecting the undervoltage and overvoltage faults. Under the assumption that exclusive voltage monitoring is often already present on electrical machines, this optimization of the framework is therefore permissible.

5.3. Generalized Model for Fault Detection

The optimizations from the previous sections lead to the approach of generalized fault detection. Instead of the specific training of neural networks for a single induction motor, an entire range with several electrical machines is considered instead. The goal is to train generalized neural networks that can be used flexibly for induction motors within a greater range. For this purpose, the procedure from Section 5.2 is repeated for several induction motors in order to generate a corresponding data set for the training process. A total of four different induction motors with squirrel cage rotors from a catalog in a power range between 0.5 and 7.5 kW are taken into account. The rated data of the respective motors are shown in

Table 5. Nameplate data of five different squirrel cage induction motors used for parameter identification and data set simulation.

	Motor No. 1	Motor No. 2	Motor No. 3	Motor No. 4
Rated power $P_{\mathrm{N}}$ [kW]	0.75	2.2	4	7.5
Rated current $I_{\mathrm{N}}$ [A]	1.75	4.4	7.9	14.3
Rated rotor speed $n_{\mathrm{N}}$ [1/min]	1450	1465	1460	1470
Power factor $\cos \phi$	0.75	0.83	0.82	0.84
Efficiency $\eta$ [%]	82.5	86.7	88.6	90.4

.

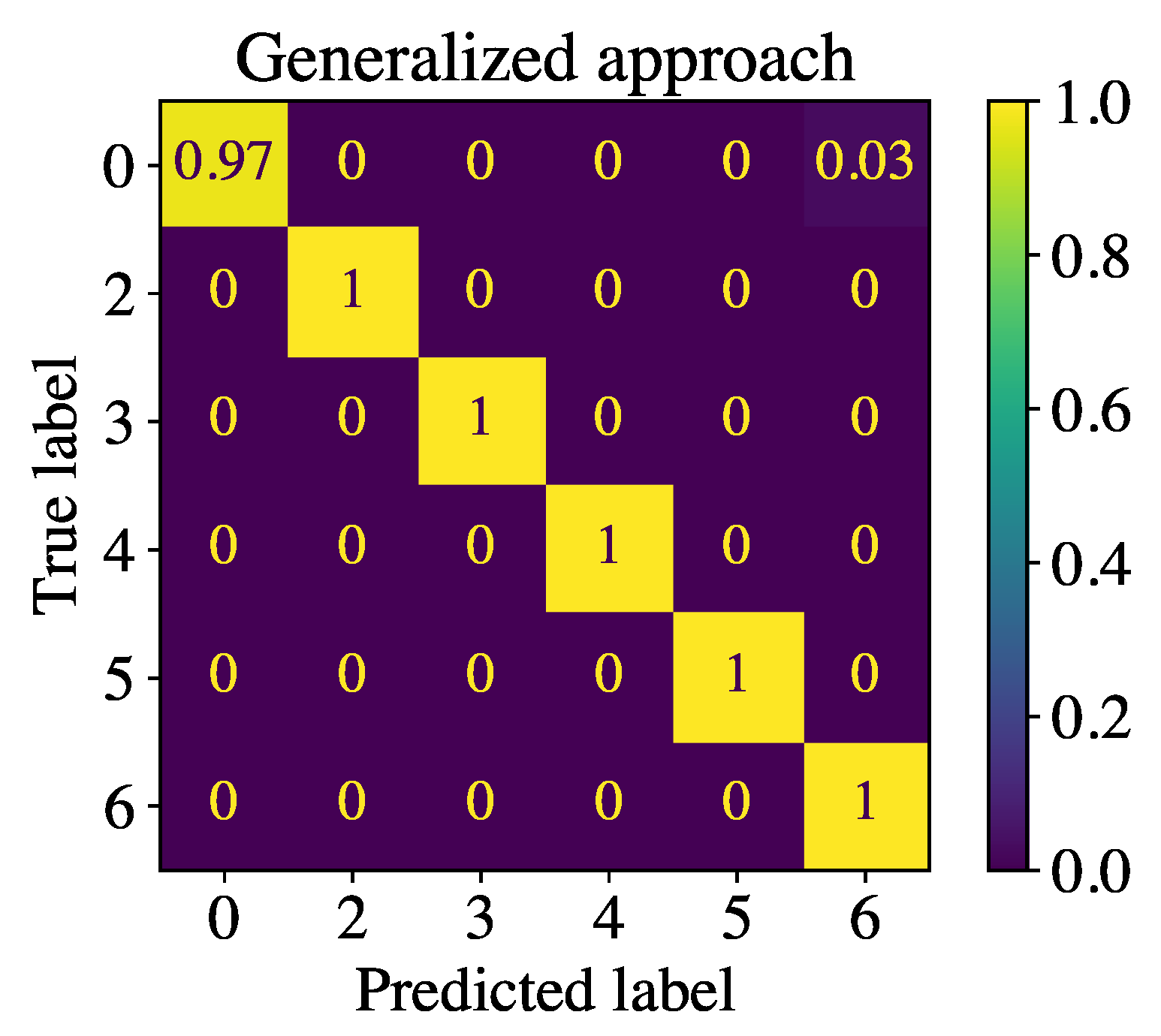
The validation with the induction motor from Section 3, which was not used as part of the training data, results in a detection accuracy of 99.56% with neglect of undervoltage. Looking at the confusion matrix in Figure 10, it is apparent that all fault cases are detected with high accuracy. Even the mixed eccentricity is now detected with great precision. As a result of the higher dispersion due to several motors, the overall performance is better than in Section 5.2. The training of a robust and generalized model for fault detection is feasible in a larger range. This has an advantageous effect on the practical suitability of the framework, as the neural networks only need to be trained once and can then be used immediately for a large number of induction motors in the corresponding power range.

5.4. Fault Detection for Larger Operating Range

After the generalized approach, the fault detection is extended to a larger operating range in order to be able to detect conditions that deviate from the rated load. As already described in Section 3.4, this requires additional simulations under specified load conditions. Also, reference measurements in the healthy state of the corresponding operating points are needed. In this case, the simulations and the reference measurements are carried out at 60, 80, 100 and 120 % rated torque. The recorded reference measurements are used as part of the data pre-processing in order to be able to analyze the deviation from the healthy state.

The results of this extension to the near operating range are very good overall. This leads to a detection accuracy of 92.89% at 60% rated load, 96.44% at 80% rated load, 96.00% at 100% rated load and 94.44% at 120% rated load with neglect of undervoltage. The respective confusion matrices for the individual operating points can be seen in Figure 11. It is apparent that all faults can also be identified in deviating load ranges. However, the greater the deviation from the rated load, the more difficult it is to distinguish between the two very similar cases of healthy state and mixed eccentricity. Nevertheless, comprehensive fault detection with good precision is possible over a wide operating range, provided that corresponding reference measurements are available in the healthy state.

The robustness to noise of the proposed methodology is considered to be high. This is due to the use of a versatile training data set with different fault and load conditions. The generation of this data set also includes the implementation of additional noise on the input voltage (see Section 5). Furthermore, the training of the neural networks focuses on a high degree of generalization and the prevention of overfitting in order to ensure robust fault characteristics for the transferability from simulated data to measured data. The robustness of the methodology is demonstrated in the successful validation with the large number of measurements in various fault and load states under real conditions in this section.

6. Prototype for Monitoring System

Another difficulty in the practical use of the framework for fault detection in an industrial environment is the necessary interaction of the software with a suitable computing environment and appropriate measurement technology. Although sensors are often already installed on existing machines, there is often a lack of a suitable platform for the software-side connection and evaluation of the measurement data. As a solution, a prototype is presented in the following, which is specially designed for use as a monitoring system.

The core of the prototype is a Raspberry Pi, on which the neural networks process the measured stator currents as input and output for an assessment of the current status of the electrical motor. The measurement data are recorded via an ESP32 microcontroller. Three split-core current transformers for measuring alternating current are connected to the 12-bit analog-to-digital converter of the microcontroller and can be easily and safely installed on the supply cables of the electrical machine. The ESP32 microcontroller uses its analog-to-digital converter to record the analog signals at a sampling rate of 30 kHz (10 kHz per phase) and forwards the recorded digital data to the Raspberry Pi via the serial interface. The hardware concept is illustrated in Figure 12.

The electronic components are covered for protection against external influences. A display is also integrated into the housing, which displays the current status of the induction motor. Depending on the requirements, the output of the neural networks can also be distributed to other systems via standardized interfaces. The complete prototype and the electrical components inside the housing can be seen in Figure 13.

The hardware concept of the monitoring system enables continuous data recording and evaluation. For the software, C is used for the data acquisition on the ESP32 and Python is used for the data evaluation on the Raspberry Pi. Finally, the stator currents can be evaluated every second or at longer time intervals as required. In each execution, the fault detection and diagnosis algorithm from Algorithm 1 is processed.

Algorithm 1. Fault detection and diagnosis algorithm

1: Measurement of the three-phase stator currents i for 0.4 s. 2: Fast Fourier transform (FFT) of the stator currents i to the frequency domain. $i_{\mathrm{fft}}=\mathrm{FFT}\left(i\right)$ 3: Normalization of the frequency spectra $i_{\mathrm{fft}}$ between 0 and 1000 Hz via basic harmonics. $i_{\mathrm{norm}}=\mathrm{norm}\left(i_{\mathrm{norm}}\right)$ 4: Calculation of difference from the frequency spectra of the reference measurement for the healthy state $i_{\mathrm{healthy}}$. $i_{\mathrm{diff}}=i_{\mathrm{norm}}-i_{\mathrm{healthy}}$ 5: Execution of feed-forward neural networks with pre-processed currents $i_{\mathrm{diff}}$ as input. $p=\mathrm{FFNN}\left(i_{\mathrm{diff}}\right)$ 6: Feedback of the probabilities p for each fault state.

The prototype offers an all-in-one solution for a monitoring system for electrical machines. The Raspberry Pi creates a cost-effective and flexible platform for the interface between software and hardware. This enables both the execution of neural networks and the connection of sensors. In addition, installation on the machine can be carried out quickly and easily using the split-core current transformers. The result is an autonomous monitoring system for use in a production process. The system can be integrated during the implementation of new machines, but can also be retrofitted to intact existing systems.

7. Conclusions

In its original form, the model- and machine learning-based framework enables early fault detection and diagnosis with high detection accuracy and acceptable practical suitability. With the help of the optimizations from this paper, the pragmatic and practice-friendly application of the framework is further increased. One of the improvements is the replacement of the fingerprint measurement with analytical current and voltage characteristics. In addition, it is possible to train a generalized model for a larger range of induction motors instead of an individual motor. At least, it is also conceivable to extend fault detection to a larger operating range deviating from the rated load.

These adjustments to the framework simplify the practical application of the monitoring for induction motors. In industrial environments, the neural networks for fault detection can be trained for a larger range of induction motors and without a prior fingerprint measurement, so that individual adaptation to the respective induction motor is no longer necessary. Thus, fault detection can be started immediately after recording a reference measurement for the healthy state of the motor. This eliminates the need for time-consuming calculations during the installation and implementation of the monitoring system. In addition, the extension of the fault detection to various load conditions ensures that all operating states of the induction motor can be considered. In future research, the effectiveness of the framework in real applications and its superiority over other methods need to be evaluated.

In combination with the prototype hardware, the model- and machine learning-based framework forms a plug-and-play-capable monitoring system that can be put into operation within a very short time. Fault detection and diagnosis can start immediately after an initial reference measurement has been recorded and subsequently enables the robust and sensitive detection of faults in a wide range of applications.