Pyrolytic Pathway of Wheat Straw Pellet by the Thermogravimetric Analyzer
Abstract
1. Introduction
2. Theoretical Approach
2.1. Kinetic Parameters
- α = conversion degree;
- (T) = reaction at absolute temperature.
- α = reactant decomposition fraction or conversion degree at the time (t);
- m, m0, mf = sample’s actual, initial, and final mass (gm).
- k = constant of reaction rate, (1/min);
- Eα = activation of energy (kJ/mole);
- lnA = pre-exponential factor (1/s);
- T = absolute temperature (°C);
- R = universal gas constant (8.314 kJ/K.mole).
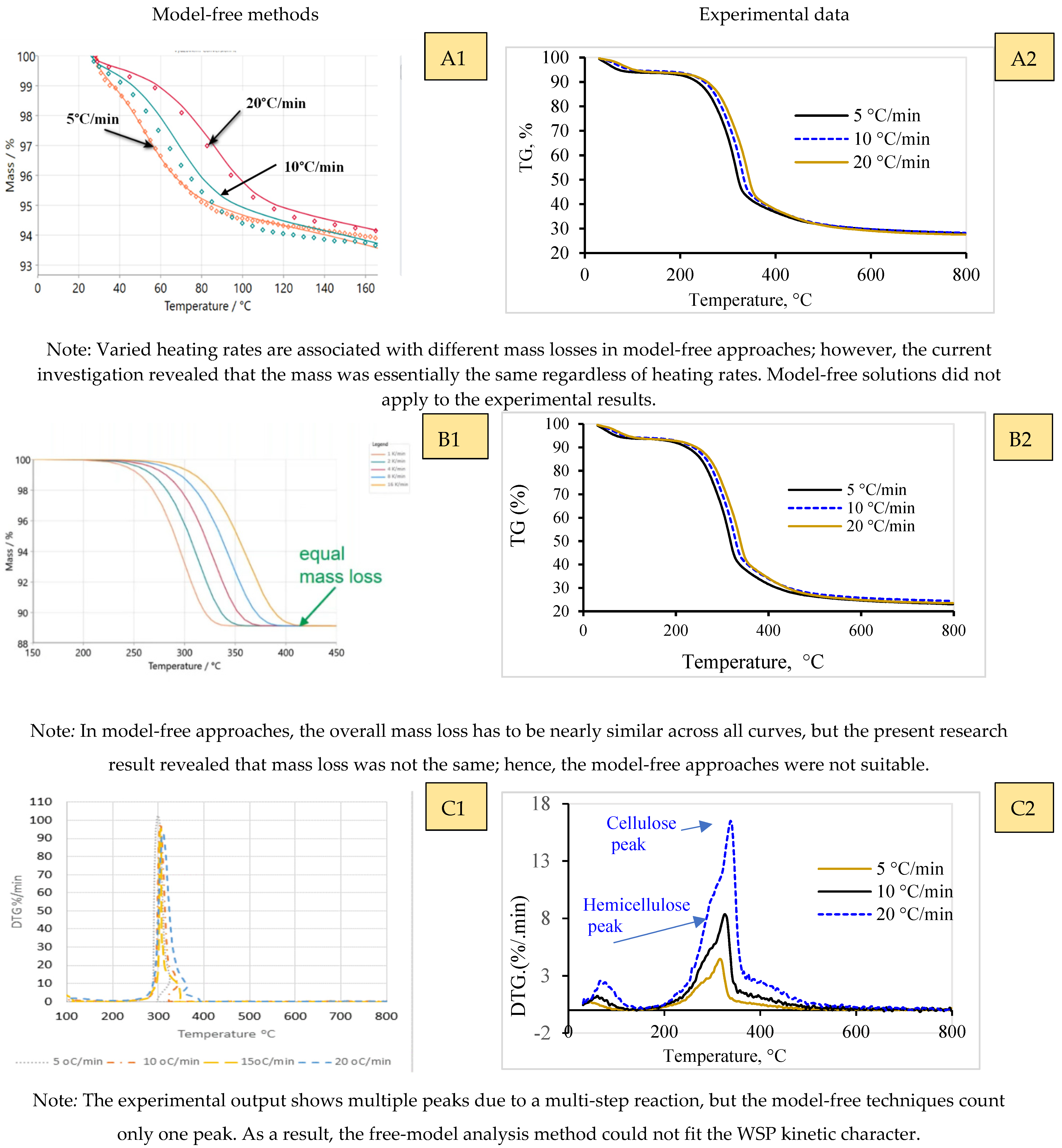
2.2. Model-Free (Iso-Conversional) Analysis
- ▪
- Only single kinetic equation, for instance, Reactants A → Products B;
- ▪
- Eα and A based on α;
- ▪
- At a consistent level of conversion, the reaction rate is solely dependent on temperature;
- ▪
- Across all curves, the overall impact (total mass loss or total peak area) should remain consistent;
- ▪
- Reaction pathway change must maintain a similar conversion value.
2.3. Model-Based Method
- ▪
- Firstly, it is implicit that the reaction comprises several distinct primary reaction stages, each characterized by its own kinetic reaction equation.
- ▪
- Additionally, it is posited that constant values exist for all kinetic factors governing the reaction.
- ▪
- Lastly, the total signal arises from aggregating individual reaction steps, each weighted accordingly. These combined steps form the foundation of the model-based kinetic analysis.
- fj(ejpj) = function of reaction type;
- ej = initial reactant concentration;
- pj = product concentration;
- lnAj = pre-exponential factor;
- j = reaction steps number.
2.4. Kinetic Reaction Model
3. Experimental Approach
3.1. Experimental Sample Preparation
3.2. Thermogravimetric Analysis
4. Results and Discussion
4.1. Physicochemical Analysis
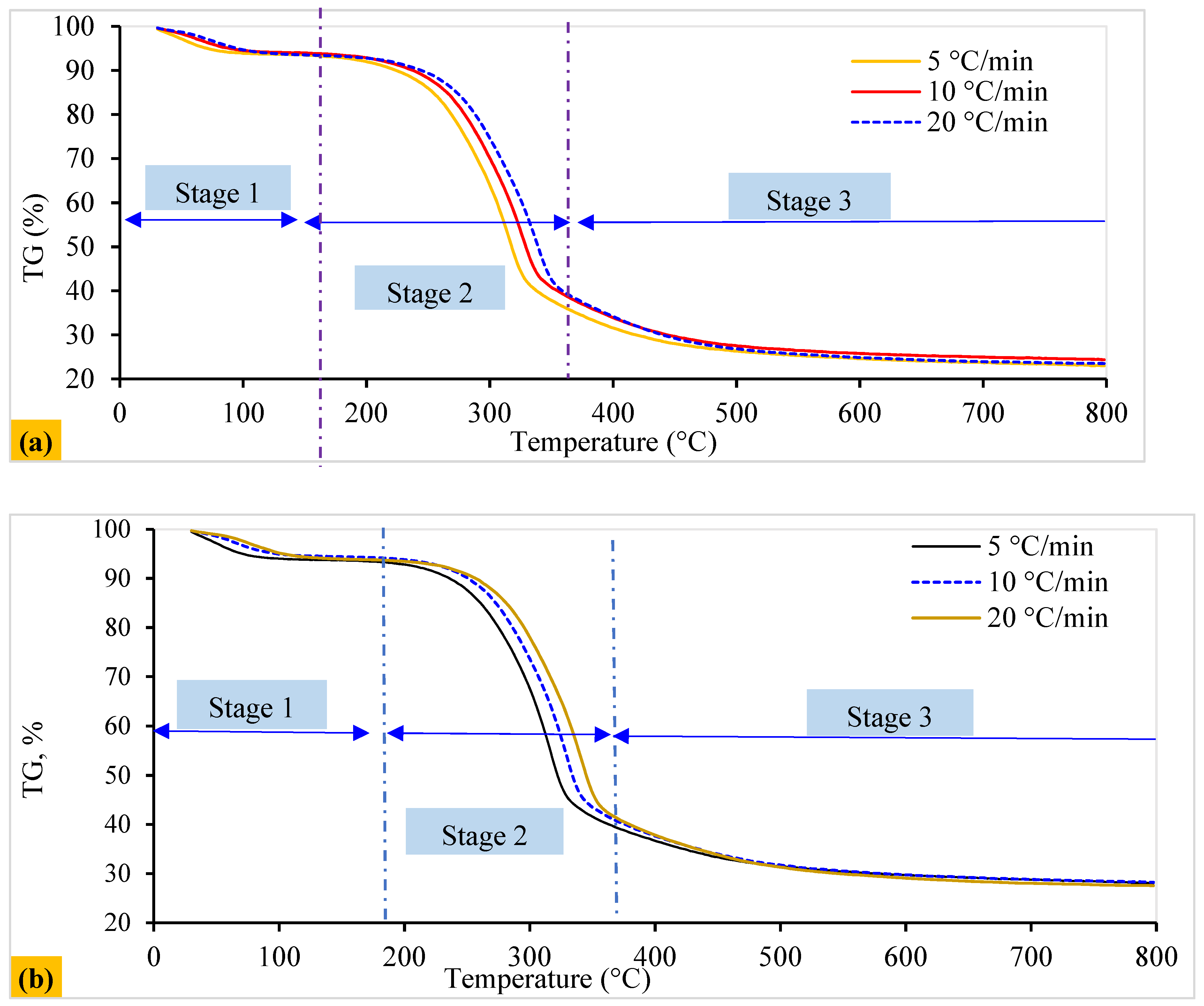
4.2. Thermokinetic Characteristics
4.3. Pyrolysis Process Assessment through a Model-Based Technique
4.4. Reaction Mechanism Analysis Based on Model-Based Results
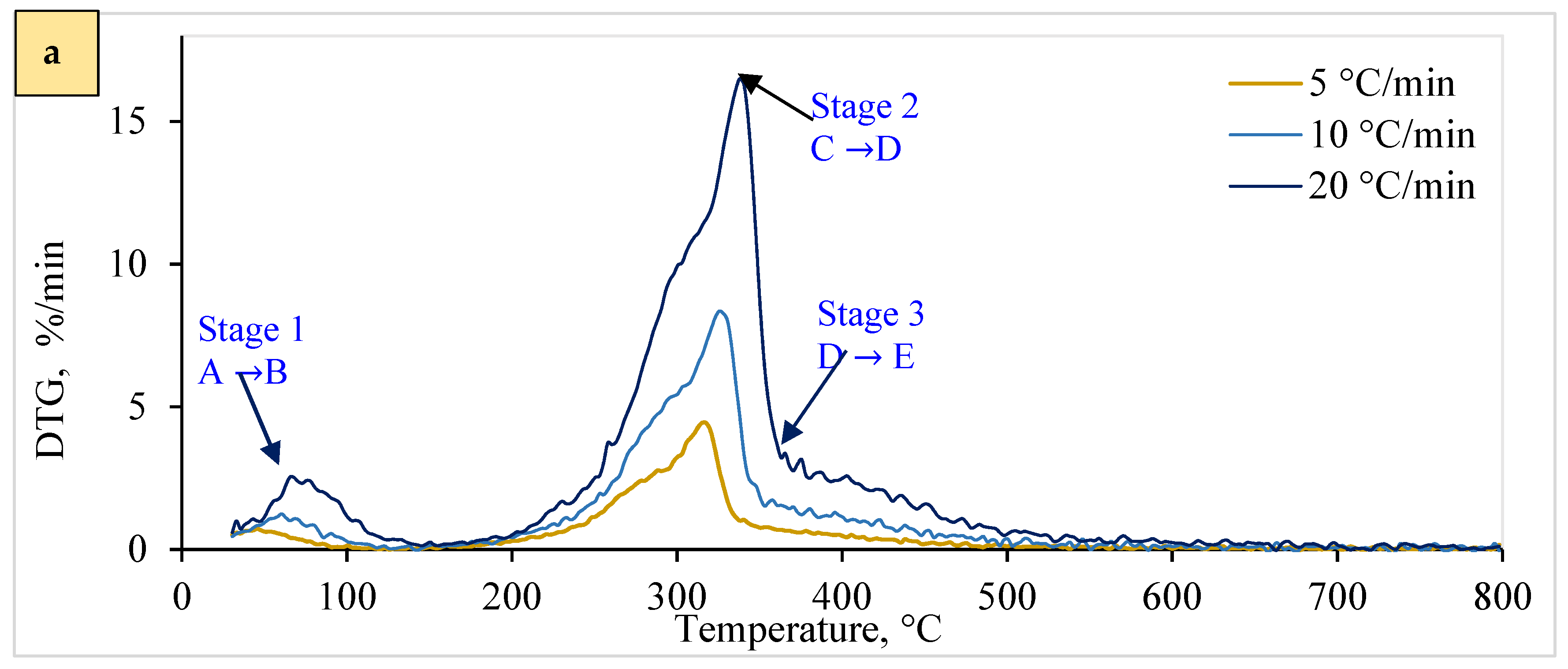
4.4.1. Kinetic Reaction Pathway and Consecutive Stages
4.4.2. Reaction Pathway and Kinetic Triplets
4.4.3. Reaction Pathway and Kinetic Reactions
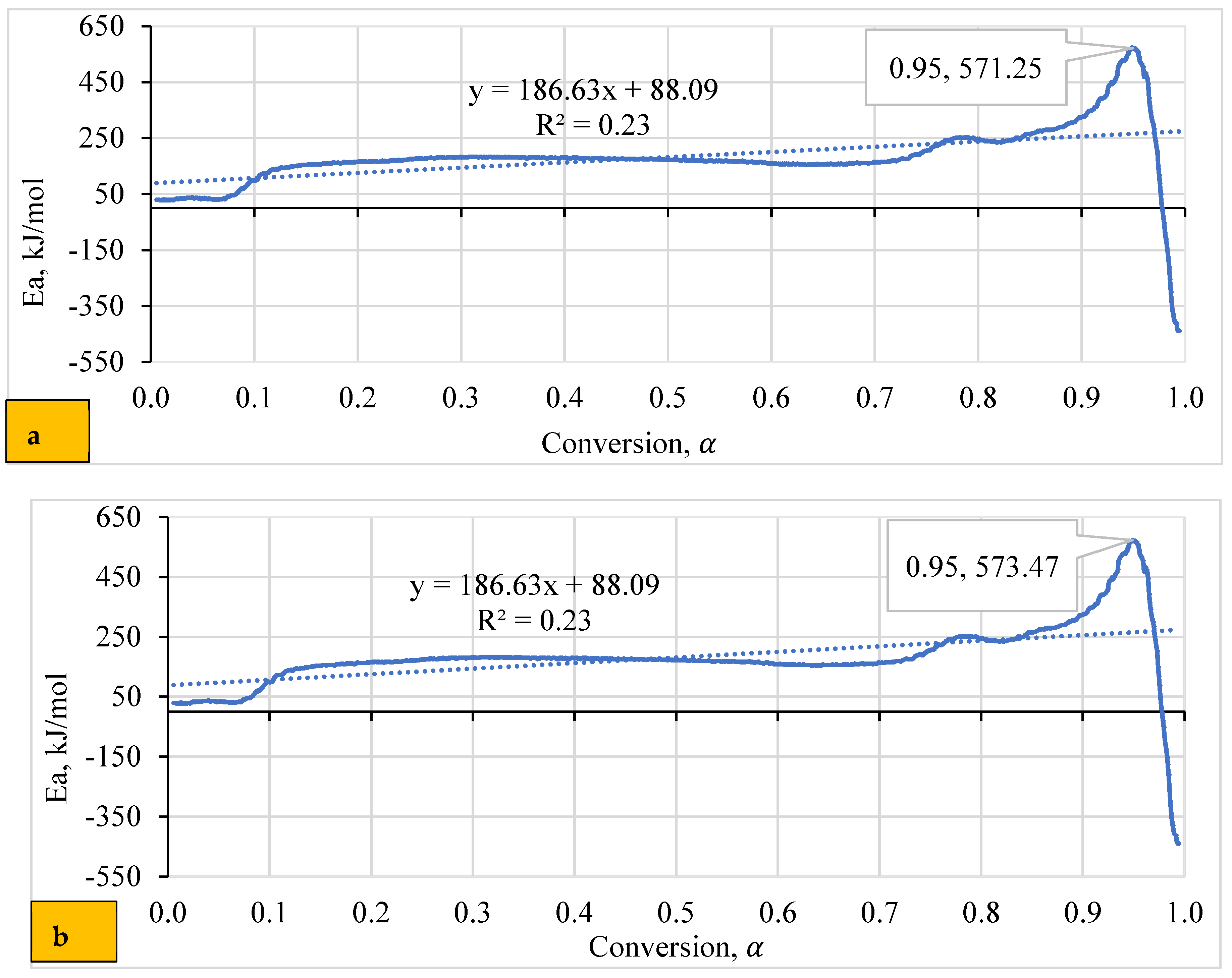
4.5. Dependence of Activation Energy (Eα) on the Degree of Conversion (α)
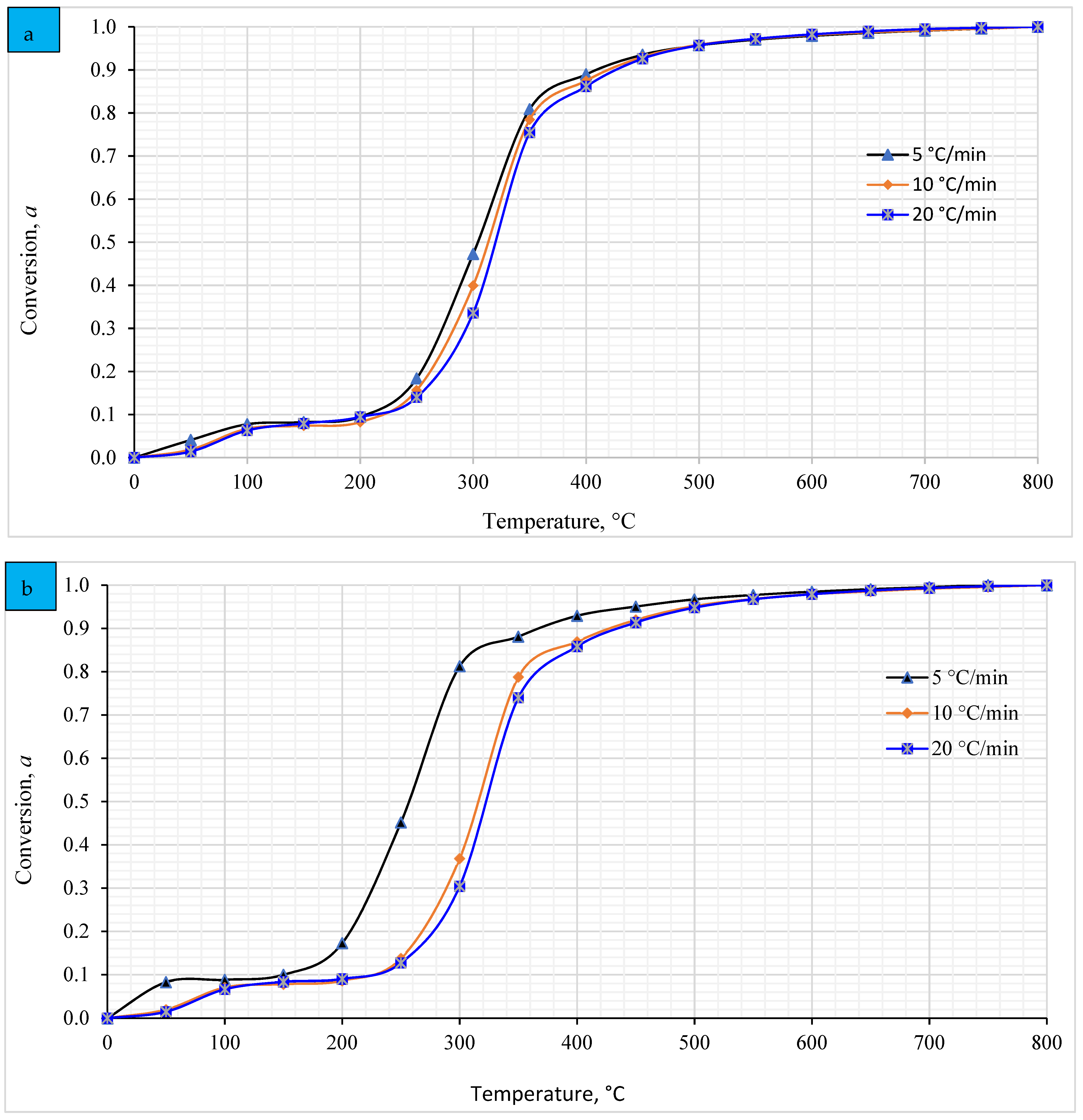
4.6. Relationship between the Temperature and the Conversion Degree (α)
4.7. Compensation Effect
5. Limitations of the Study
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mamun, A.; Glauber, J.W.; Laborde Debucquet, D. How the War in Ukraine Threatens Bangladesh’s Food Security; CGIAR: Montpellier, France, 2023. [Google Scholar]
- Erenstein, O.; Jaleta, M.; Mottaleb, K.A.; Sonder, K.; Donovan, J.; Braun, H.-J. Global trends in wheat production, consumption and trade. In Wheat Improvement: Food Security in a Changing Climate; Springer International Publishing: Cham, Switzerland, 2022; pp. 47–66. [Google Scholar]
- Perkins, G.; Bhaskar, T.; Konarova, M. Process development status of fast pyrolysis technologies for the manufacture of renewable transport fuels from biomass. Renew. Sustain. Energy Rev. 2018, 90, 292–315. [Google Scholar] [CrossRef]
- Nisar, J.; Ali, F.; Malana, M.A.; Ali, G.; Iqbal, M.; Shah, A.; Bhatti, I.A.; Khan, T.A.; Rashid, U. Kinetics of the pyrolysis of cobalt-impregnated sesame stalk biomass. Biomass Convers. Bior. 2020, 10, 1179–1187. [Google Scholar] [CrossRef]
- Czajczyńska, D.; Anguilano, L.; Ghazal, H.; Krzyżyńska, R.; Reynolds, A.; Spencer, N.; Jouhara, H. Potential of pyrolysis processes in the waste management sector. Therm. Sci. Eng. Prog. 2017, 3, 171–197. [Google Scholar] [CrossRef]
- Wuzella, G.; Kandelbauer, A.; Mahendran, A.R.; Müller, U.; Teischinger, A. Influence of thermo-analytical and rheological properties of an epoxy powder coating resin on the quality of coatings on medium density fibreboards (MDF) using in-mould technology. Prog. Org. Coat. 2014, 77, 1539–1546. [Google Scholar] [CrossRef]
- Vyazovkin, S. Isoconversional Kinetics of Thermally Stimulated Processes; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Kan, T.; Strezov, V.; Evans, T.J. Lignocellulosic biomass pyrolysis: A review of product properties and effects of pyrolysis parameters. Renew. Sustain. Energy Rev. 2016, 57, 1126–1140. [Google Scholar] [CrossRef]
- Jelić, D.; Papović, S.; Vraneš, M.; Gadžurić, S.; Berto, S.; Alladio, E.; Gajić, D.; Janković, B. Thermo-analytical and compatibility study with mechanistic explanation of degradation kinetics of ambroxol hydrochloride tablets under non-isothermal conditions. Pharmaceutics 2021, 13, 1910. [Google Scholar] [CrossRef]
- Lateef, H.U.; Kazmi, M.; Tabish, A.N.; Cheema, I.I.; Rashid, M.I. Effect of demineralization on physiochemical and thermal characteristics of wheat straw. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 1–10. [Google Scholar] [CrossRef]
- Radhaboy, G.; Pugazhvadivu, M.; Ganeshan, P.; Raja, K. Influence of kinetic parameters on Calotropis procera by TGA under pyrolytic conditions. Energy Sources Part A-Recovery Util. Environ. Eff. 2019, 45, 8257–8270. [Google Scholar]
- Nath, B.; Chen, G.; Bowtell, L.; Graham, E. Kinetic mechanism of wheat straw pellets combustion process with a thermogravimetric analyser. Heliyon 2023, 9, e20602. [Google Scholar] [CrossRef]
- Zanutto, C.P.; Paladino, E.E.; Evrard, F.; van Wachem, B.; Denner, F. Modeling of interfacial mass transfer based on a single-field formulation and an algebraic VOF method considering non-isothermal systems and large volume changes. Chem. Eng. Sci. 2022, 247, 116855. [Google Scholar] [CrossRef]
- Mureddu, M.; Dessì, F.; Orsini, A.; Ferrara, F.; Pettinau, A. Air-and oxygen-blown characterization of coal and biomass by thermogravimetric analysis. Fuel 2018, 212, 626–637. [Google Scholar] [CrossRef]
- Fonseca, F.G.; Anca-Couce, A.; Funke, A.; Dahmen, N. Challenges in Kinetic Parameter Determination for Wheat Straw Pyrolysis. Energies 2022, 15, 7240. [Google Scholar] [CrossRef]
- Paul, A.S.; Panwar, N.L.; Salvi, B.L.; Jain, S.; Sharma, D. Experimental investigation on the production of bio-oil from wheat straw. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 1–16. [Google Scholar] [CrossRef]
- Naqvi, S.R.; Ali, I.; Nasir, S.; Ali Ammar Taqvi, S.; Atabani, A.E.; Chen, W.-H. Assessment of agro-industrial residues for bioenergy potential by investigating thermo-kinetic behavior in a slow pyrolysis process. Fuel 2020, 278, 118259. [Google Scholar] [CrossRef]
- Luo, L.; Guo, X.; Zhang, Z.; Chai, M.; Rahman, M.M.; Zhang, X.; Cai, J. Insight into pyrolysis kinetics of lignocellulosic biomass: Isoconversional kinetic analysis by the modified friedman method. Energy Fuels 2020, 34, 4874–4881. [Google Scholar] [CrossRef]
- Peng, Y.; Wu, S. The structural and thermal characteristics of wheat straw hemicellulose. J. Anal. Appl. Pyrolysis 2010, 88, 134–139. [Google Scholar] [CrossRef]
- Singh, S.; Tagade, A.; Verma, A.; Sharma, A.; Tekade, S.P.; Sawarkar, A.N. Insights into kinetic and thermodynamic analyses of co-pyrolysis of wheat straw and plastic waste via thermogravimetric analysis. Bioresour. Technol. 2022, 356, 127332. [Google Scholar] [CrossRef]
- Sher, F.; Iqbal, S.Z.; Liu, H.; Imran, M.; Snape, C.E. Thermal and kinetic analysis of diverse biomass fuels under different reaction environment: A way forward to renewable energy sources. Energy Convers. Manag. 2020, 203, 112266. [Google Scholar] [CrossRef]
- Anca-Couce, A.; Tsekos, C.; Retschitzegger, S.; Zimbardi, F.; Funke, A.; Banks, S.; Kraia, T.; Marques, P.; Scharler, R.; de Jong, W.; et al. Biomass pyrolysis TGA assessment with an international round robin. Fuel 2020, 276, 118002. [Google Scholar] [CrossRef]
- Gaitán-Álvarez, J.; Moya, R.; Puente-Urbina, A.; Rodriguez-Zúñiga, A. Thermogravimetric, devolatilization rate, and differential scanning calorimetry analyses of biomass of tropical plantation species of Costa Rica torrefied at different temperatures and times. Energies 2018, 11, 696. [Google Scholar] [CrossRef]
- López Ordovás, J. Construction of a Model for the Design of a Rotary Kiln for Slow Pyrolysis of Biomass–GreenCarbon Project. Ph.D. Thesis, Aston University, Birmingham, UK, 2020. [Google Scholar]
- Khankari, G.; Rajan, D. Utilization of mill rejects with biomass pellets in the existing coal power plants-a novel approach towards sustainability & fuel security. Energy Sources Part A Recovery Util. Environ. Eff. 2023, 45, 12633–12650. [Google Scholar]
- Nath, B.; Chen, G.; Bowtell, L.; Mahmood, R.A. CFDs Modeling and Simulation of Wheat Straw Pellet Combustion in a 10 kW Fixed-Bed Downdraft Reactor. Processes 2024, 12, 863. [Google Scholar] [CrossRef]
- Janković, B. Devolatilization kinetics of swine manure solid pyrolysis using deconvolution procedure. Determination of the bio-oil/liquid yields and char gasification. Fuel Process. Technol. 2015, 138, 1–13. [Google Scholar] [CrossRef]
- Sobek, S.; Werle, S. Isoconversional determination of the apparent reaction models governing pyrolysis of wood, straw and sewage sludge, with an approach to rate modelling. Renew. Energy 2020, 161, 972–987. [Google Scholar] [CrossRef]
- Singh, R.K.; Patil, T.; Sawarkar, A.N. Pyrolysis of garlic husk biomass: Physico-chemical characterization, thermodynamic and kinetic analyses. Bioresour. Technol. Rep. 2020, 12, 100558. [Google Scholar] [CrossRef]
- Huang, J.; Liu, J.; Chen, J.; Xie, W.; Kuo, J.; Lu, X.; Chang, K.; Wen, S.; Sun, G.; Cai, H.; et al. Combustion behaviors of spent mushroom substrate using TG-MS and TG-FTIR: Thermal conversion, kinetic, thermodynamic and emission analyses. Bioresour. Technol. 2018, 266, 389–397. [Google Scholar] [CrossRef]
- Chong, C.T.; Mong, G.R.; Ng, J.-H.; Chong, W.W.F.; Ani, F.N.; Lam, S.S.; Ong, H.C. Pyrolysis characteristics and kinetic studies of horse manure using thermogravimetric analysis. Energy Convers. Manag. 2019, 180, 1260–1267. [Google Scholar] [CrossRef]
- Kartal, F.; Özveren, U. Prediction of activation energy for combustion and pyrolysis by means of machine learning. Therm. Sci. Eng. Prog. 2022, 33, 101346. [Google Scholar] [CrossRef]
- Nath, B.; Chen, G.; Bowtell, L.; Graham, E. An investigation of thermal decomposition behavior and combustion parameter of pellets from wheat straw and additive blends by thermogravimetric analysis. Int. J. Thermofluids 2024, 22, 100660. [Google Scholar] [CrossRef]
- Laidler, K.J. The development of the Arrhenius equation. J. Chem. Educ. 1984, 61, 494. [Google Scholar] [CrossRef]
- Urbanovici, E.; Popescu, C.; Segal, E. Improved iterative version of the Coats-Redfern method to evaluate non-isothermal kinetic parameters. J. Therm. Anal. Calorim. 1999, 58, 683–700. [Google Scholar] [CrossRef]
- Shagali, A.A.; Hu, S.; Li, H.; Chi, H.; Qing, H.; Xu, J.; Jiang, L.; Wang, Y.; Su, S.; Xiang, J. Thermal behavior, synergistic effect and thermodynamic parameter evaluations of biomass/plastics co–pyrolysis in a concentrating photothermal TGA. Fuel 2023, 331, 125724. [Google Scholar] [CrossRef]
- Mandal, S.; Mohalik, N.K.; Ray, S.K.; Khan, A.M.; Mishra, D.; Pandey, J.K. A comparative kinetic study between TGA & DSC techniques using model-free and model-based analyses to assess spontaneous combustion propensity of Indian coals. Process Saf. Environ. Prot. 2022, 159, 1113–1126. [Google Scholar]
- Hu, J.; Yan, Y.; Evrendilek, F.; Buyukada, M.; Liu, J. Combustion behaviors of three bamboo residues: Gas emission, kinetic, reaction mechanism and optimization patterns. J. Clean. Prod. 2019, 235, 549–561. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.; Zhang, W.; Ma, F.; Zhang, Q.; Gu, Q. Pyrolysis of heavy hydrocarbons in weathered petroleum-contaminated soil enhanced with inexpensive additives at low temperatures. J. Clean. Prod. 2021, 302, 127017. [Google Scholar] [CrossRef]
- Wang, S.; Dai, G.; Yang, H.; Luo, Z. Lignocellulosic biomass pyrolysis mechanism: A state-of-the-art review. Prog. Energy Combust. Sci. 2017, 62, 33–86. [Google Scholar] [CrossRef]
- Martín-Lara, M.; Ronda, A.; Blázquez, G.; Pérez, A.; Calero, M. Pyrolysis kinetics of the lead-impregnated olive stone by non-isothermal thermogravimetry. Process Saf. Environ. Prot. 2018, 113, 448–458. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Manić, N.; Janković, B.; Dodevski, V. Model-free and model-based kinetic analysis of Poplar fluff (Populus alba) pyrolysis process under dynamic conditions. J. Therm. Anal. Calorim. 2021, 143, 3419–3438. [Google Scholar] [CrossRef]
- Liu, H.; Xu, G.; Li, G. Pyrolysis characteristic and kinetic analysis of sewage sludge using model-free and master plots methods. Process Saf. Environ. Prot. 2021, 149, 48–55. [Google Scholar] [CrossRef]
- Nebojša, P.; Marija, I.; Kristina, Č. Organizational Culture and Job Satisfaction among University Professors in the Selected Central and Eastern European Countries. Stud. Bus. Econ. 2020, 15, 168–184. [Google Scholar] [CrossRef]
- Karaeva, J.V.; Timofeeva, S.S.; Islamova, S.I.; Gerasimov, A.V. Pyrolysis kinetics of new bioenergy feedstock from anaerobic digestate of agro-waste by thermogravimetric analysis. J. Environ. Chem. Eng. 2022, 10, 107850. [Google Scholar] [CrossRef]
- Vargeese, A.A. A kinetic investigation on the mechanism and activity of copper oxide nanorods on the thermal decomposition of propellants. Combust. Flame 2016, 165, 354–360. [Google Scholar] [CrossRef]
- Janković, B.; Manić, N.; Radović, I.; Janković, M.; Rajačić, M. Model-free and model-based kinetics of the combustion process of low rank coals with high ash contents using TGA-DTG-DTA-MS and FTIR techniques. Thermochim. Acta 2019, 679, 178337. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Favergeon, L.; Koga, N.; Moukhina, E.; Pérez-Maqueda, L.A.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for analysis of multi-step kinetics. Thermochim. Acta 2020, 689, 178597. [Google Scholar] [CrossRef]
- Safiullina, A.S.; Buzyurov, A.V.; Ziganshina, S.A.; Gerasimov, A.V.; Schick, C.; Gorbatchuk, V.V.; Ziganshin, M.A. Using fast scanning calorimetry to study solid-state cyclization of dipeptide L-leucyl-L-leucine. Thermochim. Acta 2020, 692, 178748. [Google Scholar] [CrossRef]
- Khawam, A.; Flanagan, D.R. Solid-state kinetic models: Basics and mathematical fundamentals. J. Phys. Chem. B 2006, 110, 17315–17328. [Google Scholar] [CrossRef] [PubMed]
- Dhyani, V.; Kumar, J.; Bhaskar, T. Thermal decomposition kinetics of sorghum straw via thermogravimetric analysis. Bioresour. Technol. 2017, 245, 1122–1129. [Google Scholar] [CrossRef] [PubMed]
- Nath, B.; Chen, G.; Bowtell, L.; Mahmood, R.A. Assessment of densified fuel quality parameters: A case study for wheat straw pellet. J. Bioresour. Bioprod. 2023, 8, 45–58. [Google Scholar] [CrossRef]
- Qi, K.; Liu, S.-y.; Chen, Y.; Xia, B.; Li, G.-D. A simple post-treatment with urea solution to enhance the photoelectric conversion efficiency for TiO2 dye-sensitized solar cells. Sol. Energy Mater. Sol. Cells 2018, 183, 193–199. [Google Scholar] [CrossRef]
- Ahmad, A.; Yadav, A.K.; Singh, A.; Singh, D.K. A comprehensive machine learning-coupled response surface methodology approach for predictive modeling and optimization of biogas potential in anaerobic Co-digestion of organic waste. Biomass Bioenergy 2024, 180, 106995. [Google Scholar] [CrossRef]
- Vhathvarothai, N.; Ness, J.; Yu, Q.J. An investigation of thermal behaviour of biomass and coal during copyrolysis using thermogravimetric analysis. Int. J. Energy Res. 2014, 38, 1145–1154. [Google Scholar] [CrossRef]
- Rex, P.; Miranda, L.R. Catalytic activity of acid-treated biomass for the degradation of expanded polystyrene waste. Environ. Sci. Pollut. Res. 2020, 27, 438–455. [Google Scholar] [CrossRef] [PubMed]
- Kaur, R.; Gera, P.; Jha, M.K.; Bhaskar, T. Pyrolysis kinetics and thermodynamic parameters of castor (Ricinus communis) residue using thermogravimetric analysis. Bioresour. Technol. 2018, 250, 422–428. [Google Scholar] [CrossRef] [PubMed]
- Torres, C.; Urvina, L.; de Lasa, H. A chemical equilibrium model for biomass gasification. Application to Costa Rican coffee pulp transformation unit. Biomass Bioenergy 2019, 123, 89–103. [Google Scholar] [CrossRef]
- Nath, B.; Chen, G.; Bowtell, L.; Nguyen-Huy, T. Pyrolysis of wheat straw pellets in a pilot-scale reactor: Effect of temperature and residence time. Energy Sci. Eng. 2024. [Google Scholar] [CrossRef]
- Lu, D.; Tabil, L.G.; Wang, D.; Wang, G.; Emami, S. Experimental trials to make wheat straw pellets with wood residue and binders. Biomass Bioenergy 2014, 69, 287–296. [Google Scholar] [CrossRef]
- Nanou, P.; Huijgen, W.; Carbo, M.; Kiel, J. The role of lignin in the densification of torrefied wood in relation to the final product properties. Biomass Bioenergy 2018, 111, 248–262. [Google Scholar] [CrossRef]
- Moukhina, E. Determination of kinetic mechanisms for reactions measured with thermoanalytical instruments. J. Therm. Anal. Calorim. 2012, 109, 1203–1214. [Google Scholar] [CrossRef]
- Soh, M.; Chew, J.J.; Liu, S.; Sunarso, J. Comprehensive kinetic study on the pyrolysis and combustion behaviours of five oil palm biomass by thermogravimetric-mass spectrometry (TG-MS) analyses. BioEnergy Res. 2019, 12, 370–387. [Google Scholar] [CrossRef]
- Anca-Couce, A. Reaction mechanisms and multi-scale modelling of lignocellulosic biomass pyrolysis. Prog. Energy Combust. Sci. 2016, 53, 41–79. [Google Scholar] [CrossRef]
- El-Sayed, S.A.; Mostafa, M.E. Thermal pyrolysis and kinetic parameter determination of mango leaves using common and new proposed parallel kinetic models. RSC Adv. 2020, 10, 18160–18179. [Google Scholar] [CrossRef] [PubMed]
- Mandapati, R.N.; Ghodke, P.K. Kinetics of pyrolysis of cotton stalk using model-fitting and model-free methods. Fuel 2021, 303, 121285. [Google Scholar] [CrossRef]
- Singh, R.K.; Pandey, D.; Patil, T.; Sawarkar, A.N. Pyrolysis of banana leaves biomass: Physico-chemical characterization, thermal decomposition behavior, kinetic and thermodynamic analyses. Bioresour. Technol. 2020, 310, 123464. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Nandi, B.K. Combustion characteristics of high ash Indian coal, wheat straw, wheat husk and their blends. Mater. Sci. Energy Technol. 2021, 4, 274–281. [Google Scholar] [CrossRef]
- Gupta, S.; Gupta, G.K.; Mondal, M.K. Thermal degradation characteristics, kinetics, thermodynamic, and reaction mechanism analysis of pistachio shell pyrolysis for its bioenergy potential. Biomass Convers. Bior. 2020, 12, 4847–4861. [Google Scholar] [CrossRef]
- Radojević, M.; Janković, B.; Jovanović, V.; Stojiljković, D.; Manić, N. Comparative pyrolysis kinetics of various biomasses based on model-free and DAEM approaches improved with numerical optimization procedure. PLoS ONE 2018, 13, e0206657. [Google Scholar] [CrossRef] [PubMed]
- Cai, J.; Wu, W.; Liu, R.; Huber, G.W. A distributed activation energy model for the pyrolysis of lignocellulosic biomass. Green Chem. 2013, 15, 1331–1340. [Google Scholar] [CrossRef]
- Galano, J.-M.; Lee, Y.Y.; Oger, C.; Vigor, C.; Vercauteren, J.; Durand, T.; Giera, M.; Lee, J.C.-Y. Isoprostanes, neuroprostanes and phytoprostanes: An overview of 25 years of research in chemistry and biology. Prog. Lipid Res. 2017, 68, 83–108. [Google Scholar] [CrossRef]
- Saldarriaga, J.F.; Aguado, R.; Pablos, A.; Amutio, M.; Olazar, M.; Bilbao, J. Fast characterization of biomass fuels by thermogravimetric analysis (TGA). Fuel 2015, 140, 744–751. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Y.; Lang, X.; Fan, S. Comparative evaluation of thermal oxidative decomposition for oil-plant residues via thermogravimetric analysis: Thermal conversion characteristics, kinetics, and thermodynamics. Bioresour. Technol. 2017, 243, 37–46. [Google Scholar] [CrossRef] [PubMed]
- Varma, A.K.; Lal, N.; Rathore, A.K.; Katiyar, R.; Thakur, L.S.; Shankar, R.; Mondal, P. Thermal, kinetic and thermodynamic study for co-pyrolysis of pine needles and styrofoam using thermogravimetric analysis. Energy 2021, 218, 119404. [Google Scholar] [CrossRef]
- Zhao, S.; Xu, W.; Gu, H.; Bi, X.; Chen, L.; Zhang, Y. Density functional theory and experimental study on the chemisorption and catalytic decomposition of benzene over exposed bio-char surface: The influence of unsaturated carbon atoms and potassium. Fuel 2022, 326, 125032. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, J.; Liu, J.; Xie, W.; Kuo, J.; Chang, K.; Buyukada, M.; Evrendilek, F.; Sun, S. Thermal conversion behaviors and products of spent mushroom substrate in CO2 and N2 atmospheres: Kinetic, thermodynamic, TG and Py-GC/MS analyses. J. Anal. Appl. Pyrolysis 2019, 139, 177–186. [Google Scholar] [CrossRef]
- Zhang, D.; Cao, C.-Y.; Lu, S.; Cheng, Y.; Zhang, H.-P. Experimental insight into catalytic mechanism of transition metal oxide nanoparticles on combustion of 5-Amino-1H-Tetrazole energetic propellant by multi kinetics methods and TG-FTIR-MS analysis. Fuel 2019, 245, 78–88. [Google Scholar] [CrossRef]
- Várhegyi, G.; Chen, H.; Godoy, S. Thermal decomposition of wheat, oat, barley, and Brassica carinata straws. A kinetic study. Energy Fuels 2009, 23, 646–652. [Google Scholar] [CrossRef]
- Muravyev, N.V.; Pivkina, A.N.; Koga, N. Critical appraisal of kinetic calculation methods applied to overlapping multistep reactions. Molecules 2019, 24, 2298. [Google Scholar] [CrossRef] [PubMed]
- Thakur, L.S.; Varma, A.K.; Mondal, P. Analysis of thermal behavior and pyrolytic characteristics of vetiver grass after phytoremediation through thermogravimetric analysis. J. Therm. Anal. Calorim. 2018, 131, 3053–3064. [Google Scholar] [CrossRef]
- Sharma, K. Carbohydrate-to-hydrogen production technologies: A mini-review. Renew. Sustain. Energy Rev. 2019, 105, 138–143. [Google Scholar] [CrossRef]
- Banerjee, A.; Vithusha, T.; Krishna, B.B.; Kumar, J.; Bhaskar, T.; Ghosh, D. Pyrolysis of de-oiled yeast biomass of Rhodotorula mucilaginosa IIPL32: Kinetics and thermodynamic parameters using thermogravimetric analysis. Bioresour. Technol. 2021, 340, 125534. [Google Scholar] [CrossRef]
- Soria-Verdugo, A.; Rubio-Rubio, M.; Goos, E.; Riedel, U. Combining the lumped capacitance method and the simplified distributed activation energy model to describe the pyrolysis of thermally small biomass particles. Energy Convers. Manag. 2018, 175, 164–172. [Google Scholar] [CrossRef]
- Luo, Z.; Zhou, J. Thermal conversion of biomass. In Handbook of Climate Change Mitigation and Adaptation; Springer: Berlin/Heidelberg, Germany, 2022; pp. 965–1021. [Google Scholar]
- Liang, W.; Ning, X.; Wang, G.; Zhang, J.; Li, R.; Chang, W.; Wang, C. Influence mechanism and kinetic analysis of co-gasification of biomass char and semi-coke. Renew. Energy 2021, 163, 331–341. [Google Scholar] [CrossRef]
- Chelouche, S.; Trache, D.; Tarchoun, A.F.; Abdelaziz, A.; Khimeche, K.; Mezroua, A. Organic eutectic mixture as efficient stabilizer for nitrocellulose: Kinetic modeling and stability assessment. Thermochim. Acta 2019, 673, 78–91. [Google Scholar] [CrossRef]
- Tarchoun, A.F.; Trache, D.; Klapötke, T.M.; Chelouche, S.; Derradji, M.; Bessa, W.; Mezroua, A. A promising energetic polymer from Posidonia oceanica brown algae: Synthesis, characterization, and kinetic modeling. Macromol. Chem. Phys. 2019, 220, 1900358. [Google Scholar] [CrossRef]




| Reaction | Model Name | Code | Functions |
|---|---|---|---|
| Chemical reaction | Zero-dimensional phase boundary | R0 | 0 |
| First-dimensional phase boundary | R1 | f = e | |
| Two-dimensional phase boundary | R2 | f = 2e1/2 | |
| Phase interfacial reaction | First-order reaction | F1 | f = e |
| Contracting cylinder (Second-order) | F2 | f = e2 | |
| Contracting sphere (Third-order | F3 | f = e3 | |
| Random nucleation (Fourth-order) | F4 | f = e4 | |
| Reaction of nth order | Fn | f = en | |
| Diffusion control (Jander model) | D3 | f =1.5e2/3/(1 − e1/3) | |
| Diffusion control (Ginstling model) | D4 | f = 1.5/(e−1/3 − 1) | |
| Nucleation and growth models | 2D nucleation, according to Avarami–Erofeev | A2 | f = 2e·[−ln(e)]1/2 |
| 3D nucleation, according to Avarami–Erofeev | A3 | f = 3e·[−ln(e)]2/3 | |
| n-Dimensional nucleation according to Avrami–Erofeev | An | f = n·e·[−ln(e)](n−1)/n | |
| Auto-cat reaction | Reaction of 1st order with autocatalysis byproduct | C1 | f = e·(1 + AutocatOrder·P) |
| Reaction of nth order with autocatalysis byproduct | Cn | f = en·(1 + AutocatOrder·P) |
| Sample /Pellets | Proximate Analysis, %, As Received, Dry Basis | Ultimate Analysis, %, Dry Basis | Physical Parameter | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MC | VM | FC | Ash | C | H | N | S | O * | Average Length, mm | Mean Diameter, mm | Bulk Density, Kg/m3 | |
| T1 | 6.20 | 75.61 | 11.10 | 7.09 | 44.32 | 4.90 | 0.56 | 0.11 | 50.11 | 22.0 | 8.21 | 244.79 |
| T2 | 3.50 | 53.03 | 31.60 | 11.87 | 45.87 | 6.30 | 0.72 | 0.21 | 46.90 | 37.0 | 8.13 | 607.40 |
| Treatment | Dry wt, % | ||
|---|---|---|---|
| Hemicellulose | Cellulose | Lignin | |
| T2 | 23.30 | 30.00 | 10.60 |
| T1 | 22.40 | 41.30 | 7.00 |
| T1 Pellets | ||||||
|---|---|---|---|---|---|---|
| Reaction pathway: A → B → C → D (Three-step) | ||||||
| Reaction step | Reaction type | Equation | Activation energy | Pre-exponential factor | Reaction order, n | Contribution/slope |
| 1 (A B) | F2: 2nd Order | 45.02 | 1.2 × 102 | - | 0.09 | |
| 2 (C ) | Fn: nth order | 136.04 | 3.9 × 104 | 2.76 | 0.55 | |
| 3 (D ) | Fn: nth order | 358.11 | 5.45 × 1014 | 16.88 | 0.36 | |
| T2 Pellets | ||||||
| Reaction pathway: A → B → C → D (Three-step) | ||||||
| Reaction step | Reaction type | Equation | Activation energy | Pre-exponential factor | Reaction order, n | Contribution/slope |
| 1 (A B) | F2: 2nd Order | 37.29 | 38.24 | - | 0.08 | |
| 2 (C ) | Fn: nth order | 132.87 | 2.4 × 104 | 2.35 | 0.55 | |
| 3 (D ) | Fn: nth order | 227.11 | 2.9 × 109 | 20.0 | 0.36 | |
| Model Scheme | Model Reaction Steps | Concentration Equations | |
|---|---|---|---|
| A—B C—D—E | A → B (step 1) | (10) | |
| (11) | |||
| C → D (step 2) | (12) | ||
| − | (13) | ||
| D → E (step 3) | (14) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nath, B.; Bowtell, L.; Chen, G.; Graham, E.; Nguyen-Huy, T. Pyrolytic Pathway of Wheat Straw Pellet by the Thermogravimetric Analyzer. Energies 2024, 17, 3693. https://doi.org/10.3390/en17153693
Nath B, Bowtell L, Chen G, Graham E, Nguyen-Huy T. Pyrolytic Pathway of Wheat Straw Pellet by the Thermogravimetric Analyzer. Energies. 2024; 17(15):3693. https://doi.org/10.3390/en17153693
Chicago/Turabian StyleNath, Bidhan, Les Bowtell, Guangnan Chen, Elizabeth Graham, and Thong Nguyen-Huy. 2024. "Pyrolytic Pathway of Wheat Straw Pellet by the Thermogravimetric Analyzer" Energies 17, no. 15: 3693. https://doi.org/10.3390/en17153693
APA StyleNath, B., Bowtell, L., Chen, G., Graham, E., & Nguyen-Huy, T. (2024). Pyrolytic Pathway of Wheat Straw Pellet by the Thermogravimetric Analyzer. Energies, 17(15), 3693. https://doi.org/10.3390/en17153693









