Abstract
Increasing oil production is crucial for multilayer co-production. When there are significant differences in the permeability of each layer, an interlayer contradiction arises that can impact the recovery efficiency. After a number of tests and the establishment of a mathematical model, the effects of permeability contrast on oil production for water flooding were revealed. In the meantime, the developed mathematical model was solved using the Buckley–Lever seepage equation. Ultimately, the accuracy of the established model was confirmed by comparing the simulated outcomes of the mathematical model with the experimental results. The findings indicate that when permeability contrast increases, the production ratio of the high-permeability layer will improve. This is primarily due to the low-permeability layer’s production contribution rate decreasing. The accuracy of the established model is ensured by an error of less than 5% between the results of the experiment and the simulation. When the permeability contrast is less than three, the low-permeability layer can be effectively used for three-layer commingled production. However, when the permeability contrast exceeds six, the production coefficient of the low-permeability layer will be less than 5%, which has a significant impact on the layer’s development.
1. Introduction
In recent years, although affected by the global economic slowdown, China’s import and consumption of crude oil have been rising due to the impact of new energy and the decline in international oil prices, as well as other adverse factors. China surpassed the United States in 2018 to become the world’s largest oil importer and the world’s second-largest oil consumer, according to the latest data. China imported about 500 million tons of crude oil in 2019, and its external dependence on crude oil reached a record high of 72%. In contrast, China’s crude oil production finally ended its negative growth in 2019, reaching 191 million tons. Therefore, China’s oil industry is still facing great pressure to increase and stabilize production. At the same time, affected by environmental change, how to reduce fossil fuel energy consumption is also a key consideration in the current development of oil. In order to balance the cost and benefit of exploitation and obtain greater economic benefits and recovery efficiency, oil fields adopt many methods, such as water flooding, hydrocarbon gas flooding, CO2 flooding, and so on. Water flooding is the main way to enhance oil recovery at present. Multilayer commingled production can increase well production and oil recovery. Multilayer commingled production refers to an oilfield development method that utilizes the same pressure at the wellhead to develop each layer in a multilayer oil well. The overall cost of multilayer commingled production is low, and the process is easy to realize. However, there are some differences in the production and reserve utilization of each layer in the process of water flooding when the oil reservoir is heterogeneous. Significant fingering of the water–oil front will occur during the water flooding stage for a multilayer oil reservoir when the permeability contrast is relatively serious, which has a prominent effect on the recovery efficiency (Chai et al., 2021 [1]; Salmo et al., 2021 [2]; Schlueter et al., 2016 [3]; Sorbie et al., 2020 [4]). It is necessary to take into account the influence of reservoir heterogeneity on the development result when multilayer commingled production is carried out (Chai et al., 2022 [5]; Cui et al., 2016 [6]; Shen et al., 2018 [7]; Xu et al., 2021 [8]; Guo et al., 2022 [9]; Tian et al., 2020 [10]; Yang et al., 2022 [11]). It is well known that there are some methods to investigate multilayer commingled production in oil reservoirs, and the main ways include physical simulation experiments (Fu et al., 2024 [12]; Sun et al., 2019 [13]; Huang et al., 2015 [14]) and mathematical models (Kucuk et al., 1986 [15]; Zhong et al., 2022 [16]; Guo et al., 2010 [17]). Xiong et al. (2005) designed three kinds of mathematical models of water flooding, including single-layer, two-layer, and three-layer heterogeneous models. The results showed that the production and utilization of the high-permeability layer were not affected by other layers, and the production and utilization of the middle- and low-permeability layers were determined by the gap [18]. Mo et al. (2011) conducted experiments to study the utilization of each layer in production, contribution ratio, recovery efficiency, and other influencing factors. In addition, mathematical statistics were applied to analyze the relationship between effects and various influencing factors in water flooding. The results showed that the permeability stage difference limit of multilayer injection and production was between 8 and 15. The low-permeability layer could be better utilized when the value was less than eight, and it was difficult to use the low-permeability layer when the value was greater than 15 [19]. Deng et al. (2022) designed a multi-pipe parallel waterflooding experiment and studied the effects of permeability area, water cut, pressure difference, and crude oil viscosity on the combined production in multiple zones. The findings indicate that there is less interference and a weaker difference in the physical characteristics of the layers, the smaller the permeability range. By reducing the water content between layers, interference between layers can be effectively reduced. Increasing the pressure difference can improve the oil displacement efficiency [20]. Fu et al. (2024) created a visual sand-filled pipe experiment model, simulated the oil–water two-phase flow process, and revealed the influencing factors of water-driven oil flow through microscopic flow simulation. The results show that the higher the permeability, the stronger the microheterogeneity, and the lower the overall mobility increase after flooding. The adaptation coefficient increases with increasing drive pressure difference for a given permeability. In multizone combination production, interzone interference occurs, and the greater the interzone difference, the higher the initial production capacity of the combined production well [12]. However, the high-permeability layer is easy to flood, resulting in ineffective water circulation, and the low-permeability pipe is difficult to flood completely, resulting in a slight increase in overall mobility. Through microscopic flow simulation, Li created a visual sand-filled pipe experiment model, simulated the oil–water two-phase flow process, and revealed the influencing factors of water-driven oil flow. The results show that the higher the permeability, the stronger the microheterogeneity, and the lower the overall mobility increases after flooding. The adaptation coefficient increases with increasing drive pressure difference for a given permeability. Combined production in multiple zones involves interzonal interference, and the greater the interzonal difference, the higher the initial production capacity of combined production. Tariq et al. (1978) developed a new model of multilayer commingled production in oil reservoirs, and a numerical inversion method was used to evaluate the analytical solution of the layered system problem in Laplace space. The results showed that false wellbore storage effects would appear in cases involving high-permeability contrast and a small, highly permeable layer. Also, it was found that there were two semi-log permeable layers. It was found that layered system data could be analyzed under certain circumstances to yield information about the permeability ratio and the radius of the layers [21]. Tompang et al. (1988) developed a five-bed linear model to investigate the effect of crossflow on water flooding in a stratified reservoir. The results showed that the oil recovery and crossflow index were dependent on the value of RL (effective length-to-height ratio) for favorable mobility ratios and on the value of RD (vertical-to-horizontal pressure gradients ratio) for unfavorable mobility ratios [22]. Based on the theory of oil–water two-phase unstable flow, Cui et al. (2016) established a mathematical model of multilayer combined production in water-drive reservoirs. The model takes into account interlayer differences such as permeability, oil viscosity, and remaining oil saturation. The results show that the pseudo-current resistance contrast should be less than four in layered single sampling. The model was applied to the Shengtuo oilfield, and the recovery rate increased by 6.08% [6]. Sheng et al. (2018) established a one-dimensional linear flow model and a plane radial flow model for multilayer commingled production using the Buckley–Leverett theory. The parameters, such as seepage resistance, sweep efficiency, and recovery efficiency, can be accurately evaluated by this model. The results show that the difference in seepage resistance is an important factor affecting the recovery efficiency of multilayer commingled production. When the permeability range reaches a certain value, fractional extraction must be undertaken [7]. Xu et al. (2021) used the Fedassi, Buckley–Leverett, and material balance equations to build the percolation model of multilayer commingled production with water displacement. The model was then solved using the iteration method, considering saturation, bottom flow pressure, microelement of the borehole, and oil–water relative permeability. By contrasting the model’s output with that of a standard black oil model, the model’s accuracy was confirmed [8]. Wang et al. (2023) built a mathematical model of multilayer commingled production in oil reservoirs. The simulated results demonstrated that such a validated mathematical model had been upscaled and used to precisely evaluate and forecast the dynamic co-production characteristics of a real multilayer reservoir, with overall deviations of 2.36 percent and 5.50 percent for oil production and water cut, respectively [23]. In the research process, boundary calculations are typically based on experimental data rather than theoretical models. This study focuses on exploring the permeability differential limit in water flood development within multilayer commingled production reservoirs. Initially, indoor core parallel physical simulation experiments were conducted. Through the establishment of a theoretical mathematical model and iterative solution using B-L theory, the variation in liquid production for each layer prior to water breakthrough in low-permeability layers was calculated. Additionally, the changes in recovery degree for each layer and the production contribution rate at different stages were examined. By cross-referencing the results of these analyses, the maximum permissible permeability difference in water drive multilayer commingled production reservoirs was determined. This information is vital in determining appropriate layer divisions and selecting the best development strategies for subsequent layer adjustments.
2. Experiment
The heterogeneity of the reservoir during the development process frequently results in various indices during the exploitation phase. This difference will be magnified and may even have an impact on the regular exploitation of the oil field if the reservoir is developed through water flooding and multilayer system production. Studying the law of multilayer combined oil production with waterflooding is, therefore, essential.
The water advance front of each layer varies greatly due to the highly irregular waterline advance performance of the injected water, which is generally caused by the physical characteristics of crude oil or reservoirs. Additionally, the layer with poorer physical properties is inhibited by the faster displacement of the layer with better physical properties, which has an impact on the oil field’s ability to use the low-permeability layer and, ultimately, its production rate. The middle and high water cut stages are when the majority of oil is produced because of the quick discovery of water, short anhydrous recovery period, and low anhydrous recovery efficiency. The purpose of laboratory experiments is to investigate the interlayer interference dynamic change during the combined production process, as well as the variation law of each layer’s production and other indicators in each water-cutting phase. This paper presents a quantitative characterization of the phenomenon and the law of interlayer interference in various water-bearing phases of the multilayer combined production of water-propulsion oil reservoirs using a physical simulation experiment conducted in a laboratory. These findings are critical for the precise assessment of oil well productivity under conditions of combined production and the proper division or rescheduling of development shifts.
2.1. Materials
Materials include an ISCO displacement pump, 15 sand-filled pipes (500 mm × 38 mm), a six-way valve, quartz sand (40–200 mesh), an intermediate container (oil), deionized water, and a measuring cylinder. The ions content analysis of the formation water is shown in Table 1. The formation water type is CaCl2 with a salinity of 34,880 mg/L.

Table 1.
Ions content analysis of experimental formation water sample.
2.2. Experimental Model Design
In order to further study the law of the influence of intermediate difference on the liquid production of each layer during water flood displacement of a multilayer commingled production reservoir with certain differential conditions, a laboratory physical simulation experiment of a multilayer commingled production general water flood was designed. The experimental model is shown in Figure 1.
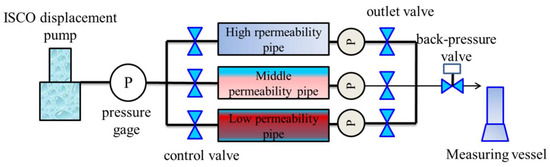
Figure 1.
Core parallel displacement model.
2.3. Experimental Procedure
- (1)
- Quartz sand of different particle sizes is mixed in a certain proportion and placed in a sand-filling pipe to obtain a sand-filling pipe core model. If the proportion of quartz sand particle size is different, the permeability of the sand-filling pipe core model is different. By changing the filling proportion of quartz sand particle size, other sand-filling pipe core models are obtained in turn.
- (2)
- Wash oil, dry, and weigh the sand-filled pipe. The porosity and permeability of each sand-filled tube are measured, respectively.
- (3)
- The sand-filled tubes were pumped out and saturated with salt water, then the effective volume of the pores was obtained, and the absolute liquid phase permeability of each tube was measured. The size and permeability of the sand-filled tubes are shown in Table 2.
- (4)
- The above saltwater-saturated pipes were displaced with crude oil. Data were recorded during the displacing process until only crude oil was produced at the liquid-producing end. At this time, the bound water saturation of each pipe was obtained, and the oil phase permeability under this saturation was measured.
- (5)
- The viscosity of crude oil is 5 mPa·s and the viscosity of aqueous solution is 1.50 mPa·s.
- (6)
- Three sand-filled pipe models were connected in parallel and water flooding was carried out. A fixed flow rate of 3 mL/min was maintained for displacement until the water content at the outlet of the high-permeability layer reached more than 98%. Liquid production and oil production at the outlet of each sand-filled pipe were collected and recorded, and the contribution rate of liquid production at the low-permeability layer was calculated.
- (7)
- Parallel models with different differences were replaced and the experiment was repeated. The physical simulation experimental device is shown in Figure 2.
 Figure 2. Physical picture of general water flood physical simulation experimental device for three-layer commingled mining.
Figure 2. Physical picture of general water flood physical simulation experimental device for three-layer commingled mining.

Table 2.
Sand-filled pipe size and permeability statistics.
Table 2.
Sand-filled pipe size and permeability statistics.
| Scheme | Permeability Max-Min Ratio | Permeability (mD) | ||
|---|---|---|---|---|
| High-Permeability Layer | Middle-Permeability Layer | Low-Permeability Layer | ||
| 1 | 2.8 | 136.4 | 92.7 | 48.9 |
| 2 | 4.2 | 207.9 | 135.2 | 49.5 |
| 3 | 5.1 | 255.51 | 153.1 | 50.1 |
| 4 | 6.2 | 308.14 | 180.5 | 49.7 |
| 5 | 7.4 | 369.26 | 212.58 | 49.9 |
| Length (cm) | 50.98~51.23 | |||
| Diameter (cm) | 3.80 | |||
2.4. Experimental Results
The liquid production of each sand-filled pipe core in each scheme was calculated. Figure 3 shows the liquid production statistics at a certain time point The liquid production multiple of high- and low-permeability layers and the liquid production contribution of low-permeability layers were calculated according to the statistical results, as shown in Table 3. It can be seen that when the step difference increases, the flow ratio of high- and low-permeability layers increases significantly, while the percentage of flow in low-permeability layers decreases significantly.

Figure 3.
Physical diagram of liquid production at each layer.

Table 3.
Data table of the relationship between the percentage of low-permeability flow and the permeability level difference.
3. Establishment of Theoretical Model
3.1. Assumptions
A three-layer water flooding seepage model was established according to the oil–water seepage theory and the following assumptions were made for the model:
- ①
- Constant injection fluid volume, injection, and production balance.
- ②
- Rigid porous media, rock, and fluid are incompressible.
- ③
- Non-piston displacement creates an oil–water two-phase zone.
- ④
- In the stable compartment, interlayer channeling is not considered.
- ⑤
- Starting pressure gradient is not taken into account.
3.2. Governing Equation
The equation of oil–water motion is as follows:
Oil phase:
Water phase:
Total seepage velocity:
The output of each layer before water emergence is calculated, respectively, and expressed as follows:
Seepage resistance:
In different regions, the pressure drop calculation method is different:
Pure oil zone pressure drop:
The water content equation is:
The formula of water drive front is:
3.3. Model Solving
The permeability of each layer is different, and the change in water drive at different stages of each layer is calculated.
Before the first layer (high-permeability layer) encounters water, the output formula for each section before water formation is
Seepage resistance is
The water drive front formula is as follows:
The initial output of each layer can be obtained by output splitting:
The cumulative liquid production of each layer is:
The formula of water drive front becomes:
The above formula of seepage resistance becomes:
is a constant, which can be obtained by numerical integration.
It is assumed that the production pressure difference between the two ends of each layer is fixed, then:
The liquid production of each layer at the first step is obtained by combining the above formula. The oil production of each layer is equal to the liquid production before the high-permeability layer encounters water. Set the time step to 1 day, and the cumulative liquid production on the first day becomes
The fluid production of the next day is calculated by repeated calculation until water is found in the high-permeability layer.
After the first layer (high-permeability) sees water, and before the second layer (medium-permeability) sees water.
After the high-permeability layer sees water, the seepage resistance of the layer is only the resistance of the oil–water two-phase zone, as follows:
The iterative calculation of the above process is repeated until water is found in the high-permeability layer, at which time the water saturation at the exit side of the reservoir is .
The liquid yield of each reservoir can be obtained by substituting the obtained into the above production formula.
Using the saturation surface movement equation, the average water saturation of the high-permeability layer is obtained:
Assuming is a constant value in the element, the water volume of the three reservoirs is obtained by an integral solution, and then the average water saturation is obtained according to it.
Through the water saturation increment of adjacent time steps, the oil production of the high-permeability layer can be obtained. Vp1 is the pore volume of the high-permeability layer, and the liquid production of the medium- and low-permeability layers is equal to the oil production.
In the same way, the water saturation at the outlet side of the medium-permeability layer was calculated. By calculating the seepage resistance, the liquid production of each layer can be obtained successively. The above calculation was repeated to calculate the liquid production of each layer when water is seen in the low-permeability layer.
According to the above calculation process, using a MATLAB programming solution, we can obtain the change in liquid production of each layer.
3.4. Study on Permeability Differential Limit
In order to explore the permeability differential limit of multilayer reservoir commingled production, its approximate range was determined according to the existing research results. The designed permeability differential ranges from 1 to 10 groups, and the permeability of the designed middle-permeability layer is the average permeability of the reservoir. The permeability of each layer under different levels of differential conditions is shown in Table 4, and the other parameters of the model are listed in Table 5.

Table 4.
Statistical table of permeability under different permeability ratios.

Table 5.
Reservoir parameters of three-layer commingled water flooding model.
The above model parameters and permeability data under different levels of poor conditions were substituted for an iterative solution, and the relationship between the contribution rate of daily production of the low-permeability layer and the multiple of daily liquid production of high- and low-permeability layers and water flooding time was calculated, as shown in Figure 4 below. The calculation result of the yield contribution rate of the low-permeability layer when the water content of the high-permeability layer reaches 98% is shown in Figure 5.
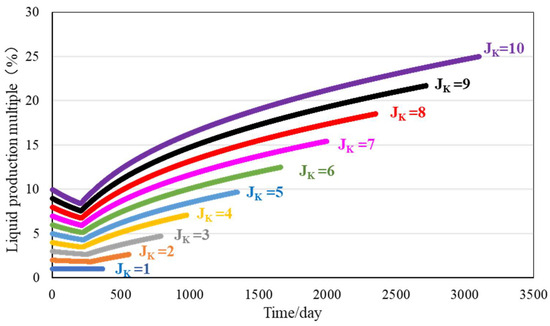
Figure 4.
Daily liquid multiples of high- and low-permeability layers.
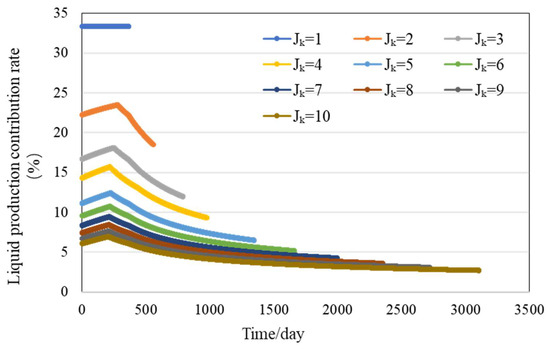
Figure 5.
Contribution rate of daily yield of low-permeability layer.
As shown in Figure 4, the multiples of high- and low-permeability layers increase with the increase in the permeability difference between layers and also increase with the passage of time. As shown in Figure 5, when the step difference increases, the contribution rate of the daily yield of the low-permeability layer decreases, while that of the high-permeability layer decreases with time after water is seen.
Taking 1000 days of injection and production as the node, when the step difference is more than three, the liquid production multiple of the high- and low-permeability layers reaches five, and the liquid production contribution rate of the low-permeability layer is less than 15%. In this case, the low-permeability layer can be utilized to a certain extent. When the gradient difference is more than six, the liquid production multiple of the high-permeability layer is 10, the liquid production contribution rate of the low-permeability layer is less than 10%, and when the low-permeability layer sees water (1500~2000 days), its production contribution rate is less than 5%. It is suggested to adjust the layers at this time, such as the single-mining low-permeability layer, to improve the utilization degree.
4. Verification and Analysis of Mathematic Model
The contribution rate of the low-permeability layer flow rate or the proportion of relative water absorption when the water content of the high-permeability layer reaches 98 percent can be used to characterize the reservoir displacement effect for multilayer commingled oil production reservoirs. Thus, the multiple relation of low-permeability layer flow rate (high-permeability layer water content: 98 percent) and the percentage of low-permeability layer flow rate obtained by the theoretical calculation and experiment were compared in accordance with the data results obtained by the above two methods. Figure 6 and Figure 7 present the comparison.
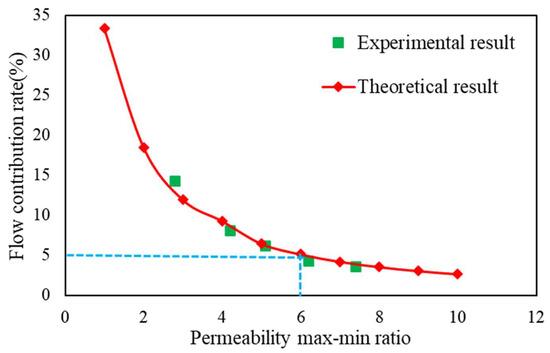
Figure 6.
Flow contribution rate of low-permeability layer (fw1 ≥ 98%).
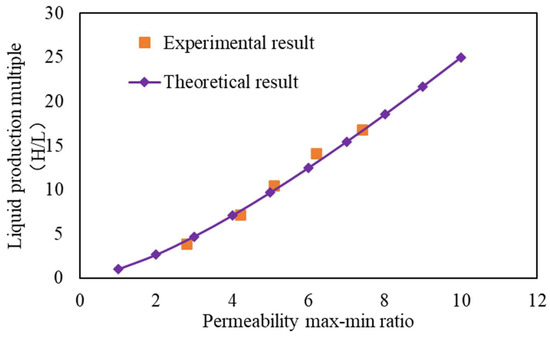
Figure 7.
High- and low-permeability flow ratio (fw1 ≥ 98%).
The similarity between the theoretical and experimental data calculation results confirms each other’s dependability. As illustrated in Figure 7, there is a certain linear relationship between the flow ratio of the high- and low-permeability layers and the grade difference when the water content of the high-permeability layer surpasses 98 percent. As multilayer combined mining develops, the grade difference causes the low-permeability layer’s flow rate to continuously decrease, which lowers the low-permeability layer’s utilization degree relative to the high-permeability layer. Simultaneously, the computation results show that the low-permeability layer’s flow ratio is greater than 4.5, and its flow contribution rate is less than 15% when the step difference is larger than three. Although there is some utility for the low-permeability layer in this situation, the flow contribution rate is minimal. The contribution rate of the low-permeability layer is less than 5%, the flow ratio of the high- and low-permeability layers is more than 12, and the low-permeability layer’s application degree is very low when the gradient difference is greater than six.
Therefore, when there is a significant classification difference, it is advised that strata adjustment be implemented to improve the utilization degree in accordance with actual development needs in order to ensure the utilization degree of the entire reservoir under normal injection–production conditions. The low-permeability layer can be utilized to some extent when the difference is less than three. In this paper, the difference limits are three and six. To increase the level of reservoir utilization, it is advised to avoid commingled production when it surpasses six.
5. Conclusions
- (1)
- The results of the displacement experiment conducted in the parallel core demonstrate that as permeability contrast increases, the production ratios of high- and low-permeability will also improve. This is primarily due to the fact that the production contribution rate for the low-permeability layer will decrease.
- (2)
- Using the Buckley–Lever (B-L) seepage equation, the mathematical model of multilayer combined production for water flooding in oil reservoirs has been established. When comparing simulated and experiment results, the error is less than 5%, demonstrating the accuracy of the established model.
- (3)
- When the permeability contrast is less than three, the experiment and the simulated results demonstrate that the low-permeability layer’s water flooding effect is superior and can be utilized to some extent. However, when the gradient difference is greater than six, the low-permeability layer’s production contribution rate is less than five percent.
Author Contributions
L.T.: Conceptualization, Investigation, Methodology, Writing-original draft. X.C.: Conceptualization, Project administration, Writing-review and editing. L.Z.: Writing-review and editing. W.Z.: Writing-review and editing. Y.Z.: Formal analysis. J.W. (Jiaxing Wang): Software. J.W. (Jianguo Wang): Resources. All authors have read and agreed to the published version of the manuscript.
Funding
National Natural Science Foundation of China (51974329) and National Major Science and Technology Projects of China (2016ZX05047-005-001).
Data Availability Statement
The datasets used during the current study available from the corresponding author on reasonable request.
Acknowledgments
The authors would like to acknowledge the funding by project (51974329), sponsored by the National Natural Science Foundation of China, and project (2016ZX05047-005-001), sponsored by the National Major Science and Technology Projects of China. The authors also thank the editors and reviewers for their critical comments, which greatly improved our manuscript.
Conflicts of Interest
Author Lei Zhang and Wenbo Zhang were employed by Tianjin Branch of CNOOC Ltd. and Cnooc Research Institute Ltd. Liability Company, respectively. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclature
| Oil phase flow velocity, m/s; | |
| Water phase seepage velocity, m/s; | |
| Total seepage velocity, m/s; | |
| Viscosity of crude, mPa·s; | |
| Viscosity of water, mPa·s; | |
| Porosity, %; | |
| Absolute permeability, mD; | |
| Oil phase relative permeability; | |
| Water phase relative permeability; | |
| Total flow, m3/s; | |
| Seepage cross section area, m2; | |
| Thickness of each reservoir, m; | |
| Seepage resistance of each layer, mPa·s/(D·m); | |
| Pressure drop in oil–water two-phase zone, MPa; | |
| Pressure drop in oil–water two-phase zone, MPa; | |
| Distance from supply edge to well row, m; | |
| Location of oil–water front in each layer, m; | |
| Water saturation, %; | |
| Oil saturation, %; | |
| Irreducible water saturation, %; | |
| Exit side water saturation, %; | |
| Derivative of fractional rate corresponding to water flooding front saturation; | |
| Pore volume of the hypertonic layer, m3; | |
| Cumulative fluid production of each reservoir, m3. |
References
- Wei, C.; Raad SM, J.; Leonenko, Y.; Hassanzadeh, H. Correlations for prediction of hydrogen gas viscosity and density for production, transportation, storage, and utilization applications. Int. J. Hydrogen Energy 2023, 48, 34930–34944. [Google Scholar] [CrossRef]
- Salmo, I.C.; Sorbie, K.S.; Skauge, A. The impact of rheology on viscous oil displacement by polymers analyzed by pore-scale network modelling. Polymers 2021, 13, 1259. [Google Scholar] [CrossRef]
- Schluter, S.; Berg, S.; Rucker, M.; Armstrong, R.T.; Vogel, H.; Hilfer, R.; Wildenschild, D. Pore-scale displacement mechanisms as a source of hysteresis for two-phase flow in porous media. Water Resour. Res. 2016, 52, 2194–2205. [Google Scholar] [CrossRef]
- Sorbie, K.S.; Al Ghafri, A.Y.; Skauge, A.; Mackay, E.J. On the modelling of immiscible viscous fingering in two-phase flow in porous media. Transp. Porous Media 2020, 135, 331–359. [Google Scholar] [CrossRef]
- Chai, X.; Tian, L.; Dong, P.; Wang, C.; Peng, L.; Wang, H. Study on recovery factor and interlayer interference mechanism of multilayer co-production in tight gas reservoir with high heterogeneity and multi-pressure systems. J. Pet. Sci. Eng. 2022, 210, 109699. [Google Scholar] [CrossRef]
- Cui, C.Z.; Xu, J.P.; Wang, D.P.; Liu, Z.-H.; Huang, Y.-S.; Geng, Z.-L. Layer regrouping for water-flooded commingled reservoirs at a high water-cut stage. Pet. Sci. 2016, 13, 272–279. [Google Scholar] [CrossRef][Green Version]
- Shen, F.; Cheng, L.; Sun, Q.; Huang, S. Evaluation of the vertical producing degree of commingled production via waterflooding for multilayer offshore heavy oil reservoirs. Energies 2018, 11, 2428. [Google Scholar] [CrossRef]
- Xu, J.; Hu, X.; Ning, B. Dynamic interference behaviors of arbitrary multilayer commingling production in heavy oil reservoirs with water flooding. ACS Omega 2021, 6, 10005–10012. [Google Scholar] [CrossRef]
- Guo, W.; Fu, S.; Li, A.; Xie, H.; Cui, S.; Nangendo, J. Experimental research on the mechanisms of improving water flooding in fractured-vuggy reservoirs. J. Pet. Sci. Eng. 2022, 213, 110383. [Google Scholar] [CrossRef]
- Chai, R.; Liu, Y.; Xue, L.; Rui, Z.; Zhao, R.; Wang, J. Formation damage of sandstone geothermal reservoirs: During decreased salinity water injection. Appl. Energy 2022, 322, 119465. [Google Scholar] [CrossRef]
- Yang, Y.; Liao, G.; Xiong, W.; Shen, R.; Zhang, J.; Li, Q.; Wang, S.; Zhang, J.; Tan, L.; Shao, G. Physical and numerical simulation of inter-fracture flooding in heterogeneous tight oil reservoirs. Energy Rep. 2022, 8, 12970–12978. [Google Scholar] [CrossRef]
- Fu, D.; Fu, Y.; Zhang, Y.J.; Wang, M. Experimental simulation study on influencing factors of liquid production capacity in heterogeneous water drive reservoirs. Phys. Fluids 2024, 36, 016612. [Google Scholar] [CrossRef]
- Sun, L.; Li, B.; Jiang, H.; Li, Y.; Jiao, Y. An injectivity evaluation model of polymer flooding in offshore multilayer reservoir. Energies 2019, 12, 1444. [Google Scholar] [CrossRef]
- Huang, S.J.; Kang, B.T.; Cheng, L.S.; Zhou, W.; Chang, S. Quantitative characterization of interzonal interference and productivity prediction of directional well in offshore common heavy oil reservoirs. Pet. Explor. Dev. 2015, 42, 488–495. [Google Scholar] [CrossRef]
- Kucuk, F.; Karakas, M.; Ayestaran, L. Well testing and analysis techniques for layered reservoirs. SPE Form. Eval. 1986, 1, 342–354. [Google Scholar] [CrossRef]
- Zhong, H.; He, Y.; Zhao, X.; Peng, X. Theoretical study on the micro-flow mechanism of polymer flooding in a double heterogeneous oil layer. Energies 2022, 15, 3236. [Google Scholar] [CrossRef]
- Chai, R.; Liu, Y.; Wang, J.; Liu, Q.; Rui, Z. CO2 utilization and sequestration in Reservoir: Effects and mechanisms of CO2 electrochemical reduction. Appl. Energy 2022, 323, 119584. [Google Scholar] [CrossRef]
- Xiong, W.; Gao, S.S.; Gao, H.J.; Long, H. Application of physical simulation results of interlayer heterogeneous reservoir to flow unit division. Daqing Pet. Geol. Dev. 2005, 2, 34–36+105. [Google Scholar]
- Mo, J.W.; Sun, W.; Yang, X.P.; Han, Z.Y.; Wu, M.J. Study on water flooding effect and influencing factors of severe interlayer heterogeneous reservoir. J. Northwest Univ. (Nat. Sci. Ed.) 2011, 41, 113–118. [Google Scholar]
- Deng, X.; Huang, X.; Ye, Q.; Li, S.; Yu, C.; Zhang, X.; Wang, Z. Experimental research on production law of multilayer heterogeneous reservoirs. Front. Earth Sci. 2022, 10, 990554. [Google Scholar] [CrossRef]
- Tariq, S.M.; Ramey, H.J. Drawdown Behavior of a Well with Storage and Skin Effect Communicating with Layers of Different Radii and Other Characteristics. In Proceedings of the SPE Annual Fall Technical Conference and Exhibition, Houston, TX, USA, 1 October 1978. [Google Scholar]
- Tompang, R.; Kelkar, B.G. Prediction of Waterflood Performance in Stratified Reservoirs. Chest 1988, 92, 657–662. [Google Scholar]
- Wei, C.; Liu, Y.; Deng, Y.; Cheng, S.; Hassanzadeh, H. Temperature transient analysis of naturally fractured geothermal reservoirs. SPE J. 2022, 27, 2723–2745. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).