Long Short-Term Memory Autoencoder and Extreme Gradient Boosting-Based Factory Energy Management Framework for Power Consumption Forecasting
Abstract
1. Introduction
- Superior predictive performance for mid to long-term forecasting: our method demonstrated significant improvements in various evaluation metrics compared to existing models, highlighting its capability in forecasting complex industrial energy systems over mid to long-term periods.
- Enhanced handling of non-standard events: by integrating event indicators and SMP data, the model adeptly handles non-standard events and holidays, which are critical for accurate mid to long-term forecasting, traditionally a weak point in existing forecasting models.
- Optimized data preprocessing: the application of EM-PCA not only improved the handling of missing data but also effectively managed feature extraction, which is critical for enhancing the predictive accuracy of complex models in mid to long-term scenarios.
2. Related Work
2.1. Energy Management in Smart Manufacturing
2.2. Data Preprocessing in Forecasting
2.3. Prediction Horizons
2.4. Time Series Forecasting Models
3. Materials and Methods
3.1. Data Preprocessing in Smart Manufacturing
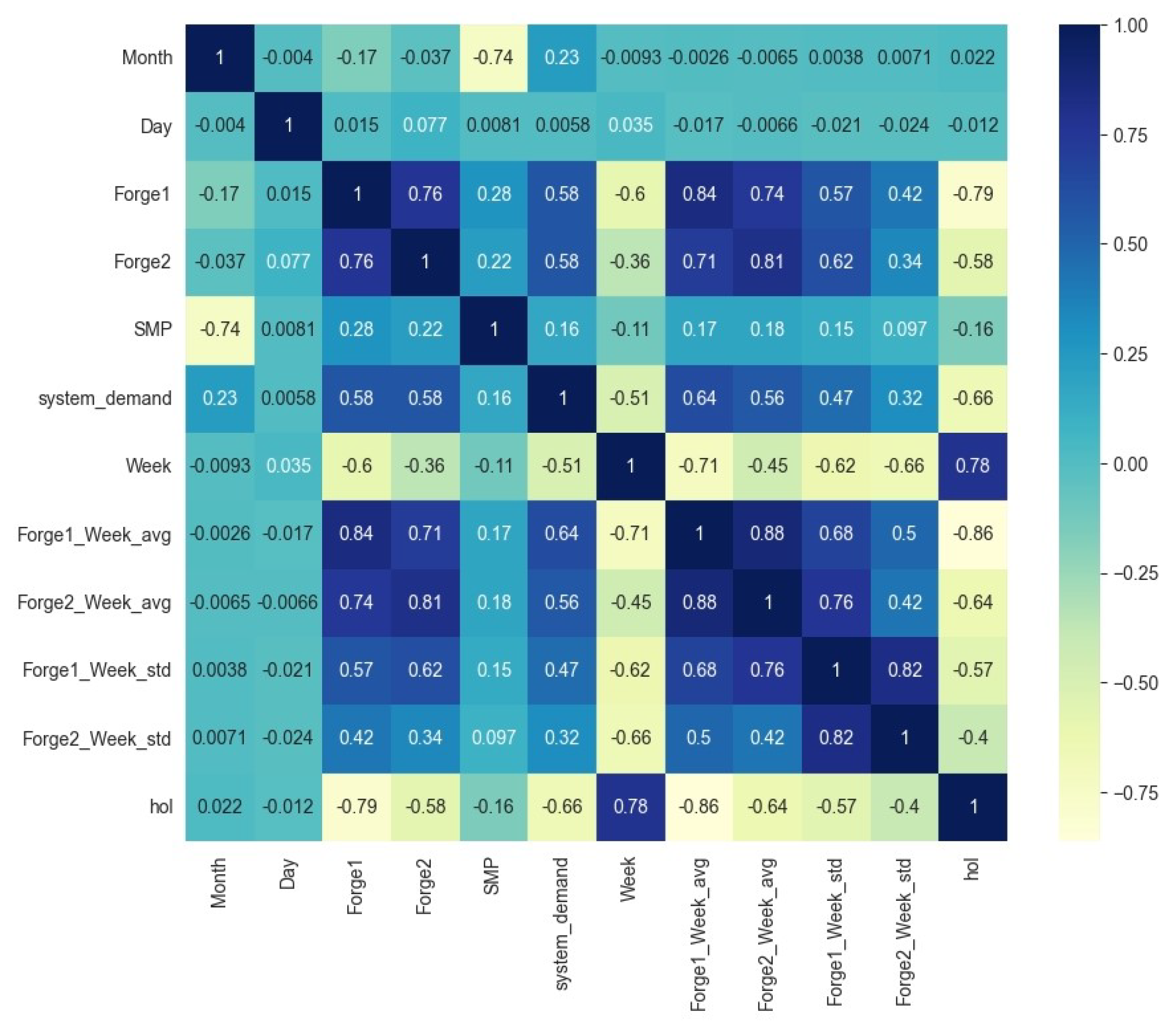
3.1.1. Key Variables and Feature Setting
3.1.2. Handling Missing Values and Outliers
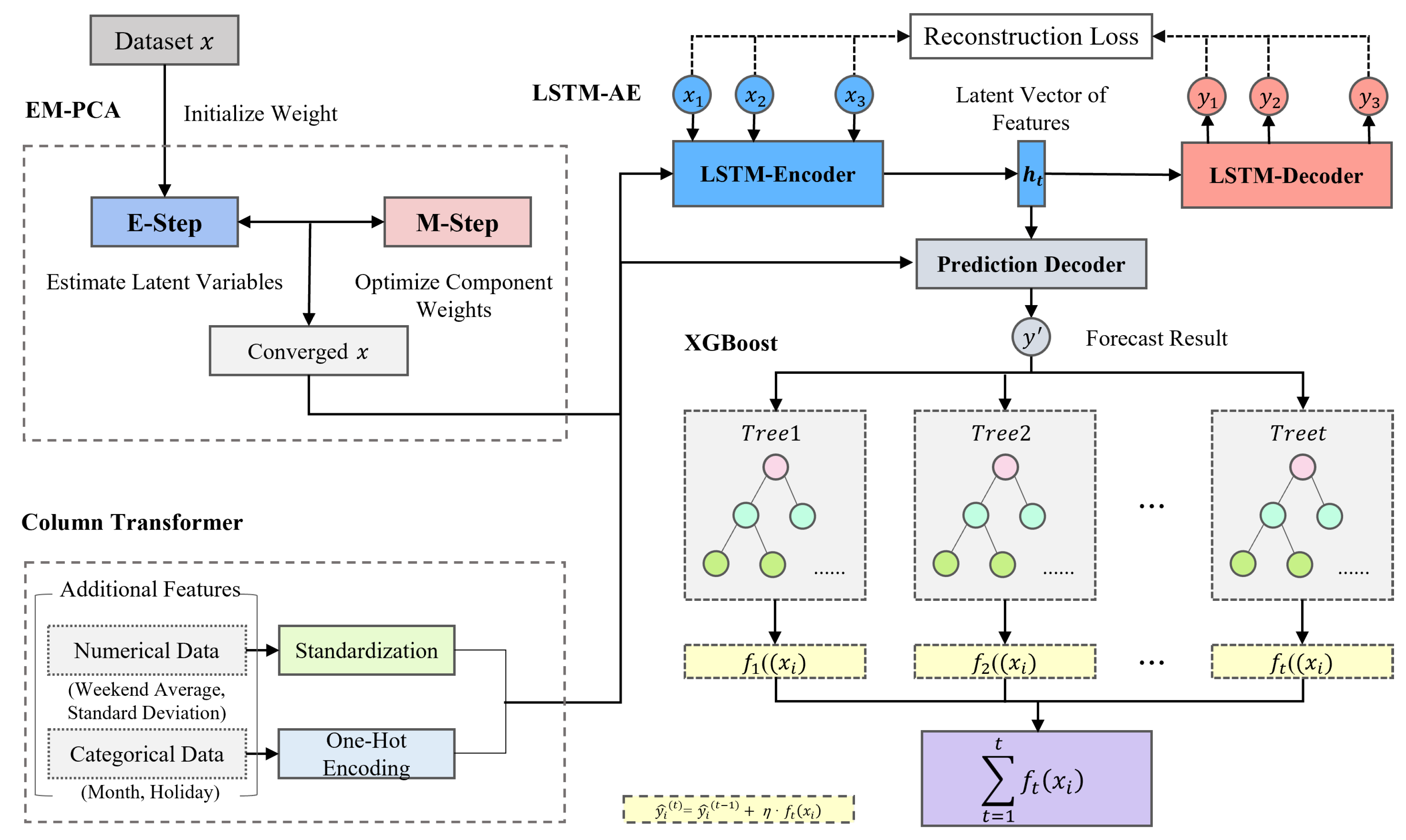
3.1.3. Data Preprocessing Optimization Using EM-PCA
- Initialization: provide initial estimates for missing data X, filling missing values with initial means or medians and performing initial principal component estimates.
- Application of EM-PCA: use EM-PCA to handle missing data, reducing dimensionality while preserving key characteristics.
- Feature extraction: extract important features from the reduced-dimensionality data for use in the modeling phase.
- E-step (expectation step) (1): calculate the expected values of missing data given the current principal component estimates.
- M-step (maximization step) (2): Use the complete data calculated in the E-step to re-estimate the principal components. Repeat E-step and M-step until convergence, producing an optimal dataset with imputed missing values.
3.1.4. Feature Extraction Preprocessing
3.2. LSTM-AE and XGBoost Model Ensemble
3.2.1. Feature Extraction Using Long Short-Term Memory Autoencoder Model
3.2.2. Prediction Using Extreme Gradient Boosting Model
3.2.3. Hyperparameter Tuning
| Algorithm 1 Hyperparameter tuning using RandomizedSearchCV |
|
4. Experiment and Results
4.1. Experimental Environment
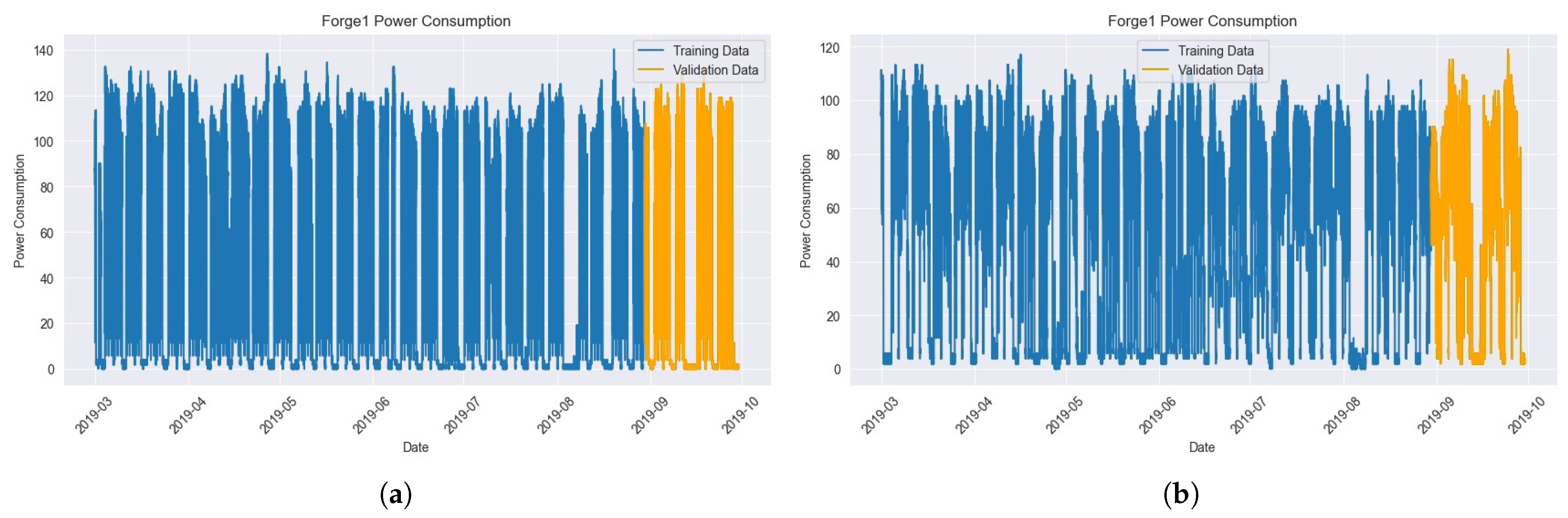
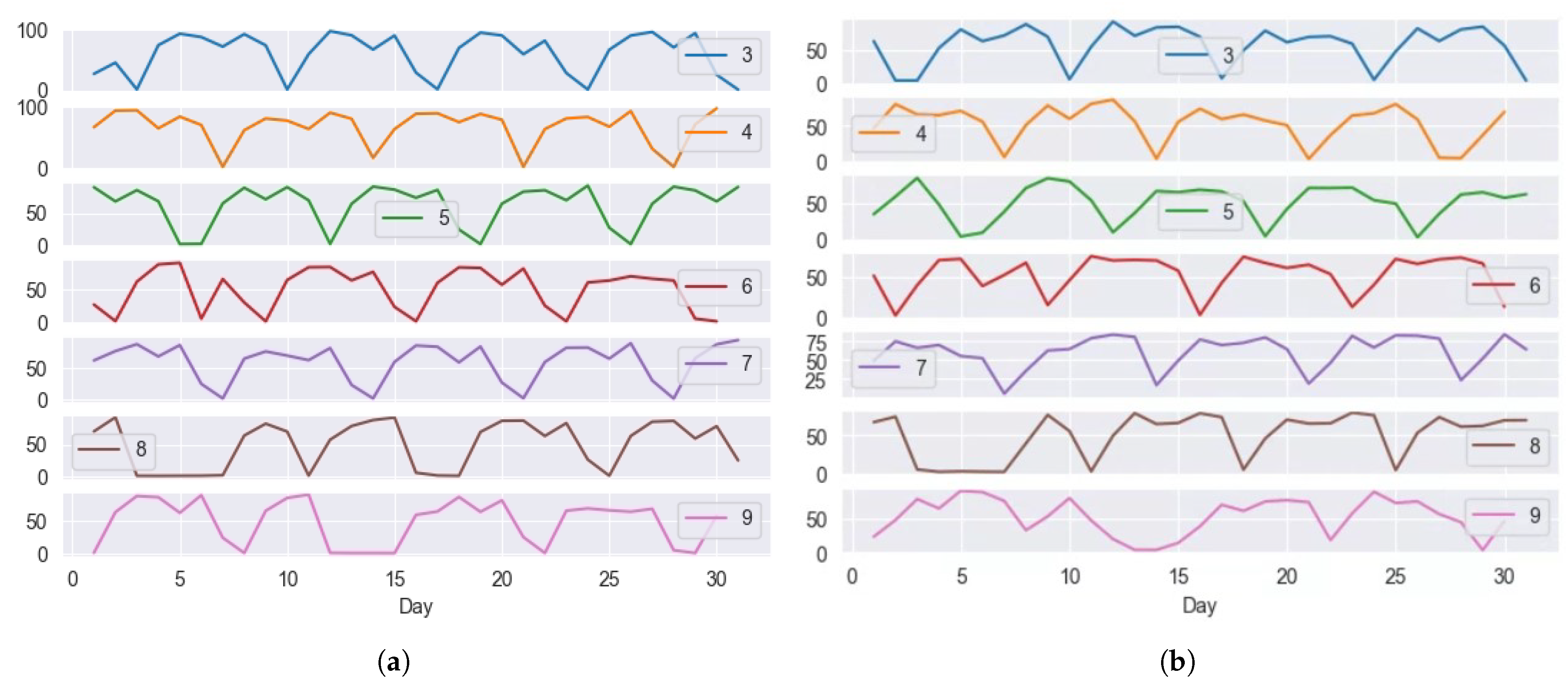
4.2. Dataset
4.3. Performance Metrics
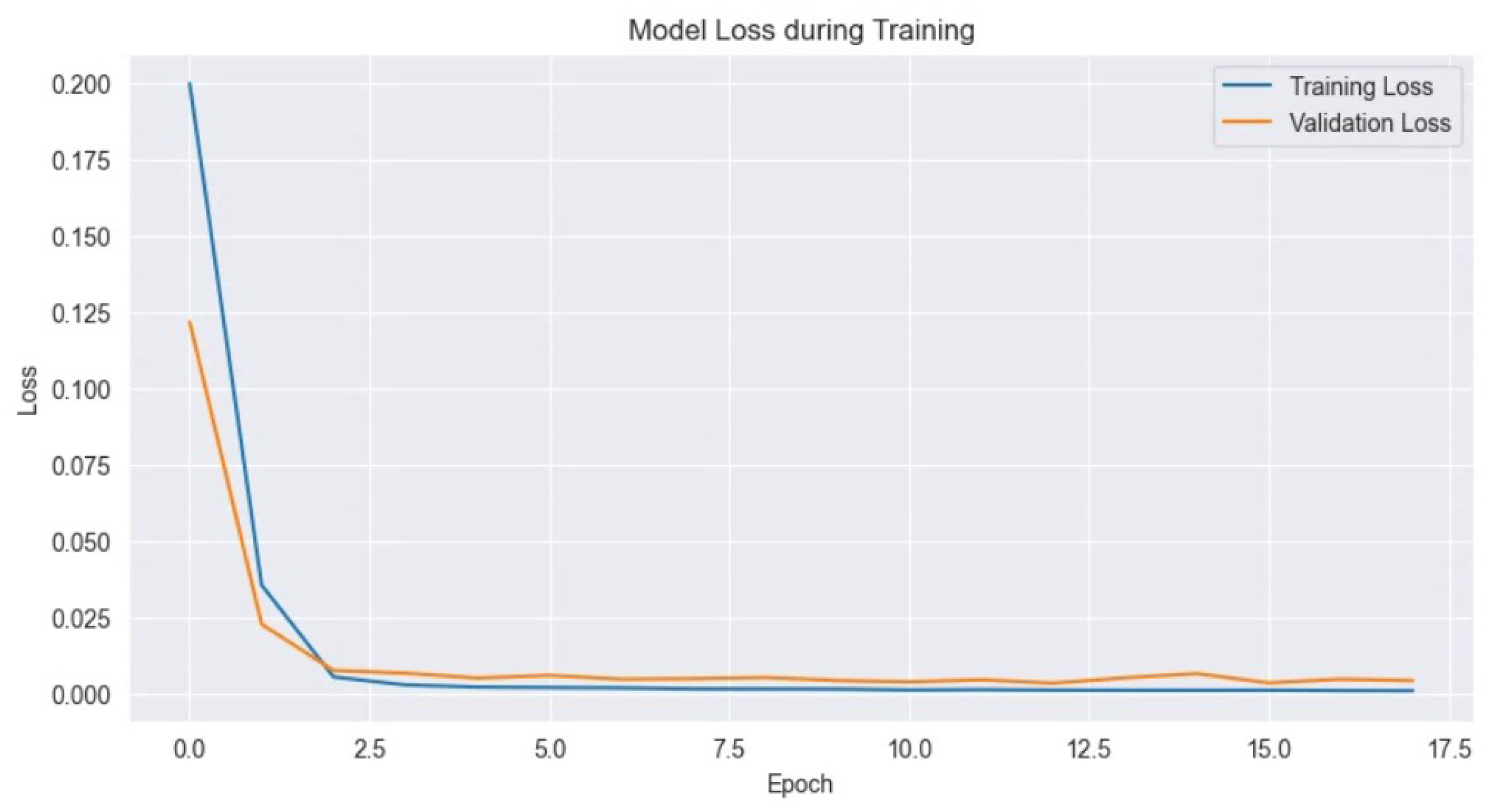
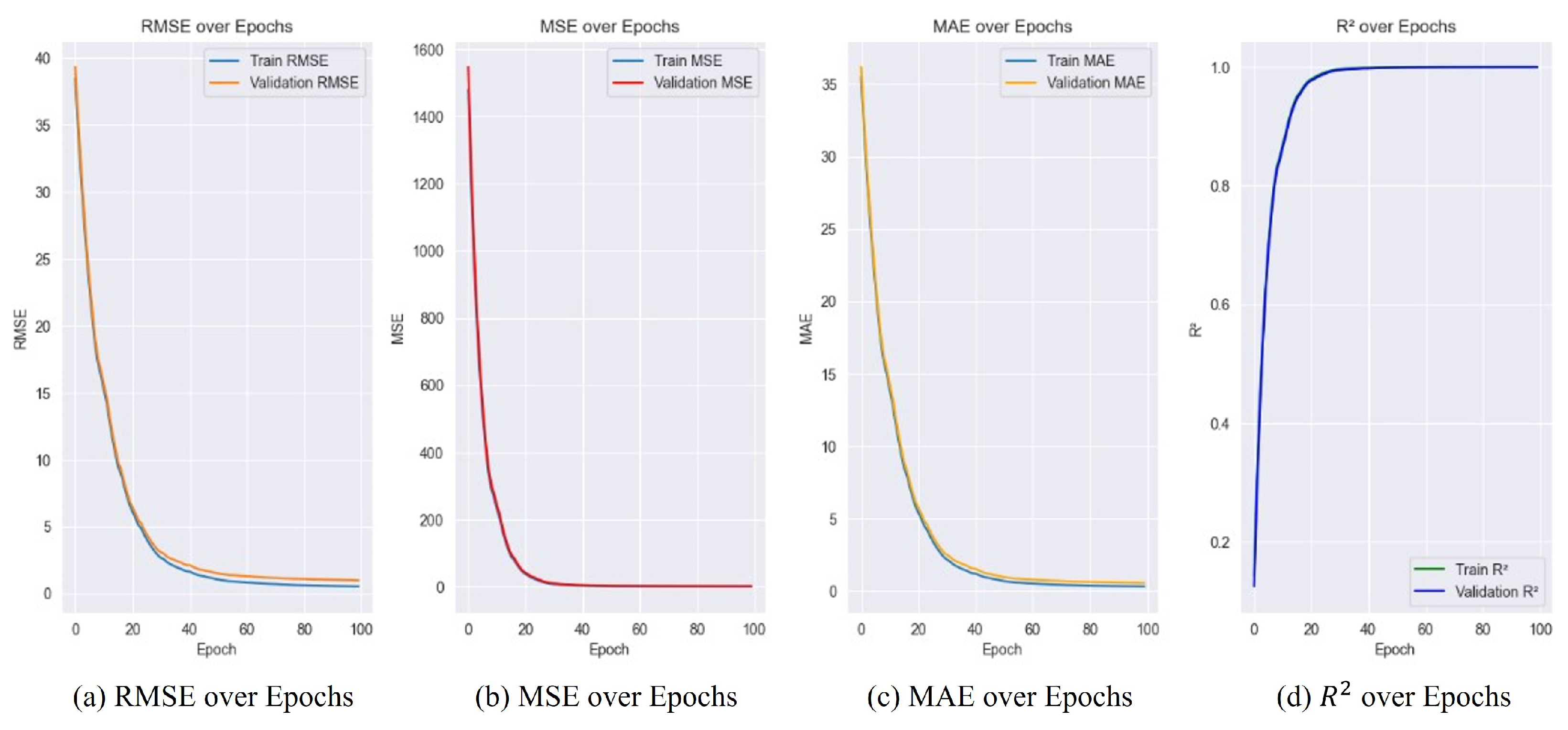
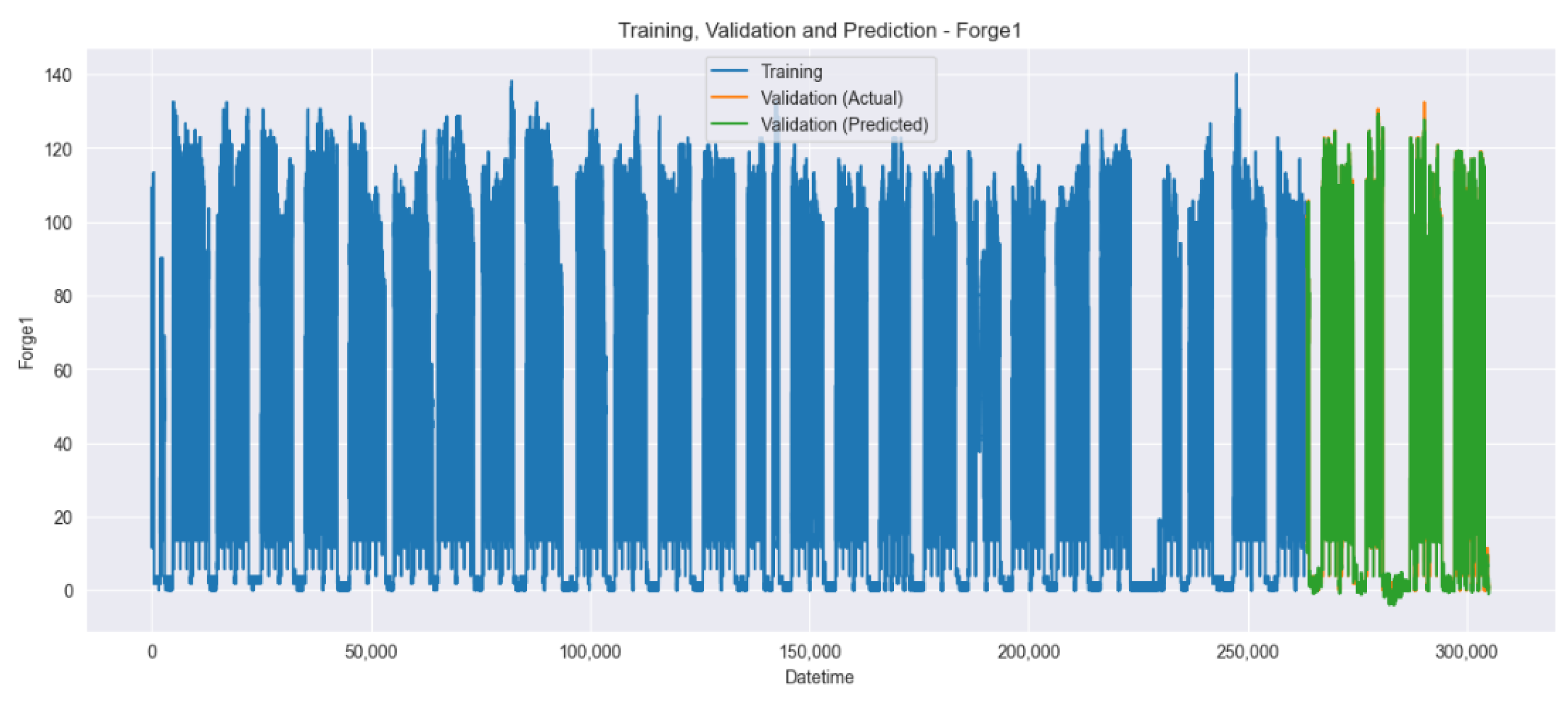
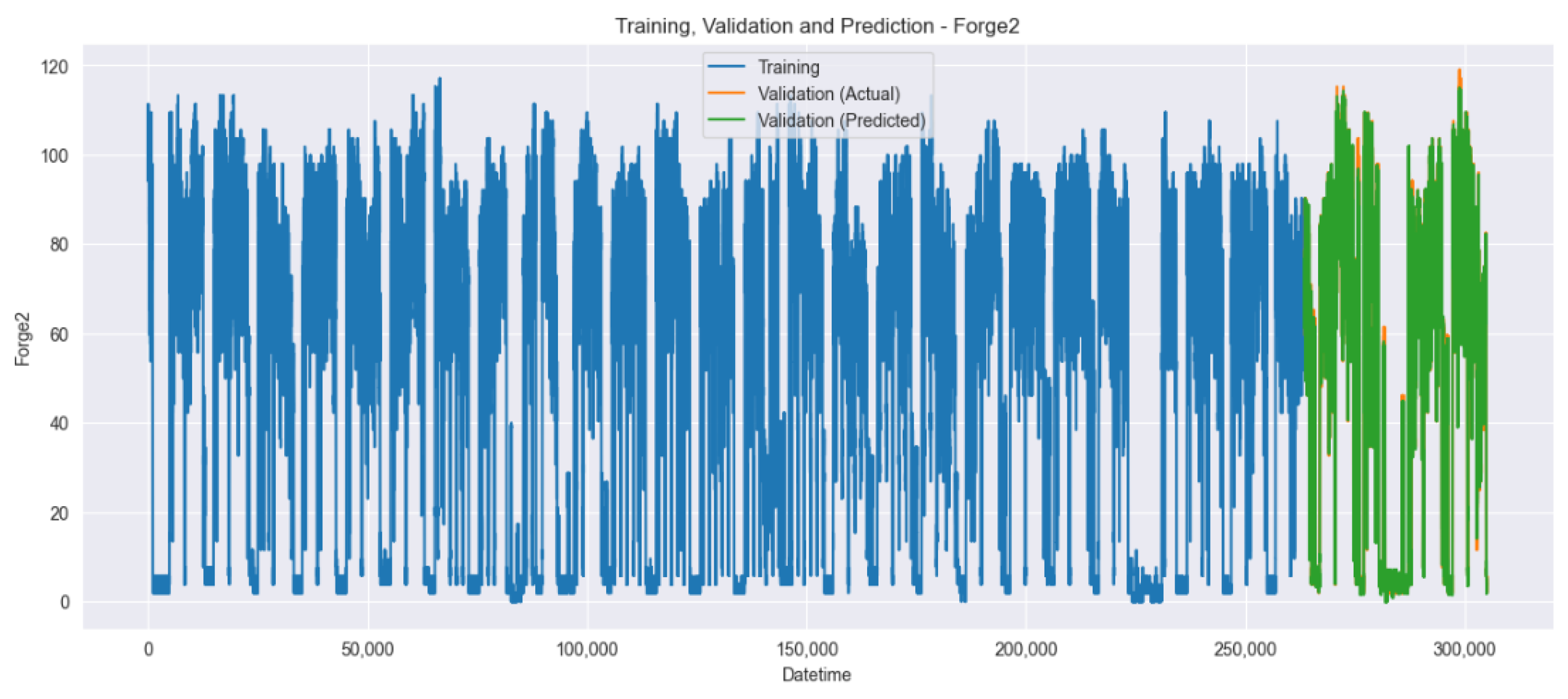
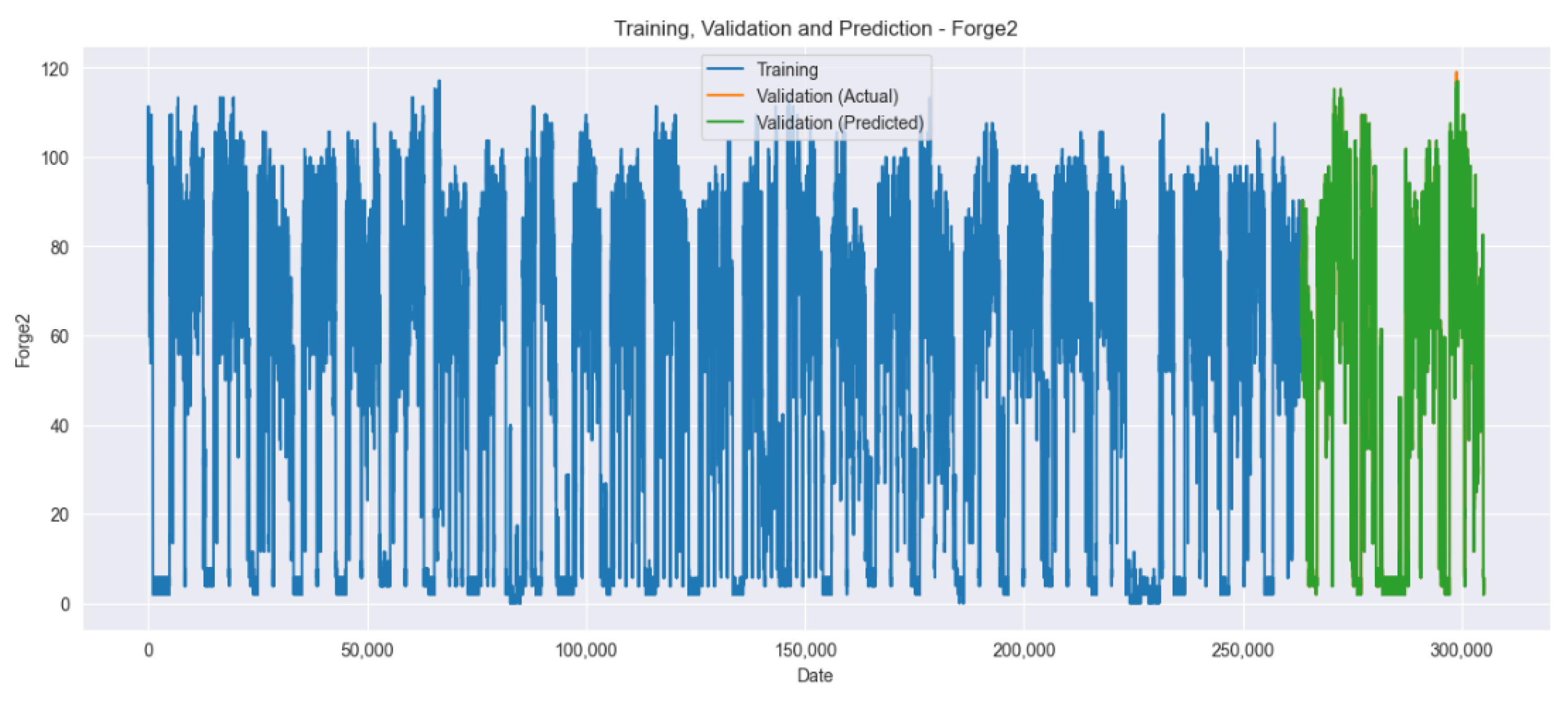
4.4. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kavousi-Fard, A.; Samet, H.; Marzbani, F. A new hybrid modified firefly algorithm and support vector regression model for accurate short term load forecasting. Expert Syst. Appl. 2014, 41, 6047–6056. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Yang, C.; Bozkurt, A. An advanced framework for net electricity consumption prediction: Incorporating novel machine learning models and optimization algorithms. Energy 2024, 296, 131259. [Google Scholar] [CrossRef]
- Lee, H.A.; Kim, D.J.; Cho, W.J.; Gu, J.H. Optimization of Energy Consumption Prediction Model of Food Factory based on LSTM for Application to FEMS. J. Environ. Therm. Eng. 2023, 18, 7–19. [Google Scholar] [CrossRef]
- Shao, X.; Kim, C.S.; Sontakke, P. Accurate deep model for electricity consumption forecasting using multi-channel and multi-scale feature fusion CNN–LSTM. Energies 2020, 13, 1881. [Google Scholar] [CrossRef]
- Zhang, J.R. Research on power load forecasting based on the improved Elman neural network. Chem. Eng. Trans. 2016, 51, 589–594. [Google Scholar]
- Zhang, S.; Chen, R.; Cao, J.; Tan, J. A CNN and LSTM-based multi-task learning architecture for short and medium-term electricity load forecasting. Electr. Power Syst. Res. 2023, 222, 109507. [Google Scholar] [CrossRef]
- Son, N.; Shin, Y. Short-and medium-term electricity consumption forecasting using Prophet and GRU. Sustainability 2023, 15, 15860. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, H.; Xie, Y.; Li, G.; Yang, D.; Hu, B. Regional short-term load forecasting method based on power load characteristics of different industries. Sustain. Energy Grids Netw. 2024, 38, 101336. [Google Scholar] [CrossRef]
- Roweis, S. EM algorithms for PCA and SPCA. Adv. Neural Inf. Process. Syst. 1997, 10, 626–632. [Google Scholar]
- Shrouf, F.; Ordieres, J.; Miragliotta, G. Smart factories in Industry 4.0: A review of the concept and of energy management approaches in production based on the Internet of Things paradigm. In Proceedings of the 2014 IEEE International Conference on Industrial Engineering and Engineering Management, Selangor, Malaysia, 9–12 December 2014; pp. 697–701. [Google Scholar]
- Lopez Research. Building Smarter Manufacturing with the Internet of Things (IoT). 2014. Available online: https://drop.ndtv.com/tvschedule/dropfiles/iot_in_manufacturing.pdf (accessed on 23 July 2024).
- Vikhorev, K.; Greenough, R.; Brown, N. An advanced energy management framework to promote energy awareness. J. Clean. Prod. 2013, 43, 103–112. [Google Scholar] [CrossRef]
- Khan, S.U.; Khan, N.; Ullah, F.U.; Kim, M.J.; Lee, M.Y.; Baik, S.W. Towards intelligent building energy management: AI-based framework for power consumption and generation forecasting. Energy Build. 2023, 279, 112705. [Google Scholar] [CrossRef]
- Lee, D.; Cheng, C.-C. Energy savings by Energy Management Systems: A Review. Renew. Sustain. Energy Rev. 2016, 56, 760–777. [Google Scholar] [CrossRef]
- Bermeo-Ayerbe, M.A.; Ocampo-Martínez, C.; Diaz-Rozo, J. Adaptive predictive control for peripheral equipment management to enhance energy efficiency in smart manufacturing systems. J. Clean. Prod. 2021, 291, 125556. [Google Scholar] [CrossRef]
- Wu, Z.; Yang, K.; Yang, J.; Cao, Y.; Gan, Y. Energy-efficiency-oriented scheduling in smart manufacturing. J. Ambient Intell. Humaniz. Comput. 2018, 10, 969–978. [Google Scholar] [CrossRef]
- Alghamdi, T.A.; Javaid, N. A survey of preprocessing methods used for analysis of big data originated from smart grids. IEEE Access 2022, 10, 29149–29171. [Google Scholar] [CrossRef]
- Li, Z.; Xue, J.; Lv, Z.; Zhang, Z.; Li, Y. Grid-constrained data cleansing method for enhanced bus load forecasting. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Trygg, J.; Gabrielsson, J.; Lundstedt, T. Background estimation, denoising, and preprocessing. In Comprehensive Chemometrics; Brown, S., Tauler, R., Walczak, B., Eds.; Elsevier: Oxford, UK, 2020; pp. 137–141. [Google Scholar]
- Alasadi, S.A.; Bhaya, W.S. Review of data preprocessing techniques in data mining. J. Eng. Appl. Sci. 2017, 12, 4102–4107. [Google Scholar]
- Zhang, C.; Li, X.; Zhang, W.; Cui, L.; Zhang, H.; Tao, X. Noise reduction in the spectral domain of hyperspectral images using denoising autoencoder methods. Chemom. Intell. Lab. Syst. 2020, 203, 104063. [Google Scholar] [CrossRef]
- Bruha, I.; Franek, F. Comparison of various routines for unknown attribute value processing: The covering paradigm. Int. J. Pattern Recognit. Artif. Intell. 1996, 10, 939–955. [Google Scholar] [CrossRef]
- Lakshminarayan, K.; Harp, S.A.; Samad, T. Imputation of Missing Data in Industrial Databases. Appl. Intell. 1999, 11, 259–275. [Google Scholar] [CrossRef]
- Hodge, V.; Austin, J. A survey of outlier detection methodologies. Artif. Intell. Rev. 2004, 22, 85–126. [Google Scholar] [CrossRef]
- Wang, H.; Bah, M.J.; Hammad, M. Progress in outlier detection techniques: A survey. IEEE Access 2019, 7, 107964–108000. [Google Scholar] [CrossRef]
- Kotsiantis, S.B.; Kanellopoulos, D.; Pintelas, P.E. Data preprocessing for supervised learning. Int. J. Comput. Sci. 2006, 1, 111–117. [Google Scholar]
- Hanifi, S.; Jaradat, M.; Salman, A.; Abujubbeh, M. A critical review of wind power forecasting methods—Past, present and future. Energies 2020, 13, 3764. [Google Scholar] [CrossRef]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M.D. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
- Pereira, A.; Proença, A. HEP-frame: Improving the efficiency of pipelined data transformation & filtering for scientific analyses. Comput. Phys. Commun. 2021, 263, 107844. [Google Scholar]
- Ferrara, M.; Guerrini, L.; Sodini, M. Nonlinear dynamics in a Solow model with delay and non-convex technology. Appl. Math. Comput. 2014, 228, 1–12. [Google Scholar] [CrossRef]
- Hu, Y.; Man, Y. Energy consumption and carbon emissions forecasting for industrial processes: Status, challenges and perspectives. Renew. Sustain. Energy Rev. 2023, 182, 113405. [Google Scholar] [CrossRef]
- Imani, M. Electrical load-temperature CNN for residential load forecasting. Energy 2021, 227, 120480. [Google Scholar] [CrossRef]
- Somu, N.; MR, G.R.; Ramamritham, K. A hybrid model for building energy consumption forecasting using long short term memory networks. Appl. Energy 2020, 261, 114131. [Google Scholar] [CrossRef]
- Hu, Y.; Li, J.; Hong, M.; Ren, J.; Lin, R.; Liu, Y.; Zhang, H.; Wang, Y.; Chen, F.; Liu, M. Short term electric load forecasting model and its verification for process industrial enterprises based on hybrid GA-PSO-BPNN algorithm—A case study of papermaking process. Energy 2019, 170, 1215–1227. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), Long Beach, CA, USA, 4–9 December 2017; pp. 3149–3157. [Google Scholar]
- Taylor, S.J.; Letham, B. Forecasting at Scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Zhu, N.; Hou, Q.; Qin, S.; Zhou, L.; Hua, D.; Wang, X.; Cheng, L. GGNet: A novel graph structure for power forecasting in renewable power plants considering temporal lead-lag correlations. Appl. Energy 2024, 364, 123194. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, T.; Zhou, S.; Zhang, F.; Zou, R.; Hu, Q. An improved Wavenet network for multi-step-ahead wind energy forecasting. Energy Convers. Manag. 2023, 278, 116709. [Google Scholar] [CrossRef]
- Zheng, H.; Yuan, J.; Chen, L. Short-term load forecasting using EMD-LSTM neural networks with a Xgboost algorithm for feature importance evaluation. Energies 2017, 10, 1168. [Google Scholar] [CrossRef]
- Lin, Y.; Luo, H.; Wang, D.; Guo, H.; Zhu, K. An ensemble model based on machine learning methods and data preprocessing for short-term electric load forecasting. Energies 2017, 10, 1186. [Google Scholar] [CrossRef]
- Tan, M.; Hu, C.; Chen, J.; Wang, L.; Li, Z. Multi-node load forecasting based on multi-task learning with modal feature extraction. Eng. Appl. Artif. Intell. 2022, 112, 104856. [Google Scholar] [CrossRef]
- Srivastava, N.; Mansimov, E.; Salakhudinov, R. Unsupervised learning of video representations using LSTMs. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 843–852. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Lee, E.; Baek, K.; Kim, J. Datasets on South Korean manufacturing factories’ electricity consumption and demand response participation. Sci. Data 2022, 9, 227. [Google Scholar] [CrossRef] [PubMed]
- Korea Power Exchange. System Marginal Price (SMP) Data. Available online: https://www.kpx.or.kr (accessed on 28 June 2024).
- Ibrahim, M.S.; Gharghory, S.M.; Kamal, H.A. A hybrid model of CNN and LSTM autoencoder-based short-term PV power generation forecasting. Electr. Eng. 2024, 105, 1–17. [Google Scholar] [CrossRef]
- Lu, M.; Hou, Q.; Qin, S.; Zhou, L.; Hua, D.; Wang, X.; Cheng, L. A stacking ensemble model of various machine learning models for daily runoff forecasting. Water 2023, 15, 1265. [Google Scholar] [CrossRef]





| Time Horizon | Range | Applications |
|---|---|---|
| Very short-term | Seconds to 30 min | Real-time grid operations, market clearing, turbine control, real-time electricity dispatch, PV storage control |
| Short-term | 30 min to 6 h | Load dispatch planning, power system operation, economic load dispatch, control of renewable energy integrated systems |
| Medium-term | 6 h to 1 day | Maintenance scheduling, operational security in the electricity market, energy trading, on-line and off-line generating decisions |
| Long-term | 1 day to 1 month | Reserve requirements, maintenance schedules, long-term power generation and distribution, optimum operating cost, operation management |
| Parameter | LSTM-AE |
|---|---|
| Number of LSTM layers | 2 |
| Units per LSTM layer | 50 |
| Dropout rate | 0.2 |
| Learning rate | 0.001 |
| Batch size | 32 |
| Epochs | 100 |
| Parameter | XGBoost |
|---|---|
| Learning rate | 0.05 |
| Max depth | 7 |
| Min child weight | 1 |
| Subsample | 0.8 |
| Colsample bytree | 1.0 |
| Number of estimators | 300 |
| Hardware | Software |
|---|---|
| • CPU: 13th Gen Intel(R) Core(TM) i9-13900KF 3.00 GHz | • Operating system: Windows 11 Pro |
| • GPU: NVIDIA GeForce RTX 4090 | • Python: 3.8.10 |
| • RAM: 64.0 GB | • IDE: PyCharm 2023.3.2 |
| • Pytorch: torch 1.13.0+cu116 | |
| • Tensorflow: 2.13.0 |
| Model | MAE | MSE | R2 | SMAPE | Training Time (min) |
|---|---|---|---|---|---|
| LSTM-AE | 0.101 | 0.021 | 0.95 | - | 17 |
| XGBoost | 0.954 | 0.533 | 0.99 | 18.00 | 4 |
| LightGBM | 0.773 | 1.143 | 0.51 | 33.79 | 0.11 |
| Prophet | 0.869 | 1.425 | 0.44 | 38.86 | 5 |
| GGNet | 0.825 | 1.161 | 0.46 | 37.45 | 19 |
| Our method | 0.020 | 0.021 | 0.99 | 4.24 | 0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moon, Y.; Lee, Y.; Hwang, Y.; Jeong, J. Long Short-Term Memory Autoencoder and Extreme Gradient Boosting-Based Factory Energy Management Framework for Power Consumption Forecasting. Energies 2024, 17, 3666. https://doi.org/10.3390/en17153666
Moon Y, Lee Y, Hwang Y, Jeong J. Long Short-Term Memory Autoencoder and Extreme Gradient Boosting-Based Factory Energy Management Framework for Power Consumption Forecasting. Energies. 2024; 17(15):3666. https://doi.org/10.3390/en17153666
Chicago/Turabian StyleMoon, Yeeun, Younjeong Lee, Yejin Hwang, and Jongpil Jeong. 2024. "Long Short-Term Memory Autoencoder and Extreme Gradient Boosting-Based Factory Energy Management Framework for Power Consumption Forecasting" Energies 17, no. 15: 3666. https://doi.org/10.3390/en17153666
APA StyleMoon, Y., Lee, Y., Hwang, Y., & Jeong, J. (2024). Long Short-Term Memory Autoencoder and Extreme Gradient Boosting-Based Factory Energy Management Framework for Power Consumption Forecasting. Energies, 17(15), 3666. https://doi.org/10.3390/en17153666







