Hybrid ANPC Grid-Tied Inverter Design with Passivity-Based Sliding Mode Control Strategy
Abstract
1. Introduction
2. Design of PSM Controller for Hybrid ANPC Grid-Tied Inverters
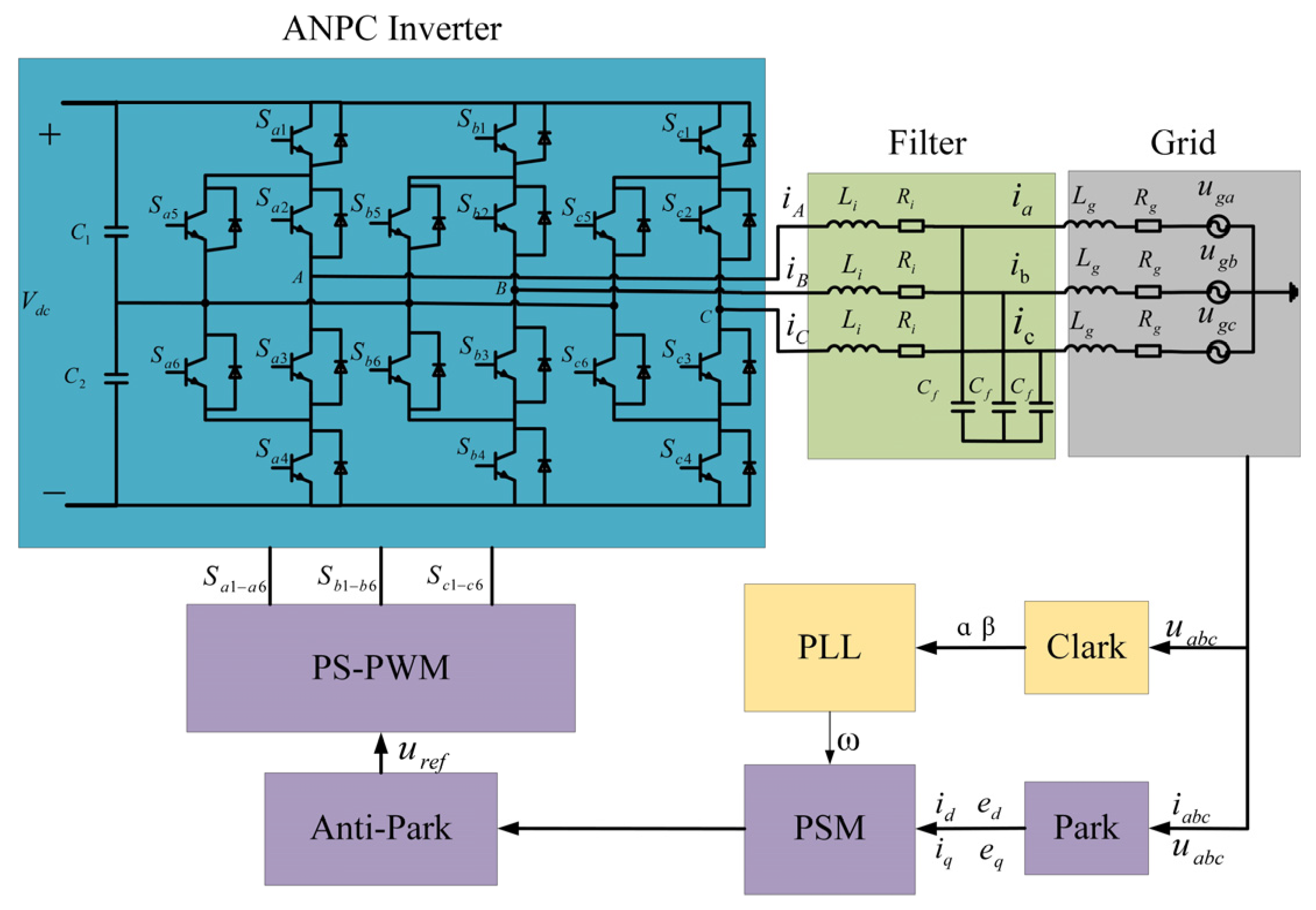
2.1. Hybrid ANPC Grid-Tied Inverter Model
2.2. Passive System and Controller Design
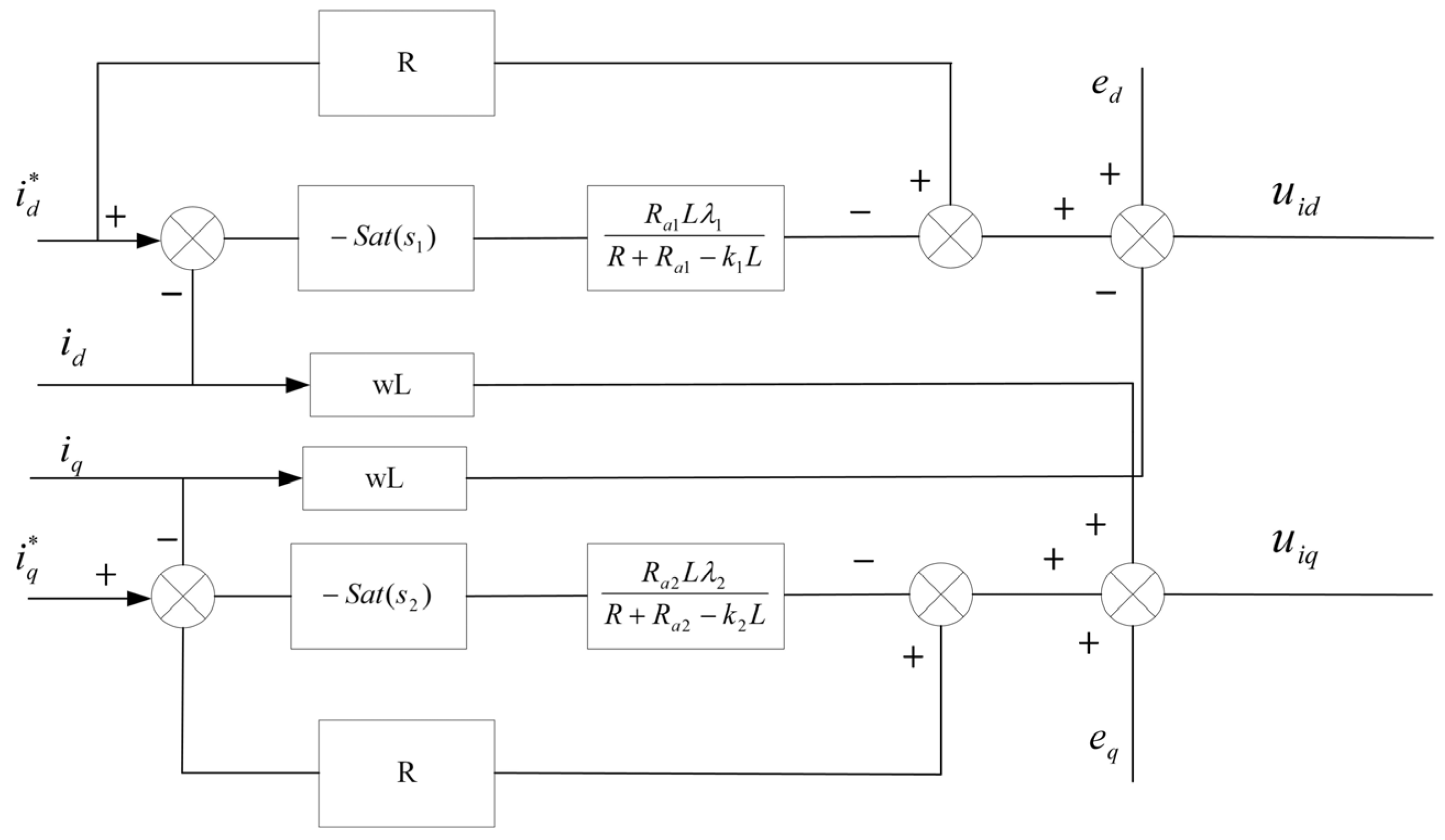
2.3. PSM Controller Design
2.4. Simulation and Results
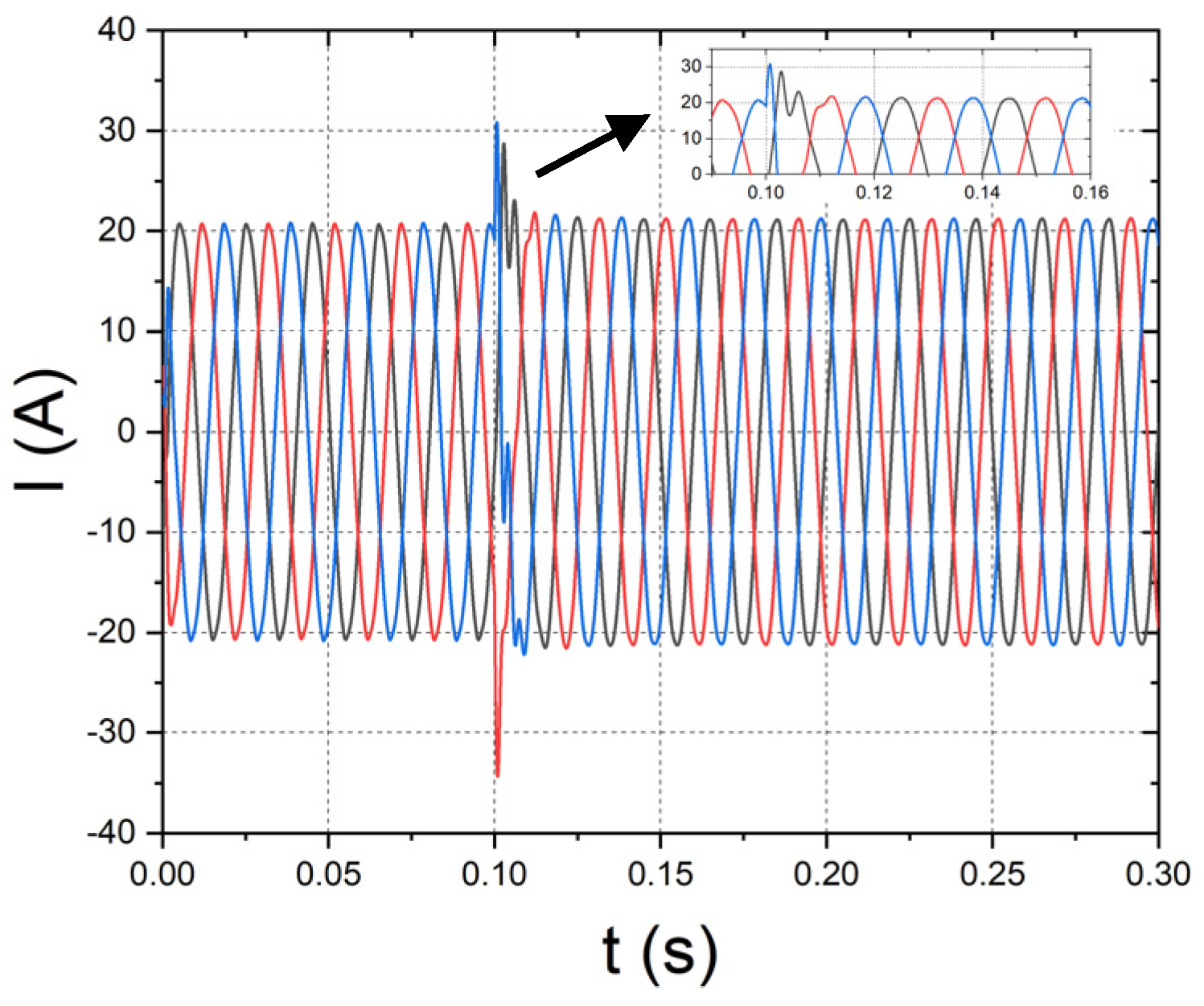
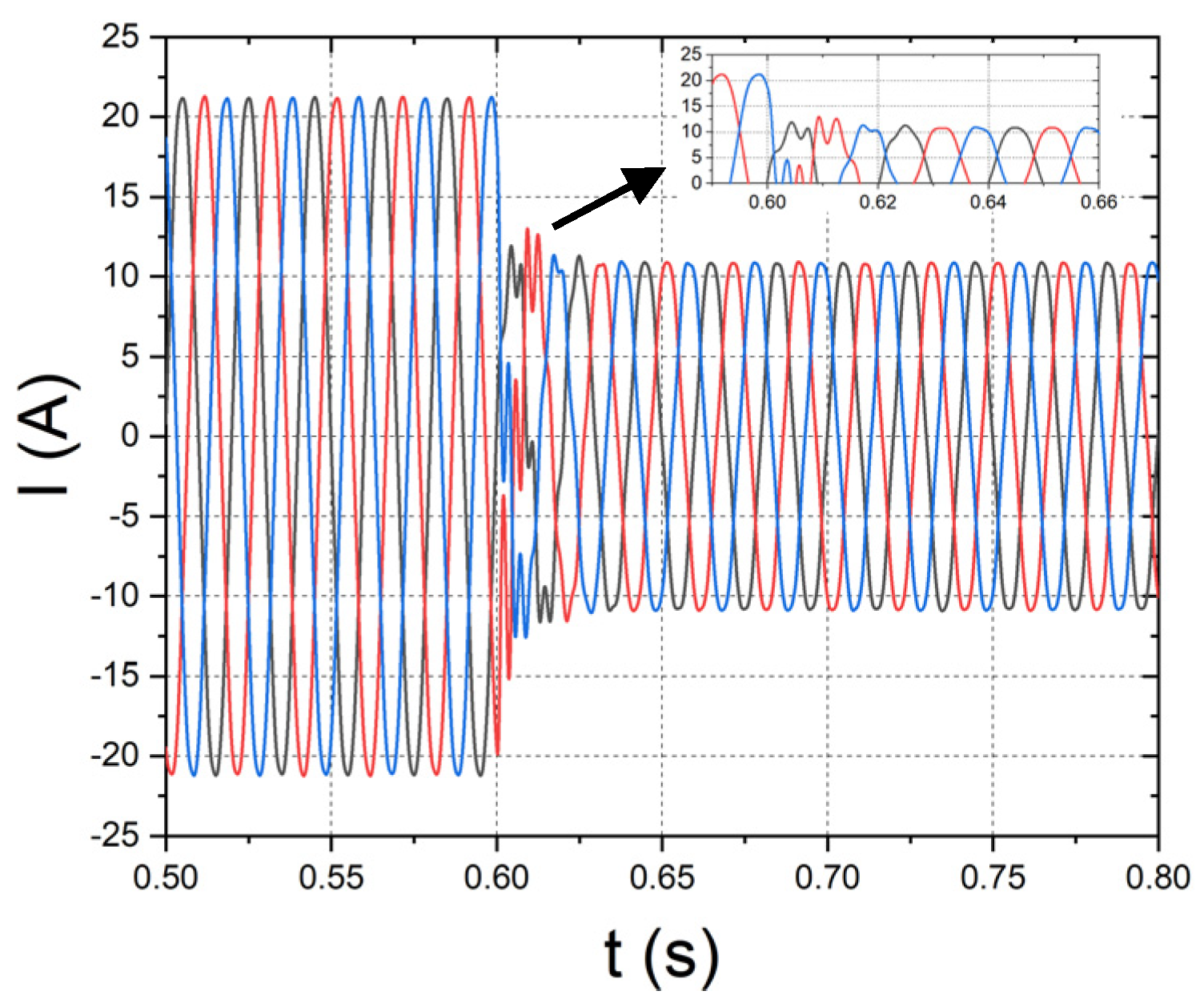
2.4.1. Impedance Variations on the Grid Side
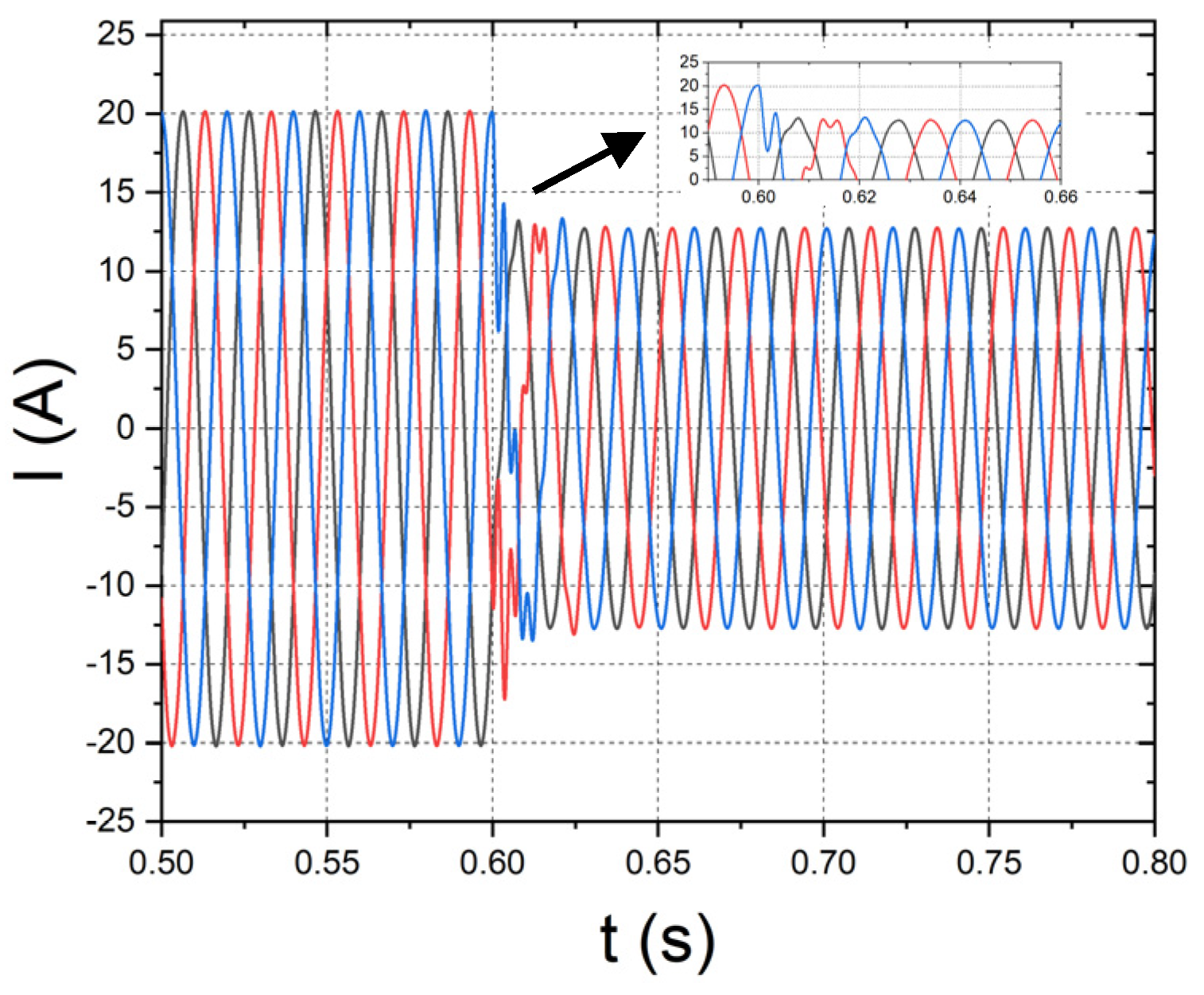
2.4.2. Changes in Output Reference Current
3. Design of Hybrid Inverter Based on Loss Analysis
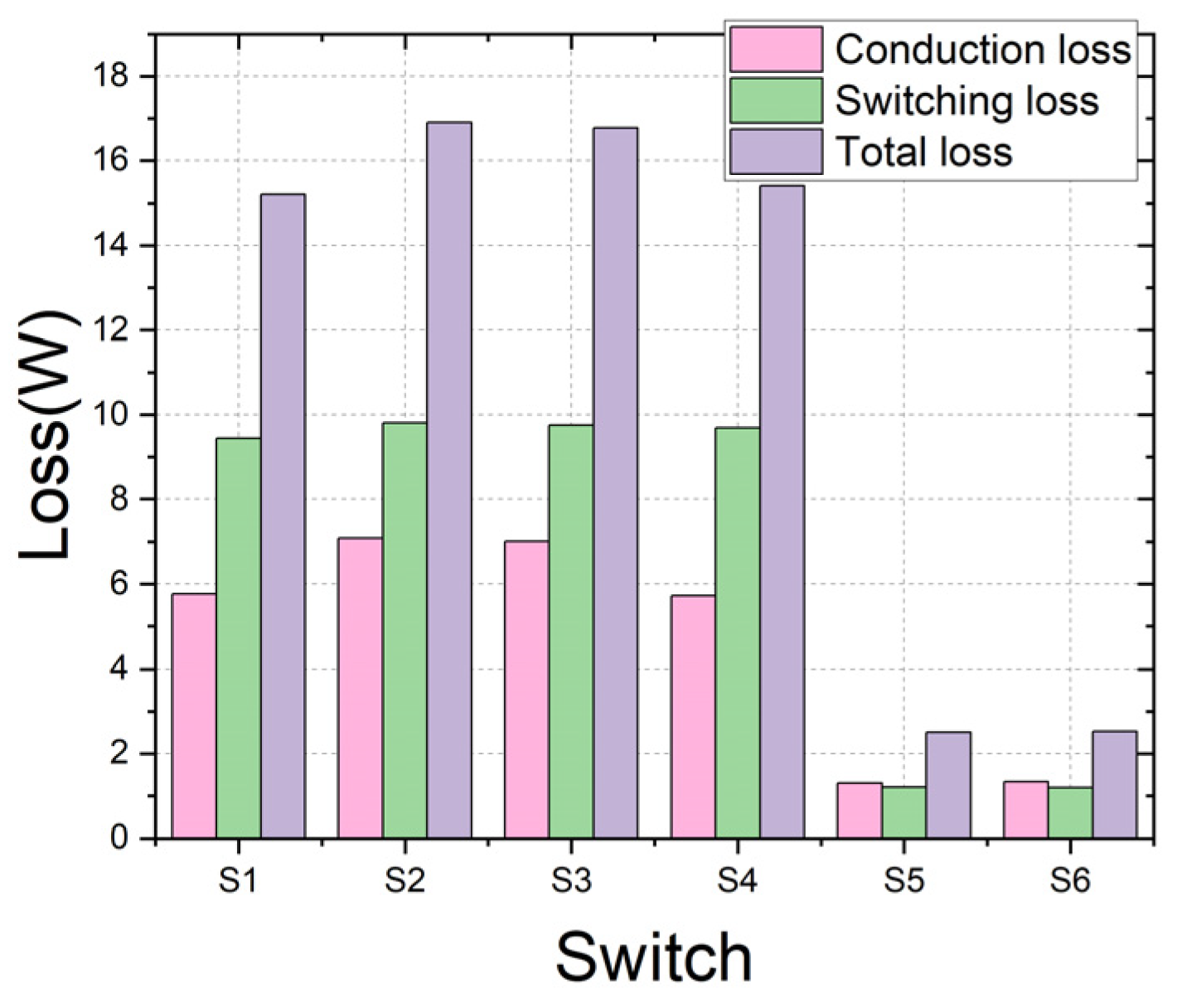
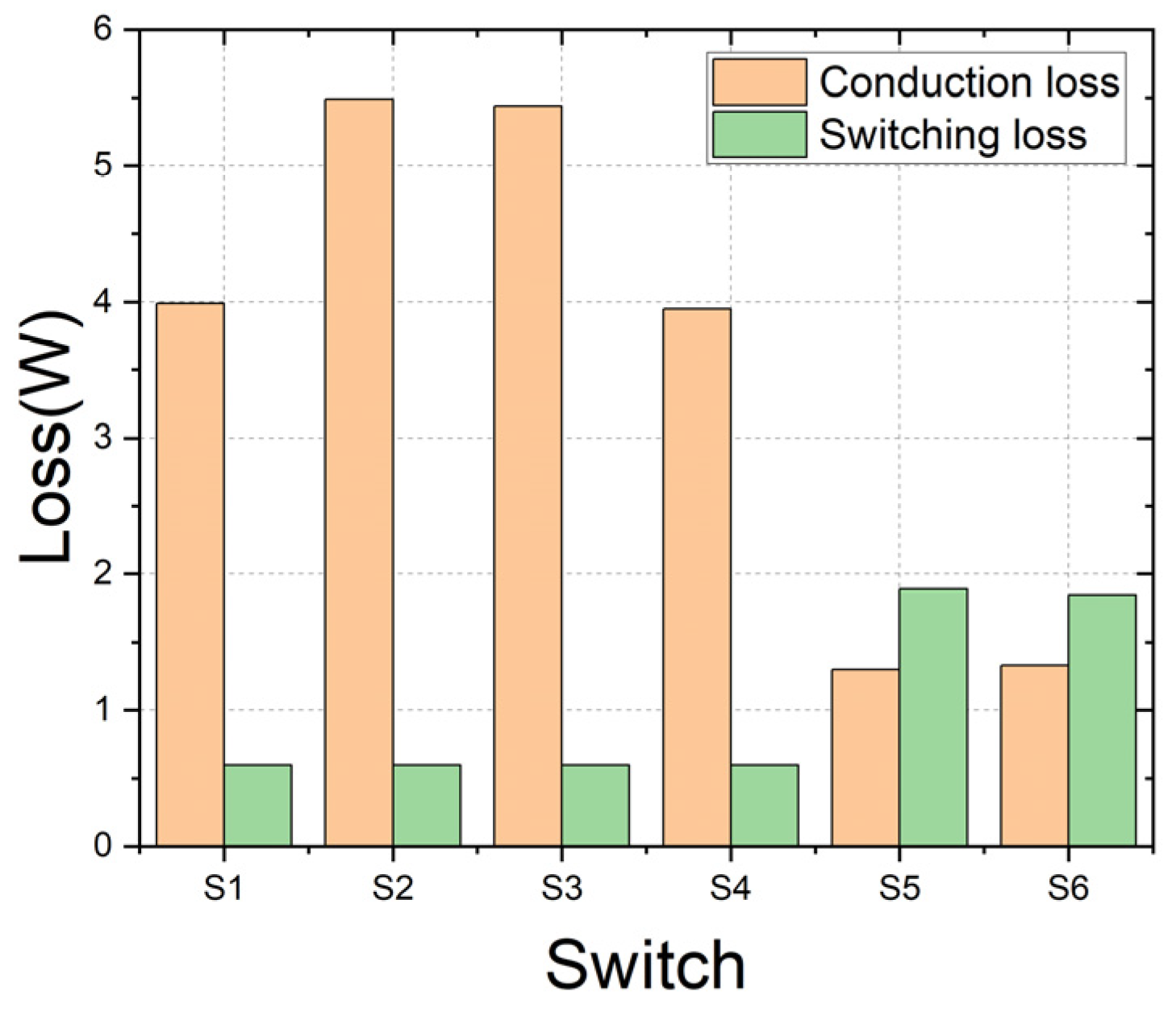
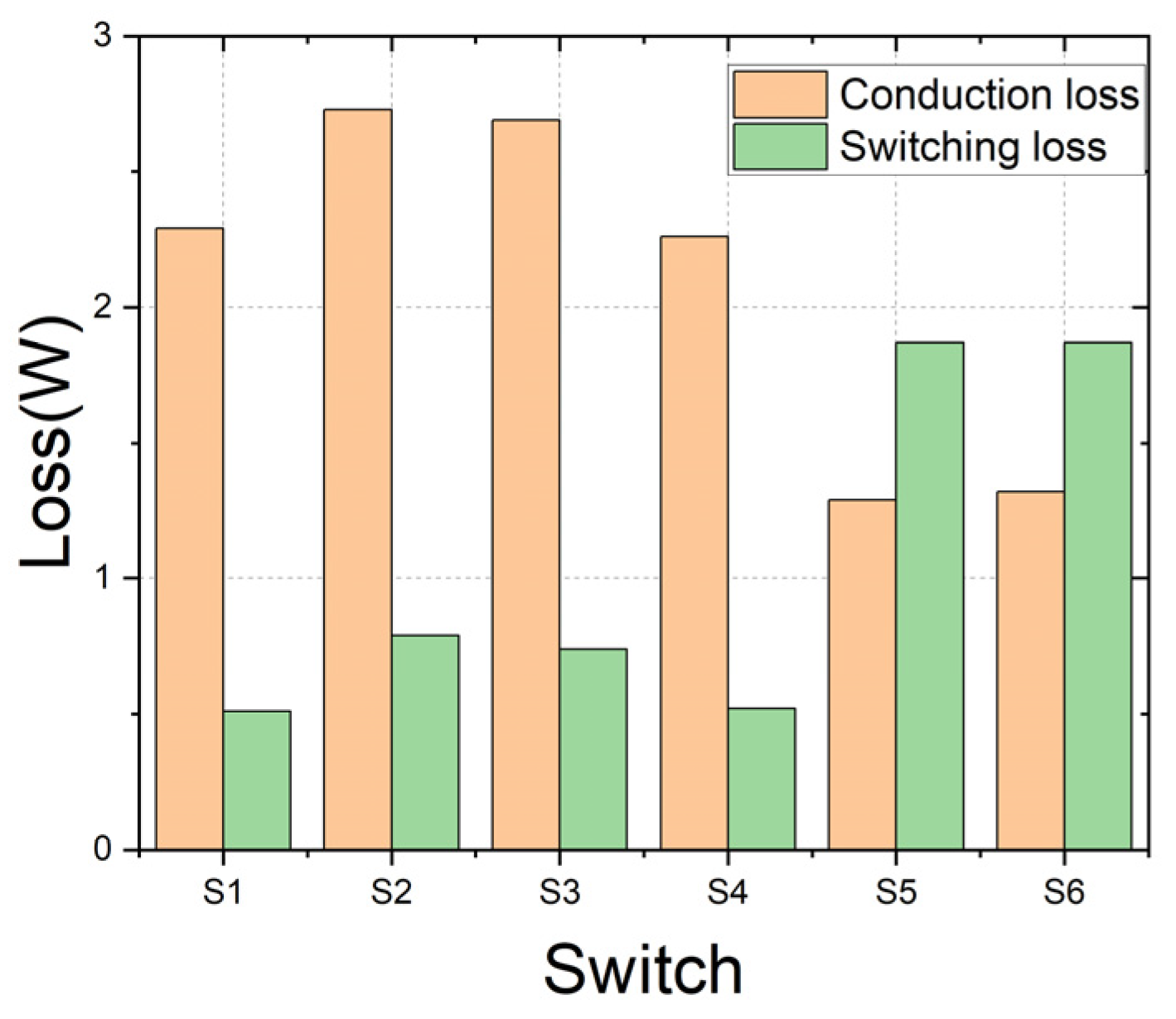
3.1. Analysis of Loss Distribution
3.2. Design of Hybrid Structure
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yao, H.; Yan, Y.; Shi, T. A novel SVPWM scheme for field-oriented vector-controlled PMSM drive system fed by cascaded H-bridge inverter. IEEE Trans. Power Electron. 2021, 36, 8988–9000. [Google Scholar] [CrossRef]
- Qanbari, T.; Tousi, B. Single-source three-phase multilevel inverter assembled by three-phase two-level inverter and two single-phase cascaded H-bridge inverters. IEEE Trans. Power Electron. 2020, 36, 5204–5212. [Google Scholar] [CrossRef]
- Shahabadini, M.; Moeini, N.; Bahrami-Fard, M.; Iman-Eini, H. Heric-based cascaded h-bridge inverter for leakage current suppression in pv systems. IEEE Trans. Power Electron. 2022, 38, 4005–4014. [Google Scholar] [CrossRef]
- Chen, M.; Loh, P.C. A dual-boost H-bridge inverter with common ground for photovoltaic interfacing. IEEE Trans. Ind. Electron. 2020, 68, 9515–9526. [Google Scholar] [CrossRef]
- Fang, J.; Blaabjerg, F.; Liu, S.; Goetz, S.M. A review of multilevel converters with parallel connectivity. IEEE Trans. Power Electron. 2021, 36, 12468–12489. [Google Scholar] [CrossRef]
- Perez, M.A.; Ceballos, S.; Konstantinou, G.; Pou, J.; Aguilera, R.P. Modular multilevel converters: Recent achievements and challenges. IEEE Open J. Ind. Electron. Soc. 2021, 2, 224–239. [Google Scholar] [CrossRef]
- Alatai, S.; Salem, M.; Ishak, D.; Das, H.S.; Nazari, M.A.; Bughneda, A.; Kamarol, M. A review on state-of-the-art power converters: Bidirectional, resonant, multilevel converters and their derivatives. Appl. Sci. 2021, 11, 10172. [Google Scholar] [CrossRef]
- Xu, S.; Huang, W.; Wang, H.; Zheng, W.; Wang, J.; Chai, Y.; Ma, M. A simultaneous diagnosis method for power switch and current sensor faults in grid-connected three-level NPC inverters. IEEE Trans. Power Electron. 2022, 38, 1104–1118. [Google Scholar] [CrossRef]
- Khan, A.A.; Khan, U.A.; Ahmed, H.F.; Cha, H.; Ahmed, S.A. Improved NPC inverters without short-circuit and dead-time issues. IEEE Trans. Power Electron. 2021, 37, 2180–2190. [Google Scholar] [CrossRef]
- Tcai, A.; Kwon, Y.; Pugliese, S.; Liserre, M. Reduction of the circulating current among parallel NPC inverters. IEEE Trans. Power Electron. 2021, 36, 12504–12514. [Google Scholar] [CrossRef]
- Wang, K.; Zheng, Z.; Xu, L.; Li, Y. Neutral-point voltage balancing method for five-level NPC inverters based on carrier-overlapped PWM. IEEE Trans. Power Electron. 2020, 36, 1428–1440. [Google Scholar] [CrossRef]
- Choi, U.M.; Ryu, T. Comparative evaluation of efficiency and reliability of single-phase five-level NPC inverters for photovoltaic systems. IEEE Access 2021, 9, 120638–120651. [Google Scholar] [CrossRef]
- Sathik, M.J.; Almakhles, D.J.; Sandeep, N.; Siddique, M.D. Experimental validation of new self-voltage balanced 9L-ANPC inverter for photovoltaic applications. Sci. Rep. 2021, 11, 5067. [Google Scholar] [CrossRef] [PubMed]
- Hakami, S.S.; Halabi, L.M.; Lee, K.B. Dual-carrier-based PWM method for DC-link capacitor lifetime extension in three-level hybrid ANPC inverters. IEEE Trans. Ind. Electron. 2022, 70, 3303–3314. [Google Scholar] [CrossRef]
- Song, J.; Chu, E.; Sun, Q. An Improved Auxiliary Resonant Pole TNPC Inverter and Its Modulation Strategy. IEEE Trans. Power Electron. 2024, 39, 9765–9776. [Google Scholar] [CrossRef]
- Muduli, U.R.; Behera, R.K. A modified high gain boost tnpc inverter with neutral point balancing for three-phase induction motor driven electric vehicle. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 16–19 December 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Roy, P.; Banerjee, A. A study on performance parameters of three-level T-type inverter based PMSM drives for electric vehicles applications. Electr. Eng. 2024, 106, 1121–1134. [Google Scholar] [CrossRef]
- Guo, F.; Ma, Z.; Diao, F.; Cao, H.; Zhao, Y. Carrier-Based Space-Vector Coordinate-Shifted DPWM Strategy for Three-Level T-type NPC Inverters in Electric Aircraft Propulsion Applications. In Proceedings of the 2024 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 25–29 February 2024; IEEE: Piscataway, NJ, USA, 2024. [Google Scholar]
- Hou, L.; Ma, Z.; Li, H.; Qiu, C.; Wang, K.; Zheng, Z. Research on Fault Tolerant Control Method of Three-Level TNPC Inverter. In Proceedings of the 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5–8 November 2023; IEEE: Piscataway, NJ, USA, 2023. [Google Scholar]
- Song, W.; Saeed, M.S.R.; Yu, B.; Li, J.; Guo, Y. Model predictive current control with reduced complexity for five-phase three-level NPC voltage-source inverters. IEEE Trans. Transp. Electrif. 2021, 8, 1906–1917. [Google Scholar] [CrossRef]
- Khoshkbar-Sadigh, A.; Naderi, R.; Dargahi, V.; Corzine, K. Thermal and performance comparison of active neutral-point-clamped (anpc) and dual flyingcapacitor anpc (dfc-anpc) inverters. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 5522–5528. [Google Scholar]
- Li, J.; Huang, A.Q.; Liang, Z.; Bhattacharya, S. Analysis and design of active NPC (ANPC) inverters for fault-tolerant operation of high-power electrical drives. IEEE Trans. Power Electron. 2011, 27, 519–533. [Google Scholar] [CrossRef]
- He, J.; Zhang, D.; Pan, D. PWM strategy for MW-scale “SiC+ Si” ANPC converter in aircraft propulsion applications. IEEE Trans. Ind. Appl. 2020, 57, 3077–3086. [Google Scholar] [CrossRef]
- Dargahi, V.; Corzine, K.A.; Enslin, J.H.; Rodríguez, J.; Blaabjerg, F. Improved active-neutral-point-clamped (I-ANPC) multilevel converter: Fundamental circuit topology, innovative modulation technique, and experimental validation. In Proceedings of the 2018 IEEE Power and Energy Conference at Illinois (PECI), Champaign, IL, USA, 22–23 February 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–8. [Google Scholar]
- Hwang, J.H.; Halabi, L.M.; Ko, Y.; Lee, K.B. Lifetime-based fault tolerant strategy for three-level hybrid ANPC inverters. J. Power Electron. 2023, 23, 363–373. [Google Scholar] [CrossRef]
- Humada, A.M.; Darweesh, S.Y.; Mohammed, K.G.; Kamil, M.; Mohammed, S.F.; Kasim, N.K.; Tahseen, T.A.; Awad, O.I.; Mekhilef, S. Modeling of PV system and parameter extraction based on experimental data: Review and investigation. Sol. Energy 2020, 199, 742–760. [Google Scholar] [CrossRef]
- Hamzat, A.K.; Sahin, A.Z.; Omisanya, M.I.; Alhems, L.M. Advances in PV and PVT cooling technologies: A review. Sustain. Energy Technol. Assess. 2021, 47, 101360. [Google Scholar] [CrossRef]
- Wang, Y.; Zou, R.; Liu, F.; Zhang, L.; Liu, Q. A review of wind speed and wind power forecasting with deep neural networks. Appl. Energy 2021, 304, 117766. [Google Scholar] [CrossRef]
- Oyekale, J.; Petrollese, M.; Tola, V.; Cau, G. Impacts of renewable energy resources on effectiveness of grid-integrated systems: Succinct review of current challenges and potential solution strategies. Energies 2020, 13, 4856. [Google Scholar] [CrossRef]
- Li, G.; Chen, Y.; Luo, A.; Wang, Y. An inertia phase locked loop for suppressing sub-synchronous resonance of renewable energy generation system under weak grid. IEEE Trans. Power Syst. 2021, 36, 4621–4631. [Google Scholar] [CrossRef]
- Naqvi, S.B.Q.; Singh, B. A PV-battery system resilient to weak grid conditions with regulated power injection and grid supportive features. IEEE Trans. Sustain. Energy 2022, 13, 1408–1419. [Google Scholar] [CrossRef]
- Yang, D.; Ruan, X.; Wu, H. Impedance shaping of the grid-connected inverter with LCL filter to improve its adaptability to the weak grid condition. IEEE Trans. Power Electron. 2014, 29, 5795–5805. [Google Scholar] [CrossRef]
- Ashabani, M.; Mohamed, Y.A.R.I. Integrating VSCs to weak grids by nonlinear power damping controller with self-synchronization capability. IEEE Trans. Power Syst. 2013, 29, 805–814. [Google Scholar] [CrossRef]
- Pal, S.; Roy, A.; Shivakumara, P.; Pal, U. Adapting a swin transformer for license plate number and text detection in drone images. Artif. Intell. Appl. 2023, 1, 145–154. [Google Scholar] [CrossRef]
- Helali, R.G.M. An Exploratory Study of Factors Affecting Research Productivity in Higher Educational Institutes Using Regression and Deep Learning Techniques. Artif. Intell. Appl. 2022, 1, 23–26. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.; Zhang, Y.; Chen, J.; Sang, Y.; Jiang, L. Passivity-based sliding-mode control design for optimal power extraction of a PMSG based variable speed wind turbine. Renew. Energy 2018, 119, 577–589. [Google Scholar] [CrossRef]
- Shunchao, K.E.; Miao, Z.H.U.; Yang, C.; Zheng, C.; Cungang, H.U. Passive sliding mode variable structure control for mmc-upfc. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2184–2189. [Google Scholar]
- Zhang, L.; Zheng, Z.; Lou, X. A review of WBG and Si devices hybrid applications. Chin. J. Electr. Eng. 2021, 7, 1–20. [Google Scholar] [CrossRef]
- Zhang, L.; Lou, X.; Li, C.; Wu, F.; Gu, Y.; Chen, G.; Xu, D. Evaluation of different Si/SiC hybrid three-level active NPC inverters for high power density. IEEE Trans. Power Electron. 2019, 35, 8224–8236. [Google Scholar] [CrossRef]
- Feng, Z.; Zhang, X.; Wang, J.; Yu, S. A high-efficiency three-level ANPC inverter based on hybrid SiC and Si devices. Energies 2020, 13, 1159. [Google Scholar] [CrossRef]
- Balaji, P.S.; Karthik SelvaKumar, K. Applications of nonlinearity in passive vibration control: A review. J. Vib. Eng. Technol. 2021, 9, 183–213. [Google Scholar] [CrossRef]
- Udabe, A.; Baraia-Etxaburu, I.; Diez, D.G. Gallium nitride power devices: A state of the art review. IEEE Access 2023, 11, 48628–48650. [Google Scholar] [CrossRef]
- Ravinchandra, K.; Freddy, T.K.S.; Thiruchelvam, V. Review of electrical characteristics for wide bandgap power devices. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition-Asia (ECCE-Asia), Singapore, 24–27 May 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Chen, J.; Du, X.; Luo, Q.; Zhang, X.; Sun, P.; Zhou, L. A review of switching oscillations of wide bandgap semiconductor devices. IEEE Trans. Power Electron. 2020, 35, 13182–13199. [Google Scholar] [CrossRef]
- Infineon IGW60T120 Trenchstop Si IGBT Datasheet. Available online: http://www.infineon.com/dgdl/Infineon-IGW60T120-DS-v02_04 (accessed on 11 February 2024).
- Cree (Wolfspeed) C2M0040120D SiC Power MOSFET Datasheet. Available online: http://www.wolfspeed.com/media/downloads/165/C2M0040120D.pdf (accessed on 15 February 2024).
- GaN Systems GS-065-060 GaN Power Transistor. Available online: https://gansystems.com/gan-transistors/gs-065-060-5-t-a/ (accessed on 11 February 2024).
- Zhang, Y.; Li, K.; Zhang, L. Loss Analysis of ANPC Inverters with Hybrid Si and WBG Devices. In Proceedings of the 2024 International Conference on Life System Modeling and Simulation (LSMS2024) and 2024 International Conference on Intelligent Computing for Sustainable Energy and Environment (ICSEE2024), Suzhou, China, 20 December–15 September 2024. [Google Scholar]

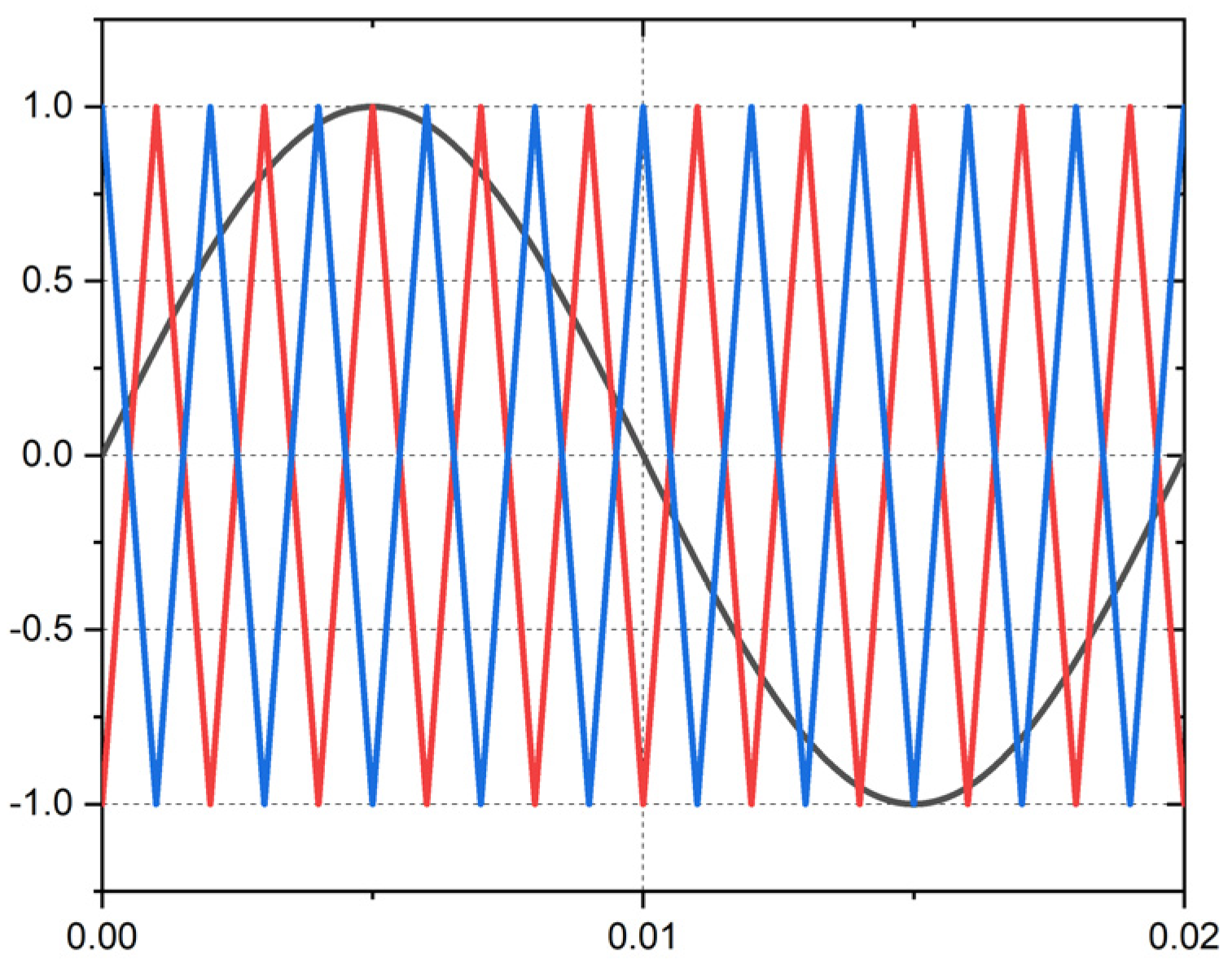
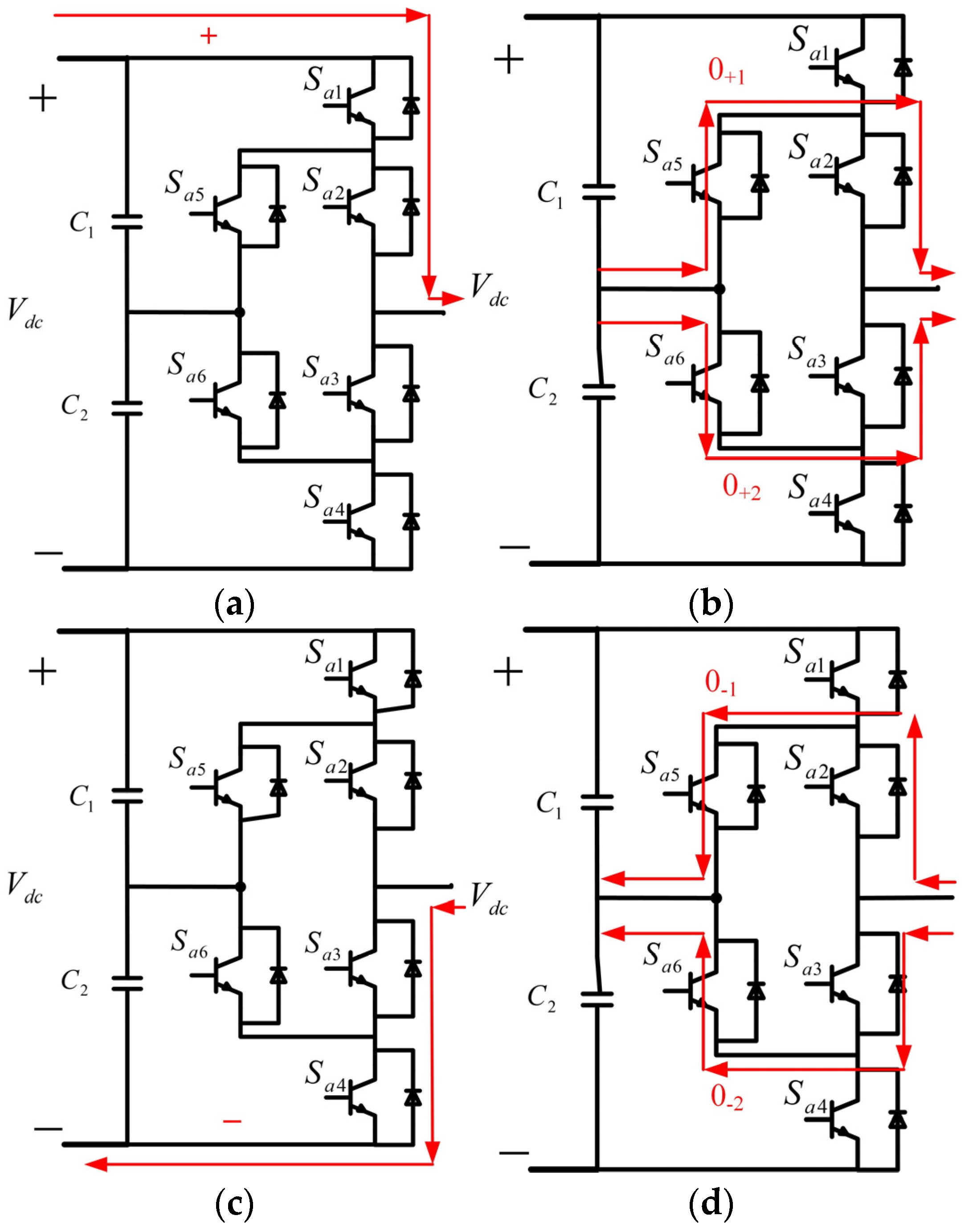
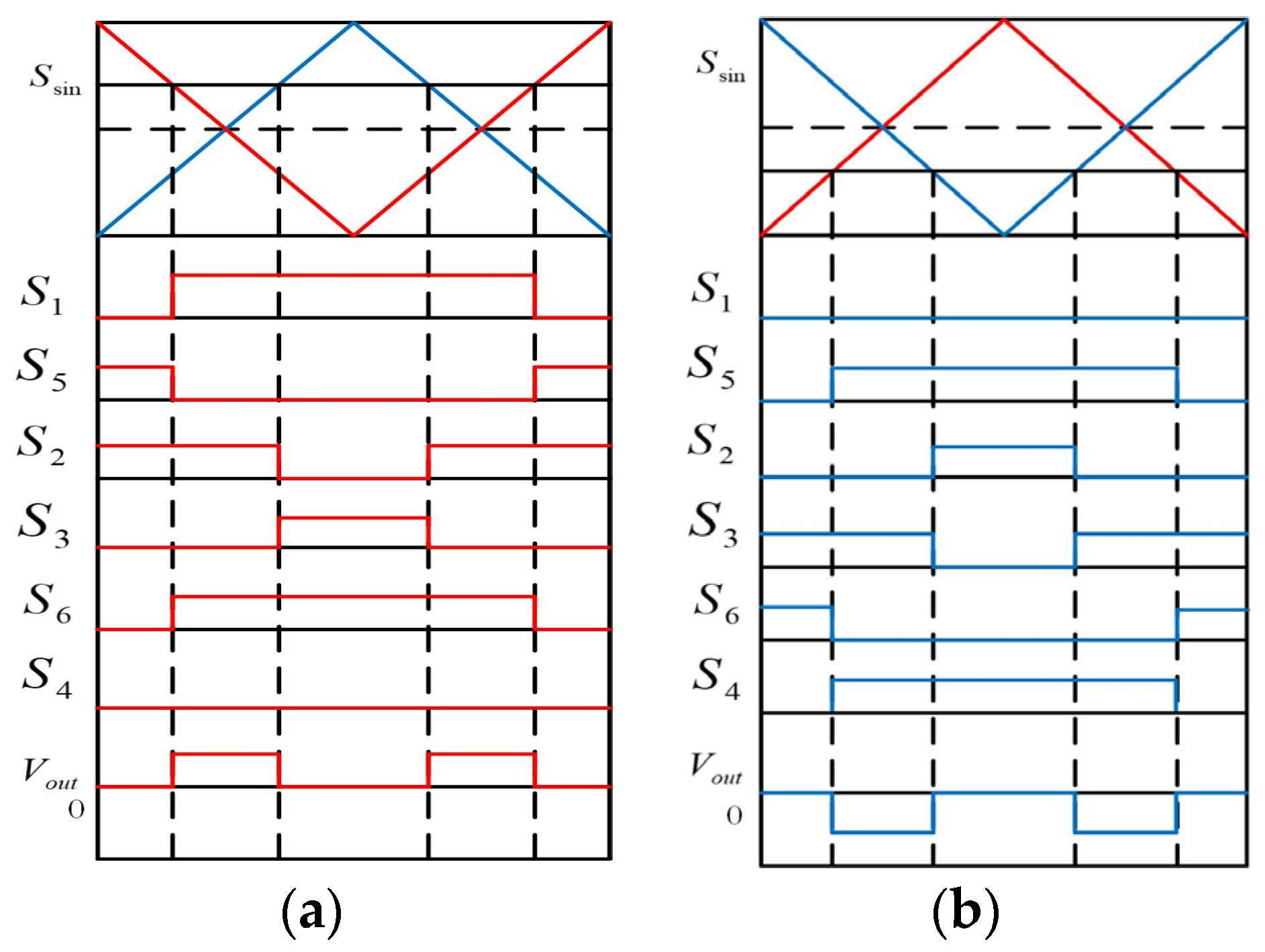
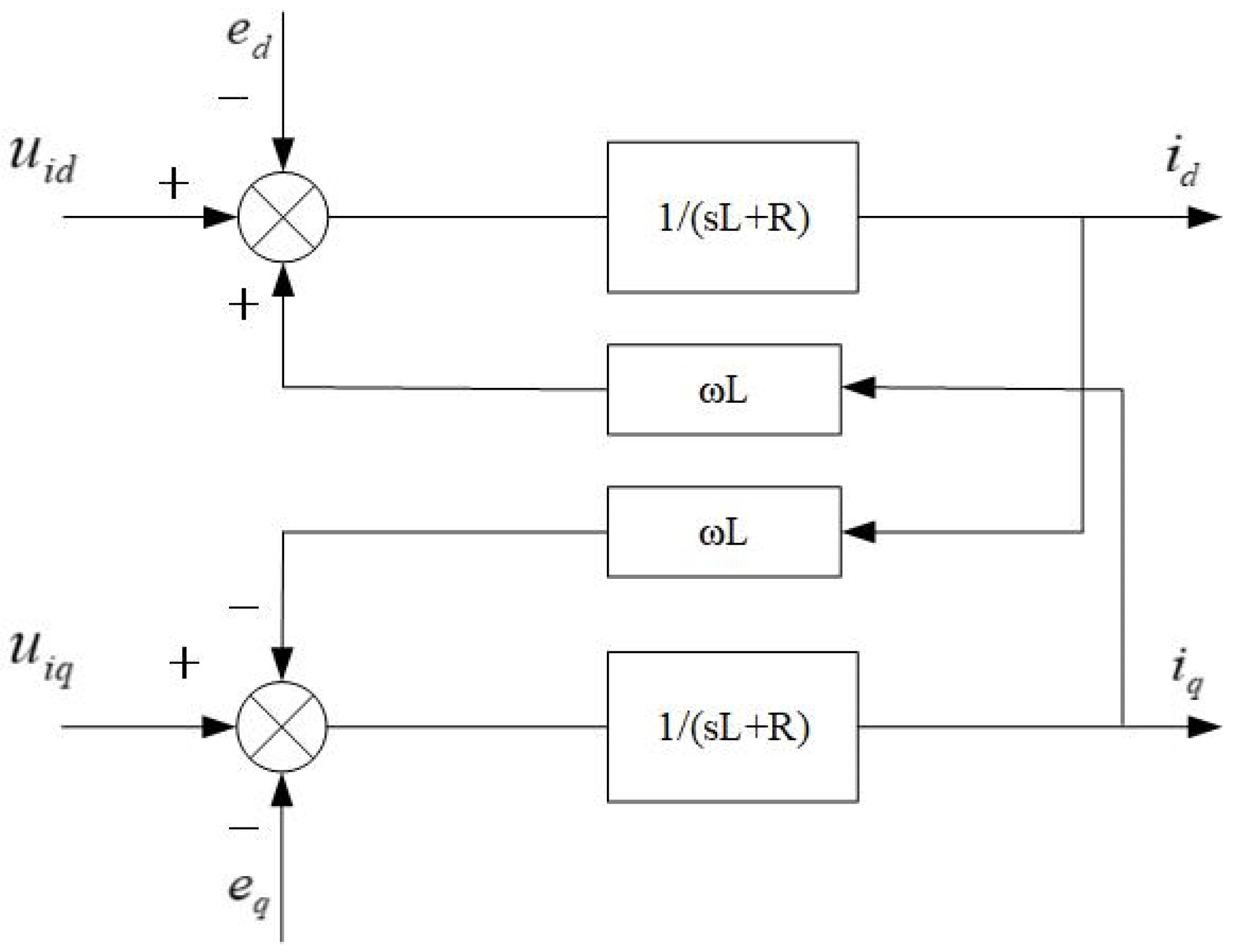




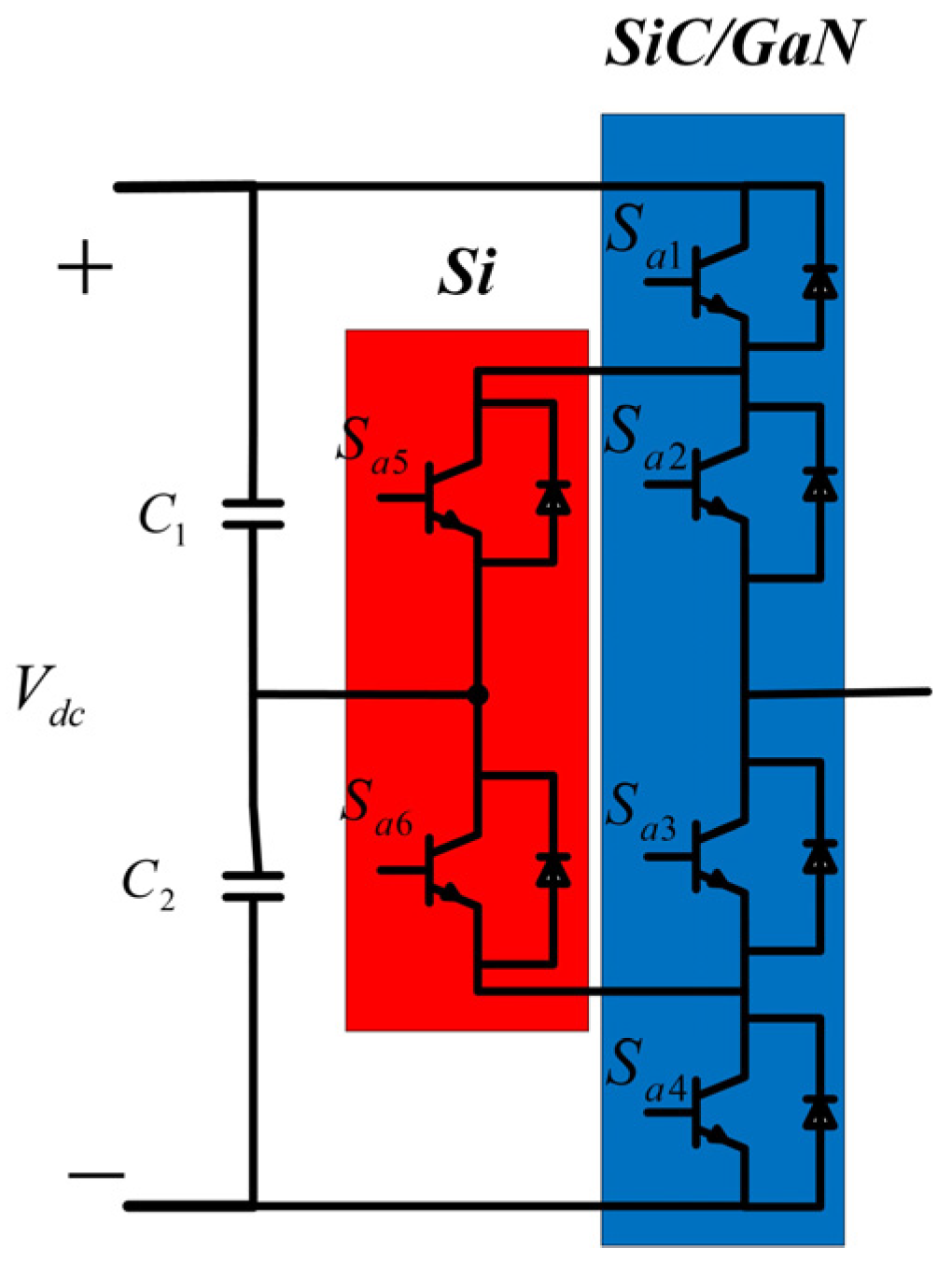
| States | Sa1 | Sa2 | Sa3 | Sa4 | Sa5 | Sa6 |
|---|---|---|---|---|---|---|
| Positive | on | on | off | off | off | on |
| 0+1 | off | on | off | off | on | off |
| 0+2 | on | off | on | off | off | on |
| 0−1 | off | on | off | on | on | off |
| 0−2 | off | off | on | off | off | on |
| Negative | off | off | on | on | on | off |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Input voltage, Vdc | 800 V | Grid-side inductance, Lgi | 1.58 mH |
| Input capacitors, C1, C2 | 5 mF | Filter capacitors, Cf | 0.1 mF |
| Filter inductance, Li | 3 mH | Grid voltage, ugi | 220 V |
| Switching frequency, fs | 10,000 Hz | Resistance of inductance, Ri | 1 mΩ |
| Grid-side resistance, Rg | 0.8929 Ω |
| Controller | Parameters | Value |
|---|---|---|
| Passive controller | R | 0.44645 |
| Ra1, Ra2 | 100 | |
| SMC | λ1, λ2 | 47 |
| R | 0.44645 | |
| k1, k2 | 20,000 | |
| PSM controller | Ra1, Ra2 | 50 |
| k1, k2 | 100 | |
| R | 0.44645 | |
| λ1, λ2 | 13,100 |
| Devices | Si | SiC | GaN |
|---|---|---|---|
| Conduction loss (W) | 28.24 | 21.97 | 11.22 |
| Switching loss (W) | 41.08 | 2.409 | 2.9 |
| Total loss (W) | 69.32 | 24.389 | 14.12 |
| Devices | Si | SiC | GaN | Si/SiC | Si/GaN |
|---|---|---|---|---|---|
| Conduction loss (W) | 28.24 | 21.97 | 11.22 | 21.5 | 12.58 |
| Switching loss (W) | 41.08 | 2.409 | 2.9 | 6.14 | 6.3 |
| Total loss (W) | 69.32 | 24.389 | 14.12 | 27.64 | 18.88 |
| Cost (USD) | 59.52 | 273.12 | 254.4 | 201.92 | 189.44 |
| Power (W) | 10,492.04 | 10,626.83 | 10,657.64 | 10,617.08 | 10,643.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Li, K.; Zhang, L. Hybrid ANPC Grid-Tied Inverter Design with Passivity-Based Sliding Mode Control Strategy. Energies 2024, 17, 3655. https://doi.org/10.3390/en17153655
Zhang Y, Li K, Zhang L. Hybrid ANPC Grid-Tied Inverter Design with Passivity-Based Sliding Mode Control Strategy. Energies. 2024; 17(15):3655. https://doi.org/10.3390/en17153655
Chicago/Turabian StyleZhang, Yifei, Kang Li, and Li Zhang. 2024. "Hybrid ANPC Grid-Tied Inverter Design with Passivity-Based Sliding Mode Control Strategy" Energies 17, no. 15: 3655. https://doi.org/10.3390/en17153655
APA StyleZhang, Y., Li, K., & Zhang, L. (2024). Hybrid ANPC Grid-Tied Inverter Design with Passivity-Based Sliding Mode Control Strategy. Energies, 17(15), 3655. https://doi.org/10.3390/en17153655







