Research on the Control and Modulation Scheme for a Novel Five-Switch Current Source Inverter

Abstract

Different from the voltage source inverter (VSI), the current source inverter (CSI) can boost the voltage and eliminate the additional passive filter and dead time. However, the DC-side inductor current is not a real current source and is generated by a DC voltage supply and an inductor. Under different switching states, the DC-side inductor will be charged or discharged, which leads to the DC-side inductor current being discontinuous or increasing. To solve the control problem of the DC-side inductor current of the CSI, a novel single-phase CSI topology with five switching tubes for grid-connected applications is proposed. Firstly, the reference calculation method and the hysteresis loop control scheme for the DC-side inductor current are proposed, and the adjustable and constant DC-side inductor current are obtained. Since the PWM signals cannot be directly implemented to the switching tubes, the modulation strategy for the single-phase CSI is proposed in this paper. Then, an active damping method based on the feedback capacitor voltage is presented to suppress the resonance peak caused by the LC filter on the grid side. Finally, the math model of the AC-side structure is established, and the optimal proportional-resonant controller parameters’ design method is explored by the amplitude–frequency characteristic curves. The simulation and experiment are implemented for the proposed CSI topology. The results show that a high-quality power with a good control performance can be obtained with the proposed CSI topology.

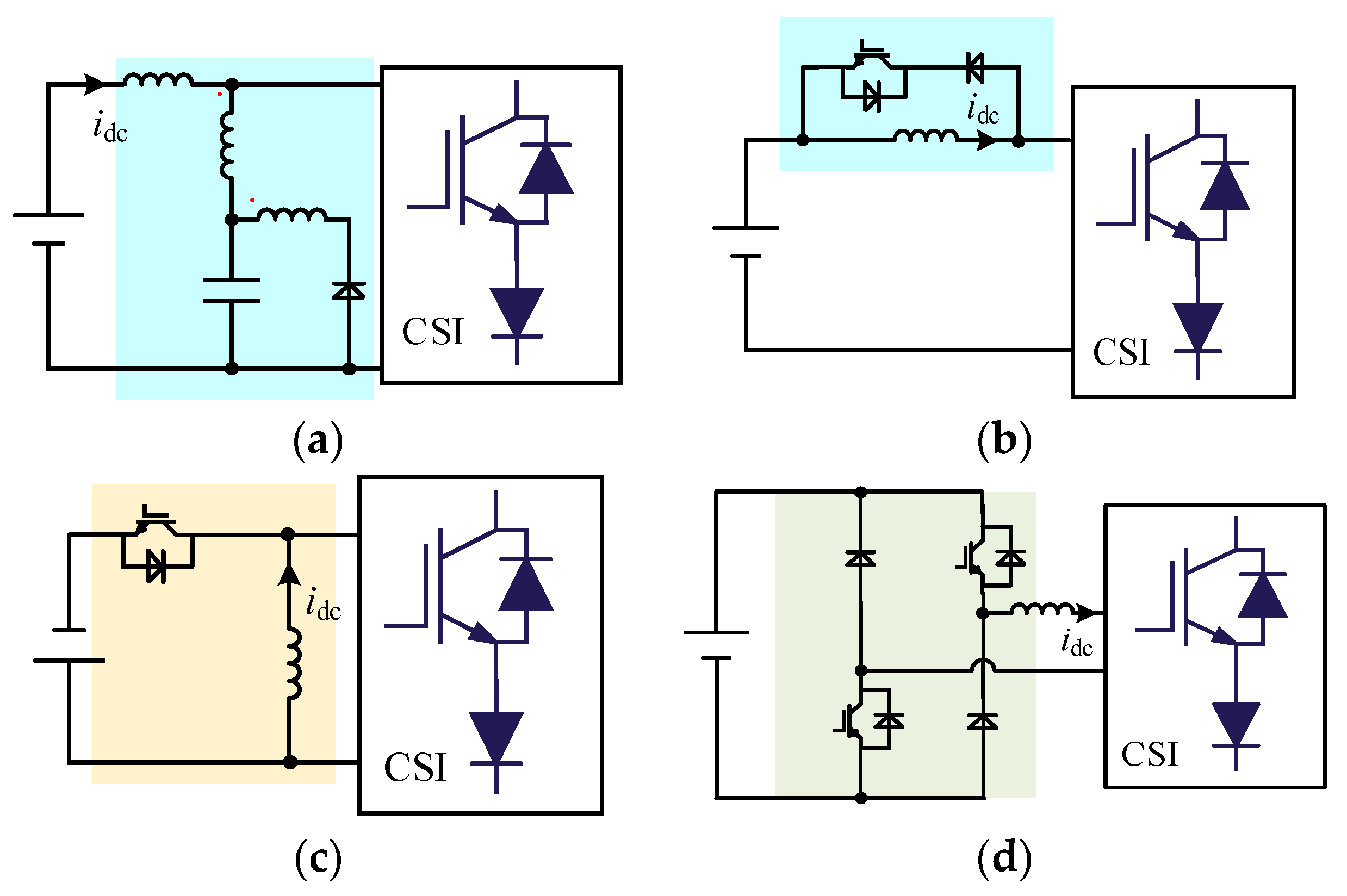
1. Introduction

To reduce carbon emissions and environmental pollution, it is imperative to accelerate the extraction of non-fossil fuels, such as wind power and photovoltaic power generation [1,2]. The inverter is the core part of a grid-connected device, used to complete the conversion of electrical energy from DC to AC, and it includes a voltage source inverter (VSI) and current source inverter (CSI) [3]. The VSIs stand out for their simple topology and flexible modulation and are employed in motor drives, electric vehicles, new energy generation, and other power conversion scenarios [4]. However, when the VSI is connected to the power grid, since the inverter output voltage contains switching harmonics, it is necessary to add a large inductor or LCL-type filter between the inverter and the grid side [5]. Although an L-type filter has a simple structure and no resonance, it has a large volume, poor dynamic characteristics, and insufficient suppression of the harmonics at the switching frequency [6]. The LCL-type filter is a third-order system, and a resonance peak occurs in the Bode plots of the LCL filter, which increases the complexity of the control system [7].

Different from VSIs, a CSI has the unique advantages of boost characteristic, protection for short circuits and overcurrent, no need for an electrolytic capacitor, and low dv/dt stress [8,9]. In the AC side, the capacitor filter and the grid-side inductor together form an LC-type second-order filter, which has a high filtering performance for high-frequency harmonics [10], and its resonance peak is lower than that of the LCL-type filter. However, the traditional CSI, shown in Figure 1, has some inherent shortcomings, which limits its wide application. Firstly, the DC-side inductor current of the CSI is not provided by a real current source, but is generated by a DC voltage source charging to the DC-side inductor. Different switching states have an impact on the charging or discharging of the DC-side inductor, and, as the DC-side inductor current and the AC-side output voltage have a coupling relationship, the control of the DC-side inductor current is necessary to improve the practicability of the CSI [11].

For example, if the initial value of the DC-side inductor current i_dc is zero, i_dc is in a discontinuous state, the amplitude of the load current i_s is relatively low, and there is an obvious low-order harmonic, which is shown in Figure 2a. This is because i_dc is too low to provide enough current for the AC-side load; the duration of the pass-through state is too short, causing the DC-side inductor to be unable to be sufficiently charged; the amplitude of i_s is lower than that of i_dc; and i_s cannot maintain a sinusoidal shape. When the initial value of i_dc is much greater than the amplitude of i_s, the simulation waveforms are as shown in Figure 2b. Within a fundamental cycle, since the charging effect of the DC-side inductor is greater than the discharging effect, i_dc continues to increase, which leads to the duration of the non-pass-through state decreasing and the duration of the pass-through state increasing. i_dc and the duty cycle of the pass-through state are a positive feedback process. Meanwhile, the higher harmonics of i_s increase with the decrease in the current utilization rate.

Secondly, the traditional CSI cannot operate in buck mode, and the waveforms are similar to those Figure 2b. Because the DC-side inductor is continuously charged, it is an unacceptable state for the CSI [12]. In summary, there is a coupling effect between the AC and DC sides of the traditional CSI, and it is difficult to control i_dc. In response to these challenges, a DC-side inductor current inner-loop controller was added into the AC control loop [11]. Due to too many state variables in the control system, this approach cannot achieve decoupling of the DC-side inductor current and the AC-side voltage. The second harmonic occurs in the DC-side inductor current, and the grid current has obvious low-order harmonic distortion. Therefore, the topology improvement of the CSI is the most widely used approach to achieve the DC-side inductor current control and voltage buck operation. A variety of two-stage improved topologies for the CSI have been proposed. The CSI with the quasi-Z source network proposed in [13] can achieve the buck operation without adding power-switching devices; this topology is shown in Figure 3a, where the red dots represent the same name terminal of the transformer. However, the introduction of too many passive devices greatly increases the complexity of the system and is not conducive to the design of the control system. Another topology, presented in [14], includes a front-stage rectifier and a back-stage inverter. This topology enables the control of the DC-side inductor current by the rectifier bridge, but it is only suitable for the wind power generation and other AC–DC–AC power conversion scenarios. Reference [15] added an SEPIC circuit on the DC side of the CSI to achieve the buck operation and common-mode current suppression. However, the SEPIC circuit includes three switching tubes, one diode, and two capacitors, which increases the loss and cost of the CSI. In [16], a switching tube and a diode were in parallel with the DC-side inductor, as shown in Figure 3b, and a new switching state was added to provide another freewheeling loop for the DC-side inductor. By switching to the pass-through state, the control and stability of i_dc can be achieved. In [17], a buck–boost CSI topology, shown in Figure 3c, was proposed to achieve the buck operation. However, the coupling between the DC side and the AC side was not eliminated by the topologies proposed in [16,17]. A CSI topology with a two-transistor forward voltage–current (V–I) converter was proposed in [18] and is shown in Figure 3d; the control for the DC-side inductor current and the buck operation can be realized. This topology also decouples the V–I converter from the CSI inverter, enabling independent control and bidirectional energy flow.

In addition to the different characteristics of the DC-side energy source, the switching signal generation method of the CSI is very different to that of VSI. Since the CSI allows bridge arm short circuits but not open circuits, the PWM signals, generated by comparison between the modulation signal and the carrier signal, cannot be directly implemented to the switching tubes of the CSI [19]. For this reason, Reference [20] proposed a logic circuit that converts two-value logic signals to three-logic logic signals, but it will increase the delay of the driving signal. In addition, the grid-side LC filter has a resonance peak phenomenon, which needs to be suppressed through the active damping method [21]. An active damping method was adopted in [22], which adopts the feedback of the AC-side capacitive current to reduce the resonance peak, but it requires additional current sensors, and the digital delay is not considered.

To fully utilize the advantages of the CSI and overcome its inherent defects, in this paper, a novel single-phase grid-connected CSI with five switching tubes is taken as the research object, and the operation principle is presented in Section 2. The reference calculation and hysteresis control scheme of the DC-side inductor current are proposed in Section 3. Aiming at the problem that the PWM signals cannot be directly implemented to the switching tubes of the CSI, the logical converter expressions are derived in Section 4. In Section 5, on the premise of introducing the capacitor voltage feedback channel, the amplitude–frequency characteristics of the closed-loop transfer function and the disturbance transfer function under different proportional resonant controller parameters are analyzed, and the method for determining the controller parameters is obtained. Finally, the simulation and experimental verifications are completed in Section 6 and Section 7, respectively. The conclusion is given in Section 8.

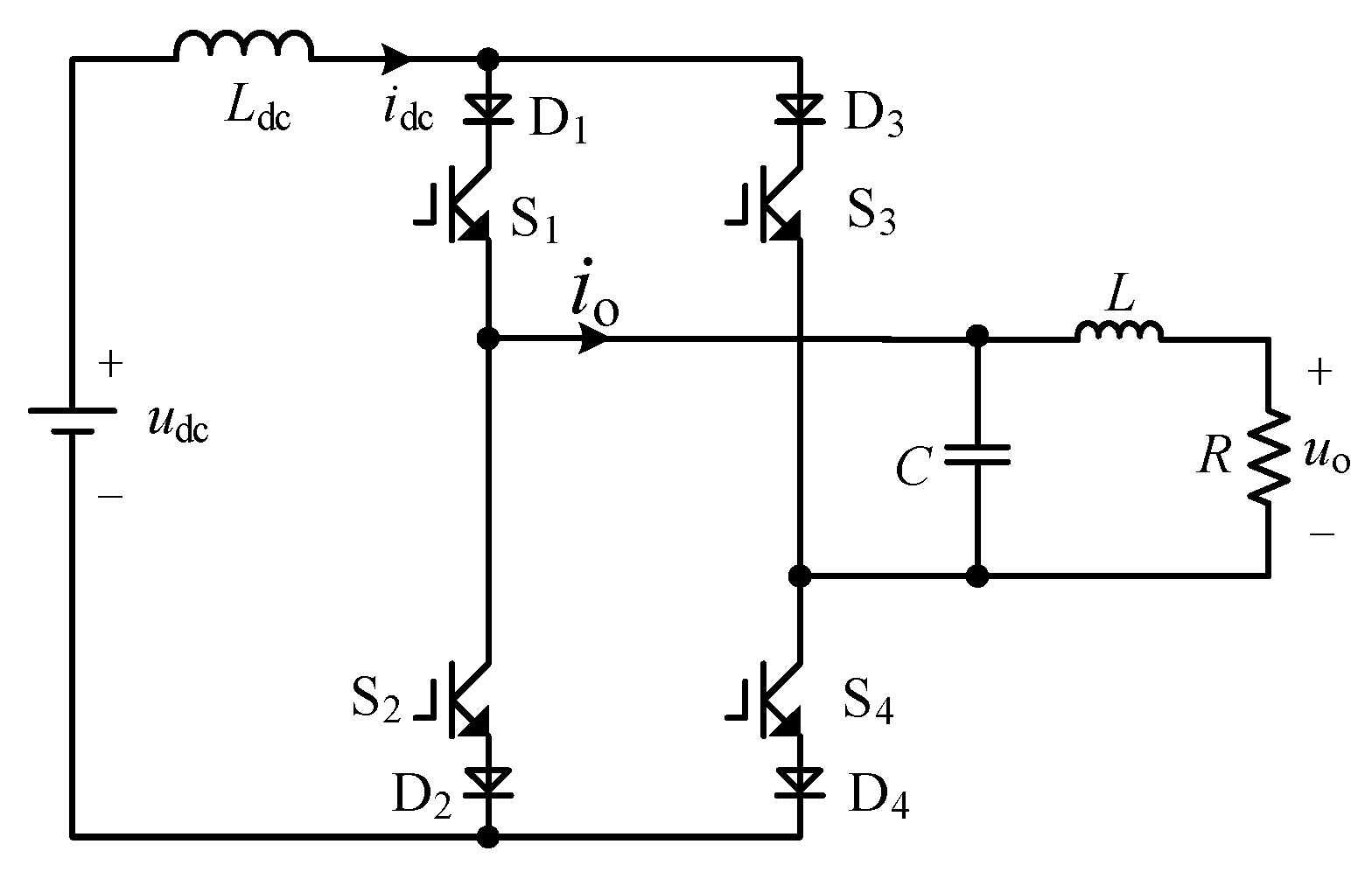
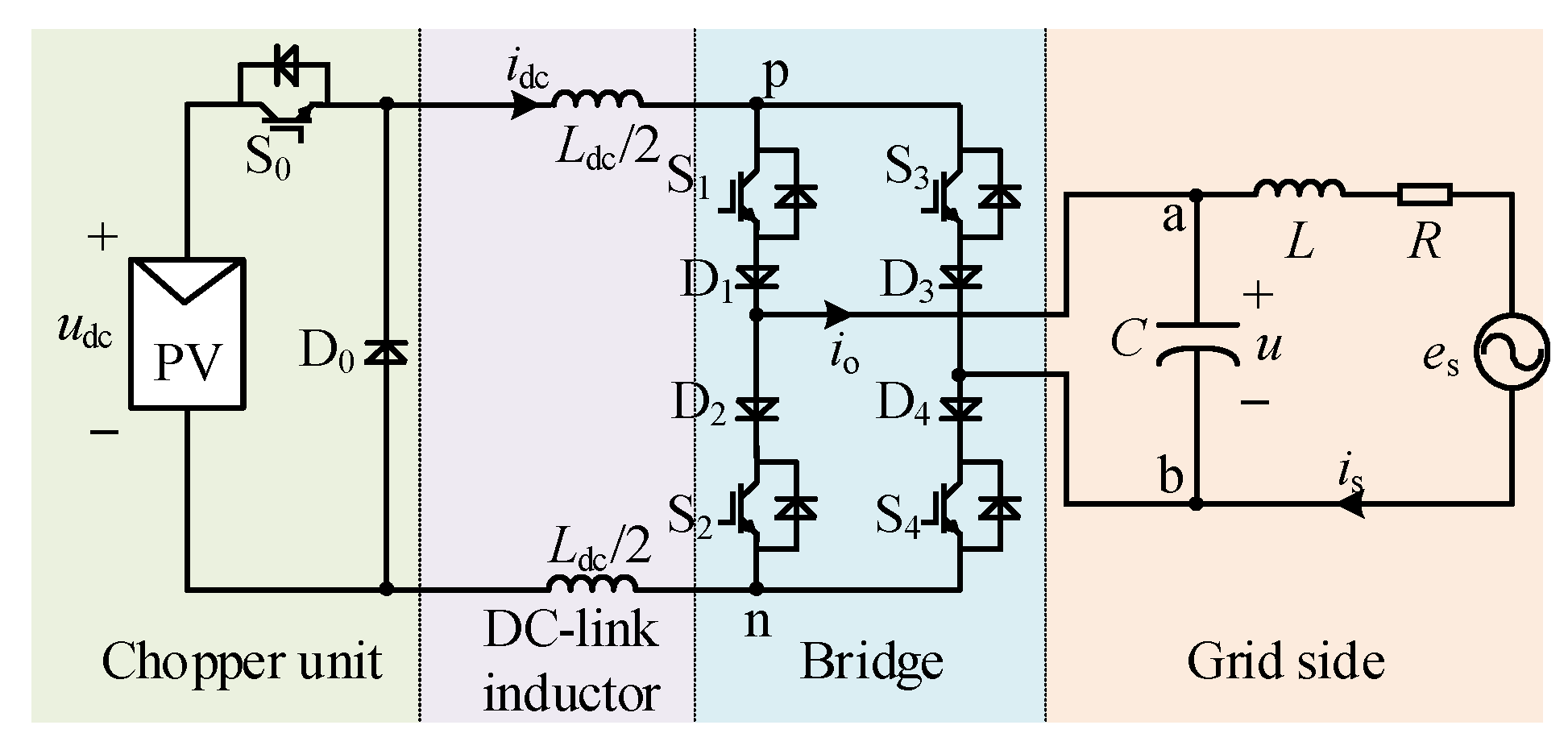
2. Topology and Operation Principle of the Proposed CSI Topology

After analyzing and comparing various improved CSI topologies, the CSI with the V–I converter proposed in [18] is the optimal topology. The DC-side inductor current can be controlled as a controlled current source, the coupling effect with the AC-side can be eliminated, and the improved CSI can operate in the buck, boost, and regeneration modes. Since the application scenario of this paper is the grid-connected system, the direction of the energy is only from the DC side to the AC side, so the V–I converter is replaced by a simple buck unit in this paper, and only one switching tube and one diode are introduced. A stable DC-side inductor current can be obtained, and the CSI can operate in the buck mode.

The proposed five-switch single-phase grid-connected CSI with a DC-buck unit is shown in Figure 4. u_dc denotes the DC-side input voltage; the switching tube S₀ and diode D₀ constitute the DC chopper unit, which realizes the adjustment of the DC-side inductor current i_dc. Switching tubes S₁–S₄ and diodes D₁–D₄ constitute the CSI bridge; L, R, C, and e_s denote the grid-side inductance, resistance, filtering capacitance, and voltage, respectively, which denotes the gird.

According to Figure 4, the state equation of the DC-side inductor current i_dc is derived as follows:

$$L_{\mathrm{dc}}{\displaystyle \frac{\mathrm{d}{i}_{\mathrm{dc}}}{\mathrm{d}t}}=u_{\mathrm{dc}}{p}_0-u_{\mathrm{pn}}$$

(1)

where p₀ denotes the switching function of the switching S₀, u_pn denotes the voltage between the upper and lower DC bus of the bridge, and u_pn satisfies the following relationship:

$$u_{\mathrm{pn}}=u_{\mathrm{ab}}{p}_{\mathrm{inv}}$$

(2)

where u_ab is the voltage of the filter capacitor and p_inv denotes the switching function, and p_inv is defined as follows:

$$p_{\mathrm{inv}}=\left\{\begin{array}{l}1{ \mathrm{S}}_1{ \mathrm{S}}_4{ \mathrm{on}, \mathrm{S}}_2{ \mathrm{S}}_3 \mathrm{off}\\ 0{ \mathrm{S}}_1{ \mathrm{S}}_2{ \mathrm{on}, \mathrm{S}}_3{ \mathrm{S}}_4 \mathrm{off} \\ -1{ \mathrm{S}}_2{ \mathrm{S}}_3{ \mathrm{on}, \mathrm{S}}_1{ \mathrm{S}}_4 \mathrm{off}\end{array}\right.$$

(3)

The state equation of u_ab can be derived and is shown as follows:

$${\displaystyle \frac{\mathrm{d}{u}_{\mathrm{ab}}}{\mathrm{d}t}}=i_{\mathrm{o}}-i_{\mathrm{s}}$$

(4)

where i_o is the output current of bridge, and i_s the grid-side current, respectively. i_o should be equal to i_dc × p_inv, and the state equation of i_s derived as follows:

$$L_{\mathrm{s}}{\displaystyle \frac{\mathrm{d}{i}_{\mathrm{s}}}{\mathrm{d}t}}=u_{\mathrm{ab}}-i_{\mathrm{s}}{R}_{\mathrm{s}}-e_{\mathrm{s}}$$

(5)

According to Equations (1) and (5), the switching action induces changes in i_dc, which in turn affects u_ab. There is a significant coupling relationship between u_ab and i_dc. To remove coupling between AC and DC sides, the DC-side inductor current and the grid current are decomposed into two separate links. The constant output of i_dc is achieved by adjusting the switching state of S₀, and the control of grid current is achieved by controlling S₁–S₄.

3. Reference Calculation and Control Scheme for DC-Side Inductor Current

The loss of the switching tubes, and the harmonic distortion of the current exhibit a positive correlation with the DC-side inductor current. Therefore, under the condition that the DC-side inductor current is capable of meeting power requirements, the current utilization rate should also be improved as much as possible.

3.1. Reference Calculation for DC-Side Inductor Current

The vector diagram of the inductor, capacitor, resistor, and grid voltage in the AC side is shown in Figure 5.

The expression for the grid voltage, e_s, is defined as follows:

$$e_{\mathrm{s}}(t)=E_{\mathrm{s}}\sin (\omega t+\theta )$$

(6)

where E_s denotes the magnitude of e_s, θ denotes the initial phase, and ω denotes the angular frequency. When the CSI operates at steady state and at unit power factor, i_s, the expression of the grid current, is defined as follows:

$$i_{\mathrm{s}}(t)=I_{\mathrm{s}}\sin (\omega t+\theta )$$

(7)

where I_s denotes the fundamental amplitude of i_s. According to the circuit, the fundamental wave expression of u_ab is defined as follows:

$$u_{\mathrm{ab}}(t)=U\sin (\omega t+\phi )$$

(8)

where U and φ denote the amplitude and phase of u_ab. They can be derived as follows:

$$\left\{\begin{array}{l}U=\sqrt{{(\omega L_{\mathrm{s}}{I}_{\mathrm{s}})}^2+{(E_{\mathrm{s}}+I_{\mathrm{s}}R)}^2}\\ \phi =\theta +\arctan ({\displaystyle \frac{\omega L_{\mathrm{s}}{I}_{\mathrm{s}}}{E_{\mathrm{s}}+I_{\mathrm{s}}R}})\end{array}\right.$$

(9)

According to the vector diagram of the AC grid side, based on the cosine theorem, the expression for the fundamental amplitude I_o of i_o can be derived as follows:

$$I_{\mathrm{o}}=\sqrt{{\omega }^2{C}^2{U}_{\mathrm{o}}^2+I_{\mathrm{s}}^2-2\omega C{U}_{\mathrm{o}}{I}_{\mathrm{s}}\sin (\phi -\theta )}$$

(10)

Substituting (9) into (10), I_o is obtained as follows:

$$I_{\mathrm{o}}=\sqrt{{\omega }^2{C}^2{(E_{\mathrm{s}}+I_{\mathrm{s}}R)}^2+{\omega }^4{C}^2{L}_{\mathrm{s}}^2{I}_{\mathrm{s}}^4+{(1-{\omega }^2{L}_{\mathrm{s}}C)}^2{I}_{\mathrm{s}}^2}$$

(11)

where i_o is modulated by i_dc. The reference of i_dc is equal to I_o/m, where m is the modulation ratio. If m is set too high, L_dc cannot be charged sufficiently in the through state; it is difficult to achieve a volt-second balance of the DC-link inductor. If m is set too low, the current utilization rate is too low, and the loss is also great. Therefore, under the condition that the DC-side inductor current is capable of meeting power requirements, the current utilization rate should also be improved as much as possible. According to [18], m is set as 0.75 in this paper.

3.2. Hysteresis Loop Control Scheme for DC-Side Inductor Current

To realize the DC-side inductor current following the reference value $i_{\mathrm{dc}}^{*}$, as shown in Figure 6, an easy-to-implement hysteresis control scheme is adopted in this paper. When i_dc is greater than the hysteresis loop upper limit setting value, S₀ is turned off, L_dc provides energy to the load alone during this period, and i_dc gradually decreases. When i_dc is lower than the hysteresis lower limit setting value, S₀ is turned on, u_dc charges L_dc in the stage of pass-through state and non-pass-through state when u_dc is greater than u_o, and i_dc continuously increases.

4. Modulation Strategy for the CSI

Different from the VSI, the PWM signals generated by the comparison between the modulation signal and the carrier signal cannot be directly implemented for the switching tubes of CSI. Instead, a logic conversion process is necessary. Since the single-phase modulation strategy is relatively simple, there is no need to adopt hardware logic circuit, and the switching signals of S₁–S₄ can be directly generated by the digital signal processor. A logic signal X is defined, and, determined by the polarity of the judgment method, is defined as follows:

$$\mathrm{X}=\left\{\begin{array}{l}1\hspace{1em}\hspace{1em}{i}_{\mathrm{o}}^{*}\ge 0\\ 0\hspace{1em}\hspace{1em}{i}_{\mathrm{o}}^{*}<0 \end{array}\right.$$

(12)

Another logic signal Y is defined; it is used to reflect the pass-through state and the non-pass-through state of CSI, and is determined by the compared result between the modulating signal and the triangular carrier signal; the judgment method is defined as follows:

$$\mathrm{Y}=\left\{\begin{array}{l}1\hspace{1em}\hspace{1em}{i}_{\mathrm{o}}^{*}/i_{\mathrm{dc}}\ge \mathrm{triangular} \mathrm{carrier}\\ 0\hspace{1em}\hspace{1em}{i}_{\mathrm{o}}^{*}/i_{\mathrm{dc}}< \mathrm{triangular} \mathrm{carrier} \end{array}\right.$$

(13)

Combining the inverter bridge switching functions shown in Equation (3), the drive logic functions p₁–p₄ for S₁–S₄ are obtained.

$$\left\{\begin{array}{l}{p}_1=\mathrm{X}|\overline{\mathrm{Y}}\\ p_2=\overline{\mathrm{X}}\&\mathrm{Y}\\ p_3=\overline{\mathrm{X}}|\overline{\mathrm{Y}}\\ p_4=\mathrm{X}\&\mathrm{Y}\end{array}\right.$$

(14)

When $i_{\mathrm{o}}^{*}$ > 0, X = 1; at this time, S₁ is turned on, and S₂ is turned off. Commutation occurs between S₃ and S₄, CSI switches between pass-through and non-pass-through states, and the diagram of p₁–p₄ is shown in Figure 7a. When $i_{\mathrm{o}}^{*}$ < 0, X = 0; at this time, S₃ is turned on, S₄ is turned off. Commutation occurs between S₁ and S₂, and the diagram of p₁–p₄ is shown in Figure 7b.

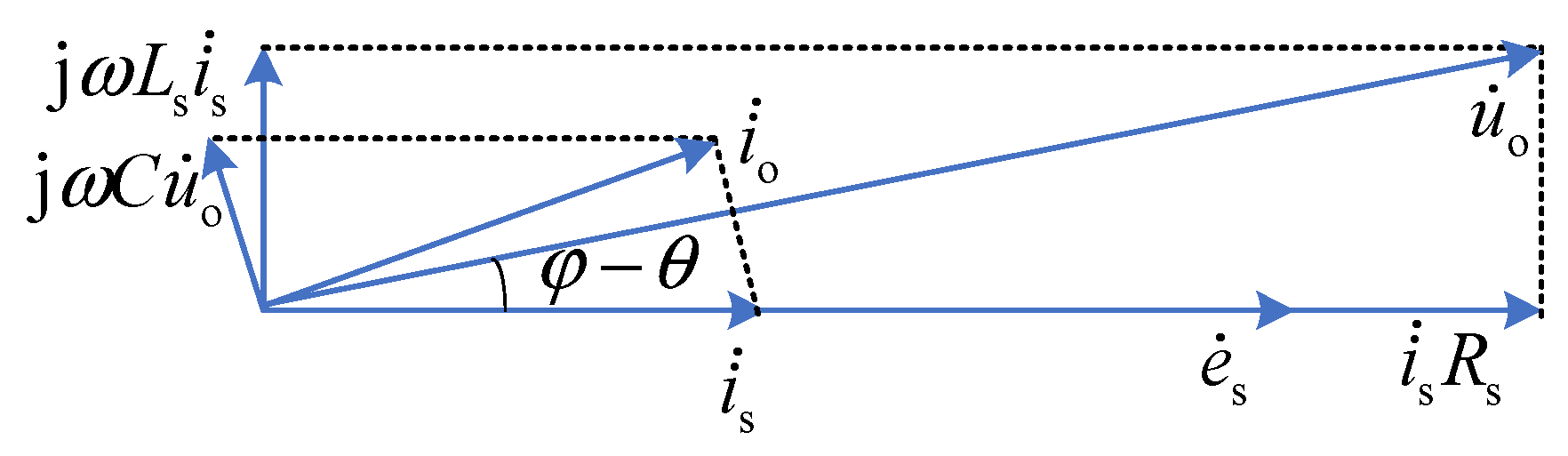
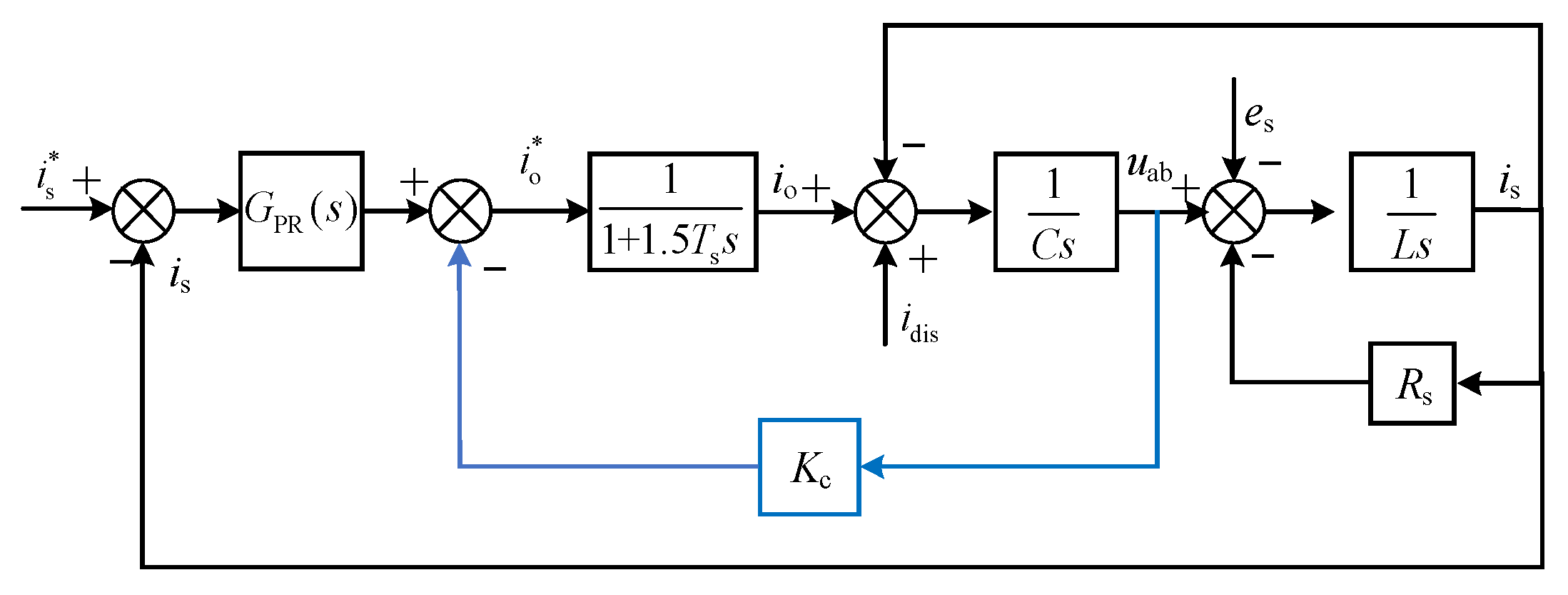
5. Grid Current Control Scheme Based on Capacitor Voltage Feedback

Compared with the VSI with an LCL-type third-order filter, the CSI has an LC second-order filter on the grid side, and the resonance peak phenomenon still exists in its Bode plot. When the line inductance increases as a result of changes in grid impedance and inductive load connection, the resonant frequency point shifts to low frequency, causing more serious low-frequency resonance, resulting in the oscillation during the system dynamic adjustment process. Therefore, before designing the controller parameters, the active damping needs to be introduced to effectively suppress the LC resonance.

5.1. Active Damping Based on Voltage Feedback

The transfer function G_io2is(s) from i_o to i_s is derived as follows:

$$G_{\mathrm{io}2\mathrm{is}}(s)={\displaystyle \frac{i_{\mathrm{s}}(s)}{i_{\mathrm{o}}(s)}}={\displaystyle \frac{1}{L_{\mathrm{s}}C{s}^2+R_{\mathrm{s}}Cs+1}}$$

(15)

R_s is the line loss and the impedance is very small, so G_io2is(s) is a second underdamped state, and a resonance peak occurs in its Bode plots. Since the capacitor voltage is easy to sample, the active damping method based on the feedback of u_ab is adopted in this paper. Firstly, a mathematical model in the s-domain of the AC-side control system is constructed, which is shown in Figure 8.

The sampling and digital delay are combined [23], and are equivalent to the first-order transfer function T(s); its expression is as follows:

$$T(s)={\displaystyle \frac{1}{1+1.5T_{\mathrm{s}}s}}$$

(16)

where T_s is the sample and carrier period. When the capacitor voltage feedback is introduced to the control loop, the transfer function of G_io2is(s) is re-expressed as follows:

$$G_{\mathrm{io}2\mathrm{is}}(s)={\displaystyle \frac{1}{L(1.5T_{\mathrm{s}}+C)s^2+(1.5T_{\mathrm{s}}R+CR+K_{\mathrm{c}}L)s+K_{\mathrm{c}}R+1}}$$

(17)

Substituting the parameter values, as shown in

Table 1. Parameters of CSI.

Parameters	Value
DC input voltage udc (V)	270
DC-side inductance Ldc (mH)	4
Amplitude of grid voltage es (V)	311
Filter capacitance C (µF)	12
Inductance L (mH)	0.5
Resistance R (Ω)	0.5
Frequency f (kHz)	10

into Equation (16), the amplitude–frequency characteristic curves of G_io2is(s) can be obtained for different values of the capacitor voltage feedback coefficient K_c, as shown in Figure 9. In all frequency bands, changes in K_c have no effect on G_io2is(s), the resonance spikes of G_io2is(s) gradually decrease with the increase in K_c, and the gains at the resonance frequencies are all less than 0 dB under K_c > 0.3. Nevertheless, with the increase in K_c, the gain of the low band will also decrease slightly. When K_c is too large, the inverter needs to output i_o with a larger amplitude to generate the same grid-side current. However, the DC-side inductor current is limited, and excessive K_c will cause overmodulation, resulting in the amplitude error of grid current, so K_c is set as 0.3.

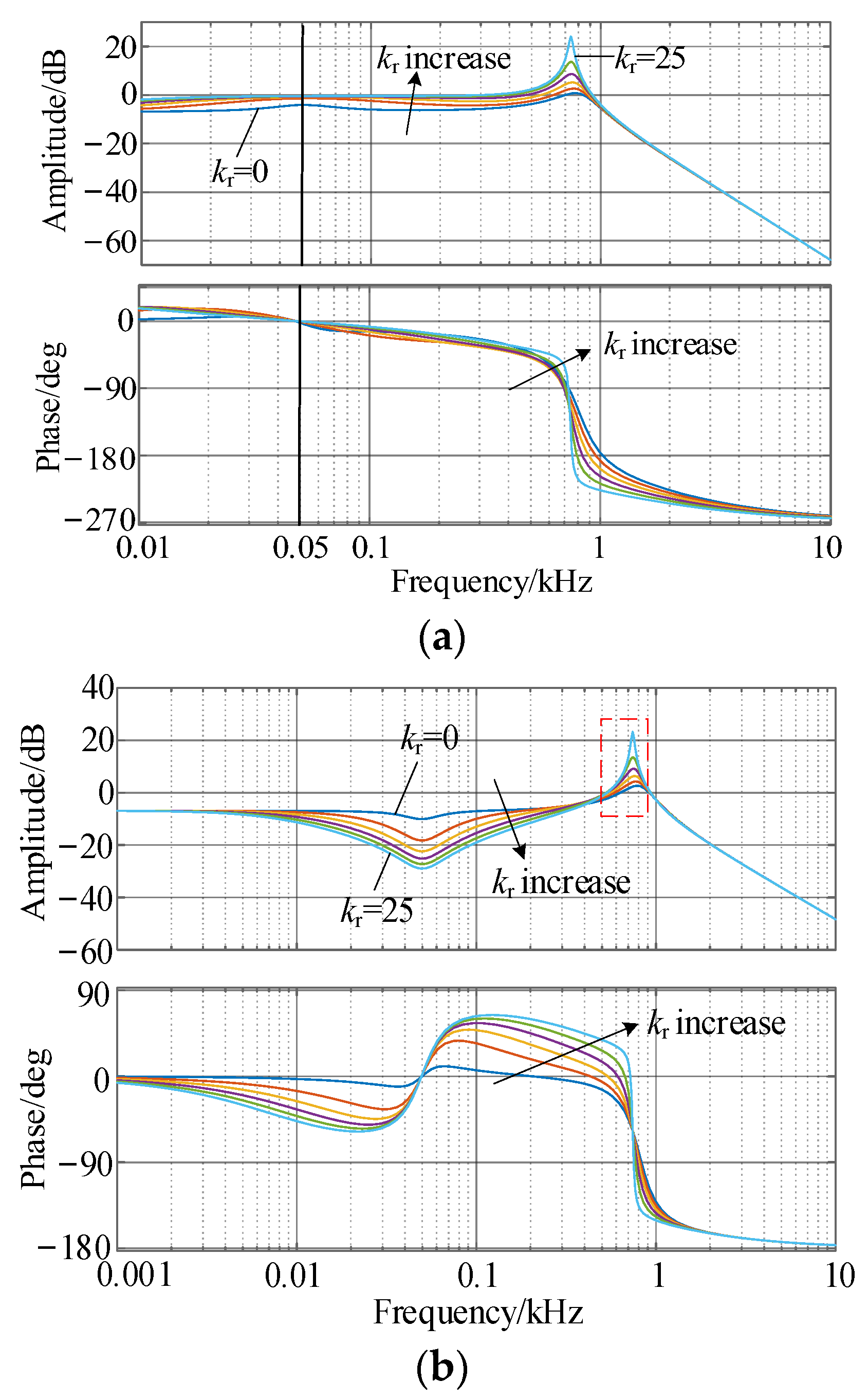
5.2. Controller Parameter Design Method

For the single-phase system, since only one AC component cannot be mapped to DC component by the Park transformation, the PI control algorithm in the rotating coordinate system cannot be applied [20]. Reference [11] proposed a method of constructing orthogonal imaginary axis components to achieve conversion from AC to DC systems, but this will increase the execution time of the program and reduce the robustness of the system. Therefore, in this paper, a proportional resonance (PR) controller G_PR(s) is adopted to realize a single closed-loop control of i_s, and the transfer function of G_PR(s) is shown as follows:

$$G_{\mathrm{PR}}(s)=k_{\mathrm{p}}+{\displaystyle \frac{2k_{\mathrm{c}}\zeta {\omega }_{0}s}{s^2+2\zeta {\omega }_{0}s+{{\omega }_0}^2}}$$

(18)

where k_p is the proportional coefficient, k_c is the resonance coefficient, and ζ is the resonance damping, which is set as 0.5 in this paper. ω₀ is the angular frequency and is equal to 100π. The open-loop transfer function G_open(s) can be expressed as follows:

$$G_{\mathrm{open}}(s)=G_{\mathrm{PR}}(s)T(s)G_{\mathrm{io}2\mathrm{is}}(s)$$

(19)

The closed-loop transfer function G_close(s) can be expressed as follows:

$$G_{\mathrm{close}}(s)={\displaystyle \frac{G_{\mathrm{open}}(s)}{1+G_{\mathrm{open}}(s)}}$$

(20)

During the modulation process, i_o has abundant sideband harmonics at the carrier frequency and its multiples. It is also necessary to delay the turn-off signal to prevent the DC-side inductor current from breaking, resulting in the presence of 5th, 7th, 11th, and 13th harmonic components in i_o. In the modeling process, the low and high harmonics are equated to the disturbance current i_dis in Figure 5, and the transfer function G_idis2is(s) from i_dis to i_s can be derived as follows:

$$G_{\mathrm{idis}2\mathrm{is}}(s)={\displaystyle \frac{G_{\mathrm{io}2\mathrm{is}}(s)}{1+G_{\mathrm{open}}(s)}}$$

(21)

Subsequently, the individual impacts of k_p and k_r on the performance of the control system are discussed in detail. Firstly, k_p is set as 0, and the amplitude–frequency characteristics and phase-frequency characteristic curves of G_close(s) and G_idis2is(s) under different k_r are drawn, as shown in Figure 10a,b. As k_r increases, G_close(s) gradually approaches the 0 dB line in the low-frequency band, and i_s and i_a remain in the same phase at 50 Hz. In the high-frequency band, k_r has no effect on G_close(s). However, in Figure 10b, it can be seen that in the frequency band from 500 Hz to 950 Hz, G_idis2is(s) produces a large spike as k_r increases. It will amplify the perturbing effect of the 11th and 13th harmonics in i_dis on i_s.

Next, k_r is set as 15, and the amplitude–frequency characteristics and phase-frequency characteristic curves of G_close(s) and G_idis2is(s) under different k_p are drawn, as shown in Figure 11a,b. In the low-frequency band, k_p has little effect on G_close(s), while in the high-frequency band, the cutoff frequency of G_close(s) increases with the increase in k_p. But when k_p > 10, the cutoff frequency is 2 kHz, and the sensitivity to k_p becomes smaller. In Figure 11b, the amplitude–frequency characteristic curve of G_idis2is(s) gradually decreases with the increase in k_p, and when k_p > 5, the amplitude gain of G_idis2is(s) is lower than 0 dB in the whole frequency band, which means that the control system is capable of attenuating all the harmonics generated by the modulation process.

Combining the above analysis, the parameters of the PR controller in this paper are set as k_p = 10 and k_r = 5.

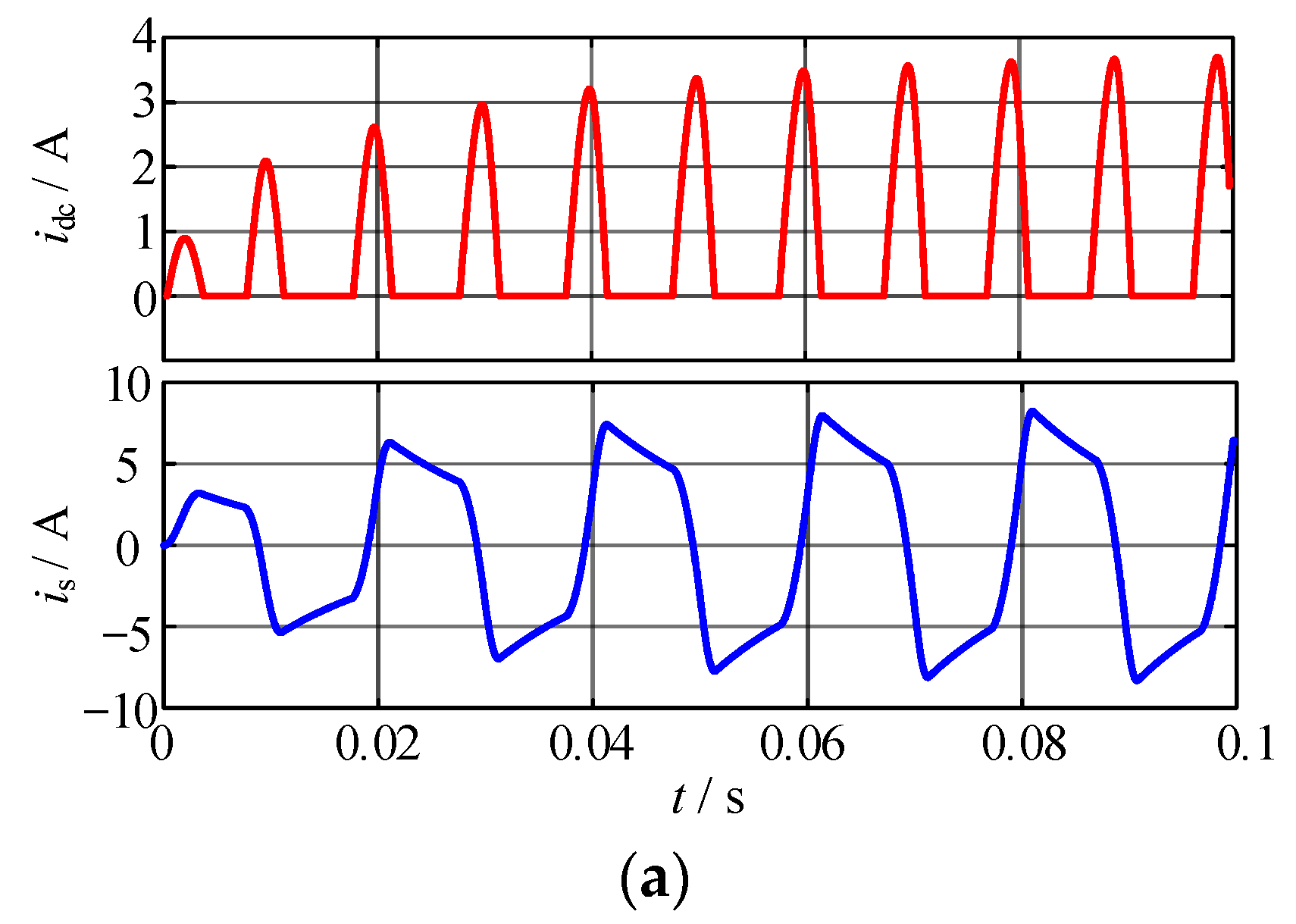
6. Simulink Results and Analysis

The simulation model of the proposed topology, modulation, and control scheme are established in the Matlab2021b/Simulink environment, and the Simulink parameters are listed in Table 1. The correctness of the calculation method for the DC-side inductor current and the effectiveness of the hysteresis loop control strategy are simulated and verified. The reference amplitude of i_s is set as 10 A, and the parameters shown in Table 1 are substituted into Equation (11) to obtain the optimal value of $i_{\mathrm{dc}}^{*}$ of 14 A. The simulation is carried out for this case, and the simulated waveforms of i_s and i_dc, as well as the results of the FFT analysis of i_s, are shown in Figure 12a. To show that $i_{\mathrm{dc}}^{*}$ = 14 A is in the optimal range, simulation is carried out for the two cases of $i_{\mathrm{dc}}^{*}$ = 12.5 A and $i_{\mathrm{dc}}^{*}$ = 15.5 A, and the simulation waveforms are shown in Figure 12b,c. The three sets of simulation results shown in Figure 10 indicate that the i_dc can accurately follow $i_{\mathrm{dc}}^{*}$, so the effectiveness of the DC-side inductor current hysteresis loop control strategy proposed in Section 3.2 has been verified. When $i_{\mathrm{dc}}^{*}$ = 12.5 A, the amplitude of i_s is only 9.85 A, which is lower than the reference amplitude of 10 A, and there are obvious low harmonic distortions. When $i_{\mathrm{dc}}^{*}$= 15.5 A, i_s has no steady-state error, but the third harmonic component and THD are greater than those under $i_{\mathrm{dc}}^{*}$= 14 A. The above simulation results can prove the correctness of the calculation method for the reference of the DC-side inductor current.

The effectiveness of the active damping method based on the capacitor voltage feedback is simulated and verified, the simulation is also carried out under the operating condition of $i_{\mathrm{dc}}^{*}$ = 14 A, and the reference amplitude of i_s is set as 10 A. For the capacitive voltage feedback channel not introduced, the simulation waveform of i_s is shown in Figure 13a, and it can be seen that there is an obvious current ripple in i_s. For the capacitor voltage feedback coefficient K_c set as 0.5, the simulation waveform is shown in Figure 13b. Although there is no obvious harmonic distortion, the amplitude of i_s is only 8.6 A. Comparing the two aspects of control performance and power quality, the simulation results under K_c = 0.3, shown in Figure 13a, are better than those under K_c = 0 and K_c = 0.5, which indicates the feasibility of the transfer function derivation and capacitor voltage feedback coefficient determination methods.

7. Experimental Results and Analysis

As shown in Figure 14, a grid-connected CSI experimental platform is established. The TMS320F28335 (TEXAS Instruments, Dallas, TX, USA) is used to execute the control algorithm and generate the switching signals, the switching tube and diode models are FF100R12RT4 (Infineon, Neubiberg, Germany) and MEK75-12DA (Infineon, Neubiberg, Germany), and other passive device parameters and carrier frequency are consistent with Table 1.

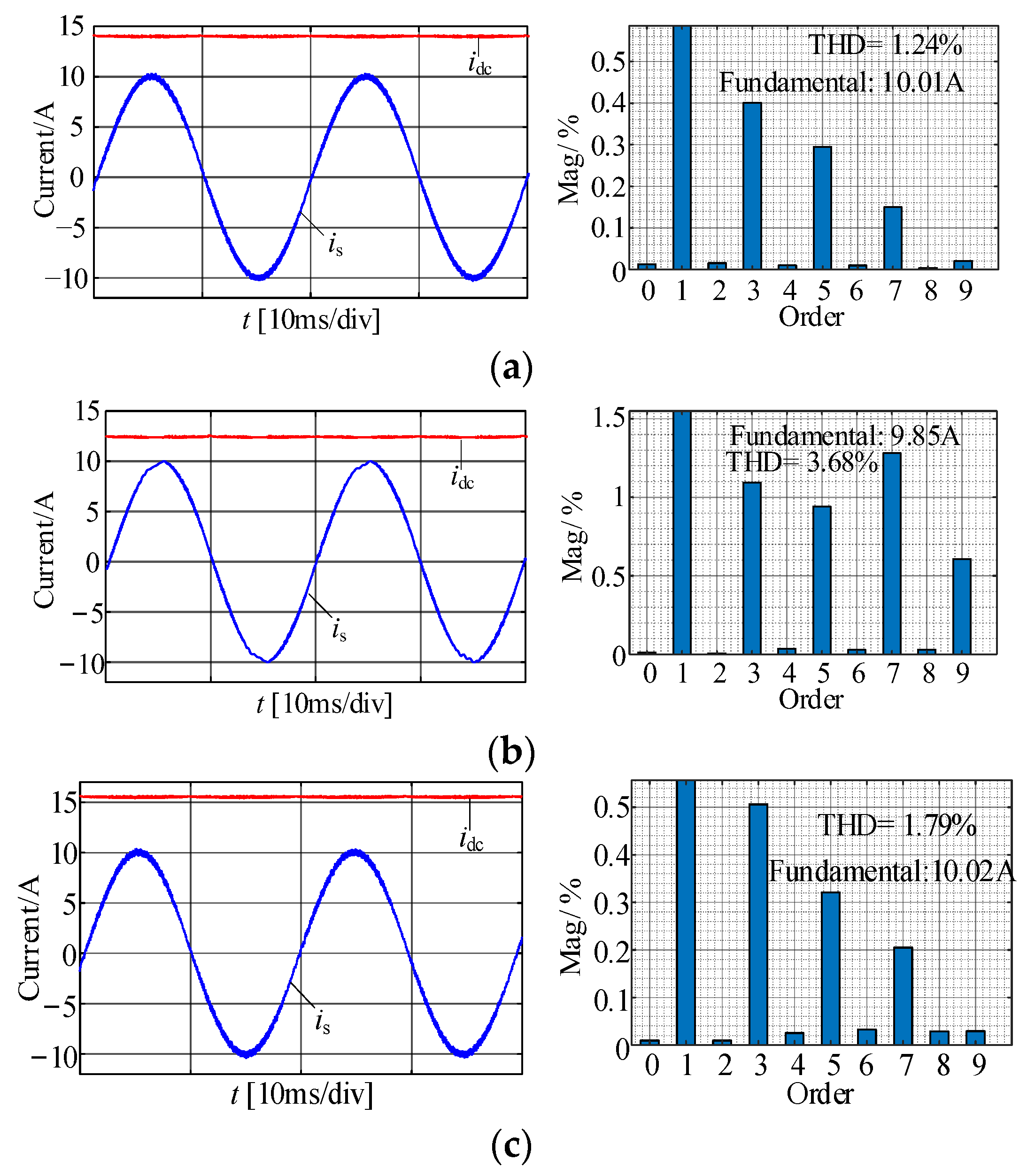
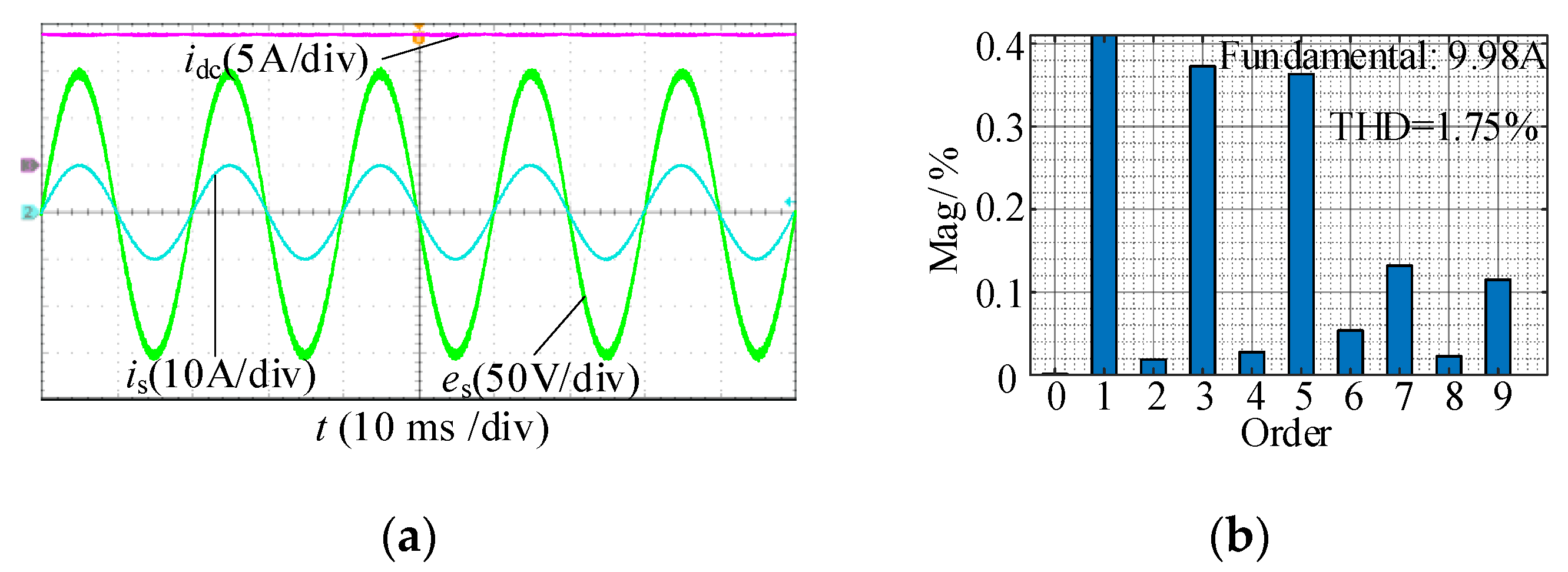
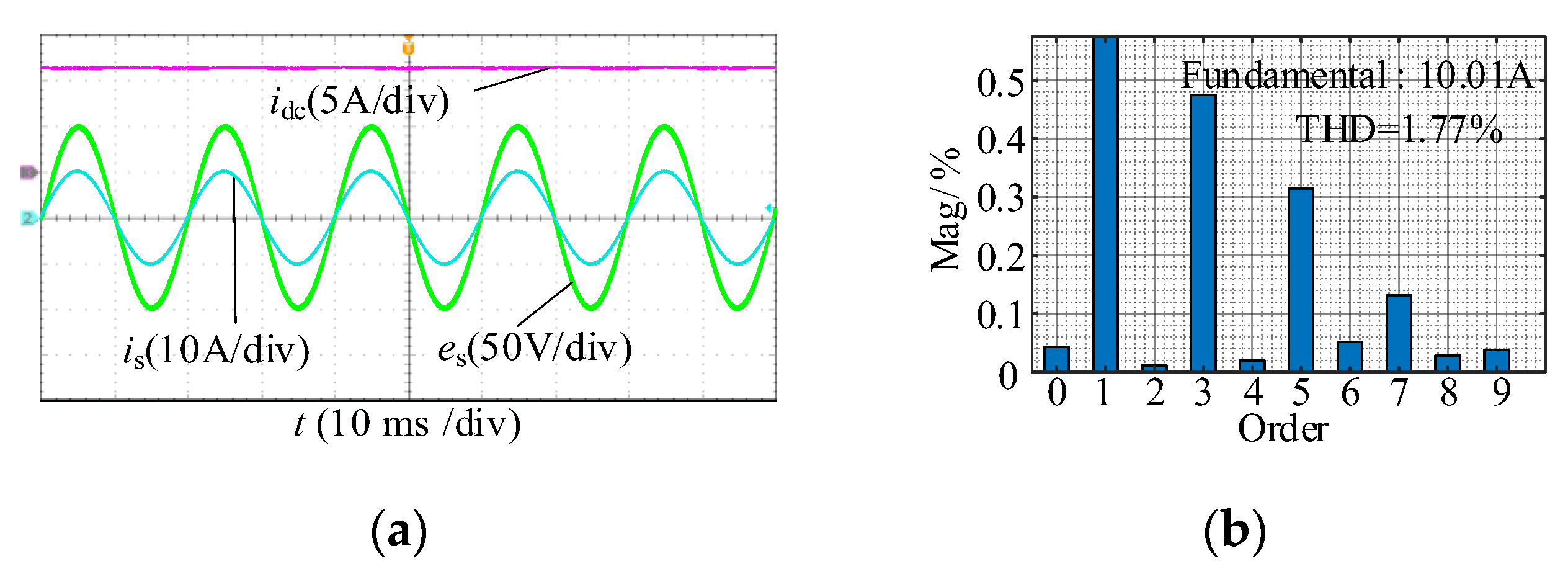
7.1. Steady-State Verification

The experimental verification is firstly carried out in the boost mode, where u_dc is regulated to 100 V and the programmable grid simulator outputs an AC voltage with a frequency of 50 Hz and an amplitude of 150 V. Similar to the simulation, the reference amplitude of i_s is set as 10 A and the phase is synchronized with the grid voltage. Substituting into Equation (10) yields $i_{\mathrm{dc}}^{*}$= 14 A. Under the proposed DC-side inductor current hysteresis controller and the PR controller of the grid current, the steady-state experimental waveforms are shown in Figure 15a, and the results of the FFT analysis are shown in Figure 15b. The CSI maintains the unit power factor operation without steady-state error, and the content of each low-order harmonic is within 0.4%, while the i_dc is capable of accurately tracking the reference.

Next, u_dc is increased to 270 V, and the system operates in the buck mode. $i_{\mathrm{dc}}^{*}$ is set as 11.3 A. The steady-state experimental waveforms are shown in Figure 16a, and the FFT analysis results are shown in Figure 16b, the excellent steady-state performance and power output quality can be obtained, which shows that the DC-side inductor current control and modulation scheme proposed for the five switches single-phase CSI is correct and feasible, while solving the inherent defect of traditional CSI that cannot operate in buck mode.

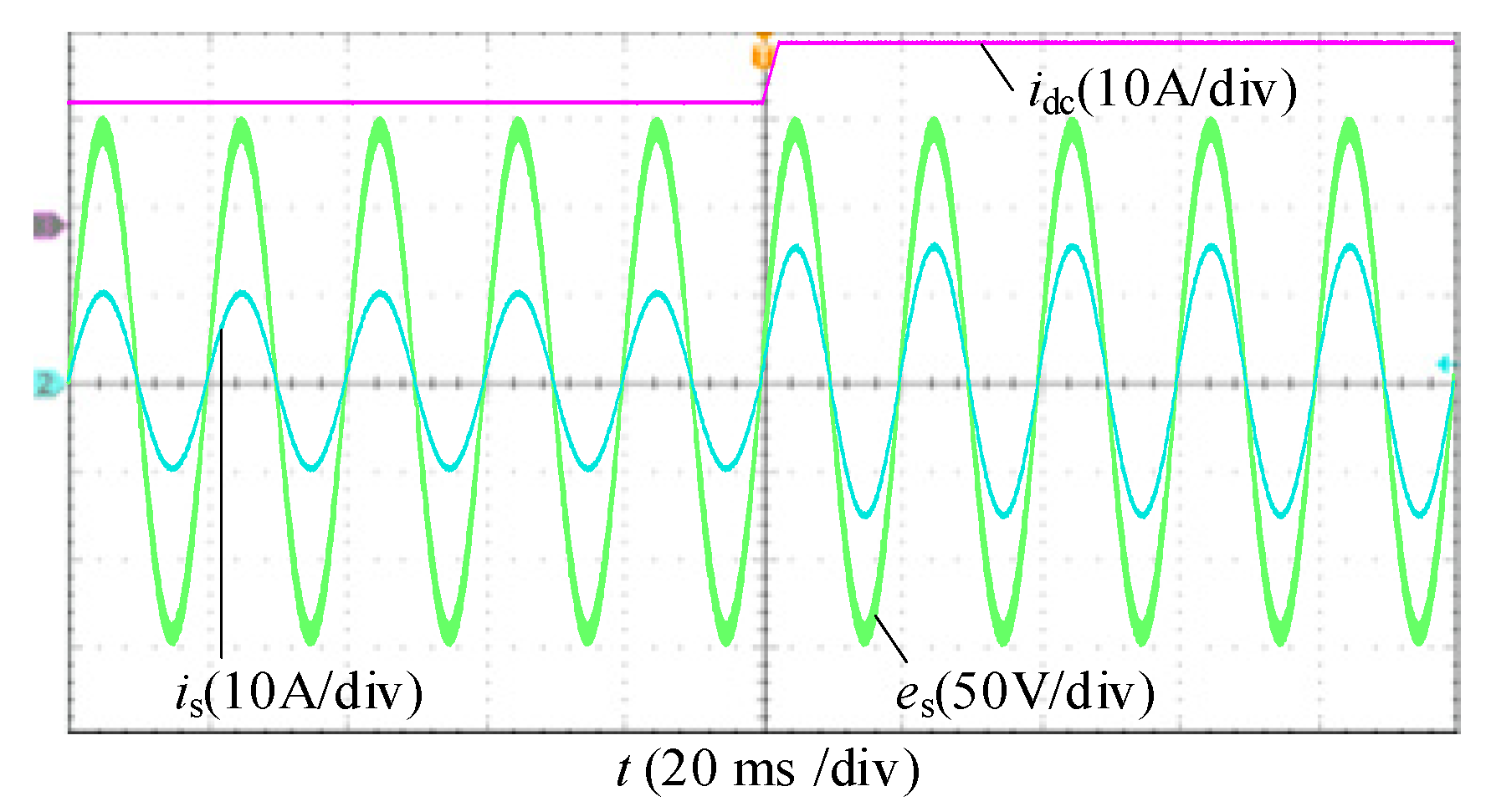
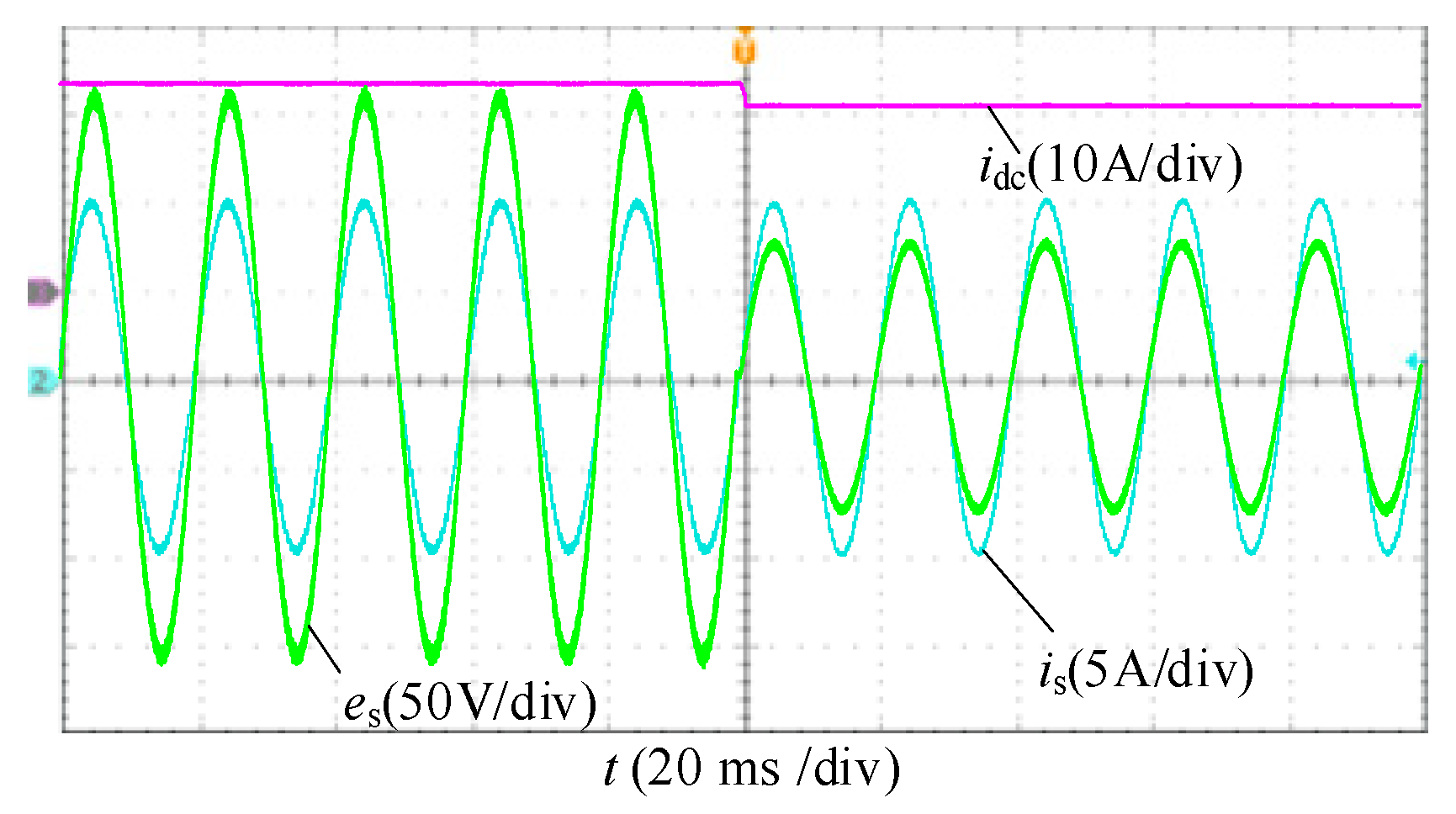
7.2. Dynamic Verification

The CSI operates in boost operation, and the reference amplitude of i_s is adjusted from 10 A to 15 A, and $i_{\mathrm{dc}}^{*}$ is set from 14 A to 20.8 A according to Equation (11). The dynamic experimental waveforms of this process are shown in Figure 17. i_dc restores to the steady state after 3 ms, and there is no steady-state error and overshoot. Due to the short dynamic adjustment process of i_dc, it can provide sufficient current output for the grid side. Under the adjustment of the designed PR controller, i_s can track the reference within half a cycle and remain in the same phase with e_s.

The amplitude of the grid voltage decreases from 160 V to 80 V, the CSI operates from boost mode to buck mode, and the reference amplitude of the grid current is still 10 A. According to the calculation method for the DC-side inductor current under different operation modes in Section 3.1, $i_{\mathrm{dc}}^{*}$ should be reduced from 13.6 A to 10.6 A. The experimental waveforms are shown in Figure 18. i_dc quickly drops to the reference, and under the effect of the PR controller, the amplitude of i_s is restored to 10 A immediately. The experimental results show that a good dynamic performance can be obtained by the DC-side inductor current hysteresis loop controller and the grid current PR controller designed in this paper.

8. Conclusions

To solve the problem that the DC-side inductor current is not stable and controlled in the traditional topology of a CSI, a novel single-phase CSI topology with five switching tubes was taken as the research object. The calculation for the reference of the DC-side inductor current, the modulation scheme for the single-phase CSI, and the optimal parameters design method of the proportional-resonance controller based on the feedback capacitor voltage were proposed in this paper. Finally, the simulation and experimental results were tested for the proposed CSI topology to validate the effectiveness of the proposed control and modulation scheme. The main conclusions of this paper are included below:

(1)

The control method of the DC-side inductor current is proposed in this paper, which can give the DC side the characteristics of the controlled current source. Hence, it can realize the independent control of the DC side and the AC grid side, improving the reliability and practicality of the CSI.

(2)

Based on output current polarity, the proposed logic conversion method can convert the PWM signals into switching signals of the single-phase CSI; there is no need to add hardware logic circuits.

(3)

The proposed active damping method based on the feedback capacitor voltage can effectively suppress the resonance peak caused by the LC filter on the grid side.

(4)

The optimization design of the PR controller is analyzed in this paper. The results show that increasing the resonance coefficient can eliminate the steady-state error, and the suppression ability of the harmonic components can be improved by increasing the proportional coefficient.