Numerical Simulation Method of Hydraulic Power Take-Off of Point-Absorbing Wave Energy Device Based on Simulink

Abstract

Wave energy has a high energy density and strong predictability, presenting encouraging prospects for development. So far, there are dozens of different wave energy devices (WECs), but the mechanism that ultimately converts wave energy into electrical energy in these devices has always been the focus of research by scholars from various countries. The energy conversion mechanism in wave energy devices is called PTO (power take-off). According to different working principles, PTOs can be classified into the linear motor type, hydraulic type, and mechanical type. Hydraulic PTOs are characterized by their high efficiency, low cost, and simple installation. They are widely used in the energy conversion links of various wave energy devices. However, apart from experimental methods, there is currently almost no concise numerical method to predict and evaluate the power generation performance of hydraulic PTO. Therefore, based on the working principle of hydraulic PTO, this paper proposes a numerical method to simulate the performance of a hydraulic PTO using MATLAB(2018b) Simulink^®. Using a point-absorption wave energy device as a carrier, a float hydraulic system power-generation numerical model is built. The method is validated by comparison with previous experimental results. The predicted power generation and conversion efficiency of the point-absorption wave energy device under different regular and irregular wave conditions are compared. Key factors affecting the power generation performance of the device were investigated, providing insight for the subsequent optimal design of the device, which is of great significance to the development and utilization of wave energy resources.

1. Introduction

Wave energy is an important form of marine renewable energy, which has numerous advantages including safety, cleanliness, high energy density, and accessibility [1]. According to statistics, the current economic value of global wave energy utilization is between 100 million and 1 billion watts, while China’s theoretical reserves of wave energy are about 70 million kilowatts, which has great commercial prospects and strategic value [2].

As shown in Figure 1, wave energy convertors (WECs) can be classified into oscillating water column type, wave crossing type, and oscillation type according to the different forms of wave energy [2]. Among them exist the most common types of oscillating wave energy devices [3], such as point-absorption type (also known as oscillating float type), pendulum type, raft type, nodding duck type, etc. [4]. The point-absorption type has been widely used due to its early development and mature technology [5].

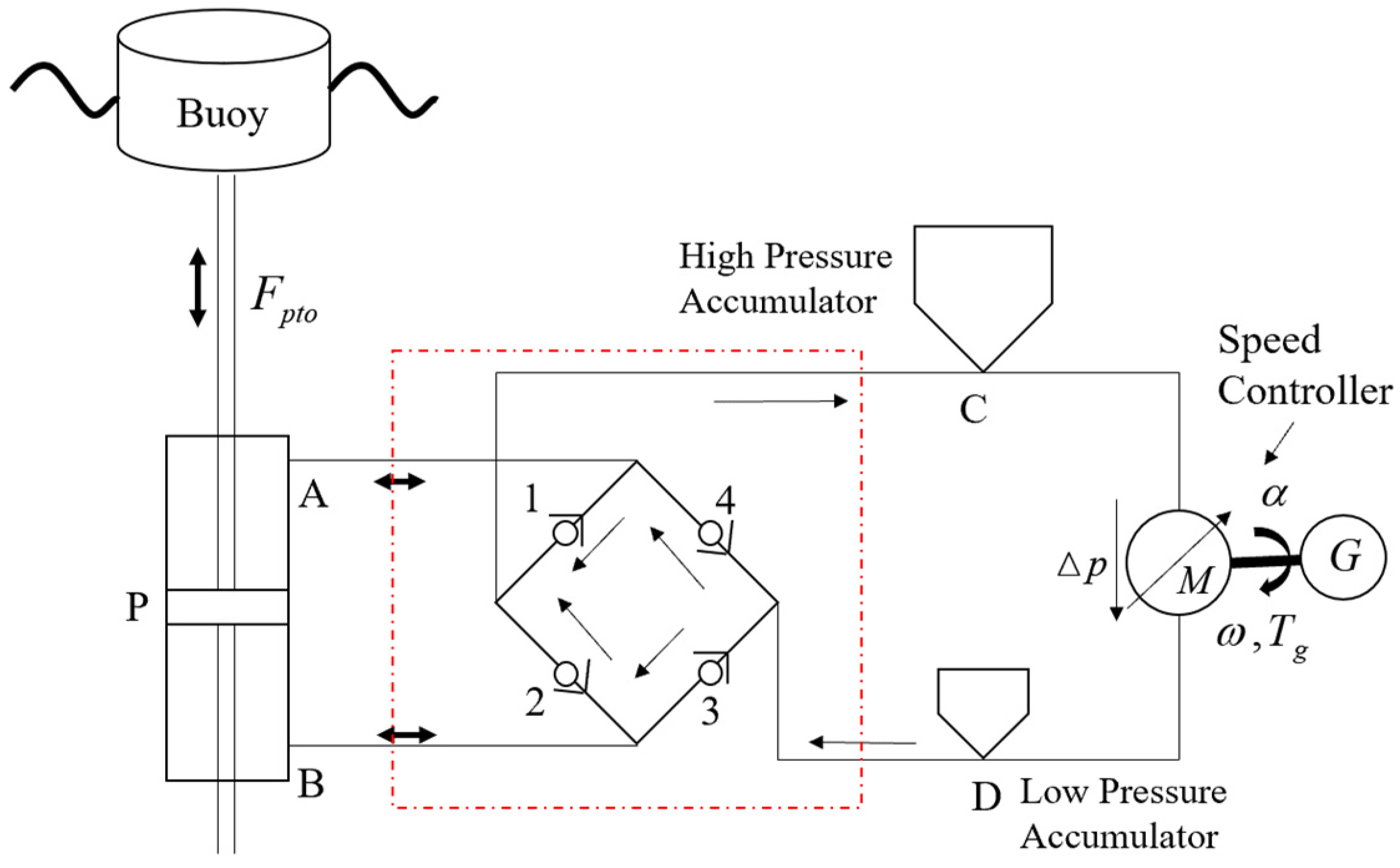
The power take-off system (PTO), shown in the yellow dotted box in Figure 1, is the key component that determines the performance level of the wave energy device [6], which can usually be divided into mechanical, hydraulic, magnetic, etc. [7], including air turbines, hydraulic turbines, hydraulic systems, mechanical transmission systems, etc. These systems efficiently harness aerodynamic energy, hydrokinetic energy, hydraulic energy, mechanical energy, etc., and transform them into energy forms compatible with power-generation systems. Ultimately, mechanical energy is converted into electrical energy through linear motors, magnetic fluid motors, and similar mechanisms [8]. Among the above three forms of PTO, hydraulic PTO has the characteristics of stable transmission, convenient and reliable speed adjustment, and relatively large power density, so it is widely used in wave energy power generation devices.

In the actual operation process of the wave energy conversion device, the influence of unstable sea conditions, bad weather, and other factors often extends the rated cycle of the hydraulic cylinder. The rated speed of the generator or the rated torque of the output shaft decreases, so that the final conversion efficiency of the device decreases. Consequently, the hydraulic PTO has to be actively controlled to offset the negative impact of the environment on the device and ensure that the device can operate efficiently and in a stable manner under different wave conditions [9]. The most commonly used control method is PID control, that is, through the combination of three basic control functions, proportional, integral, and derivative, to achieve accurate control of each part of the hydraulic PTO [10]. Umesh A. Koredel et al. completed the speed control of hydraulic PTO of the linear generator by PID control [11]; Marian P. Kazmierkowski et al. performed PID control for voltage at the load side and achieved good results [12].

Additionally, the PID control method can also predict the movement law of the wave energy device with the wave according to the information collected by the system. This approach enhances both the generated power and efficiency of the system. Daniele Cavaglieri developed the Kalman prediction algorithm based on the PID control method, which used Doppler radar to collect and predict wave data in the nearby sea area, and adjusted the parameters of the hydraulic PTO based on this to ensure that the power generation efficiency of the device was maintained at about 21.75% [13]. Rajapakse, G [14] carried out a model predictive control study on the PTO of an oscillating water column gas turbine, where the generator speed was controlled by optimizing the permanent magnet synchronous generator and the IGBT rectifier module, which effectively improved the system power. Falco [15] controlled the frequency response of the point-absorbing wave energy conversion device based on PID feedback control, which captured the resonance of the system and further improved the power generation. In addition, Amon [16] established an MPPT control algorithm for linear generators based on the PID control theory and completed the experimental test. Based on the developed MPPT method, Boyin [17] simulated the generator damping using the fixed-step climbing method, which provided further theoretical support for the performance optimization of the hydraulic PTO.

In summary, optimization of the system performance of the WEC mainly depends on the control of its hydraulic PTO. PID control has been widely used in the industrial field because of its adaptability, robustness and scalability. It has become the preferred control method of the mainstream wave energy conversion device, offering significant benefits in enhancing the energy conversion efficiency of the device. However, at present, the research on the effect of the PID control method on the control of hydraulic PTO performance is still limited to the experimental stage, and there is not an accurate and concise numerical model to simulate the operation of the system under this control method.

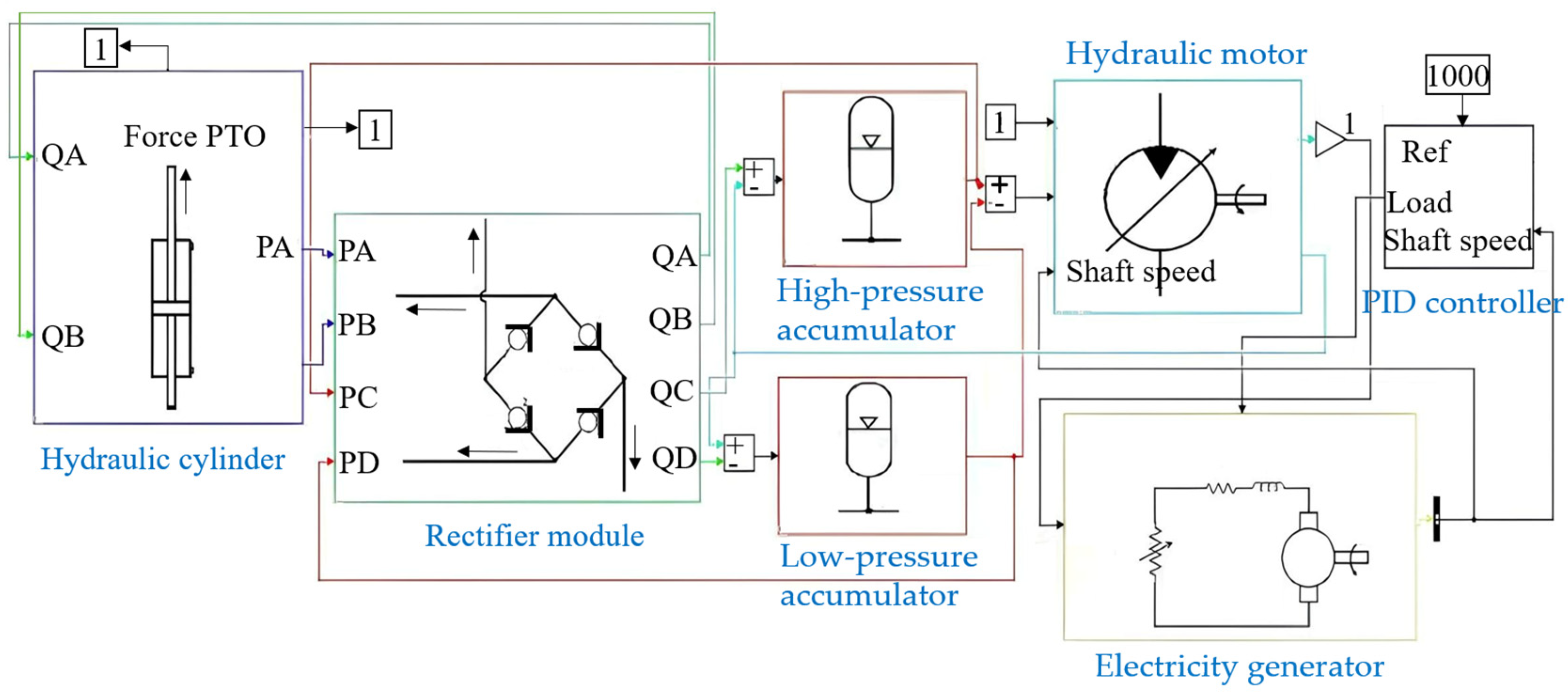
Based on the background of this problem, this paper takes the point-absorbing wave energy conversion device as the research object and proposes a new feasible numerical evaluation method. By innovatively using the MATLAB Simulink^® wave energy conversion device open-source program WEC-Sim, developed by the U.S. Renewable Energy Laboratory (NREL), the numerical simulation model of the starting point-absorbing wave energy device is constructed in the way of secondary development, and the correctness and credibility of the model are verified. The key parameters of the hydraulic PTO are controlled by using the PID control module, and output results of this type of device are obtained at different conditions. The PID control module is then used to control the key parameters of the hydraulic PTO, and the output results, such as the power conversion efficiency, of this kind of device under different working conditions and design parameters are obtained. This provides data support for the improvement of the subsequent device design, thus filling the technological gaps in the related fields.

2. Physical Model and Motion Equations

The point-absorption wave energy power generation device is composed of a float, connecting mechanism, support column, hydraulic PTO, and other parts. The float is the main energy-gaining part of the device. Through its vertical motion, it can convert the wave energy to mechanical energy, and finally convert it into electrical energy through the subsequent hydraulic PTO action. In addition, the hydraulic PTO is the core part of the whole set of equipment that realizes the conversion of mechanical energy to electric energy, which is composed of a hydraulic cylinder, rectifier circuit, pressurization device, speed control module, alternator, and other parts. The precursor mainly uses hydraulic energy to achieve energy transfer, and finally uses the alternator to realize the conversion of mechanical energy into electrical energy. The float motion of the buoyancy absorbs the energy in the wave through a heave motion which can be expressed by the following equation:

$$(m+M)\ddot{x}+(C+C_{PTO})\dot{x}+Kx=F_{F-K}$$

(1)

$(m+M)$ represents the sum of the mass of the float during motion and the additional mass of the heave, $(C+C_{PTO})$ is the additional damping of the heave and the damping of the heaving direction of the PTO system, $K$ is the recovery stiffness coefficient of the heave direction resulting from buoyancy, and $F_{F-X}$ is the first-order excitation wave force in heave.

To facilitate the analysis, the displacement $x$ is transformed in the complex frequency domain $x=\mathrm{Re}(\overline{X}{e}^{-\mathrm{i}\omega t})$, and the expression in the complex frequency domain is further derived

$$-{\omega }^2(m+M)\overline{X}-i\omega (C+C_{PTO})\overline{X}+K\overline{X}=\overline{F}$$

(2)

When the incident wave is a unit amplitude, the amplitude of the displacement $|\overline{X}|$ is called the amplitude response operator, which can be written as

$$|\overline{X}|=|{\displaystyle \frac{\overline{F}}{-{\omega }^2(m+M)-i\omega (C+C_{PTO})+K}}|$$

(3)

Then, the general frequency domain governing equation of the hydraulic PTO connected to the float is as follows:

$$F_e(\omega )=i\omega \left[m+M(\omega )\right]U(\omega )+B(\omega )U(\omega )+{\displaystyle \frac{c}{i\omega }}U(\omega )+F_{pto}(\omega )$$

(4)

Among them, $F_e(\omega )$ is the wave excitation force after the Fourier transform, $\mathrm{i}=\sqrt{-1}$, $U(\omega )$ is the velocity after the Fourier transform, $m$ is the dry weight of the wave energy device, $M(\omega )$ is the additional mass of the device, $c$ is the linearized elastic force coefficient, and $F_{pto}(\omega )$ is the PTO damping force of the device.

The excitation force $F_e(\omega )$ and the PTO force $F_{pto}(\omega )$ can be regarded as external forces, while other forces can be regarded as internal forces. The internal forces can be expressed by the intrinsic impedance and velocity of the wave energy device. Thus, the above equation can be simplified as follows:

$$F_e(\omega )=Z(\omega )U(\omega )+F_{pto}(\omega )$$

(5)

$Z(\omega )$ is the intrinsic impedance of the wave energy device, i.e.,

$$Z(\omega )=B(\omega )+\mathrm{i}(\omega \left[m+M(\omega )\right]-{\displaystyle \frac{c}{\omega }})$$

(6)

$W(\omega )$ is the excitation coefficient. It defines the transfer function between the wave elevation and the excitation force:

$$F_e(\omega )=W(\omega )H(\omega )$$

(7)

$H(\omega )$ is the wave lift function after the Fourier transform $\eta (t)$. Due to the symmetry in the direction of the device of the vertical axis, $W(\omega )$ can be written as:

$$|W(\omega ){|}^2={\displaystyle \frac{4\rho g{c}_g(\omega ,h)}{k(\omega ,h)}}B(\omega )$$

(8)

where $c_g(\omega ,h)$ is the group velocity, $k(\omega ,h)$ which is the number of waves, and $h$w is the depth of the seawater.

The force on a hydraulic PTO system depends on the load impedance and the incoming flow velocity:

$$F_{pto}(\omega )=Z_{pto}(\omega )U(\omega )$$

(9)

$Z_{pto}(\omega )$ is the load impedance of the system. The hydraulic PTO impedance, for the system to achieve optimal energy capture at a given wave frequency, is the conjugate complex impedance of the intrinsic impedance at this frequency:

$${\tilde{Z}}_{pto}(\omega )=Z^{\ast }(\omega )$$

(10)

The intrinsic impedance of a PTO system is the internal property of the system itself when the influence of external forces (excitation force and hydraulic force) on the system is not considered, namely:

$${\tilde{Z}}_{pto}(\omega )=-i\omega \left[m+M(\omega )\right]+B(\omega )-{\displaystyle \frac{c}{i\omega }}$$

(11)

Theoretically, PTO damping forces can be abstracted into mass-damping-spring systems with frequency-dependent PTO coefficients:

$${\tilde{F}}_{pto}(\omega )=\left[i\omega {\overline{M}}_{pto}(\omega )+{\tilde{B}}_{pto}(\omega )+{\displaystyle \frac{{\tilde{C}}_{pto}(\omega )}{i\omega }}\right]U(\omega )$$

(12)

3. Parameters of PTO Systems

The hydraulic PTO system’s average absorbed power serves as a key metric for the system performance. In practice, the discrete Fourier transform (DFT) of velocity data is employed to ascertain this average output power. Plancherel theorem [18,19], which is derived from the DFT, facilitates the representation of power absorbed by the linear hydraulic PTO system. This is particularly pertinent when the wave energy transfer is formulated as a function of wave characteristics. By leveraging these analytical tools, a precise evaluation of the system’s energy conversion efficiency can be achieved, providing a robust framework for performance analysis in the context of wave energy utilization. The energy calculation formula for hydraulic PTO systems can be simplified. The average power input from outside to the hydraulic PTO over a time interval containing N samples is the average of the instantaneous power of each sample:

$$P_A={\displaystyle \frac{1}{N}}{\displaystyle \sum _{n=0}^{N-1}{f}_{pto}}(t_n)u(t_n)$$

(13)

The hydraulic circuit causes the damping force and velocity to change periodically, and the power absorbed by the WEC can be expressed as follows:

$$P_A={\displaystyle \sum _{j=0}^{N/2-1}{P}_A}({\omega }_j)={\displaystyle \frac{2}{N^2}}{\displaystyle \sum _{j=0}^{N/2-1}\mathfrak{R}}\left\{F_{pto}({\omega }_j)U^{\ast }({\omega }_j)\right\}$$

(14)

When the PTO force is a linear function of velocity in (9), the above equation can be simplified as follows:

$$P_A={\displaystyle \frac{2}{N^2}}{\displaystyle \sum _{j=0}^{N/2-1}{B}_{pto}}({\omega }_j)|U({\omega }_j){|}^2$$

(15)

Combining (4) and (7), the velocity $U({\omega }_j)$ can be defined as follows:

$$U({\omega }_j)=Z_{net}^{-1}({\omega }_j)W({\omega }_j)H({\omega }_j)$$

(16)

$Z_{net}^{-1}({\omega }_j)$ represents the inverse matrix of the scalar quantity sought. The average absorbed power of the generalized wave energy utilization device is obtained:

$$P_A={\displaystyle \frac{2}{N^2}}{\displaystyle \sum _{j=0}^{N/2-1}{B}_{pto}}({\omega }_j)|Z_{net}^{-1}({\omega }_j){|}^2|W({\omega }_j){|}^2|H({\omega }_j){|}^2$$

(17)

For point-absorbing wave energy devices, the main one is the heave motion, and the diffraction behavior is not considered. Substituting (17) in (8), the average absorbed power can be written as:

$$P_A={\displaystyle \frac{8\rho g}{N^2}}{\displaystyle \sum _{j=0}^{N/2-1}\frac{B_{pto}({\omega }_j)c_g({\omega }_j,h)B({\omega }_j)|H({\omega }_j){|}^2}{k({\omega }_j,h)|Z_{net}({\omega }_j){|}^2}}$$

(18)

The unit wavefront power of a wave with a frequency of ${\omega }_s$ is defined as follows:

$$P_{IW}({\omega }_s)={\displaystyle \frac{\rho g}{2}}{c}_g({\omega }_s,h)|H({\omega }_s){|}^2$$

(19)

where $H({\omega }_s)$ is the wave height, and the wave group velocity $c_g(\omega ,h)$ can be defined as follows:

$$c_g({\omega }_s,h)={\displaystyle \frac{g}{2{\omega }_s}}D({\omega }_s,h)$$

(20)

$D({\omega }_s,h)$ is a function of wave frequency and water depth:

$$D({\omega }_s,h)=\tan h(k({\omega }_s,h)h)\left[1+{\displaystyle \frac{2k({\omega }_s,h)h}{\sin h(2k({\omega }_s,h)h)}}\right]$$

(21)

In deep-water conditions ($kh\gg 1$), $D({\omega }_s,h)$ tends to be fixed, and the group velocity $c_g(\omega ,h)$ is independent of depth:

$$c_g({\omega }_s)\approx {\displaystyle \frac{g}{2{\omega }_s}}$$

(22)

In summary, the unit wavefront power at the small amplitude scale is as follows:

$$P_{IW}={\displaystyle \sum _{j=0}^{N/2-1}{P}_{IW}}({\omega }_j)={\displaystyle \frac{2\rho g}{N^2}}{\displaystyle \sum _{j=0}^{N/2-1}{c}_g}({\omega }_j,h)|H({\omega }_j){|}^2$$

(23)

The capture width is a measure of the performance of a wave energy generator and is defined as the ratio of the wave energy captured by the float to the energy transmitted by the wave:

$$C_W={\displaystyle \frac{P_A}{P_{IW}}}$$

(24)

For short-period waves, the wave energy transmission is linear with the wave spectrum, assuming that the float heave velocity is linear and periodic relative to the wave height, the capture width can be written as follows:

$$C_W={\displaystyle \frac{{\displaystyle \sum _{j=0}^{N/2-1}{B}_{pto}}({\omega }_j)|Z_{net}^{-1}{|}^2|W({\omega }_j){|}^2|H({\omega }_j){|}^2}{{\displaystyle \sum _{i=0}^{N/2-1}\rho g{c}_g({\omega }_I,h)|H({\omega }_I){|}^2}}}$$

(25)

There is a special case, under deep-water conditions, where the WEC geometrically moves symmetrically and in the direction of only one degree of freedom of draping, in which case the wave capture width becomes the following:

$$C_W^s({\omega }_s)={\displaystyle \frac{4g{B}_{pto}({\omega }_s)B({\omega }_s)}{{\omega }_s^2|Z_{net}({\omega }_s){|}^2}}$$

(26)

Let the final output electrical power be and $P_{output}$ the diameter of the wave energy float is $D$; then, the energy conversion rate of the device is as follows:

$$\eta ={\displaystyle \frac{P_{output}}{C_W·D}}$$

(27)

4. Numerical Calculation Based on Simulink

4.1. Numerical Model Construction

A typical hydraulic PTO consists mainly of a hydraulic cylinder, a rectifier device, a high (low)-pressure accumulator, a hydraulic motor, a generator, and other parts. Its physical model is shown in Figure 2. Through the action of the hydraulic PTO, the heave motion of the float can eventually be converted into mechanical energy for the generator. The float, in the role of the wave oscillation movement, reciprocates the wave force into the hydraulic piston up and down movement of mechanical energy, and causes the hydraulic cylinder in the two oil outlets of the oil pressure to produce cyclical changes in the rectifier loop composed of four spherical valves, which can be adjusted according to the changes in the oil pressure in a timely manner to ensure the subsequent one-way stability of the work of the hydraulic motor. Immediately after that, by adjusting the volume of the oil bladder of the high (low)-pressure accumulator in the circuit, the pressure difference between the two sides of the hydraulic motor can be increased and stabilized, thus driving the hydraulic motor to run smoothly at high speed. The generator is connected to the hydraulic motor through a coupling, on which a speed control module is installed, so that the speed of the generator can be adjusted according to the needs, and finally the wave energy can be converted into a stable output of electric energy.

In this paper, the MATLAB^®(2018b) open-source software WEC-Sim is used to simulate the working process of the point-absorbing wave energy power generation device and its hydraulic PTO. The definition of the internal hydraulic piston, rectifier valve, and accumulators are completed through programming. A numerical model of the energy conversion of the hydraulic PTO was built in Simulink, as shown in Figure 3. This includes a hydraulic cylinder, a rectifier module, a high-pressure accumulator module, a low-pressure accumulator module, a hydraulic motor module, an electricity generator module, and other components. The speed of the motor is adjusted through the PID speed control module, as shown in Figure 4. The principle is to compare the difference between the actual speed and the expected speed; the combination of $K_p$ proportional, $K_d$ differential, and $K_i$ integral gain regulates the rotational speed to a stable value.

The parameters of each component and their corresponding environmental parameters are defined through the pre-processing file. This includes the wave period of the regular wave, the irregular spectrum, the piston stroke of the hydraulic cylinder, the opening of the rectifier valve, and the initial energy storage values of the high- and low-pressure accumulators. These definitions enable the power generation performance of the wave energy device under different working conditions. Additionally, it is convenient to evaluate the influence of different PTO parameters on the power generation efficiency of the wave energy device.

4.2. Validation of the Numerical Model

The wave energy capture width, influenced by geometry and PTO selection, is an important parameter to characterize the performance of the wave energy conversion device (WEC). It is used to describe the performance of the linearized WEC under monochromatic waves and multi-frequency waves. It is greatly affected by PTO damping, so it is necessary to select specific PTO damping in the design to ensure the reliability of the results. The same parameters used by A. A. E. Price [20] were used for the point-absorbing WEC shown in

Table 1. Physical parameters of the example float.

Physical Parameter	Symbol	Value
Radius	$r$	2.5 m
Density	$\rho$	1000 kg/m3
Mass	$m=2\pi r^3\rho /3$	32,725 kg
Spring	$c=\pi r^2\rho g$	192,423 N/m

. The PTO damping and other related coefficients were calculated using the MATLAB preprocessing file, so as to obtain the wave energy capture width of the device at a specific wave frequency. The numerical simulation model of the device is shown in Figure 5, modeling in WEC-Sim.

The capture width of the point-absorbing wave energy device is closely related to the damping of the PTO system. Based on the mass-spring-damping control method, Price calculates the wave capture width in monochromatic waves under different wave frequencies of the hydraulic PTO. Figure 6 shows the wave energy capture width of the spherical float at different oscillation frequencies in the monochromatic wave when the optimal control mode ($\omega =0.5\mathrm{rad}/\mathrm{s}$) is selected.

When using the simulation model, the normalized energy capture width is compared to the ideal calculation provided by Price’s work [20], using the monochromatic wave capture width multiplied by the wavenumber k.

As can be seen from the data in Figure 6, the calculated data curve has the same trend as the ideal value, and the maximum error is not more than 20.17%. Additionally, the energy capture width of the device is the same when both reach the natural frequency.

In addition to Price’s mass-spring-damper controlled wave energy device scheme, Zanuttig [21] carried out an experiment of a wave energy generator model DEXA 302 at Aalborg University in Denmark. This device can also be represented as a variant of the point-absorbing wave energy generator device. He used a 1/30 scale model in his experiments with a length of 2.1 m, width of 0.81 m, and a total weight of 33 kg. The system was equipped with a hydraulic PTO system weighing about 10 kg, and he eventually gave the output power of the hydraulic PTO under different mooring conditions in his experimental results. In this subsection of the validation work, the authors geometrically constructed Zunatting’s experimental model and obtained the output power dimensionless results of the hydraulic PTO under the same working condition settings by the evaluation method proposed in this paper, and the comparison between the two is shown in Figure 7.

It can be seen that the results obtained using the WEC performance evaluation method proposed in this paper have the same trend as the measured data of the DEXA 302 power generator, especially in the wave frequency range of 1.0–2.0 rad/s, which is well fitted with a maximum error of no more than 10.17%. The energy capture peaks of the experimental and simulation results are very close to each other, and all of them appear near the intrinsic frequency, and the above comparison results are within the error tolerance, so it can be considered that this method is suitable for the performance evaluation of WEC with high accuracy.

From the above analysis, it can be concluded that the Simulink-based numerical simulation method of hydraulic PTO of point-absorption wave energy power generation device proposed in this paper can accurately and effectively predict the power output performance of the device with better accuracy than the traditional mass-spring-damper control system description scheme. At the same time, it is conducive to the structural optimization of specific hydraulic PTO systems.

5. Results and Discussion

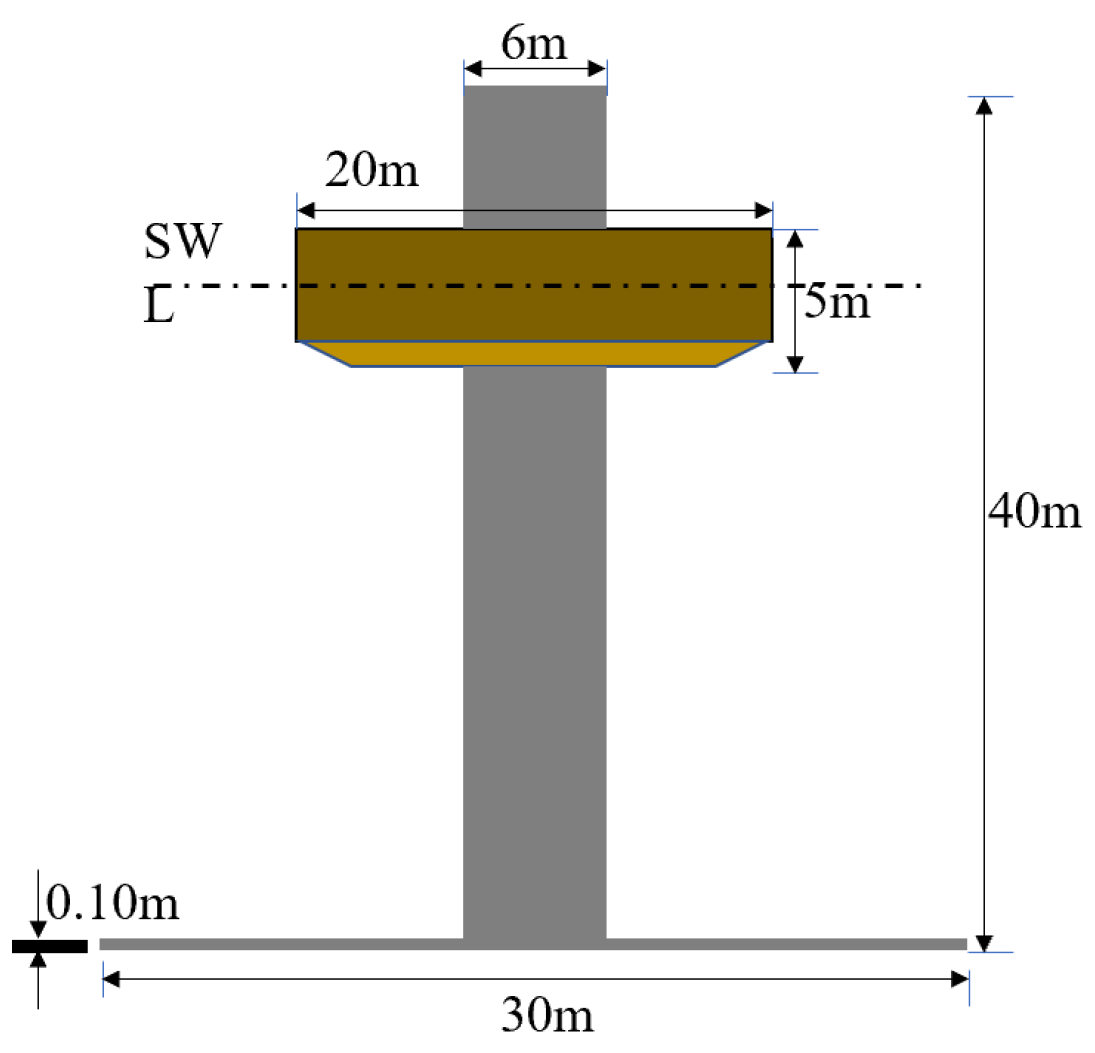
The numerical simulation method proposed in this paper can define the specific parameters affecting the elasticity and damping coefficient of the system through the preprocessing file, which is more accurate than the traditional “one-time definition method” and facilitates the study of specific parameters affecting the performance of hydraulic PTO. Based on this method, the authors studied the output performance of the classical oscillating float-type wave energy device under regular and irregular waves, and the influence of some hydraulic parameters on the system, such as the design dimensions of the device, are given in Figure 8. The corresponding Simulink model is built by imitating Figure 5, and the working conditions such as wave height, period, irregular wave spectrum, and peak period are set in the preprocessing file to initialize the hydraulic PTO parameters.

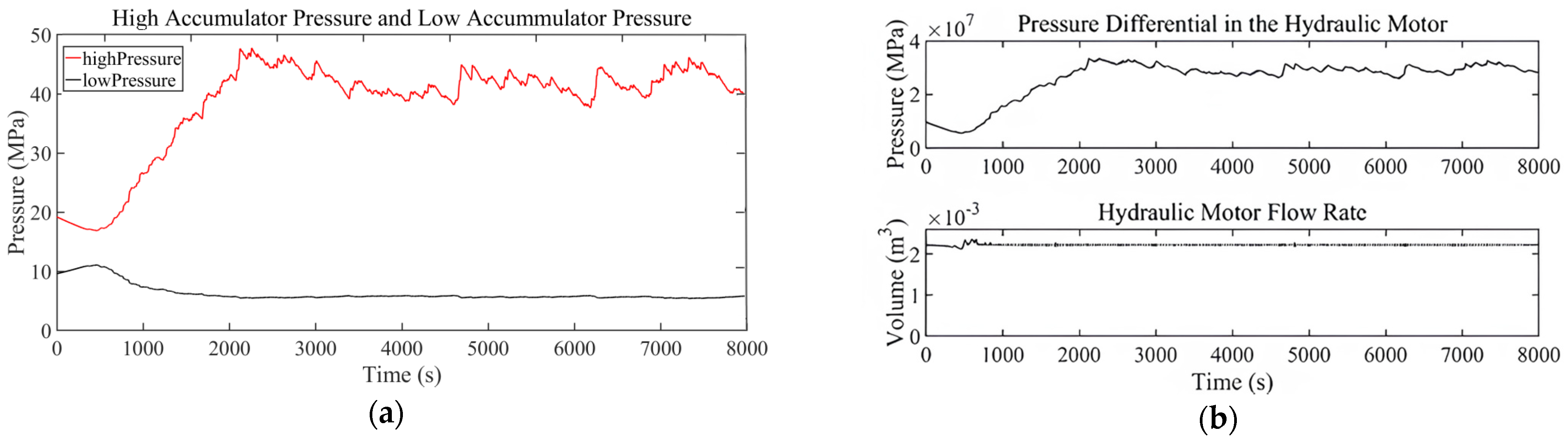
Firstly, the variation in internal parameters during the operation of the hydraulic PTO is considered under a regular wave with a period of $T=8 \mathrm{s}$ and a wave height of $H=3 \mathrm{m}$. Since the variation in the circuit pressure will directly affect the operation of the generator, Figure 9 gives the simulation results of the pressure variation at both ends of the accumulator and hydraulic motor in the hydraulic circuit. In Figure 9, after a short period of time, the pressure difference between the output of the high- and low-pressure accumulators is finally stabilized at about 45 MPa; at the same time, as shown in Figure 9b, the pressure difference at the hydraulic motor starts to rise slowly from the initial stage and can be finally stabilized at 45 MPa, which indicates that the maximum pressure that can be provided by the hydraulic circuit at this time is 45 MPa.

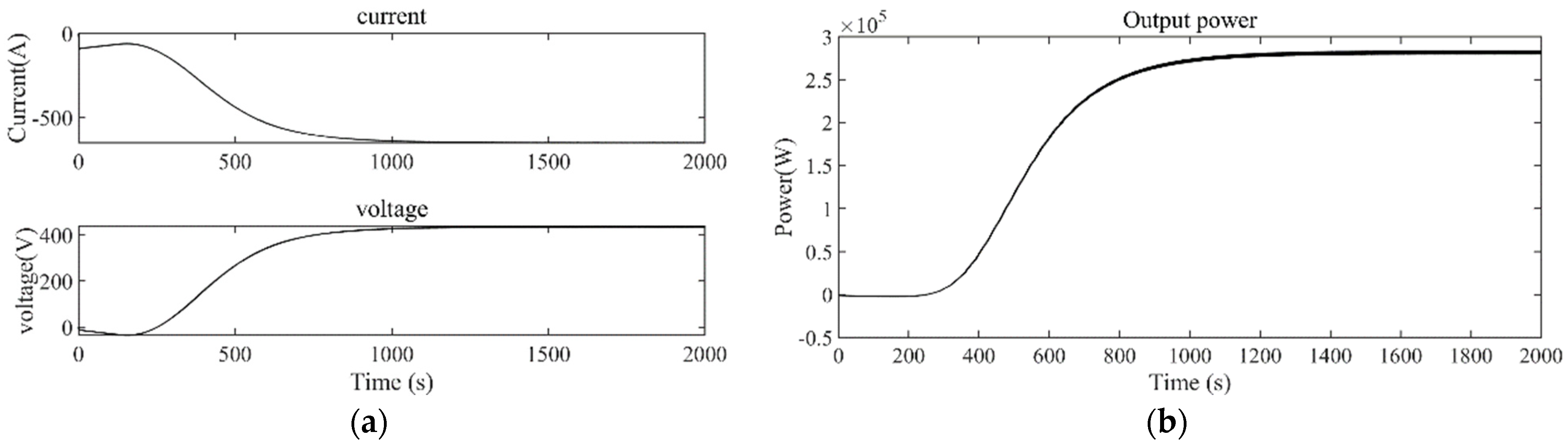
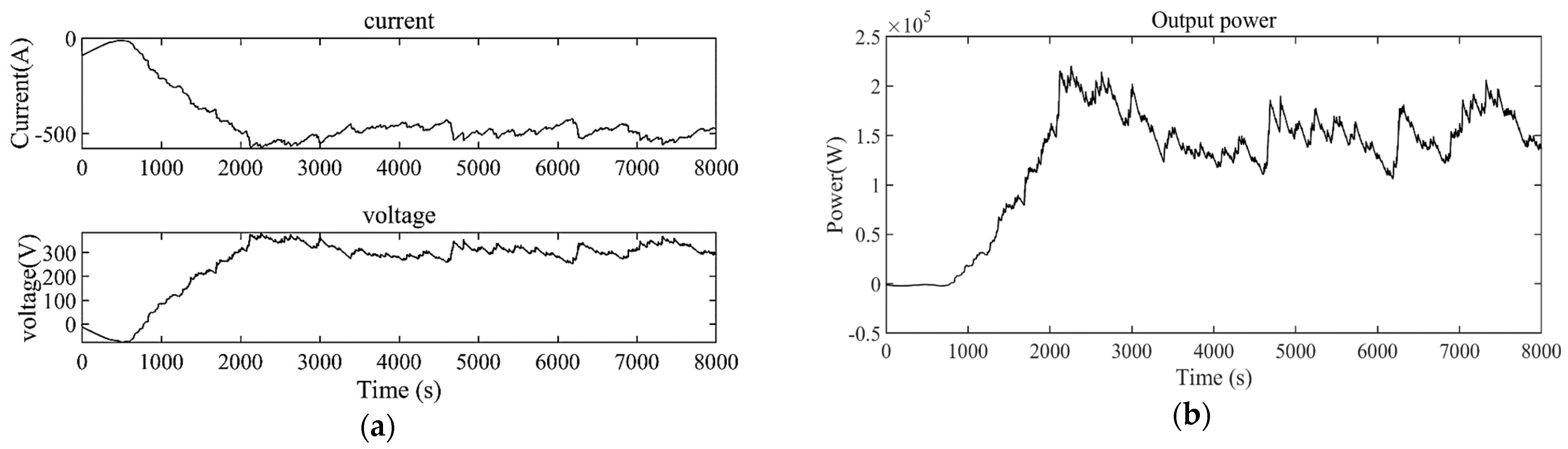
Figure 10 shows the voltage, current, and power generated by the generator circuit. As shown in Figure 10a, after the system is stabilized, the directions of the voltage and current are opposite, the generator is in the power generation stage, and the current generated can reach 700 A when stable at the corresponding voltage of 405 V. In Figure 10b, the generator can output up to 2.75 × 10⁵ W of power during this time.

Furthermore, the wave energy capture width and energy gain efficiency at wave heights of 3 m and 2.5 m were studied. As shown in

Table 2. Energy acquisition efficiency of hydraulic PTO under rule wave.

Wave Height H (m)	Period T (s)	Average Power P (kW)	Capture Width (kW/m)	Power Efficiency
3	8	284.3	68.9	10.32%
2.5	8	141.8	47.9	7.40%

, when the regular wave height is 3 m, the energy gain efficiency is 10.32%, which is close to the current theoretical energy gain efficiency of this type of device; when the wave height drops to 2.5 m, the energy gain efficiency drops to 7.40%.

In addition, this article considers the case of irregular waves. The JONSWAP wave spectrum was selected, taking the spectral peak period $T_P=8 \mathrm{s}$ and the significant wave height $H_s=3 \mathrm{m}$. Simulation calculations are also carried out for the changes in physical quantities of each component of the hydraulic PTO during the operation of the wave energy device to derive the energy output for the corresponding case.

As shown in Figure 11, the liquid pressure at the high-pressure accumulator always fluctuates up and down around a certain value under irregular wave action compared to that under regular wave action, while the liquid pressure at the low-pressure accumulator is more stable. The steady state pressure difference is Δp = 27.98 Mpa, and the hydraulic energy obtained by the hydraulic motor is therefore reduced as a result.

Figure 12 shows the voltage, current, and output power under the corresponding operating conditions. Comparing Figure 11 and Figure 12, it can be seen that under the same working conditions, the output current under irregular waves is I = 500 A, the output voltage is V = 305 V, and the average output power is 1.725 × 10⁵ W.

At the same time, the energy efficiency of PTO under irregular waves was evaluated, and the predictions are shown in

Table 3. Energy acquisition efficiency of hydraulic PTO under irregular waves.

Significant Wave Height HS (s)	Spectral Peak Period TP (s)	Average Power (kW)	Capture Width (kW/m)	Power Efficiency
3	8	273.4	42.8	15.97%
2.5	8	155.3	20.5	18.94%

. When the peak period is fixed, the energy efficiency and sense wave height of the device decrease. Compared with the regular wave, when the device works under irregular wave conditions, the energy efficiency is significantly reduced, down to 15.97% with the wave energy capture width being 42.8 kW/m. Due to the decrease in the wave energy capture width of the float under irregular waves, the mechanical energy conversion ability of the hydraulic PTO decreases, and the energy gain efficiency of the device decreases.

6. Conclusions

In this paper, a hydraulic PTO performance evaluation method based on the open-source code WEC-Sim is proposed, which can more intuitively and accurately simulate the output performance of hydraulic PTOs under various working conditions compared with the traditional numerical methods. The following is a summary of the work undertaken and main conclusions:

1. The working principle of the point-absorption wave energy power generation device is explained, and the kinetic equation and the energy conversion model of the internal hydraulic PTO are presented.

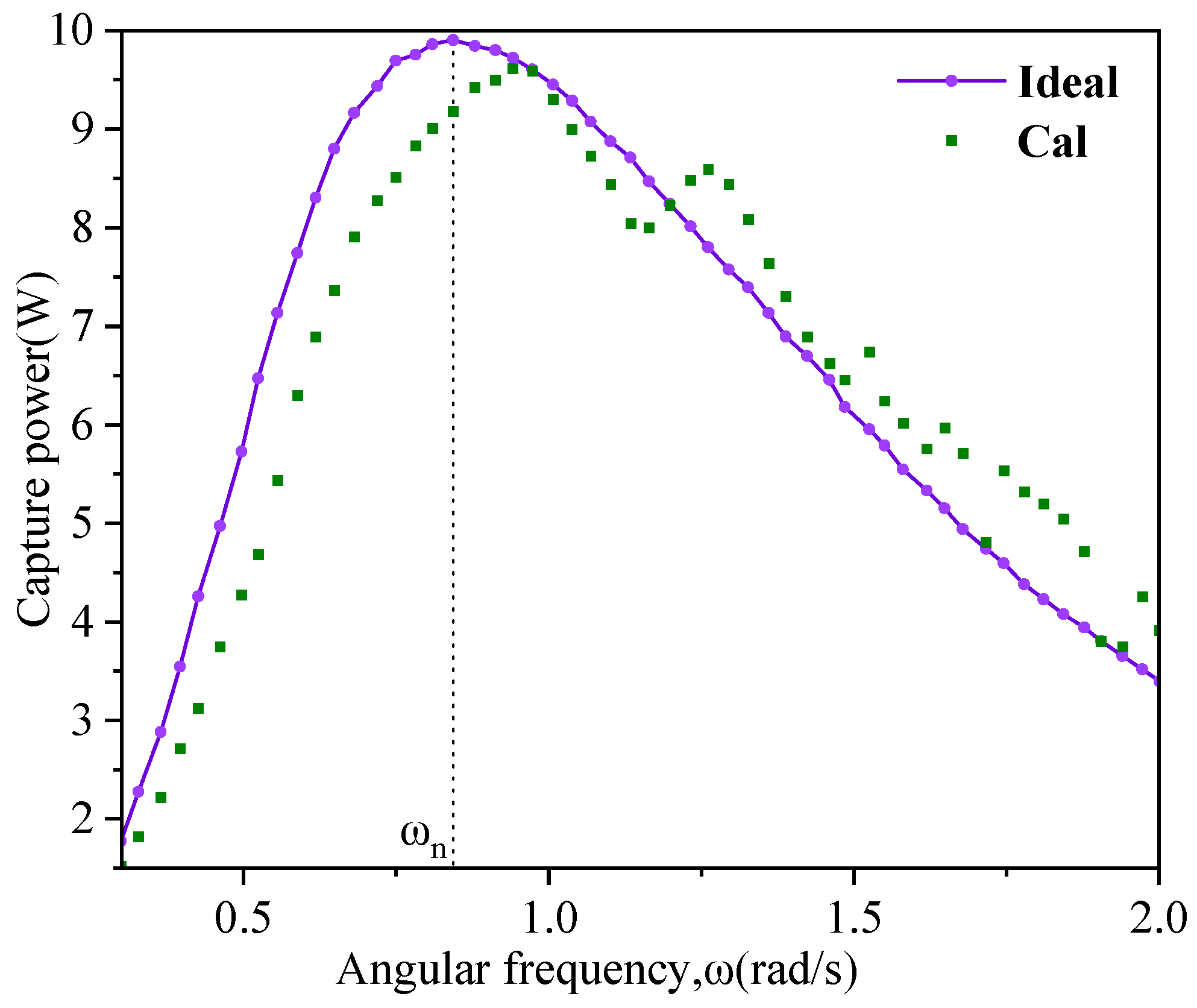
2. The numerical model WEC-Sim simulated the hydraulic performance of the PTO. The reliability of the calculation method was verified by calculating the energy harvesting width of the spherical float under monochromatic wave, and the results were compared with the calculation data of the DEXA 302 device. The power generation efficiency of the device was comprehensively analyzed, and it was found that, compared with the traditional PTO performance evaluation method, the method had the advantages of accuracy, high visualization degree, and simple operation.

3. The proposed numerical method predicts that for a point-absorbing wave energy power generation device that can be integrated into an offshore wind turbine platform, an energy harvesting efficiency of 15.97% can be achieved under regular wave conditions, while this decreases to 10.32% for irregular waves. The simulation data can reliably set the parameters of various parts of the hydraulic PTO, the liquid pressure of the high-pressure (low-pressure) accumulator of the process volume, the hydraulic distribution of the hydraulic motor, and the voltage and current at the generator were also evaluated, which provided data support for the next optimization work.