Advancements and Perspectives in Embedded Discrete Fracture Models (EDFM)

Abstract

The Embedded Discrete Fracture Model (EDFM) has emerged as a prominent piece of technology used for embedding the hydraulic behavior of rock joints in reservoir numerical models. This paper critically reviews its fundamentals, the latest developments, and opportunities for further research. The literature is extensive regarding novel algorithms attempting to reach more accurate and computationally effective estimates. While hydraulic fracture models seem suitable for their purposes, their assumptions might be excessively simplistic and unrealistic when assessing naturally fractured reservoirs. The paper begins by examining fractures as physical characteristics and the key mechanisms to be considered when integrating them into numerical flow simulators. The use of the EDFM technique shows promise for simulating capillary continuity and buoyancy effects in multiphase and multicomponent cases. However, there are significant limitations that hinder its widespread field-scale adoption for reservoir performance evaluation. In this regard, the lack of public-domain realistic benchmarks to validate and compare the potential of each method reinforces the difficulties of performing broader applications of the EDFM techniques in large-scale models.

1. Introduction

The economic development of hydrocarbon resources has become increasingly complex as newer oil discoveries slow down and occur in intricate geological formations. On one hand, in conventional mature fields, conventional carbonate Naturally Fractured Reservoirs (NFRs) hold most of the reserves worldwide [1], and Enhanced Oil Recovery (EOR) techniques demand a thorough understanding of fluid flow and wettability alterations in the presence of injected smart fluids [2,3]. On the other hand, non-conventional new discoveries have pushed technology towards hydraulic fractured setups. The fluid flow behavior inside fractures and its interaction in a nano-darcy context thus becomes the key process [4].

The role of emerging computing techniques in their development is evident as a means to increase oil and gas recovery, especially with the fast growth of artificial intelligence in all its flavors. Given the availability of unprecedented computational power, the use of numerical models to characterize, forecast, and support design decisions has become standard practice. Probabilistic models have become daily tools for engineers and geoscientists to test hypotheses and bound expectations, and effectively communicate with stakeholders during the decision-making process [5].

The optimal modeling technique depends on data availability and the physical understanding of the problem under analysis [6]. In terms of fracture characterization, most workflows start distributing discrete fractures in the so-called Design Fracture Network (DFN) of the reservoir. Each fracture or each set of fractures in the DFN is then upscaled into numerical counterparts optimizing accuracy and computational cost as needed [6].

The first classification of fractures regards their genesis, specifically whether they are originally present in the field as Natural Fractures (NFs) or as artificially man-made features such as Hydraulic Fractures (HFs). While NFs are sparsely distributed across the reservoir domain, HFs are stimulation techniques used to enhance the well–reservoir coupling. The literature is comprehensive in both cases. It is important to consider HFs and NFs in distinct ways because of their unique spatial position and geometry for the gradient distribution of field pressure.

There is reasonable information on fracture attributes for HF modeling: their geometries are anticipated as a design parameter, and their permeabilities are a consequence of the proppant or can be estimated from the residual aperture. While dealing with NFs, however, the fracture network geometry and hydraulic conductivity are highly uncertain, being fundamentally based on geoscience conceptualization and analogs. Unlike intact rock, it is impractical to sample fractures or retain their in situ conditions and behavior on the way to the laboratory. Hence, numerical calibration eventually relies on production data that cannot characterize individual joints, but rather the overall behavior of the network as an equivalent continuum. The lack of physical meaning of the parameters may lead to history matching into unpredictable results [7].

Intuitively, one cannot expect a single model to fit all possible NF scenarios. A thorough geologic understanding of the genesis of the fractures is the definite starting point. A multidisciplinary team must investigate and promote sensible data acquisition from production instruments, logs, laboratory, and well-testing. Data interpretation and statistical analysis must be used sensibly together, as concluding deterministic or long single runs is misleading since they offer little or no predictability [8]. Hence, probabilistic models, sensitivity analyses, and history matching are preferred and demand fast optimization loops.

The challenge is, therefore, to navigate existing technologies to enable physically consistent fracture-aware workflows, providing fast assessment cycles while coping with high uncertainties. While each technology has its particular application niche, this paper focuses on recent progress in developing EDFM. EDFM has received significant attention in the past decade, with significant advancements reported. The idea of embedding fractures as nonconforming entities into existing models has been proven to accurately solve field-scale models with notable performance [9].

This paper assesses the current state of the art in discrete fracture modeling from an engineering perspective, providing context, pros, and cons related to recent technology. Although detailed geological, geophysical, and data acquisition workflows and techniques are fundamental for a complete understanding of the topic, they are outside the scope of this manuscript.

The text is organized into brief sections, each discussing one essential aspect of fracture modeling. The next section begins with the physical conceptualization of fractures and rock joints, along with the relevant phenomena to model in their numerical counterparts. Then, the history and state-of-the-art fracture models and EDFM are presented, acknowledging recent progress and areas of research interest. Finally, the Conclusion summarizes current technology and open issues requiring future work.

2. Fractures as Physical Features

Fractures are defined as breaks or mechanical discontinuities in rock that consist of two rough surfaces in partial contact, are complex in shape, and are often filled with mineral precipitates or transport materials [10]. Their occurrence is linked to deformation after mechanical stress or to physical diagenesis [8]. If connected void spaces are present along the fracture, they may comprise low-porosity fluid conduits, potentially being a primary drainage mechanism of the reservoir. However, when cracks are filled with fine impermeable material, the fluid transmissibility is significantly penalized perpendicularly to its faces.

A Naturally Fractured Reservoir (NFR) is defined as a reservoir in which naturally occurring fractures either have or are predicted to have a significant effect on reservoir fluid flow [8]. The author classifies NFRs according to the relevance of the fractures to the fluid flow as follows: Type 1—fractures are essential for drainage, providing essential porosity and permeability; Types 2 and 3—fractures offer essential or assistance permeability enhancement (both the fracture network and the matrix continuum contribute to fluid flow); Type 4—fractures negatively impact fluid flow as barriers or as a high-conducting path, incurring in a strong flow anisotropy.

Identifying the NFR type is the first step to optimally translating the fractures into the models. In Type 1, for example, the fracture network controls the overall reservoir drainage, likely with fluid channeling and slow matrix imbibition; in Type 3, on the other limit, fluid flow is likely to occur more homogeneously, as matrix–matrix flow is non-negligible.

Man-made HFs are engineering-designed and positioned across the well to enhance well productivity or injectivity. They are mostly considered tensile in nature and are supported either by added proppant or wall roughness in case of nonuniform acidizing. The uncertainties in HF geometry are bounded by operational parameters, analog wells, well logs, and pressure tests. It is reasonable to assume planar geometry, although some authors show that HFs are rarely planar and are, in fact, complex networks to be calibrated to an effective planar representation [11,12,13,14].

NF studies present distinct challenges. NF genesis is multifactorial, resulting in wide ranges of uncertainties and site-dependent behavior [15,16]. NFs can be cemented or open, span from seismic to millimetric scales, be interconnected or standalone, etc., so that rules of thumb do not apply [17]. Authors have tried for many years to find correlations to understand the hydraulic behavior through estimates of fracture aperture, rugosity, contact area, and geometry, but with limited success [10,18]. Nevertheless, the lubrication theory (also known as the cubic law) is often used to characterize fluid flow inside an NF, even though the complexity of NF networks departs by far from the assumptions behind the equations. Recent work shows that the cubic law estimates result in excessive transmissibility by up to 100-fold and cannot forecast the varied degrees of flow anisotropy seen in a typical fracture network [19,20].

As HFs are designed to be major fluid channels to the well, large pressure gradients are expected from the fracture to the surrounding matrix. In this case, cubic law may be reasonably approximated, and viscous fluid transport is likely to control the fracture–matrix fluid exchange. In NFs, on the other hand, pressure gradients are typically not expected to be significant across matrix blocks due to the small pressure gradient along the surrounding fractures. In these cases, capillary continuity, buoyancy, and multiphase interaction physics become more relevant than Darcy’s straightforward viscous flow. Designers must now consider various mechanisms, like counter- and co-current flows and capillary continuity [21,22,23]. Although intrinsically scale-dependent, building up a solid laboratory test program is the key to understanding the reservoir’s fundamental drainage mechanisms, and results must be used after upscaling considerations [24,25].

3. Fractures as Numerical Entities

Mathematical models of fractured reservoirs date back to the 1960s and have evolved into many different technologies. This section briefly discusses the most popular models, as summarized in Figure 1 and Table 1.

The early models represented fractures as a collection of joints with regular geometry approximated by an effective continuum. Barenblatt [26] understood the need to deal with the fracture collection as a whole, considering it impractical to model each fracture individually. At the time, the models were targeted to transient well test interpretations of naturally fractured conventional reservoirs, and authors could define two numerical parameters to describe the network dynamics as follows: a characteristic time and a characteristic distance. After that, following the evolution and commercial adoption of flow simulators, more interest was seen in numerical models for fractures, using the idealized concepts as a basis for the framework.

Long et al. [27] discussed the scale of the fractures and their interconnectivity in high-permeability large-scale paths. From the author’s perspective, single fractures are only relevant as segments of large features and will not significantly impact global system drainage unless combined into large-scale effective elements. Gilman and Kazemi [28,29] extended the model to multiphase to account for capillary forces, which were not considered so far, and formulated the multiphase mathematical background still used today in modern simulators.

Multiphase physics were further investigated by Hinkley and Davis [30], and more recently by Elputranto et al. [31], who were concerned with capillary end effects in fractured tight rocks. The issue is that the capillary pressure discontinuity, as idealized in early models, may mislead the analysis. As natural fractures are distributed irregularly, much more capillary continuity is expected than in idealized geometries. This means that one can expect a significant contribution from gravity-driven co-current flows and an environment that is more favorable to recovery factors [22,24,32,33].

A Discrete Fracture Network (DFN) is a geometrical description of a set of fractures and their interconnections, both explicitly and individually. While the literature is not uniform in classifying the different numerical approaches to modeling a DFN and its impact on drainage, this work divides fracture models into two major classes: (1) conforming and (2) non-conforming. In conforming fracture models, the features are explicitly represented in the numerical mesh. In contrast, in non-conforming models, they are embedded as an equivalent continuum with no impact in the original mesh.

Conforming meshes algorithms represent the fractures by Local Grid Refinements (LGR) [15,34] or as elements reduced (or mixed) in dimensions—i.e., 2D elements in a 3D environment, or 1D elements in a 2D environment. In LGR, the low porosity and high permeability of the narrow elements representing the fractures have a high computational cost and are impractical for most applications. Improvements and practical aspects in light of simulation time and numerical limitations, such as effective fracture aperture, are discussed in detail by Reiss [35].

Using elements of reduced dimensions benefits from the fact that the fracture aperture is orders of magnitude smaller than its length and height, and that no significant pressure drop or flow is expected inside the fracture along the thin axis. Hence, this dimension may be reduced analytically. Still, this approach is only suitable for small domains due to the high computational when many fractures are to be mapped. Moreover, just like any conforming algorithm, any modification in fracture geometry requires full re-meshing and costly model re-processing, which harms iterative workflows.

Non-conforming approaches are preferred in field-scale models where performance is critical, and fracture geometries carry high uncertainty. In this case, fractures are embedded in the continuum either as an effective medium or by introducing additional Representative Elementary Volumes (REV) for each fracture, such as in classic dual porosity and dual permeability models (DKDP) or embedded models, like EDFM.

DKDP was proposed originally by Barenblatt [26] and applied to well-testing interpretation by Warren and Root [29]. The idea was to include two equivalent media (matrix and fractures) with the same grid block distribution and size. Transfer functions (or shape factors) were originally proposed by Gilman and Kazemi [29,36] to quantify the communication between the two media. Those formulations assume quasi-steady-state flow, which is valid for most cases of interest. The Multiple Interacting Continua (MINC) method offers an alternative whenever long transients are to be investigated. This might be the case for non-isothermal or accurate multiphase flows, in which characteristic times of heat and fluid exchange between the fracture and matrix can be long.

In all cases, upscaling processes must be used to find the effective continuum parameters for the DFN (mainly porosity, permeability, and shape factors), which are later calibrated during data assimilation (interchangeably known as history matching), as by Long [27], Oda [37] and Elfeel [38].

Accurate results have been reported in conforming and non-conforming models for large-scale fractures with known geometries. In the case of diffuse fracture geometries, many features are present, and discrete fracture models may add too many degrees of freedom to the model. As the approach works for small models, field-scale models may become overcomplex and counterproductive, and design teams may lose intellectual control of the model. In this case, embedding fractures in the continua either by classic models or upscaled effective discrete models is generally more sensible.

Table 1. Relevant fracture models published in the literature.

Fracture Geometry	Fracture Models	Reference
Non-conforming	Effective continuum model (1ϕ)	[39]
	Warren and Root (2ϕ2K)	[26,40]
	Multiporosity	[41,42]
	MINC	[43]
	EDFM	[44]
	pEDFM	[45]
	cEDFM	[46]
	XFEM	[47]
Conforming	Lower-dimensional elements	[37,48]
	Local Grid Refinement (LGR)	[15,34]

Table 1. Relevant fracture models published in the literature.

Fracture Geometry	Fracture Models	Reference
Non-conforming	Effective continuum model (1ϕ)	[39]
	Warren and Root (2ϕ2K)	[26,40]
	Multiporosity	[41,42]
	MINC	[43]
	EDFM	[44]
	pEDFM	[45]
	cEDFM	[46]
	XFEM	[47]
Conforming	Lower-dimensional elements	[37,48]
	Local Grid Refinement (LGR)	[15,34]

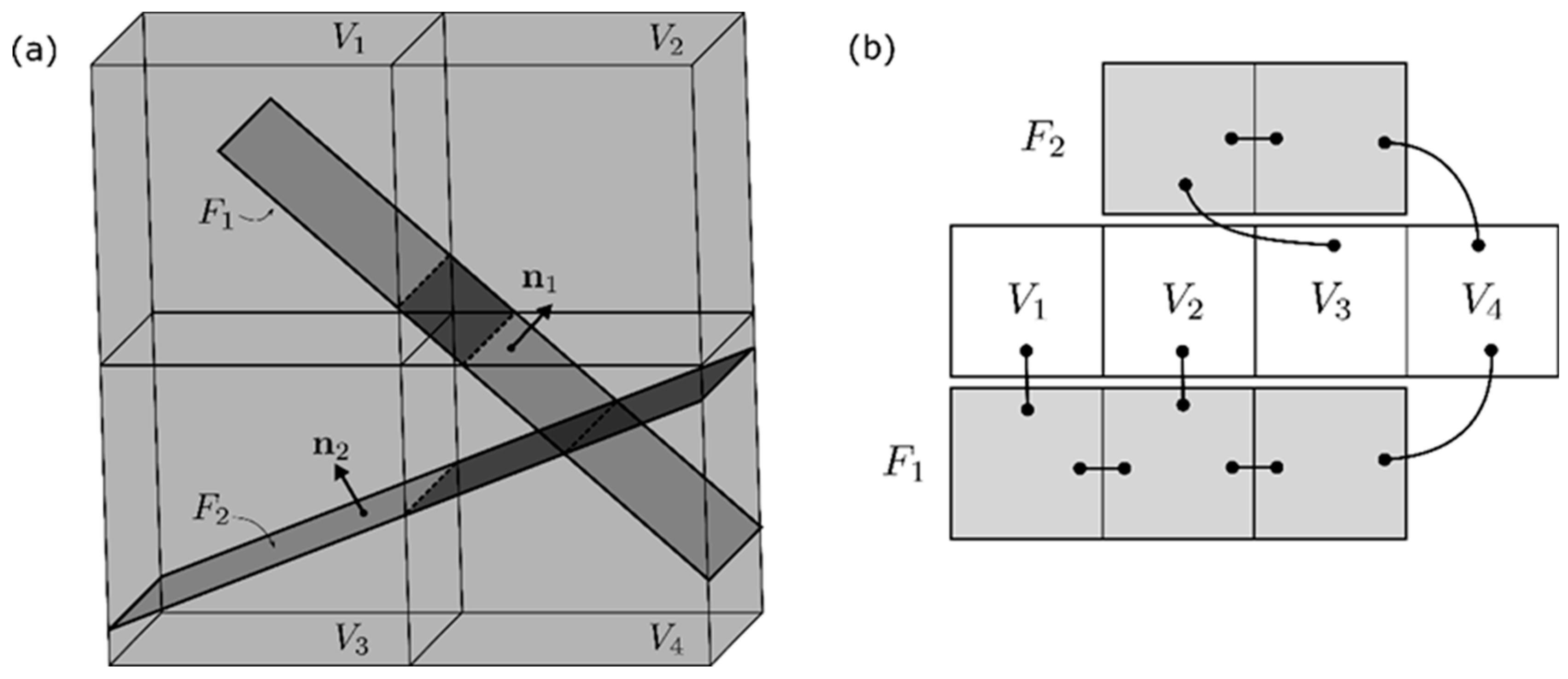
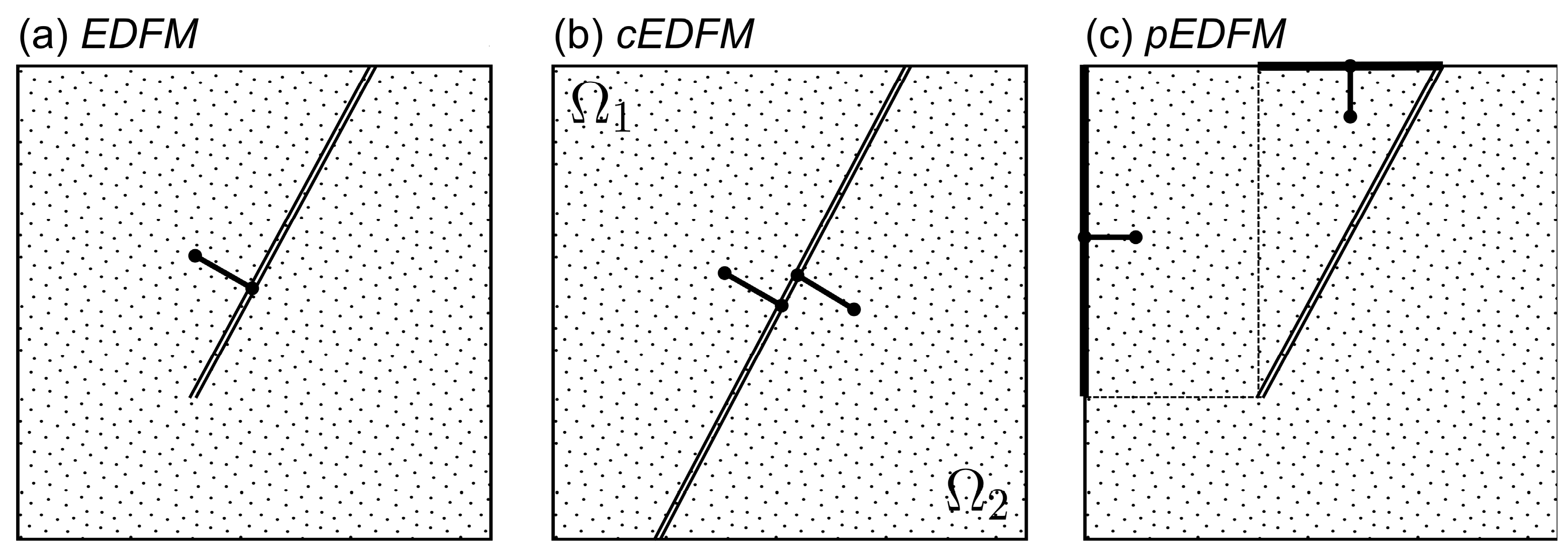
4. EDFM Formulation

This section reviews the EDFM history and common grounds. Extensive discussion and validation of the technique are found in [44,49,50,51].

The first use of the EDFM principles was proposed by Hearn [52], and, a few years later, Lee [16] and Li [53] made progress on similar grounds. At the time, formulations were limited to Cartesian meshes and simplified fracture geometries. Moinfar [44] expanded the idea for a 3D environment with inclined fractures and proposed EDFM naming for the method family. In the following years, many researchers expanded EDFM in different directions by incorporating more complex mesh setups and fracture geometries, chemo-thermo mechanics, and new formulations in various target applications.

EDFM workflow starts by characterizing the fracture network as a set of discrete lower dimensional entities (2D in a 3D model, or 1D in a 2D model). Additional REVs are assigned for each effective discrete entity, and the new REVs are then analytically connected to the geometrically co-located elements by redefining element connectivity. As the fracture REVs are not present in the mesh of matrix elements, special non-neighboring connections link the fracture REVs to the original matrix ones. Conventional well-established reservoir flow simulators can then solve the new model so that the original EDFM engines can be seen as a preprocessor.

The elementary entity of the method is a fracture segment, defined as the slice of a given fracture intersecting a matrix block (Figure 2). The segment will be associated with a new REV, with an assigned fluid volume and connectivity to the matrix blocks. The REV porosity represents the fluid volume and is defined as follows:

$${\varphi }_f={\displaystyle \frac{w S}{V_b}}$$

(1)

where $w$ is the fracture aperture, $S$ is the surface area of the segment, and $V_b$ is the bulk volume of the numerical element in which the segment will be represented.

In field-scale models, w is in the order of millimeters, whereas $V_b$ is typically in the 10²–10⁶ m³ range. Hence, ${\varphi }_f$ will tend to be small (<0.01%) and drive the solver into numerical issues. It is a common practice to set a lower bound to ${\varphi }_f$ to avoid numerical issues.

The additional connectivity (or transmissibility) to be added to the model must account for (i) the fluid flow throughout the interconnected fracture segments $T_F$; (ii) the fluid flow between intersecting fractures $T_I$; and (iii) the fluid flow from the fracture to the surrounding matrix block $T_{FM}$. The flow equations formulation for two segments of the same fracture follows a two-point flux approximation that is

$$T_F={\displaystyle \frac{T_i+T_j}{T_i{T}_j}}, T_i={\kappa }_f{\displaystyle \frac{A_i}{d_i}}, T_j={\kappa }_f{\displaystyle \frac{A_j}{d_j}}$$

(2)

where $T_i$ and $T_j$ are the transmissibility of each segment to their contact, ${\kappa }_f$ stands for the fracture permeability, $A_i$ is the contact area between the two segments, and $d_i$ is the distance from the fracture centroid to the common face.

In cases of fracture intersection, the transmissibility between the intersecting fractures is

$$T_{Ii}={\kappa }_f{\displaystyle \frac{w_i{L}_i}{d_{ij}}}, d_{ij}={\displaystyle \frac{{\int }_{S_i}{x}_{n}d{S}_i+{\int }_{S_j}{x}_{n}d{S}_j}{S_i+S_j}}$$

(3)

where $w_i$ is the aperture of the fracture segment $i$, $L_i$ is the length of the intersecting segment, $d_{ij}$ is the weighted average distance from each segment centroid to the intersection line $j$, $x_n$ is the distance from the fracture area differential element to the intersection, and $S_i$ and $d{S}_i$ refer to the total area of the fracture and its differential element.

Finally, the transmissibility from the fracture to the surrounding matrix block is geometrically estimated as

$$T_{FM}={\displaystyle \frac{2A_f\left({\mathit{\kappa }}_{\mathit{M}}·\mathbf{n}\right)·\mathbf{n}}{d_{FM}}}, d_{FM}={\displaystyle \frac{{\int }_V{x}_{n}dV}{V}}$$

(4)

where $A_f$ is the area of the fracture segment open to flow, $\mathbf{n}$ is the vector normal to the fracture surface, ${\kappa }_M$ is the matrix permeability tensor, $d_{FM}$ is the normal average distance between the fracture and the matrix, and $x_n$ is the shortest distance measured from each infinitesimal volume in $V$ to the fracture plane.

As described, the original developments in EDFM could represent planar fractures in 2D Cartesian meshes. Later, the technology was deployed towards more complex mesh descriptions, namely corner-point [54] and unstructured grids [55]. The novel formulations enabled mixed representations: that is, fractures can now be represented by lower dimensional and embedded elements on the same numerical framework. Moreover, preexisting models may now be used as bases for EDFM studies, avoiding costly mesh conversions.

Limitations on fracture geometry were overcome by Xu [51]. The authors validated EDFM on the representation of complex natural fracture networks and complex networks of hydraulic fractures whose geometry was estimated by numerical simulators.

5. Low-Permeability Fractures

As discussed previously, fracture simulation techniques were originally thought of to incorporate additional flow permeability into the existing matrix REVs. However, natural fractures appear in different flavors; while continuous open joints enhance fluid flow, cemented fractures are restrictions. Such restrictions are traditionally added to the matrix REVs during the DFN upscaling or naturally emerge during history matching.

The ability to deal with low-permeability fractures using EDFM was proposed by Tene [45], called projection-based EDFM (pEDFM). The idea is to penalize the original matrix-to-matrix transmissibilities at the cell interfaces (Figure 3c). pEDFM adds value to history matching and uncertainty assessment, as the overall mesh is kept static, enabling fast optimization loops even with extreme anisotropy ratios.

pEDFM projects the fracture path at the matrix cells’ interfaces along each dimension $x_e$, with surface areas $A_{if\perp x_e}$. The M-M transmissibilities are

$$T_{i{i}_e}={\kappa }_{i{i}_e}{\displaystyle \frac{A_e-A_{if\perp x_e}}{\mathsf{\Delta }{x}_e}}$$

(5)

where ${\kappa }_{i{i}_e}$ is the fluid mobility between the matrix cell $i$ and its neighbor in the direction $x_e$. The fracture transmissibility enhancements are similar to the base EDFM technique, except that they are projected to the matrix cell interfaces as

$$T_{i{i}_e}={\kappa }_{i_{e}f}{\displaystyle \frac{A_{if\perp x_e}}{d_{i_e}f}}$$

(6)

The limiting condition of a fluid-blocking fracture would represent a split between the reservoir volumes (compartmentalization), and a significant error might emerge if large cells are used. One might also consider that volumes might be confined between two blocking fractures if they are mapped to opposing faces of the volume, which would not be physical or would drop excessive volumes apart. Such an approach suggests that pEDFM requires fine meshes near the fluid-blocking fractures.

Li et al. [56] investigated this problem. Their simulation results show significant deviations when pEDFM is used to map low-permeability fractures. As a solution, they proposed flow-based EDFM (fEDFM) [56]. However, the excessive refinement and complexity in adaptive remeshing may be unattractive for field-scale models.

Chai [46] proposes a more assertive approach with compartmental EDFM (cEDFM). The idea is to enable an unstructured cell volume split (Figure 3b) when a large cell is cut by fluid-blocking fractures. In cEDFM, the matrix cell is split into separate domains, one on each fracture side, non-conforming to the mesh. After the splitting process, a connection graph is built, in which the REVs are represented as nodes and the transmissibilities as edges. This data structure is convenient for applying upscaling methods and calculating the necessary transmissibilities between the fracture volumes and the surrounding matrix blocks. Details of the cEDFM transmissibility calculations follow similar EDFM ideas and are out of the scope of this manuscript.

Although cEDFM was validated in a proprietary simulator with the freedom to modify the core code, it seems possible to implement it as a preprocessor of commercial simulators. As the number of new volume domains increases with the network’s complexity, upscaling techniques for the cEDFM connectivity graph are a natural improvement to seek in an effort to minimize the number of effective numerical entities representing the DFN.

6. Enhanced Transmissibility Calculation

Significant effort has been devoted to improving transmissibility calculations. This is the case for integrally EDFM (iEDFM) [57], where the fracture network inside a given block is considered altogether in a simple yet powerful upscaling technique. The advantage is the reduction in the number of new REVs and connectivity as neighboring fractures are merged. Similarly, there has also been progress in using multiscale simulations to compute the transmissibility calculations, allowing for the numerical incorporation of complex physics into the field-scale models. Losapio [58] developed an algorithm in that direction. However, the solution is costly and significantly increases the design optimization loops. As the author points out, this might be an interesting research topic for machine learning and artificial intelligence algorithms.

One weakness of most EDFM transmissibility calculation strategies concerns disregarding multiphase aspects and relying on highly uncertain data. After all, field data reveals the connectivity among the joints only globally and at a later time when the field has already been developed. Pursuing highly accurate characterization without reliable data for calibration is pointless. One alternative is to build up local fine-grained and physically rich models, which are more suitable for addressing phenomenological approaches. The idea would be to enhance overall physical understanding and constrain the uncertainties of large-scale models. This seems like a fruitful research topic to be explored, especially considering data-driven multiscale strategies.

7. Geological Considerations

Fracture modeling has poor and highly uncertain calibration data regarding quality and spatiality. The predictability of a fracture model eventually relies on the physical understanding of the problem derived from geoscience studies. That means that the quality of a model is directly linked to its ability to enhance multidisciplinary communication and implement and test high-level understandings of the fracture network attributes. Hence, design cycles and numerical methodologies must include geosciences and human interventions, both in adding new interpretations to the models and receiving feedback from them.

It is challenging or even impossible to build a generic correlation between fracture geometry and hydraulic behavior, and the simplistic idea of fracture flow controlled by average apertures and planar geometries is unrealistic. A geometrical description must include, besides the fracture’s large-scale geometry path, at least its roughness, aperture, contact area, and history [10,59]. Frash [20] and Pyrak-Nolte [60] show, for example, that the lubrication theory in parallel plates (cubic law) is not applicable for natural fractures, as a geometry-to-transmissibility correlation is complex, and the lubrication theory assumptions are excessively restrictive. Moreover, laboratory investigations have important scale and mechanical limitations that usually invalidate the findings.

Hence, the design team must agree on the nature of the fracture network and essential attributes before assigning fracture conductivity. Even though EDFM provides a framework to model discrete fractures, one must be aware of detaching the geometry of the fracture from its numerical counterpart. As much as W&R models map complex natural fracture networks as a continuum by assuming the equivalent geometry of regularly spaced cubic blocks, discrete fractures must be interpreted as numerical representations of interconnected multiscale joints. The best approach, thus, is to seek higher-level parameters in geosciences to characterize the fractured medium as effective features.

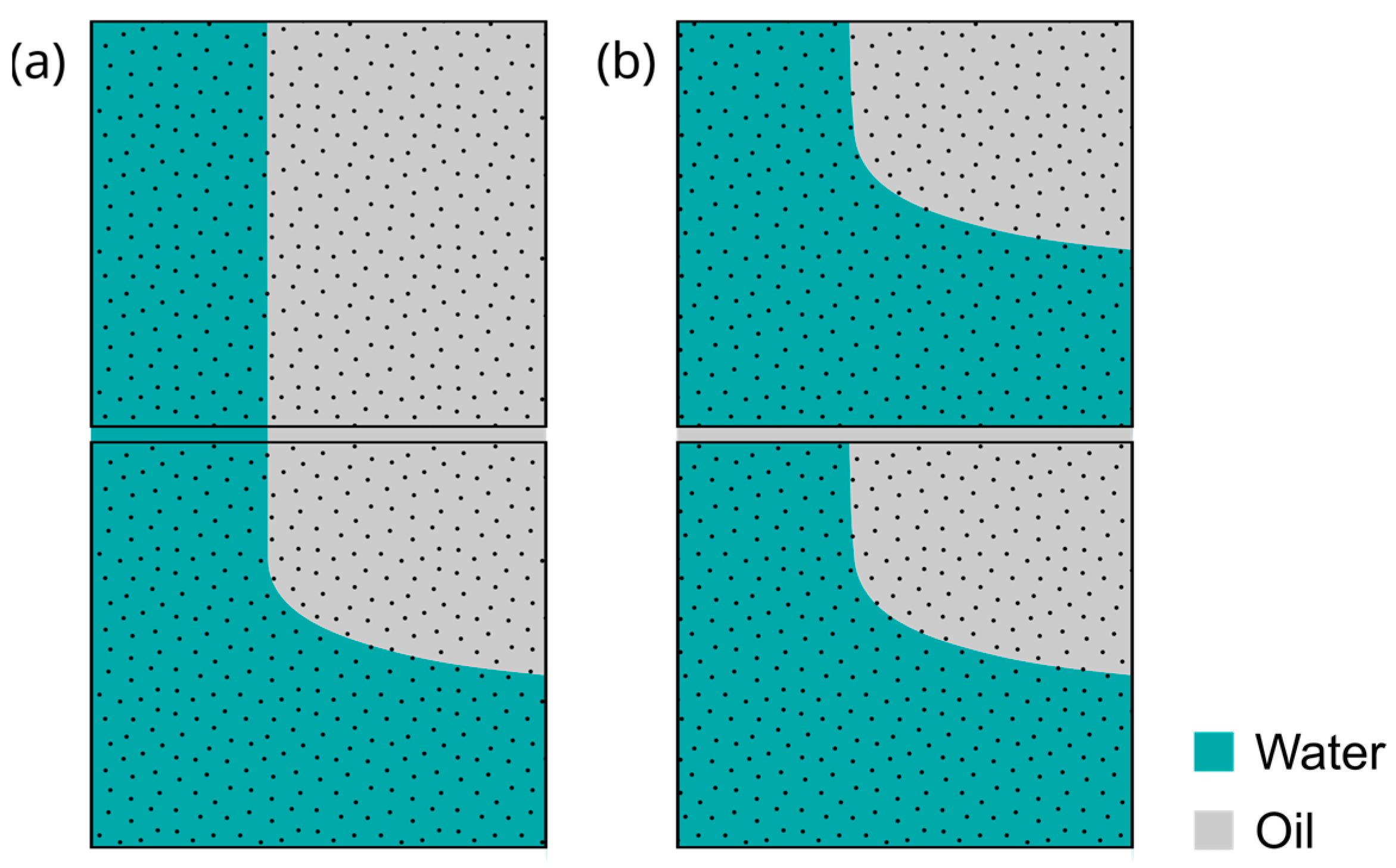
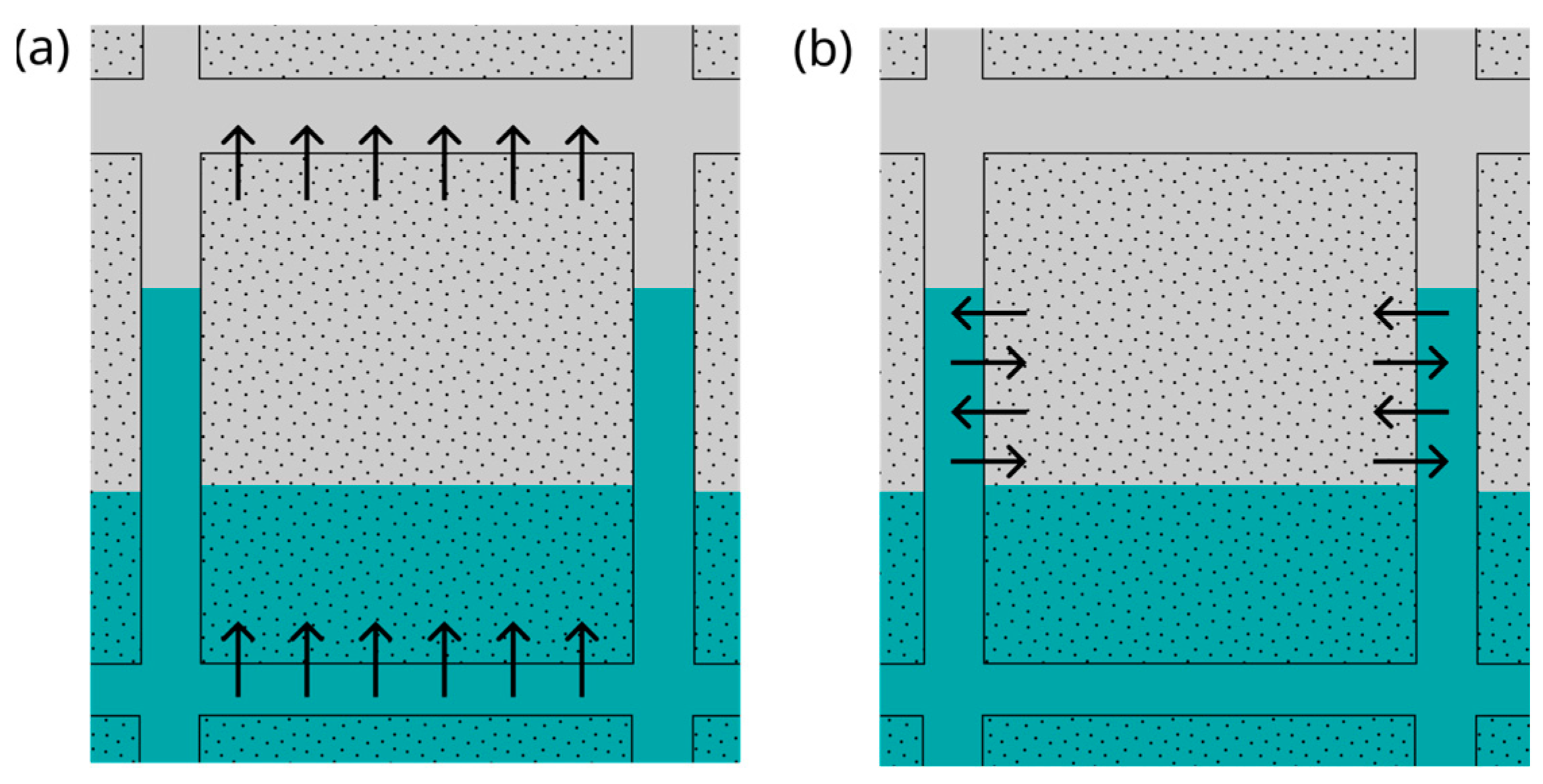
8. Multiphase Flow

The drainage mechanisms in a flow simulator are the forces in the domain that control the rock and fluid interactions. The major forces to consider in a given porous media are gravitational, viscous, and capillary. Their preponderance in the overall equilibrium varies with the composition of the materials, the geometry of the pore structure, the height of the reservoir, and the pressure gradients imposed, etc.

When calculations are performed in idealized geometries and multiphase flow is left open for the reader’s discretion, considering capillary pressure and relative permeability as a function of fluid saturation might be enough to embed multiphase physics into the NFR numerical models. However, in naturally fractured reservoirs, many aspects of capillary continuity, spontaneous imbibition, counter-current, co-current flow patterns, and their numerical counterparts remain open and have received little attention from the EDFM community [25,33,61,62].

As relative permeability embeds capillary-controlled behavior into larger scale Darcy’s viscous flow formulation [63], its use in NFR is not straightforward. When derived from laboratory tests, relative permeabilities map the behavior along the matrix. Similarly, along the fractures, capillary pressure is routinely considered negligible, and relative permeabilities are set as linear, close to an X-shape [64]. However, work by Pieters [65] shows this is untrue even for idealized parallel plates. When capillary forces are considered, Firoozabadi [66] and Karimi-Fard [48] show additional deviation, with a bias to produce over-pessimistic recovery estimates when the X-shape is used. After all, multiphase flow in the fracture and porous medium depends on complex physics and fluid-rock interactions, and predicting relative permeabilities is not straightforward and likely impossible with current technology (Figure 4 and Figure 5).

The imbibition dynamics of NFRs subject to waterflooding enhance oil recovery in water-wet (WW) formations, reduces oil recovery in strongly oil-wet formations, and, in mixed wet rocks, the recovery varies and can be even more favorable than the WW scenarios [23,48,67,68]. The assumption that fluid flow in an NFR occurs mainly inside fractures breaks down when multiphase effects are considered: as the capillary pressure inside fractures is usually non-negligible, capillary continuity throughout a fracture set is probably greater than anticipated, and both gravity and the co-current flow play a role as primary drainage mechanisms and imbibition of the natural fractures delay the water breakthrough (Figure 6).

It must be underlined that although laboratory testing of fractured rock is not trivial, the investigation of the imbibition mechanisms of a given rock in the pore scale is fundamental so that fracture models and overall analysis can go beyond simplistic idealized geometries, and successfully find representative realistic estimates.

Similar issues arise in the evaluation of gas injection and carbon storage. March [69] presented strategies in a dual porosity model concerning the non-wetting nature of the injected fluid and the need for specialized transfer functions. Machado [70] explored a similar idea by comparing EDFM, LGR, and dual porosity models, additionally considering chemical reactions. In all cases, the presence of fractures cannot be neglected when estimating the optimal injection strategy and the site’s storage capacity.

Wu [71] further discussed potential numerical issues. Finite difference flow simulators use upstream approximations for the derivatives as a numerical stabilization technique. This implies that the fracture’s relative permeability dominates the process when fluid flows from the fracture to the matrix. This is unrealistic, as the permeability of the most restrictive block controls the equivalent permeability between two blocks with contrasting permeability. The proposed solution is to model the fracture–matrix interface physics instead of relying on matrix and fracture parameters alone. While EDFM seems like an interesting approach to controlling capillary continuity and buoyancy of each numerical effective feature, a clear recommendation is still an open research area.

Benchmarks and validation procedures for multiphase flow in NFRs are scarce, as work found in the literature tends to focus on the assessment of the accuracy and performance of algorithms in single-phase flow scenarios [72,73]. The strategy is indeed suitable for estimates related to stimulated wells and hydraulic fractures but eventually misleads and oversimplifies the analysis for naturally fractured reservoirs.

9. Thermo-Hydro-Chemo Mechanics (THCM)

Most of the advancements seen in EDFM lately relate to applications beyond hydraulic flow. Pei [74] recently used EDFM to model fully coupled mechanics and hydraulic flow, which can handle time-dependent aspects of fracture transmissibility as a response to stress and pressure dynamics. Ren [75] presented an algorithm to model isothermal complex fracture propagation in a hybrid XFEM–EDFM strategy. One key aspect is the ability to track the fracture path, an important degree of freedom in this class of algorithms. Despite historical research efforts, strategies for fracture tracking in THM-coupled processes in 3D environments are not yet consolidated.

EDFM has also been extended to Enhanced Geothermal Systems (EGS), in which the coupling between energy exchange and fluid flow is primary for the design [76,77,78,79]. Besides the understanding of the energy exchange along the reservoir, thermal stresses are likely to trigger mechanical events, such as fracture propagation, fault reactivation, and well integrity. These events in EGS applications differ significantly from stimulation jobs. As the latter are operated for a few hours with generally neglected localized thermal stresses, EGS operates for years, and thermally induced stresses are likely propagating fractures in non-planar geometries. It is unclear how to map secondary fractures as effective discrete fractures and the numerical simulation of long-term propagation are still areas of active development.

Most simulators dealing with mechanical coupling restrict the analysis to linear time-dependent transmissibilities as a response to linear elasticity. That is, the fracture conductivity reduces as effective stresses rise due to depletion or cooling [74,80]. Proppant distribution and crushing due to elevated effective stresses have also been studied, for example, by Yu [81]. However, fundamental nonlinear phenomena, such as plasticity, creep, hysteresis, and large strains, are often neglected or left as future work.

Recently, with the emergent interest in Carbon Capture and Storage (CCS), workflows are challenged to model reactive transport [70]. EDFM has been computationally effective and could capture reactive phenomena inside each fracture individually. Most importantly, EDFM could be used as a preprocessor, taking advantage of the existing commercial simulator engines for thermodynamically intensive computation.

10. Data Assimilation under Uncertainties

Fracture-aware workflows and optimization loops must cope with a highly uncertain characterization environment. Narrowing data uncertainty is a long-term ongoing effort, although the physical attributes of the problem limit the range of success. The data assimilation and sensitivity analysis approach must consider probabilistic tools to enhance understanding and provide reliable results under uncertainty. Estimating the uncertainty degree of each piece of information is challenging, but awareness is crucial to avoid time-consuming, over-accurate optimization processes that are impossible to calibrate.

The optimization method in use cannot assume the fracture network or individual fracture conductivities are known. A better approach is to consider every simulation run as a probabilistic realization to be interpreted as an intermediate result to feed the global probabilistic interpretation. Moreover, designers must avoid an excessive number of parameters.

Depending on the scale of analysis, a fracture network may consist of thousands to millions of fractures. There is a need to control higher-level parameters—like fracture genesis, large-scale path, anisotropy, or global transmissibility multipliers—to gain control of the optimization process. In these loops, upscaling methods control the fracture network in each realization, an open area for research that may take advantage of recent AI and multiscale data assimilation techniques [82,83,84].

The evolution of such algorithms and automatic history matching, e.g., by Canchumuni [85], shows the potential to reduce human interaction times. However, optimization workflows still demand visualization, assessment, and validation in postprocessing, which is limiting for many applications of novel methods. The work by Sousa Junior et al. [80] is one example where visually interpreting coupled geomechanically processes in fractures was central.

We acknowledge that the use of EDFM in standard industry workflows has made significant progress as the tools become more user-friendly, fast, reliable, and integrated into existing workflows. For now, pre- and post-processing tools and optimization loops are likely the limiting ones. Consistent results visualization is essential for calibrating, extracting information, and communicating with geoscientists and stakeholders.

11. Performance and Accuracy

Reservoir flow models are currently composed of as many as 100 million active elements. As models grow, performance becomes an issue even for modern computers. EDFM has proven to be a computationally efficient framework to model discrete fractures, preventing local grid refinement while maintaining accuracy. One must pay special attention to the grid sensitivity of each algorithm. As EDFM and related models are supposed to oppose local grid refinement, they lose value as the grid is refined. Effective techniques must be tested and validated for grid sensitivity and present accurate results with sufficient large meshes.

Yu [9] successfully stressed the idea of a large model with a million fractures. In single-phase benchmarks, it has also been competitive in accuracy and computational cost [72,73]. Unlike most other methods, EDFM can use commercial simulator engines, meaning that multiphase behavior, complex thermodynamics, well control, pre- and post-processing, and uncertainty analysis framework are available with no extra development.

As methodologies are proposed, benchmarking against simplistic approaches must be avoided. For example, single-porosity or LGR are rarely used in real-life field-scale simulations. Instead, commercial software has consolidated dual-porosity W&R variations, which work well for dense sets of NFs. To the best of our knowledge, there are no consistent public-domain benchmarks for multiphase flow assessment in fractured porous media. As discussed in previous sections, while single-phase tests are enough for Hydraulic Fractured Wells, that is certainly not true for Naturally Fractured Reservoirs. Proposing comprehensive, public-domain NFR benchmarks and reference metrics for accuracy and computational performance is an important research area.

Finally, the validation of a given model must assess the ability of the model to predicting the behavior of the reservoir, in opposition to simply history matching the data. This may be true even for well-established dual-porosity models, in which many parameters are offered as degrees of freedom to history matching but may lack physical meaning and hence, predictability [7].

Table 2. Recommended techniques for selected fracture types and application scenarios.

	Recommended Technique	Reasoning
Hydraulic Fracture	EDFM or Conforming	Fractures are designed with a well-known geometry, and multiphase flow is less relevant. EDFM can be faithful to the fracture geometry and is computationally efficient. Conforming methods are also suitable and efficient for low-density fracture networks with known geometries.
Natural Fracture (Type 1)	EDFM or Effective continuum (1ϕ)	The matrix is irrelevant for the flow and for connate fluid storage. Fracture distribution and their connectivity can be represented by EDFM or by an upscaled single porosity effective continuum model.
Natural Fracture (Type 2, 3)	EDFM or 2ϕ2K	The contrast between matrix and fracture conductivities can be modeled as a continuum using dual porosity or directly related to an effective geometry with EDFM.
Natural Fracture (Type 4)	pEDFM, cEDFM or Conforming	Fractures with large extensions whose geometry is mapped from seismic data with low uncertainty can be conformed to the grid. Sub-seismic features are likely to take advantage of pEDFM or cEDFM flexibility
Waterflooding	EDFM or 2ϕ2K	Multiphase flow raises concerns about how to represent the fracture’s role in this context in both approaches and how to calibrate the transfer function in the DPDK approach.
Gas-EOR and Storage	EDFM or 2ϕ2K	Multiphase flow raises concerns about representing the fracture’s role in this context. However, EDFM tends to be computationally more efficient in reactive transport.
Steamflooding	2ϕ2K or MINC	It’s unclear if EDFM can handle heat flow when coupled with commercial simulators.
Iterative workflows	2ϕ2K or EDFM	One must avoid costly operations like re-meshing and property redistribution during iterative workflows. Hence, more flexible schemes are preferred.

presents a summary and recommendations of modeling formulations for selected scenarios.

12. Conclusions and Recommendations

This manuscript looked into the latest development of EDFM frameworks, aiming to identify important open issues and research opportunities. While the technique’s progress is evident, fundamental questions remain open, such as:

• The multidisciplinary fracture characterization culture has long seen distancing between geoscientists and simulation engineers. Narrowing this gap will enable the assimilation of stochastic techniques built after data and interpretation from outcrops, cores, image logs, seismic surveys, and field measurements. With such a framework in place, history matching to field data and uncertainty assessment of the DFN attributes enhance team communication and aggregate phenomenological findings.
• The consolidation of upscaling processes and field-data assimilation techniques still needs thorough investigation. Considering that numerical discrete fractures are effective representations of large collections of complex smaller joints, their attributes, like fracture aperture or roughness, cannot be derived from direct correlation to direct geometrical observation. Instead, the attributes are intrinsically multiscale, multifactorial, and highly uncertain.
• A comprehensive set of geologically consistent, public-domain benchmarks covering a wide range of complex fracture networks would enable the assessment of available methodologies’ actual scalability and accuracy. Current benchmarks are notably simplistic and limited to single-phase flow in isothermal and mechanically stable environments. Remarkably, the significant differences in drainage mechanisms between NFs and HFs suggest that each case demands particular setups.
• Novel discrete fracture models must assess multiphase capillary-driven fluid imbibition dynamics, especially when targeting naturally fractured reservoirs. Similarly, thermally induced fracture opening and extension and their mechanical interactions still need further understanding.
• Most of the techniques discussed in this paper are still limited to academic investigation. Establishing a discrete fracture framework in commercial software for field-scale at industry standards is the key to moving forward. Training of subsurface technicians has been extensive in dual porosity strategies for a long time, and shifting to a discrete modeling culture is costly and not immediate. For example, the lack of integrated pre- and post-processing tools for fluid flow simulation and visualization is crucial in human-assisted history matching. This limits the use of the models across decision-making chains.