IIP-Mixer: Intra–Inter-Patch Mixing Architecture for Battery Remaining Useful Life Prediction
Abstract
1. Introduction
- Novel architecture: The IIP-Mixer architecture introduces parallel dual-head mixer layers: the intra-patch mixing MLP, which captures local temporal patterns in the short-term period, and the inter-patch mixing MLP, which captures global temporal patterns in the long-term period. This parallel dual-head approach allows the model to effectively learn from both short-term and long-term data patterns.
- Weighted loss function: To address the varying importance of features in RUL prediction, we introduce a weighted loss function in the MLP-Mixer-based architecture. This innovation marks the first time such an approach has been employed in this context, enhancing the model’s ability to prioritize more critical features during training.
- Performance and efficiency: Our experiments demonstrate that the IIP-Mixer achieves competitive performance in battery RUL prediction, outperforming other popular time series frameworks. Furthermore, the simplicity of the MLP-based design results in faster training times compared to attention-based models like Transformers, making it a more efficient solution for real-time applications.
2. Related Work
2.1. Physics-Based Approaches
- Semi-empirical methods map degradation parameters to key battery metrics like static capacity and impedance under different loads and environmental conditions through offline testing. Sankararaman et al. [23] extended the first-order second-moment method (FOSM) and first-order reliability method (FORM) for use with state space models, creating a computational framework to determine the entire probability distribution of RUL predictions. Coulombic efficiency, a critical battery parameter, is closely linked to lithium inventory loss, the main aging factor for lithium-ion batteries. Leveraging this relationship, Yang et al. [24] developed a semi-empirical model to capture capacity degradation.
- Empirical methods continuously update their model parameters through online measurement and estimation of battery states. Given the nonlinear and non-Gaussian capacity degradation characteristics of lithium-ion batteries (LIBs), Zhang et al. [25] proposed an RUL prediction method using an exponential model and particle filter. In real environments, the discharge current of LIBs changes randomly within a charge–discharge cycle, significantly affecting battery life. Shen et al. [26] developed a two-stage Wiener process model, incorporating the unscented particle filtering algorithm, to predict the RUL considering variable discharge currents.
2.2. Data-Driven Approaches
- MLP-based architecture: A multilayer perceptron (MLP) is a type of artificial neural network with a forward structure, consisting of an input layer, an output layer, and several hidden layers. Kim et al. [30] proposed a practical State of Health (SOH) classification scheme based on an MLP, performing classification using only data from discrete life spans. Das et al. [31] introduced a multilayer perceptron-based encoder–decoder model, the Time Series Dense Encoder (TiDE), for long-term time series forecasting. This model combined the simplicity and speed of linear models with the ability to handle covariates and nonlinear dependencies.
- RNN-based architecture: Recurrent neural networks (RNNs) are designed for processing sequential data. In [32], differential thermal voltammetry (DTV) signal analysis methods are combined with RNN-based data-driven methods to track battery degradation. De Brouwer et al. [33] introduced a continuous-time version of the Gated Recurrent Unit (GRU), built upon Ordinary Differential Equations, along with a Bayesian update network for processing sporadically observed time series.
- Transformer-based architecture: The Transformer employs an attention network to precisely capture sequential information, thereby enhancing neural network training performance. Chen et al. [34] introduced a model based on the Transformer to tackle challenges in capturing long-term dependencies and complex degradation patterns. This model integrated a position-sensitive self-attention (PSA) unit, which improved the model’s ability to incorporate local context by focusing on positional relationships in input data at each time step. To handle noisy battery capacity data, particularly during charge/discharge cycles, Chen et al. [13] developed a Transformer-based neural network using a Denoising Auto-Encoder (DAE) to learn from corrupted input and reconstruct data, effectively processing noisy battery capacity data.
3. Methods
3.1. Problem Formulation
- Input data: the input data consist of multiple time series variables collected over a series of cycles, representing various sensor measurements, such as voltage, current, and capacity.
- Output data: the output is the predicted future values , from which the remaining useful life of the battery can be determined.
- Objective: the goal is to develop a model that can accurately predict the future values based on the historical data .
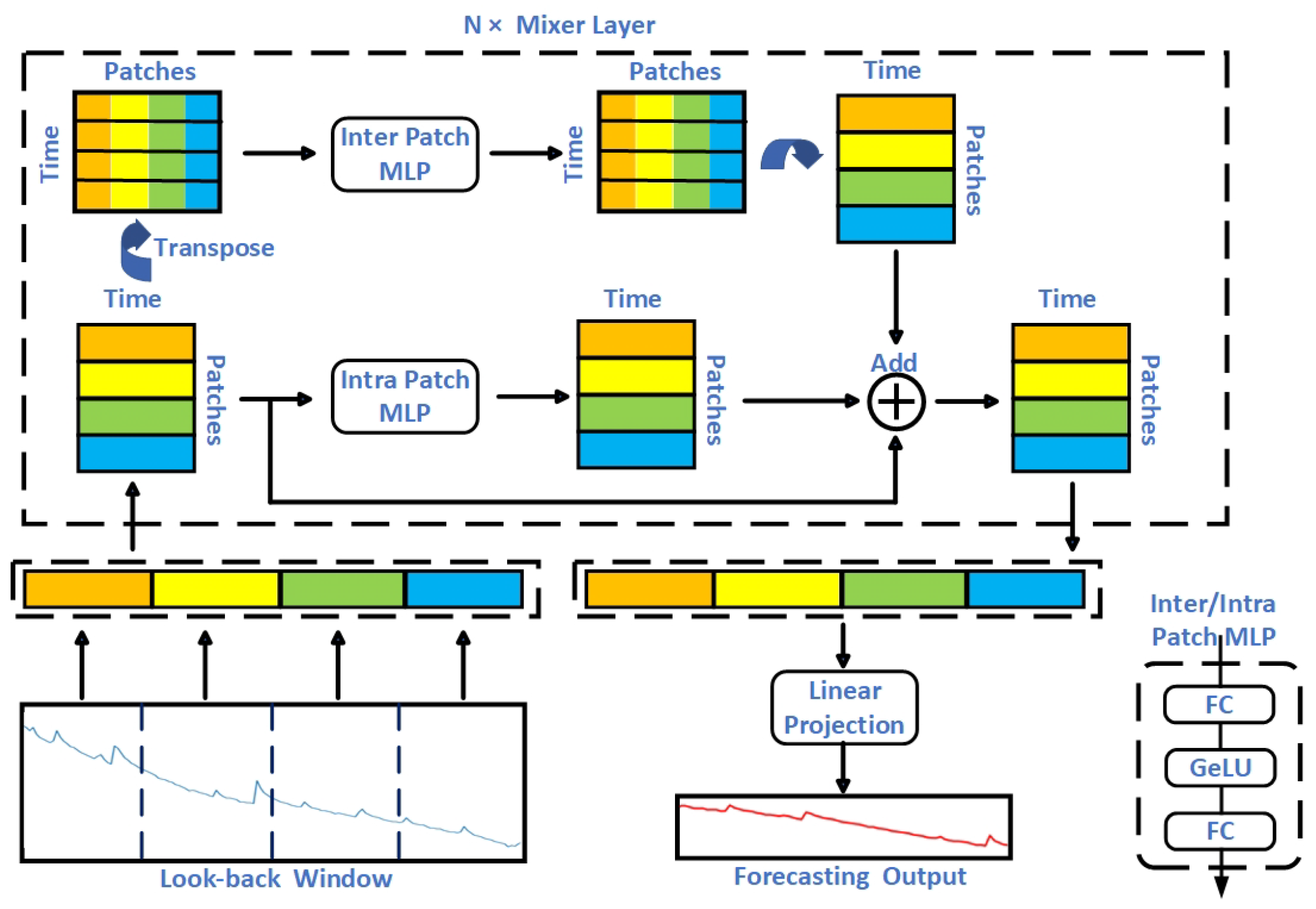
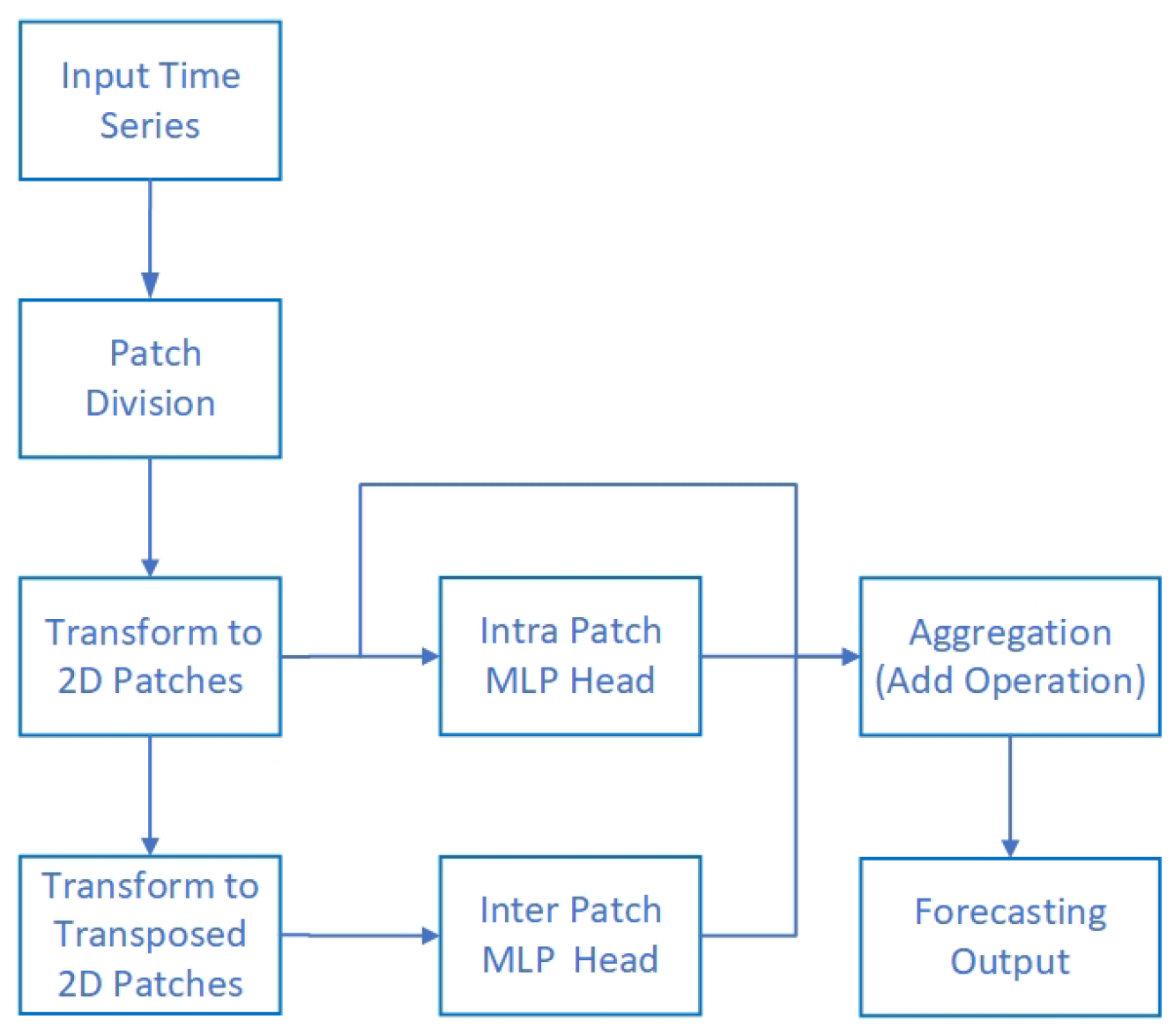
3.2. The Framework
3.2.1. Major Components of the Framework
3.2.2. Data Processing Procedure
3.3. The Multivariate Time Series
3.4. Dual-Head MLP
| Algorithm 1: IIP-Mixer: PyTorch-like pseudocode. |
: segments of the univariate time series the transposition of input x params: parameters of the network: mixer + fc for x in loader: # load a minibatch # transform from 1D to 2D for i in range (N) # loop number of mixer layer x = mixer # the i-th mixer layer ft(x) # flatten from 2D to 1D pred # full connection layer loss = WMSELoss ( pred, true ) # weighted MSE loss function loss.backward() # back-propagate update(params) # SGD update # mixer layers def mixer (x): # intra-patch mixing MLP # inter-patch mixing MLP # aggregate output information return x |
3.5. Differences between IIP-Mixer and MLP-Mixer
- First, in IIP-Mixer, unlike MLP-Mixer’s patches and features, the two dimensions represent patches and time steps, allowing us to capture both local and global temporal patterns simultaneously. Particularly, the global temporal patterns captured from time steps are crucial for battery RUL prediction, as demonstrated in Table 5.
- Second, unlike MLP-Mixer’s serial structure of dual-head MLP, in IIP-Mixer, we introduce a parallel structure for inter-patch mixing and intra-patch mixing to capture temporal patterns simultaneously. As shown in Table 6, the parallel heads’ structure clearly outperforms the serial structure in battery RUL prediction.
- Consequently, unlike MLP-Mixer’s traditional loss function, we propose a weighted mean square error loss function that accounts for the varying importance of features in battery RUL prediction. This approach results in a 5% relative improvement in MAE.
4. Experiments
4.1. Datasets
4.2. Baselines
- MLP: A multilayer perceptron is like a mathematical function that maps input and output values. Multiple layers are used to learn the battery’s dynamic and nonlinear degradation trend.
- Transformer: Transformer is a model that uses an attention mechanism for model training; it mainly consists of two components: an encoder and a decoder, with which we can predict the capacity degradation trend of the battery.
- Informer: A variant of the Transformer architecture that efficiently handles extremely long input sequences by highlighting the dominating attention by halving the cascading layer input. It predicts the long time series sequences in one forward operation rather than in a step-by-step way, which drastically improves the inference speed.
- DLinear: In consideration of permutation-invariant and “anti-ordering” to some extent of the Transformer-based architecture [16], DLinear decomposes the time series into a trend and a remainder series and employs two one-layer linear networks to extract the temporal relations among an ordering set of continuous points.
4.3. Implementation
4.3.1. Parameter Selection and Optimization
- MLP: The MLP model was configured with one hidden layer. The optimal values for the learning rate and hidden dimension were determined through a grid search, resulting in 0.0005 and 32, respectively.
- Transformer and Informer models utilized two encoder layers and one decoder layer, each with 8 attention heads. The optimal values for the learning rate, hidden dimension, and dropout rate, identified through a grid search, were 0.0001, 512, and 0.05, respectively.
- For the DLinear model, we adopted the architecture parameters proposed in the original paper. The best performance was achieved with a decomposition kernel size of 25 and a learning rate of 0.0015, as determined through a grid search.
- IIP-Mixer: Our model includes six key parameters: patch size, learning rate, dropout rate, patch length, number of mixer blocks, and number of principal features of the time series. The optimal values, determined through a grid search, were 4, 0.001, 0.05, 4, 1, and 6, respectively. Detailed information about the training process is provided in Table 1.
4.3.2. Evaluation Metrics
5. Results
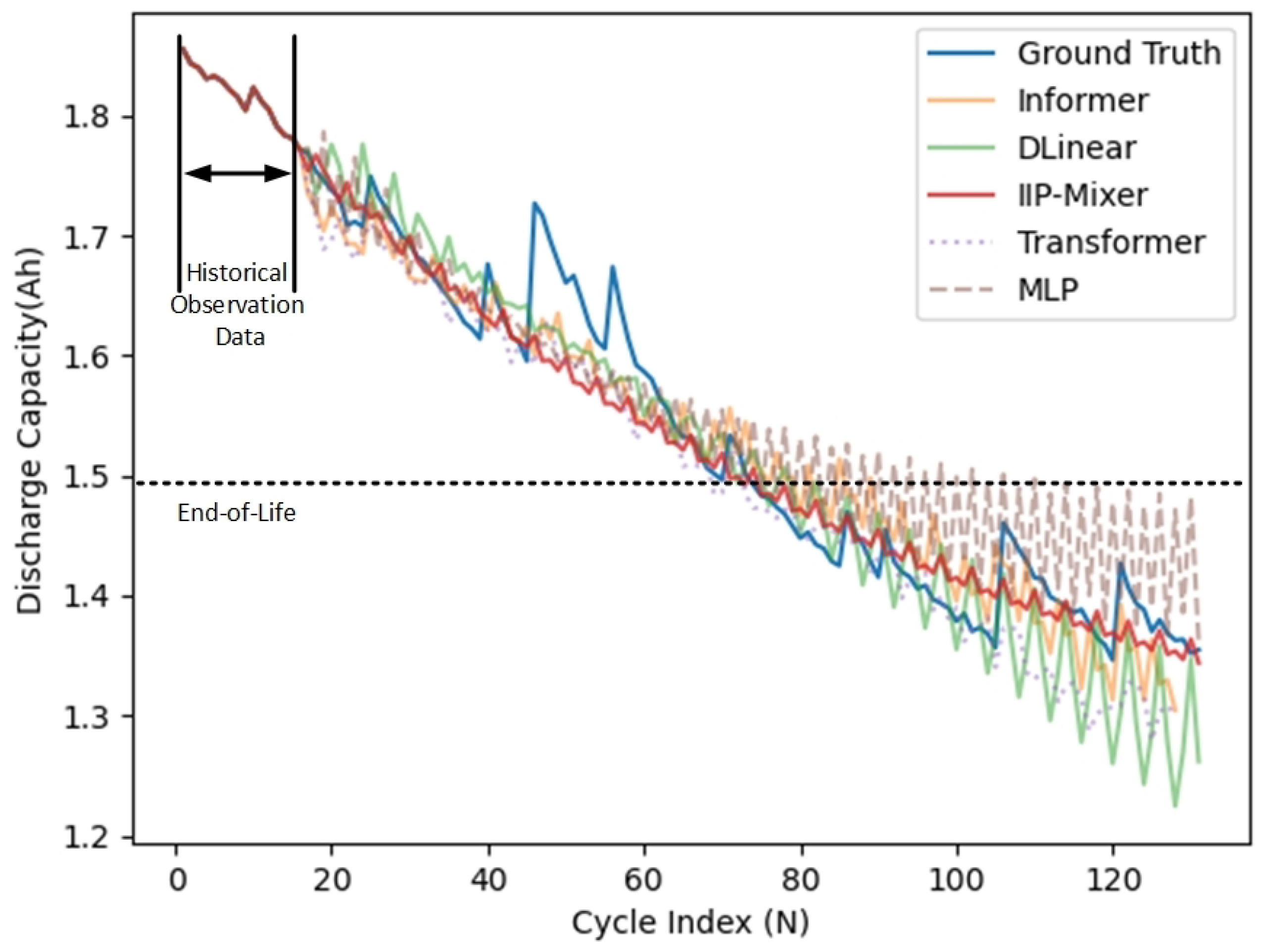
5.1. Performance of IIP-Mixer
- The Transformer and its variant, the Informer model, excel in modeling both long-term and short-term dependencies, showcasing superior performance on long-time series data. However, it is worth noting that they can easily lead to overfitting for small datasets, such as the NASA PCoE battery dataset.
- The MPL model is adept at capturing global temporal patterns but may struggle to capture local temporal patterns from time series data. Consequently, its performance remained average across all evaluation metrics compared to other methods.
- The DLinear model decomposes the time series into a trend and a remainder series. It utilizes two one-layer linear networks to extract temporal relations among an ordered set of continuous points, making it adept at capturing both the trend and season of a time series.
- Among all the baseline methods, our proposed model IIP-Mixer achieved the best experimental results. As shown in Figure 3, IIP-Mixer could capture the local and global temporal patterns in time series data; this is a great help for battery RUL prediction, especially in the overall degeneration trend of discharge capacity.
- LSTM and its variants, the GRU [40] and Dual-LSTM [41] models, are types of neural networks designed for processing sequential data. These models can handle examples of varying lengths by sharing parameters across different parts of the network. However, recurrent neural networks, including LSTM networks, can experience performance degradation due to long-term dependencies, which impacts their effectiveness in battery RUL prediction.
- DeTransformer [13], a variant of Transformer, leverages the strength of the self-attention mechanism, excelling at extracting semantic correlations between paired elements in a long sequence, regardless of their order, thanks to its permutation-invariant nature. However, in time series analysis, the primary focus is on modeling the temporal dynamics among a continuous set of points, where the order of the data points is crucial [16]. This affects the effectiveness of Transformers in predicting battery RUL.
- IIP-Mixer, a straightforward MLP-Mixer-based architecture, is well suited for learning temporal patterns due to its time-step-dependent characteristics, as demonstrated by recent work [35]. Our results also highlight the importance of efficiently utilizing MLPs to capture both local and global temporal information, thereby improving the performance of time series forecasting. In summary, this approach achieved superior performance compared to RNN-based and Transformer-based architectures.
5.2. Computation Efficiency
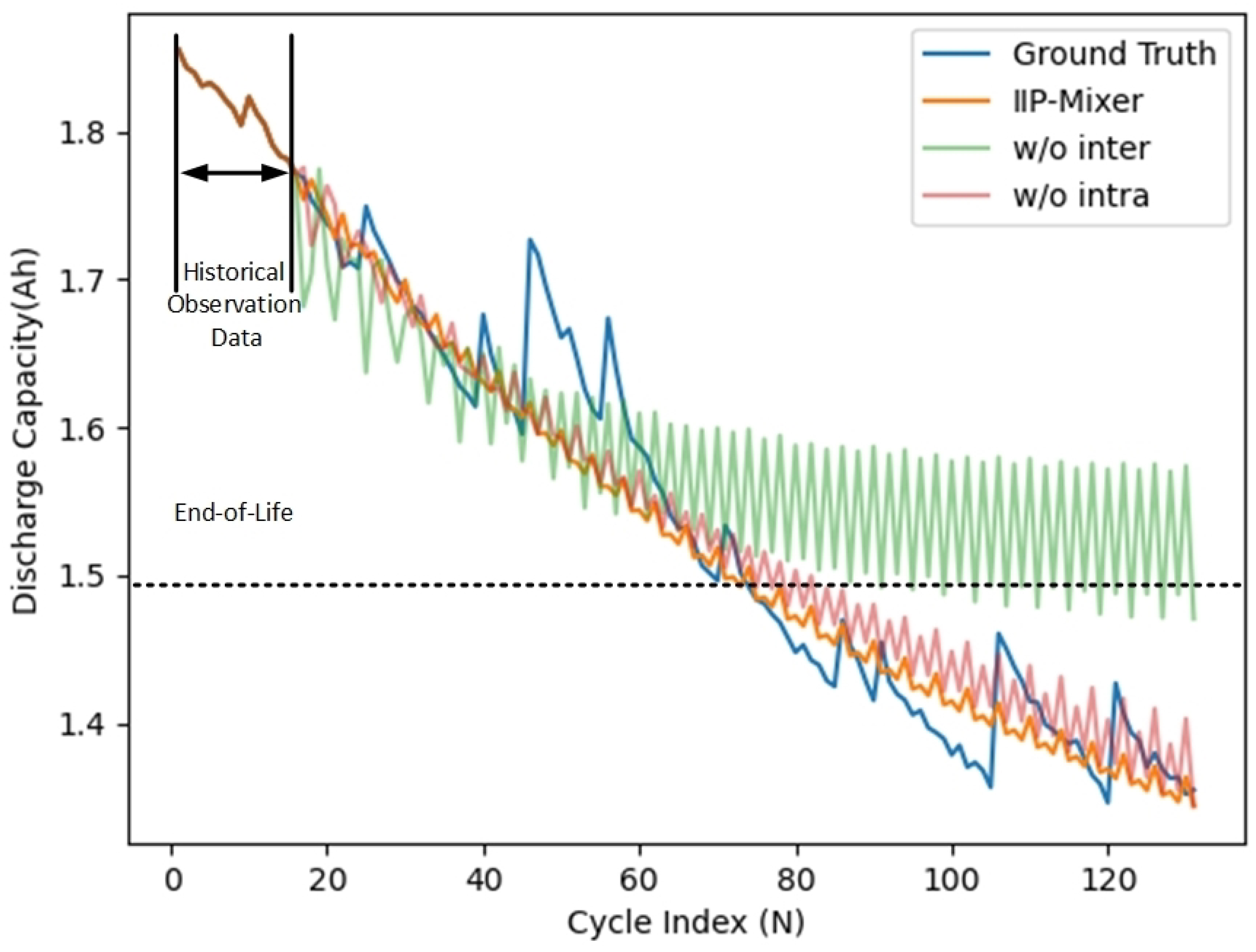
5.3. Ablation Study
5.3.1. Effect of Dual-Head MLP
5.3.2. Serial vs. Parallel Heads
5.3.3. Effect of Weighted Loss Function
5.3.4. Effect of Multivariate Time Series
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alsuwian, T.; Ansari, S.; Zainuri, M.A.A.M.; Ayob, A.; Hussain, A.; Lipu, M.H.; Alhawari, A.R.; Almawgani, A.; Almasabi, S.; Hindi, A.T. A Review of Expert Hybrid and Co-Estimation Techniques for SOH and RUL Estimation in Battery Management System with Electric Vehicle Application. Expert Syst. Appl. 2024, 246, 123123. [Google Scholar] [CrossRef]
- Wei, M.; Gu, H.; Ye, M.; Wang, Q.; Xu, X.; Wu, C. Remaining useful life prediction of lithium-ion batteries based on Monte Carlo Dropout and gated recurrent unit. Energy Rep. 2021, 7, 2862–2871. [Google Scholar] [CrossRef]
- Xu, Q.; Wu, M.; Khoo, E.; Chen, Z.; Li, X. A hybrid ensemble deep learning approach for early prediction of battery remaining useful life. IEEE/CAA J. Autom. Sin. 2023, 10, 177–187. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; Guo, Q.; Ramadass, P.; White, R.E. Review of models for predicting the cycling performance of lithium-ion batteries. J. Power Sources 2006, 156, 620–628. [Google Scholar] [CrossRef]
- Kemper, P.; Li, S.E.; Kum, D. Simplification of pseudo two-dimensional battery model using dynamic profile of lithium concentration. J. Power Sources 2015, 286, 510–525. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, S.; Li, C.; Wu, L.; Wang, Y. A data-driven method with mode decomposition mechanism for remaining useful life prediction of lithium-ion batteries. IEEE Trans. Power Electron. 2022, 37, 13684–13695. [Google Scholar] [CrossRef]
- Guo, H.; Liu, X.; Song, L. Dynamic programming approach for segmentation of multivariate time series. Stoch. Environ. Res. Risk Assess. 2015, 29, 265–273. [Google Scholar] [CrossRef]
- Roberts, S.; Osborne, M.; Ebden, M.; Reece, S.; Gibson, N.; Aigrain, S. Gaussian processes for time-series modelling. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 2013, 371, 20110550. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Lobato, J.M.; Lloyd, J.R.; Hernández-Lobato, D. Gaussian process conditional copulas with applications to financial time series. Adv. Neural Inf. Process. Syst. 2013, 2, 1736–1744. [Google Scholar]
- Wang, S.; Fan, Y.; Jin, S.; Takyi-Aninakwa, P.; Fernandez, C. Improved anti-noise adaptive long short-term memory neural network modeling for the robust remaining useful life prediction of lithium-ion batteries. Reliab. Eng. Syst. Saf. 2023, 230, 108920. [Google Scholar] [CrossRef]
- Rincón-Maya, C.; Guevara-Carazas, F.; Hernández-Barajas, F.; Patino-Rodriguez, C.; Usuga-Manco, O. Remaining Useful Life Prediction of Lithium-Ion Battery Using ICC-CNN-LSTM Methodology. Energies 2023, 16, 7081. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, C.; Chow, M.Y.; Li, X.; Tian, J.; Luo, H.; Yin, S. A data-model interactive remaining useful life prediction approach of lithium-ion batteries based on PF-BiGRU-TSAM. IEEE Trans. Ind. Inform. 2023, 20, 1144–1154. [Google Scholar] [CrossRef]
- Chen, D.; Hong, W.; Zhou, X. Transformer network for remaining useful life prediction of lithium-ion batteries. IEEE Access 2022, 10, 19621–19628. [Google Scholar] [CrossRef]
- Han, Y.; Li, C.; Zheng, L.; Lei, G.; Li, L. Remaining useful life prediction of lithium-ion batteries by using a denoising transformer-based neural network. Energies 2023, 16, 6328. [Google Scholar] [CrossRef]
- Ye, J.; Gu, J.; Dash, A.; Deek, F.P.; Wang, G.G. Prediction with time-series mixer for the S&P500 index. In Proceedings of the 2023 IEEE 39th International Conference on Data Engineering Workshops (ICDEW), Anaheim, CA, USA, 3–7 April 2023; pp. 20–27. [Google Scholar]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are transformers effective for time series forecasting? In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 11121–11128. [Google Scholar] [CrossRef]
- Wei, Y.; Wu, D. State of health and remaining useful life prediction of lithium-ion batteries with conditional graph convolutional network. Expert Syst. Appl. 2024, 238, 122041. [Google Scholar] [CrossRef]
- Tolstikhin, I.O.; Houlsby, N.; Kolesnikov, A.; Beyer, L.; Zhai, X.; Unterthiner, T.; Yung, J.; Steiner, A.; Keysers, D.; Uszkoreit, J.; et al. Mlp-mixer: An all-mlp architecture for vision. Adv. Neural Inf. Process. Syst. 2021, 34, 24261–24272. [Google Scholar]
- Hasib, S.A.; Islam, S.; Chakrabortty, R.K.; Ryan, M.J.; Saha, D.K.; Ahamed, M.H.; Moyeen, S.I.; Das, S.K.; Ali, M.F.; Islam, M.R.; et al. A comprehensive review of available battery datasets, RUL prediction approaches, and advanced battery management. IEEE Access 2021, 9, 86166–86193. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Shchegolkov, A.; Komarov, F.; Lipkin, M.; Milchanin, O.; Parfimovich, I.; Shchegolkov, A.; Semenkova, A.; Velichko, A.; Chebotov, K.; Nokhaeva, V. Synthesis and study of cathode materials based on carbon nanotubes for lithium-ion batteries. Inorg. Mater. Appl. Res. 2021, 12, 1281–1287. [Google Scholar] [CrossRef]
- Kamali, A.R.; Fray, D.J. Tin-based materials as advanced anode materials for lithium ion batteries: A review. Rev. Adv. Mater. Sci. 2011, 27, 14–24. [Google Scholar]
- Sankararaman, S.; Daigle, M.J.; Goebel, K. Uncertainty quantification in remaining useful life prediction using first-order reliability methods. IEEE Trans. Reliab. 2014, 63, 603–619. [Google Scholar] [CrossRef]
- Yang, F.; Song, X.; Dong, G.; Tsui, K.L. A coulombic efficiency-based model for prognostics and health estimation of lithium-ion batteries. Energy 2019, 171, 1173–1182. [Google Scholar] [CrossRef]
- Zhang, L.; Mu, Z.; Sun, C. Remaining useful life prediction for lithium-ion batteries based on exponential model and particle filter. IEEE Access 2018, 6, 17729–17740. [Google Scholar] [CrossRef]
- Shen, D.; Wu, L.; Kang, G.; Guan, Y.; Peng, Z. A novel online method for predicting the remaining useful life of lithium-ion batteries considering random variable discharge current. Energy 2021, 218, 119490. [Google Scholar] [CrossRef]
- Su, C.; Chen, H. A review on prognostics approaches for remaining useful life of lithium-ion battery. In Proceedings of the IOP Conference Series: Earth and Environmental Science; 2017; Volume 93, p. 012040. [Google Scholar]
- Safavi, V.; Mohammadi Vaniar, A.; Bazmohammadi, N.; Vasquez, J.C.; Guerrero, J.M. Battery Remaining Useful Life Prediction Using Machine Learning Models: A Comparative Study. Information 2024, 15, 124. [Google Scholar] [CrossRef]
- Khalid, A.; Sundararajan, A.; Acharya, I.; Sarwat, A.I. Prediction of li-ion battery state of charge using multilayer perceptron and long short-term memory models. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 19–21 June 2019; pp. 1–6. [Google Scholar]
- Kim, J.; Yu, J.; Kim, M.; Kim, K.; Han, S. Estimation of Li-ion battery state of health based on multilayer perceptron: As an EV application. IFAC-PapersOnLine 2018, 51, 392–397. [Google Scholar] [CrossRef]
- Das, A.; Kong, W.; Leach, A.; Mathur, S.; Sen, R.; Yu, R. Long-term forecasting with tide: Time-series dense encoder. arXiv 2023, arXiv:2304.08424. [Google Scholar]
- Ma, B.; Yang, S.; Zhang, L.; Wang, W.; Chen, S.; Yang, X.; Xie, H.; Yu, H.; Wang, H.; Liu, X. Remaining useful life and state of health prediction for lithium batteries based on differential thermal voltammetry and a deep-learning model. J. Power Sources 2022, 548, 232030. [Google Scholar] [CrossRef]
- De Brouwer, E.; Simm, J.; Arany, A.; Moreau, Y. GRU-ODE-Bayes: Continuous modeling of sporadically-observed time series. Adv. Neural Inf. Process. Syst. 2019, 32, 7379–7390. [Google Scholar]
- Chen, X. A novel transformer-based DL model enhanced by position-sensitive attention and gated hierarchical LSTM for aero-engine RUL prediction. Sci. Rep. 2024, 14, 10061. [Google Scholar] [CrossRef]
- Chen, S.A.; Li, C.L.; Yoder, N.; Arik, S.O.; Pfister, T. Tsmixer: An all-mlp architecture for time series forecasting. arXiv 2023, arXiv:2303.06053. [Google Scholar]
- Gong, Z.; Tang, Y.; Liang, J. Patchmixer: A patch-mixing architecture for long-term time series forecasting. arXiv 2023, arXiv:2310.00655. [Google Scholar]
- Hwang, S.W.; Chung, H.; Lee, T.; Kim, J.; Kim, Y.; Kim, J.C.; Kwak, H.W.; Choi, I.G.; Yeo, H. Feature importance measures from random forest regressor using near-infrared spectra for predicting carbonization characteristics of kraft lignin-derived hydrochar. J. Wood Sci. 2023, 69, 1. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Zhang, M.; Kang, G.; Wu, L.; Guan, Y. A method for capacity prediction of lithium-ion batteries under small sample conditions. Energy 2022, 238, 122094. [Google Scholar] [CrossRef]
- Xiao, B.; Liu, Y.; Xiao, B. Accurate state-of-charge estimation approach for lithium-ion batteries by gated recurrent unit with ensemble optimizer. IEEE Access 2019, 7, 54192–54202. [Google Scholar] [CrossRef]
- Shi, Z.; Chehade, A. A dual-LSTM framework combining change point detection and remaining useful life prediction. Reliab. Eng. Syst. Saf. 2021, 205, 107257. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries. IEEE Trans. Veh. Technol. 2018, 67, 5695–5705. [Google Scholar] [CrossRef]
| Hyper-Parameter | Range of Values |
|---|---|
| Patch size | {2, 4, 8} |
| Learning rate | {0.0001, 0.0005, 0.001} |
| Dropout | {0.05, 0.1, 0.2} |
| Length of patch | {2, 4, 8} |
| # of mixer blocks | {1, 2, 3, 4} |
| # of principal features | {1,2,4,6,8,10,12,14,16} |
| Methods | MAE (Ah) | RMSE (Ah) | MAPE (%) | ARE (%) |
|---|---|---|---|---|
| Transformer | 0.055 | 0.073 | 3.697 | 9.589 |
| Informer | 0.049 | 0.063 | 3.281 | 4.110 |
| MLP | 0.050 | 0.066 | 3.402 | 6.393 |
| DLinear | 0.041 | 0.052 | 2.732 | 3.196 |
| IIP-Mixer | 0.037 | 0.048 | 2.480 | 1.370 |
| Methods | MAE(Ah) | RMSE(Ah) | ARE |
|---|---|---|---|
| LSTM [42] | 0.083 | 0.091 | 0.265 |
| Dual-LSTM [41] | 0.082 | 0.088 | 0.256 |
| GRU [40] | 0.081 | 0.092 | 0.304 |
| DeTransformer [13] | 0.071 | 0.080 | 0.225 |
| IIP-Mixer (ours) | 0.037 | 0.048 | 0.014 |
| Methods | Training | Testing | |
|---|---|---|---|
| Time | Memory | Step | |
| Transformer | L | ||
| Informer | 1 | ||
| MLP | 1 | ||
| DLinear | 1 | ||
| IIP-Mixer | 1 | ||
| Methods | MAE (Ah) | RMSE (Ah) | MAPE (%) | ARE (%) |
|---|---|---|---|---|
| w/o inter | 0.081 | 0.095 | 5.443 | 34.703 |
| w/o intra | 0.044 | 0.055 | 2.940 | 5.023 |
| IIP-Mixer | 0.037 | 0.048 | 2.480 | 1.370 |
| Methods | MAE (Ah) | RMSE (Ah) | MAPE (%) | ARE (%) |
|---|---|---|---|---|
| Serial heads (inter-first) | 0.063 | 0.076 | 4.258 | 15.068 |
| Serial heads (intra-first) | 0.045 | 0.056 | 3.032 | 4.110 |
| Parallel heads | 0.037 | 0.048 | 2.480 | 1.370 |
| Methods | MAE (Ah) | RMSE (Ah) | MAPE (%) | ARE (%) |
|---|---|---|---|---|
| w/o weighting | 0.039 | 0.049 | 2.562 | 1.370 |
| With weighting | 0.037 | 0.048 | 2.480 | 1.370 |
| Methods | MAE (Ah) | RMSE (Ah) | MAPE (%) | ARE (%) |
|---|---|---|---|---|
| Univariate | 0.042 | 0.054 | 2.822 | 3.653 |
| Multivariate (full) | 0.052 | 0.064 | 3.510 | 7.306 |
| Multivariate (principal) | 0.037 | 0.048 | 2.480 | 1.370 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, G.; Feng, L.; Guo, J.; Chen, Y. IIP-Mixer: Intra–Inter-Patch Mixing Architecture for Battery Remaining Useful Life Prediction. Energies 2024, 17, 3553. https://doi.org/10.3390/en17143553
Ye G, Feng L, Guo J, Chen Y. IIP-Mixer: Intra–Inter-Patch Mixing Architecture for Battery Remaining Useful Life Prediction. Energies. 2024; 17(14):3553. https://doi.org/10.3390/en17143553
Chicago/Turabian StyleYe, Guangzai, Li Feng, Jianlan Guo, and Yuqiang Chen. 2024. "IIP-Mixer: Intra–Inter-Patch Mixing Architecture for Battery Remaining Useful Life Prediction" Energies 17, no. 14: 3553. https://doi.org/10.3390/en17143553
APA StyleYe, G., Feng, L., Guo, J., & Chen, Y. (2024). IIP-Mixer: Intra–Inter-Patch Mixing Architecture for Battery Remaining Useful Life Prediction. Energies, 17(14), 3553. https://doi.org/10.3390/en17143553






