Effect of Thickness on the Breakdown Characteristics of Organic Insulation Materials under Microsecond Pulse Voltage
Abstract
1. Introduction
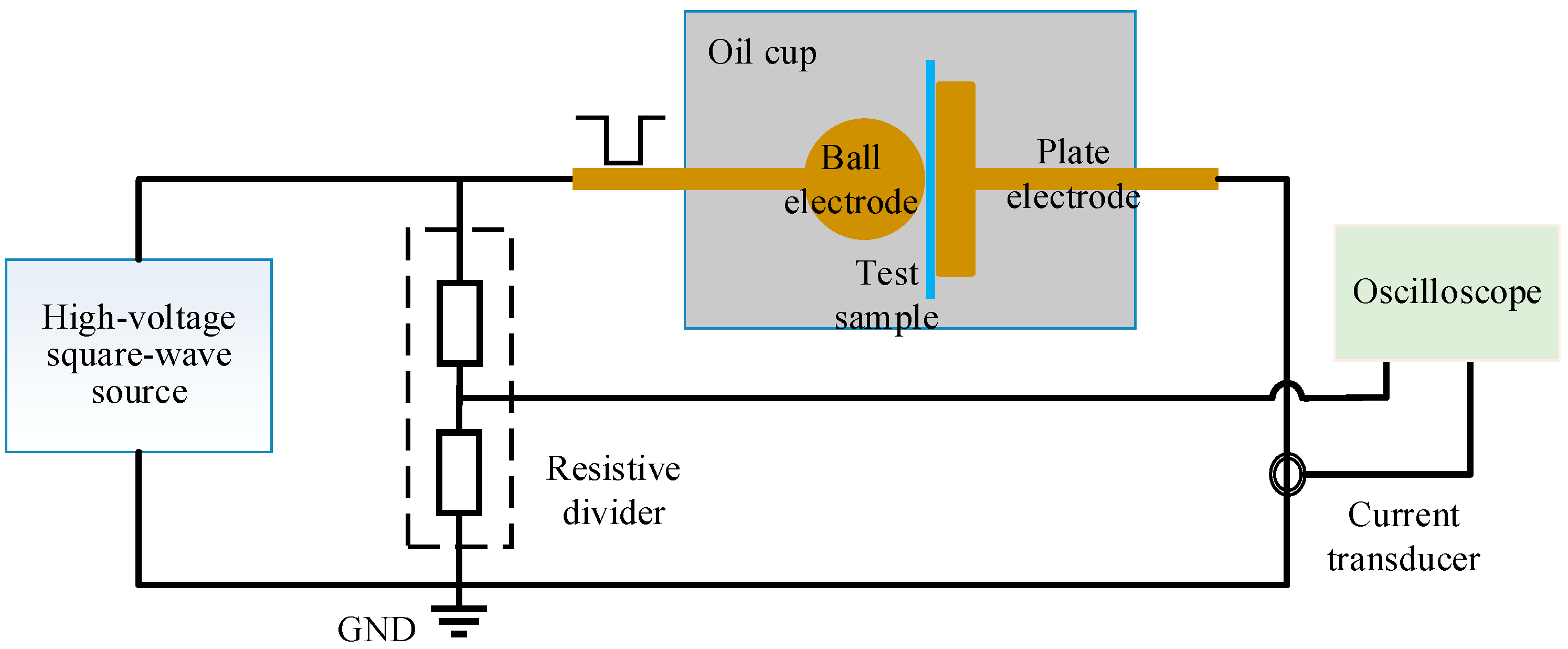
2. Experimental Setup
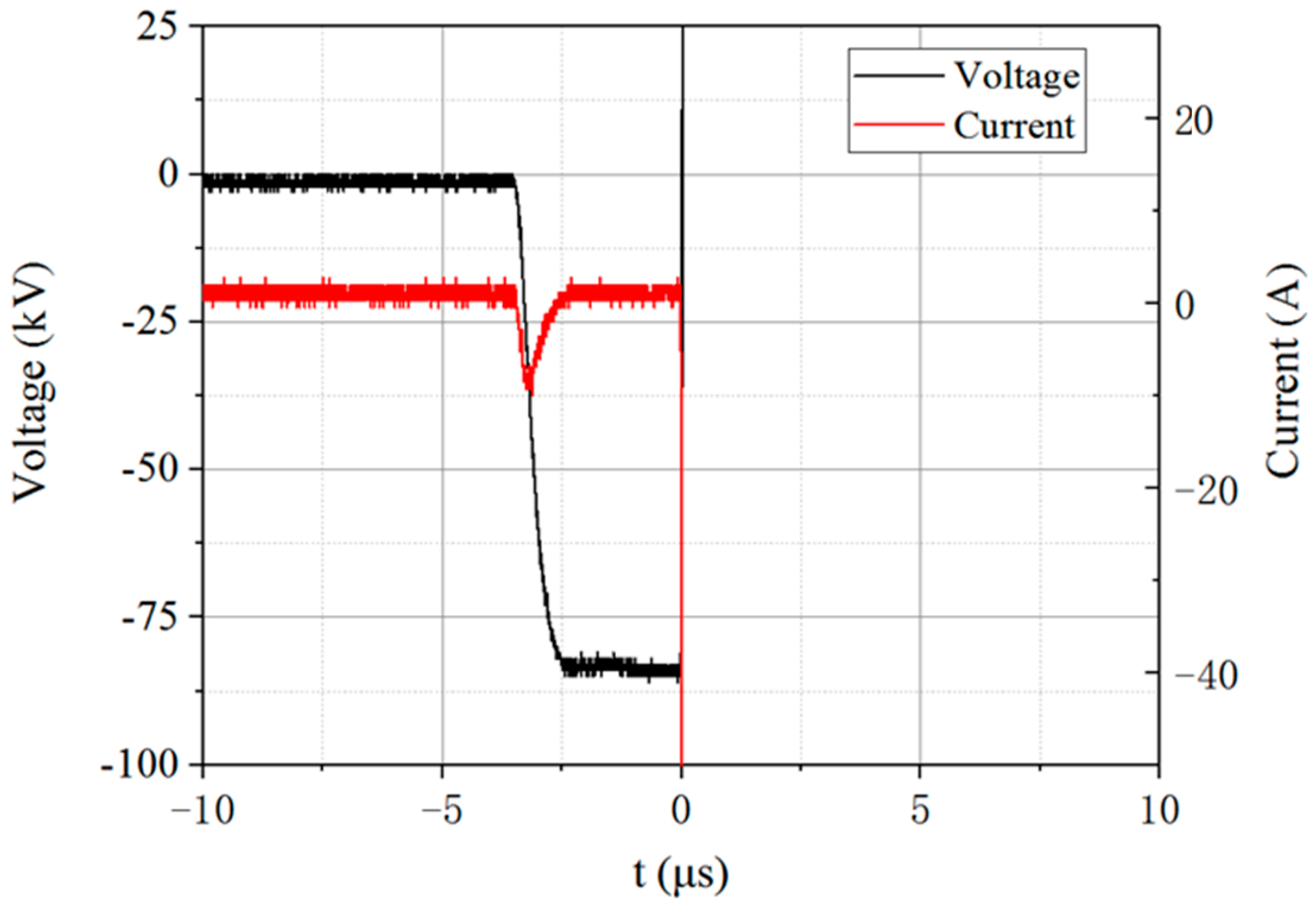
3. Experimental Results
4. Effect of Thickness on Breakdown Characteristics
4.1. Theoretical Analysis
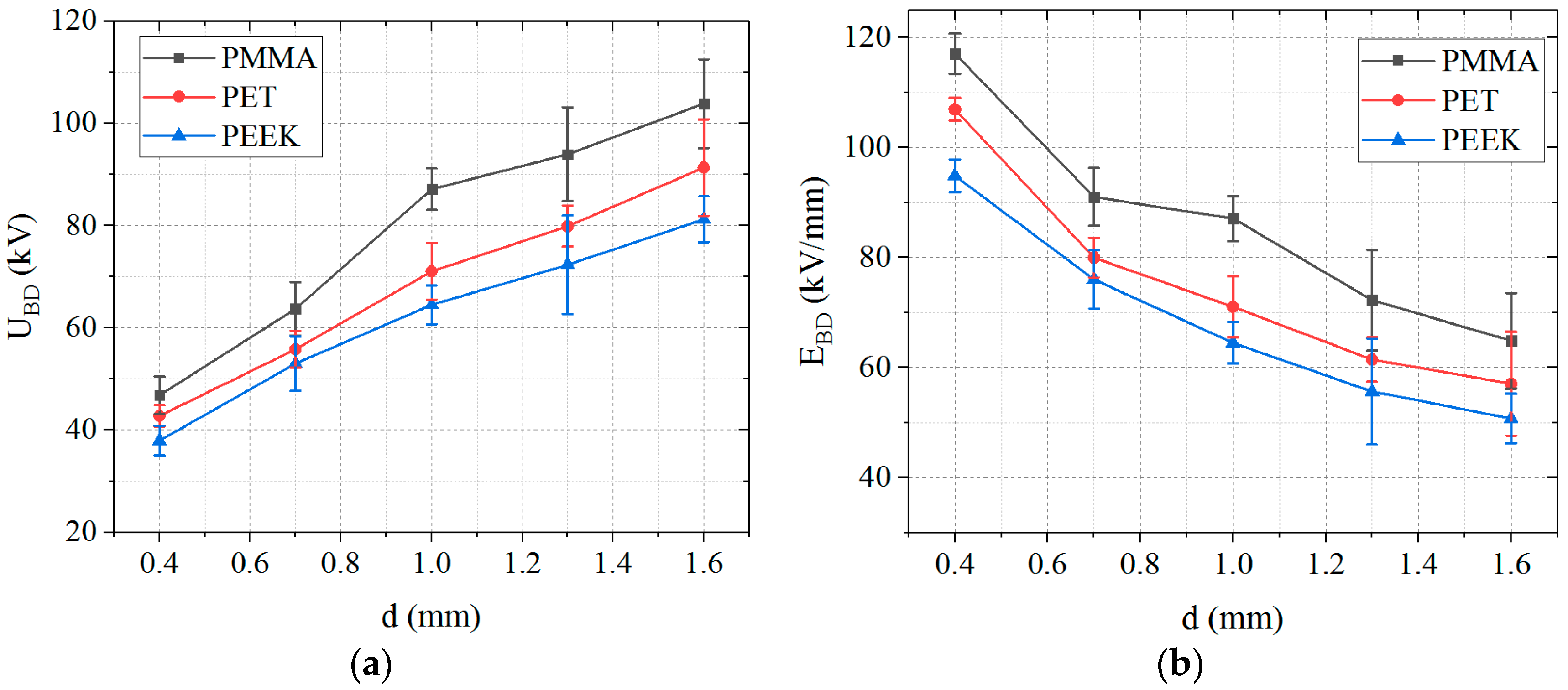
4.2. Analysis of the Relationship between EBD and d
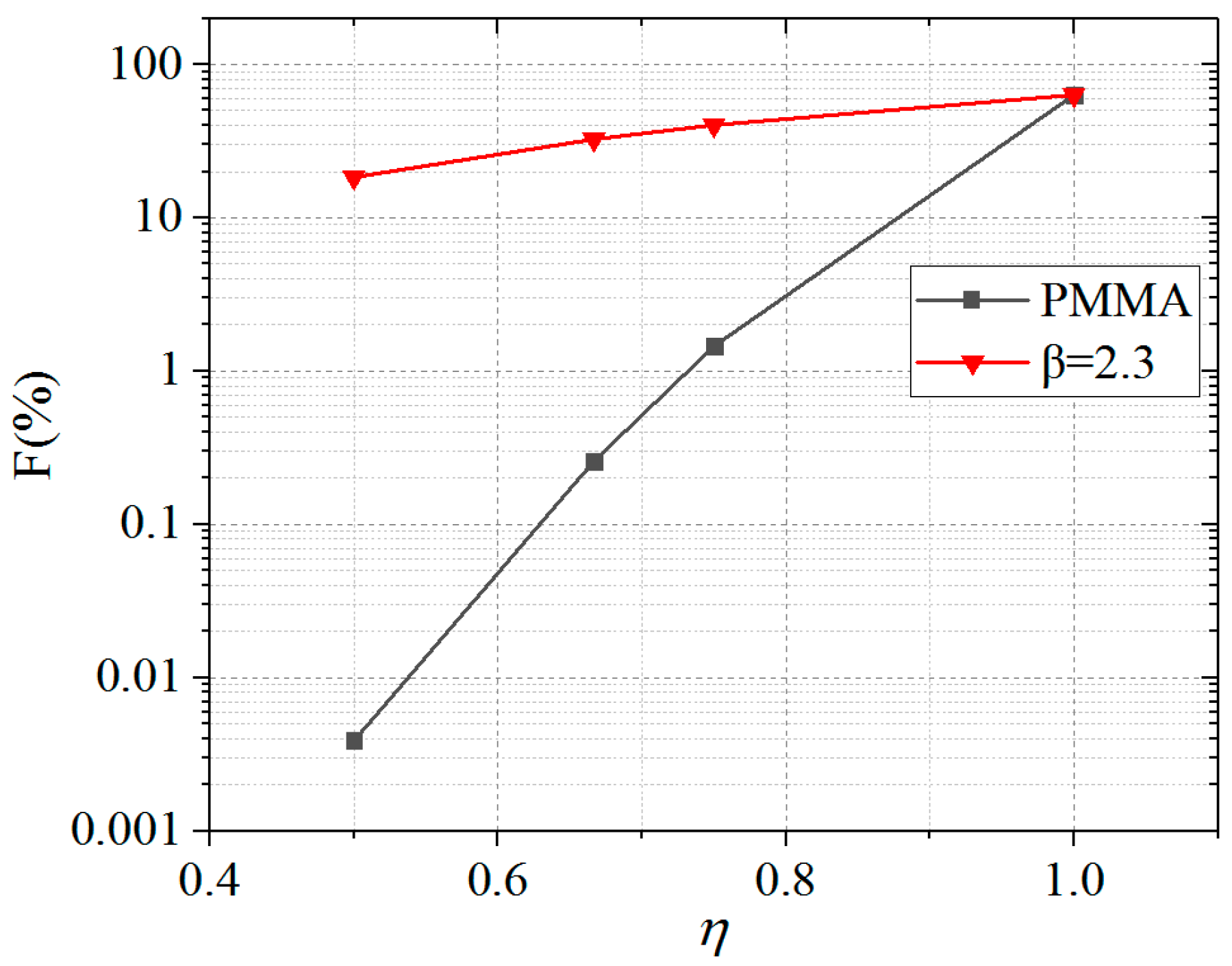
4.3. Prediction of Breakdown Probability of OIM under MSPV
5. Discussion on the Breakdown Mechanism of OIM under MSPV
5.1. Electric Breakdown
5.2. The Space Charge Effect
5.3. Pulse Thermal Breakdown
5.4. Electromechanical Breakdown
5.5. Breakdown Mechanism Speculaiton
6. Analysis of Energy Accumulation Characteristics of OIM under MSPV
6.1. Theoretical Analysis of Energy Accumulation Characteristics
6.2. Analysis of Calculation Results of Energy Accumulation Characteristics
7. Conclusions
- (1)
- Under MSPV, the UBD of the three materials increased with the increment of d, and the corresponding EBD decreased with the increment of d. The decrease value of EBD became smaller with increasing d.
- (2)
- The relationship between the characteristic EBD and d satisfied the inverse power model for all the three materials under MSPV, and their inverse power coefficients were close to each other, with a value of about 1/2.3. This value was much larger than the inverse power coefficient under nanosecond pulse voltage, which meant that the decrease trend of EBD with the increase of d under MSPV was more pronounced than that under nanosecond pulse voltage, indicating a different breakdown mechanism of the OIMs under MSPV.
- (3)
- A general breakdown probability prediction model of the OIMs under MSPV was established based on the Weibull distribution and β = 2.3, which could be applied to guide engineering designs in the absence of basic test data.
- (4)
- The breakdown mechanism of the OIMs under MSPV was attributed to an energy-related composite physical breakdown mechanism, which was verified through analyses of the energy accumulation characteristics as well as the experimental evidence of the little influence of pulse width on EBD under MSPV.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, X. High Pulsed Power Technology; National Defense Industry Press: Beijing, China, 2007; pp. 1–3. [Google Scholar]
- Martin, J.C. Nanosecond pulse techniques. Proc. IEEE 1992, 80, 934–945. [Google Scholar] [CrossRef]
- Akiyama, H.; Sakugawa, T.; Namihira, T.; Takaki, K.; Minamitani, Y.; Shimomura, N. Industrial applications of pulsed power technology. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 1051–1064. [Google Scholar] [CrossRef]
- Barber, P.; Balasubramanian, S.; Anguchamy, Y.; Gong, S.; Wibowo, A.; Gao, H.; Ploehn, H.J.; Zur Loye, H.C. Polymer composite and nanocomposite dielectric materials for pulse power energy storage. Materials 2009, 2, 1697–1733. [Google Scholar] [CrossRef]
- Jin, S.; Chen, J.; Li, Z.; Zhang, C.; Zhao, Y.; Fang, Z. Novel RDD pulse shaping method for high-power high-voltage pulse current power supply in DBD application. IEEE Trans. Ind. Electron. 2022, 69, 12653–12664. [Google Scholar] [CrossRef]
- Korovin, S.D.; Rostov, V.V.; Polevin, S.D.; Pegel, I.V.; Schamiloglu, E.; Fuks, M.I.; Barker, R.J. Pulsed power-driven high-power microwave sources. Proc. IEEE 2004, 92, 1082–1095. [Google Scholar] [CrossRef]
- Hosseinzadehtaher, M.; Khan, A.; Easley, M.; Shadmand, M.B.; Fajri, P. Self-healing predictive control of battery system in naval power system with pulsed power loads. IEEE Trans. Energy Convers. 2020, 36, 1056–1069. [Google Scholar] [CrossRef]
- Zhao, L.; Su, J.; Liu, C. Review of developments on polymers’ breakdown characteristics and mechanisms on a nanosecond time scale. AIP Adv. 2020, 10, 035206. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, G.Z.; Su, J.C.; Pan, Y.F.; Zhang, X.B. Investigation of thickness effect on electric breakdown strength of polymers under nanosecond pulses. IEEE Trans. Plasma Sci. 2011, 7, 1613–1618. [Google Scholar] [CrossRef]
- Mankowski, J.; Dickens, J.; Kristiansen, M. A subnanosecond high voltage pulser for the investigation of dielectric breakdown. In Proceedings of the 11th IEEE International Pulsed Power Conference, Baltimore, MA, USA, 29 June–2 July 1997. [Google Scholar]
- Zhao, L.; Su, J.C.; Pan, Y.F.; Zhang, X.B. The effect of polymer type on electric breakdown strength on a nanosecond time scale. Chin. Phys. B 2012, 21, 033102. [Google Scholar] [CrossRef]
- Guo, R.; Wang, Z.; He, C.; Zhang, X.; Jin, Y.; Sun, Z.; Li, J. Experimental study on the effect of lightning impulse oscillation frequency on pressboard flashover in oil. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 431–439. [Google Scholar] [CrossRef]
- Ni, H.; Zhang, Q.; Guo, C.; Wen, T. Breakdown and streamer behavior in double-layer oil-paper insulation under impulses of varying front time. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 103–111. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, G.; Guo, R.; Yang, F. The breakdown characteristics of thermostable insulation materials under high-frequency square waveform. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 1073–1080. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, G.; Guo, R.; Wan, L.; Liu, Y.; Yang, F. Breakdown characteristics of heat-resistant inter-turn insulation materials in high-frequency transformers. High Volt. Eng. 2020, 46, 657–665. [Google Scholar]
- Qian, K.; Su, P.; Wu, J.D.; Yin, Y. The effect of thickness on breakdown strength in high voltage direct current cable insulation at different temperatures. Proc. CSEE 2018, 38, 7121–7130. [Google Scholar]
- Cygan, S.; Laghari, J.R. Dependence of the electric strength on thickness area and volume of polypropylene. IEEE Trans. Electr. Insul. 1987, 22, 835–837. [Google Scholar] [CrossRef]
- Primo, V.A.; García, B.; Burgos, J.C.; Pérez-Rosa, D. Investigation of the lightning impulse breakdown voltage of mineral oil based Fe3O4 nanofluids. Coatings 2019, 9, 799. [Google Scholar] [CrossRef]
- Yoshino, K.; Harada, S.; Kyokane, J.; Inuishi, Y. Electrical properties of hexatriacontane single crystal. J. Phys. D Appl. Phys. 1979, 12, 1535. [Google Scholar] [CrossRef]
- IEC 60243-1:2013; Electric Strength of Insulating Materials-Test Methods—Part 1: Test at Power Frequencies. IEC: Geneva, Switzerland, 2013.
- IEC 60243-3:2013; Electric Strength of Insulating Materials-Test Methods—Part 3: Additional Requirements for 1.2/50 μs Impulse Tests. IEC: Geneva, Switzerland, 2013.
- Mazzanti, G. Reliability evaluation of insulation subjected to harmonic voltages within the limits set by international standards. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 2037–2046. [Google Scholar] [CrossRef]
- Baek, S.M.; Joung, J.M.; Kim, S.H. Electrical insulation design and withstand test of model coils for 6.6 kV class HTSFCL. IEEE Trans. Appl. Supercond. 2004, 14, 843–846. [Google Scholar] [CrossRef]
- Rozhkov, V.M. Electrical breakdown in solid insulators: Duration of the discharge channel formation. Tech. Phys. 2003, 48, 48–51. [Google Scholar] [CrossRef]
- Zhao, L. Theoretical calculation on formative time lag in polymer breakdown on a nanosecond time scale. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 1051–1058. [Google Scholar] [CrossRef]
- Zhong, L.; Li, S.; Xu, C. Engineering Dielectric Physics and Dielectric Phenomena; Xi’an Jiaotong University Press: Xi’an, China, 2013. [Google Scholar]
- Watson, D.B. The impulse electric strength of polythene as a function of voltage rise time. J. Phys. D Appl. Phys. 1971, 4, L19. [Google Scholar] [CrossRef]
- Wang, H.; Ma, L.; Zeng, Z. Electric breakdown model for dielectric strength of 10 um level polyester foil. High Power Laser Part. Beams 2008, 20, 1749–1752. [Google Scholar]
- Pitike, K.C.; Hong, W. Phase-field model for dielectric breakdown in solids. J. Appl. Phys. 2014, 115, 044101. [Google Scholar] [CrossRef]


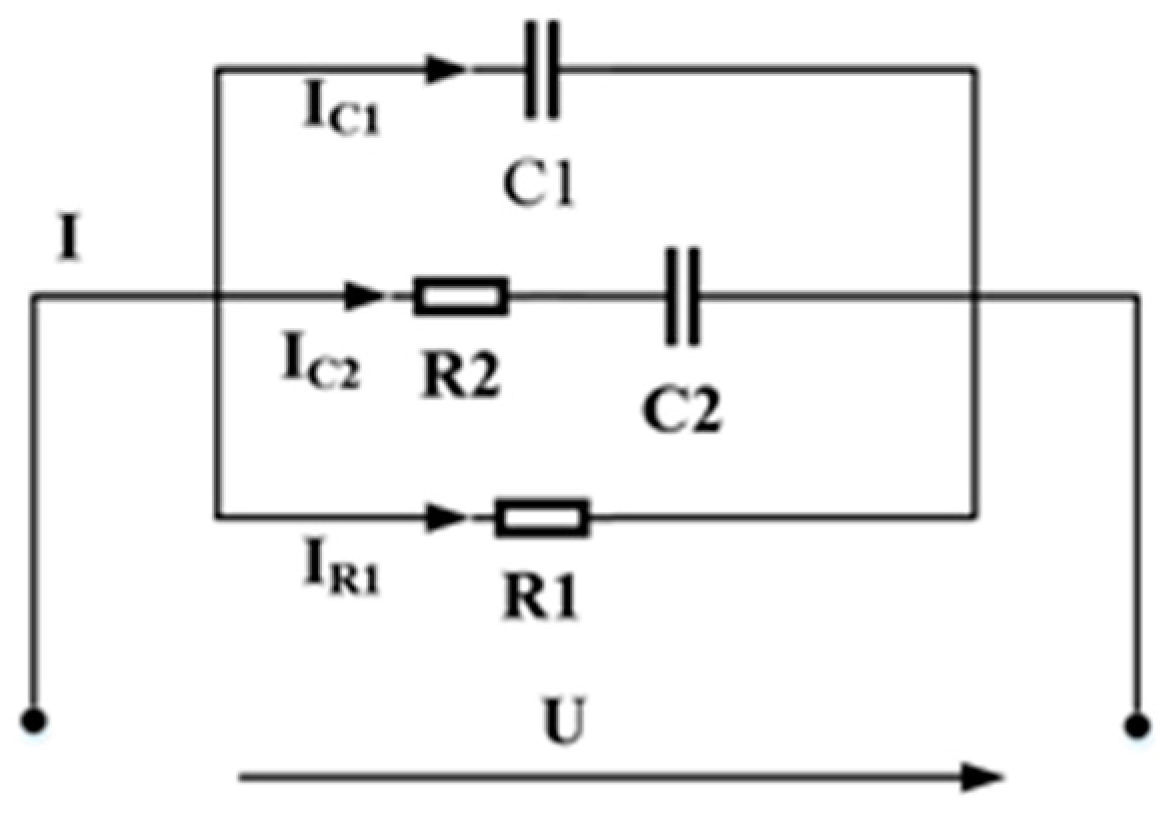
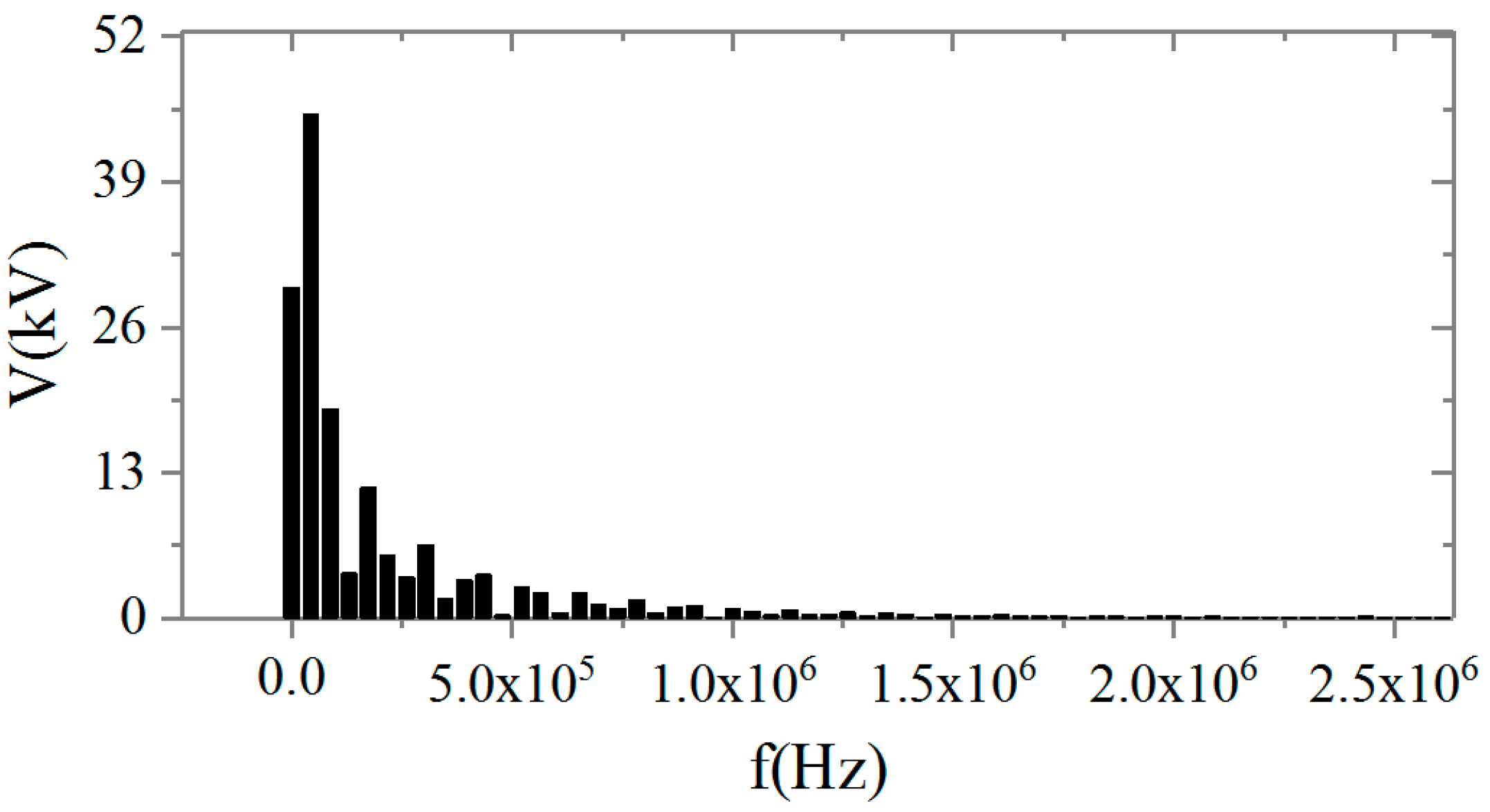
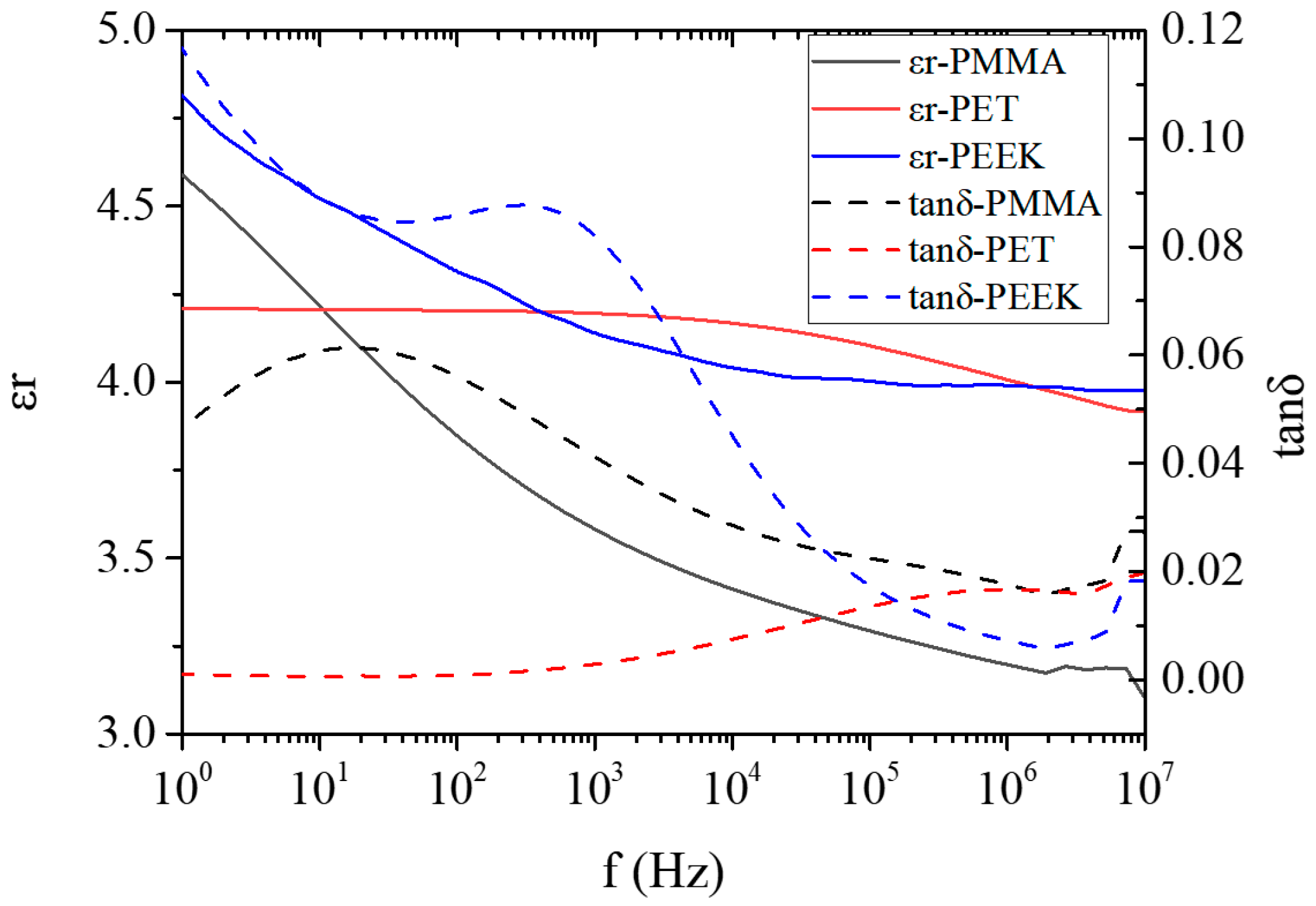

| Material | d (mm) | α (kV/mm) | β | βm |
|---|---|---|---|---|
| PMMA | 0.4 | 121.15 | 14.41 | 14.69 |
| 0.7 | 94.90 | 13.97 | ||
| 1 | 89.30 | 17.89 | ||
| 1.3 | 75.06 | 13.71 | ||
| 1.6 | 67.32 | 13.47 | ||
| PET | 0.4 | 109.43 | 21.62 | 18.43 |
| 0.7 | 82.24 | 17.64 | ||
| 1 | 73.85 | 15.39 | ||
| 1.3 | 62.77 | 23.98 | ||
| 1.6 | 59.65 | 13.49 | ||
| PEEK | 0.4 | 98.37 | 12.97 | 13.11 |
| 0.7 | 81.42 | 11.22 | ||
| 1 | 66.37 | 19.55 | ||
| 1.3 | 58.53 | 9.79 | ||
| 1.6 | 52.29 | 12.00 |
| Material | 1/β | Goodness of Fit (R2) |
|---|---|---|
| PMMA | 1/2.45 | 0.97 |
| PET | 1/2.27 | 0.99 |
| PEEK | 1/2.17 | 0.99 |
| Material | Average EBD (kV/mm) | ||
|---|---|---|---|
| 4 μs | 6 μs | 8 μs | |
| PMMA | 86.57 | 87.94 | 87.11 |
| PET | 72.31 | 70.33 | 71.06 |
| PEEK | 63.65 | 65.87 | 64.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Liu, X.; Ru, J.; Zeng, Z.; Bian, H.; Li, Y.; Zhong, H.; Chen, L. Effect of Thickness on the Breakdown Characteristics of Organic Insulation Materials under Microsecond Pulse Voltage. Energies 2024, 17, 3538. https://doi.org/10.3390/en17143538
Li X, Liu X, Ru J, Zeng Z, Bian H, Li Y, Zhong H, Chen L. Effect of Thickness on the Breakdown Characteristics of Organic Insulation Materials under Microsecond Pulse Voltage. Energies. 2024; 17(14):3538. https://doi.org/10.3390/en17143538
Chicago/Turabian StyleLi, Xudong, Xin Liu, Jiasheng Ru, Zhibin Zeng, Haoran Bian, Yuefang Li, Hua Zhong, and Lei Chen. 2024. "Effect of Thickness on the Breakdown Characteristics of Organic Insulation Materials under Microsecond Pulse Voltage" Energies 17, no. 14: 3538. https://doi.org/10.3390/en17143538
APA StyleLi, X., Liu, X., Ru, J., Zeng, Z., Bian, H., Li, Y., Zhong, H., & Chen, L. (2024). Effect of Thickness on the Breakdown Characteristics of Organic Insulation Materials under Microsecond Pulse Voltage. Energies, 17(14), 3538. https://doi.org/10.3390/en17143538





