Fluid-Structure Numerical Study of an In-Pipe Axial Turbine with Circular Blades
Abstract
1. Introduction
- Providing the scientific literature with a methodology to analyze the hydrodynamic performance and structural (static, modal, and harmonic) behavior of an axial propeller-type turbine with circular blades for in-pipe installation in water distribution systems. Previous fluid–structure analyses reported in the scientific literature do not structurally study this type of turbine with a constant thickness curved blade, especially considering resonance and fatigue conditions for different materials which can be scaled to other types of turbomachines.
- Offering the scientific community a couple of open-source computational tools to perform the grid convergence study by applying the Grid Convergence Index method (GCI) recommended by The American Society of Mechanical Engineers (ASME) and provide the meridional coordinates of the circular blade to obtain its three-dimensional model.
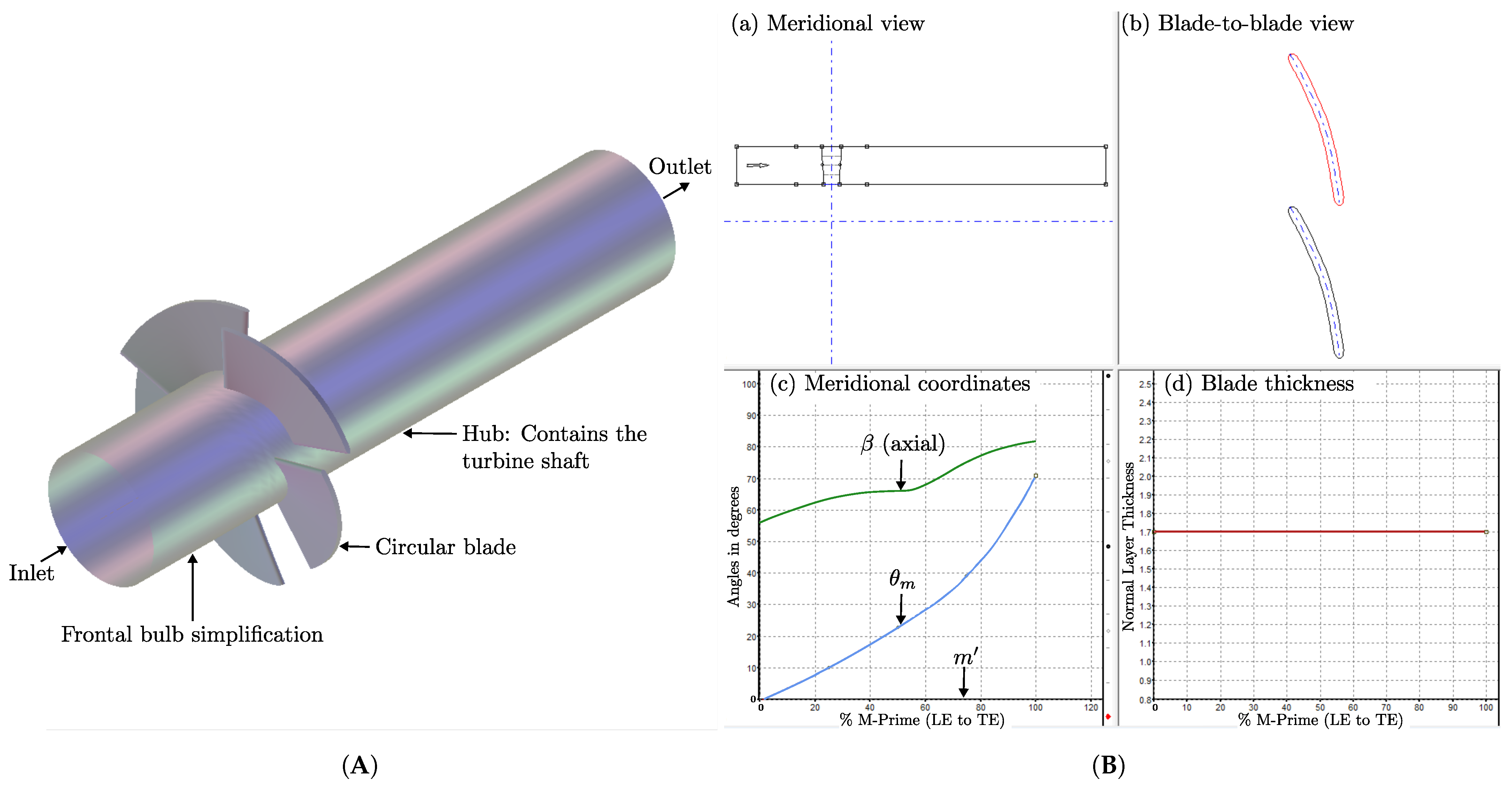
2. Circular Blade 3D Model
2.1. Design Parameters Selection
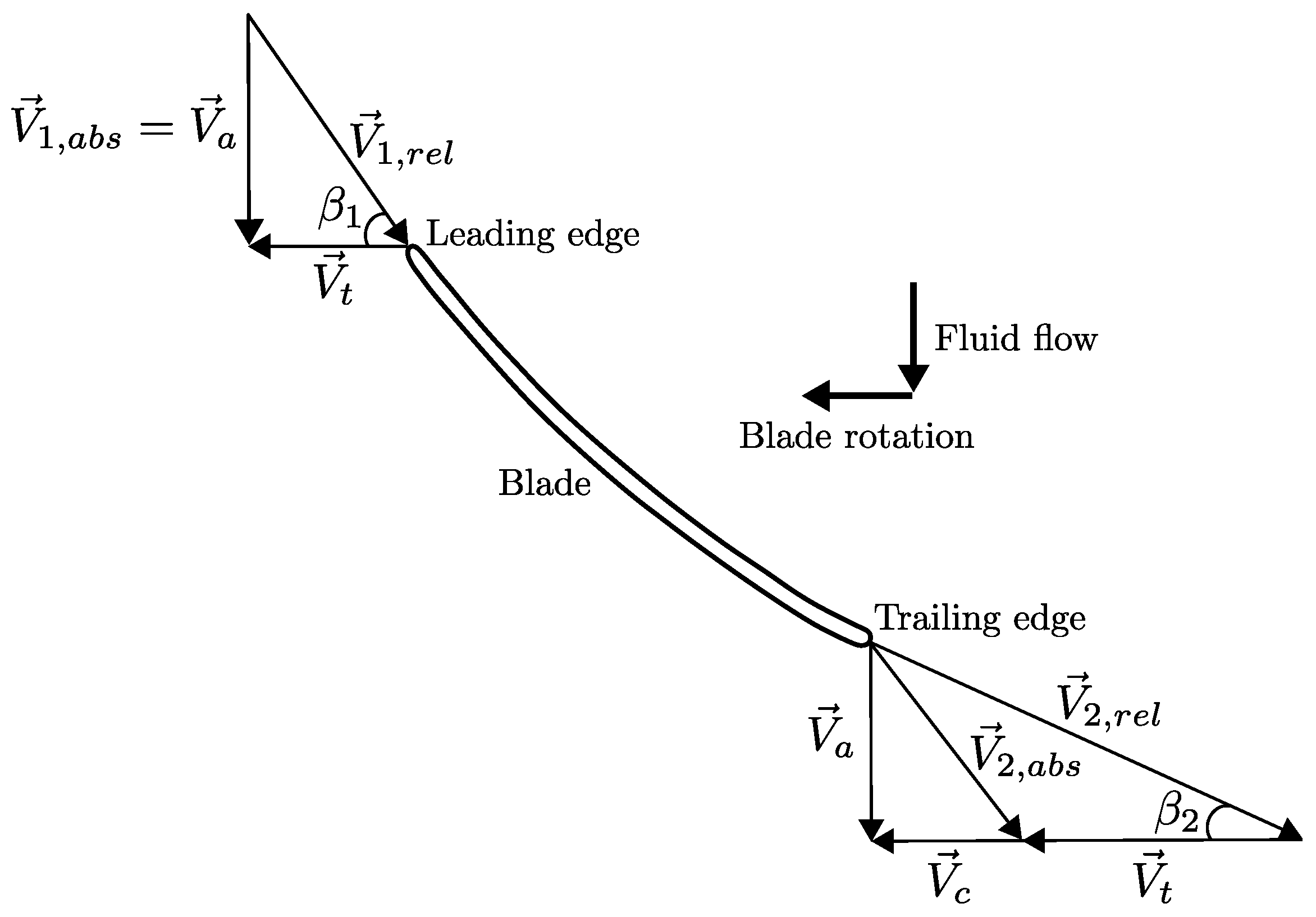
2.2. Theoretical Design
2.3. Design Methodology
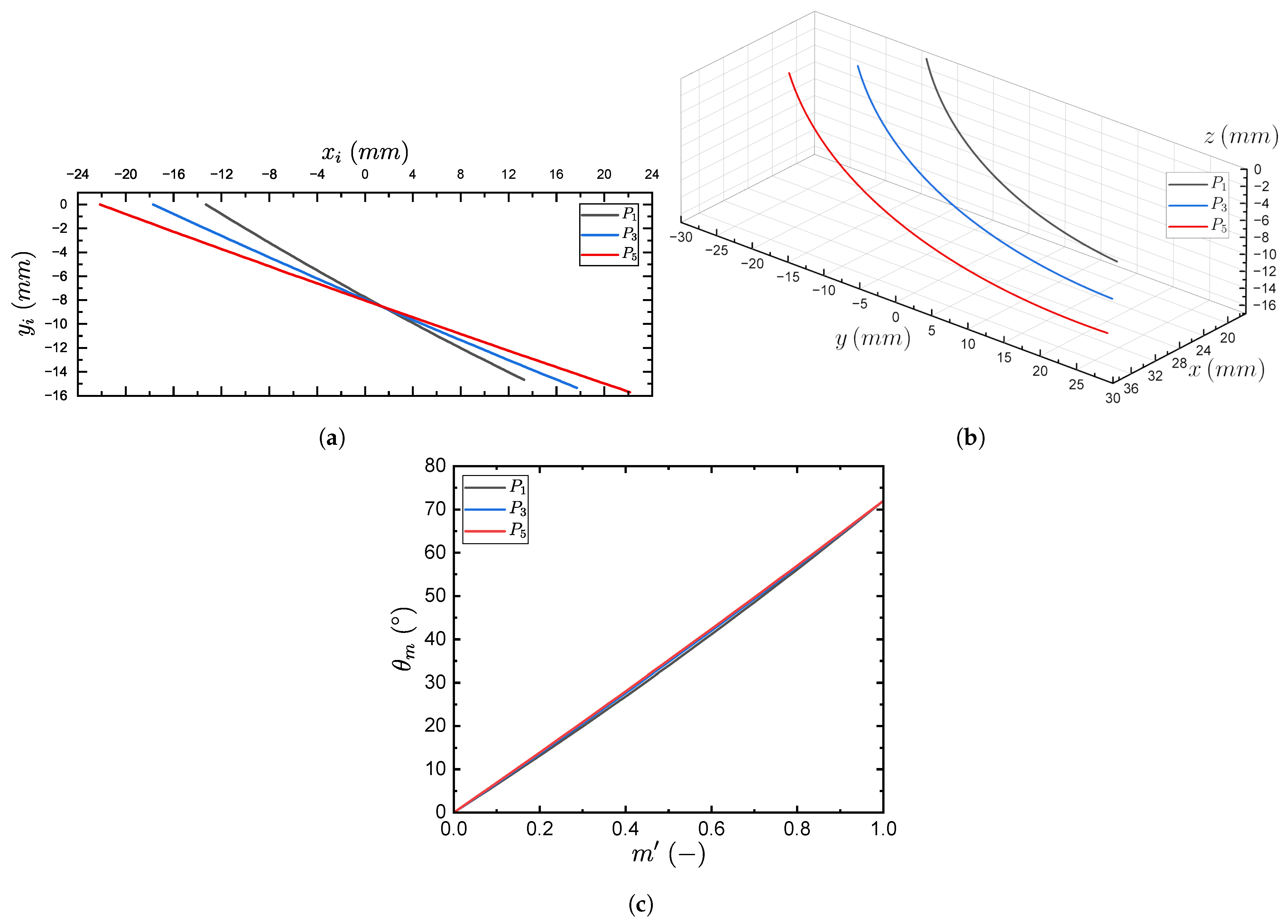
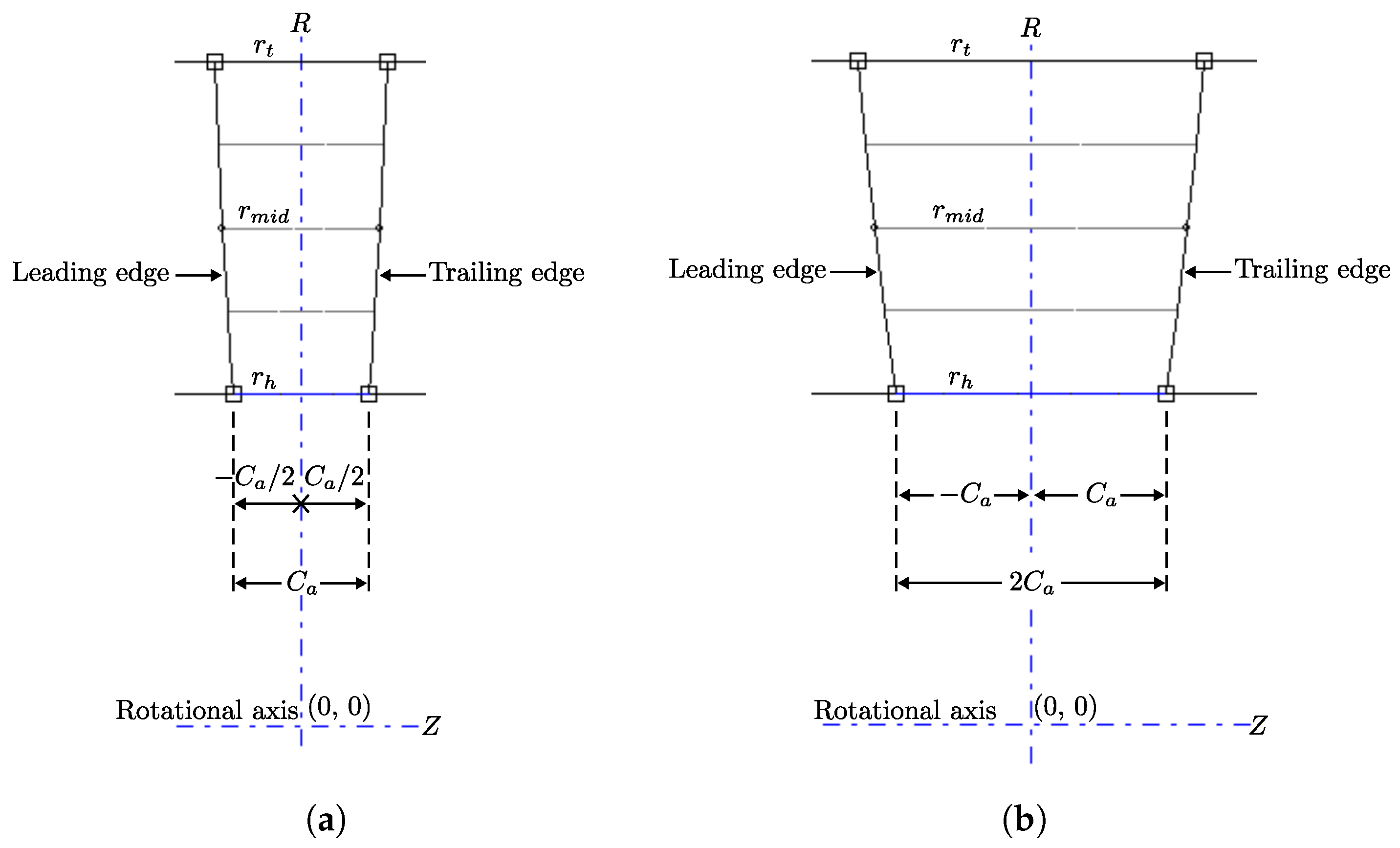
2.3.1. Coordinates Transformation
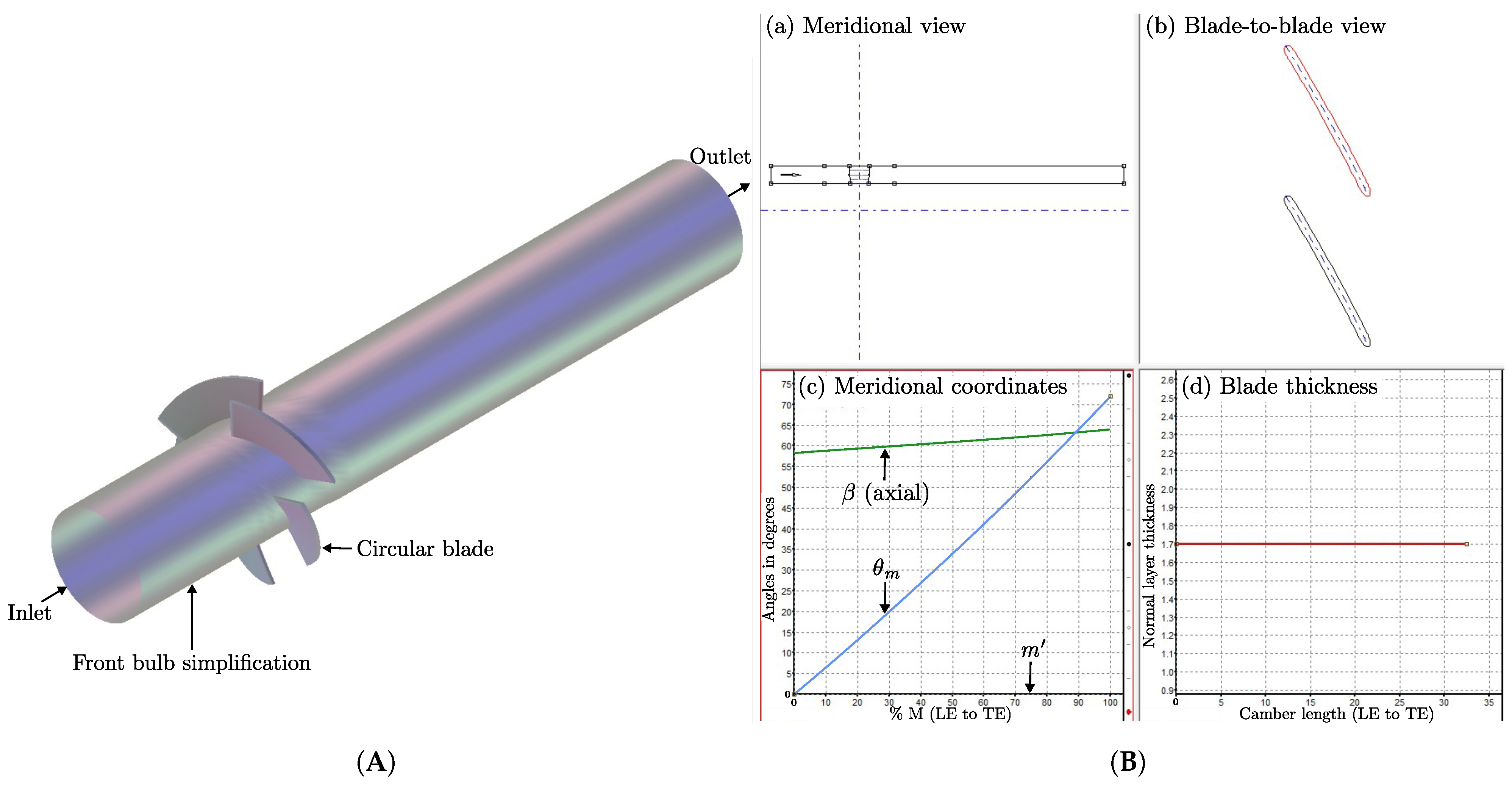
2.3.2. BladeGen Geometry Generation
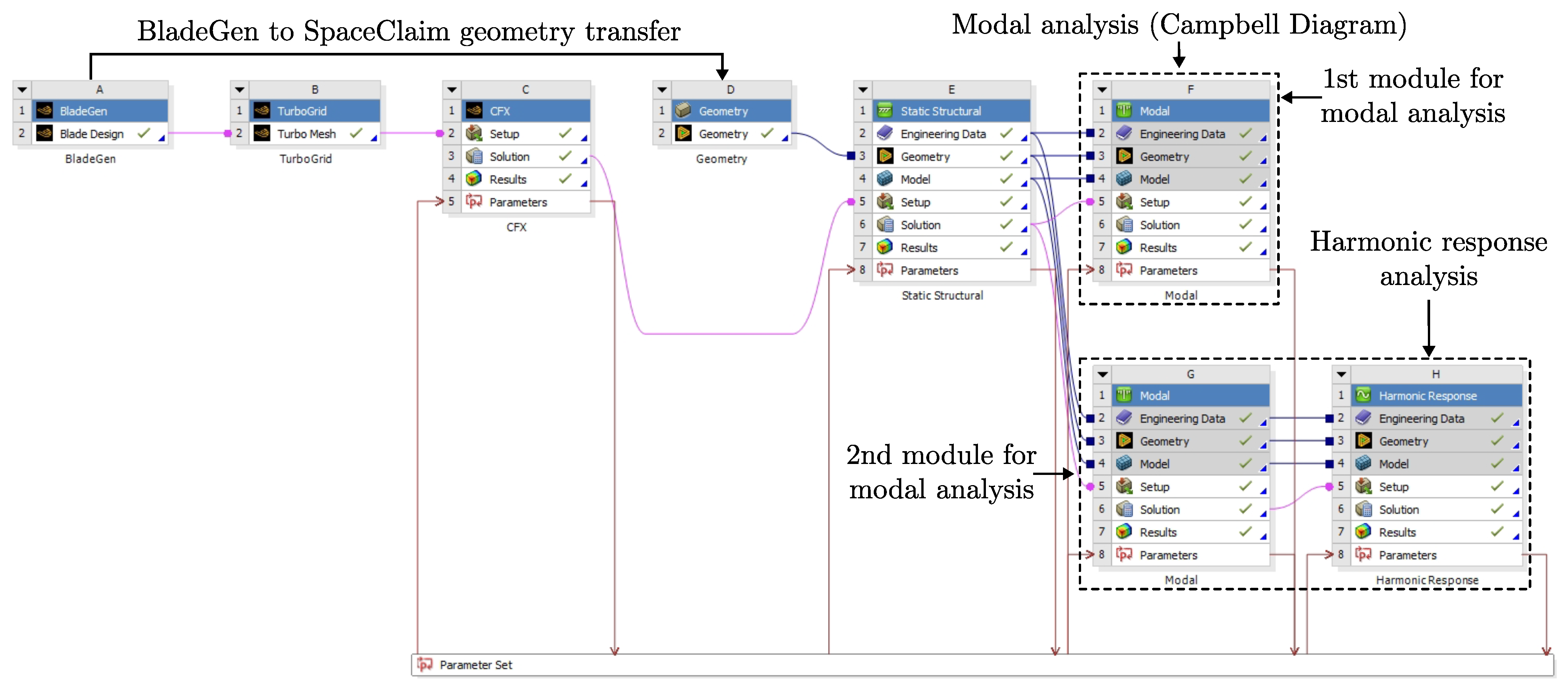
3. Fluid–Structure Interaction (FSI) Simulations
3.1. Proposed Methodology
3.2. CFD Parametric Simulations
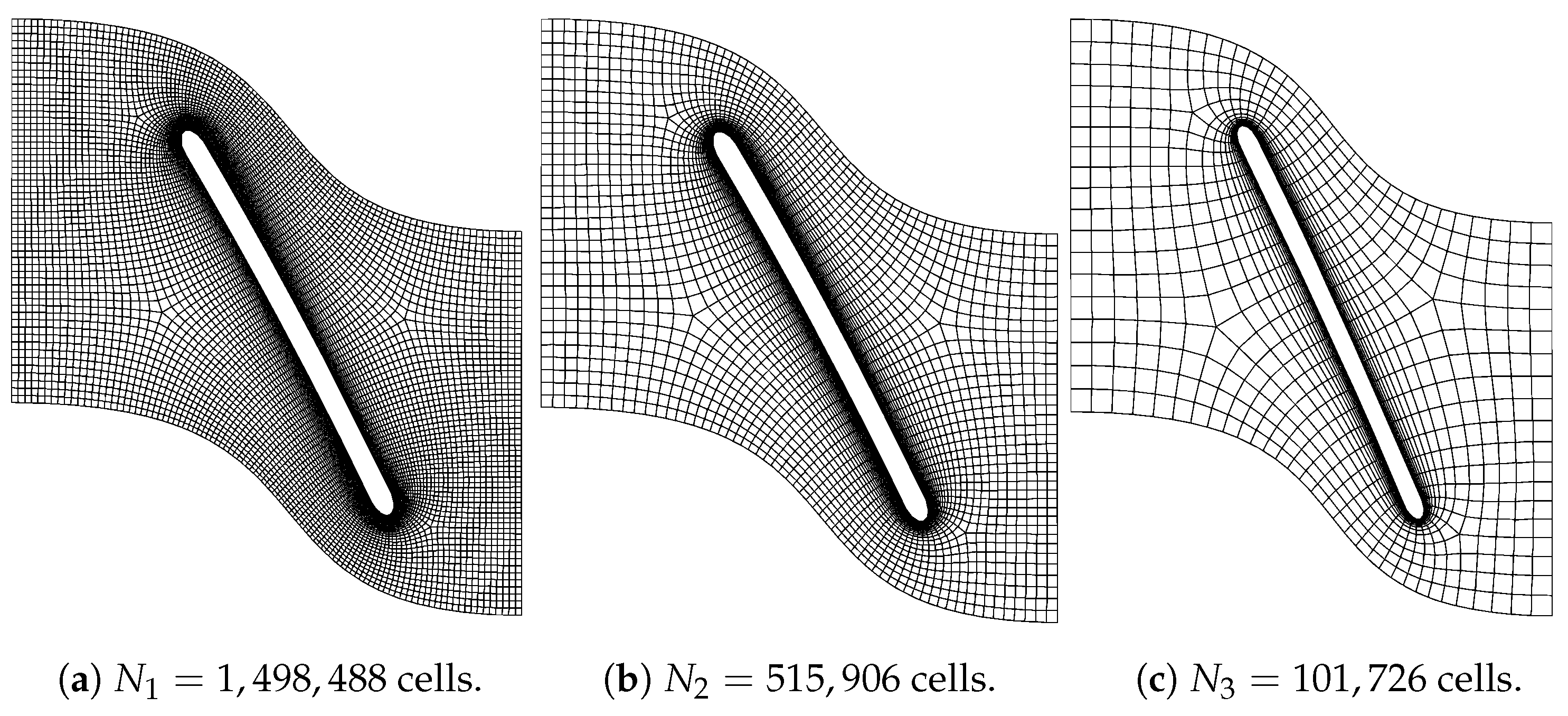
3.2.1. Spatial Discretization
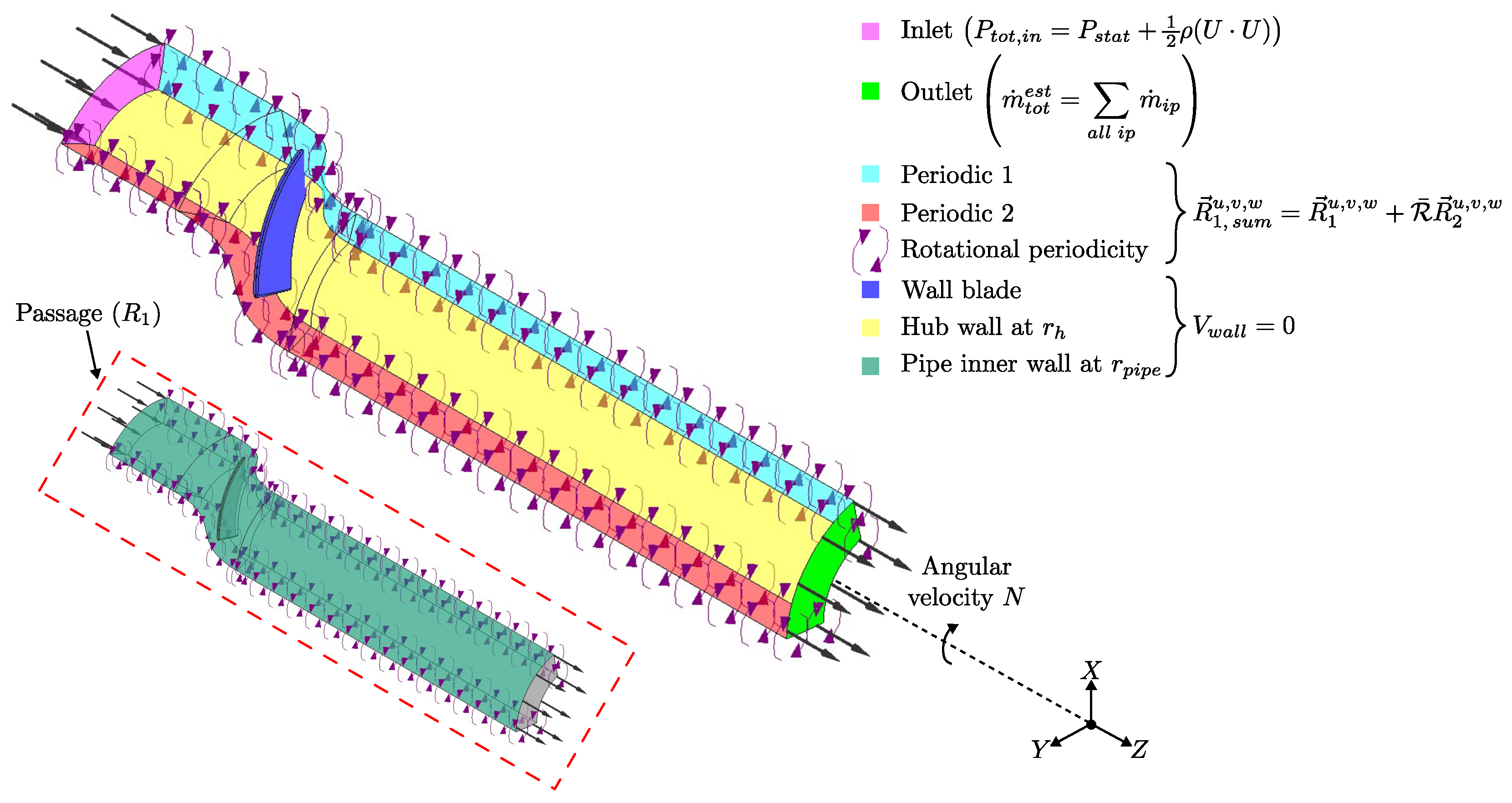
3.2.2. CFD Boundary Conditions and Parametric Study
3.3. Structural Parametric Simulations
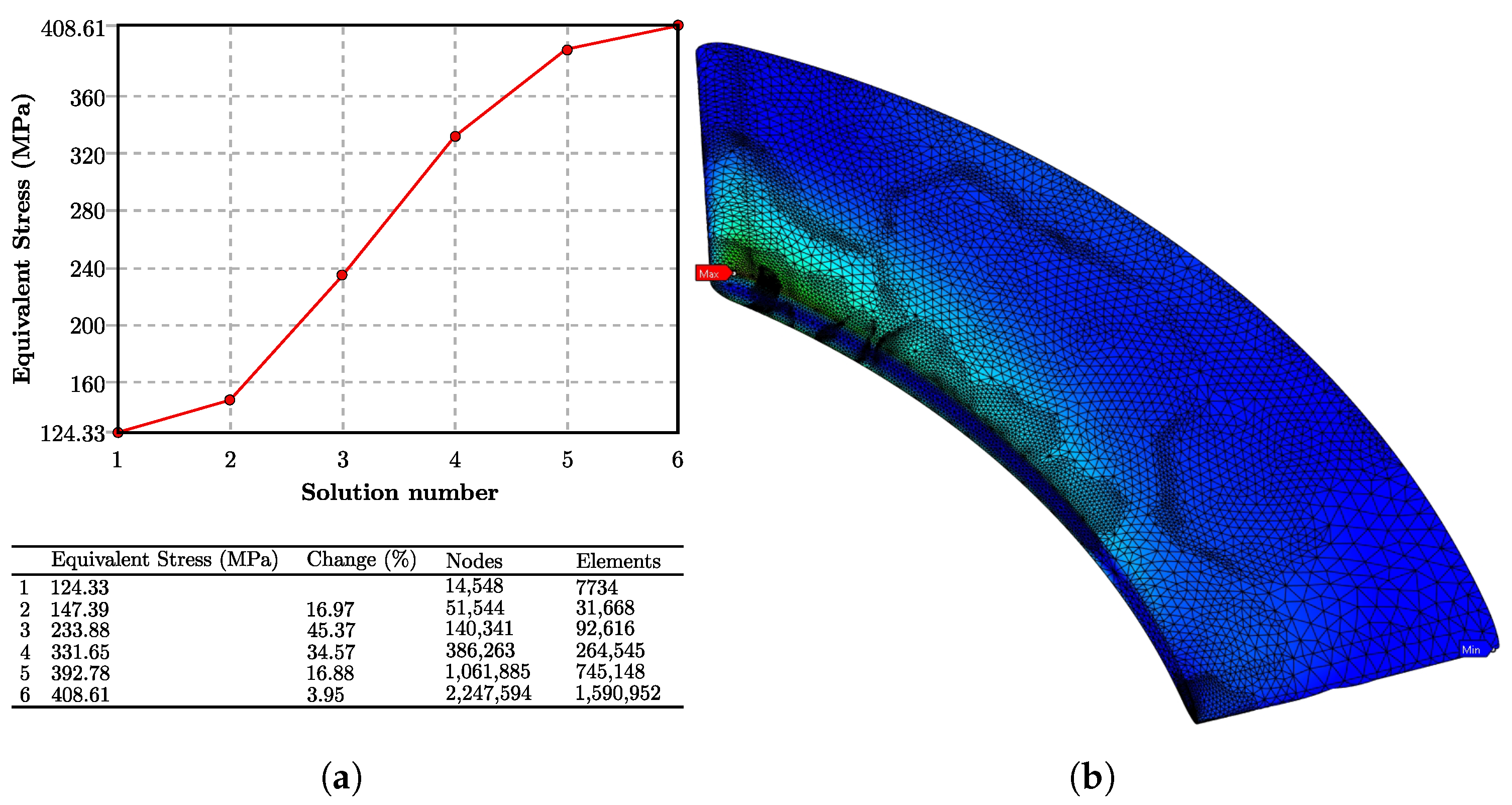
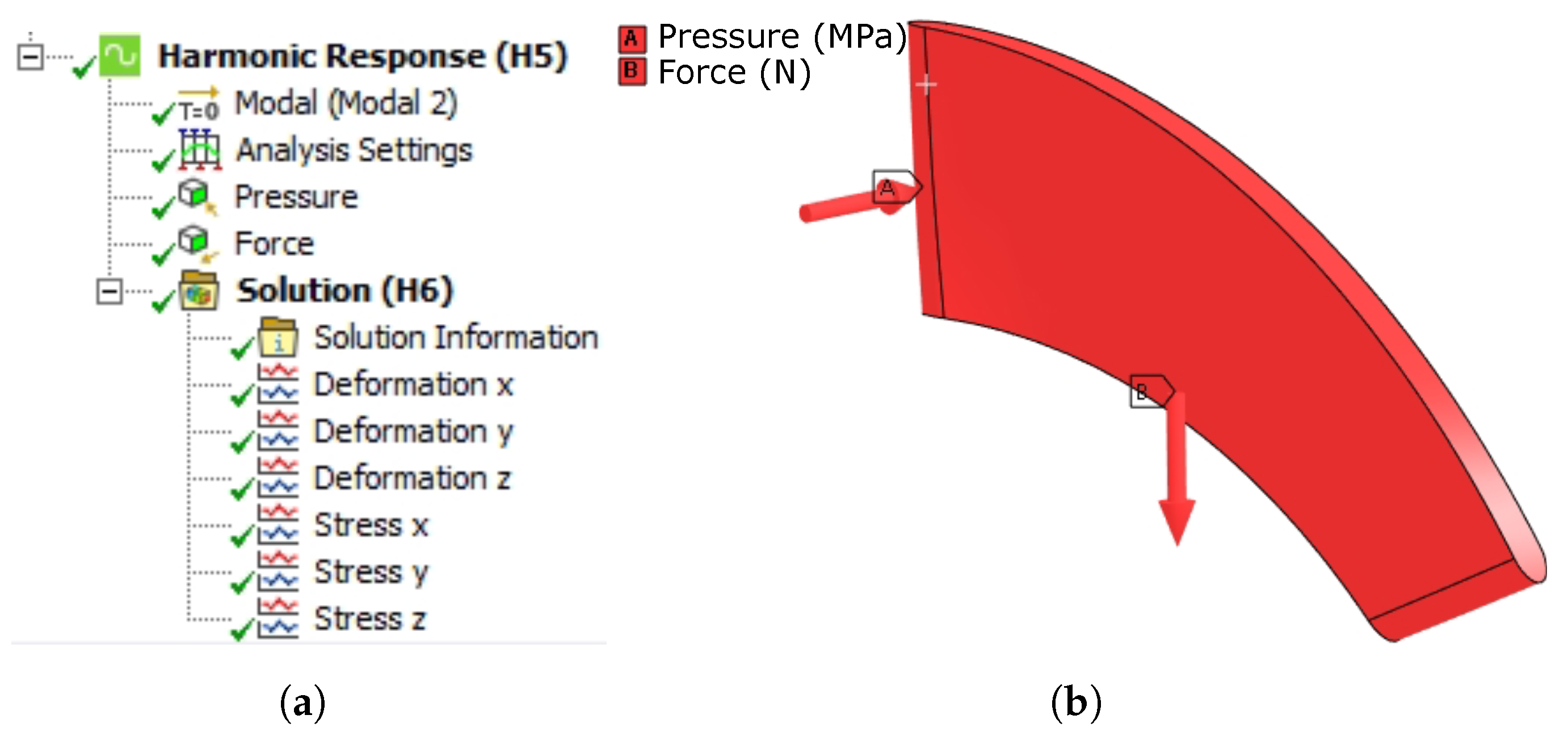
3.3.1. Static Structural
3.3.2. Dynamic Structural
4. Results
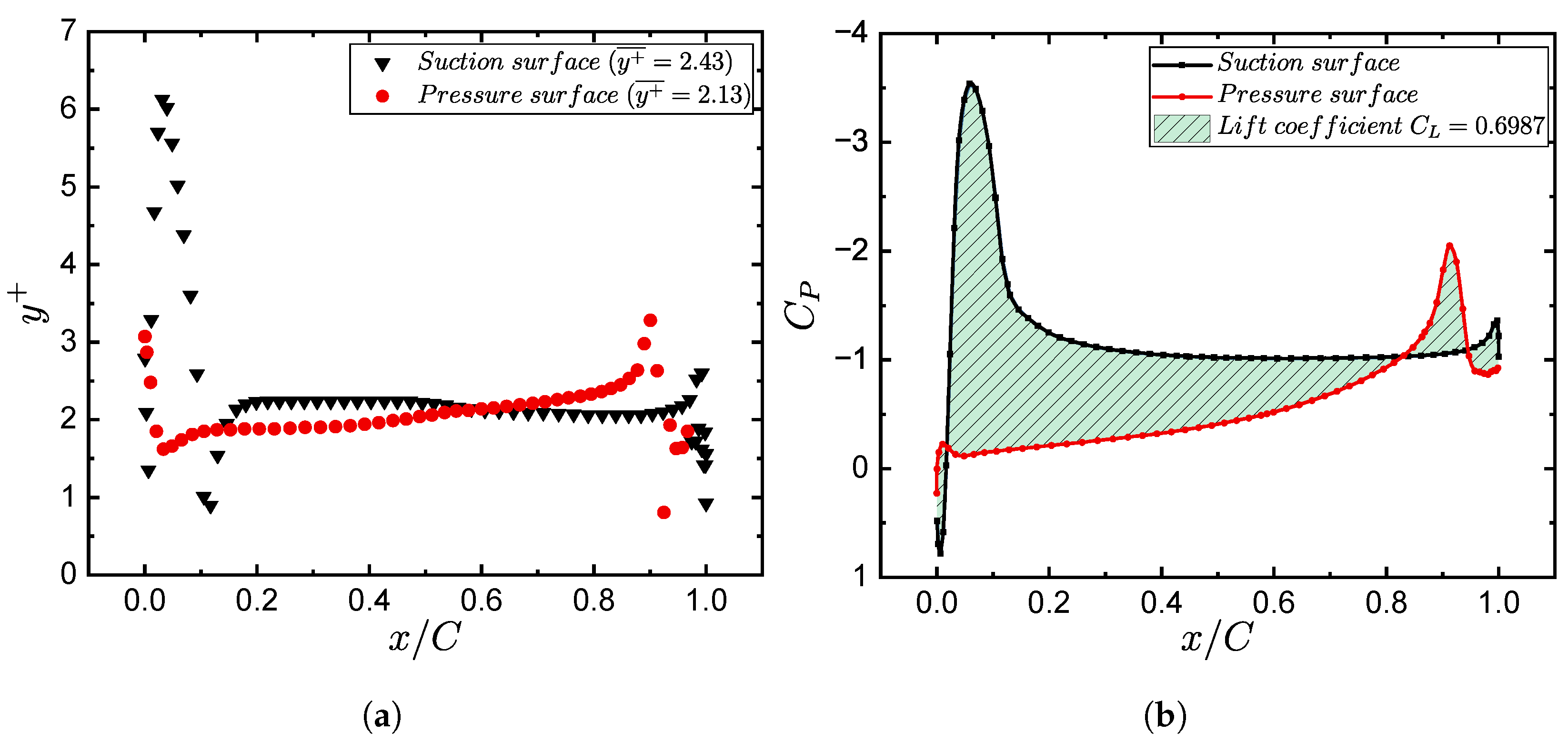
4.1. Numerical Model Validation
4.1.1. Steady-State Analysis
4.1.2. Transient Analysis
- The study of the influence of the time-step size on the numerical solution, where corresponds to the fraction of time of each iteration of the transient solution. With the obtained results, the temporal grid convergence index (GCI) method was applied to the time-step .
- The study of the influence of the total physical time of the transient simulation.
- 1.
- Study of the influence of the time-step size :
- 2.
- Study of the influence of the total physical time of the transient simulation:
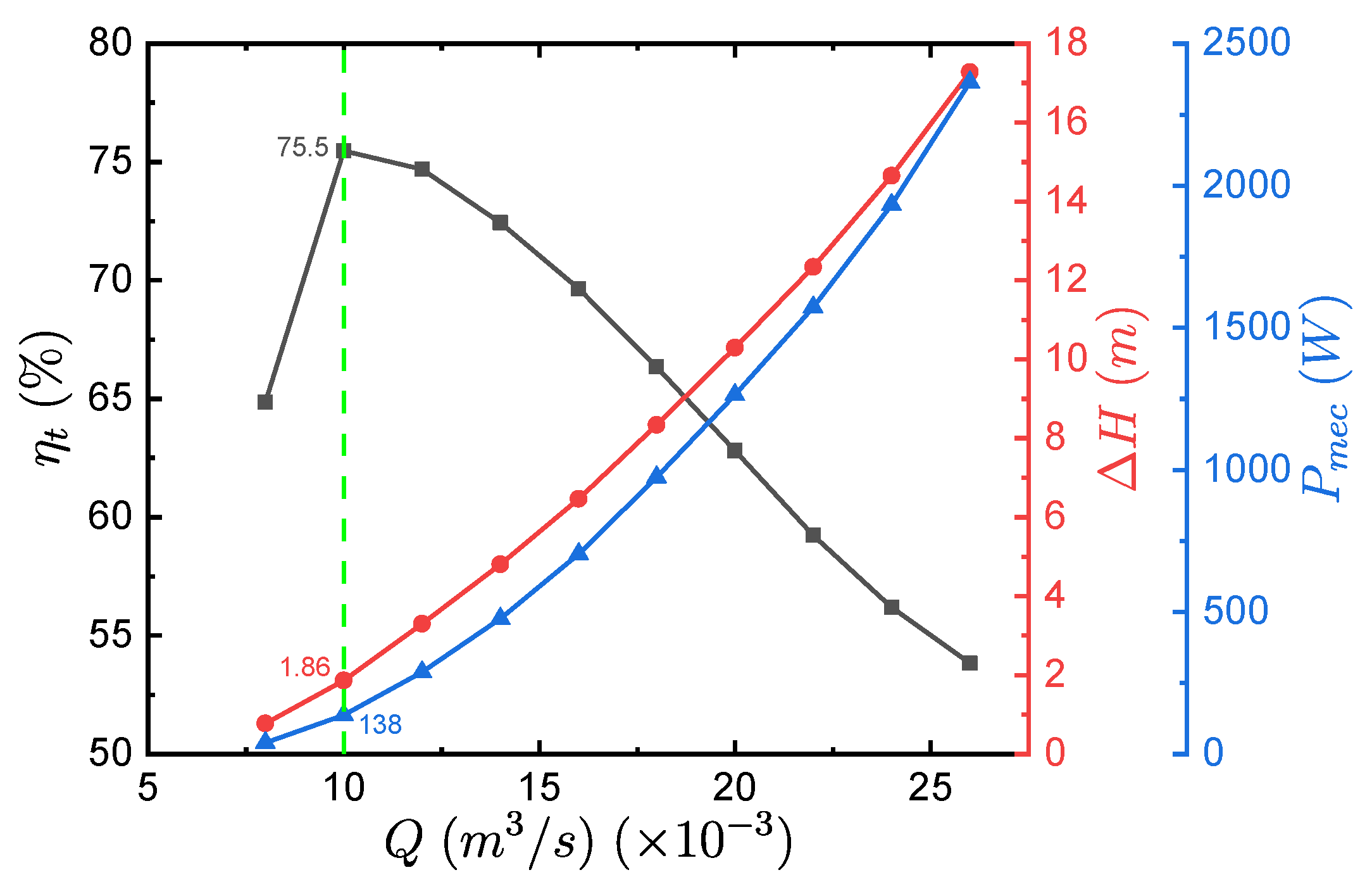
4.2. Fluid Dynamic Results
4.3. Structural Results
4.3.1. Static Structural Results
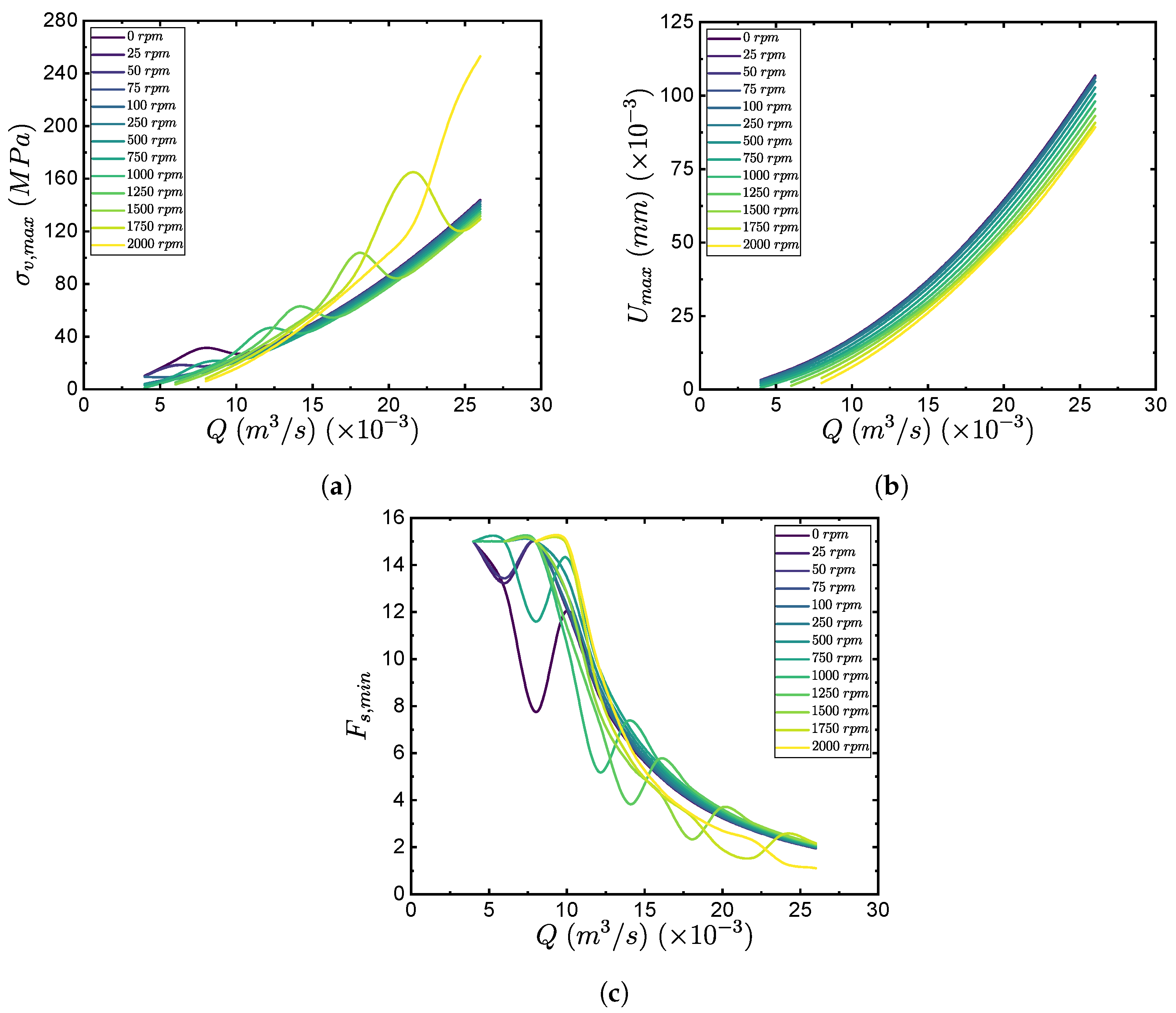
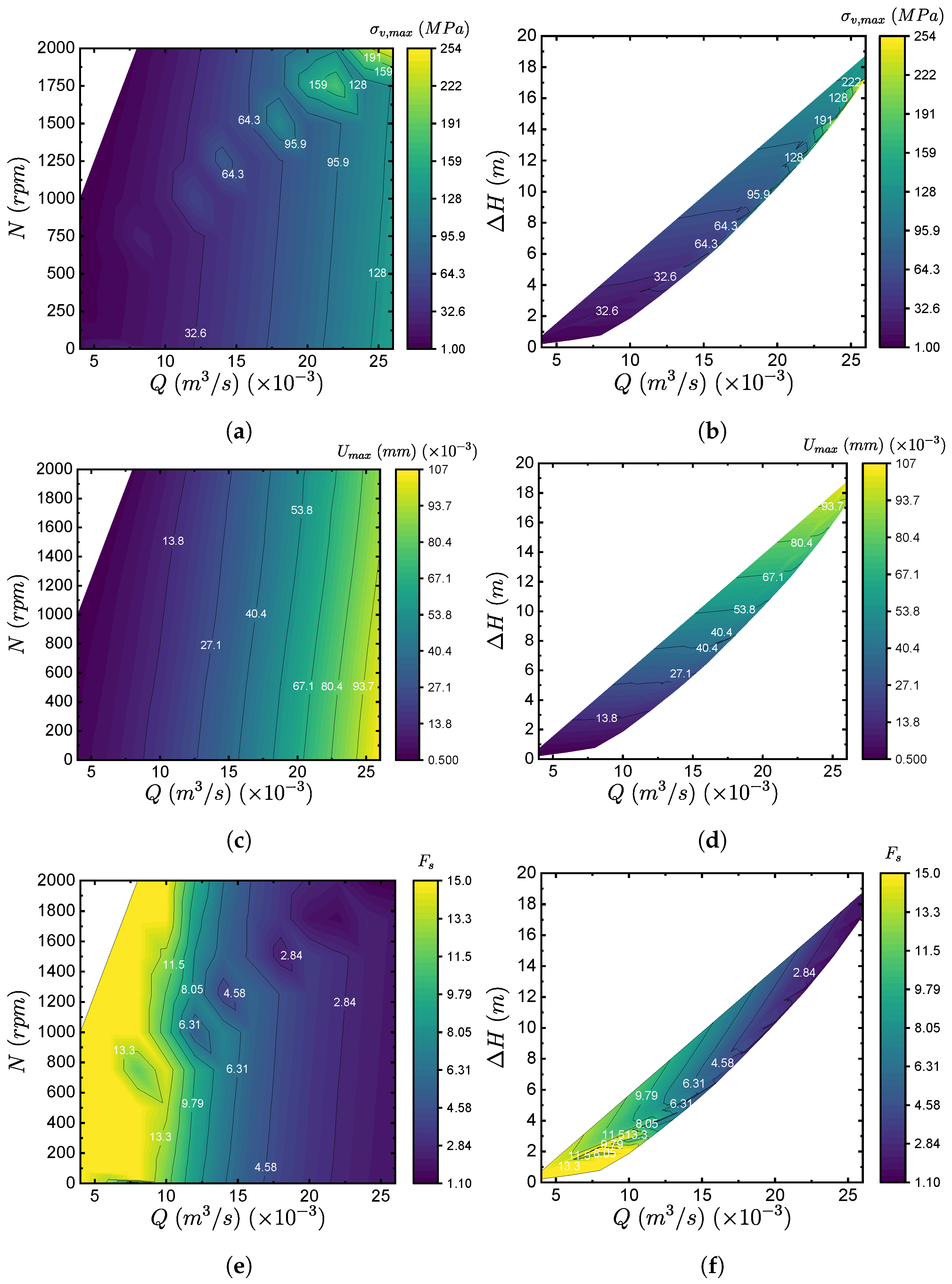
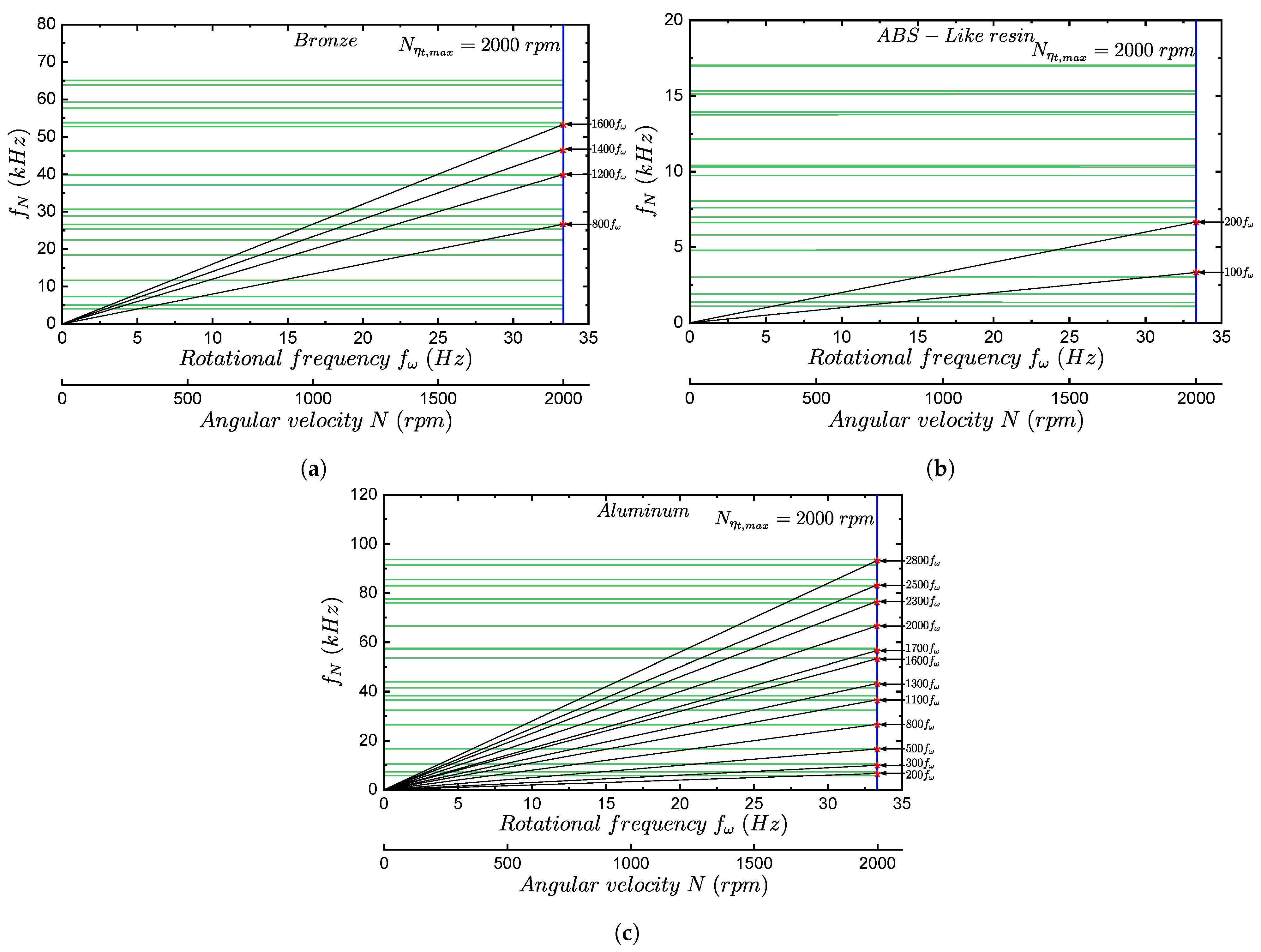
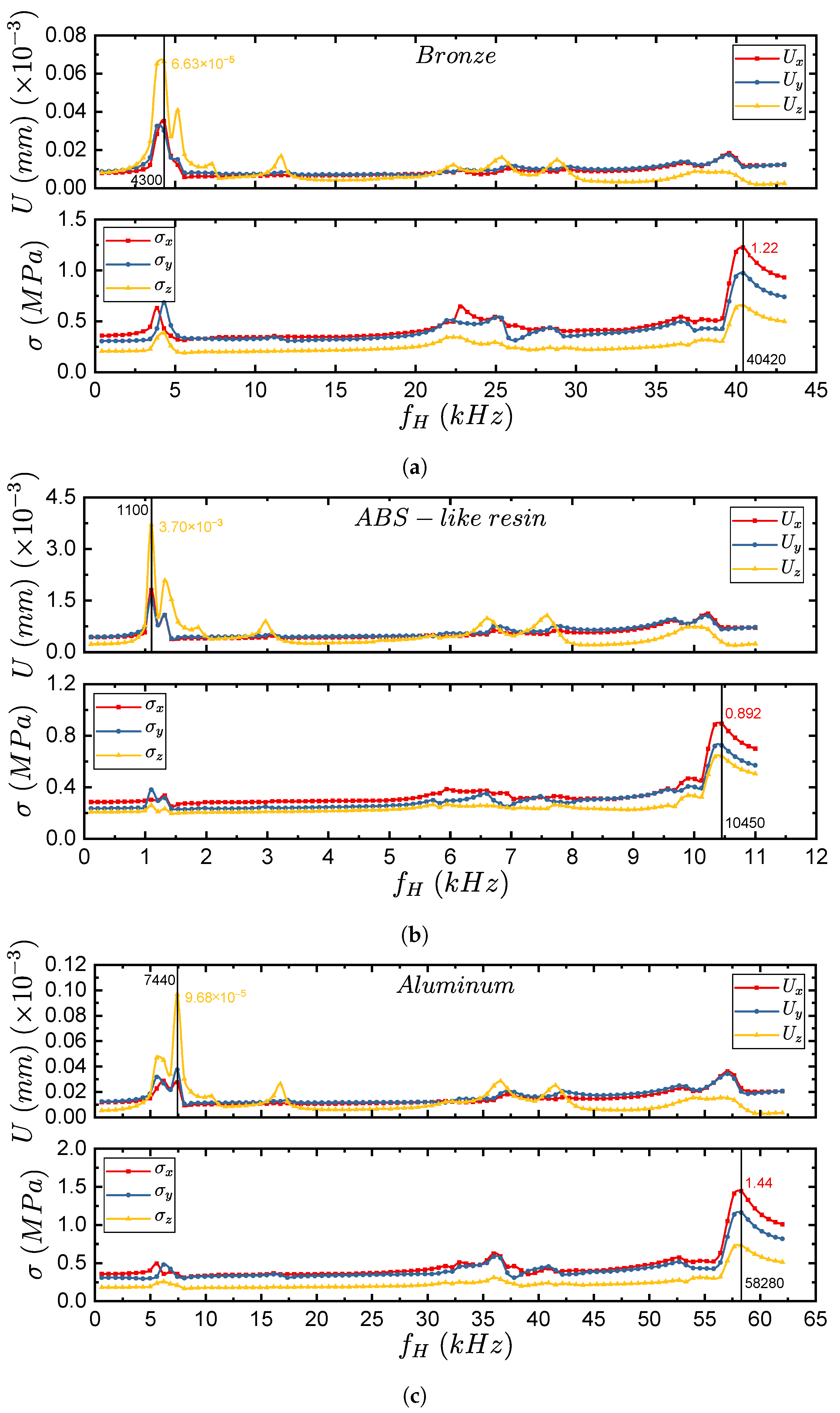
4.3.2. Dynamic Structural Results
- Modal analysis
- Harmonic analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Roman letters | |
| A | Characteristic area () |
| Axial chord length (m) | |
| Lift coefficient | |
| Pressure coefficient | |
| Turbine tip diameter (m) | |
| Turbine hub diameter (m) | |
| Pipe inner diameter (m) | |
| Hub-to-tip ratio | |
| Safety factor | |
| Natural frequency of the mode shapes (Hz) | |
| Harmonic frequency range (Hz) |
| Rotational frequency (Hz) | |
| g | Gravitational constant (m/) |
| Convergence index for the fine grid | |
| Convergence index for the medium grid | |
| H | Available head pressure (m) |
| Head pressure drop (m) | |
| k | Free-vortex constant (/s) |
| L | Characteristic length (m) |
| Meridional coordinates | |
| Mass flow rate (kg/s) | |
| N | Turbine angular velocity () |
| Total number of iterations | |
| Total number of turbine rotations | |
| r | Characteristic radius (m) |
| Cylindrical coordinates (m, °, m) | |
| Hydraulic power (W) | |
| Mechanical power (W) | |
| Static pressure (Pa) | |
| Total pressure (Pa) | |
| Far-field pressure (Pa) | |
| Q | Flow rate (/s) |
| T | Torque (Nm) |
| t | time; blade thickness (s, m) |
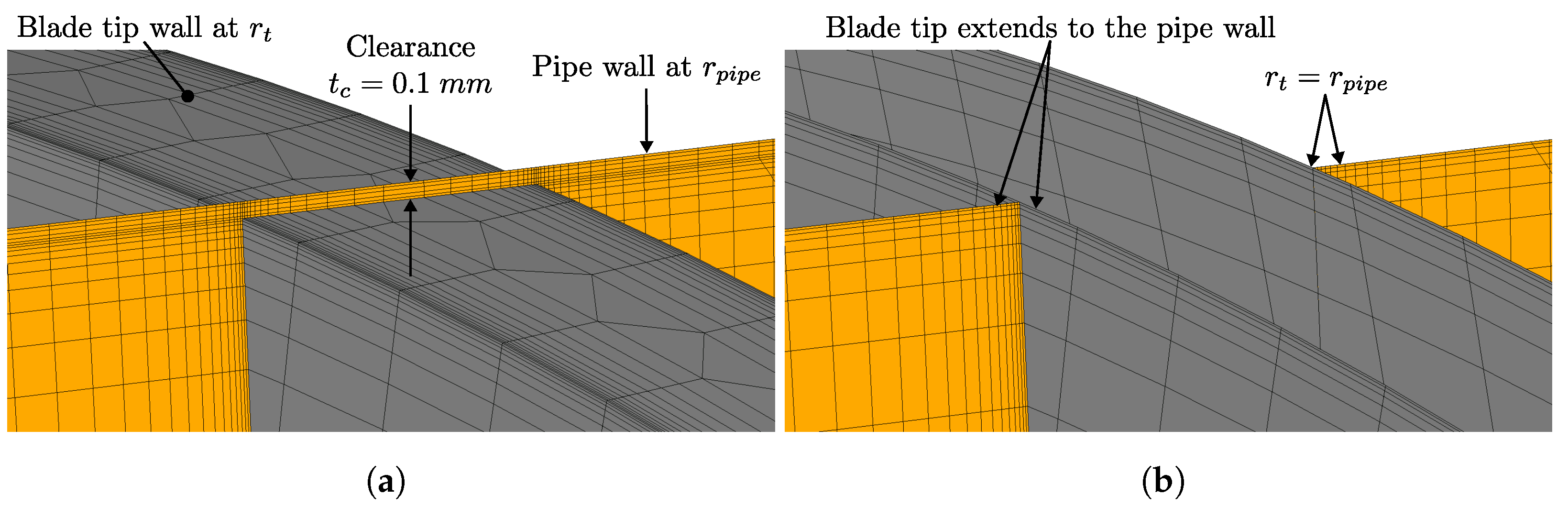
| Blade clearance (m) | |
| Time-step size (s) | |
| U | Total deformation (m) |
| Far-field velocity (m/s) | |
| Axial velocity vector (m/s) | |
| Tangential velocity vector (m/s) | |
| Circumferential velocity vector (m/s) | |
| 2D Cartesian coordinates (m) | |
| 3D Cartesian coordinates (m) | |
| Dimensionless wall distance | |
| z | Turbine blade number |
| Greek letters | |
| Leading and trailing edge blade angles | |
| Specific weight (N/) | |
| Turbine hydraulic efficiency | |
| Circular blade wrap angle | |
| Turbine rotational angle for each iteration | |
| Density; far-field density (kg/) | |
| Normal stress (Pa) | |
| Von Mises stress (Pa) | |
| Mode shape (Pa) | |
| Angular velocity (rad/s) |
| Abbreviations | |
| ASME | American Society of Mechanical Engineers |
| BEP | Best Efficiency Point |
| CFD | Computational Fluid Dynamics |
| FSI | Fluid–Structure Interaction |
| FEM | Finite Element Method |
| GCI | Grid Convergence Index |
| DOF | Degrees of Freedom |
| PAT | Pump as Turbine |
| SST | Shear Stress Transport |
| SSL | Spatial Relative Streamline |
Appendix A. Governing Equations of Fluid Dynamics
Appendix A.1. Navier-Stokes Equations
Appendix A.2. The k − ω SST Turbulence Model
Appendix B. Governing Equations of Structural Dynamics
Appendix B.1. Static Structural
Appendix B.2. Modal Analysis
- Valid for all degrees of freedom concerning structures and fluids.
- The structure has constant mass and stiffness effects.
- No damping is imposed by default unless defined by the user.
- The structure has no time-varying quantities such as forces, displacements, pressures, or temperatures.
Appendix B.3. Harmonic Response
- Valid for structural, fluid, magnetic and electrical degrees of freedom. Thermal degrees of freedom may be present in a coupled field harmonic response analysis using structural DOFs.
- The entire structure has constant or frequency-dependent stiffness, damping, and mass effects.
- All loads and displacements vary sinusoidally at the same known frequency (although not necessarily in phase).
- Solution method: Mode Superposition
- Non-zero imposed harmonic displacements are not allowed.
- There are no element damping matrices. However, there are several types of damping of the system.
References
- Ji, Y.; Song, H.; Xue, Z.; Li, Z.; Tong, M.; Li, H. A Review of the Efficiency Improvement of Hydraulic Turbines in Energy Recovery. Processes 2023, 11, 1815. [Google Scholar] [CrossRef]
- Du, J.; Shen, Z.; Yang, H. Numerical study on the impact of runner inlet arc angle on the performance of inline cross-flow turbine used in urban water mains. Energy 2018, 158, 228–237. [Google Scholar] [CrossRef]
- Payambarpour, S.A.; Najafi, A.F.; Magagnato, F. Investigation of blade number effect on hydraulic performance of in-pipe hydro savonius turbine. Int. J. Rotating Mach. 2019, 2019, 8394191. [Google Scholar] [CrossRef]
- Yang, W.; Hou, Y.; Jia, H.; Liu, B.; Xiao, R. Lift-type and drag-type hydro turbine with vertical axis for power generation from water pipelines. Energy 2019, 188, 116070. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H.M. PAT design strategy for energy recovery in water distribution networks by electrical regulation. Energies 2013, 6, 411–424. [Google Scholar] [CrossRef]
- Samora, I.; Hasmatuchi, V.; Münch-Alligné, C.; Franca, M.J.; Schleiss, A.J.; Ramos, H.M. Experimental characterization of a five blade tubular propeller turbine for pipe inline installation. Renew. Energy 2016, 95, 356–366. [Google Scholar] [CrossRef]
- Ministry of Environment, Housing and Territorial Development, Republic of Colombia. General Aspects of Drinking Water Supply and Basic Sanitation Systems, Title A. Available online: https://www.minvivienda.gov.co/sites/default/files/documentos/010710_ras_titulo_a_.pdf. (accessed on 29 April 2024). (In Spanish)
- Ministry of Environment, Housing and Territorial Development, Republic of Colombia. Water Supply Systems, Title B. Available online: https://www.minvivienda.gov.co/sites/default/files/documentos/titulob-030714.pdf. (accessed on 29 April 2024). (In Spanish)
- Hannachi, M.; Ketata, A.; Sinagra, M.; Arico, C.; Tucciarelli, T.; Driss, Z. A novel pressure regulation system based on Banki hydro turbine for energy recovery under in-range and out-range discharge conditions. Energy Convers. Manag. 2021, 243, 114417. [Google Scholar] [CrossRef]
- Pasha, M.F.K.; Weathers, M.; Smith, B. Investigating energy flow in water-energy storage for hydropower generation in water distribution systems. Water Resour. Manag. 2020, 34, 1609–1622. [Google Scholar] [CrossRef]
- Waqas, M.; Ahmad, N. Computation of stress distribution in hydraulic horizontal propeller turbine runner based on fluid–structure interaction analysis. Arab. J. Sci. Eng. 2020, 45, 9325–9337. [Google Scholar] [CrossRef]
- Chica, E.; Rubio-Clemente, A. Design of Zero Head Turbines for Power Generation; IntechOpen: London, UK, 2017. [Google Scholar] [CrossRef]
- Gonabadi, H.; Oila, A.; Yadav, A.; Bull, S. Structural performance of composite tidal turbine blades. Compos. Struct. 2021, 278, 114679. [Google Scholar] [CrossRef]
- Luo, Y.; Yang, G.; Cao, J.; Yang, J.; Chen, J.; Zhao, H.; Wang, Z. Multibody dynamics analysis of a Kaplan turbine runner in full operating conditions. J. Energy Storage 2023, 72, 108269. [Google Scholar] [CrossRef]
- Saeed, R.A.; Galybin, A.; Popov, V. Modelling of flow-induced stresses in a Francis turbine runner. Adv. Eng. Softw. 2010, 41, 1245–1255. [Google Scholar] [CrossRef]
- Yazik, M.H.M.; Zawawi, M.H.; Ahmed, A.N.; Sidek, L.M.; Basri, H.; Ismail, F. One-way fluid structure interaction analysis of a static savonius hydrokinetic turbine under different velocity and surface roughness with different blade materials. Ocean Eng. 2024, 291, 116373. [Google Scholar] [CrossRef]
- Presas, A.; Luo, Y.; Wang, Z.; Guo, B. Fatigue life estimation of Francis turbines based on experimental strain measurements: Review of the actual data and future trends. Renew. Sustain. Energy Rev. 2019, 102, 96–110. [Google Scholar] [CrossRef]
- Thapa, B.S.; Dahlhaug, O.G.; Thapa, B. Sediment erosion induced leakage flow from guide vane clearance gap in a low specific speed Francis turbine. Renew. Energy 2017, 107, 253–261. [Google Scholar] [CrossRef]
- Cao, J.; Tian, H.; Ahn, S.H.; Duo, W.; Bi, H.; Zhao, L.; Zhao, G.; Gao, H.; Wang, M.; Ma, G.; et al. Fatigue analysis in rotor of a prototype bulb turbine based on fluid-structure interaction. Eng. Fail. Anal. 2022, 132, 105940. [Google Scholar] [CrossRef]
- Xia, X.; Luo, H.; Li, S.; Wang, F.; Zhou, L.; Wang, Z. Characteristics and factors of mode families of axial turbine runner. Int. J. Mech. Sci. 2023, 251, 108356. [Google Scholar] [CrossRef]
- An, X.; Wang, P.; Ye, M.; He, R.; Li, C.; Lessard, L. Tip clearance influence on hydrodynamic performance and pressure fluctuation of a composite ducted propeller using a two-way FSI method. Ocean Eng. 2023, 282, 114698. [Google Scholar] [CrossRef]
- Lin, C.S.; Chiang, H.T.; Hsu, C.H.; Lin, M.H.; Liu, J.K.; Bai, C.J. Modal Verification and Strength Analysis of Bladed Rotors of Turbine in Rated Working Conditions. Appl. Sci. 2021, 11, 6306. [Google Scholar] [CrossRef]
- Gauthier, J.; Giroux, A.; Etienne, S.; Gosselin, F. A numerical method for the determination of flow-induced damping in hydroelectric turbines. J. Fluids Struct. 2017, 69, 341–354. [Google Scholar] [CrossRef]
- Castorrini, A.; Corsini, A.; Rispoli, F.; Takizawa, K.; Tezduyar, T.E. A stabilized ALE method for computational fluid–structure interaction analysis of passive morphing in turbomachinery. Math. Models Methods Appl. Sci. 2019, 29, 967–994. [Google Scholar] [CrossRef]
- Ubulom, I.; Shankar, K.; Neely, A. Turbine Blade Life Prediction Using Fluid-Thermal-Structural Interaction Modelling. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Montreal, QC, Canada, 15–19 June 2015; American Society of Mechanical Engineers: New York, NY, USA; Volume 56765, p. V07AT28A008. [Google Scholar] [CrossRef]
- Krishna, V.R.; Sanaka, S.P.; Pardhasaradhi, N.; Rao, B.R. Hydro-elastic computational analysis of a marine propeller using two-way fluid structure interaction. J. Ocean Eng. Sci. 2022, 7, 280–291. [Google Scholar] [CrossRef]
- Nishi, Y.; Kobayashi, Y.; Inagaki, T.; Kikuchi, N. The design method of axial flow runners focusing on axial flow velocity uniformization and its application to an ultra-small axial flow hydraulic turbine. Int. J. Rotating Mach. 2016, 2016, 5390360. [Google Scholar] [CrossRef]
- Ohiemi, I.E.; Sheng, Y.S.; Singh, P.; Li, Y. Experimental investigation on the effect of axial gap on performance and unsteady pressure pulsations of low head axial flow hydraulic turbine. Flow Meas. Instrum. 2022, 88, 102255. [Google Scholar] [CrossRef]
- Demetriades, G.; Williams, A.; Smith, N. A simplified propeller turbine runner design for stand alone micro-hydro power generation units. Int. J. Ambient Energy 1996, 17, 151–156. [Google Scholar] [CrossRef]
- Alexander, K.; Giddens, E.; Fuller, A. Axial-flow turbines for low head microhydro systems. Renew. Energy 2009, 34, 35–47. [Google Scholar] [CrossRef]
- Singh, P.; Nestmann, F. Experimental optimization of a free vortex propeller runner for micro hydro application. Exp. Therm. Fluid Sci. 2009, 33, 991–1002. [Google Scholar] [CrossRef]
- Singh, P.; Nestmann, F. Experimental investigation of the influence of blade height and blade number on the performance of low head axial flow turbines. Renew. Energy 2011, 36, 272–281. [Google Scholar] [CrossRef]
- Ho-Yan, B. Design of a Low Head Pico Hydro Turbine for Rural Electrification in Cameroon. Master’s Thesis, University of Guelph, Guelph, ON, Canada, 2012. Available online: http://hdl.handle.net/10214/3552 (accessed on 29 April 2024).
- Ramos, H.M.; Simão, M.; Borga, A. Experiments and CFD analyses for a new reaction microhydro propeller with five blades. J. Energy Eng. 2013, 139, 109–117. [Google Scholar] [CrossRef]
- Byeon, S.S.; Kim, Y.J. Influence of blade number on the flow characteristics in the vertical axis propeller hydro turbine. Int. J. Fluid Mach. Syst. 2013, 6, 144–151. [Google Scholar] [CrossRef]
- Nan, D.; Shigemitsu, T.; Zhao, S.; Ikebuchi, T.; Takeshima, Y. Study on performance of contra-rotating small hydro-turbine with thinner blade and longer front hub. Renew. Energy 2018, 117, 184–192. [Google Scholar] [CrossRef]
- Tran, B.N.; Kim, J.H. Design and analysis of a pico propeller hydro turbine applied in fish farms using CFD and experimental method. J. Korean Soc. Mar. Environ. Saf. 2019, 25, 373–380. [Google Scholar] [CrossRef]
- Kurniawan, R.; Himawanto, D.; Widodo, P. The performance of numbers of blade towards picohydro propeller turbine. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Jakarta, Indonesia, 22–23 November 2018; IOP Publishing: Bristol, UK, 2019; Volume 508, p. 012057. [Google Scholar] [CrossRef]
- Pienika, R.; Rodríguez, N.; Rovira, I. Design and scale model manufacturing of a micro hydraulic axial turbine. In Proceedings of the IV Latin American on Hydro Power and Systems Meeting–IAHR, Panama City, Panama, 1–6 September 2019. [Google Scholar]
- Vivas, A.; Viedma, A.; Kaiser, A. In-pipe axial pico-hydraulic tailored turbine design: A novel approach using a dimensionless design chart. Energy Convers. Manag. 2021, 250, 114884. [Google Scholar] [CrossRef]
- Suprayetno, N.; Sutikno, P.; Tandian, N.P.; Hartono, F. Numerical Simulation of Cascade Flow: Vortex Element Method for Inviscid Flow Analysis and Axial Turbine Blade Design. J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 85, 14–23. [Google Scholar] [CrossRef]
- Yang, F.; Chang, P.; Hu, W.; Mao, B.; Liu, C.; Li, Z. Numerical study on pressure pulsation in a slanted axial-flow pump device under partial loads. Processes 2021, 9, 1404. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, X.; Yang, X.; Ding, J.; Zhu, D.; Tao, R.; Wang, H.; Xiao, R. Prediction of the influence of runner tip clearance on the performance of tubular turbine. J. Mar. Sci. Eng. 2022, 10, 136. [Google Scholar] [CrossRef]
- Wegiel, T.; Borkowski, D.; Liszka, D. Efficiency analysis of an energy conversion system for a variable speed small hydropower plant. In Proceedings of the E3S Web of Conferences. EDP Sciences, Krakow, Poland, 17–19 May 2016; Volume 10, p. 00100. [Google Scholar] [CrossRef]
- Tran, B.N.; Jeong, H.; Kim, J.H.; Park, J.S.; Yang, C. Effects of tip clearance size on energy performance and pressure fluctuation of a tidal propeller turbine. Energies 2020, 13, 4055. [Google Scholar] [CrossRef]
- Monsalve-Cifuentes, O.D.; Velez-Garcia, S.; Revuelta-Acosta, J.D. Influence of Blade Number on the Hydrodynamic Performance of a Propeller-Type Axial Turbine for In-Pipe Installation. CFD Lett. 2024, 16, 134–158. [Google Scholar] [CrossRef]
- Dixon, S.L.; Hall, C. Fluid Mechanics and Thermodynamics of Turbomachinery; Butterworth-Heinemann: Oxford, UK, 2013; ISBN 978-0-12-415954-9. [Google Scholar]
- ANSYS Inc. Ansys CFX-Solver Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2023; pp. 1–746. [Google Scholar]
- Chen, Y.; Zhou, J.; Karney, B.; Guo, Q.; Zhang, J. Analytical Implementation and Prediction of Hydraulic Characteristics for a Francis Turbine Runner Operated at BEP. Sustainability 2022, 14, 1965. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng.-Trans. ASME 2008, 130, 078001. [Google Scholar] [CrossRef]
- ANSYS Inc. Theory Reference for the Mechanical APDL and Mechanical Applications; ANSYS Inc.: Canonsburg, PA, USA, 2023; pp. 1–1226. [Google Scholar]
- NASA Glenn Research Center. Examining Spatial (Grid) Convergence. Available online: https://www.grc.nasa.gov/www/wind/valid/tutorial/spatconv.html (accessed on 29 April 2024).
- Almohammadi, K.; Ingham, D.; Ma, L.; Pourkashan, M. Computational fluid dynamics (CFD) mesh independency techniques for a straight blade vertical axis wind turbine. Energy 2013, 58, 483–493. [Google Scholar] [CrossRef]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications; Butterworth-Heinemann: Oxford, UK, 2015; ISBN 978-0-08-099995-1. [Google Scholar]
- Ocepek, M.; Peršin, Z.; Kern, I.; Djelić, V.; Muhič, S.; Lipej, A. Experimental and Numerical Analysis of Cavitation and Pressure Fluctuations in Large High Head Propeller Turbine. IOP Conf. Ser. Earth Environ. Sci. 2019, 405, 012032. [Google Scholar] [CrossRef]
- Amjadi, H.; Khashehchi, M.; Soltani, J. Experimental Investigation and Numerical Simulation of an Inline Low-Head Microhydroturbine for Applications in Water Pipelines. IET Renew. Power Gener. 2020, 14, 3209–3219. [Google Scholar] [CrossRef]
- Junginger, B.; Riedelbauch, S. Numerical Analysis of a Propeller Turbine Operated in Part Load Conditions. In High Performance Computing in Science and Engineering ’17: Transactions of the High Performance Computing Center, Stuttgart (HLRS) 2017; Springer: Berlin/Heidelberg, Germany, 2018; pp. 355–368. [Google Scholar] [CrossRef]
- Nagel, W.E.; Kröner, D.H.; Resch, M.M. Numerical Investigation of a Full Load Operation Point for a Low Head Propeller Turbine. In High Performance Computing in Science and Engineering ’15: Transactions of the High Performance Computing Center, Stuttgart (HLRS) 2015; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–701. [Google Scholar] [CrossRef]
- Gagnon, J.M.; Deschênes, C. Numerical Simulation with Flow Feature Extraction of a Propeller Turbine Unsteady Rotor-Stator Interaction. In Computational Methods and Experimental Measurements XIII; WIT Press: Billerica MA, USA, 2007; Volume 1, pp. 55–64. [Google Scholar] [CrossRef]
- Maulana Bs, Q.; Susatyo, A.; Fathul, M.H.; Suherman. Numerical Simulation of the Effect of Flow Direction Angle at Inlet Boundary Condition on Flow Characteristics and Performance of Axial Flow Hydraulic Propeller Turbine Runner. In Proceedings of the 2015 International Conference on Sustainable Energy Engineering and Application (ICSEEA 2015), Jakarta, Indonesia, 3–5 October 2016; pp. 88–94. [Google Scholar] [CrossRef]
- ANSYS Inc. Ansys Granta: Materials Information Management. Available online: https://www.ansys.com/products/materials (accessed on 29 April 2024).
- SUNLU. SUNLU ABS-Like UV Resin Technical Datasheet. Available online: https://cdn.shopify.com/s/files/1/0152/6507/1190/files/SUNLU_ABS-Like_UV_Resin_Data_Sheet.pdf?v=1691779412 (accessed on 29 April 2024).
- Singh, R.; Tiwari, S.; Mishra, S.K. Cavitation erosion in hydraulic turbine components and mitigation by coatings: Current status and future needs. J. Mater. Eng. Perform. 2012, 21, 1539–1551. [Google Scholar] [CrossRef]
- Khalid Mohammed Ridha, W.; Reza Kashyzadeh, K.; Ghorbani, S. Common failures in hydraulic Kaplan turbine blades and practical solutions. Materials 2023, 16, 3303. [Google Scholar] [CrossRef] [PubMed]
- Kharat, V.J.; Singh, P.; Raju, G.S.; Yadav, D.K.; Gupta, M.S.; Arun, V.; Majeed, A.H.; Singh, N. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Mater. Today Proc. 2023, 143, 172–196. [Google Scholar] [CrossRef]
- An, X.; Mu, Y.; Liang, J.; Li, J.; Zhou, Y.; Sun, X. Stereolithography 3D printing of ceramic cores for hollow aeroengine turbine blades. J. Mater. Sci. Technol. 2022, 127, 177–182. [Google Scholar] [CrossRef]
- Rouway, M.; Nachtane, M.; Tarfaoui, M.; Chakhchaoui, N.; Omari, L.E.H.; Fraija, F.; Cherkaoui, O. 3D printing: Rapid manufacturing of a new small-scale tidal turbine blade. Int. J. Adv. Manuf. Technol. 2021, 115, 61–76. [Google Scholar] [CrossRef]
- Patil, H.; Jeyakarthikeyan, P. Mesh convergence study and estimation of discretization error of hub in clutch disc with integration of ANSYS. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Kattankulathur, India, 22–24 March 2018; IOP Publishing: Bristol, UK, 2018; Volume 402, p. 012065. [Google Scholar] [CrossRef]
- ANSYS Inc. Harmonic Response Analysis in Ansys Mechanical. Available online: https://innovationspace.ansys.com/product/harmonic-response-analysis-in-ansys-mechanical/ (accessed on 29 April 2024).
- Nishi, Y.; Kobori, T.; Mori, N.; Inagaki, T.; Kikuchi, N. Study of the internal flow structure of an ultra-small axial flow hydraulic turbine. Renew. Energy 2019, 139, 1000–1011. [Google Scholar] [CrossRef]
- ANSYS Inc. Modal Analysis in Ansys Mechanical. Available online: https://innovationspace.ansys.com/product/modal-analysis-in-ansys-mechanical/ (accessed on 29 April 2024).
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]




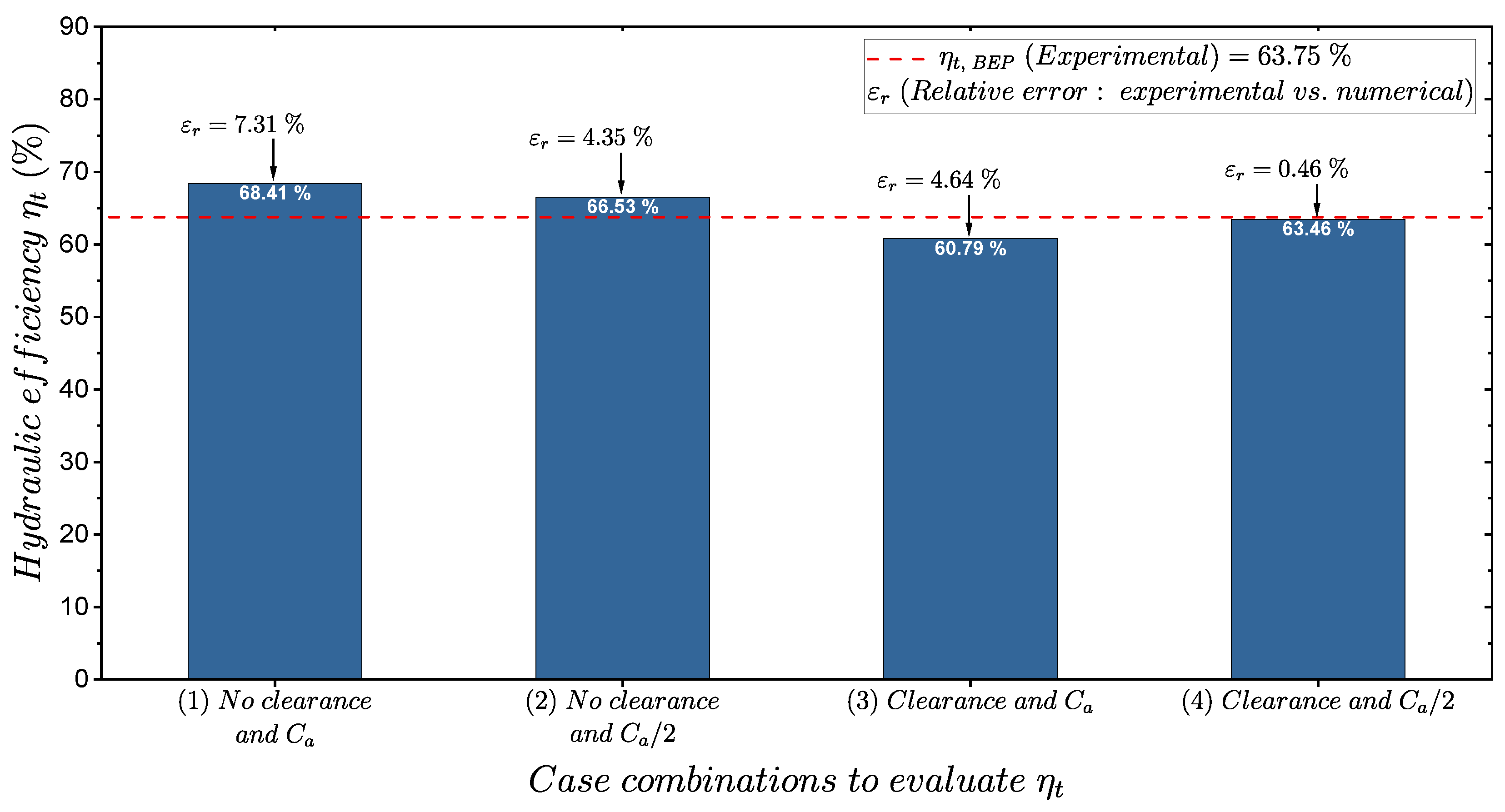
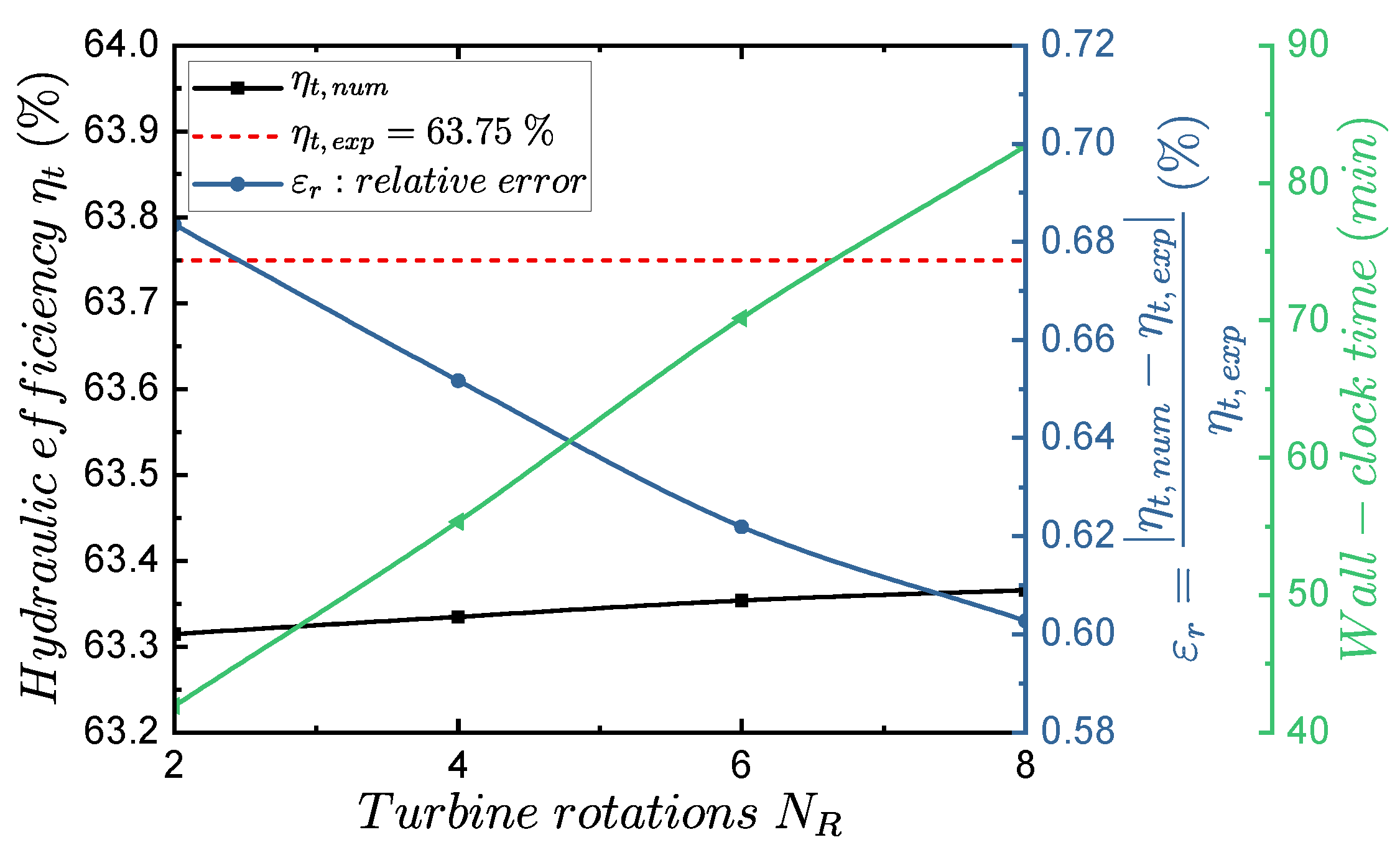
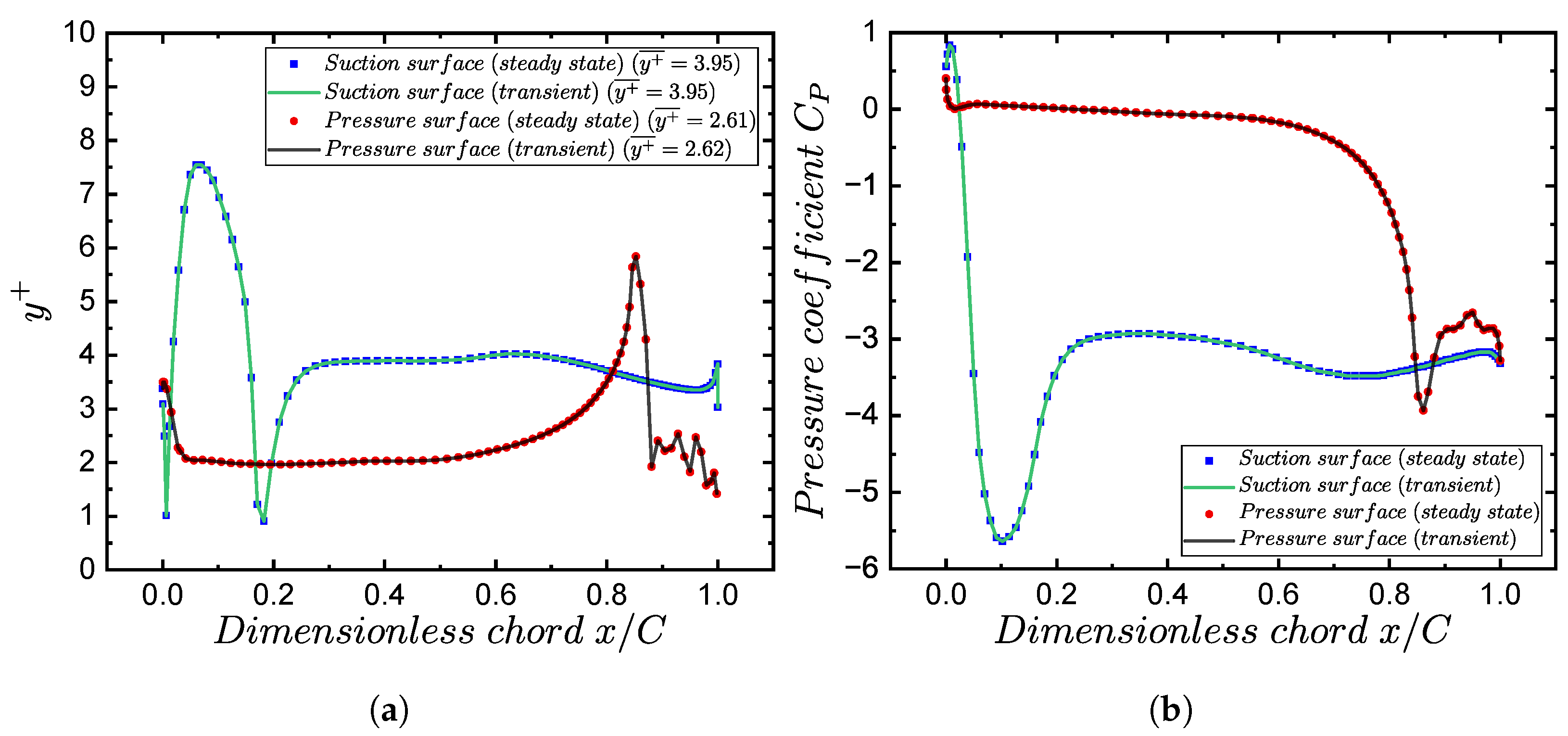
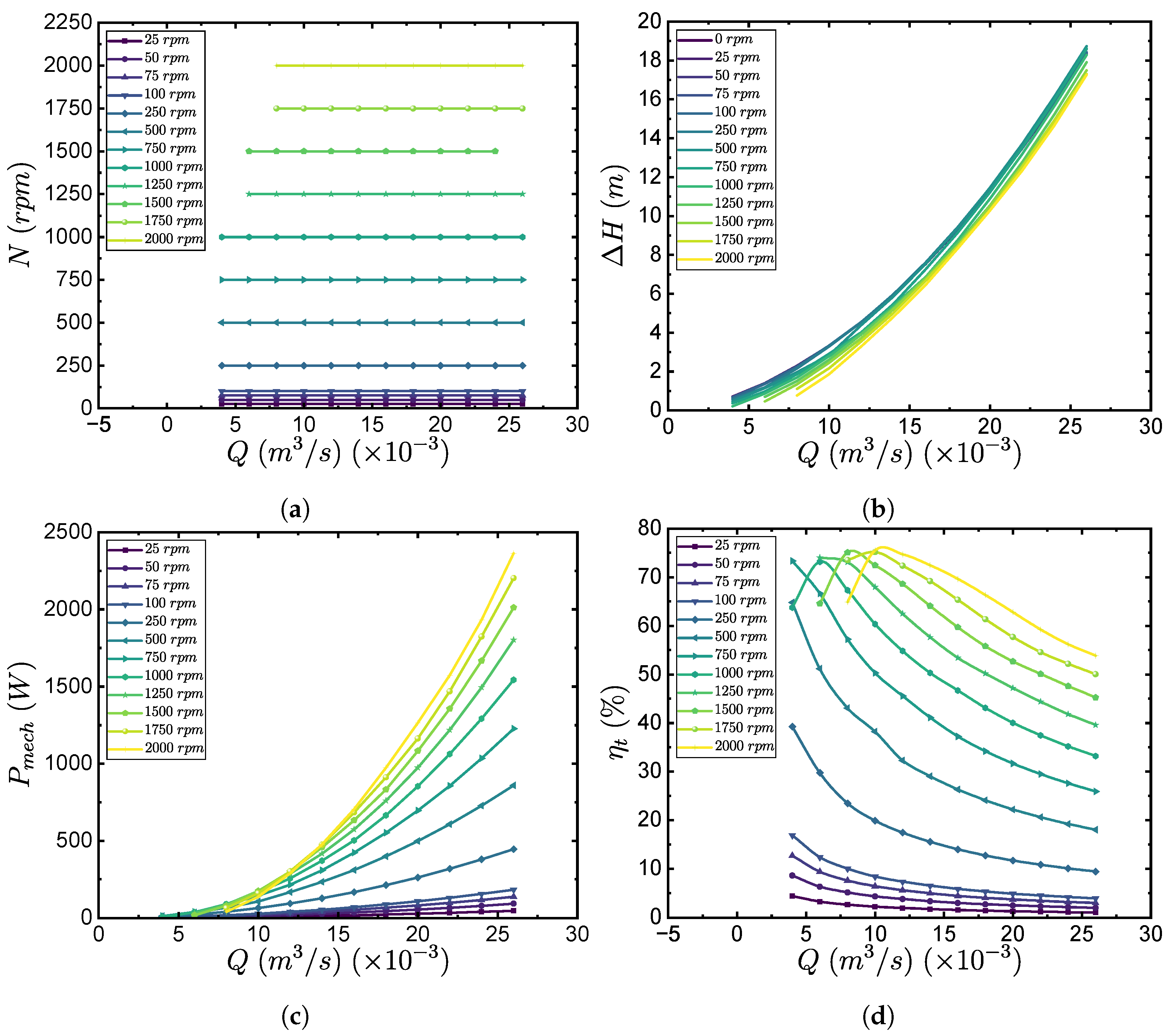


| Ref. | Year | Q (l/s) | H (m) | (%) | N (rpm) | (W) | (mm) | z | |
|---|---|---|---|---|---|---|---|---|---|
| [29] | 1996 | 72 | 2 | 72 | 1560 | 1000 | 149 | 0.403 | 4 |
| [30] | 2009 | 32 | 4.31 | 74.7 | 1500 | 1000 | 131 | 0.643 | 4 |
| [31] | 2009 | 75 | 1.75 | 75 | 1000 | 962.8 | 200 | 0.3 | 5 |
| [32] | 2011 | 75.50 | 1.75 | 65 | 900 | 850 | 200 | 0.42 | 6 |
| [33] | 2012 | 25 | 2 | 78 | 1500 | 255 | 130 | 0.55 | 4 |
| [34] | 2013 | 4 | 0.12 | 100 | 300 | 108 | 100 | 0.5 | 5 |
| [35] | 2013 | 3.5 | 80 | 200 | 249.2 | 400 | 0.3 | 4 | |
| [27] | 2016 | 7.80 | 1.5 | 65.9 | 2460 | 75.5 | 68.1 | 0.443 | 4 |
| [36] | 2018 | 4.82 | 1.3 | 60 | 2300 | 37 | 58 | 0.5 | 4 |
| [37] | 2019 | 250 | 2 | 80 | 450 | 3000 | 380 | 0.4 | 4 |
| [38] | 2019 | 11.40 | 2 | 60 | 1500 | 134 | 88 | 0.68 | 6 |
| [39] | 2019 | 1800 | 3.1 | 71 | 760 | 566 | 0.32 | 3 | |
| [40] | 2021 | 4.44 | 0.37 | 70 | 1000 | 10 | 84 | 0.69 | 7 |
| [41] | 2021 | 1.2 | 5 | 90 | - | 5.2 | 600 | 0.35 | 5 |
| [42] | 2021 | 3.5 | 50 | 250 | - | 1680 | 0.402 | 4 | |
| [43,44] | 2022 | 3000 | 3 | 55 | 150 | 400 | 0.3 | 4 |
| Design Parameter | Magnitude | Unit | Description |
|---|---|---|---|
| Turbine and pipe sizing parameters | |||
| 75.3 | mm | Pipe inner diameter (3″, Schedule 40) | |
| 0.1 | mm | Blade clearance | |
| 75.1 | mm | Tip turbine diameter (outer) | |
| 0.6 | - | Turbine hub-to-tip ratio | |
| 45.06 | mm | Hub turbine diameter (inner) | |
| t | 1.7 | mm | Blade thickness |
| z | 5 | - | Blade number |
| Hydraulic parameters | |||
| Q | 15 | l/s | Flow rate |
| H | 3 | m | Available head pressure |
| 65 | % | Assumed turbine efficiency | |
| N | 3600 | rpm | Turbine angular velocity |
| Design Point | Circular Blade Geometric Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
(mm) | (°) | (°) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | |
| 22.59 | 31.72 | 26.06 | 26.56 | −13.28 | 13.28 | 307.34 | 148.29 | 261.44 | 14.65 | |
| 30.12 | 24.87 | 21.98 | 35.41 | −17.70 | 17.70 | 765.68 | 304.27 | 694.69 | 15.34 | |
| 37.65 | 20.34 | 18.71 | 44.26 | −22.13 | 22.13 | 1644.34 | 549.55 | 1541.76 | 15.70 | |
| Parameter | Response Variables | |
|---|---|---|
| Torque | Pressure Drop | |
| = 1,498,488, = 515,906, = 101,726 | ||
| 1.4268 | 1.4268 | |
| 1.7181 | 1.7181 | |
| 0.0942 (Nm) | 0.9424 (m) | |
| 0.0969 (Nm) | 0.9725 (m) | |
| 0.1104 (Nm) | 1.1061 (m) | |
| 4.9861 | 4.4454 | |
| p | 2.5475 | 2.3087 |
| 0.0923 (Nm) | 0.9188 (m) | |
| 2.8758 | 3.1908 | |
| 1.9911 | 2.5733 | |
| 13.9381 | 13.7458 | |
| 4.9242 | 5.8462 | |
| 2.4403 | 3.1360 | |
| 5.8664 | 6.9041 | |
| Ref. | Turbine Type | Regime | Turbulence Model | Used | Software |
|---|---|---|---|---|---|
| [55] | Propeller (Kaplan Mount) | Transient | SST | 0 < | NUMECA FINE/Open v17.0 |
| [56] | Savonius | Transient | SST | - | ANSYS-FLUENT v19.0 |
| [57] | Propeller | Transient | SST, SAS-SST, SBES | 0 < | ANSYS-CFX v16.0, v17.2, v18.0 |
| [58] | Propeller | Transient | SST, SAS-SST | 1.4 < | ANSYS-CFX v16.0 |
| [59] | Propeller (Kaplan Mount) | Transient | URANS | 30 < | ANSYS-CFX v7.0 |
| [60] | Propeller | Steady | SST | - | ANSYS-CFX v9.0 |
| Material | (kg/) | () | (—) | E (GPa) | G (GPa) | (MPa) | (MPa) |
|---|---|---|---|---|---|---|---|
| Aluminum 6061-T6 [61] | 2770 | 0.33 | 71 | 26.69 | 280 | 310 | |
| Bronze C51000 [61] | 8715 | 0.34 | 107.7 | 40.04 | 505 | 574.5 | |
| ABS-like resin [62] | 1220 | 0.41 | 1.02 | 0.36 | 34 | 36.26 |
| Design Parameter | Magnitude | Unit | Description |
|---|---|---|---|
| 0.0424 | m | Outer radius of the turbine | |
| 0.0212 | m | Inner radius of the turbine | |
| 0.0425 | m | Inner radius of the pipe | |
| 0.0001 | m | Blade clearance | |
| Q | 0.00443 | /s | Flow rate |
| 0.347 | bar | Head pressure drop of the turbine | |
| N | 750 | rpm | Angular velocity of the turbine |
| 63.75 | % | Hydraulic efficiency of the turbine | |
| z | 5 | − | Number of blades of the turbine |
| Design Point | Validation Study Circular Blade Geometry | ||||||||
|---|---|---|---|---|---|---|---|---|---|
(mm) | (°) | (°) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | |
| 21.20 | 32.13 | 4.07 | 26.64 | −13.32 | 13.32 | 57.80 | 17.42 | 48.95 | |
| 31.80 | 22.72 | 5.34 | 39.96 | −19.98 | 19.98 | 136.31 | 32.67 | 125.73 | |
| 42.40 | 17.44 | 6.06 | 53.28 | −26.64 | 26.64 | 274.63 | 55.65 | 262.02 | |
| Design Radius | (mm) | Case 1: (mm) | Case 2: (mm) |
|---|---|---|---|
| 21.20 | 8.7084 | 4.3542 | |
| 31.80 | 9.9864 | 4.9932 | |
| 42.40 | 11.0815 | 5.5408 |
| Input Parameters | Output Parameters | ||||
|---|---|---|---|---|---|
| (°) | (rad/s) | (s) | (s) | ||
| 20 | 4 | 78.54 | 72 | 0.32 | |
| 10 | 4 | 78.54 | 144 | 0.32 | |
| 5 | 4 | 78.54 | 288 | 0.32 | |
| 1 | 4 | 78.54 | 1440 | 0.32 | |
| Parameter | Response Variables | |
|---|---|---|
| Torque | Pressure Drop | |
| (s) | ||
| 1.709976 | 1.709976 | |
| 1.587401 | 1.587401 | |
| 0.072505 (Nm) | 1.037496 (m) | |
| 0.072501 (Nm) | 1.037639 (m) | |
| 0.072511(Nm) | 1.037976 (m) | |
| p | 1.904328 | 2.041669 |
| 0.072502 (Nm) | 1.037424 (m) | |
| 0.004752 | 0.008666 | |
| 0.005711 | 0.025908 | |
| Input Parameters | Output Parameters | ||||
|---|---|---|---|---|---|
| (°) | (rad/s) | (s) | (s) | ||
| 5 | 2 | 78.54 | 144 | 0.16 | |
| 5 | 4 | 78.54 | 288 | 0.32 | |
| 5 | 6 | 78.54 | 432 | 0.48 | |
| 5 | 8 | 78.54 | 576 | 0.64 | |
| Input Parameters | Output Parameters | |||||
|---|---|---|---|---|---|---|
| Critical Conditions | Material | (/s) | (rpm) | (MPa) | (mm) | |
| Aluminum | 10 | 2000 | 15.20 | 7.44 | 15 | |
| Aluminum | 26 | 2000 | 253.01 | 89.26 | 1.11 | |
| Aluminum | 26 | 0 | 143.84 | 106.85 | 1.95 | |
| Bronze | 10 | 2000 | 15.24 | 4.87 | 15 | |
| Bronze | 26 | 0 | 143.66 | 69.82 | 3.52 | |
| ABS-like resin | 10 | 2000 | 10.29 | 490.89 | 3.30 | |
| ABS-like resin | 26 | 0 | 408.61 | 7107.39 | 0.08 | |
| Material | von Mises Stress Contours | Total Deformation Contours |
|---|---|---|
| Aluminum |  |  |
| Bronze |  | 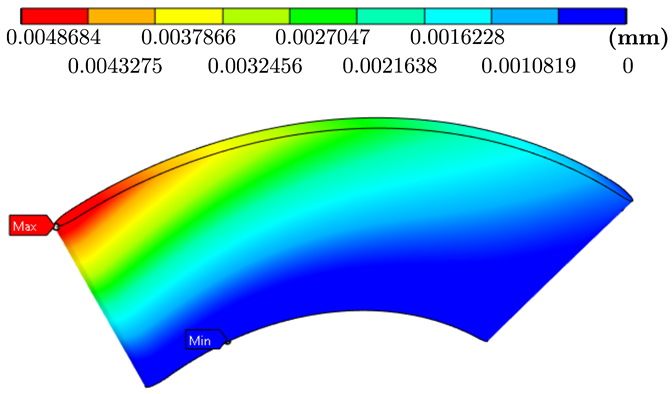 |
| ABS | 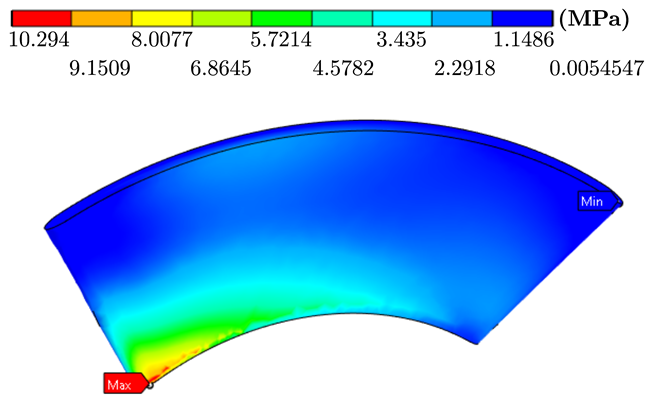 |  |
| Material | Total Deformation U for | von Mises Stress for |
|---|---|---|
| Bronze |  | 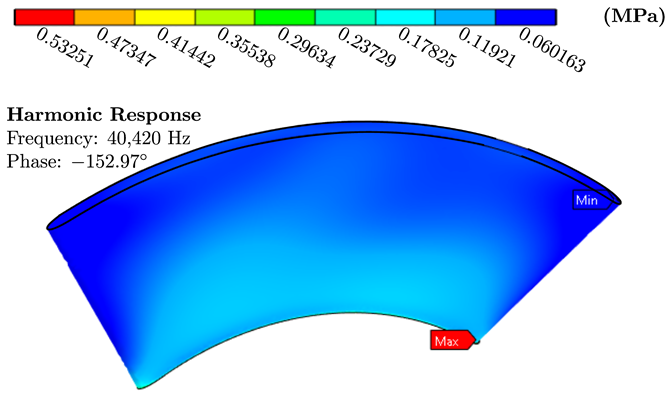 |
| ABS |  | 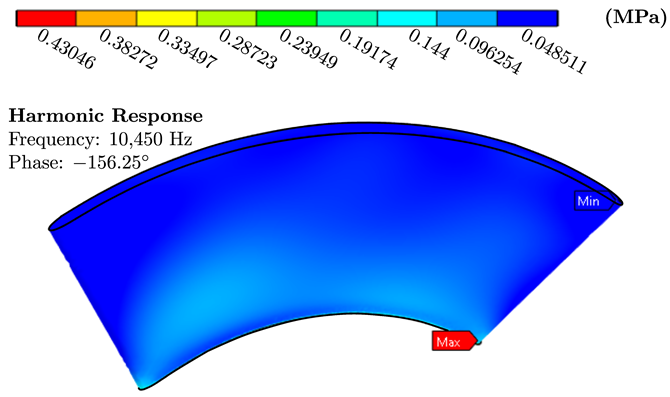 |
| Aluminum | 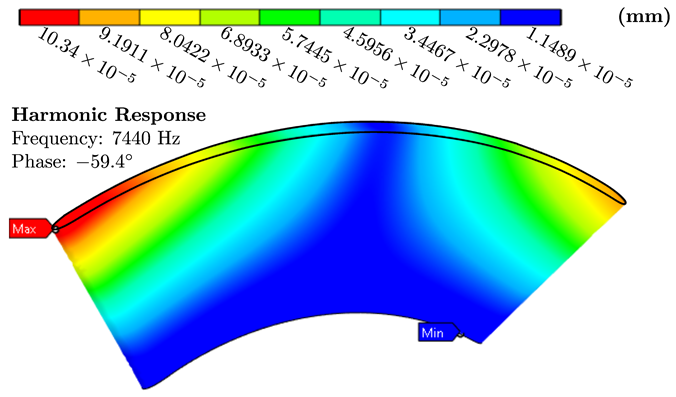 | 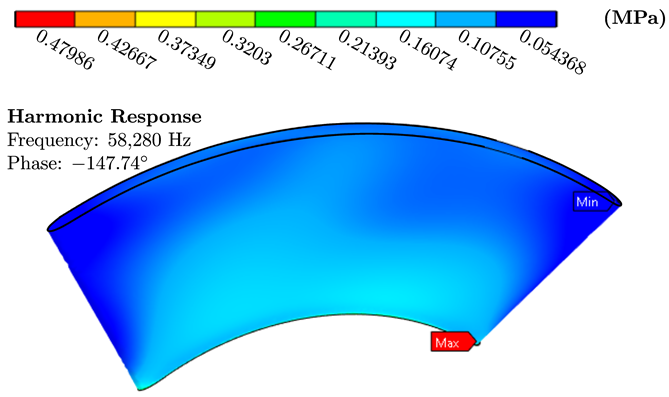 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monsalve-Cifuentes, O.D.; Vélez-García, S.; Sanín-Villa, D.; Revuelta-Acosta, J.D. Fluid-Structure Numerical Study of an In-Pipe Axial Turbine with Circular Blades. Energies 2024, 17, 3539. https://doi.org/10.3390/en17143539
Monsalve-Cifuentes OD, Vélez-García S, Sanín-Villa D, Revuelta-Acosta JD. Fluid-Structure Numerical Study of an In-Pipe Axial Turbine with Circular Blades. Energies. 2024; 17(14):3539. https://doi.org/10.3390/en17143539
Chicago/Turabian StyleMonsalve-Cifuentes, Oscar D., Sebastián Vélez-García, Daniel Sanín-Villa, and Josept David Revuelta-Acosta. 2024. "Fluid-Structure Numerical Study of an In-Pipe Axial Turbine with Circular Blades" Energies 17, no. 14: 3539. https://doi.org/10.3390/en17143539
APA StyleMonsalve-Cifuentes, O. D., Vélez-García, S., Sanín-Villa, D., & Revuelta-Acosta, J. D. (2024). Fluid-Structure Numerical Study of an In-Pipe Axial Turbine with Circular Blades. Energies, 17(14), 3539. https://doi.org/10.3390/en17143539








