A Stochastic Model Predictive Control Method for Tie-Line Power Smoothing under Uncertainty
Abstract
1. Introduction
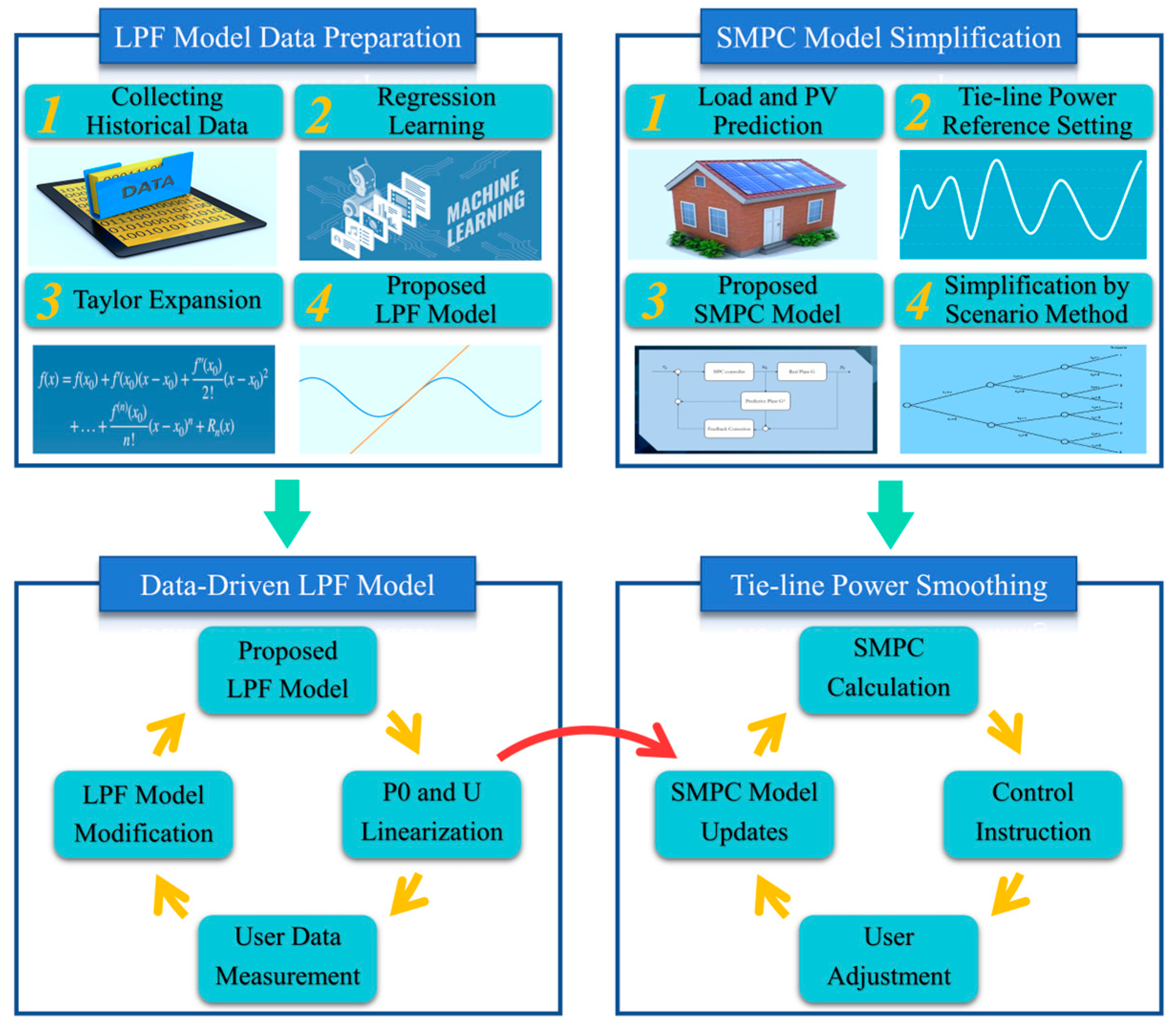
2. Methods
2.1. LPF Model
2.2. Derivation of the SMPC Model
2.3. Simplification of the Objective Function and Chance Constraints
3. Results
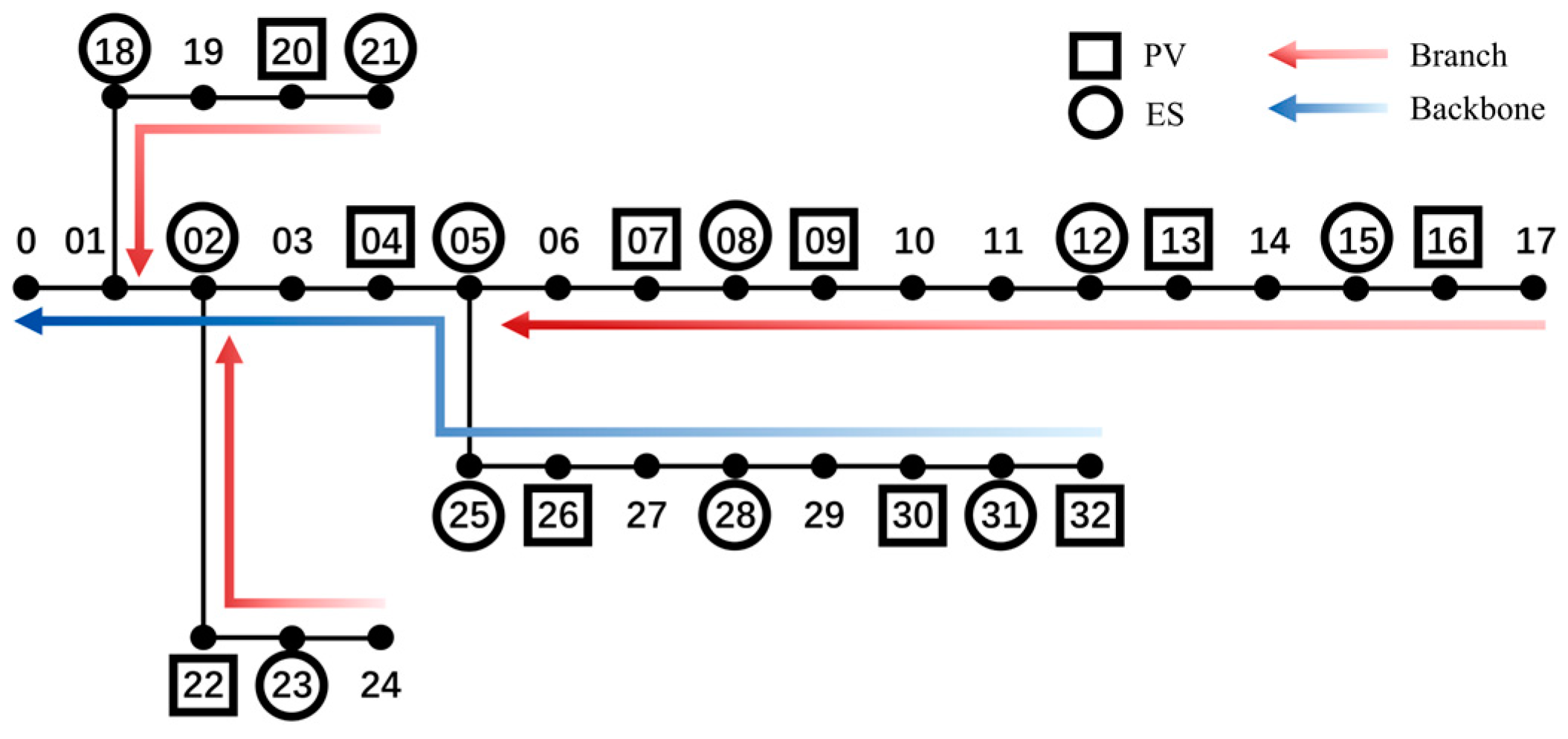
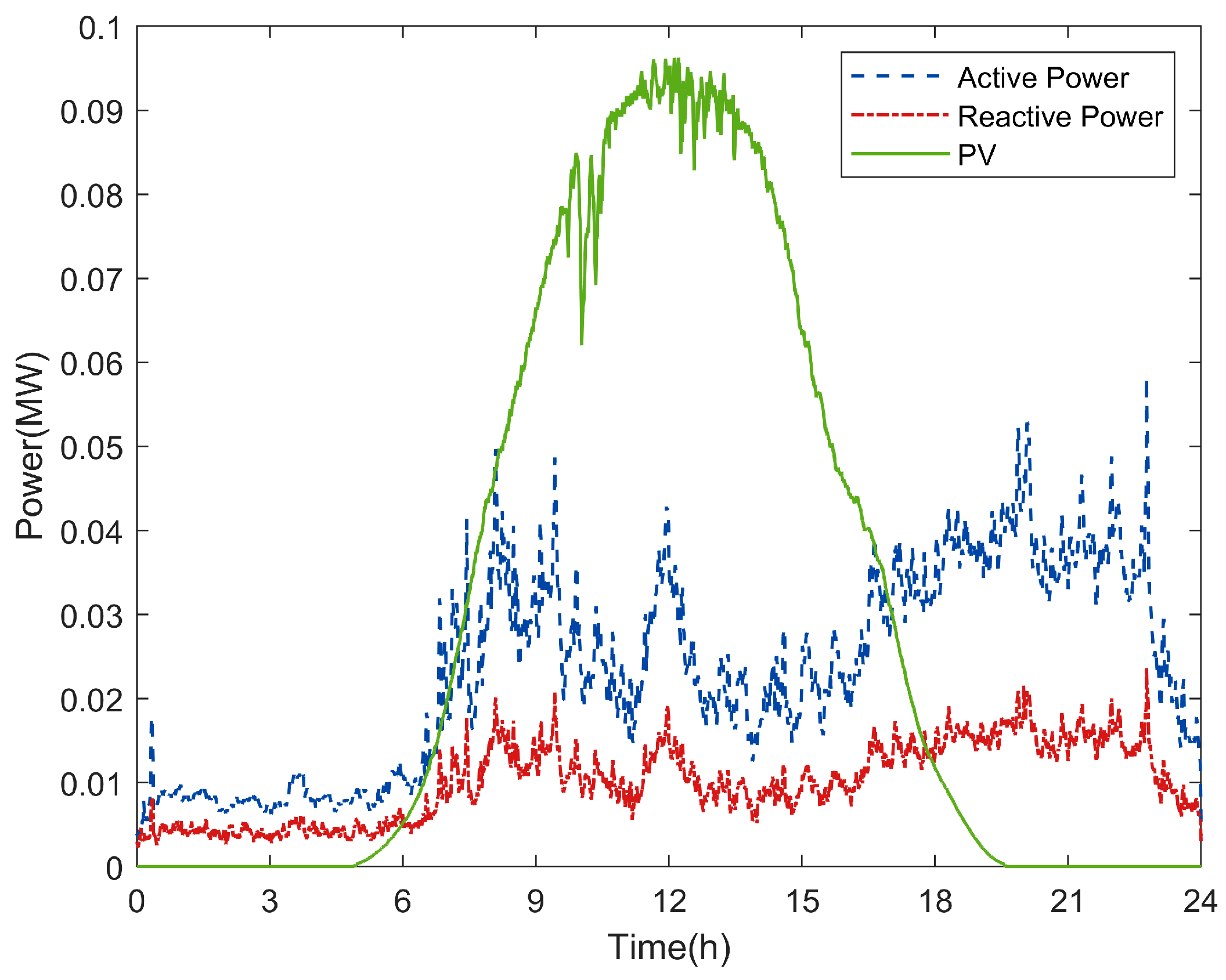
3.1. Data Preparation
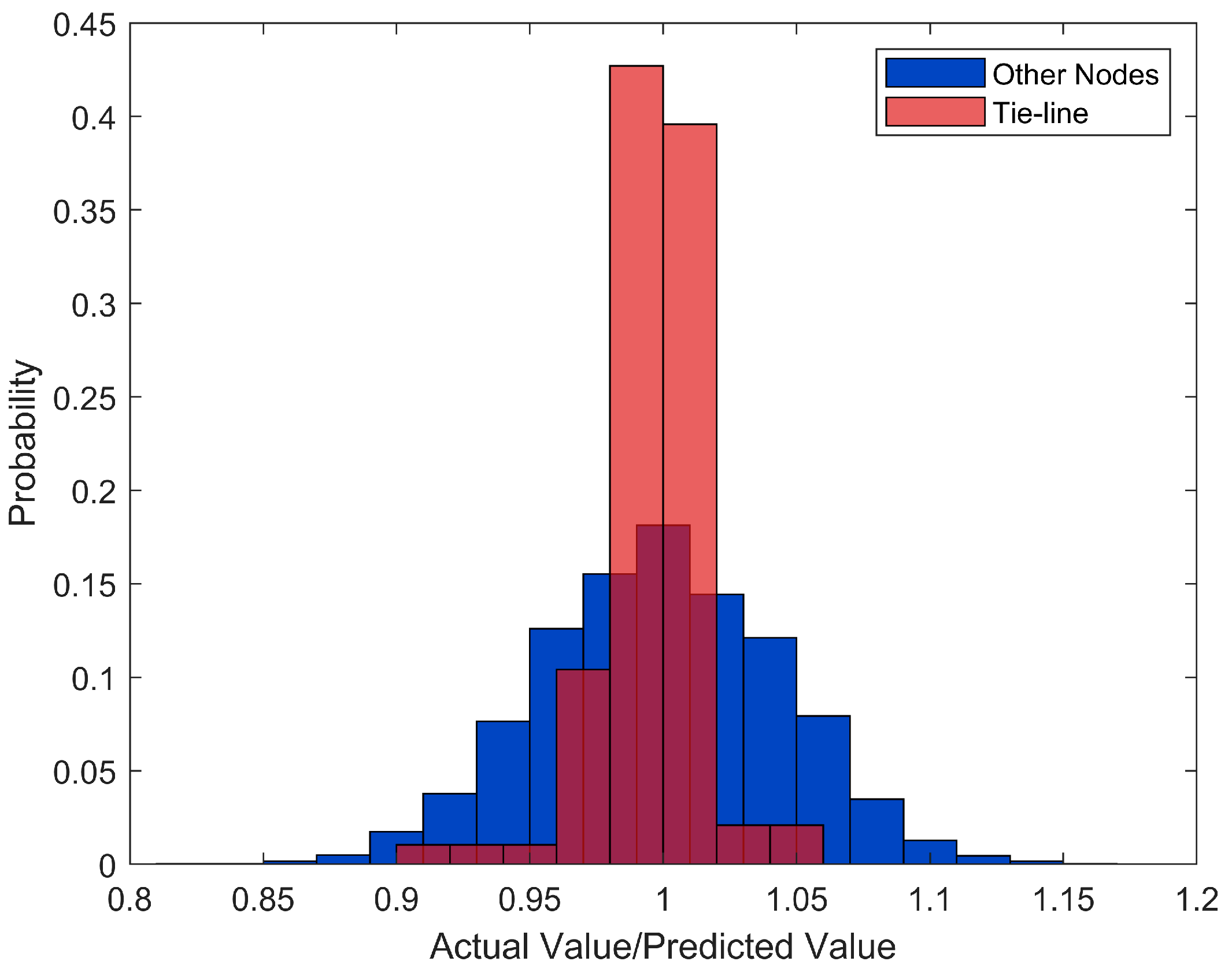
3.2. Performance Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Z.M.; Xu, Y.; Wang, P.; Xiao, G.X. Restoration of a Multi-Energy Distribution System With Joint District Network Reconfiguration via Distributed Stochastic Programming. IEEE Trans. Smart Grid 2024, 15, 2667–2680. [Google Scholar] [CrossRef]
- Dall’Anese, E.; Dhople, S.V.; Giannakis, G.B. Photovoltaic Inverter Controllers Seeking AC Optimal Power Flow Solutions. IEEE Trans. Power Syst. 2016, 31, 2809–2823. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.Z.; Xin, H.H.; Gooi, H.B.; Pan, J.F. Distributed Optimal Tie-Line Power Flow Control for Multiple Interconnected AC Microgrids. IEEE Trans. Power Syst. 2019, 34, 1869–1880. [Google Scholar] [CrossRef]
- Zhang, C.; Lin, W.; Ke, D.P.; Sun, Y.Z. Smoothing Tie-Line Power Fluctuations for Industrial Microgrids by Demand Side Control: An Output Regulation Approach. IEEE Trans. Power Syst. 2019, 34, 3716–3728. [Google Scholar] [CrossRef]
- Zhang, R.; Yu, J.L. External tie line power fluctuations smoothing strategy of new urban power grid. Int. J. Electr. Power Energy Syst. 2023, 153, 109289. [Google Scholar] [CrossRef]
- Said, S.M.; Ali, A.; Hartmann, B. Tie-line Power Flow Control Method for Grid-connected Microgrids with SMES Based on Optimization and Fuzzy Logic. J. Mod. Power Syst. Clean Energy 2020, 8, 941–950. [Google Scholar] [CrossRef]
- Xiao, Z.X.; Guerrero, J.M.; Shuang, J.; Sera, D.; Schaltz, E.; Vásquez, J.C. Flat tie-line power scheduling control of grid-connected hybrid microgrids. Appl. Energy 2018, 210, 786–799. [Google Scholar] [CrossRef]
- Che, Y.B.; Zhou, J.H.; Lin, T.J.; Li, W.X.; Xu, J.M. A Simplified Control Method for Tie-Line Power of DC Micro-Grid. Energies 2018, 11, 933. [Google Scholar] [CrossRef]
- Ding, Y.; Xie, D.J.; Hui, H.X.; Xu, Y.; Siano, P. Game-Theoretic Demand Side Management of Thermostatically Controlled Loads for Smoothing Tie-Line Power of Microgrids. IEEE Trans. Power Syst. 2021, 36, 4089–4101. [Google Scholar] [CrossRef]
- Mudaliyar, S.; Duggal, B.; Mishra, S. Distributed Tie-Line Power Flow Control of Autonomous DC Microgrid Clusters. IEEE Trans. Power Electron. 2020, 35, 11250–11266. [Google Scholar] [CrossRef]
- Wang, D.; Zhi, Y.Q.; Yu, B.; Chen, Z.Y.; An, Q.S.; Cheng, L.; Fan, M.H. Optimal Coordination Control Strategy of Hybrid Energy Storage Systems for Tie-line Smoothing Services in Integrated Community Energy Systems. CSEE J. Power Energy 2018, 4, 408–416. [Google Scholar] [CrossRef]
- Khavari, F.; Badri, A.; Zangeneh, A. A tie-line power smoothing via a novel dynamic real-time pricing mechanism in MMGs. Int. J. Electr. Power Energy Syst. 2022, 136, 107671. [Google Scholar] [CrossRef]
- Islam, M.; Yang, F.W.; Amin, M. Dynamic control of grid-connected microgrids for tie-line smoothing. Int. Trans. Electr. Energy Syst. 2020, 30, 12557. [Google Scholar] [CrossRef]
- Xu, J.; Liao, S.Y.; Jiang, H.Y.; Zhang, D.N.; Sun, Y.Z.; Ke, D.P.; Li, X.; Yang, J.; Peng, X.T.; Yao, L.Z. A Multi-time Scale Tie-line Energy and Reserve Allocation Model Considering Wind Power Uncertainties for Multi-area Systems. CSEE J. Power Energy 2021, 7, 677–687. [Google Scholar] [CrossRef]
- Li, Z.M.; Xu, Y.; Wang, P.; Xiao, G.X. Coordinated preparation and recovery of a post-disaster Multi-energy distribution system considering thermal inertia and diverse uncertainties. Appl. Energy 2023, 336, 120736. [Google Scholar] [CrossRef]
- Fan, S.; He, G.Y.; Zhou, X.Y.; Cui, M.J. Online Optimization for Networked Distributed Energy Resources With Time-Coupling Constraints. IEEE Trans. Smart Grid 2021, 12, 251–267. [Google Scholar] [CrossRef]
- Chen, S.; Wang, C.F.; Zhang, Z.W. Multitime Scale Active and Reactive Power Coordinated Optimal Dispatch in Active Distribution Network Considering Multiple Correlation of Renewable Energy Sources. IEEE Trans. Ind. Appl. 2021, 57, 5614–5625. [Google Scholar] [CrossRef]
- Guo, Y.F.; Wu, Q.W.; Gao, H.L.; Huang, S.; Zhou, B.; Li, C.B. Double-Time-Scale Coordinated Voltage Control in Active Distribution Networks Based on MPC. IEEE Trans. Sustain. Energy 2020, 11, 294–303. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.Y.; Tan, R.M. Distributed Model Predictive Control for On-Connected Microgrid Power Management. IEEE Trans. Control. Syst. Technol. 2018, 26, 1028–1039. [Google Scholar] [CrossRef]
- Cai, S.; Xie, Y.Y.; Wu, Q.W.; Zhang, M.L.; Jin, X.L.; Xiang, Z.R. Active and Reactive Power Coordinated Two-Stage MG Scheduling for Resilient Distribution Systems Under Uncertainties. IEEE Trans. Smart Grid 2022, 13, 2986–2998. [Google Scholar] [CrossRef]
- Ding, Y.F.; Morstyn, T.; McCulloch, M.D. Distributionally Robust Joint Chance-Constrained Optimization for Networked Microgrids Considering Contingencies and Renewable Uncertainty. IEEE Trans. Smart Grid 2022, 13, 2467–2478. [Google Scholar] [CrossRef]
- Mesbah, A. Stochastic Model Predictive Control: An Overview and Perspectives for Future Research. IEEE Control. Syst. Mag. 2016, 36, 30–44. [Google Scholar] [CrossRef]
- Zhao, Z.L.; Guo, J.T.; Luo, X.; Lai, C.S.; Yang, P.; Lai, L.L.; Li, P.; Guerrero, J.M.; Shahidehpour, M. Distributed Robust Model Predictive Control-Based Energy Management Strategy for Islanded Multi-Microgrids Considering Uncertainty. IEEE Trans. Smart Grid 2022, 13, 2107–2120. [Google Scholar] [CrossRef]
- Zhang, Z.W.; Wang, C.F.; Wu, Q.W.; Dong, X.M. Optimal dispatch for cross-regional integrated energy system with renewable energy uncertainties: A unified spatial-temporal cooperative framework. Energy 2024, 292, 130433. [Google Scholar] [CrossRef]
- Jabr, R.A. Linear Decision Rules for Control of Reactive Power by Distributed Photovoltaic Generators. IEEE Trans. Power Syst. 2018, 33, 2165–2174. [Google Scholar] [CrossRef]
- Yang, Z.F.; Zhong, H.W.; Bose, A.; Zheng, T.X.; Xia, Q.; Kang, C.Q. A Linearized OPF Model with Reactive Power and Voltage Magnitude: A Pathway to Improve the MW-Only DC OPF. IEEE Trans. Power Syst. 2018, 33, 1734–1745. [Google Scholar] [CrossRef]
- Wang, B.B.; Tang, N.; Bo, R.; Li, F.X. Three-phase DLMP model based on linearized power flow for distribution with application to DER benefit studies. Int. J. Electr. Power Energy Syst. 2021, 130, 106884. [Google Scholar] [CrossRef]
- Sperr, F.; Stai, E.; Venkatraman, A.; Krause, T.; Hug, G. Service Restoration in the Medium Voltage Grid Minimizing the SAIDI Contribution After Primary Substation Failures. IEEE Trans. Power Syst. 2024, 39, 66–82. [Google Scholar] [CrossRef]
- Tan, Y.; Chen, Y.Y.; Li, Y.; Cao, Y.J. Linearizing Power Flow Model: A Hybrid Physical Model-Driven and Data-Driven Approach. IEEE Trans. Power Syst. 2020, 35, 2475–2478. [Google Scholar] [CrossRef]
- Li, Z.G.; Yu, J.Y.; Wu, Q.H. Approximate Linear Power Flow Using Logarithmic Transform of Voltage Magnitudes with Reactive Power and Transmission Loss Consideration. IEEE Trans. Power Syst. 2018, 33, 4593–4603. [Google Scholar] [CrossRef]
- Liu, Y.T.; Li, Z.S.; Zhou, Y. Data-Driven-Aided Linear Three-Phase Power Flow Model for Distribution Power Systems. IEEE Trans. Power Syst. 2022, 37, 2783–2795. [Google Scholar] [CrossRef]
- Shao, Z.T.; Zhai, Q.Z.; Wu, J.; Guan, X.H. Data Based Linear Power Flow Model: Investigation of a Least-Squares Based Approximation. IEEE Trans. Power Syst. 2021, 36, 4246–4258. [Google Scholar] [CrossRef]
- Liu, Y.T.; Li, Z.S.; Zhao, J.B. Robust Data-Driven Linear Power Flow Model with Probability Constrained Worst-Case Errors. IEEE Trans. Power Syst. 2022, 37, 4113–4116. [Google Scholar] [CrossRef]
- Liu, Y.X.; Wang, Y.; Zhang, N.; Lu, D.; Kang, C.Q. A Data-Driven Approach to Linearize Power Flow Equations Considering Measurement Noise. IEEE Trans. Smart Grid 2020, 11, 2576–2587. [Google Scholar] [CrossRef]
- Liu, Y.X.; Zhang, N.; Wang, Y.; Yang, J.W.; Kang, C.Q. Data-Driven Power Flow Linearization: A Regression Approach. IEEE Trans. Smart Grid 2019, 10, 2569–2580. [Google Scholar] [CrossRef]
- An, M.L.; Lu, T.G.; Han, X.S. An online updated linear power flow model based on regression learning. IET Gener. Transm. Distrib. 2024, 18, 2006–2019. [Google Scholar] [CrossRef]
- Li, Z.M.; Wu, L.; Xu, Y.; Wang, L.H.; Yang, N. Distributed tri-layer risk-averse stochastic game approach for energy trading among multi-energy microgrids. Appl. Energy 2023, 331, 120282. [Google Scholar] [CrossRef]
- Bertsekas, D.P.; Tsitsiklis, J.N.; Tsitsiklis, J.N. Introduction to Probability, 2nd ed.; Athena Scientific: Belmont, MA, USA, 2008. [Google Scholar]
- Alamo, T.; Tempo, R.; Luque, A. On the Sample Complexity of Randomized Approaches to the Analysis and Design under Uncertainty. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 4671–4676. [Google Scholar]
- Campi, M.C.; Garatti, S. A Sampling-and-Discarding Approach to Chance-Constrained Optimization: Feasibility and Optimality. J. Optim. Theory Appl. 2011, 148, 257–280. [Google Scholar] [CrossRef]
- Cannon, M.; Kouvaritakis, B.; Wu, X. Model predictive control for systems with stochastic multiplicative uncertainty and probabilistic constraints. Automatica 2009, 45, 167–172. [Google Scholar] [CrossRef]
- Cannon, M.; Kouvaritakis, B.; Wu, X.J. Probabilistic Constrained MPC for Multiplicative and Additive Stochastic Uncertainty. IEEE Trans. Autom. Control 2009, 54, 1626–1632. [Google Scholar] [CrossRef]
- Campi, M.C.; Garatti, S.; Prandini, M. The scenario approach for systems and control design. Annu. Rev. Control 2009, 33, 149–157. [Google Scholar] [CrossRef]
- Chen, Y.B.; Wu, C.; Qi, J.J. Data-driven Power Flow Method Based on Exact Linear Regression Equations. J. Mod. Power Syst. Clean Energy 2022, 10, 800–804. [Google Scholar] [CrossRef]


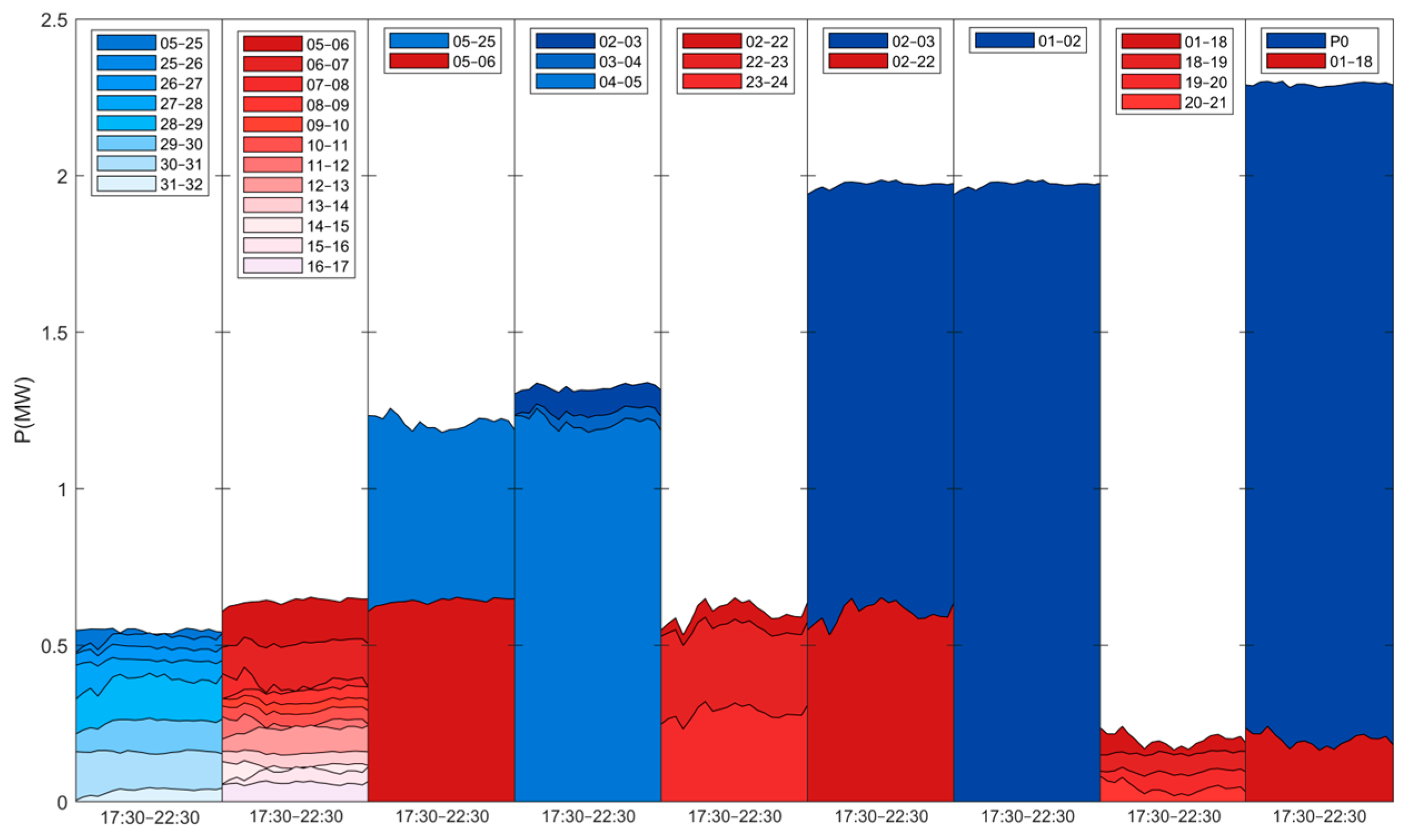

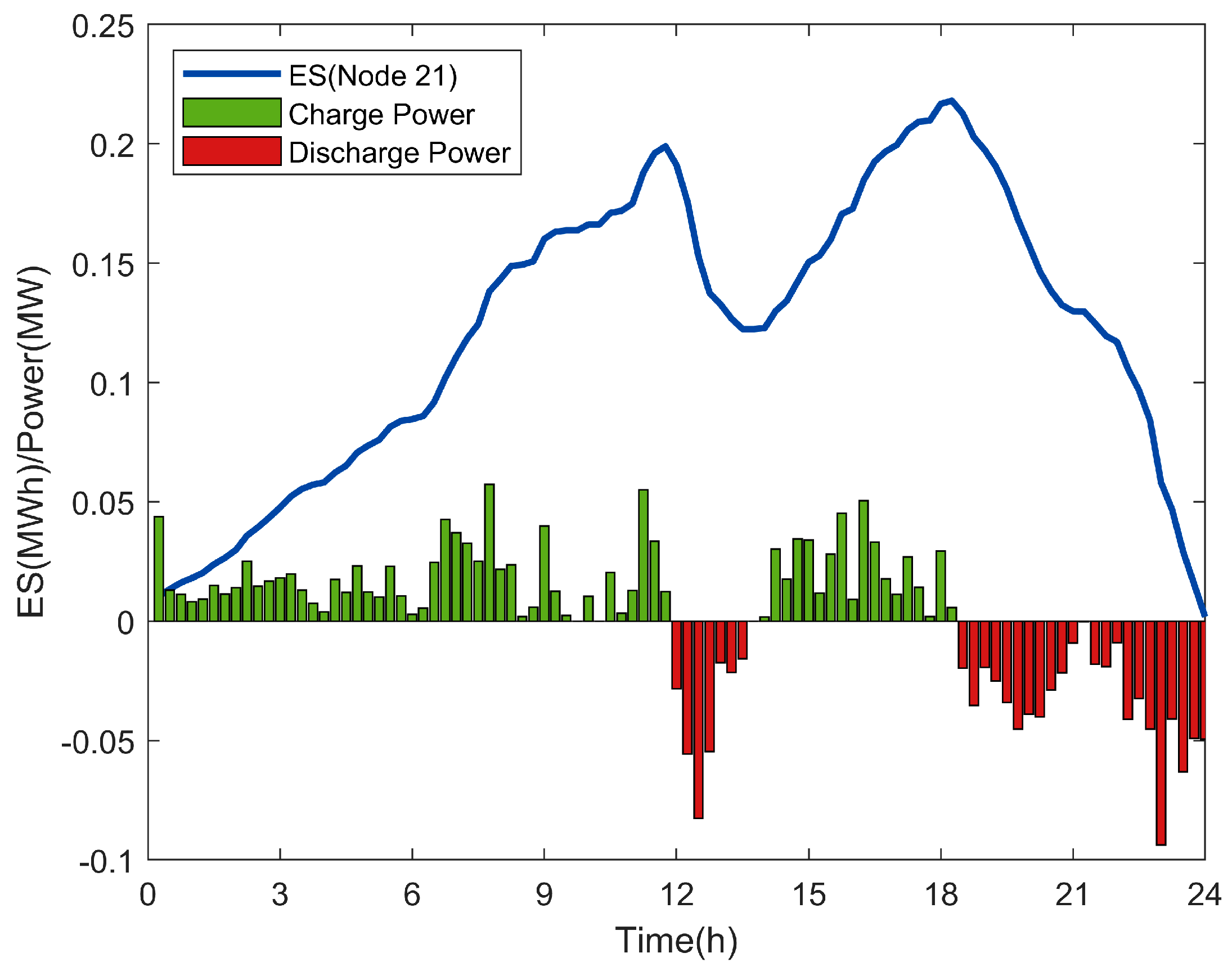
| Literature | Methodology | Voltage Control | ES | Uncertainty | Time Scale | Power Flow | Control Method |
|---|---|---|---|---|---|---|---|
| [3] | Distributed optimal tie-line power flow control for the multiple-MG system. | Not considered | Not considered | Not considered | Long | Nonlinear | Optimization |
| [4] | Output regulation approach combined with LQ optimal control | Considered | Not considered | Not considered | Short | Linear | Modern Control |
| [5] | External tie line power fluctuations smoothing strategy of new urban power grid | Not considered | Considered | Considered | Long | Nonlinear | Optimization |
| [6] | Fuzzy logic control based and optimized fuzzy logic control based SMES method | Considered | Considered | Not considered | Short | Nonlinear | Optimization |
| [7] | Flat tie-line power scheduling control of grid-connected hybrid MGs | Considered | Considered | Not considered | Short | Nonlinear | Classical Control |
| [8] | Improved droop control strategy for tie-line power of DC-MG | Considered | Considered | Not considered | Short | Nonlinear | Classical Control |
| [9] | Game-theoretic demand side management for smoothing tie-line power | Not considered | Not considered | Considered | Long | Nonlinear | Game Theory |
| [10] | A unifying hierarchical control scheme based on distributed communication | Considered | Considered | Not considered | Short | Nonlinear | Classical Control |
| [11] | Optimal coordination control for tie-line smoothing in hybrid energy storage systems | Not considered | Considered | Not considered | Long | Nonlinear | Modern Control |
| [12] | A tie-line power smoothing via a novel dynamic real-time pricing mechanism in multi-MG | Not considered | Considered | Considered | Short | Linear | Optimization |
| [13] | Dynamic control of grid-connected MGs for tie-line smoothing | Considered | Considered | Not considered | Short | Nonlinear | Modern Control |
| [14] | A multi-time-scale tie-line energy and reserve allocation model | Not considered | Not considered | Considered | Long | Linear | Optimization |
| This paper | SMPC for the tie-line power smoothing with a novel data-driven LPF model | Considered | Considered | Considered | Long | Linear | SMPC |
| Section | Index | The Traditional Data-Driven LPF | The Proposed Method | Improvement |
|---|---|---|---|---|
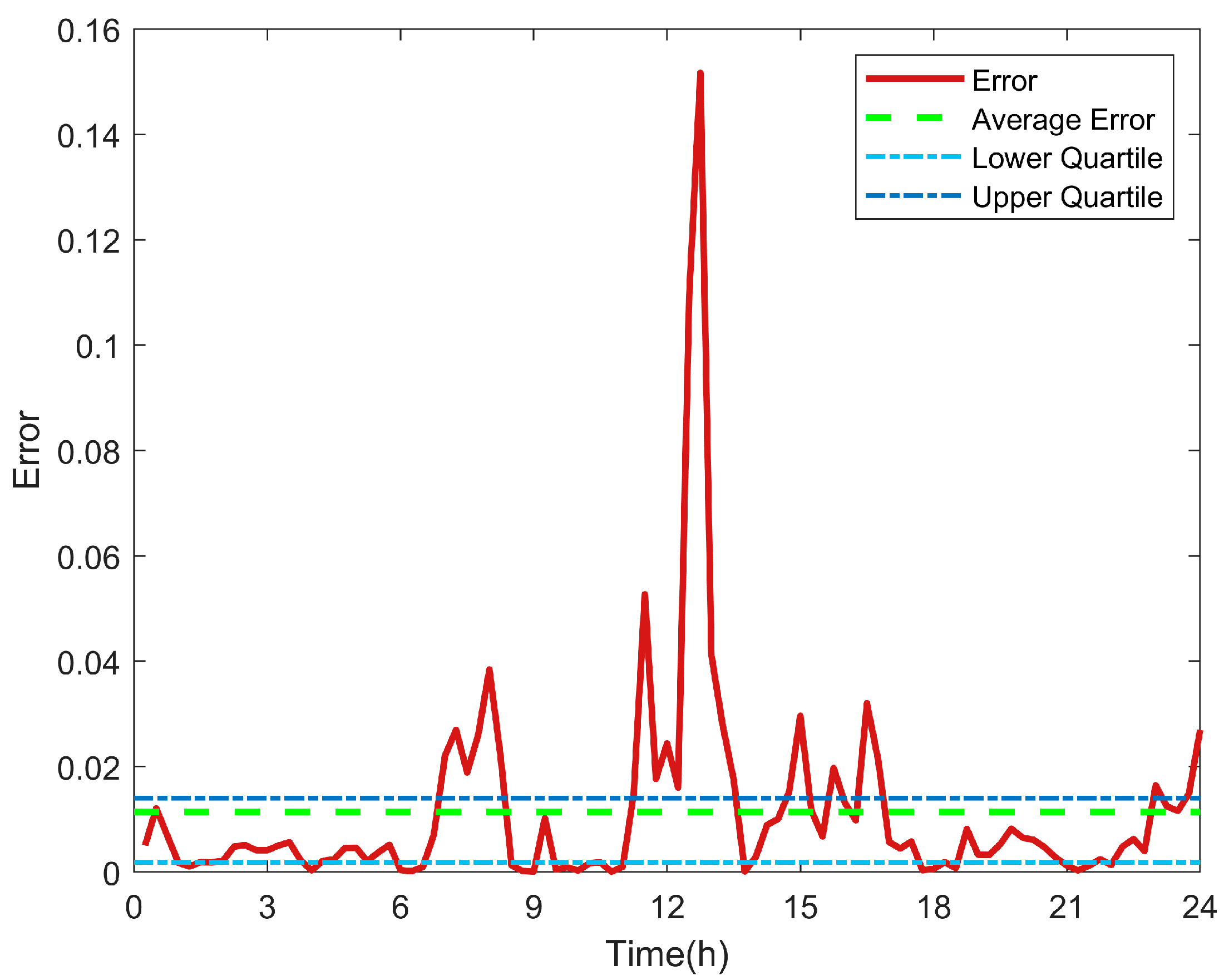
| Error | Maximum of relative error | 1.73960% | 0.32083% | 81.56% |
| Upper quartile of relative error | 0.43340% | 0.01578% | 96.36% | |
| Mean of relative error | 0.27041% | 0.01317% | 95.13% | |
| Median of relative error | 0.15968% | 0.00421% | 97.36% | |
| Lower quartile of relative error | 0.04535% | 0.00070% | 98.47% | |
| Minimum of relative error | 0.00019% | 0% | 100% | |
| Efficiency | Time for initializing | 0.016 s | 24.88 s | / |
| Data burden for initializing | 1455 KB | 678 KB | 53.40% | |
| Time for model updating once | 0.016 s | 0.002 s | 87.50% | |
| Data burden for model updating once | 1455 KB | 96 KB | 93.40% | |
| Time for total operation (per minute in 7 days) | 161.28 s | 45.04 s | 72.07% | |
| Data burden for total operation (per minute in 7 days) | 13.987 GB | 0.923 GB | 93.40% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, M.; Han, X.; Lu, T. A Stochastic Model Predictive Control Method for Tie-Line Power Smoothing under Uncertainty. Energies 2024, 17, 3515. https://doi.org/10.3390/en17143515
An M, Han X, Lu T. A Stochastic Model Predictive Control Method for Tie-Line Power Smoothing under Uncertainty. Energies. 2024; 17(14):3515. https://doi.org/10.3390/en17143515
Chicago/Turabian StyleAn, Molin, Xueshan Han, and Tianguang Lu. 2024. "A Stochastic Model Predictive Control Method for Tie-Line Power Smoothing under Uncertainty" Energies 17, no. 14: 3515. https://doi.org/10.3390/en17143515
APA StyleAn, M., Han, X., & Lu, T. (2024). A Stochastic Model Predictive Control Method for Tie-Line Power Smoothing under Uncertainty. Energies, 17(14), 3515. https://doi.org/10.3390/en17143515










