A Productivity Prediction Method of Fracture-Vuggy Reservoirs Based on the PSO-BP Neural Network
Abstract
1. Introduction
2. Methods
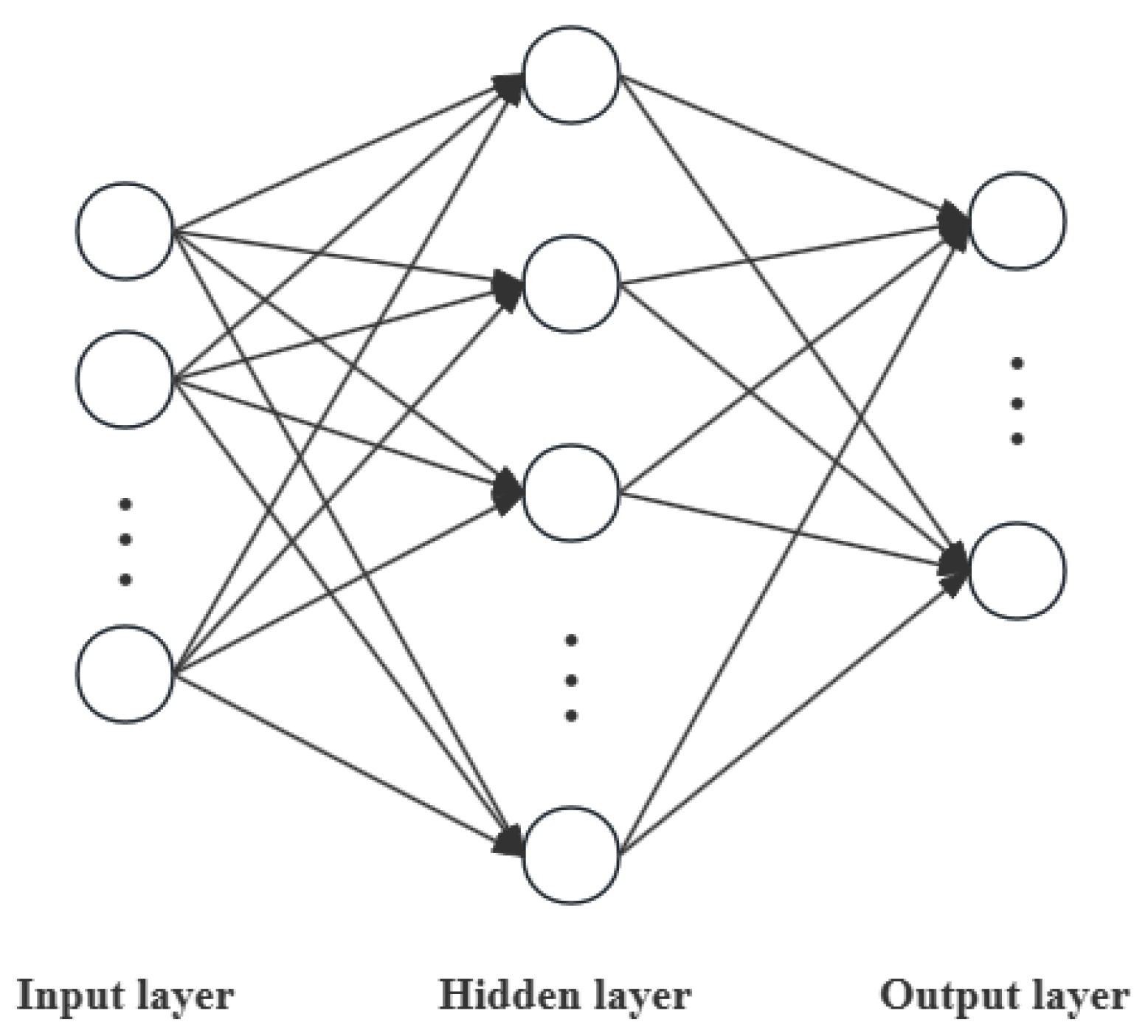
2.1. BP Neural Network Algorithm
2.2. PSO Algorithm
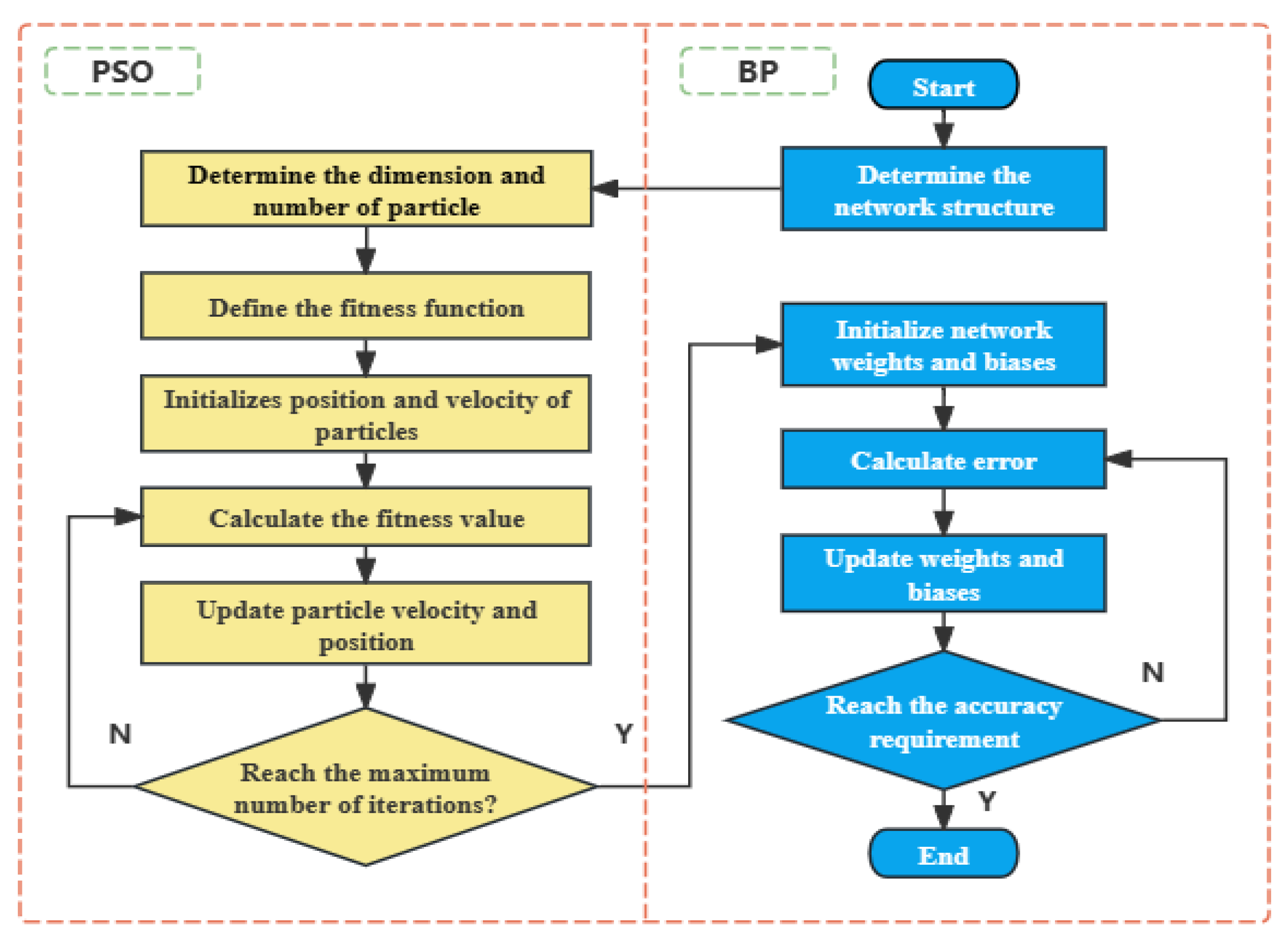
2.3. PSO-BP Algorithm
3. Data
3.1. Feature Data
- Distance from fault: During this study, we found that the dissolution cavity and fracture are closely associated, and the high-angle fracture under the unconformity plays an important role in promoting the development of weathering karstification, while the low-angle fracture has a good correspondence with the burial dissolution, and the fault is an important factor affecting the reservoir in the Tahe area. Therefore, we considered the vertical distance between the well location and the fracture as one of the factors affecting the production of wells.
- Root mean square of amplitude (RMS Amplitude): Because the amplitude value is squared in the process of calculation, it becomes more sensitive to changes in amplitude, and is thus suitable for the analysis of carbonate karst reservoirs.
- Amplitude change rate: This attribute has a similar effect to the RMS amplitude, and is sensitive to abrupt changes in amplitude in the formation. It can identify the size and scale of karst caverns in carbonate reservoirs, and is thus a key attribute for identifying fracture-vuggy reservoirs.
- Percentage of frequency attenuation: If porosity has developed in a reservoir and is filled with oil or gas, seismic wave absorption increases, high-frequency absorption attenuation intensifies, and low-frequency energy increases. The frequency attenuation percentage attribute is the percentage of high-frequency attenuation, and is thus widely used in hydrocarbon detection and is sensitive to gas reservoirs.
- Sweetness: The sweetness value is obtained by the ratio of the instantaneous amplitude of the seismic wave to the instantaneous frequency of the root mean square. Lateral changes in transient amplitudes are usually related to lithology and hydrocarbon accumulation, and the instantaneous frequency can provide information on the effective frequency absorption effect of the seismic event, fracture effects, and reservoir thickness. We can extract the maximum value, minimum value, arithmetic mean value, and geometric mean value of sweetness based on the obtained sweetness value.
- Beaded area: A fracture-cavity reservoir is mainly characterized by a string of bead-shaped seismic reflections, and the size of the beaded area provides important mapping of a fracture-cavity reservoir product.
3.2. Feature Optimization
- (1)
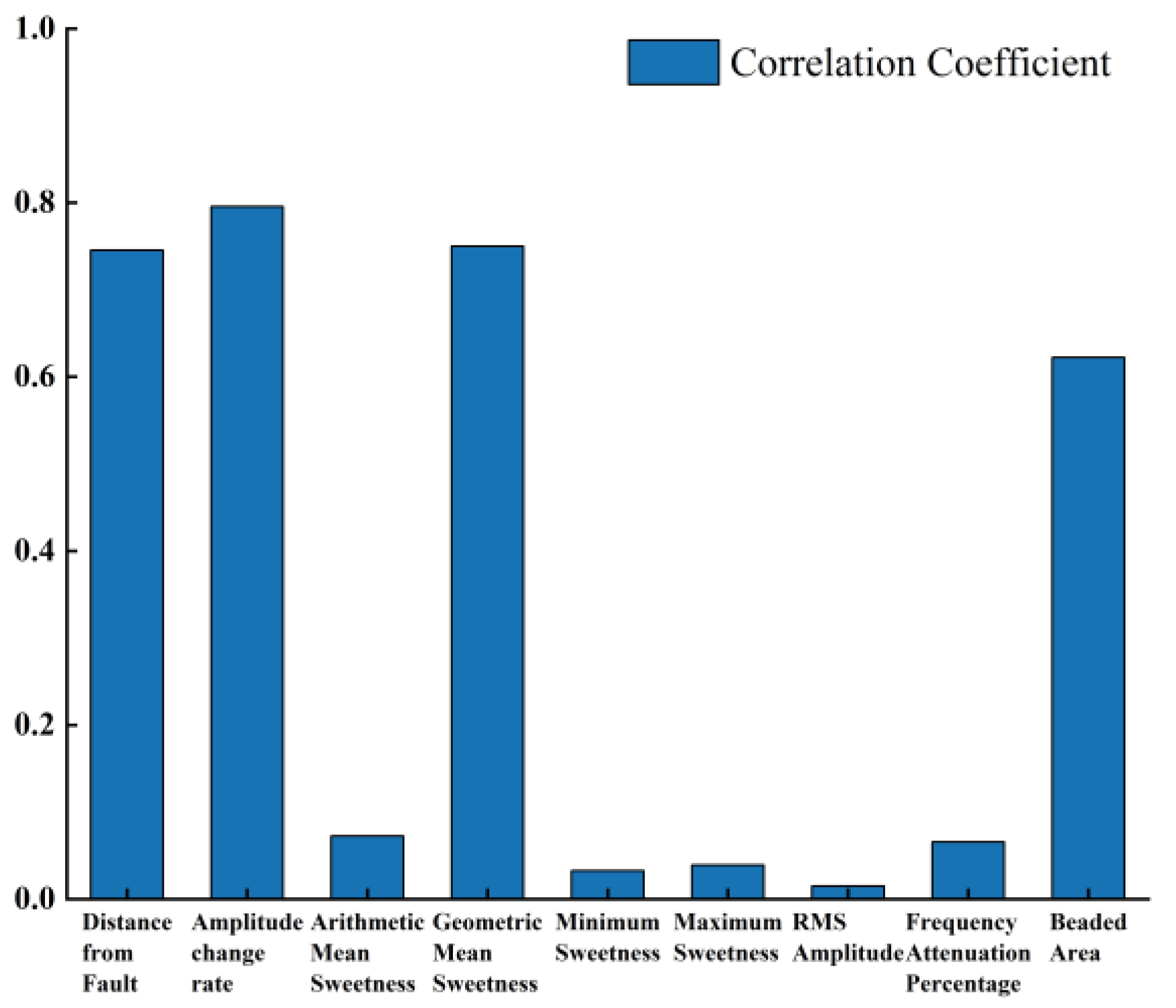
- Some seismic attributes may have nothing to do with the target layer, but reflect the change in interference; if the input attributes are not identified, it will cause confusion, as shown in Figure 3, where there is no clear correlation between some seismic attributes and well production;
- (2)
- The increase in attributes will bring about computational difficulties, and too much data will take up a lot of storage space and cause a long computation time;
- (3)
- A large number of attributes will mean that there are a lot of interrelated factors, resulting in duplication and a waste of information.

4. Results
4.1. Pretreatment
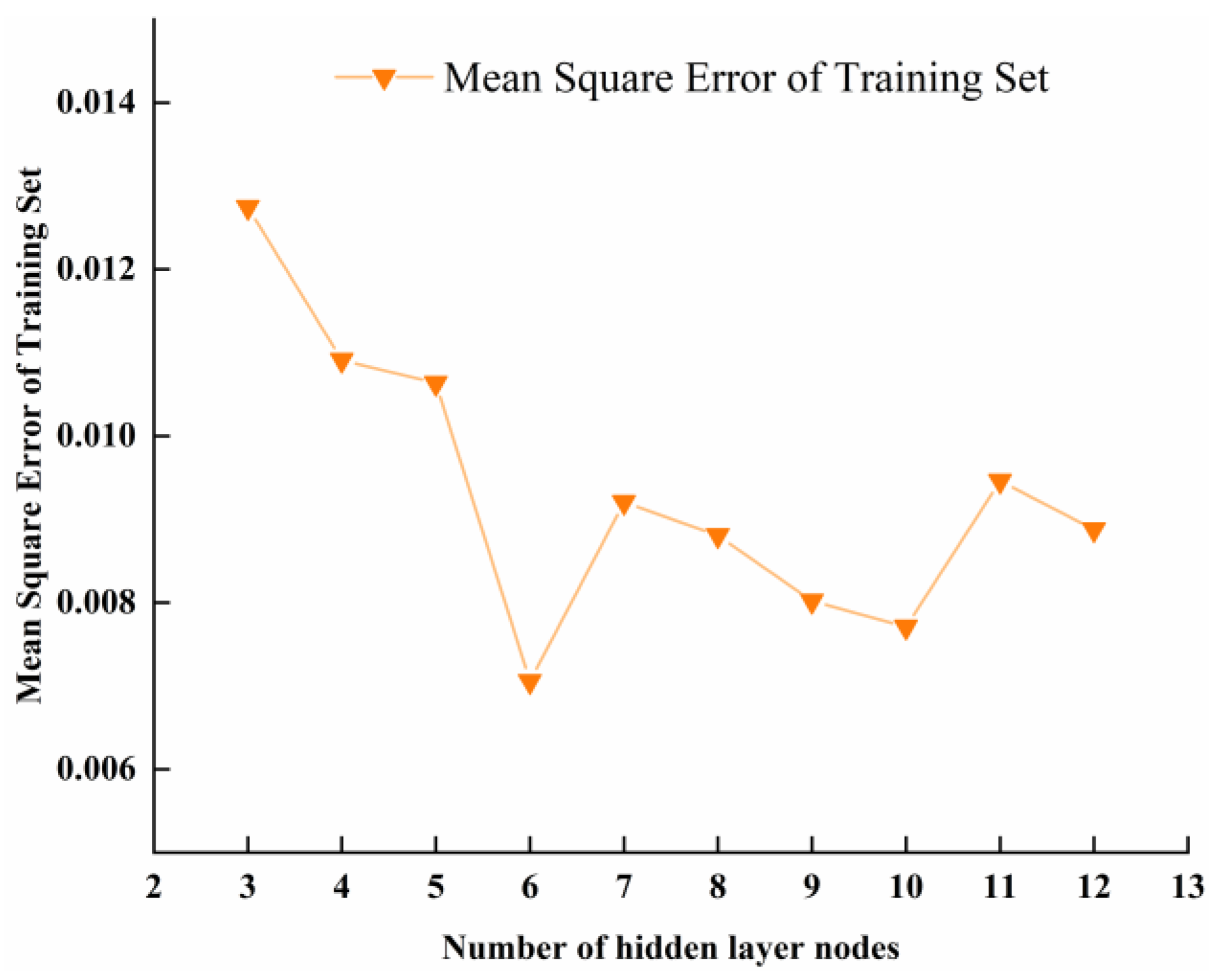
4.2. Model Setting
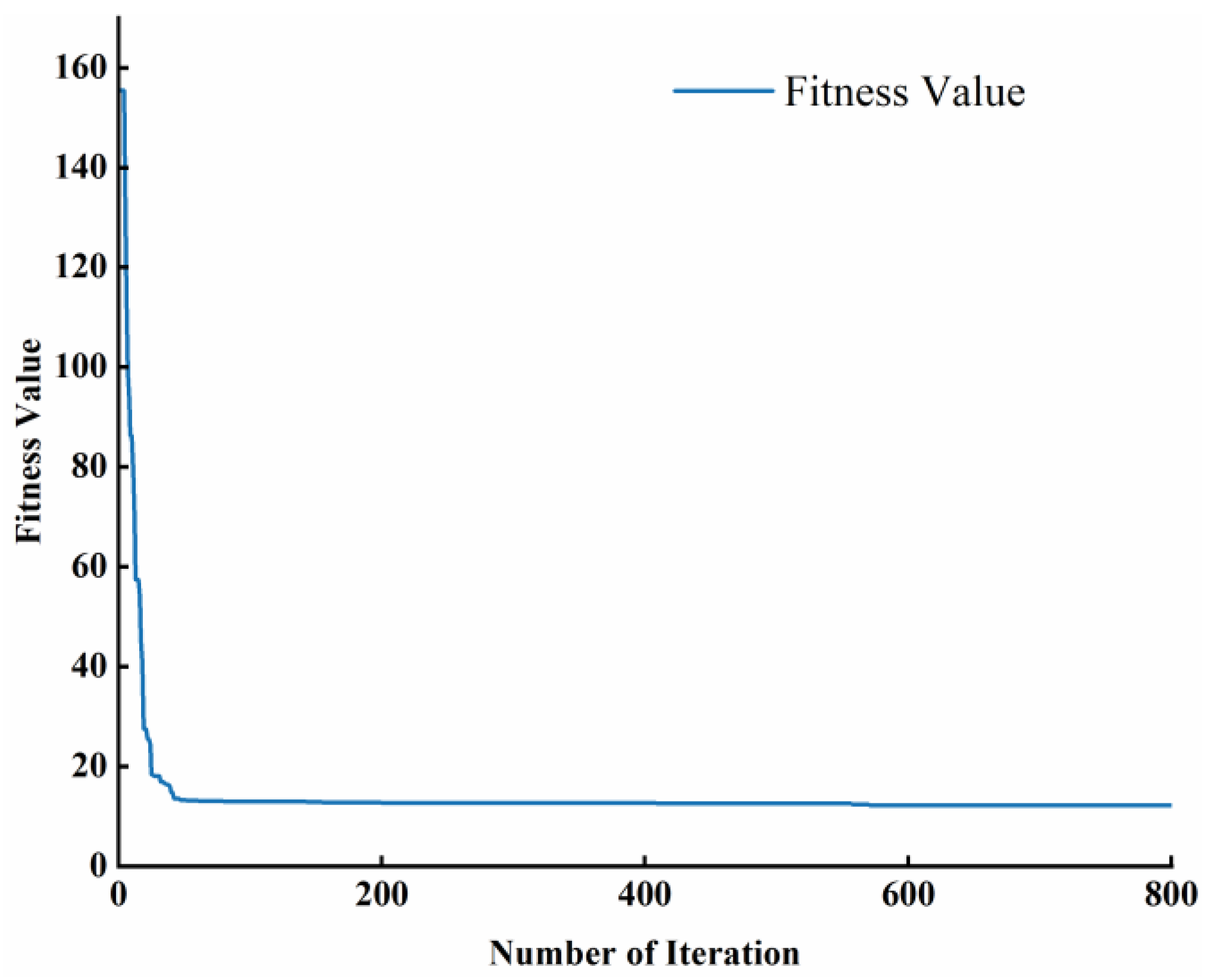
4.3. Productivity Prediction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, Z.-X.; Li, S.-Y.; Li, B.-F.; Chen, D.-Q.; Liu, Z.-Y.; Li, Z.-M. A review of development methods and EOR technologies for carbonate reservoirs. Pet. Sci. 2020, 17, 990–1013. [Google Scholar] [CrossRef]
- Liang, T.; Hou, J.; Qu, M.; Song, C.; Li, J.; Tan, T.; Lu, X.; Zheng, Y. Flow behaviors of nitrogen and foams in micro-visual fracture-vuggy structures. RSC Adv. 2021, 11, 28169–28177. [Google Scholar] [CrossRef] [PubMed]
- Qu, M.; Hou, J.; Qi, P.; Zhao, F.; Ma, S.; Churchwell, L.; Wang, Q.; Li, H.; Yang, T. Experimental study of fluid behaviors from water and nitrogen floods on a 3-D visual fractured-vuggy model. J. Pet. Sci. Eng. 2018, 166, 871–879. [Google Scholar] [CrossRef]
- Nwonodi, R.I. A novel model for predicting the productivity index of horizontal/vertical wells based on Darcy’s law, drainage radius, and flow convergence. Heliyon 2024, 10, e25073. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Xie, P.; Zhang, H.; Liu, Y.; Yang, A. Fracture-vuggy carbonate reservoir characterization based on multiple geological information fusion. Front. Earth Sci. 2024, 11, 1345028. [Google Scholar] [CrossRef]
- He, S.; Chen, B.; Yuan, F.; Wang, X.; Wang, T. Dynamic Reserve Calculation Method of Fractured-Vuggy Reservoir Based on Modified Comprehensive Compression Coefficient. Processes 2024, 12, 640. [Google Scholar] [CrossRef]
- Niu, W.; Lu, J.; Sun, Y. An improved empirical model for rapid and accurate production prediction of shale gas wells. J. Pet. Sci. Eng. 2022, 208, 109800. [Google Scholar] [CrossRef]
- Liang, H.-B.; Zhang, L.-H.; Zhao, Y.-L.; Zhang, B.-N.; Chang, C.; Chen, M.; Bai, M.-X. Empirical methods of decline-curve analysis for shale gas reservoirs: Review, evaluation, and application. J. Nat. Gas Sci. Eng. 2020, 83, 103531. [Google Scholar] [CrossRef]
- Makinde, I.; Lee, W.J. Production Forecasting in Shale Volatile Oil Reservoirs Using Reservoir Simulation, Empirical and Analytical Methods. In Proceedings of the 4th Unconventional Resources Technology Conference, San Antonio, TX, USA, 1–3 August 2016. [Google Scholar]
- Ozkan, E.; Brown, M.; Raghavan, R.; Kazemi, H. Comparison of fractured-horizontal-well performance in tight sand and shale reservoirs. SPE Reserv. Eval. Eng. 2011, 14, 248–259. [Google Scholar] [CrossRef]
- Arumugham, A.J.; Li, L.; Huang, J.; Luo, C.; Du, F.; Liu, Y.; Ulkhaq, M.M.; Kocisko, M.; Goyal, R.K.; Yusmawiza, W.A.; et al. Study on Productivity Numerical Simulation of Highly Deviated and Fractured Wells in Deep Oil and Gas Reservoirs. In Proceedings of the 2016 The 3rd International Conference on Industrial Engineering and Applications (ICIEA 2016), Hong Kong, China, 28–30 April 2016; Volume 68. [Google Scholar]
- Liu, L.; Fan, W.; Sun, X.; Huang, Z.; Yao, J.; Liu, Y.; Zeng, Q.; Wang, X. Gas condensate well productivity in fractured vuggy carbonate reservoirs: A numerical modeling study. Geoenergy Sci. Eng. 2023, 225, 211694. [Google Scholar] [CrossRef]
- Nie, J.; Wang, H.; Hao, Y. Rapid productivity prediction method for frac hits affected wells based on gas reservoir numerical simulation and probability method. Open Phys. 2023, 21, 20220233. [Google Scholar] [CrossRef]
- Bi, G.; Han, F.; Li, M.; Wu, J.; Cui, Y.; Wang, X. Research on Productivity Prediction Model of Three-Dimensional Directional Wells in Different Reservoirs. J. Energy Eng. 2023, 149, 04023020. [Google Scholar] [CrossRef]
- Sircar, A.; Yadav, K.; Rayavarapu, K.; Bist, N.; Oza, H. Application of machine learning and artificial intelligence in oil and gas industry. Pet. Res. 2021, 6, 379–391. [Google Scholar] [CrossRef]
- Kuang, L.; Liu, H.; Ren, Y.; Luo, K.; Shi, M.; Su, J.; Li, X. Application and development trend of artificial intelligence in petroleum exploration and development. Pet. Explor. Dev. 2021, 48, 1–14. [Google Scholar] [CrossRef]
- Li, H.; Yu, H.; Cao, N.; Tian, H.; Cheng, S. Applications of Artificial Intelligence in Oil and Gas Development. Arch. Comput. Methods Eng. 2020, 28, 937–949. [Google Scholar] [CrossRef]
- Kong, X.; Liu, Y.; Xue, L.; Li, G.; Zhu, D. A Hybrid Oil Production Prediction Model Based on Artificial Intelligence Technology. Energies 2023, 16, 1027. [Google Scholar] [CrossRef]
- Hajizadeh, Y. Machine learning in oil and gas; a SWOT analysis approach. J. Pet. Sci. Eng. 2019, 176, 661–663. [Google Scholar] [CrossRef]
- Fan, Z.; Liu, X.; Wang, Z.; Liu, P.; Wang, Y. A Novel Ensemble Machine Learning Model for Oil Production Prediction with Two-Stage Data Preprocessing. Processes 2024, 12, 587. [Google Scholar] [CrossRef]
- Mohamed, A.; Hamdi, M.S.; Tahar, S. A Machine Learning Approach for Big Data in Oil and Gas Pipelines. In Proceedings of the 2015 3rd International Conference on Future Internet of Things and Cloud, Rome, Italy, 24–26 August 2015; pp. 585–590. [Google Scholar]
- Ning, Y.; Kazemi, H.; Tahmasebi, P. A comparative machine learning study for time series oil production forecasting: ARIMA, LSTM, and Prophet. Comput. Geosci. 2022, 164, 105126. [Google Scholar] [CrossRef]
- Han, D.; Jung, J.; Kwon, S. Comparative Study on Supervised Learning Models for Productivity Forecasting of Shale Reservoirs Based on a Data-Driven Approach. Appl. Sci. 2020, 10, 1267. [Google Scholar] [CrossRef]
- Wang, T.; Wang, Q.; Shi, J.; Zhang, W.; Ren, W.; Wang, H.; Tian, S. Productivity Prediction of Fractured Horizontal Well in Shale Gas Reservoirs with Machine Learning Algorithms. Appl. Sci. 2021, 11, 12064. [Google Scholar] [CrossRef]
- Yuan, Z.; Huang, H.; Jiang, Y.; Li, J. Hybrid deep neural networks for reservoir production prediction. J. Pet. Sci. Eng. 2021, 197, 108111. [Google Scholar] [CrossRef]
- Abdullayeva, F.; Imamverdiyev, Y. Development of Oil Production Forecasting Method based on Deep Learning. Stat. Optim. Inf. Comput. 2019, 7, 826–839. [Google Scholar] [CrossRef]
- Zhang, L.; Dou, H.; Wang, T.; Wang, H.; Peng, Y.; Zhang, J.; Liu, Z.; Mi, L.; Jiang, L. A production prediction method of single well in water flooding oilfield based on integrated temporal convolutional network model. Pet. Explor. Dev. 2022, 49, 1150–1160. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; McClelland, J.L.; Group, P.R. Parallel Distributed Processing, Volume 1: Explorations in the Microstructure of Cognition: Foundations; The MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Eberhart, R.; Kennedy, J. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Citeseer: University Park, PA, USA, 1995; pp. 1942–1948. [Google Scholar]
- Hampson, D.P.; Schuelke, J.S.; Quirein, J.A. Use of multiattribute transforms to predict log properties from seismic data. Geophysics 2001, 66, 220–236. [Google Scholar] [CrossRef]
- Schultz, P.S.; Ronen, S.; Hattori, M.; Corbett, C. Seismic-guided estimation of log properties (Part 1: A data-driven interpretation methodology). Lead. Edge 1994, 13, 305–310. [Google Scholar] [CrossRef]
- Zahmatkesh, I.; Kadkhodaie, A.; Soleimani, B.; Azarpour, M. Integration of well log-derived facies and 3D seismic attributes for seismic facies mapping: A case study from mansuri oil field, SW Iran. J. Pet. Sci. Eng. 2021, 202, 108563. [Google Scholar] [CrossRef]
- Liu, X.; Yang, J.; Li, Z.; Wang, Y. A new methodology on reservoir modeling in the fracture-cavity carbonate rock of Tahe Oilfield. In Proceedings of the SPE International Oil and Gas Conference and Exhibition in China, Beijing, China, 5–7 December 2006; SPE: Richardson, TX, USA, 2006; p. SPE-104429-MS. [Google Scholar]
- Chatterjee, S. A New Coefficient of Correlation. J. Am. Stat. Assoc. 2020, 116, 2009–2022. [Google Scholar] [CrossRef]

| Correlation Extent | Value |
|---|---|
| Non-correlation | 0.0~0.09 |
| Low-correlation | 0.1~0.3 |
| Middle-correlation | 0.3~0.5 |
| High-correlation | 0.5~1.0 |
| Method | MSE | RMSE | MAE | SSE × 103 | R-Square |
|---|---|---|---|---|---|
| PSO-BP | 80.5880 | 8.9771 | 6.4155 | 3.0623 | 0.9316 |
| BP | 104.0693 | 10.2014 | 7.8672 | 3.9546 | 0.9117 |
| SVM-R | 209.4602 | 14.4727 | 11.6104 | 7.9595 | 0.8223 |
| Linear-Regress | 128.9415 | 11.3552 | 9.2737 | 4.8998 | 0.8906 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, K.; Kang, Z.; Kang, Z. A Productivity Prediction Method of Fracture-Vuggy Reservoirs Based on the PSO-BP Neural Network. Energies 2024, 17, 3482. https://doi.org/10.3390/en17143482
Tian K, Kang Z, Kang Z. A Productivity Prediction Method of Fracture-Vuggy Reservoirs Based on the PSO-BP Neural Network. Energies. 2024; 17(14):3482. https://doi.org/10.3390/en17143482
Chicago/Turabian StyleTian, Kunming, Zhihong Kang, and Zhijiang Kang. 2024. "A Productivity Prediction Method of Fracture-Vuggy Reservoirs Based on the PSO-BP Neural Network" Energies 17, no. 14: 3482. https://doi.org/10.3390/en17143482
APA StyleTian, K., Kang, Z., & Kang, Z. (2024). A Productivity Prediction Method of Fracture-Vuggy Reservoirs Based on the PSO-BP Neural Network. Energies, 17(14), 3482. https://doi.org/10.3390/en17143482





