A Design Tool for Battery/Supercapacitor Hybrid Energy Storage Systems Based on the Physical–Electrochemical Degradation Battery Model BaSiS
Abstract
1. Introduction
1.1. Application of HESS for Grid Frequency Support
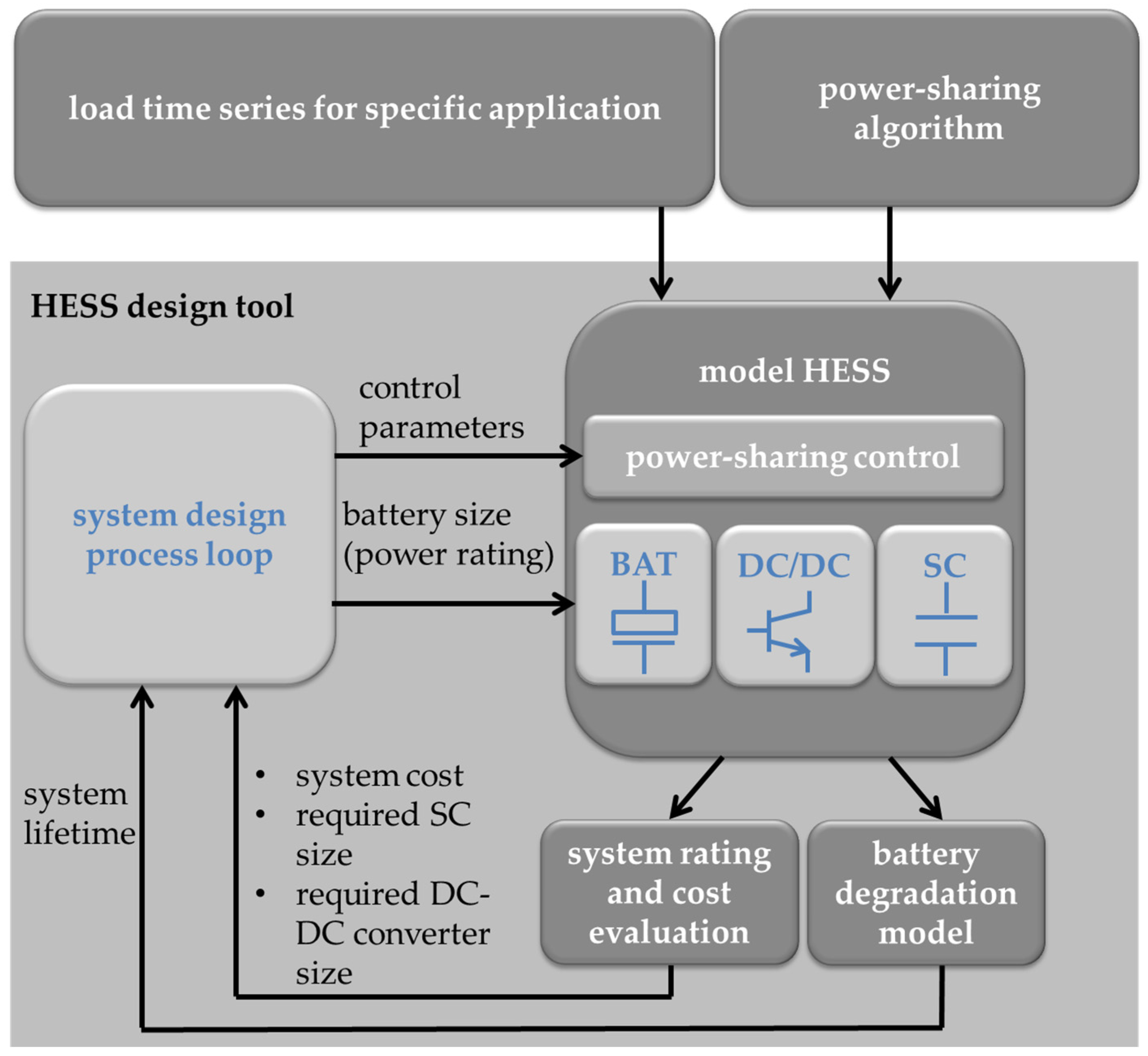
1.2. Concept and Structure of Design Tool
- How much impact does an additional SC module of a given size have on the battery lifetime?
- By how much can the battery size in the HESS be reduced, to achieve a pre-defined lifetime?
- In comparison, the general advantages of PEC degradation models are the following:
- The parameters to be determined in PEC models are properties of physical and electrochemical equations that express the internal aging processes in the battery cells (e.g., the growth of the SEI layer, evolution of cracks, etc.). Once the parameters have been determined, the model can extrapolate the battery performance and degradation to any temperatures, values, and current profiles. A comprehensive comparison with the cyclic testing results is usually conducted only for validation purposes in the final step.
- Different aspects of aging are considered in PEC models, which cause the loss of capacity and an increase in impedance. These aspects include passivation and the decrease of active surfaces, the increase of internal resistance, the growth of the SEI layer, loss of active lithium ions (Li-ions), and loss of active material, etc. As a result of battery aging, changes in other electrical characteristics critical to practical applications can also be examined, such as capacity, voltage profile, power profile, charging/discharging efficiency, and heat production, etc. Additionally, the PEC model can provide insights into the individual contributions of the different mechanisms to the aging process.
2. Evaluation of Battery Degradation with Detailed Physical–Electrochemical (PEC) Model
2.1. Description of the Physical–Electrochemical Battery Model
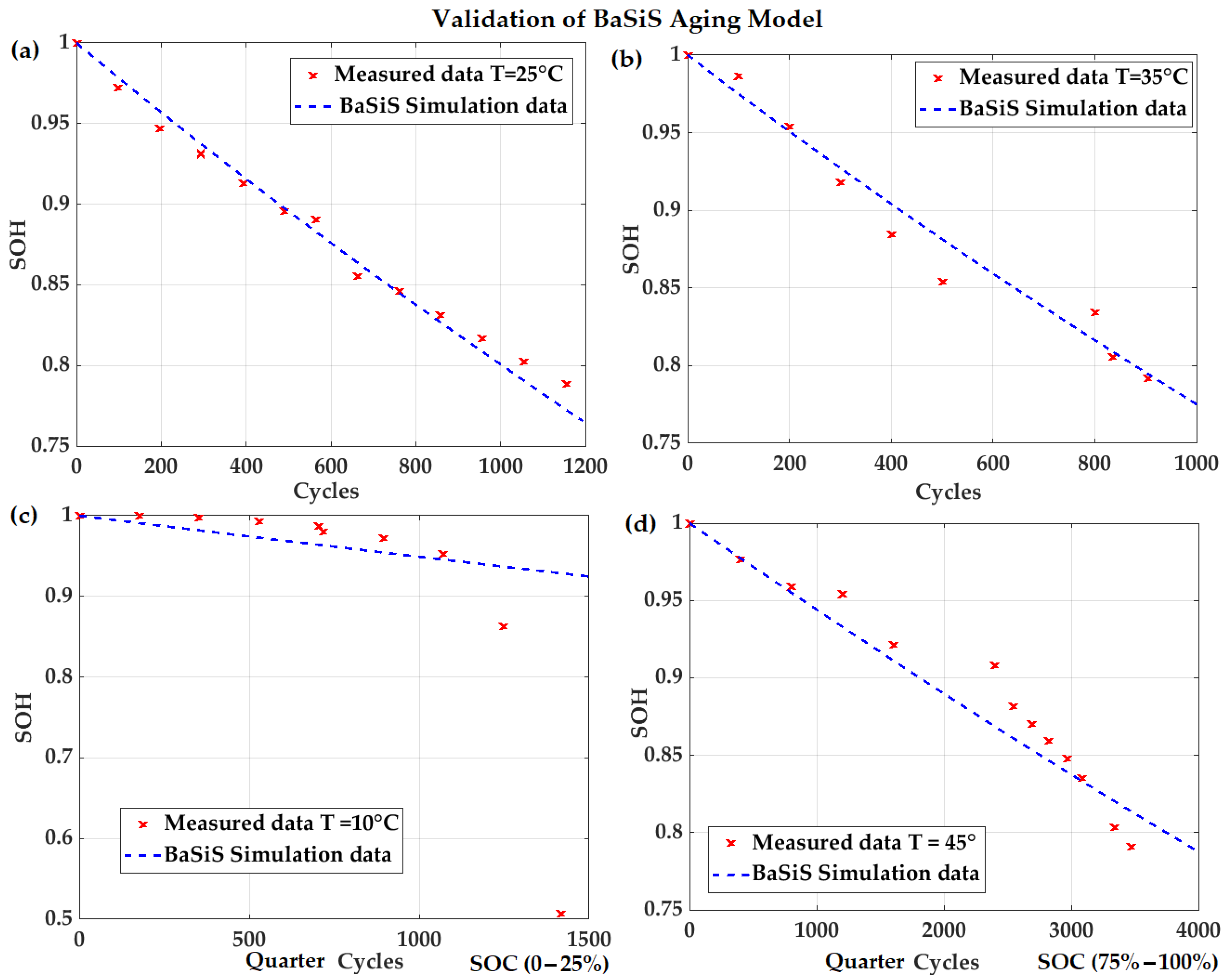
2.2. Model Characterization and Validation
2.2.1. Measured Batteries
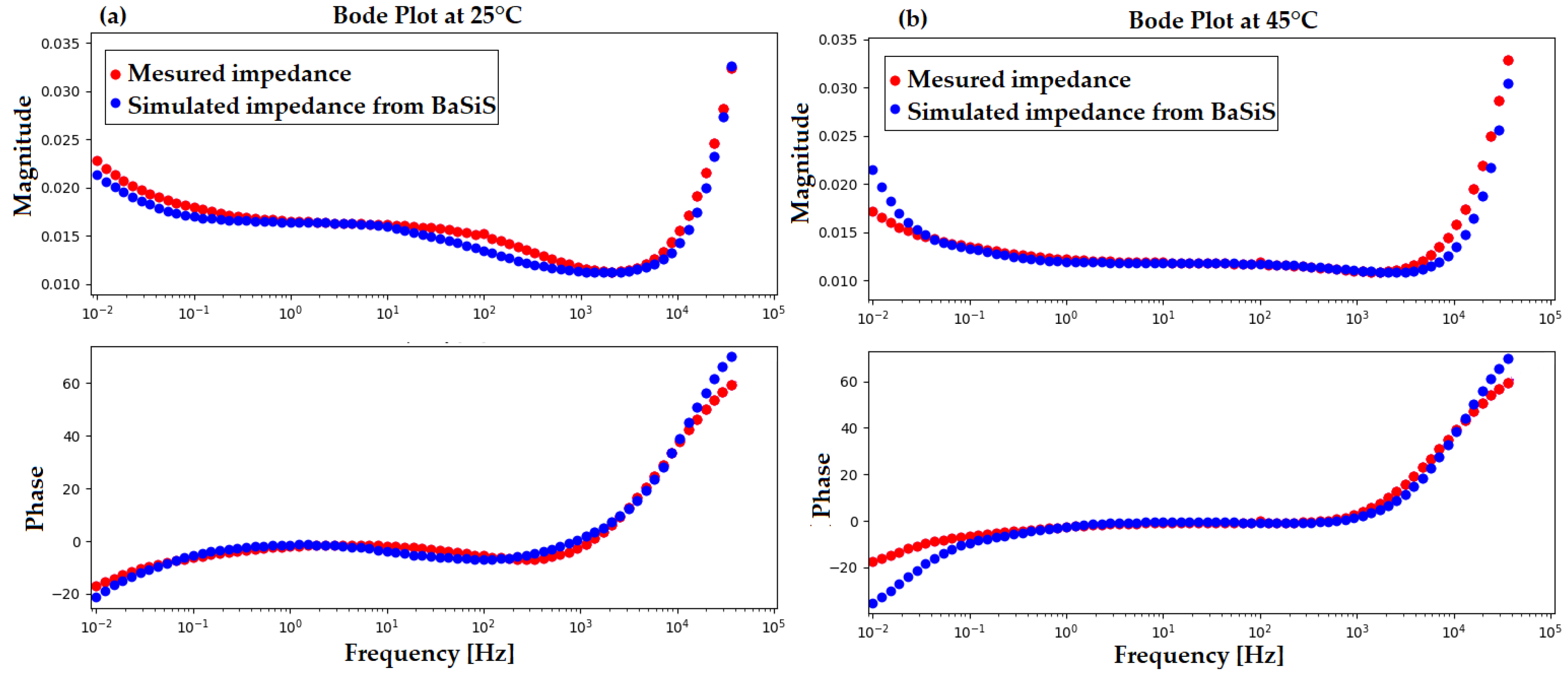
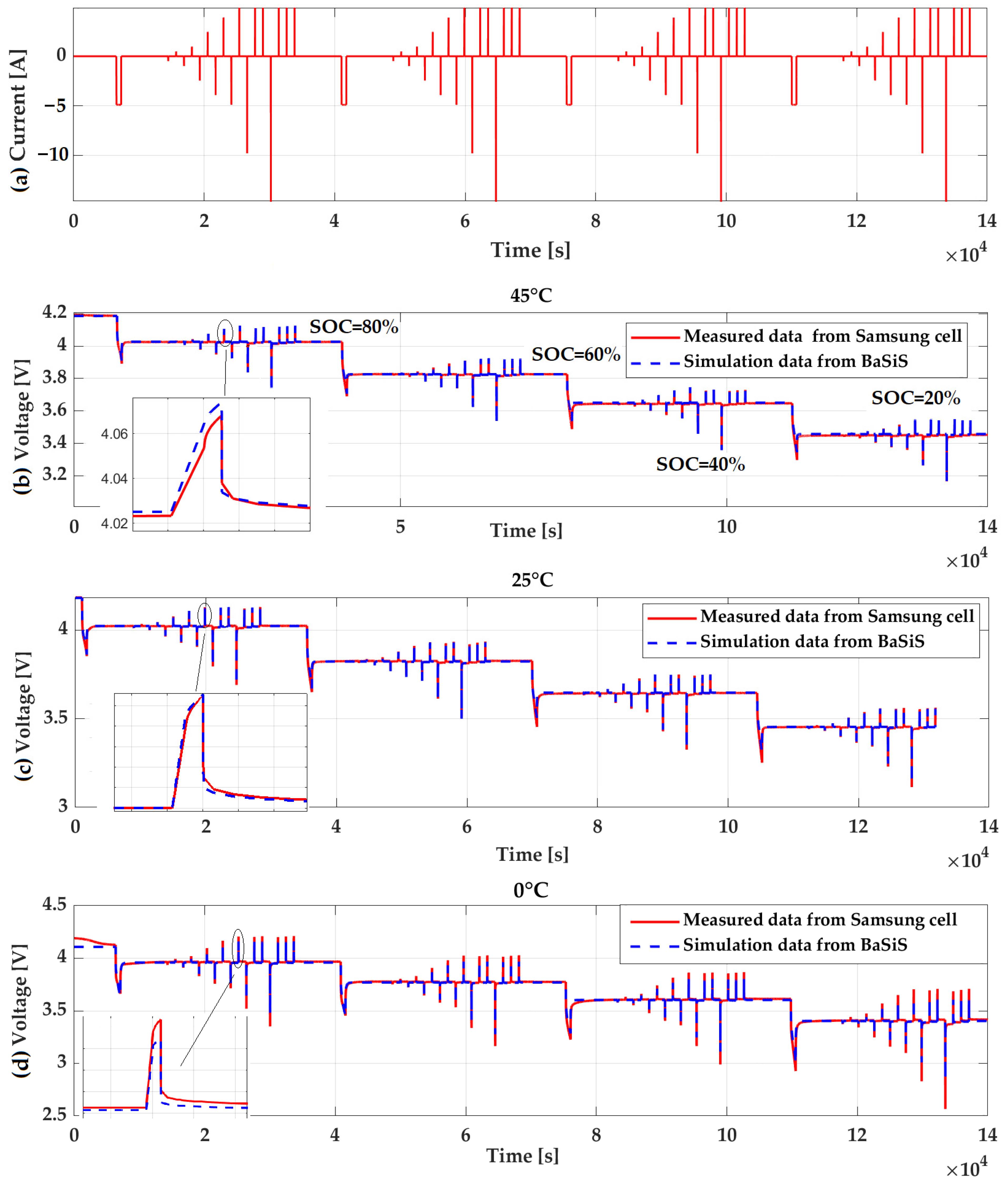
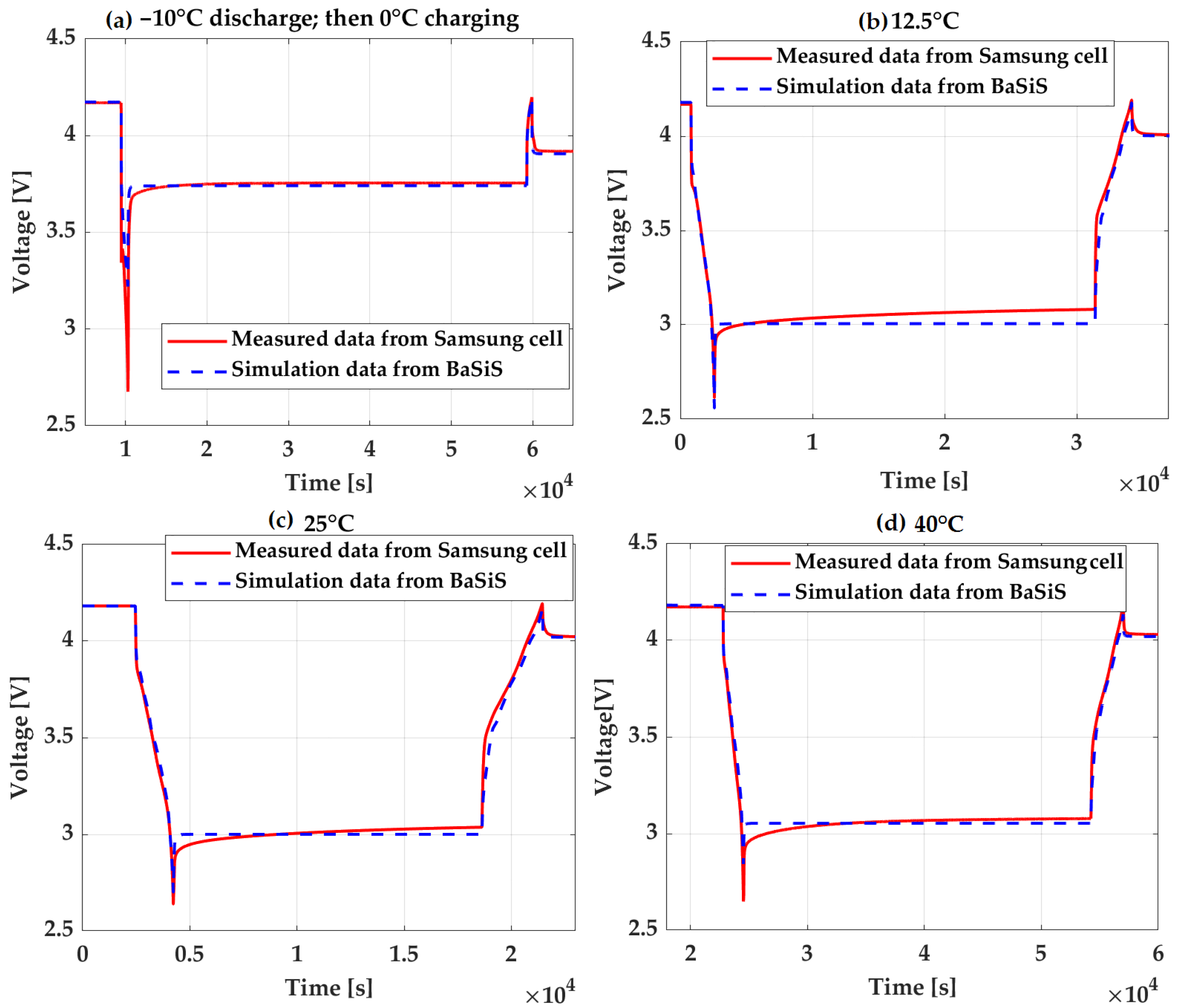
2.2.2. Performance Characterization and Validation
2.2.3. Degradation Characterization and Validation
3. Hybrid Energy Storage System (HESS)
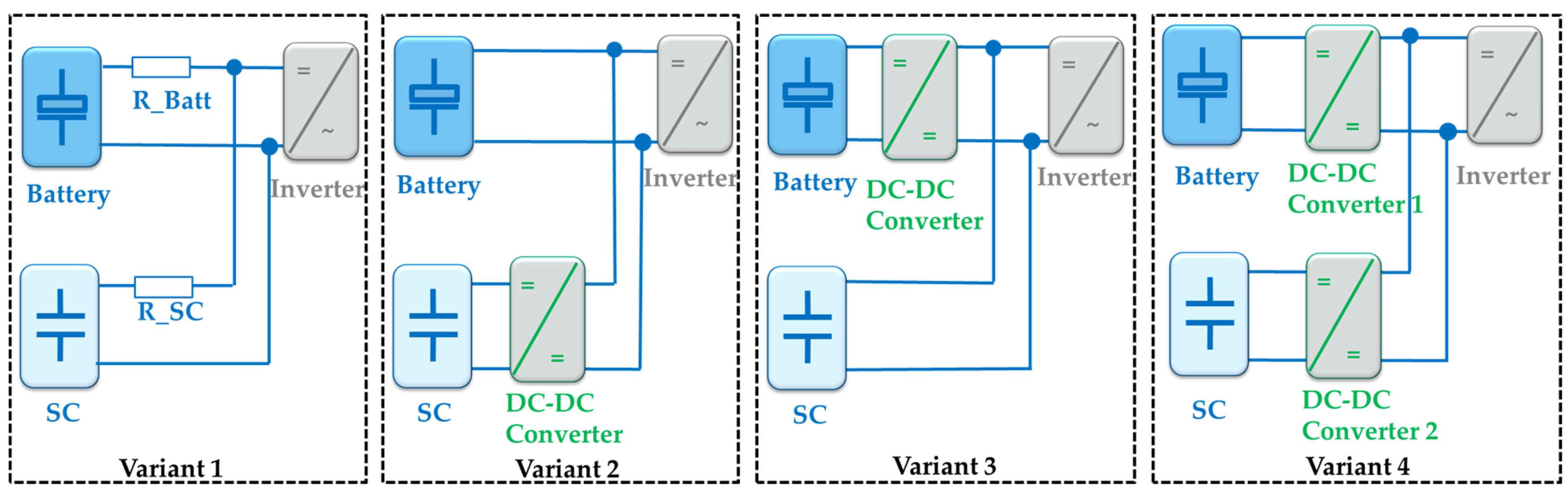
3.1. Topologies of Hybrid Energy Storage Systems
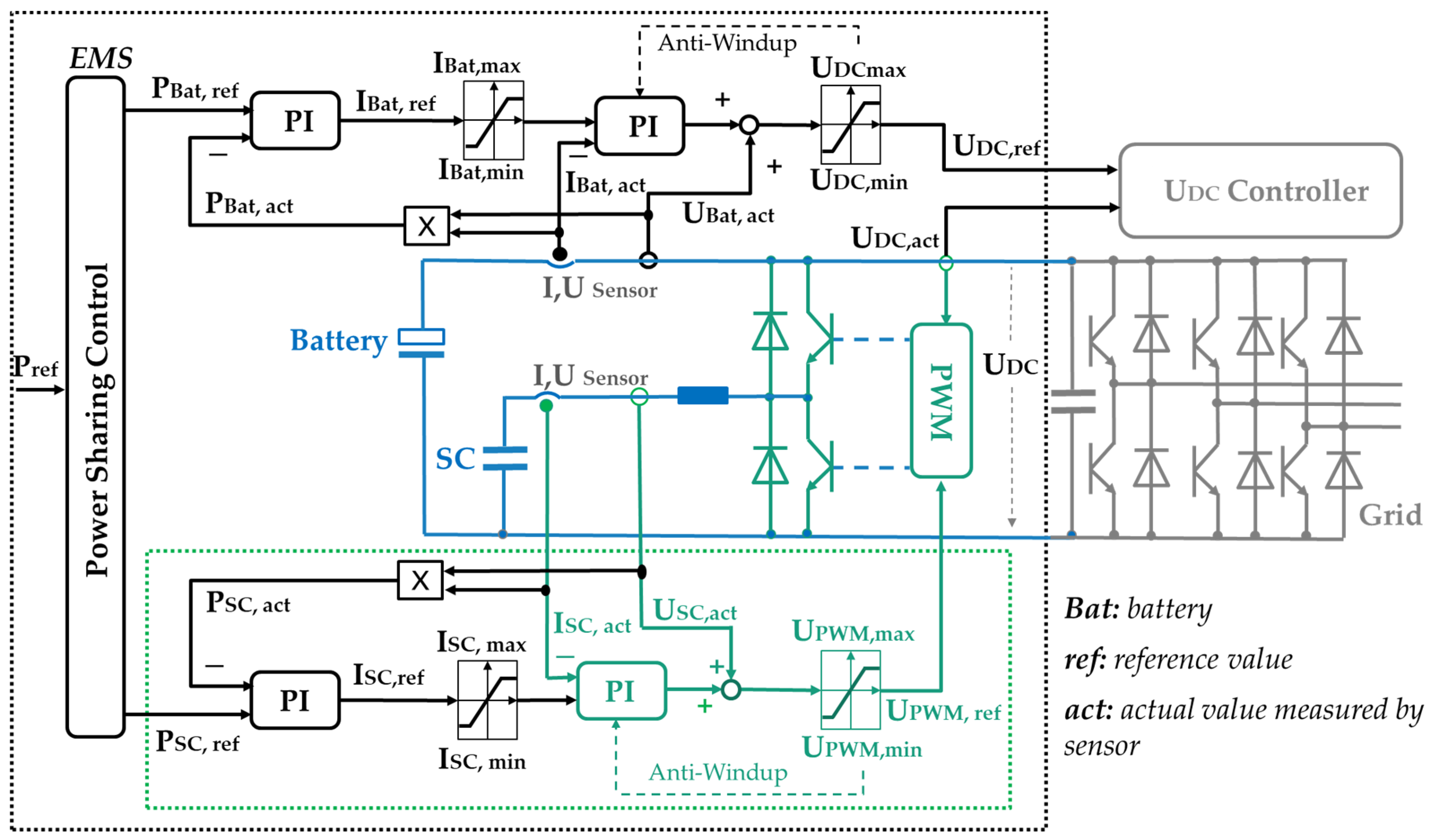
3.2. Energy Management System (EMS) of HESS
4. Optimal Design Toolbox
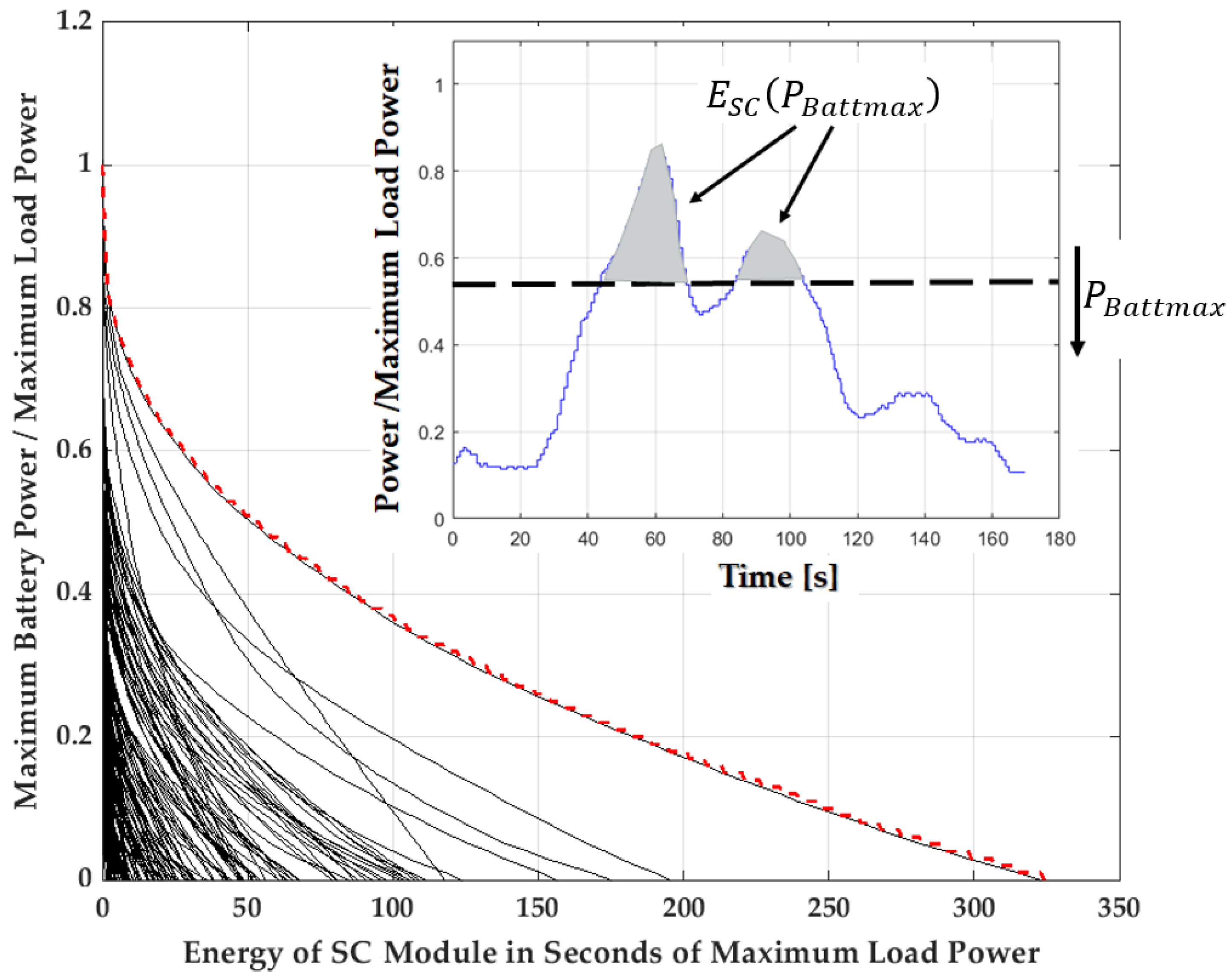
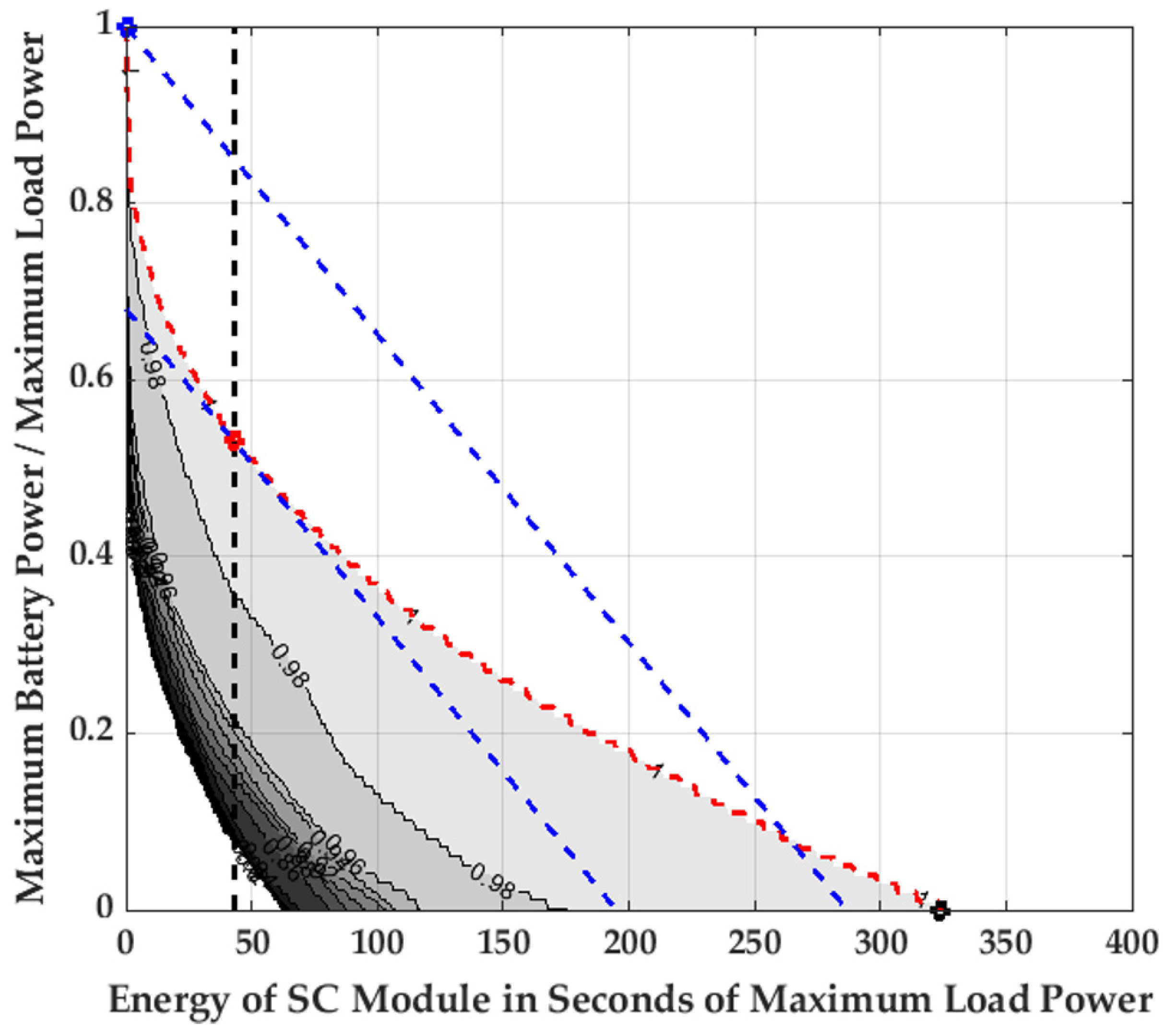
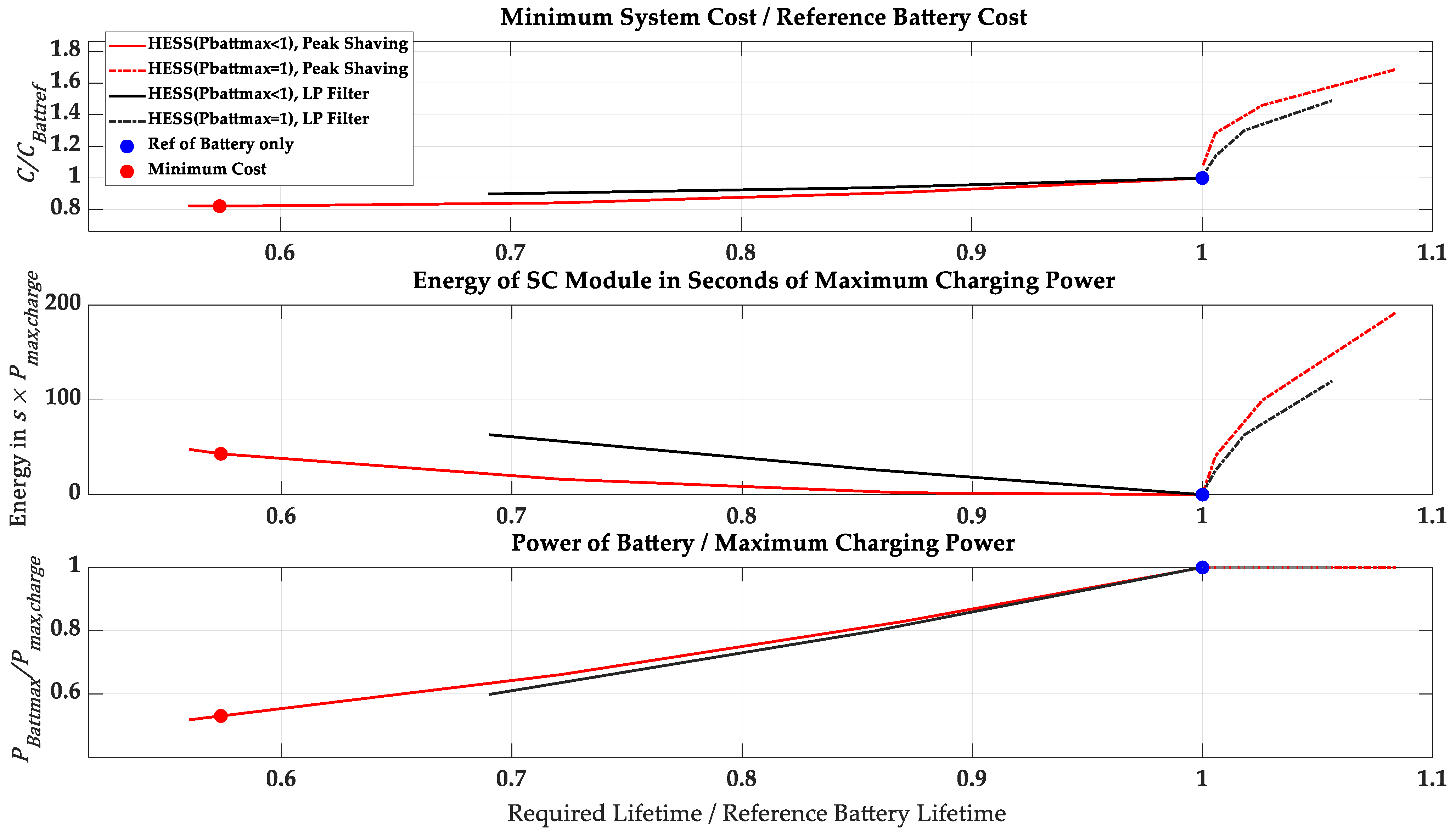
4.1. Step 1: Find Battery/SC Module Combination for Minimum Investment Costs
4.2. Step 2: Select Best System for Required Lifetime
- Required minimum battery module capacity;
- Required minimum SC module capacity;
- Required minimum DC-DC converter power rating;
- Component and overall system costs.
- Two strategies are investigated for HESS system design:
- Battery Size Reduction: For that design strategy, the maximum battery charging power and consequently the battery size is reduced. In this way, a cost reduction compared to the reference battery-only system can be achieved. However, reducing the size of the battery module increases the current amplitude for each individual cell, which in turn increases the number of full cycles. Consequently, a reduction in the system lifetime must be accepted.
- Lifetime Prolongation: For this strategy, the battery size remains constant, while an additional SC module is equipped to effectively reduce power peaks. This approach can extend battery lifetime. It is important to note that the HESS system will incur higher investment cost compared to the reference battery-only system.
5. Hybrid Storage Energy System in Grid Application: Case Study
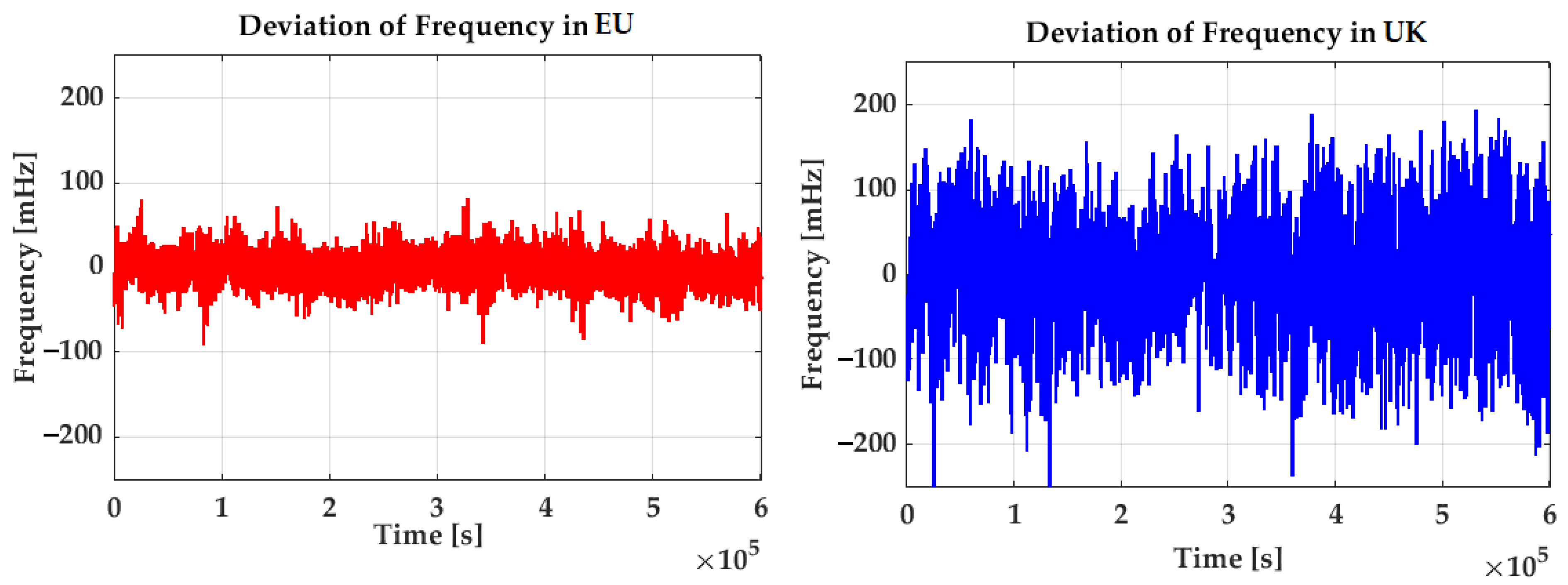
5.1. Description of Grid Application
- BESSs are well-suited and state-of-the-art for providing conventional grid services like PR;
- For a BESS, these new requirements result in high power peaks of short duration, leading to high charging (or discharging) current ratings and fast degradation.
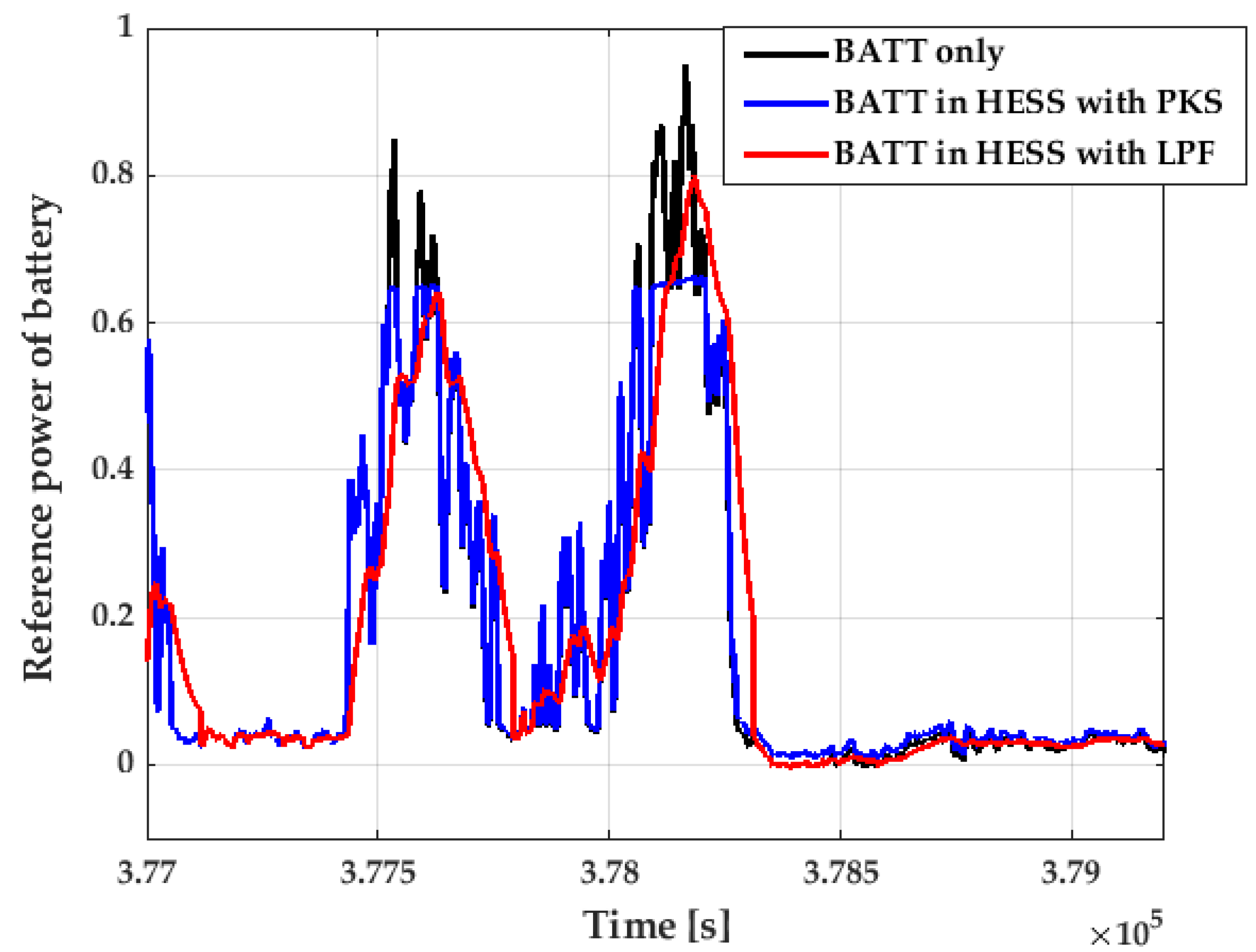
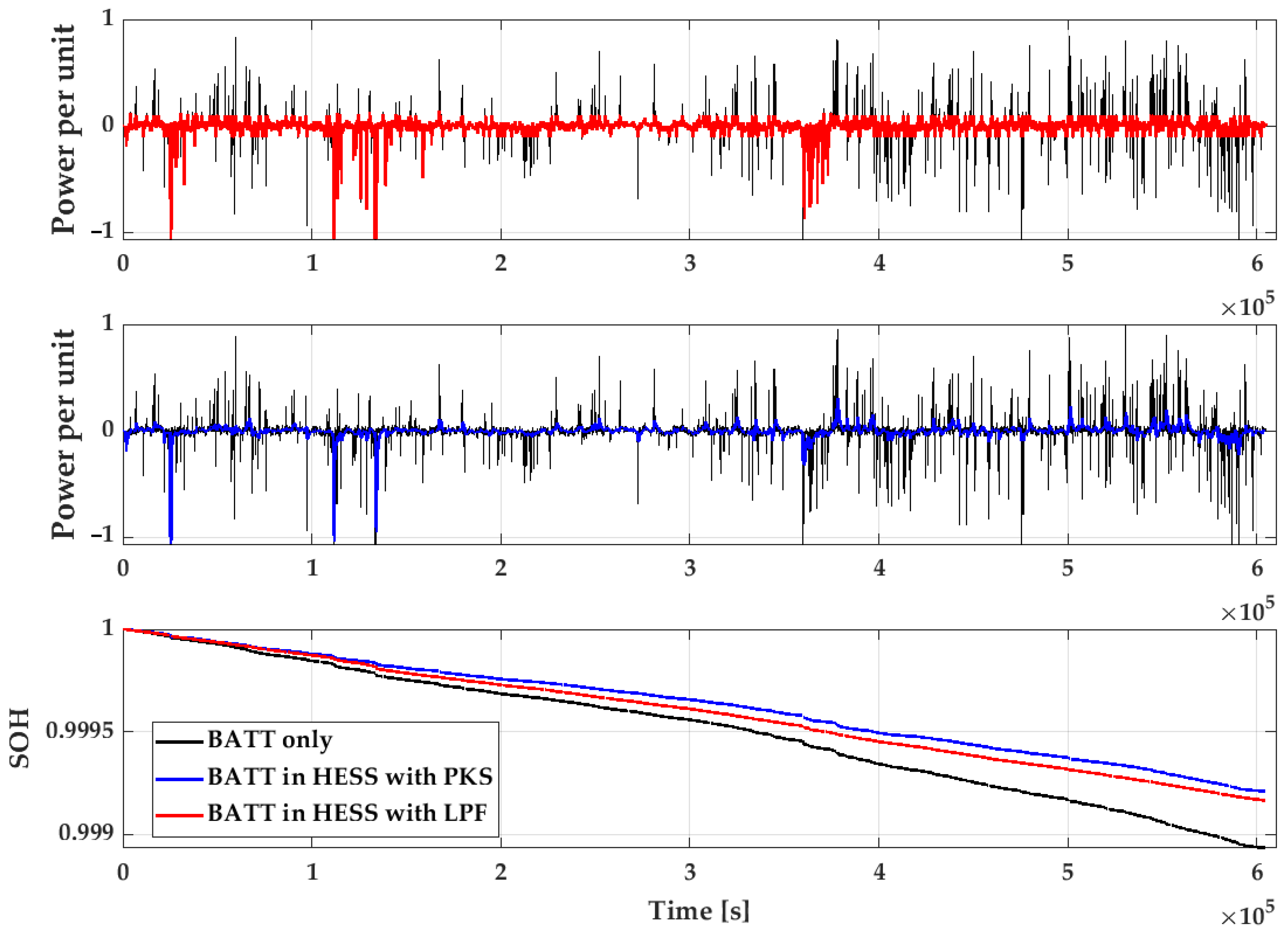
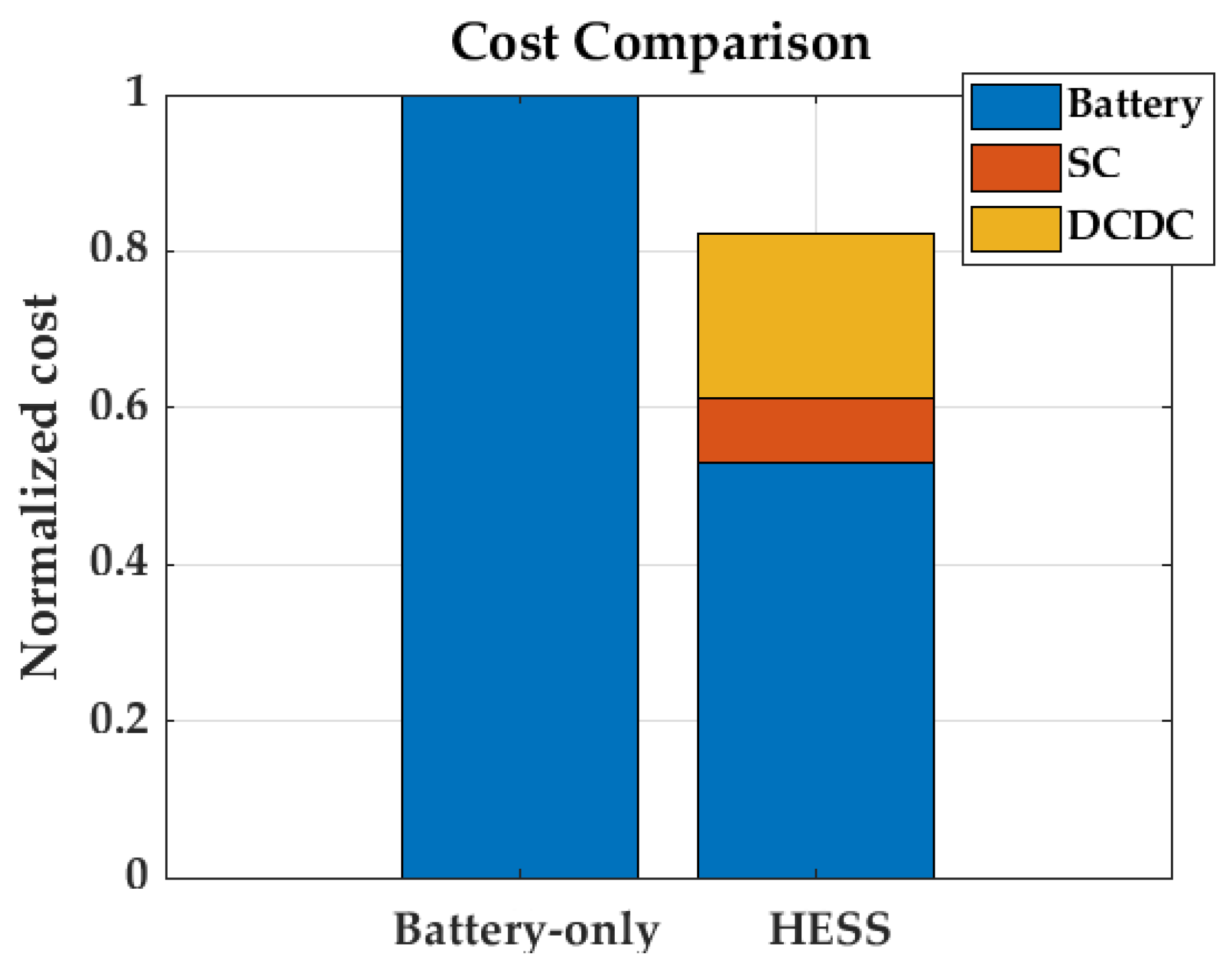
5.2. Results of Case Study
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khalid, M. A Review on the selected application of battery-supercapacitor hybrid energy storage. Energies 2019, 12, 4559. [Google Scholar] [CrossRef]
- Jing, W.L.; Lai, C.H.; Wallace, S.H.; Wong, M.I.; Wong, D. A comprehensive study of battery-supercapacitor hybrid energy storage system for standalone PV power system in rural electrification. Appl. Energy 2018, 224, 340–356. [Google Scholar] [CrossRef]
- Hesse, H.C.; Schimpe, M.; Kucevic, D.; Jossen, A. Lithium-Ion battery storage for the grid-A review of stationary battery storage system design tailored for applications in modern power grid. Energies 2017, 10, 2107. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Ricco, M.; Swierczynski, M.; Stroe, D.; Teodorescu, R. Overview of Lithium-Ion battery modelling methods for State-of-Charge estimation in electrical vehicles. Appl. Sci. 2018, 8, 659. [Google Scholar] [CrossRef]
- Brivio, C.; Mandelli, S.; Merlo, M. Battery energy storage system for primary control reserve and energy arbitrage. Sustain. Energy Grid Netw. 2016, 6, 152–165. [Google Scholar] [CrossRef]
- ESO. New Dynamic Services (DC/DM/DR). 2024. Available online: https://www.nationalgrideso.com/industry-information/balancing-services/frequency-response-services/new-dynamic-services-dcdmdr (accessed on 10 February 2024).
- Zhang, C.; Wang, D.; Wang, B.; Tong, F. Battery degradation minimization-oriented hybrid energy storage system for electric vehicles. Energies 2020, 13, 246. [Google Scholar] [CrossRef]
- Yi, F.; Lu, D.; Wang, X.; Pan, C.; Tao, Y.; Zhou, J.; Zhao, C. Energy management strategy for hybrid energy storage electric vehicles based on pontryagin’s minimum principle considering battery degradation. Sustainability 2022, 14, 1214. [Google Scholar] [CrossRef]
- Vulturescu, B.; Butterbach, S.; Forgez, C.; Coquery, G.; Freidich, G. Ageing study of a supercapacitor-battery storage system. In Proceedings of the ICEM 2010, Rome, Italy, 6–8 September 2010. [Google Scholar]
- Sahin, M.E.; Blaabjerg, F. A hybrid PV-battery/supercapacitor system and a basis active power control proposal in MATLAB/Simulink. Electronic 2020, 9, 129. [Google Scholar] [CrossRef]
- Wang, J.; Purewal, J.; Liu, P.; Hicks-Garner, J.; Soukazian, S.; Sherman, E.; Sorenson, A.; Vu, L.; Tataria, H.; Verbrugge, M.W. Degradation of lithium-ion batteries employing graphite negatives and nickel-cobalt-manganese oxide spinel manganese oxide positives: Part 1, aging mechanisms and life estimation. J. Power Sources 2014, 269, 937–948. [Google Scholar] [CrossRef]
- Xu, B.; Oudalov, A.; Ulbig, A.; Andersson, G. Modelling of Lithium-Ion battery degradation for cell life assessment. IEEE Trans. Smart Grid 2016, 9, 1131–1140. [Google Scholar] [CrossRef]
- Newman, J.; Thomas, K.E.; Hafezi, H.; Wheeler, D.R. Modelling of lithium-ion batteries. J. Power Sources 2003, 119–121, 838–843. [Google Scholar] [CrossRef]
- Newman, J.; Thomas-Alyea, K.E. Electrochemical Systems, 3rd ed.; Electrochemical Society Series; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Doyle, M.; Newman, J. The use of mathematical modelling in the design of lithium/polymer battery systems. Electrochem. Acta 1995, 40, 2191–2196. [Google Scholar] [CrossRef]
- He, W.; Pecht, M.; Flynn, D.; Dinmohammdi, F. A physic-based electrochemical model for lithium battery State-of-Charge estimation solved by an optimised projection-based method and moving window filter. Energies 2018, 11, 2120. [Google Scholar] [CrossRef]
- Smith, K.W.C.-Y. Solid-state diffusion limitations on pulse operation of a lithium-ion cell for hybrid electric vehicles. J. Power Sources 2006, 161, 628–639. [Google Scholar] [CrossRef]
- Liu, L.; Park, J.; Lin, X.; Sastry, A.M.; Lu, W. A thermal-electrochemical 185 model that gives spatial-dependent growth of solid electrolyte interphase in a Li-ion battery. J. Power Sources 2014, 268, 482–490. [Google Scholar] [CrossRef]
- Maheshwari, A.; Heck, M.; Santarelli, M. Cycle aging studies of lithium nickel manganese cobalt oxide-based batteries using electrochemical impedance spectroscopy. Electrochim. Acta 2018, 273, 335–348. [Google Scholar] [CrossRef]
- Käbitz, S.; Gerschler, J.B.; Ecker, M.; Yurdagel, Y.; Emmermacher, B.; André, D.; Mitsch, T.; Sauer, D.U. Cycle and calendar life study of a graphite |LiNi1/3Mn1/3Co1/3O2|Li-ion high energy system. Part A: Full cell characterization. J. Power Sources 2013, 239, 572–583. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, D.; Yang, B.; Cui, X.; Li, X. Electrochemical model of lithium-ion battery for wide frequency range applications. Electrochim. Acta 2020, 343, 136094. [Google Scholar] [CrossRef]
- Grün, T.; Smith, A.; Ehrenberg, H.; Doppelbauer, M. Passive hybrid storage systems: Influence of circuit and system design on performance and lifetime. Energy Procedia 2018, 155, 336–349. [Google Scholar] [CrossRef]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design, 2nd ed.; Wiley: Hoboken, NJ, USA, 2005; ISBN 978-0-470-01167-6. [Google Scholar]
- Kazmierkowski, M.P.; Malesani, L. Current control techniques for three-phase voltage-source PWM converters: A survey. IEEE Trans. Ind. Electron. 1998, 45, 691–703. [Google Scholar] [CrossRef]
- Rao, R.K.; Srinivas, P.; Kumar, M.V.S. Design and analysis of various inverters using different PWM techniques. In Proceedings of the International Conference on Innovations in Electrical & Electronics Engineering (ICIEEE-2014), IJES Special Issue 2014, London, UK, 2–4 July 2014; pp. 41–51. [Google Scholar]
- Keerthana, M.; Manoharan, P.S.; Ravi, A. Design of control strategy for battery-supercapacitor hybrid storage system. In Proceedings of the 2022 7th International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 22–24 June 2022; pp. 798–803. [Google Scholar] [CrossRef]
- Rahmoun, A.; Biechl, H. Modelling of Li-Ion batteries using equivalent circuit diagrams. Prz. Elektrotechniczny 2012, 88, 152–156. [Google Scholar]
- Navas, S.J.; Gonzalez, G.M.C.; Pino, F.J.; Guerra, J.J. Modelling Li-ion batteries using equivalent circuits for renewable energy applications. Energy Rep. 2023, 9, 4456–4465. [Google Scholar] [CrossRef]
- He, X.; Zhang, X. A comprehensive review of supercapacitors: Properties, electrodes, electrolytes and thermal management systems based on phase change materials. J. Energy Storage 2022, 56, 106023. [Google Scholar] [CrossRef]
- Joshi, P.S.; Sutrave, D.S. Supercapacitor: Basics and Overview. J. Inf. Comput. Sci. 2019, 9, 609–625. [Google Scholar]
- Rajan, R.S.; Rahman, M.M. Lifetime analysis of super capacitor for many power electronics applications. IOSR-JEEE 2014, 9, 55–58. [Google Scholar] [CrossRef]
- ESO System Frequency. Available online: https://www.nationalgrideso.com/data-portal/system-frequency-data (accessed on 10 February 2024).
- Engels, J.; Claessens, B.; Deconinck, G. Optimal combination of frequency control and peak shaving with battery storage system. IEEE Trans. Smart Grid 2020, 11, 3270–3279. [Google Scholar] [CrossRef]
- Sankaran, G.; Venkatesan, S. An Overview of Lithium-Ion Batteries for Electric Mobility and Energy Storage Applications; IOP Conference Series: Earth and Environmental Science, Volume 1042; IOP Publishing Ltd.: Bristol, UK, 2022. [Google Scholar] [CrossRef]
- Nitta, N.; Wu, F.; Lee, J.T.; Yushin, G. Li-ion battery materials: Present and future. Materialstody 2015, 18, 252–264. [Google Scholar] [CrossRef]
- Chen, T.; Jin, Y.; Lv, H.; Yang, A.; Liu, M.; Chen, B.; Xie, Y.; Chen, Q. Applications of lithium-Ion batteries in grid-scale energy storage systems. Trans. Tianjing Univ. 2020, 26, 208–217. [Google Scholar] [CrossRef]
- Choi, D.; Shamin, N.; Crawfor, A.; Huang, Q.; Vartanian, C.K.; Viswanathan, V.V.; Paiss, M.D.; Alam, M.; Reed, D.M.; Sprenkle, V.L. Li-ion battery technology for grid application. J. Power Source 2021, 511, 230419. [Google Scholar] [CrossRef]
- Mödl, R.; Braun, A.; Kallis, L. Simulation and Evaluation of Battery Aging in Electric Hybrid Storage Systems; SAE Technical Paper 2024-01-2903; SAE: Warrendale, PA, USA, 2024. [Google Scholar] [CrossRef]


| Topic | PR | DM | DC | DR |
|---|---|---|---|---|
| Speed of response | 30 s | 1 s | 1 s | 2 s |
| Initial time | 5 s | 0.5 s | 0.5 s | 10 s |
| Deadband (delivery %) | 15 mHz (0%) | |||
| Knee point | no knee point | with knee point | with knee point | no knee point |
| Initial linear range (delivery %) | none | 15–100 mHz (0–5%) | 15–200 mHz (0–5%) | none |
| Linear range (delivery %) | 15–200 mHz (0–100%) | 100–200 mHz (5–100%) | 00–500 mHz (5–100%) | 15–200 mHz (0–100%) |
| Delivery Duration | 15 min | 30 min | 15 min | 60 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, W.; Schwalm, M.; Shan, M. A Design Tool for Battery/Supercapacitor Hybrid Energy Storage Systems Based on the Physical–Electrochemical Degradation Battery Model BaSiS. Energies 2024, 17, 3481. https://doi.org/10.3390/en17143481
Shan W, Schwalm M, Shan M. A Design Tool for Battery/Supercapacitor Hybrid Energy Storage Systems Based on the Physical–Electrochemical Degradation Battery Model BaSiS. Energies. 2024; 17(14):3481. https://doi.org/10.3390/en17143481
Chicago/Turabian StyleShan, Weiwei, Michael Schwalm, and Martin Shan. 2024. "A Design Tool for Battery/Supercapacitor Hybrid Energy Storage Systems Based on the Physical–Electrochemical Degradation Battery Model BaSiS" Energies 17, no. 14: 3481. https://doi.org/10.3390/en17143481
APA StyleShan, W., Schwalm, M., & Shan, M. (2024). A Design Tool for Battery/Supercapacitor Hybrid Energy Storage Systems Based on the Physical–Electrochemical Degradation Battery Model BaSiS. Energies, 17(14), 3481. https://doi.org/10.3390/en17143481






