Novel Frequency Regulation Scenarios Generation Method Serving for Battery Energy Storage System Participating in PJM Market
Abstract
1. Introduction
- The proposed typical frequency regulation scenarios, composed of two features with a 15-min resolution, are generated based on their joint probability distribution. The two features, calculated based on the RegD signal and BESS parameters, capture the influence of the RegD signal on BESS operation and the characteristic of energy neutrality during 15 min of the RegD signal;
- The effectiveness of typical regulation scenarios generated based on K-means clustering and FSR in prior research is validated, which is from the perspective of accuracy in estimating regulation revenue and the consistency of probability distribution.
2. Market Rule
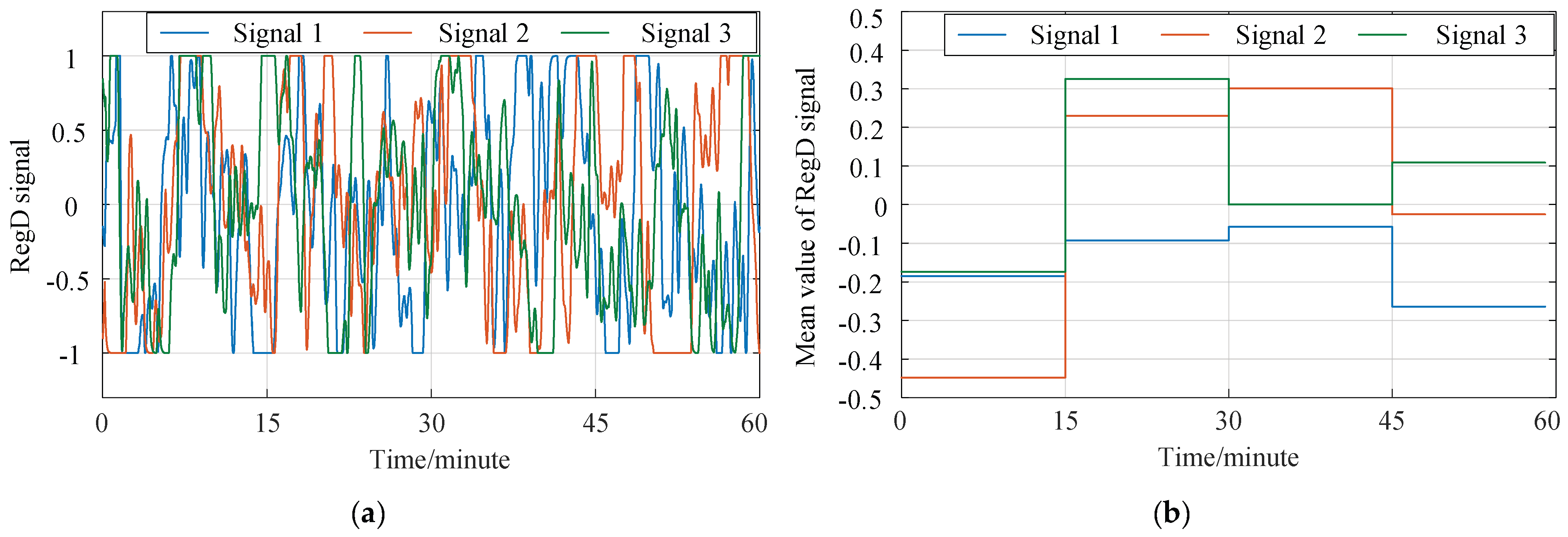
2.1. RegD Signal
2.2. Frequency Regulation Market Rule
2.3. Framework of Optimizing BESS Sizing
3. Frequency Regulation Scenarios Generation
3.1. Regulation Scenario Analysis
3.2. Proposed Method for Generating Frequency Scenarios
- (1)
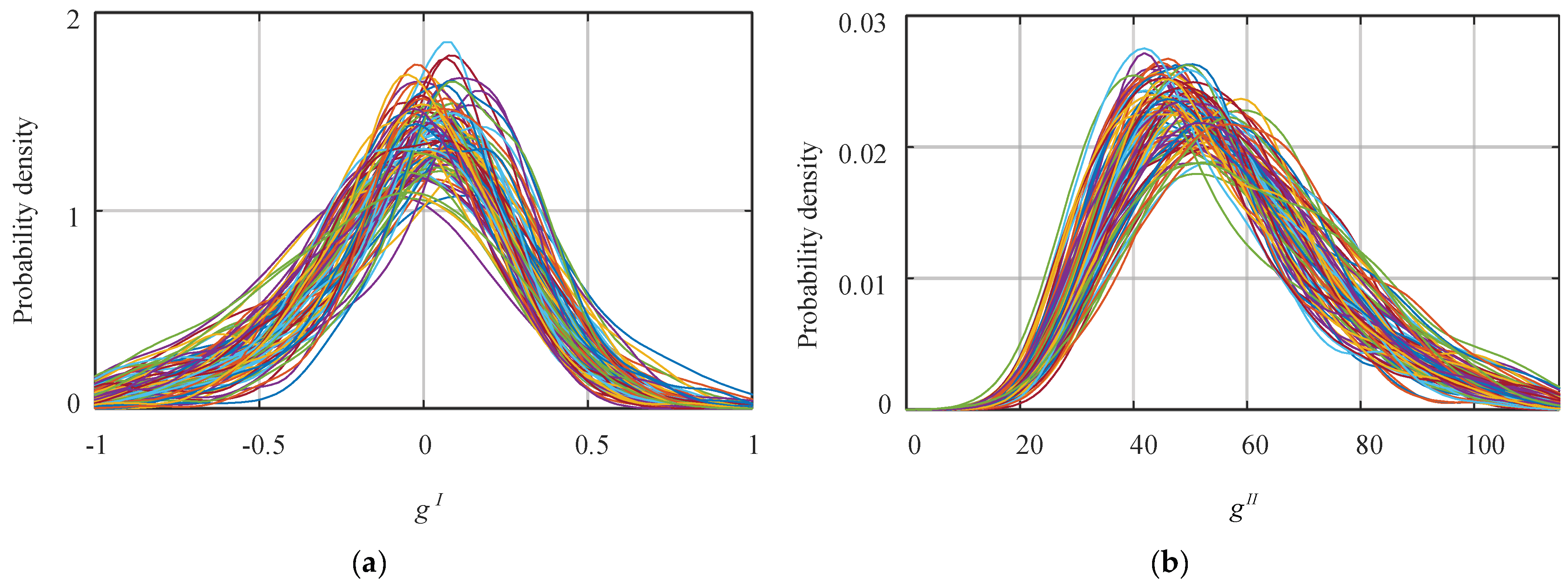
- To obtain the probability distribution of and the historical RegD signal lasting for a year (366 days) is employed in this section. Based on (5) and (6), the original RegD signal with a resolution of 2 s lasting for 15 min is converted into two features {}. Finally, 366 × 96 groups of {} data are obtained.
- (2)
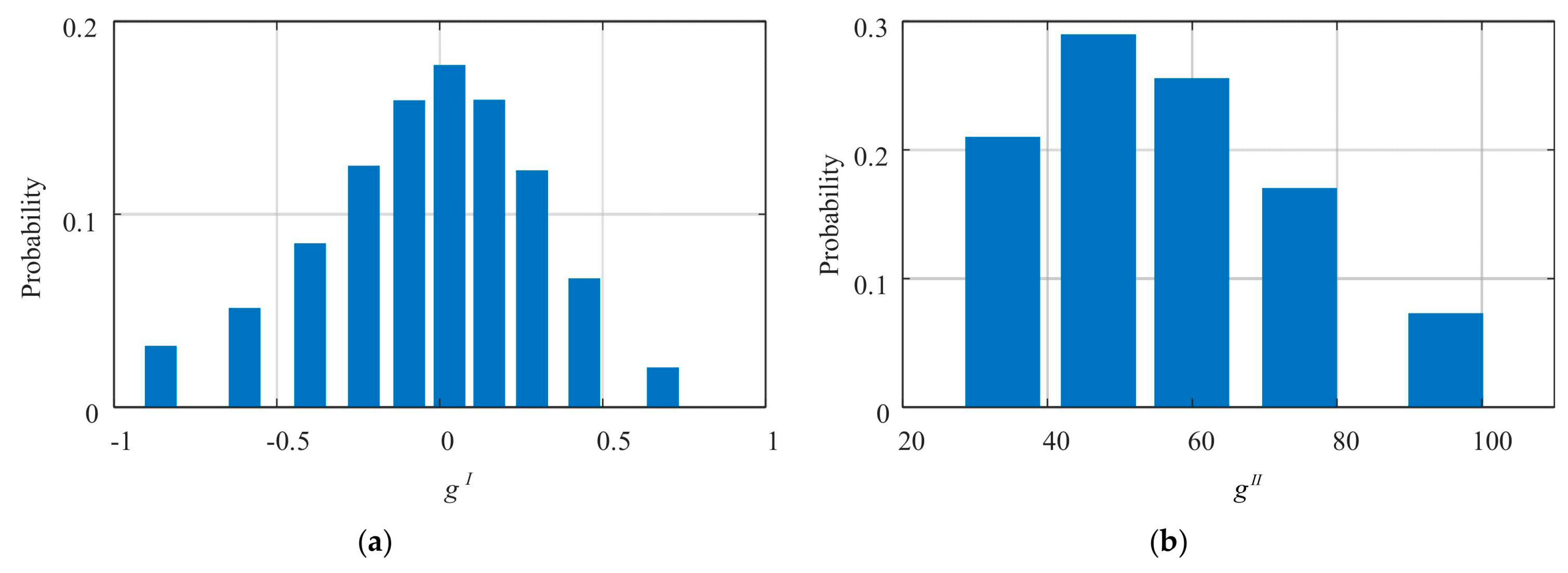
- A cluster analysis is executed for and separately using the K-means method. For , set the number of cluster center as M. Then, partition 366 × 96 groups of data into M clusters based on the minimum Euclidean distance. For each cluster, calculate its centroid associated with probability according to (18) and (19).where, and are the centroid and probability of cluster m, respectively. is a set that includes all data in cluster m. Num(·) is utilized for counting the number of in cluster m.Similarly, set the number of cluster centers for as N. The centroids associated with probabilities of the N clusters are calculated according to (20) and (21).
- (3)
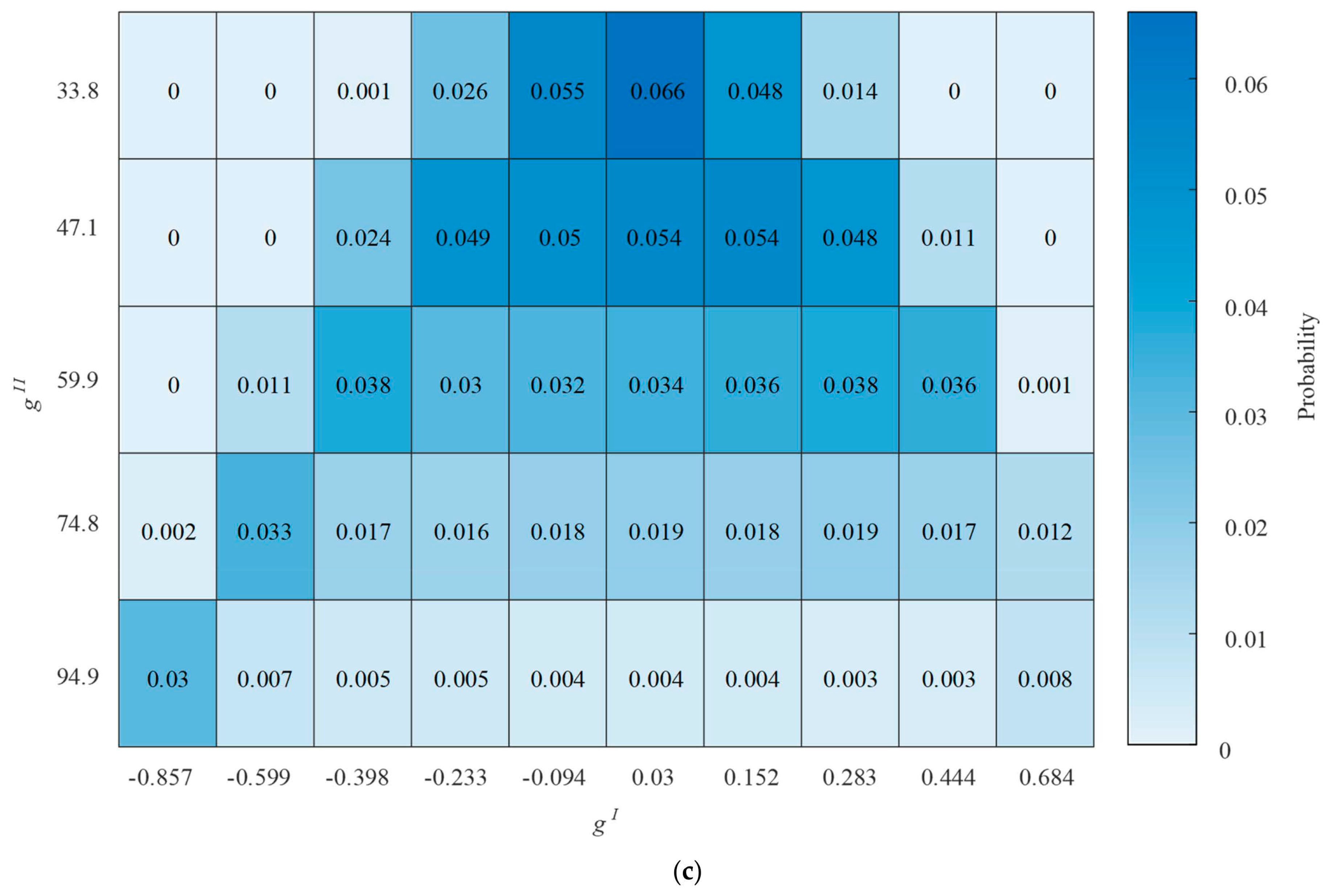
- Calculate the discrete joint probability of centroids and based on the clustering analysis for and Concretely, when a group of data {, } belongs to set m and n at the same time, it will be assigned into the set m × n. Consequently, the joint probabilities are calculated based on the number of the intersections of and , as shown in (22).
- (4)
- J regulation scenarios are generated based on the joint probability distribution of and . Each scenario consists of 96 groups of {}, representing 96 moments in a day.
- (5)
- To select the typical scenarios that have the most consistent probability distribution with the actual one, a cluster analysis is performed for each generated scenario. Here, and are utilized to represent the centroids of and of the generated scenario j. and denote their probabilities. To measure the difference in probability distribution, an index E is proposed in (23). Equal weight is assigned to the two features to measure their difference. And, it is necessary to eliminate the difference in dimension of and by normalization.where, Nor() denotes the normalization step.Finally, S scenarios with the smallest difference E will be employed as the typical regulation scenarios.
4. Case Study
4.1. Typical Regulation Scenarios Generation
4.2. Comparison of Monthly Revenue
4.3. Cluster Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PJM | Pennsylvania-New Jersey-Maryland Interconnection |
| RegD | Regulation D |
| RegA | Regulation A |
| BESS | Battery energy storage system |
| FFR | Fast frequency regulation |
| MISO | Midwest Independent Transmission System Operator |
| NYISO | New York Independent System Operator |
| AGC | Automatic generation control |
| ACE | Area control error |
| FSR | Forward scenario reduction |
| SOC | State of charge |
| LFP | Lithium iron phosphate battery |
References
- Mohd Razif, A.S.; Ab Aziz, N.F.; Ab Kadir, M.Z.A.; Kamil, K. Accelerating Energy Transition through Battery Energy Storage Systems Deployment: A Review on Current Status, Potential and Challenges in Malaysia. Energy Strat. Rev. 2024, 52, 101346. [Google Scholar] [CrossRef]
- Abdalla, A.A.; Moursi, M.S.E.; El-Fouly, T.H.M.; Hosani, K.H.A. Reliant Monotonic Charging Controllers for Parallel-Connected Battery Storage Units to Reduce PV Power Ramp Rate and Battery Aging. IEEE Trans. Smart Grid 2023, 14, 4424–4438. [Google Scholar] [CrossRef]
- Wang, X.; Li, F.; Zhang, Q.; Shi, Q.; Wang, J. Profit-Oriented BESS Siting and Sizing in Deregulated Distribution Systems. IEEE Trans. Smart Grid 2023, 14, 1528–1540. [Google Scholar] [CrossRef]
- Kong, W.; Luo, F.; Jia, Y.; Dong, Z.Y.; Liu, J. Benefits of Home Energy Storage Utilization: An Australian Case Study of Demand Charge Practices in Residential Sector. IEEE Trans. Smart Grid 2021, 12, 3086–3096. [Google Scholar] [CrossRef]
- Zhang, Y.; Anvari-Moghaddam, A.; Peyghami, S.; Dragičević, T.; Li, Y.; Blaabjerg, F. Optimal Sizing of Behind-the-Meter BESS for Providing Stackable Services. In Proceedings of the 2022 IEEE 13th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Kiel, Germany, 26–29 June 2022. [Google Scholar]
- Krata, J.; Saha, T.K. Real-Time Coordinated Voltage Support With Battery Energy Storage in a Distribution Grid Equipped With Medium-Scale PV Generation. IEEE Trans. Smart Grid 2019, 10, 3486–3497. [Google Scholar] [CrossRef]
- Bhandari, A.; Ramasubramanian, D.; Singhvi, V.; Gaikwad, A. Considerations for Electric Utilities to Determine Energy Storage Size for Transmission Deferral to Increase Hosting Capacity. In Proceedings of the 2020 52nd North American Power Symposium (NAPS), Tempe, AZ, USA, 11–13 April 2021. [Google Scholar]
- Liu, J.; Jian, L.; Wang, W.; Qiu, Z.; Zhang, J.; Dastbaz, P. The Role of Energy Storage Systems in Resilience Enhancement of Health Care Centers with Critical Loads. J. Energy Storage 2021, 33, 102086. [Google Scholar] [CrossRef]
- Yamujala, S.; Jain, A.; Bhakar, R.; Mathur, J. Multi-Service Based Economic Valuation of Grid-Connected Battery Energy Storage Systems. J. Energy Storage 2022, 52, 104657. [Google Scholar] [CrossRef]
- Cheng, B.; Asamov, T.; Powell, W.B. Low-Rank Value Function Approximation for Co-Optimization of Battery Storage. IEEE Trans. Smart Grid 2018, 9, 6590–6598. [Google Scholar] [CrossRef]
- Hao, H.; Wu, D.; Lian, J.; Yang, T. Optimal Coordination of Building Loads and Energy Storage for Power Grid and End User Services. IEEE Trans. Smart Grid 2018, 9, 4335–4345. [Google Scholar] [CrossRef]
- Tian, Y.; Bera, A.; Benidris, M.; Mitra, J. Stacked Revenue and Technical Benefits of a Grid-Connected Energy Storage System. IEEE Trans. Ind. Appl. 2018, 54, 3034–3043. [Google Scholar] [CrossRef]
- Brahma, S.; Khurram, A.; Ossareh, H.; Almassalkhi, M. Optimal Frequency Regulation Using Packetized Energy Management. IEEE Trans. Smart Grid 2023, 14, 341–353. [Google Scholar] [CrossRef]
- M12. Available online: https://www.pjm.com/~/media/documents/manuals/m12.ashx (accessed on 17 November 2023).
- Ma, Q.; Wei, W.; Wu, L.; Mei, S. Life-Aware Operation of Battery Energy Storage in Frequency Regulation. IEEE Trans. Sustain. Energy 2023, 14, 1725–1736. [Google Scholar] [CrossRef]
- Miao, Y.; Chen, T.; Bu, S.; Liang, H.; Han, Z. Co-Optimizing Battery Storage for Energy Arbitrage and Frequency Regulation in Real-Time Markets Using Deep Reinforcement Learning. Energies 2021, 14, 8365. [Google Scholar] [CrossRef]
- Engels, J.; Claessens, B.; Deconinck, G. Optimal Combination of Frequency Control and Peak Shaving With Battery Storage Systems. IEEE Trans. Smart Grid 2020, 11, 3270–3279. [Google Scholar] [CrossRef]
- Su, H.; Feng, D.; Zhao, Y.; Zhou, Y.; Zhou, Q.; Fang, C.; Rahman, U. Optimization of Customer-Side Battery Storage for Multiple Service Provision: Arbitrage, Peak Shaving, and Regulation. IEEE Trans. Ind. Appl. 2022, 58, 2559–2573. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, J.; Conejo, A.J. Optimal Battery Sizing for Frequency Regulation and Energy Arbitrage. IEEE Trans. Power Deliv. 2022, 37, 2016–2023. [Google Scholar] [CrossRef]
- Zhang, Y.; Anvari-Moghaddam, A.; Peyghami, S.; Li, Y.; Dragičević, T.; Blaabjerg, F. Optimal Sizing of Behind-the-Meter Battery Storage for Providing Profit-Oriented Stackable Services. IEEE Trans. Smart Grid 2024, 15, 1481–1494. [Google Scholar] [CrossRef]
- Arias, N.B.; López, J.C.; Hashemi, S.; Franco, J.F.; Rider, M.J. Multi-Objective Sizing of Battery Energy Storage Systems for Stackable Grid Applications. IEEE Trans. Smart Grid 2021, 12, 2708–2721. [Google Scholar] [CrossRef]
- Zheng, X.; Su, Y.; Wei, L.; Zhang, J.; Shen, X.; Sun, H. Cost-Benefit Evaluation for Battery Energy Storage Considering Degradation and Data Clustering in Performance-Based Frequency Regulation Service. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020. [Google Scholar]
- Awad, A.S.A.; EL-Fouly, T.H.M.; Salama, M.M.A. Optimal ESS Allocation for Benefit Maximization in Distribution Networks. IEEE Trans. Smart Grid 2017, 8, 1668–1678. [Google Scholar] [CrossRef]
- Shi, Y.; Xu, B.; Wang, D.; Zhang, B. Using Battery Storage for Peak Shaving and Frequency Regulation: Joint Optimization for Superlinear Gains. IEEE Trans. Power Syst. 2018, 33, 2882–2894. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, A.; He, H.; Xia, Z.; Zhou, Y. Correlation analysis of weather factors and outage duration. In Proceedings of the 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28–30 May 2021. [Google Scholar]
- PJM Historical Regulation Market Data. Available online: https://dataminer2.pjm.com/feed/reg_market_results/definition (accessed on 17 November 2023).
- RTO Regulation Signal Data. Available online: https://www.pjm.com/markets-and-operations/ancillary-services (accessed on 17 November 2023).

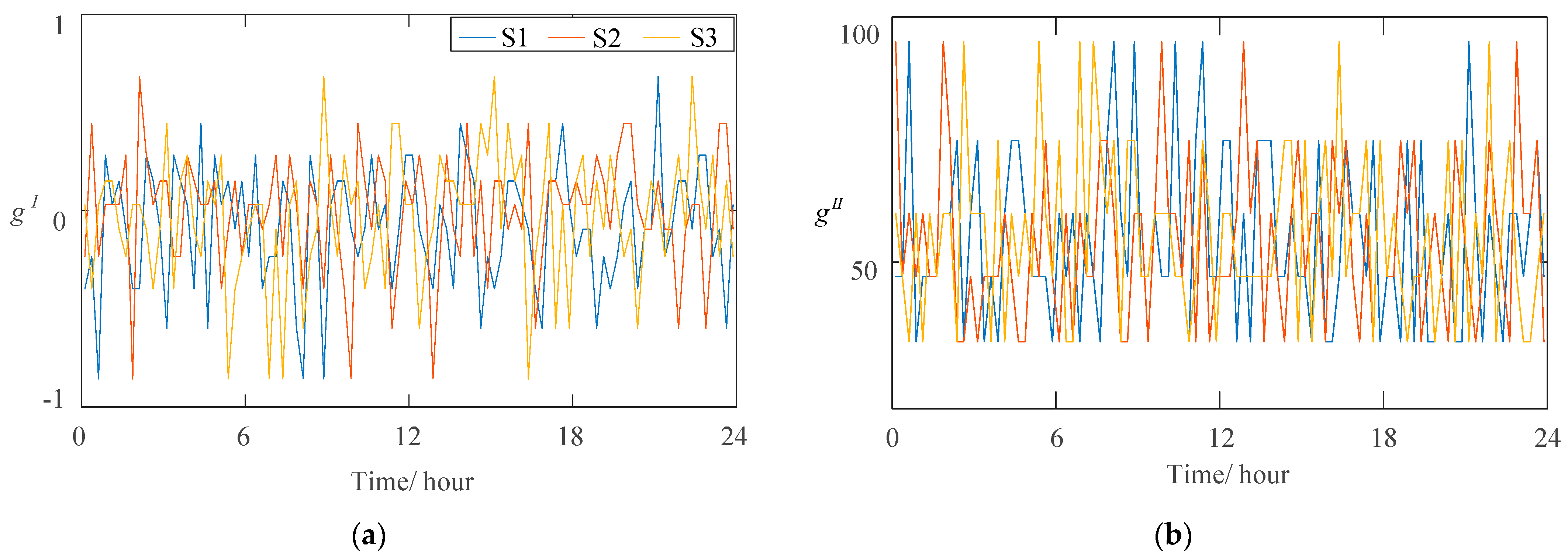
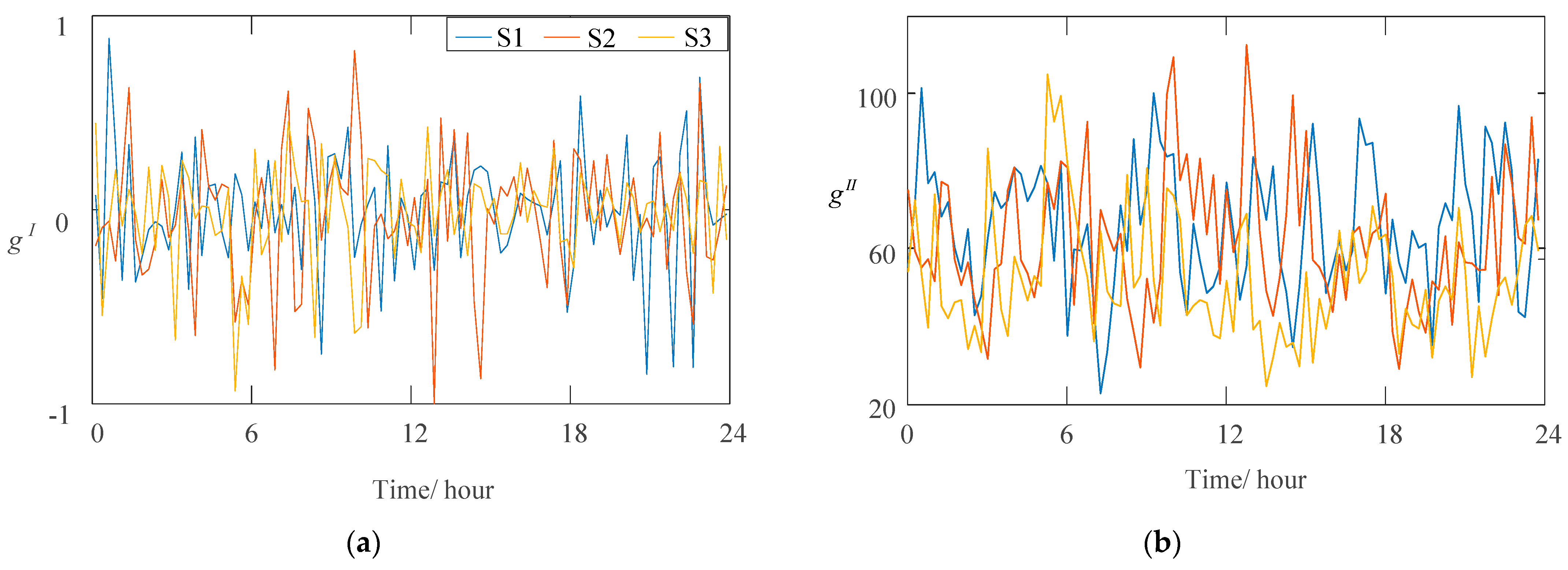

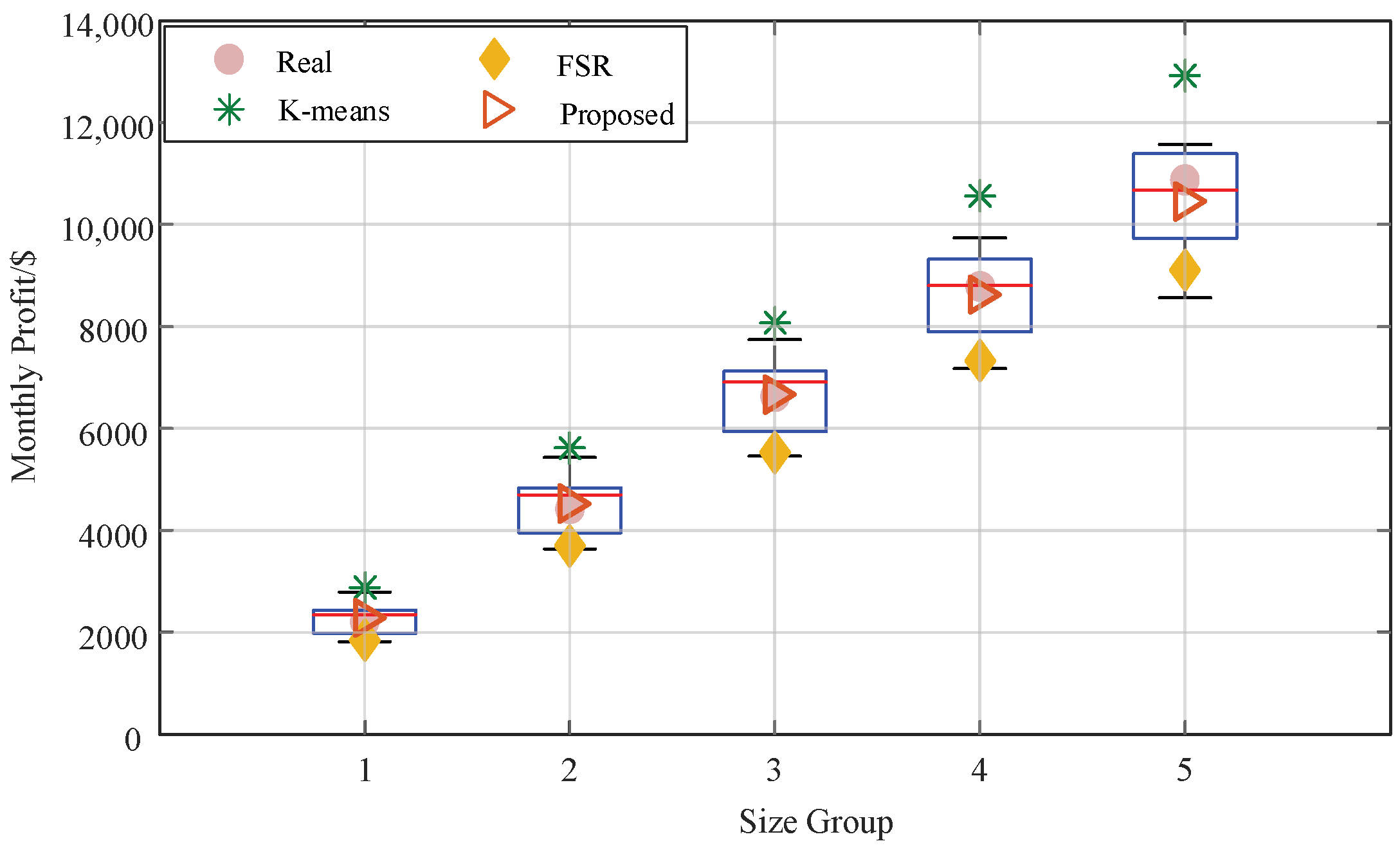
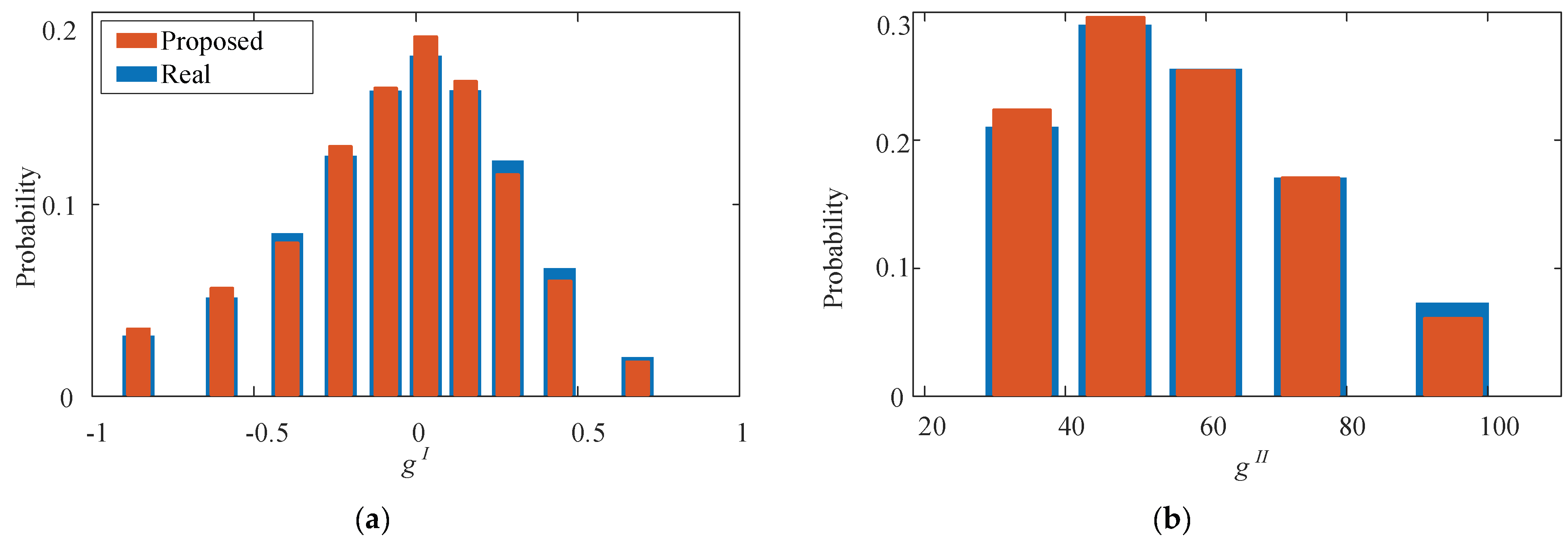
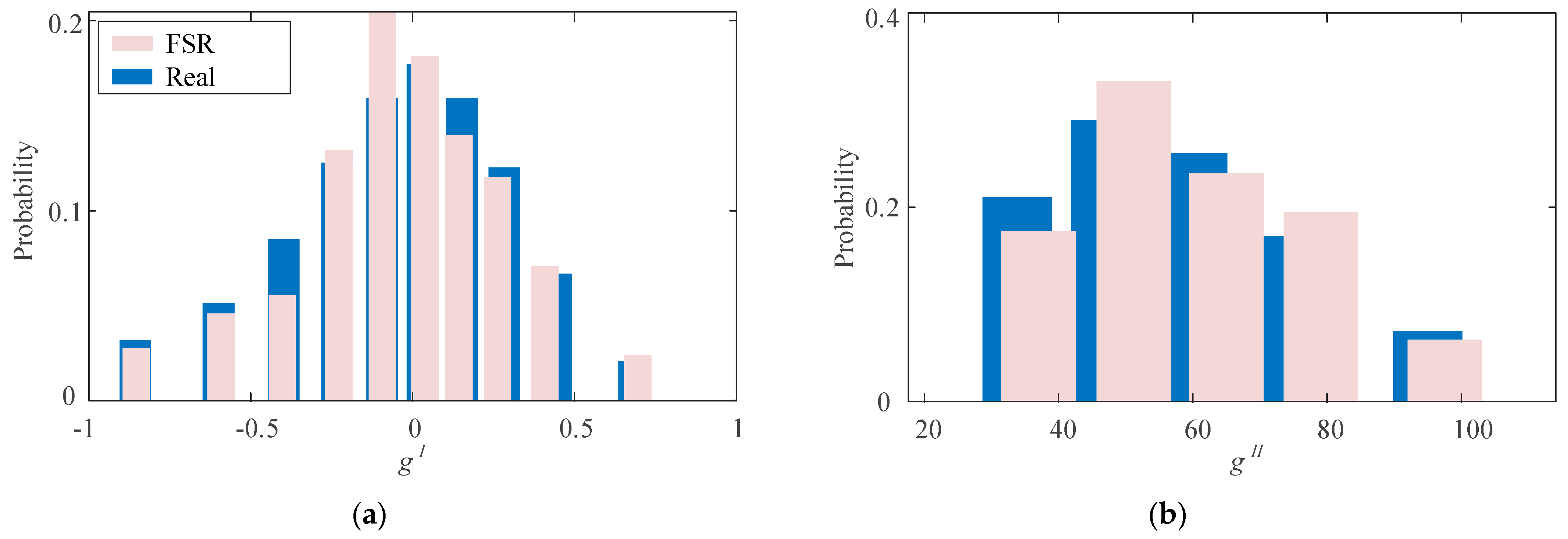
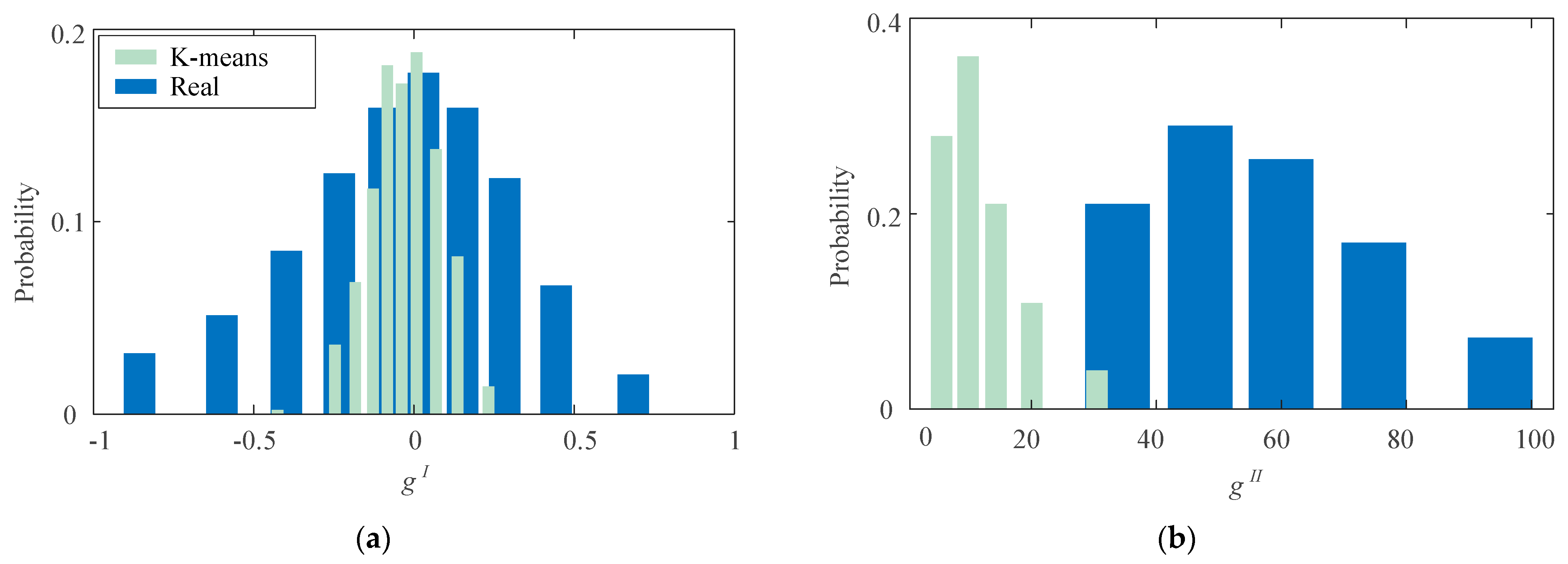
| Parameters | M | N | J | S |
|---|---|---|---|---|
| Values | 10 | 5 | 1000 | 10 |
| Parameters | Efficiency (%) | Range of SOC (%) | Degradation Cost per MWh ($/MWh) |
|---|---|---|---|
| Values | 95 | 15–90 | 18.75 |
| Size Group | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| BESS Size | 0.4 MW, 1 MWh | 0.8 MW, 1 MWh | 1.2 MW, 1 MWh | 1.6 MW, 1 MWh | 2 MW, 1 MWh |
| PE | Size Group | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Proposed method | 3.24 | 2.34 | 0.57 | −1.77 | −3.89 |
| FSR | −16.4 | −16.39 | −16.54 | −16.56 | −16.28 |
| K-means clustering | 30.07 | 27 | 21.88 | 20.29 | 18.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Anvari-Moghaddam, A.; Peyghami, S.; Blaabjerg, F. Novel Frequency Regulation Scenarios Generation Method Serving for Battery Energy Storage System Participating in PJM Market. Energies 2024, 17, 3479. https://doi.org/10.3390/en17143479
Zhang Y, Anvari-Moghaddam A, Peyghami S, Blaabjerg F. Novel Frequency Regulation Scenarios Generation Method Serving for Battery Energy Storage System Participating in PJM Market. Energies. 2024; 17(14):3479. https://doi.org/10.3390/en17143479
Chicago/Turabian StyleZhang, Yichao, Amjad Anvari-Moghaddam, Saeed Peyghami, and Frede Blaabjerg. 2024. "Novel Frequency Regulation Scenarios Generation Method Serving for Battery Energy Storage System Participating in PJM Market" Energies 17, no. 14: 3479. https://doi.org/10.3390/en17143479
APA StyleZhang, Y., Anvari-Moghaddam, A., Peyghami, S., & Blaabjerg, F. (2024). Novel Frequency Regulation Scenarios Generation Method Serving for Battery Energy Storage System Participating in PJM Market. Energies, 17(14), 3479. https://doi.org/10.3390/en17143479








