An Economic Performance Improving and Analysis for Offshore Wind Farm-Based Islanded Green Hydrogen System
Abstract
1. Introduction
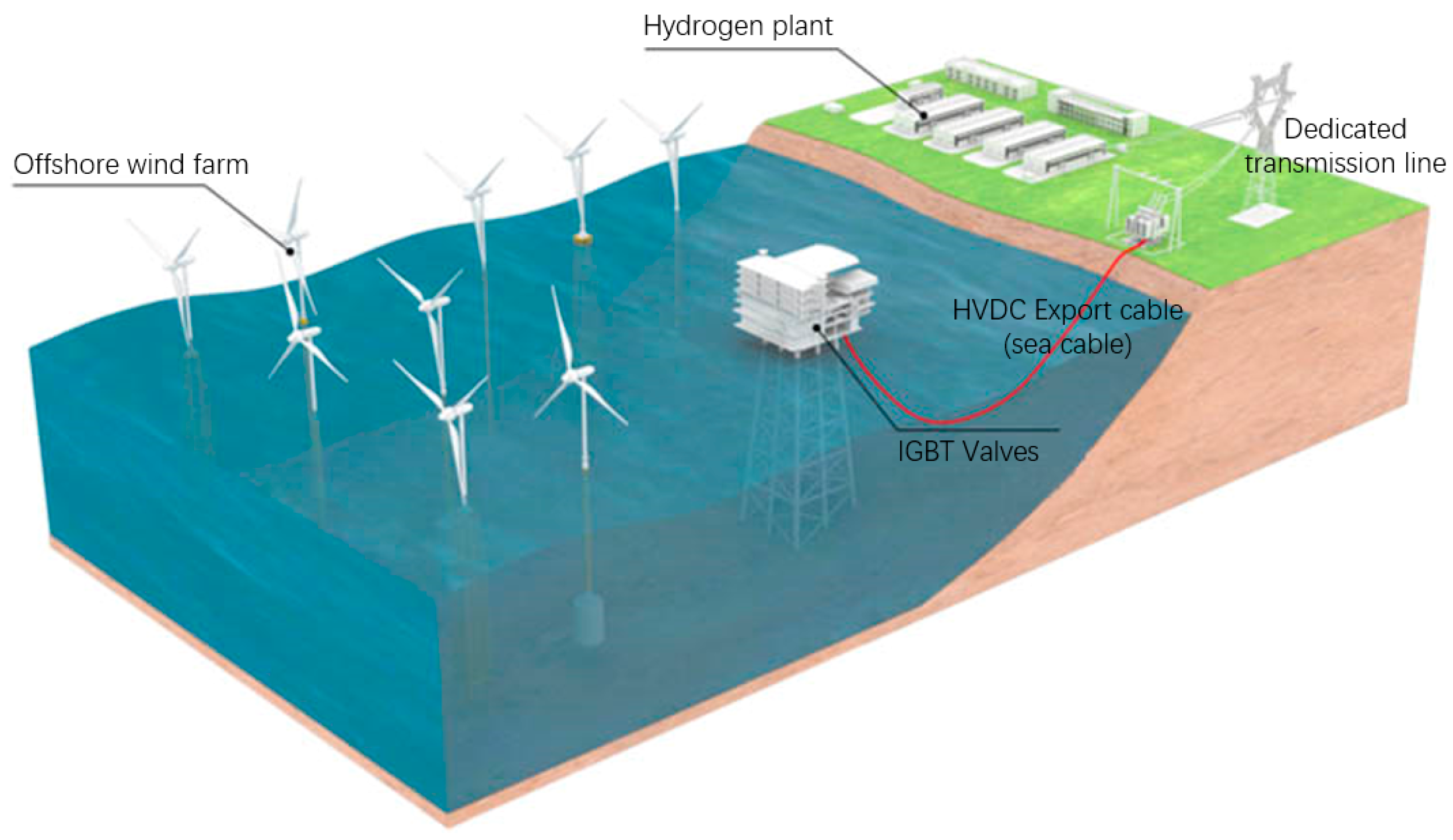
2. Islanded Wind-Hydrogen System
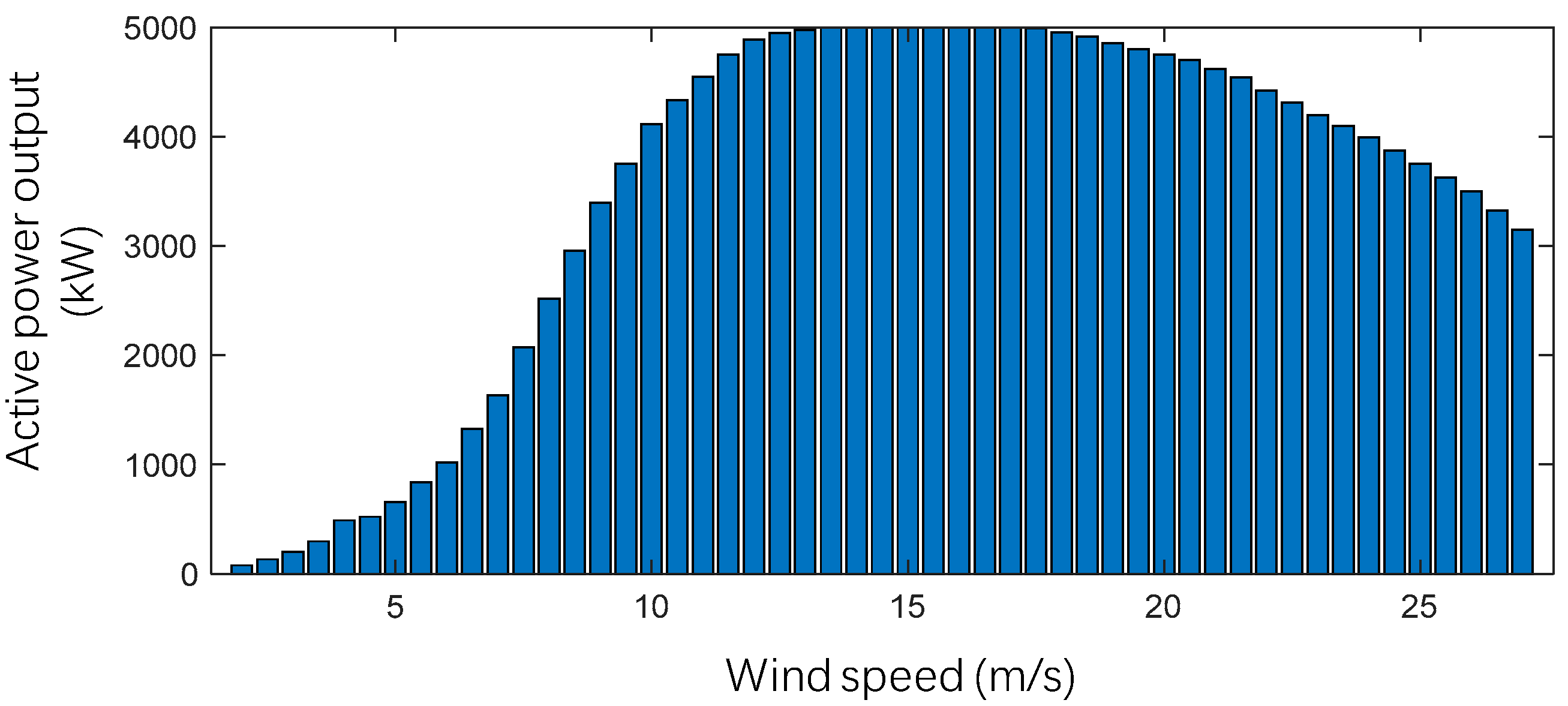
2.1. Offshore Wind Farm
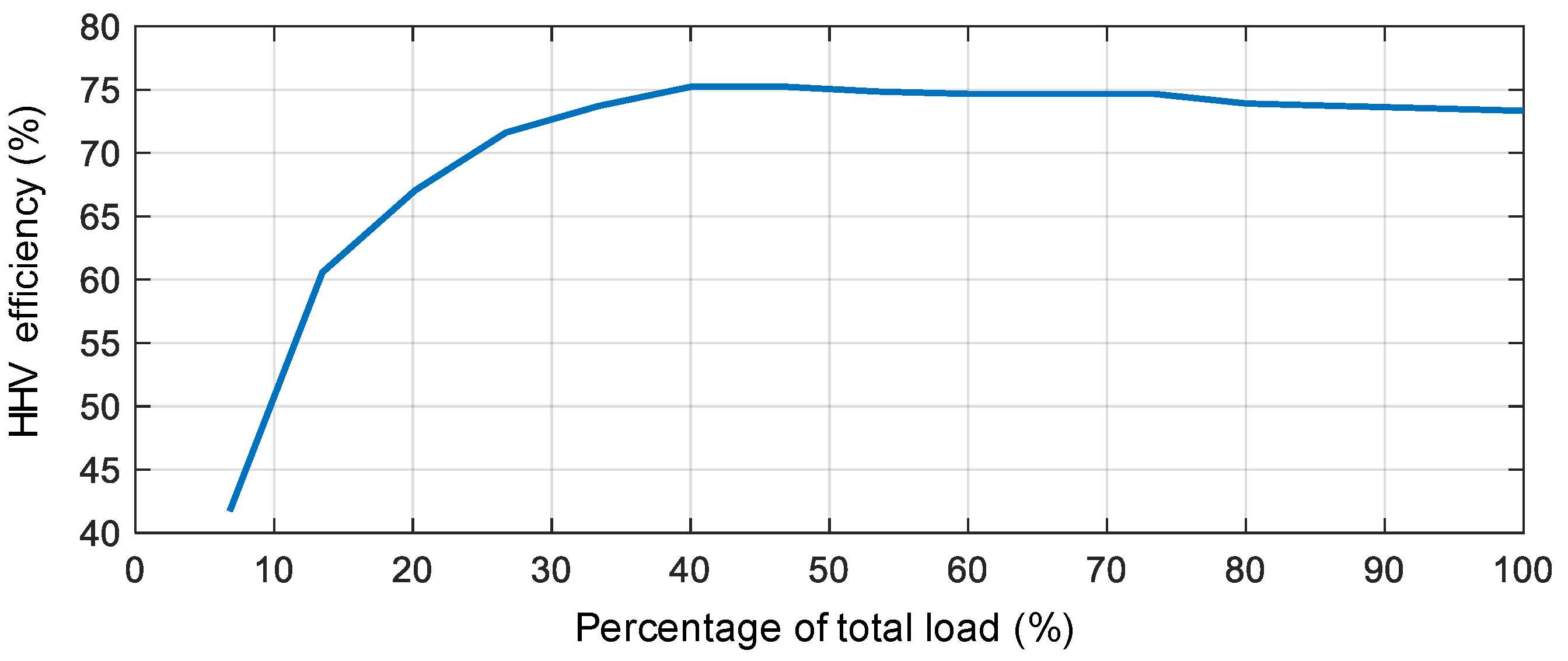
2.2. Hydrogen Plant
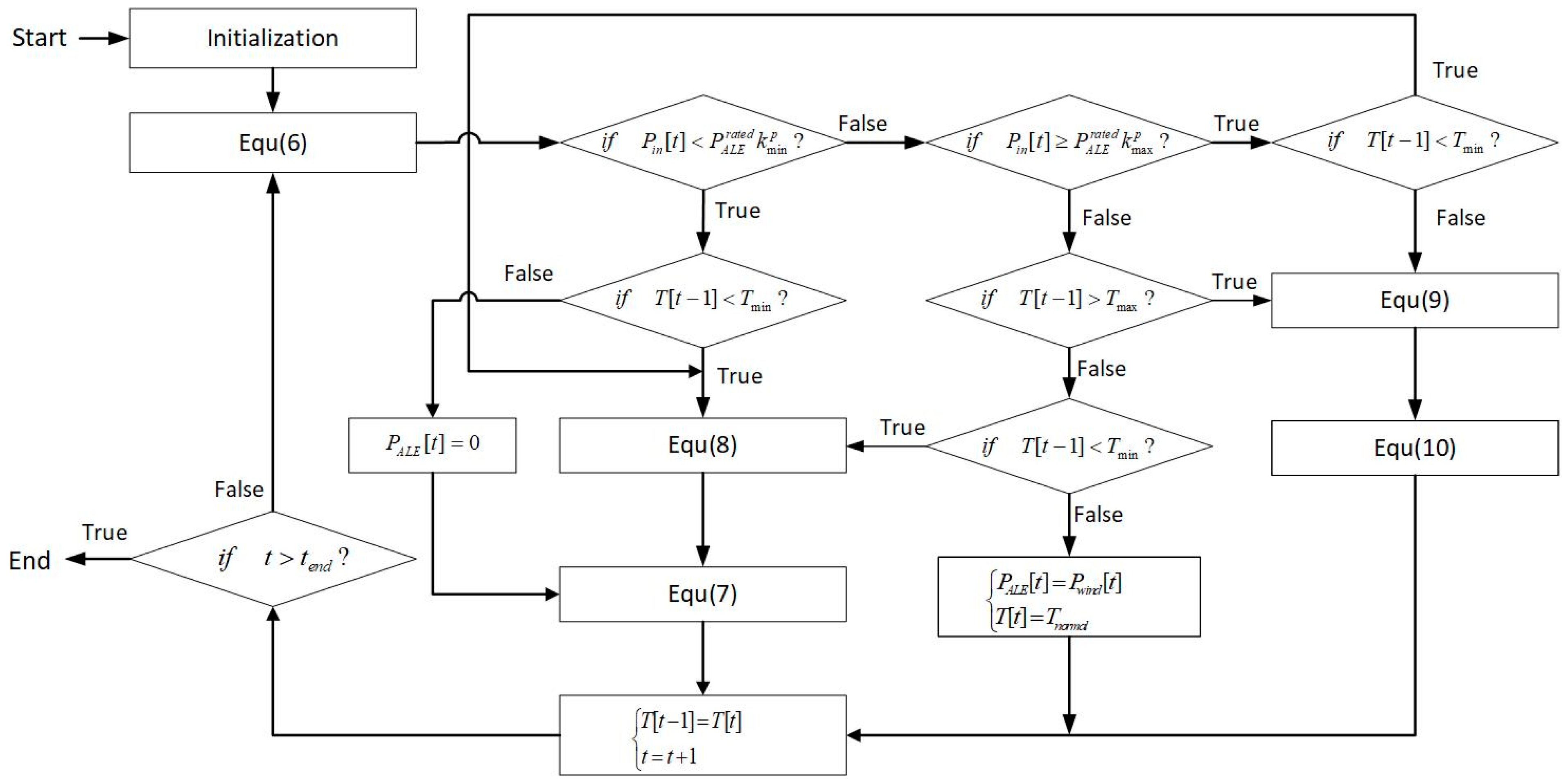
3. Proposed Operation Strategy and Simplified Techno-Economic Analysis Model
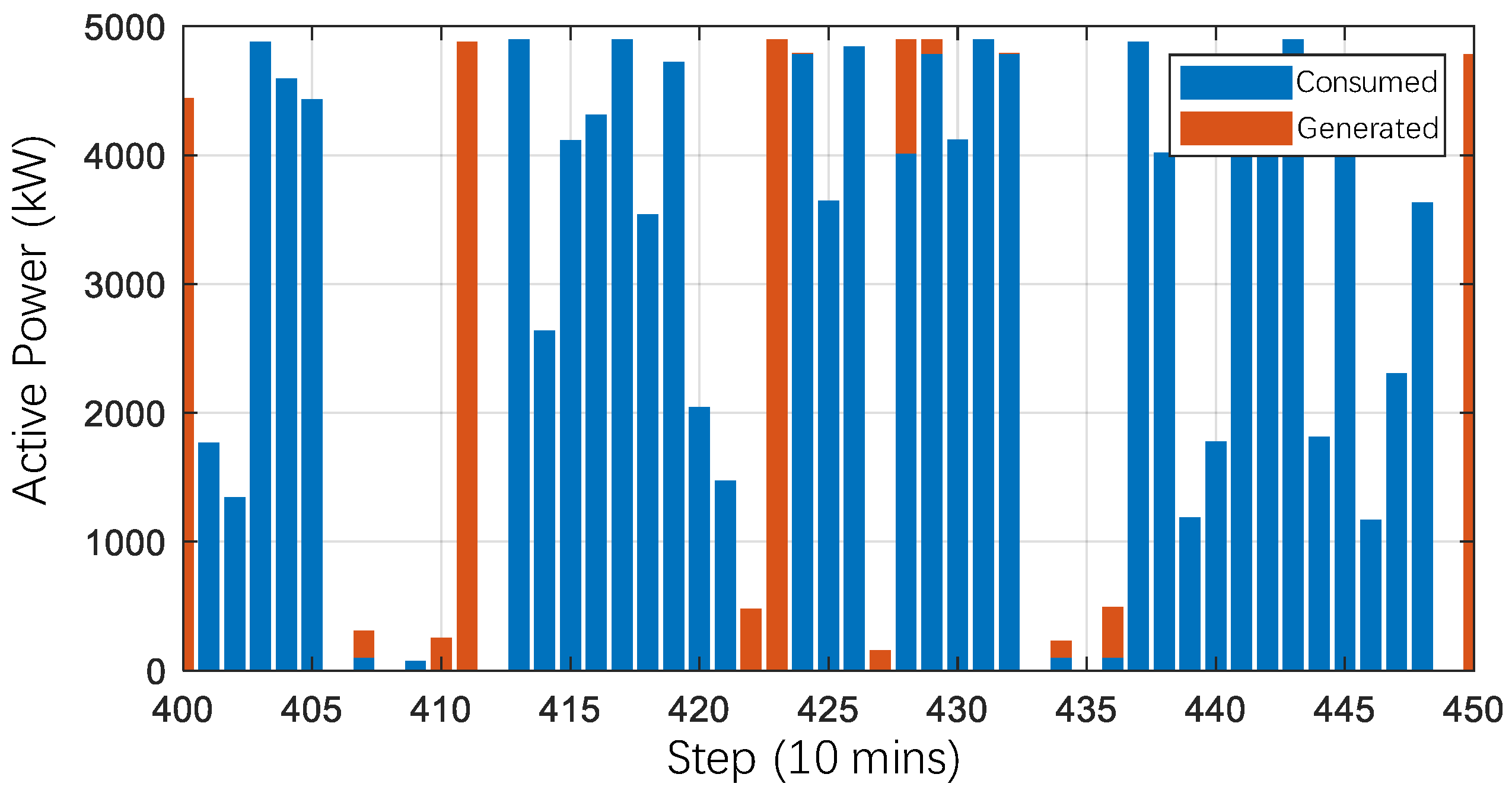
4. Simulation Verification
4.1. Testing Scenario 1
4.2. Testing Scenario 2
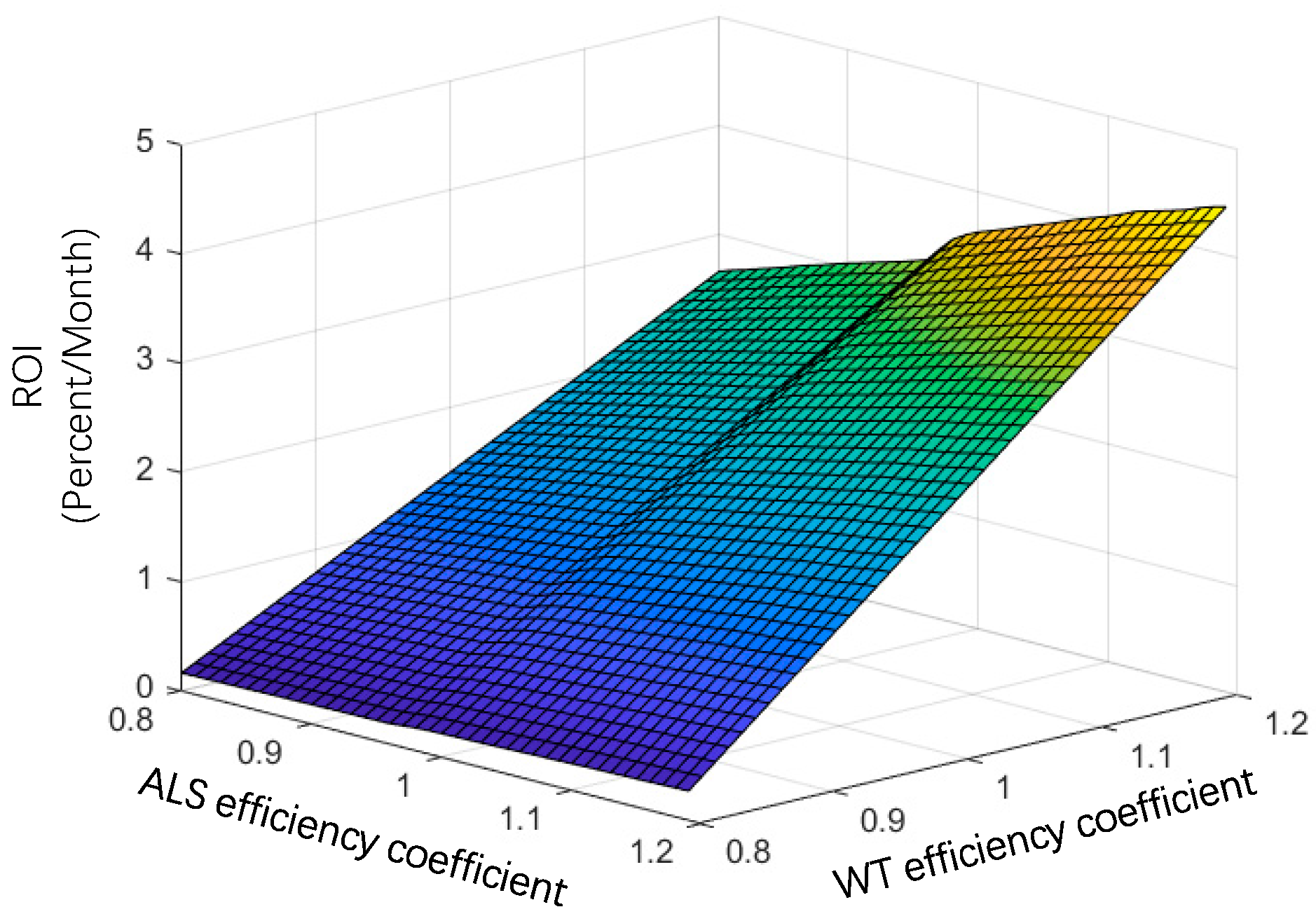
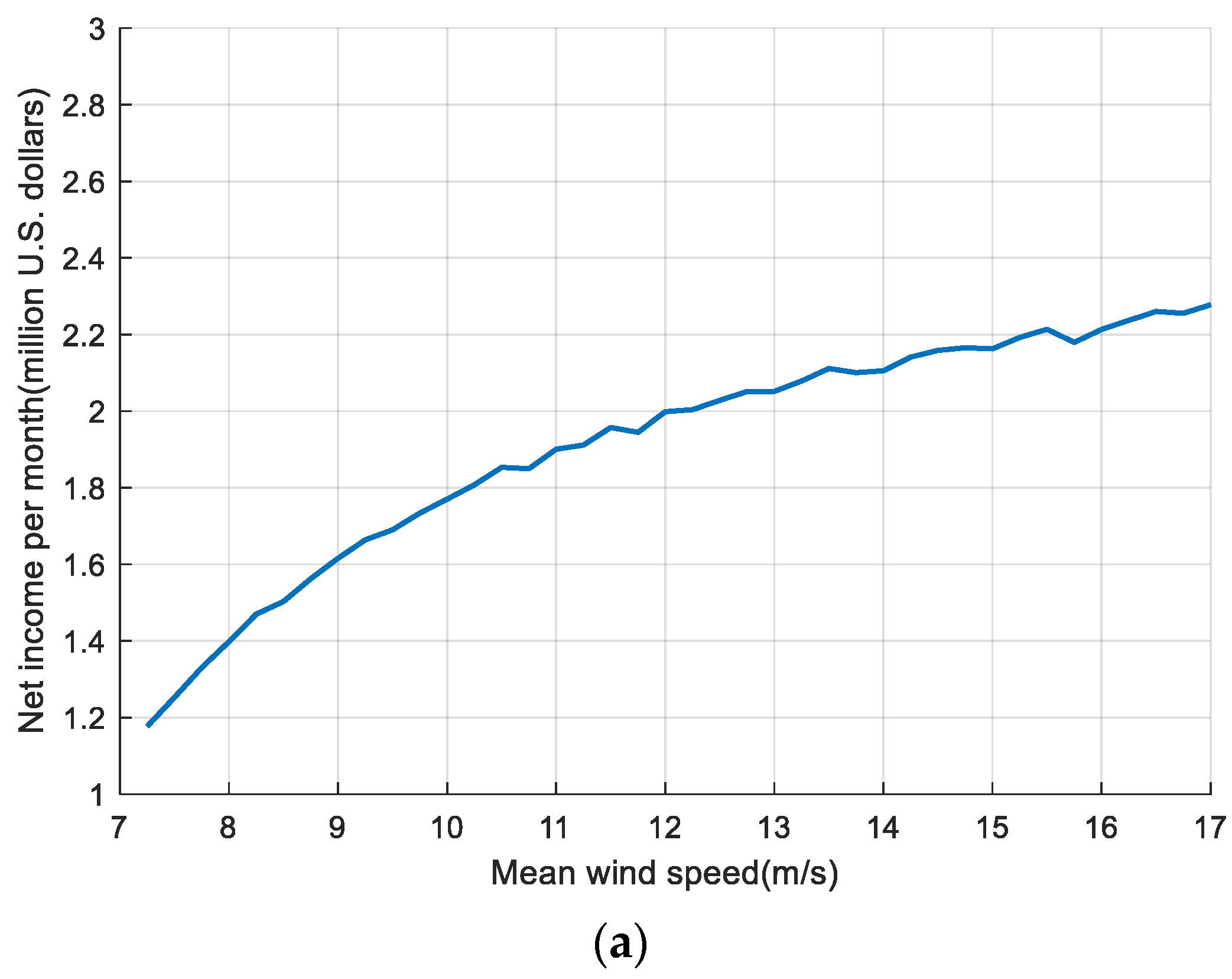
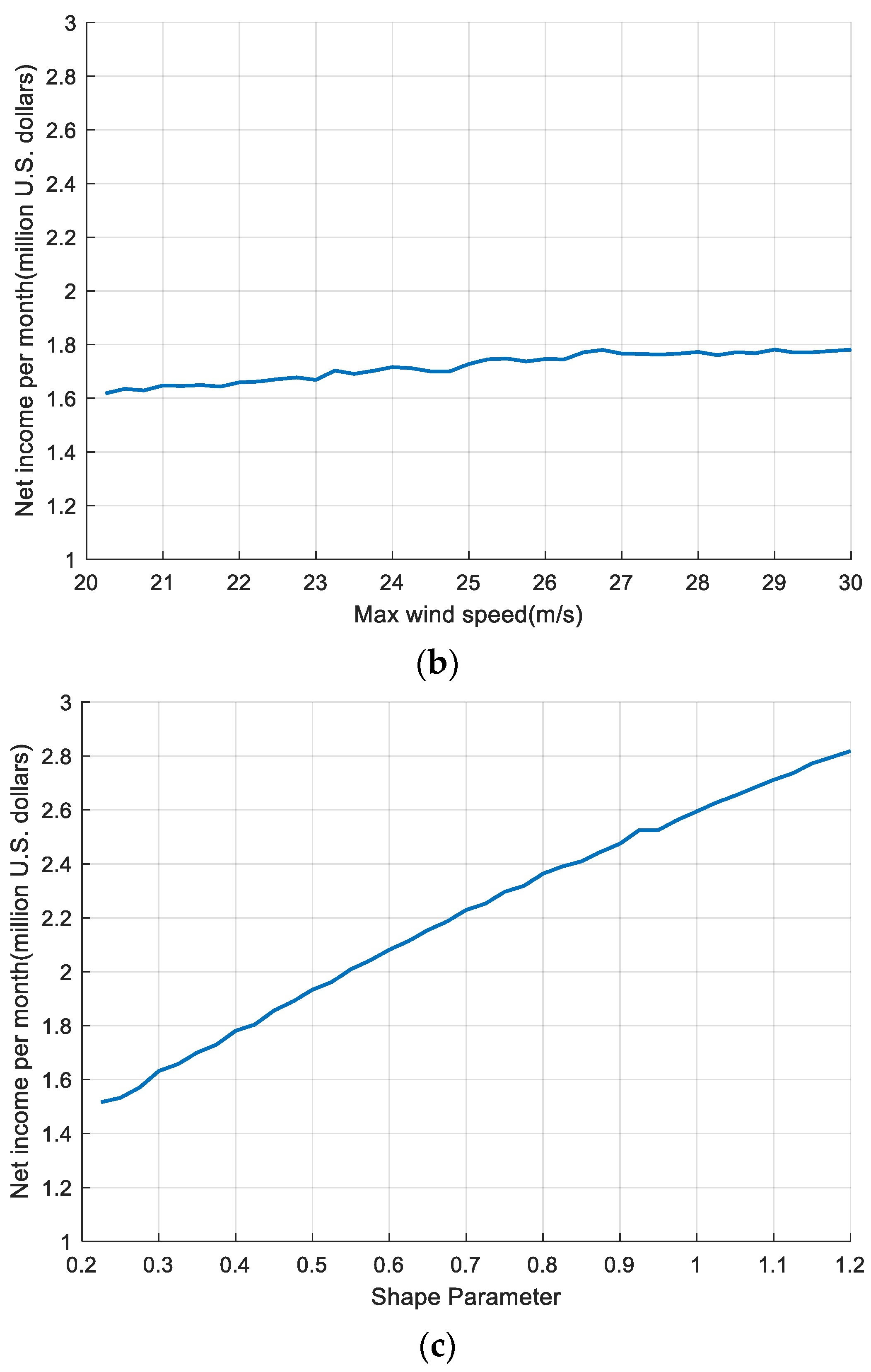
4.3. Sensitivity Analysis
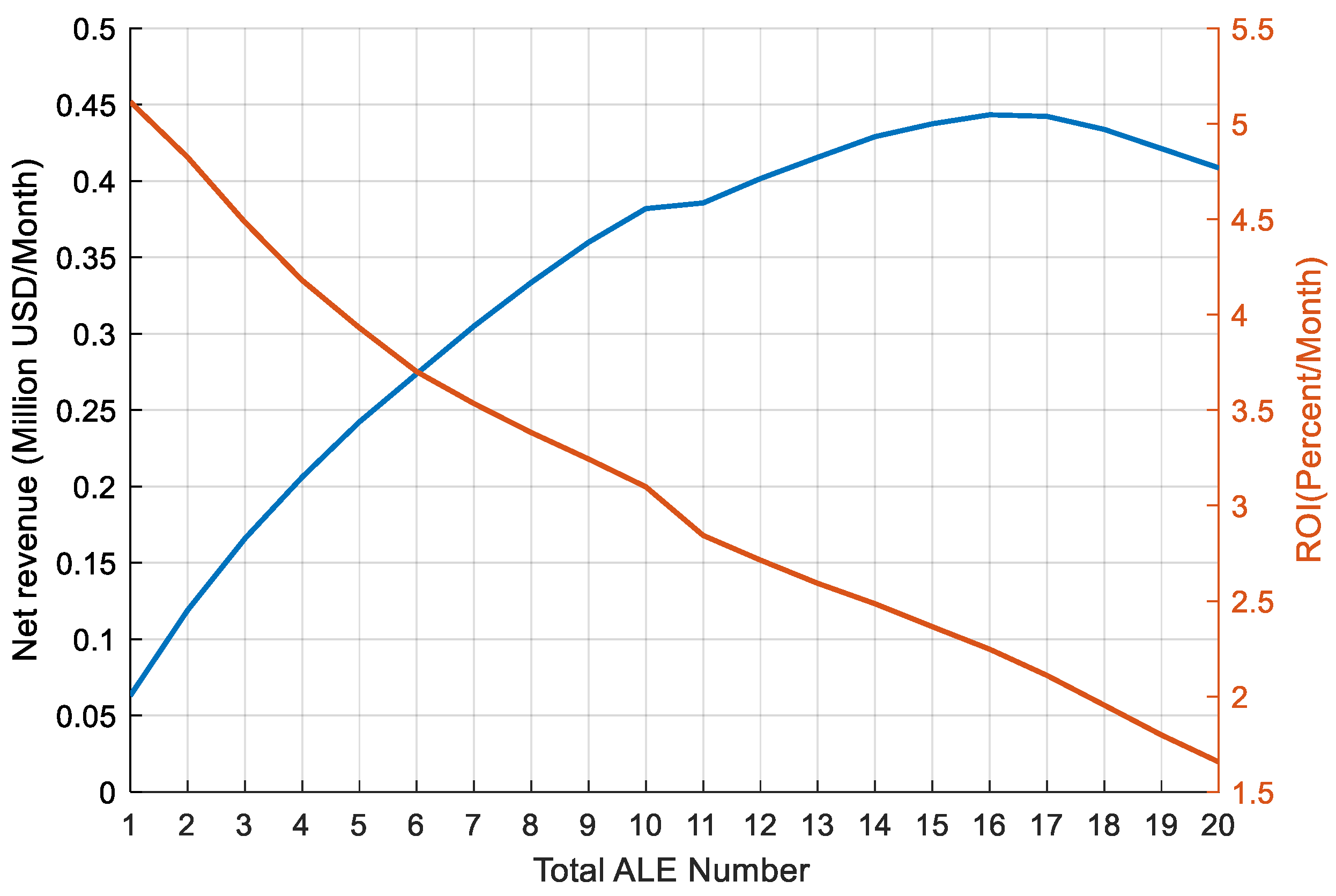
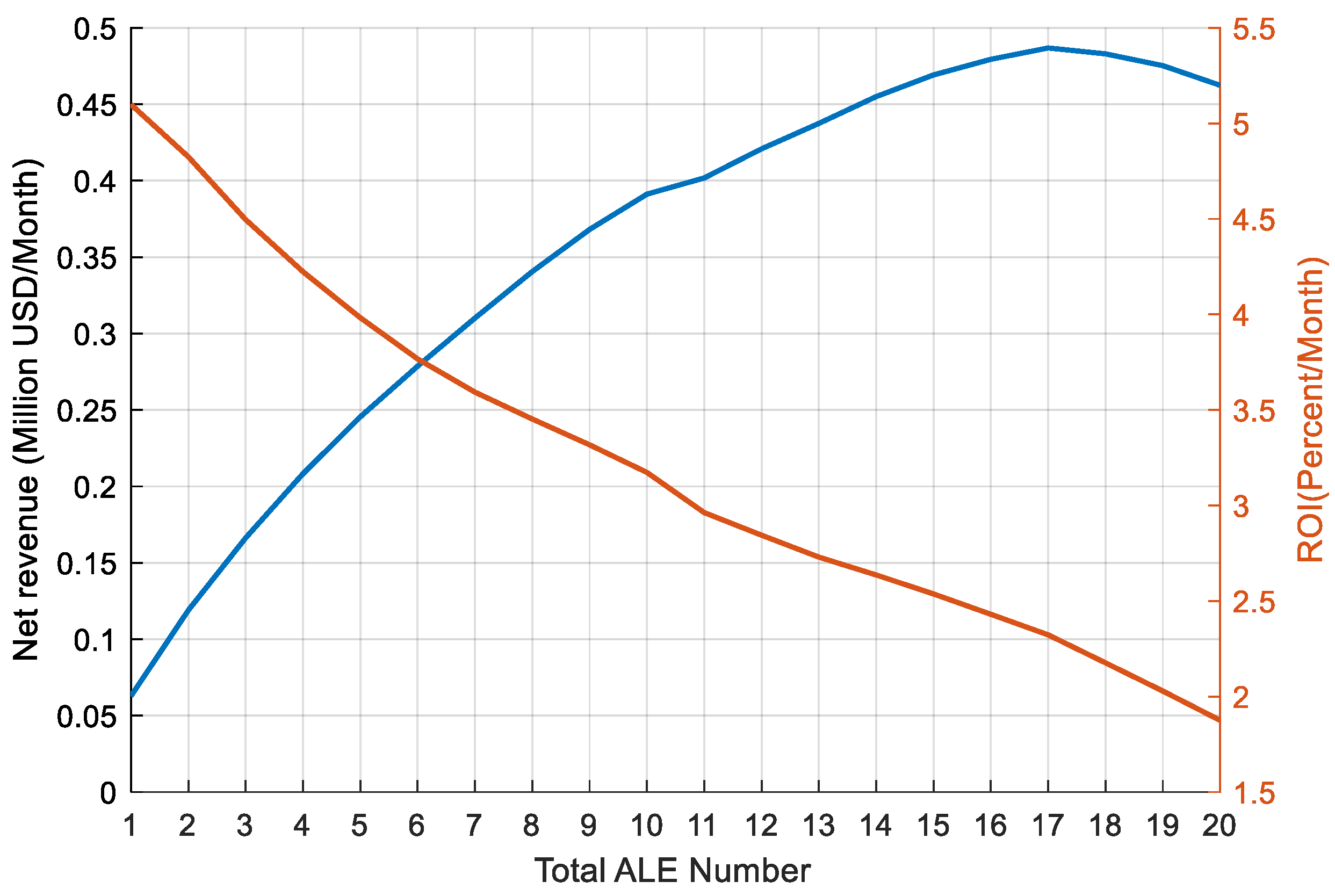
4.4. Capacity Allocation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AEC | Alkaline Electrolyser Cell |
| ALE | Alkaline electrolyzer |
| ALS | Alkaline solution |
| CAPEX | Capital expenditure |
| EMS | Energy management system |
| ESS | Energy storage system |
| HHV | Higher Heating Value |
| HVDC | High-voltage direct current |
| IGBT | Insulated Gate Bipolar Transistor |
| LCOE | Levelized Cost of Electricity |
| LCOH | Levelized Cost of Hydrogen |
| PEMEC | Proton exchange membrane electrolysis cells |
| PtX | Power-to-X |
| ROI | Return on investment |
| SOEC | Solid oxide electrolyzer cell |
| WT | Wind turbine |
References
- PtX i Danmark før 2030; Report 18/07002-7; Energinet: Fredericia, Denmark, 2019.
- Nye Vinde til Brint—PtX Strategisk Handlingsplan; Report 19/07995-21; Energinet: Fredericia, Denmark, 2020.
- Perner, J.; Bothe, D. International Aspects of a Power-to-X Roadmap. Front. Econ. 2018, 156. [Google Scholar]
- Wang, Z.; Shi, J.; Zhao, Y.; Gao, H.; Tao, Y.; Kat, C.; Qin, H.; Liu, M.; Zhao, J.; Cao, B.; et al. China Wind Power Development Roadmap 2050; Energy Research Institute, China National Development and Reform Commission: Beijing, China, 2014. [Google Scholar]
- Recalde Melo, D.F.; Chang-Chien, L.-R. Synergistic Control Between Hydrogen Storage System and Offshore Wind Farm for Grid Operation. IEEE Trans. Sustain. Energy 2014, 5, 18–27. [Google Scholar] [CrossRef]
- Senjyu, T.; Nakaji, T.; Uezato, K.; Funabashi, T. A hybrid power system using alternative energy facilities in isolated island. IEEE Trans. Energy Convers. 2005, 20, 406–414. [Google Scholar] [CrossRef]
- Ursua, A.; Gandia, L.M.; Sanchis, P. Hydrogen Production From Water Electrolysis: Current Status and Future Trends. Proc. IEEE 2012, 100, 410–426. [Google Scholar] [CrossRef]
- Diaaeldin, I.M.; Attia, M.A.; Khamees, A.K.; Omar, O.A.M.; Badr, A.O. A Novel Multiobjective Formulation for Optimal Wind Speed Modeling via a Mixture Probability Density Function. Mathematics 2023, 11, 1463. [Google Scholar] [CrossRef]
- Yang, N.; Huang, Y.; Hou, D.; Liu, S.; Ye, D.; Dong, B.; Fan, Y. Adaptive Nonparametric Kernel Density Estimation Approach for Joint Probability Density Function Modeling of Multiple Wind Farms. Energies 2019, 12, 1356. [Google Scholar] [CrossRef]
- Omar, O.A.M.; Ahmed, H.M.; Elbarkouky, R.A. Wind turbines new criteria optimal site matching under new capacity factor probabilistic approaches. Energy Syst. 2023, 14, 419–444. [Google Scholar] [CrossRef]
- Tahara, S.; Koiwa, K.; Umemura, A.; Takahashi, R.; Tamura, J. A new method to control frequency fluctuation of power system with wind farm by using hydrogen generating system. In Proceedings of the 3rd Renewable Power Generation Conference (RPG 2014), Naples, Italy, 24–25 September 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Zhai, D.; Yao, L.; Liao, S.; Xu, J.; Mao, B.; Xie, B. A Coordinated Control Strategy of Wind Power/Hydrogen Integrated System. In Proceedings of the 2022 7th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 23–26 September 2022; pp. 838–843. [Google Scholar] [CrossRef]
- Koiwa, K.; Takahashi, R.; Tamura, J. A study of hydrogen production in stand-alone wind farm. In Proceedings of the 2012 International Conference on Renewable Energy Research and Applications (ICRERA), Nagasaki, Japan, 11–14 November 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Nistor, S.; Carr, S.; Sooriyabandara, M. The Island Hydrogen Project: Electrolytic Generated Hydrogen for Automotive and Maritime Applications. IEEE Electrif. Mag. 2018, 6, 55–60. [Google Scholar] [CrossRef]
- Chu, W.; Zhang, Y. The Efficiency and Economic Feasibility Study on Wind-Hydrogen System. In Proceedings of the 2020 IEEE Sustainable Power and Energy Conference (iSPEC), Chengdu, China, 23–25 November 2020; pp. 1198–1203. [Google Scholar] [CrossRef]
- Ioannou, A.; Brennan, F. A preliminary techno-economic comparison between a grid-connected and non-grid connected offshore floating wind farm. In Proceedings of the Offshore Energy and Storage Summit (OSES), BREST, France, 10–12 July 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Koiwa, K.; Umemura, A.; Takahashi, R.; Tamura, J. Stand-alone hydrogen production system composed of wind generators and electrolyzer. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 1873–1879. [Google Scholar] [CrossRef]
- Tebibel, H. Wind Turbine Power System for Hydrogen Production and Storage: Techno-economic Analysis. In Proceedings of the 2018 International Conference on Wind Energy and Applications in Algeria (ICWEAA), Algiers, Algeria, 6–7 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Sayed, K.; Khamies, M.; Abokhalil, A.G.; Aref, M.; Mossa, M.A.; Almalki, M.M.; Alghamdi, T.A. Feasibility Study and Economic Analysis of PV/Wind-Powered Hydrogen Production Plant. IEEE Access 2024, 12, 76304–76318. [Google Scholar] [CrossRef]
- González-Longatt, F.; Wall, P.; Terzija, V. Wake effect in wind farm performance: Steady-state and dynamic behavior. Renew. Energy 2012, 39, 329–338. [Google Scholar] [CrossRef]
- The Wind Power. The Wind Power Database. Available online: https://www.thewindpower.net/ (accessed on 10 April 2024).
- Schmidt, O.; Gambhir, A.; Staffell, I.; Hawkes, A.; Nelson, J.; Few, S. Future cost and performance of water electrolysis: An expert elicitation study. Int. J. Hydrogen Energy 2017, 42, 30470–30492. [Google Scholar] [CrossRef]
- Bartholomy, O. A Technical, Economic, and Environmental Assessment of the Production of Renewable Hydrogen from Wind in California. Master’s Thesis, California Polytechnic State University, San Luis Obispo, CA, USA, 2002. [Google Scholar]
- Ozay, C.; Celiktas, M.S. Statistical analysis of wind speed using two-parameter Weibull distribution in Alaçatı region. Energy Convers. Manag. 2016, 121, 49–54. [Google Scholar] [CrossRef]
- Abdelsalam, R.A.; Abdallah, Y.S.; Shabar, N.M.; Afifi, O.A.; Fouda, M.H.; El-Deib, A.A. Energy Management and Techno-Economic Optimization of an Isolated Hybrid AC/DC Microgrid with Green Hydrogen Storage System. In Proceedings of the 2023 IEEE Conference on Power Electronics and Renewable Energy (CPERE), Luxor, Egypt, 19–21 February 2023; pp. 1–7. [Google Scholar]
- Fueling the Future of Mobility: Hydrogen Electrolyzers. Monitor Deloitte. 2021. Available online: https://www2.deloitte.com/content/dam/Deloitte/fr/Documents/energie-et-ressources/Publications/fueling-the-future-of-mobility-hydrogen-electrolyzers.pdf (accessed on 25 April 2024).

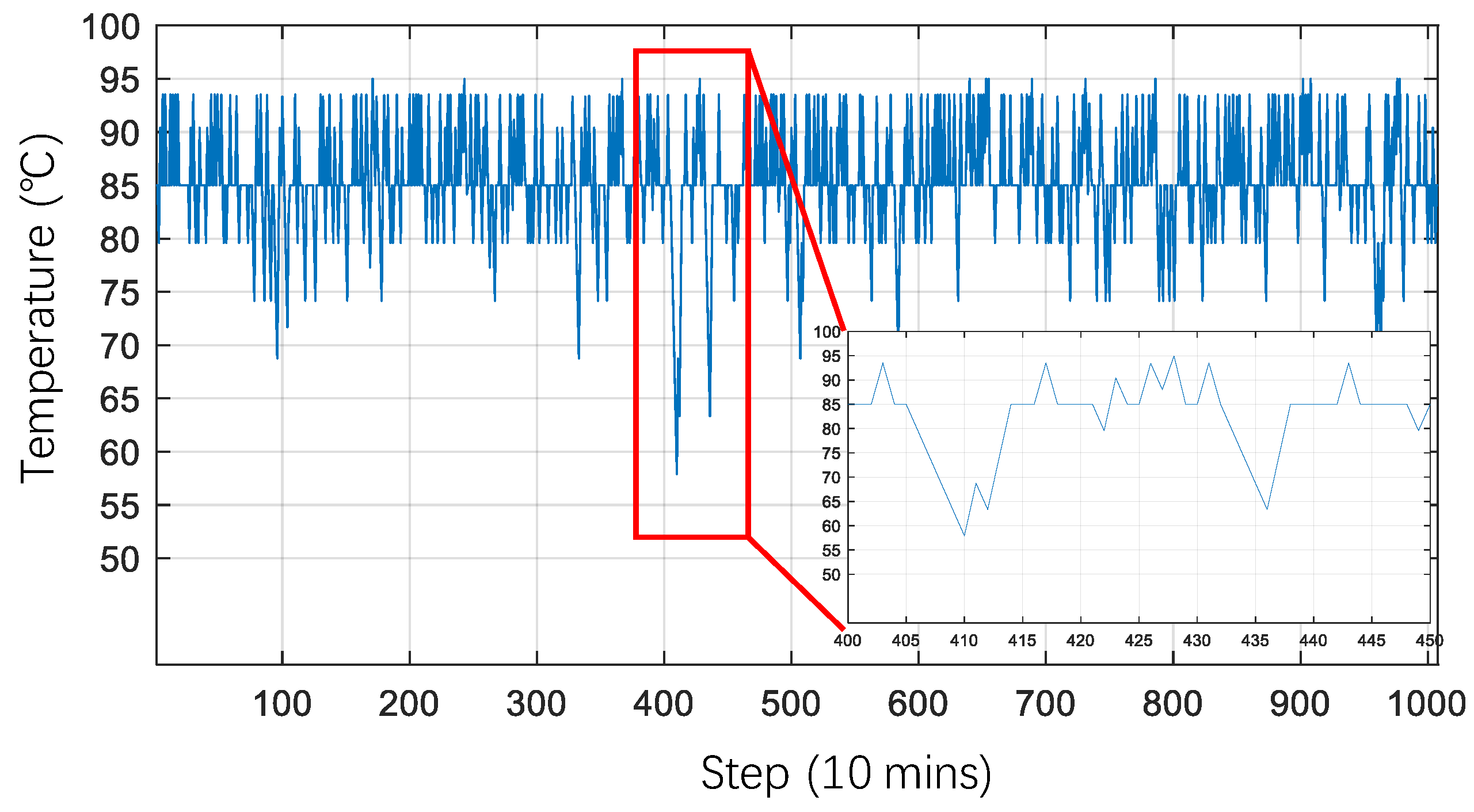

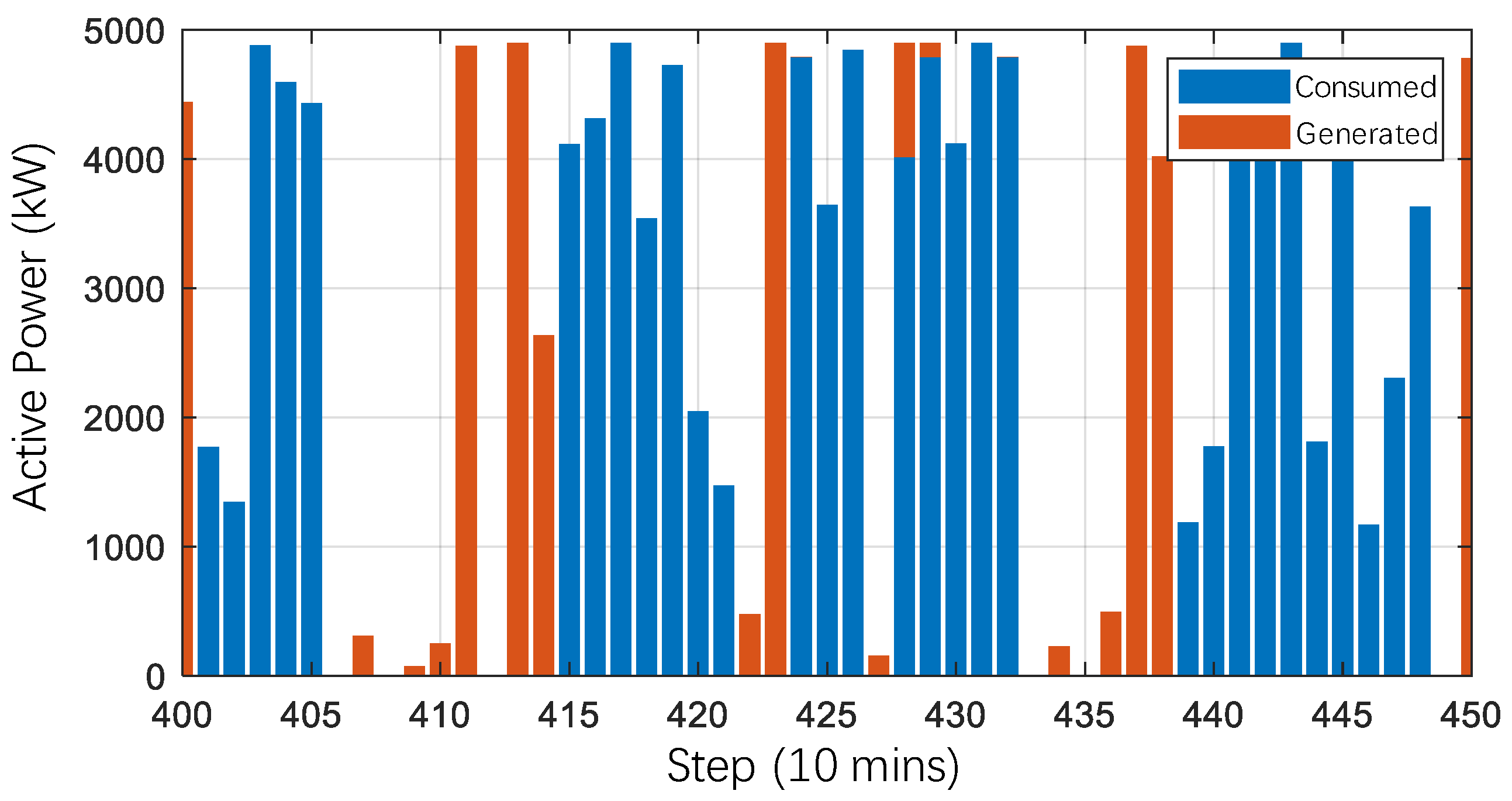
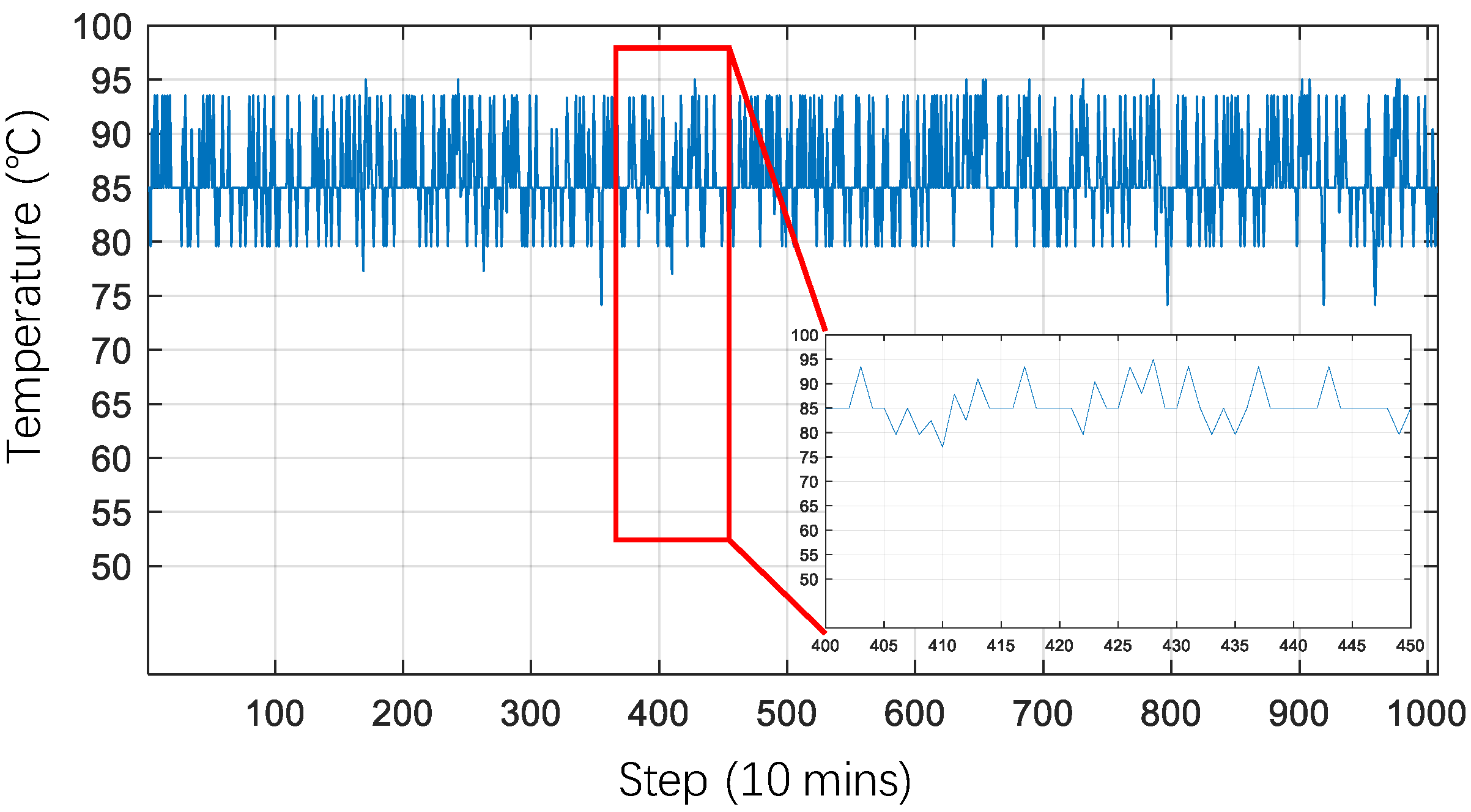
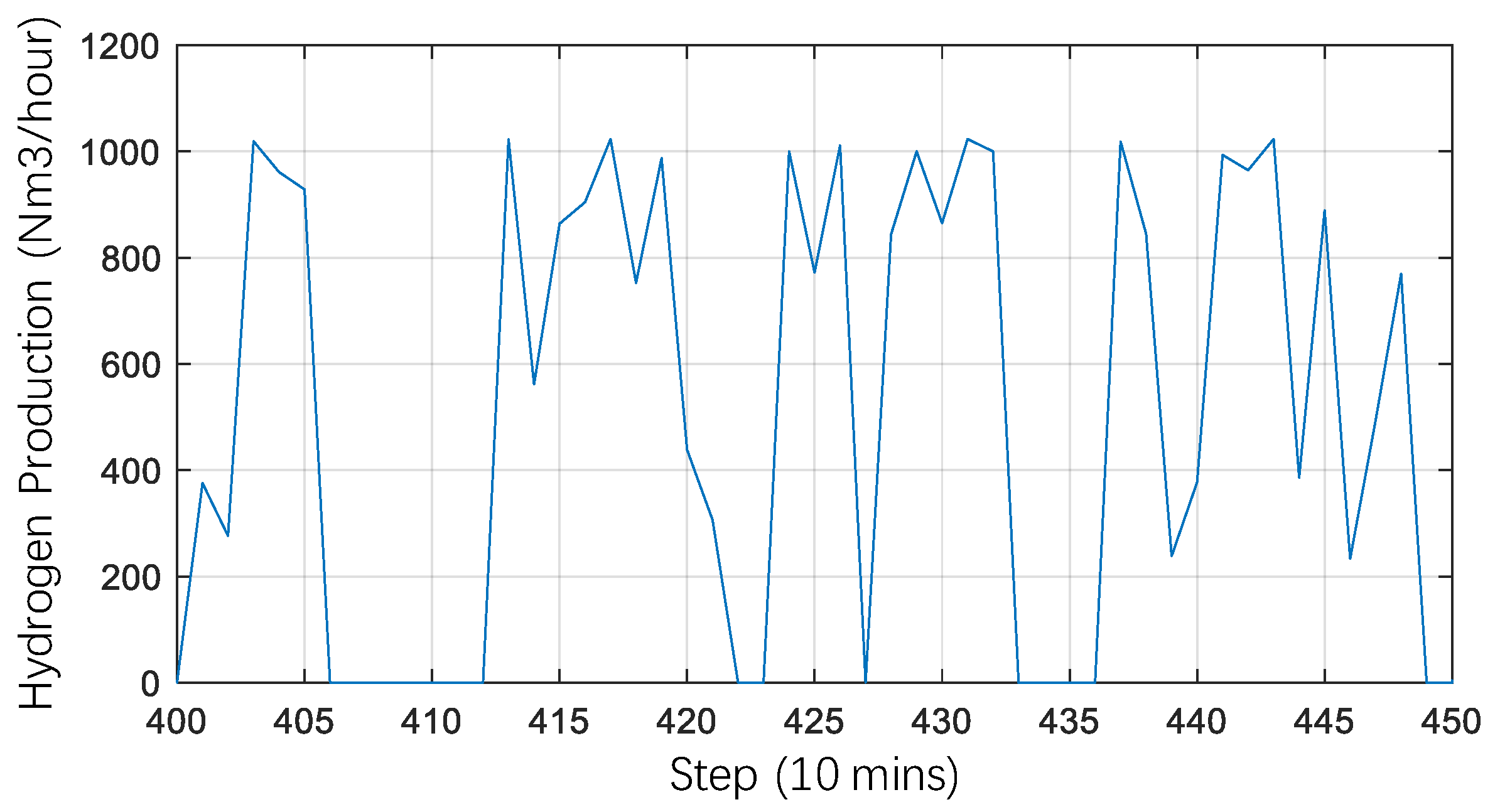
| Symbol | Description | Value | Unit |
|---|---|---|---|
| Simulation step | 10 | min/step | |
| Rated capacity of ALE | 4788.8 | kW | |
| Rated hydrogen production of a single ALE | 1000 | Nm3/h | |
| Cost of total ALE | 1,230,079 | $ | |
| Electricity price (Dedicated source) | 0.027 | $/kWh | |
| Hydrogen price | 4.67 | $/kg | |
| Volume factor | 11.2 | Nm3/kg | |
| The rated capacity of WT | 5000 | kW | |
| Number of WT | 20 | n.a. | |
| Efficiency factor of cons and transmission line | 0.98 | n.a. | |
| Efficiency coefficient of WT | 1 | n.a. | |
| Efficiency coefficient of ALE | 1 | n.a. | |
| Minimum power coefficient | 0.2 | n.a. | |
| Maximum power coefficient | 1.3 | n.a. | |
| Minimum temperature of ALE | 80 | °C | |
| Maximum temperature of ALE | 90 | ||
| Overload temperature of ALE | 95 | ||
| The normal temperature of ALE | 85 | ||
| Ambient temperature | 25 | ||
| Cooling factor | 5.4167 | °C/step | |
| Maximum simulation steps of overload ALE | 2 | n.a. | |
| The capacity of the additional heating system | 100 | kW | |
| Amount of heat required for a 1 °C change in ALS | 4.1 × 106 | J |
| Item | Value |
|---|---|
| Total hydrogen production | 220,218.2182 Nm3 |
| Total electricity consumption | 1,049,678.2675 kWh |
| Total energy utilization | 62.0768% |
| Total hydrogen sales revenue | USD 1.83 million |
| Total electricity cost | USD 0.57 million |
| CAPEX | USD 24.6 million |
| ROI | 5.1303%/Month |
| Item | Value |
|---|---|
| Total hydrogen production | 256,247.0256 Nm3 |
| Total electricity consumption | 1,226,636.3042 kWh |
| Total energy utilization | 72.5419% |
| Total hydrogen sales revenue | USD 2.13 million |
| Total electricity cost | USD 0.67 million |
| CAPEX | USD 24.6 million |
| ROI | 5.9581%/Month |
| Symbol | Item | Value |
|---|---|---|
| T | Total lifetime | 25 year |
| Ts | Stack lifetime | 75,000 h |
| Ht | Total hydrogen production | 3,074,964.3 Nm3/year |
| Ft | Total electricity cost | 8.04 million USD/year |
| O | O&M cost | 5% of CAPEX |
| I | CAPEX | USD 24.6 million |
| LCOH | Total electricity cost | 2.01 USD/kg |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, W.; Yang, L.; Sun, K.; Zhou, Y.; Yuan, Z. An Economic Performance Improving and Analysis for Offshore Wind Farm-Based Islanded Green Hydrogen System. Energies 2024, 17, 3460. https://doi.org/10.3390/en17143460
Feng W, Yang L, Sun K, Zhou Y, Yuan Z. An Economic Performance Improving and Analysis for Offshore Wind Farm-Based Islanded Green Hydrogen System. Energies. 2024; 17(14):3460. https://doi.org/10.3390/en17143460
Chicago/Turabian StyleFeng, Wei, Liu Yang, Kai Sun, Yuebin Zhou, and Zhiyong Yuan. 2024. "An Economic Performance Improving and Analysis for Offshore Wind Farm-Based Islanded Green Hydrogen System" Energies 17, no. 14: 3460. https://doi.org/10.3390/en17143460
APA StyleFeng, W., Yang, L., Sun, K., Zhou, Y., & Yuan, Z. (2024). An Economic Performance Improving and Analysis for Offshore Wind Farm-Based Islanded Green Hydrogen System. Energies, 17(14), 3460. https://doi.org/10.3390/en17143460






