Abstract
Net zero and electrification targets are continuing to enforce a need for the development of high-performance electrical machines, increasingly based on the use of rare earth permanent magnets. Biased flux motors have the potential to overcome some of the disadvantages associated with more conventional electrical machines. Since their introduction, there has been a consistent trend towards new and improved topologies, all relying on the same principles of operation. In this paper, a new alternative operation is proposed where the magnetic flux density offset of each module is different. The resulting asymmetric biased excitations of the magnets leads to a flux concentration in the air gap. Placement of magnets in the slot-opening area is shown to produce a higher average torque at a higher power factor. It is mathematically shown that the conventional methods used to investigate the effect of each group of magnets separately cannot be used for the explanation of this operation principle. Therefore, it is necessary to simultaneously consider both groups of magnets in the magnetic equivalent circuit. Due to the use of magnets in these motors, thermal conditions are also investigated. Finally, a comprehensive comparison between several stator-situated-magnet motors is presented. The performance of the proposed motor is improved in terms of average torque, torque density, PM torque density, power factor, and overload capability. The torque density specifically has increased by 9%. Moreover, both motors have suitable thermal behaviour which confirms the validity of the demagnetization analysis.
1. Introduction
In recent years, stator permanent magnet (PM) motors have gained significant attention in the realm of electric machines, primarily attributed to their potential for mitigating mechanical and thermal stress on PMs [1,2]. Compared to rotor-PM structures, these motors are robust and have thermal and mechanical advantages of the rotor when compared to rotor-PM structures. Apart from the recognized thermal and mechanical advantages [3], they are known to exhibit high-efficiency performance at low speed, thanks to their magnetic gearing effect [2,4]. The stator-PM division encompasses distinct categories of machine, characterized by unique features. It is helpful to discuss them in order to explain the evolution of the topology considered in this paper.
1. Stator-slot PM (SSPM) motors [5] have the PMs in the slot opening of the stator, preventing them from being in series with the armature magnetic field and therefore providing effective protection for the PMs [6]. However, the PM-driven flux tends to short-circuit in the stator yoke, leading to a reduction in torque density.
2. Flux-switching PM (FSPM) motors [7] offer heightened average torque at the expense of compromised PM safety. PMs are enclosed by armature windings, which, although they hinder direct access, does result in increased torque density.
3. Flux-reversal PM (FRPM) motors also achieve high torque density, but this comes at the cost of compromised PM safety [8]. The proximity of PMs to the air gap in this design makes it challenging to cool them effectively through heat transfer to the stator yoke [9].
4. The doubly salient PM (DSPM) motor strategically positions the PM as far as the air gap in the stator yoke [10]. However, since its introduction this motor has been operated with a square-wave current, resulting in elevated torque ripple due to inherent imbalances in the reluctance network of each phase [11,12,13,14,15]. Various solutions have been proposed to equalize the reluctance network of each phase. To reduce the torque ripple, other methods, such as bevelled tooth and slot, can be used, but this deteriorates the torque profile, efficiency, and current-torque profile [16].
5. The biased-flux PM (BFPM) motor is a recently proposed novel type of DSPM motor. All PMs are placed in the stator yoke, facilitating easier thermal monitoring compared to FSPM, FRPM, and SSPM topologies [17]. Although the BFPM structure offers more slot/pole combinations compared to DSPM, resulting in reduced torque ripple, it does not generate a significantly higher average torque [18]. To address torque density, improvements have been proposed for BFPM motors. An analysis in [19] explores the impact of multi-tooth structures on torque density, revealing that BFPM motors with a multi-tooth stator exhibit higher torque density and lower torque ripple.
6. The combination of SSPM and BFPM structures is termed biased-flux slot PM (BFSPM) and presents a more competitive solution, offering a higher torque density with a lower torque ripple [20].
7. An inter-modular PM (IMPM) motor has bar PMs positioned between stator modules [21]. The primary advantage of this topology lies in the circulation of magnetic flux by the armature winding [22]. Given that the PMs are not entirely in series with the armature, the power factor of the IMPM motor surpasses that of the BFSPM topology. Additionally, the placement of the PMs provides complete and unique accessibility for monitoring their temperature status.
A shared characteristic among all BFPM topologies, including IMPM, is their operational principle centred around the variation of a biased magnetic point. Various BFPM structures exhibit distinct biased magnetic points and fluctuation amplitudes. Nevertheless, this operating principle has not undergone extensive refinement. In essence, a closer examination of their operational principles offers an opportunity to optimize the torque profiles of these structures. Innovative flux-focusing solutions can be devised without compromising the fundamental operational principle of these topologies.
In this paper, a new IMPM motor, namely slot-IMPM (SIMPM), is proposed based on scrutinizing the operation principle of the IMPM topology. To enable the flux-focusing effect, slot PMs with different synergistic directions are considered. Those slot PMs will intensify or reduce the biased operating point in the middle teeth, helping the IMPM to regain its high torque density while protecting the PMs from demagnetization and also increasing the power factor. Although this asymmetric flux distribution improves the SIMPM motor’s performance, it complicates the prediction of how each PM group contributes to the total flux distribution. In most of our works and by using the symmetry condition of flux distribution, we could simplify our analysis by considering only a small portion of the stator. However, in the SIMPM motor we have to investigate a larger portion of the stator to fully analyse the flux density distribution in the air gap. Due to the stator teeth saturation caused by the slot PMs, the slot and inter-module PMs cannot be investigated independently.
In response to this complexity, this paper proposes an analytical method which investigates both slot and inter-module PMs simultaneously. Harmonic components of the flux density are analysed using flux modulation theory (FMT). Finally, the Maxwell stress tensor has been used to determine the contribution of each harmonic component to the electromagnetic torque generation.
Section 2 fully addresses the topology of the proposed motor and its operation principle. It also establishes the proposed structure’s flux modulation and identifies the working harmonics. The FMT method is a well-known analytical method for solving electromagnetic problems and is currently widely used due to its fast approach. Section 3 delves into the optimization algorithms and design parameters. The no-load and full-load operations are explored in Section 4 through finite element analysis (FEA), and a comparative study is also delivered in this section to better evaluate the advantages of the proposed IMPM. Furthermore, the PMs have been fully studied from the perspective of demagnetization and thermal stress. Finally, a conclusion is provided in Section 5.
2. Operation Schemes
This section begins by outlining the fundamental principles governing the operation of the IMPM motor and then describes the new operational principle through magnetic equivalent circuit modelling.
2.1. IMPM’s Operation Principle
Figure 1c,d illustrate the structure of an IMPM motor. The motor’s pole-pair number is equal to the number of rotor teeth, in this case 11. The direction of PM magnetization and winding connection is demonstrated in Figure 1. It is worth noting that the coils of each phase are connected in series. M470-50A is used as the lamination material of the rotor and stator. The rotation of the rotor is linked to the displacement of its magnetic balance point—the pivotal location where all magnetic forces acting on the rotor attain equilibrium. This delicate balance is perturbed when the armature windings are energized, compelling the rotor to realign itself with the magnetic balance point. In configurations featuring biased-flux, each stator module is predisposed to a fixed magnetic point. Upon activation of the armature, the stator modules undergo oscillations around this predetermined point, inducing a consequential shift in the rotor’s balance point.
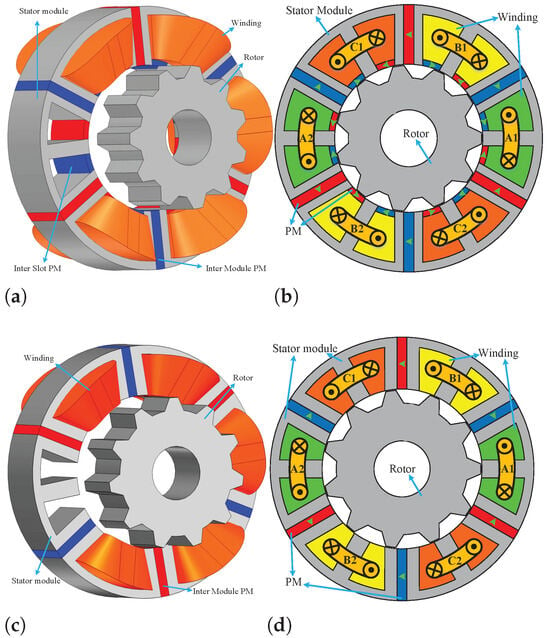
Figure 1.
Structure of the (a) SIMPM in 3D, (b) SIMPM in 2D, (c) IMPM in 3D, and (d) IMPM in 2D.
2.2. Asymmetric-Biased-Flux Operation
The manipulation of the biased magnetic point for each module offers a viable means to augment the concentration of flux density in the air gap. Introducing asymmetry into the flux density profile can be achieved by placing PMs within the stator slot opening. The added advantage of the supplementary PMs lies not only in their safeguarding against demagnetization, owing to their parallel alignment with the armature windings, but also in their ability to selectively amplify or diminish the flux density in the air gap, based on their orientation.
2.3. Mathematical Verification
This section provides the mathematical analysis of the asymmetric-biased-flux operation for this structure. It is essential to highlight a key distinction in operational principles—specifically, the ineffectiveness of the superposition principle in this context. Unlike the conventional approach, the interplay of inter-modular magnets alters the saturation point of the stator middle teeth. Consequently, the slot magnets encounter varying reluctance in the stator core. As a result, the involvement of each PM in torque production is contingent upon the saturation conditions induced by the presence and influence of other PMs. Figure 2a illustrates the flux density profile in the air gap under no-load conditions induced by individual sets of PMs. Each case considers only one set of PMs at a time. The observation reveals that the summation of flux densities generated by each PM independently does not align with the no-load flux density of the SIMPM when all PMs are collectively modeled. In Figure 2b, the flux density profiles are depicted under conditions where a narrow air gap is introduced in the stator middle tooth. This gap serves to prevent short-circuiting of the slot PMs in the stator core, with the exclusion of the inter-modular magnets in the modelling. Clearly, in comparison with the preceding scenario, the combined flux density contribution from both slot PM and IMPM is closer to the flux density in the SIMPM model.
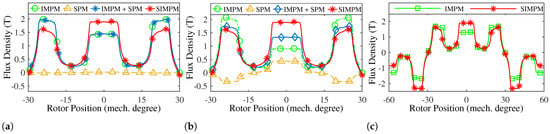
Figure 2.
Normal flux density distribution: (a) the effect of each PM is individually considered; (b) there is a gap in the stator middle teeth to prevent the slot PM’s flux short circuit; (c) comparison between the SIMPM and IMPM.
Having established the ineffectiveness of the superposition principle in analytically exploring this operational principle, an alternative mathematical approach is required to differentiate between SIMPM and IMPM. Figure 2c illustrates how the flux density under one stator module significantly differs from its neighboring modules. The magnetic equivalent circuit (MEC) of the structures is shown in Figure 3. This diagram provides an overview of various reluctances influenced by the saturation effects of inter-modular magnets. Simplifying this circuit, we can isolate an individual module, as shown in Figure 4a. A more streamlined perspective into the magnetic circuit is presented in Figure 4b by eliminating certain core reluctances. Once the magnetic circuit is established, the impact of each PM can be studied under a specific condition: the SPMs undergo variable reluctance adjusted by the inter-modular magnets. Figure 4c,d display this condition, providing a nuanced understanding of the magnetic interactions within the structure.
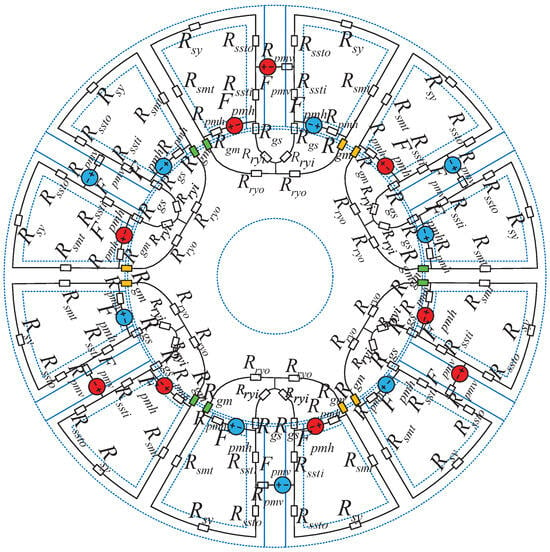
Figure 3.
General magnetic equivalent circuit.

Figure 4.
SIMPM’s one-module magnetic equivalent circuit when (a) all of the core reluctances are modelled, (b) just the necessary ones are modelled, (c) only the inter-modular magnets are modelled, and (d) only the slot PMs are modelled.
Equation (1) shows the flux linkage of two adjacent modules in the SIMPM. and are the flux linkage induced by SPMs and and represent the inter-modular magnets’ flux linkages.
where and can be calculated as
and and can be formulated by solving the magnetic circuit in Figure 4d.
It is evident that the flux density in SIMPM’s module is either subtracted or added with (3).
2.4. Space Harmonics
To examine distinct harmonic orders in the SIMPM topology, the flux modulation theory is applied, isolating PM-MMF and armature MMF, as depicted in Figure 5. Each structure adjusts the primary PM-MMF and armature MMF using stator and rotor teeth, and the values of (), (), (), (), (), (), and () shown in Figure 5 are calculated. Employing a fast Fourier transform (FFT) and leveraging the evident even symmetry in Figure 6a, the primary PM-MMF of the SIMPM can be formulated, as illustrated in (4). Notably, the Fourier coefficient () of the SIMPM differs from the IMPM configuration, as the asymmetric-biased-flux operation introduces an additional DC term ().
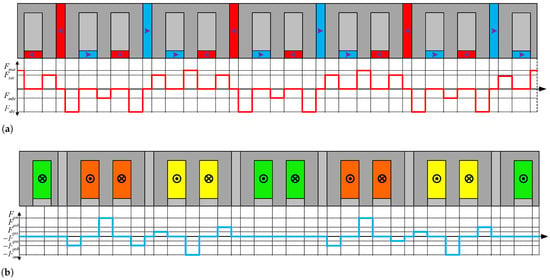
Figure 5.
SIMPM’s (a) PM MMF and (b) armature MMF.

Figure 6.
(a) SIMPM’s normal flux density for PM-only-enabled condition, (b) its FFT, (c) IMPM’s normal flux density for armature-only-enabled condition, and (d) its FFT.

Table 1.
Harmonic groups of the PM flux density.
The same procedure can be applied to armature MMF, as shown in (7),
to build up the armature flux density (Figure 6c and (8)),
Table 2 categorizes the different armature harmonics shown in (8). To generate average torque, each PM MMF harmonic shall be synchronized with the same space harmonic in Table 1.

Table 2.
Harmonic groups of the armature flux density.
Using the Maxwell stress tensor, the contribution of each PM flux density harmonic is calculated as shown in Table 3. It should be noted that the first 40 harmonics are considered and the major ones are analysed for their effective contribution.

Table 3.
Contribution of each PM flux density harmonic group to the torque production.
The sum of the torque contribution of each harmonic component (Table 3) is not equal to 100% as some harmonic components are missing.
3. Optimization
Figure 7 delineates the optimization parameters utilized for both configurations. Employing random search algorithms and multi-objective optimization techniques, the objective is to augment torque density while concurrently minimizing torque ripple in the structures. Notably, the optimization process places a premium on enhancing torque density. In this research, a genetic algorithm (GA) is used to optimize the motors. The cost function or objective function is defined as shown in (9).
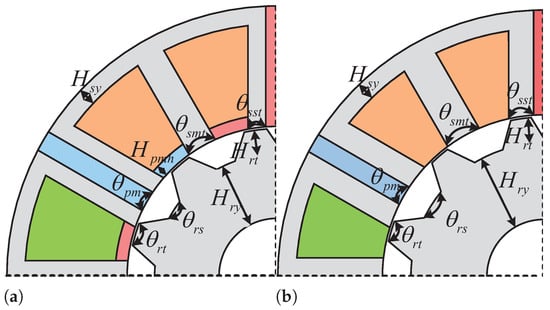
Figure 7.
Optimization parameters for the (a) SIMPM and (b) IMPM.
In (9), CFM, ATC, TRC, PAT, and PTR represent the cost function margin, the average torque coefficient, the torque ripple coefficient, the predicted average torque, and the predicted torque ripple, respectively. Also, and represent the average torque and torque ripple values measured in the simulation. In IMPM’s and SIMPM’s optimization, CFM, ATC, TRC, PAT, and PTR values are equal to 1.3, 0.75, 0.25, 2, and 0.005, respectively.
As illustrated in Figure 8, the optimization generates multiple samples, with the best-performing sample for each structure marked in red. The conclusive values for the optimization parameters are detailed in Table 4. This optimization approach does not impose specific constraints on copper loss or PM mass. Instead, the primary constraints are centered around total volume and current density considerations.
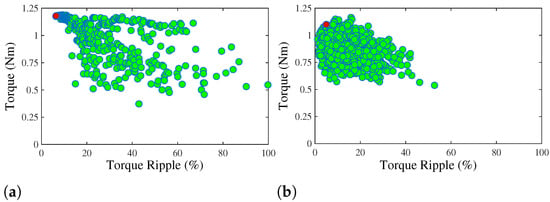
Figure 8.
Optimization samples for the (a) SIMPM and (b) IMPM.

Table 4.
Optimized design variables.
Both motors are optimized to improve the average torque and torque ripple. Each of the structural parameters is changed in a specific range. The maximum and minimum values of these ranges are defined according to the motor geometry. For every optimization sample, the rotor yoke thickness along with other structural parameters are changed, and these variations result in a different motor geometry with different performances in terms of average torque and torque ripple. According to the average torque and torque ripple of each sample, the cost function is calculated. Considering the cost of each sample, the optimum sample is chosen.
A Sensitivity analysis is conducted to investigate the effect of rotor yoke thickness on the motor’s performance in terms of average torque and torque ripple. Other motor structural parameters are not changed during the sensitivity analysis. The results are demonstrated in Figure 9a,b. As Figure 9a shows, decreasing the rotor yoke width causes a decrease in the average torque. Also, decreasing the rotor yoke width causes an increase in the torque ripple, which has been shown in Figure 9b. So, although decreasing the rotor yoke thickness lowers the rotor’s weight, it does not have any positive effect on the motor performance.
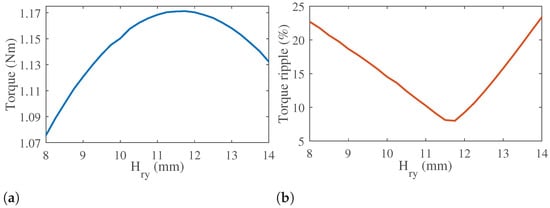
Figure 9.
Effect of different rotor yoke thicknesses on the (a) average torque and (b) torque ripple.
4. FEA Study
This section covers the performance analysis of both the SIMPM and an optimized IMPM including no-load indices such as flux density distributions and back-EMF voltages. Subsequently, the examination extends to full-load parameters, encompassing torque profiles and overload capabilities in the following subsection. To highlight the superior performance of the proposed SIMPM, a comparative analysis is conducted under equitable conditions. Additionally, a comprehensive investigation into the demagnetization of the permanent magnets is carried out, accompanied by a three-dimensional thermal verification. These simulation results are derived using the ANSYS Electronic Desktop software package.
4.1. No-Load Performances
The magnetic flux density distributions of the presented structures under no-load conditions are depicted in Figure 10. It is evident that neither of the motors experiences global saturation. Notably, the flux line representation in Figure 10 illustrates that the SIMPM effectively directs the PM flux towards the air gap, thereby amplifying torque density. The back-EMF waveforms for the motors are displayed in Figure 11.
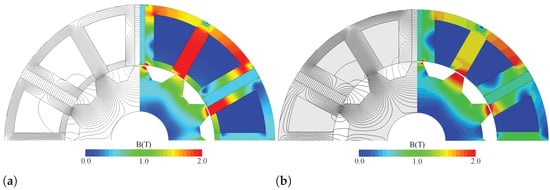
Figure 10.
No-load flux density and flux lines: (a) SIMPM and (b) IMPM.
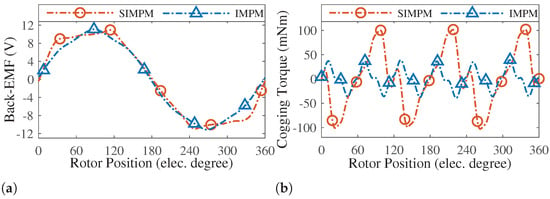
Figure 11.
Comparison of (a) back-EMF and (b) cogging torque.
Given the concentrated flux density in the air gap of the SIMPM, it is reasonable to observe a higher amplitude in the back-EMF waveform. Furthermore, the cogging torque curves, plotted for a 360 electrical degrees period in Figure 11b, reveal that the cogging torque peaks for SIMPM are elevated. This is attributed to the higher flux leakage from the air gap in this structure, as depicted in Figure 10.
4.2. Full Load
Figure 12 illustrates the magnetic flux density distributions of the presented SIMPM at a rated current density of 6 A/mm2 and a speed of 900 rpm. Figure 13 displays the full-load torque profiles. The proposed structures produced approximately 9% more average torque compared to the IMPM. This is because of the flux concentration of the PMs and increased effective harmonics. In other words, reluctance torque is negligible.
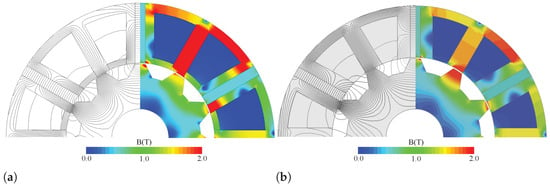
Figure 12.
Full-load flux density and flux lines: (a) SIMPM and (b) IMPM.
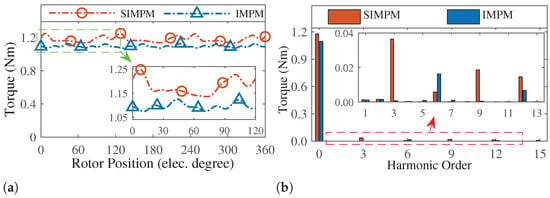
Figure 13.
Comparison of (a) torque profile and (b) torque profile FFT.
In terms of overload capability, both of the structures maintain their average torque value difference while increasing the armature current (Figure 14a). Figure 14b also shows that electromagnetic torque is the main source of produced torque for both of the structures.
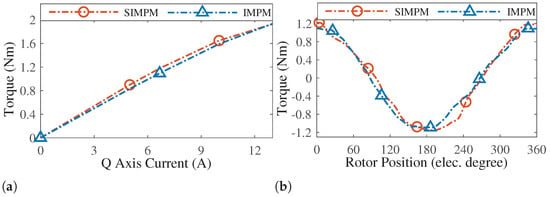
Figure 14.
Comparison of (a) overload capability and (b) static torque profile.
Table 5 compares the SIMPM with conventional topologies. It can be seen that the efficiency, torque density, and power factor of the proposed topology exceed others. The torque density of the SIMPM is significantly higher than IMPM, which proves the efficient utilization of the PMs in this structure. It is worth noting that, although this study has not considered cost, to make a fair comparison between the previous motors we must implement the simulation using the same specifications, such as the outer diameter and stack length. Moreover, some conventional motors are simulated and optimized using the same specifications and assumptions.

Table 5.
Comparison between different stator-PM topologies (In DSPM [23], the material of the PMs is NdFeB-30SH and the material of the core is Transil310-50. In PMaSRM [6], the material of the PMs is NdFeB42 and the material of the core is M19-26G. The efficiency of DSPM [23] is calculated without considering core loss).
To make a fair comparison between the proposed SIMPM and conventional IMPM motors, both motors are simulated in the same main dimensions, such as the outer stator diameter, stack length, and shaft radius. Other dimensions for both motors are optimized to improve the average torque and torque ripple, and the motors’ dimensions are changed during the optimization. Although some parts of the motor structure are narrowed, causing an increased flux density in these parts, none of the motors are saturated globally. As Table 5 shows, the torque density and torque per PM volume increases by 8.2% and 3.2%, respectively. Moreover, the core loss and efficiency are two parameters that can investigate the motor’s global magnetic condition. Therefore, the slot PMs have not drastically increased the core loss in the SIMPM.
Figure 15 also shows the efficiency maps of the two structures. SIMPM topology has an increased torque-speed region compared to the conventional IMPM. On the other hand, the high-efficiency region of IMPM is a little more extended than SIMPM. This resulted from reduced core loss due to the absence of slot PMs.
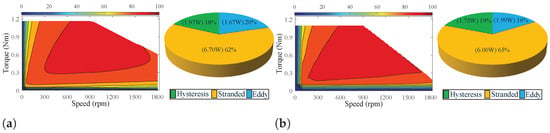
Figure 15.
Efficiency map: (a) SIMPM and (b) IMPM.
The demagnetization state of the proposed SIMPM is analysed, as depicted in Figure 16a. Notably, none of the PMs approach the demagnetization region of NdFeB-42. It can be seen that both motors’ PMs are far from the irreversible demagnetization region [26].
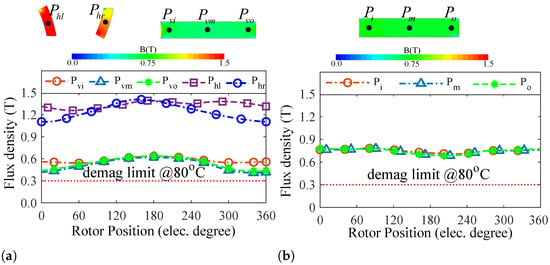
Figure 16.
Demagnetization assessment: (a) SIMPM and (b) IMPM.
Figure 17 summarizes the comparison between SIMPM and IMPM. This shows that, due to the insertion of slot PMs, the torque per PM density has decreased for the SIMPM. However, the torque density has increased by approximately 9%. The other difference lies in the power factor in which the SIMPM takes the lead compared to the IMPM because of higher back-EMF and lower magnetic reluctance.
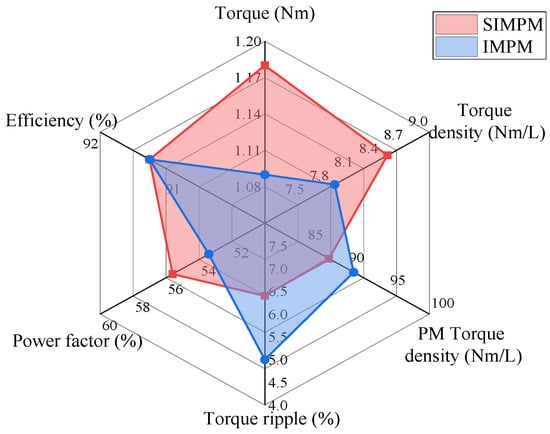
Figure 17.
Exclusive comparison between SIMPM and IMPM.
4.3. Thermal
For both IMPM and SIMPM motors, thermal studies are conducted by Ansys Maxwell–Icepack to validate the PM temperature. The natural convection defaults is set as the cooling type. For both IMPM and SIMPM motors, the frequency is equal to 165 Hz. The magnetic field sampling is equal to 20 times per electrical cycle. Therefore, the frequency of the magnetic field measurement is equal to 3300 Hz. Also, the material’s thermal conductivity and specific heat is listed in Table 6. Illustrated in Figure 18, the simulation depicts the temperature distribution of SIMPM. Notably, all PMs maintain temperatures below 70 °C (10 °C lower than the demagnetization temperature). It can be seen that there are lower temperatures at the outer face of the magnets, where they come into contact with the dissipator. Due to the axial airflow assumption, both motors have temperature variations in the axial direction. It is worth noting that no forced cooling mechanism is used in the simulation, but an axial natural airflow assumption is more like real conditions. Figure 19 demonstrates the thermal analysis results (TAR) at the same scale. In comparison to the FSPM topologies, the temperature distribution of the SIMPM is notably more uniform, fluctuating within ±1 °C. This uniformity stems from the distinctive structure where the PM is not enveloped by the armature. This design choice therefore has the additional advantage of enabling temperature regulation of the PM’s inner face through control of the outer face temperature.

Table 6.
The specific heat and thermal conductivity of motors’ materials.

Figure 18.
Thermal analysis: (a) SIMPM’s stator, (b) SIMPM’s PMs, (c) SIMPM’s rotor, (d) SIMPM’s coils, (e) IMPM’s stator, (f) IMPM’s PMs, (g) IMPM’s rotor, (h) IMPM’s coils.
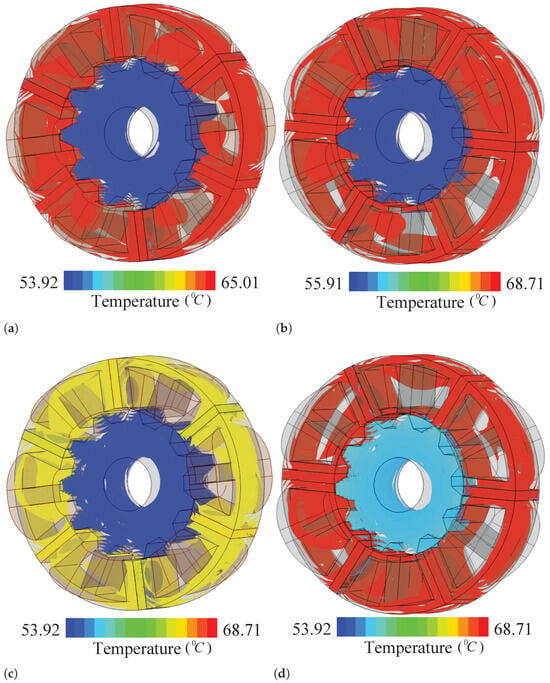
Figure 19.
Thermal analysis results in a common scale for (a) IMPM motor and (b) SIMPM motor. (c) IMPM and (d) SIMPM thermal analysis results with the same range.
5. Conclusions
This paper introduced a new operational principle for biased-flux motors by introducing small circumferentially magnetised magnets into the stator slots. The resulting magnetic field is asymmetric and concentrated in the air gap. The added magnets are shielded from demagnetization and mitigate flux fluctuations induced by the armature winding. Mathematical proof of the machine performance was presented, establishing that the superposition principle is no longer a viable tool for analysing the impact of each set of PMs in this configuration. A finite element analysis investigation of optimised topologies suggests the proposed structure has a significant increase in torque density. Analytical evidence supported the assertion that the DC offset resulting from asymmetric biased point operation positively contributed to the average torque. The additional stator slot magnets increased the simulated torque by nearly 20% and the torque density by 9% and improved the power factor from 0.54 to 0.56 whilst reducing the torque ripple by 2%. The efficiency was unaltered. Thermal analysis ensured that the SIMPM topology posed no risk of demagnetizing the PMs, and the uniformity of PM temperature distribution was identified as an additional advantage. Comparative assessments with other biased-flux or stator-PM topologies underscored the SIMPM motor’s distinctive superiority in terms of torque density and overall efficiency. This innovative motor configuration presents a significant leap forward in the realm of biased-flux motors, offering a promising avenue for enhanced performance.
Author Contributions
Conceptualization, M.A. (Mohammad Amirkhani); methodology, M.A. (Mohammad Afrank), M.A. (Mohammad Amirkhani), and A.K.; software, M.A. (Mohammad Afrank) and E.F.F.; validation, E.F.F.; formal analysis, M.A. (Mohammad Afrank) and M.A. (Mohammad Amirkhani); investigation, M.A. (Mohammad Afrank) and M.A. (Mohammad Amirkhani); resources, M.M.; data curation, M.A. (Mohammad Afrank) and M.A. (Mohammad Amirkhani); writing—original draft preparation, M.A. (Mohammad Amirkhani); writing—review and editing, M.A. (Mohammad Afrank), M.A. (Mohammad Amirkhani), E.F.F., M.M., A.K. and N.J.B.; visualization, M.A. (Mohammad Afrank); supervision, M.M., A.K. and N.J.B.; project administration, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
Some of the authors of this work are supported by Engineering and Physical Science Research Council Grant number EP/V040758/1.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, Q.; Zhao, X.; Niu, S. Flux-Modulated Permanent Magnet Machines: Challenges and Opportunities. World Electr. Veh. J. 2021, 12, 13. [Google Scholar] [CrossRef]
- Cai, S.; Kirtley, J.L.; Lee, C.H. Critical Review of Direct-Drive Electrical Machine Systems for Electric and Hybrid Electric Vehicles. IEEE Trans. Energy Convers. 2022, 37, 2657–2668. [Google Scholar] [CrossRef]
- Huang, Z.; Ding, Z.; Pang, M.; Chen, B. Multidisciplinary Design Overview and Comparison for Two Case Studies of High Speed Permanent Magnet Machines. IEEE Trans. Transp. Electrif. 2022, 8, 4242–4254. [Google Scholar] [CrossRef]
- Cheng, M.; Hua, W.; Zhang, J.; Zhao, W. Overview of stator-permanent magnet brushless machines. IEEE Trans. Ind. Electron. 2011, 58, 5087–5101. [Google Scholar] [CrossRef]
- Qu, H.; Zhu, Z.Q. Analysis of split-tooth stator slot PM machine. IEEE Trans. Ind. Electron. 2020, 68, 10580–10591. [Google Scholar] [CrossRef]
- Farahani, E.F.; Kondelaji, M.A.J.; Mirsalim, M. An innovative hybrid-excited multi-tooth switched reluctance motor for torque enhancement. IEEE Trans. Ind. Electron. 2020, 68, 982–992. [Google Scholar] [CrossRef]
- Farahani, E.F.; Baker, N.J.; Mahmouditabar, F. An Innovative H-Type Flux Switching Permanent Magnet Linear Generator for Thrust Force Enhancement. Energies 2023, 16, 5976. [Google Scholar] [CrossRef]
- Sarshar, M.R.; Kondelaji, M.A.J.; Mirsalim, M. Analysis of a Synthesized Slot Permanent Magnet Flux Reversal Motor. In Proceedings of the 2023 3rd International Conference on Electrical Machines and Drives (ICEMD), Tehran, Iran, 20–21 December 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Gao, Y.; Qu, R.; Li, D.; Li, J.; Zhou, G. Consequent-pole flux-reversal permanent-magnet machine for electric vehicle propulsion. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Liao, Y.; Liang, F.; Lipo, T.A. A novel permanent magnet motor with doubly salient structure. IEEE Trans. Ind. Appl. 1995, 31, 1069–1078. [Google Scholar] [CrossRef]
- Kondelaji, M.A.J.; Mirsalim, M. Segmented-rotor modular switched reluctance motor with high torque and low torque ripple. IEEE Trans. Transp. Electrif. 2020, 6, 62–72. [Google Scholar] [CrossRef]
- Farahani, E.F.; Masoumi, M.; Amirkhani, M.; Kondelaji, M.A.J.; Mirsalim, M. A comprehensive analysis of an axial flux switched reluctance motor with different number of rotor poles. In Proceedings of the 2020 11th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tehran, Iran, 4–6 February 2020; pp. 1–5. [Google Scholar]
- Radmanesh, H.; Farmahini Farahani, E. Performance evaluation of a new modular split-tooth permanent magnet-assisted switched reluctance motor. IET Electr. Power Appl. 2023, 17, 441–451. [Google Scholar] [CrossRef]
- Radmanesh, H.; Farahani, E.F. Analysis of a permanent magnet switched reluctance motor with new arrangements for permanent magnets. In Proceedings of the 2022 13th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tehran, Iran, 1–3 February 2022; pp. 96–100. [Google Scholar]
- Farmahini Farahani, E.; Mirsalim, M. Comprehensive study on divided-teeth and permanent magnet assisted outer-rotor switched reluctance motors. IET Electr. Power Appl. 2020, 14, 2293–2300. [Google Scholar] [CrossRef]
- Lordoglu, A.; Gulbahce, M.O.; Kocabas, D.A. A comprehensive disturbing effect analysis of multi-sectional rotor slot geometry for induction machines in electrical vehicles. IEEE Access 2021, 9, 49590–49600. [Google Scholar] [CrossRef]
- Wu, D.; Shi, J.T.; Zhu, Z.; Liu, X. Electromagnetic performance of novel synchronous machines with permanent magnets in stator yoke. IEEE Trans. Magn. 2014, 50, 1–9. [Google Scholar] [CrossRef]
- Ming, G.; Wu, L.; Zhang, L.; Niu, F.; Yan, Y.; Fang, Y.; Zhu, Z. Comparative study of biased flux PM machines having different stator core segments and armature winding configurations. IEEE Trans. Transp. Electrif. 2022, 8, 3379–3389. [Google Scholar] [CrossRef]
- Amirkhani, M.; Ghanbari, M.A.; Kondelaji, M.A.J.; Mirsalim, M.; Khorsandi, A. Performance Analysis of Outer Rotor Multi-Tooth Biased Flux Permanent Magnet Motors. IEEE Trans. Energy Convers. 2023, 38, 1738–1752. [Google Scholar] [CrossRef]
- Amirkhani, M.; Kondelaji, M.A.J.; Ghaffarpour, A.; Mirsalim, M.; Vaez-Zadeh, S. Study of boosted toothed biased flux permanent magnet motors. IEEE Trans. Transp. Electrif. 2022, 8, 2549–2564. [Google Scholar] [CrossRef]
- Amirkhani, M.; Farahani, E.F.; Mirsalim, M. Study of An Improved Biased Flux Intermodular Permanent Magnet Motor. IEEE Trans. Transp. Electrif. 2023, 10, 4455–4469. [Google Scholar] [CrossRef]
- Afrank, M.; Eikani, A.; Farahani, E.F.; Mirsalim, M. Comparative Study of Alternative-Pole Flux Switching and Inter-Modular Biased-Flux Permanent Magnet Motors. In Proceedings of the 2023 3rd International Conference on Electrical Machines and Drives (ICEMD), Tehran, Iran, 20–21 December 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Cai, S.; Zhu, Z.; Mipo, J.; Personnaz, S. Investigation of novel doubly salient hybrid excited machine with non-overlapped field winding. IEEE Trans. Energy Convers. 2020, 36, 2261–2275. [Google Scholar] [CrossRef]
- Zheng, M.; Zhu, Z.; Cai, S.; Li, H.; Liu, Y. Influence of magnetic saturation and rotor eccentricity on back EMF of novel hybrid-excited stator slot-opening permanent magnet machine. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar]
- Amirkhani, M.; Mirsalim, M. An improved biased-flux doubly salient shifted permanent magnet motor. In Proceedings of the 2022 13th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tehran, Iran, 1–3 February 2022; pp. 619–623. [Google Scholar]
- Kim, H.K.; Hur, J. Dynamic characteristic analysis of irreversible demagnetization in SPM and IPM type BLDC motor. Trans. Ind. Appl. 2016, 53, 982–990. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).