1. Introduction
Electricity price forecasting is an important issue for producers and consumers in today’s competitive electricity markets. As electricity cannot be efficiently and economically stored in large quantities using current technologies, a slight shift in demand can result in a massive change in electricity prices and, hence, pose a significant risk for traders in the markets. Accurate forecasts empower energy companies to optimize their production schedules, mitigate risks, and make informed trading decisions. Moreover, the end consumers also benefit from improved budgeting and strategic consumption planning. Meanwhile, electricity price forecasting is a challenging task due to its specific features [
1].
It is well known that time series of electricity prices are characterized by both long-term and periodic (yearly, weekly, and daily) behaviors, calendar effect, spikes and/or level shifts as well as short-term serial dependence [
2,
3]. All these components have been considered in several ways in the literature, but we can divide them into methods considering some components as deterministic and others as stochastic, and methods that model all the components as stochastic. In the first case, the usual approach is filtering the deterministic components by some procedure, for example, using smoothing spline and stochastically modeling the residual component [
4]. For example, ref. [
5] proposed a semi-parametric component-based model consisting of a non-parametric (smoothing spline) and a parametric (autoregressive moving average (ARMA) model) component. To capture different characteristics of day-ahead electricity prices, ref. [
6] proposed a model based on the improved empirical mode decomposition (IEMD), ARMA with exogenous terms (ARMAX), exponential generalized autoregressive conditional heteroscedasticity (EGARCH) and adaptive network-based fuzzy inference system (ANFIS). The non-parametric regression techniques and semi-functional partial linear models are used by [
7] for electricity demand and price prediction. In this case, the deterministic components are filtered out first, and then the residual component is modeled with a suitable stochastic process.
In the second case, all components are jointly accounted by a single stochastic model [
8,
9,
10]. For instance, ref. [
11] studied the periodic behavior of the electricity prices using the seasonal Reg-ARFIMA-GARCH model that explains the conditional mean and variance of electricity prices. Ref. [
12] studied the performance of AR-GARCH models on the Indian spot electricity price series. Different seasonalities are captured in the model using hourly, weekly, and daily dummy variables. The conditional mean and conditional variance equations for different variants of the model are estimated, and the forecasting performance of the calibrated models is assessed using standard accuracy measures. The study suggested that AR-GARCH and AR-EGARCH outperform the competitors. Ref. [
13] compared the forecasting performance of different approaches, including transfer function, ARIMA, wavelet, and artificial NN used for electricity price forecasting. Ref. [
14] studied the performance of univariate time series models for forecasting electricity demand using both components jointly.
Apart from the two approaches described above, researchers used different classical and machine learning techniques to model and forecast electricity prices [
15,
16,
17]. For instance, ref. [
18] performed short-term price prediction using regression trees to predict the electricity price. The results of the proposed method are compared with alternative methods like ARIMA, exponential smoothing, and neural networks (NN). The empirical results show that the proposed method performs better than the competitors. Ref. [
19] used a variable-segmented support vector machine-based model (VS-SVM) for day-ahead price forecasting in Ontario’s electricity market. The author used the heuristic model, simulation model (Monte Carlo simulation approach), multiple linear regression (MLR), NN model, neuro-fuzzy, ARIMA, dynamic regression model (DRM), and transfer function model (TFM) to compare with the proposed hybrid model. The results indicated that the VS-SVM model outperformed all the other models in terms of MAPE and RMSE. Ref. [
20] proposed a fuzzy neural network-based method for short-term price forecasting for mainland Spain’s electricity market. The author compared the proposed model with other fuzzy regression models and hybrid approaches based on NN and fuzzy logic, ARIMA, wavelet-ARIMA, multi-layer perceptron (MLP) and radial basis function (RBF) neural networks. The results indicated that the proposed method outperformed other methods in terms of forecasting accuracy and robustness against outliers and non-stationary behavior of the price series. The use of these forecasting models is not limited to the electricity market as they are extensively used in other research fields [
21,
22,
23]. A summary of previous studies concerning electricity market forecasting is given in
Table 1.
In the last years, a promising approach to deal with the complex behavior of electricity markets time series is that based on functional data analysis. Functional modeling can handle high-dimensional data and facilitates the transformation of long forecast horizons into a one-step-ahead functional forecast [
24,
25]. Considering functional data allows one to obtain forecasts for ultra-short periods, which is not possible with traditional techniques. In addition, it is particularly useful to describe daily periodic profiles of some market variables. In the electricity prices time series literature, when the functional approach has been involved, the separate estimation has always been used. While a separate estimation permits to highlight the role of each component, a joint estimation could account for those inter-relations among components that a separate modeling process usually ignores, possibly improving prediction. In this work, we try to fill the gap by suggesting a functional model that allows for the joint estimation of the components. To investigate the issue, we consider and compare the predictive performance of different predictors referring to both the separate and the joint component estimation. In more detail, we consider two models based on the separate component estimation which use smoothing splines (SS) in the first step and SARIMA (SS-SAR) models or standard functional autoregressive (SS-FAR) models in the second step. For the joint estimation, we consider an extension of the standard FAR model which includes exogenous variables describing the deterministic components (FARX). A suitable estimation procedure based on principal components is proposed. For a deeper insight, we also consider a predictor based on a combination of the two approaches. We test the predictive performances of the models on the hourly electricity prices of the northern zone of the Italian electricity market (IPEX) and show that, using functional models, the joint components estimation leads to significantly better prediction than the separate estimation.
Table 1.
Summary of literature review.
Table 1.
Summary of literature review.
| No. | Authors | Market | Forecasting | Methods | Accuracy Measures |
|---|
| 1 | Marcjasz et al. (2023) [26] | Germany | Day-ahead | DNN | MAE, RMSE, CRPS |
| 2 | Alberto et al. (2011) [27] | Spain | Day-ahead | double seasonal ARIMA, ES model | SSR, MAPE |
| 3 | Girish (2016) [12] | India | Hour-ahead | AR-GARCH, ARIMA-EGARCH | RMSE, MAE, MAPE |
| 4 | Zhang et al. (2019) [5] | Spain, Australia | Day-ahead | IEMD, ARMAX, EGARCH, ANFIS | MAE, RMSE, MAPE |
| 5 | Aggarwal et al. (2009) [19] | Canada | Hour-Ahead | VS-SVM, MLR, NN, DRM | RMSE, MAPE |
| 6 | Amjady (2006) [20] | Spain | Day-ahead | ARIMA, Wavelet-ARIMA, MLP, RBF | TE, DME |
| 7 | Shah et al. (2020) [28] | Italy | Day-ahead | AR, NPAR, FAR, NPFAR | MAE, MAPE, |
| 8 | Vilar et al. (2012) [7] | Spain | Day-ahead | ARIMA, FNP, SFPL | DEs, SE |
| 9 | Conejo et al. (2005) [29] | Spain | Day-ahead | wavelet transform, ARIMA | DEs, HE |
| 10 | Dudek (2015) [18] | Poland | Day-ahead | RF, ARIMA, ES, NN | RMSE |
The rest of the paper is structured as follows. The general framework within which we move is described in
Section 2.
Section 3 provides a basic introduction to functional data and the details of the functional models we use. The description of the data, as well as of our forecasting exercise, are contained in
Section 4.
Section 5 concludes the paper.
2. General Framework
The general framework within which we move in this work is the following.
Let us denote by
the time series of the price for day
t and load period (hour)
h,
and
. We assume that its logarithm, log
, can be decomposed in several additive components:
where
represents the long-run (trend component),
is the annual periodic component,
is the weekly cycles,
is the calendar component describing the effect of bank holidays and other possible calendar effects. Finally,
describes the short-run dynamics of the price series. Note that since expression (
1) refers to a given time slot
j, the daily component, due to the periodicity over the hours of the day, is not present. This is why, in the rest of the work, when not necessary, we will omit the hour subscript
j.
Usually, the trend is represented through the sequence , the yearly component by the sequence or by trigonometric functions, the weekly period by the sequence , while bank holidays are described by dummy variables.
In the literature, these components have been treated in several ways: using different models or approaches, assuming that the first four components are deterministic while the residual component is stochastic [
30] or treating all components as stochastic [
31], estimating them separately or jointly. In this work, we compare the predictive performance of functional models when the components are separately or jointly modeled. To the best of our knowledge, the joint estimation of the components using functional methods is new within energy markets.
In the separate approach, the deterministic and the stochastic components are usually estimated using a two-step procedure. First the deterministic components are estimated, then the stochastic component is obtained as the residual difference
The series
are then modeled following some stochastic approach.
In this work, for each given time period
j, we estimate the deterministic components using the non-parametric additive model:
where
is a constant parameter defining the bank holidays effect and
are functions describing the relations between
, which are jointly estimated through smoothing splines.
After the residual component
has been estimated using expression (
2), we put together the series
to convert them in functional time series. To this end, we use B-spline basis functions, so that we can write
where
are constant parameters,
represent the B-spline basis functions, and
K is the number of basis functions used.
Once the functional time series is available, we model it by means of functional autoregressive models (FAR).
The final prediction is obtained by summing the individual forecast:
When the joint estimation approach is considered, both deterministic and stochastic components are estimated using a single-step procedure. This helps to account for possible relationships between deterministic and stochastic components. While joint estimation of the components is not a novelty, it is new in the energy field using functional models.
For the joint estimation, we consider a functional autoregressive model with suitable exogenous variables (FARX), allowing us to include the effects of scalar or functional exogenous drivers. The estimation of such a model is challenging since the computational burden increases more than linearly with the lag orders of endogenous and exogenous variables. In addition, in many cases, the estimation is unfeasible due to the unboundedness of the inverse of covariance operators. Thus, a feasible and adaptable strategy is required. In this work, we use the principle component analysis (PCA) to reduce the number of variables while retaining most information included in the endogenous and exogenous variables. In this case, first log(
) is converted into a functional time series using the methodology explained in
Section 2 and, then, a suitable FARX model is estimated using the PCA approach. The estimated model also allows for the series prediction.
3. Functional Data Analysis
3.1. Preliminaries
This section provides a basic introduction to functional data analysis which is essential to understand the contents of this work. In the following, we will use the mathcal font to denote functional objects, bold fonts for vectors and matrices, and normal fonts for scalar quantities.
Let be a time series of functional observations, where and . Usually the interval is normalized to . For each t, the observation belongs to the Hilbert space of square integrable functions which is equipped with a norm induced by the inner product .
For a generic time series
, defined on a probability space
, with mean function
, the covariance function
, with
, is defined as
The covariance function (
6) can also be expressed using the following spectral decomposition:
where
is the inner product,
is the strictly positive decreasing sequence of eigenvalues of (
6) and
denotes the corresponding sequence of eigenfunctions which form an orthonormal basis system for
.
The functional time series
can also be represented using the principal component approach, based on the Karhunen-Loève representation [
32]. If
, we can write:
where
denotes the
functional principal component score while
are the function principal components (FPC). The functional principal component constitutes an uncorrelated set of random variables with zero mean and variance
. The
s are such that
.
The main advantage of expansion (
8) is it allows dimension reduction as the first
d terms often provide a good enough approximation to the infinite sum and, thus, the information contained in
can be adequately summarized considering only the first
d principal components. The approximated process is given by
More details on functional principal components and their practical applications are given in [
33,
34].
In practice, all the previously defined quantities have to be estimated starting from an observed time series,
, representing a finite realization of the underlying random process. To this end, the following estimators can be used:
The authors of [
35] showed that the estimators (
10) and (
11) are consistent estimators for weekly dependent processes. Then, using the KL expansion, the realizations of the random process
can be written as
where
is the
estimated functional principle component score for the
observation,
is the
functional principle components and
is an estimated white noise. This formulation allows us to describe the FAR and FARX models, which will be used to forecast
.
3.2. Functional Autoregressive Models
One of the simplest ways to model a functional time series
is to use a functional autoregressive model of order
p,
[
36]. A FAR(p) model, which is the generalization of an
model to the case of functional objects, is defined as
where
are the functional parameters of the model,
are lagged functional variables and
is a strong
-white noise with zero mean and finite second moment (
). The FAR(p) model can be further generalized by including, besides
lagged variables, other exogenous (possibly lagged) regressors. These exogenous variables may be scalars (
), vector-valued (
) or functional (
). The FARX(
) model can be defined as
where
denotes the functional exogenous variables,
are the scalar exogenous variables and
is a strong
-white noise as in (14). Often, the exogenous variables are previously demeaned.
,
,
B,
and
,
are functional (the first two) and scalar (the third one) model parameters.
3.3. Building FAR(p) and FARX() Models
Building FAR and FARX models requires one to identify the orders
p,
m and
r as well as to estimate the model parameters. A partial theoretical estimation procedure for FAR(
p) is given in [
36]. This is based on the Shibata-Mourid [
37] statistics; however, practical estimation issues are completely ignored by the author. The procedure works in the case of FAR(1); however, it is not clear how to apply it to real data for generic FAR(p) models. In the case of FAR(1), the PCs’ use is useful since the covariance operator behaves erratically due to the unboundedness of its inverse, and thus, the data are projected onto a suitable finite-dimensional subspace, generally spanned by the first few largest eigenvectors.
In this work, we estimate the FAR(p) and FARX() using the principle components approach. This ensures a fair model estimation as well as computational efficiency since most of the variation in the endogenous and exogenous variables is summarized by the first PCs. Clearly, in this case, the identification step requires the selection of the lag orders () and the number of FPCs (d) used in the approximation. To this end, to select p and d, the following algorithm is used
- (a)
For a demeaned functional dataset , fix a dimension d and, using (8), compute the vector , containing the first d FPC scores.
- (b)
For each functional exogenous variables fix the value of m and use the data to compute the vector , containing the first m FPC scores of the exogenous variable lag matrix.
- (c)
combine all the exogenous variables vectors into a single vector, ,
Using and , consider an appropriate multivariate model, for example vector autoregressive model,, to obtain a one-step ahead forecast for as
Choose the order
p and
d using
Section 3.4 and obtain
for the optimal
p and
d.
Use the KL expansion to compute the one-step-ahead forecast
3.4. Selection of Orders and Number of PCs d
The performance of functional models FAR(p) and FARX() crucially depends on the appropriate selection of the order and of the suitable number of PCs d. In this section, we show that they can be jointly estimated using the functional final prediction error (FFPE) criterion.
We start by considering the mean squared error (MSE). Since the eigenfunctions
are orthogonal and the PCs
are uncorrelated, it can be written as
Here, the usual
Euclidean norm of vectors is represented by
. Assuming the stationarity of the process
, a
d-variate VAR(
p) has the form
where
is a white noise process such that [
38]
where
= vec
is the least squares estimator of
= vec
, and
= Var[vec
and
. Suppose that the
are estimated from independent training sample
. It follows then
The independence of
and
yields that
By using (
15), the last term can be approximated as
Replacing
by
,
16 can be written as
Thus, the order
p and the number of components
d are simultaneously selected by minimizing the functional final perdition error criterion as
The use of FFPE makes the forecasting procedure completely data-driven and does not require any subjective specification of parameters (see [
39] for more technical details).
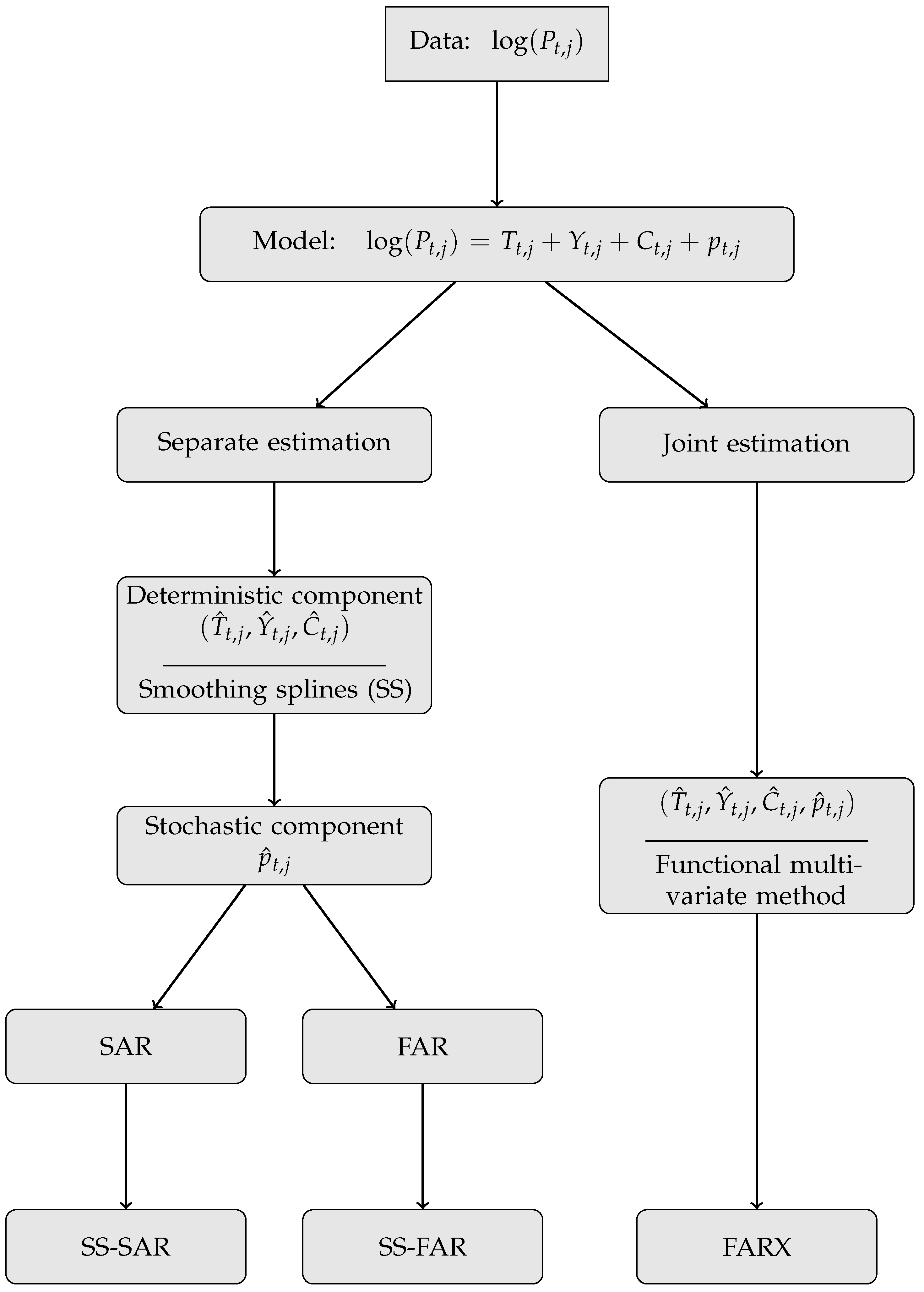
A flowchart of the proposed modeling framework using a separate or joint estimation approach is given in
Figure 1. It explains that model estimation is a two-step procedure in the separate modeling approach, while all the components are modeled and forecasted in a single step in the joint approach.
5. Conclusions
In this work, we faced the issue of modeling and forecasting electricity prices within the functional approach. As this is often conducted by estimating and predicting the different components of the price dynamics, we wondered if a joint modeling of the components could improve prediction with respect to a separate modeling process. The basic idea is that a joint estimation could consider those inter-relations among components that a separate modeling usually ignores. To investigate this issue, we compared the predictive performance of four different predictors: the first two are based on separate modeling, the third is based on joint modeling, and the fourth one is a combination of the two approaches.
In particular, the first two models use smoothing splines to estimate the deterministic components and SARIMA (SS-SAR) and FAR (SS-FAR) models to describe the dynamics of the stochastic component. The third model, the FARX model, follows a one-step procedure to jointly estimate all the components by suitably including exogenous variables. For empirical analysis, electricity price data from the northern zone of the Italian electricity market, from January 2015 to December 2019, are used. The first four years are used for model estimation, and the entire year 2019 is used for one-day-ahead out-of-sample forecasts. Forecasting performances are evaluated in terms of MAE, MAPE, and RMSE and statistically assessed by means of the Diebold and Mariano test.
The results suggest that the functional modeling approach is efficient in predicting electricity prices as it produces lower forecasting errors than the non-functional model used in the study, i.e., the SS-SAR model. Within the functional models, the FARX model, which jointly estimates all the components, significantly outperforms its competitors except the combined predictor. The last one, however, seems mainly affected by the good performance of the FARX model and gives numerical results worse than those of the FARX model.
Finally, this study’s findings suggest that the forecasting errors are generally higher on (a) Sunday and Monday, (b) from hours 3 to 6 in the morning and 14 to 15 in the afternoon, and (c) June and December. On the other hand, prices are relatively lower on (a) Wednesday, Thursday, and Friday, (b) from hour 20 to 1 a.m., and (c) January and February.
 ), a statistical computing language, is used to implement the models [44]. In the comparison, all the computations have been performed using an Intel(R)-Core(TM) i7-4770 CPU running at 3.40 GHz.
), a statistical computing language, is used to implement the models [44]. In the comparison, all the computations have been performed using an Intel(R)-Core(TM) i7-4770 CPU running at 3.40 GHz.