Stability Control of Grid-Connected Converter Considering Phase-Locked Loop Frequency Coupling Effect
Abstract
1. Introduction
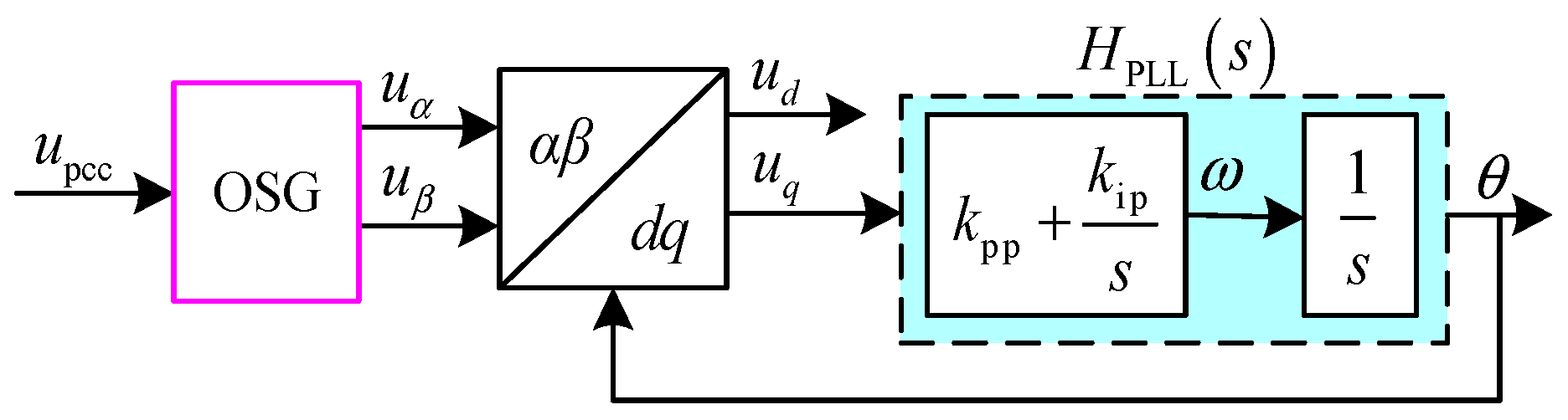
2. Frequency Coupling Mechanism of PLL
3. Impact of PLL-FCE on the Output Impedance and Operating Characteristics of GCCs
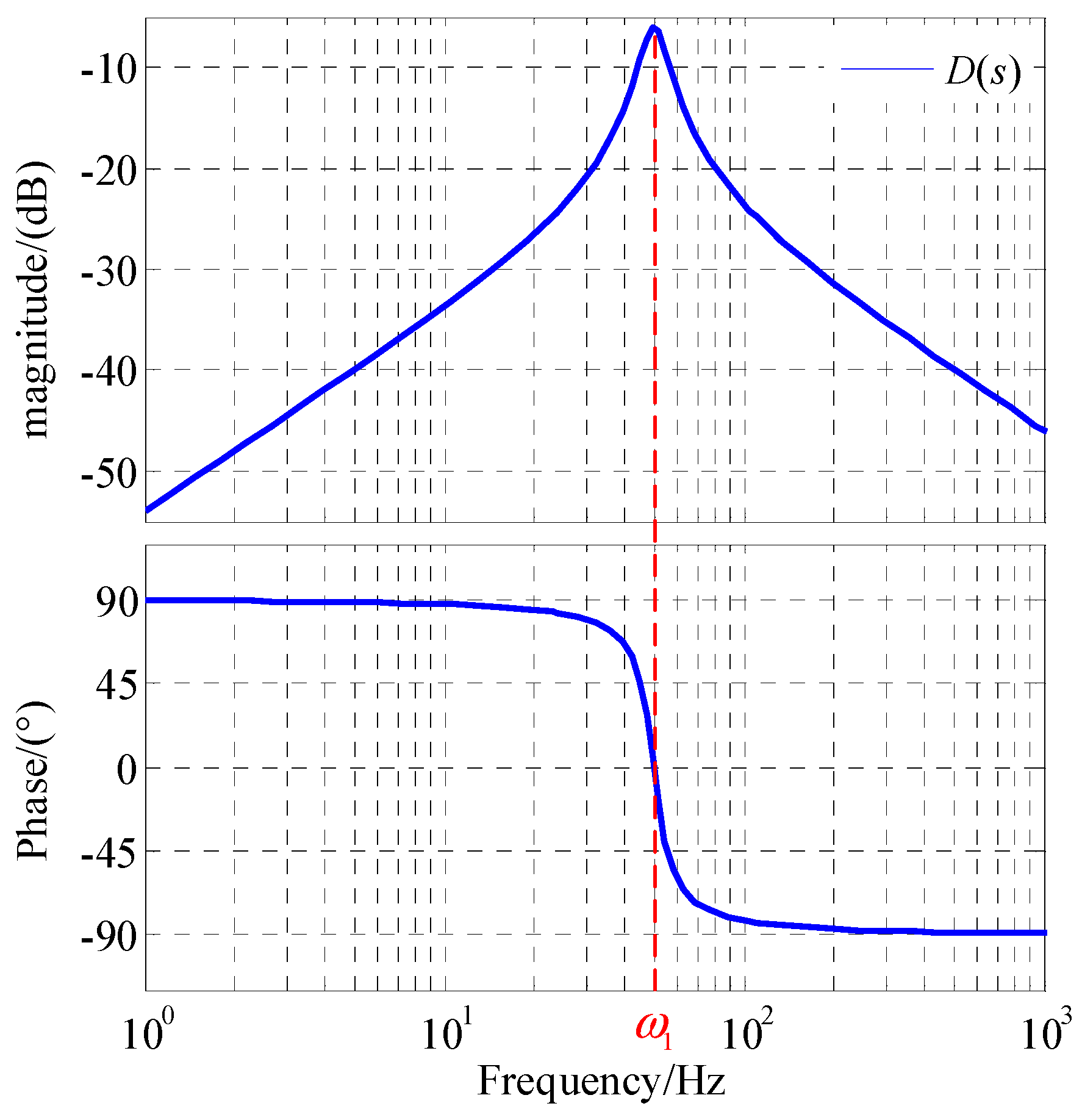
3.1. Coupling Admittance Modeling
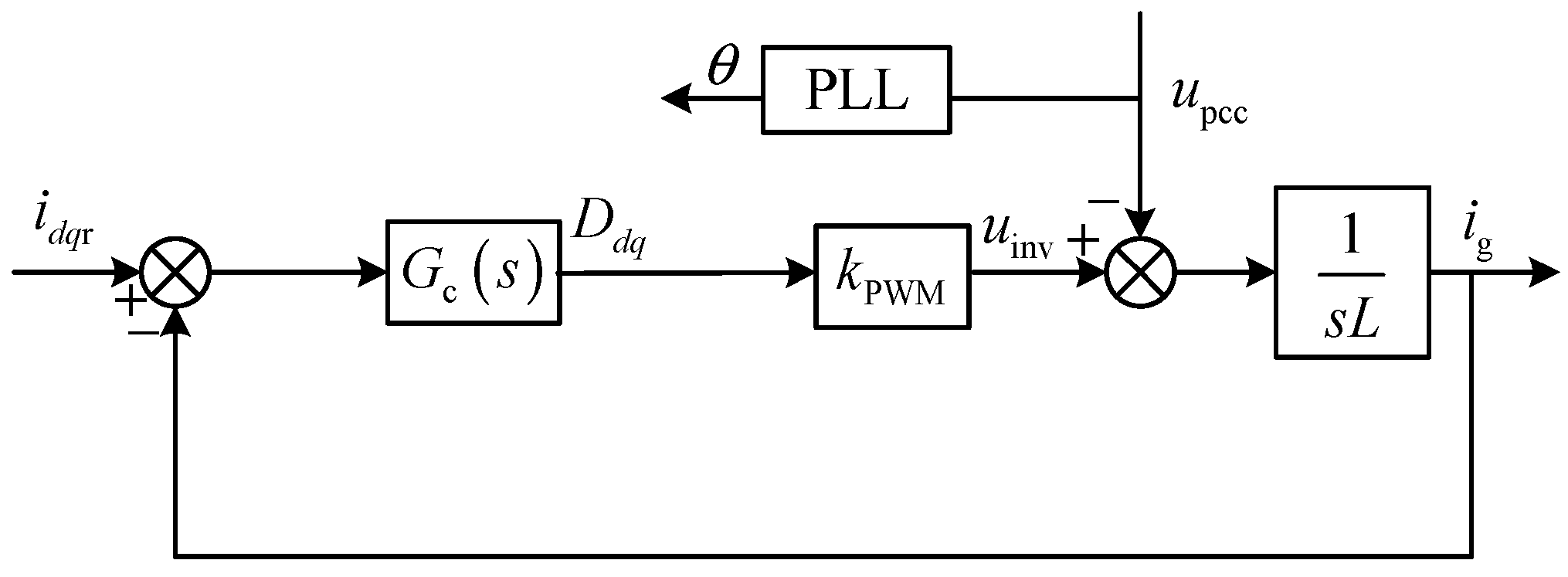
3.2. Output Impedance Modeling for GCCs under the PLL Frequency Coupling Characteristics
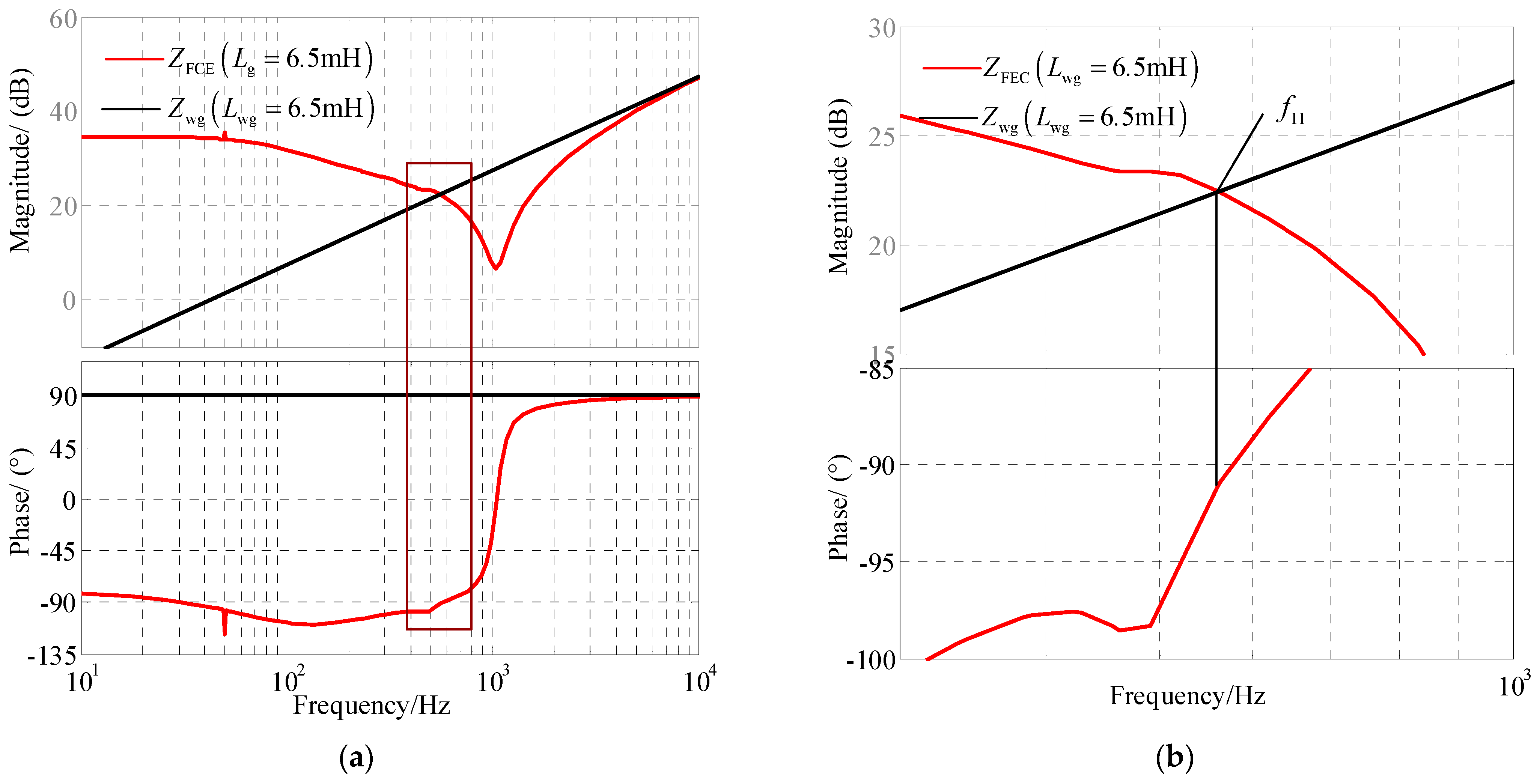
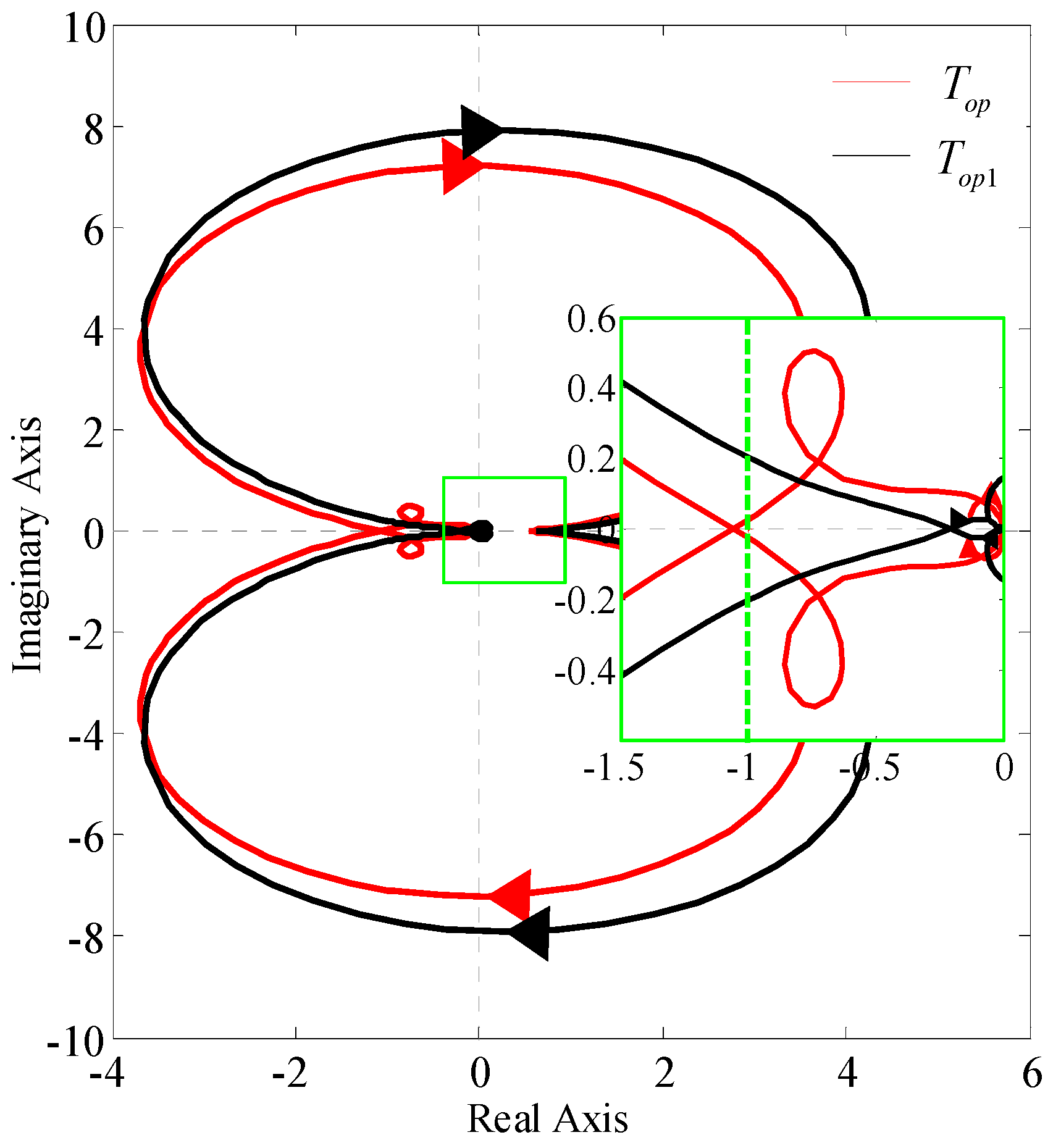
3.3. Stability Analysis of GCCs under PLL Frequency Coupling Characteristics
4. Strategy to Suppress the PLL-FCE
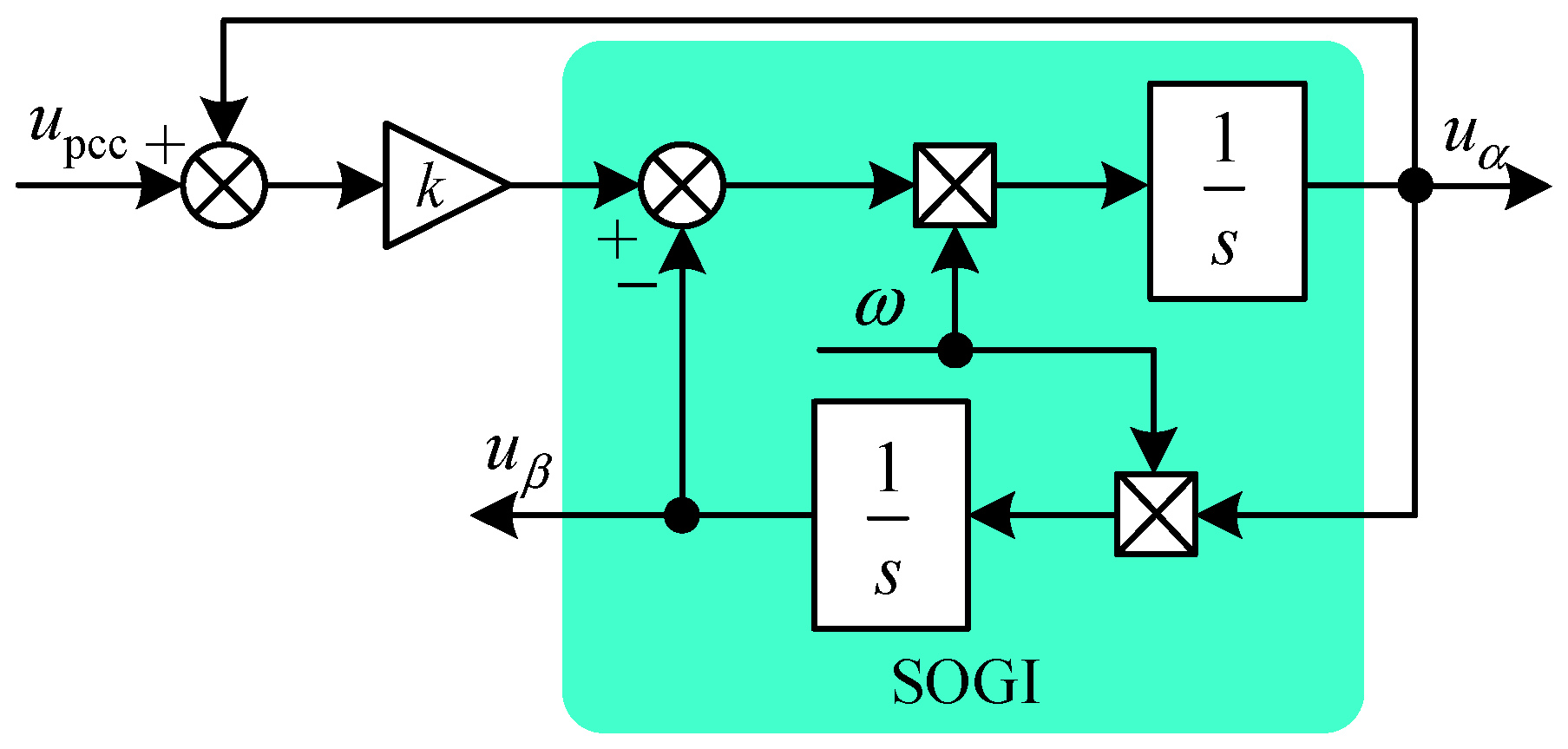
4.1. Second-Order Generalized Integral-Based PLL
4.2. Performance of SOGI-PLL
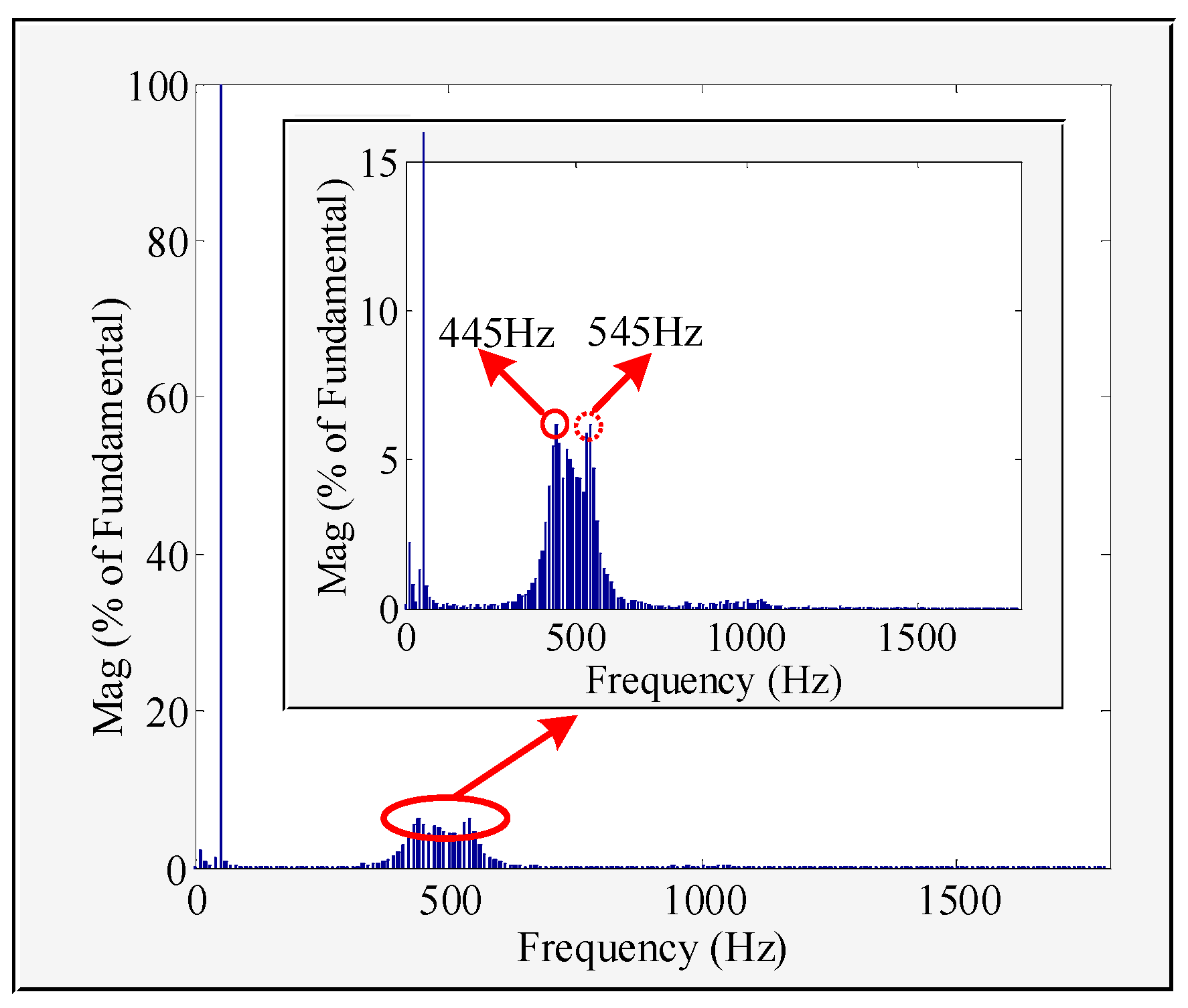
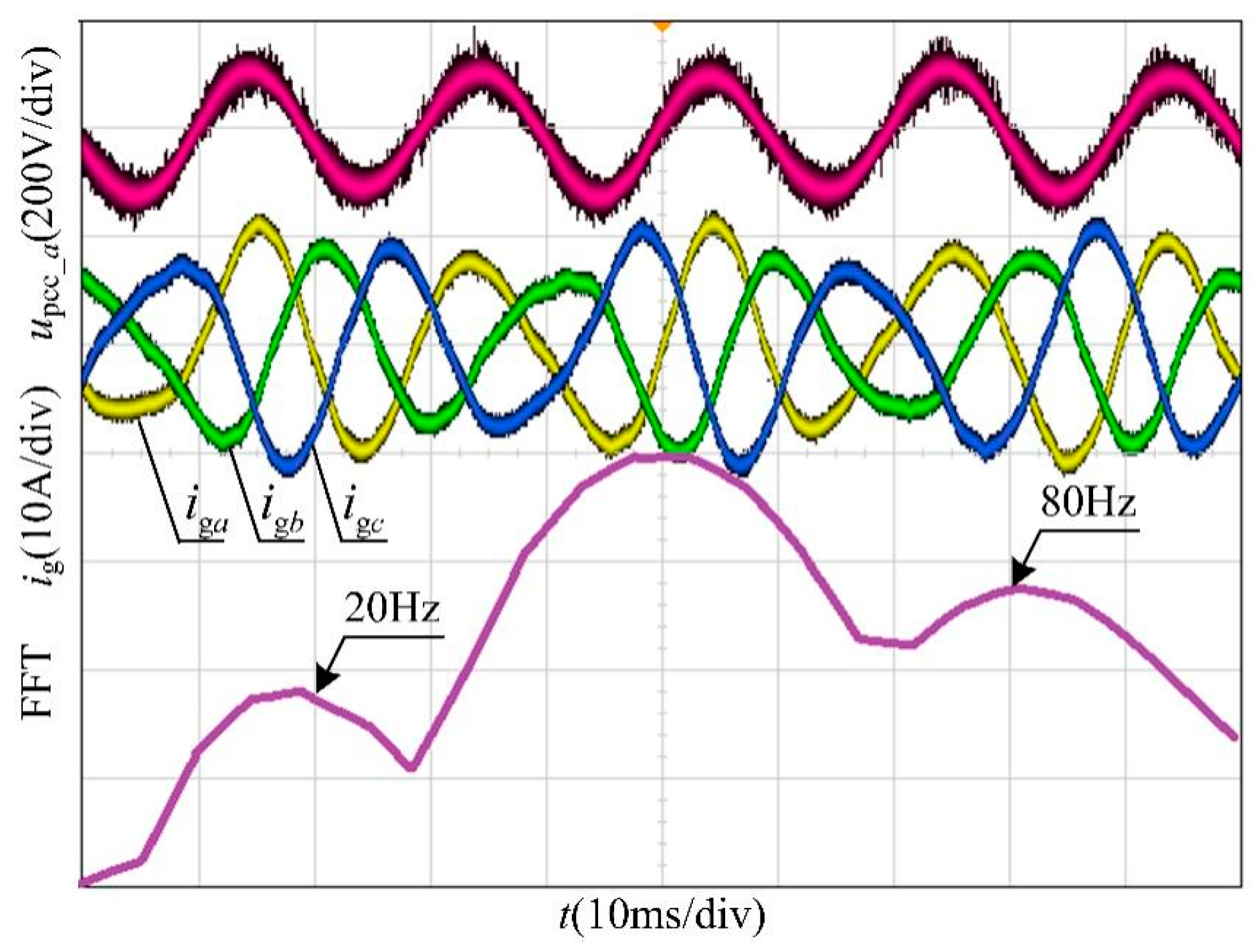
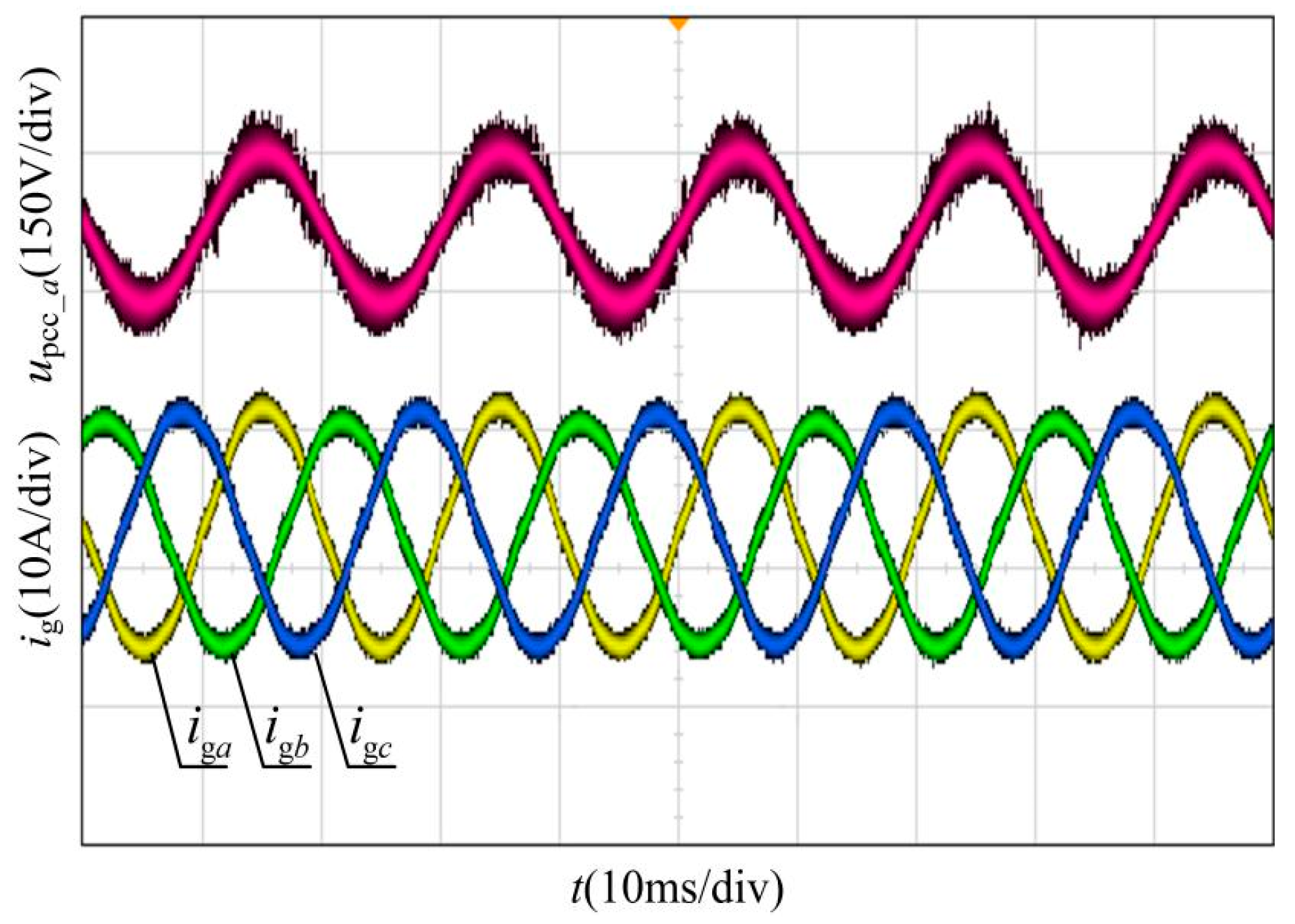
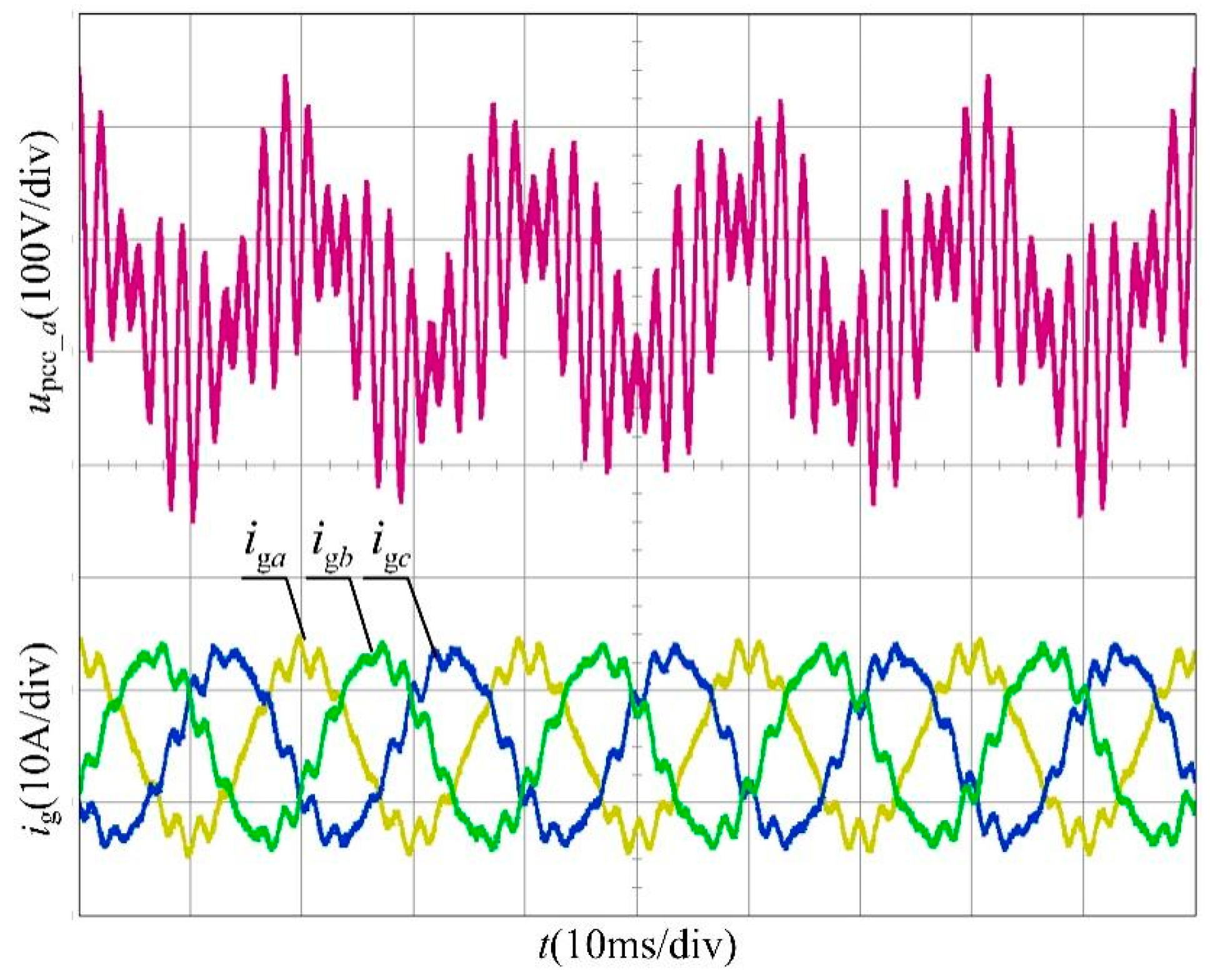
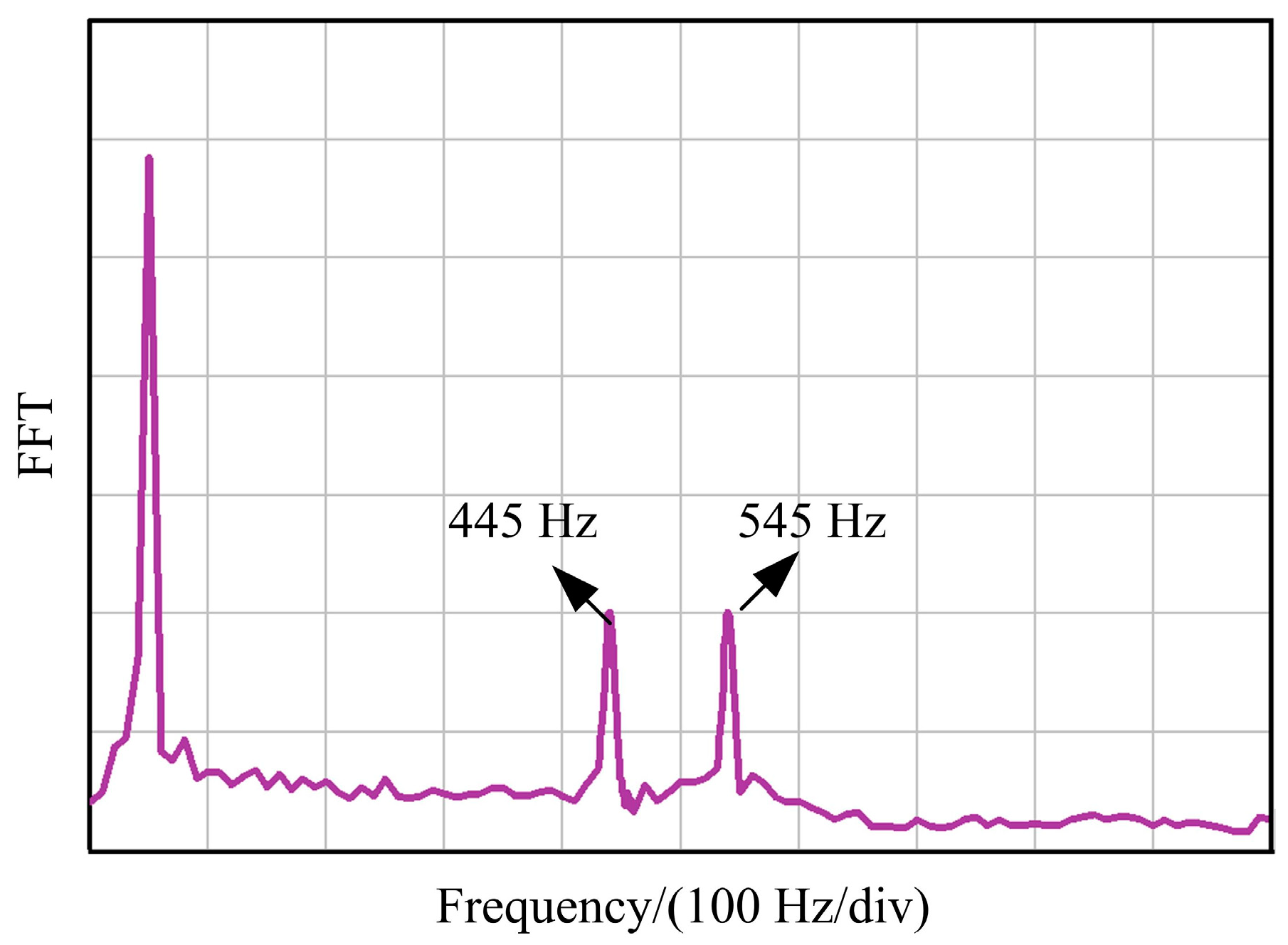
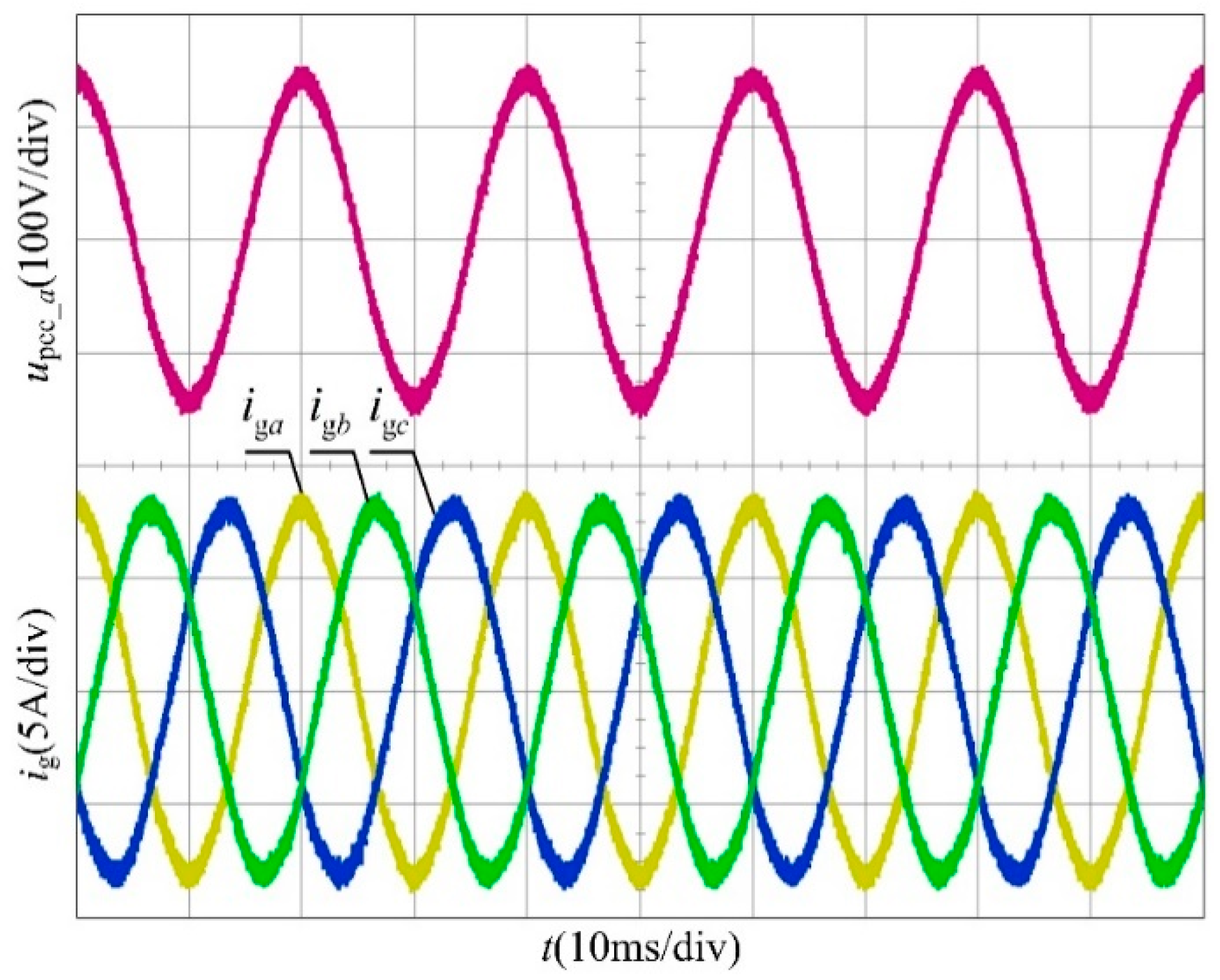
5. Simulation and Experimentation Verification
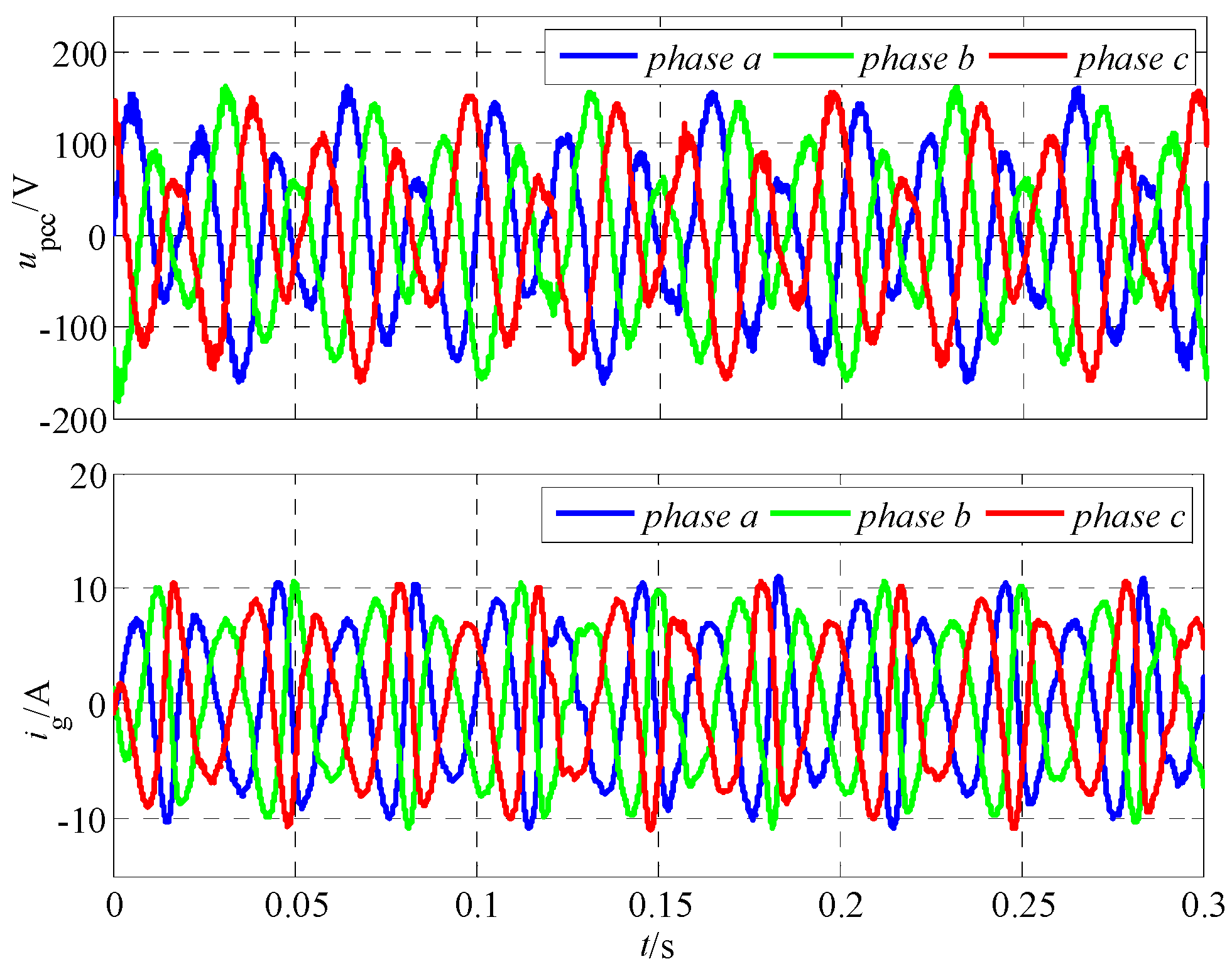
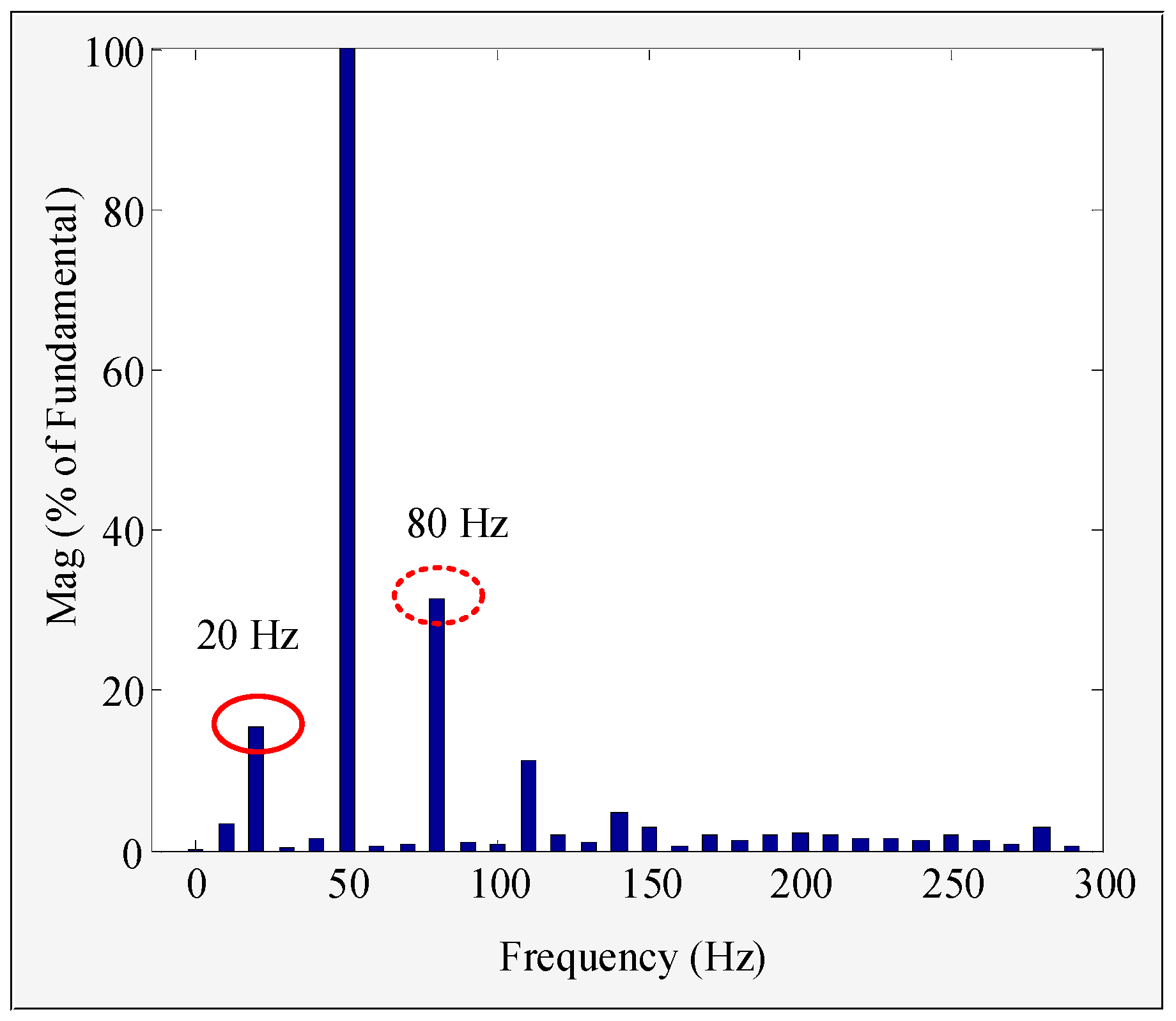
5.1. Simulation Results
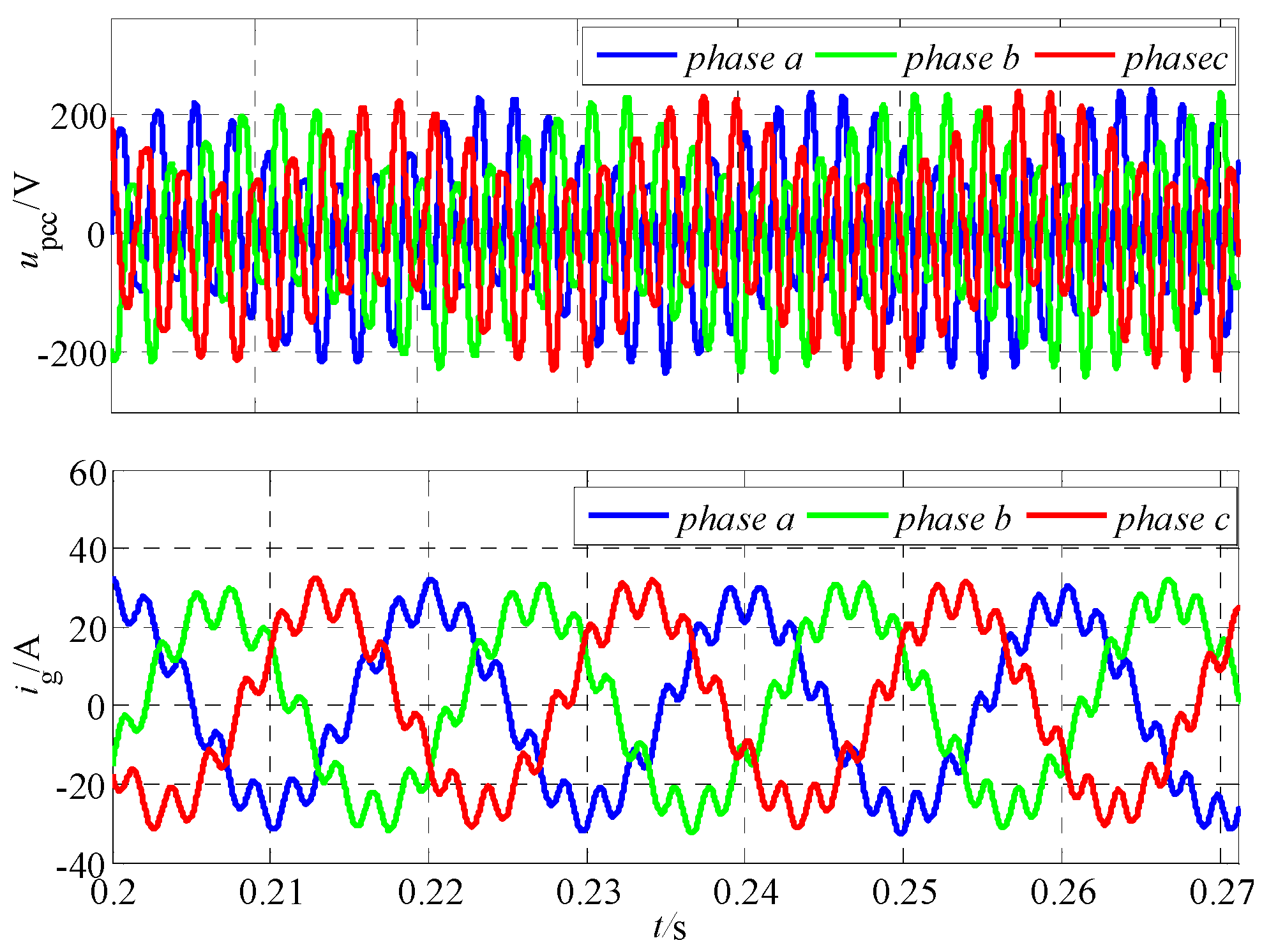
5.2. Experiment Results
6. Conclusions
- (1)
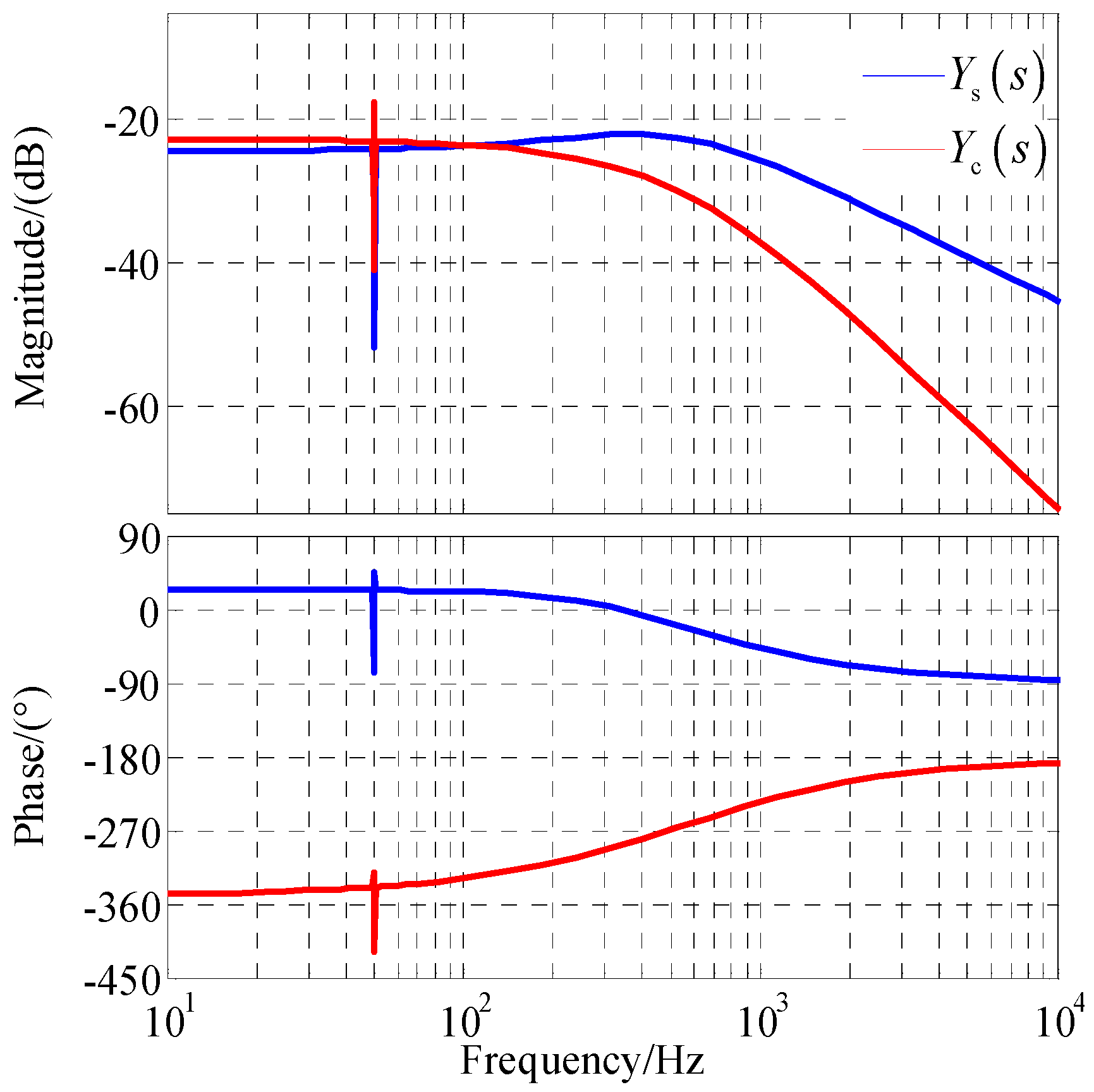
- The analysis of the coupling admittance modeling reveals that the PLL-FCE significantly impacts the output impedance characteristics of the GCC, particularly in the range of medium and low frequency.
- (2)
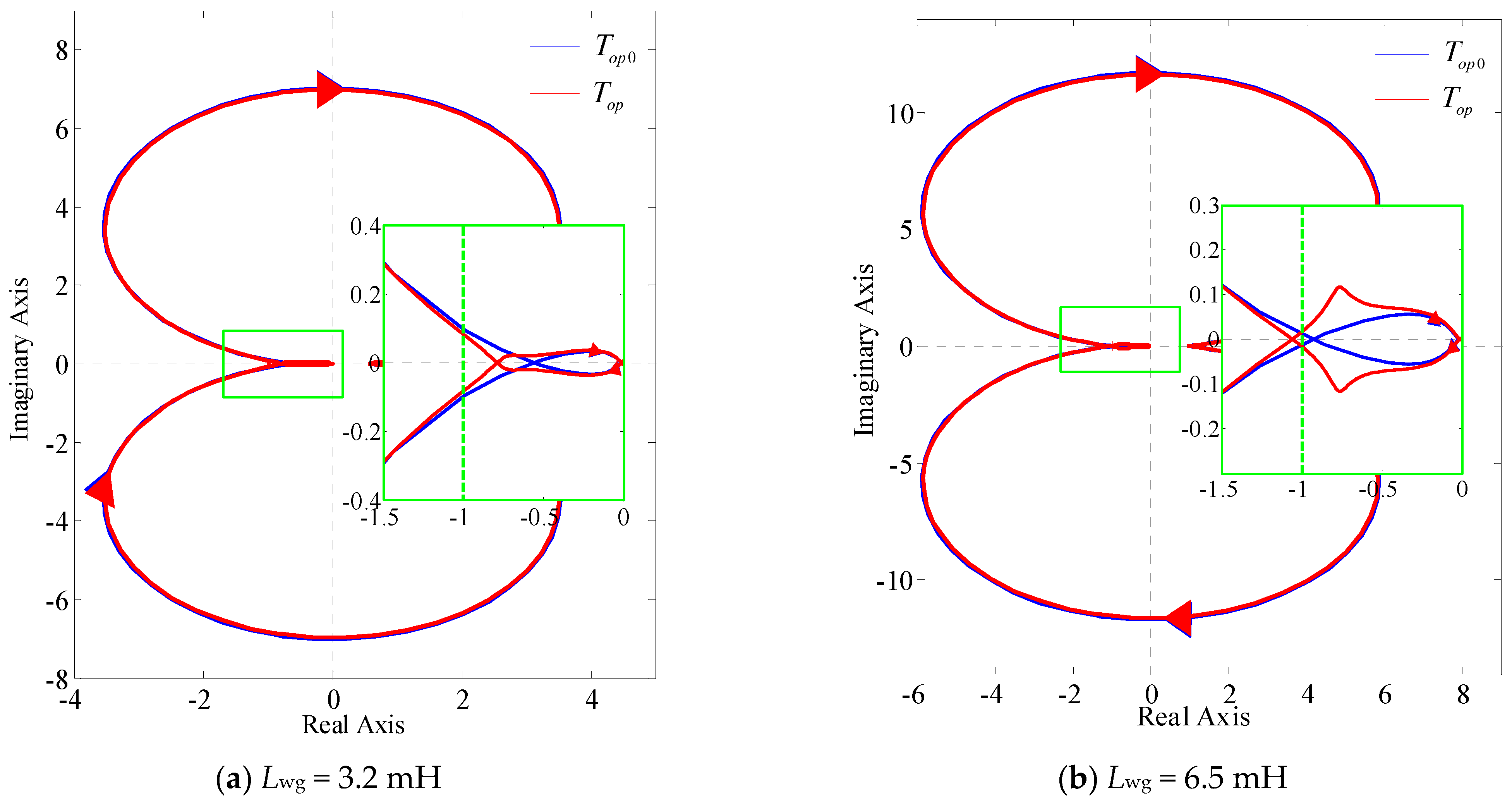
- The impedance of the GCC is influenced not only by the coupling admittance but also by the grid impedance, particularly through the PLL-FCE. As the grid impedance increases, the coupling effect becomes more pronounced. The interplay between these factors shapes a negative impact on the overall performance and stability of the converter system and increases the risk of its instability.
- (3)
- The SOGI-PLL introduced in this paper serves to mitigate coupling admittance, thereby effectively suppressing the PLL-FCE. As the grid impedance escalates, this approach can ameliorate system instability stemming from PLL-FCEs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Whazaei, J.; Tu, Z.; Asrari, A.; Liu, W. Feedback linearization control of converters with LCL filter for weak AC grid integration. IEEE Trans. Power Syst. 2021, 36, 3740–3750. [Google Scholar]
- Negri, S.; Ubezio, G.; Faranda, R.S. Fault-Tolerant Multiport Converter for Hybrid Distribution Systems: Configuration, Control Principles and Fault Analysis. Appl. Sci. 2024, 14, 4024. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F. Harmonic stability in power electronic-based power systems: Concept, modeling, and analysis. IEEE Trans. Smart Grid 2019, 10, 2858–2870. [Google Scholar] [CrossRef]
- Sun, J.; Wang, G.; Du, X.; Wang, H. A theory for harmonics created by resonance in converter-grid systems. IEEE Trans. Power Electron. 2019, 34, 3025–3029. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C. Three-phase PLLs: A review of recent advances. IEEE Trans. Power Electron. 2017, 32, 1894–1907. [Google Scholar] [CrossRef]
- Hu, Q.; Fu, L.; Ma, F.; Ji, F. Large signal synchronizing instability of PLL-based VSC connected to weak AC grid. IEEE Trans. Power Syst. 2019, 34, 3220–3229. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, S.; Li, H.; Zhong, C. An Optimized method of PLL for grid-connected inverter in the weak grid. Chin. J. Sci. Instrum. 2022, 43, 234–243. [Google Scholar]
- Wu, W.; Zhou, L.; Chen, Y.; Luo, A.; Dong, Y.; Zhou, X.; Xu, Q.; Yang, L.; Guerrero, J.M. Sequence-impedance-based stability comparison between VSGs and traditional grid-connected inverters. IEEE Trans. Power Electron. 2019, 34, 46–52. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Zhang, Y.; Chen, J.; Gong, C. Frequency characteristics analysis and stability research of phase locked loop for three-phase grid-connected inverters. Proc. CSEE 2017, 37, 3843–3853. [Google Scholar]
- Nian, H.; Xun, Y.; Chen, L.; Li, G. Frequency coupling characteristic modeling of grid-connected inverter and system stability analysis. Proc. CSEE 2019, 39, 1421–1431. [Google Scholar]
- Wang, X.; Harnefors, L.; Blaabjerg, F. Unified impedance model of grid-connected voltage-source converters. IEEE Trans. Power Electron. 2018, 33, 1775–1787. [Google Scholar] [CrossRef]
- Li, Z.; Tang, X.; He, Y.; Liu, P.; Li, X. Admittance reshaping method of converter for suppressing background harmonic of grid. Proc. CSEE 2024, 44, 704–713. [Google Scholar]
- Gong, H.; Wang, X.; Harnefors, L. Rethinking current controller design for PLL-synchronized VSCs in weak grids. IEEE Trans. Power Electron. 2022, 37, 1369–1381. [Google Scholar] [CrossRef]
- Tang, X.; Li, Z.; Li, Y.; He, Y. Frequency coupling oscillation analysis and decoupling control design of grid connected converter. Proc. CSEE 2023, 43, 3127–3136. [Google Scholar]
- Guan, W.; Li, H.; Liu, Y.; Xu, M.; Chen, X.; Rong, S.; Song, B. Low-frequency coupling resonance suppression method of PLL-based current controlled converter based on coordinated control. In Proceedings of the 2022 IEEE 2nd International Conference on Power, Electronics and Computer Applications (ICPECA), Shenyang, China, 21–23 January 2022; pp. 1151–1157. [Google Scholar]
- Xiao, S.; Xu, L. Analysis of key factors and suppression measures for sub-synchronous oscillation of direct-drive PMSG based on frequency coupled impedance. Power Syst. Technol. 2023, 47, 1641–1652. [Google Scholar]
- Wu, X.; Wang, Y.; Chen, X.; Chen, J.; He, G.; Li, G. Sequence impedance model and interaction stability research of three-phase grid-connected inverters with considering coupling effects. Proc. CSEE 2020, 40, 1605–1616. [Google Scholar]
- Xu, J.; Bian, S.; Qian, Q.; Qian, H.; Xie, S. Robustness improvement of single-phase inverters under weak grid cases by adding grid current feed-forward in delay-based phase-locked loop. IEEE Access 2020, 8, 124275–124287. [Google Scholar] [CrossRef]
- Zhang, X.; Fu, S.; Chen, W.; Zhao, N.; Wang, G.; Xu, D. A symmetrical control method for grid-connected converters to suppress the frequency coupling under weak grid conditions. IEEE Trans. Power Electron. 2020, 35, 13488–13499. [Google Scholar] [CrossRef]
- Lin, X.; Yu, R.; Yu, J.; Wen, H. Constant-coupling-effect-based PLL for synchronization stability enhancement of grid-connected converter under weak grids. IEEE Trans. Ind. Electron. 2023, 70, 11310–11323. [Google Scholar] [CrossRef]
- Yang, D.; Wang, X.; Liu, F.; Xin, K.; Liu, Y.; Blaabjerg, F. Symmetrical PLL for SISO impedance modeling and enhanced stability in weak grids. IEEE Trans. Power Electron. 2020, 35, 1473–1483. [Google Scholar] [CrossRef]
- Li, J.; Ding, J.; Chai, T.; Lewis, F.; Jagannathan, S. Adaptive interleaved reinforcement learning: Robust stability of affine nonlinear systems with unknown uncertainty. IEEE Trans. Neural Netw. Learn. Syst. 2024, 33, 270–280. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wang, S.; Shi, H.; Wang, L.; Su, C.; LI, P. Robust asynchronous fuzzy predictive fault-tolerant tracking control for nonlinear multi-phase batch processes with time-varying reference trajectories. Eng. Appl. Artif. Intell. 2024, 133, 108415. [Google Scholar] [CrossRef]
- Shi, H.; Zuo, L.; Wang, S.; Yuan, Y.; Su, C.; Li, P. Robust predictive fault-tolerant switching control for discrete linear systems with actuator random failures. Comput. Chem. Eng. 2024, 181, 108554. [Google Scholar] [CrossRef]
- Wang, G.; Du, X.; Shi, Y.; Tai, H.; Ji, Y. Mechanism analysis and stabilization of three-phase grid-inverter systems considering frequency coupling. J. Power Electron. 2018, 18, 853–862. [Google Scholar]
- Zou, X.; Du, X.; Wang, G.; Yang, Y.; Ji, Y. The single equivalent inverter admittance model of three-phase grid-connected inverter system considering frequency coupling. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 4994–4999. [Google Scholar]
- Zhang, Y.; Tian, M.; Zhang, H.; Song, J.; Zhang, W. Admittance modeling and stability enhancement of grid-connected inverter considering frequency coupling in weak grids. Electr. Power Syst. Res. 2022, 209, 108034. [Google Scholar] [CrossRef]
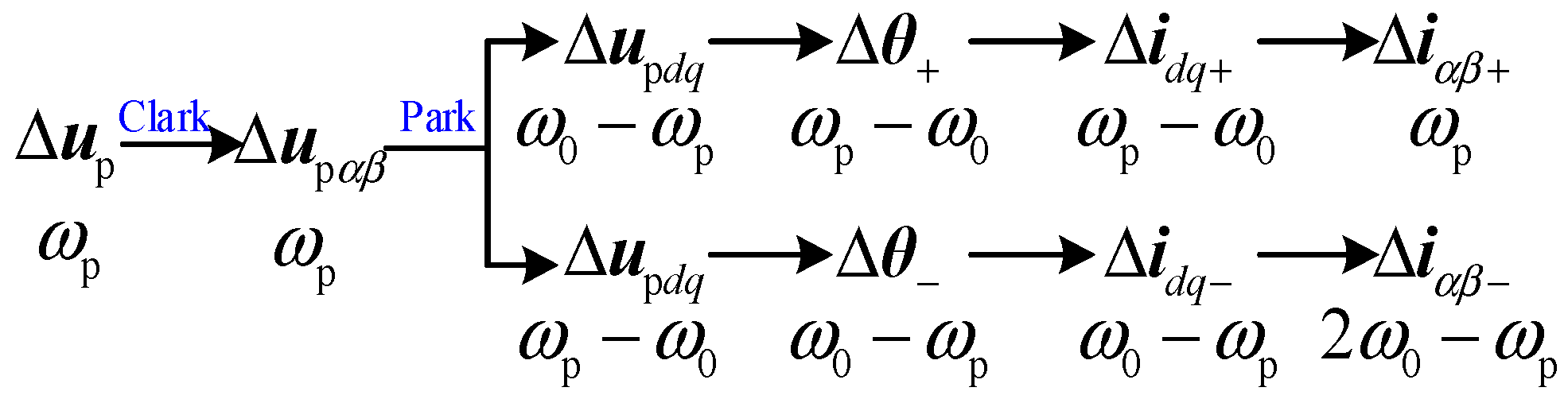




| Parameter | Notation | Value/Unit |
|---|---|---|
| Capacity | S | 4.0 kVA |
| DC source | Vdc | 400 V |
| Inductance | Lwg | 3.2/6.5 mH |
| PCC voltage | upcc | 110 V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Pen, H.; Zhang, X. Stability Control of Grid-Connected Converter Considering Phase-Locked Loop Frequency Coupling Effect. Energies 2024, 17, 3438. https://doi.org/10.3390/en17143438
Zhang Y, Pen H, Zhang X. Stability Control of Grid-Connected Converter Considering Phase-Locked Loop Frequency Coupling Effect. Energies. 2024; 17(14):3438. https://doi.org/10.3390/en17143438
Chicago/Turabian StyleZhang, Ye, Haibo Pen, and Xiaoyu Zhang. 2024. "Stability Control of Grid-Connected Converter Considering Phase-Locked Loop Frequency Coupling Effect" Energies 17, no. 14: 3438. https://doi.org/10.3390/en17143438
APA StyleZhang, Y., Pen, H., & Zhang, X. (2024). Stability Control of Grid-Connected Converter Considering Phase-Locked Loop Frequency Coupling Effect. Energies, 17(14), 3438. https://doi.org/10.3390/en17143438







