Capacity Expansion Planning of Hydrogen-Enabled Industrial Energy Systems for Carbon Dioxide Peaking
Abstract
1. Introduction
2. Problem Formulation
2.1. Capacity Expansion and Retirement
2.2. System-Level Constraints of Energy Exchange
2.3. Constraints of Distributed Power Grid
2.4. Operation Constraints of HIES
2.5. Operation Constraints of CES
3. Solution Methodology
4. Numerical Testing Results
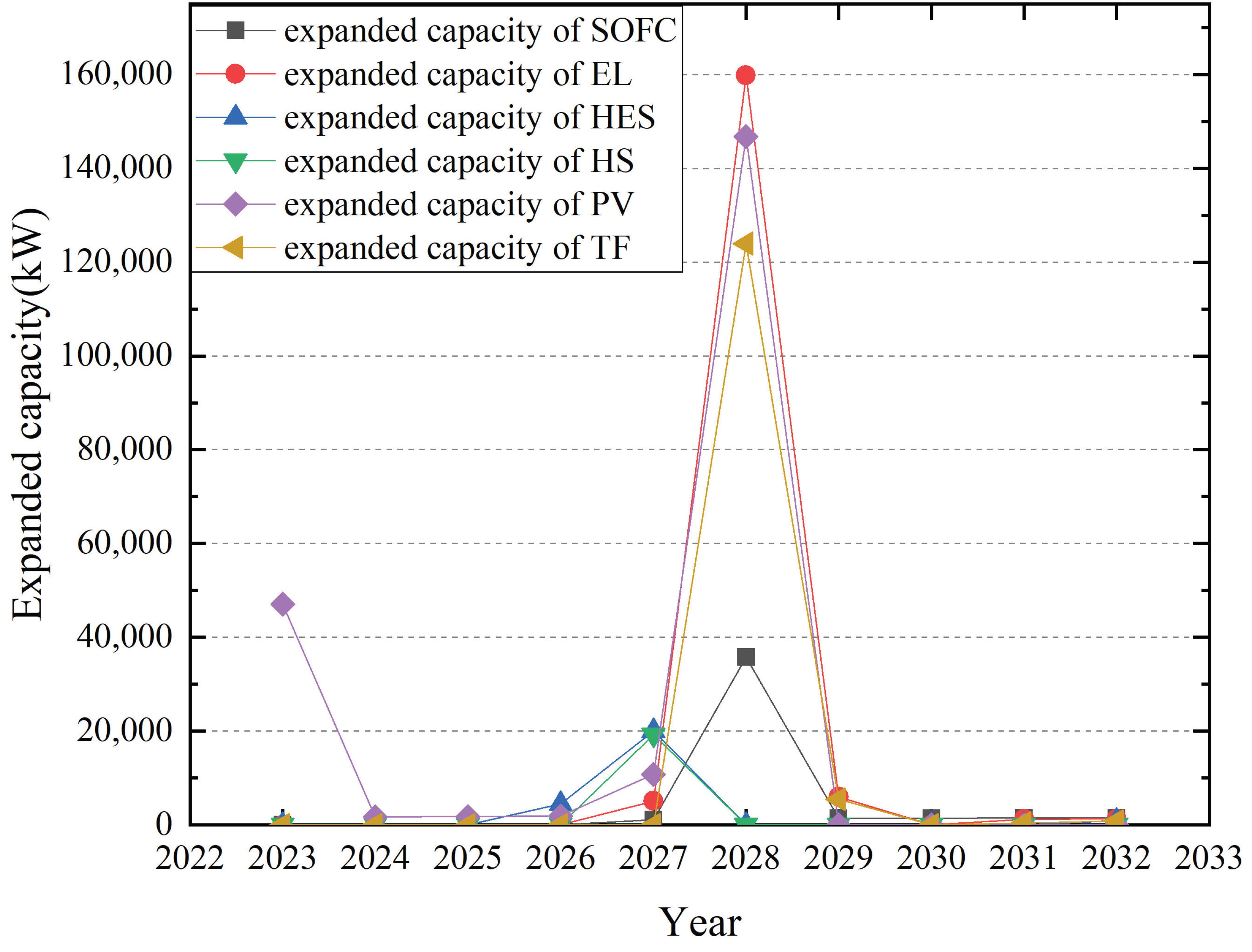
4.1. Optimization Results
4.2. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HIES | Hydrogen-enabled industrial energy system |
| CES | Coal-driven energy system |
| SOFC | Solid oxide fuel cell |
| HS | Hydrogen storage tank |
| EL | Electrolyzer |
| BPT | Back-pressure turbine |
| HES | Heating energy storage |
| HEX | Heat exchanger |
| PV | Photovoltaic |
| CB | Coal-fired boiler |
| CG | Coal-fired generator |
| TOU | Time-of-use |
References
- Tong, Y.; Wang, K.; Liu, J.; Zhang, Y.; Gao, J.; Dan, M.; Yue, T.; Zuo, P.; Zhao, Z. Refined assessment and decomposition analysis of carbon emissions in high-energy intensive industrial sectors in China. Sci. Total Environ. 2023, 872, 162161. [Google Scholar] [CrossRef] [PubMed]
- Dong, X.; Wu, J.; Xu, Z.; Liu, K.; Guan, X. Optimal coordination of hydrogen-based integrated energy systems with combination of hydrogen and water storage. Appl. Energy 2022, 308, 118274. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, H.; Zhang, Y.; Wang, H.; Lyu, J.; Yue, G. Efficiency and emissions of gas-fired industrial boiler fueled with hydrogen-enriched nature gas: A case study of 108 t/h steam boiler. Int. J. Hydrogen Energy 2022, 47, 28188–28203. [Google Scholar] [CrossRef]
- Chang, Y.; Wan, F.; Yao, X.; Wang, J.; Han, Y.; Li, H. Influence of hydrogen production on the CO2 emissions reduction of hydrogen metallurgy transformation in iron and steel industry. Energy Rep. 2023, 9, 3057–3071. [Google Scholar] [CrossRef]
- Lin, J.; Cai, R. Optimal planning for industrial park-integrated energy system with hydrogen energy industry chain. Int. J. Hydrogen Energy 2023, 48, 19046–19059. [Google Scholar] [CrossRef]
- Ahmadi, F.; Nazeri Tahroudi, M.; Mirabbasi, R.; Khalili, K.; Jhajharia, D. Spatiotemporal trend and abrupt change analysis of temperature in Iran. Meteorol. Appl. 2018, 25, 314–321. [Google Scholar] [CrossRef]
- Dong, X.; Liu, Y.; Xu, Z.; Wu, J.; Liu, J.; Guan, X. Optimal Scheduling of Distributed Hydrogen-based Multi-Energy Systems for Building Energy Cost and Carbon Emission Reduction. IEEE Int. Conf. Autom. Sci. Eng. 2020, 2020, 1526–1531. [Google Scholar] [CrossRef]
- Mu, C.; Ding, T.; Qu, M.; Zhou, Q.; Li, F.; Shahidehpour, M. Decentralized optimization operation for the multiple integrated energy systems with energy cascade utilization. Appl. Energy 2020, 280, 115989. [Google Scholar] [CrossRef]
- Staffell, I. Zero carbon infinite COP heat from fuel cell CHP. Appl. Energy 2015, 147, 373–385. [Google Scholar] [CrossRef]
- Bartela, Ł.; Skorek-Osikowska, A.; Kotowicz, J. An analysis of the investment risk related to the integration of a supercritical coal-fired combined heat and power plant with an absorption installation for CO2 separation. Appl. Energy 2015, 156, 423–435. [Google Scholar] [CrossRef]
- Zhao, S.; Ge, Z.; Sun, J.; Ding, Y.; Yang, Y. Comparative study of flexibility enhancement technologies for the coal-fired combined heat and power plant. Energy Convers. Manag. 2019, 184, 15–23. [Google Scholar] [CrossRef]
- Whiston, M.M.; Azevedo, I.M.; Litster, S.; Samaras, C.; Whitefoot, K.S.; Whitacre, J.F. Meeting US solid oxide fuel cell targets. Joule 2019, 3, 2060–2065. [Google Scholar] [CrossRef]
- Pfenninger, S.; Staffell, I. Renewables.ninja. Available online: https://www.renewables.ninja/ (accessed on 1 June 2022).
- Liu, J.; Xu, Z.; Wu, J.; Liu, K.; Guan, X. Optimal planning of distributed hydrogen-based multi-energy systems. Appl. Energy 2021, 281, 116107. [Google Scholar] [CrossRef]
- Al-Khori, K.; Bicer, Y.; Koç, M. Comparative techno-economic assessment of integrated PV-SOFC and PV-Battery hybrid system for natural gas processing plants. Energy 2021, 222, 119923. [Google Scholar] [CrossRef]
- Kler, A.; Stepanova, E.; Maksimov, A. Investigating the efficiency of a steam-turbine heating plant with a back-pressure steam turbine and waste-heat recovery. Thermophys. Aeromechanics 2018, 25, 929–938. [Google Scholar] [CrossRef]


| Time (hour) | Price (RMB/kWh) |
|---|---|
| 22:00–6:00 | 0.298 |
| 6:00–8:00, 11:00–18:00, 21:00–22:00 | 0.593 |
| 8:00–11:00, 18:00–21:00 | 1.021 |
| Equipment | Cost |
|---|---|
| SOFC | 455,539–5050 RMB/kW [12,15] |
| Electrolyzer | RMB 2100/kW |
| Back-pressure turbine | RMB 406.2/kW [16] |
| Hydrogen storage tank | RMB 3385/kg |
| Heating energy storage | RMB 33.85/kWh |
| Coal-fired generator | RMB 13,464/kW [10] |
| Coal-fired boiler | RMB 1292/kW [11] |
| PV panels | RMB 900/ |
| Peaking Time | Overall Cost (RMB) | Costs of Purchasing Allowance (RMB) | Emission Peak (kg) |
|---|---|---|---|
| 2030 | 3.191 × 109 | 9.870 × 109 | 5.819 × 1010 |
| 2028 | 3.191 × 109 | 9.870 × 109 | 5.819 × 1010 |
| 2026 | 3.238 × 109 | 5.765 × 109 | 5.611 × 1010 |
| 2024 | 3.248 × 109 | 5.902 × 109 | 5.218 × 1010 |
| Emission Targets in 2030 Compared with 2022 | Overall Cost (RMB) | Costs of Purchasing Allowance (RMB) | Emission Peak (kg) | Emission in 2030 (kg) |
|---|---|---|---|---|
| 100% | 3.191 × 109 | 9.870 × 109 | 5.819 × 1010 | 3.516 × 1010 |
| 75% | 3.191 × 109 | 9.870 × 109 | 5.819 × 1010 | 3.516 × 1010 |
| 50% | 3.197 × 109 | 1.151 × 1010 | 5.819 × 1010 | 2.516 × 1010 |
| 25% | 3.204 × 109 | 1.386 × 1010 | 5.819 × 1010 | 1.258 × 1010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Dong, X.; Li, C.; Zhao, Y.; Liu, K. Capacity Expansion Planning of Hydrogen-Enabled Industrial Energy Systems for Carbon Dioxide Peaking. Energies 2024, 17, 3400. https://doi.org/10.3390/en17143400
Zhang K, Dong X, Li C, Zhao Y, Liu K. Capacity Expansion Planning of Hydrogen-Enabled Industrial Energy Systems for Carbon Dioxide Peaking. Energies. 2024; 17(14):3400. https://doi.org/10.3390/en17143400
Chicago/Turabian StyleZhang, Kai, Xiangxiang Dong, Chaofeng Li, Yanling Zhao, and Kun Liu. 2024. "Capacity Expansion Planning of Hydrogen-Enabled Industrial Energy Systems for Carbon Dioxide Peaking" Energies 17, no. 14: 3400. https://doi.org/10.3390/en17143400
APA StyleZhang, K., Dong, X., Li, C., Zhao, Y., & Liu, K. (2024). Capacity Expansion Planning of Hydrogen-Enabled Industrial Energy Systems for Carbon Dioxide Peaking. Energies, 17(14), 3400. https://doi.org/10.3390/en17143400






