Influence of Wind and Rainfall on the Performance of a Photovoltaic Module in a Dusty Environment
Abstract
1. Introduction
- Factors that immediately affect the total amount, incidence angles, and/or spectral distribution of solar radiation reaching the semiconductor, e.g., shading, clouds, aerosol particles, humidity, surface soiling or wetness, etc.
- Factors that have effect on the deposition, retention, accumulation, and cementation of soiling particles on a module’s surface (and thereby influence the fraction of incident radiation absorbed by the cell), including wind, precipitation, relative humidity, air temperature, etc.
- Factors that influence cell temperature via heat transfer, such as wind, precipitation, and air temperature (Many studies have investigated the effect of wind, including some considering the local variations in module temperature [23,24]. Typically, higher wind speed results in enhanced heat transfer and a reduction in the temperature of the module, which is beneficial for its power output. However, contrary results have also been reported as a consequence of uneven cooling [25]. In addition to wind speed, wind direction has also been considered as an important factor [26,27], for it determines the windward side of the module and the development of the boundary layers. Nevertheless, in some studies its effect has been found to be rather small or insignificant [28,29]).
2. Materials and Methods
- The average power of the module was calculated from the measured voltage.
- The current-voltage curve of the PV module was determined according to the aforementioned PVLIB-Python implementation of the six-parameter SDM based on the calculated global in-plane irradiance and the measured average back temperature of the module. The theoretical power output of the module was obtained via an optimization algorithm, which finds the voltage (and thus power) on the given curve corresponding to the connected constant resistive load () (In essence, the algorithm finds the intersection of the two curves—that of the module and that of the load).
3. Results and Discussion
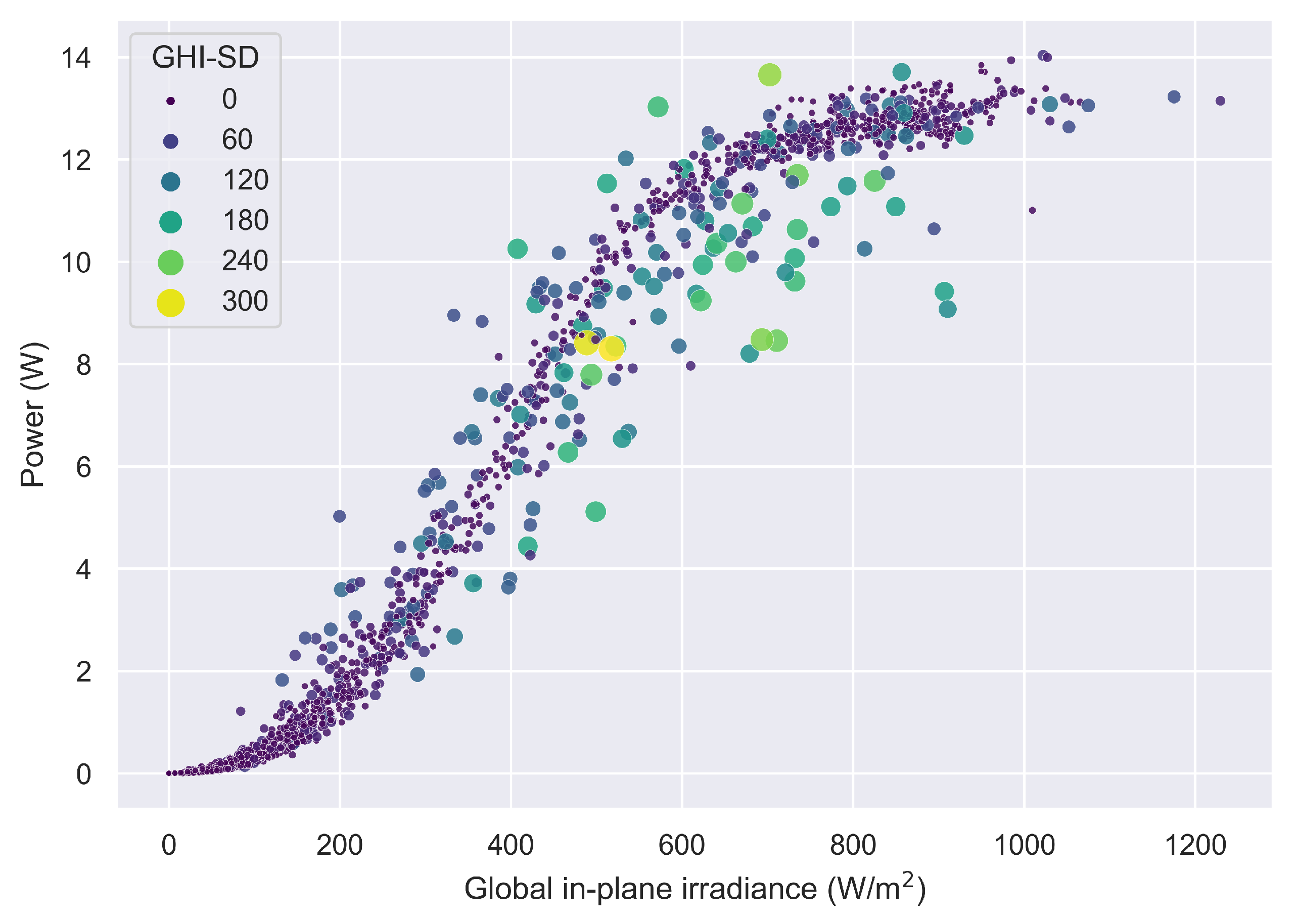
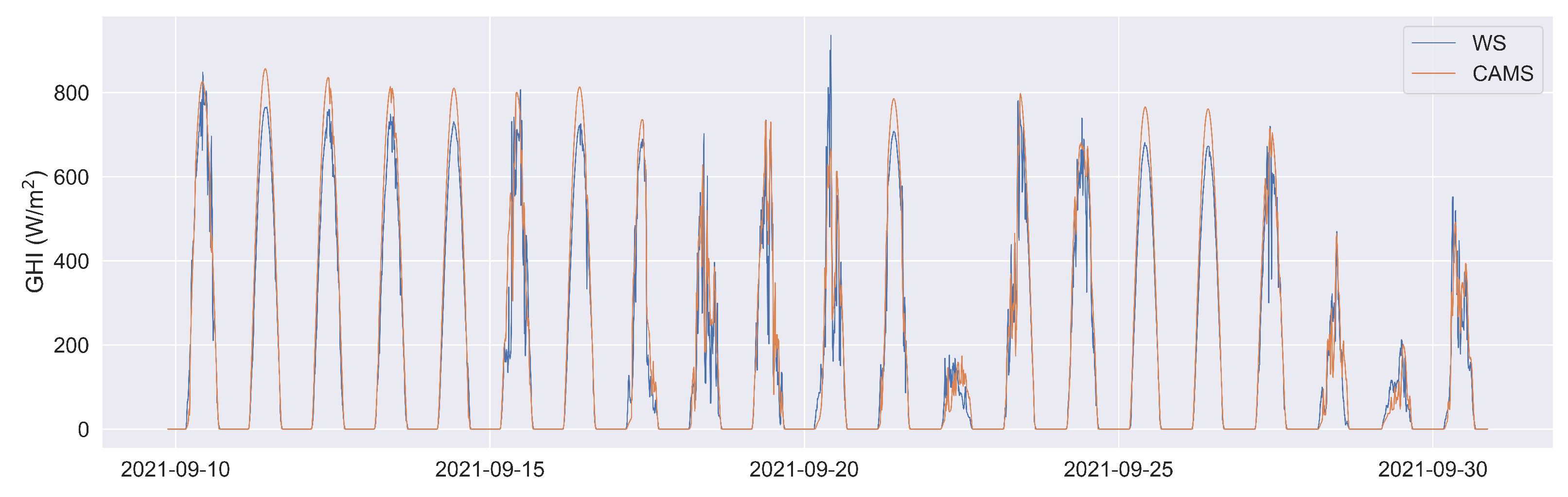
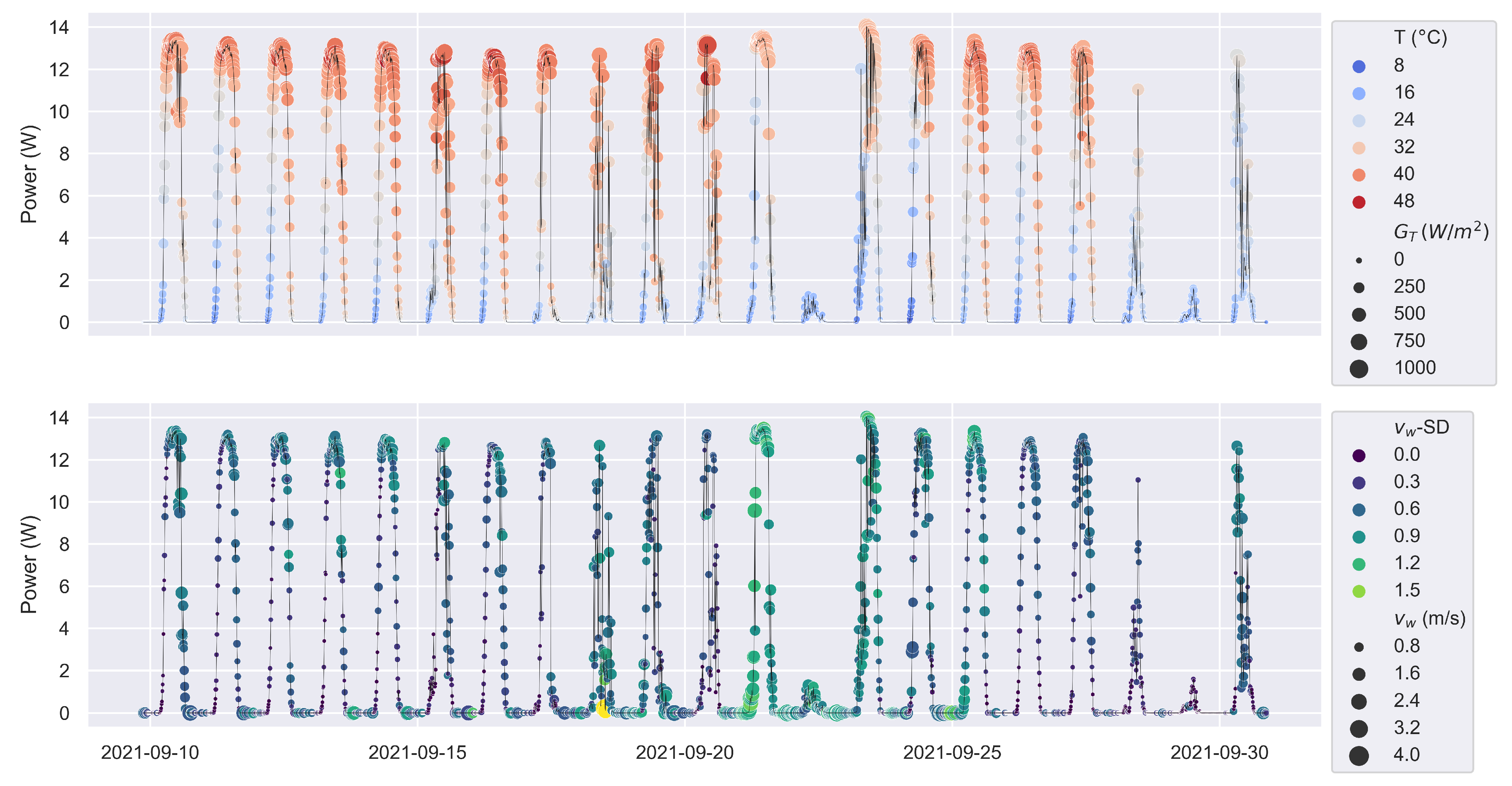
3.1. General Observations
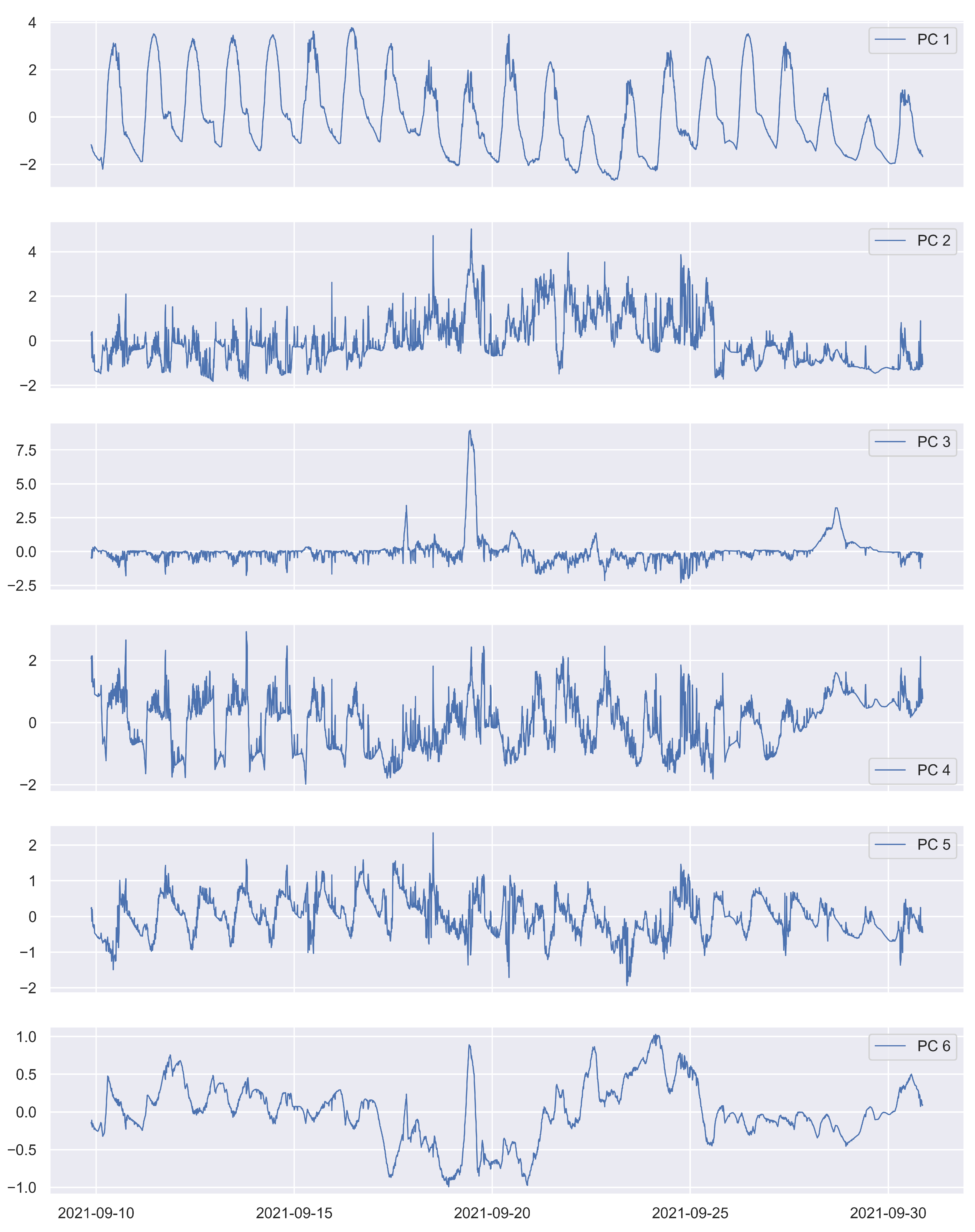
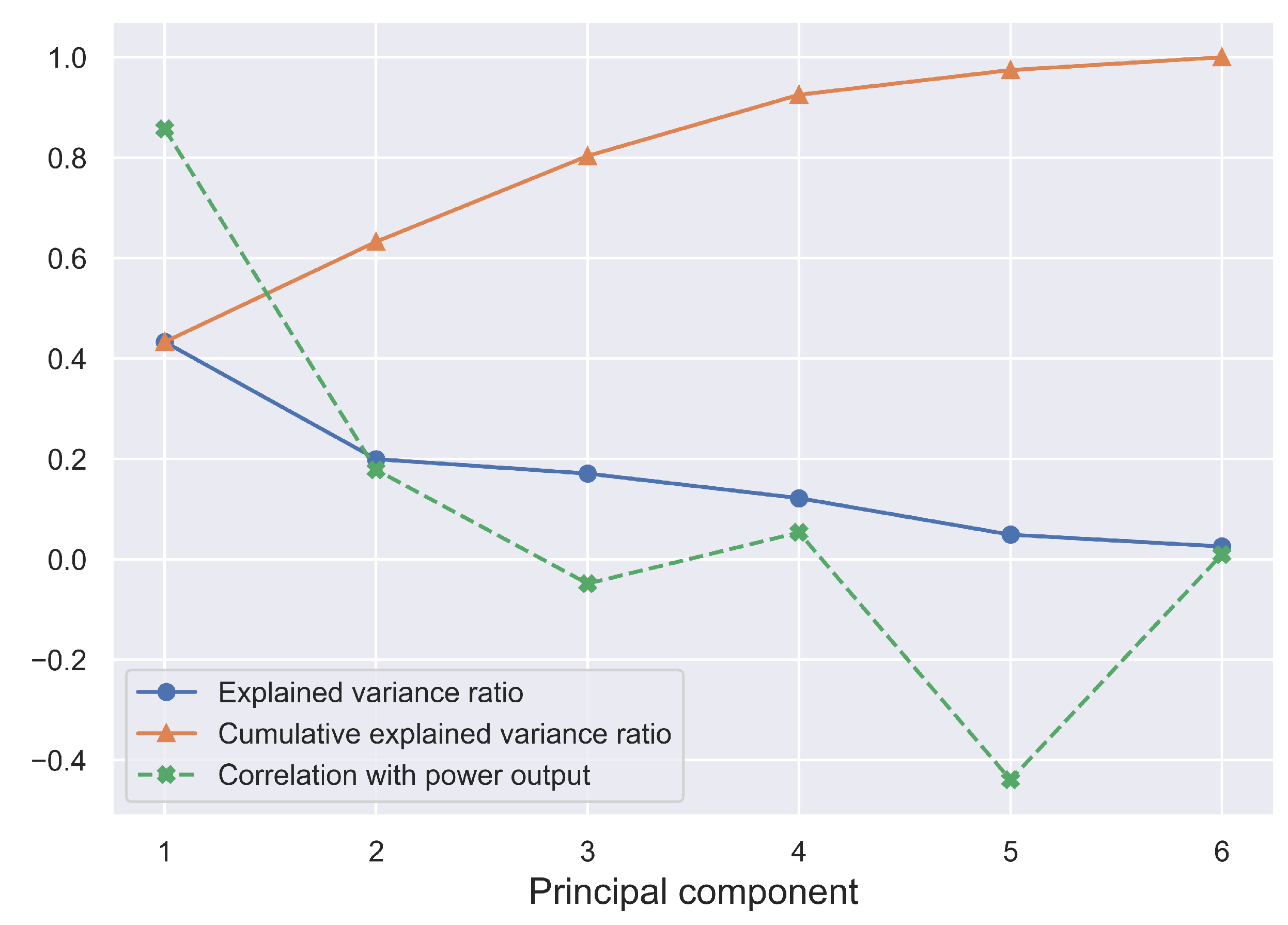
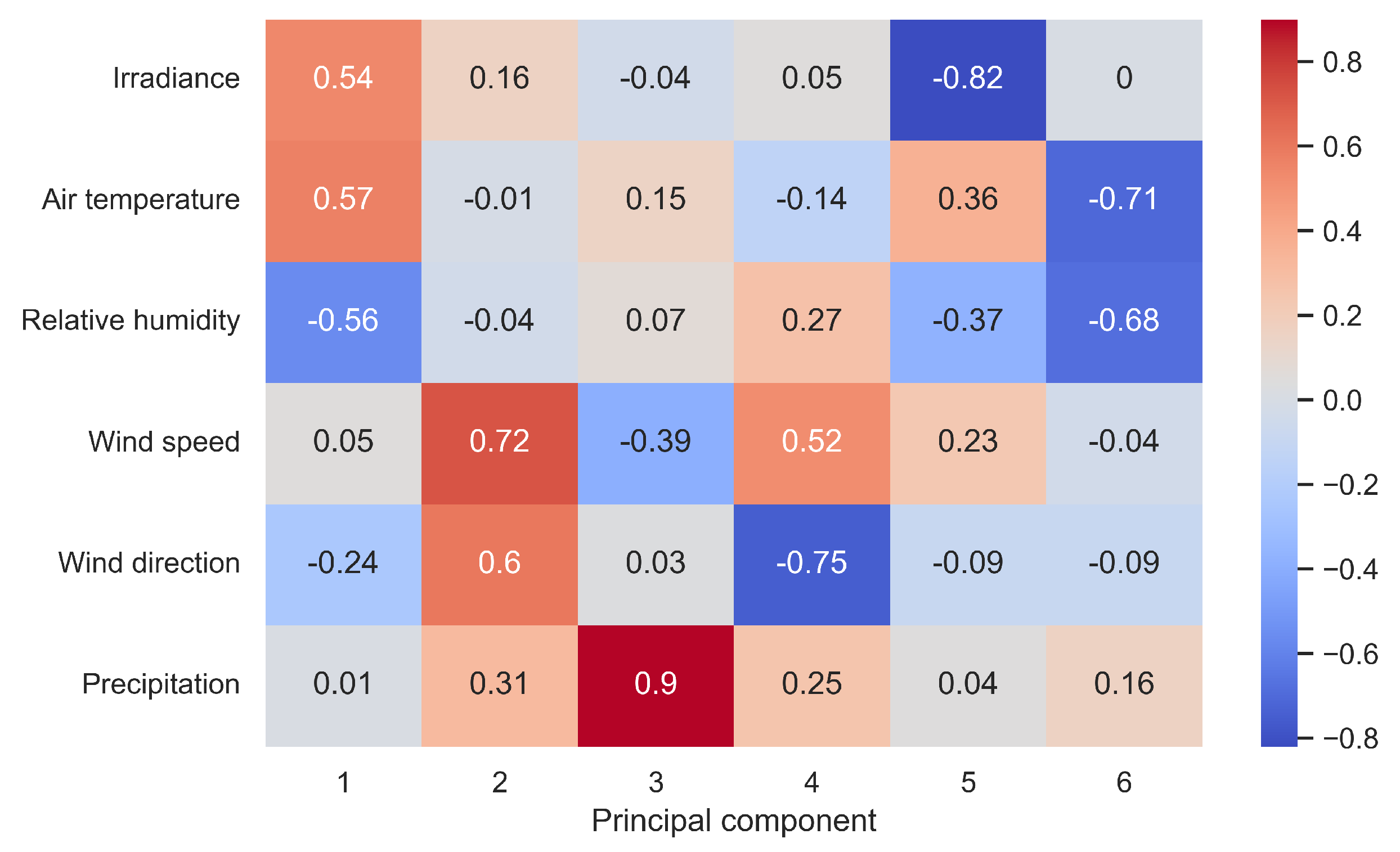
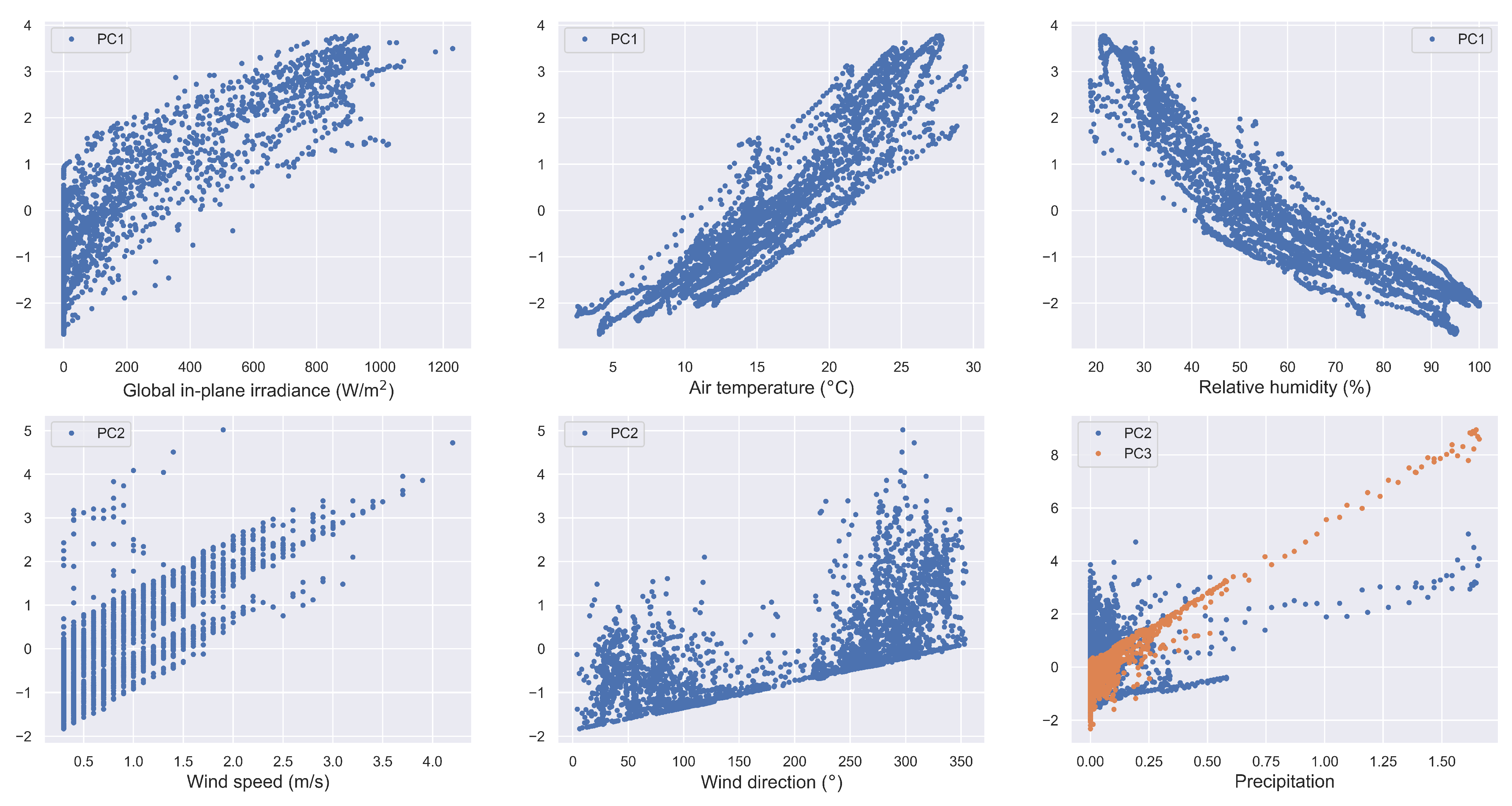
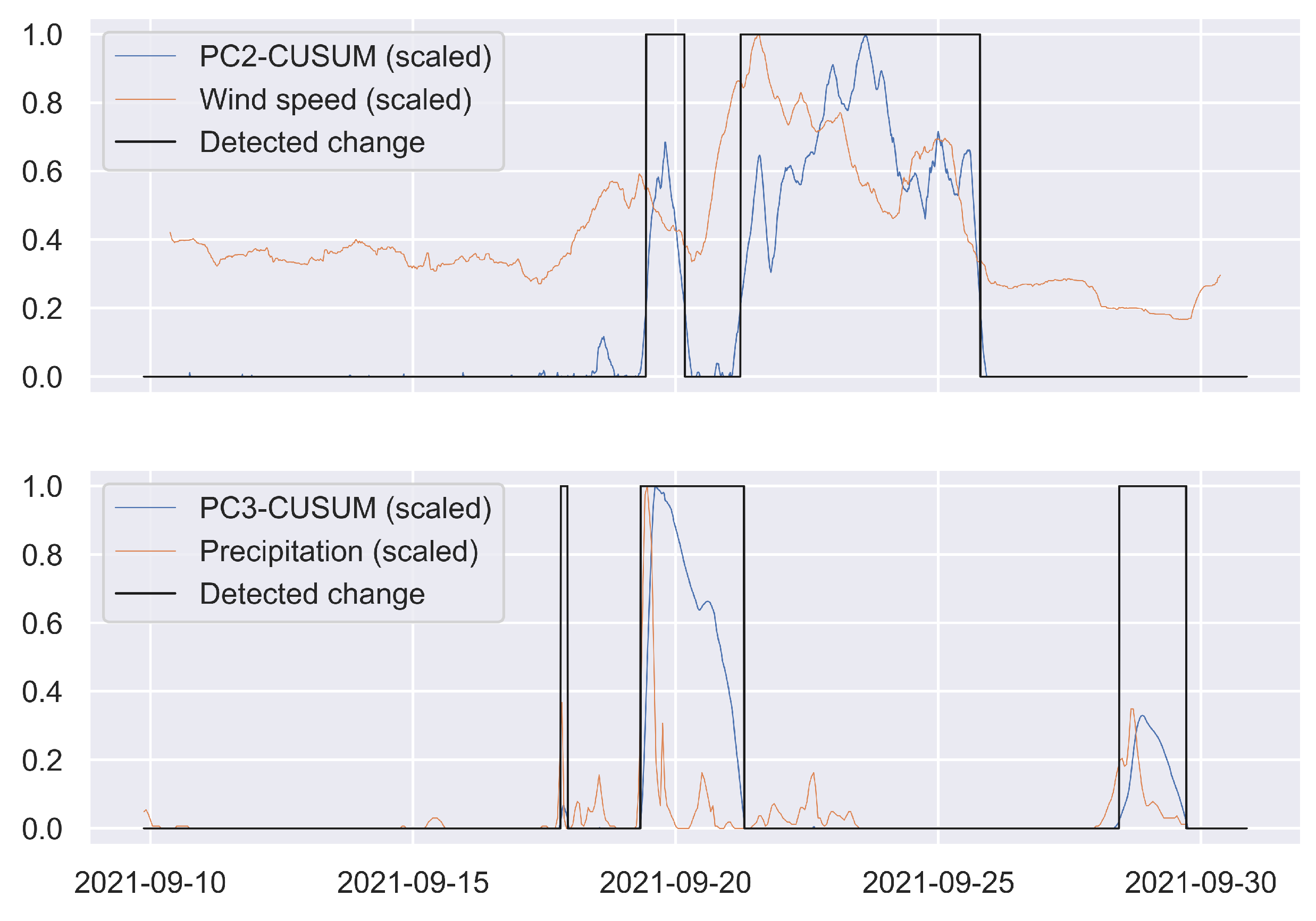
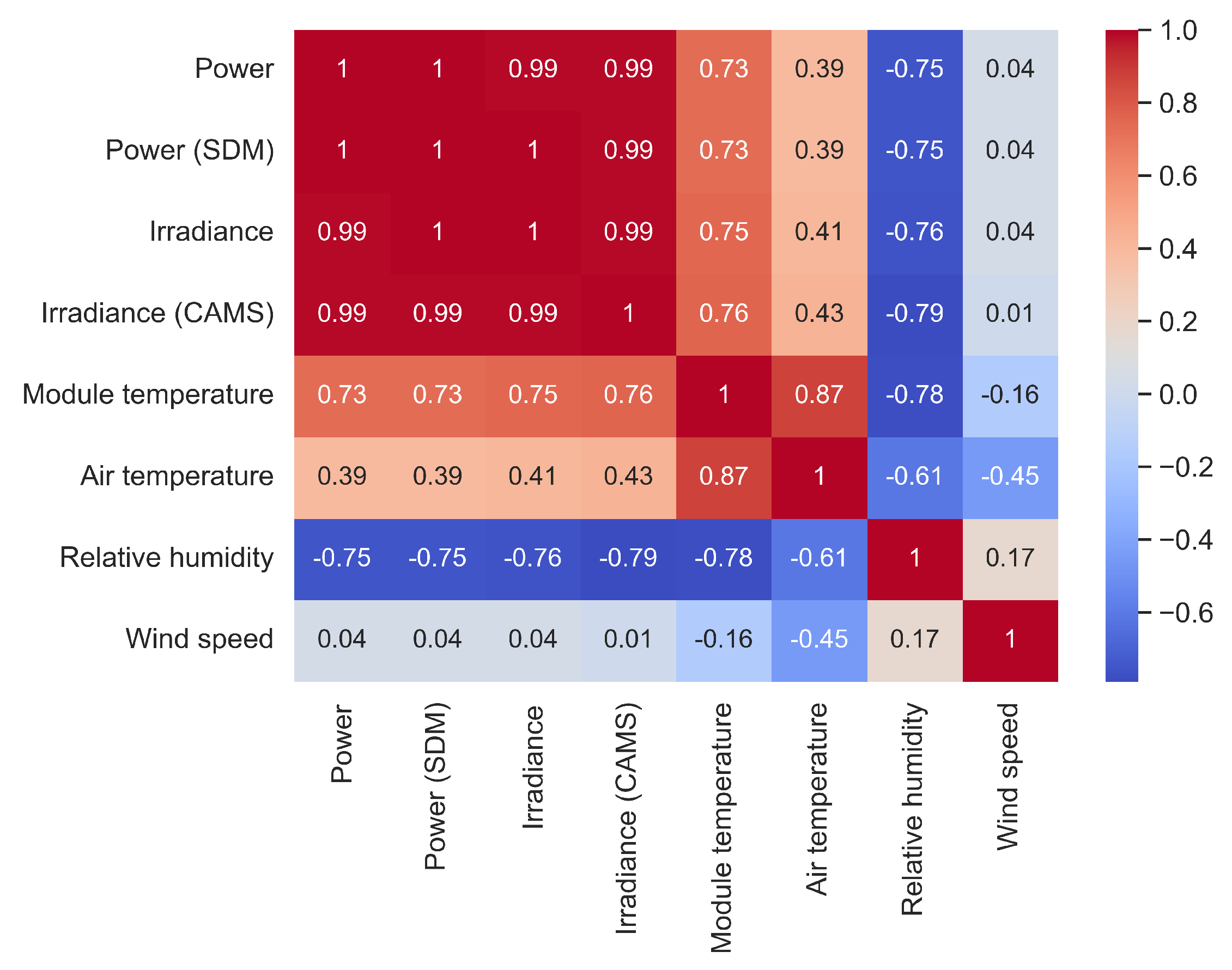
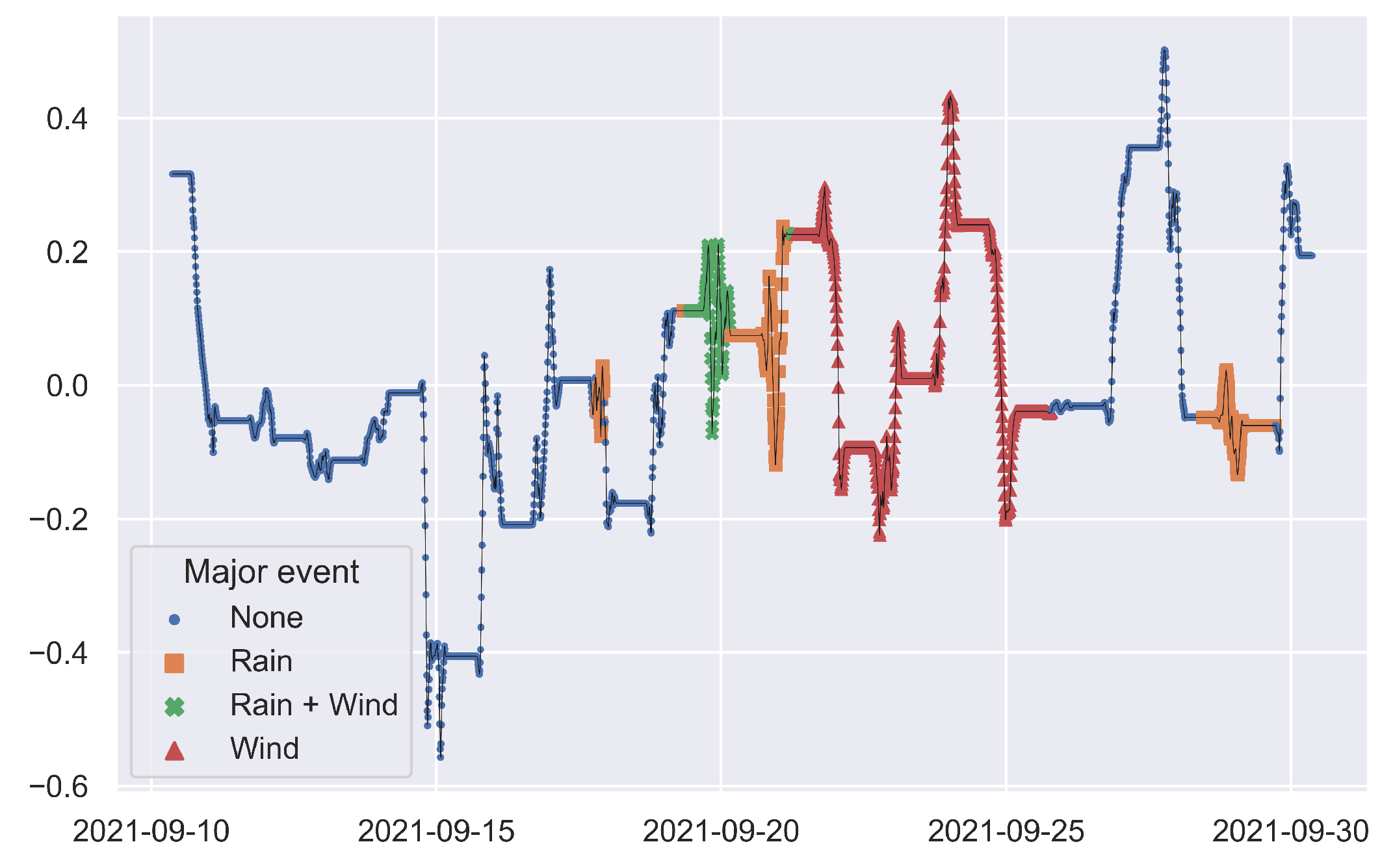
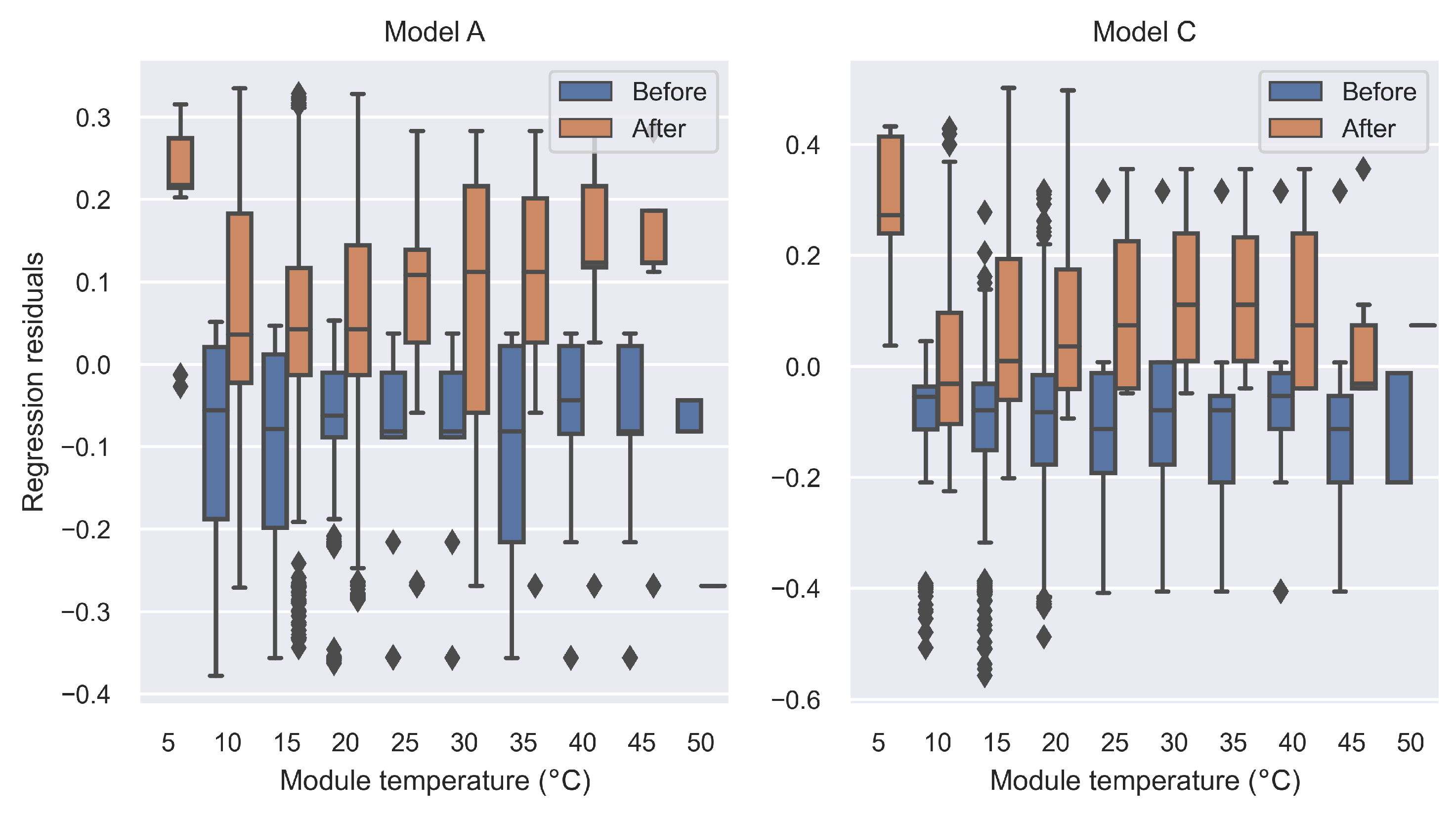
3.2. Principal Component Analysis and Change Detection
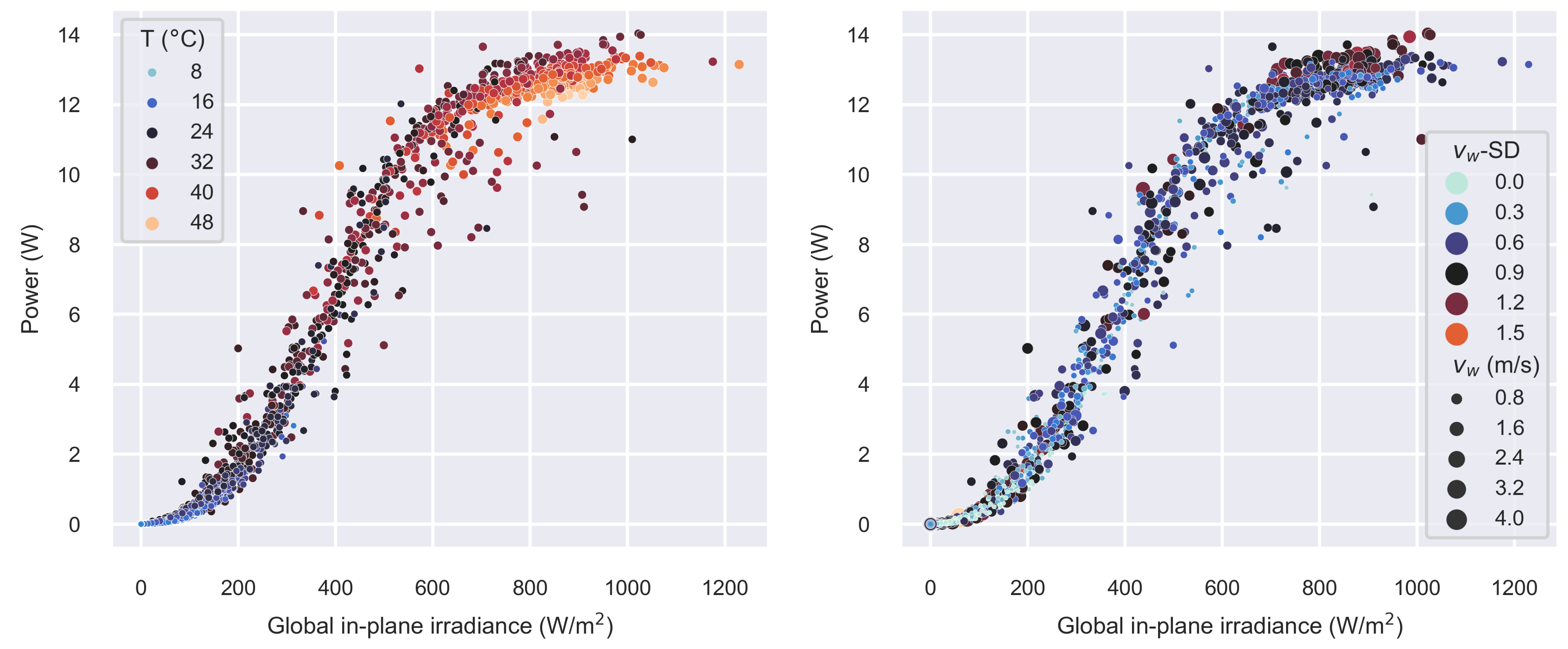
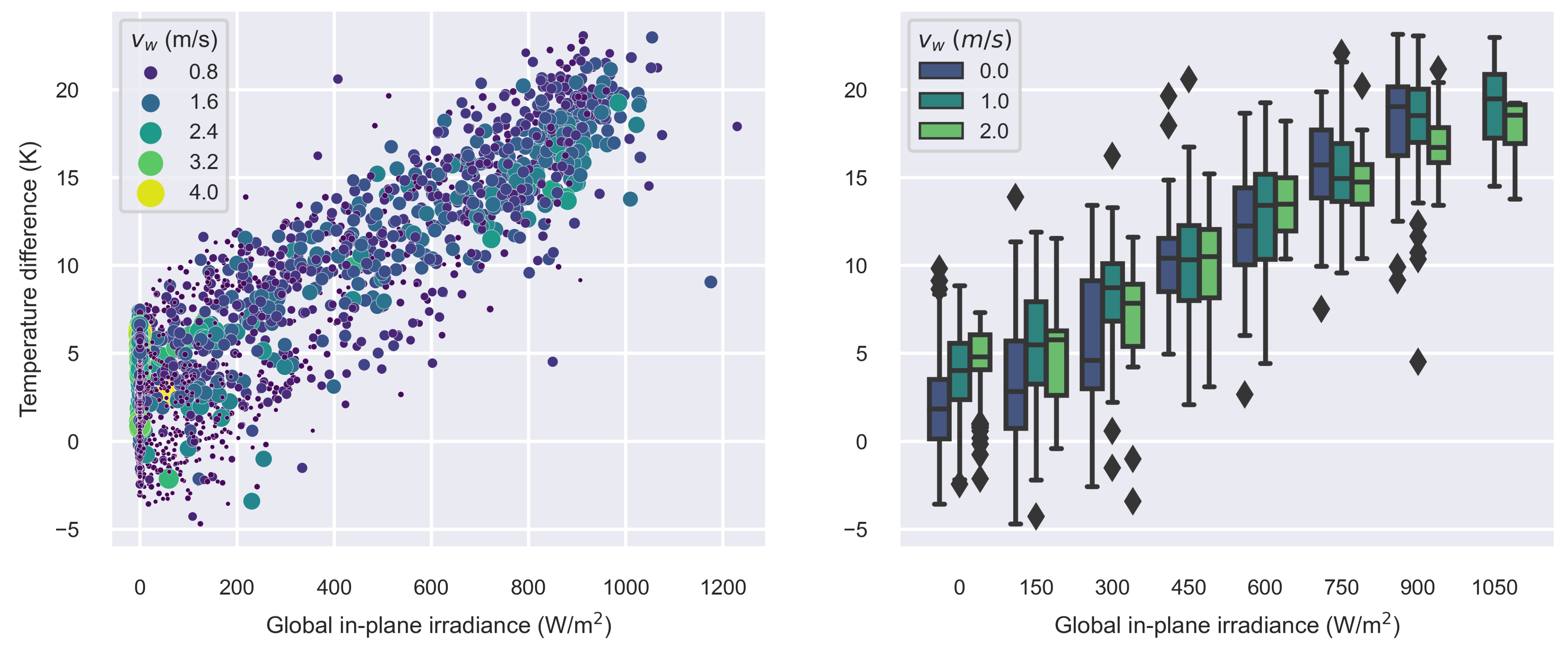
3.3. Wind Speed and Module Temperature
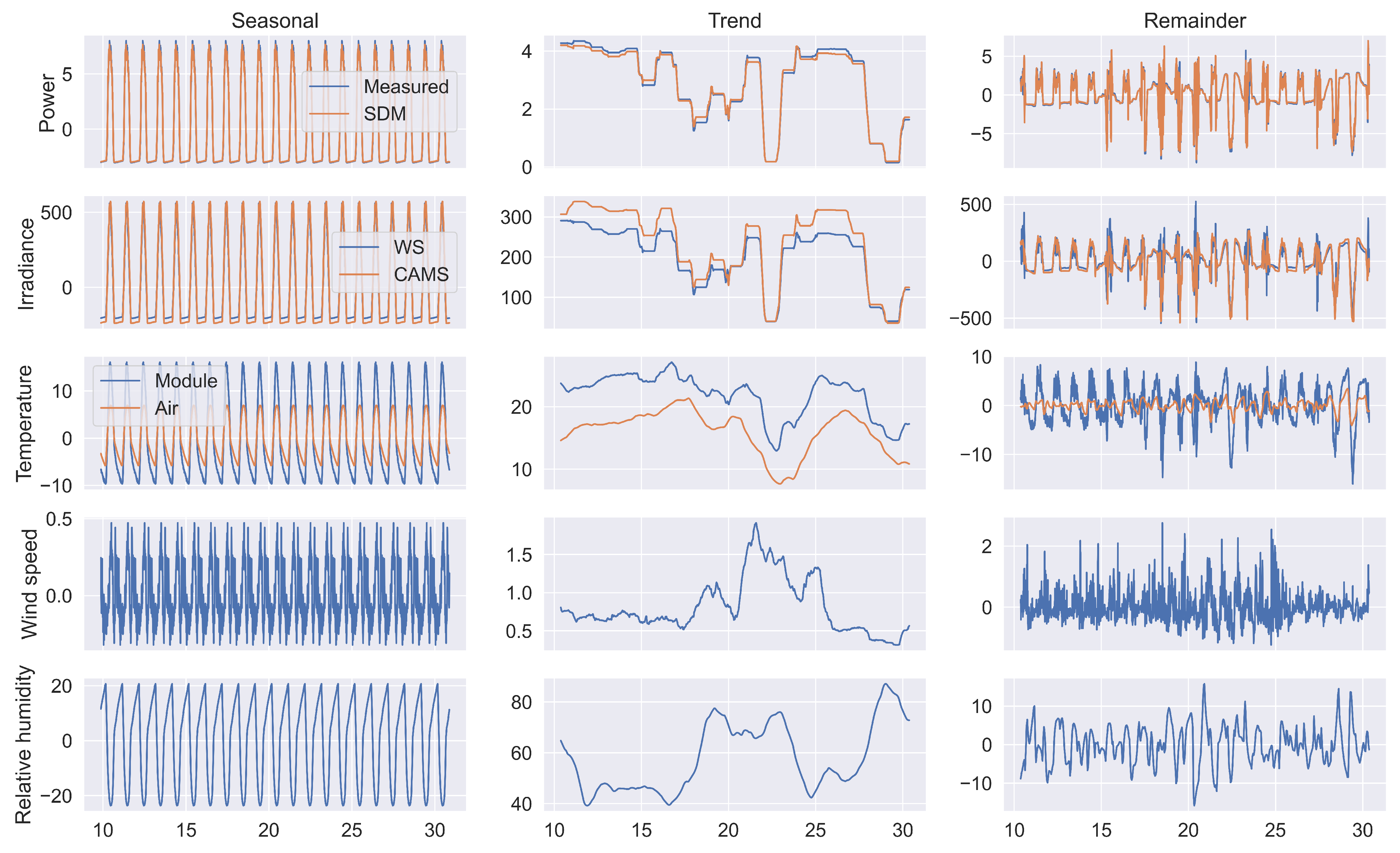
3.4. Seasonal-Trend Decomposition
4. Conclusions
- Soiling is one of the most detrimental factors affecting PV performance, while among the various pollutants, limestone particles are a common cause for concern.
- In field measurements, the problem with soiling also affects the irradiance sensors, which can obscure the actual magnitude of PV performance deterioration;
- Rainfall with sufficient intensity can effectively clean soiled surfaces, even if not completely, which makes the issue of soiling much less severe in some climates.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CAMS | Copernicus Atmosphere Monitoring Service |
| CUSUM | Cumulative Sum Method |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| GHI | Global Horizontal Irradiance |
| HDKR | Hay-Davies-Klucher-Reindl model |
| I-V | Current-Voltage |
| LOESS | Locally Estimated Scatterplot Smoothing |
| MPP | Maximum Power Point |
| NASA | National Aeronautics and Space Administration |
| PC | Principal Component |
| PCA | Principal Component Analysis |
| POWER | Prediction Of Worldwide Energy Resources |
| PV | Photovoltaic |
| SD | Standard Deviation |
| SDM | Single-Diode Model |
| STL | Seasonal-Trend decomposition using LOESS |
References
- Kruitwagen, L.; Story, K.T.; Friedrich, J.; Byers, L.; Skillman, S.; Hepburn, C. A global inventory of photovoltaic solar energy generating units. Nature 2021, 598, 604–610. [Google Scholar] [CrossRef] [PubMed]
- Haegel, N.M.; Verlinden, P.; Victoria, M.; Altermatt, P.; Atwater, H.; Barnes, T.; Breyer, C.; Case, C.; Wolf, S.D.; Deline, C.; et al. Photovoltaics at multi-terawatt scale: Waiting is not an option. Science 2023, 380, 39–42. [Google Scholar] [CrossRef]
- Borah, P.; Micheli, L.; Sarmah, N. Analysis of Soiling Loss in Photovoltaic Modules: A Review of the Impact of Atmospheric Parameters, Soil Properties, and Mitigation Approaches. Sustainability 2023, 15, 6669. [Google Scholar] [CrossRef]
- Li, X.; Mauzerall, D.L.; Bergin, M.H. Global reduction of solar power generation efficiency due to aerosols and panel soiling. Nat. Sustain. 2020, 3, 720–727. [Google Scholar] [CrossRef]
- Jaxa-Rozen, M.; Trutnevyte, E. Sources of uncertainty in long-term global scenarios of solar photovoltaic technology. Nat. Clim. Chang. 2021, 11, 266–273. [Google Scholar] [CrossRef]
- Haegel, N.M.; Atwater, H.; Barnes, T.; Breyer, C.; Burrell, A.; Chiang, Y.M.; Wolf, S.D.; Dimmler, B.; Feldman, D.; Glunz, S.; et al. Terawatt-scale photovoltaics: Transform global energy. Science 2019, 364, 836–838. [Google Scholar] [CrossRef] [PubMed]
- Shukla, A.K.; Sudhakar, K.; Baredar, P. Recent advancement in BIPV product technologies: A review. Energy Build. 2017, 140, 188–195. [Google Scholar] [CrossRef]
- Naderi, M.; Palmer, D.; Smith, M.J.; Ballantyne, E.E.F.; Stone, D.A.; Foster, M.P.; Gladwin, D.T.; Khazali, A.; Al-Wreikat, Y.; Cruden, A.; et al. Techno-Economic Planning of a Fully Renewable Energy-Based Autonomous Microgrid with Both Single and Hybrid Energy Storage Systems. Energies 2024, 17, 788. [Google Scholar] [CrossRef]
- Fikiin, K.; Stankov, B. Integration of Renewable Energy in Refrigerated Warehouses. In Handbook of Research on Advances and Applications in Refrigeration Systems and Technologies; IGI Global: Hershey, PA, USA, 2015; pp. 803–853. [Google Scholar] [CrossRef]
- Walczewski, M.J.; Wöhrle, H. Prediction of Electricity Generation Using Onshore Wind and Solar Energy in Germany. Energies 2024, 17, 844. [Google Scholar] [CrossRef]
- Feron, S.; Cordero, R.R.; Damiani, A.; Jackson, R.B. Climate change extremes and photovoltaic power output. Nat. Sustain. 2021, 4, 270–276. [Google Scholar] [CrossRef]
- Van de Ven, D.J.; Capellan-Peréz, I.; Arto, I.; Cazcarro, I.; de Castro, C.; Patel, P.; Gonzalez-Eguino, M. The potential land requirements and related land use change emissions of solar energy. Sci. Rep. 2021, 11, 2907. [Google Scholar] [CrossRef] [PubMed]
- Sills, J.; Serrano, D.; Margalida, A.; Pérez-García, J.M.; Juste, J.; Traba, J.; Valera, F.; Carrete, M.; Aihartza, J.; Real, J.; et al. Renewables in Spain threaten biodiversity. Science 2020, 370, 1282–1283. [Google Scholar] [CrossRef]
- Ortiz, A.; Negandhi, D.; Mysorekar, S.R.; Nagaraju, S.K.; Kiesecker, J.; Robinson, C.; Bhatia, P.; Khurana, A.; Wang, J.; Oviedo, F.; et al. An Artificial Intelligence Dataset for Solar Energy Locations in India. Sci. Data 2022, 9, 497. [Google Scholar] [CrossRef] [PubMed]
- Bao, K.; Thrän, D.; Schröter, B. Land resource allocation between biomass and ground-mounted PV under consideration of the food–water–energy nexus framework at regional scale. Renew. Energy 2023, 203, 323–333. [Google Scholar] [CrossRef]
- Rodziewicz, T.; Rajfur, M.; Teneta, J.; Świsłowski, P.; Wacławek, M. Modelling and analysis of the influence of solar spectrum on the efficiency of photovoltaic modules. Energy Rep. 2021, 7, 565–574. [Google Scholar] [CrossRef]
- Polman, A.; Knight, M.; Garnett, E.C.; Ehrler, B.; Sinke, W.C. Photovoltaic materials: Present efficiencies and future challenges. Science 2016, 352, aad4424. [Google Scholar] [CrossRef]
- Daxini, R.; Wu, Y. Review of methods to account for the solar spectral influence on photovoltaic device performance. Energy 2024, 286, 129461. [Google Scholar] [CrossRef]
- Nazir, S.; Ali, A.; Aftab, A.; Muqeet, H.A.; Mirsaeidi, S.; Zhang, J.M. Techno-Economic and Environmental Perspectives of Solar Cell Technologies: A Comprehensive Review. Energies 2023, 16, 4959. [Google Scholar] [CrossRef]
- Honsberg, C.; Bowden, S. Photovoltaics Education Website. 2019. Available online: https://www.pveducation.org (accessed on 5 April 2024).
- Löper, P.; Pysch, D.; Richter, A.; Hermle, M.; Janz, S.; Zacharias, M.; Glunz, S. Analysis of the Temperature Dependence of the Open-Circuit Voltage. Energy Procedia 2012, 27, 135–142. [Google Scholar] [CrossRef]
- Skoplaki, E.; Palyvos, J. On the temperature dependence of photovoltaic module electrical performance: A review of efficiency/power correlations. Sol. Energy 2009, 83, 614–624. [Google Scholar] [CrossRef]
- Nižetić, S.; Grubišić- Čabo, F.; Marinić-Kragić, I.; Papadopoulos, A. Experimental and numerical investigation of a backside convective cooling mechanism on photovoltaic panels. Energy 2016, 111, 211–225. [Google Scholar] [CrossRef]
- Goverde, H.; Goossens, D.; Govaerts, J.; Catthoor, F.; Baert, K.; Poortmans, J.; Driesen, J. Spatial and temporal analysis of wind effects on PV modules: Consequences for electrical power evaluation. Sol. Energy 2017, 147, 292–299. [Google Scholar] [CrossRef]
- Rossa, C. Energy losses in photovoltaic generators due to wind patterns. Commun. Eng. 2023, 2, 66. [Google Scholar] [CrossRef]
- Waterworth, D.; Armstrong, A. Southerly winds increase the electricity generated by solar photovoltaic systems. Sol. Energy 2020, 202, 123–135. [Google Scholar] [CrossRef]
- Kaplani, E.; Kaplanis, S. Thermal modelling and experimental assessment of the dependence of PV module temperature on wind velocity and direction, module orientation and inclination. Sol. Energy 2014, 107, 443–460. [Google Scholar] [CrossRef]
- Ghabuzyan, L.; Pan, K.; Fatahi, A.; Kuo, J.; Baldus-Jeursen, C. Thermal Effects on Photovoltaic Array Performance: Experimentation, Modeling, and Simulation. Appl. Sci. 2021, 11, 1460. [Google Scholar] [CrossRef]
- Sharples, S.; Charlesworth, P. Full-scale measurements of wind-induced convective heat transfer from a roof-mounted flat plate solar collector. Sol. Energy 1998, 62, 69–77. [Google Scholar] [CrossRef]
- Segbefia, O.K.; Imenes, A.G.; Sætre, T.O. Moisture ingress in photovoltaic modules: A review. Sol. Energy 2021, 224, 889–906. [Google Scholar] [CrossRef]
- Mekhilef, S.; Saidur, R.; Kamalisarvestani, M. Effect of dust, humidity and air velocity on efficiency of photovoltaic cells. Renew. Sustain. Energy Rev. 2012, 16, 2920–2925. [Google Scholar] [CrossRef]
- Jordan, D.C.; Perry, K.; White, R.; Deline, C. Extreme Weather and PV Performance. IEEE J. Photovolt. 2023, 13, 830–835. [Google Scholar] [CrossRef]
- Bošnjaković, M.; Stojkov, M.; Katinić, M.; Lacković, I. Effects of Extreme Weather Conditions on PV Systems. Sustainability 2023, 15, 6044. [Google Scholar] [CrossRef]
- Ammari, N.; Mehdi, M.; Alami Merrouni, A.; El Gallassi, H.; Chaabelasri, E.; Ghennioui, A. Experimental study on the impact of soiling on the modules temperature and performance of two different PV technologies under hot arid climate. Heliyon 2022, 8, e11395. [Google Scholar] [CrossRef] [PubMed]
- Kaldellis, J.; Fragos, P.; Kapsali, M. Systematic experimental study of the pollution deposition impact on the energy yield of photovoltaic installations. Renew. Energy 2011, 36, 2717–2724. [Google Scholar] [CrossRef]
- Kaldellis, J.; Kapsali, M. Simulating the dust effect on the energy performance of photovoltaic generators based on experimental measurements. Energy 2011, 36, 5154–5161. [Google Scholar] [CrossRef]
- Mustafa, R.J.; Gomaa, M.R.; Al-Dhaifallah, M.; Rezk, H. Environmental Impacts on the Performance of Solar Photovoltaic Systems. Sustainability 2020, 12, 608. [Google Scholar] [CrossRef]
- Nezamisavojbolaghi, M.; Davodian, E.; Bouich, A.; Tlemçani, M.; Mesbahi, O.; Janeiro, F.M. The Impact of Dust Deposition on PV Panels’ Efficiency and Mitigation Solutions: Review Article. Energies 2023, 16, 8022. [Google Scholar] [CrossRef]
- Klugmann-Radziemska, E. Degradation of electrical performance of a crystalline photovoltaic module due to dust deposition in northern Poland. Renew. Energy 2015, 78, 418–426. [Google Scholar] [CrossRef]
- Maghami, M.R.; Hizam, H.; Gomes, C.; Radzi, M.A.; Rezadad, M.I.; Hajighorbani, S. Power loss due to soiling on solar panel: A review. Renew. Sustain. Energy Rev. 2016, 59, 1307–1316. [Google Scholar] [CrossRef]
- Ghazi, S.; Ip, K. The effect of weather conditions on the efficiency of PV panels in the southeast of UK. Renew. Energy 2014, 69, 50–59. [Google Scholar] [CrossRef]
- Ilse, K.; Micheli, L.; Figgis, B.W.; Lange, K.; Daßler, D.; Hanifi, H.; Wolfertstetter, F.; Naumann, V.; Hagendorf, C.; Gottschalg, R.; et al. Techno-Economic Assessment of Soiling Losses and Mitigation Strategies for Solar Power Generation. Joule 2019, 3, 2303–2321. [Google Scholar] [CrossRef]
- Alkharusi, T.; Huang, G.; Markides, C.N. Characterisation of soiling on glass surfaces and their impact on optical and solar photovoltaic performance. Renew. Energy 2024, 220, 119422. [Google Scholar] [CrossRef]
- Sarver, T.; Al-Qaraghuli, A.; Kazmerski, L.L. A comprehensive review of the impact of dust on the use of solar energy: History, investigations, results, literature, and mitigation approaches. Renew. Sustain. Energy Rev. 2013, 22, 698–733. [Google Scholar] [CrossRef]
- Appels, R.; Muthirayan, B.; Beerten, A.; Paesen, R.; Driesen, J.; Poortmans, J. The effect of dust deposition on photovoltaic modules. In Proceedings of the 2012 38th IEEE Photovoltaic Specialists Conference, Austin, TX, USA, 3–8 June 2012; pp. 1886–1889. [Google Scholar] [CrossRef]
- Zahedi, R.; Ranjbaran, P.; Gharehpetian, G.B.; Mohammadi, F.; Ahmadiahangar, R. Cleaning of Floating Photovoltaic Systems: A Critical Review on Approaches from Technical and Economic Perspectives. Energies 2021, 14, 2018. [Google Scholar] [CrossRef]
- Brahma, H.; Pant, S.; Micheli, L.; Smestad, G.P.; Sarmah, N. Effect of Environmental Factors on Photovoltaic Soiling: Experimental and Statistical Analysis. Energies 2023, 16, 45. [Google Scholar] [CrossRef]
- Javed, W.; Guo, B.; Figgis, B.; Martin Pomares, L.; Aïssa, B. Multi-year field assessment of seasonal variability of photovoltaic soiling and environmental factors in a desert environment. Sol. Energy 2020, 211, 1392–1402. [Google Scholar] [CrossRef]
- Del Pero, C.; Aste, N.; Leonforte, F. The effect of rain on photovoltaic systems. Renew. Energy 2021, 179, 1803–1814. [Google Scholar] [CrossRef]
- Picotti, G.; Borghesani, P.; Cholette, M.; Manzolini, G. Soiling of solar collectors—Modelling approaches for airborne dust and its interactions with surfaces. Renew. Sustain. Energy Rev. 2018, 81, 2343–2357. [Google Scholar] [CrossRef]
- Amer Dahham, I.; Mohd Zainuri, M.A.A.; Abdullah, A.A.; Fauzan, M.F. Modeling the Effect of Dust and Wind Speed on Solar Panel Performance in Iraq. Energies 2023, 16, 6397. [Google Scholar] [CrossRef]
- Goossens, D.; Van Kerschaever, E. Aeolian dust deposition on photovoltaic solar cells: The effects of wind velocity and airborne dust concentration on cell performance. Sol. Energy 1999, 66, 277–289. [Google Scholar] [CrossRef]
- Jiang, Y.; Lu, L.; Ferro, A.R.; Ahmadi, G. Analyzing wind cleaning process on the accumulated dust on solar photovoltaic (PV) modules on flat surfaces. Sol. Energy 2018, 159, 1031–1036. [Google Scholar] [CrossRef]
- Mani, M.; Pillai, R. Impact of dust on solar photovoltaic (PV) performance: Research status, challenges and recommendations. Renew. Sustain. Energy Rev. 2010, 14, 3124–3131. [Google Scholar] [CrossRef]
- Said, S.A.; Walwil, H.M. Fundamental studies on dust fouling effects on PV module performance. Sol. Energy 2014, 107, 328–337. [Google Scholar] [CrossRef]
- Figgis, B.; Ennaoui, A.; Ahzi, S.; Rémond, Y. Review of PV soiling particle mechanics in desert environments. Renew. Sustain. Energy Rev. 2017, 76, 872–881. [Google Scholar] [CrossRef]
- Ramirez-Vergara, J.; Bosman, L.B.; Wollega, E.; Leon-Salas, W.D. Review of forecasting methods to support photovoltaic predictive maintenance. Clean. Eng. Technol. 2022, 8, 100460. [Google Scholar] [CrossRef]
- Araujo Costa Silva, L.; Baca Ruiz, L.G.; Criado-Ramón, D.; Gabriel Bessa, J.; Micheli, L.; del Carmen Pegalajar Jiménez, M. Assessing the impact of soiling on photovoltaic efficiency using supervised learning techniques. Expert Syst. Appl. 2023, 231, 120816. [Google Scholar] [CrossRef]
- Bosman, L.B.; Leon-Salas, W.D.; Hutzel, W.; Soto, E.A. PV System Predictive Maintenance: Challenges, Current Approaches, and Opportunities. Energies 2020, 13, 1398. [Google Scholar] [CrossRef]
- Bessa, J.G.; Micheli, L.; Almonacid, F.; Fernández, E.F. Monitoring photovoltaic soiling: Assessment, challenges, and perspectives of current and potential strategies. iScience 2021, 24, 102165. [Google Scholar] [CrossRef] [PubMed]
- Duffie, J.A.; Beckman, W.A.; Blair, N. Design of Photovoltaic Systems. In Solar Engineering of Thermal Processes, Photovoltaics and Wind; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Dobos, A.P. An Improved Coefficient Calculator for the California Energy Commission 6 Parameter Photovoltaic Module Model. J. Sol. Energy Eng. 2012, 134, 021011. [Google Scholar] [CrossRef]
- Andrews, R.W.; Stein, J.S.; Hansen, C.; Riley, D. Introduction to the open source PV LIB for python Photovoltaic system modelling package. In Proceedings of the 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC), Denver, CO, USA, 8–13 June 2014; pp. 170–174. [Google Scholar] [CrossRef]
- Anderson, K.S.; Hansen, C.W.; Holmgren, W.F.; Jensen, A.R.; Mikofski, M.A.; Driesse, A. pvlib python: 2023 project update. J. Open Source Softw. 2023, 8, 5994. [Google Scholar] [CrossRef]
- NASA Prediction of Worldwide Energy Resources (POWER). Available online: https://power.larc.nasa.gov (accessed on 1 April 2024).
- CAMS Solar Radiation Time-Series. Copernicus Atmosphere Monitoring Service (CAMS) Atmosphere Data Store (ADS). Available online: https://ads.atmosphere.copernicus.eu/cdsapp#!/dataset/cams-solar-radiation-timeseries?tab=overview (accessed on 5 April 2024).
- Qu, Z.; Oumbe, A.; Blanc, P.; Espinar, B.; Gesell, G.; Gschwind, B.; Klüser, L.; Lefèvre, M.; Saboret, L.; Schroedter-Homscheidt, M.; et al. Fast radiative transfer parameterisation for assessing the surface solar irradiance: The Heliosat-4 method. Meteorol. Z. 2017, 26, 33–57. [Google Scholar] [CrossRef]
- Schroedter-Homscheidt, M.; Azam, F.; Betcke, J.; Hanrieder, N.; Lefèvre, M.; Saboret, L.; Saint-Drenan, Y.M. Surface solar irradiation retrieval from MSG/SEVIRI based on APOLLO Next Generation and HELIOSAT-4 methods. Meteorol. Z. 2022, 31, 455–476. [Google Scholar] [CrossRef]
- Gschwind, B.; Wald, L.; Blanc, P.; Lefèvre, M.; Schroedter?Homscheidt, M.; Arola, A. Improving the McClear model estimating the downwelling solar radiation at ground level in cloud?free conditions—McClear-v3. Meteorol. Z. 2019, 28, 147–163. [Google Scholar] [CrossRef]
- Lefèvre, M.; Oumbe, A.; Blanc, P.; Espinar, B.; Gschwind, B.; Qu, Z.; Wald, L.; Schroedter-Homscheidt, M.; Hoyer-Klick, C.; Arola, A.; et al. McClear: A new model estimating downwelling solar radiation at ground level in clear-sky conditions. Atmos. Meas. Tech. 2013, 6, 2403–2418. [Google Scholar] [CrossRef]
- Erbs, D.; Klein, S.; Duffie, J. Estimation of the diffuse radiation fraction for hourly, daily and monthly-average global radiation. Sol. Energy 1982, 28, 293–302. [Google Scholar] [CrossRef]
- Kasten, F.; Young, A.T. Revised optical air mass tables and approximation formula. Appl. Optics 1989, 28, 4735–4738. [Google Scholar] [CrossRef]
- Osterwald, C.R.; Adelstein, J.; del Cueto, J.A.; Sekulic, W.; Trudell, D.; McNutt, P.; Hansen, R.; Rummel, S.; Anderberg, A.; Moriarty, T. Resistive loading of photovoltaic modules and arrays for long-term exposure testing. Prog. Photovolt. Res. Appl. 2006, 14, 567–575. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- The Pandas Development Team. Pandas-Dev/Pandas: Pandas. 2023. Available online: https://zenodo.org/records/10957263 (accessed on 1 April 2024).
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 56–61. [Google Scholar] [CrossRef]
- McKinney, W. Python for Data Analysis: Data Wrangling with Pandas, NumPy, and Jupyter; O’Reilly: Sebastopol, CA, USA, 2022. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Waskom, M.L. seaborn: Statistical data visualization. J. Open Source Softw. 2021, 6, 3021. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. Basis Expansions and Regularization. In The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; pp. 139–189. [Google Scholar] [CrossRef]
- Seabold, S.; Perktold, J. statsmodels: Econometric and statistical modeling with Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 92–96. [Google Scholar] [CrossRef]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition procedure based on Loess. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Greenacre, M.; Groenen, P.J.F.; Hastie, T.; D’Enza, A.I.; Markos, A.; Tuzhilina, E. Principal component analysis. Nat. Rev. Methods Prim. 2022, 2, 100. [Google Scholar] [CrossRef]
- Faizi, N.; Alvi, Y. Chapter 6—Correlation. In Biostatistics Manual for Health Research; Faizi, N., Alvi, Y., Eds.; Academic Press: Cambridge, MA, USA, 2023; pp. 109–126. [Google Scholar] [CrossRef]
- Orioli, A.; Di Gangi, A. A Criterion for Rating the Usability and Accuracy of the One-Diode Models for Photovoltaic Modules. Energies 2016, 9, 427. [Google Scholar] [CrossRef]
- Mihaylov, B.; Betts, T.R.; Pozza, A.; Müllejans, H.; Gottschalg, R. Uncertainty Estimation of Temperature Coefficient Measurements of PV Modules. IEEE J. Photovolt. 2016, 6, 1554–1563. [Google Scholar] [CrossRef]
- Feuermann, D.; Zemel, A. Dust-induced degradation of pyranometer sensitivity. Sol. Energy 1993, 50, 483–486. [Google Scholar] [CrossRef]
- Geuder, N.; Quaschning, V. Soiling of irradiation sensors and methods for soiling correction. Sol. Energy 2006, 80, 1402–1409. [Google Scholar] [CrossRef]
- Ghosh, A. Soiling Losses: A Barrier for India’s Energy Security Dependency from Photovoltaic Power. Challenges 2020, 11, 9. [Google Scholar] [CrossRef]
- Cleveland, W.S. Robust Locally Weighted Regression and Smoothing Scatterplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
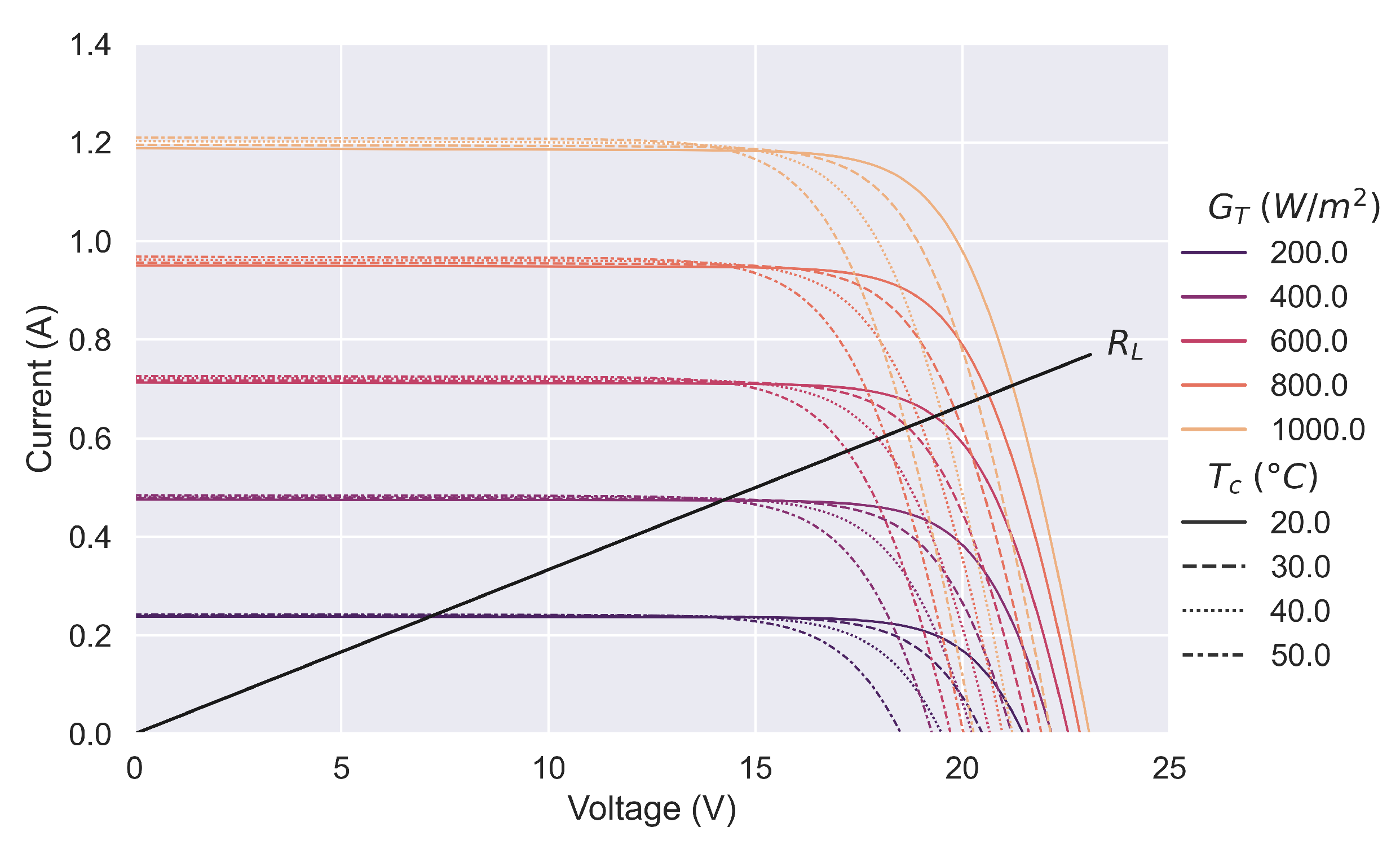


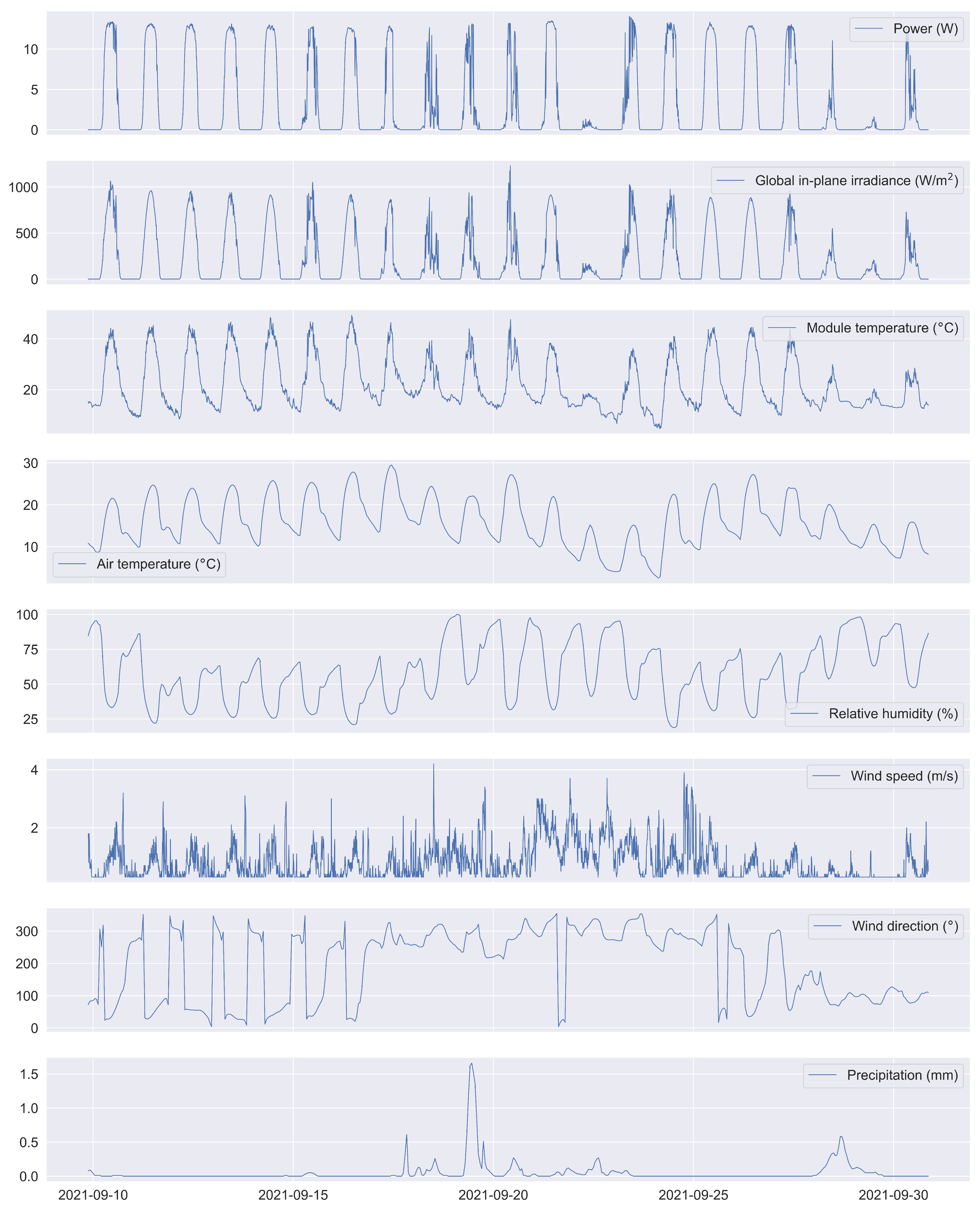
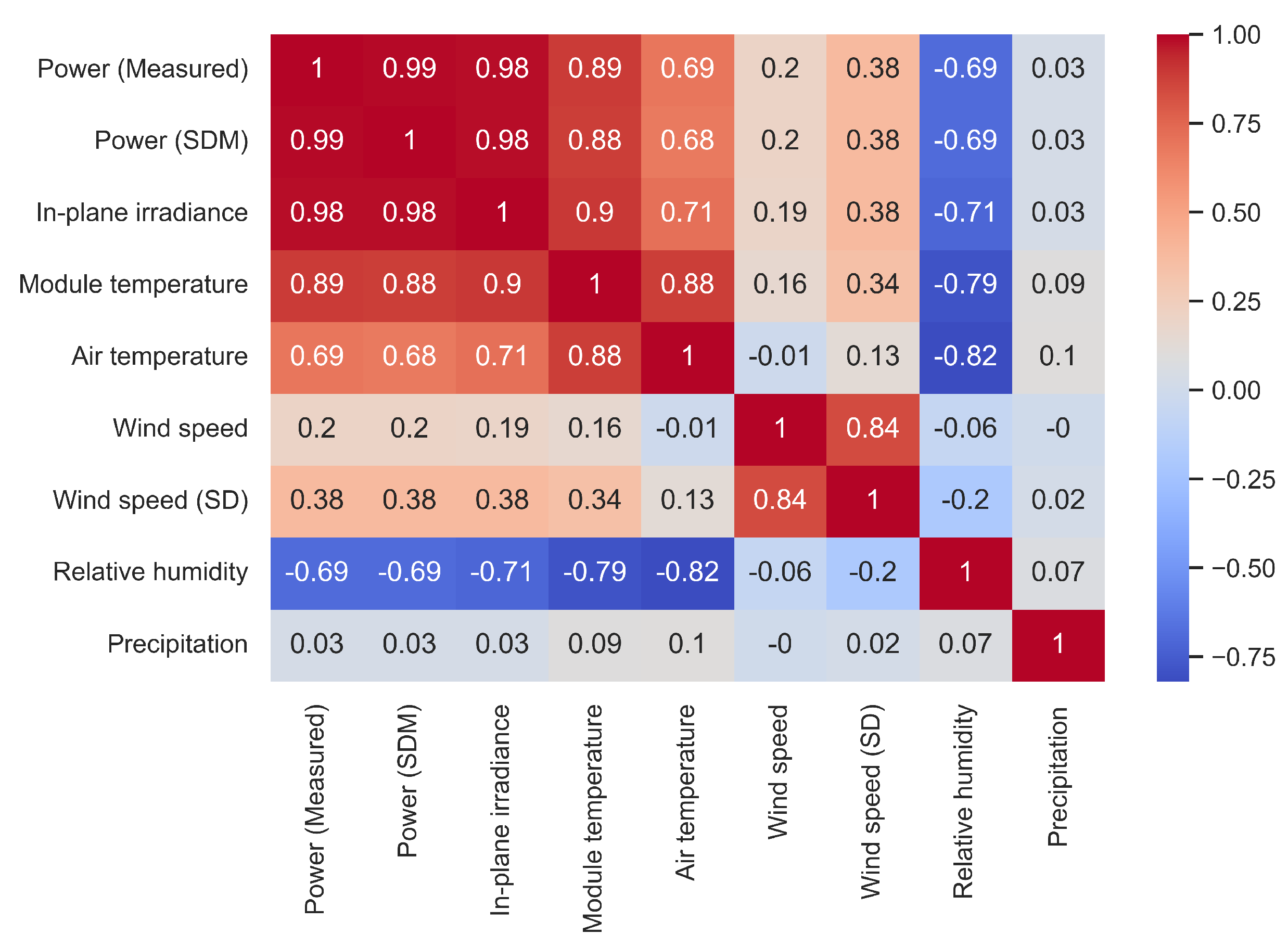
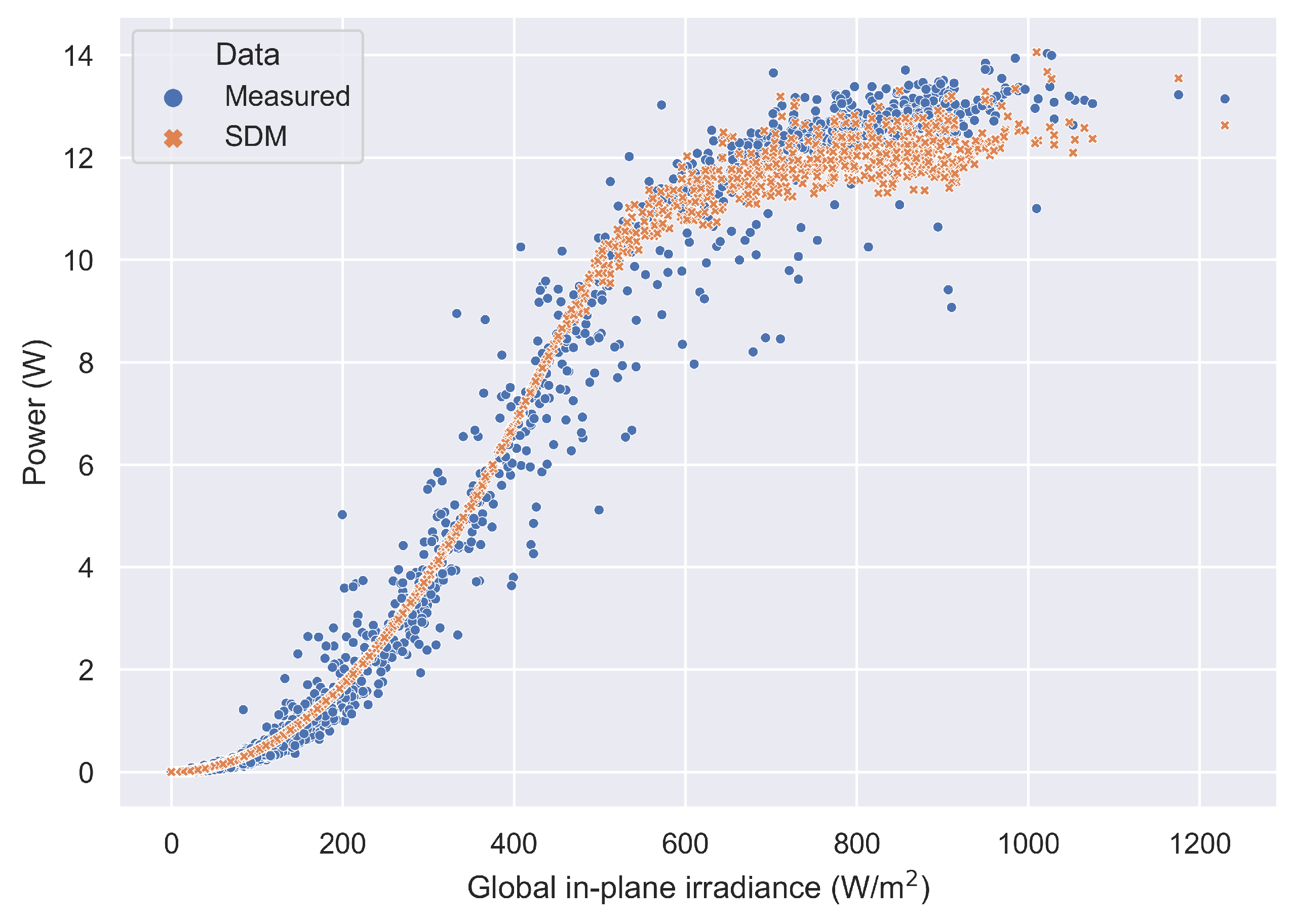

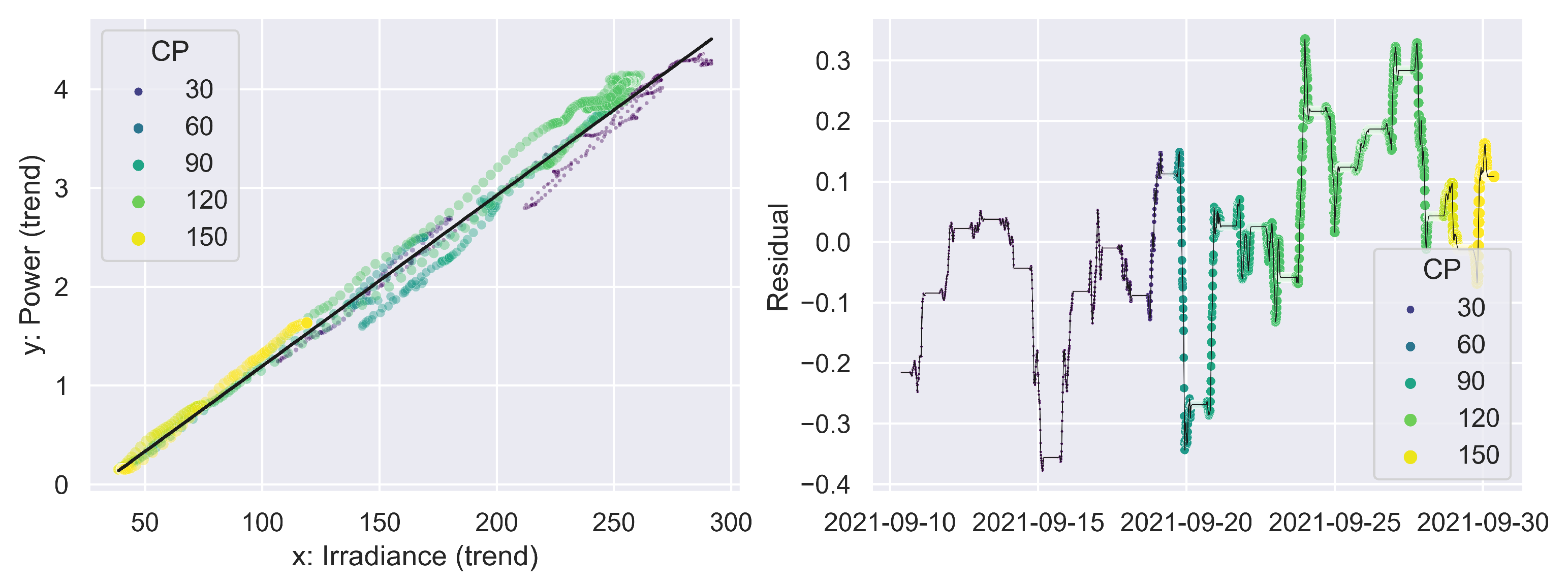
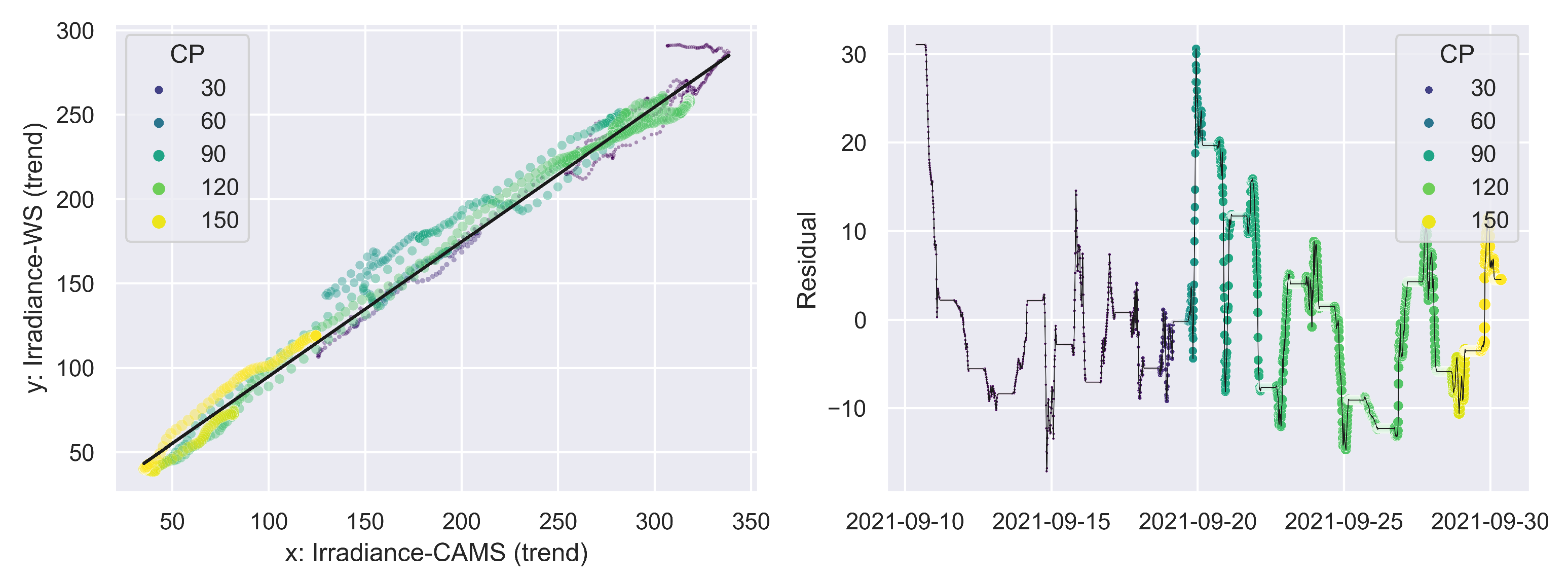

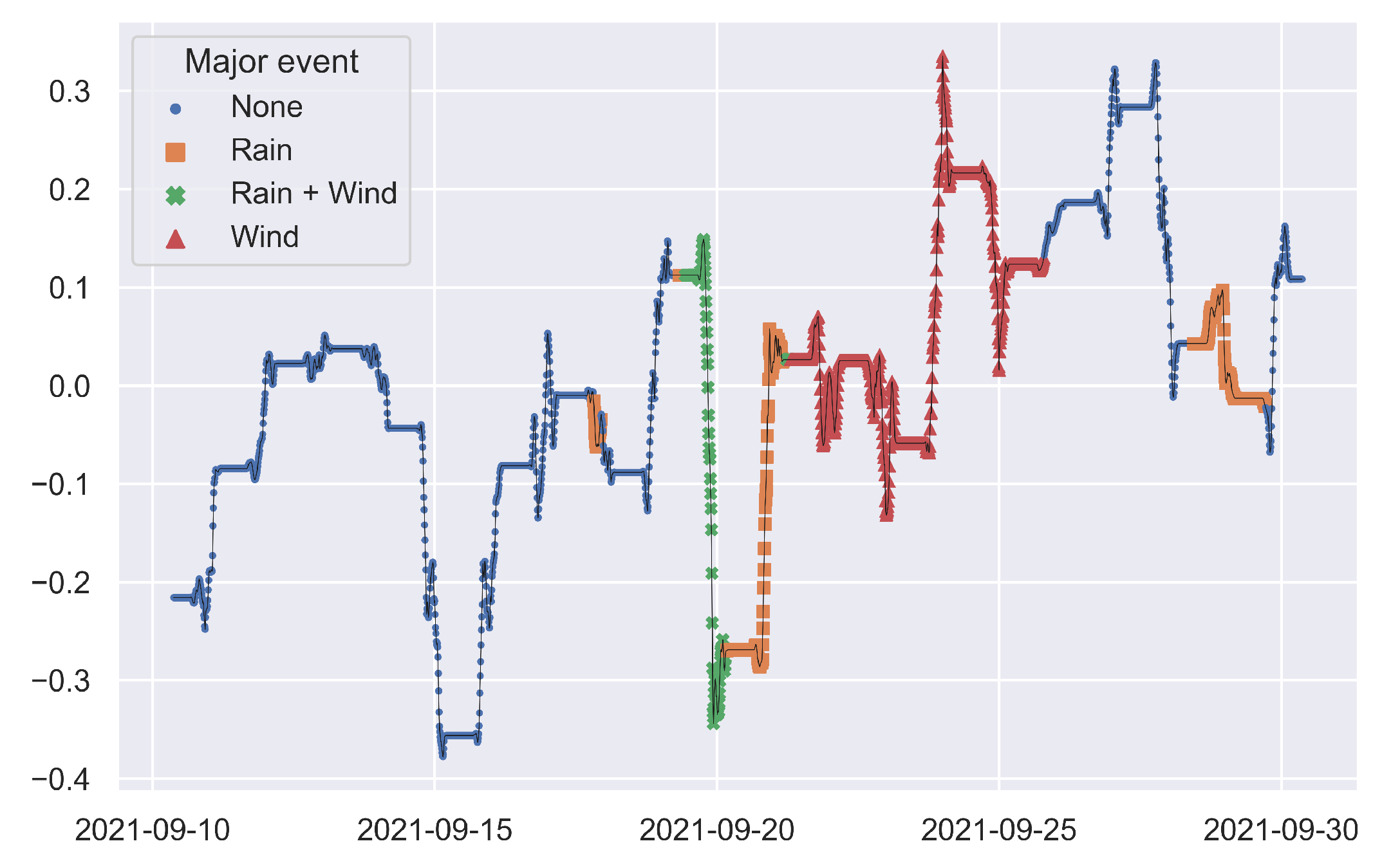
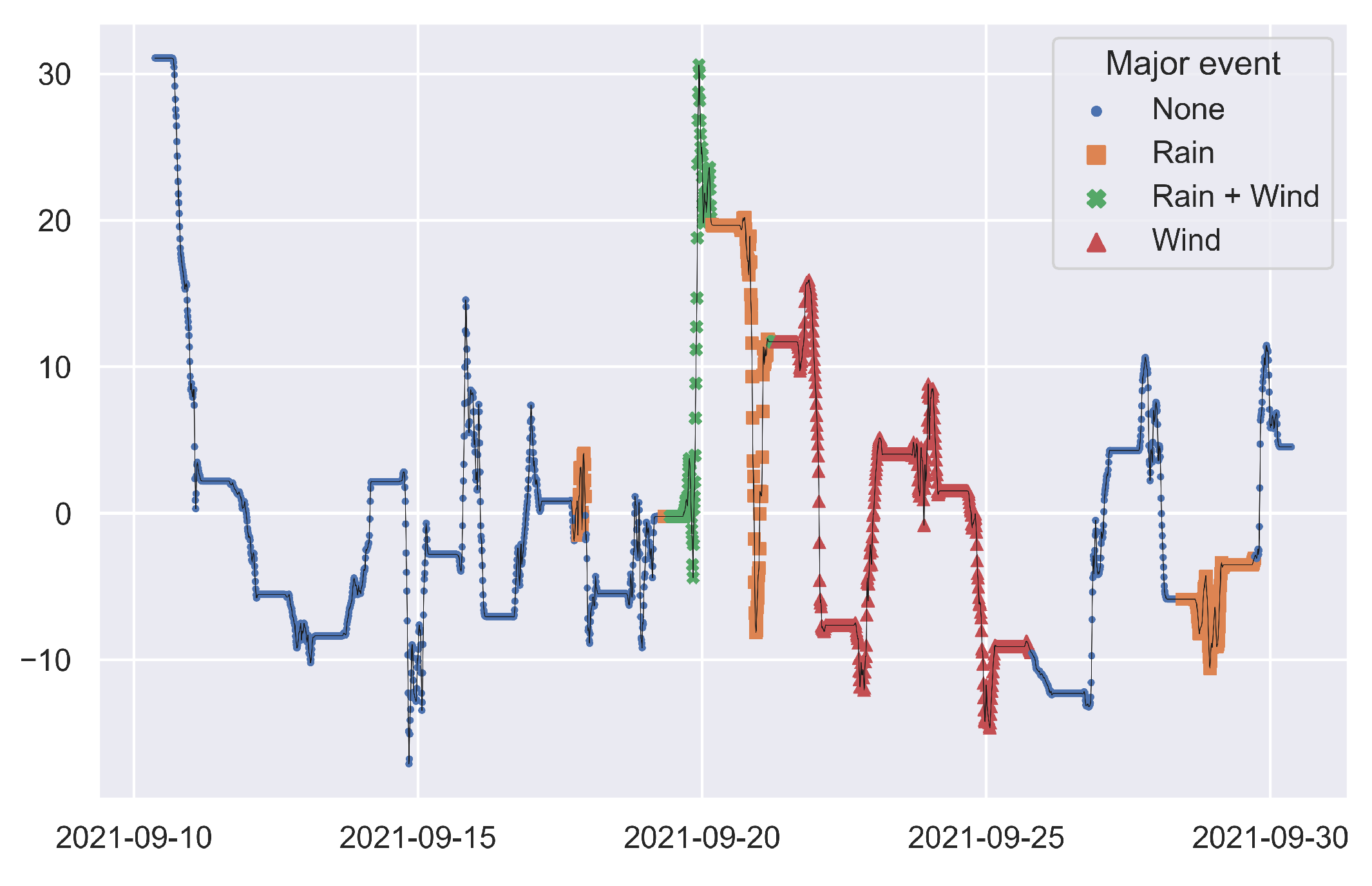

| Coefficient | Value | Uncertainty |
|---|---|---|
| Temperature coeffcient of short-circuit current, | 0.065 %/K | %/K |
| Temperature coeffcient of open-circuit voltage, | −0.40 %/K | %/K |
| Temperature coeffcient of maximum power, | −0.5 %/K | %/K |
| Intercept | Slope | R2 | |
|---|---|---|---|
| Model A | −0.53005 | 0.01727 | 0.987 |
| Model B | 15.30717 | 0.79717 | 0.985 |
| Model C | −0.28131 | 0.01384 | 0.982 |
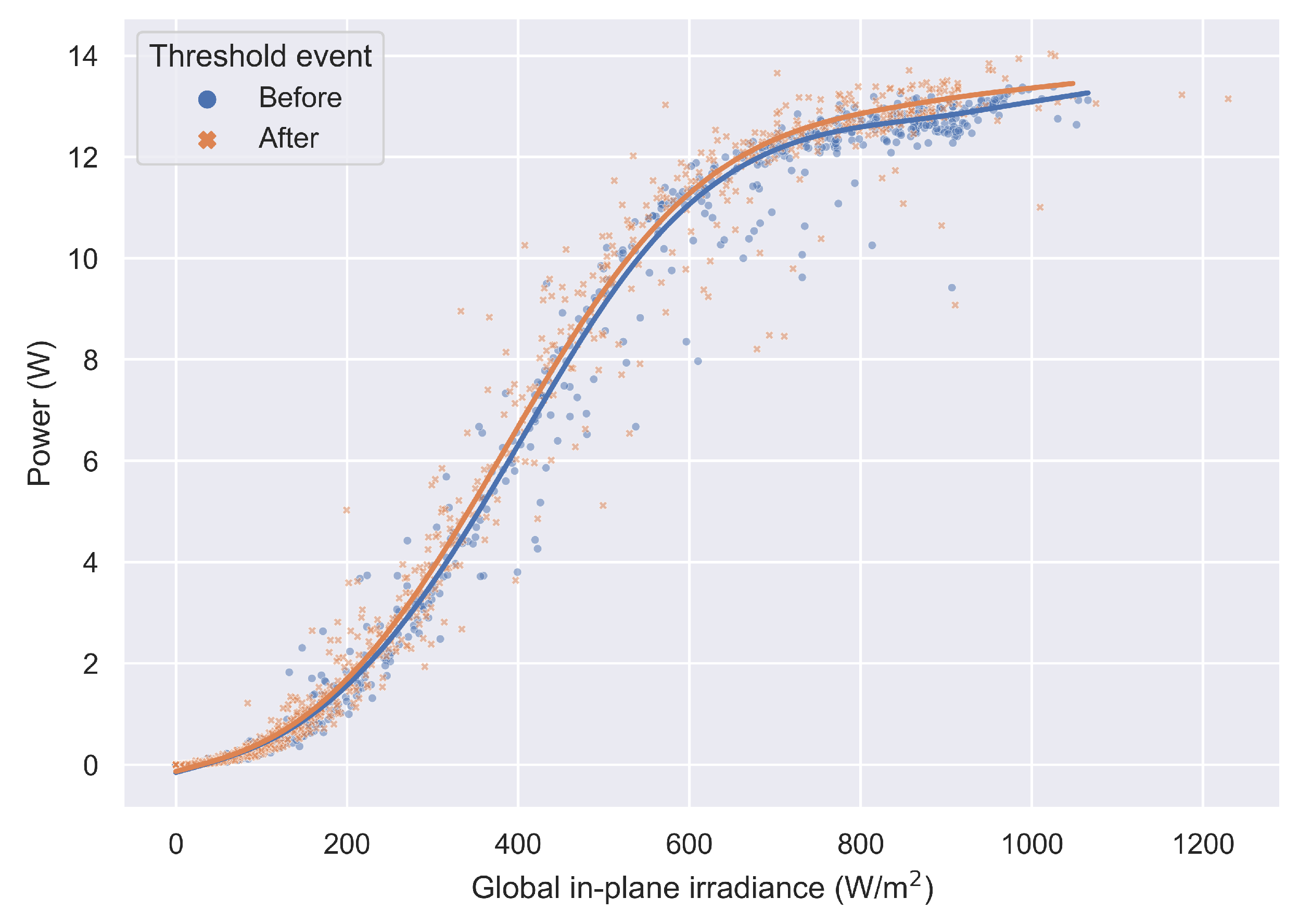
| GHI Data | Threshold Event | Intercept | Slope | R2 |
|---|---|---|---|---|
| On-site measurements | Before | −0.49129 | 0.01423 | 0.972 |
| After | −0.30546 | 0.01433 | 0.990 | |
| CAMS | Before | −0.63597 | 0.01736 | 0.985 |
| After | −0.57407 | 0.01789 | 0.991 |
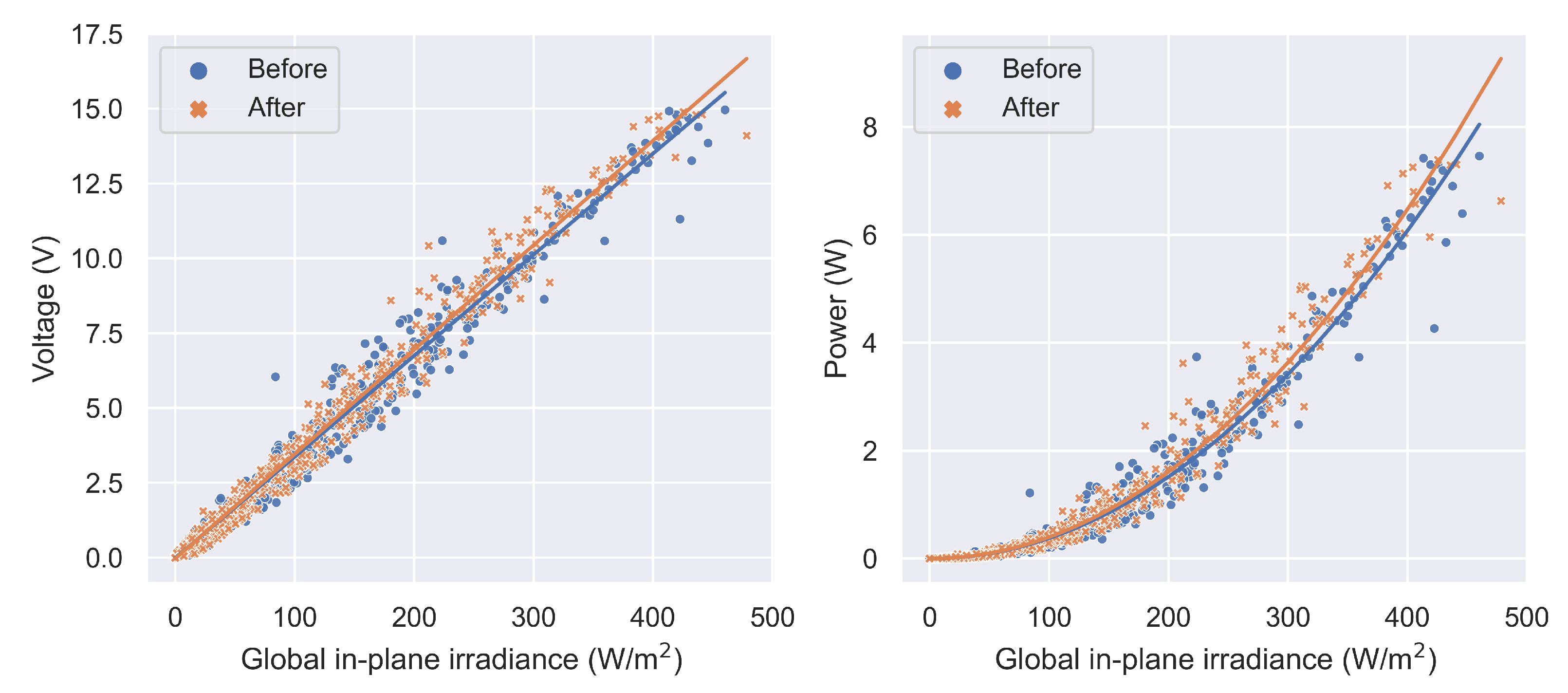
| Threshold Event | Intercept | Slope | R2 |
|---|---|---|---|
| Before | −0.01221 | 0.03378 | 0.987 |
| After | −0.03322 | 0.03492 | 0.988 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stankov, B.; Terziev, A.; Vassilev, M.; Ivanov, M. Influence of Wind and Rainfall on the Performance of a Photovoltaic Module in a Dusty Environment. Energies 2024, 17, 3394. https://doi.org/10.3390/en17143394
Stankov B, Terziev A, Vassilev M, Ivanov M. Influence of Wind and Rainfall on the Performance of a Photovoltaic Module in a Dusty Environment. Energies. 2024; 17(14):3394. https://doi.org/10.3390/en17143394
Chicago/Turabian StyleStankov, Borislav, Angel Terziev, Momchil Vassilev, and Martin Ivanov. 2024. "Influence of Wind and Rainfall on the Performance of a Photovoltaic Module in a Dusty Environment" Energies 17, no. 14: 3394. https://doi.org/10.3390/en17143394
APA StyleStankov, B., Terziev, A., Vassilev, M., & Ivanov, M. (2024). Influence of Wind and Rainfall on the Performance of a Photovoltaic Module in a Dusty Environment. Energies, 17(14), 3394. https://doi.org/10.3390/en17143394









