The Evolution of Flow Structures and Coolant Coverage in Double-Row Film Cooling with Upstream Forward Jets and Downstream Backward Jets
Abstract
1. Introduction
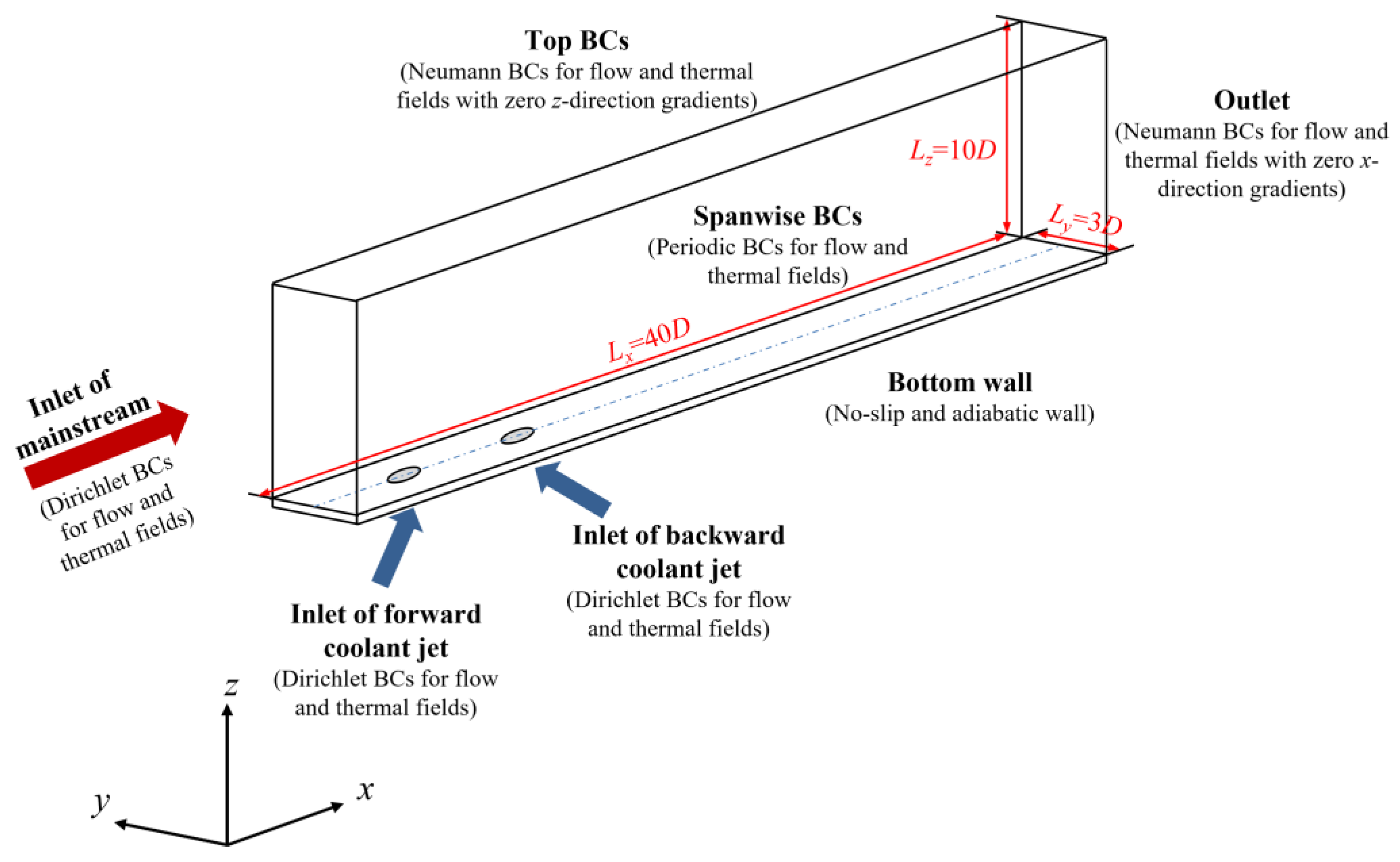
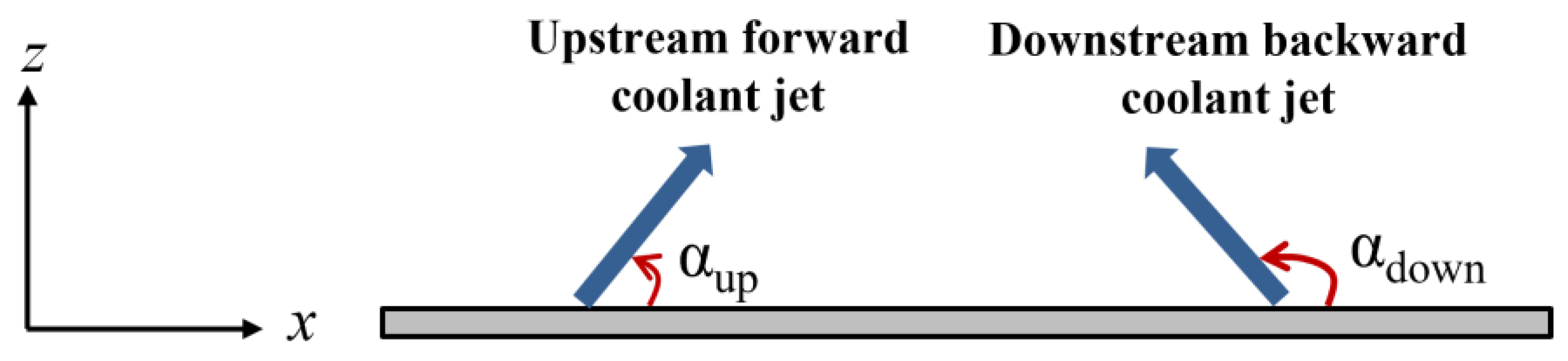
2. Computational Domain and Boundary Conditions
3. Governing Equations and Turbulence Model
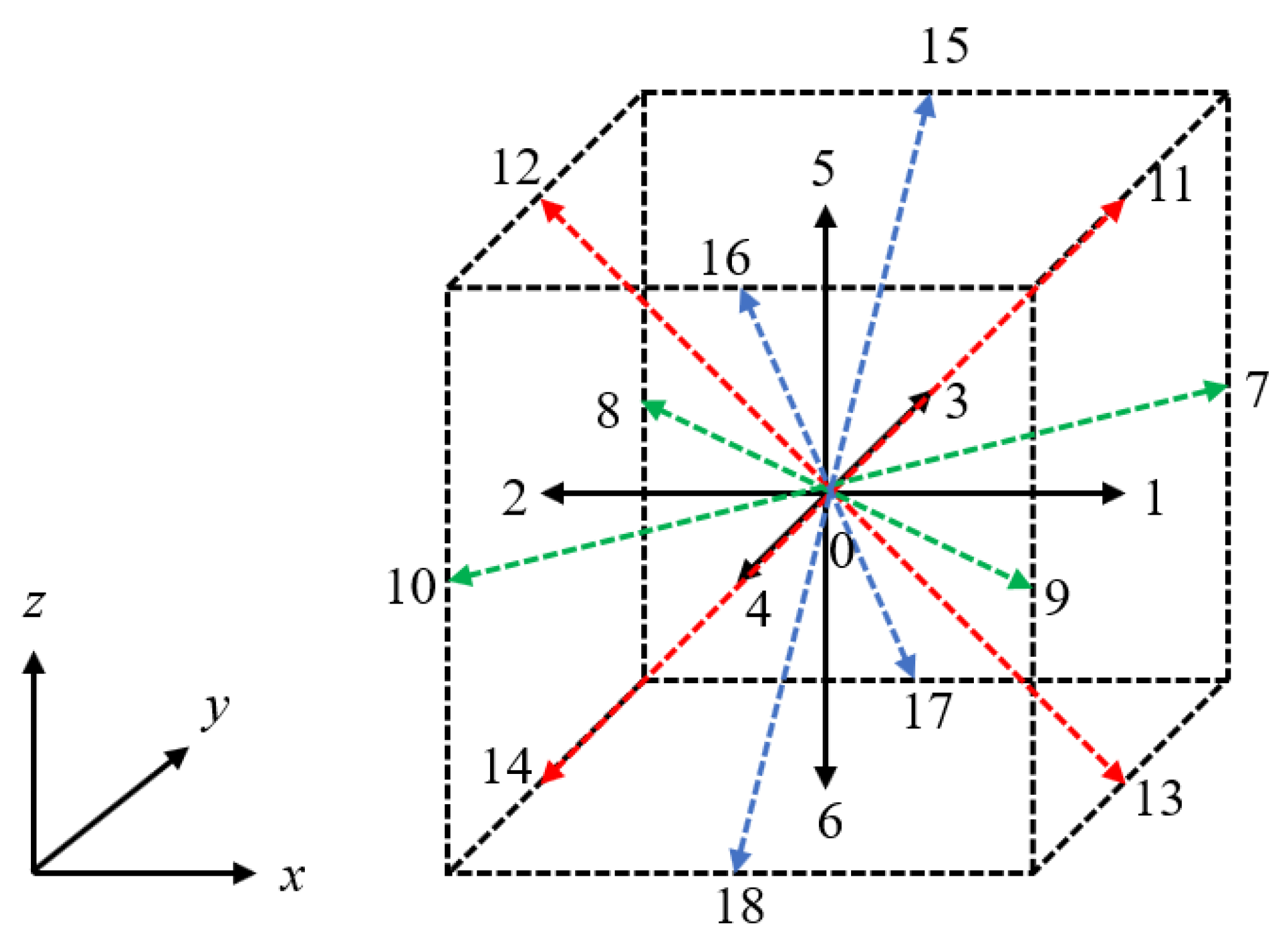
3.1. Simplified Thermal Lattice Boltzmann Method
3.2. Smagorinsky Subgrid-Scale Stress Model
3.3. Numerical Validation and Grid-Sensitivity Study
4. Results and Discussion
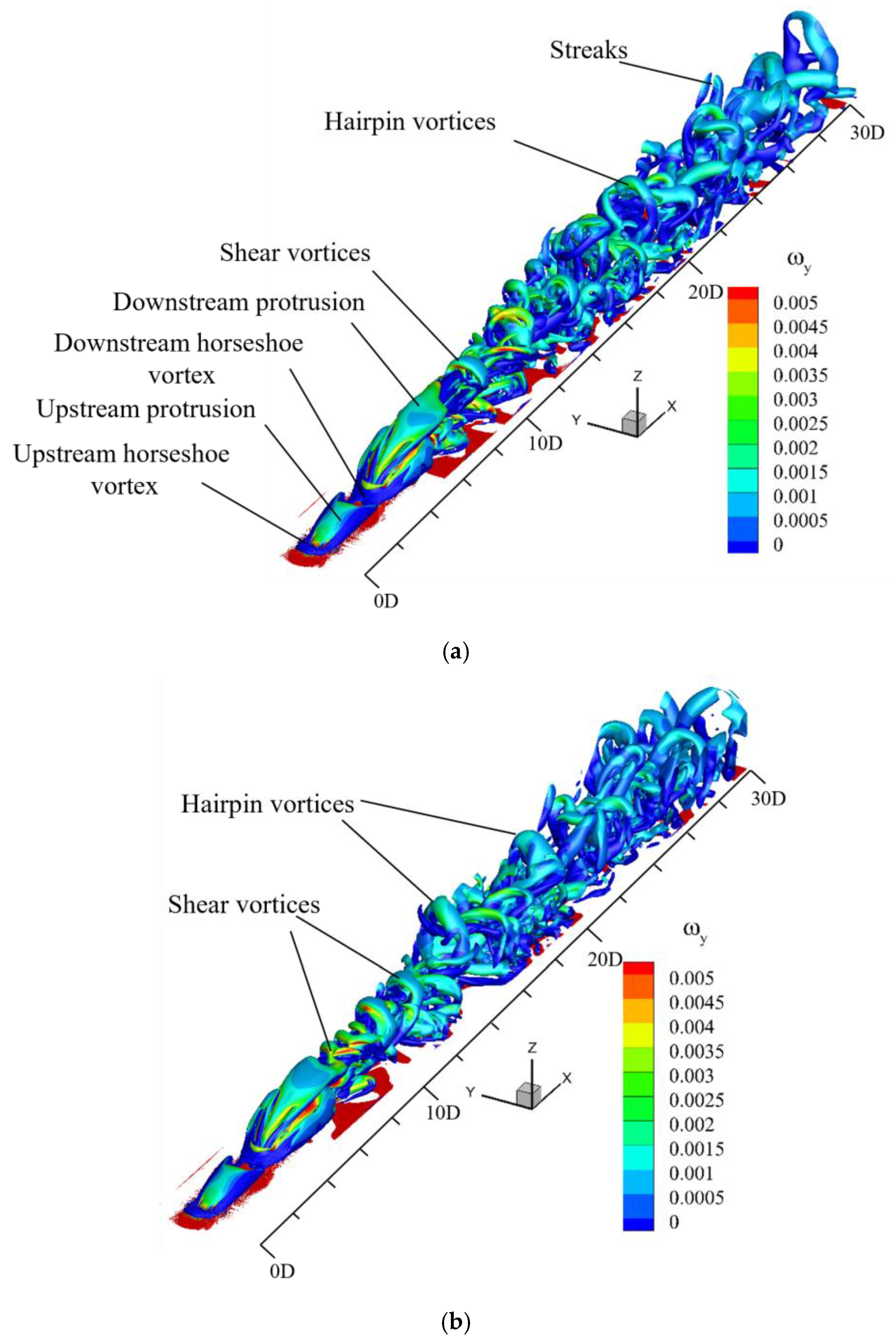
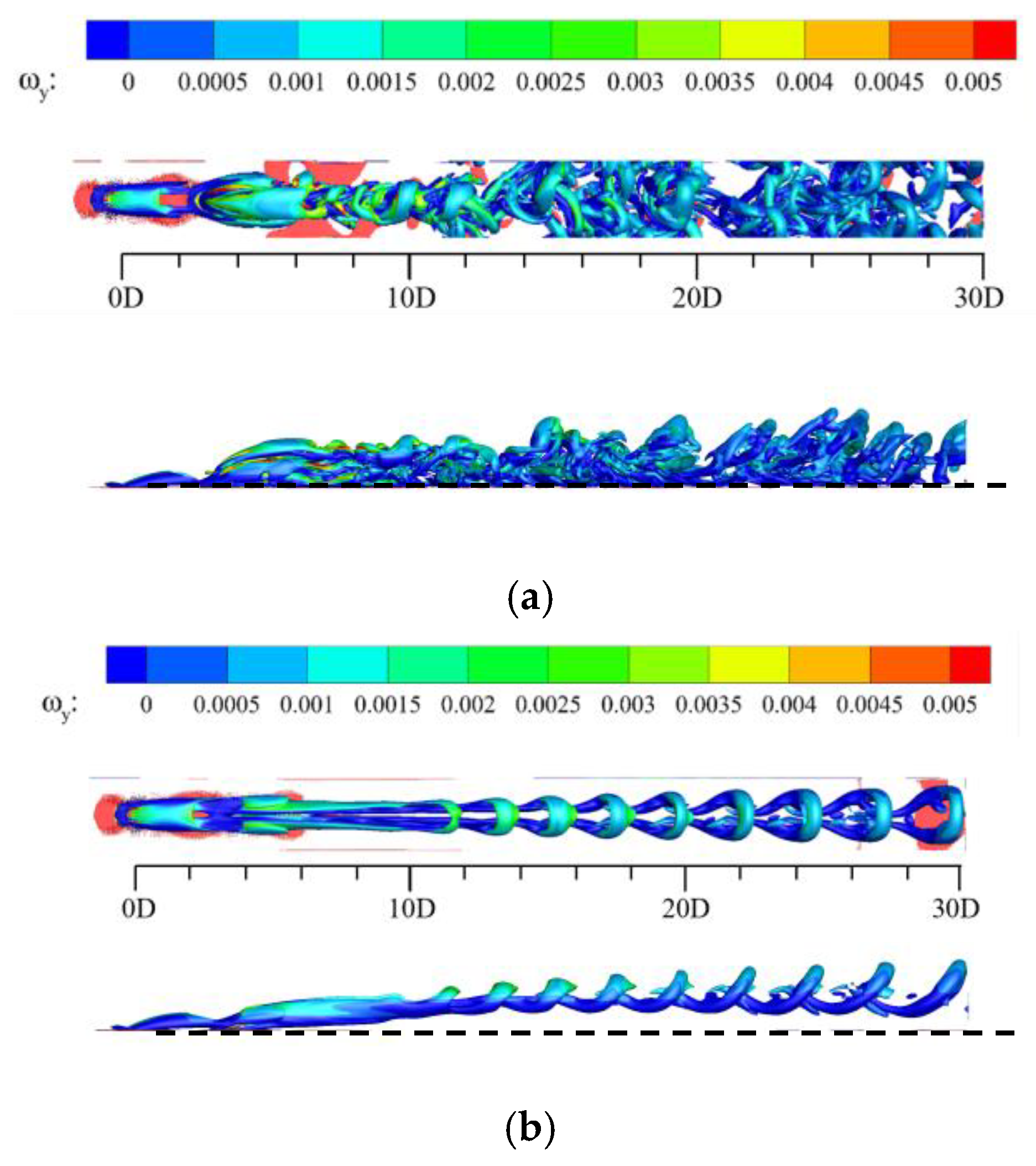
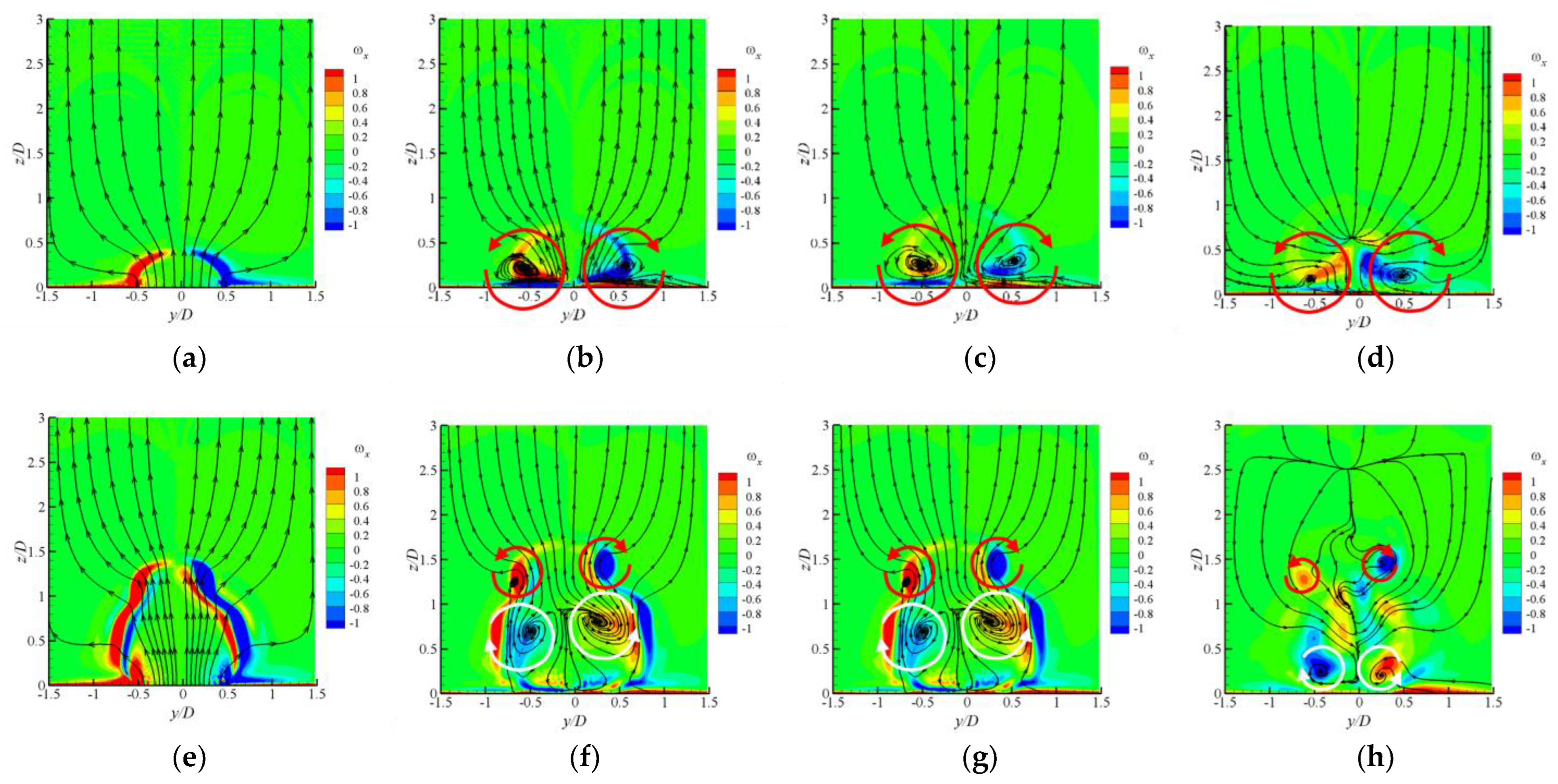
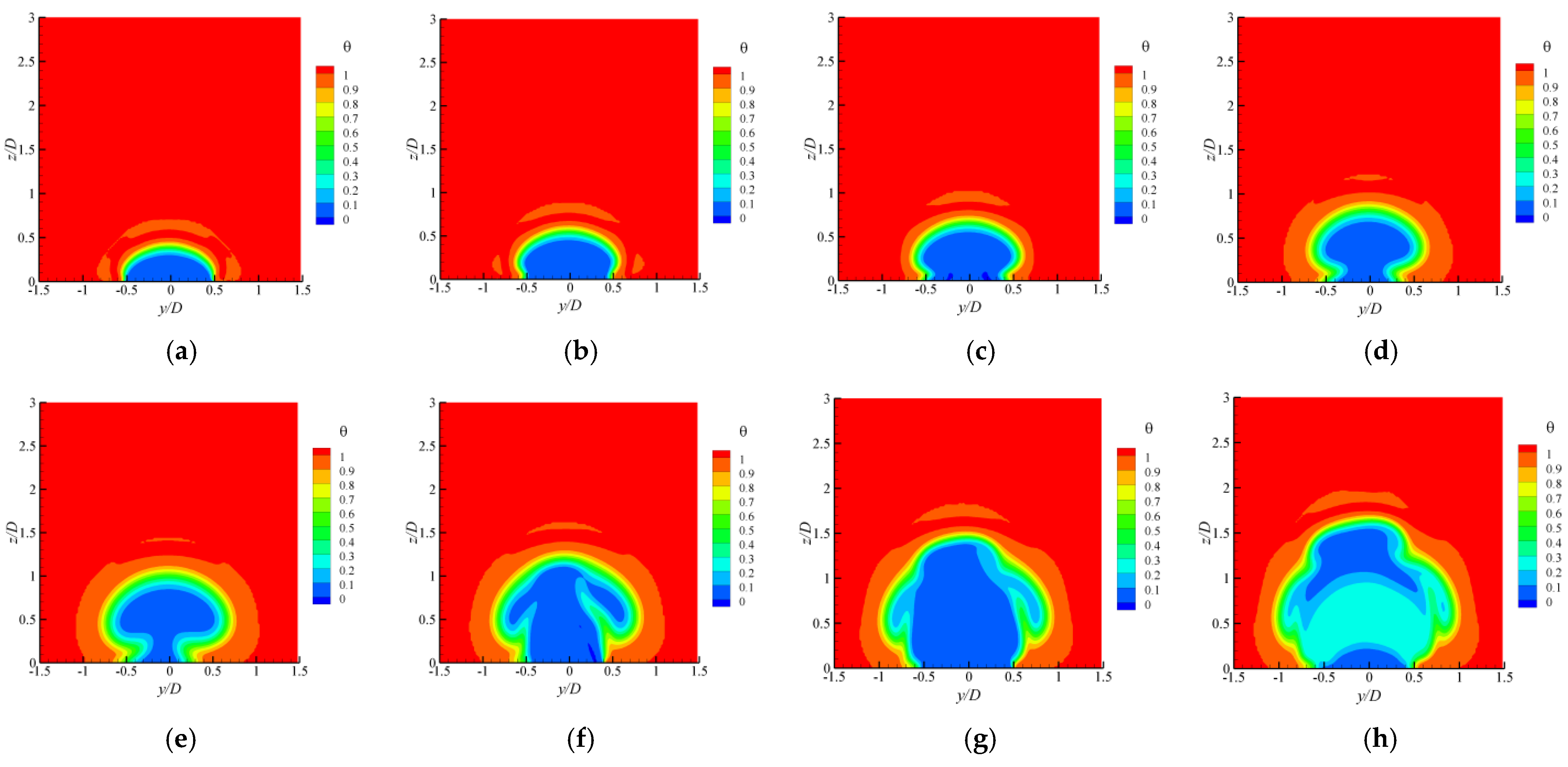
4.1. The Evolutions of Flow Structures
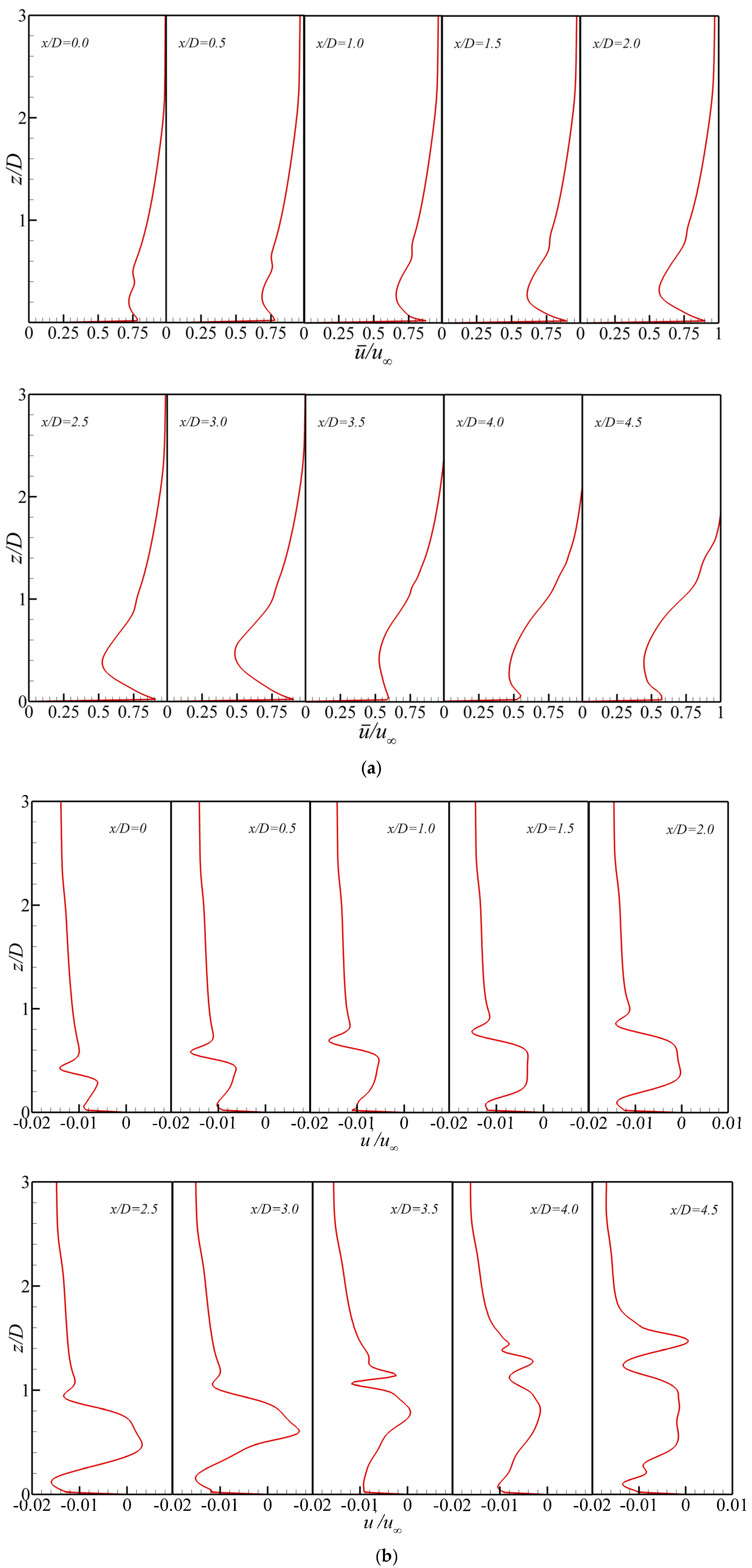
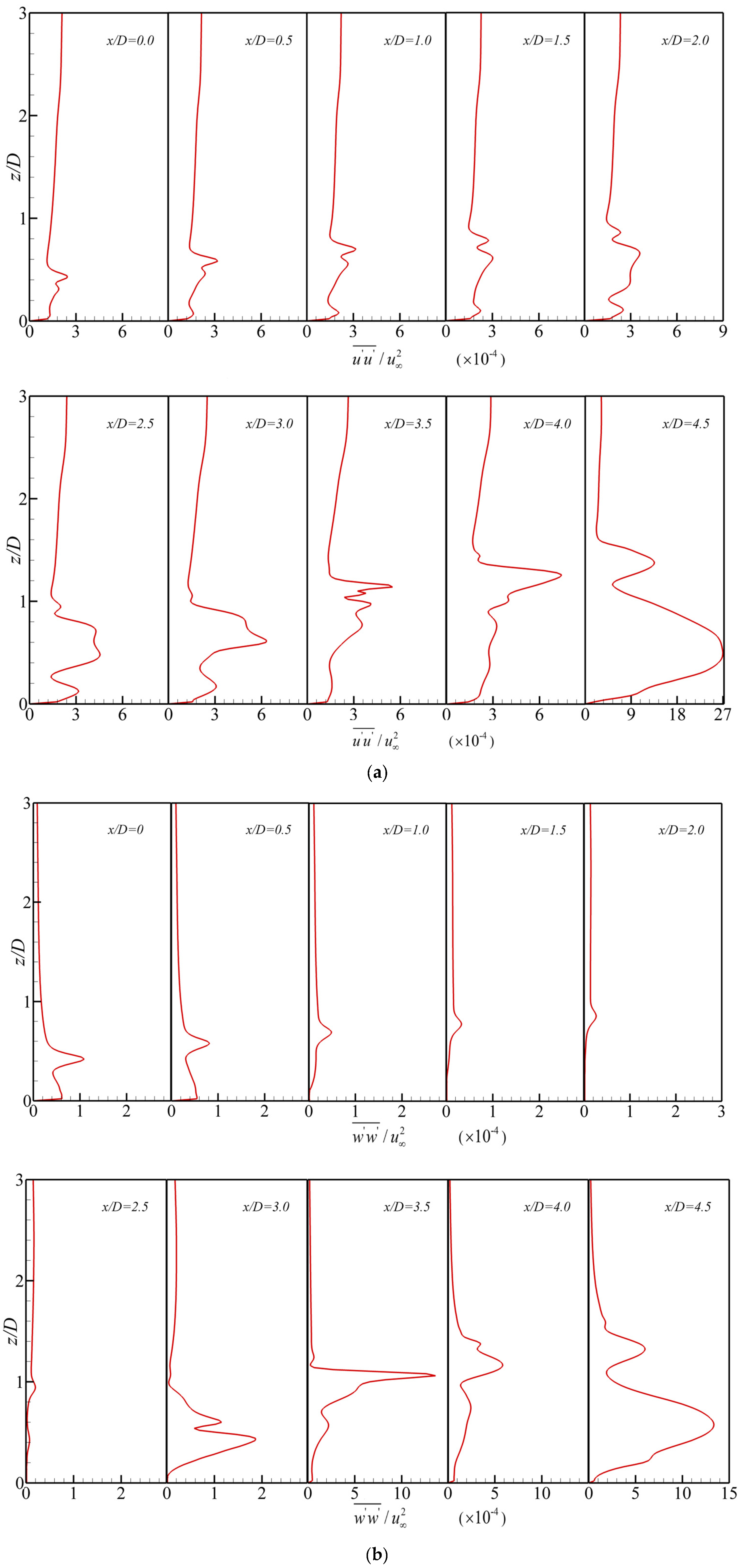
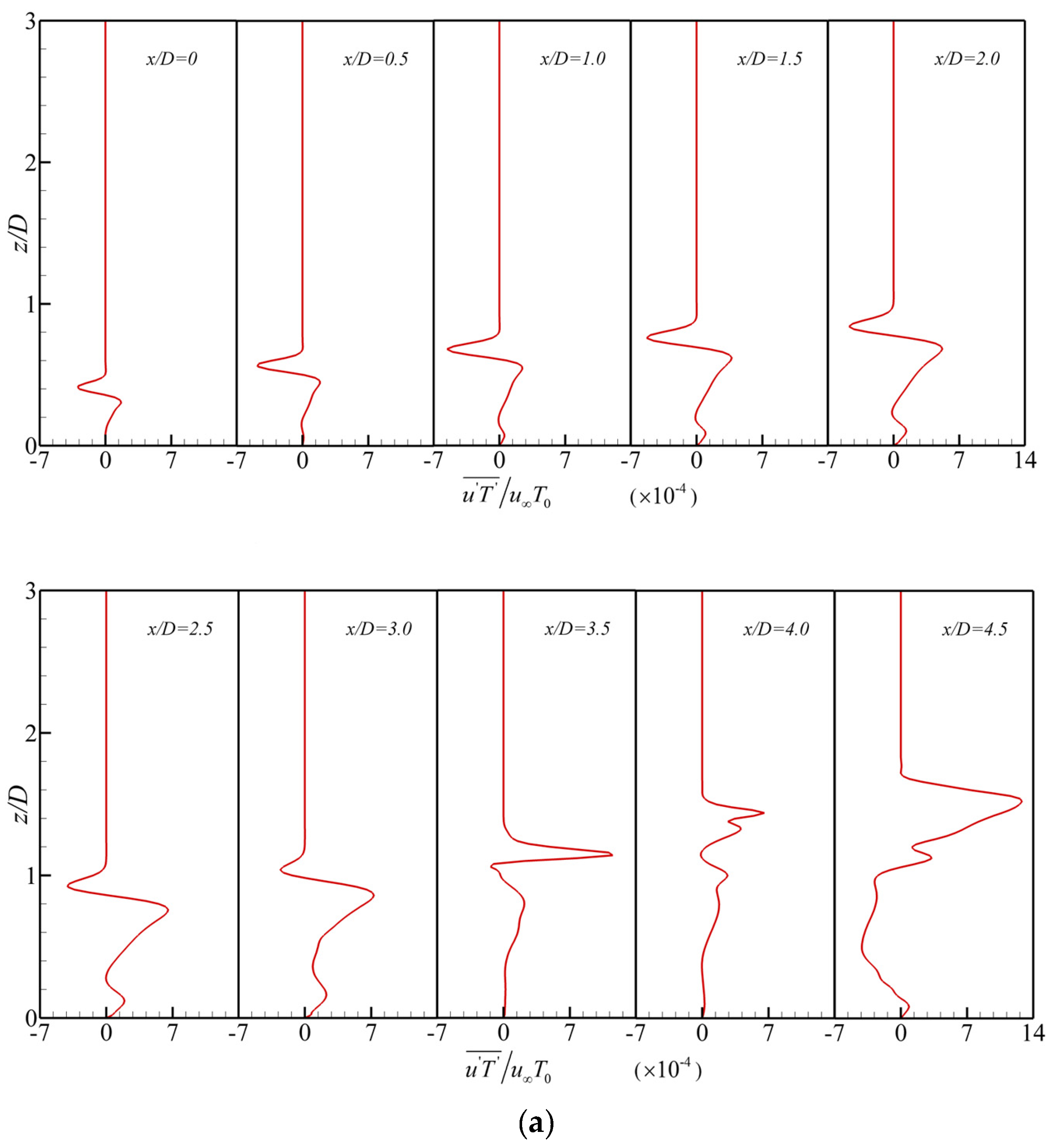
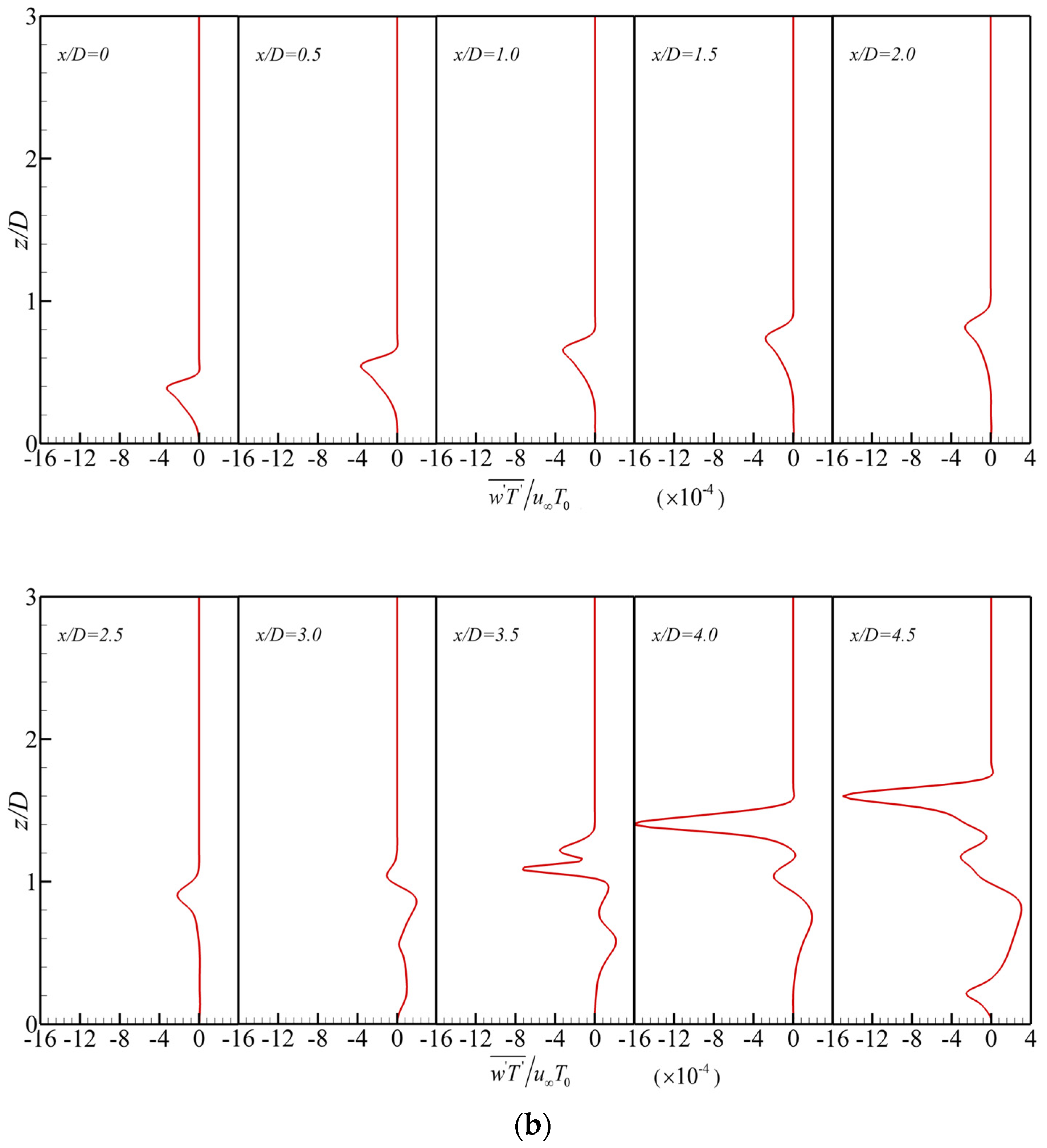
4.2. Momentum and Heat Flux Transport in the Region between Rows
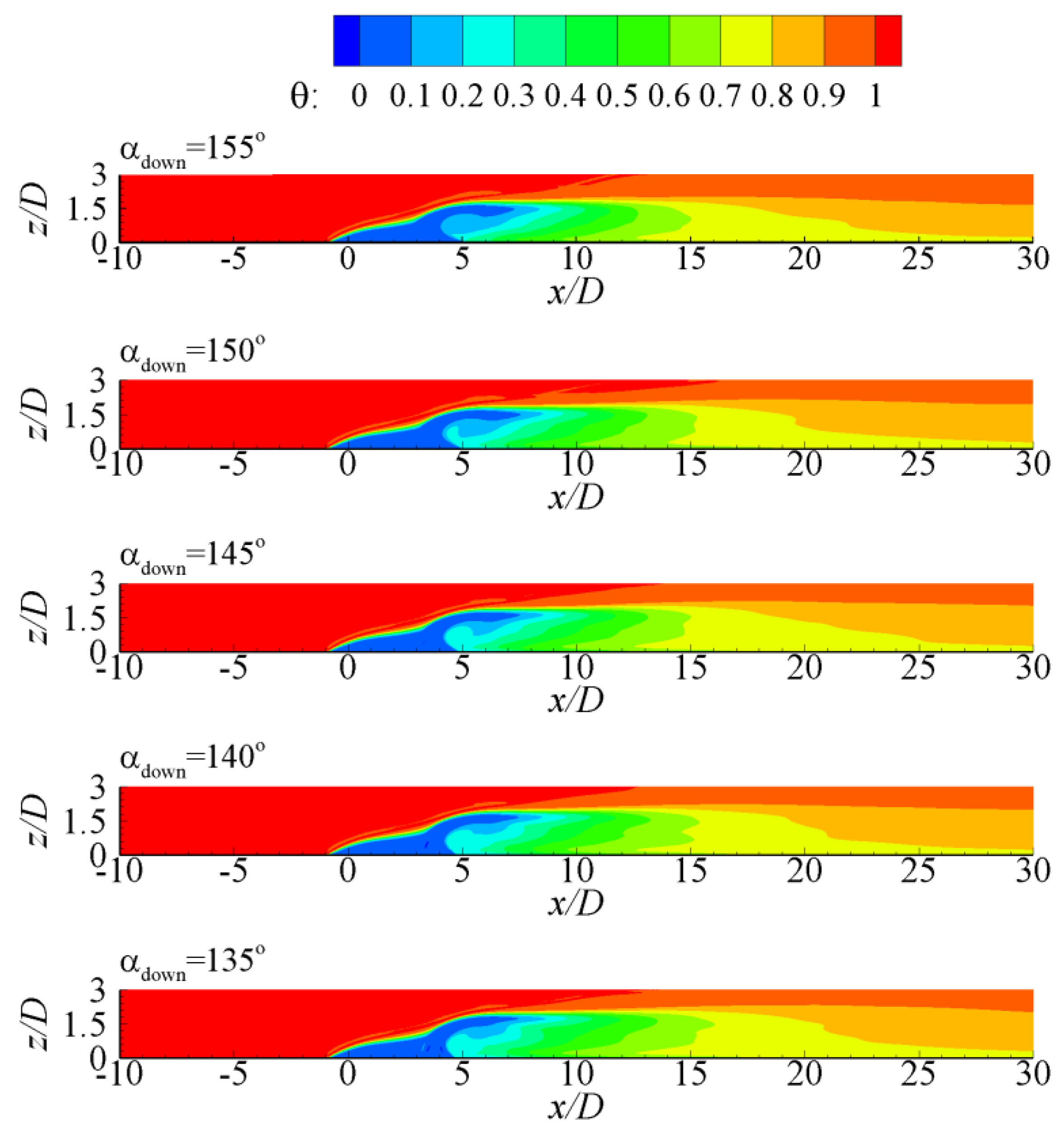
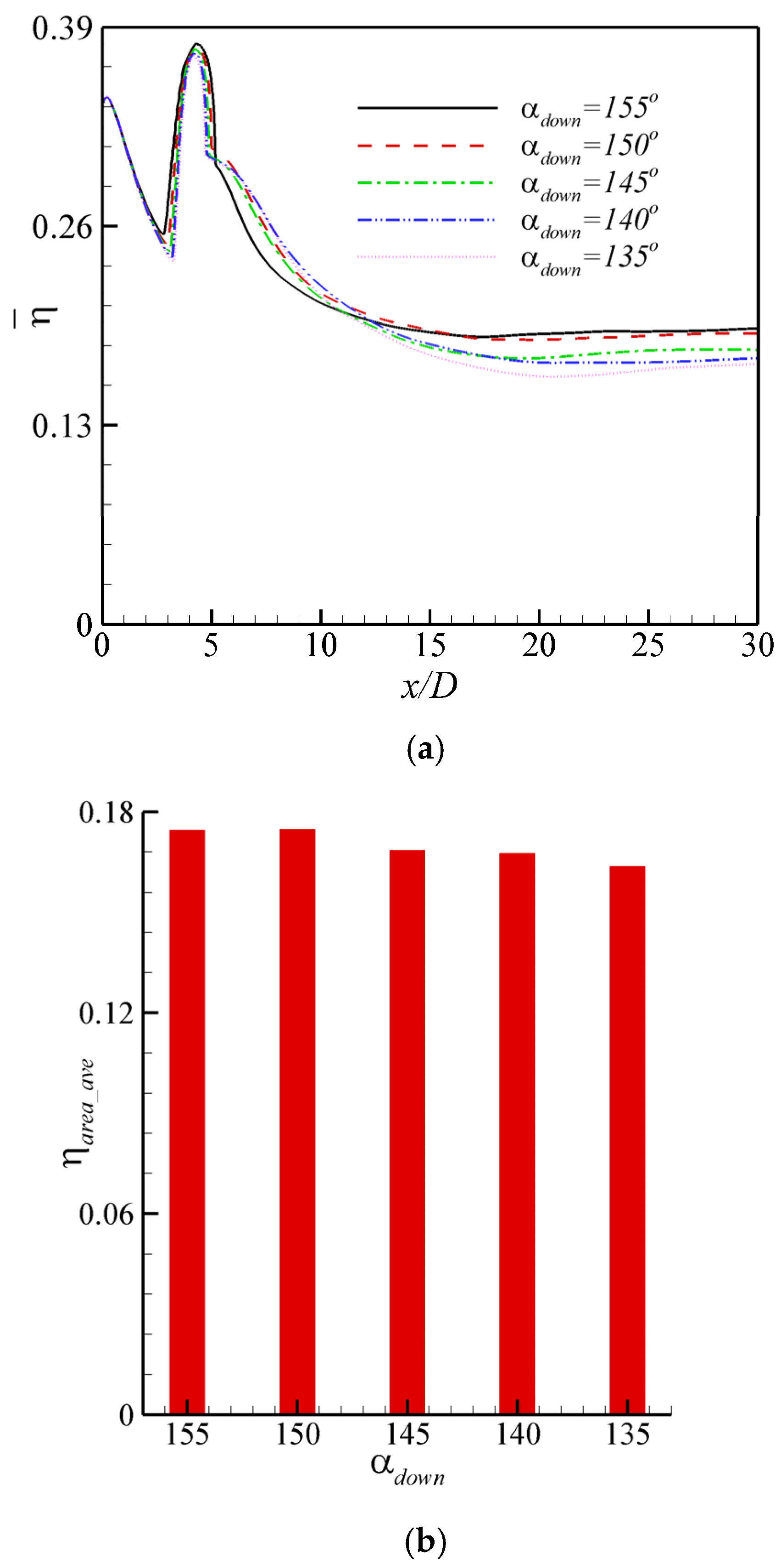
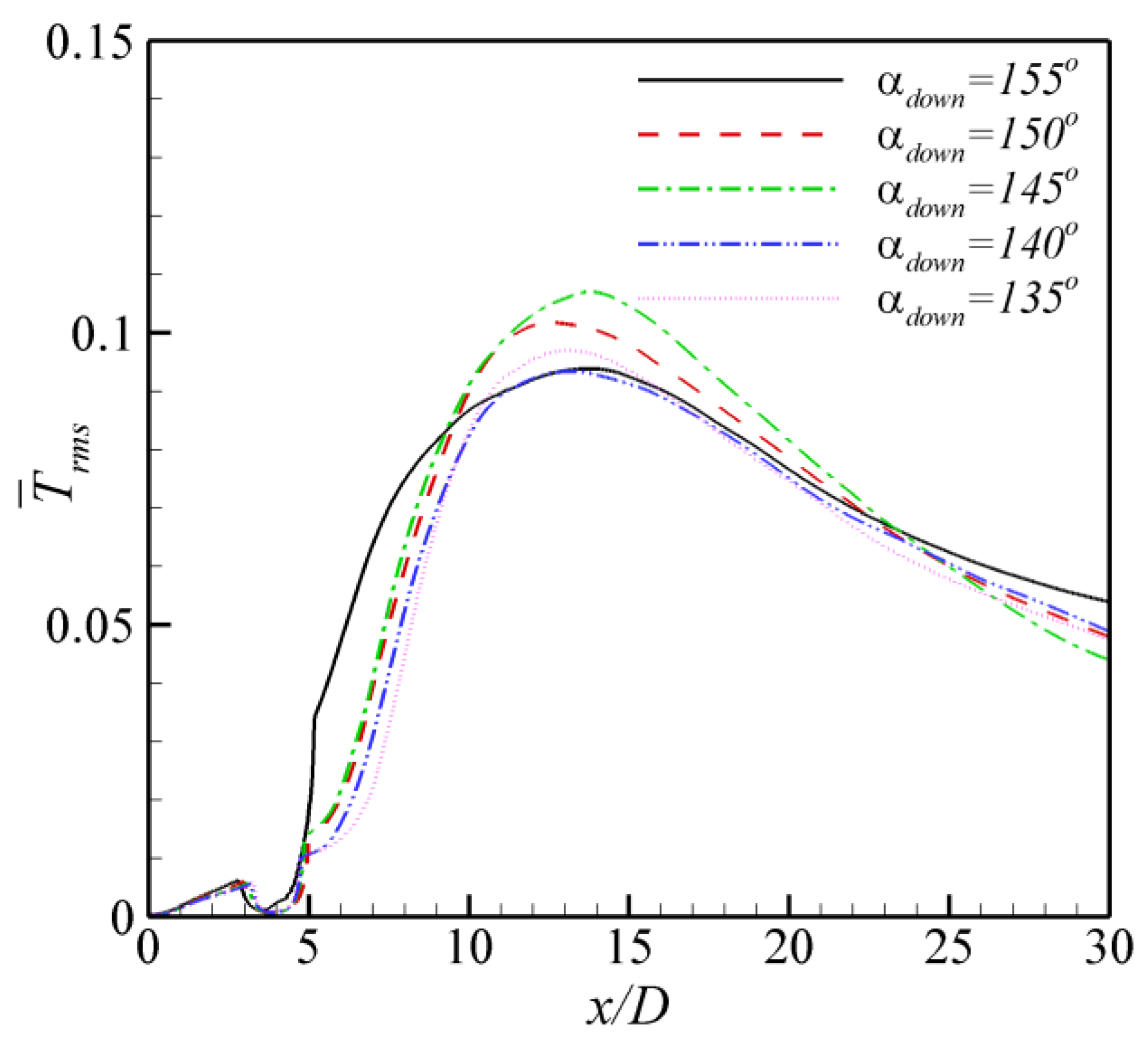
4.3. Effect of Injection Angle of Downstream Backward Jet
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tan, Z.P.; Bibik, O.; Shcherbik, D.; Zinn, B.T.; Patel, N. The regimes of twin-fluid jet-in-crossflow at atmospheric and jet-engine operating conditions. Phys. Fluids 2018, 30, 025101. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, X.; He, C.; Wen, X.; Zhao, J.; Liu, Y. Simultaneous measurements of time-resolved velocity and concentration fields behind a sand dune-inspired jet in crossflow. Phys. Fluids 2021, 33, 115101. [Google Scholar] [CrossRef]
- Bogard, D.G.; Thole, K.A. Gas turbine film cooling. J. Propul. Power 2006, 22, 249–270. [Google Scholar] [CrossRef]
- Bunker, R.S. A review of shaped hole turbine film-cooling technology. J. Heat Transf. 2005, 127, 441–453. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, K.C.; Yuan, T.J.; Wen, X.; Peng, D.; Liu, Y.Z. Spatiotemporal distributions of sweeping jet film cooling with a compact geometry. Phys. Fluids 2022, 34, 025113. [Google Scholar] [CrossRef]
- Kamotani, Y.; Greber, I. Experiments on a turbulent jet in a cross flow. AIAA J. 1972, 10, 1425–1429. [Google Scholar] [CrossRef]
- Walters, D.K.; Leylek, J.H. A detailed analysis of film-cooling physics: Part I-Streamwise injection with cylindrical holes. J. Turbomach. 2000, 122, 102–112. [Google Scholar] [CrossRef]
- McGovern, K.T.; Leylek, J.H. A detailed analysis of film cooling physics: Part II-Compound-angle injection with cylindrical holes. J. Turbomach. 2000, 122, 113–121. [Google Scholar] [CrossRef]
- Muldoon, F.; Acharya, S. DNS study of pulsed film cooling for enhanced cooling effectiveness. Int. J. Heat Mass Transf. 2009, 52, 3118–3127. [Google Scholar] [CrossRef]
- Sultan, Q.; Lalizel, G.; Fenot, M.; Dorignac, E. Influence of coolant jet pulsation on the convective film cooling of an adiabatic wall. J. Heat Trans. 2017, 139, 022201. [Google Scholar] [CrossRef]
- Ellis, C.D.; Xia, H. Impact of inflow turbulence on large-eddy simulation of film cooling flows. Int. J. Heat Mass Transf. 2022, 195, 123172. [Google Scholar] [CrossRef]
- An, B.T.; Liu, J.J.; Zhou, S.J. Effects of mainstream turbulence intensity and coolant-to-mainstream density ratio on film cooling effectiveness of multirow diffusion slot holes. J. Heat Transf. 2019, 141, 122001. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, K.; Yao, J.; Wu, J.; Lei, J.; Su, P.; Fang, Y. Experimental and numerical investigation of vane endwall film cooling with different density ratios. Int. Commun. Heat Mass Transf. 2023, 144, 106778. [Google Scholar] [CrossRef]
- Cao, N.; Li, X.; Wu, Z.Y.; Luo, X. Effect of film hole geometry and blowing ratio on film cooling performance. Appl. Therm. Eng. 2020, 165, 114578. [Google Scholar] [CrossRef]
- Han, F.; Guo, H.; Ding, X.F.; Zhang, D.W.; Li, H.W. Experimental investigation on the effects of hole pitch and blowing ratio on the leading edge region film cooling of a rotating twist turbine blade. Int. J. Heat Mass Transf. 2020, 150, 119380. [Google Scholar] [CrossRef]
- Chen, D.; Du, Q.; Xu, Q.; Xu, G.; Liu, H. Film cooling and aerodynamic loss performance of turbine vanes with fan-shaped and wave -trenched holes. Appl. Therm. Eng. 2023, 230, 120643. [Google Scholar]
- Liu, C.L.; Ye, L.; Zhang, F.; Huang, R.; Li, B.R. Film cooling performance evaluation of the furcate hole with cross-flow coolant injection: A comparative study. Int. J. Heat Mass Transf. 2021, 164, 120457. [Google Scholar] [CrossRef]
- Zhou, W.; Hu, H. Improvements of film cooling effectiveness by using Barchan dune shaped ramps. Int. J. Heat Mass Transf. 2016, 103, 443–456. [Google Scholar] [CrossRef]
- Zhao, M.J.; Bian, Y.F.; Xu, J.J.; He, T.H. Large eddy simulation of film cooling with different upstream obstacles. Int. J. Therm. Sci. 2021, 161, 106722. [Google Scholar] [CrossRef]
- Subbuswamy, G.; Li, X.C.; Gharat, K. Numerical simulation of backward film cooling with fan-shaped holes. In Proceedings of the ASME 2013 Heat Transfer Summer Conference, HT2013-17801, Minneapolis, MN, USA, 14–19 July 2013. [Google Scholar]
- Subbuswamy, G.; Li, X.C.; Gharat, K. Numerical study of aerodynamic performance of film cooling with backward injection holes. In Proceedings of the ASME 2013 Heat Transfer Summer Conference, HT2013-17803, Minneapolis, MN, USA, 14–19 July 2013. [Google Scholar]
- Li, X.C. Numerical simulation on fluid flow and heat transfer of film cooling with backward injection. In Proceedings of the ASME International Heat Transfer Conference-2010, Washington, DC, USA, 8–13 August 2010; Volume 5, pp. 257–265. [Google Scholar]
- Park, S.; Jung, E.Y.; Kim, S.H.; Sohn, H.S.; Cho, H.H. Enhancement of film cooling effectiveness using backward injection holes. Int. J. Therm. Sci. 2016, 110, 314–324. [Google Scholar] [CrossRef]
- Singh, K.; Premachandran, B.; Ravi, M.R. Experimental and numerical studies on film cooling with reverse/backward coolant injection. Int. J. Therm. Sci. 2017, 111, 390–408. [Google Scholar] [CrossRef]
- Zhao, Z.C.; He, L.M.; Dai, S.J.; Shao, S. Computational research on film cooling performance of different shaped holes with backward and forward injection. AIP Adv. 2019, 9, 055009. [Google Scholar] [CrossRef]
- Chen, A.F.; Li, S.J.; Han, J.C. Film cooling with forward and backward injection for cylindrical and fan-shaped holes using PSP measurement technique. In Proceedings of the ASME Turbo Expo 2014, GT2014-26232, Dusseldorf, Germany, 16–20 June 2014. [Google Scholar]
- Singh, A.K.; Singh, K.; Singh, D.; Sahoo, M. Large eddy simulations for film cooling assessment of cylindrical and laidback fan-shaped holes with reverse injection. J. Therm. Sci. Eng. Appl. 2021, 13, 031027. [Google Scholar] [CrossRef]
- Shangguan, Y.Q.; Cao, F. An LBM-based investigation on the mixing mechanism of double rows film cooling with the combination of forward and backward jets. Energies 2022, 15, 4848. [Google Scholar] [CrossRef]
- Zhai, Y.N.; Liu, C.L.; He, Y.H.; Zhou, Z.X. Investigation on the film cooling performance of diffuser shaped holes with different inclination angles. Int. J. Turbo. Jet Engines 2017, 34, 123–139. [Google Scholar] [CrossRef]
- An, B.T.; Liu, J.J.; Zhou, S.J. Effects of inclination angle, orientation angle, and hole length on film cooling effectiveness of rectangular diffusion holes. J. Turbomach. 2018, 140, 071003. [Google Scholar] [CrossRef]
- Shangguan, Y.Q.; Wang, X.; Cao, F.; Zhu, Y.D. High resolution simulation of film cooling with blowing ratio and inclination angle effects based on hybrid thermal lattice Boltzmann method. Therm. Sci. 2022, 26, 3491–3503. [Google Scholar] [CrossRef]
- Chen, S.Y.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Chen, Z.; Shu, C.; Tan, D. Three-dimensional simplified and unconditionally stable lattice Boltzmann method for incompressible isothermal and thermal flows. Phys. Fluids 2017, 29, 053601. [Google Scholar] [CrossRef]
- Chen, Z.; Shu, C.; Yang, L.M.; Zhao, X.; Liu, N. Immersed boundary-simplified thermal lattice Boltzmann method for incompressible thermal flows. Phys. Fluids 2020, 32, 031605. [Google Scholar] [CrossRef]
- Chen, Z.; Shu, C.; Tan, D. A simplified thermal lattice Boltzmann method without evolution of distribution functions. Int. J. Heat Mass Transf. 2017, 105, 741–757. [Google Scholar] [CrossRef]
- Hirsch, G. Numerical Computation of Internal and External Flows; John Wiley: Hoboken, NJ, USA, 1988. [Google Scholar]
- Hou, S.; Sterling, J.; Chen, S.; Doolen, G.D. A lattice Boltzmann subgrid model for high Reynolds number flows. Fields Inst. Commun. 1994, 6, 151–168. [Google Scholar]
- Wang, X.; Shangguan, Y.Q.; Onodera, N.; Kobayashi, H.; Aoki, T. Direct numerical simulation and large eddy simulation on a turbulent wall-bounded flow using lattice Boltzmann method and multiple GPUs. Math. Probl. Eng. 2014, 2014, 742432. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary-Layer Theory; Springer: Berlin, Germany, 2000. [Google Scholar]
- Shangguan, Y.Q.; Wang, X.; Li, Y.M. Investigation on the mixing mechanism of single-jet film cooling with various blowing ratios based on hybrid thermal lattice Boltzmann method. Int. J. Heat Mass Transf. 2016, 97, 880–890. [Google Scholar] [CrossRef]
- Chen, A.F.; Li, S.J.; Han, J.C. Film cooling for cylindrical and fan-shaped holes using pressure-sensitive paint measurement technique. J. Thermophys. Heat Transf. 2015, 29, 75–784. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shangguan, Y.; Cao, F. The Evolution of Flow Structures and Coolant Coverage in Double-Row Film Cooling with Upstream Forward Jets and Downstream Backward Jets. Energies 2024, 17, 3387. https://doi.org/10.3390/en17143387
Shangguan Y, Cao F. The Evolution of Flow Structures and Coolant Coverage in Double-Row Film Cooling with Upstream Forward Jets and Downstream Backward Jets. Energies. 2024; 17(14):3387. https://doi.org/10.3390/en17143387
Chicago/Turabian StyleShangguan, Yanqin, and Fei Cao. 2024. "The Evolution of Flow Structures and Coolant Coverage in Double-Row Film Cooling with Upstream Forward Jets and Downstream Backward Jets" Energies 17, no. 14: 3387. https://doi.org/10.3390/en17143387
APA StyleShangguan, Y., & Cao, F. (2024). The Evolution of Flow Structures and Coolant Coverage in Double-Row Film Cooling with Upstream Forward Jets and Downstream Backward Jets. Energies, 17(14), 3387. https://doi.org/10.3390/en17143387





