The Distributed Parameter Model of an Electro-Pneumatic System Actuated by Pneumatic Artificial Muscles with PWM-Based Position Control
Abstract
1. Introduction
| Authors, Year | Type of Model | Additional Control Method | PWM Frequency, Hz | PAM Characteristics |
|---|---|---|---|---|
| Ville T. Jouppila et al., 2014 [21] | geometric [42] | SMC | 100 | diameter: 30 mm length: 100 mm |
| Xie S. et al., 2016 [12] | empirical [47] | PID | 100–180 | diameter: 20 mm length: 500 mm |
| Pipan M., and Harakovic N. 2018 [22] | no data | PID | 250 | diameter: 20 mm length: 200 mm |
| Rimar M. et al., 2019 [23] | geometric [25] | – | 50 | diameter: 40 mm length: 1000 mm |
- The models mentioned above consider the pneumatic artificial muscle as an object with lumped parameters.
- As can be seen from Table 1, the impact of the design parameters of PAMs and PWM frequency of the control valve have not been studied in previous works. Also, in these works, the geometric and empirical mathematical models of PAMs are applied.
- to develop a distributed parameter mathematical model of the PAM with the connected pipeline;
- to carry out the numerical investigations of pressure change in the end of the bladder;
- to explore the impact of the parameters of the pneumatic artificial muscle and pneumatic circuit on the wave processes;
- to create a methodology for finding out undesirable PWM frequencies of the control pressure.
2. Methods
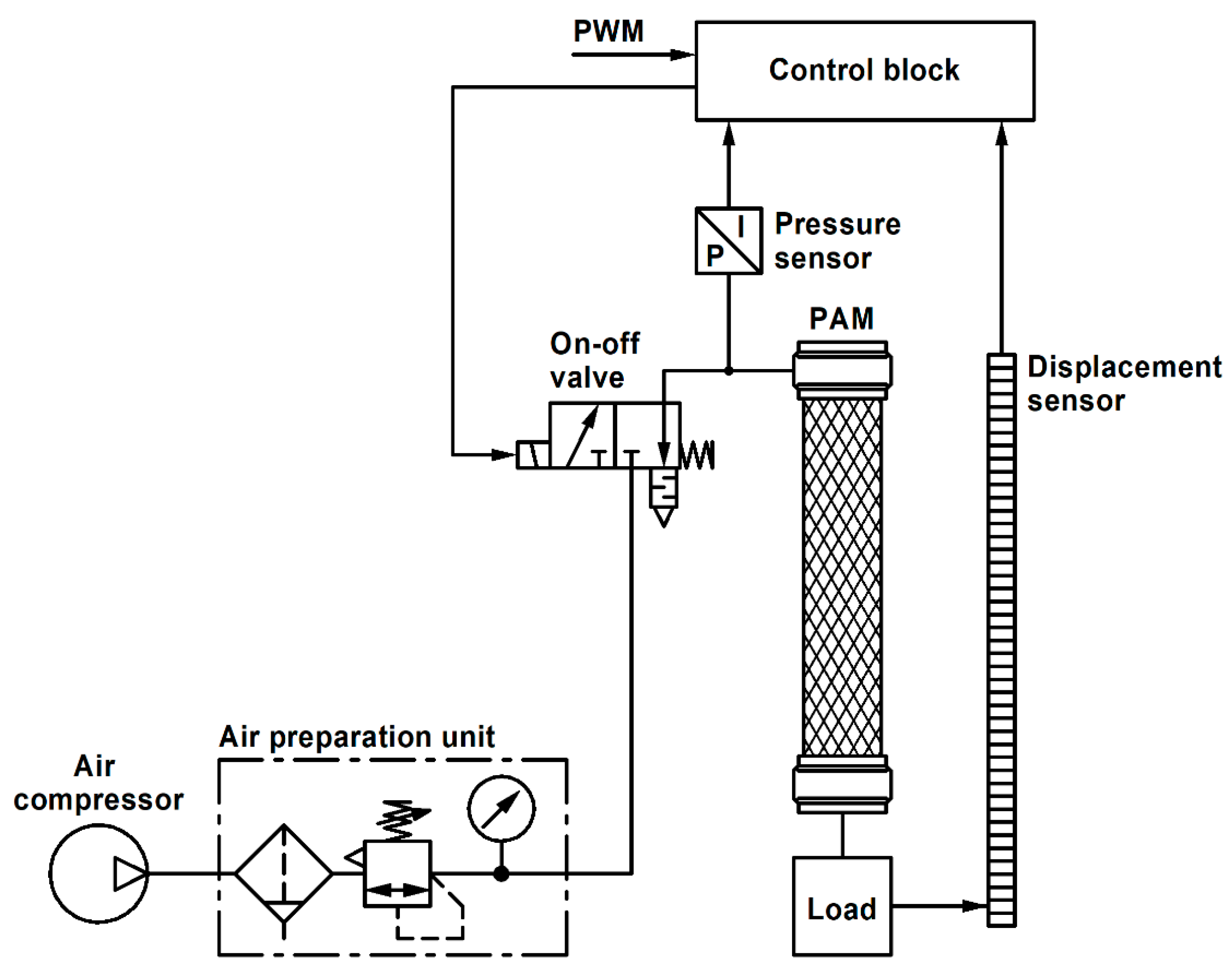
2.1. Object of the Study
2.2. Proposed Approach
- To estimate possibility of gas oscillation occurrence at the positioning point, it is necessary to obtain the pressure change characteristics at the end of the PAM instead of this distribution along the bladder length.
- At the positioning point, the amplitude of the output link oscillations is negligible compared to the PAM’s entire length. Therefore, the change in the bladder length can be neglected and we can consider a PAM as a pipeline.
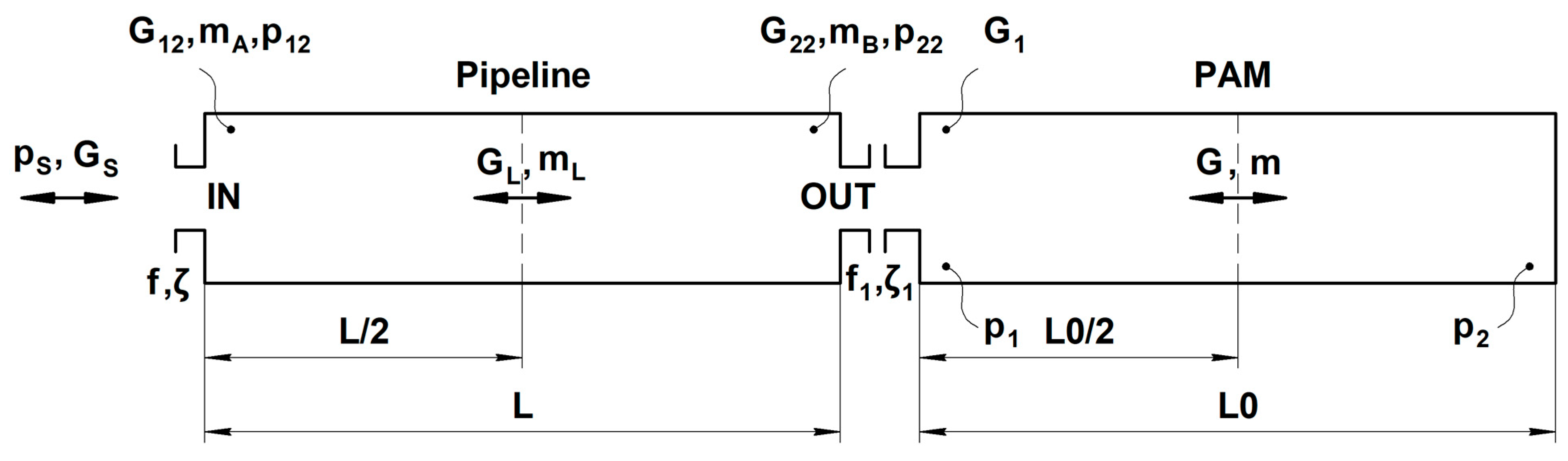
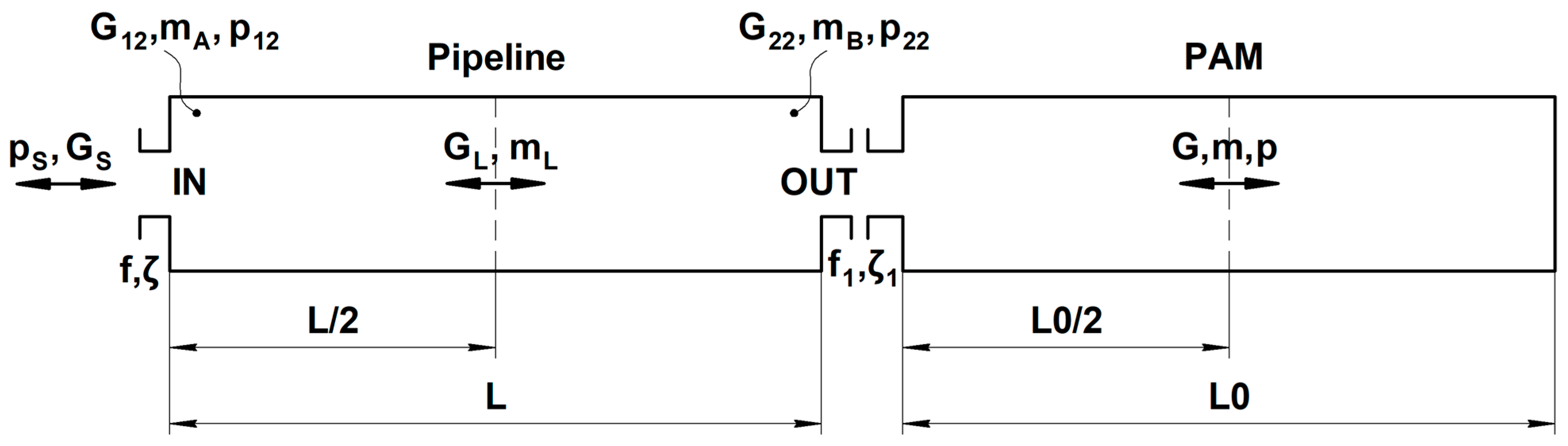
2.3. Distributed Parameter Mathematical Model
- The process of the gas mass acceleration leads to change in the flow rate inside the bladder and the pipeline.
- The process of the gas mass change due to the filling/emptying processes leads to change in the gas pressure, density, and mass flow rate.
- The process of the pressure change at the ends of the bladder and the pipeline is due to the wave processes.
- The equation of the gas motion in the pipeline.
- The equation of the gas motion in the bladder.
- The equations of the average mass flow rate and flow rates at the inlet and at the outlet of the pipeline.
- The equations of the average mass flow rate and the mass flow rate at the inlet of the PAM bladder.
- The gas mass movement is one-dimensional, i.e., the gas parameters are the functions of the z coordinate passing along the axis of the line.
- The considered processes are isothermal since the temperature change is negligible in most cases in pipelines of industrial systems.
- The length and the diameter of the pipeline and the PAM are constant (see the assumptions made in Section 2).
- The gas mass movement through the valves is quasi-static, i.e., the instantaneous value of gas consumption at the inlet in the transition processes is the same as in the steady-state flow at the same pressure drop.
- Dependence of the friction loss per the Reynolds number at the transitional process is the same as at the steady state [57]:
- During the time of wave propagation, i.e., t < L0/c, the pressure at the end of the bladder is constant and equal to its initial value p20. At this time, the speed of the gas at the end of the bladder is equal to zero, which leads to gas layer compression.
- After time t = L0/c, the pressure changes abruptly from p20 to some value p2 and then changes permanently to the steady value.
3. Results
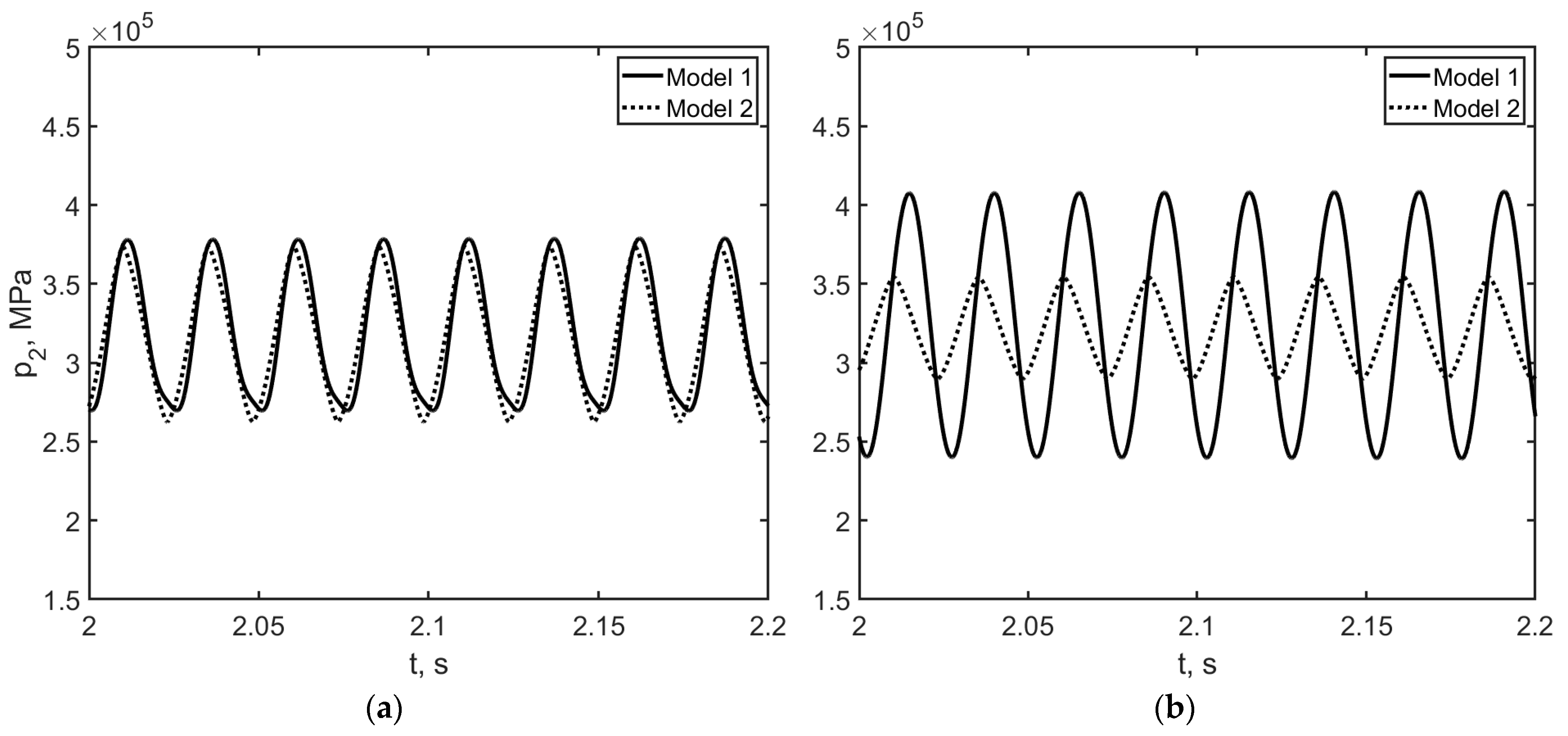
3.1. Numerical Results of the Pressure Change at the End of the PAM
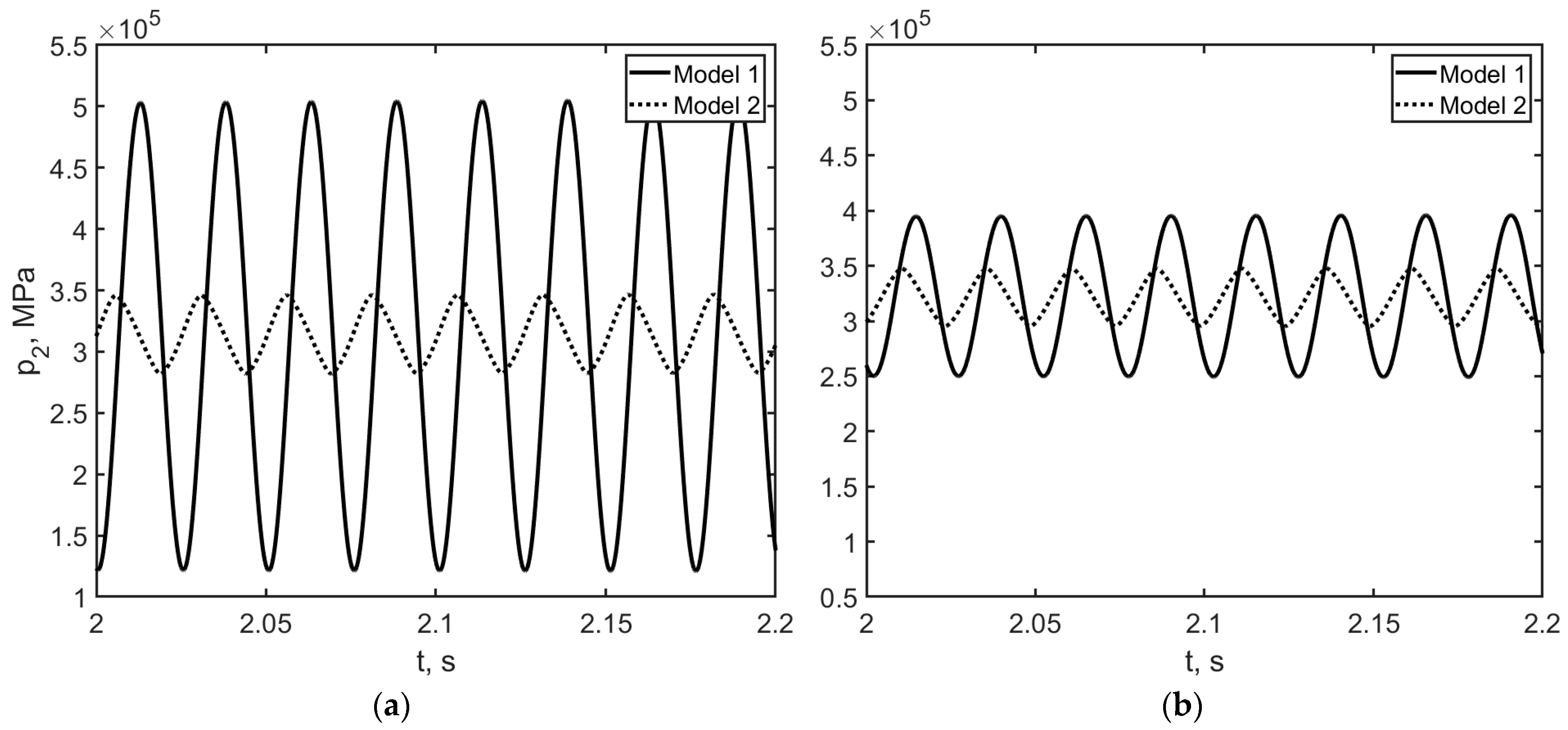
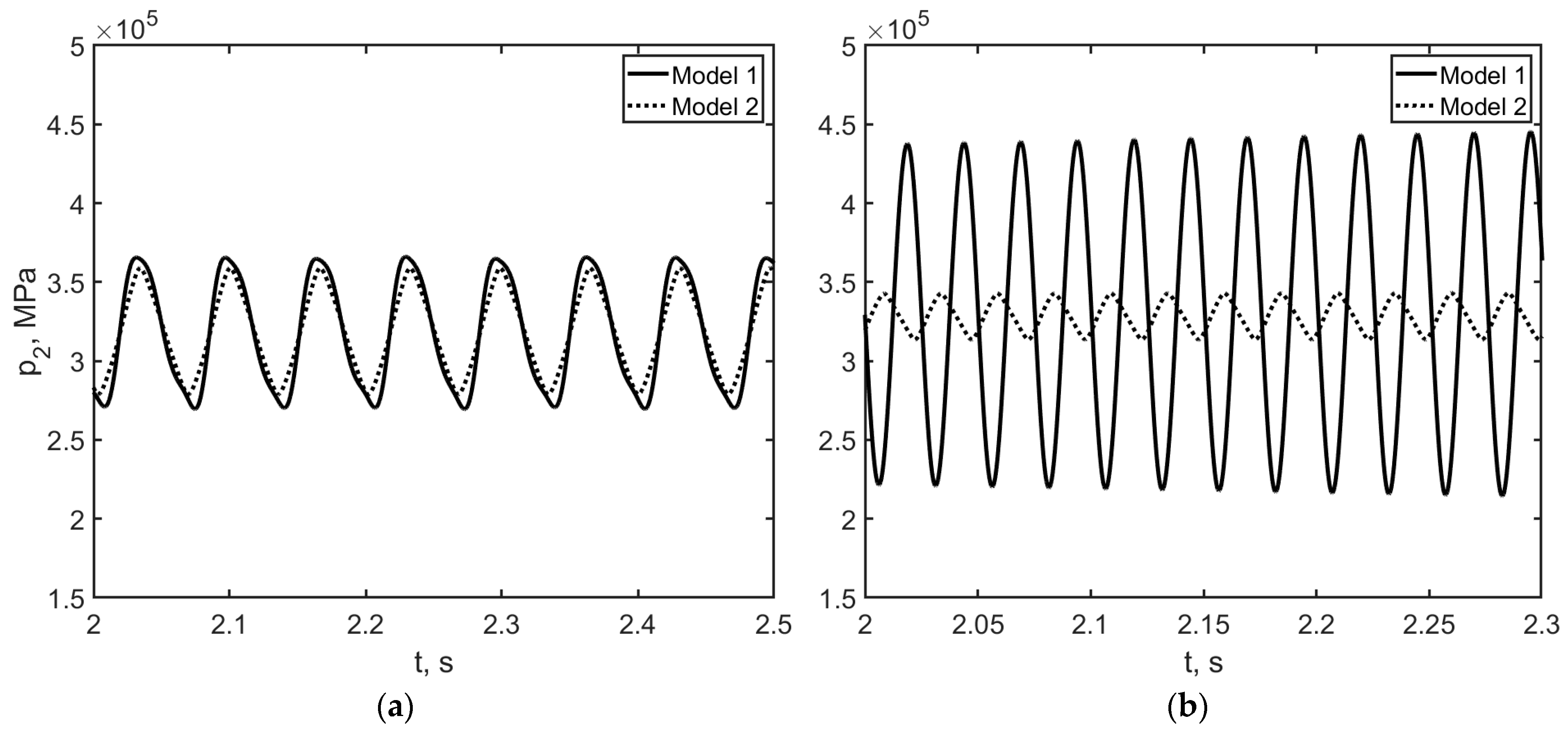
3.1.1. Different Initial Lengths of the PAM Bladder
3.1.2. Different Lengths of the Supply Pipeline
3.1.3. Different Operating Frequencies
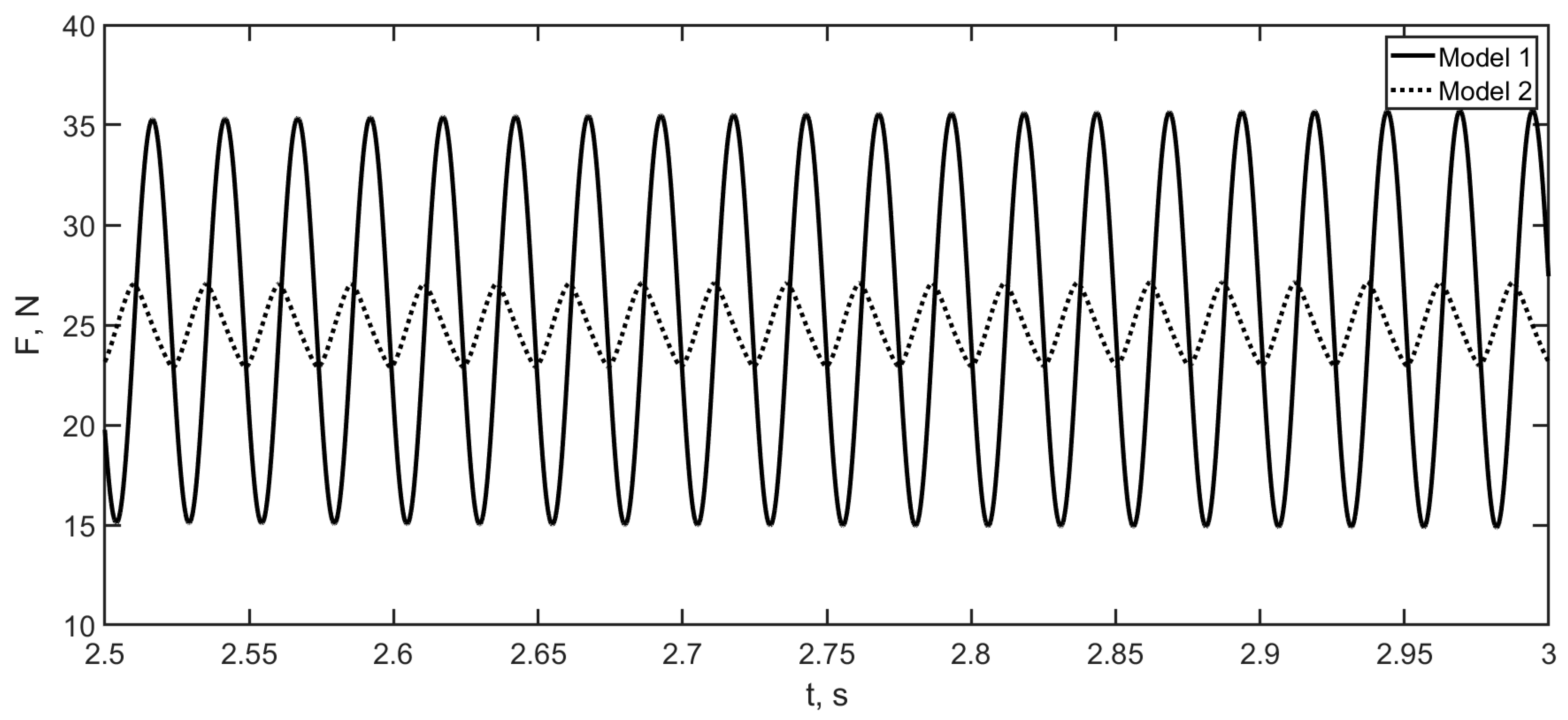
3.2. Numerical Results of the Pressure Force at the End of the PAM
3.3. The Calculation Algorithm
- Step 1. Calculate the pressure change at the end of the bladder with Model 1 (Equation (A1)), taking into account the length and diameter of the bladder and the pipeline.
- Step 2. Calculate the pressure change at the end of the bladder with Model 2 (Equation (A2)), eliminating the wave processes in the bladder.
- Step 4. If the discrepancy between the results is large, then correction of the frequency of the PWM signal is required. Correct the valve operating frequency to eliminate the discrepancy until the curves match.
- Step 5. Then, continue the calculations using the models of the PAMs that take into account change in the design parameters, for example, with the model elaborated in [41] that describes static and dynamic characteristics of the PAM.
4. Conclusions
- It allows estimating dynamic characteristics of the pressure change at the end of the bladder and avoiding undesirable PWM frequencies.
- It takes into consideration the wave processes in the supply pipeline, since the pipeline length can reach large values.
- It consists of ODEs instead of PDEs, which simplifies the calculations of dynamic characteristics.
- This model is universal for all types of PAMs since it consider the PAM as a pipeline.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| L | the length of the pipeline, m; |
| DL | the diameter of the pipeline, m; |
| VL | the value of the gas volume in the pipeline, m3; |
| fL | the cross-section area of the pipeline, m2; |
| f | the cross-section area of the pipeline inlet, m2; |
| d | the diameter of the pipeline inlet, m; |
| L0 | the initial length of the PAM, m; |
| D0 | the initial diameter of the PAM, m; |
| V0 | the value of the gas volume in the PAM, m3; |
| f0 | the cross-section area of the PAM, m2; |
| f1 | the cross-section area of the inlet of the PAM, m2; |
| d1 | the diameter of the PAM inlet, m; |
| pS | the supply pressure/the time-varying pressure, MPa; |
| pS0 | the pressure delivered from the air compressor, MPa; |
| pA | the atmospheric pressure, MPa; |
| pFR | the friction loss in the pipeline, MPa; |
| pFR0 | the friction loss in the PAM, MPa; |
| p12 | the pressure down the inlet of the pipeline, MPa; |
| p22* | the current pressure at the end of the pipeline, MPa; |
| p220 | the initial pressure at the end of the pipeline, MPa; |
| p22 | the pressure characterizing the dynamics of gas layer compression at the end of the pipeline, MPa; |
| p1 | the pressure down the PAM inlet, MPa; |
| p2* | the current pressure at the end of the PAM, MPa; |
| p20 | the initial pressure at the end of the PAM, MPa; |
| p2 | the pressure characterizing the dynamics of gas compressing at the end of the PAM, MPa; |
| p | the pressure at the end of the bladder (lumped parameters), MPa; |
| F | the pressure force at the end of the bladder (lumped parameters), H; |
| F2 | the pressure force at the end of the bladder (distributed parameters), H; |
| t | the time of the wave propagation, s; |
| c | the speed of the sound, m/s; |
| TS | the gas temperature in the pipeline and in the bladder, K; |
| R | the gas constant, J/kg·K; |
| k | the polytropic coefficient; |
| λ | the air resistance coefficient; |
| ρ | the average gas density in the pipeline, kg/m3; |
| ρ0 | the average gas density in the PAM, kg/m3; |
| υ | the average speed of the gas of the pipeline, m/s; |
| υ’ | the acceleration of the gas mass in the pipeline, m/s2; |
| υ0 | the average speed of the gas in the PAM, m/s; |
| the acceleration of the gas mass in the PAM, m/s2; | |
| ζ | the resistance coefficient of the pipeline inlet; |
| ζ1 | the resistance coefficient of the PAM inlet; |
| n | the operating frequency of the valve, Hz; |
| GL | the average mass flow rate in the pipeline, m3/s; |
| GS | the mass flow rate at the inlet of the pipeline, m3/s; |
| mL | the current value of the gas mass in the pipeline, kg; |
| mA | the current value of the gas mass at the inlet of the pipeline, kg; |
| mB | the current value of the gas mass at the outlet of the pipeline, kg; |
| m12 | the current value of the gas mass in the left half of the pipeline, m3/s; |
| the mass flow rate in the left half of the pipeline, m3/s; | |
| m22 | the current value of the gas mass in the second half of the pipeline, m3/s; |
| the mass flow rate in the second half of the pipeline, m3/s; | |
| m’A, G12 | the mass flow rate down the inlet of the pipeline, m3/s; |
| m’B, G22 | the mass flow rate at the outlet of the pipeline, m3/s; |
| m’, G | the average mass flow rate in the PAM, m3/s; |
| G1 | the mass flow rate down the inlet of the PAM, m3/s; |
| m | the current value of the gas mass in the PAM, kg; |
| the Heaviside step function |
Appendix A
| Authors | Year | Description of the Model | Type of Model | Type of PAM |
|---|---|---|---|---|
| Gaylord R.H. [34] | 1958 | elaborated the basic equation using the principle of energy conservation | geometric | McKibben |
| Schulte H.F. [35] | 1961 | geometric | McKibben | |
| Chou C.-P. and Hannaford B. [25] | 1996 | added wall thickness of bladder to the basic equation in [31] | geometric | McKibben |
| Repperger D.W. et al. [51] | 1998 | presented model consisting of a spring element, viscous damping element, contractile force element arranged in parallel | phenomenological | McKibben |
| Tondu B. and Lopez P. [5] | 2000 | proposed the equation equivalent to [23]; added empirical parameter k(p); elaborated the friction model | geometric empirical | McKibben |
| Tsagarakis N., Caldwell D.G. [36] | 2000 | considered the geometry of the end-cap surface; calculated radial elasticity | geometric | McKibben |
| Klute G.K. and Hannaford B. [37] | 2000 | considered elastic energy storage in the bladder | phenomenological | McKibben |
| Colbrunn R.W. et al. [56] | 2001 | elaborated the model consisting of a spring, viscous damper, and Coulomb friction arranged in parallel | phenomenological | McKibben |
| Hesse S. [42] | 2003 | proposed the equation of the static force | geometric | FESTO |
| Reynolds D.B. et al. [55] | 2003 | improved and experimentally tested the model in [47] | phenomenological | McKibben |
| Davis S. et al. [38] | 2003 | considered extension of the fiber strand | geometric | McKibben |
| Hildebrandt A. et al. [43] | 2005 | a pneumatic artificial muscle is proposed as combination of a pneumatic piston and mechanical spring | empirical | FESTO |
| Davis S. et al. [40] | 2006 | proposed the braid strands stress analysis; improved the friction model presented in [5] | geometric | McKibben |
| Kerscher T. et al. [44] | 2006 | added empirical function μ(p) in the equation in [5] | geometric empirical | FESTO |
| Doumit M. et al. [39] | 2009 | presented a fully analytical static model; considered the muscle end-fixture-diameter effect | geometric | McKibben |
| Wickramatunge K.C., Leephakpreeda T. [45] | 2010 | a pneumatic artificial muscle is modeled as a spring system and static force is presented as a function of stiffness and stretched length | empirical | FESTO |
| Joupilla V.T. [46] | 2010 | the static force is presented as a function of length contraction and the pressure and deducted from the maximum muscle force | empirical | FESTO |
| Pujana A.A. et al. [47] | 2010 | the static force is presented as a linear function of the internal pressure and length | empirical | FESTO |
| Hosovsky A. Havran M. [48] | 2012 | presented an approximation model of the static force using a polynomial function | empirical | FESTO |
| Sarosi J. et al. [49] | 2015 | presented an approximation model of the static force using an exponential function | empirical | FESTO |
| Donskoj et. al. [50] | 2019 | proposed an equation of the static force and a mathematical model of dynamic characteristics | geometric empirical | FESTO |
Appendix B
References
- Ahn, K.K.; Chau, N.U.T. Intelligent switching control of pneumatic muscle robot arm using learning vector quantization neural network. Mechatronics 2007, 17, 255–262. [Google Scholar] [CrossRef]
- Dolgih, E.V. Manipulator for Performance of Operations Related to Changing the Purpose of the Processing or Product in the Space. RU Patent 118 578 U1, 27 July 2012. [Google Scholar]
- Zhu, X.; Tao, G.; Yao, D.; Cao, J. Adaptive robust posture control of a parallel manipulator driven by pneumatic muscles. Automatica 2009, 44, 2248–2257. [Google Scholar] [CrossRef]
- Tondu, B.; Lopez, P. The McKibben muscle and its use in actuating robot-arms showing similarities with human arm behaviour. Ind. Robot. Int. J. 1997, 24, 432–439. [Google Scholar] [CrossRef]
- Tondu, B.; Lopez, P. Modelling and control of McKibben artificial muscle robot actuators. IEEE Contr. Syst. Mag. 2000, 20, 15–38. [Google Scholar] [CrossRef]
- Verrelst, B.; Vanderborght, B.; Van Ham, R.; Daerden, F.; Lefeber, D.; Vermeulen, J. The pneumatic biped “Lucy” actuated with pleated pneumatic artificial muscles. Auton. Robot. 2005, 18, 201–213. [Google Scholar] [CrossRef]
- Noritisugu, T.; Tanaka, T. Application of rubber artificial muscle manipulator as a rehabilitation robot. IEEE/ASME Trans. Mechatron. 1997, 2, 259–267. [Google Scholar] [CrossRef]
- Belforte, G.; Eula, G.; Ivanov, A.; Sirolli, S. Soft pneumatic actuators for rehabilitation. Actuators 2014, 3, 84–106. [Google Scholar] [CrossRef]
- Chi, H.; Su, H.; Liang, W.; Ren, Q. Control of a Rehabilitation Robotic Device Driven by Antagonistic Soft Actuators. Actuators 2021, 10, 123. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Trinh, V.C.; Le, T.D. An Adaptive Fast Terminal Sliding Mode Controller of Exercise-Assisted Robotic Arm for Elbow Joint Rehabilitation Featuring Pneumatic Artificial Muscle Actuator. Actuators 2020, 9, 118. [Google Scholar] [CrossRef]
- Nguyen, T.; Leavitt, J.; Jabbari, F.; Bobrow, J. Accurate sliding-mode control of pneumatic system using low-cost solenoid valves. IEEE/ASME Trans. Mechatron. 2007, 12, 216–219. [Google Scholar] [CrossRef]
- Xie, S.; Mei, J.; Liu, H.; Wang, P. Motion control of pneumatic muscle actuator using fast switching valve. In Mechanism and Machine Science; Springer: Singapore, 2017; pp. 1439–1451. [Google Scholar] [CrossRef]
- Lin, Z.; Wei, Q.; Ji, R.; Huang, X.; Yuan, Y.; Zhao, Z. An electro-pneumatic force tracking system using fuzzy logic based volume flow control. Energies 2019, 12, 4011. [Google Scholar] [CrossRef]
- Shin, M.C.; Ma, M.A. Position control of a pneumatic rodless cylinder using sliding mode MD-PWM control the high speed solenoid valves. JSME Int. J. Ser C Mech. Elem. Manuf. 1998, 41, 236–241. [Google Scholar] [CrossRef]
- Ahn, K.; Yokota, S. Intelligent switching control of pneumatic actuator using on/off solenoid valves. Mechatronics 2005, 15, 683–702. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, J.-F.; Yang, C.-J.; Niu, B. Design and hybrid control of the pneumatic force-feedback systems for arm-exoskeleton by using on/off valve. Mechatronics 2007, 17, 325–335. [Google Scholar] [CrossRef]
- Najjari, B.; Barakari, S.; Mohammadi, A.; Futohi, M.; Bostanian, M. Position control of an electro-pneumatic system based on PWM technique and FLC. ISA Trans. 2014, 53, 647–657. [Google Scholar] [CrossRef]
- Hodgson, S.; Tavakoli, M.; Pham, M.; Leleve, A. Nonlinear discontinuous dynamics averaging and PWM-based sliding control of solenoid-valve pneumatic actuators. IEEE/ASME Trans. Mechatron. 2015, 20, 876–888. [Google Scholar] [CrossRef]
- Lin, Z.; Zhang, T.; Xie, Q.; Wei, Q. Intelligent electro-pneumatic position tracking system using improved mode-switching sliding control with fuzzy nonlinear gain. IEEE Access 2018, 6, 34462–34476. [Google Scholar] [CrossRef]
- Leephakpreeda, T. Fuzzy logic based PWM control and neural controlled-variable estimation of pneumatic artifical muscle actuators. Expert. Syst. Appl. 2011, 38, 7837–7850. [Google Scholar] [CrossRef]
- Jouppila, V.T.; Gadsden, S.A.; Bone, G.M.; Ellman, A.U.; Habibi, S.R. Sliding mode control of a pneumatic muscle actuator system with a PWM strategy. Int. J. Fluid Power 2014, 15, 19–31. [Google Scholar] [CrossRef]
- Pipan, M.; Harakovic, N. Closed-loop volume flow control algorithm for fast switching pneumatic valves with PWM signal. Control Eng. Pract. 2018, 70, 114–120. [Google Scholar] [CrossRef]
- Rimar, M.; Fedak, M.; Corny, I.; Kulikov, A.; Kuna, S.; Kulikova, O.; Vahovsky, J. Pulse width modulation modelling for efficient pneumatic artificial muscle control. Adv. Mech. Eng. 2019, 11, 1687814019895439. [Google Scholar] [CrossRef]
- Pipan, M.; Herakovic, N. Volume flow characterization of PWM-controlled fast-switching pneumatic valves with PWM signal. Stroj. Vestn. J. Mech. Eng. 2016, 62, 543–550. [Google Scholar] [CrossRef]
- Chou, C.P.; Hannaford, B. Measurement and modelling of McKibben pneumatic artificial muscle. IEEE Trans. Robot. Autom. 1996, 6, 90–102. [Google Scholar] [CrossRef]
- Sheikh, S.M.; Sadigh, M.J.; Zareinejad, M. Precise dynamic modeling of pneumatic muscle actuators with modified Bouw–Wen hysteresis model. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 235, 1449–1457. [Google Scholar] [CrossRef]
- Fluidic Muscle DMSP/MAS. Available online: https://www.festo.com/rep/en_corp/assets/pdf/info_501_en.pdf (accessed on 20 March 2024).
- Bergemann, D.; Lorenz, B.; Thallemer, A. Actuating Means. U.S. Patent 6,349,746 B1, 26 February 2002. [Google Scholar]
- Takosoglu, J.E.; Laski, P.A.; Blasiak, S.; Bracha, S.; Bracha, G.; Pietrala, D. Determining the static characteristics of pneumatic muscles. Meas. Control 2016, 49, 62–71. [Google Scholar] [CrossRef]
- Takagi, T.; Sakaguchi, Y. Pneumatic Actuator for Manipulator. U.S. Patent 4,615,260 A, 7 October 1986. [Google Scholar]
- Kalita, B.; Leonessa, A.; Dwivedy, S.K. A review on the development of pneumatic artificial muscle actuators: Force model and application. Actuators 2022, 11, 288. [Google Scholar] [CrossRef]
- Daerden, F.; Lefeber, D. Pneumatic artificial muscles: Actuators for robotics and automation. Eur. J. Mech. Environ. Eng. 2002, 47, 11–21. [Google Scholar]
- Oguntosin, V.; Akindele, A. Design and characterization of artificial muscles from wedge-like pneumatic soft modules. Sens. Actuators A Phys. 2019, 297, 111523. [Google Scholar] [CrossRef]
- Gaylord, R.H. Fluid Actuated Motor System and Stroking Device. U.S. Patent 2,844,126 A, 22 July 1958. [Google Scholar]
- Schulte, H.F. The characteristics of the McKibben artificial muscle. In The Application of External Power in Prosthetics and Orthotics; National Academy of Sciences-National Research Council: Washington, DC, USA, 1961; pp. 94–115. [Google Scholar]
- Tsagarakis, N.; Caldwell, D.G. Improved modelling and assessment of pneumatic muscle actuators. In Proceedings of the 2000 ICRA. Millennium Conference, IEEE International Conference on Robotics and Automation, Symposia Proceedings (Cat. No.00CH37065), San Francisco, CA, USA, 24–28 April 2000; Volume 4, pp. 3641–3646. [Google Scholar] [CrossRef]
- Klute, G.K.; Hannaford, B. Accounting for elastic energy storage in McKibben artificial muscle actuators. J. Dyn. Sys. Meas. Control 2000, 122, 386–388. [Google Scholar] [CrossRef]
- Davis, S.; Tsagarakis, N.; Canderle, J.; Caldwell, D.G. Enhanced modelling and performance in braided pneumatic muscle actuators. Int. J. Robot. Res. 2003, 22, 213–227. [Google Scholar] [CrossRef]
- Doumit, M.; Fahim, A.; Munro, M. Analytical modeling and experimental validation of the braided pneumatic muscle. IEEE Trans. Robot. 2009, 25, 1282–1291. [Google Scholar] [CrossRef]
- Davis, S.; Caldwell, D.G. Braid effects on contractile range and friction modeling in pneumatic muscle actuators. Int. J. Robot. Res. 2006, 25, 359–369. [Google Scholar] [CrossRef]
- Kotkas, L.; Zhurkin, N.; Donskoy, A.; Zharkovsky, A. Design and mathematical modeling of a pneumatic artificial muscle-actuated system for industrial manipulators. Machines 2022, 10, 885. [Google Scholar] [CrossRef]
- Hesse, S. The Fluidic Muscle in Application, 150 Practical Examples Using the Pneumatic Muscle; Blue Digest on Automation, Festo: Esslingen, Germany, 2003. [Google Scholar]
- Hildebrandt, A.; Sawodny, O. Cascaded control concept of a robot with two degrees of freedom driven by four pneumatic muscle actuators. In Proceedings of the 2005, American Control Conference, 2005, Portland, OR, USA, 8–10 June 2005; Volume 1, pp. 680–685. [Google Scholar] [CrossRef]
- Kerscher, T.; Albiez, J.; Zollner, J.M.; Dillmann, R. Evaluation of the dynamic model of fluidic muscles using quick-release. In Proceedings of the First IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics, BioRob 2006, Pisa, Italy, 20–22 February 2006; pp. 637–642. [Google Scholar] [CrossRef]
- Wickramatunge, K.C.; Leephakpreeda, T. Study on mechanical behaviours of pneumatic artificial muscle. Int. J. Eng. Sci. 2010, 48, 188–198. [Google Scholar] [CrossRef]
- Jouppila, V.T. Modelling and identification of a pneumatic muscle actuator system controlled by an on/off solenoid valve. In Proceedings of the 7th International Fluid Power Conference, Aachen, Germany, 22–24 March 2010; pp. 1–11. [Google Scholar]
- Pujana-Arrese, A.; Mendizabal, A.; Arenas, J.; Prestamero, R.; Landaluze, J. Modelling in Modelica and position control of a 1-DoF set-up powered by pneumatic muscles. Mechatronics 2010, 20, 535–552. [Google Scholar] [CrossRef]
- Hosovsky, A.; Havran, M. Dynamic modelling of one degree of freedom pneumatic muscle-based actuator for industrial applications. Teh. Vjesn. 2012, 19, 673–681. [Google Scholar]
- Sarosi, J.; Biro, L.; Nemeth, J.; Cveticanin, L. Dynamic modelling of a pneumatic muscle actuator with two-direction motion. Mech. Mach. Theory 2015, 85, 25–34. [Google Scholar] [CrossRef]
- Donskoj, A.S.; Kotkas, L.A.; Salova, T.P.; Barilovich, V.; Girshov, V.; Mertens, K.K.; Cherkesov, G.; Fokin, G.; Akhmetova, I.G. Modelling the static and dynamic characteristics of pneumatic muscle. IOP Conf. Ser. Earth Environ. Sci. 2019, 337, 012042. [Google Scholar] [CrossRef]
- Trojanova, M.; Hosovsky, A.; Cakurda, T. Evaluation of machine learning-based parsimonious models for static modelling of fluidic muscles in compliant mechanisms. Mathematics 2023, 11, 149. [Google Scholar] [CrossRef]
- Repperger, D.W.; Johnson, K.R.; Philips, C.A. A VSC position tracking system involving a large scale pneumatic muscle actuator. In Proceedings of the 37th IEEE Conference on Decision & Control (Cat. No.98CH36171), Tampa, FL, USA, 18 December 1998; Volume 4, pp. 4302–4307. [Google Scholar] [CrossRef]
- Serres, J.L.; Reynolds, D.B.; Philips, C.A.; Gerschutz, M.J.; Repperger, D.W. Characterization of a phenomenological model for commercial pneumatic muscle actuators. Comput. Methods Biomech. Biomed. Eng. 2009, 12, 423–430. [Google Scholar] [CrossRef]
- Kalita, B.; Dwivedy, S.K. Nonlinear dynamic response of pneumatic artificial muscle: A theoretical and experimental study. Int. J. Non-Linear Mech. 2020, 125, 103544. [Google Scholar] [CrossRef]
- Reynolds, D.B.; Repperger, D.W.; Phillips, C.A.; Bandry, G. Modelling the dynamic characteristics of pneumatic muscle. Ann. Biomed. Eng. 2003, 31, 310–317. [Google Scholar] [CrossRef]
- Colbrunn, R.W.; Nelson, G.M.; Quinn, R.D. Modelling of braided pneumatic actuators for robotic control. In Proceedings of the 2001, IEEE/RSJ International Conference on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the Next Millennium (Cat. No. 01CH37180), Maui, HI, USA, 29 October–3 November 2001; IEEE: Piscataway, NJ, USA, 2001; Volume 4, pp. 1964–1970. [Google Scholar] [CrossRef]
- Donskoy, A.S. Simulation of pressure fluctuations in pneumatic objects using ordinary differential equations. Izv. Vyss. Uchebnykh Zaved. Seriya Teknol. Tekst. Promyshlennosti 1997, 4, 94–97. [Google Scholar]
- Krichel, S.V.; Sawodny, O. Non-linear friction modelling and simulation of long pneumatic transmission lines. Math. Comput. Model. Dyn. Syst. 2013, 20, 23–44. [Google Scholar] [CrossRef]
- Stecki, J.S.; Davis, D.C. Fluid transmission lines—Distributed parameter models, part 1: A review of the state of the art. Proc. Inst. Mech. Eng. Part A 1986, 200, 215–228. [Google Scholar] [CrossRef]
- Stecki, J.S.; Davis, D.C. Fluid transmission lines—Distributed parameter models part 2: Comparison of models. Proc. Inst. Mech. Eng. Part A 1986, 200, 229–236. [Google Scholar] [CrossRef]
- Nikitin, N.V. Direct numerical modelling of three-dimensional turbulent flows in pipes of circular cross section. Fluid. Dynam. 1994, 29, 749–758. [Google Scholar] [CrossRef]
- Kern, R. Physical modelling of a long pneumatic transmission line: Models of successively defreasing complexity and their experimental validation. Math. Comput. Modell. Dyn. Syst. 2017, 23, 1–18. [Google Scholar] [CrossRef]
- Watton, J.; Tadmori, M. A comparison of techniques for the analysis of transmission line dynamics in electrohydraulic control systems. Appl. Math. Modell. 1988, 12, 457–466. [Google Scholar] [CrossRef]
- Makinen, J.; Piche, R.; Ellman, A. Fluid transmission line modelling using a variational method. J. Dyn. Syst. Meas. Control 2000, 122, 153–162. [Google Scholar] [CrossRef]
- Trukhanov, K.I. Methods for Designing Optimal Servo Pneumatic Devices for Controlling Systems with Liquid Working Media. Ph.D. Thesis, Moscow Bauman Moscow State Technical University, Moscow, Russia, 2019. [Google Scholar]
- Tseyrov, E.M. Issues of Gas Dynamics of Air Circuit Breakers; Gosenergoizdat, USSR: Moscow, Russia, 1961. [Google Scholar]
- Donskoy, A.S. Method of analytical calculation of processes in pneumatic pipelines. In Proceedings of the IX International Science and Technical Conference, Hydraulic Machines, Hydraulic Drives and Hydropneumatic Automation, Current State and Development Prospects, St. Petersburg, Russia, 7–8 June 2016; SpbPU: St. Petersburg, Russia, 2016; pp. 327–338. [Google Scholar]
- Gercz, E.V.; Krejnin, G.V. The Calculation of Pneumatic Actuators. Reference Manual; Mechanical engineering, USSR: Moscow, Russia, 1975. [Google Scholar]
- Shcherba, V.E.; Khait, A.; Pavlyuchenko, E.A.; Bulgakova, I.Y. Development and Research of a Promising Pumpless Liquid Cooling System for Reciprocating Compressors. Energies 2023, 16, 1191. [Google Scholar] [CrossRef]
| Symbol | Value | Unit |
|---|---|---|
| R | 287 | [J/kg∙K] |
| k | 1.4 | - |
| TS | 293 | [K] |
| c | 340 | [m/s] |
| λ | 0.03 | - |
| pA | 0.098 | [MPa] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kotkas, L.; Donskoy, A.; Zharkovskii, A.; Zhurkin, N. The Distributed Parameter Model of an Electro-Pneumatic System Actuated by Pneumatic Artificial Muscles with PWM-Based Position Control. Energies 2024, 17, 3381. https://doi.org/10.3390/en17143381
Kotkas L, Donskoy A, Zharkovskii A, Zhurkin N. The Distributed Parameter Model of an Electro-Pneumatic System Actuated by Pneumatic Artificial Muscles with PWM-Based Position Control. Energies. 2024; 17(14):3381. https://doi.org/10.3390/en17143381
Chicago/Turabian StyleKotkas, Lyubov, Anatolij Donskoy, Aleksandr Zharkovskii, and Nikita Zhurkin. 2024. "The Distributed Parameter Model of an Electro-Pneumatic System Actuated by Pneumatic Artificial Muscles with PWM-Based Position Control" Energies 17, no. 14: 3381. https://doi.org/10.3390/en17143381
APA StyleKotkas, L., Donskoy, A., Zharkovskii, A., & Zhurkin, N. (2024). The Distributed Parameter Model of an Electro-Pneumatic System Actuated by Pneumatic Artificial Muscles with PWM-Based Position Control. Energies, 17(14), 3381. https://doi.org/10.3390/en17143381






