Parameter Estimation and Preliminary Fault Diagnosis for Photovoltaic Modules Using a Three-Diode Model

Abstract

Accurate estimation of photovoltaic (PV) power generation can ensure the stability of regional voltage control, provide a smooth PV output voltage and reduce the impact on power systems with many PV units. The internal parameters of solar cells that affect their PV power output may change over a period of operation and must be re-estimated to produce a power output close to the actual value. To accurately estimate the power output for PV modules, a three-diode model is used to simulate the PV power generation. The three-diode model is more accurate but more complex than single-diode and two-diode models. Different from the traditional methods, the 9 parameters of the three-diode model are transformed into 16 parameters to further provide more refined estimates. To accurately estimate the 16 parameters in the model, an optimization tool that combines enhanced swarm intelligence (ESI) algorithms and the dynamic crowing distance (DCD) index is used based on actual historical PV power data and the associated weather information. When the 16 parameters for a three-diode model are accurately estimated, the I–V (current-voltage) curves for different solar irradiances are plotted, and the possible failures of PV modules can be predicted at an early stage. The proposed method is verified using a 200 kWp PV power generation system. Three different diode models that are optimized using different ESI algorithms are compared for different weather conditions. The results affirm the reliability of the proposed ESI algorithms and the value of creating more refined estimation models with more parameters. Preliminary fault diagnosis results based on the differences between the actual and estimated I–V curves are provided to operators for early maintenance reference.

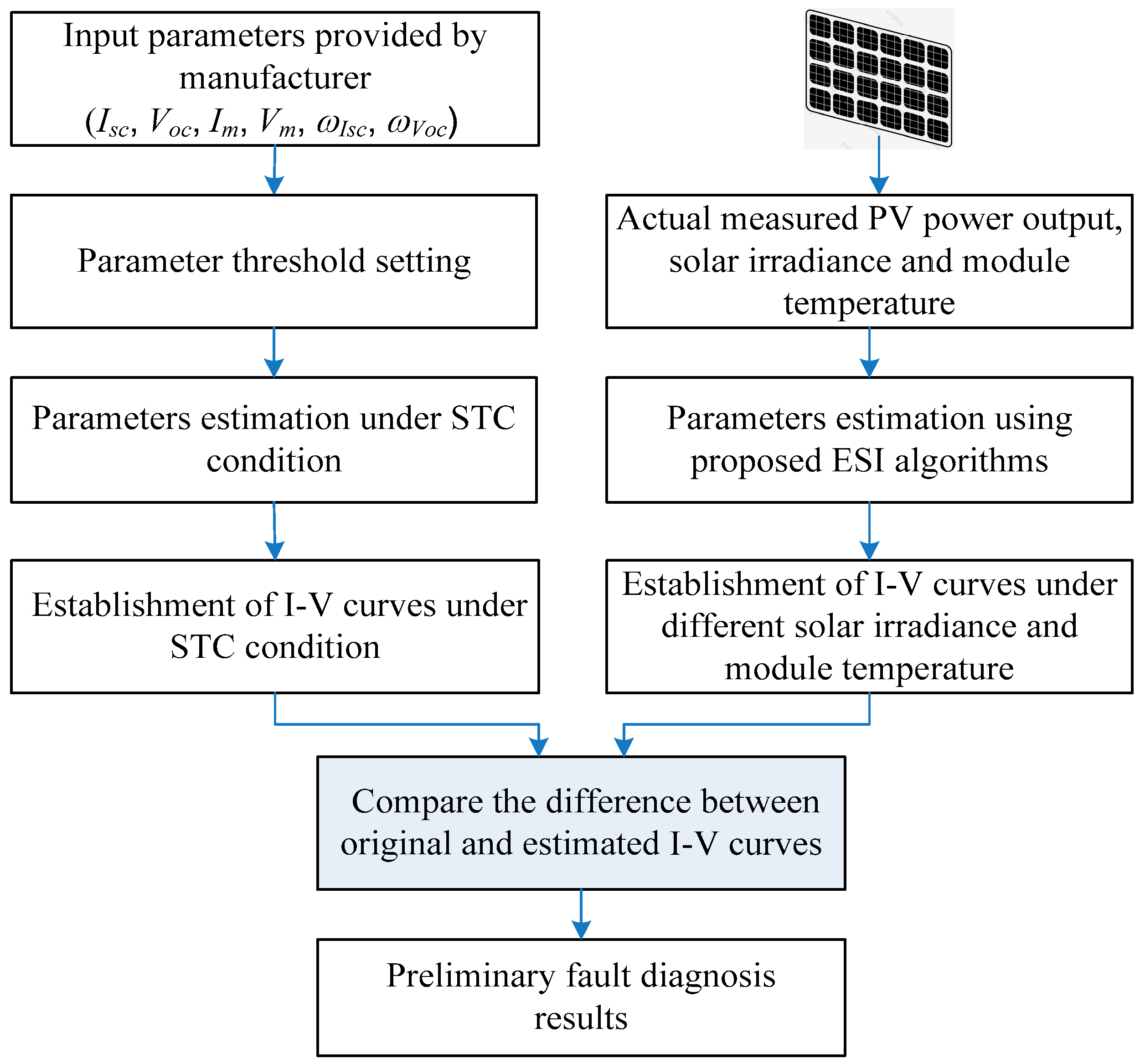
1. Introduction

The power output from solar cells is easily affected by climate and lighting. The quality of the power supply is more unstable than the supply from thermal generation systems because the power generated by photovoltaics (PVs) is intermittent and only generates electricity during the day. A high number of PV power sources may cause grid instability and threaten the security of the grid. The addition of a large amount of PV power also makes adjustment of the system frequency more sensitive. When a large-scale accident occurs, a decrease in the power system frequency is more significant, so maintaining the reliability of system operation is more challenging.

In order to reduce the impact of a large amount of PV power being added to the system, accurate PV power estimation is necessary to reduce the instability in the power generation system. If the power forecast is too high, the energy management system (EMS) must reserve more power for the grid, increasing operating costs. However, if the power forecast is too low, insufficient power reservation will cause system instability.

Precise parameter estimation for PV modules allows for accurate power estimation and reduces the instability for the EMS. Because weather conditions change regularly, an accurate and reliable parameter predictive model to represent the actual behavior of a PV power system is crucial [1]. When PV modules are produced, the manufacturer specifies the parameters for the standard test condition (STC), such as the open-circuit voltage, the short-circuit current, the output voltage and current for the maximum power point, the temperature coefficient for the short-circuit current and the temperature coefficient for open-circuit voltage. These parameters may change over a period of operation. A correction is required to produce an accurate PV power output.

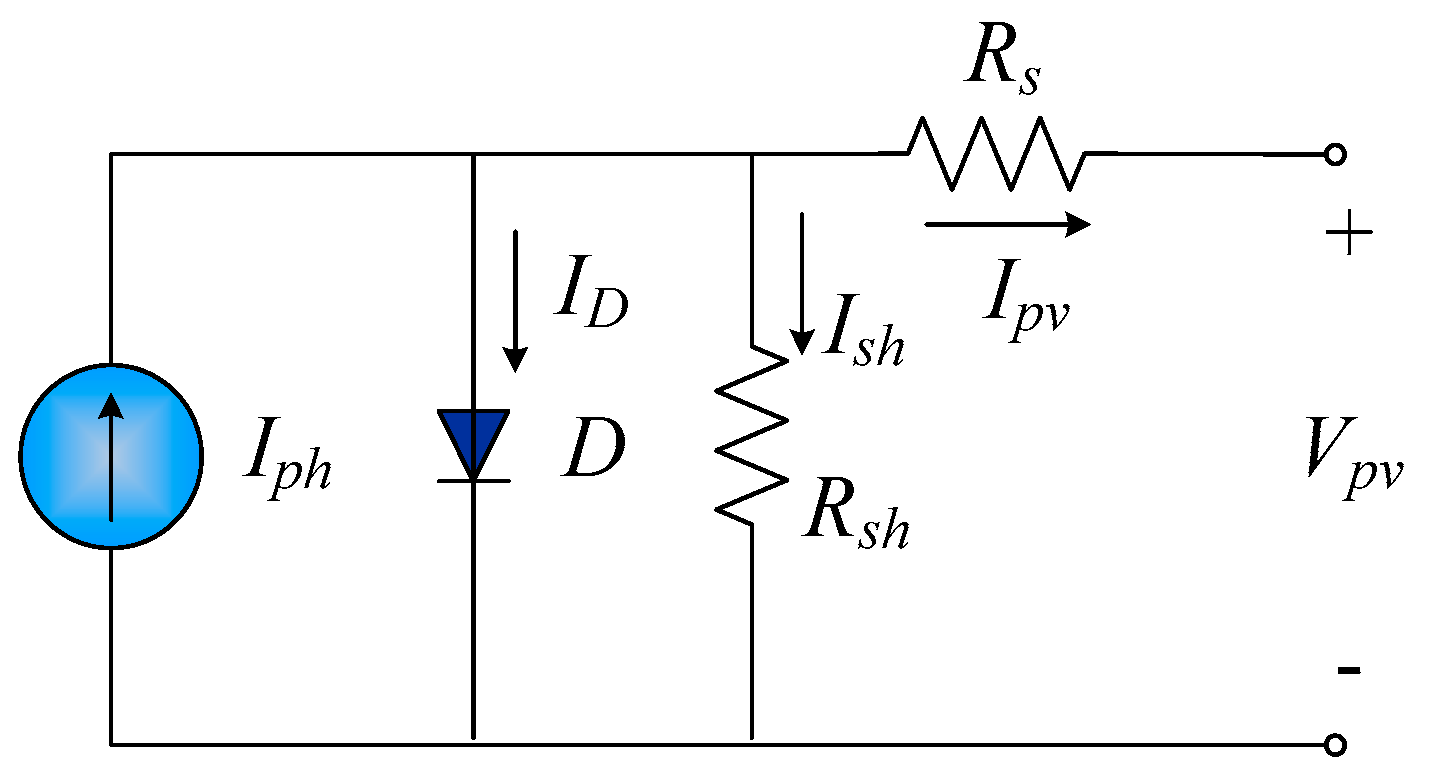
The physical models of PV modules presented in the literature include a single-diode model, a two-diode model and a three-diode model. The single-diode model [2,3,4,5] is the most widely used method, which consists of a four-parameter model and a five-parameter model. The internal parameters for a four-parameter model include photocurrent, dark saturation current, ideality factor and series resistance. This model assumes that the parallel resistance is infinite, so the open-circuit voltage decreases and does not fully reflect the leakage current for a P-N junction, which results in a large difference between the predicted and actual power. The five-parameter model considers the effect of parallel resistors, so the complexity of the model increases, but the predicted power is more accurate than that of a four-parameter model.

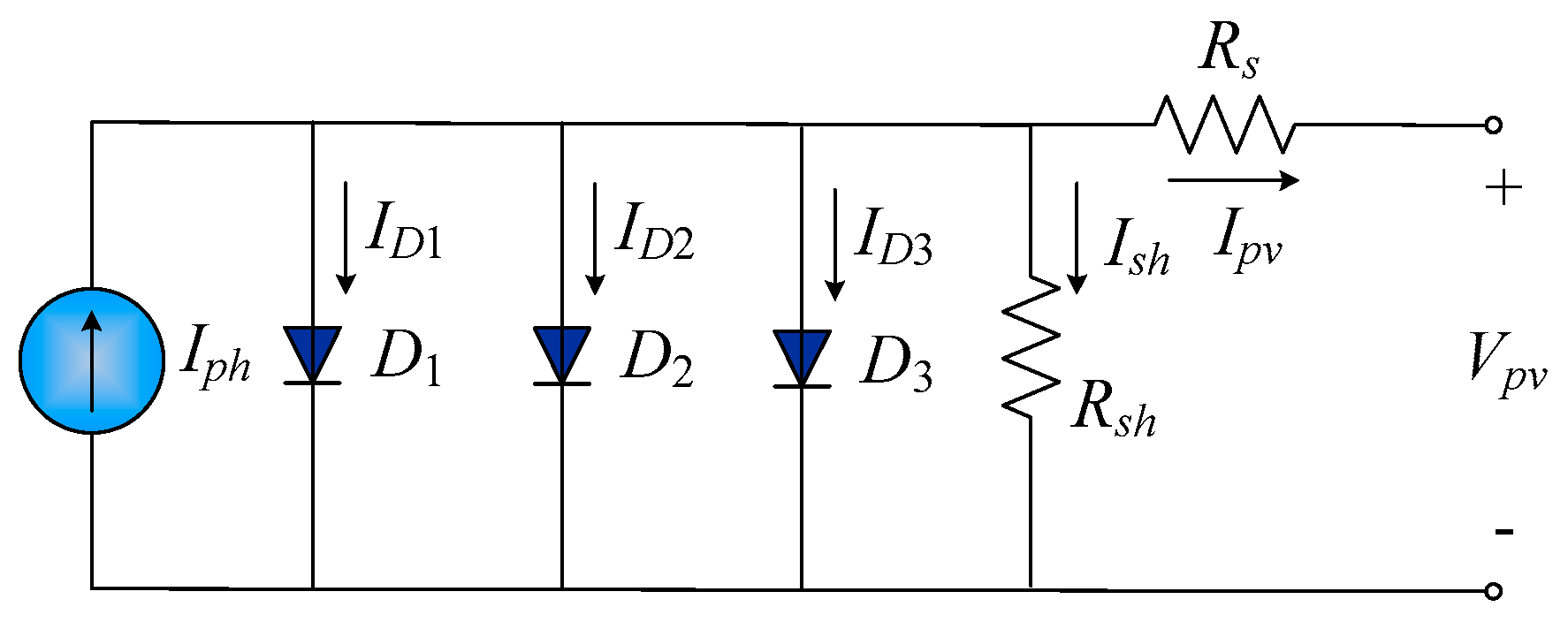
The two-diode model [6,7,8,9] is more complex than the single-diode model because there is an extra diode. For a two-diode model, the dark saturation current corresponds to two diodes and is produced by diffusion and recombination in the space charge region. This model gives an accurate prediction if there is low irradiance and shading, but there is an extra exponential term in the mathematical model, so the computational burden is increased. For a three-diode model [10,11,12,13,14,15], the dark saturation current is generated by three diodes and includes the diffusion and the recombination current for the emitter and the P-N junction, the recombination current for the depletion region and the current that is generated by the leakage current and the grain boundary effect. A three-diode model additionally uses the grain boundary effect and the influence of the leakage current, so it is more accurate. However, the number of parameters increases to nine, so the model is more complicated.

In addition to diode models, one study [16] used an analytical method to determine the internal parameters of solar cells via I–V (current–voltage) curves. This method may not perform well for a certain range of solar cell fill factors (FFs). Taking this problem into account, study [17] used an explicit two-piece quadratic model (ETPQM) to improve the accuracy of the I–V curves with higher consistency over a wider FF range. To further improve the accuracy of the ETPQM model and shorten the execution time, a low-complexity search-based parameter extraction method was proposed in study [18]. This method used a new I–V point condition to allow all the model parameters to be expressed as functions of auxiliary parameters belonging to a subset of unit intervals, whose complexity is further reduced. Most methods that use I–V curves to extract parameters only focus on five-parameter models, which may not be sufficient to accurately represent the characteristics of solar cells. The three-diode model used in this study considers nine parameters and can provide more accurate estimates than using the I–V curve method.

In addition to providing accurate power estimation results, precise parameter estimation also aids in preliminary fault diagnosis for PV modules. The main internal parameters of PV modules consist of the photocurrent, dark saturation current, ideality factor, series resistance and parallel resistance. If the estimated series resistance increases, the efficiency of the PV modules will decrease, and the solar cells begin to degrade. If the estimated parallel resistance is reduced, the solar cells may become oxidized due to thermal cycles. When the estimated values for the ideality factor and dark saturation current increase, this means that the PV modules will degrade faster.

The use of parameter estimation results for preliminary fault diagnosis of PV modules is cost-effective. Possible faults in PV power generation systems include module faults, power electronics (converter) faults or grid-side faults [19]. This study involves preliminary fault diagnosis for PV modules. To address the preliminary fault diagnosis problem, one study [20] proposed a low-cost I–V curve tracking method. An I–V curve with 26 points can be constructed within 200 ms. The real-time measurement data are used to extract the fault features for the five parameters of a single-diode model or the main characteristics of the I–V curves. The results show that the method using the main characteristics can accurately determine the degradation of the series and shunt resistances, while the method using the estimated parameters can be used to monitor long-term degradation effects. Using measurements for I–V curves, one study [21] proposed a fault diagnosis program that defines the current ratio (the ratio of the maximum current to the short-circuit current) and the voltage ratio (the maximum voltage to the open-circuit voltage). Possible faults are determined by accurately calculating the current ratio and the voltage ratio. In study [22], a standard error method was proposed to compare the difference in the I–V curves for normal operation and shading, which is used to determine whether there is a shading fault. Another study [23] provides a literature review of parameter estimation and fault detection for PV systems.

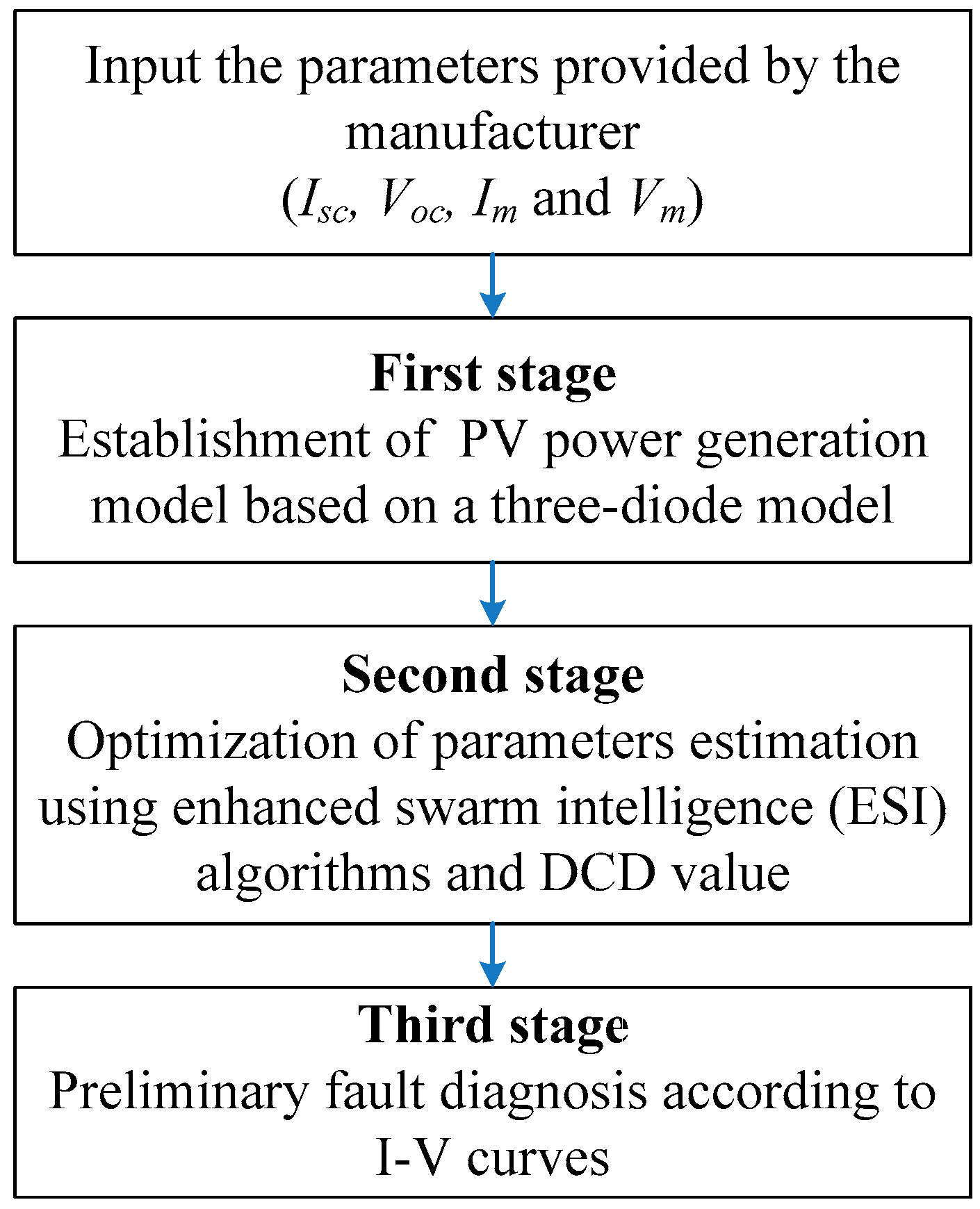
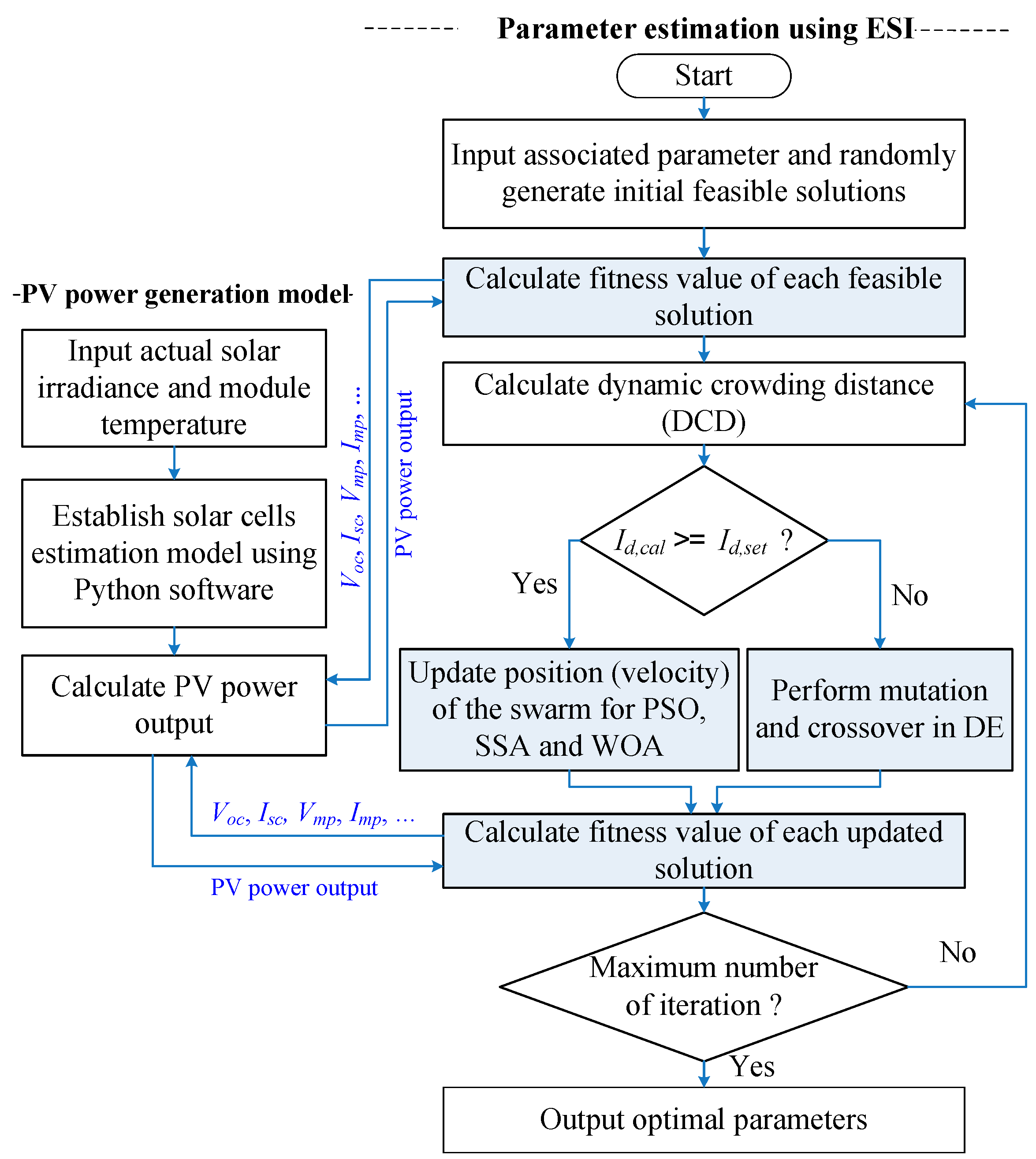
As mentioned in [10,11,12,13,14,15], distinct optimization algorithms have been proposed to optimize the nine parameters for a three-diode model. In this study, to create a more refined estimation model, the 9 parameters are transformed into 16 parameters for different solar irradiances and module temperatures. To accurately estimate the parameter values, an enhanced swarm intelligence (ESI) algorithm is used to optimize these parameters. An index of the dynamic crowing distance (DCD) is used to check whether the mutation and crossover operations in DE are performed to increase the estimation accuracy of the three-diode model. The enhanced swarm intelligence algorithms that are used are enhanced particle swarm optimization (EPSO), the enhanced salp swarm algorithm (ESSA) and the enhanced whale optimization algorithm (EWOA). When the parameters of the three-diode model are accurately estimated using an ESI algorithm, the I–V curves for different solar irradiances are established using the obtained parameters. Possible faults for PV modules are then predicted at an early stage using changes in the I–V curves.

The main contributions of this paper are the following:

• Three different diode models are used to establish a PV power generation model using the same database. The three-diode model is confirmed to be more accurate than single- and two-diode models. Different from the existing methods, the 9 parameters of the three-diode model are transformed into 16 parameters to further provide more accurate and refined estimates.
• Three enhanced swarm intelligence (ESI) algorithms such as EPSO, ESSA and EWOA are used to compare the differences in parameter estimation results. In ESI, the mutation and crossover operations in DE are used to enhance the randomness and variability of the population based on an index of the dynamic crowing distance. The reliability of the proposed ESI algorithms is confirmed using different testing data sets.
• The proposed preliminary fault diagnosis method does not require any additional detection devices, which is cost-effective for predicting possible preliminary faults in PV modules at an early stage. Changes in the I–V curve as well as changes in the series resistance, parallel resistance, ideality factor and dark saturation current indicate that the PV modules may be oxidized and degraded, which must be further addressed by maintenance operators.

The rest of this paper is organized as follows. Section 2 introduces the PV power generation models, including single-, two- and three-diode models. Section 3 describes the proposed ESI algorithms for parameter estimation. The preliminary fault diagnosis method is also introduced in this section. In Section 4, the simulation results for a 200 kWp PV power generation system are presented. Conclusions are given in Section 5.

2. Physical Models for PV Power Generation

2.1. The Single-Diode Model

The single-diode model consists of a photocurrent ($I_{ph}$), a dark saturation current ($I_{sat}$), an ideality factor ($n_{dl}$), series resistance ($R_s$) and parallel resistance ($R_{sh}$). $I_{sat}$ is a measure of the recombination in a solar cell. Greater recombination results in a larger value for $I_{sat}$. $I_{sat}$ increases as the module temperature increases and decreases as material quality increases. $R_s$ includes the material resistance, the sheet resistance, the electrode resistance and the electrode and silicon contact resistance for solar cells. $R_{sh}$ is caused by defects during manufacturing. Figure 1 shows a single-diode model. The output current is expressed as

$$I_{pv}=I_{ph}-I_{sat}\left[\mathit{exp}\left(\frac{V_{pv}+I_{pv}{R}_s}{n_{dl}{V}_T}\right)-1\right]-\frac{V_{pv}+I_{pv}{R}_s}{R_{sh}},$$

(1)

where $I_{pv}$ is the output current, $V_{pv}$ is the output voltage and $V_T$ is the thermal voltage.

Equation (1) shows that the output current ($I_{pv}$) is affected by $I_{ph}, { I}_{sat}, n_{dl}, { R}_s$ and $R_{sh}.$ These parameters are calculated using representative points on the PV characteristic curve, including the short-circuit current point ($I_{sc}$), the open-circuit voltage point ($V_{oc}$) and the maximum power point ($V_m,I_m$) as [2,3,4,5]

$$I_{ph}=\left(1+\frac{R_s}{R_{sh}}\right)I_{sc},$$

(2)

$$R_{sh}=\left(\frac{I_{sc}}{I_{ph}-I_{sc}}\right)R_s,$$

(3)

$$I_{sat}=\left(I_{sc}-\frac{V_{oc}}{R_{sh}}\right)\left[\mathit{exp}\left(-\frac{V_{oc}}{n_{dl}{V}_T}\right)\right],$$

(4)

$$N_{dl}=n_{dl}{V}_T=I_{sat}\left(\frac{V_m+I_m{R}_s}{I_m}\right)exp\left(\frac{V_m+I_m{R}_s}{n_{dl}{V}_T}\right),$$

(5)

$$R_s=\frac{\left(I_{sat}\left(\frac{V_m+I_m{R}_s}{I_m}\right)exp\left(\frac{V_m+I_m{R}_s}{n_{dl}{V}_T}\right)\right)ln\left(\frac{I_{sc}-I_m}{I_{sat}}\right)-V_m}{I_m}.$$

(6)

As shown in Equations (1)–(6), there is a recursive relationship between parameters. A traditional Newtonian iteration method [24] is usually used to solve this problem. Figure 2 shows the scheme for calculating the output current $I_{pv}$. The steps are as follows:

• Step 1: Input the initial parameters $I_{sc}$, $V_{oc}$, $V_m$ and $I_m$, as detailed in the specification sheet that is provided by the PV manufacturers.
• Step 2: Use an iterative programming method, such as the Newtonian iterative method, to solve $R_s, n_{dl}$ and $I_{sat}$ as follows.
• Step 2.1: Let $x_1={(R}_s, n_{dl}, I_{sat})$ and assign the objective function as follows:

$${f\left(x_1\right)=R}_s-\frac{\left(I_{sat}\left(\frac{V_m+I_m{R}_s}{I_m}\right)exp\left(\frac{V_m+I_m{R}_s}{n_{dl}{V}_T}\right)\right)ln\left(\frac{I_{sc}-I_m}{I_{sat}}\right)-V_m}{I_m}=0.$$

(7)

• Step 2.2: Randomly generate a set of initial $x_1$ values, $x_1^{\left(0\right)}$, and calculate ${f(x}_1^{\left(0\right)})$ and ${f^{\prime }(x}_1^{\left(0\right)})$.
• Step 2.3: Modify the $x_1$ value, namely $x_1^{\left(1\right)}$ as

$$x_1^{\left(1\right)}=x_1^{\left(0\right)}-\frac{{f(x}_1^{\left(0\right)})}{{f^{\prime }(x}_1^{\left(0\right)})}.$$

(8)

• Step 2.4: Calculate ${f(x}_1^{\left(1\right)}).$ If this value is less than the tolerance error (usually a value close to 0), then stop the convergence and record the converged value for $x_1{(R}_s, n_{dl}, I_{sat})$; otherwise, repeat step 2.3.
• Step 3: When $R_s, n_{dl}$ and $I_{sat}$ are calculated, substitute $n_{dl}$ into (5) to calculate $N_{dl}$, and substitute $I_{sat}$ into (4) to calculate $R_{sh}$. Finally, substitute $R_s$ and $R_{sh}$ into (2) to calculate $I_{ph}$.
• Step 4: Use the Newtonian iterative method and the obtained parameter values of $I_{ph}, I_{sat}, n_{dl}, R_s$ and $R_{sh}$ to calculate the output current $I_{pv}$ as follows:
• Step 4.1: Let $x_2=I_{pv}$ and assign the objective function as

$$f\left(x_2\right)=I_{pv}-\left\{I_{ph}-I_{sat}\left[\mathit{exp}\left(\frac{V_{pv}+I_{pv}{R}_s}{n_{dl}{V}_T}\right)-1\right]-\frac{V_{pv}+I_{pv}{R}_s}{R_{sh}}\right\}=0.$$

(9)

• Step 4.2: Randomly generate an initial $I_{pv}$ value, namely $x_2^{\left(0\right)}$, and calculate ${f(x}_2^{\left(0\right)})$ and ${f^{\prime }(x}_2^{\left(0\right)})$.
• Step 4.3: Modify the value of $x_2$, namely $x_2^{\left(1\right)}$, as

$$x_2^{\left(1\right)}=x_2^{\left(0\right)}-\frac{{f(x}_2^{\left(0\right)})}{{f^{\prime }(x}_1^{\left(0\right)})}.$$

(10)

• Step 4.4: Calculate ${f(x}_2^{\left(1\right)}).$ If this value is less than the tolerance error, then stop the convergence and record the converged value for $x_2\left(I_{pv}\right)$; otherwise, repeat step 4.3.

As mentioned above, the parameters for $I_{ph}, { I}_{sat}, n_{dl}, R_s$ and $R_{sh}$ are affected by $I_{sc}$, $V_{oc}$, $V_m$and $I_m$. However, these four parameters are also affected by different values of solar irradiance and module temperature as

$$I_{sc}=\frac{G}{G_r}{I}_{scr}+{\omega }_{I_{sc}}\left(T-T_r\right),$$

(11)

$$V_{oc}=V_{ocr}+{\omega }_{V_{oc}}\left(T-T_r\right),$$

(12)

$$I_m=\frac{G}{G_r}{I}_{mr}+{\omega }_{I_{sc}}\left(T-T_r\right),$$

(13)

$$V_m=V_{mr}+{\omega }_{V_{oc}}\left(T-T_r\right),$$

(14)

where $I_{scr}$, $V_{ocr}$, $V_{mr}$ and $I_{mr}$, respectively, represent the short-circuit current, the open-circuit voltage, the current at the maximum power point and the voltage at the maximum power point for the STC. ${\omega }_{I_{sc}}$ is the temperature coefficient for the short-circuit current, and ${\omega }_{V_{oc}}$ is the temperature coefficient for the open-circuit voltage. The STC is a test environment for PV modules with an irradiance of 1000 $(\mathrm{W}/{\mathrm{m}}^2)$, a module temperature of 298 (K) and an air mass of 1.5.

2.2. The Two-Diode Model

For the two-diode model, the dark saturation current is produced by diffusion and recombination in the space charge region. Figure 3 shows the equivalent circuit for a two-diode model. The output current is calculated as

$$I_{pv}=I_{ph}-I_{sat1}\left[\mathit{exp}\left(\frac{V_{pv}+I_{pv}{R}_s}{n_{dl,1}{V}_T}\right)-1\right]-I_{sat2}\left[\mathit{exp}\left(\frac{V_{pv}+I_{pv}{R}_s}{n_{dl,2}{V}_T}\right)-1\right]-\frac{V_{pv}+I_{pv}{R}_s}{R_{sh}},$$

(15)

where $I_{sat1}$ represents the dark saturation current in the neutral region, and $I_{sat2}$ is used to compensate for the recombination loss in the depletion region [25].

As shown in (15), seven parameters must be estimated: $I_{ph}$, $I_{sat1}$, $I_{sat2}$, $n_{dl,1}$, $n_{dl,2}$, $R_s$ and $R_{sh}$. The process of using the Newtonian iteration method to solve the seven parameters in the two-diode model is more complex than in the single-diode model. In order to simplify the solution process, Ishaque et al. [26] assumed that $I_{sat1}$ = $I_{sat2}=I_{sat}$ and, according to the Schockley diode diffusion theory [27], selected $n_{dl,1}$ = 1 and $n_{dl,2}$ ≥ 1.2 to produce the best fitting results. Based on these basic assumptions, the solution process for solving the output current of the two-diode model is similar to that of the single-diode model, except that the variable $x_1={(R}_s,n_{dl},I_{sat})$ in step 2.1 is changed to ${(R}_s,n_{dl,2},I_{sat})$ and Equation (9) is replaced with a two-diode model. The two-diode model is more complex than the single-diode model but gives a more accurate estimate for low irradiance and shading.

2.3. The Three-Diode Model

For a three-diode model, the dark saturation current is produced by three diodes. As shown in Figure 4, $I_{D1}$ is the diffusion and recombination current for the emitter and the P-N junction, $I_{D2}$ is the recombination current for the depletion region and $I_{D3}$ is derived using the leakage current and the effect of the grain boundaries. The output current from a three-diode model is calculated as

$$I_{pv}=I_{ph}-I_{sat1}\left[\mathit{exp}\left(\frac{V_{pv}+I_{pv}{R}_s}{n_{dl,1}{V}_T}\right)-1\right]-I_{sat2}\left[\mathit{exp}\left(\frac{V_{pv}+I_{pv}{R}_s}{n_{dl,2}{V}_T}\right)-1\right]-I_{sat3}\left[\mathit{exp}\left(\frac{V_{pv}+I_{pv}{R}_s}{n_{dl,3}{V}_T}\right)-1\right]-\frac{V_{pv}+I_{pv}{R}_s}{R_{sh}}.$$

(16)

Equation (16) has a total of nine parameters: $I_{ph}$, $I_{sat1}$, $I_{sat2}$,$I_{sat3}$, $n_{dl,1}$, $n_{dl,2}$,$n_{dl,3}$, $R_s$ and $R_{sh}.$ 

Table 1. Comparisons of different diode models.

Model	Parameter	Advantage	Disadvantage
Single-diode	$I_{ph},I_{sat},n_{idl},$$\mathrm{and} R_s$	simplest suitable when high precision is not required	output current cannot be accurately estimated at higher temperature
	$I_{ph}, I_{sat}, n_{dl}, R_s$$\mathrm{and} R_{sh}$	more accurate than a four-parameter model at higher temperature widely used	does not produce accurate estimation for low irradiance and shading
Two-diode	$I_{ph},{ I}_{sat1},$ $I_{sat2},$ $n_{dl,1},$ $n_{dl,2}, R_s$ $\mathrm{and} R_{sh}$	more accurate than a single-diode model	solution process is complicated when using a Newtonian iteration method
Three-diode	$I_{ph}, I_{sat1}, I_{sat2}, { I}_{sat3},$$n_{dl,1}, n_{dl,2}, n_{dl,3}, R_s$ $\mathrm{and} R_{sh}$	also considers the effect of the grain boundary and the impact of the leakage current most accurate	most complex usually requires a multi-agent optimization algorithm to solve parameters

compares the models with different numbers of diodes.

Similar to in the single-diode model, the Newtonian iteration method can be used to calculate the nine parameter values. However, the method of using the Newtonian iteration method to solve the nine parameters in a three-diode model may easily fall into local optimal solutions due to its high complexity. A multi-agent optimization algorithm is usually used to estimate these parameter values [28]. To further provide more accurate and finer estimation for a three-diode model, the 9 parameters are transformed into 16 parameters based on different solar irradiances and module temperatures, as follows:

$$\begin{gathered} \left[I_{ph},I_{sat1},I_{sat2}, I_{sat3},n_{dl,1},n_{dl,2}, n_{dl,3},R_s,R_{sh}\right] \\ =f[I_{scr}, V_{ocr},{ I}_{mr}, V_{mr}, {I_{sat1}, I}_{sat2}, I_{sat3},{ n}_{dl1},{ n}_{dl2},{{ n}_{dl3}, G}_r,{ T}_r,{ R}_s,{ R}_{sh}, {\omega }_{I_{sc}},{ \omega }_{V_{oc}}]. \end{gathered}$$

(17)

Equation (17) is integrated from (2)–(6) and (11)–(14), which shows that the 9 parameters are controlled by the 16 parameters. This study uses ESI algorithms to optimize the 16 parameters. Once the 16 parameters are determined using ESI, the output current ${(I}_{pv})$ as well as the output power can be calculated using (16).

3. The Proposed Method

As shown in Figure 5, the proposed method consists of three stages: establishment of a PV power generation model using a three-diode model, optimization of the parameter estimation using ESI algorithms and preliminary fault diagnosis using the actual measured I–V curves. The following describes the methods for parameter optimization and preliminary fault diagnosis.

3.1. Parameter Estimation

As described in Section 2, the three-diode model is more accurate but more complex than the single- and two-diode models. The traditional method to optimize these parameters using Newtonian iteration is time-consuming, and convergence is problematic. ESI algorithms such as EPSO, ESSA and EWOA, combined with an index of the DCD, are used to optimize these parameter values. Figure 6 shows a schematic diagram of the proposed parameter estimation method. The following describes the proposed ESI methods and the steps to optimize the 16 parameters.

3.1.1. PSO Algorithm

PSO is a multi-agent algorithm that updates the position and velocity of particles based on the swarm and its own experiences as follows [29]:

$$v_d\left(t+1\right)=w{v}_d\left(t\right)+c_1\times r_1\times \left(R_{b,d}\left(t\right)-p_d\left(t\right)\right)+c_2\times r_2\times \left(G_{b,d}\left(t\right)-p_d\left(t\right)\right),$$

(18)

where $v_d\left(t\right)$ is the velocity of the dth particle at the tth iteration; $w$ is an inertial weight, which is used to balance the local search and global search of particles; $c_1$ and $c_2$ are acceleration factors that, respectively, control the movement of particles towards the optimal position for an individual and the group. If the value of the acceleration factor is too large, the particles deviate from the optimal solution. The movement of particles is restricted if the value for the acceleration factor is too small. $r_1$ and $r_2$ are random numbers between 0 and 1, which are used to maintain the diversity of the group. $p_d\left(t\right)$ is the position of the dth particle at the tth iteration,$R_{b,d}\left(t\right)$ is the best position for the dth particle at the tth iteration and $G_{b,d}\left(t\right)$ is the best position for the group at the tth iteration.

3.1.2. The SSA

The SSA simulates the group activities for a salp swarm chain to perform exploration and exploitation strategies [30,31]. During foraging, salps naturally form a group chain that consists of a leader salp and follower salps. The leader salp swims in front and guides the group forward. Follower salps update their position using the position of the leader salp. The leader salp updates the swimming direction according to the best (food) position as

$$p_1^j(t+1)=\left\{\begin{array}{c}{p}_b^j\left(t\right)+k_1\left(\left(p_{1, max}^j-p_{1, min}^j\right)\times k_2+p_{1, min}^j\right), k_3\le 0.5 \\ p_b^j\left(t\right)-k_1\left(\left(p_{1, max}^j-p_{1, min}^j\right)\times k_2+p_{1, min}^j\right), k_3>0.5,\end{array}\right.$$

(19)

where $p_1^j(t+1)$ is the updated position of the jth variable for the leader salp, $p_b^j\left(t\right)$ is the best position for the jth variable, $p_{1, max}^j$ and $p_{1, min}^j$ are the upper and lower limits for the jth variable,$k_2$ and $k_3$ are uniform random variables between 0 and 1 and $k_1$ is used to maintain the balance between exploration and exploitation, with

$$k_1=2exp\left(-{\left(\frac{4t}{t_m}\right)}^2\right),$$

(20)

where t is the current number of iterations and $t_m$ is the maximum number of iterations.

When the position of the leader salp is updated, the positions of the follower salps are updated using the formula

$$p_i^j\left(t+1\right)=\frac{1}{2}\left(p_i^j\left(t\right){+p}_{i-1}^j\left(t\right)\right),$$

(21)

where $i=2, 3, \dots , F_s$ and $F_s$ are the number of follower salps.

3.1.3. The WOA

A WOA is a multi-agent optimization tool that simulates the predation behavior of humpback whale groups [32]. A WOA uses surrounding prey and bubble net attacking strategies to catch fish as follows.

$$\overrightarrow{p}\left(t+1\right)=\left\{\begin{array}{c}{\overrightarrow{p}}_b\left(t\right)-\overrightarrow{Y}·\overrightarrow{Z}, if r<0.5 \\ \left|{\overrightarrow{p}}_b\left(t\right)-\overrightarrow{p}\left(t\right)\right|·e^{bl}·\mathit{cos}\left(2\pi l\right)+{\overrightarrow{p}}_b\left(t\right), if r \ge 0.5, \end{array}\right.$$

(22)

$$\overrightarrow{Z}=\left|\overrightarrow{W}·{\overrightarrow{p}}_b\left(t\right)-\overrightarrow{p}\left(t\right)\right|,$$

(23)

where $\overrightarrow{p}\left(t\right)$ is the position vector for a humpback whale, ${\overrightarrow{p}}_b\left(t\right)$ is the best position and $\overrightarrow{Y}$ and $\overrightarrow{Z}$ are coefficient vectors, where $\overrightarrow{Y}=2\overrightarrow{d}·\overrightarrow{q}-\overrightarrow{d}$ and $\overrightarrow{W}=2·\overrightarrow{q}$. The value of d decreases linearly from 2 to 0 during the iteration process, and $\overrightarrow{q}$ is a random vector between 0 and 1. The value of b is a constant that defines the logarithmic spiral, l is a random variable between 0 and 1 and the term $\left|{\overrightarrow{p}}_b\left(t\right)-\overrightarrow{p}\left(t\right)\right|$ represents the distance between the humpback whale and the prey.

A WOA also uses a “search for prey” strategy to explore for other prey.

$$\overrightarrow{p}\left(t+1\right)={\overrightarrow{p}}_r-\overrightarrow{Y}·\overrightarrow{Z},$$

(24)

where $\overrightarrow{Z}=\left|\overrightarrow{W}·{\overrightarrow{p}}_r-\overrightarrow{p}\right|$ and ${\overrightarrow{p}}_r$ is the current random position vector.

3.1.4. DE Algorithm

A DE is a stochastic evolutionary algorithm that uses mutation and crossover to evolve offspring [33]. Mutation is performed by randomly selecting three parent variables for differential operation as follows.

$$p_i^j\left(t+1\right)=p_i^{r_1}\left(t\right)+R_m\left(p_i^{r_2}\left(t\right)-p_i^{r_3}\left(t\right)\right),$$

(25)

where $p_i^j\left(t+1\right)$ is the jth variable for the ith offspring particle, $p_i^{r_1}\left(t\right), p_i^{r_2}\left(t\right)$ and $p_i^{r_3}\left(t\right)$ are three randomly selected parent variables and $R_m$ is the mutation rate.

To increase the diversity of the population, after mutation, the variables are then subject to a crossover process to determine new offspring. The form of the offspring is determined by the crossover rate (CR) as

$$z_i^j\left(t+1\right)=\left\{\begin{array}{c}{p}_i^j\left(t+1\right), if \mu \le CR\\ p_i^j\left(t\right), otherwise \end{array}\right.,$$

(26)

where $\mu$ is a random number between 0 and 1. Equation (26) shows that if the randomly generated $\mu$ is less than or equal to the crossover rate, the jth variable for the offspring updates to the value after mutation (as shown in (25)). Otherwise, the jth variable for the offspring retains the value before mutation.

As mentioned above, PSO, the SSA, the WOA and DE have been developed individually to optimize the parameters of solar cells [29,30,31,32,33]. PSO, the SSA and the WOA are swarm intelligence (SI) algorithms that use a multi-agent method to perform exploration and exploitation strategies based on different group activities. The results show that the SI algorithm allows for an efficient solution for parameter estimation with solar cells. To further enhance the randomness and variability of the population, DE is used based on an index of the DCD value. The DCD is calculated as [34]

$$I_{d,cal}=\frac{\sum _{k=1,k\ne \mathrm{i}}^{N_s}\left|f_{MSE,i}-f_{MSE,k}\right|}{f_{MSE,\mathrm{m}\mathrm{a}\mathrm{x}}-f_{MSE,\mathrm{m}\mathrm{i}\mathrm{n}}},$$

(27)

where $f_{MSE,i}$ is the fitness value for the ith feasible solution, $f_{MSE,k}$ is the fitness value for the kth feasible solution, $f_{MSE,\mathrm{m}\mathrm{a}\mathrm{x}}$ and $f_{MSE,\mathrm{m}\mathrm{i}\mathrm{n}}$ are the maximum and minimum fitness values. Equation (27) shows that the smaller the DCD value, the denser the population.

If the calculated DCD value is less than the setting value, the population is relatively crowded, and the mutation and crossover operations in DE need to be performed to disperse individuals. Details of the steps of the parameter estimation process using ESI algorithms are described below.

3.1.5. Steps of the Parameter Estimation Process

As shown in Figure 6, the steps for the proposed parameter estimation process are described in the following:

• Step 1: Input the parameters provided by the manufacturer. Set the parameters that are required for ESI algorithms.
• Step 2: Randomly generate initial feasible solutions as follows:

$$p_i^j\left(0\right)=p_{i,min}^j+r_{\mathrm{a}}\left(p_{i,u}^j-p_{i,L}^j\right), j=1, 2, \dots , D i=1, 2, \dots , N_s,$$

(28)

where $p_i^j\left(0\right)$ is the initial solution for the jth parameter (variable) of the ith particle, $p_{i,u}^j$ and $p_{i,L}^j$ are the upper and lower limits for the parameters, $r_{\mathrm{a}}$ is a uniform random variable between 0 and 1, $D$ is the number of parameters (variables) and $N_s$ is the number of particles. Equation (28) constrains each parameter value to the lower and upper bounds of each feasible solution.

For this study, the position vector for the ith particle for the three-diode model is

$$p_i\left(t\right)=\left[I_{ph},I_{sat1},I_{sat2},I_{sat3},n_{i,1},{ n}_{i,2},{ n}_{i,3},R_s, R_{sh}\right].$$

(29)

For different values of solar irradiance and module temperature, (29) becomes

$$p_i\left(t\right)=\left[I_{scr}, V_{ocr},{ I}_{mr}, V_{mr}, {I_{sat1}, I}_{sat2}, I_{sat3},{ n}_{dl1},{ n}_{dl2}, n_{dl3},{ G}_r, T_r,{ R}_s,{ R}_{sh}, {\omega }_{I_{sc}},{\omega }_{V_{oc}}\right].$$

(30)

• Step 3: Calculate the fitness value for each feasible solution as

$$f_{MSE}=\frac{1}{N}\sum _{i=1}^N{(P_i-{\widehat{P}}_i)}^2,$$

(31)

where $f_{MSE}$ is the fitness value using the mean squared error (MSE), $P_i$ is the actual PV power, ${\widehat{P}}_i$ is the estimated PV power and N is the number of data points that are used. The MSE is used because it gives a smoother and differentiable curve for the estimation error. As shown in Figure 6, a subroutine for the three-diode power generation model is used to calculate the fitness value for each particle.

• Step 4: Calculate the DCD value as shown in (27). If the calculated DCD value ($I_{d,cal}$) is greater than or equal to the setting DCD value ($I_{d,set}$), update the position (or velocity) of the swarm for the ESI algorithms such as PSO, the SSA and the WOA from (18)–(24). Otherwise, perform mutation and crossover operations in DE from (25)–(26) to disperse the population. In this study, the value for $I_{d,set}$ is set at 0.8.
• Step 5: Calculate the fitness value for each updated solution using (31).
• Step 6: Determine whether the maximum number of iterations has been achieved. If this condition is satisfied, output the optimal parameter solution; otherwise, repeat steps 4 to 5 until the stopping condition is achieved.

3.2. Preliminary Fault Diagnosis

A PV module may fail during long-term operation. For the three-diode model, nine parameters affect the PV power output and the deviation in the I–V curves. Changes in the I–V curves are used to determine the preliminary faults for a PV module. The parameters that affect any change in the I–V curves are described in the following.

3.2.1. Series Resistance ($R_s$)

The series resistance is the sum of the resistance of a solar cell and the connection resistance between the sheets. An increase in series resistance occurs if there is a mismatch in the electrical characteristics between cells in the panel due to damage or erosion of the interconnecting busbars. This is also indicative of cell degradation due to daily thermal cycling [35]. Any change in the series resistance is observed using the I–V curve. If the series resistance increases, the gradient of the I–V curve decreases and efficiency decreases because the solar cells begin to degrade [36].

3.2.2. Parallel Resistance ($R_{sh}$)

Parallel resistance is caused by defects in the P-N junction. The significance of the defect affects the leakage current for the P-N junction, so a short circuit is possible. The effect of parallel resistance on the I–V curve is reflected in the gradient of the curve for the short-circuit current versus the maximum power point. Smaller parallel resistance will produce a larger slope and greater oxidation due to thermal cycling of solar cells exposed to sunlight for a long time. [37]. As the parallel resistance approaches infinity, the gradient is zero.

3.2.3. Ideality Factor ($n_{dl}$) and the Dark Saturation Current ($I_{sat}$)

The values for the ideality factor and the dark saturation current for a solar cell increase over time. If there are crystal defects at the P-N junction or the solar cell has a high density of defects, the increase in the value is more significant [38]. The ideality factor is also used to detect panel corrosion and a decrease in potential due to a parasitic current. An increase in the value of the ideality factor and the dark saturation current accelerate the degradation of the PV modules.

Figure 7 shows the preliminary fault diagnosis process using the I–V curves. The original I–V curves are first created under the STC. The estimated I–V curves are created using the obtained parameters for different values of solar irradiance and module temperature. The preliminary fault diagnosis process involves a comparison of the original and estimated I–V curves.

4. Numerical Results

The proposed method is applied to a 200 kWp PV power generation system. Data were collected in 2019 from January to December with a resolution of one hour and include historical PV power output, solar irradiance and module temperature, which were provided by the cooperation company. The historical PV power data are collected using a Hioki power meter, while the data on solar irradiance and module temperature are collected using a Fluke luminometer which satisfies the international test requirements [39]. When outlier data are deleted, 80% of the remaining data are used for training, and 20% are used for testing. During the training stage, ESI algorithms are used to determine the parameter values for a three-diode power generation model. During the testing stage, data for 10 days, which include five different weather types, such as sunny, light cloud, cloudy, heavy cloud and rain, are used to verify the performance of the constructed PV power generation model. These five weather types are taken from the weather forecasts of the Taiwan Central Weather Administration (TCWA). The program is executed using Python version 3.9.12 software in a Win-11 system with i7-10700 CPU.

The criterion for the mean relative error (MRE) is used to determine the estimation accuracy.

$$MRE=\frac{1}{N_m}{\sum }_{i=1}^{N_m}\left|\frac{P_i-{\widehat{P}}_i}{P_{cap}}\right|\times 100\%,$$

(32)

where $P_i$ is the actual power, ${\widehat{P}}_i$ is the estimated power, $P_{cap}$ is the capacity of the PV power generation system and $N_m$ is the number of data to be estimated.

4.1. Parameter Estimation Results

The PV manufacturer specifies values for six basic parameters: open-circuit voltage ($V_{OC}$), short-circuit current ($I_{SC}$), maximum voltage ($V_m$), maximum current ($I_m$), the temperature coefficient for a short-circuit current (${\omega }_{I_{sc}}$) and the temperature coefficient for open-circuit voltage (${\omega }_{V_{oc}}$). Values for other parameters that are not provided by the manufacturer must be set according to the experience of the operators or determined using a Newtonian iteration method.

Table 2. The range of parameter settings.

Parameter	Range	Parameter	Range
VOCr (V)	66.4~69	ωIsc (A/K)	0.000681~0.00069
ISCr (A)	3.66~5.40	ωVoc (V/K)	−0.166~−0.05
Vmr (A)	52~55	Isat1 (A)	1.16 $\times {10}^{-15}$~1.16 ${\times 10}^{-7}$
Imr (A)	3.51~3.65	Isat2 (A)	1.16 ${\times 10}^{-15}$~1.16 ${\times 10}^{-7}$
Gr (W/m2)	1000~1050	Isat3 (A)	1.16 $\times {10}^{-15}$~1.16 ${\times 10}^{-7}$
Tr (K)	298~310	ndl,1	1.0~1.2
Rsh (Ω)	80~150	ndl,2	1.2~2.0
Rs (Ω)	2.4~4.0	ndl,3	1.2~2.0

shows the range of parameter settings for a three-diode power generation model.

Table 3. Parameter values for PSO algorithm, SSA and WOA.

PSO			SSA	WOA
$\mathit{w}$	${\mathit{c}}_1$	${\mathit{c}}_2$	${\mathit{k}}_1$	$\overrightarrow{\mathit{Y}}$	$\overrightarrow{\mathit{W}}$
0.4	0.5	0.55	${5\times 10}^{-4}exp\left({-\left(\frac{0.65t}{t_m}\right)}^2\right)$	$0.45\overrightarrow{d}·\overrightarrow{q}-\overrightarrow{d}$	$0.85·\overrightarrow{q}$

shows the parameter values for the PSO algorithm, SSA and WOA.

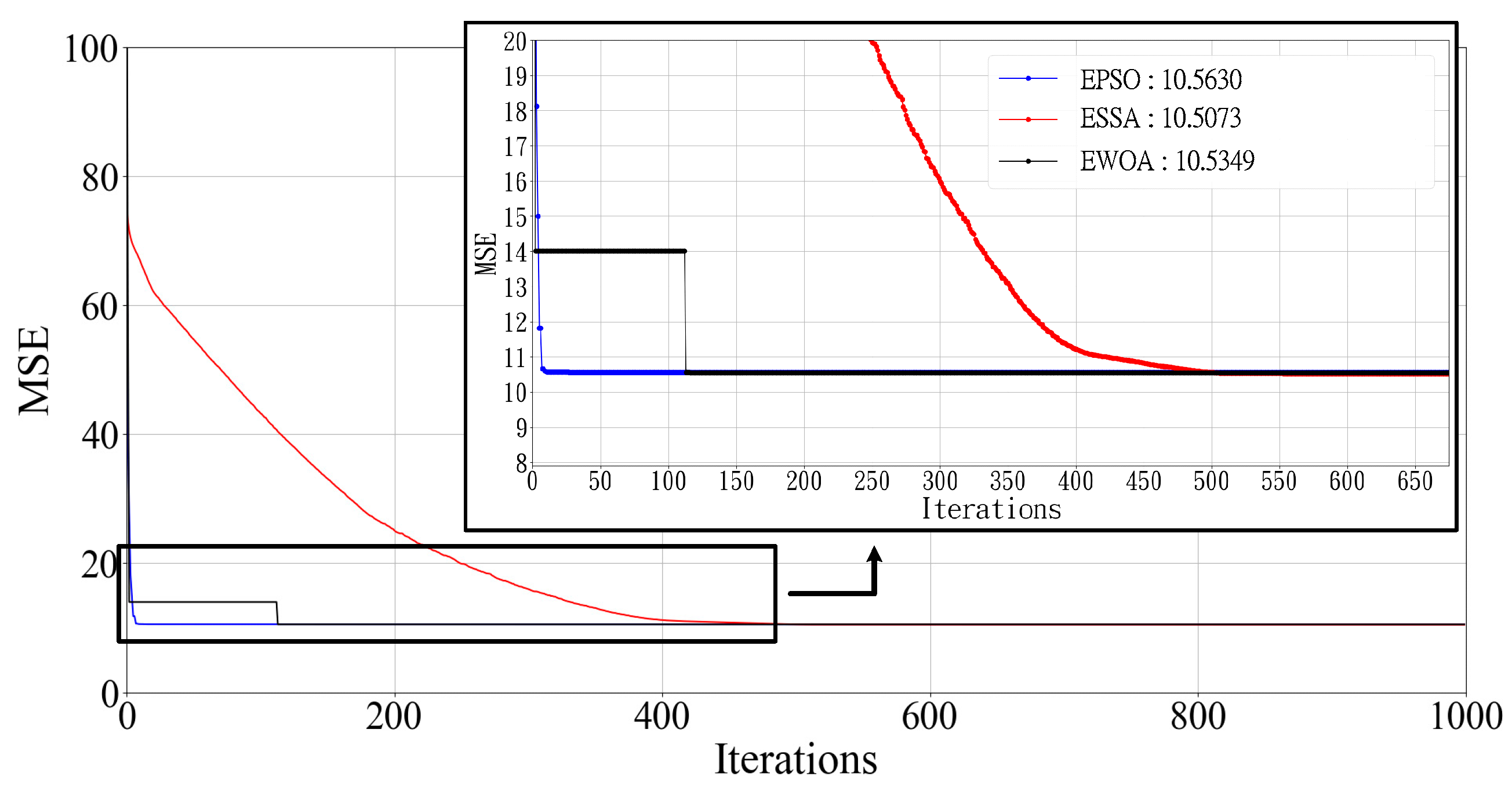
The optimization process uses a population size of 60 and 1000 iterations. Figure 8 shows the convergence of the three optimization algorithms. EPSO converges faster than the ESSA and EWOA methods. The execution time for 1000 iterations of each of the three algorithms is about 1 h 20 min to 1 h 30 min. The respective fitness values (MSE) using EPSO, the ESSA and the EWOA are 10.563, 10.507 and 10.535.

Table 4. The parameter values before and after optimization.

Parameter	Before Optimization	After Optimization
	Newton *	EPSO	ESSA	EWOA
VOCr (V)	66.4	68.25	66.57	66.4
ISCr (A)	3.66	3.75	3.72	3.68
Vmr (A)	52	54.67	54.43	52.0
Imr (A)	3.51	3.56	3.55	3.51
Gr (W/m2)	1000	1031.23	1035.99	1000
Tr (K)	298	300.63	298	298
Rsh (Ω)	150	86.81	92.60	81.09
Rs (Ω)	2.4	3.2742	3.0712	2.4248
ωIsc (A/K)	0.000681	0.000686	0.000681	0.00681
ωVoc (V/K)	−0.166	−0.069	−0.145	−0.164
Isat1 (A)	1.16 ${\times 10}^{-15}$	2.50 ${\times 10}^{-10}$	3.55 ${\times 10}^{-10}$	1.44 ${\times 10}^{-11}$
Isat2 (A)	1.16 ${\times 10}^{-15}$	1.23 $\times {10}^{-11}$	2.65 ${\times 10}^{-11}$	0.12 ${\times 10}^{-10}$
Isat3 (A)	1.16 $\times {10}^{-15}$	1.41 $\times {10}^{-11}$	2.14 ${\times 10}^{-11}$	8.32 $\times {10}^{-10}$
ndl,1	1.2	1.1541	1.1864	1.0024
ndl,2	1.8609	1.891	1.7684	1.2124
ndl,3	1.8609	1.648	1.7634	1.2124

* Parameter values are obtained from PV manufacturer, set by operator experience or determined using Newtonian iteration method.

shows the parameter values before and after optimization. Figure 9 shows the estimation results for four different weather types. The curves marked with “Actual” in the figure represent the actual measured values of the PV power data. Regardless of the weather conditions, the estimation results for the three ESI methods are very close.

Table 5. Estimation results for 10 testing days (MRE%).

Date	Weather Type	Newton	EPSO	ESSA	EWOA
1/11	Cloudy	4.581	0.918	0.933	0.938
7/13	Cloudy	5.775	2.063	2.056	2.061
1/19	Heavy cloud	1.828	0.445	0.424	0.424
6/19	Heavy cloud	1.118	0.773	0.740	0.751
2/12	Light cloud	5.830	1.837	1.838	1.854
5/14	Light cloud	5.515	1.984	1.978	1.987
1/21	Rainy	0.573	0.670	0.626	0.633
3/11	Rainy	0.402	1.013	0.961	0.962
8/7	Sunny	5.048	1.058	1.043	1.059
7/12	Sunny	4.981	0.835	0.824	0.815
	Average	3.565	1.159	1.142	1.148

shows the estimation results for 10 testing days. The respective average estimation errors for EPSO, the ESSA and the EWOA are 1.159%, 1.142% and 1.148%, which is better than the estimation error of 3.565% using the Newtonian iteration method. However, the estimation errors produced by using Newtonian iteration method on two rainy days are so small that the three ESI algorithms are unable to find parameters that produce lower estimation errors.

To affirm the reliability of the proposed ESI algorithms, another 10 days of data from five different weather types are used for testing. As shown in

Table 6. Estimation results for another 10 testing days (MRE%).

Date	Weather Type	Newton	EPSO	ESSA	EWOA
6/13	Cloudy	4.758	1.105	1.201	1.041
6/30	Cloudy	4.925	1.952	1.924	1.885
3/3	Heavy cloud	2.025	0.564	0.557	0.553
4/21	Heavy cloud	2.215	0.625	0.713	0.670
1/31	Light cloud	4.885	2.012	1.986	2.059
10/16	Light cloud	5.054	2.051	1.924	2.095
3/25	Rainy	0.502	0.625	0.700	0.756
4/16	Rainy	0.512	0.755	0.825	0.666
4/25	Sunny	4.885	1.111	0.892	1.015
9/11	Sunny	5.187	0.905	0.771	0.785
	Average	3.565	1.171	1.149	1.152

, the respective average estimation errors for EPSO, the ESSA and the EWOA are 1.171%, 1.149% and 1.152%, which gives a better estimation accuracy than the Newtonian iteration method. Compared with the results in Table 5, the estimation results of the proposed ESI algorithms are stable, and the estimation errors are very close. Similarly, the proposed ESI algorithms cannot find better estimates than the Newtonian iteration method on two rainy days.

In addition, to verify the effect of DE on the proposed ESI algorithms, the results for the swarm intelligence (SI) and ESI algorithms for a three-diode model are provided in

Table 7. The effect of DE in the proposed ESI algorithms for a three-diode model (MRE%).

Date	Weather Type	PSO	EPSO	SSA	ESSA	WOA	EWOA
1/11	Cloudy	0.932	0.918	1.323	1.201	1.093	0.938
7/13	Cloudy	2.152	2.063	2.012	1.924	2.125	2.061
1/19	Heavy cloud	0.445	0.445	0.563	0.557	0.472	0.424
6/19	Heavy cloud	0.786	0.773	0.752	0.713	0.781	0.751
2/12	Light cloud	1.865	1.837	2.013	1.986	1.866	1.854
5/14	Light cloud	1.985	1.984	1.925	1.924	2.092	1.987
1/21	Rainy	0.686	0.670	0.702	0.700	0.686	0.633
3/11	Rainy	1.013	1.013	0.835	0.825	0.972	0.962
8/7	Sunny	1.122	1.058	0.912	0.892	1.101	1.059
7/12	Sunny	0.904	0.835	0.804	0.771	0.845	0.815
	Average	1.189	1.159	1.184	1.142	1.203	1.148

. The results show that the average estimation errors for PSO, EPSO, the SSA, the ESSA, the WOA and the EWOA are 1.189%, 1.159%, 1.184%, 1.142%, 1.203% and 1.148%, respectively. These results show that the proposed ESI algorithms have better search capabilities and give lower estimation errors than the SI algorithms.

4.2. Comparisons of Different Diode Models

To evaluate the estimation results for models with different numbers of diodes, the proposed algorithms are also used to optimize the parameter values of different models.

Table 8. Estimation results for different diode models using an EPSO method (MRE%).

Date	Weather Type	Newton	Single-Diode 1	Two-Diode 2	Three-Diode 3
1/11	Cloudy	4.581	0.997	0.935	0.918
7/13	Cloudy	5.775	2.096	2.074	2.063
1/19	Heavy cloud	1.828	0.714	0.460	0.445
6/19	Heavy cloud	1.118	1.082	0.781	0.773
2/12	Light cloud	5.830	1.877	1.863	1.837
5/14	Light cloud	5.515	2.035	1.994	1.984
1/21	Rainy	0.573	0.882	0.685	0.670
3/11	Rainy	0.402	1.107	1.039	1.013
8/7	Sunny	5.048	0.664	1.035	1.058
7/12	Sunny	4.981	0.491	0.810	0.835
	Average	3.565	1.194	1.167	1.159

¹ Estimation results using 12 parameters. ² Estimation results using 14 parameters. ³ Estimation results using 16 parameters.

shows the estimation results using an EPSO algorithm. Except for two rainy days on Jan. 21 and March 11, the EPSO algorithm gives a better estimate for the three different diode models. The respective average estimation errors for the single-, two- and three-diode models are 1.194%, 1.167% and 1.159%, all of which are more accurate than the estimation error of 3.565% using the Newtonian iteration method. The three-diode model produces more accurate estimation results than the single- and two-diode models. Note that there are 12, 14 and 16 parameters to be optimized for the single-, two- and three-diode models, respectively.

Table 9. Estimation results for different diode models using an ESSA method (MRE%).

Date	Weather Type	Newton	Single-Diode	Two-Diode	Three-Diode
1/11	Cloudy	4.581	0.996	0.934	0.933
7/13	Cloudy	5.775	2.105	2.058	2.056
1/19	Heavy cloud	1.828	0.676	0.429	0.424
6/19	Heavy cloud	1.118	1.052	0.752	0.740
2/12	Light cloud	5.830	1.881	1.845	1.838
5/14	Light cloud	5.515	2.045	1.981	1.978
1/21	Rainy	0.573	0.857	0.636	0.626
3/11	Rainy	0.402	1.093	0.969	0.961
8/7	Sunny	5.048	0.645	1.041	1.043
7/12	Sunny	4.981	0.476	0.815	0.824
	Average	3.565	1.182	1.146	1.142

shows the estimation results using an ESSA. Similarly, except for the two rainy days, the SSA gives better estimates for the three different diode models. The respective average estimation errors for the single-, two- and three-diode models are 1.182%, 1.146% and 1.142%. The three-diode model gives better estimation results than the other two diode models.

Table 10. Estimation results for different diode models using an EWOA method (MRE%).

Date	Weather Type	Newton	Single-Diode	Two-Diode	Three-Diode
1/11	Cloudy	4.581	1.001	0.940	0.938
7/13	Cloudy	5.775	2.106	2.062	2.061
1/19	Heavy cloud	1.828	0.611	0.424	0.424
6/19	Heavy cloud	1.118	0.972	0.752	0.751
2/12	Light cloud	5.830	1.879	1.855	1.854
5/14	Light cloud	5.515	2.040	1.988	1.987
1/21	Rainy	0.573	0.797	0.634	0.633
3/11	Rainy	0.402	1.049	0.962	0.962
8/7	Sunny	5.048	0.673	1.056	1.059
7/12	Sunny	4.981	0.517	0.813	0.815
	Average	3.565	1.165	1.149	1.148

shows the estimation results using an EWOA, which gives similar results for the 10 testing days.

To verify the reliability of parameter estimation for different diode models, the results of another 10 days of testing data are provided in

Table 11. Results of another 10 testing days for different models using an EPSO method (MRE%).

Date	Weather Type	Newton	Single-Diode	Two-Diode	Three-Diode
6/13	Cloudy	4.758	1.341	1.127	1.105
6/30	Cloudy	4.925	2.101	2.002	1.952
3/3	Heavy cloud	2.025	0.828	0.667	0.564
4/21	Heavy cloud	2.215	0.872	0.832	0.625
1/31	Light cloud	4.885	2.570	2.135	2.012
10/16	Light cloud	5.054	2.184	2.169	2.051
3/25	Rainy	0.502	1.185	1.086	0.625
4/16	Rainy	0.512	1.483	1.314	0.755
4/25	Sunny	4.885	0.782	0.931	1.111
6/13	Sunny	5.187	1.080	1.121	0.905
	Average	3.495	1.443	1.338	1.171

. The respective average estimation errors for the single-, two- and three-diode models are 1.443%, 1.338% and 1.171%, all of which are more accurate than the estimation error of 3.495% using the Newtonian iteration method. Similar to the results shown in Table 8, Table 9 and Table 10, EPSO failed to produce better estimates than the Newtonian iteration method on two rainy days. Overall, the three-diode model produces more accurate estimates than the other diode models in term of average MRE values.

4.3. Comparison Using Different Number of Parameters

As described previously, to create a more refined estimation model, this study transforms the 9 parameters into 16 parameters for a three-diode model. Similarly, the 5 parameters in a single-diode model and the 7 parameters in a two-diode model can be transformed into 12 and 14 parameters, respectively.

Table 12. Comparison using different numbers of parameters for different diode models using an EPSO method (MRE%).

Date	Weather Type	Single-Diode Model		Two-Diode Model		Three-Diode Model
		Five Parameters	Proposed 1	Seven Parameters	Proposed 2	Nine Parameters	Proposed 3
1/11	Cloudy	1.225	0.997	1.205	0.935	1.194	0.918
7/13	Cloudy	2.330	2.096	2.313	2.074	2.065	2.063
1/19	Heavy cloud	0.801	0.714	0.801	0.460	0.735	0.445
6/19	Heavy cloud	1.089	1.082	1.081	0.781	0.834	0.773
2/12	Light cloud	2.307	1.877	2.222	1.863	2.161	1.837
5/14	Light cloud	2.952	2.035	2.853	1.994	2.173	1.984
1/21	Rainy	1.773	0.882	1.251	0.685	1.087	0.670
3/11	Rainy	1.625	1.107	1.611	1.039	1.301	1.013
8/7	Sunny	1.845	0.664	1.313	1.035	1.232	1.058
7/12	Sunny	1.622	0.491	1.450	0.810	1.137	0.835
	Average	1.757	1.194	1.610	1.167	1.392	1.159

¹ Estimation results of single-diode model using 12 parameters. ² Estimation results of two-diode model using 14 parameters. ³ Estimation results of three-diode model using 16 parameters.

shows a comparison of the different numbers of parameters used by different diode models. All the diode models are optimized using the same EPSO algorithm. As shown in the table, the respective average estimation errors for the 5-, 7- and 9-parameter models are 1.757%, 1.610% and 1.392%, while the proposed 12-, 14- and 16-parameter models obtained are 1.194%, 1.167% and 1.159%, respectively. The results show that the diode models converted into finer models provide better estimates than the unconverted diode models. Even a single-diode model using 12 parameters gives a better estimation accuracy than a three-diode model using 9 parameters.

The average execution time after 1000 iterations for the 5-, 7- and 9-parameter models is about 50 min to 1 h, while the proposed 12-, 14- and 16-parameter models need about 1 h 10 min to 1 h 30 min.

4.4. Preliminary Fault Diagnosis Results

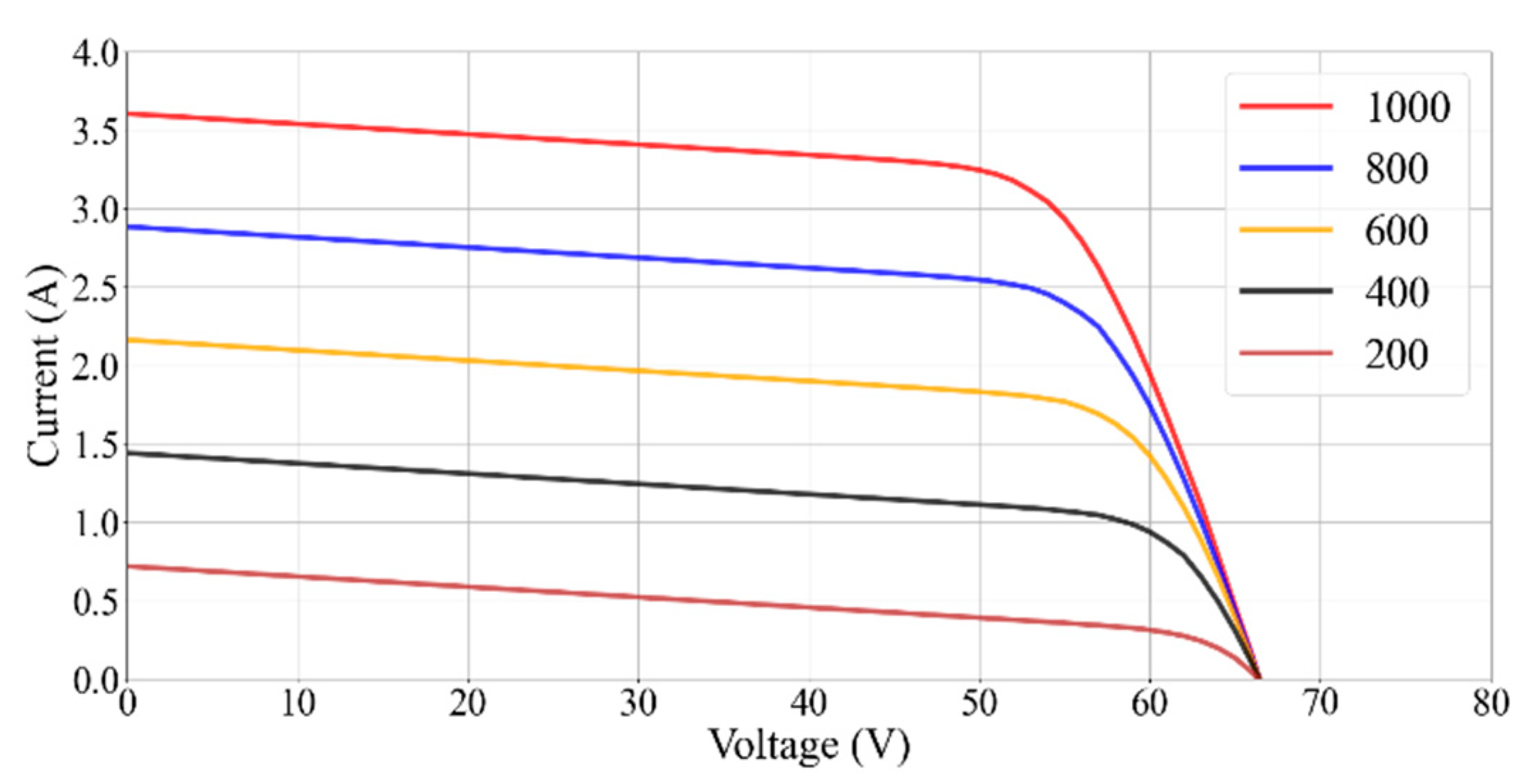
The I–V curve for solar cells is affected by solar irradiance, module temperature and the equivalent impedance of the material. Figure 10 shows the I–V curves for different solar irradiance values for a fixed module temperature of 298 (K) using the parameter values that are provided by the manufacturer. The current and power are significantly affected by the amount of solar irradiance, but the voltage for the solar cells does not change significantly. Figure 11 shows the I–V curves for different module temperatures and a constant solar irradiance of 1000 (W/m²). If the model temperature of a solar cell increases, the current increases slightly, but the voltage decreases significantly. Therefore, power output is significantly affected by solar irradiance but only slightly affected by the module temperature. As shown in Figure 10 and Figure 11, the I–V curves constructed using the parameters that are provided by the manufacturer are consistent with the actual situation of PV power generation.

Figure 12 shows the I–V curves for different solar irradiances for a temperature of 298 (K) using the proposed ESI algorithms and a three-diode model. The preliminary fault diagnosis analysis in Section 3.2 shows that the change in parameters is reflected in the I–V characteristic curves. Figure 12a shows the I–V curves for the three ESI algorithms for a solar irradiance of 1000 (W/m²). The original I–V curve for the STC is also shown for comparison. The curves marked with “Original” in the figure represent that the curves were produced using the original parameters provided by the PV manufacturer. The gradient of the I–V curves at around 40–60 volts is changed because the series resistance increases, so the current decreases significantly during this interval. If the module temperature is constant but the solar irradiance decreases to 800 (W/m²) and 600 (W/m²), as shown in Figure 12b,c, the current also decreases significantly. These results show that the PV modules may be oxidized and degraded, so maintenance is required to increase the power output.

4.5. Discussions

The following observations are yielded from the above results:

• For the single-diode model, the average estimation error for the EWOA is 1.165%, which is the lowest error for the three ESI algorithms. However, the ESSA, which allows for better exploration and exploitation strategies, gives the best estimation results for the two- and three-diode models.
• The single-diode model gives better estimates on sunny days, and the two- and three-diode models give a more accurate estimate for the other four weather types. Overall, the average estimation error for the three-diode model is smaller than that of the single- and two-diode models. Similar results are verified on another 10 testing days using the EPSO algorithm, as shown in Table 11.
• In terms of the estimation results for two rainy days, the errors that are produced using the original parameters provided by the manufacturer are quite small, so the three ESI algorithms cannot find parameters to produce a lower estimation error.
• As mentioned in the literature, most methods that use I–V curves to extract parameters only focus on a five-parameter model. Converting the I–V curves into a nine-parameter model is possible but may not be accurate enough to represent the characteristics of solar cells.
• The preliminary fault diagnosis results indicate that the PV modules may be oxidized and degraded, so maintenance is required to increase their power output. Since there are many factors that cause the oxidation and degradation of PV modules, the practical fault factors and fault locations still require further inspection by the operators.

5. Conclusions

A three-diode model is used for this study to establish a power generation model for a PV module. The 9 parameters are transformed into 16 parameters for different solar irradiances and module temperatures to establish a more refined estimation model. The ESI algorithms are used to accurately estimate the parameters that can produce a power output close to the actual value. When the parameters for a three-diode model are accurately estimated, the I–V curves for different solar irradiances are established, and possible faults in a PV array are predicted at an early stage. For tests using a 200 kWp PV power generation system, the primary findings and future research directions of the study are summarized as follows:

(1)

In terms of the estimation error, the three-diode model is more accurate than the single-diode and two-diode models.

(2)

Except for two rainy days, the proposed ESI algorithms (such as EPSO, the EWOA and the ESSA) give more accurate estimation results than the parameter estimation results using the traditional Newton iteration method.

(3)

The I–V curves show that the PV modules may undergo oxidation and degradation, which must be addressed by maintenance operators.

(4)

Testing on different data sets shows that the proposed ESI algorithms are reliable and their estimation errors are very close. In addition, the diode models converted into a finer model with more parameters provide better estimates than the unconverted diode models.

(5)

Future study will use an ensemble estimation method that combines the Newtonian iteration method and the ESI algorithms to increase the accuracy of PV power generation estimation, especially for rainy days.