Artificial Neural Networks as a Tool to Understand Complex Energy Poverty Relationships: The Case of Greece
Abstract
1. Introduction
1.1. The Problem of Energy Poverty
1.2. Artificial Neural Networks and Energy Poverty
2. Materials and Methods
- The “10% required” indicator, according to which a household is considered energy poor if it needs to spend more than 10% of its disposable income on its theoretically required annual energy expenses [44].
- The “NEPI” indicator, i.e., National Energy Poverty Index, according to which a household is considered energy poor if two conditions are simultaneously met: (i) the total annual energy cost of the household is below 80% of the amount theoretically required to meet energy needs, and (ii) the total income of the household (equivalized, based on the OECD equivalence scale) is below the poverty line, as defined in Greece, i.e., is less than 60% of the median equivalized income of all households in the country [4,45].
- The “IW” indicator, expressing the inability to keep a home adequately warm, as also measured by Eurostat (EU Statistics on Income and Living Conditions-EU SILC survey) [46].
- The “AB” indicator, expressing the arrears on energy bills, simulating the “Arrears on utility bills” indicator measured by Eurostat (EU SILC survey) [47], but more precisely focusing on energy expenses.
- The “DL” indicator, expressing the problems of a leaking roof, damp walls/floors/foundation, or rot in window frames or floor, as also measured by Eurostat (EU SILC survey) [48].
| Input Variables | Output Indicators (One Per Time) | ||||||
|---|---|---|---|---|---|---|---|
| House age | “10% actual” indicator | “10%” required indicator | “CEN” indicator | “NEPI” indicator | “IW” indicator | “AB” indicator | “DL” indicator |
| Ownership status | |||||||
| Household size | |||||||
| House area | |||||||
| Elevation | |||||||
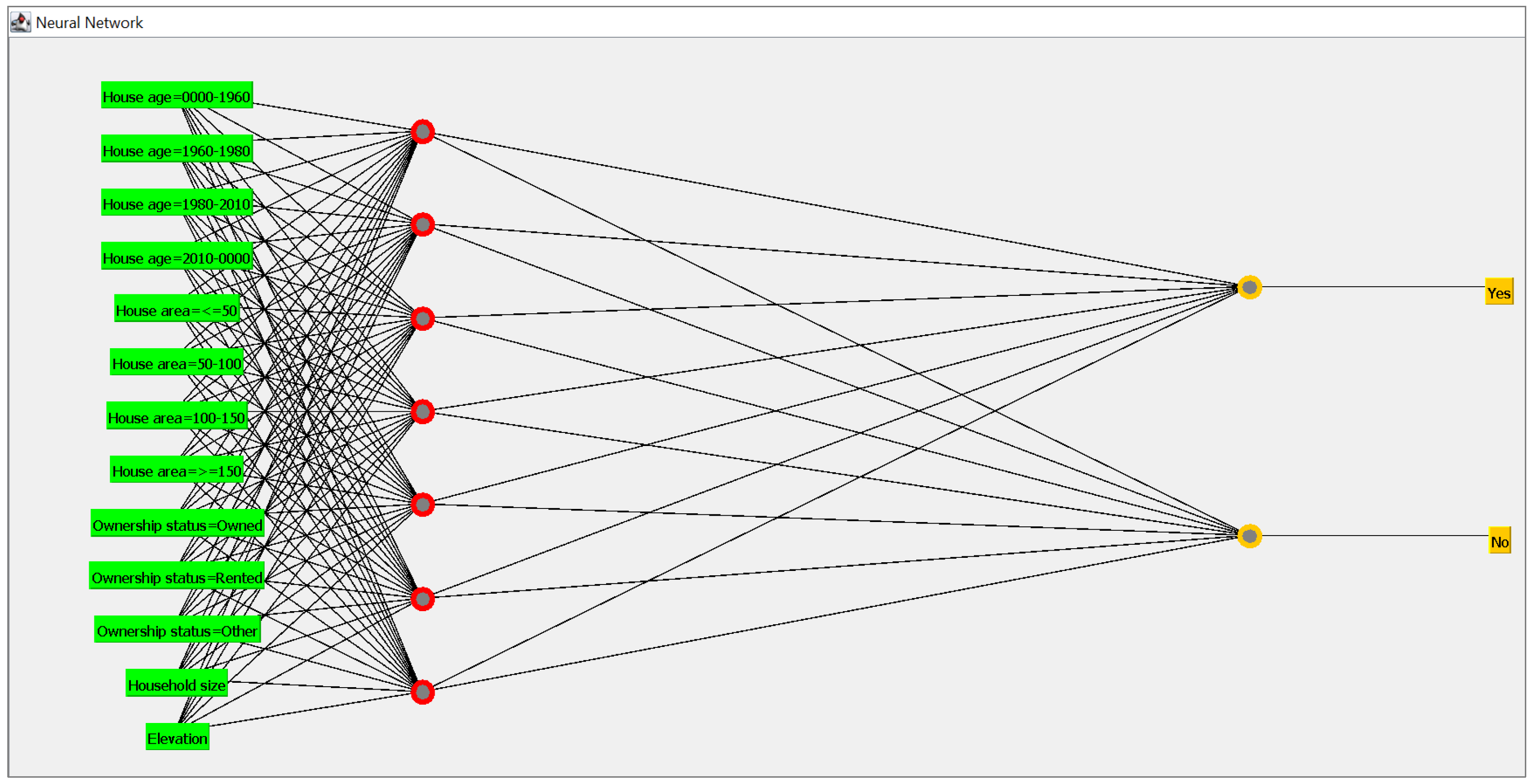
- Model A: house age, ownership status and household size.
- Model B: house age, ownership status, household size and house area.
- Model C: house age, ownership status, household size, house area and elevation.
| Models | Output Indicators (One Per Time) | ||||||
|---|---|---|---|---|---|---|---|
| Model A: House age Ownership status HH size | “10% actual” indicator | “10%” required indicator | “CEN” indicator | “NEPI” indicator | “IW” indicator | “AB” indicator | “DL” indicator |
| Model B: Model A + House area | |||||||
| Model C: Model B + Elevation | |||||||
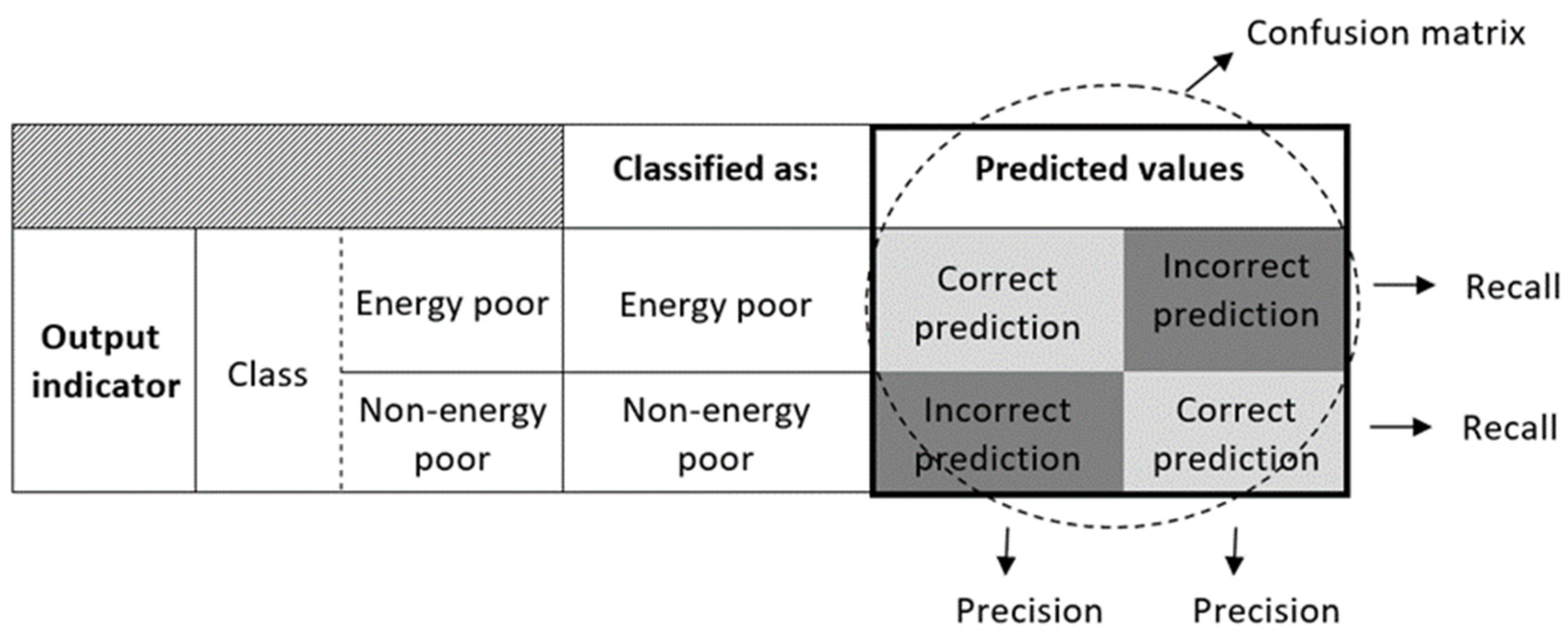
- “Precision” reflects the share of correct predictions of a class within the total correct predictions of the class and incorrect predictions of the other class (sum of instances classified as a given class category of the output indicator) (Figure 1).
- “Recall” represents the share of correct predictions of a class within the total predictions of the class (correct and incorrect) (Figure 1).
- “F-Measure” combines “Precision” and “Recall” and is utilized as a general metric considering the costs of incorrect predictions.
- “ROC Area”, or “Receiver Operator Characteristic Area under the curve”, serves as an accuracy measure of the model, indicating the level of a random model’s prediction and, ideally, aims to be the highest possible. Notably, “ROC Area” provides insights about the actual appropriateness of the neural network.
3. Results and Discussion
3.1. Prediction of the “10% Actual” Indicator
| Prediction of “10% Actual” Indicator | ||||||||
|---|---|---|---|---|---|---|---|---|
| Input Variables | Precision | Recall | F-Measure | ROC Area | Class | Accuracy | Confusion Matrix | |
| Model A: House age Ownership status HH size | 0.600 | 0.978 | 0.744 | 0.549 | Yes | 59.96% | 98% | 2% |
| 0.579 | 0.044 | 0.081 | 0.549 | No | 96% | 4% | ||
| 0.592 | 0.600 | 0.476 | 0.549 | (weighted avg) | ||||
| Model B: Model A + House area | 0.602 | 0.968 | 0.742 | 0.570 | Yes | 59.96% | 97% | 3% |
| 0.556 | 0.060 | 0.108 | 0.570 | No | 96% | 6% | ||
| 0.583 | 0.600 | 0.485 | 0.570 | (weighted avg) | ||||
| Model C: Model B + Elevation | 0.743 | 0.741 | 0.742 | 0.712 | Yes | 69.29% | 74% | 26% |
| 0.621 | 0.623 | 0.622 | 0.712 | No | 38% | 62% | ||
| 0.693 | 0.693 | 0.693 | 0.712 | (weighted avg) | ||||
3.2. Prediction of the “10% Required” Indicator
| Prediction of “10% Required” Indicator | ||||||||
|---|---|---|---|---|---|---|---|---|
| Input Variables | Precision | Recall | F-Measure | ROC Area | Class | Accuracy | Confusion Matrix | |
| Model A: House age Ownership status HH size | 0.876 | 0.755 | 0.811 | 0.774 | Yes | 73.05% | 75% | 25% |
| 0.448 | 0.652 | 0.531 | 0.774 | No | 35% | 65% | ||
| 0.776 | 0.730 | 0.745 | 0.774 | (weighted avg) | ||||
| Model B: Model A + House area | 0.860 | 0.769 | 0.812 | 0.783 | Yes | 72.70% | 77% | 23% |
| 0.438 | 0.591 | 0.503 | 0.783 | No | 41% | 59% | ||
| 0.761 | 0.727 | 0.740 | 0.783 | (weighted avg) | ||||
| Model C: Model B + Elevation | 0.929 | 0.815 | 0.868 | 0.856 | Yes | 81.03% | 81% | 19% |
| 0.568 | 0.795 | 0.662 | 0.856 | No | 20% | 80% | ||
| 0.844 | 0.810 | 0.820 | 0.856 | (weighted avg) | ||||
3.3. Prediction of the “CEN” Indicator
| Prediction of “CEN” Indicator | ||||||||
|---|---|---|---|---|---|---|---|---|
| Input Variables | Precision | Recall | F-Measure | ROC Area | Class | Accuracy | Confusion Matrix | |
| Model A: House age Ownership status HH size | 0.724 | 0.792 | 0.757 | 0.785 | Yes | 73.52% | 79% | 21% |
| 0.750 | 0.674 | 0.710 | 0.785 | No | 33% | 67% | ||
| 0.737 | 0.735 | 0.734 | 0.785 | (weighted avg) | ||||
| Model B: Model A + House area | 0.731 | 0.776 | 0.753 | 0.780 | Yes | 73.52% | 78% | 22% |
| 0.741 | 0.691 | 0.715 | 0.780 | No | 31% | 69% | ||
| 0.736 | 0.735 | 0.735 | 0.780 | (weighted avg) | ||||
| Model C: Model B + Elevation | 0.707 | 0.816 | 0.758 | 0.783 | Yes | 72.91% | 82% | 18% |
| 0.761 | 0.636 | 0.693 | 0.783 | No | 36% | 64% | ||
| 0.733 | 0.729 | 0.727 | 0.783 | (weighted avg) | ||||
3.4. Prediction of the “NEPI” Indicator
| Prediction of “NEPI” Indicator | ||||||||
|---|---|---|---|---|---|---|---|---|
| Input Variables | Precision | Recall | F-Measure | ROC Area | Class | Accuracy | Confusion Matrix | |
| Model A: House age Ownership status HH size | 0.651 | 0.433 | 0.520 | 0.768 | Yes | 71.25% | 43% | 57% |
| 0.732 | 0.869 | 0.795 | 0.768 | No | 13% | 87% | ||
| 0.703 | 0.712 | 0.696 | 0.768 | (weighted avg) | ||||
| Model B: Model A + House area | 0.680 | 0.520 | 0.589 | 0.769 | Yes | 73.94% | 52% | 48% |
| 0.762 | 0.863 | 0.809 | 0.769 | No | 14% | 86% | ||
| 0.732 | 0.739 | 0.730 | 0.769 | (weighted avg) | ||||
| Model C: Model B + Elevation | 0.777 | 0.728 | 0.752 | 0.877 | Yes | 82.72% | 73% | 27% |
| 0.853 | 0.883 | 0.867 | 0.877 | No | 12% | 88% | ||
| 0.825 | 0.827 | 0.826 | 0.877 | (weighted avg) | ||||
3.5. Prediction of the “IW” Indicator
| Prediction of “IW” Indicator | ||||||||
|---|---|---|---|---|---|---|---|---|
| Input Variables | Precision | Recall | F-Measure | ROC Area | Class | Accuracy | Confusion Matrix | |
| Model A: House age Ownership status HH size | 0.549 | 0.425 | 0.479 | 0.603 | Yes | 56.83% | 43% | 57% |
| 0.579 | 0.694 | 0.631 | 0.603 | No | 31% | 69% | ||
| 0.565 | 0.568 | 0.560 | 0.603 | (weighted avg) | ||||
| Model B: Model A + House area | 0.508 | 0.658 | 0.573 | 0.562 | Yes | 54.19% | 66% | 34% |
| 0.594 | 0.440 | 0.506 | 0.562 | No | 56% | 44% | ||
| 0.554 | 0.542 | 0.537 | 0.562 | (weighted avg) | ||||
| Model C: Model B + Elevation | 0.635 | 0.538 | 0.583 | 0.678 | Yes | 63.98% | 54% | 46% |
| 0.643 | 0.729 | 0.683 | 0.678 | No | 27% | 73% | ||
| 0.639 | 0.640 | 0.636 | 0.678 | (weighted avg) | ||||
3.6. Prediction of the “AB” Indicator
| Prediction of “AB” Indicator | ||||||||
|---|---|---|---|---|---|---|---|---|
| Input Variables | Precision | Recall | F-Measure | ROC Area | Class | Accuracy | Confusion Matrix | |
| Model A: House age Ownership status HH size | 0.398 | 0.122 | 0.187 | 0.600 | Yes | 57.04% | 12% | 88% |
| 0.595 | 0.875 | 0.708 | 0.600 | No | 13% | 87% | ||
| 0.515 | 0.570 | 0.497 | 0.600 | (weighted avg) | ||||
| Model B: Model A + House area | 0.573 | 0.693 | 0.628 | 0.682 | Yes | 66.76% | 69% | 31% |
| 0.758 | 0.650 | 0.700 | 0.682 | No | 35% | 65% | ||
| 0.683 | 0.668 | 0.671 | 0.682 | (weighted avg) | ||||
| Model C: Model B + Elevation | 0.694 | 0.697 | 0.696 | 0,769 | Yes | 75.35% | 70% | 31% |
| 0.794 | 0.792 | 0.793 | 0.769 | No | 21% | 79% | ||
| 0.754 | 0.754 | 0.754 | 0.769 | (weighted avg) | ||||
3.7. Prediction of the “DL” Indicator
| Prediction of “DL” Indicator | ||||||||
|---|---|---|---|---|---|---|---|---|
| Input variables | Precision | Recall | F-Measure | ROC Area | Class | Accuracy | Confusion Matrix | |
| Model A: House age Ownership status HH size | 0.513 | 0.302 | 0.380 | 0.543 | Yes | 56.12% | 30% | 70% |
| 0.578 | 0.770 | 0.660 | 0.543 | No | 23% | 77% | ||
| 0.549 | 0.561 | 0.535 | 0.543 | (weighted avg) | ||||
| Model B: Model A + House area | 0.547 | 0.275 | 0.366 | 0.589 | Yes | 57.52% | 27% | 73% |
| 0.583 | 0.817 | 0.681 | 0.589 | No | 18% | 82% | ||
| 0.567 | 0.575 | 0.540 | 0.589 | (weighted avg) | ||||
| Model C: Model B + Elevation | 0.562 | 0.639 | 0.598 | 0.648 | Yes | 61.71% | 64% | 36% |
| 0.674 | 0.599 | 0.634 | 0.648 | No | 40% | 60% | ||
| 0.624 | 0.617 | 0.618 | 0.648 | (weighted avg) | ||||
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IEA. SDG7: Data and Projections. IEA, 2023. Available online: https://www.iea.org/reports/sdg7-data-and-projections (accessed on 20 April 2024).
- Papada, L.; Kaliampakos, D. A Stochastic Model for energy poverty analysis. Energy Policy 2018, 116, 153–164. [Google Scholar] [CrossRef]
- Eurostat. People at Risk of Poverty or Social Exclusion. 2023. Available online: https://ec.europa.eu/eurostat/databrowser/view/sdg_01_10/default/table?lang=en (accessed on 25 April 2024).
- Kalfountzou, E.; Tourkolias, C.; Mirasgedis, S.; Damigos, D. Identifying Energy-Poor Households with Publicly Available Information: Promising Practices and Lessons Learned from the Athens Urban Area, Greece. Energies 2024, 17, 919. [Google Scholar] [CrossRef]
- Atsalis, A.; Mirasgedis, S.; Tourkolias, C.; Diakoulaki, D. Fuel poverty in Greece: Quantitative analysis and implications for policy. Energy Build. 2016, 131, 87–98. [Google Scholar] [CrossRef]
- Papada, L.; Kaliampakos, D. Measuring energy poverty in Greece. Energy Policy 2016, 94, 157–165. [Google Scholar] [CrossRef]
- Papada, L.; Kaliampakos, D. Energy poverty in Greek mountainous areas: A comparative study. J. Mt. Sci. 2017, 14, 1229–1240. [Google Scholar] [CrossRef]
- Palmos Analysis. Thessaloniki: 190,000 Households Vulnerable or in a State of Energy Poverty. Available online: https://parallaximag.gr/life/energiaki-ftochia-stopoleodomiko-sigkrotima-thessalonikis (accessed on 20 April 2024).
- Boemi, S.-N.; Avdimiotis, S.; Papadopoulos, A.M. Domestic energy deprivation in Greece: A field study. Energy Build. 2017, 144, 167–174. [Google Scholar] [CrossRef]
- Ntaintasis, E.; Mirasgedis, S.; Tourkolias, C. Comparing different methodological approaches for measuring energy poverty: Evidence from a survey in the region of Attika, Greece. Energy Policy 2019, 125, 160–169. [Google Scholar] [CrossRef]
- Spiliotis, E.; Arsenopoulos, A.; Kanellou, E.; Psarras, J.; Kontogiorgos, P. A multi-sourced data based framework for assisting utilities identify energy poor households: A case-study in Greece. Energy Sources Part B Econ. Plan. Policy 2020, 15, 49–71. [Google Scholar] [CrossRef]
- Papada, L.; Kaliampakos, D. Being forced to skimp on energy needs: A new look at energy poverty in Greece. Energy Res. Soc. Sci. 2020, 64, 101450. [Google Scholar] [CrossRef]
- Lyra, K.; Mirasgedis, S.; Tourkolias, C. From measuring fuel poverty to identification of fuel poor households: A case study in Greece. Energy Effic. 2022, 15, 6. [Google Scholar] [CrossRef]
- Kalfountzou, E.; Papada, L.; Damigos, D.; Degiannakis, S. Predicting energy poverty in Greece through statistical data analysis. Int. J. Sustain. Energy 2022, 41, 1605–1622. [Google Scholar] [CrossRef]
- Halkos, G.; Kostakis, I. Exploring the persistence and transience of energy poverty: Evidence from a Greek household survey. Energy Effic. 2023, 16, 50. [Google Scholar] [CrossRef]
- Géron, A. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems, 2nd ed.; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2019. [Google Scholar]
- Hong, Z.; Park, I.K. Comparative Analysis of Energy Poverty Prediction Models Using Machine Learning Algorithms. JKPA 2021, 56, 239–255. [Google Scholar] [CrossRef]
- Pino-Mejías, R.; Pérez-Fargallo, A.; Rubio-Bellido, C.; Pulido-Arcas, J.A. Artificial neural networks and linear regression prediction models for social housing allocation: Fuel Poverty Potential Risk Index. Energy 2018, 164, 627–641. [Google Scholar] [CrossRef]
- Hassani, H.; Yeganegi, M.R.; Beneki, C.; Unger, S.; Moradghaffari, M. Big Data and Energy Poverty Alleviation. BDCC 2019, 3, 50. [Google Scholar] [CrossRef]
- Benardos, A. Artificial intelligence in underground development: A study of TBM performance. In Proceedings of the UNDERGROUND SPACES 2008, New Forest, UK, 8–10 September 2008; pp. 21–32. [Google Scholar] [CrossRef]
- Moon, J.W.; Kim, J.-J. ANN-based thermal control models for residential buildings. Build. Environ. 2010, 45, 1612–1625. [Google Scholar] [CrossRef]
- Seo, J.; Kim, S.; Lee, S.; Jeong, H.; Kim, T.; Kim, J. Data-driven approach to predicting the energy performance of residential buildings using minimal input data. Build. Environ. 2022, 214, 108911. [Google Scholar] [CrossRef]
- Michailidis, P.; Michailidis, I.T.; Gkelios, S.; Karatzinis, G.; Kosmatopoulos, E.B. Neuro-distributed cognitive adaptive optimization for training neural networks in a parallel and asynchronous manner. ICA 2023, 31, 19–41. [Google Scholar] [CrossRef]
- Elbeltagi, E.; Wefki, H. Predicting energy consumption for residential buildings using ANN through parametric modeling. Energy Rep. 2021, 7, 2534–2545. [Google Scholar] [CrossRef]
- Tu, J.V. Advantages and disadvantages of using artificial neural networks versus logistic regression for predicting medical outcomes. J. Clin. Epidemiol. 1996, 49, 1225–1231. [Google Scholar] [CrossRef]
- Papada, L.; Kaliampakos, D. Exploring Energy Poverty Indicators Through Artificial Neural Networks. In Artificial Intelligence and Sustainable Computing; Pandit, M., Gaur, M.K., Rana, P.S., Tiwari, A., Eds.; Algorithms for Intelligent Systems; Springer Nature: Singapore, 2022; pp. 231–242. [Google Scholar] [CrossRef]
- Fausett, L.V. Fundamentals of Neural Networks: Architectures, Algorithms, and Applications; Pearson Education: New Delhi, India, 2008. [Google Scholar]
- Sietsma, J.; Dow, R.J.F. Creating artificial neural networks that generalize. Neural Netw. 1991, 4, 67–79. [Google Scholar] [CrossRef]
- Rajić, M.N.; Milovanović, M.B.; Antić, D.S.; Maksimović, R.M.; Milosavljević, P.M.; Pavlović, D.L. Analyzing energy poverty using intelligent approach. Energy Environ. 2020, 31, 1448–1472. [Google Scholar] [CrossRef]
- Cheng-wen, Y.; Jian, Y. Application of ANN for the prediction of building energy consumption at different climate zones with HDD and CDD. In 2010 2nd International Conference on Future Computer and Communication; IEEE: Wuhan, China, 2010; pp. V3-286–V3-289. [Google Scholar] [CrossRef]
- Pavićević, M.; Popović, T. Forecasting Day-Ahead Electricity Metrics with Artificial Neural Networks. Sensors 2022, 22, 1051. [Google Scholar] [CrossRef]
- Heghedus, C.; Segarra, S.; Chakravorty, A.; Rong, C. Neural Network Architectures for Electricity Consumption Forecasting. In 2019 International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData); IEEE: Atlanta, GA, USA, 2019; pp. 776–783. [Google Scholar] [CrossRef]
- Tardioli, G.; Kerrigan, R.; Oates, M.; O’Donnell, J.; Finn, D. A Data-Driven Modelling Approach for Large Scale Demand Profiling of Residential Buildings. In Proceedings of the BS 2017: Conference of International Building Performance Simulation Association, San Francisco, CA, USA, 7–9 August 2017; Barnaby, C.S., Wetter, M., Eds.; International Building Performance Simulation Association: Rapid City, SD, USA, 2017. [Google Scholar]
- López-Vargas, A.; Ledezma-Espino, A.; Sanchis-de-Miguel, A. Methods, data sources and applications of the Artificial Intelligence in the Energy Poverty context: A review. Energy Build. 2022, 268, 112233. [Google Scholar] [CrossRef]
- Longa, F.D.; Sweerts, B.; Van Der Zwaan, B. Exploring the complex origins of energy poverty in The Netherlands with machine learning. Energy Policy 2021, 156, 112373. [Google Scholar] [CrossRef]
- Al Kez, D.; Foley, A.; Abdul, Z.K.; Del Rio, D.F. Energy poverty prediction in the United Kingdom: A machine learning approach. Energy Policy 2024, 184, 113909. [Google Scholar] [CrossRef]
- Bienvenido-Huertas, D.; Pérez-Fargallo, A.; Alvarado-Amador, R.; Rubio-Bellido, C. Influence of climate on the creation of multilayer perceptrons to analyse the risk of fuel poverty. Energy Build. 2019, 198, 38–60. [Google Scholar] [CrossRef]
- Bienvenido-Huertas, D.; Sánchez-García, D.; Marín-García, D.; Rubio-Bellido, C. Analysing energy poverty in warm climate zones in Spain through artificial intelligence. J. Build. Eng. 2023, 68, 106116. [Google Scholar] [CrossRef]
- Abbas, K.; Butt, K.M.; Xu, D.; Ali, M.; Baz, K.; Kharl, S.H.; Ahmed, M. Measurements and determinants of extreme multidimensional energy poverty using machine learning. Energy 2022, 251, 123977. [Google Scholar] [CrossRef]
- Balaskas, A.; Papada, L.; Katsoulakos, N.; Damigos, D.; Kaliampakos, D. Energy poverty in the mountainous town of Metsovo, Greece. J. Mt. Sci. 2021, 18, 2240–2254. [Google Scholar] [CrossRef]
- Papada, L.; Balaskas, A.; Katsoulakos, N.; Kaliampakos, D.; Damigos, D. Fighting Energy Poverty Using User-Driven Approaches in Mountainous Greece: Lessons Learnt from a Living Lab. Energies 2021, 14, 1525. [Google Scholar] [CrossRef]
- Karani, I.; Papada, L.; Kaliampakos, D. Energy poverty signs in mountainous Greek areas: The case of Agrafa. Int. J. Sustain. Energy 2022, 41, 1408–1433. [Google Scholar] [CrossRef]
- Roberts, D.; Vera-Toscano, E.; Phimister, E. Fuel poverty in the UK: Is there a difference between rural and urban areas? Energy Policy 2015, 87, 216–223. [Google Scholar] [CrossRef]
- DECC (Dept for Energy and Climate Change). Annual Fuel Poverty Statistics Report 2015. DECC: London, UK, 2015. Available online: https://assets.publishing.service.gov.uk/media/5a814b3340f0b6230269684c/Fuel_Poverty_Report_2015.pdf (accessed on 25 April 2024).
- Annual Progress Report of the Action Plan for combating Energy Poverty year 2021 (in Greek). Ministry of Environment & Energy, 2021. Available online: https://ypen.gov.gr/wp-content/uploads/2022/04/SDEE-Annual-report-2021-v4-14032022-clean.pdf (accessed on 15 April 2024).
- EU Statistics on Income and Living Conditions. Eurostat, 2024. Available online: https://ec.europa.eu/eurostat/web/microdata/european-union-statistics-on-income-and-living-conditions (accessed on 25 April 2024).
- ‘Arrears on Utility Bills’. Eurostat, 2024. Available online: https://ec.europa.eu/eurostat/web/products-eurostat-news/-/DDN-20200120-1 (accessed on 25 April 2024).
- ‘EU Statistics on Income and Living Conditions (EU-SILC) Methodology—Housing Deprivation’. Eurostat, 2024. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=EU_statistics_on_income_and_living_conditions_(EU-SILC)_methodology_-_housing_deprivation (accessed on 25 April 2024).
- European Commission. An Energy Policy for Customers. Commission Staff Working Paper; European Commission: Brussels, Belgium, 2010. [Google Scholar]
- Papada, L.; Kaliampakos, D. Developing the energy profile of mountainous areas. Energy 2016, 107, 205–214. [Google Scholar] [CrossRef]
- Frank, E.; Hall, M.A.; Witten, I.H. The WEKA Workbench. Data Mining. Practical Machine Learning Tools and Techniques, 4th ed.; Morgan Kaufmann: Waikato, New Zealand, 2016. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papada, L.; Kaliampakos, D. Artificial Neural Networks as a Tool to Understand Complex Energy Poverty Relationships: The Case of Greece. Energies 2024, 17, 3163. https://doi.org/10.3390/en17133163
Papada L, Kaliampakos D. Artificial Neural Networks as a Tool to Understand Complex Energy Poverty Relationships: The Case of Greece. Energies. 2024; 17(13):3163. https://doi.org/10.3390/en17133163
Chicago/Turabian StylePapada, Lefkothea, and Dimitris Kaliampakos. 2024. "Artificial Neural Networks as a Tool to Understand Complex Energy Poverty Relationships: The Case of Greece" Energies 17, no. 13: 3163. https://doi.org/10.3390/en17133163
APA StylePapada, L., & Kaliampakos, D. (2024). Artificial Neural Networks as a Tool to Understand Complex Energy Poverty Relationships: The Case of Greece. Energies, 17(13), 3163. https://doi.org/10.3390/en17133163







