Abstract
As the regulations and consumer preferences in Europe tend to favor more energy-efficient household appliances, companies have to find innovative ways of saving electric energy during the operations of those appliances. One such method in dishwasher design is to reduce heat energy loss to the surrounding environment and reuse heat energy during the washing cycle, thus minimizing the time that heaters are operating. In this study, a numerical simulation involving computational fluid dynamics is implemented to speed up the iterative process of improving efficiency. The washing cycle has been simplified to include only the most critical moments of dishwasher work, and non-important components have been excluded. A workflow of simulations and numerical methods employed for this task is presented. The numerical simulations are compared with real-life experiments to assess their accuracy and verify boundary conditions. Geometric and washing cycle improvements are compared with the base design and show satisfactory results.
1. Introduction
The European Union energy label [1] is one of the examples that shows a large amount of pressure on energy efficiency in the European Union. In terms of the profitability of production of producers of household appliances, by maintaining or increasing market share, the critical element defining the competitiveness of the device will not be the ISO EN requirements constituting conditions for market admission but guidelines for the requirement for labeling devices, which in the case of large household appliances may play an important role in the consumer’s decision [2,3,4]. As the ways of saving energy in household appliances become more sophisticated, so do the geometry and materials used in the design. Verification of these improvements also becomes more costly. In recent years, the amount of computational power available in average workstations and computing stations has greatly increased, thus allowing computational fluid dynamics (CFD) calculations to gain popularity in companies specializing in the design of household appliances [5,6,7]. The aim of the experiment was to create a theoretical model to map the energy losses in the working system of a dishwasher and to perform an optimization analysis of the energy flow in the working systems in order to reduce energy consumption. Previous research proved that waste heat can be recovered by changing the dishwasher design, thus minimizing energy consumption [8,9,10,11]. The working system of the dishwasher was created using geometry and input data based on the real model of the dishwasher.
The complexity of the dishwasher washing cycle requires analytical simplification in order to capture all relations between different components [12,13]; thus, authors have made simplifications to the washing cycle. Due to this complexity, dishwashers can be optimized in many different ways [14] and require model-based design optimization in order for the changes to be beneficial in all aspects [15,16]. The geometry was prepared for calculations in ANSYS SpaceClaim 2023R1 software. The computational model was created in ANSYS Fluent 2022R2 software using the finite volume method to solve the fluid mechanics equations (i.e., the Navier–Stokes equations). Further references to analyses using this method will be identified by the acronym CFD. The geometry used to create the system was taken from actual models of commercially available dishwasher components, which were then modified for computational purposes to form a coherent whole. Model simplifications were made to reduce the size of the computational model, thereby reducing the time required to generate results. The material data for the different materials and fluids used in the model were derived from the ANSYS Fluent 2022R2 material database or taken from the literature. During the calculations, simplifications of the physical phenomena and boundary conditions were made to improve the convergence of the non-linear calculations.
The purpose of the computer simulation of the dishwasher was to identify areas of heat loss and to introduce a change in the design of the heat exchanger that would allow cold water to be preheated by recovering heat from the water that is discharged into the wastewater after the washing cycle.
2. Models and Methods
2.1. Numerical Theory
ANSYS Fluent is a CFD software package widely used to simulate fluid-flow and heat-transfer phenomena. It employs the finite volume method to discretize the governing equations of fluid flow and solve them numerically. The primary equations used by ANSYS Fluent [17] to model fluid flow include:
- Continuity equations (based on mass conservation);
- Navier–Stokes equations (based on momentum conservation);
- Energy equation (optional).
By solving these governing equations along with the appropriate boundary conditions, ANSYS Fluent predicts the behavior of fluid flow, including velocity profiles, pressure distributions, temperature fields, and turbulence characteristics within the simulated domain. By the addition of other equations and calculation methods (such as the radiative transfer equation for radiation modeling), it is possible to calculate complex flow phenomena inside the ANSYS Fluent package.
Most of the daily flow that is encountered can be classified as turbulent flow. It is thus worth noting that the vast majority of ANSYS Fluent calculations use the Reynolds-Averaged Navier–Stokes (RANS) approach to model turbulent flow. The important feature of RANS is that the turbulent flow field is decomposed into time-averaged mean flow and fluctuating turbulent components. Turbulent quantities such as velocity, pressure, and viscosity are modeled using empirical turbulence models, which solve additional transport equations for parameters such as turbulent kinetic energy and its dissipation rate. The effect of turbulence on the mean flow is represented statistically, assuming that the turbulent fluctuations are well-behaved and can be represented by a time-averaged model. An alternative to RANS is a large eddy simulation (LES). In LES, the large turbulent eddies are explicitly resolved in the simulation, while the smaller eddies are modeled or filtered out. The LES captures the large-scale, energetic turbulent structures directly, resolving their spatial and temporal variations while modeling the effects of smaller-scale turbulence using sub-grid-scale (SGS) models. Unlike RANS, a LES does not require empirical turbulence closure models for the resolved scales of turbulence. The LES requires finer spatial and temporal resolutions to resolve the large turbulent structures accurately. As a result, LES simulations are more computationally demanding compared to RANS, especially for high-Reynolds-number flow or flow with fine-scale turbulent features. However, LES provides more detailed information about the flow field, including turbulence spectra, coherent structures, and turbulent mixing processes. The LES requires finer spatial and temporal resolutions to resolve the large turbulent structures accurately. In this application, the authors have chosen the RANS approach. As a result, a turbulence model had to be chosen. An effective turbulence model to begin is a k-omega shear-stress transport (SST) approach, which (as of recently) is also the default ANSYS Fluent turbulence model. Developed by Menter [18], this model combines the advantages of both the k-omega and k-epsilon turbulence models to provide accurate predictions for a wide range of turbulent flow, including boundary layers, separated flow, and free shear flow. The “shear-stress transport” in the model’s name refers to its ability to account for the transport of shear stresses, in addition to turbulent kinetic energy and dissipation rate. This improves the accuracy of predictions for flow with strong adverse pressure gradients and separation. Besides the continuity equation and momentum equation, ANSYS Fluent also solves turbulent kinetic energy (k) and specific rate of dissipation (omega) equations [17,18].
The turbulent kinetic energy equation (k-equation) is given by
The turbulent kinetic energy dissipation rate equation (omega-equation) is written as
where represents density; denotes vector velocity; refers to molecular dynamic viscosity; signifies turbulent viscosity; is turbulent kinetic energy; is the specific turbulent dissipation rate; is the production of turbulent kinetic energy due to mean velocity gradients; is the dissipation rate of turbulent kinetic energy; is the Reynolds stress tensor; are constants for the model; and denotes a Kronecker delta.
To represent distinct interfaces between water and air inside the computational Eulerian domain, the authors have chosen a volume of fluid (VOF) analysis since it allows the modeling of two or more immiscible fluids by solving a single set of momentum equations and tracking the volume fraction of each of the fluids throughout the domain. Tracking the interface(s) between the phases is accomplished by the solution of a continuity equation for the volume fraction of one (or more) of the phases [1]. For the phase, this equation has the following form:
The interface representation is based on linear geometric reconstruction, thus also allowing the calculation of phase interaction phenomena such as surface tension effects. The interface representation by linear segments compared to the actual interface shape is shown in Figure 1 [17,19].
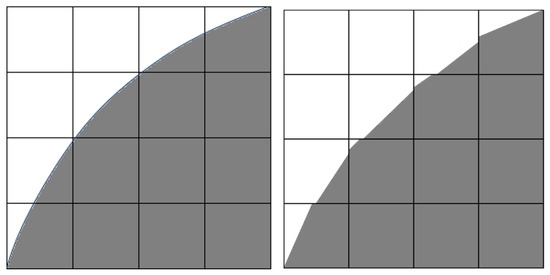
Figure 1.
Comparison between the actual water (gray)–air (white) interface and the one computed via ANSYS Fluent using the VOF method.
During the project, a need for modeling free convection arose. A free convection mechanism is driven by the spatial differences in temperature in a given fluid, which results in an uneven density of the fluid. The less dense fluid tends to be on top of the denser one, thus giving rise to a mass flow. In order to capture that behavior, gravity has to be present in the model. There are many models available in ANSYS Fluent that can capture buoyancy-driven flow, but the authors have chosen the Boussinesq model [20] since it is relatively simple and non-demanding in terms of calculational resources. It does not explicitly model changes in the density of the fluid but rather includes an internal momentum equation, i.e.,
where denotes density, represents temperature, is gravitational acceleration, and is the coefficient of thermal expansion.
This approximation for the buoyancy flow is only accurate for relatively small differences in temperature. The applicability can be estimated by the following condition:
where is temperature, and is the coefficient of thermal expansion. In this work, the above condition has been satisfied for water.
2.2. Dishwasher Washing Cycle
To show how the dishwasher thermal efficiency has been increased, it is useful to initially list all of the washing stages, present in the referred logic for the eco-program, since only some of them have been considered. These stages can be represented in a graphical diagram, as presented in Figure 2.
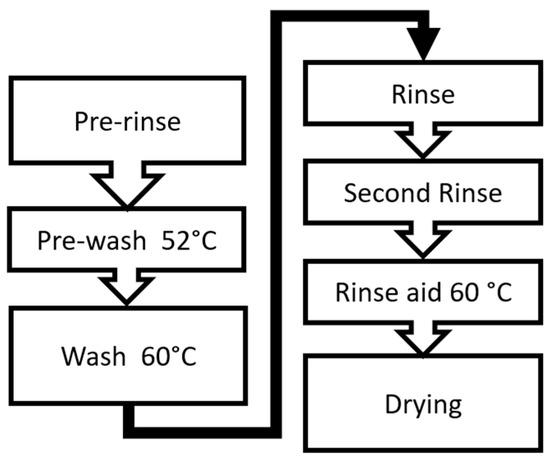
Figure 2.
Seven distinct stages for an average dishwasher washing cycle.
A short description of each of the stages is now given as follows:
- Pre-rinse (softening up of the soil): In the pre-rinse stage, the dishwasher sprays water onto the dishes to remove any loose food particles or debris before the main washing cycle begins. This helps to prevent food soil from sticking to the dishes during the wash cycle.
- Pre-wash 52 °C (pre-heat load): The pre-wash stage involves spraying the dishes with water heated to around 52 °C. This temperature helps to soften and loosen any stubborn food residues, making them easier to remove during the main wash cycle.
- Wash at 60 °C: During the wash cycle, the dishwasher fills with hot water, typically heated to around 60 °C. Detergent is also added at this stage to help break down grease and food particles on the dishes. The water jets spray the dishes, thoroughly cleaning them.
- Rinse: After the wash cycle, the dishwasher drains the dirty water and fills with clean water for the rinse cycle. The rinse stage involves spraying the dishes with hot water to remove any remaining detergent and debris, leaving them clean and ready for drying.
- Second rinse: Some dishwashers have an additional rinse cycle known as the second rinse. This stage provides an extra rinse to ensure that all detergent residue is thoroughly removed from the dishes, reducing the risk of leaving behind any soapy residue.
- Rinse aid at 60 °C: The rinse aid stage involves adding a rinse aid solution to the final rinse water. Rinse aid helps to prevent water spots and streaks from forming on the dishes during the drying process and also deactivates alkaline detergent residue. The water temperature during this stage is typically maintained at around 60 °C.
- Drying: Once the dishes have been thoroughly rinsed, the dishwasher begins the drying cycle. During this stage, the dishwasher may use a combination of heated air (using the heat energy accumulated in the load) and/or fan-assisted drying to evaporate any remaining moisture from the dishes, leaving them clean, dry, and ready for use.
2.3. Heat Exchanger Operating Principle
The location of the highest thermal flux is the interface between the heat exchanger and the washing chamber. A heat exchanger is often a wide, flat tank that adheres directly to the dishwasher chamber. A block diagram of a washing program that includes its role in each heat exchanger operating step is presented in Figure 3.
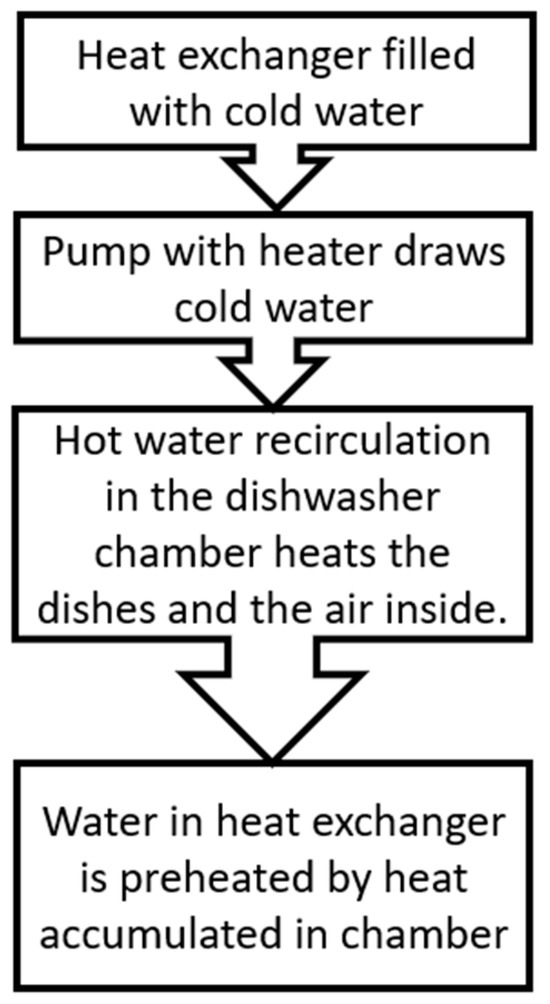
Figure 3.
Heat exchanger stages for an average dishwasher washing cycle.
There are several factors that have to be considered in order to increase the thermal efficiency of a dishwasher with regard to the heat exchanger [21,22,23]. The most important are:
- Temperature difference: The heat exchanger typically operates at a lower temperature compared to the dishwasher chamber during the heating phases of the cycle. This temperature gradient drives heat transfer from the heat exchanger to the dishwasher chamber, resulting in a higher heat flux.
- Large surface area: Heat exchangers are designed with a large surface area to maximize contact with the fluid (i.e., either water or steam) flowing through them. This increased surface area enhances heat transfer between the heat exchanger and the dishwasher chamber, leading to higher heat flux.
- Regulation and control: The heat flux between the heat exchanger and dishwasher chamber is typically regulated and controlled by the dishwasher’s heating system. Sensors and controls monitor the temperature and adjust the heat exchanger’s operation to maintain the desired temperature and optimize energy efficiency.
- Internal design: Dishwasher manufacturers optimize the internal design of the heat exchanger to ensure efficient heat transfer during the dishwasher’s working cycle. Factors such as flow rates, turbulence, and baffle structure are carefully considered to maximize heat flux while minimizing energy consumption and cycle times.
In this study, the authors consider changing the internal design of the heat exchanger as well as the materials of the heat exchanger’s internal structure. The effect of detergents on the hydrodynamic and thermophysical properties was intentionally ignored. Due to low concentration of detergents in overall water mass, authors concluded that they do not influence heat-transfer phenomenon.
3. Numerical Model
Due to the significant length of the dishwasher eco-cycle (about two hours) and the large number of phenomena occurring during a single cycle, it was necessary to isolate time intervals and key system elements to identify areas exposed to heat loss. In addition, the division of the dishwasher cycle into several pseudo-steady states was supported by the fact that there are significant movements of the free surface of the water in the water tank of the heat exchanger and the turbulent nature of the free surface sprayed into the washing chamber. The CFD analyses using algorithms that simulate the dynamic motion of a free surface are much more computationally demanding than algorithms that do not model changes in the location of the free surface. The dishwasher was filled with a load consisting of the geometric representation of ceramic and glass vessels based on a normative load derived from PN-EN 60436 [24].
The critical moment in the dishwasher’s operating cycle was the moment when cold water from the network (at a temperature of about 11 °C) was poured into the water tank in the heat exchanger. At this moment, water at a temperature of approximately 60 °C is injected into the center of the washing chamber, and the temperature field away from the contact of the heat exchanger with the walls of the dishwasher chamber is in a steady state. This is due to a sufficiently long water injection time before the water tank begins to fill. The whole model, without simplifications, can be seen in Figure 4.
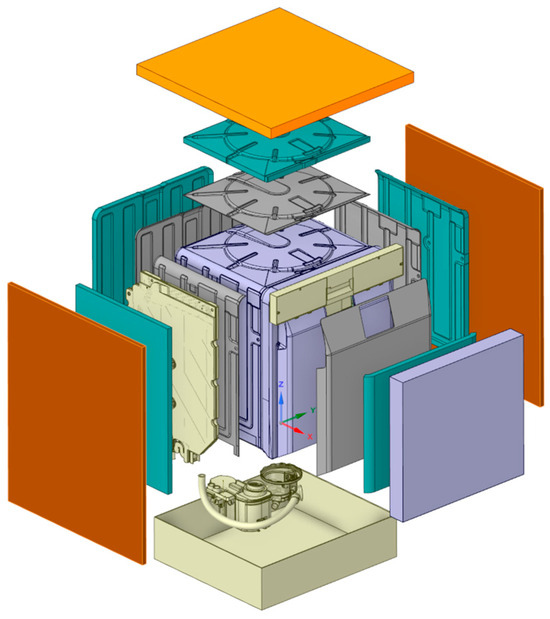
Figure 4.
Dishwasher and adjacent elements representation CAD model without simplifications.
The spatial simplification assumes the omission of direct modeling of the air volume surrounding the dishwasher chamber. This volume is, at least, between the outer surface of the felt mat and the oak countertop. This simplification assumes the boundary condition of convection on the outer walls of the dishwasher chamber. To achieve this goal, it was necessary to determine the heat transfer coefficient α for given surfaces in contact with the air surrounding the system. This coefficient, later referred to in the report as the heat transfer coefficient (HTC), was determined by a separate experiment performed in the lab, which was then reproduced in the computational environment. The description of the experiment and the methodology for its mapping in ANSYS Fluent 2022R2 are presented in Section 4.
Due to the complex geometry of some of the system components (in particular, the heat exchanger and the walls of the wash chamber), it was necessary to simplify them. In addition, minor modifications to the geometry were necessary to prepare it for CFD analyses. The simplification of the reverse-engineered geometry was additionally aimed at:
- Reducing the number of surfaces present in the model to more easily manageable boundary conditions;
- Facilitating the finite element mesh-generation process;
- Reducing the number of finite elements in the model;
- Facilitating the achievement of a finite element mesh with good quality parameters.
Figure 5 shows a section of the reverse-engineered model, which has been drastically simplified. The authors had to sculpt the geometry to mimic the real supposed geometry. This figure also shows a drastic reduction in the amount of fillets and geometrical gaps. As a result, the ANSYS Fluent Meshing can represent this geometry with a smaller amount of cells. The only problem was the generation of mesh on a thin-walled solid geometry since the version of ANSYS Fluent Meshing that the authors had used did not allow the easy creation of hexahedral elements with given amounts of cell layers in the thickness direction, and a polyhedral mesh had to be used. In the current release of the software, given the time of publication, this function should be available. The necessity of geometrical modeling of thin mats was due to the need to capture their heat capacity, as it cannot be simplified by using, for example, a shell conduction model.
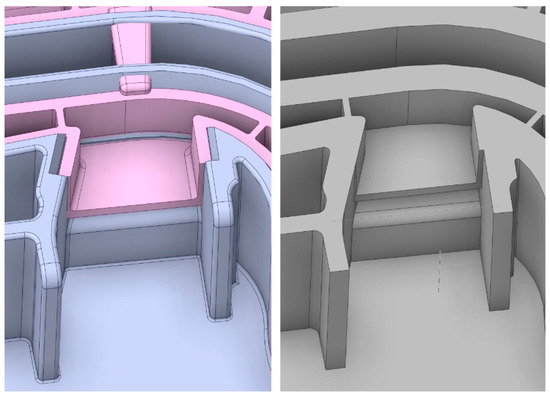
Figure 5.
Comparison of the heat exchanger geometry before (left) and after geometrical simplification (right).
3.1. Finite Volume Mesh for Heater Experiment
The mesh of finite volumes distributed over the model had to be sufficiently dense to accurately reproduce the phenomena of heat exchange and air and water movement. It also needed to be sparse enough to minimize computational time. The default mesh for the entire model used in the experiment with heating coils (no mixing/interaction between phases) consisted of 3,135,187 polyhedral elements with a minimum orthogonal quality of 0.15. The global appearance of the mesh is shown in Figure 6. Figure 7 shows the mesh for the volume of water (dark gray) and air (other colors) located inside the heat exchanger. It shows the water level between the dark gray water domain and the orange air domain.

Figure 6.
Volume mesh for the representation of the experimental heater model.
Figure 7.
Finite volume mesh for the fluid domains within the heat exchanger.
3.2. Calibration and Verification of Numerical Model
The heat transfer mechanism in a dishwasher is extremely complex, both in the ways the heat can flow across the model and how the boundary conditions change as the washing cycle progresses. It was necessary to conduct a simple experiment in which some of the model parameters could be tested. The straightforward experiment that was chosen consisted of placing four heating elements freely inside the washing chamber so that they were positioned close to the center of the chamber and did not touch any of the walls. This setup can be seen in Figure 8.

Figure 8.
Experimental setup of the fan and heating elements inside the dishwasher.
Together, these heating elements could generate 500 watts of power and were programmed such that they would turn off when the air temperature inside the chamber rose above 60 °C; thus, they could maintain a constant temperature after the initial warm-up. There was only a two-millimeter layer of butyl mat on the outside of the chamber. The heat exchanger adjacent to the chamber wall was filled up with water to a given level. The water inside the heat exchanger was not pumped in or out throughout the duration of the test, thus giving rise to a buoyancy-driven circulation of the water as it heats up. The starting temperature of the whole setup was 20.4 °C, as this was the temperature inside the laboratory. To counteract the stratification of the air inside the washing chamber during the heating process, a fan was placed at the center of the chamber to create a forced airflow toward the bottom of the chamber. The ventilation hole occurring between the heat exchanger and the washing chamber was capped off to minimize the amount of heat escaping out of the system. The capping surface is marked in red in Figure 9, which shows the heat exchanger model in the CAD environment. In reality, this hole provides a path for heated air to escape to the outside of the system. It therefore had to be plugged since a correct representation of the air exhaust through the hole would have required the simultaneous inclusion of gaps in other parts of the chamber, through which room-temperature air would have entered the chamber to balance the mass of air in the chamber. Correctly accounting for the gaps would have required a considerable amount of work, so an easier path was carried out for the experiment in the form of a closed system, where only heat had the opportunity to escape outside the system. The largest gap was present between the dishwasher door and the washing chamber; it was filled up in the numerical model.
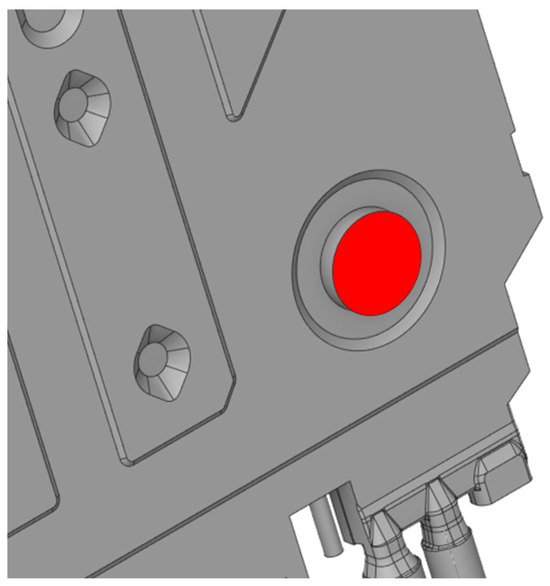
Figure 9.
Capped ventilation hole representation in the CAD environment.
This setup was also recreated in simulation software with some simplifications, as can be seen in Figure 10.
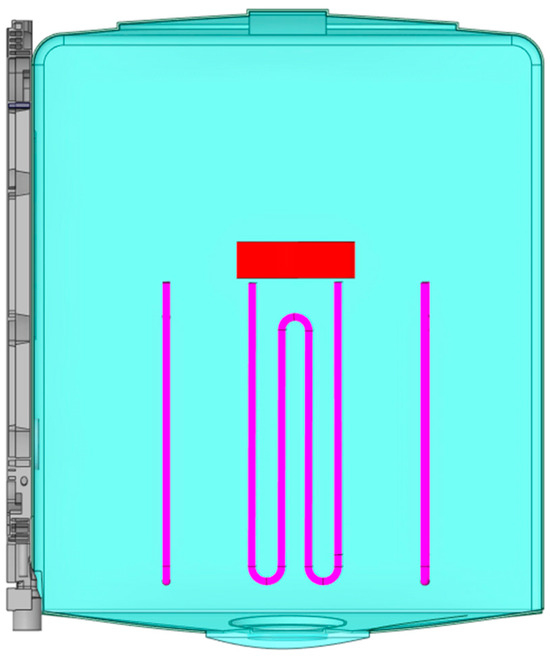
Figure 10.
CAD model of experimental setup with simplifications.
This experiment can show differences between the free convection inside the water tank, and it can be used to calculate the heat transfer coefficient of air. To verify that the geometric shape of the chamber, together with the heaters and the rotor, can be replaced by a convective boundary condition, where the HTC is determined from calculations for the entire model, a mesh was also created that consisted of the heat exchanger itself, the mat, and the sheet metal between the chamber and the mat.
3.3. Boundary Conditions for the Heater Experiment
Material parameters for water and air were taken from the ANSYS Fluent 2022R2 material database. The Boussinesq approximation was used to represent the movement of water due to the buoyancy during its local heating. The lack of free water surface movement did not require activation of the multiphase model. Due to the air motion in the turbulent range, the viscosity model used in the calculations was the k-omega SST with default values. The pressure–velocity coupling used the “coupled” scheme, and the spatial discretization of the pressure used the “PRESTO!” method. The rest of the spatial discretization methods used second-order upwind methods. From the technical parameters of the fan, the mass flow of air was determined, which was 0.041136 kg/s. This condition (i.e., the mass flow inlet) was set for the bottom surface of the cylinder representing the fan. The inside of the cylinder was an inactive domain (so-called void). The upper surface of the fan had an outflow condition from the domain (pressure outlet). On this surface, the program calculated the mass-averaged temperature, which was set as the temperature condition on the lower surface of the cylinder. This ensured that the air drawn into the fan was the same temperature as the air flowing out of it, thus conserving energy in the system.
The four heaters were modeled as solids with a volumetric heat source. Based on the volume of one heater, which was 5.746158 × 10−5 m3, it was calculated that the required power of the heat source was 2,175,366.5 W/m3. This gave a power of 500 W for all four heaters during operation. Deactivation of the heat source occurred when the average air temperature in the chamber exceeded 60 °C. Due to the creation of the mesh in two separate files (one containing the heat exchanger, the mat at the exchanger, and the sheet at the exchanger, and the other for the rest of the system), it was necessary to create an interface between the surface of the sheet and the chamber volume. A convection boundary condition was applied at the points of contact between the chamber volume and the air surrounding the system, which considered the thickness of the sheet metal.
The fluid temperature for the convection boundary condition, i.e., the air temperature around the chamber, was 20.4, and the HTC was determined by numerical calculations so that the results coincided with the experimental results. Its optimum value was 3.5 W/(m2 K). For the chamber–heat exchanger interface, due to the forced air movement, the HTC had a much higher value of 8.279 W/(m2 K) for a fluid temperature of 60 degrees. This value was obtained from the global model for the last time step. A coupled condition that considers the sheet thickness was also assumed between the mats, distant from the heat exchanger and the chamber volume. The outer surfaces of the butyl mats, as well as the outer surfaces of the heat exchanger, were given a direct convection condition with a fluid temperature of 20.4 °C and an HTC equal to the HTC from the chamber volume condition versus the ambient air. The initialization of the model assumed zero velocity and a homogeneous system temperature of 20.4 °C. The entire numerical simulation simulated 204 min of real-time in which the dishwasher was operating, which corresponded to the length of the experiment. The initial time step of the analysis was 0.01 min, and as the stability of the calculation increased, this was increased to a value of 0.2 min after converting 3 min of analysis time.
3.4. Optimization of the Heat Exchanger
The purpose of the calculations was, among other things, to propose changes to the design of the dishwasher water system and the water flow diagram in order to improve energy efficiency. Based on our experience, it was decided to analyze a modified heat exchanger system through which a 0.4 mm thick aluminum tube was routed. Hot water would flow through this tube after the rinsing process. At the same time, cold water from the mains will be poured into the water tank, which will be in direct contact with the outer walls of the aluminum tube. The opposite movement of the liquid is intended to increase the amount of heat transferred. In the performed analyses, the inner part of the tube was not coated to protect the aluminum from the corrosive effect of the heated detergent water after the rinsing process. The real-world model should take such a surface into account and investigate its effect on the results in the calculation environment.
The inner and outer surfaces of the tube remain smooth after the manufacturing process, so it was not necessary to take roughness into account during the numerical calculations. The geometry of the heat exchanger before and after the changes is shown in Figure 11 and Figure 12. The cold-water inlet from the mains for both geometries is located in the same places (represented by the slender red cylinders in Figure 13), but in the changed geometry, immediately after the inlet to the bottom of the cylinder, the cold water is directed to the red inlet on the right-hand side. This inlet is adjacent to the hot water outlet of the aluminum tube. The inlet and outlet of the aluminum tube are next to each other. This altered geometry completely eliminates the ventilation hole marked in Figure 9. In Figure 13, marked in red, is the hole that was created to inlet water from the mains to the water storage tank. The cyan color denotes the lateral surface of the grid water flow path. The new heat exchanger geometry maximizes the surface area and the time in which the heated water has the opportunity to transfer heat to the main water. In addition, the use of aluminum greatly increases heat transfer due to its relatively high thermal conductivity coefficient.
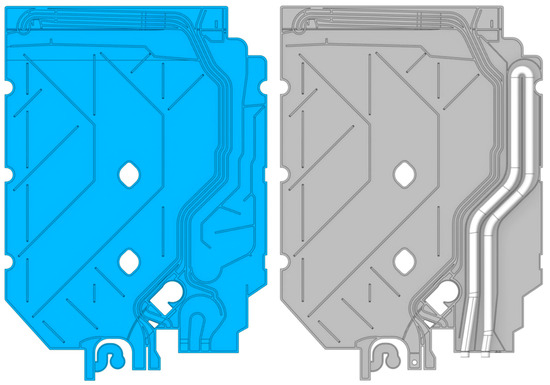
Figure 11.
Comparison of heat exchanger reference geometry before (left) and after (right) evaluated changes.
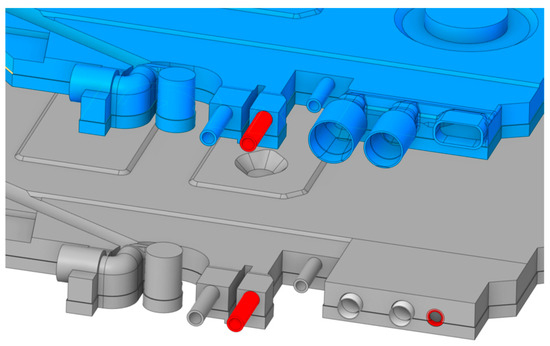
Figure 12.
Comparison of heat exchanger geometry before (top) and after (bottom) changes.
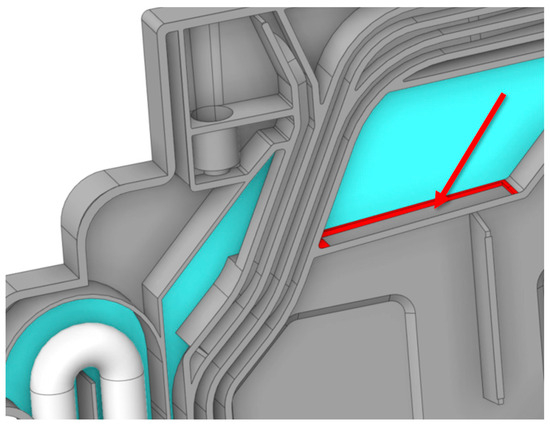
Figure 13.
New additional hole through which water flows into the water storage tank indicated with red contour and arrow.
3.5. Defining the Most Important Working Point in the Washing Cycle
The simulation, crucial for determining the thermal yield, involved filling the storage tank with mains water at 11 °C. The volume of water that was to be in the filled tank was 3.15 L. During the filling of the water storage tank, there is a load inside the chamber consisting of vessels, and water (at a temperature of 60 °C) is injected from the spray arms. Thus, it was necessary to model the heat-transfer processes inside the chamber due to the lack of knowledge of the HTC between the sheet at the heat exchanger and the interior of the chamber. In the chamber, spraying water creates a moving free surface, which was mapped using the volume of fluid (VoF) method. This was necessary in order to accurately determine the HTC coefficient of the sheet surface at the heat exchanger because some of the heated water falls directly on this surface and significantly increases heat transfer. The two heat exchanger geometries presented in Section 3.4 were simulated. Since the HTC coefficient at the sheet metal interface did not depend on the geometry of the heat exchanger (this assumption was verified computationally), the simulation of the original heat exchanger geometry only considered the geometry of the heat exchanger along with the mat and sheet directly adjacent to its wall. Since the dishwasher chamber is in a steady state during the water-pouring process, it was decided to replace the geometry of the chamber sheet, butyl mats, and felt mats with a boundary condition (i.e., a layer shell conduction). A similar condition was set for the rear wall of the heat exchanger in contact with the felt mat. The established temperature field also made it possible to disregard the geometry of the baskets inside the chamber, which have complex geometries (they would cause a large increase in the number of elements) but have little effect on the water-splash process.
3.6. Main Simulation Geometry
Figure 14 and Figure 15 show the geometric form of the system in the computational environment for the changed geometry of the heat exchanger. Figure 14 displays an isometric projection, from which it can be seen that the transparent volume of the chamber contains voids for the vessels (the voids were automatically filled with mesh during the meshing process) and flat cylinders containing spray arms in the center. These cylinders, along with the voids for the arm geometries (here, the voids were left as a void type during the calculation), are shown in Figure 15. The outer surfaces of the cylinders provided a rotating interface with the rest of the chamber, allowing for the rotation of the spray arms to be mapped. Because of the increased computational accuracy around the aluminum tube, it was decided to represent it geometrically in the computational model.
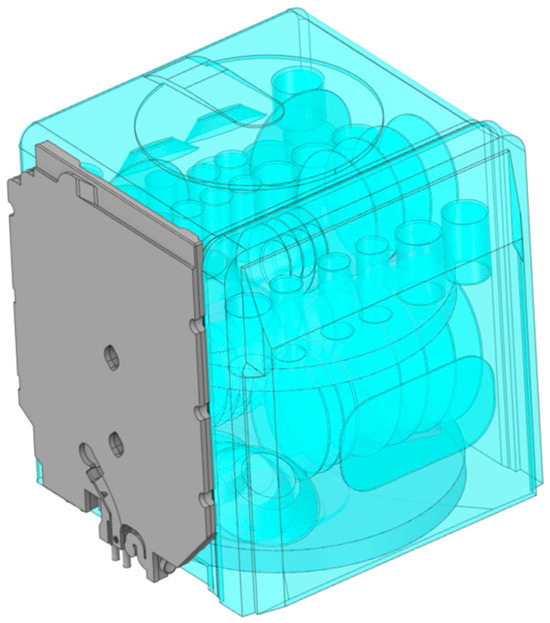
Figure 14.
Geometric form of the system with a modified heat exchanger.
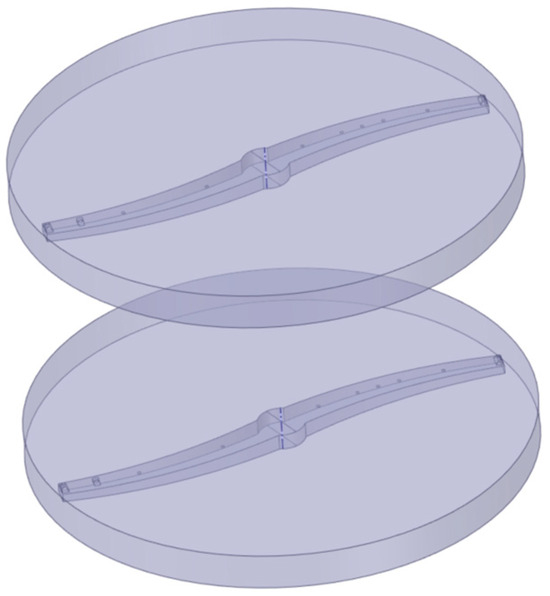
Figure 15.
Volumes around the spray arms.
3.7. Finite Volume Mesh for the Main Simulation
As in Section 3.1, an optimal mesh size was created. For the geometry of the revised heat exchanger, including the wash chamber, a mesh was created consisting of 4,588,633 elements with a minimum orthogonal quality of 0.1507. For the geometry of the original heat exchanger, the number of elements was 1,685,725, and the quality was 0.151. Figure 16 shows the finite volume mesh for the cross-section of the new heat exchanger geometry at the ends of the aluminum tube. It shows the density of the mesh around the tube. Figure 17 shows the mesh spanned by the chamber inlet and the walls of the spray arms. Figure 18 simultaneously displays the mesh on the XY and YZ cross-sections for the chamber and the new heat exchanger geometry. The YZ cross-section shows the interface between the rotating volume around the spray arm and the chamber.

Figure 16.
Finite volume mesh for the cross-section of the new heat exchanger geometry at the ends of the aluminum tube.

Figure 17.
Finite volume mesh for chamber load and spray arm walls.
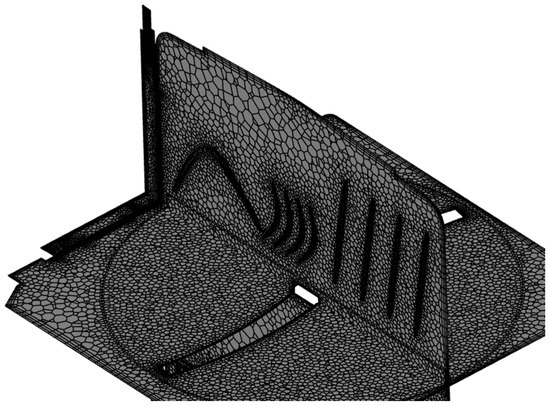
Figure 18.
Finite volume mesh for simultaneous XY and YZ sections for the chamber and the new heat exchanger geometry.
3.8. Boundary Conditions for the Main Model
The material parameters for water and air were taken from the ANSYS Fluent 2022R2 material database. Due to the forced flow of water, the Boussinesq approximation was not used. The viscosity model used in the calculations was the k-omega SST with default values. Pressure–velocity coupling used the “PISO” scheme, spatial discretization of pressure employed the “PRESTO!” method, and discretization of volume contribution utilized the “compressive” method. The rest of the spatial discretization methods used were first-order upwind methods. The optimal time step for the analysis with the chamber (the new heat exchanger geometry) was 0.025 s, and for the analysis without the chamber (the original heat exchanger geometry), it was 0.05 s. The speed of the spray arms was 20 rpm. The mass flux for both spray arms was 0.041583 kg/s, and the temperature of the sprayed water was 60 °C. At the bottom of the chamber, there were two openings through which water and air could flow out of the design domain (i.e., the pressure outlet). A convection condition was assumed for the outer walls, which considered the thickness of each layer of material (the layer shell conduction). This condition used an HTC of 3.5 W/(m2 K) (a value determined from the heater experiment), and the temperature of the fluid around the domain was 23 °C. For the analysis of the new heat exchanger geometry, a mass flow rate of mains water at 11 °C was assumed to be equal to 0.05708 kg/s, which corresponded to filling 3.15 L of water storage volume in 60 s. The same flow rate was set for the water at the inlet to the aluminum tube; the water temperature was 60 °C.
For the analysis of the original heat exchanger geometry, the sheet metal contact with the chamber was replaced by a convection boundary condition with an HTC of 29.15 W/(m2 K) and a fluid temperature of 60 °C. The HTC value was taken as the averaged HTC value from the results of the analysis with the chamber. The mass flow rate of main water at 11 °C for the original geometry of the heat exchanger had a value of 0.01902 kg/s, which allowed the water tank to be filled in 180 s. The values of mass flow were tested by the Ordering Party (SANHUA AWECO Appliance Systems). The initialization of solutions consisted of setting zero velocity and an equal temperature of 23 °C in the domain for the analysis of the original heat exchanger geometry. For the new geometry, these values were the same; however, the interior of the chamber had an initial temperature of 60 °C and zero velocity. A quick pseudo-determination of the temperature field in the model allowed this simplification of the initial conditions.
4. Results
4.1. Results of the Heater Experiment
The figures included in this subsection show the results for the last time step, i.e., for 204 min. Figure 19 shows a map of vectors on the cross-section of the chamber and heat exchanger. The vectors are of equal length, but their color depends on the fluid velocity at a given location. The contour maps for the chamber are pseudo-fixed in nature, i.e., they may vary slightly between successive time steps. This is due to the turbulent nature of the flow inside the chamber. Figure 20 shows the temperature distribution over the same cross-section. A significant temperature gradient between the water in the water tank and the chamber is clearly visible. Figure 21 and Figure 22 show, in turn, the temperature distribution in the cross-section of the volume of water contained in the storage tank as well as on the outer surfaces of this volume. Clearly noticeable is the stratification of temperature in the vertical direction as well as in the direction normal to the lateral surface of the chamber. Figure 23 shows a graph comparing experimental results with global model calculations. The global model, in this case, is considered to include the volume of the chamber, including the mats, heaters, and fans. The graph shows good agreement between the calculations and experimental results. Figure 24 shows a comparison of the results of the global model with the local model. It shows good overlap between the two models for the whole duration of simulation.
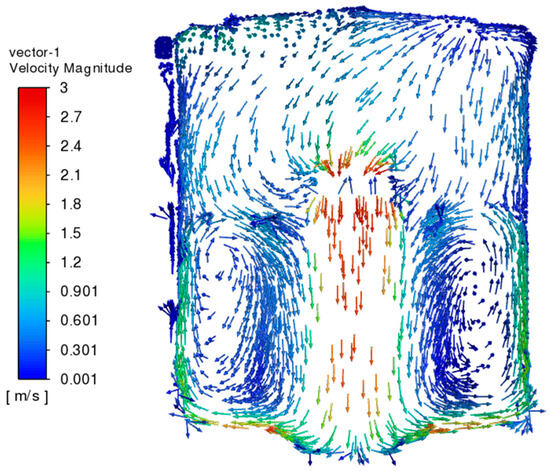
Figure 19.
Map of velocity vectors on the cross-section of the chamber and heat exchanger.
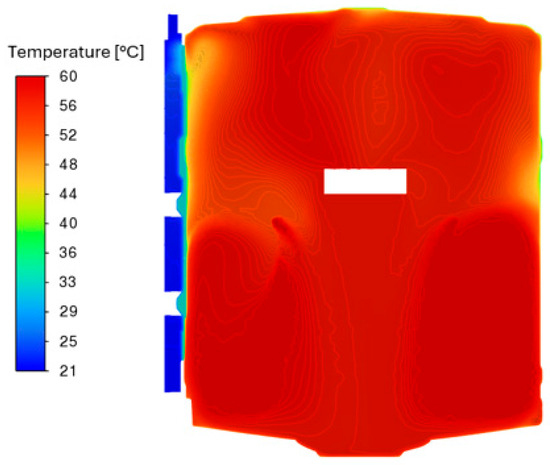
Figure 20.
Contour temperature map on the cross-section of the chamber and heat exchanger.
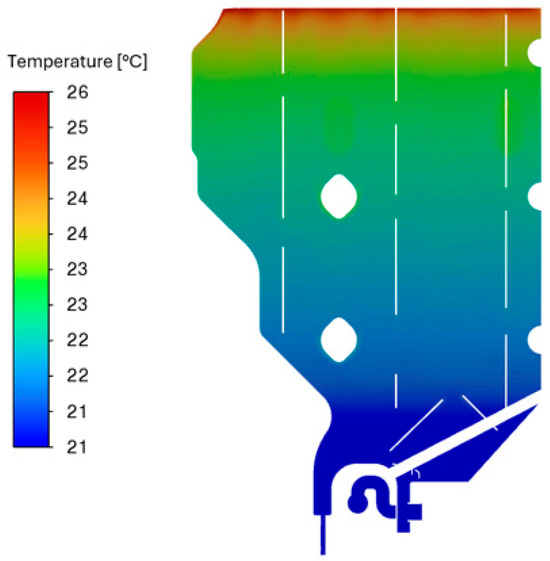
Figure 21.
Temperature distribution in the tank cross-section showing only the volume of water.
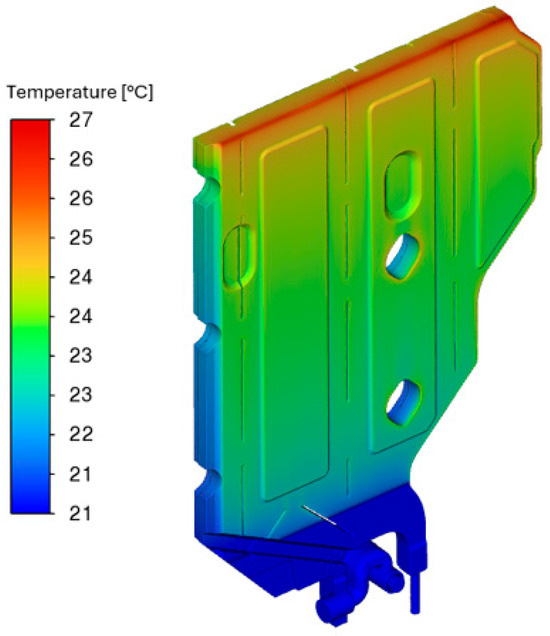
Figure 22.
Temperature distribution on the outer surfaces of the water volume in the storage tank.
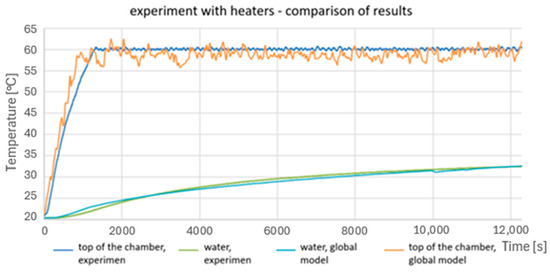
Figure 23.
Graph showing a comparison of experimental results with global model calculations.
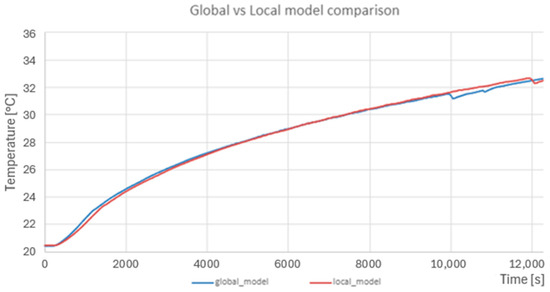
Figure 24.
Graph showing a comparison of the results of the global model with the local model.
4.2. Results for the Main Model
The figures in this subsection show the results for the final time step, i.e., 60 s for the analysis of the new heat exchanger geometry and 180 s for the analysis of the original heat exchanger geometry. Figure 25 shows the distribution of the volume fraction of water in each cell on a section through the new heat exchanger. A value of 1 indicates a complete filling of the cell with water, and a value of 0 indicates a complete filling with air. The figure shows a blurring of the water–air interface due to the use of the sharp/dispersed interface modeling option and the relatively large time step of the analysis. However, this blurring should not affect the heat conduction results because the interface around the aluminum tube is clear. Figure 26 shows a similar contour map for the original heat exchanger geometry. Due to the less turbulent water flow and slower mass flux, the water-air interface has a clearly defined shape. Figure 27 and Figure 28 compare the temperature distributions at the same cross-sections for the analysis of the new and original heat exchanger geometries in turn. In addition, Figure 29 and Figure 30 show the temperature distributions on the cross-sections for the new heat exchanger.
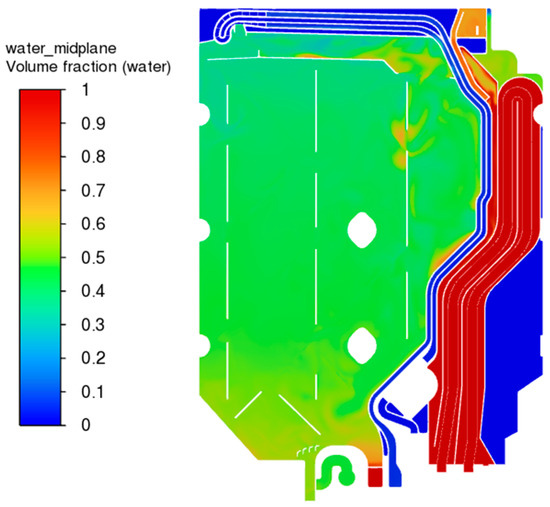
Figure 25.
Volume distribution of water and air in the cross-section of the new heat exchanger.
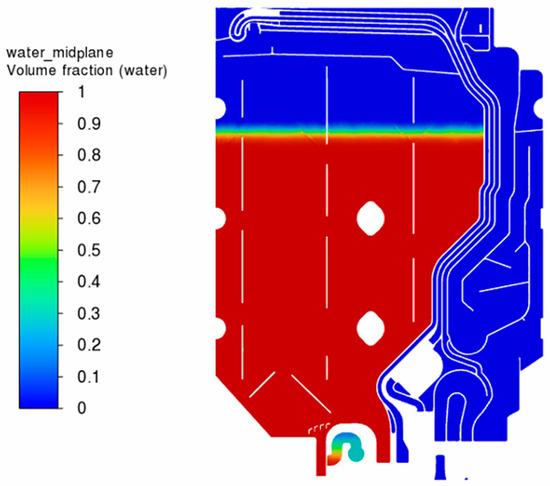
Figure 26.
Volume distribution of water and air in the cross-section of the original heat exchanger.
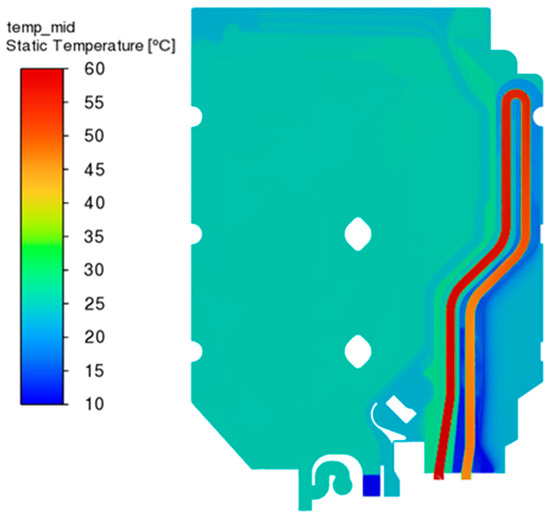
Figure 27.
Temperature distribution in the cross-section of the new heat exchanger.
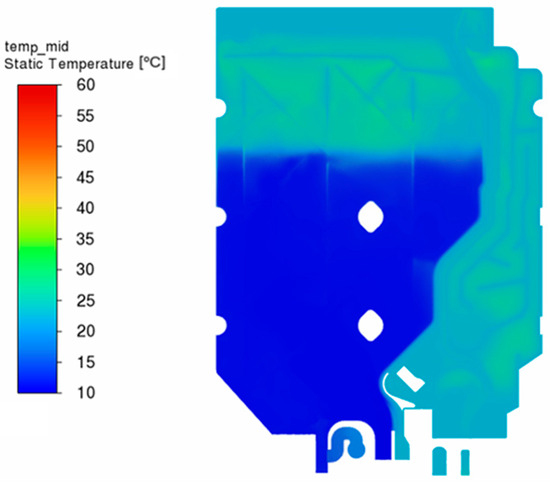
Figure 28.
Temperature distribution in the cross-section of the original heat exchanger.

Figure 29.
Temperature distribution in the XY section of the new heat exchanger and chamber.
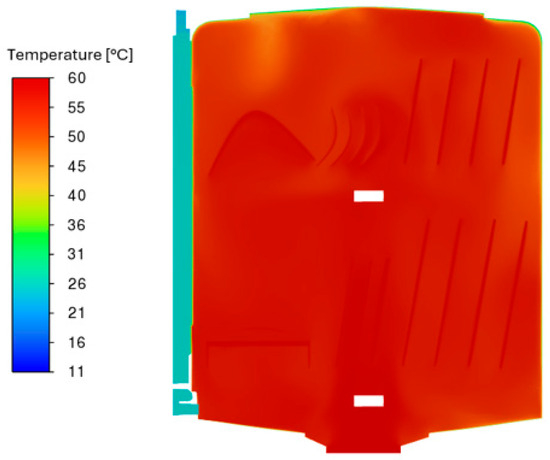
Figure 30.
Temperature distribution in the YZ section of the new heat exchanger and chamber.
In order to identify areas of the system exposed to heat loss, a contour map of the heat flux leaving the system was created, which is shown in Figure 31 and Figure 32.
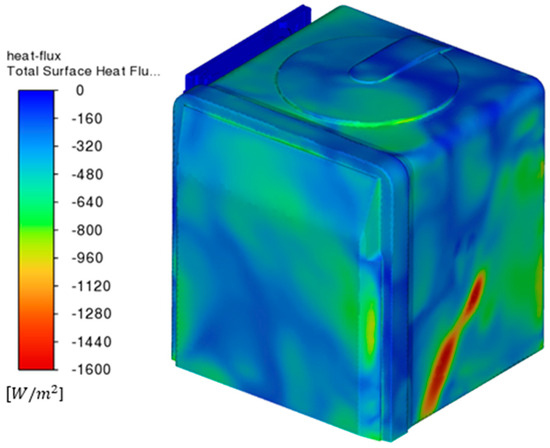
Figure 31.
Distribution of heat flux leaving the system, viewed from the upper-right corner.
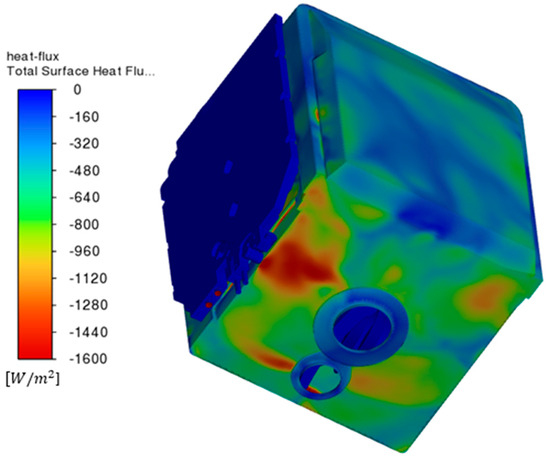
Figure 32.
Distribution of heat flux leaving the system, viewed from the bottom-left corner.
This map shows that the heat exchanger is not an easy pathway by which heat can escape. The situation is different for the walls of the chamber, in which the highest flux occurs where the water currently originates from the spray arms. As the water flows through the heat pipe, it reduces its temperature from 60 to 45 °C, thus giving an average heat transfer at the end of the analysis of 3.59 kW, assuming a specific heat of water of 4200 J/(kg K). The average water temperature in the new heat exchanger geometry at the end of the analysis was 24.82 °C compared to 13.26 °C for the original geometry (87.18% temperature increase). This provides a theoretical yield when filling the water tank of 152.94 kJ.
The amount of heat transferred through the chamber walls to the environment (excluding the sheet metal-HEX interface) for the case with the new heat exchanger geometry is 55.48 kJ in 60 s, which provides a heat flux equal to 924.62 W. This value will be similar to the case with the original heat exchanger geometry because the results are obtained at a significant distance from the heat exchanger. The large heat flux value is due to the replacement of the geometric form of the sheet and the bitumen and felt mat with a boundary condition (layer shell conduction) that does not consider the influence of specific heat and thermal inertia of the individual layers.
The additional heat energy accumulated in the loading due to spraying (relative to the initial temperature) is 526.73 kJ. This loading considers the vessel baskets. This value is the same for both geometries of the heat exchanger. Due to the replacement of the geometric form of the sheet and bitumen and felt mat with a boundary condition, it was not possible to determine the thermal energy stored in these bodies. The heat exchanger was spatially discretized, and the value of heat stored in its volume for the original geometry is –18.64 kJ. For the new geometry, the value is 3.46 kJ. The negative value for the original geometry is due to the significant volume of cool water from the grid inside it (negative energy causes condensation drying).
5. Conclusions and Recommendations
Due to the complexity of the real system, the dishwasher and its washing cycle were simplified so that simplifications had minimal impact on the obtained results. The parameters of fluid temperature and flow velocity in the various parts of the system allowed us to represent the heat flow for the critical moment of the dishwasher cycle, which was the stage of filling the water tank. Conducting an additional test, assuming no movement of the free water surface, allowed for checking the correctness of the modeled system and determining the HTC for convection boundary conditions for the outer surfaces of the system. The areas of highest instantaneous heat transfer are identified in Figure 31 and Figure 32. Increasing the level of insulation can be undertaken by applying a bituminous or felt mat to the exposed sheet metal surfaces of the washing chamber. The proposed changes to the geometry of the heat exchanger and the alteration of the flow of heated water, so that it runs through the heat exchanger, allowed for a significant thermal yield of 152.94 kJ when filling the water tank. This gives a yield of 305.88 kJ during the dishwasher’s entire cycle and a yield of 85,646.4 kJ in terms of the dishwasher’s annual operation.
It is worth noting that incompressible smoothed particle hydrodynamics (ISPH) stands out as a promising numerical modeling method since it is being actively developed in commercial numerical software, such as Particleworks (v8), at the time of writing this paper. Unlike the volume of fluid (VOF) method, ISPH offers inherent advantages in handling free surfaces without the need for explicit interface tracking. Utilizing particles to represent the fluid domain, ISPH naturally captures intricate surface deformations, such as splashing, waves, and foam formation, which are characteristic of dishwasher environments. Moreover, ISPH’s meshless nature eliminates the need for a fixed computational grid, making it adaptable to the irregular geometries and moving boundaries often encountered in dishwasher chambers. Its numerical stability, even in highly dynamic flow, and potentially lower computational costs further solidify ISPH’s appeal as a robust and efficient approach for simulating the complex fluid dynamics inherent in dishwasher operations.
Author Contributions
Conceptualization, W.S. and M.S. (Michał Sobota); methodology, W.S. and M.S. (Michał Sobota); software, M.S. (Michał Sobota) and P.A.; validation, M.S. (Michał Sobota) and P.A.; formal analysis, M.S. (Michał Sobota) and W.S.; investigation, W.S., M.S. (Michał Sobota), M.S. (Michał Skarka) and P.A.; resources, M.S. (Michał Sobota), P.A. and M.S. (Michał Skarka); data curation, M.S. (Michał Sobota) and P.A.; writing—original draft preparation, M.S. (Michał Sobota) and P.A.; writing—review and editing, W.S. and M.S. (Michał Skarka); visualization, M.S. (Michał Sobota) and P.A.; supervision, W.S.; project administration, W.S. and M.S. (Michał Skarka); funding acquisition, W.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Polish National Centre of Research and Development from the project POIR.01.01.01-00-1408/20 titled Dishwasher Hybrid & Energy efficient water management system with Advanced Recovery Technology.
Data Availability Statement
Data are contained within the paper.
Acknowledgments
The authors would like to express their gratitude to SANHUA AWECO Appliance Systems for technical and organizational assistance in carrying out the research.
Conflicts of Interest
Authors Michał Sobota, Piotr Antys and Michał Skarka were employed by the company SkyTech eLab LLC. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Regulation of the European Parliament and of the Council of 4 July 2017 (EU) 2017/1369. Available online: https://eur-lex.europa.eu/legal-content/EN/ALL/?uri=celex%3A32017R1369 (accessed on 10 April 2024).
- Heinzle, S.L.; Wüstenhagen, R. Dynamic Adjustment of Eco-labeling Schemes and Consumer Choice—The Revision of the EU Energy Label as a Missed Opportunity? Bus. Strat. Env. 2012, 21, 60–70. [Google Scholar] [CrossRef]
- Andor, M.A.; Gerster, A.; Götte, L. How effective is the European Union energy label? Evidence from a real-stakes experiment. Environ. Res. Lett. 2019, 14, 044001. [Google Scholar] [CrossRef]
- Solà, M.M.; Escapa, M.; Galarraga, I. Effectiveness of monetary information in promoting the purchase of energy-efficient appliances: Evidence from a field experiment in Spain. Energy Res. Soc. Sci. 2023, 95, 102887. [Google Scholar] [CrossRef]
- Minde, M. Validation of Dishwasher CFD Model Using PIV. Master’s Thesis, Luleå University of Technology, Luleå, Sweden, 2011. [Google Scholar]
- Wang, W.; Liu, X.; Shi, Z.; Liu, H. Investigation of heat transfer and energy distribution inside dishwasher based on a coupled 3D-1D simulation method. Case Stud. Therm. Eng. 2023, 49, 103355. [Google Scholar] [CrossRef]
- Erik, Ö.B. Hydraulic Design Optimization and Performance Evaluation for a Dishwasher. Unpublished. Master’s Thesis, Izmir Institute of Technology, Izmir, Turkey, 2019. Available online: https://gcris.iyte.edu.tr/handle/11147/10918 (accessed on 13 January 2024).
- Bengtsson, P.; Berghel, J.; Renström, R. A household dishwasher heated by a heat pump system using an energy storage unit with water as the heat source. Int. J. Refrig. 2015, 49, 19–27. [Google Scholar] [CrossRef]
- Selimli, S.; Karabas, T.; Taskin, Y.; Karatas, M.B. Experimental study of the performance of heat recovery by a fin and tube heat exchange tank attached to the dishwasher greywater line. Sustain. Energy Technol. Assess. 2019, 36, 100552. [Google Scholar] [CrossRef]
- Selimli, K.M.A. Abajja, Recovery of greywater thermal energy with a wire on a tube heat exchanger attached to a dishwasher. Water Environ. Res. 2021, 93, 1333–1345. [Google Scholar] [CrossRef]
- Atasoy, E.; Çetin, B.; Bayer, Ö. Experiment-based optimization of an energy-efficient heat pump integrated water heater for household appliances. Energy 2022, 245, 123308. [Google Scholar] [CrossRef]
- Habibi Khorasani, S.M. Hydraulic Simulation Model for Dishwasher. Master’s Thesis, KTH, School of Engineering Sciences, Stockholm, Sweeden, 2018. Available online: https://www.diva-portal.org/smash/record.jsf?pid=diva2%3A1381816&dswid=3220 (accessed on 13 January 2024).
- Tang, J.S. Modelling Study of Dishwasher Hydraulic Filtration System. In Proceedings of the World Congress on Engineering and Computer Science, San Francisco, CA, USA, 22–24 October 2019. [Google Scholar]
- Kobielski, M.J.; Skarka, W.; Mazur, M.; Kądzielawa, D. Evaluation of Strong Cation Ion-Exchange Resin Cost Efficiency in Manufacturing Applications—A Case Study. Polymers 2022, 14, 2391. [Google Scholar] [CrossRef] [PubMed]
- Mateja, K.; Skarka, W.; Peciak, M.; Niestrój, R.; Gude, M. Energy Autonomy Simulation Model of Solar Powered UAV. Energies 2023, 16, 479. [Google Scholar] [CrossRef]
- Peciak, M.; Skarka, W. Assessment of the Potential of Electric Propulsion for General Aviation Using Model-Based System Engineering (MBSE) Methodology. Aerospace 2022, 9, 74. [Google Scholar] [CrossRef]
- Ansys Inc. Ansys Help; Ansys Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- Menter, F.R. Zonal Two Equation Kappa-Omega Turbulence Models for Aerodynamic Flows. In Proceedings of the AIAA Fluid Dynamics Conference, Orlando, FL, USA, 6–9 July 1993. [Google Scholar]
- Andersson, B.; Andersson, R.; Håkansson, L.; Mortensen, M.; Sudiyo, R.; van Wachem, B. Computational Fluid Dynamics for Engineers; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Zeytounian, K.R. Joseph Boussinesq and his approximation: A contemporary view. Comptes Rendus Mec. 2003, 331, 575–586. [Google Scholar] [CrossRef]
- Cengel, Y.A. Heat Transfer A practical Approach; Mcgraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Kaminski, D.A.; Jensen, M.K. Introduction to Thermal and Fluids Engineering; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Kundu, P.K.; Cohen, I.M.; Dowling, D.R. Fluid Mechanics, 5th ed.; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- EN 50242:2016; Electric Dishwashers for Household Use—Methods for Measuring the Performance. European Committee for Electrotechnical Standardization: Brussels, Belgium, 1 July 2016.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).