1. Introduction
Nuclear fusion is a process where the collision of light nuclei causes the further formation of one or more heavier nuclei and subatomic particles [
1] and is characterized by the release of a substantial amount of energy. As is known, this process is currently of high significance for humanity due to its potential to become a clean, safe, and abundant energy source in the near future [
2]. At present, a sufficient number of fusion devices and projects with different fusion reactor concepts [
3] exist, especially large tokamaks such as the International Thermonuclear Experimental Reactor (ITER) [
4] and the Joint European Torus (JET) [
5], using strong and powerful magnetic fields to confine hot plasma at temperatures exceeding 150 million °C. Although significant progress has been made in fusion research and various fusion devices and installations are utilized nowadays, it is still unknown and uncertain when fusion reactors will finally become commercially viable. According to ITER estimations, the main D-T fusion experiments are planned for 2035, with final completion expected around 2040 [
6]. It is a well-known fact that the ITER specialists expect at least a 10-fold increase in the energy of the fusion reactor, which corresponds to the production of 500 MW of fusion energy with external heating of 50 MW. Therefore, the development of nuclear fusion research and the proposal of alternative fusion reactor concepts with various methods of plasma confinement (not only tokamaks) remain one of the most crucial challenges of the current century.
The leading types of plasma confinement methods used in fusion research are magnetic confinement (JET, ITER) [
7], inertial confinement (National Ignition Facility, Omega Laser Facility, Laser Mégajoule) [
8], and magneto-inertial confinement (Z Facility, Tri Alpha Energy, Helion Energy, General Fusion) [
3,
9]. The particle density required for controlled nuclear fusion reaches 10
20 m
−3 in magnetic confinement fusion devices and 10
31 m
−3 in inertial confinement fusion devices. Both of these values can be achieved at temperatures of about 10 keV. Regarding the last concept, magneto-inertial confinement, as a new approach to energy production [
3], combines the general principles of both magnetic and inertial fusion. One of the great examples is MagLIF (Magnetized Liner Inertial Fusion) experiments conducted in the Z machine at Sandia National Laboratories [
10,
11,
12]. This concept involves using a Z-pinch to compress a magnetized fusion fuel [
9,
13,
14,
15,
16,
17,
18], typically deuterium–tritium (D-T) or deuterium–deuterium (D-D), to achieve the conditions necessary for fusion reactions. Since magnetic and inertial fusion devices are well studied and taking into account the above statements about the commerciality of fusion reactors, Z-pinches based on the magneto-inertial fusion concept can be considered as a promising alternative method of controlled fusion research.
Concerning the most promising types of fusion fuel, the main fusion fuel used in research and experiments is deuterium–tritium (D-T) fuel [
19,
20,
21] because D-T fusion reactions release a significant amount of energy and occur at lower temperatures (approximately at about 10 keV) compared to other fusion reactions. Although deuterium is an abundant fuel source, it is essential to generate tritium from lithium-containing breeder blankets during neutron irradiation [
22,
23]. In contrast, fuel sources such as deuterium–deuterium (D-D) and deuterium–helium-3 (D-
3He) can also be used in fusion reactors in the future as alternative options [
24]. However, these fuel types burn efficiently at temperatures of 30 keV and above. Therefore, deuterium–tritium (D-T) remains the primary fusion fuel due to its energy yield and lower temperature required for nuclear fusion.
The main aim of the present work is to extend the methods developed in [
25,
26], where the burning of hot, dense plasma containing D-T and D-
3He fuel capsules is considered within magnetic–inertial facilities. Although D-T fuel was considered in [
26], the main focus of the research was on D
3He fusion in hot, dense-state plasma with a minimal neutron fraction in magnetic–inertial facilities. In contrast, this work focuses on the detailed theoretical description of the D-T fuel burning rate in a Z-pinch device with magneto-inertial plasma confinement along with corresponding numerical methods for solving the particle and balance equations. The fusion reactions in the mixed D-T-
3He cycle (D+T, D+D, D+
3He,
3He+
3He, and T+T) are considered, taking into account all produced charged ions (p, D, T,
3He,
4He). The plasma is in a hot, ultra-dense state under the quasi-neutrality condition, with initial deuterium and tritium densities of
cm
−3 and an electron density of
cm
−3. The average ion and electron temperature was equal, with an initial value of 10 keV, achieved by fast laser ignition. The time dependencies of the ion densities, plasma temperature, energy yield from charged ions and neutrons, fusion power density, and bremsstrahlung radiation loss were studied.
2. Methods
D-T fuel burning initiated by a laser pulse in a Z-pinch device was considered in this paper. A deuterium–tritium gas mixture was contained in a cylindrical capsule under high pressure. The ultrashort laser pulse was essential for fast and effective ignition of the fuel mixture. An electron–photon converter designed with a high-Z element, such as tantalum (Ta), was positioned at the left end of the capsule. This converter facilitated the conversion of part of the energy from fast-moving electrons into a stream of bremsstrahlung photons. A powerful mega-ampere electrical pulse propagates through the system along the direction of the capsule axis. This scheme of nuclear fusion with the example of D-
3He fuel was first proposed by Voronchev V.T. and Kukulin V.I. [
25] and further developed by Seksembayev et al. [
26]. The authors offered
9Be as a material for the capsule. However, since D-T fuel is considered in this paper, it would be interesting to use
6Li in a mixture with
9Be as a potential material and an additional source of tritium.
The burning rate of D-T fuel in Z-pinch devices with magneto-inertial fusion is investigated in this paper. Specifically, only deuterium and tritium were contained in the liner of a pinch. Although deuterium–tritium (D-T) fuel is considered in the calculations, to achieve realistic results, it is essential to take into account the densities of various charged ions produced during nuclear fusion reactions. The main process is the D-T fusion reaction with emission of α-particles and neutrons. However, despite the lower fusion cross-section compared to D-T fusion, there is also a possibility of D-D and T-T fusion reactions, so that charged particles like protons, tritium, and
3He ions can be additionally produced during fusion. Thus, the following reactions were used for accurate and precise calculations:
where the reaction energies (
Q values) are expressed in units of MeV.
The burning rate of thermonuclear fusion fuel is influenced by different factors: the fuel type, the electron and ion densities and temperatures, and the fusion cross-sections of light nuclei contained and produced in a fuel mixture. Among the nuclear reactions given in Equations (1)–(6), the D-T fusion reaction had the largest cross-section, which had a broad maximum at a center-of-mass energy of 64 keV [
27]. The D-T and D-
3He fusion reactions were resonant [
28,
29], while the D-D, T-T, and
3He-
3He fusion reactions had a non-resonant nature. As a result, due to a wide resonance, the D-T and D-
3He fusion reactions had higher fusion cross-sections compared to the other reactions.
Although fusion cross-sections significantly influence the burning rate of fuel, it is essential to take into account the fact that particles in plasma are distributed depending on their velocities (kinetic energies). Therefore, a more principal physical value for nuclear fusion is the reaction rate. Assuming the Maxwellian distribution of particles, the thermally averaged reaction rate can be obtained as follows [
30]:
where
is the fusion cross-section,
is the particle velocity, and
is the Maxwellian distribution function.
In this paper, the reaction rates obtained by the approximation formulas [
30,
31] are utilized. The logarithmic reaction rates for the reactions from Equations (1)–(4) were taken from [
30] and are expressed as
where the temperature,
, is expressed in units of eV. The approximation coefficients,
and
, are defined in [
30] and listed in
Table 1.
Table 1 presents the values of the approximation coefficients,
and
, for the logarithmic reaction rates of the reactions described in Equations (1)–(4). For all four reactions given in Equations (1)–(4),
and
.
The reaction rates for the reactions corresponding to Equations (5) and (6) were obtained from the approximation formulas [
31] as follows:
where the temperature,
, is expressed in keV. The reaction rates in Equations (8)–(11) are expressed in units of cm
3/s.
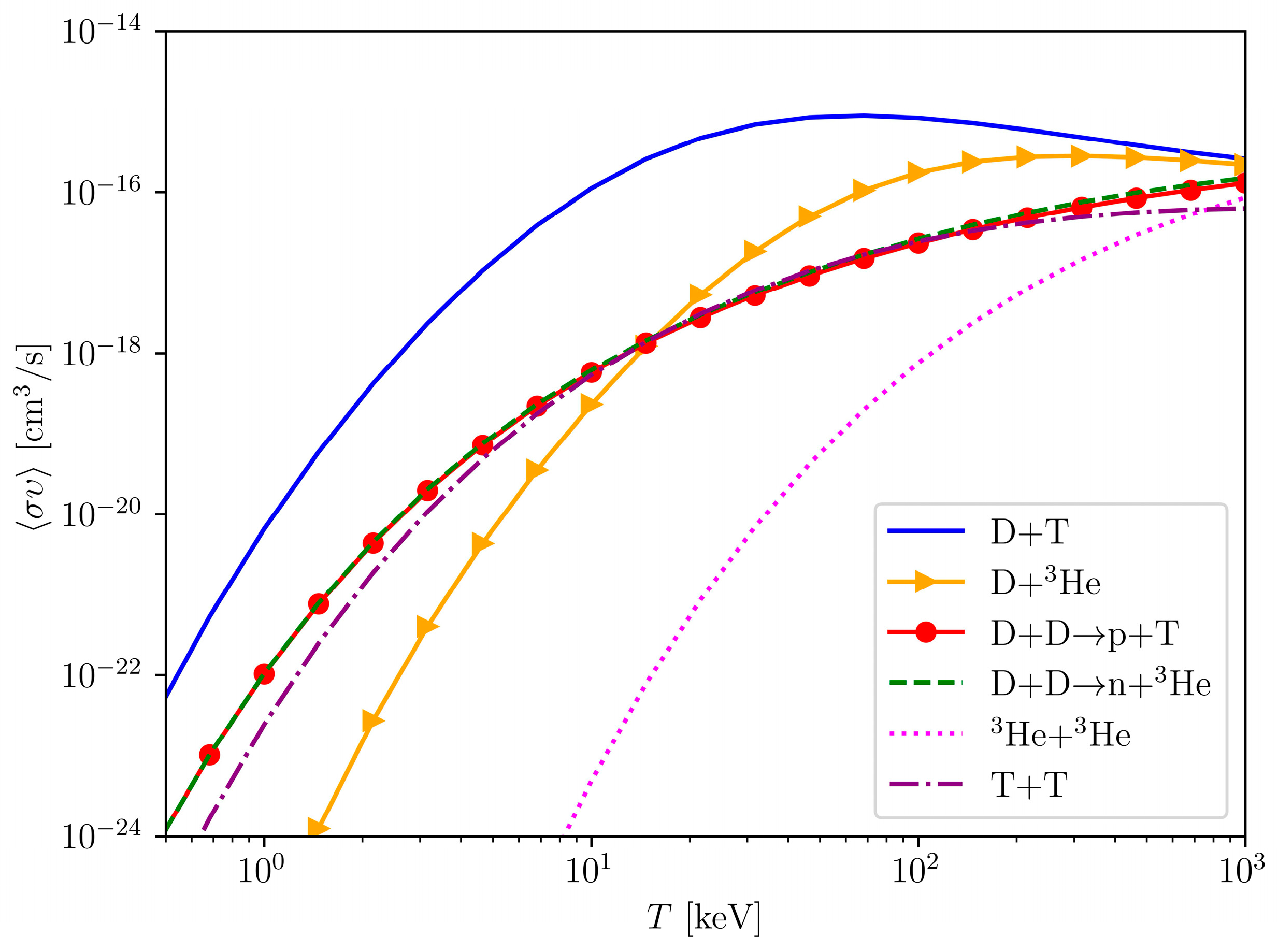
Figure 1 shows the reaction rate values of the nuclear reactions corresponding to Equations (1)–(6) depending on temperatures in the center-of-mass energy frame, obtained by the parametrization formulas given in Equations (8)–(10). From the results illustrated in
Figure 1, it can be noted that the reaction rate of the D-T fusion reaction was dominant compared to other reactions at temperatures up to 1000 keV, while that of D-
3He was the second highest from 10 keV and above. However, at higher temperatures, the reaction rates of other processes significantly increased and approached the values of the deuterium–tritium fusion reaction. At lower energies, up to 10 keV, the T-T fusion reaction rate was slightly lower than that of D-D fusion (nuclear reactions (2) and (3) were considered separately), but almost equal from 10 keV to 200 keV. Additionally, the reaction rate of
3He-
3He fusion was the lowest among all reactions considered in this paper.
The burning rate of the D-T fusion in dense, hot plasma was defined through a set of particle and energy balance equations, which involved the reaction rates depending on the plasma temperature. The particle balance equations describe the change in the ion densities of fuel components. Initially, the fuel mixture contained only deuterium and tritium ions and electrons. As a result of the fusion reactions, the fuel mixture was filled with protons, tritium,
3He, and
4He ions. Thus, based on the rates of fusion reactions corresponding to Equations (1)–(6), the set of particle balance equations can be defined as follows:
where
is the density of the
i-th ion (
i = p, D, T,
3He, α) and
is the fusion reaction rate for reactions (1)–(6). The rates of reactions of identical particles are multiplied by a factor of 1/2. It should be noted that in Equations (11)–(15), the particle number is taken into account, not reactions. Thus, for example, in Equation (12), since two deuterium nuclei are lost during the D-D fusion reactions, the number of particles is proportional to
and
, while the corresponding reaction rates are
and
. Similarly, the formation of 2 protons in the reaction in Equation (6) is taken into account, as well as the loss of 2 tritium/helium-3 nuclei in the reactions corresponding to Equations (5) and (6).
The total energy density of plasma depends on the kinetic energies of both electrons and ions. Generally, the temperatures of electrons and ions are different. Moreover, in a fuel mixture, there are different hydrogen and helium ions as well as other impurities in the plasma. In addition, it is worth noting that the plasma temperature is primarily influenced by the charged ions. Thus, assuming equal average ion and electron temperatures, the total energy density,
, can be obtained as follows:
where
is the electron density,
is the average electron temperature, and
is the average ion temperature. In terms of the quasi-neutrality condition for the plasma, the electron density is defined as
where
and
are the charge and density of the
i-th ion, respectively.
The energy balance equation shows the difference between the fusion power density and radiation losses, and can be defined for Z-pinch devices with magneto-inertial confinement in the following way:
where
is the fusion power density of charged ions,
is the bremsstrahlung radiation power density loss, and
is the synchrotron radiation power density loss. Since the electromagnetic fields, which compress and confine the plasma in a Z-pinch configuration, are generated by the plasma itself, no external resources are needed. Thus, auxiliary power is not essential, except for laser ignition, which is required for the plasma to achieve a minimum fusion temperature of 10 keV. In fact, a temperature of 10 keV was initially chosen for the calculations in this paper. In addition, taking into account that the magnetic field is strong, we may assume that the transport losses can be neglected. Therefore, in a Z-pinch device, there is only thermonuclear energy from charged hydrogen and helium ions, partially emitting as bremsstrahlung radiation. In addition, we considered the central (hottest) areas of the plasma in Z-pinch devices, which were not affected by synchrotron radiation. Therefore, the synchrotron radiation power density loss can be neglected.
The fusion power density, based on the energy yield of charged particles in reactions (1)–(6), is obtained as
where
is the reaction energy (
Q value) and
is the kinetic energy of a charged particle. Here, the values of energy densities are expressed in MeV/cm
3. It is worth noting that the full fusion power density is the sum of the power densities of charged ions and neutrons. However, as mentioned before, the plasma temperature was affected only by the fusion power of charged ions.
The fusion power density of neutrons is defined as follows:
where
,
,
, and
are the kinetic energies of the neutrons from the fusion reactions corresponding to Equations (1), (3) and (5).
The bremsstrahlung radiation power density loss is defined as follows [
32]:
Here, the power density loss is measured in MeV/cm3.
The set of particle and energy balance Equations (11)–(18) was solved numerically using general integration of ordinary differential equations, employing the SciPy module in Python [
33].
3. Results and Discussion
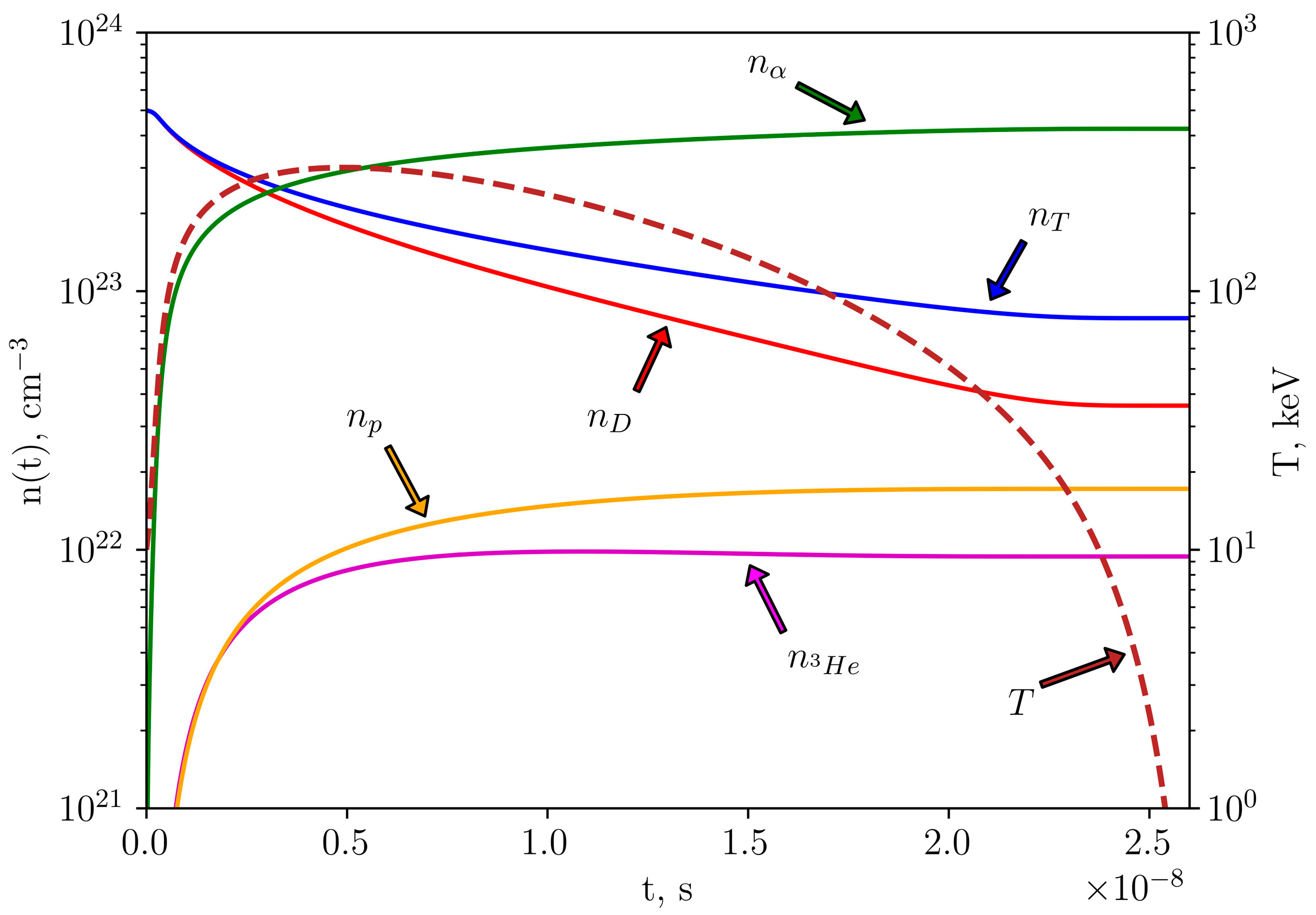
Figure 2 shows the time-dependent changes in ion densities and plasma temperature during the D-T fuel burning in a Z-pinch device with magneto-inertial confinement, which corresponds to the numerical results from Equations (11)–(18). The initial fuel mixture contained only deuterium and tritium atoms. The initial densities of deuterium and tritium were chosen, equal to
cm
−3. Taking into account the quasi-neutrality condition for the plasma, the density of electrons was equal to
cm
−3. The full burning time of the D-T fuel reached
seconds. The plasma temperature increased rapidly, achieving the maximum of 300.38 keV at
seconds. As expected, since the cross-section of the D-T fusion was dominant among other fusion reactions, the number of produced alpha particles exceeded the number of other produced ions during burning. As a result of a rapid increase in the temperature, reactions (2)–(6) significantly influenced the burning rate of the D-T fuel, increasing the production of charged ions, especially protons and
3He ions, and further burning of the produced deuterium and tritium ions. From the results illustrated in
Figure 2, it is worth noting that the effective burning time reached the value of
seconds, and throughout the remaining burning time, the plasma temperature dramatically dropped to
keV, thereby causing the fusion process to stop.
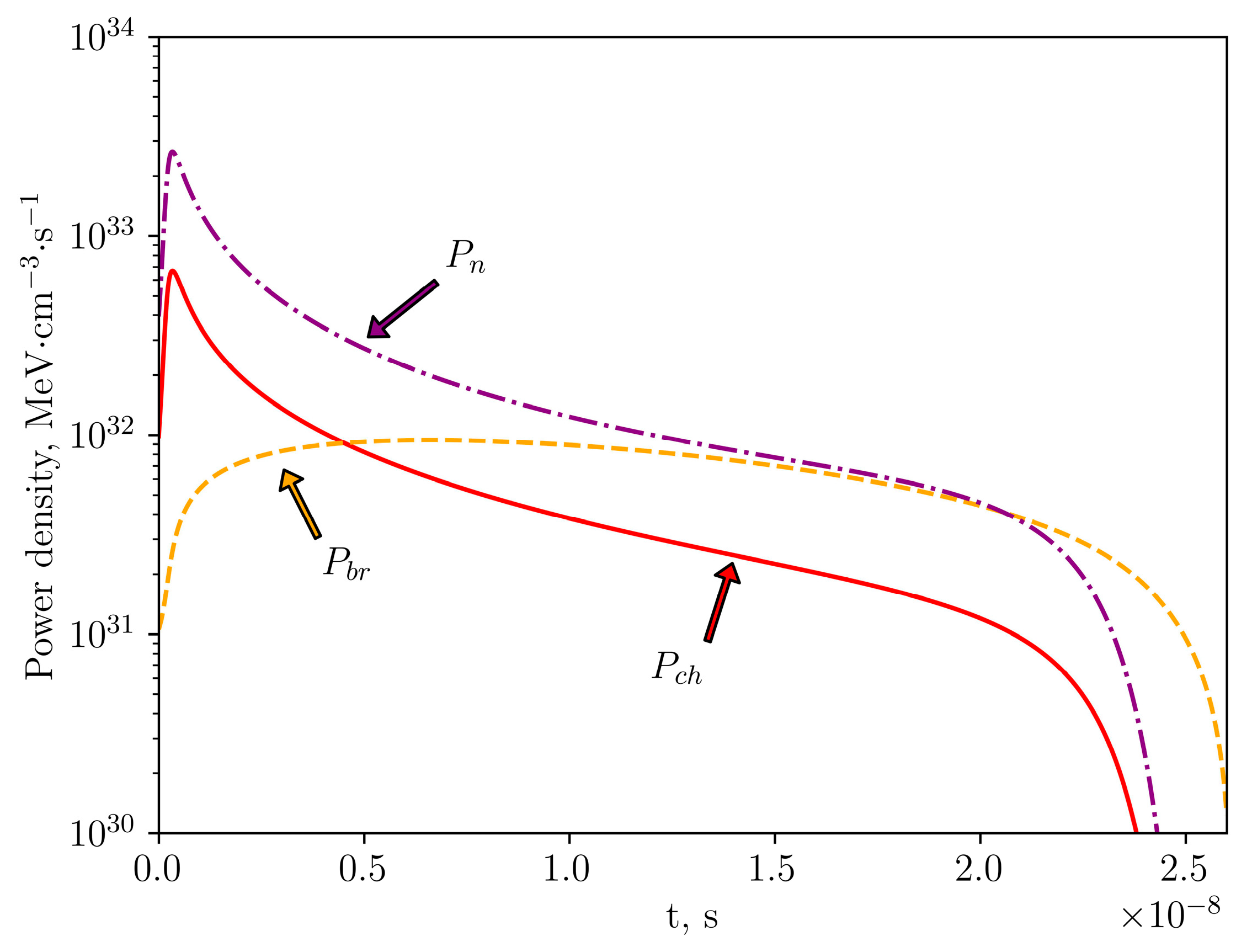
Figure 3 illustrates the fusion power density of charged ions and neutrons as well as the bremsstrahlung radiation power density loss per unit of volume depending on the D-T fuel burning time. The fusion power density of charged ions increased significantly from the starting point of the fuel burning, reaching a peak of
MeV·cm
−3·s
−1 at
seconds. The same pattern of a rapid increase was observed for the fusion power density of neutrons, with a maximum of
MeV·cm
−3·s
−1 at
seconds. After achieving the peak, the fusion power density of both charged ions and neutrons decreased sharply over the rest of the burning time. The bremsstrahlung radiation power density loss increased rapidly up to
MeV·cm
−3·s
−1 in
seconds, and after that, it declined gradually over the remaining period of time. From the results presented on
Figure 3, it can be concluded that the fusion power density of charged ions is almost half an order of magnitude lower than that of neutrons.
Figure 4 shows the energy yield of charged ions and neutrons and the energy of the bremsstrahlung radiation loss per unit of volume, as well as the plasma temperature depending on the D-T fuel burning time. It is worth noting that the time dependencies of the energy yield for both charged ions and neutrons were proportional over the entire burning time of D-T fuel. However, the energy yield of charged particles was almost half an order of magnitude lower than that of neutrons. The energy of the bremsstrahlung radiation was almost one order of magnitude lower than the energy yield of charged ions up to
seconds. Starting from
seconds, the bremsstrahlung radiation grew significantly, and as a result of a fast decrease in the plasma temperature, it finally reached the value of the energy yield of charged ions, stopping the fusion process. From the results presented in
Figure 4, it can be concluded that the time dependency of the energy yield of charged ions and neutrons as well as the energy of the bremsstrahlung radiation were linear up to
seconds, while after that, the burning rate of D-T fuel changed significantly, leading to non-linear changes in the plasma temperature and energy yield of particles. As a fact, one can say that the effective burning of D-T fuel in a Z-pinch device starts in a couple of nanoseconds. As is well known, at low temperatures of about 10 keV, the dominant reaction is the D-T fusion reaction, and other reactions become effective at greater temperatures (about 30 keV for the D-D and D-
3He fusion reactions). Therefore, effective burning means that all of the reactions corresponding to Equations (1)–(6) were involved in fusion, changing the burning rate of the D-T fuel significantly.
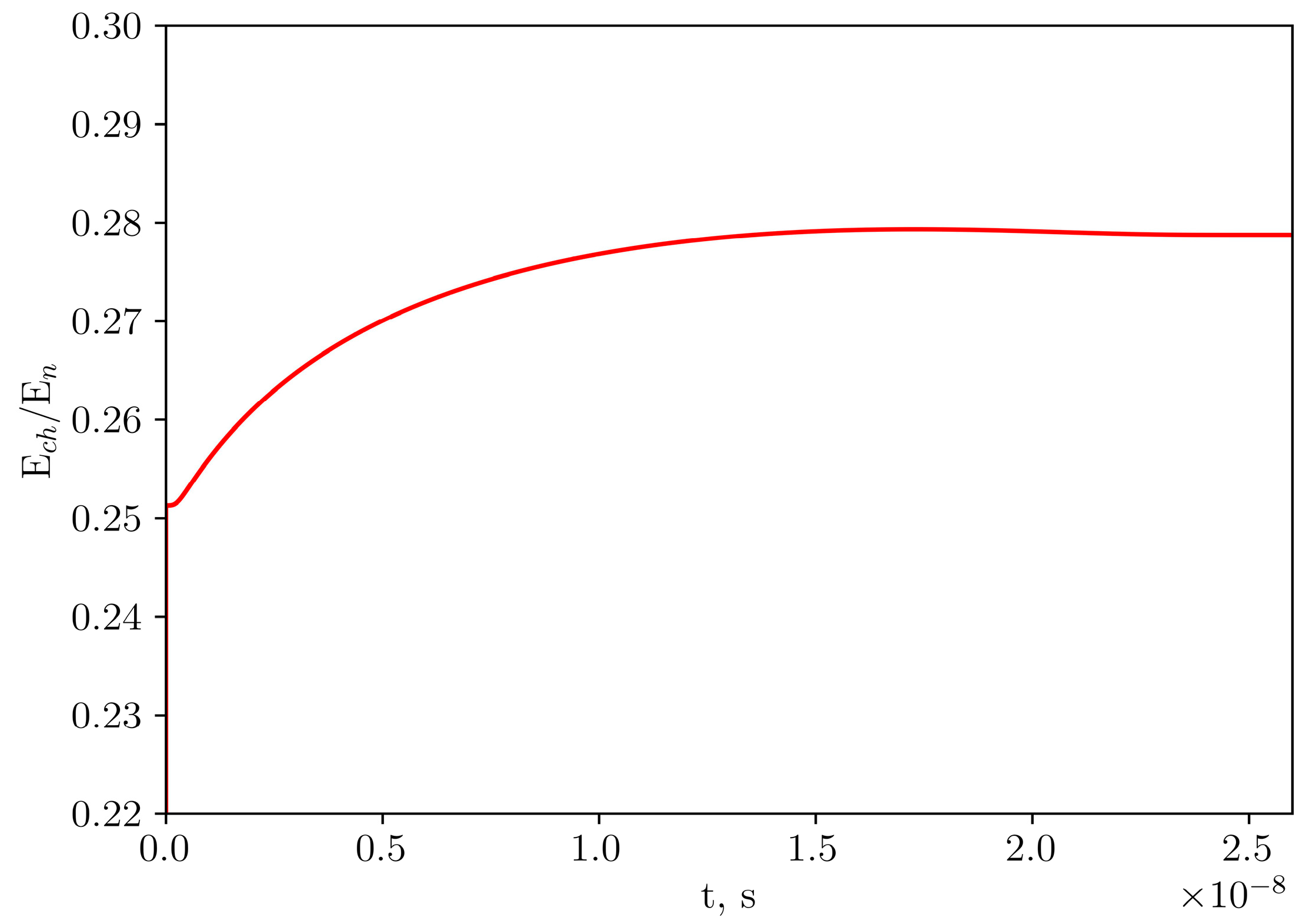
Figure 5 illustrates the ratio between the energy yield produced from charged ions and neutrons during the D-T fuel burning. Initially, it reached a value of just over
and then increased gradually, achieving a peak of
at
seconds. After that, the ratio of the energy yield of charged particles to neutrons remained almost the same over the rest of the period of D-T fuel burning. As is known, 80% of the kinetic energy in the D-T fusion reaction corresponding to Equation (1) goes to neutrons, while 20% goes to produced alpha particles. Therefore, taking this fact into account, from the results presented in
Figure 5, it can be concluded that reactions corresponding to Equations (2)–(6) influenced the burning rate of the D-T fuel significantly, generating almost 12% of the alpha particles’ energy produced in the D-T fusion reaction.
Comparing the obtained results for the D-T fuel burning rate with the findings of Seksembayev et al. [
26], the following conclusions can be drawn:
The plasma temperature rapidly increased in an ultra-short period of time (in the range of 5 nanoseconds) due to fast laser ignition, which increased the D-T fuel burning rate by initiating the fusion reactions corresponding to Equations (1)–(6). The time dependency of the plasma temperature was characterized by a similar pattern, as in [
26]. However, taking into account the ion densities of protons and alpha particles, the temperature peak reached 300.38 keV at
seconds, whereas in [
26], it reached 430 keV at
seconds. This difference in the temperature peaks can be explained by the increased bremsstrahlung radiation loss of alpha particles.
The same picture was obtained for the time dependency of ion densities. The burning rate of deuterium and tritium was almost the same, while in the present work, the ion density of
3He was slightly lower than in [
26]. The ion density of protons is slightly greater than that of
3He because the D-
3He fusion reaction becomes as effective as the D-T fusion reaction at high temperatures, thereby leading to enhanced consumption of
3He ions for further fusion.
In the present paper, the ratio of energy yield between charged ions and neutrons,
, reached values in the range of 0.25–0.28. This corresponds to 78–80% of the total energy produced by neutrons, which was obtained as the fraction of energy released per neutron component in the total released energy and is defined as
. In contrast, in [
26], this ratio achieves 80–84%, since the density of protons was not considered in the calculations. Therefore, the efficiency of the D-T fuel burning in this work was greater than that in [
26].
4. Conclusions
In this paper, we investigate the burning rate of D-T fuel with fast laser ignition at an initial temperature of 10 keV in Z-pinch devices with magneto-inertial confinement. The mixed D-T-3He cycle (D+T, D+D, D+3He, 3He+3He, and T+T) of fusion reactions in a hot, dense, quasi-neutral plasma state with initial deuterium and tritium densities of cm−3 and an electron density of cm−3 was investigated. The full spectrum of charged ions (p, D, T, 3He, and 4He) were considered in this study.
The results obtained in this paper indicate that the plasma temperature rises rapidly in an ultra-short period of time (approximately 5 nanoseconds) to 300.38 keV due to fast laser ignition with a subsequent fast decrease over the remaining burning time. The time dependencies of plasma temperature and ion densities were quite similar to the results of the previous study [
26], except for the
3He ion density, which was slightly lower. The ratio between the energy yield produced from charged ions and neutrons exceeded that of the previous research [
26], thereby leading to enhanced efficiency in D-T fuel burning. By including the ion densities of protons and alpha particles in the set of particle balance equations in addition to the densities of deuterium, tritium and
3He ions, we have a more realistic picture of the D-T fuel burning in Z-pinch devices in comparison with the previous study [
26].
Overall, the present research leads to a deeper theoretical understanding of D-T fuel burning in Z-pinch facilities, which is important for the future development of fusion energy.