Optimal Scheduling of Source–Load Synergy in Rural Integrated Energy Systems Considering Complementary Biogas–Wind–Solar Utilization

Abstract

To address the issues of the low usage efficiency and illogical structure in rural regions, this study builds a rural integrated energy system (RIES) that incorporates the complementary use of biogas, wind, and light. For resolving the RIES optimum-low-carbon-economic-dispatch problem, a source–load-cooperative optimal-dispatch strategy is proposed. Firstly, a multi-energy integrated demand response (IDR) model based on time-of-use tariffs and time-varying biogas costs is established on the demand side. Secondly, power-to-gas devices are added on the supply side to optimize the system’s electricity–gas-coupling relationship and increase the wind power output space. Thirdly, an RIES-oriented carbon-trading model is constructed by considering the actual carbon emissions of gas loads and the stepped-carbon-trading mechanism. Finally, an optimal-dispatch model is built with the objective function of reducing the total energy cost, wind abandonment cost, IDR cost, and carbon emission cost, while the problem is transformed into a mixed-integer linear problem and solved using CPLEX 12.9. By setting up four scenarios for example analysis, the results show that on typical days in spring, summer, autumn, and winter, the total operating costs of the stepped-carbon-trading system (Scenario 1), taking into account the source-side power-to-gas (P2G) device and the load-side IDR, are reduced by 12.25%, 11.25%, 12.42%, and 11.56%, respectively, compared to the system without the introduction of the IDR (Scenario 3). In contrast to the system that lacks a P2G device at the source end (Scenario 2), the overall costs are decreased by 4.97%, 3.07%, 5.02%, and 5.36%, but the wind power consumption rates are increased by 11.63%, 7.93%, 11.54%, and 11.65%, respectively. Stepped emission trading (Scenario 1) reduces the total operating costs by 5.12%, 3.15%, 5.21%, and 6.84%, respectively, while reducing the biogas costs by 9.75%, 7.74%, 9.67%, and 9.57%, respectively, in comparison to traditional emission trading (Scenario 4). The example results demonstrate the economics, effectiveness, and reliability of a stepped-carbon-trading system with an integrated P2G load-side energy demand response.

1. Introduction

The “rural revitalization” strategy was first proposed and included in the report of the 19th National Party Congress of the People’s Republic of China in October 2017. The “Rural Revitalization Strategy (2018–2022)” was released in September 2018 by the State Council of the People’s Republic of China and aims to improve living conditions, encourage economic development, and realize the coordinated development of the countryside in both urban and rural areas, as well as overall progress. The plan suggests optimizing the structure of the rural energy supply, advancing the modernization of the rural energy sector, and stimulating the rapid growth of renewable energy sources, such as biomass, light, and wind. By increasing the energy supply stability, lowering the reliance on conventional fossil fuels, and simultaneously lowering carbon emissions and environmental pollution, the development of clean-energy power generation facilities in rural areas is a pragmatic means of erecting a new kind of energy system and fostering rural revitalization. However, China’s rural areas still face several problems, such as irrational energy structures, low utilization efficiencies, unstable supplies, and irrational planning and allocation [1]. According to the goals of “strong agriculture, beautiful scenery, and rich farmers”, “carbon peaking and carbon neutrality”, and “strong agriculture”, we should make resolving the “three rural problems” the primary focus of all national efforts. The nationwide energy revolution and the all-encompassing promotion of rural regeneration plans are being propelled by these forces. The development of a low-carbon economy in the countryside, the construction of a green and low-carbon energy system, and the advancement of the deep substitution of rural electricity have become major issues facing the energy industry under the guidance of ecological civilization and the directive to make solving the “three rural issues” “the top priority of the work of the whole nation”. Thus, it is critical to hasten the transformation of rural energy usage toward cleaner, more efficient, and sustainable forms.

In terms of rural energy consumption and development, this study analyzed the energy supply and consumption in rural areas over a one-year period based on quantitative data. Studies have shown that biomass fuels dominate the rural energy supply in West Africa, Southern Ethiopia [2,3], and that firewood is the main source of cooking fuel in the rural energy supply in China [4]. It has also been found that rural energy supplies and consumption are dominated by common biomass fuels and large amounts of biomass, while wind and light energy are not utilized but have great potential for use in power generation. The spatio-temporal nature of energy in agricultural production and people’s lives in rural China was further analyzed through spatio-temporal modeling, and the proportions of various energy consumptions were analyzed to create a fair market mechanism to support energy upgrading, but no specific options for research planning were proposed for this [5]. Rural areas are rich in natural resources, but the main source of energy in these areas is the direct combustion of coal and biomass. This leads to a mismatch between the energy supply and demand, low energy utilization, increased carbon emissions, and environmental pollution.

Optimizing integrated rural energy systems and rural energy development: From the perspective of the dual optimization of technology and economics, it was found that the development of an integrated energy system in the rural areas of Uttarakhand, India, was highly feasible [6], as was the development of a model of the energy system suitable for the existing energy structure, development, and utilization of the various rural areas of China by targeting the abundant plant fuels and wind and light energy in the region alone [7]. An off-grid energy system model and optimization framework has been developed from the perspective of energy use patterns, incorporating biomass, solar, and wind energy into the consideration of the energy consumption patterns in remote rural areas in order to achieve stable, continuous, reliable, and cost-effective system operations [8]. A framework model of an integrated rural energy system considering biomass biogas production has been constructed from the perspective of the dual optimization of economics and energy use efficiency [9]. The development and optimization of integrated energy systems (IESs) in rural areas has significant advantages. Rural areas can provide IESs with a wide range of available resources, such as crop waste, livestock manure, and crop residues. Moreover, IESs can further contribute to the production of agricultural biomass resources, improve people’s living standards, and contribute to the revitalization of rural areas if different forms of energy are used in agricultural production. The role of biomass resources in meeting the energy needs of rural households and achieving energy substitution has also been identified [10]. However, most of the existing studies on integrated rural energy system optimization and energy development are considered from a single technical perspective, an economic perspective, an energy-use-rate perspective, or an energy-use-pattern perspective and are rarely constructed from a combination of perspectives, and they lack a variety of energy source combinations for development and utilization.

Rural regions are rich in natural resources and provide both “source” and “load” conditions for energy production and usage, but the question of how to manage a rural integrated energy system (RIES) that includes numerous renewable energy sources, such as wind, light, and biomass, is crucial. The timing of RIESs is crucial to the issue. The “double carbon” aim has led to a gradual shift in the research focus from traditional economic dispatch to low-carbon economic dispatch. To lower the running costs and encourage the use of new energy sources, a variety of energy conversion devices have been added to IESs based on the complementary properties of the electricity, heat, and gas loads at the source.

Considerations from the source end of an integrated energy system: Based on the linked thermal–electric-dispatching model, air-source heat pumps (HPs) were introduced, improving the system’s economics and energy consumption efficiency while realizing the combined heat supply of the heat pumps [11]. The role of power-to-gas (P2G) in natural gas with a high percentage of renewable energy sources and distribution systems was investigated in more depth, and the results show that P2G is very valuable in reducing the operating costs of IESs [12]. Furthermore, the P2G’s integration with a gas turbine creates a closed-loop electricity–gas–electricity-system IES, enabling the multi-level utilization of diverse energy sources and confirming P2G’s efficacy in fostering new energy consumption and a low-carbon economy [13]. It was taken into consideration that Combined Heat and Power (CHP) units have an adjustable hot-spot ratio, which enhances their energy supply flexibility and maximizes the system’s economical operation [14]. In Denmark, for example, heat pumps with variable operating conditions are being introduced into the integrated energy systems (IESs) of buildings, improving the thermal flexibilities of residential buildings and reducing household energy costs [15]. An electric boiler was introduced into the IES system, and the effect of the configuration of the electric boiler on wind energy consumption was studied, confirming the importance of the electric boiler in heat network losses [16]. The above studies have explored the positive effect of considering only P2G to promote new energy consumption or only air-source HPs to promote the economy of the system, but they have not considered the synergy between the coupling characteristics of P2G, air-source HPs, and CHP units in terms of new energy consumption, reducing the overall operating costs of the system, and reducing carbon emissions.

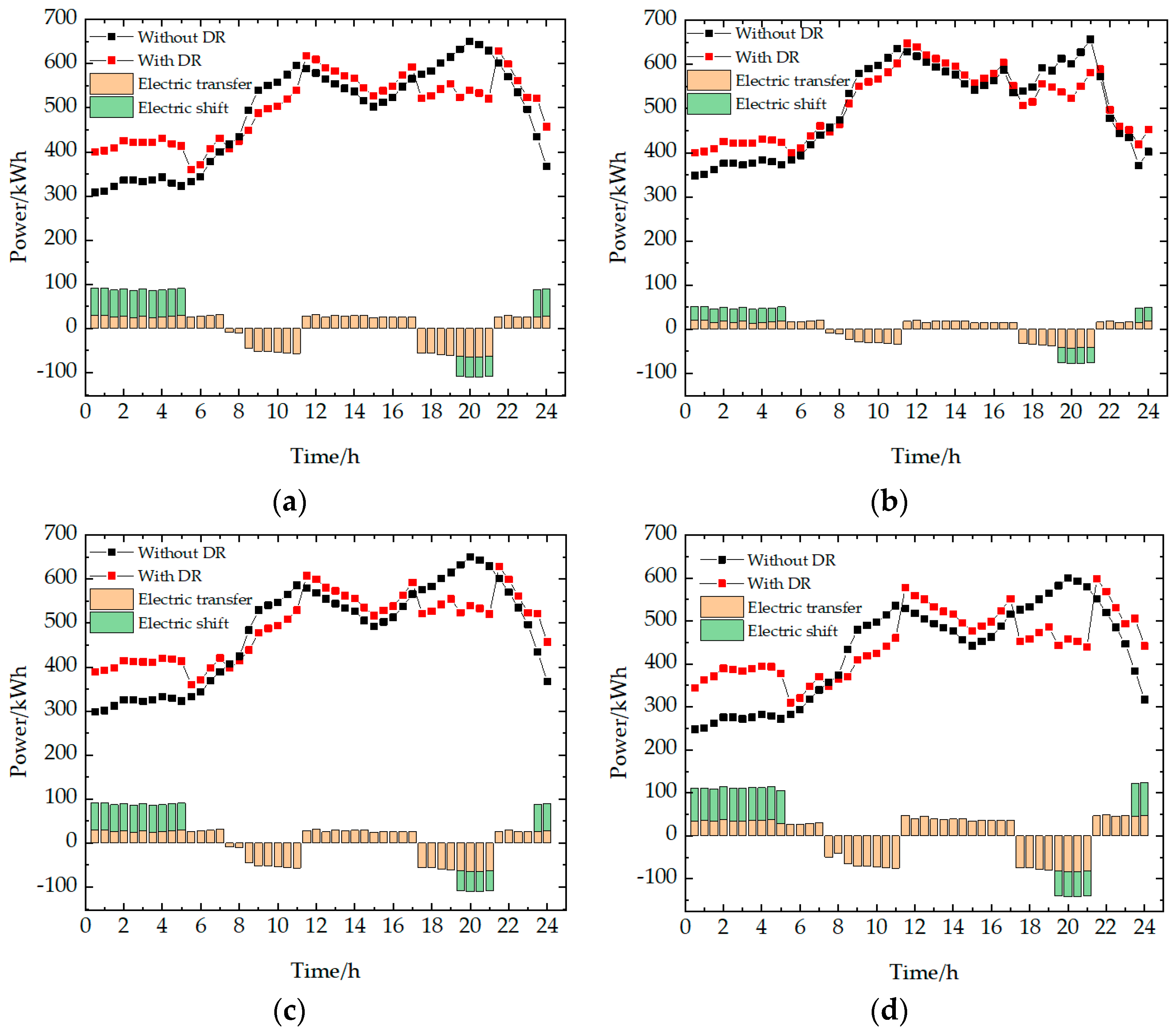
Considerations from the Dutch end of the integrated energy system: The load side coordinates the way users use energy through the demand response (DR) to further optimize the energy supply and demand [17]. An integrated demand response (IDR) model considering tariff intervals is further proposed to optimize the electrical-load profile through different tariff scenarios and interval probabilities, while the coordinated scheduling of the integrated energy system is achieved by optimizing the configuration of each piece of energy supply equipment [18]. The DR of the electrical and thermal loads is also considered, and the electrical and thermal loads are optimized hierarchically over multiple time scales [19]. The electric-load DR was introduced based on the constructed energy hub, which achieves the reduction in electricity consumption by certain energy compensation during the peak energy consumption period [20]. The electric-load DR based on time-of-day tariffs in an integrated energy system was considered. The results of the example show that the user’s initiative to shift part of the electrical load, guided by the tariff, makes a significant contribution to relieving the pressure on the utility [20]. An IES coupled with several heterogeneous energy sources was constructed, and the supply pressure and operating costs of the equipment were effectively reduced by the introduction of the IDR [21]. The impact of introducing the DR on the stability and economics of IES dispatching was studied, and the results showed that the DR achieved good results in reducing the randomness [22]. In the above-mentioned study, only electric and thermal loads were considered, and the form of the DR was limited to the superimposition of a single form of energy, while the dispatchable value of the gas load in question was not explored. In addition, considering only the load-shedding and switching characteristics may affect the user’s energy experience to some extent, while the switching characteristics between loads have little impact on the user’s actual satisfaction with the energy use. Therefore, it is important to build a comprehensive DR model with load shifting on the load side.

The low-carbon perspective of integrated energy systems: Most of the existing studies only considered traditional carbon trading in the IES and analyzed the impact of carbon-trading quotas on the environmental and economic performance of the system [23], without optimizing on this basis. Additionally, stepped carbon trading has been introduced based on the consideration of source-side energy conversion devices and load-side IDRs, and the role of carbon trading in energy saving and emission reduction has been explored. Under the stepped-carbon-trading mechanism, the user’s demand response mode is changed to prioritize the thermal demand response, which enables the user to reduce the carbon emissions and total operating costs while accomplishing the peak shaving target, which further improves the low-carbon and economic performance of park users [24]. Existing studies have proposed low-carbon-economic-dispatch models for integrated energy systems that include carbon capture devices. The carbon-trading price has a positive impact on the dispatch results, which can be better utilized to achieve energy savings and emission reductions [25]. Firstly, the difference between the traditional carbon-trading mechanism and the laddered-carbon-trading mechanism is analyzed, and the rationality of the laddered-carbon-trading mechanism is explained. Secondly, the carbon-trading mechanism is introduced into the model to compare the low-carbon and economic performance of the system under different carbon-trading mechanisms. Finally, it verifies the effectiveness of the laddered-carbon-trading mechanism at reducing the carbon emissions of the system to provide a reference for the low-carbon scheduling operation of the integrated energy system [26]. A comparative analysis of the carbon penalty mechanism and carbon-trading mechanism in terms of the limit and trading system based on the consideration of carbon emissions was studied, proving that the carbon-trading mechanism can further promote carbon emission reductions within a specific range of carbon quotas [27]. In the above study, it was proved that the combination of stepped carbon trading and traditional carbon trading is more beneficial to energy saving and emission reduction, but, during the period, only carbon emissions from equipment such as upper-tier coal units, CHP units, and gas-fired boilers were considered, none of which took into account carbon emissions generated by gas loads. Gas loads are consumed through combustion, which also generates some carbon emissions. Therefore, it is extremely important to take into account the carbon emissions from gas loads when considering the combination of stepped carbon trading and traditional carbon trading in the carbon-trading market. To further summarize the current statuses of the above studies, a brief comparison is provided in

Table 1. Comparison of literature.

References	Source-Side	Electric-Load DR	Thermal-Load DR	Gas-Load DR	Traditional Carbon Trading	Layered Carbon Trading	Rural Area	Parks
[9]	√	×	×	×	×	×	√	×
[10]	√	×	×	×	×	×	√	×
[11]	√	×	×	×	×	×	×	√
[13]	√	×	×	×	×	×	×	√
[16]	√	×	×	×	×	×	×	√
[18]	×	√	×	×	×	×	×	√
[19]	×	√	√	×	×	×	×	√
[20]	×	√	×	×	×	×	×	√
[21]	√	√	×	√	×	×	×	√
[22]	√	√	√	×	×	×	×	√
[23]	×	√	×	√	×	×	×	√
[24]	√	×	×	×	×	√	×	√
[25]	√	√	√	×	×	√	×	√
[26]	√	√	×	×	√	×	×	√
[27]	×	√	×	×	√	√	×	√
[28]	√	√	×	×	√	√	×	√
This paper	√	√	√	√	√	√	√	×

Note: √—Adopt this option; ×—Do not adopt this option.

.

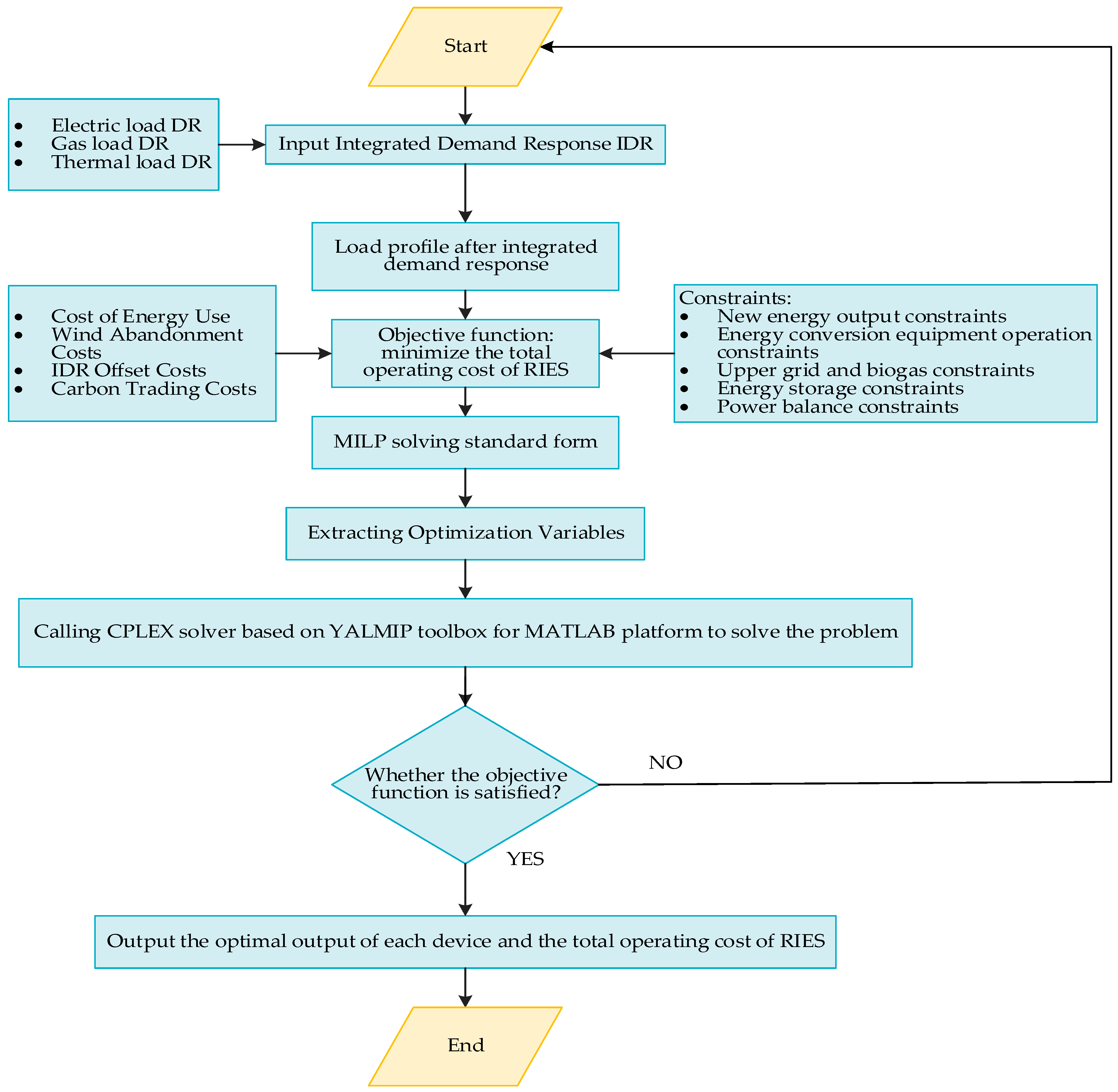
As can be seen from the comparison of the literature in Table 1, the existing studies on planning integrated energy systems have mainly focused on industrial parks. In contrast, the research on rural integrated energy systems is mainly described in terms of development directions and planning frameworks. There is little research on integrated energy systems that makes full use of combined biomass, wind, and solar energy. Few studies on the optimal low-carbon economic dispatch consider both the synergistic optimization of the source and load and a stepped-carbon-trading mechanism. With regard to this, based on the established integrated rural energy system with complementary biogas–wind–light utilization, this paper proposes an RIES optimal-dispatch model that integrates source–load co-optimization and stepped carbon trading. The data on a typical rural integrated energy system in the Panxi region of Sichuan Province, China, were used as the basis for real-life simulation analyses under non-extreme weather conditions in four seasons to verify the upper limit that can be achieved in practice. The main contributions are as follows:

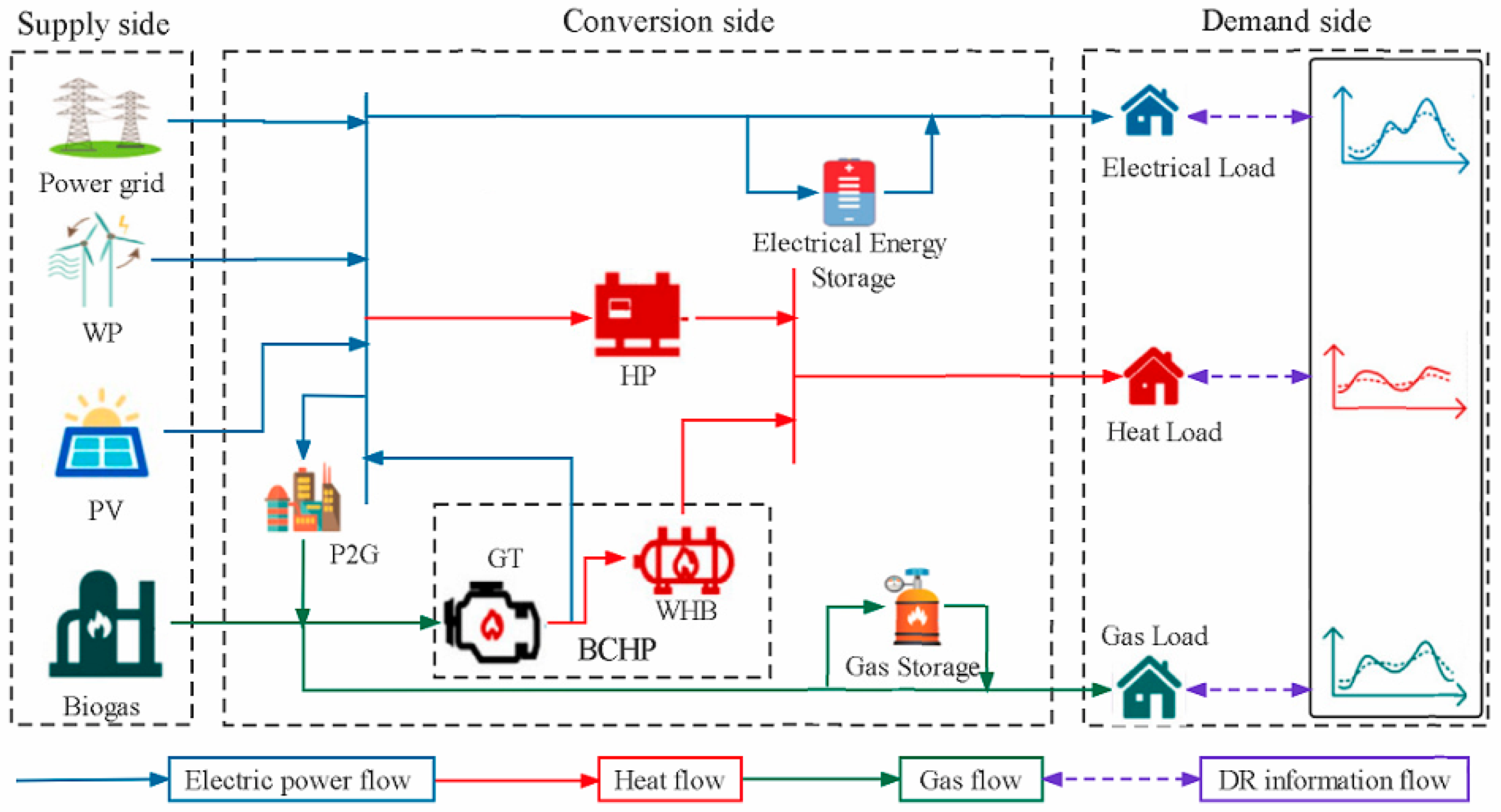
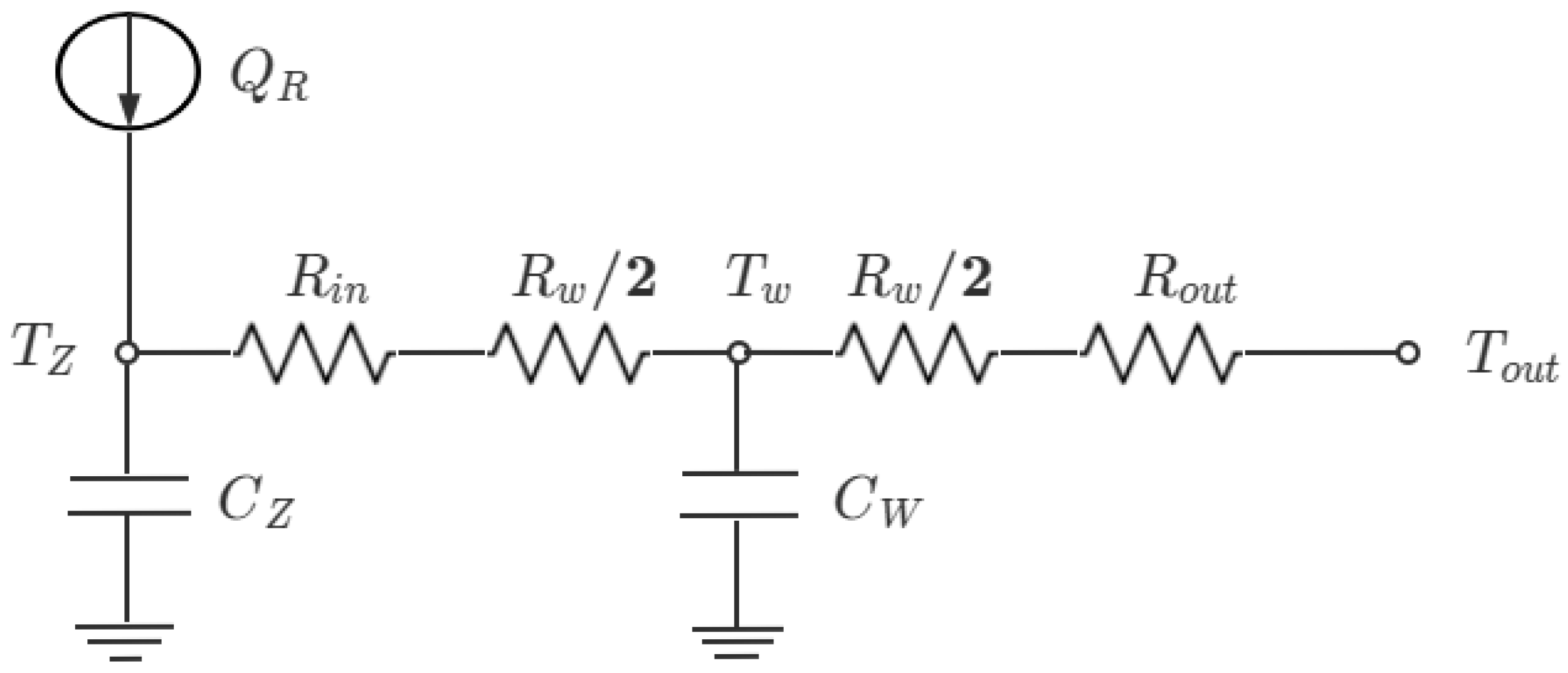
• An RIES with the complementary use of biogas, wind, and solar energy was constructed, together with a model of the temperature dynamics of the digester and consideration of the cost of using biogas;
• A source–load-coordinated optimized-low-carbon-economic-dispatch model based on P2G at the source end and consideration of the electricity-, heat-, and gas-load-shifting, -switching, and -curtailing characteristics at the load end is developed, and the impacts of both the source and load on the RIES low-carbon economy are analyzed in depth;
• A carbon quota mechanism suitable for the characteristics of the RIES low-carbon-economy operation is proposed, and a stepped-carbon-trading model that takes into account the actual carbon emissions of the gas load is introduced to realize the RIES low-carbon-economy operation.

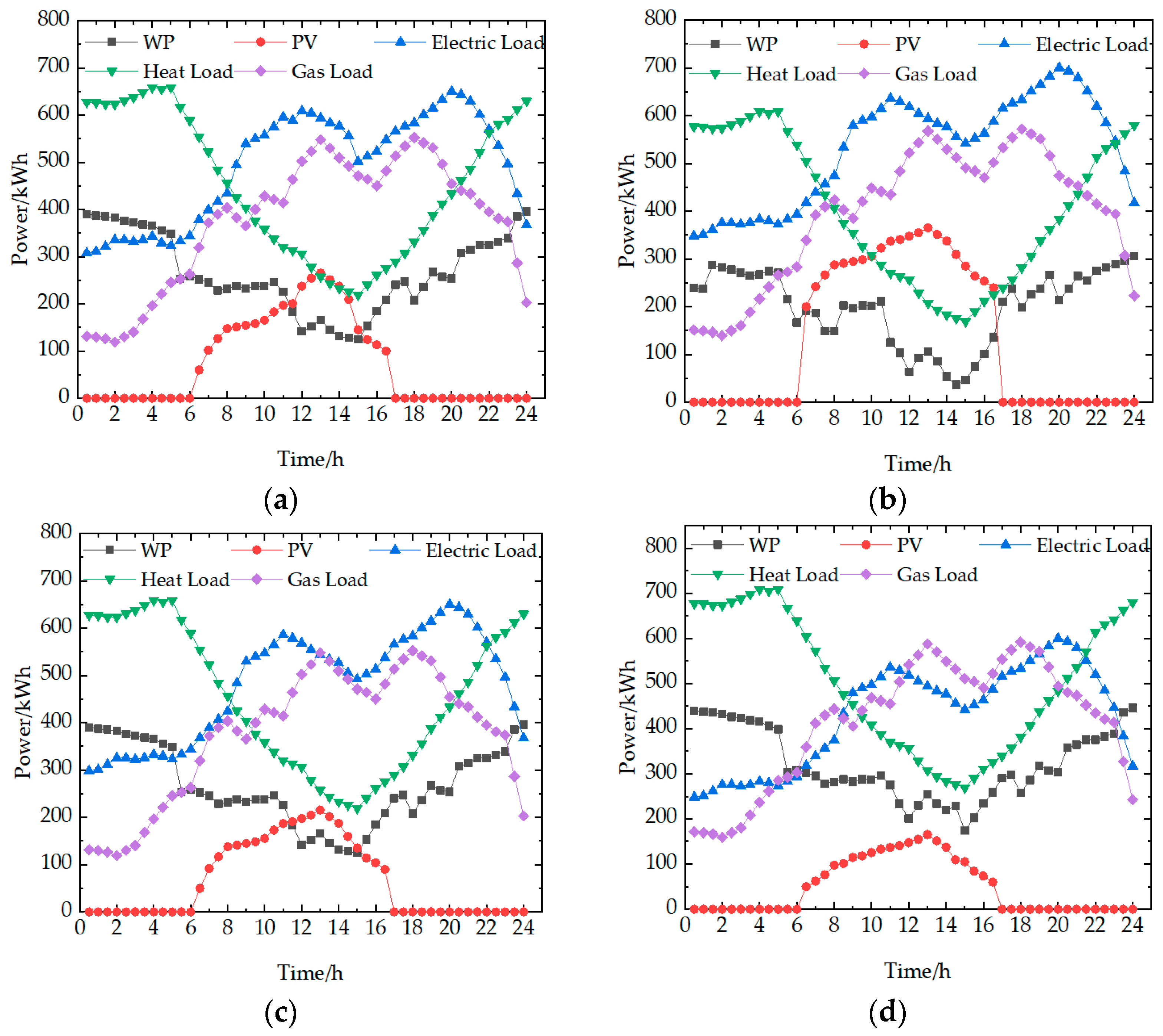
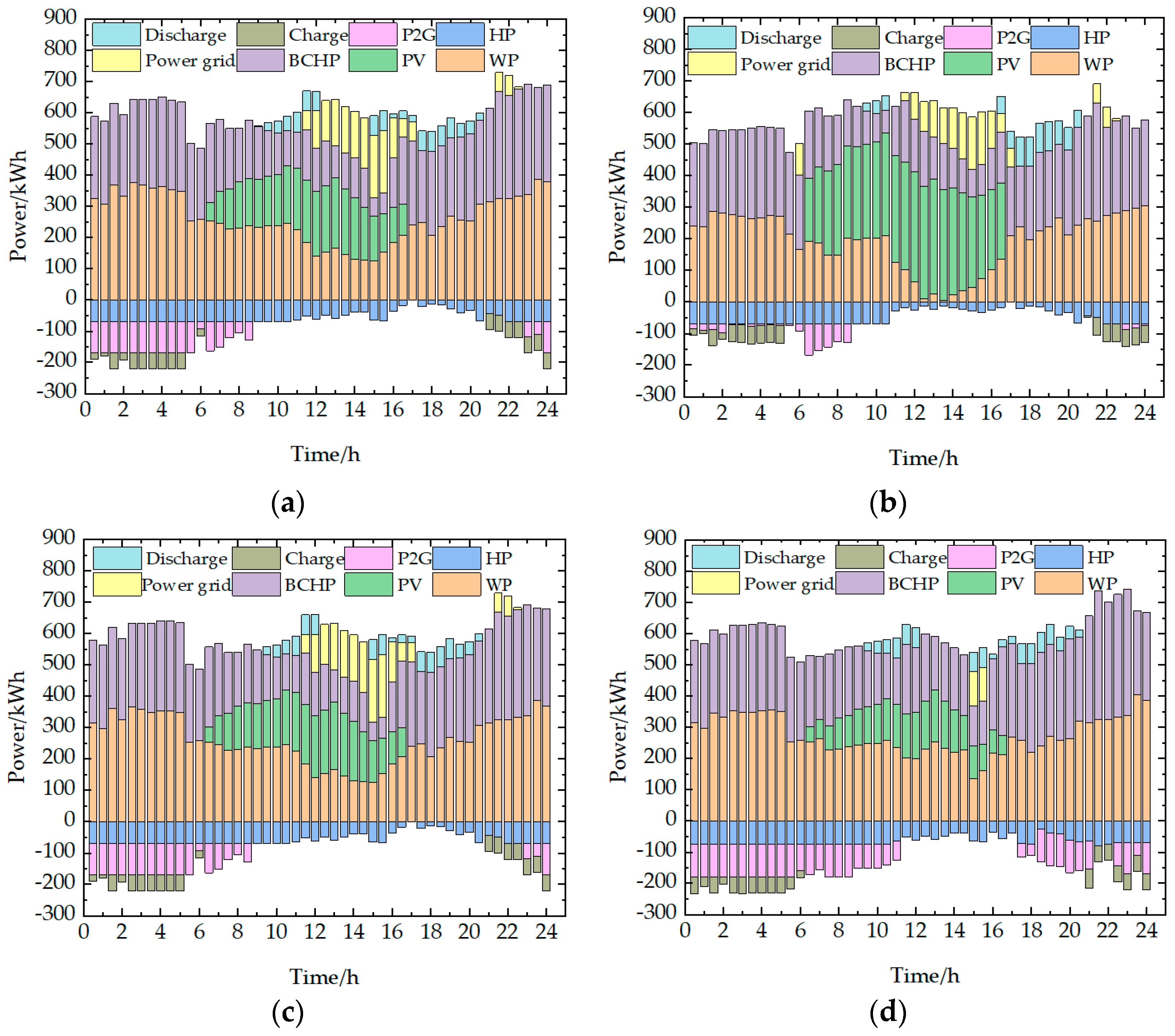
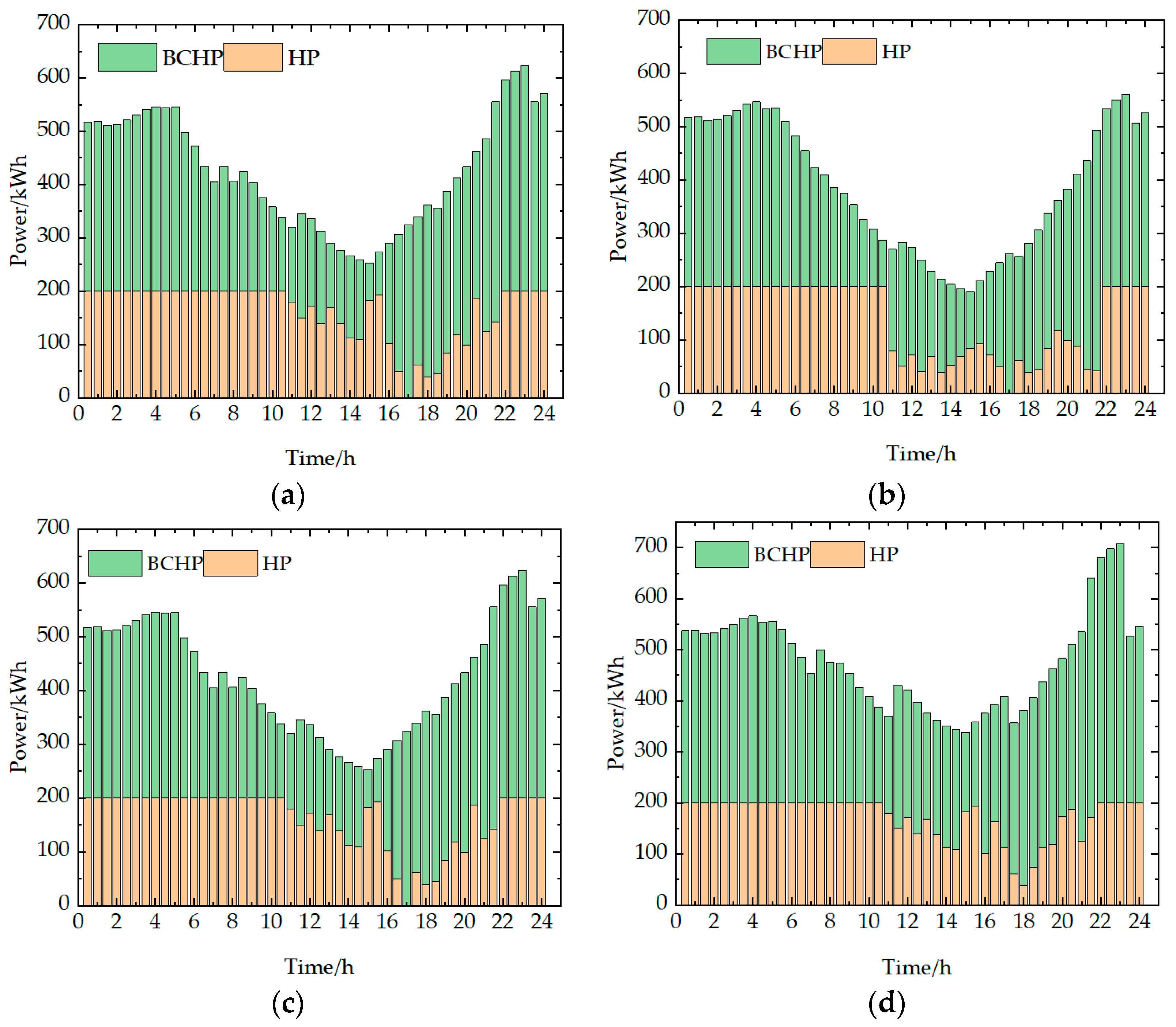
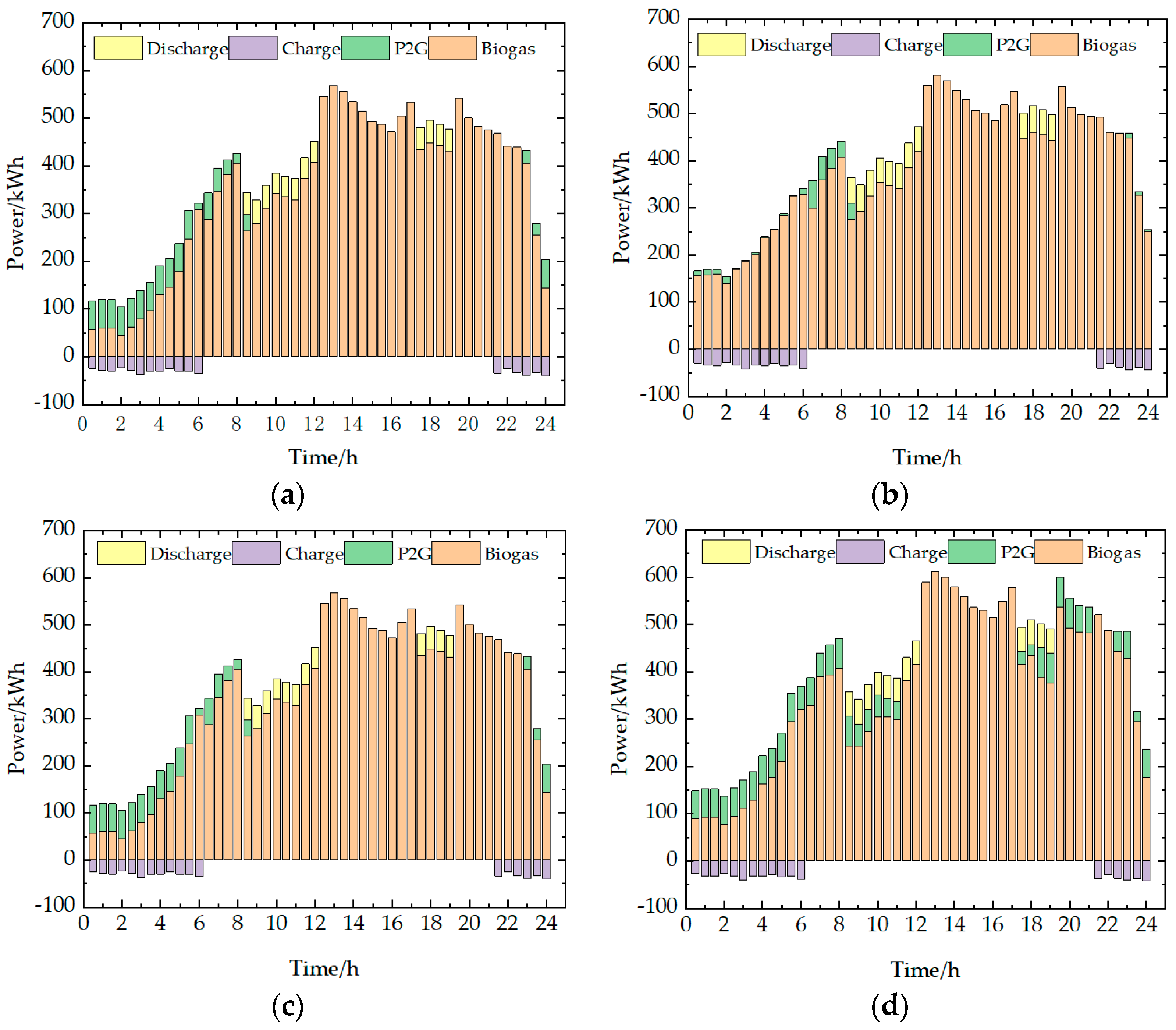
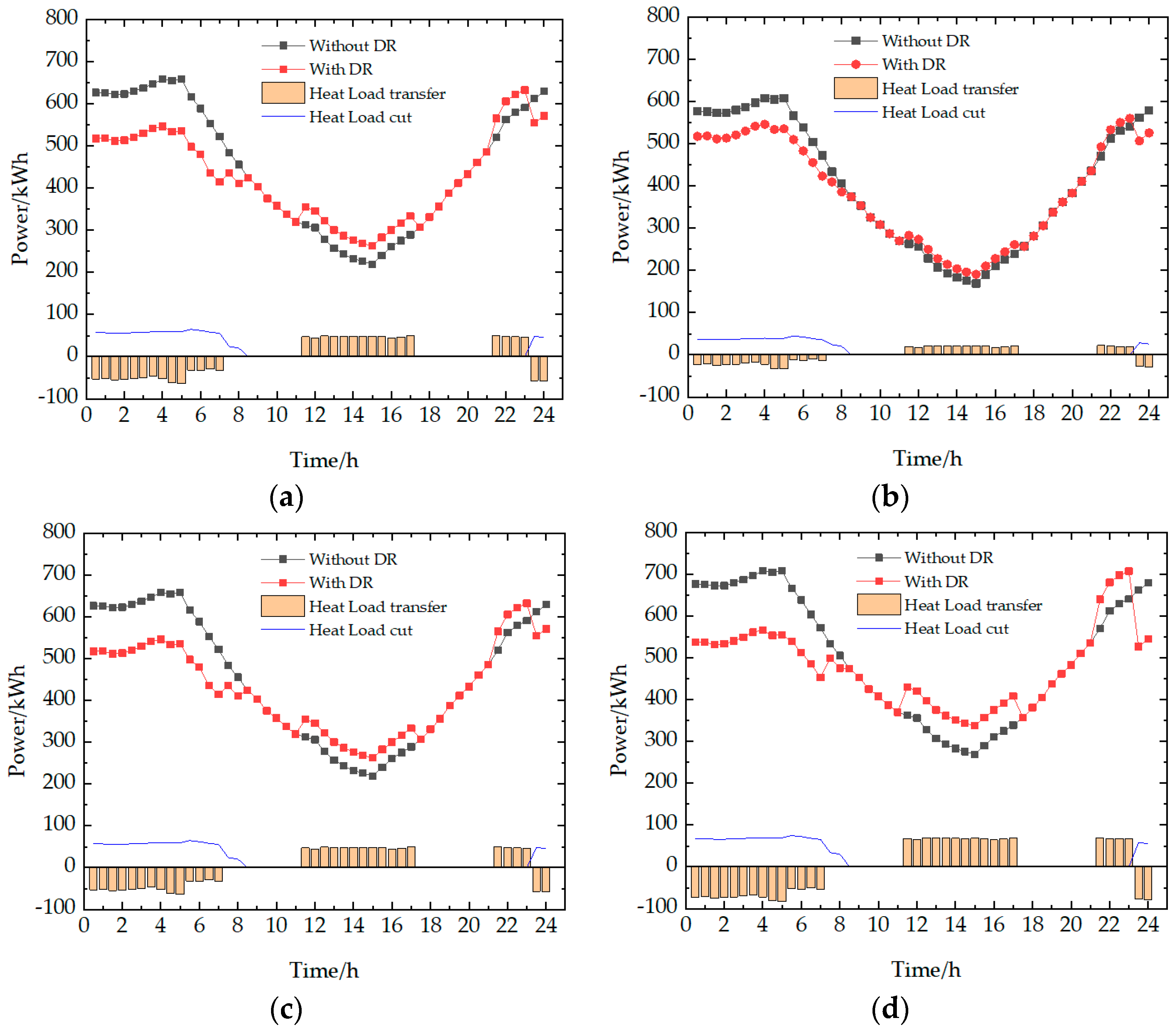
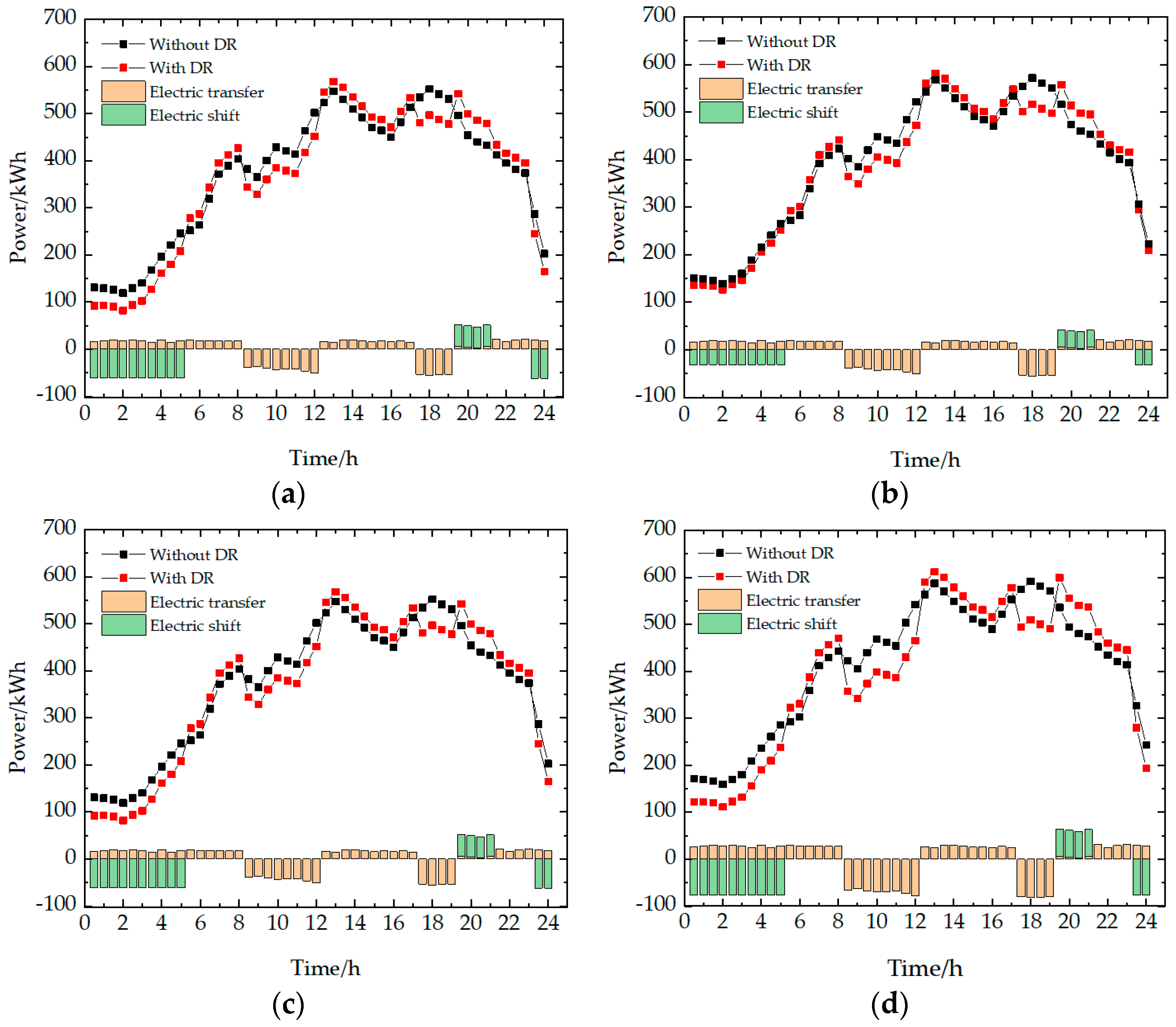
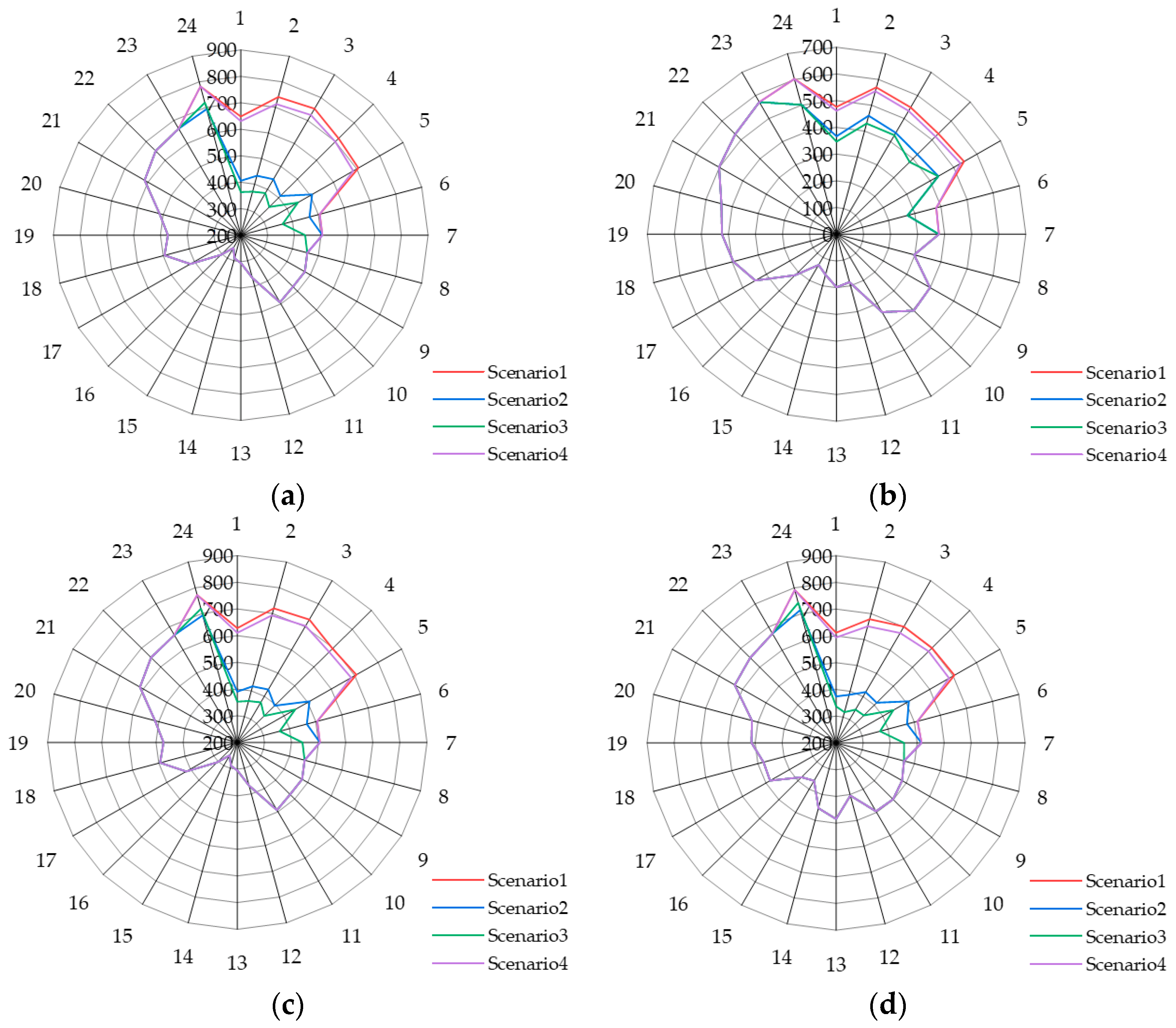
The rest of the section is organized as follows. In Section 2, the RIES structure and model based on biogas–wind–light and the IDR is presented. In Section 3, a stepped-carbon-trading model is developed that takes into account the actual carbon emissions of the gas load. In Section 4, an RIES source–load synergistic optimization operational model is developed. In Section 5, four case studies of four scenarios are conducted for typical days in four seasons to verify the feasibility and effectiveness of the scheme proposed in this paper. In Section 6, the conclusions of the paper are summarized.

2. Structure and Model of RIES Based on Biogas–Wind–Light and IDR

2.1. RIES System Architecture

The RIES can achieve the complementary use of electricity, heat, and gas, which solves the problems of a single form of energy use and inefficient energy use in rural areas. Meanwhile, under the constraints of the IDR and the stepped-carbon-trading mechanism, it can optimize both the operating costs and carbon emissions of the system. In this paper, the structure of the RIES considering the complementary utilization of biogas–wind–light and the load-side IDR is shown in Figure 1, which includes three parts: the energy supply side, the conversion side, and the demand side.

As shown in Figure 1, the energy supply side of the RIES includes the power grid, wind power, photovoltaic power, and biomass biogas units. The energy conversion equipment includes P2G, Biomass Combined Heat and Power (BCHP), and an HP, where the BCHP consists of a gas turbine (GT) and a Waste Heat Boiler (WHB). The P2G consumes wind power and satisfies part of the gas load, while the HP decouples the operating mode of the BCHP “heat to set the electricity” and also improves the wind power grid connection capacity. The demand side includes three loads of electricity, heat, and gas, and the introduction of the IDR can not only smooth the load curve, realize the interactive coupling between loads, and improve the coordination and flexibility between various pieces of energy supply equipment but can also reduce the system operation cost. In addition, the carbon emissions generated by the operation of the RIES are incorporated into the carbon-trading market and participate in trading.

2.2. Biogas Digester Output Model

Biogas is a mixed gas produced by the anaerobic fermentation of organic waste, such as animal and poultry manure, plant residues, and household garbage. Its uses include power generation, heating, gas stoves, and other forms, which are widely used in households, agriculture, and other fields. As one of the most critical factors in biogas production, temperature can cause low gas production or no production if it is too high or too low. The optimal temperature for biogas production is around 35 °C [28]. Therefore, assuming that there are sufficient biomass resources for biogas production in rural areas and ignoring the effects of other external factors on biogas production, the relationship between biogas production and temperature is given in the following equation:

$$E_{biogas}=m\left|T_Z-T_0\right|+n$$

(1)

where $E_{biogas}$ is the production of biogas per unit time; $T_Z$ and $T_0$ are the actual and optimal temperatures of the digester reaction, respectively. In this paper, $T_0$ is taken as 35 °C, and $m$ and $n$ are the parameters obtained from fitting the data.

Due to the temperature difference between the inside and outside of the biogas digester walls, Fourier’s law of heat conduction is used to describe it, and its basic form is as follows:

$$q_x=-r\frac{dT}{dy}$$

(2)

where $q_x$ is the heat flux passing through the per unit area ($\mathrm{W}\cdot {\mathrm{m}}^{-2}$); $r$ is the thermal conductivity of the biogas digester wall (W·m⁻¹·°C⁻¹); $T$ is the temperature at which the heat transfer takes place in the digester (°C); $y$ is the coordinate at which the heat transfer takes place in the digester ($m$).

Further modeling of the heat conduction inside and outside the biogas digester walls is conducted, and $T_Z$ is solved using Fourier’s law of heat conduction and the nodal heat balance equation. The schematic diagram of the biogas digester wall heat conduction principle is shown in Figure 2.

$$\begin{array}{l}\frac{T_W-T_Z}{R_{in}+R_w/2}+Q_R=C_Z\frac{d{T}_Z}{dt}\\ \frac{T_Z-T_W}{R_{in}+R_w/2}+\frac{T_{out}-T_W}{R_{out}+R_w/2}=C_W\frac{d{T}_W}{dt}\end{array}$$

(3)

where $Q_R$ is the energy injected into the biogas from outside the system (W); $R_{in}$, $R_{out}$, and $R_w$ are the heat transfer thermal resistances of the digester interior, exterior, and walls, respectively (°C/W); $T_{out}$ and $T_W$ are the temperatures of the digester’s exterior and walls, respectively (°C); $C_Z$ and $C_W$ are the heat capacities of the digester interior and walls, respectively (J/°C); and $t$ is the heat conduction time ($s$).

2.3. IDR Model

(1)

Electrical-Load DR

The forms of electricity consumption in rural areas mainly include electricity for agricultural production and household life. According to their DR characteristics, electrical loads can be classified into dispatchable loads and non-dispatchable loads, of which dispatchable loads are further classified into transferable loads and convertible loads. Transferable loads can be shifted from high tariffs to tariff troughs under the guidance of time-of-use tariffs, and the total amount of the load does not change during a dispatch cycle. Convertible loads, in contrast, choose a different form of energy use by comparing the price signals of heterogeneous energy sources during a dispatch cycle. Non-dispatchable loads are not dispatched. In summary, the electric-load DR model is as follows:

$$\left\{\begin{array}{l}\begin{array}{l}{P}_{e,load}(t)=P_{e,load}^s(t)+P_{e,load}^m(t)+\Delta P_{e,load}^c(t)\hfill \\ P_{e,load}^{m,\min }(t)\le \left|P_{e,load}^m(t)\right|\le P_{e,load}^{m,\max }(t)\hfill \end{array}\hfill \\ {\displaystyle \sum _{t=1}^T{P}_{e,load}^m(t)=0}\hfill \\ \Delta P_{e,load}^c(t)={\xi }_e^{c,in}(t)P_{e,load}^{c,in}(t)-{\xi }_e^{c,out}(t)P_{e,load}^{c,out}\hfill \\ \begin{array}{l}{\xi }_e^{c,in}(t)+{\xi }_e^{c,out}(t)=1\\ P_{e,load}^{c,\min }(t)\le \left|\Delta P_{e,load}^c(t)\right|\le P_{e,load}^{c,\max }(t)\end{array}\hfill \end{array}\right.$$

(4)

where $P_{e,load}(t)$ and $P_{e,load}^s(t)$ are the electrical loads after and before the IDR at time period t, respectively (kW); $P_{e,load}^m(t)$ is the electrical load transferred at time period t, in which the transfer-in period is positive and the transfer-out period is negative (kW); $\Delta P_{e,load}^c(t)$ is the electrical load converted at time period t (kW); $P_{e,load}^{m,\min }(t)$ and $P_{e,load}^{m,\max }(t)$ are the minimum and maximum values of the transferred electrical load at time period t, respectively, which account for 15% of the total load (kW); $P_{e,load}^{c,in}(t)$ and $P_{e,load}^{c,out}(t)$ are the powers of the incoming and outgoing conversion electric loads during time period t (kW); ${\xi }_e^{c,in}(t)$ and ${\xi }_e^{c,out}(t)$ are binary variables representing the parameters for the incoming and outgoing conversion electric loads during time period t, respectively (${\xi }_e^{c,in}(t),{\xi }_e^{c,out}(t)\in \left\{0,\left.1\right\}\right.$); $P_{e,load}^{c,\min }(t)$ and $P_{e,load}^{c,\max }(t)$, respectively, are the minimum and maximum values of the converted electric load during time period t, which account for 10% of the total load (kW).

(2)

Heat-Load DR

Analogous to the electric load, the heat load is also time-transferable. Under the conditions of time-sharing tariffs and time-varying biogas usage costs, the transferable heat load can be dispatched by shifting them to the time period with the lowest system operating costs according to the load characteristics. At the same time, studies have shown that the user’s perception of the heat-load temperature is somewhat ambiguous (i.e., when the indoor temperature fluctuates within a certain range, the user’s thermal comfort is not significantly affected) [29]. Therefore, the heat load can be reduced to a certain extent without affecting the energy comfort of the user. The heat-load DR model is as follows:

$$\left\{\begin{array}{l}{P}_{h,load}=P_{h,load}^s(t)+P_{h,load}^m(t)-P_{h,load}^{cut}(t)\hfill \\ P_{h,load}^{m,\min }(t)\le \left|P_{h,load}^m(t)\right|\le P_{h,load}^{m,\max }(t)\hfill \\ {\displaystyle \sum _{t=1}^T{P}_{h,load}^m(t)=0}\hfill \\ 0\le P_{h,load}^{cut}\le P_{h,load}^{cut,\max }(t)\hfill \end{array}\right.$$

(5)

where $P_{h,load}(t)$ and $P_{h,load}^s(t)$ are the heat loads after and before the IDR at time t, respectively (kW); $P_{h,load}^m(t)$ is the heat load transferred at time t, in which the transfer-in period is positive and the transfer-out period is negative (kW); $P_{\mathrm{h},load}^{\mathrm{m},\min }(t)$ and $P_{\mathrm{h},load}^{\mathrm{m},\max }(t)$ are the minimum and maximum values of the heat load transferred at time t, respectively, which account for 15% of the total load (kW); $P_{h,load}^{cut}(t)$ is the heat load curtailed at time t (kW); $P_{h,load}^{cut,\max }(t)$ is the maximum value of the heat load curtailed at time t, which accounts for 10% of the total load (kW).

(3)

Gas-Load DR

Similar to the electric-load characteristics, the dispatchable gas load is also time- and space-dispatchable under time-varying biogas usage costs. Therefore, the dispatchable gas load has both a transferable load and a convertible load. The DR model for gas loads is as follows:

$$\left\{\begin{array}{l}\begin{array}{l}{P}_{g,load}(t)=P_{g,load}^s(t)+P_{g,load}^m(t)+\Delta P_{g,load}^c(t)\hfill \\ P_{g,load}^{m,\min }(t)\le \left|P_{g,load}^m(t)\right|\le P_{g,load}^{m,\max }(t)\hfill \end{array}\hfill \\ {\displaystyle \sum _{t=1}^T{P}_{g,load}^m(t)=0}\hfill \\ \Delta P_{g,load}^c(t)={\xi }_g^{c,in}{P}_{g,load}^{c,in}(t)-{\xi }_g^{c,out}{P}_{g,load}^{c,out}(t)\hfill \\ \begin{array}{l}{\xi }_g^{c,in}+{\xi }_g^{c,out}=1\\ P_{g,load}^{c,\min }(t)\le \left|\Delta P_{g,load}^{\mathrm{c}}(t)\right|\le P_{g,load}^{c,\max }(t)\end{array}\hfill \end{array}\right.$$

(6)

where $P_{g,load}(t)$ and $P_{g,load}^s(t)$ are the gas loads after and before the IDR at time period t, respectively (kW); $P_{g,load}^m(t)$ is the gas load transferred at time period t, in which the transfer-in period is positive and the transfer-out period is negative (kW); $\Delta P_{g,load}^c(t)$ is the gas load converted at time period t (kW); $P_{g,load}^{\mathrm{m},\min }(t)$ and $P_{g,load}^{\mathrm{m},\max }(t)$ are the minimum and maximum values of the transferred gas load at time period t, respectively, which account for 15% of the total load (kW); $P_{g,load}^{c,in}(t)$ and $P_{g,load}^{c,out}(t)$ are the power of the converted gas load for the transfer in and the transfer out, respectively, at time period t (kW); ${\xi }_g^{c,in}(t)$ and ${\xi }_g^{c,out}(t)$ are binary variables representing the parameters for the incoming and outgoing conversion gas loads during time period t, respectively (${\xi }_g^{c,in}(t),{\xi }_g^{c,out}(t)\in \left\{0,\left.1\right\}\right.$); $P_{\mathrm{g},load}^{c,\min }(t)$ and $P_{\mathrm{g},load}^{c,\max }(t)$ are the minimum and maximum values of the converted gas loads at time period t, respectively, which account for 10% of the total load (kW).

3. Stepped-Carbon-Trading Mechanism

Carbon trading is a policy tool that uses market mechanisms and economic incentives to reduce greenhouse gas emissions. It involves placing carbon emission rights on the carbon market for trading. The promotion and implementation of a carbon-trading mechanism can facilitate actions to reduce emissions, promote the development of clean technologies, and direct financial flows to low-carbon areas. The basis of carbon trading is carbon emission rights, which represent a specific amount of greenhouse gas emissions. The government formulates relevant carbon emission rules and allocates a certain amount of carbon emission rights to enterprises. Enterprises can then buy or sell carbon emission rights based on their own emission situations and emission reduction targets when engaging in carbon trading. In the carbon-trading model, if a company’s actual emissions are lower than the allocated carbon emission rights, it can sell the excess emission rights to a company with higher emissions and obtain an economic return. When a company’s actual emissions exceed the allocated carbon credits, it needs to buy additional credits to make up the difference. The carbon-trading model comprises three parts: the initial carbon emission quota, the actual carbon emissions, and the carbon-trading cost.

3.1. Initial Carbon Emission Quota Model

At present, China mainly adopts the gratuitous allocation method for the initial carbon emission allowances [30]. In the RIES, the carbon emission sources are mainly power purchased from the superior grid, BCHP, and gas loads. The initial carbon allowance model of the system is as follows:

$$\left\{\begin{array}{l}{E}_{RIES}=E_{e,Buy}+E_{BCHP}+E_{g,load}\hfill \\ E_{e,Buy}={\kappa }_e{\displaystyle \sum _{t=1}^T{P}_{e,Buy}(t)}\hfill \\ E_{CHP}={\kappa }_h{\displaystyle \sum _{t=1}^T({\phi }_{e,h}{P}_{e,BCHP}(t)+P_{h,BCHP}(t))}\hfill \\ E_{g,load}={\kappa }_g{\displaystyle \sum _{t=1}^T{P}_{g,load}(t)}\hfill \end{array}\right.$$

(7)

where $E_{RIES}$, $E_{e,Buy}$, $E_{BCHP}$, and $E_{g,load}$ are the carbon emission allowances of the RIES, power purchased from the grid, BCHP units, and gas loads in a dispatch cycle, respectively (kg); $P_{e,Buy}(t)$ is the amount of power purchased from the grid by the system at time period t (kW); $P_{e,BCHP}(t)$ and $P_{\mathrm{h},BCHP}(t)$ are the electric and thermal power outputs from the BCHP units at time period t, respectively (kW); $P_{g,load}(t)$ is the gas loads at time period t (kW); ${\kappa }_e$, ${\kappa }_h$, and ${\kappa }_g$ are the carbon emission allocations per unit of electric power, per unit of heat load, and per unit of gas load, respectively (kg); ${\phi }_{e,h}$ is the conversion coefficient from power to heat ($\%$).

3.2. Actual Carbon Emission Model

The P2G unit absorbs some of the CO₂ during operation, while the gas load is primarily used for combustion, which also generates actual carbon emissions. When considering carbon emissions from an RIES, it is important to take into account both the P2G unit and gas loads. The model for the actual carbon emissions from the RIES is as follows:

$$\left\{\begin{array}{l}\begin{array}{l}{E}_{RIES,a}=E_{e,Buy,a}+E_{BCHP,a}+E_{g,load,a}-E_{P2G,a}\hfill \\ E_{e,Buy,a}={\chi }_e{\displaystyle \sum _{t=1}^T{P}_{e,Buy}(t)}\hfill \end{array}\hfill \\ E_{BCHP,a}={\chi }_h{\displaystyle \sum _{t=1}^T({\phi }_{e,h}{P}_{e,BCHP}(t)+P_{h,BCHP}(t))}\hfill \\ E_{g,load,a}={\chi }_g{\displaystyle \sum _{t=1}^T{P}_{g,load}(t)}\hfill \\ E_{P2G,a}={\chi }_{P2G}{\displaystyle \sum _{t=1}^T{P}_{P2G}(t)}\hfill \end{array}\right.$$

(8)

where $E_{RIES,a}$ is the actual carbon emissions generated by the system in one dispatch cycle (kg); $E_{e,Buy,a}$ is the actual carbon emissions generated by the power purchased from the grid by the RIES system (kg); $E_{BCHP,a}$ is the actual carbon emissions generated by the operation of the BCHP unit in one dispatch cycle (kg); $E_{g,load,a}$ is the actual carbon emissions generated by the gas load in one dispatch cycle (kg); $E_{P2G,a}$ is the amount of CO₂ absorbed by the operation of the P2G in one dispatch cycle (kg);$P_{P2G}(t)$ is the output power of the P2G at time t (kW); ${\chi }_e$, ${\chi }_h$, and ${\chi }_g$ are the carbon emission coefficients per unit of electric power, per unit of heat load, and per unit of gas load, respectively ($\%$); ${\chi }_{P2G}$ is the coefficient of CO₂ absorption by the P2G operation ($\%$). In summary, it can be seen that the actual participation of the RIES in carbon trading is as follows:

$$E_{RIES,t}=E_{RIES,a}-E_{RIES}$$

(9)

3.3. Carbon-Trading Cost Model

The stepped-carbon-trading model is a highly effective mechanism in the carbon market that gradually increases the price of carbon emission quotas. It is important to note that this model has been extensively tested and has proven to be a reliable and efficient method for reducing carbon emissions. The initial price of carbon emission quotas is set at a relatively low level, and the purchase price increases proportionally with the amount of purchased carbon emission quotas. This paper divides the purchasing of carbon emission allowances into five intervals, and the specific model for calculating the cost of stepped trading is presented below:

$$F_{C{O}_2}=\left\{\begin{array}{l}\begin{array}{l}\mu E_{RIES,t},E_{RIES,t}\le L\hfill \\ \mu (1+\nu )(E_{RIES,t}-L)+\mu L,L<E_{RIES,t}\le 2L\hfill \end{array}\hfill \\ \mu (1+2\nu )(E_{RIES,t}-2L)+\mu (2+\nu )L,2L<E_{RIES,t}\le 3L\hfill \\ \mu (1+3\nu )(E_{RIES,t}-3L)+\mu (3+3\nu )L,3L<E_{RIES,t}\le 4L\hfill \\ \mu (1+4\nu )(E_{RIES,t}-4L)+\mu (4+6\nu )L,4L<E_{RIES,t}\hfill \end{array}\right.$$

(10)

where $\mu$ is the carbon-trading price (RMB); $\nu$ is the carbon-trading-price growth rate (%); $L$ is the length of the carbon emission interval.

4. RIES Source–Load-Coordinated Optimization Operation Model

4.1. Objective Function

The RIES coordinated optimization model considers the P2G and IDR under the stepped-carbon-trading mechanism to achieve the optimal low-carbon and economic operation of the system while adhering to the system operation constraints. The aim of this paper is to minimize the total operating cost of the RIES, which includes the energy use cost ($F_{\mathit{Buy}}$), wind abandonment cost ($F_{WP}$), IDR compensation cost ($F_{IDR}$), and carbon-trading cost ($F_{{\mathrm{CO}}_2}$):

$$F_{RIES}=\min (F_{\mathit{Buy}}+F_{WP}+F_{IDR}+F_{{\mathrm{CO}}_2})$$

(1)

Energy cost:

$$F_{Buy}={\displaystyle \sum _{t=1}^T{\delta }_{e,t}{P}_{e,Buy}(t)}+{\displaystyle \sum _{\mathrm{t}=1}^T{\delta }_{Biogas,t}(P_{g,Biogas}(t)+P_{BCHP}(t))}$$

(11)

where ${\delta }_{e,t}$ is the electricity price at time period t ($\mathrm{RMB}/\mathrm{kWh}$); ${\delta }_{Biogas,t}$ is the cost of biogas use at time period t ($\mathrm{RMB}/\mathrm{kWh}$);

(2)

Wind abandonment cost:

$$F_{WP}={\displaystyle \sum _{t=1}^T{\eta }_{WP,cut}{P}_{WP,cut}(t)}$$

(12)

where ${\eta }_{WP,cut}$ is the unit penalty cost of the wind abandonment ($\mathrm{RMB}/\mathrm{kWh}$); $P_{WP,cut}(t)$ is the power of the wind abandonment at time period t (kW);

(3)

IDR compensation cost:

$$\begin{array}{c}{F}_{DR}={\displaystyle \sum _{t=1}^T{\alpha }_{mov}(\left|P_{e,mov}(t)\right|+\left|P_{h,mov}(t)\right|+\left|P_{g,mov}(t)\right|)}\\ +\frac{1}{2}{\displaystyle \sum _{t=1}^T{\alpha }_{change}(\left|P_{e,change}(t)\right|+\left|P_{g,change}(t)\right|)}\\ +{\displaystyle \sum _{t=1}^T{\alpha }_{h,cut}{P}_{h,cut}(t)}\end{array}$$

(13)

where ${\alpha }_{mov}$, ${\alpha }_{change}$, and ${\alpha }_{h,cut}$ are the unit compensation costs for the transferable, convertible, and curtailable loads, respectively ($\mathrm{RMB}/\mathrm{kWh}$);

(4)

Carbon-trading cost

Refer to Formula (10).

4.2. Constraint Conditions

(1)

New energy output constraints:

$$0\le P_{PV}(t)\le P_{PV,his}(t)$$

(14)

$$0\le P_{WP}(t)\le P_{WP,his}(t)$$

(15)

where $P_{PV,his}(t)$ and $P_{WP,his}(t)$ are the historical production data of the PV and WP at time period t, respectively (kW);

(2)

Operational constraints for energy conversion equipment:

a)

BCHP constraints:

$$\left\{\begin{array}{l}{P}_{e,BCHP}(t)=P_{BCHP}(t)\cdot {\Upsilon }_{BCHP}\hfill \\ P_{h,BCHP}(t)=P_{e,BCHP}(t)\cdot {\eta }_{BCHP}\hfill \\ P_{e,BCHP}^{\min }\le P_{e,BCHP}(t)\le P_{e,BCHP}^{\max }\hfill \\ \Delta P_{e,BCHP}^{\min }\le P_{e,BCHP}(t+1)-P_{e,BCHP}(t)\le \Delta P_{e,BCHP}^{\max }\hfill \end{array}\right.$$

(16)

where $P_{BCHP}(t)$ is the power of the biogas consumed at time period t ($kW$); ${\Upsilon }_{BCHP}$ and ${\eta }_{BCHP}$ are the electrical conversion efficiency and the thermoelectric ratio of the BCHP, respectively ($\%$); $P_{e,BCHP}^{\min }$ and $P_{e,BCHP}^{\max }$ are the minimum and maximum values of the BCHP’s output electrical power, respectively (kW); $\Delta P_{e,BCHP}^{\min }$ and $\Delta P_{e,BCHP}^{\max }$ are the upper and lower limits of the rate of change of the BCHP’s output electrical power, respectively (kW);

b)

HP constraints:

$$\left\{\begin{array}{l}{P}_{h,HP}=P_{HP}(t)\cdot {\eta }_{HP}\hfill \\ P_{h,HP}^{\min }\le P_{HP}(t)\le P_{h,HP}^{\max }\hfill \end{array}\right.$$

(17)

where $P_{HP}(t)$ is the input electric power of the HP at time period t (kW); ${\eta }_{HP}$ is the thermoelectric ratio of the HP ($\%$); $P_{h,HP}^{\min }$ and $P_{h,HP}^{\max }$ are the minimum and maximum values of the output power of the HP, respectively (kW);

c)

P2G constraints:

$$\left\{\begin{array}{l}{P}_{g,P2G}=P_{P2G}(t)\cdot {\eta }_{P2G}\hfill \\ P_{P2G}^{\min }\le P_{P2G}(t)\le P_{P2G}^{\max }\hfill \end{array}\right.$$

(18)

where $P_{P2G}(t)$ is the input electric power of the P2G at time period t (kW); ${\eta }_{P2G}$ is the conversion efficiency of the P2G ($\%$); $P_{P2G}^{\min }$ and $P_{P2G}^{\max }$ are the minimum and maximum values of the output power of the P2G, respectively (kW);

(3)

Constraints of the higher-level power grid and biogas

a)

Grid interconnection constraints:

$$\left\{\begin{array}{l}{P}_{e,Buy}^{\min }\le P_{e,Buy}(t)\le P_{e,Buy}^{\max }\hfill \\ \Delta P_{e,Buy}^{\min }\le P_{e,Buy}(t+1)-P_{e,Buy}(t)\le \Delta P_{e,Buy}^{\max }\hfill \end{array}\right.$$

(19)

where $P_{e,Buy}^{\min }$ and $P_{e,Buy}^{\max }$ are the minimum and maximum values of the grid output power, respectively (kW); $\Delta P_{e,Buy}^{\min }$ and $\Delta P_{e,Buy}^{\max }$ are the minimum and maximum values of the rate of change of the grid output power, respectively (kW);

b)

Constraints on biogas:

$$\left\{\begin{array}{l}{P}_{g,Biogas}^{\min }\le P_{g,Biogas}(t)\le P_{g,Biogas}^{\max }\hfill \\ T_Z^{\min }\le T_Z(t)\le T_Z^{\max }\hfill \end{array}\right.$$

(20)

where $P_{g,Biogas}^{\min }$ and $P_{g,Biogas}^{\max }$ are the minimum and maximum values of the biogas output power, respectively (kW); $T_Z^{\min }$ and $T_Z^{\max }$ are the minimum and maximum values of the biogas reactor temperature, respectively (°C);

(4)

Energy storage constraints

In order to further improve the flexibility of the operation scheduling of the energy system built in this paper, the electricity storage device and the gas storage devices are considered, and the unified modeling is as follows:

$$\left\{\begin{array}{l}\begin{array}{l}0\le P_{n,es}^{ch}(t)\le B_{n,es}^{ch}(t)P_{n,es}^{\max }\hfill \\ 0\le P_{n,es}^{dch}(t)\le B_{n,es}^{dch}(t)P_{n,es}^{\max }\hfill \\ P_{n,es}(t)=P_{n,es}^{ch}/{\eta }_{n,es}^{ch}-P_{n,es}^{dch}\cdot {\eta }_{n,es}^{dch}\hfill \\ S_n(t)=S_n(t-1)+P_{n,es}(t)/P_{n,es}^{cap}\hfill \end{array}\hfill \\ S_n(1)=S_n(T)\hfill \\ B_{n,es}^{ch}(t)+B_{n,es}^{dch}(t)=1\hfill \\ S_n^{\min }\le S_n(t)\le S_n^{\max }\hfill \end{array}\right.$$

(21)

where $P_{n,es}^{ch}(t)$ and $P_{n,es}^{dch}(t)$ are the charging power and the discharging power of the energy storage device (n) at time period t, respectively (kW); $P_{n,es}^{\max }$ is the maximum power of charging and discharging (kW); $B_{n,es}^{ch}$ and $B_{n,es}^{dch}$ are binary variables, which are the charging and discharging states of the energy storage device (n) at time period t, respectively ($B_{n,es}^{ch},B_{n,es}^{dch}\in \left\{0,\left.1\right\}\right.$); $P_{n,es}(t)$ is the output power of the energy storage device (n) at time period t (kW); ${\eta }_{n,es}^{ch}$ and ${\eta }_{n,es}^{dch}$ are the charging and discharging efficiencies of the energy storage device (n) at time period t, respectively ($\%$); $S_n(t)$ is the capacity of the energy storage device (n) at time period t (kWh); $P_{n,es}^{cap}$ is the rated capacity of the energy storage device (n) at t (kW); $S_n^{\min }$ and $S_n^{\max }$ are the minimum and maximum values of the capacity of the energy storage device (n), respectively, at t (kWh);

(5)

Power balance constraints

a)

Electric power balance constraints:

$$\begin{array}{c}{P}_{e,load}(t)=P_{e,Buy}(t)+P_{PV}(t)+P_{WP}(t)+P_{e,BCHP}(t)\\ +P_{e,es}(t)-P_{HP}(t)-P_{P2G}(t)\end{array}$$

(22)

b)

Heat power balance constraints:

$$P_{h,load}(t)=P_{h,HP}(t)+P_{h,BCHP}(t)$$

(23)

c)

Gas power balance constraints:

$$P_{g,load}(t)=P_{g,Biogas}(t)+P_{g,P2G}(t)+P_{g,es}(t)$$

(24)

d)

Electric-load-conversion balance constraints:

$$\Delta P_{e,load}^c(t)+\Delta P_{g,load}^c(t)=0$$

(25)

(6)

User energy satisfaction constraints

Satisfaction with the energy use is an important indicator of whether or not the user actively participates in the load IDR. Because energy conversion only changes the form of energy used by the customer without affecting the customer’s energy demand, the customer’s energy satisfaction constraints are as follows.

$$S=1-\frac{{\displaystyle \sum _{t=1}^T(P_{e,mov}(t)+P_{h,cut}(t)+P_{g,mov}(t))}}{{\displaystyle \sum _{t=1}^T(P_{e,load}(t)+P_{h,load}(t)+P_{g,load}(t))}}\ge S_0$$

(26)

where $S_0$ is the minimum value of the user satisfaction with the energy use, which is 0.9 in this paper.

4.3. Model Solution Method

This paper presents the RIES optimal-scheduling model, which effectively solves a mixed-integer linear programming (MILP) problem. The decision variables comprise the operation strategy and energy supply allocation, among other factors. The system has several constraints, which include the new energy output, energy conversion equipment operation, upper grid, biogas, energy storage, power balance, and user satisfaction. The objective function aims to minimize the total operating cost. Various algorithms exist for solving models, such as particle swarm and genetic algorithms. However, these algorithms may become trapped in local optimal solutions, failing to reach the global optimal solution. The CPLEX solver, based on YALMIP, includes a mixed-integer optimizer that overcomes this limitation and guarantees finding the global optimal solution with confidence. This study used YALMIP R2021a in MATLAB for the mathematical modeling and invoked the CPLEX solver for solving with confidence and professionalism. The standard form of the solution is Equation (27), and the solution process is shown in Figure 3.

$$\begin{array}{c}\min c^{T}x\\ s.t.\left\{\begin{array}{l}{A}_{eq}x=b_{eq}\hfill \\ A_{ineq}x\ge b_{ineq}\hfill \\ x_{\max }\ge x_i\ge x_{\min },i\in I\hfill \\ x_j\in \left\{0,1\right\},j\in J\hfill \end{array}\right.\end{array}$$

(27)

where the optimization variable ($x$) represents the output of each piece of energy supply equipment, energy conversion equipment, and energy storage equipment of the system. The equation constraints represent the energy balance equations of the system, the biogas heat transfer balance equations, and the balance equations of the energy storage equipment. The inequality constraints represent the output of each piece of equipment in the system.

5. Case Study Analysis

5.1. Basic Parameters

The Panxi region in Sichuan Province, China, is an ideal location for renewable energy systems due to its favorable conditions for agriculture, forestry, animal husbandry, and by-products, as well as its abundance of biomass and wind energy. Its potential for sustainable energy development is undeniable. Establishing a wind and biogas energy conversion facility in this densely populated area with high energy consumption can be achieved with a well-planned approach. To effectively contribute to rural revitalization, the establishment of a source–load synergistic optimal-scheduling model for a rural integrated energy system is recommended. This model should consider the complementary utilization of biogas, wind, and solar energy. For the purpose of analysis and research, we selected the data from an integrated energy system in a village situated in the Panxi region of Sichuan, China. As shown in Figure 1, the system structure was considered.

Typical days of the four seasons in a year were studied, and the typical daily historical data of the new energy output and electricity, heat, and gas loads are shown in Figure 4. The parameters of the individual energy supply equipment and energy conversion devices in the system are shown in

Table 2. System equipment parameters.

Equipment	Efficiency	Output Lower Limit/kW	Output Upper Limit (kW)
BCHP	0.35	0	500
P2G	0.6	0	100
HP	2.85	0	200
Power grid	1	0	200
Biogas	1	0	600

, while the parameters of the energy storage devices are shown in

Table 3. Energy storage equipment parameters.

Equipment	Capacity/kWh	Upper- and Lower-Limit Capacity Constraints	Charging and Discharging Efficiency
Energy storage (electricity)	450	0.2, 0.9	0.9
Energy storage (gas)	300	0.2, 0.9	0.9

. The system is dispatched in a 24 h cycle with a time interval of 0.5 h. The time-varying cost of biogas [31] and the time-sharing tariff [32] are shown in

Table 4. Time-of-use electricity rates.

Category	Time/h	Unit Price/kWh
High electricity price	09:00–11:00	1.09
	18:00–21:00
Flat electricity price	07:00–08:00	0.5
	12:00–17:00
Low electricity price	22:00–06:00	0.29

.

In order to verify the feasibility and validity of the modeling scheme of this paper and its basic features (the low-carbon economic operation of the system and the equipment output of wind power consumption) under non-extreme weather conditions in four seasons, this study set up the four scenarios for simulation analysis. The scenarios are shown in

Table 5. Scenario settings.

Scenario	P2G	DR	Layered Carbon Trading	Traditional Carbon Trading
1	√	√	√	×
2	×	√	√	×
3	√	×	√	×
4	√	√	×	√

Note: √—Adopt this option; ×—Do not adopt this option.

.

5.2. Economic Analysis of Different Scheduling Scenarios in the System

The operating-cost dispatch results for the four scenarios mentioned above are shown in

Table 6. Operating costs of RIES in different scenarios.

(a) Typical Spring Day
Cost/RMB	Scenario 1	Scenario 2	Scenario 3	Scenario 4
Biogas cost	5215.88	5312.17	5727.96	5779.06
Electricity purchase cost	413.77	413.77	440.66	281.82
Wind power curtailment cost	27.02	175.39	208.05	39.63
Cost in IDR	194.78	267.95	0	188.93
Carbon-trading cost	1320.93	1382.18	1797.19	1269.62
Total cost	7172.38	7547.46	8173.86	7559.06
(b) Typical Summer Day
Cost/RMB	Scenario 1	Scenario 2	Scenario 3	Scenario 4
Biogas cost	5336.48	5380.57	5861.41	5783.81
Electricity purchase cost	428.31	428.31	460.12	279.75
Wind power curtailment cost	0	96.89	110.54	16.95
Cost in IDR	145.39	201.84	0	150.14
Carbon-trading cost	1398.28	1432.03	1803.19	1315.27
Total cost	7308.46	7539.64	8235.26	7545.92
(c) Typical Autumn Day
Cost/RMB	Scenario 1	Scenario 2	Scenario 3	Scenario 4
Biogas cost	5224.76	5310.33	5734.7	5783.81
Electricity purchase cost	410.19	410.19	441.53	279.75
Wind power curtailment cost	33.71	181.06	213.88	44.95
Cost in IDR	186.65	259.76	0	188.93
Carbon-trading cost	1305.28	1377.41	1786.37	1256.75
Total cost	7160.59	7538.75	8176.48	7554.19
(d) Typical Winter Day
Cost/RMB	Scenario 1	Scenario 2	Scenario 3	Scenario 4
Biogas cost	5266.47	5352.49	5781.92	5823.25
Electricity purchase cost	11.02	11.02	19.34	7.58
Wind power curtailment cost	40.89	189.92	223.23	52.93
Cost in IDR	271.76	352.03	0	278.02
Carbon-trading cost	1364.55	1442.91	1839.14	1303.46
Total cost	6954.69	7348.37	7863.63	7465.24

.

(1)

Comparative analysis of Scenario 1 and Scenario 2

According to Table 6, the operating cost of Scenario 1 is RMB 7172.38 on a typical day in spring. Compared to Scenario 2, the biogas cost, wind abandonment penalty cost, IDR cost, and carbon-trading cost are reduced by 1.74%, 84.59%, 27.31%, and 4.43%, respectively. On a typical day in summer, Scenario 1 has an operating cost of RMB 7308.46. Compared to Scenario 2, the biogas cost, wind abandonment penalty cost, IDR cost, and carbon-trading cost are reduced by 0.81%, 100%, 27.96%, and 2.35%, respectively. On a typical day in autumn, the operating cost of Scenario 1 is RMB 7160.59, and compared to Scenario 2, the biogas cost, wind abandonment penalty cost, IDR cost, and carbon-trading cost are reduced by 1.61%, 81.38%, 28.15%, and 5.24%, respectively. On a typical winter day, the operating cost of Scenario 1 is RMB 6954.69. Compared to Scenario 2, the biogas cost, wind abandonment penalty cost, IDR cost, and carbon-trading cost are reduced by 1.60%, 78.46%, 22.80%, and 5.43%, respectively. In the absence of P2G, the surplus wind is forced to be wasted, resulting in higher abandonment penalty costs. In addition, the gas load can only be met by biogas, which increases the biogas cost and carbon-trading cost and also makes the system inflexible, leading to a higher IDR cost. As a result, the total operating costs for Scenario 1 are reduced by 4.97%, 3.71%, 5.02%, and 5.36% for typical days in spring, summer, autumn, and winter, respectively;

(2)

Comparative analysis of Scenario 1 and Scenario 3

In contrast to Scenario 1, Scenario 3 has no IDRs and relies only on coordinated optimization by the energy conversion devices in the system, which lacks flexibility. In contrast, the introduction of the IDR in Scenario 1 allows users to flexibly change their electricity and gas consumption habits based on different price signals and incentives. This can not only promote the consumption of wind power but can also reduce the pressure of each unit of energy supply equipment and reduce carbon emissions, balancing the economy and environmental protection during the system operation. From Table 5, it can be seen that on a typical day in spring, compared to Scenario 3, the wind power penalty cost and total operating cost of Scenario 1 are reduced by 87.01% and 12.25%, respectively. On a typical day in summer, compared to Scenario 3, Scenario 1’s wind power penalty cost and total operating cost are reduced by 100% and 11.25%, respectively. On a typical day in autumn, compared to Scenario 3, Scenario 1’s wind penalty cost and total operating cost are reduced by 84.24% and 12.42%, respectively. On a typical day in winter, the wind penalty cost and total operating cost for Scenario 1 are reduced by 81.68% and 11.56%, respectively, compared to Scenario 3;

(3)

Comparative analysis of Scenario 1 and Scenario 4

Compared to Scenario 1, Scenario 4 does not consider the stepped-carbon-trading mechanism. Although traditional carbon trading has some constraints on the system carbon emissions, its fixed-pricing model makes a limited contribution to system emission reductions. Combined with Table 6, it can be seen that on a typical day in spring, compared to Scenario 4, the Scenario 1 biogas cost is reduced by 9.74% and the total operating cost is reduced by 5.11%. On a typical day in summer, compared to Scenario 4, the Scenario 1 biogas cost is reduced by 7.73% and the total operating cost is reduced by 3.14%. On a typical day in autumn, compared to Scenario 4, the Scenario 1 biogas cost is reduced by 9.67% and the total operating cost is reduced by 5.21%. On a typical day in winter, compared to Scenario 4, the Scenario 1 biogas cost is reduced by 9.56% and the total operating cost is reduced by 6.83%. Stepped carbon trading further effectively reduces carbon emissions from the system.

Based on the above analysis, it can be seen that the introduction of P2G promotes the consumption of wind power at night, and, at the same time, enriches the source of the gas load, decoupling the single mode of the gas load that can only be supplied by biogas. The introduction of the IDR at the load side effectively coordinates the user’s energy consumption habits, enabling the system to choose a more economical way of energy consumption, further promoting the consumption of wind power. The introduction of the stepped-carbon-trading mechanism strengthens the degree of the emission reduction of the system. Therefore, the modeling scheme proposed in this paper can effectively balance the economy and low-carbon nature of the system operation. Next, the scheduling results of Scenario 1 are selected for the analysis of the output of each device of the RIES system and the IDR analysis during typical days in spring, summer, autumn, and winter, together with a comparative analysis of the wind power consumption, system carbon emissions, and user satisfaction.

5.3. Analysis of System Equipment Output

After the introduction of the P2G and IDR at the source and load ends, respectively, as well as the consideration of the stepped-carbon-trading mechanism, the output of each unit of equipment of the system is shown in Figure 5, Figure 6 and Figure 7.

(1)

Output of electrical-load equipment

As can be seen in Figure 5, it can be seen that the wind power output is large during the periods of 22:00–05:00 and the electric-load demand is not high, so the system electric load relies on wind power and biomass biogas power generation to satisfy the system electric load during this time, and the excess wind power is used for the P2G, HP, and power storage to promote the consumption of wind power and reduce the operating cost. During the periods of 09:00–11:00, although the power purchase price is at its peak, the BCHP reduces its output, as the PV is connected to reduce carbon emissions, taking into account the low-carbon nature of the system. During the 18:00–21:00 time period when the power purchase price is at its peak and the load demand is high, the PV output is zero and the BCHP increases the output to alleviate the power tension. During the periods of 7:00–8:00 and 12:00–17:00, when the power purchase price is flat and the load demand slows down, the system relies on wind, PV, and biomass biogas generation to balance the load, while the grid fluctuates to meet the operation of the HP, which has a higher thermal efficiency. The power storage device stores electricity when the electricity price is low and wind power is abundant, and it discharges it when the electricity price is high, which further ensures the economy and stability of the system;

(2)

Output of heat-load equipment

As can be seen in Figure 6, the heat load is supplied by the BCHP and HP jointly. During the period of 22:00–06:00, wind power resources are sufficient, and the heat pump runs at full power, decoupling the operation mode of the BCHP “heat to set the electricity”, maximally relieving the pressure of the BCHP heat supply, and expanding the space of the wind power grid connection. During the period of 07:00–16:00, with the output of photovoltaics, the system uses the electricity-consuming HP for heating in order to consume renewable energy as much as possible. Therefore, even if the electricity price is high during this period, the output power of the HP is still large. At the same time, because the demand for the heat load is reduced during this period, the output of the BCHP is also reduced to lower the cost and carbon emissions of the biogas utilization. During the period of 18:00–21:00, when the purchasing price is at its peak, the output of photovoltaics is zero, and the demand for the thermal load increases. The biomass CHP system increases its output to meet the thermal-load demand. Due to the increase in the carbon emission cost of BCHP and the discharging of energy storage devices under the stepped-carbon-trading mechanism, the HP also fluctuates its output slightly to ensure the economic and environmental performance of the system;

(3)

Output of gas-load equipment

As can be seen in Figure 7, the gas load is supplied by a combination of P2G, purchased gas, and gas storage units. The gas-load demand in the 23:00–08:00 time period is relatively low, the wind power resources are abundant, and the cost of biogas is at a low price, so the gas load is mainly balanced by the purchased gas and P2G in this time period, and, at the same time, in addition to fulfilling the user’s gas-load demand, in order to fully absorb the wind power resources and reduce the operating cost of the system, the excess gas is supplied to other gas-consuming equipment or is stored in the gas storage tanks. During 09:00–12:00 and 18:00–19:00, the gas-load demand gradually increases, and the cost of biogas is at its peak, so the system gives priority to the use of gas in the storage tanks to ensure the economy during this period, and the shortfall in supply is balanced by the purchased gas. During 13:00–17:00 and 20:00–22:00, the gas-load demand is higher and the cost of biogas and purchased electricity are at a flat value; however, due to the conversion efficiency of the P2G, running the P2G through purchased electricity would result in a greater economic cost, so the gas load is fully met by the purchased gas during this time.

5.4. Integrated Demand Response Analysis of Electricity, Heat, and Gas Loads

(1)

Analysis of DR for electric load

As can be seen from Figure 8, the participation of the electric load in the DR plays a good role in peak shaving and valley filling, smoothing the load curve. Under the guidance of time-sharing tariffs, the electric load is transferred during the peak tariff hours of 09:00–11:00 and 18:00–21:00, which reduces the load during these times, increases the load at the valley and flat values of the tariffs, smooths the load curve, and reduces the system operation cost and energy supply pressure of each piece of energy-supplying equipment. A portion of the gas load is replaced by the electric load during 23:00–05:00 h, which not only improves the consumption capacity of wind power at night but also reduces the carbon emissions of the system. Meanwhile, the price of electricity is much higher than the price of gas during the period of 18:00–21:00, and there is a certain amount of energy loss in the conversion of biogas through the BCHP, so the system replaces part of the electric load with the gas load during this period to further alleviate the pressure on the power supply;

(2)

Analysis of DR for heat load

As can be seen from Figure 9, the system heat-load demand is at its peak during the 23:00–05:00 time period, and the BCHP leads to a large amount of wind power waste in order to satisfy the heat-load demand, so the system transfers the heat load during this time period to the 12:00–17:00 and 22:00–23:00 time periods, when the electricity tariffs are at parity and prices are low, and, at the same time, selects HPs with higher energy efficiency ratios to carry out the auxiliary heat supply to reduce the pressure on the heat supply from the BCHP. When the electricity price is at its peak during 09:00–11:00 and 18:00–21:00, no heat-load transfer is carried out to ensure the economy of the system. Further, under the constraint of meeting the maximum heat-load reduction, heat-load reduction is carried out for the 23:00–08:00 time period to further reduce the heat supply pressure of the BCHP on the basis of heat-load shifting in order to reduce the carbon emissions and improve the economics;

(3)

Analysis of DR for gas load

As can be seen from Figure 10, biogas costs are guided by time-sharing signals, and the gas load is transferred during the peak gas price hours of 09:00–12:00 and 18:00–19:00, which reduces the load during the peak gas price hours and increases the load at the valley and flat values of the electricity price, which improves the flexibility of the system to choose a more economical way of purchasing energy. During the 23:00–05:00 period, when electricity prices are low and wind abandonment exists, a portion of the gas load is met by selecting the electric load, resulting in a reduction in the final gas load during this period, which further reduces the carbon emissions of the system. During the period 18:00–21:00, when the tariff is at its peak, some of the electric load is also replaced by the gas load, which mitigates the high carbon emissions of the coal power units and cogeneration equipment and ultimately reduces the total carbon emissions and operating cost of the system to some extent.

5.5. Analysis of Wind Power Consumption Improvement

Figure 11 and

Table 7. Wind power consumption situation.

(a) Typical Spring Day
Scenario	Total Wind Power Consumption/kWh	Wind Power Curtailment Rate/%
1	12,611.1	2.35
2	11,117.8	13.98
3	10,688.7	16.07
4	12,498.5	3.38
(b) Typical Summer Day
Scenario	Total Wind Power Consumption/kWh	Wind Power Curtailment Rate/%
1	9572.5	0
2	8812.8	7.93
3	8712.2	8.98
4	9497.4	0.78
(c) Typical Autumn Day
Scenario	Total Wind Power Consumption/kWh	Wind Power Curtailment Rate/%
1	12,438.7	2.64
2	10,964.5	14.18
3	10,635.9	16.75
4	12,326.1	3.52
(d) Typical Winter Day
Scenario	Total Wind Power Consumption/kWh	Wind Power Curtailment Rate/%
1	13,992.4	3.36
2	12,576.9	15.01
3	12,123.5	17.47
4	13,879.6	4.55

show the consumption of wind power in each scenario. As the wind power output is larger at night, the heat load is at peak, the demand of the electric load is not high, and the BCHP has the operation mode of “heat to set the electricity”. Therefore, from Figure 11, it can be seen that wind abandonment mainly occurs during 24:00–07:00. Table 7 shows that on a typical day in spring, compared with Scenario 2, Scenario 3, and Scenario 4, the wind power consumption of Scenario 1 is increased by 11.63%, 13.72%, and 1.03% respectively, and finally reaches a consumption rate of 97.93%. On a typical day in summer, the wind power consumption of Scenario 1 is increased by 7.93%, 8.98%, and 0.78% compared to Scenarios 2, 3, and 4, respectively, and finally reaches 100%. On a typical day in autumn, compared to Scenario 2, Scenario 3, and Scenario 4, Scenario 1’s wind power consumption improves by 11.54%, 14.11%, and 0.88%, respectively, and eventually reaches a 97.36% consumption rate. On a typical day in winter, compared with Scenario 2, Scenario 3, and Scenario 4, the wind power consumption of Scenario 1 is enhanced by 11.65%, 14.11%, and 1.19%, respectively, and finally reaches a consumption rate of 96.78%. It has an obvious enhancement effect, which verifies the enhancement effect of the source-side introduction of P2G and the load-side introduction of the IDR on the wind power consumption proposed in this paper, which effectively enhances the level of wind power consumption in the RIES, and also extends the value and variety of the P2G and load-side IDR in the integrated energy system.

5.6. Analysis of System Carbon Emissions and User Satisfaction

The carbon emission results and user satisfaction for each scenario are shown in

Table 8. Carbon emission results and user satisfaction.

(a) Typical Spring Day
Scenario	Carbon Emissions/kg	User Satisfaction/%
1	9254.17	95.45
2	9689.65	93.88
3	12,598.22	100
4	10,546.62	94.41
(b) Typical Summer Day
Scenario	Carbon Emissions/kg	User Satisfaction/%
1	9800.96	95.96
2	10,040.11	93.38
3	12,640.27	100
4	10,869.05	94.86
(c) Typical Autumn Day
Scenario	Carbon Emissions/kg	User Satisfaction/%
1	9149.04	95.71
2	9654.61	93.11
3	12,521.12	100
4	10448.5	94.62
(d) Typical Winter Day
Scenario	Carbon Emissions/kg	User Satisfaction/%
1	9920.08	95.46
2	10,110.21	93.36
3	12,850.55	100
4	10,798.96	94.22

. We compared the carbon emission results of the system with or without P2G, the integrated demand response, and the stepped-carbon-trading mechanism under the same conditions in order to analyze the impact of the scenarios containing the P2G, IDR, and stepped-carbon-trading mechanism on the system’s environmental benefits. After comparing the results of Scenario 1 with those of Scenario 2, Scenario 3, and Scenario 4, it was found that the carbon emissions of the system were reduced to a certain extent. Among them, as shown in Table 7, on a typical day in spring, compared with Scenario 2, Scenario 3, and Scenario 4, the carbon emissions of the system in Scenario 1 are reduced by 435.48 kg, 3344.05 kg, and 1292.45 kg, which are decreases of 4.49%, 26.54%, and 12.25%, respectively. On a typical day in summer, compared with Scenario 2, Scenario 3, and Scenario 4, the system carbon emissions of Scenario 1 are reduced by 239.15 kg, 2839.31 kg, and 1068.09 kg, or by 2.38%, 22.46%, and 9.82%, respectively. On a typical day in autumn, compared with Scenario 2, Scenario 3, and Scenario 4, the system carbon emissions of Scenario 1 are reduced by 505.57 kg, 3372.08 kg, and 1299.46 kg, or by 5.23%, 26.93%, and 12.44%, respectively. On a typical day in winter, compared with Scenario 2, Scenario 3, and Scenario 4, the systematic carbon emissions of Scenario 1 are reduced by 190.13 kg, 2930.47 kg, and 878.88 kg, which are decreases of 1.88%, 22.80%, and 8.13%, respectively. After considering the stepped-carbon-trading mechanism, the scheme proposed in this paper will arrange the scheduling of the system’s various equipment outputs according to the electricity price, biogas cost, and transaction cost of using carbon-generating equipment, so that the system can meet the lowest total operating cost while reducing the CO₂ emissions as much as possible, taking into account the system’s economy and environment. In summary, by optimizing the output of the gas-consuming equipment and electricity-consuming equipment, as well as the distribution of each load, the model and scheme proposed in this paper can effectively reduce the carbon emissions of the system to improve environmental protection, while, at the same time, not losing the economy of the system operation. In addition, as can be seen from Table 8, load participation in the IDR has an impact on the user’s comprehensive energy satisfaction, which is 100%, as Scenario 3 does not participate in the IDR. On a typical day in spring, compared with Scenario 2 and Scenario 4, the user satisfaction in Scenario 1 increased by 1.64% and 1.08%, respectively. On a typical day in summer, compared with Scenario 2 and Scenario 4, the user satisfaction in Scenario 1 increased by 2.68% and 1.14%, respectively. On a typical day in autumn, compared with Scenario 2 and Scenario 4, the user satisfaction in Scenario 1 increased by 2.85% and 1.14%, respectively. On a typical day in winter, compared with Scenario 2 and Scenario 4, the user satisfaction in Scenario 1 increased by 2.85% and 1.14%, respectively. This proves that the scenarios considering P2G and the stepped-carbon-trading mechanism in this paper have less impact on the user satisfaction.

6. Conclusions

In this paper, an RIES based on the complementary utilization of biogas–wind–light is constructed by combining the natural resource endowment of rural areas. A source–load synergistic optimization model with the lowest system operation cost and considering the biogas usage cost, carbon-trading cost, and IDR compensation cost is established for the RIES low-carbon-economic-dispatch problem. Through the simulation analysis based on non-extreme weather conditions in four seasons and based on the data in Table 6(a–d), the following relevant conclusions that can guide the upper bound of practice are drawn:

• The introduction of the IDR can effectively improve the economics and stability of the system operation. Under the time-sharing tariff and time-varying biogas cost, customers can promote the system consumption of wind power and relieve pressure on the equipment supply by transferring, shifting, or curtailing part of the load during periods of peak energy use and high energy purchase prices. Compared to no IDR, the system in this paper reduces the wind penalty cost and total operating cost by 87.01% and 12.25%; 100% and 11.25%; 84.24% and 12.42%; 81.68% and 11.56%, respectively, for typical days in spring, summer, autumn, and winter;
• With the introduction of the IDR mechanism, the consideration of P2G at the source end allows for the further optimization of the economics and low-carbon nature of the system. In the absence of P2G, the surplus wind power is forced to be wasted, which leads to an increase in the abandonment penalty cost, and also further leads to the gas load being met only by biogas, which increases the biogas cost and carbon-trading cost. Compared to no P2G, the system in this paper shows reductions in the biogas costs, wind abandonment penalty costs, and carbon-trading costs on typical days in spring, summer, autumn, and winter of 1.81%, 84.59%, and 4.43%; 0.82%, 100%, and 2.35%; 1.61%, 81.38%, and 5.24%; and 1.60%, 78.46%, and 5.43%, respectively;
• The introduction of a stepped-carbon-trading mechanism can further promote energy saving and emission reduction in the system. Compared with traditional carbon trading, the strategy proposed in this paper reduces the biogas cost and operating cost by 9.75% and 5.12%; 7.74% and 3.15%; 9.67% and 5.21%; and 9.57% and 6.84%, respectively, on typical days in spring, summer, autumn, and winter. The effective reduction in carbon emissions from the system also improves the economics of the system operation.

In summary, the research work in this paper not only provides a novel perspective for the planning and construction of RIESs but also effectively promotes rural revitalization. However, the effects of multiple uncertainties, such as the wind power output and load forecast curves in the integrated energy system, have not yet been taken into account, and the demand-side cooling load of customer loads has not been considered, which will be analyzed and discussed in future studies.