Numerically Investigating the Energy-Harvesting Performance of an Oscillating Flat Plate with Leading and Trailing Flaps
Abstract
1. Introduction
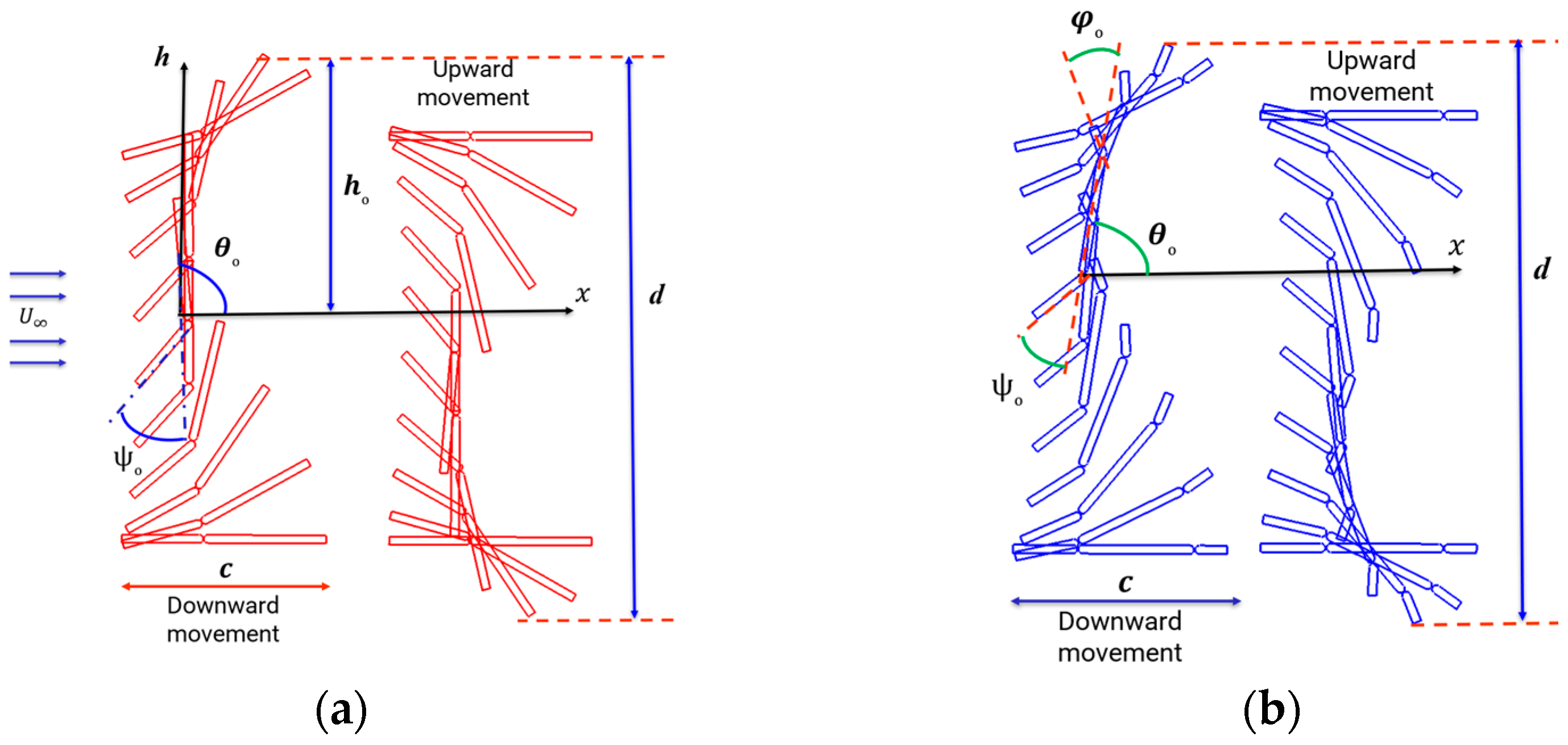
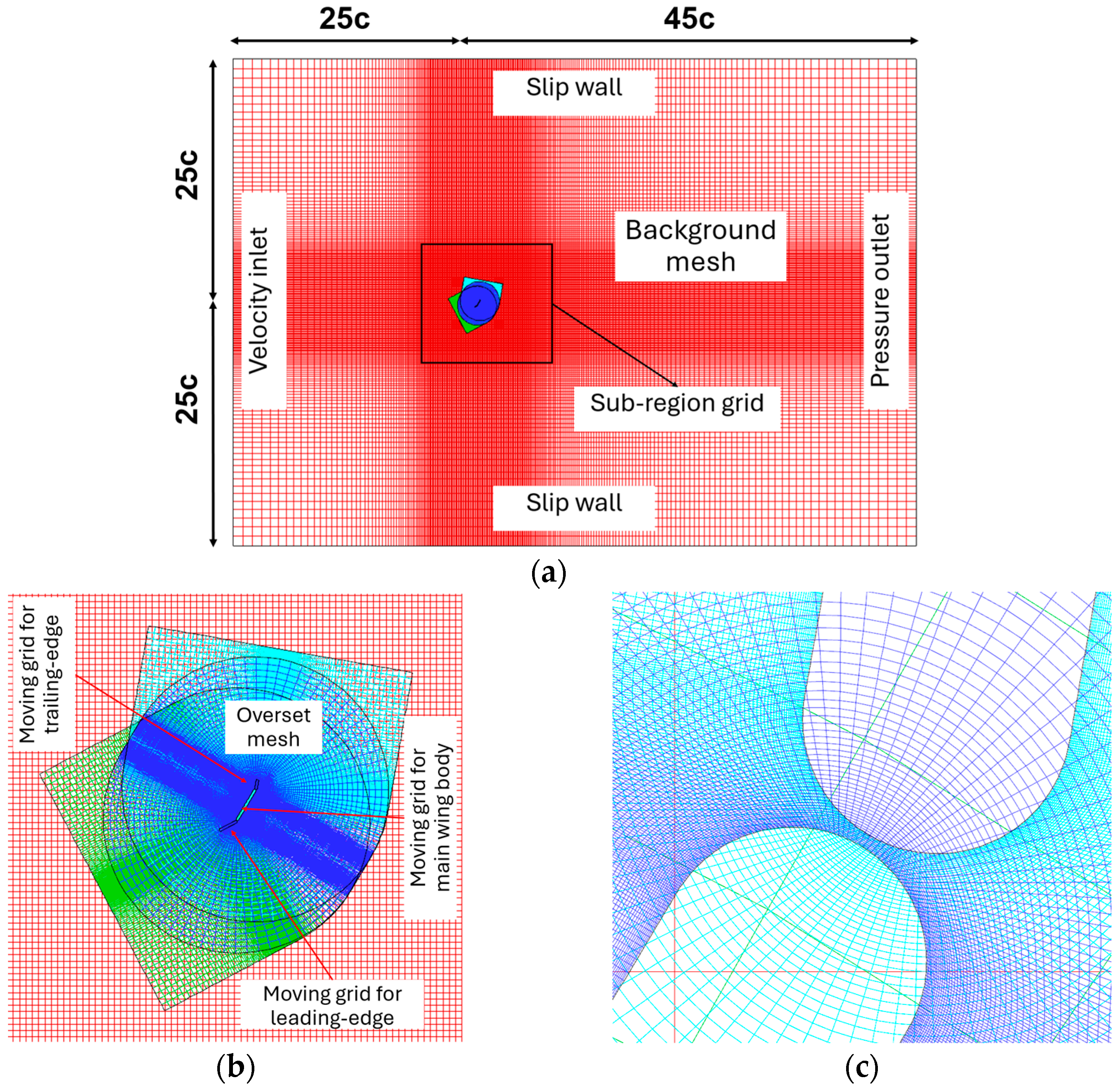
2. Numerical Methodology
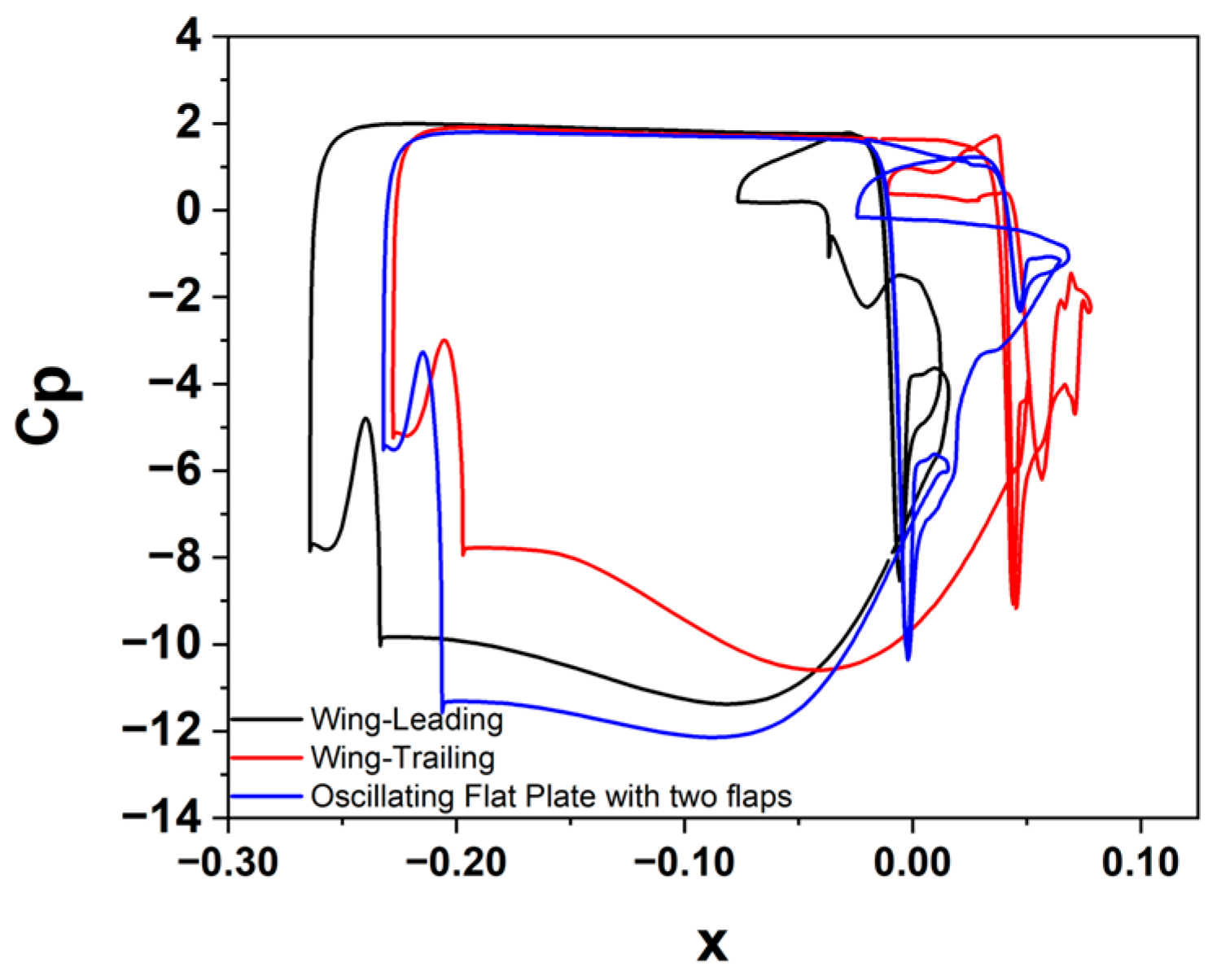
3. Results and Discussion
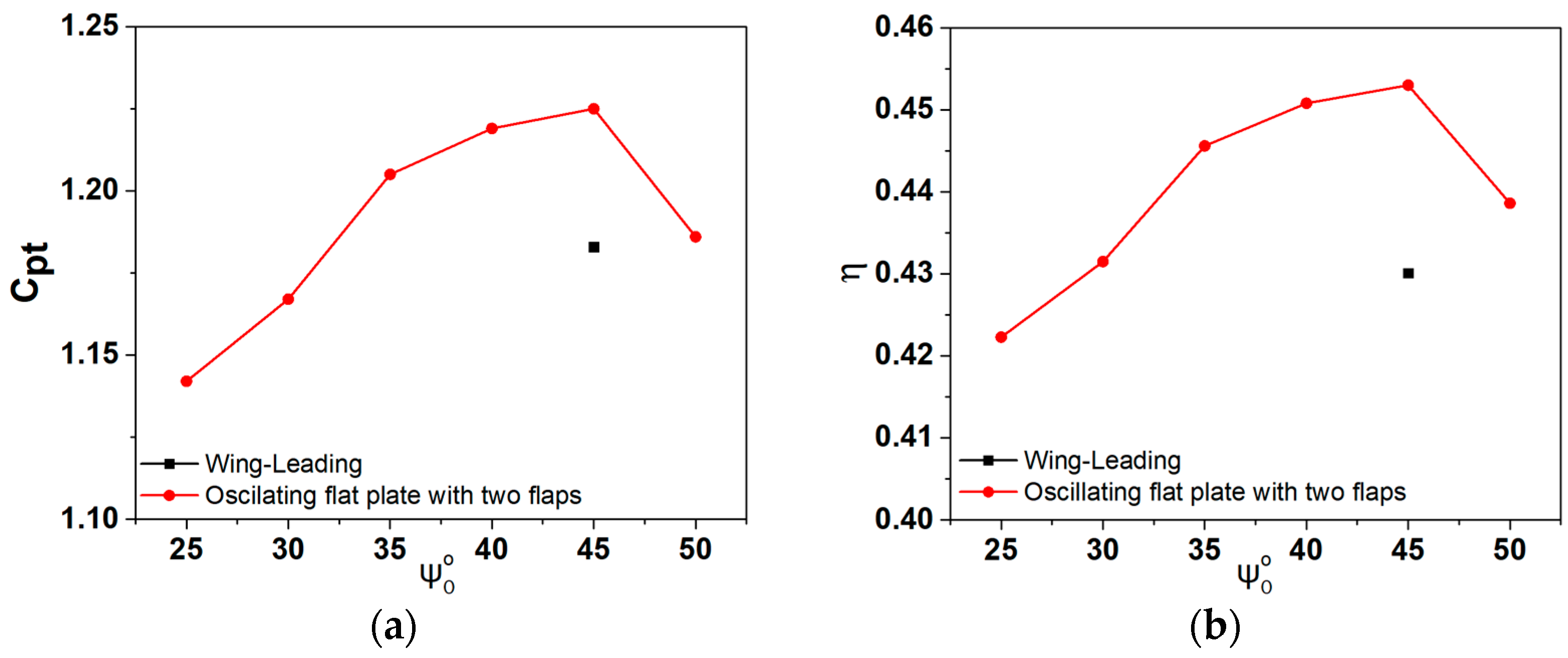
3.1. Effect of the Leading Flap’s Pitch Angles on an Oscillating Flat Plate with Two Flaps
3.2. Effect of the Trailing Flap’s Pitch Angles on an Oscillating Flat Plate with Two Flaps
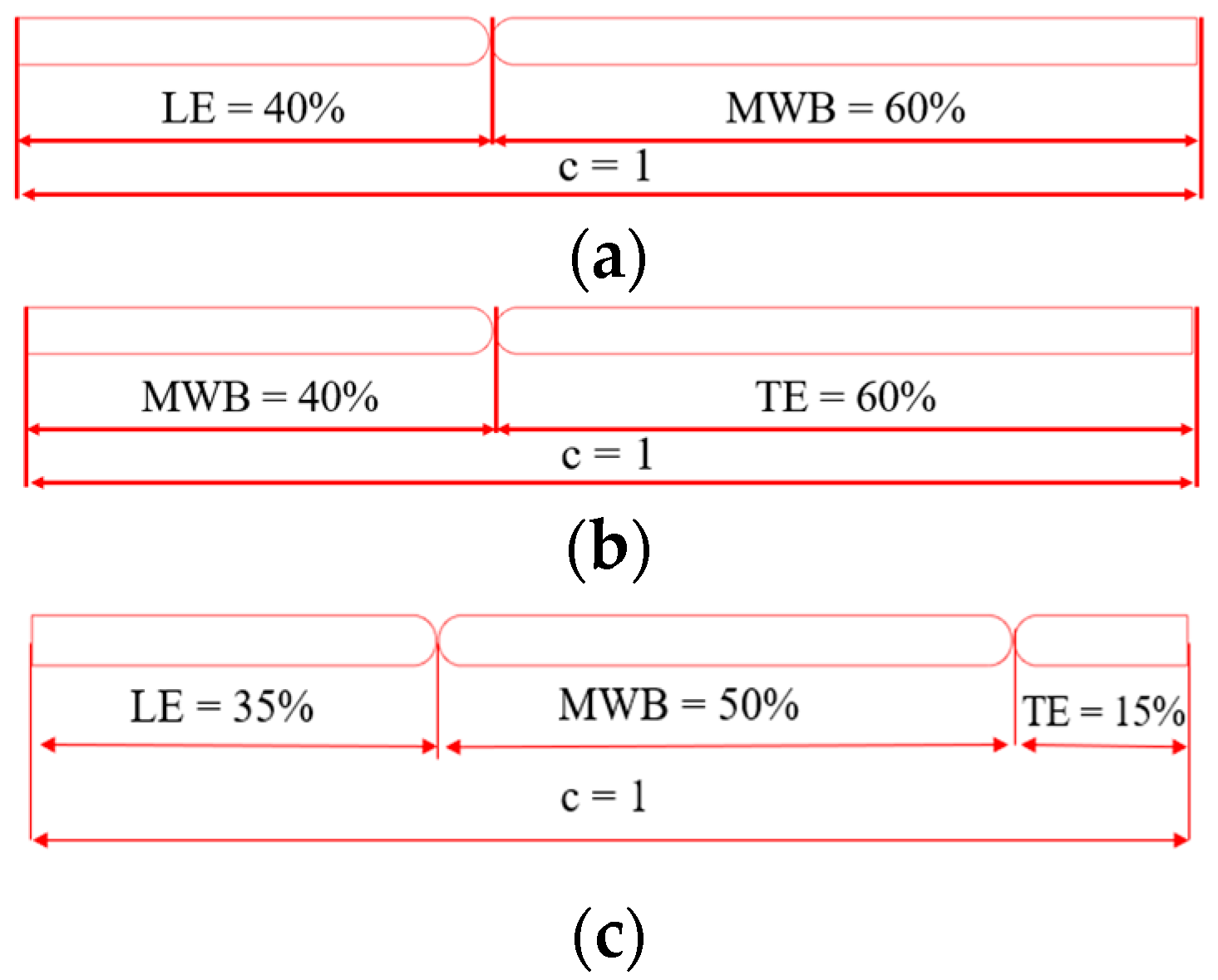
3.3. Effect of Flap Lengths on an Oscillating Flat Plate with Two Flaps
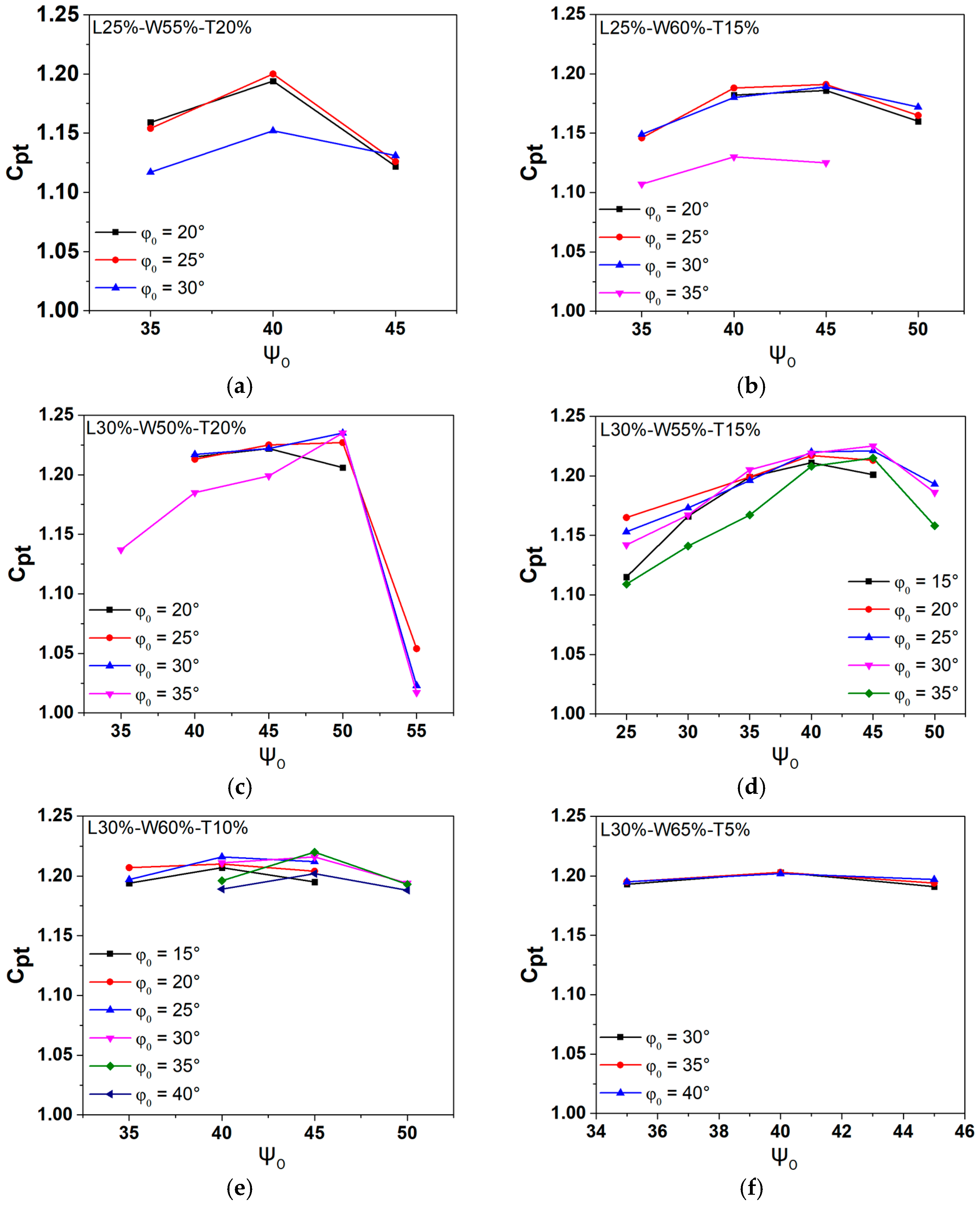
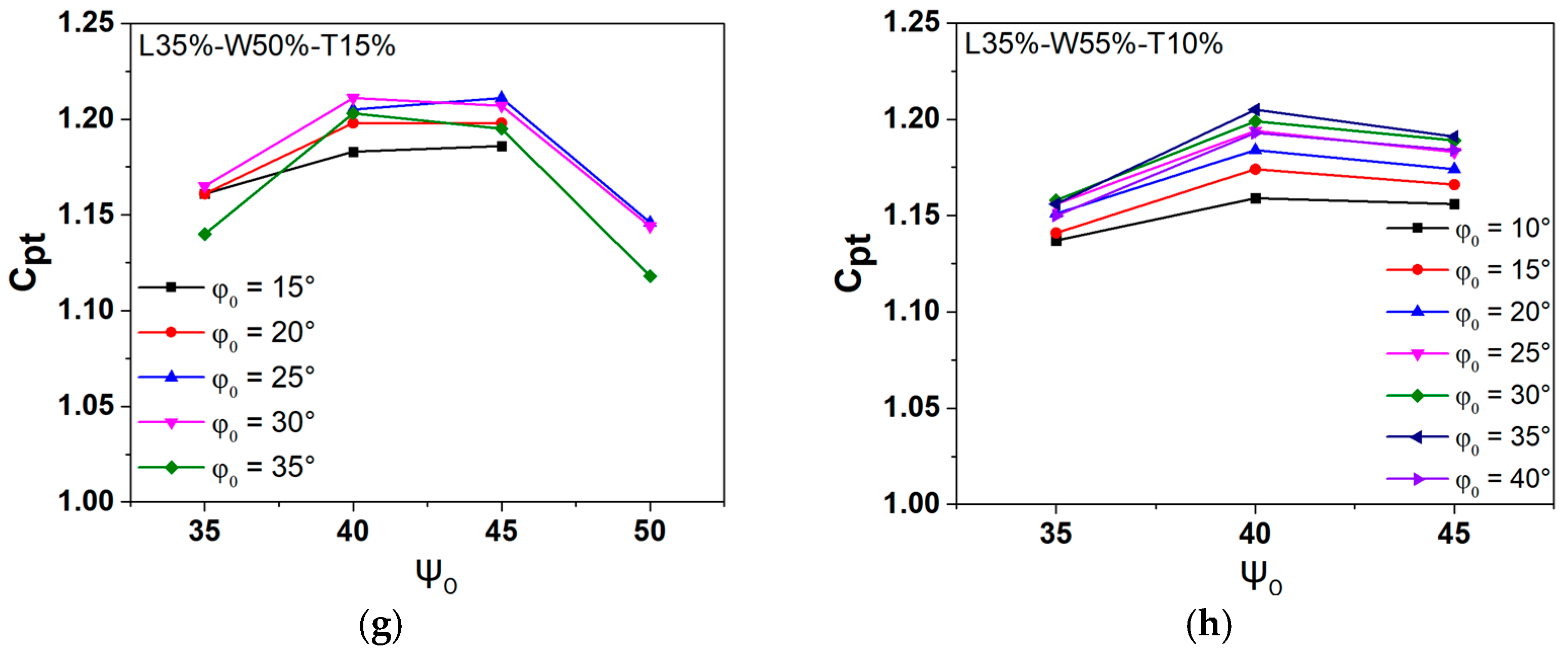
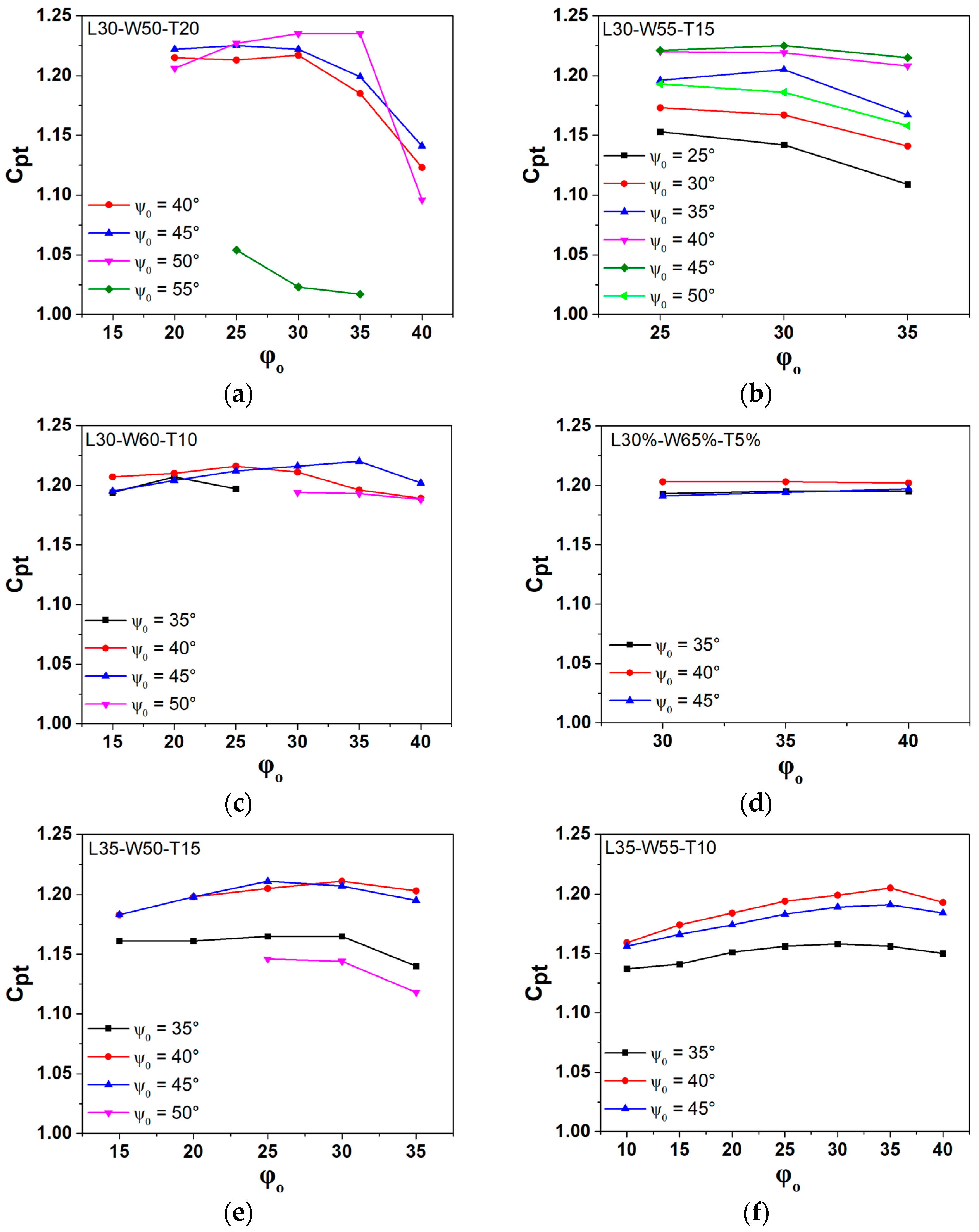
3.4. Effect of the Combination of Lengths and Pitch Angles on an Oscillating Flat Plate with Two Flaps
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- García-Olivares, A.; Solé, J.; Osychenko, O. Transportation in a 100% renewable energy system. Energy Convers. Manag. 2018, 158, 266–285. [Google Scholar] [CrossRef]
- Paiva, A.S.S.; Rivera-Castro, M.A.; Andrade, R.F.S. DCCA analysis of renewable and conventional energy prices. Phys. A Stat. Mech. Its Appl. 2018, 490, 1408–1414. [Google Scholar] [CrossRef]
- Jones, K.D.; Davids, S.; Platzer, M.F. Oscillating-wing power generator. In Proceedings of the 3rd ASME/JSME Joint Fluids Engineering Conference, San Francisco, CA, USA, 18–23 July 1999; American Society of Mechanical Engineers: New York, NY, USA, 1999. [Google Scholar]
- Shimizu, E.; Isogai, K.; Obayashi, S. Multiobjective design study of a flapping wing power generator. J. Fluids Eng. 2008, 130, 021104. [Google Scholar] [CrossRef]
- Wu, T.Y.-t. Extraction of flow energy by a wing oscillating in waves. J. Ship Res. 1972, 16, 66–78. [Google Scholar] [CrossRef]
- McKinney, W.; DeLaurier, J. Wingmill: An oscillating-wing windmill. J. Energy 1981, 5, 109–115. [Google Scholar] [CrossRef]
- Lindsey, K. A Feasibility Study of Oscillating-Wing Power Generators; Naval Postgraduate School: Monterey, CA, USA, 2002. [Google Scholar]
- Xie, Y.; Lu, K.; Zhang, D. Investigation on energy extraction performance of an oscillating foil with modified flapping motion. Renew. Energy 2014, 63, 550–557. [Google Scholar] [CrossRef]
- Zhu, B.; Han, W.; Sun, X.; Wang, Y.; Cao, Y.; Wu, G.; Huang, D.; Zheng, Z.C. Research on energy extraction characteristics of an adaptive deformation oscillating-wing. J. Renew. Sustain. Energy 2015, 7, 023101. [Google Scholar] [CrossRef]
- Rushen, J.; Siala, F.; Totpal, A.D.; Planck, C.J.; Liburdy, J.A. The effects of a passively actuated trailing edge on the aerodynamics of an oscillating wing. In Proceedings of the Fluids Engineering Division Summer Meeting, Chicago, IL, USA, 3–7 August 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014; p. V01BT12A012. [Google Scholar]
- Zhu, B.; Xia, P.; Huang, Y.; Zhang, W. Energy extraction properties of a flapping wing with an arc-deformable airfoil. J. Renew. Sustain. Energy 2019, 11, 023302. [Google Scholar] [CrossRef]
- Sun, G.; Wang, Y.; Xie, Y.; Ma, P.; Zhang, Y. Hydrodynamic and energy extraction properties of oscillating hydrofoils with a trailing edge flap. Appl. Ocean Res. 2021, 110, 102530. [Google Scholar] [CrossRef]
- Drost, K.; Linvog, H.; Apte, S.; Liburdy, J. Low reynolds number flow dynamics of a thin airfoil with an actuated leading edge. In Proceedings of the 41st AIAA Fluid Dynamics Conference and Exhibit, Honolulu, HI, USA, 27–30 June 2011; p. 3904. [Google Scholar]
- Davids, S.T. A computational and Experimental Investigation of a Flutter Generator; Naval Postgraduate School: Monterey, CA, USA, 1999. [Google Scholar]
- Jones, K.; Platzer, M. Numerical computation of flapping-wing propulsion and power extraction. In Proceedings of the 35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1997; p. 826. [Google Scholar]
- Kinsey, T.; Dumas, G. Parametric study of an oscillating airfoil in a power-extraction regime. AIAA J. 2008, 46, 1318–1330. [Google Scholar] [CrossRef]
- Aramendia, I.; Saenz-Aguirre, A.; Boyano, A.; Fernandez-Gamiz, U.; Zulueta, E. Oscillating U-shaped body for underwater piezoelectric energy harvester power optimization. Micromachines 2019, 10, 737. [Google Scholar] [CrossRef]
- Teso-Fz-Betoño, D.; Aramendia, I.; Martinez-Rico, J.; Fernandez-Gamiz, U.; Zulueta, E. Piezoelectric energy harvesting controlled with an IGBT H-bridge and bidirectional buck–boost for low-cost 4G devices. Sensors 2020, 20, 7039. [Google Scholar] [CrossRef]
- Esfahani, J.; Barati, E.; Karbasian, H.R. Fluid structures of flapping airfoil with elliptical motion trajectory. Comput. Fluids 2015, 108, 142–155. [Google Scholar] [CrossRef]
- Karbasian, H.R.; Kim, K.C. Numerical investigations on flow structure and behavior of vortices in the dynamic stall of an oscillating pitching hydrofoil. Ocean Eng. 2016, 127, 200–211. [Google Scholar] [CrossRef]
- Zhu, Q. Optimal frequency for flow energy harvesting of a flapping foil. J. Fluid Mech. 2011, 675, 495–517. [Google Scholar] [CrossRef]
- He, G.; Yang, H.; Mo, W.; Zhao, Z.; Wang, W.; Ghassemi, H. Influence of inter-foil spacing on energy extraction of tandem oscillating hydrofoils. Ocean Eng. 2022, 259, 111953. [Google Scholar] [CrossRef]
- Dahmani, F.; Sohn, C. Effect of convergent duct geometry on the energy extraction performance of tandem oscillating hydrofoils system. J. Fluids Struct. 2020, 95, 102949. [Google Scholar] [CrossRef]
- Dahmani, F.; Sohn, C. Effects of the downstream spatial configuration on the energy extraction performance of tandem/parallel combined oscillating hydrofoils. J. Mech. Sci. Technol. 2020, 34, 2035–2046. [Google Scholar] [CrossRef]
- Wang, G.; Ng, B.F. Energy harvesting performance of a tandem-hydrofoil based closely-interconnected tidal array. Energy Convers. Manag. 2023, 280, 116796. [Google Scholar] [CrossRef]
- Hover, F.; Haugsdal, Ø.; Triantafyllou, M. Effect of angle of attack profiles in flapping foil propulsion. J. Fluids Struct. 2004, 19, 37–47. [Google Scholar] [CrossRef]
- Xiao, Q.; Liao, W. Numerical study of asymmetric effect on a pitching foil. Int. J. Mod. Phys. C 2009, 20, 1663–1680. [Google Scholar] [CrossRef]
- Xiao, Q.; Liao, W. Numerical investigation of angle of attack profile on propulsion performance of an oscillating foil. Comput. Fluids 2010, 39, 1366–1380. [Google Scholar] [CrossRef]
- Shanmugam, A.R.; Park, K.S.; Sohn, C.H. Comparison of the Power Extraction Performance of an Oscillating Hydrofoil Turbine with Different Deflector Designs. Energies 2023, 16, 3420. [Google Scholar] [CrossRef]
- Wang, J.; Deng, J.; Kandel, P.; Sun, L. Numerical study on the energy extraction performance by flapping foils in a density stratified flow. J. Fluids Struct. 2023, 118, 103865. [Google Scholar] [CrossRef]
- Swain, P.K.; Dora, S.P.; Barik, A.K. Energy extraction performance of tandem flapping foil undergoing elliptical motion trajectory. Ocean Eng. 2023, 268, 113390. [Google Scholar] [CrossRef]
- Sitorus, P.E.; Ko, J.H. Power extraction performance of three types of flapping hydrofoils at a Reynolds number of 1.7 E6. Renew. Energy 2019, 132, 106–118. [Google Scholar] [CrossRef]
- Xiao, Q.; Liao, W.; Yang, S.; Peng, Y. How motion trajectory affects energy extraction performance of a biomimic energy generator with an oscillating foil? Renew. Energy 2012, 37, 61–75. [Google Scholar] [CrossRef]
- Lu, K.; Xie, Y.; Zhang, D. Nonsinusoidal motion effects on energy extraction performance of a flapping foil. Renew. Energy 2014, 64, 283–293. [Google Scholar] [CrossRef]
- Deng, J.; Teng, L.; Pan, D.; Shao, X. Inertial effects of the semi-passive flapping foil on its energy extraction efficiency. Phys. Fluids 2015, 27, 053103. [Google Scholar]
- Teng, L.; Deng, J.; Pan, D.; Shao, X. Effects of non-sinusoidal pitching motion on energy extraction performance of a semi-active flapping foil. Renew. Energy 2016, 85, 810–818. [Google Scholar] [CrossRef]
- Li, W.; Wang, W.-Q.; Yan, Y.; Tian, F.-B. Effects of pitching motion profile on energy harvesting performance of a semi-active flapping foil using immersed boundary method. Ocean Eng. 2018, 163, 94–106. [Google Scholar] [CrossRef]
- Saleh, S.; Sohn, C.-H. Power Extraction Performance by a Hybrid Non-Sinusoidal Pitching Motion of an Oscillating Energy Harvester. Energies 2024, 17, 2451. [Google Scholar] [CrossRef]
- Kral, L.D. Active Flow Control Technology; ASME Fluids Engineering Technical Brief; Washington University: St. Louis, MI, USA, 2000; pp. 1–28. [Google Scholar]
- Yin, B.; Luo, H. Effect of wing inertia on hovering performance of flexible flapping wings. Phys. Fluids 2010, 22, 111902. [Google Scholar] [CrossRef]
- Le, T.Q.; Ko, J.H.; Byun, D. Morphological effect of a scallop shell on a flapping-type tidal stream generator. Bioinspiration Biomim. 2013, 8, 036009. [Google Scholar] [CrossRef]
- Zhu, B.; Huang, Y.; Zhang, Y. Energy harvesting properties of a flapping wing with an adaptive Gurney flap. Energy 2018, 152, 119–128. [Google Scholar] [CrossRef]
- Xie, Y.; Jiang, W.; Lu, K.; Zhang, D. Numerical investigation into energy extraction of flapping airfoil with Gurney flaps. Energy 2016, 109, 694–702. [Google Scholar] [CrossRef]
- Petikidis, N.; Papadakis, G. Investigation of Submergence Depth and Wave-Induced Effects on the Performance of a Fully Passive Energy Harvesting Flapping Foil Operating Beneath the Free Surface. J. Mar. Sci. Eng. 2023, 11, 1559. [Google Scholar] [CrossRef]
- Balam-Tamayo, D.; Málaga, C.; Figueroa-Espinoza, B. Numerical study of an oscillating-wing wingmill for ocean current energy harvesting: Fluid-solid-body interaction with feedback control. J. Mar. Sci. Eng. 2020, 9, 23. [Google Scholar] [CrossRef]
- Jiang, W.; Mei, Z.; Wu, F.; Han, A.; Xie, Y.; Xie, D. Effect of shroud on the energy extraction performance of oscillating foil. Energy 2022, 239, 122387. [Google Scholar] [CrossRef]
- Hou, L.; Yang, P.; Du, D.; Zhu, B. An adaptive plate at flapping wing’s trailing edge in promoting energy extraction performance. J. Mech. Sci. Technol. 2021, 35, 591–600. [Google Scholar] [CrossRef]
- Shi, F.; Sun, X. Study on Performance Enhancement of a Flapping Foil Energy Harvester Using Circulation Control. J. Fluids Eng. 2021, 143, 071207. [Google Scholar] [CrossRef]
- MahboubiDoust, A.; Ramiar, A.; Dardel, M. Numerical investigation of plasma actuated and non-actuated Gurney flaps on aerodynamic characteristics of a plunging airfoil. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 230, 1423–1437. [Google Scholar] [CrossRef]
- Lee, T.; Su, Y. Unsteady airfoil with a harmonically deflected trailing-edge flap. J. Fluids Struct. 2011, 27, 1411–1424. [Google Scholar] [CrossRef]
- Visconti, U.; Eun, W.; Sim, J.; Lee, S.; Shin, S. Design improvements and flap deflection evaluations with considering centrifugal load on active trailing edge flap. Aircr. Eng. Aerosp. Technol. 2019, 91, 10–19. [Google Scholar] [CrossRef]
- He, G.; Mo, W.; Gao, Y.; Zhang, Z.; Wang, J.; Wang, W.; Liu, P.; Ghassemi, H. Modification of effective angle of attack on hydrofoil power extraction. Ocean Eng. 2021, 240, 109919. [Google Scholar] [CrossRef]
- Alam, M.; Sohn, C.H. Enhanced Performance of Oscillating Wing Energy Harvester Using Active Controlled Flap. J. Mech. Sci. Technol. 2023, 37, 2405–2415. [Google Scholar] [CrossRef]
- Alam, M.; Sohn, C.H. Parametric analysis of an oscillating wing energy harvester with a trailing edge flap. J. Mech. Sci. Technol. 2023, 37, 3563–3573. [Google Scholar] [CrossRef]
- Alam, M.; Sohn, C.H. Enhancing the Performance of an Oscillating Wing Energy Harvester Using a Leading-Edge Flap. J. Mar. Sci. Eng. 2023, 12, 62. [Google Scholar] [CrossRef]
- Bianchini, A.; Balduzzi, F.; Di Rosa, D.; Ferrara, G. On the use of Gurney Flaps for the aerodynamic performance augmentation of Darrieus wind turbines. Energy Convers. Manag. 2019, 184, 402–415. [Google Scholar] [CrossRef]
- Bofeng, X.; Junheng, F.; Qing, L.; Chang, X.; Zhenzhou, Z.; Yue, Y. Aerodynamic performance analysis of a trailing-edge flap for wind turbines. J. Phys. Conf. Ser. 2018, 1037, 022020. [Google Scholar] [CrossRef]
- Liu, Q.; Miao, W.; Li, C.; Hao, W.; Zhu, H.; Deng, Y. Effects of trailing-edge movable flap on aerodynamic performance and noise characteristics of VAWT. Energy 2019, 189, 116271. [Google Scholar] [CrossRef]
- Liu, F.-R.; Zhang, W.-M.; Zhao, L.-C.; Zou, H.-X.; Tan, T.; Peng, Z.-K.; Meng, G. Performance enhancement of wind energy harvester utilizing wake flow induced by double upstream flat-plates. Appl. Energy 2020, 257, 114034. [Google Scholar] [CrossRef]
- Maruai, N.M.; Mat Ali, M.S.; Ismail, M.H.; Shaikh Salim, S.A.Z. Downstream flat plate as the flow-induced vibration enhancer for energy harvesting. J. Vib. Control 2018, 24, 3555–3568. [Google Scholar] [CrossRef]
- Soylak, M. Experimental investigation of aerodynamic performance of oscillating wings at low Re numbers. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 230, 1882–1902. [Google Scholar] [CrossRef]
- Usoh, C.; Young, J.; Lai, J.; Ashraf, M. Numerical analysis of a non-profiled plate for flapping wing turbines. In Proceedings of the 18th Australasian Fluid Mechanics Conference, Launceston, Australia, 3–7 December 2021. [Google Scholar]
- Wang, B.; Zhu, B.; Zhang, W. New type of motion trajectory for increasing the power extraction efficiency of flapping wing devices. Energy 2019, 189, 116072. [Google Scholar] [CrossRef]
- Ansys, Inc. ANSYS Fluent User’s Guide, Release 2021 R1; Ansys, Inc.: Canonsburg, PA, USA, 2021. [Google Scholar]
- Kinsey, T.; Dumas, G. Computational fluid dynamics analysis of a hydrokinetic turbine based on oscillating hydrofoils. J. Fluids Eng. 2012, 134, 021104. [Google Scholar] [CrossRef]




| Grid Type | No. of Moving Body Elements | No. of Stationary Body Elements | Time Steps/Cycle | (%) | (%) | |
|---|---|---|---|---|---|---|
| Coarse | 2000 | 0.891 | ||||
| Medium | 500 | 0.904 | ||||
| 2000 | 0.887 | 0.44 | 1.88 | |||
| 4000 | 0.883 | 0.45 | ||||
| Fine | 2000 | 0.886 | 0.11 |
| Wing Configuration | Wing without Any Flaps | Wing with Leading Flap | Wing with Trailing Flap | ||
|---|---|---|---|---|---|
| Flap Configuration | Wing | Wing | Leading | Wing | Trailing |
| Length percentage | 100% | 60% | 40% | 40% | 60% |
| Pitch angle | = 75° | = 95° | = 45° | = 50° | = 45° |
| Configuration Type | Wing with Leading Flap | Wing with Trailing Flap | Oscillating Flat Plate with Leading and Trailing Flaps | |||||
|---|---|---|---|---|---|---|---|---|
| Pitch angle, | 25° | 30° | 35° | 40° | 45° | 50° | ||
| 1.544 | 1.429 | 1.188 | 1.356 | 1.422 | 1.458 | 1.489 | 1.432 | |
| −0.360 | −0.251 | −0.045 | −0.188 | −0.216 | −0.239 | −0.263 | −0.246 | |
| 1.183 | 1.177 | 1.142 | 1.167 | 1.205 | 1.219 | 1.225 | 1.186 | |
| (%) | − | − | −3.46 | −1.35 | 1.85 | 3.04 | 3.55 | 0.25 |
| η | 43.01 | 43.49 | 42.23 | 43.15 | 44.56 | 45.08 | 45.30 | 43.86 |
| (%) | − | − | −1.82 | 0.32 | 3.59 | 4.79 | 5.32 | 1.95 |
| Configuration Type | Wing with Leading Flap | Wing with Trailing Flap | Oscillating Flat Plate with Leading and Trailing Flaps | |||||
|---|---|---|---|---|---|---|---|---|
| Pitch angle, | 10° | 15° | 20° | 25° | 30° | 35° | ||
| 1.544 | 1.429 | 1.423 | 1.450 | 1.470 | 1.483 | 1.489 | 1.473 | |
| −0.360 | −0.251 | −0.234 | −0.248 | −0.257 | −0.261 | 0.263 | −0.258 | |
| 1.183 | 1.177 | 1.189 | 1.201 | 1.213 | 1.221 | 1.225 | 1.215 | |
| (%) | − | − | 0.50 | 1.52 | 2.53 | 3.21 | 3.55 | 2.70 |
| η | 43.01 | 43.49 | 44.29 | 44.64 | 44.99 | 45.22 | 45.30 | 44.86 |
| (%) | 2.97 | 3.78 | 4.58 | 5.12 | 5.32 | 4.29 | ||
| Leading Flap Length | Wing Length | Trailing Flap Length | η | |||
|---|---|---|---|---|---|---|
| 35% | 55% | 10% | 1.469 | −0.279 | 1.189 | 44.23 |
| 30% | 55% | 15% | 1.489 | −0.263 | 1.225 | 45.30 |
| 25% | 55% | 20% | 1.456 | −0.324 | 1.132 | 41.58 |
| 40% | 50% | 10% | 1.422 | −0.288 | 1.133 | 42.15 |
| 35% | 50% | 15% | 1.514 | −0.307 | 1.207 | 44.63 |
| 30% | 50% | 20% | 1.495 | −0.272 | 1.222 | 44.89 |
| Leading Flap Length | Wing Length | Trailing Flap Length | η | |||
|---|---|---|---|---|---|---|
| 25% | 60% | 15% | 1.479 | −0.307 | 1.172 | 43.32 |
| 30% | 55% | 15% | 1.432 | −0.246 | 1.186 | 43.86 |
| 30% | 60% | 10% | 1.437 | −0.242 | 1.194 | 44.42 |
| 35% | 50% | 15% | 1.369 | −0.224 | 1.144 | 42.30 |
| 30% | 50% | 20% | 1.532 | −0.296 | 1.235 | 45.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saleh, S.; Sohn, C.-H. Numerically Investigating the Energy-Harvesting Performance of an Oscillating Flat Plate with Leading and Trailing Flaps. Energies 2024, 17, 3010. https://doi.org/10.3390/en17123010
Saleh S, Sohn C-H. Numerically Investigating the Energy-Harvesting Performance of an Oscillating Flat Plate with Leading and Trailing Flaps. Energies. 2024; 17(12):3010. https://doi.org/10.3390/en17123010
Chicago/Turabian StyleSaleh, Suleiman, and Chang-Hyun Sohn. 2024. "Numerically Investigating the Energy-Harvesting Performance of an Oscillating Flat Plate with Leading and Trailing Flaps" Energies 17, no. 12: 3010. https://doi.org/10.3390/en17123010
APA StyleSaleh, S., & Sohn, C.-H. (2024). Numerically Investigating the Energy-Harvesting Performance of an Oscillating Flat Plate with Leading and Trailing Flaps. Energies, 17(12), 3010. https://doi.org/10.3390/en17123010






