A Multiscale Hybrid Wind Power Prediction Model Based on Least Squares Support Vector Regression–Regularized Extreme Learning Machine–Multi-Head Attention–Bidirectional Gated Recurrent Unit and Data Decomposition
Abstract
1. Introduction
- (1)
- This paper proposed a multiscale wind power prediction hybrid model combining data decomposition, LSSVR, RELM, and MHA-BiGRU.
- (2)
- This paper introduced the ICEEMDAN and PE methods to process the original wind energy series. These methods can effectively address mode mixing and residual noise, thereby better handling the nonlinear and non-stationary characteristics of wind power series.
- (3)
- This paper introduced the multi-head attention mechanism in the prediction of low-frequency signals, utilizing its strong ability to capture inter-data correlations. Combined with the BiGRU model, this mechanism avoids information loss.
- (4)
- This paper introduced the DBO optimization algorithm to optimize four parameters including the learning rate, the number of BiGRU neurons, the number of heads in multi-head attention, and the number of filters and regularization parameters. This addresses the limitations and arbitrariness of manual tuning when the MHA-BiGRU model has too many parameters.
- (5)
- This paper considered the characteristics of information in different frequency bands, used different applicable models, and summed up the results to achieve multiscale hybrid prediction. This overcomes the limitation of insufficient prediction accuracy of a single model.
2. Methods
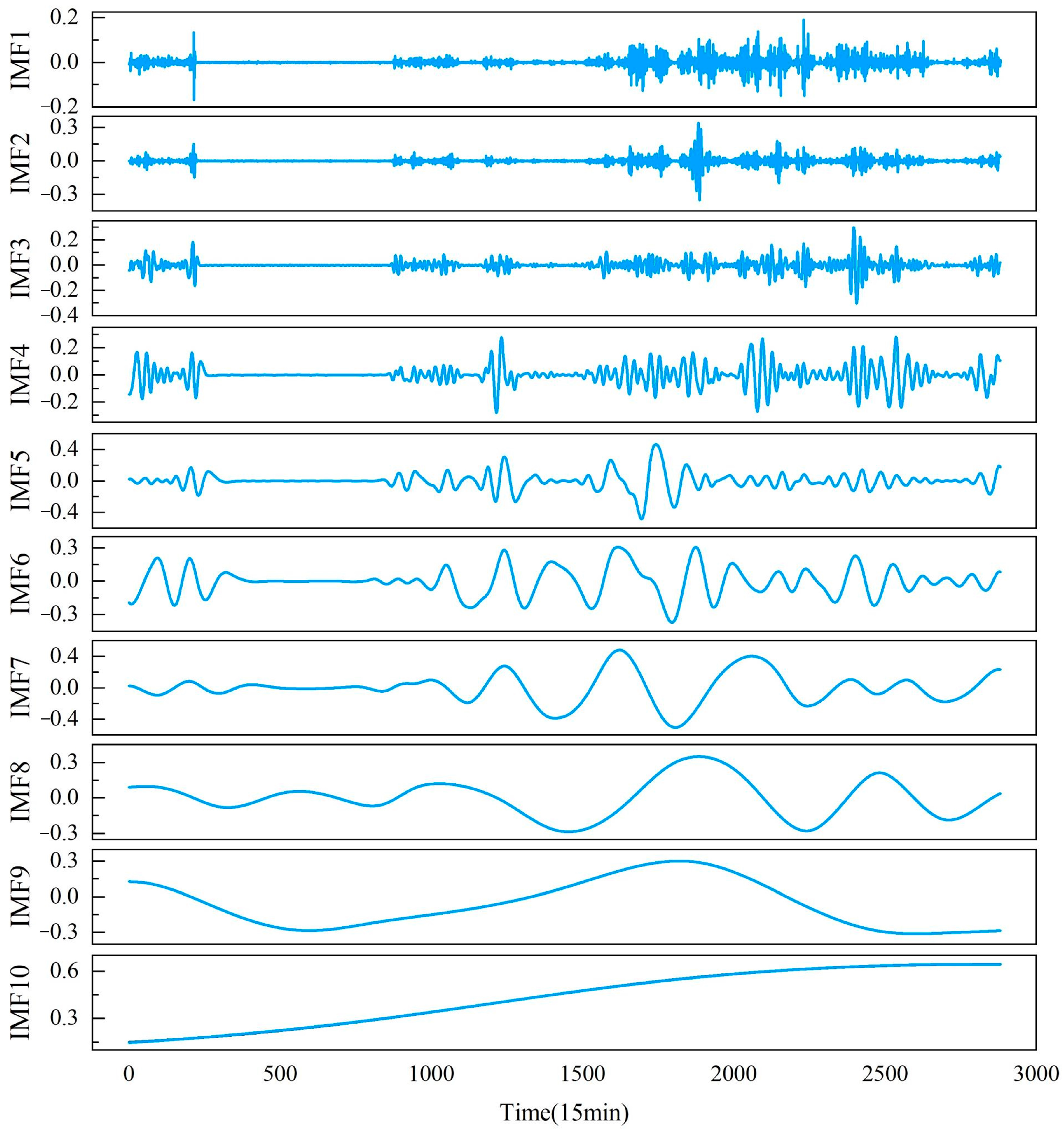
2.1. Intrinsic Combined Ensemble Empirical Mode Decomposition with Adaptive Noise
- Based on the original wind power signal s, construct a new sequence by adding i groups of white noise to s, resulting in the first group of residues .In Equation (1), represents the k-th mode component generated by EMD decomposition, represents the local mean of the signal generated by the EMD algorithm, and represents the overall mean.
- Calculate the first mode component iteratively to obtain the k-th group of residues and mode component .In Equation (2), can be expressed as .
- Repeat step 2 until the calculation is complete to obtain all wind power sequence mode components and the final residue.
2.2. Permutation Entroy
- Consider a wind power generation sequence , where i represent the number one of the wind power sequence.
- Perform phase space reconstruction on the time series, resulting in a reconstruction matrix Z with a given dimension m and time delay .In Equation (4), .
- Sort the elements of in ascending order and record the sequence of elements in each row of the reconstruction matrix. Calculate the probability of occurrence for each element sequence to obtain .
- Define the permutation entropy of wind power sequence X as:In Equation (5), represents the probability of each element size relationship permutation in the reconstruction matrix Z, m is the given dimension, k is the number of subsequences, and q is the total number of elements.
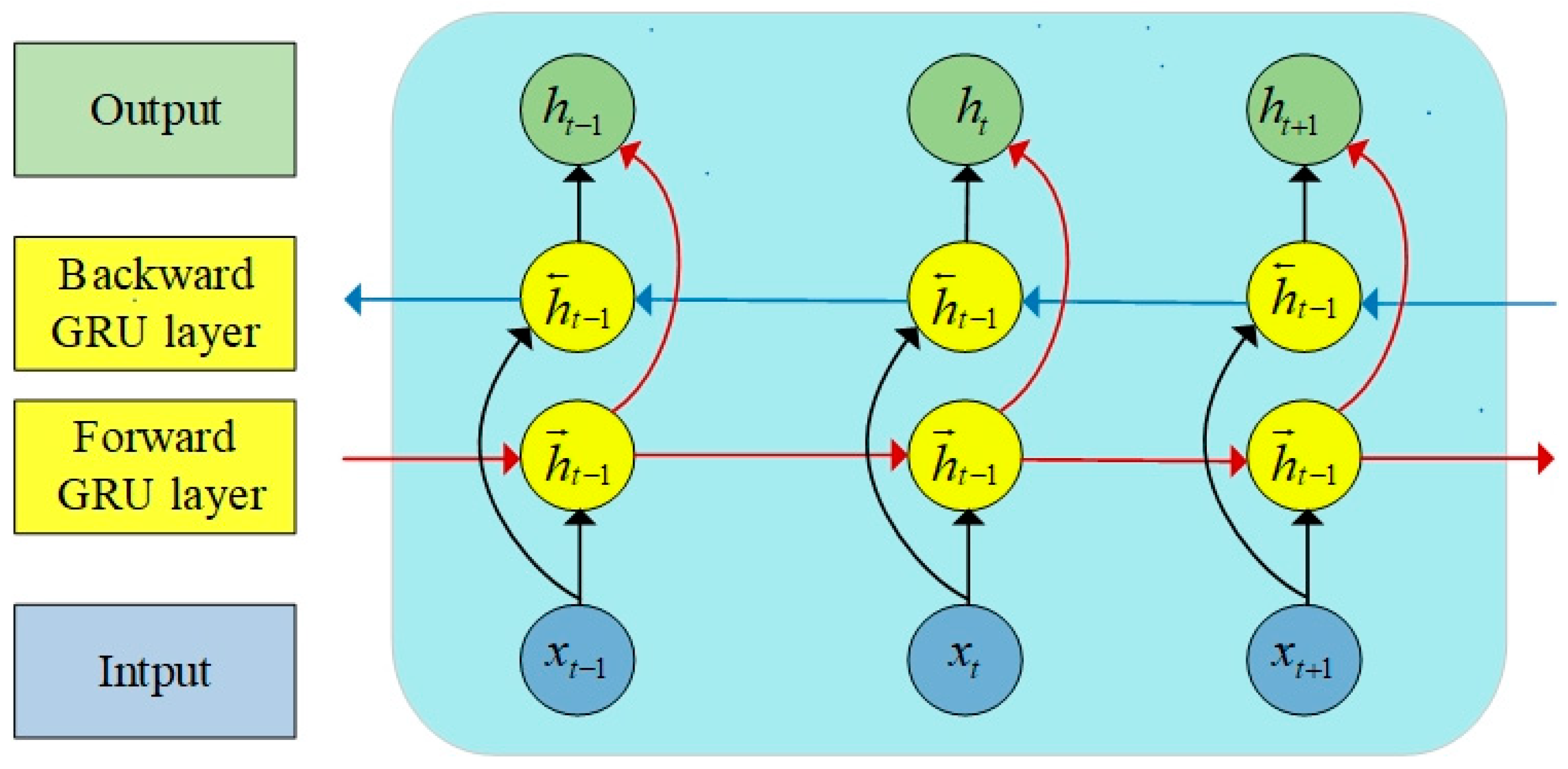
2.3. Bidirectional Gated Recurrent Unit
2.4. Multi-Head Attention
2.5. MHA-Bidirectional Gated Recurrent Unit
2.6. DBO-MHA-Bidirectional Gated Recurrent Unit
2.7. Least Squares Support Vector Regression
2.8. Regularized Extreme Learning Machine
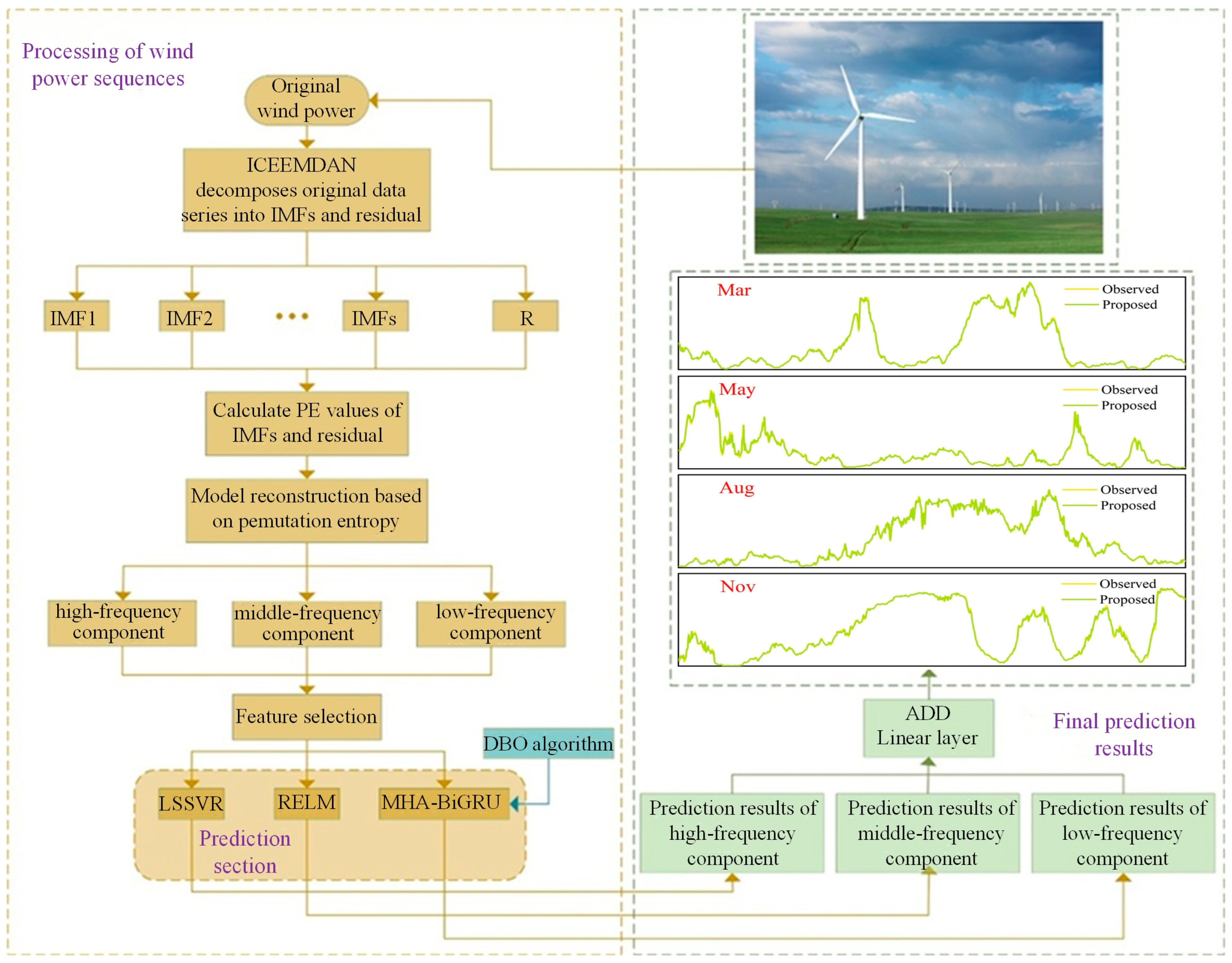
2.9. Composition of the Proposed Model
3. Research Study
3.1. Data Description
3.2. Performance Metrics
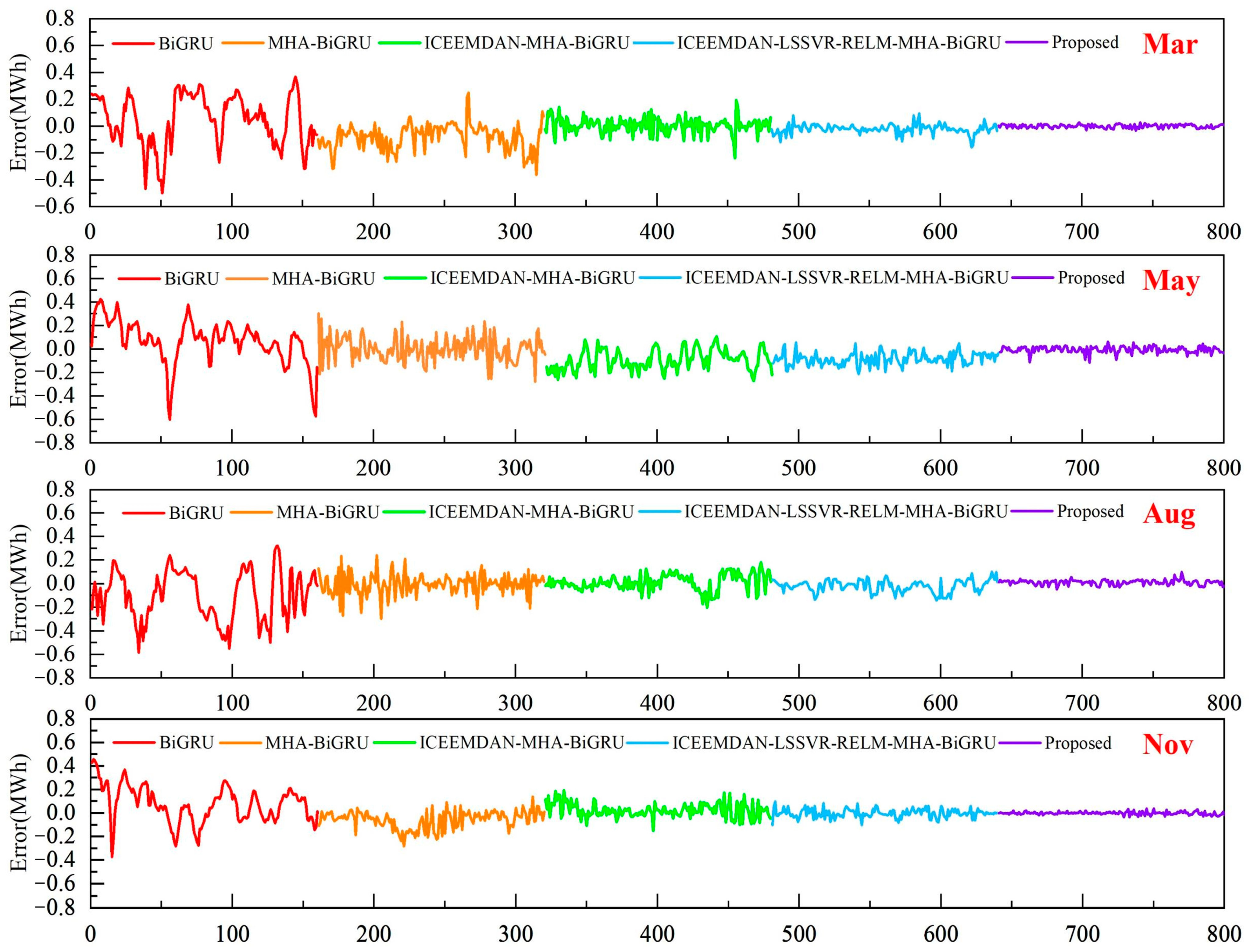
4. Comparative Results
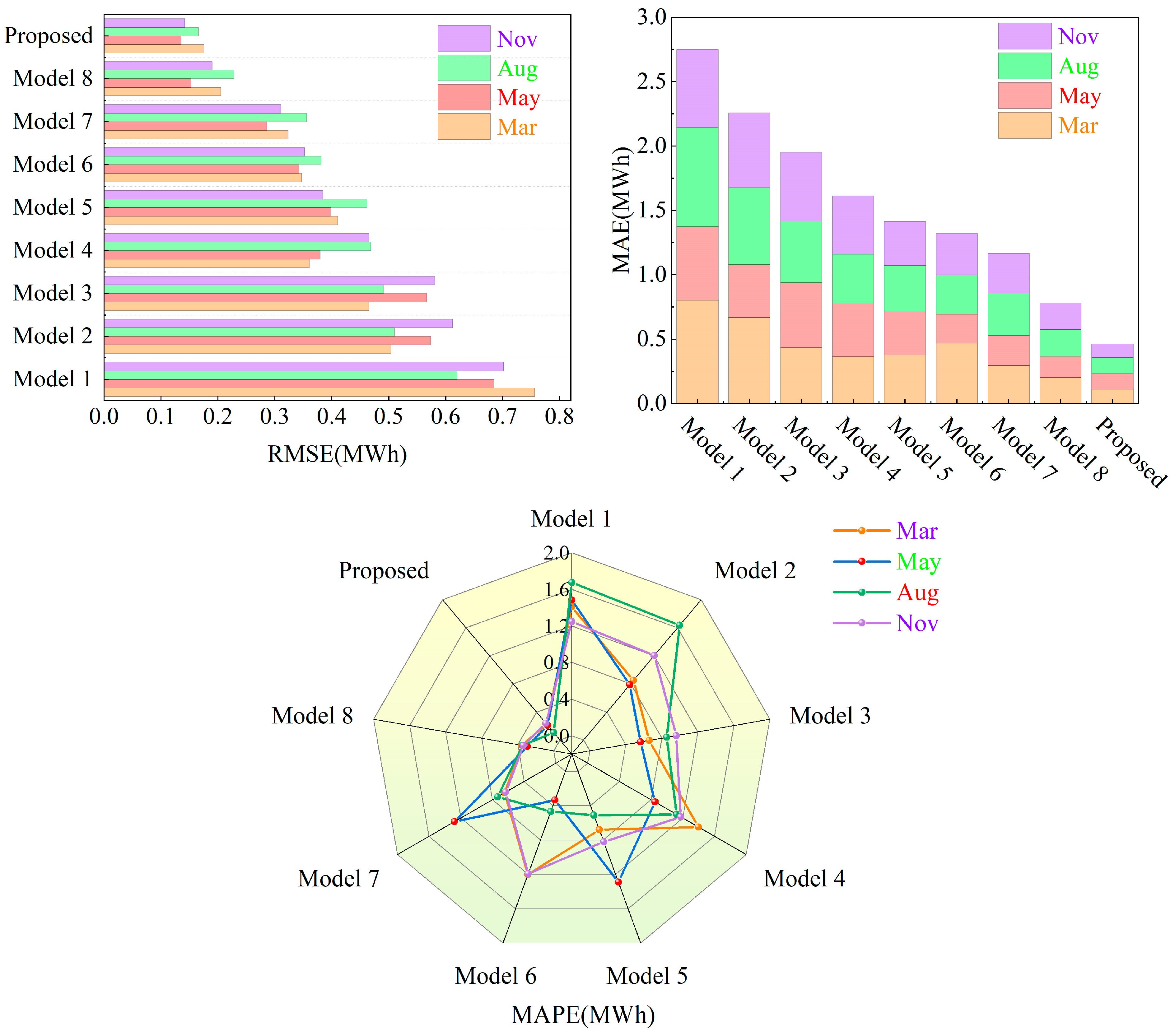
- The comparison of the LSSVR, RELM, and BiGRU models suggests that multiscale hybrid models outperform single-scale models in wind power sequence prediction.
- The evaluation of the BiGRU and MHA-BiGRU models reveals a notable decrease of 18.72% in RMSE and 7.08% in MAE for the May forecast. Additionally, for the March forecasts, the RMSE values decrease by approximately 10%, indicating that the incorporation of multi-head attention mechanisms enhances predictive accuracy.
- The inclusion of decomposition algorithms generally enhances predictive performance in wind power prediction compared with single models. For example, in the August metrics, the LSSVR, RELM, and BiGRU models incorporating the ICEEMDAN decomposition algorithm exhibit reductions of 25.57%, 25.29%, and 27.63% in RMSE values, respectively, along with approximately 20% decreases in the other metrics. This underscores the effectiveness of models incorporating decomposition algorithms in improving prediction accuracy.
- The comparison between Model 8 and the single-scale models combined with decomposition algorithms indicates that hybrid algorithms generally exhibit superior predictive performance. For instance, in the radar chart of MAPE values in Figure 7, the proposed model consistently exhibits the lowest values along its axes. Furthermore, in terms of RMSE values for March, Model 8 demonstrates a 57.20% reduction compared with Model 5. This underscores the advantage of multiscale hybrid algorithms in achieving smaller errors and higher predictive accuracy.
- The evaluation of Model 8 against the proposed model highlights improvements in predictive performance with the introduction of DBO optimization algorithms. For instance, in the November forecast, there are reductions of 25.59%, 46.40%, and 28.96% in the RMSE, MAE, and MAPE values, respectively. This indicates that the incorporation of DBO optimization algorithms enhances predictive performance, rendering the model proposed in this study more suitable for wind power sequence prediction.
5. Discussion
- This study relies solely on historical wind power data without considering additional factors such as geographical conditions and turbine statuses, which can significantly influence wind power prediction accuracy. Thus, future research could explore integrating multiple factors to enable multi-step prediction.
- The dataset used in this study is limited to a single wind farm, which may restrict the model’s ability to generalize across different environments. Future endeavors should aim to validate the proposed model using data from multiple wind farms to enhance its robustness and applicability.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Academic name |
| LSSVR | Least Squares Support Vector Regression |
| RELM | Regularized Extreme Learning Machine |
| BiGRU | Bidirectional Gated Recurrent Unit |
| MHA | multi-head attention |
| ICEEMDAN | Improved Complementary Ensemble Empirical Mode Decomposition with Adaptive Noise |
| DBO | Dung Beetle Optimizer optimization algorithm |
| PE | permutation entropy |
| LSTM | Long Short-Term Memory |
References
- Global Wind Energy Council. 2022 Global Wind Report; Global Wind Energy Council (GWEC): Brussels, Belgium, 2023; pp. 6–7. [Google Scholar]
- Yuan, X.; Chen, C.; Yuan, Y.; Huang, Y.; Tan, Q. Short-term wind power prediction based on LSSVM–GSA model. Energy Convers. 2015, 101, 393–401. [Google Scholar] [CrossRef]
- Hu, S.; Xiang, Y.; Zhang, H.; Xie, S.; Li, J.; Gu, C.; Sun, W.; Liu, J. Hybrid forecasting method for wind power integrating spatial correlation and corrected numerical weather prediction. Appl. Energy 2021, 293, 116951. [Google Scholar] [CrossRef]
- Ye, L.; Dai, B.; Li, Z.; Pei, M.; Zhao, Y.; Lu, P. An ensemble method for short-term wind power prediction considering error correction strategy. Appl. Energy 2022, 322, 119475. [Google Scholar] [CrossRef]
- Wang, J.; Hu, J.; Ma, K.; Zhang, Y. A self-adaptive hybrid approach for wind speed forecasting. Renew. Energy 2015, 78, 374–385. [Google Scholar] [CrossRef]
- Xiong, B.; Meng, X.; Xiong, G.; Ma, H.; Lou, L.; Wang, Z. Multi-branch wind power prediction based on optimized variational mode decomposition. Energy 2022, 8, 11181–11191. [Google Scholar]
- Costa, A.; Crespo, A.; Navarro, J.; Lizcano, G.; Madsen, H.; Feitosa, E. A review on the young history of the wind power short-term prediction. Renew. Sustain. Energy 2008, 12, 1725–1744. [Google Scholar] [CrossRef]
- Wang, H.; Han, S.; Liu, Y.; Yan, J.; Li, L. Sequence transfer correction algorithm for numerical weather prediction wind speed and its application in a wind power forecasting system. Appl. Energy 2019, 237, 1–10. [Google Scholar] [CrossRef]
- Liang, T.; Zhao, Q.; Lv, Q.; Sun, H. A novel wind speed prediction strategy based on Bi-LSTM, MOOFADA and transfer learning for centralized control centers. Energy 2021, 230, 120904. [Google Scholar] [CrossRef]
- Erdem, E.; Shi, J. ARMA based approaches for forecasting the tuple of wind speed and direction. Energy 2011, 88, 1405–1414. [Google Scholar] [CrossRef]
- Valipour, M.; Banihabib, M.; Behbahani, S. Comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir. J. Hydrol 2013, 476, 433–441. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machines; Springer: Berlin/Heidelberg, Germany, 2015; pp. 67–80. [Google Scholar]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the Conference Extreme Learning Machine: A New Learning Scheme of Feedforward Neural Networks, Budapest, Hungary, 25–29 July 2004; Volume 2, pp. 985–990. [Google Scholar]
- Li, C.; Tang, G.; Xue, X.; Saeed, A.; Hu, X. Short-term wind speed interval prediction based on ensemble GRU Model. IEEE Trans. Sustain. Energy 2020, 11, 1370–1380. [Google Scholar] [CrossRef]
- Wang, X.; Wang, C.; Li, Q. Short-term wind power prediction using GA-ELM. Open Electr. Electron. Eng. J. 2017, 11, 48–56. [Google Scholar] [CrossRef]
- Zhai, X.; Ma, L. Medium and long-term wind power prediction based on artificial fish swarm algorithm combined with extreme learning machine. Int. Core J. Eng. 2019, 5, 265–272. [Google Scholar]
- Tan, L.; Han, J.; Zhang, H. Ultra-short-term wind power prediction by salp swarm algorithm-based optimizing extreme learning machine. IEEE Access 2020, 8, 44470–44484. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Multi-Sequence LSTM-RNN Deep Learning and Metaheuristics for Electric Load Forecasting. Energies 2020, 13, 391. [Google Scholar] [CrossRef]
- Gundu, V.; Simon, S.P. PSO–LSTM for short term forecast of heterogeneous time series electricity price signals. J. Ambient. Intell. Hum. Comput. 2021, 12, 2375–2385. [Google Scholar] [CrossRef]
- Meng, Y.; Chang, C.; Huo, J.; Zhang, Y.; Mohammed Al-Neshmi, H.M.; Xu, J.; Xie, T. Research on Ultra-Short-Term Prediction Model ofWind Power Based on Attention Mechanism and CNN-BiGRU Combined. Front. Energy Res. 2022, 10, 920835. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Chen, X.; Zeng, X.; Kong, Y.; Sun, S.; Guo, Y.; Liu, Y. Short-term load forecasting for industrial customers based on TCN-LightGBM. IEEE Trans. Power Syst. 2021, 36, 1984–1997. [Google Scholar] [CrossRef]
- Chi, D.; Yang, C. Wind power prediction based on WT-BiGRU-attention-TCN model. Front. Energy Res. 2023, 11, 1156007. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Sun, D.; Jin, K.; Gu, Y. Short-Term Wind Power Forecasting Based on VMD and a Hybrid SSA-TCN-BiGRU Network. Appl. Sci. 2023, 13, 9888. [Google Scholar] [CrossRef]
- Gao, X.; Li, X.; Zhao, B.; Ji, W.; Jing, X.; He, Y. Short-term Electricity Load Forecasting Model based on EMD-GRU with Feature Selection. Energies 2019, 12, 1140. [Google Scholar] [CrossRef]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E.; Flandrin, P. Noise-assisted EMD methods in action. Adv. Adapt. Data Anal. 2012, 4, 1250025. [Google Scholar] [CrossRef]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved complete ensemble EMD:A suitable tool for biomedical signal processing. Biomed. Signal Process. Control 2014, 14, 19–29. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2003, 79, 7305–7336. [Google Scholar] [CrossRef]
- Xiong, J.; Peng, T.; Tao, Z.; Zhang, C.; Song, S.; Nazir, M.S. A dual-scale deep learning model based on ELM-BiLSTM and improved reptile search algorithm for wind power prediction. Energy 2022, 266, 126419. [Google Scholar] [CrossRef]


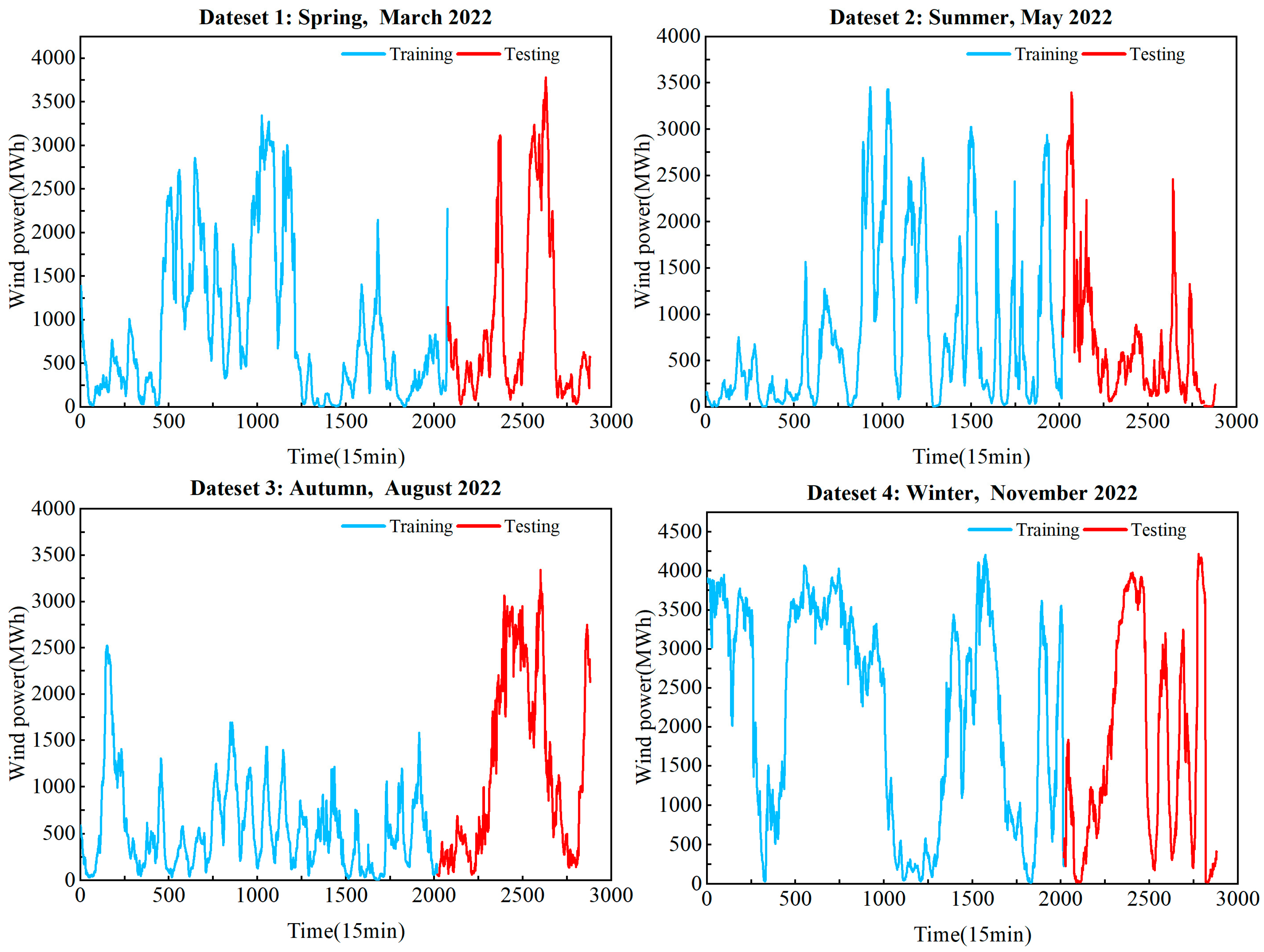
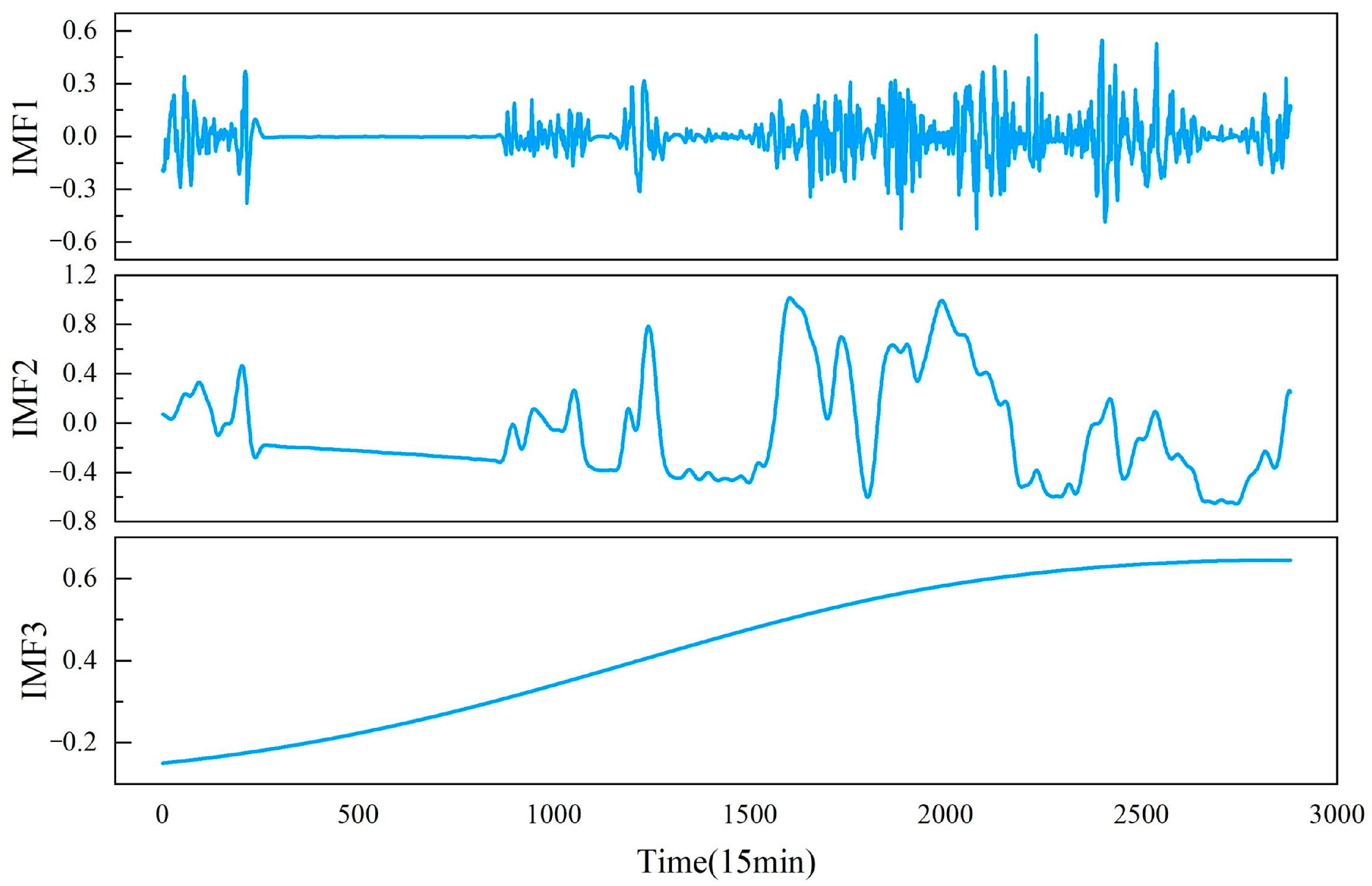

| Months | Dataset | Data Length | Max | Min | Mean | Std Dev |
|---|---|---|---|---|---|---|
| March | All (MWh) | 2880 | 3780.86 | 1.43 | 920.67 | 911.52 |
| Training (MWh) | 2016 | 3780.86 | 16.51 | 1146.53 | 976.85 | |
| Testing (MWh) | 864 | 2271.29 | 1.43 | 393.69 | 382.49 | |
| May | All (MWh) | 2880 | 3483.90 | 0.21 | 862.15 | 918.57 |
| Training (MWh) | 2016 | 3455.84 | 0.21 | 784.92 | 869.87 | |
| Testing (MWh) | 864 | 3483.90 | 2.18 | 1042.35 | 1000.30 | |
| August | All (MWh) | 2880 | 2751.17 | 2.53 | 580.44 | 482.30 |
| Training (MWh) | 2016 | 2523.70 | 2.53 | 543.60 | 457.46 | |
| Testing (MWh) | 864 | 2751.17 | 7.70 | 666.39 | 525.85 | |
| November | All (MWh) | 2880 | 4206.60 | 6.31 | 2082.61 | 1361.31 |
| Training (MWh) | 2016 | 4206.60 | 18.08 | 2229.31 | 1345.26 | |
| Testing (MWh) | 864 | 3810.65 | 6.31 | 1740.32 | 1336.83 |
| Component | PE |
|---|---|
| IMF 1 | 0.9936 |
| IMF 2 | 0.8908 |
| IMF 3 | 0.7174 |
| IMF 4 | 0.5798 |
| IMF 5 | 0.4913 |
| IMF 6 | 0.4424 |
| IMF 7 | 0.4135 |
| IMF 8 | 0.3999 |
| IMF 9 | 0.3911 |
| IMF 10 | 0.0451 |
| Name | Model |
|---|---|
| Model 1 | LSSVR |
| Model 2 | RELM |
| Model 3 | BiGRU |
| Model 4 | MHA-BiGRU |
| Model 5 | ICEEMDAN-LSSVR |
| Model 6 | ICEEMDAN-RELM |
| Model 7 | ICEEMDAN-MHA-BiGRU |
| Model 8 | ICEEMDAN-LSSVR-RELM-MHA-BiGRU |
| Proposed | ICEEMDAN-LSSVR-RELM-DBO-MHA-BiGRU |
| Dataset | Models | RMSE | MAE | MAPE |
|---|---|---|---|---|
| March | Model 1 | 0.7563 | 0.8021 | 1.4089 |
| Model 2 | 0.5039 | 0.6671 | 0.8476 | |
| Model 3 | 0.4657 | 0.4332 | 0.6599 | |
| Model 4 | 0.3605 | 0.3624 | 1.3988 | |
| Model 5 | 0.4105 | 0.3766 | 0.6821 | |
| Model 6 | 0.4710 | 0.5691 | 1.2042 | |
| Model 7 | 0.3933 | 0.2968 | 0.6470 | |
| Model 8 | 0.2053 | 0.2012 | 0.3535 | |
| Proposed | 0.1757 | 0.1133 | 0.2297 | |
| May | Model 1 | 0.6852 | 0.5711 | 1.4820 |
| Model 2 | 0.5743 | 0.6113 | 0.7851 | |
| Model 3 | 0.5670 | 0.5053 | 0.5627 | |
| Model 4 | 0.3798 | 0.4182 | 0.8501 | |
| Model 5 | 0.3983 | 0.3398 | 1.2908 | |
| Model 6 | 0.3422 | 0.2243 | 0.3348 | |
| Model 7 | 0.2862 | 0.2331 | 1.2788 | |
| Model 8 | 0.1528 | 0.1662 | 0.2924 | |
| Proposed | 0.1354 | 0.1178 | 0.2102 | |
| August | Model 1 | 0.6203 | 0.7706 | 1.675 |
| Model 2 | 0.5104 | 0.5963 | 1.6358 | |
| Model 3 | 0.4915 | 0.4784 | 0.85306 | |
| Model 4 | 0.4688 | 0.3796 | 1.1223 | |
| Model 5 | 0.4617 | 0.3554 | 0.5117 | |
| Model 6 | 0.3813 | 0.3048 | 0.4701 | |
| Model 7 | 0.3557 | 0.3291 | 0.7367 | |
| Model 8 | 0.2285 | 0.2093 | 0.3467 | |
| Proposed | 0.1661 | 0.1243 | 0.1069 | |
| November | Model 1 | 0.7021 | 0.6053 | 1.2463 |
| Model 2 | 0.6120 | 0.5825 | 1.2038 | |
| Model 3 | 0.5811 | 0.5351 | 0.9602 | |
| Model 4 | 0.4655 | 0.4528 | 1.1745 | |
| Model 5 | 0.3842 | 0.3413 | 0.8221 | |
| Model 6 | 0.3522 | 0.3227 | 1.1934 | |
| Model 7 | 0.3106 | 0.3067 | 0.6332 | |
| Model 8 | 0.1903 | 0.2026 | 0.3374 | |
| Proposed | 0.1416 | 0.1086 | 0.2397 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zhang, S. A Multiscale Hybrid Wind Power Prediction Model Based on Least Squares Support Vector Regression–Regularized Extreme Learning Machine–Multi-Head Attention–Bidirectional Gated Recurrent Unit and Data Decomposition. Energies 2024, 17, 2923. https://doi.org/10.3390/en17122923
Sun Y, Zhang S. A Multiscale Hybrid Wind Power Prediction Model Based on Least Squares Support Vector Regression–Regularized Extreme Learning Machine–Multi-Head Attention–Bidirectional Gated Recurrent Unit and Data Decomposition. Energies. 2024; 17(12):2923. https://doi.org/10.3390/en17122923
Chicago/Turabian StyleSun, Yuan, and Shiyang Zhang. 2024. "A Multiscale Hybrid Wind Power Prediction Model Based on Least Squares Support Vector Regression–Regularized Extreme Learning Machine–Multi-Head Attention–Bidirectional Gated Recurrent Unit and Data Decomposition" Energies 17, no. 12: 2923. https://doi.org/10.3390/en17122923
APA StyleSun, Y., & Zhang, S. (2024). A Multiscale Hybrid Wind Power Prediction Model Based on Least Squares Support Vector Regression–Regularized Extreme Learning Machine–Multi-Head Attention–Bidirectional Gated Recurrent Unit and Data Decomposition. Energies, 17(12), 2923. https://doi.org/10.3390/en17122923





