Thermal Evaluation of the Initial Concept 3.X Vehicle at Mach 7 †
Abstract
1. Introduction
2. Methodology
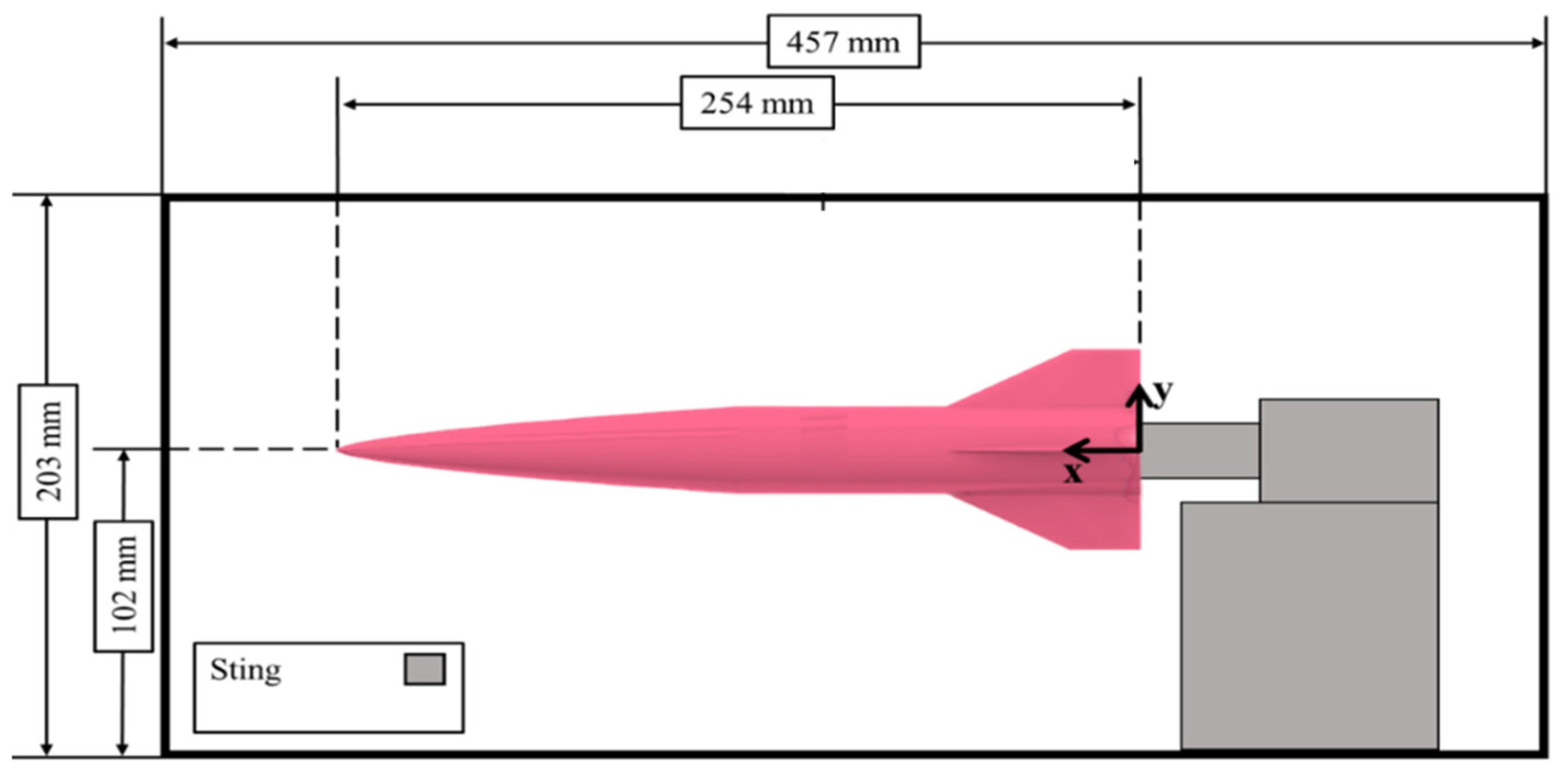
2.1. Wind Tunnel
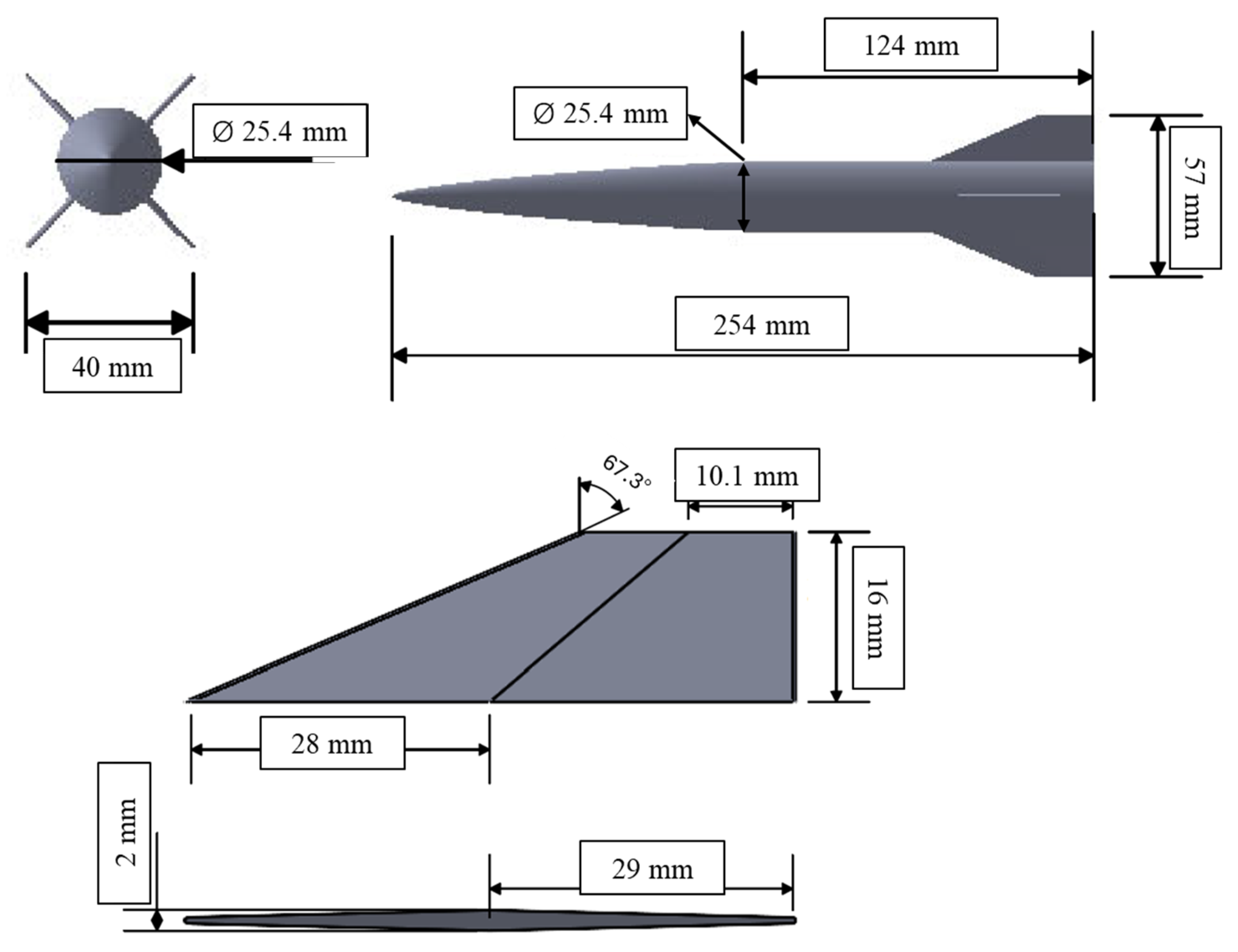
2.2. Model Geometry
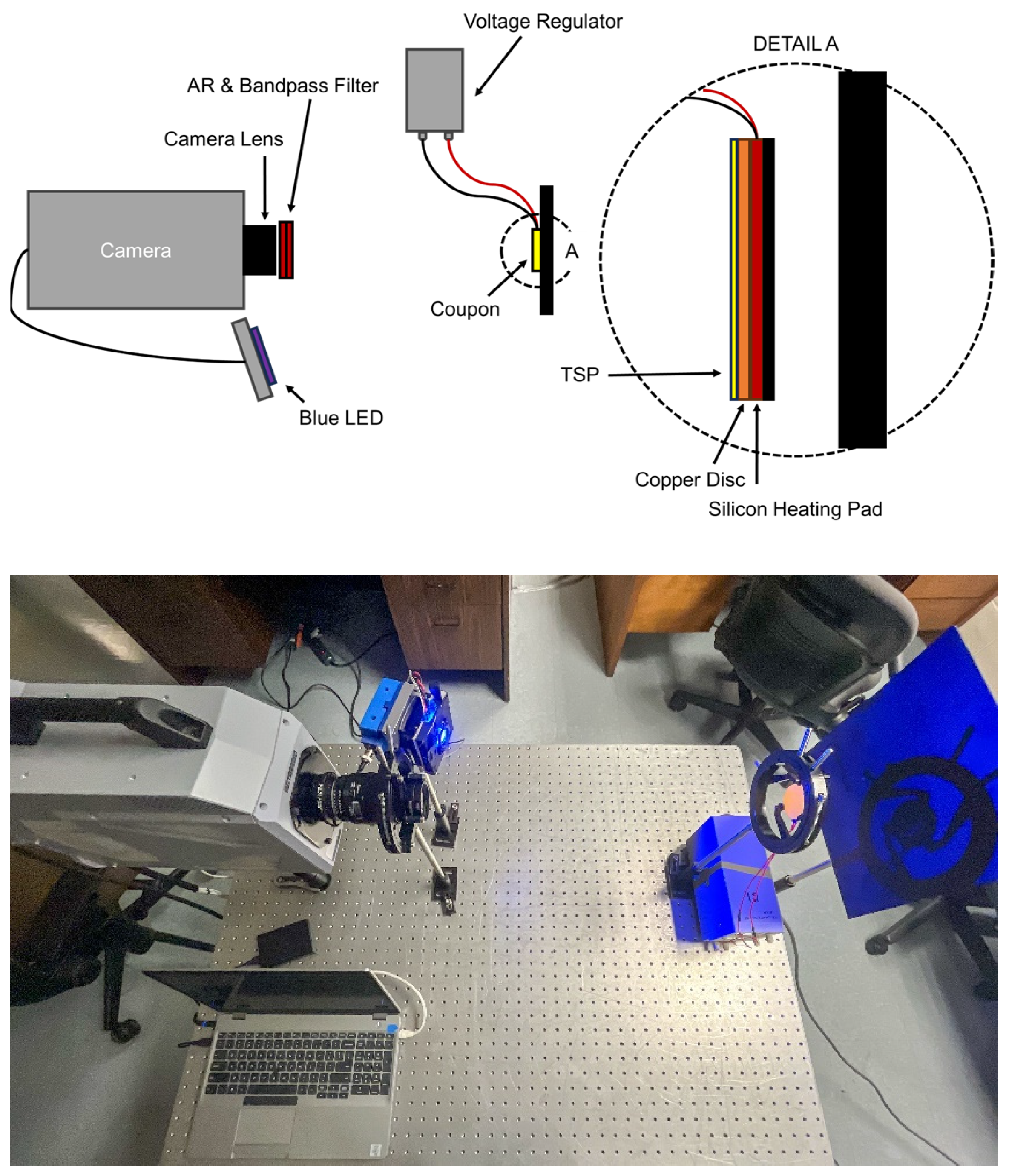
2.3. Fast-TSP Preparation and Application
2.4. Experimental Setup and Data Processing
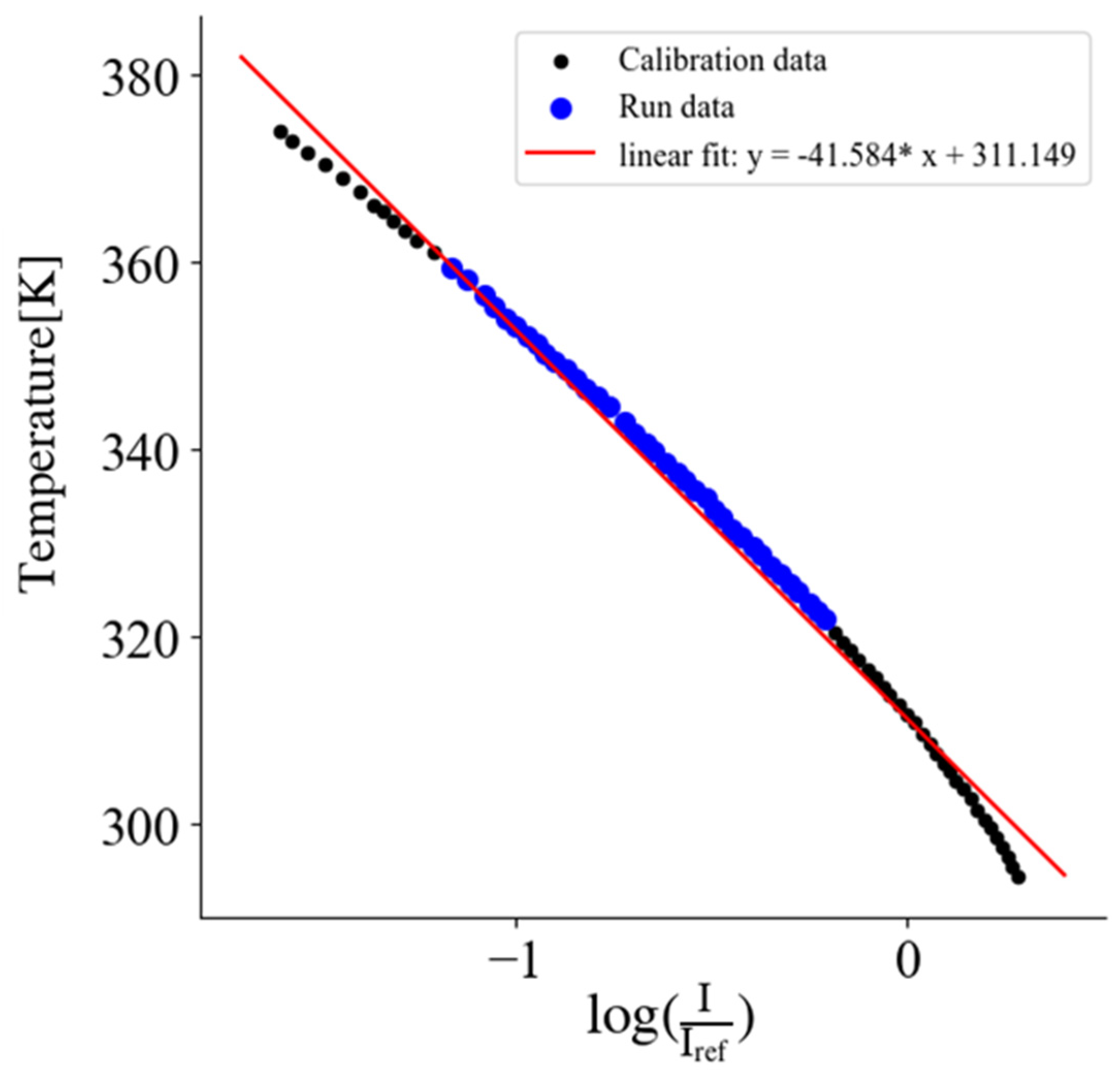
3. Static Calibration
4. Surface Temperature Measurements
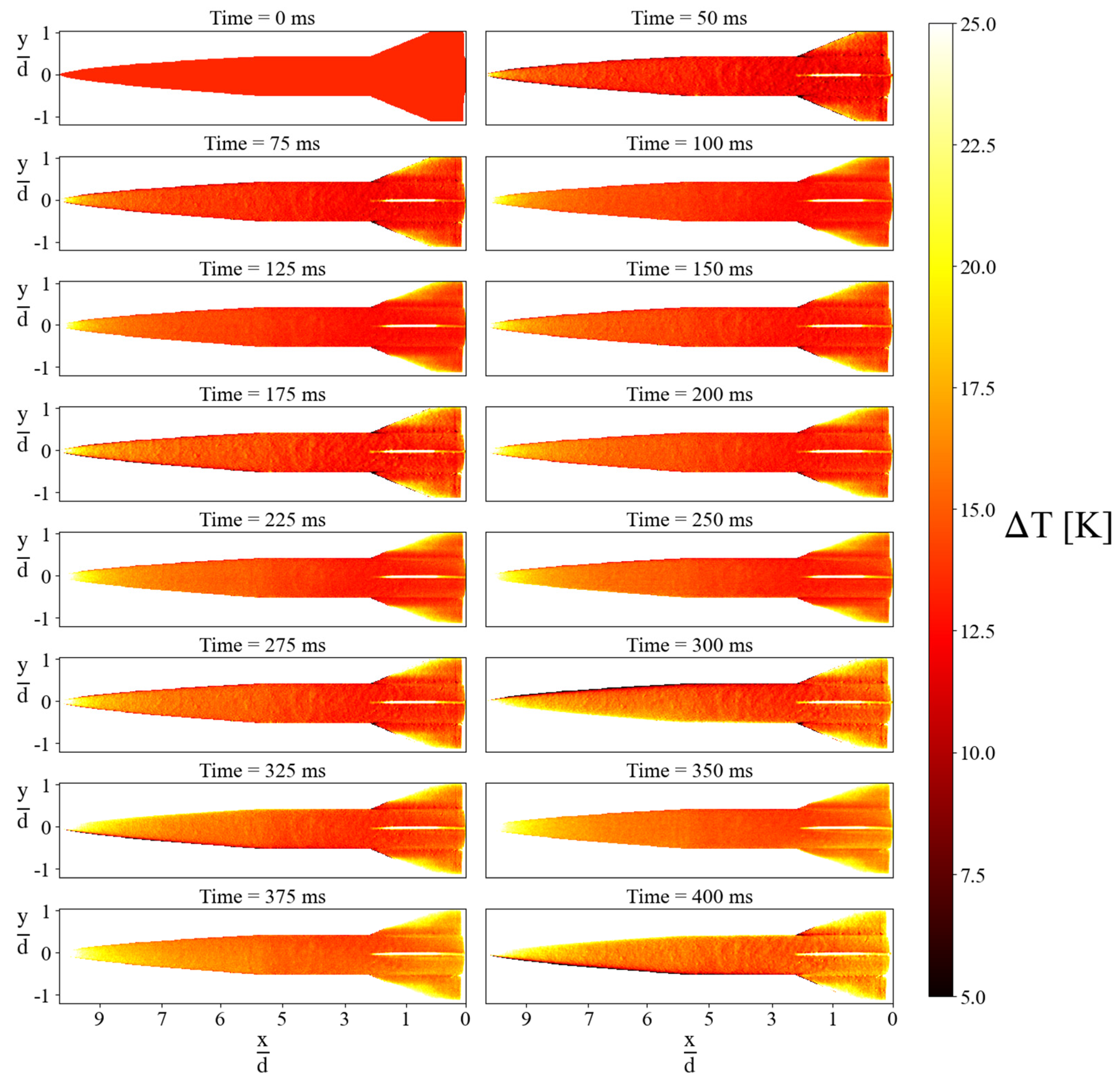
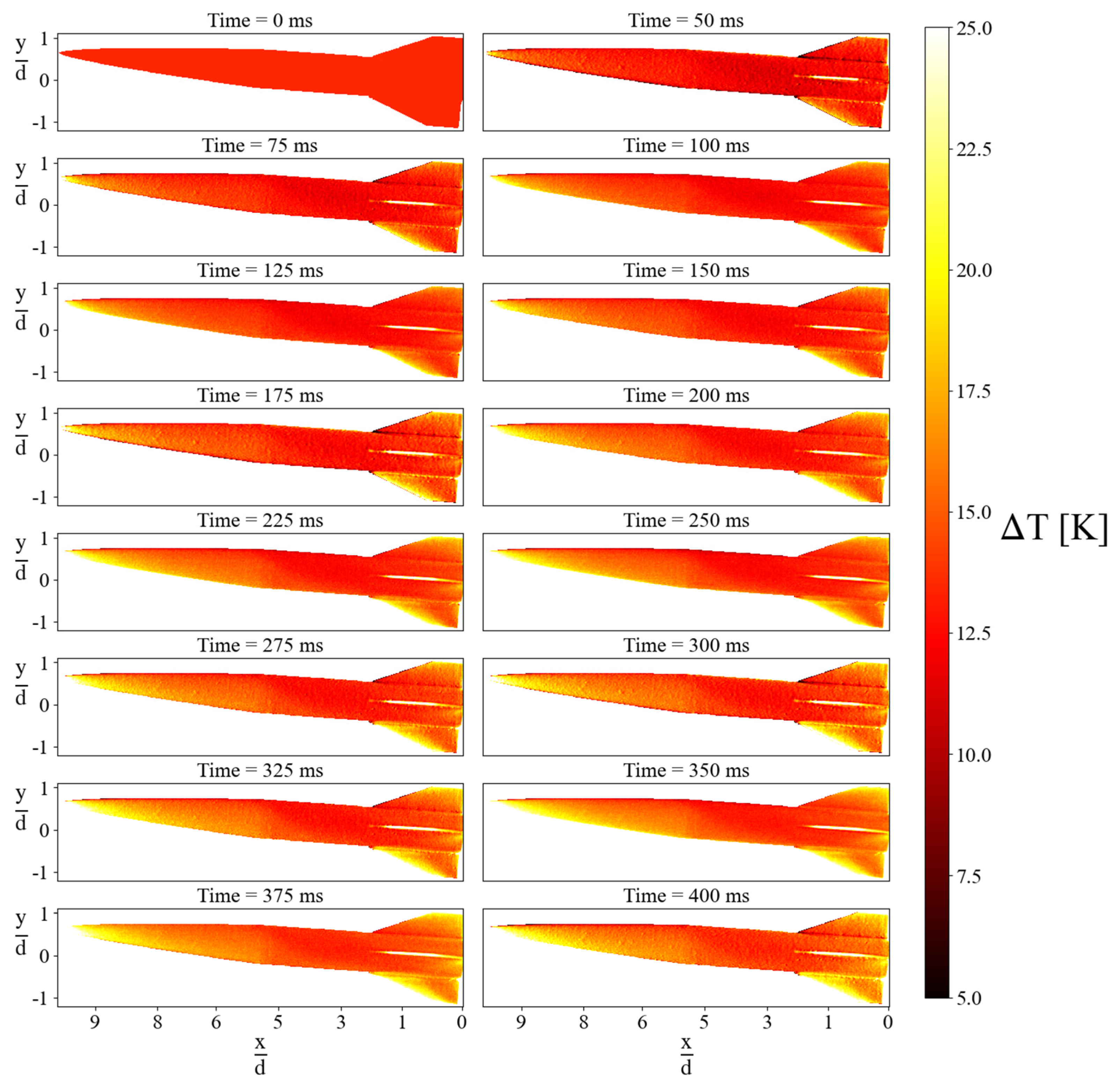
4.1. Instantaneous Temperature Fields
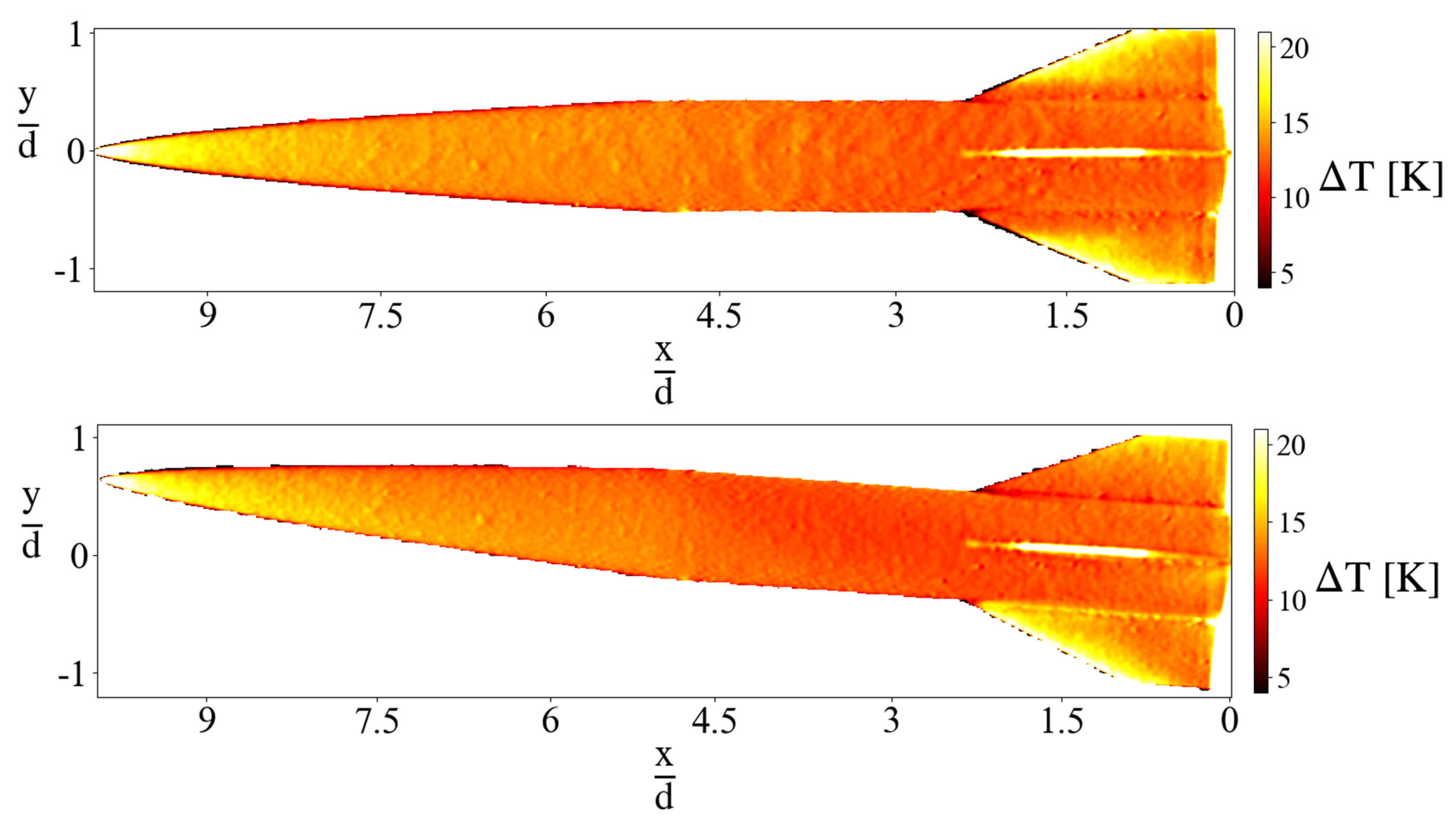
4.2. Mean Surface Temperature
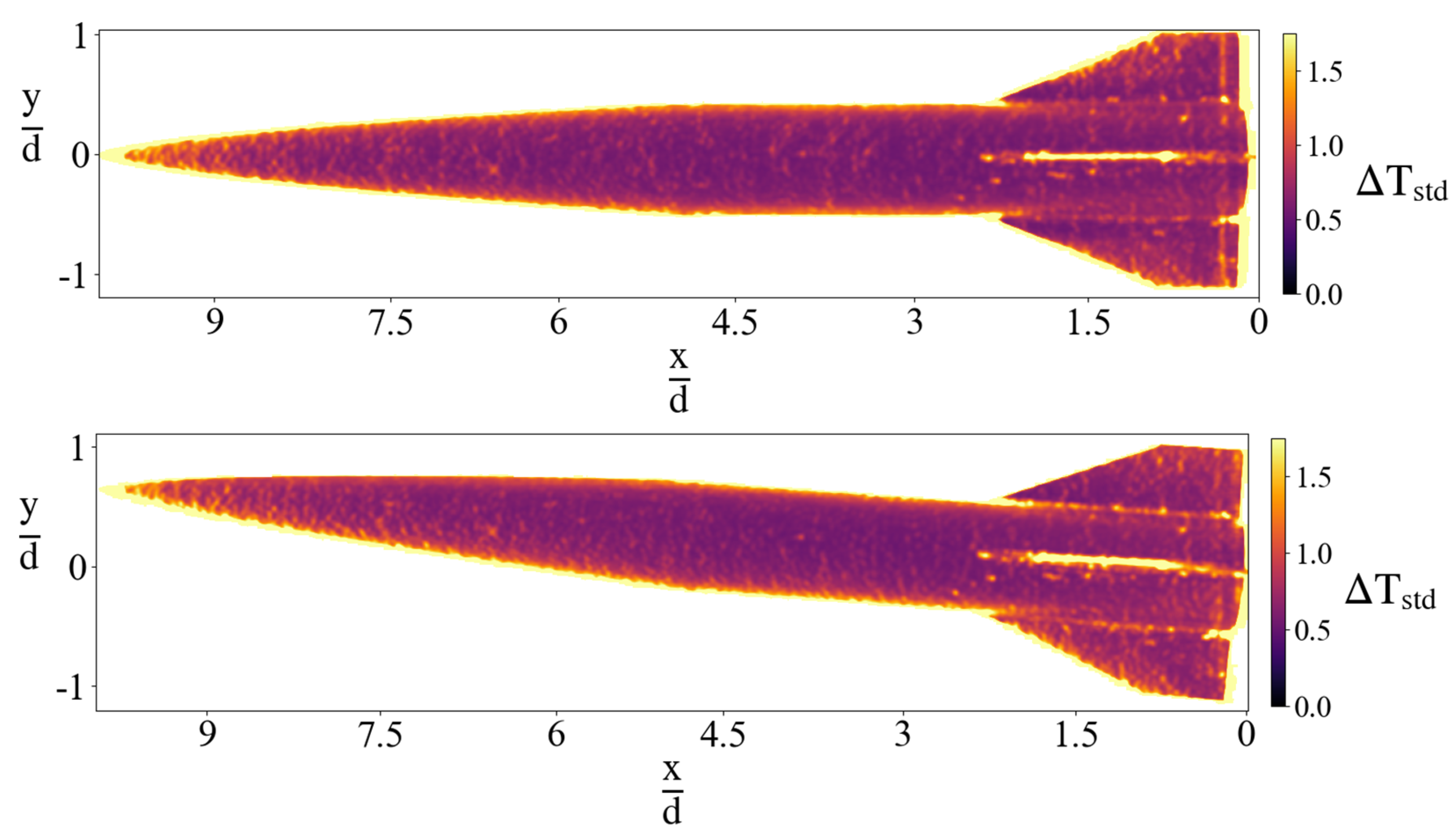
4.3. Standard Deviation
4.4. Temporal Temperature Gradients
5. Heat Flux
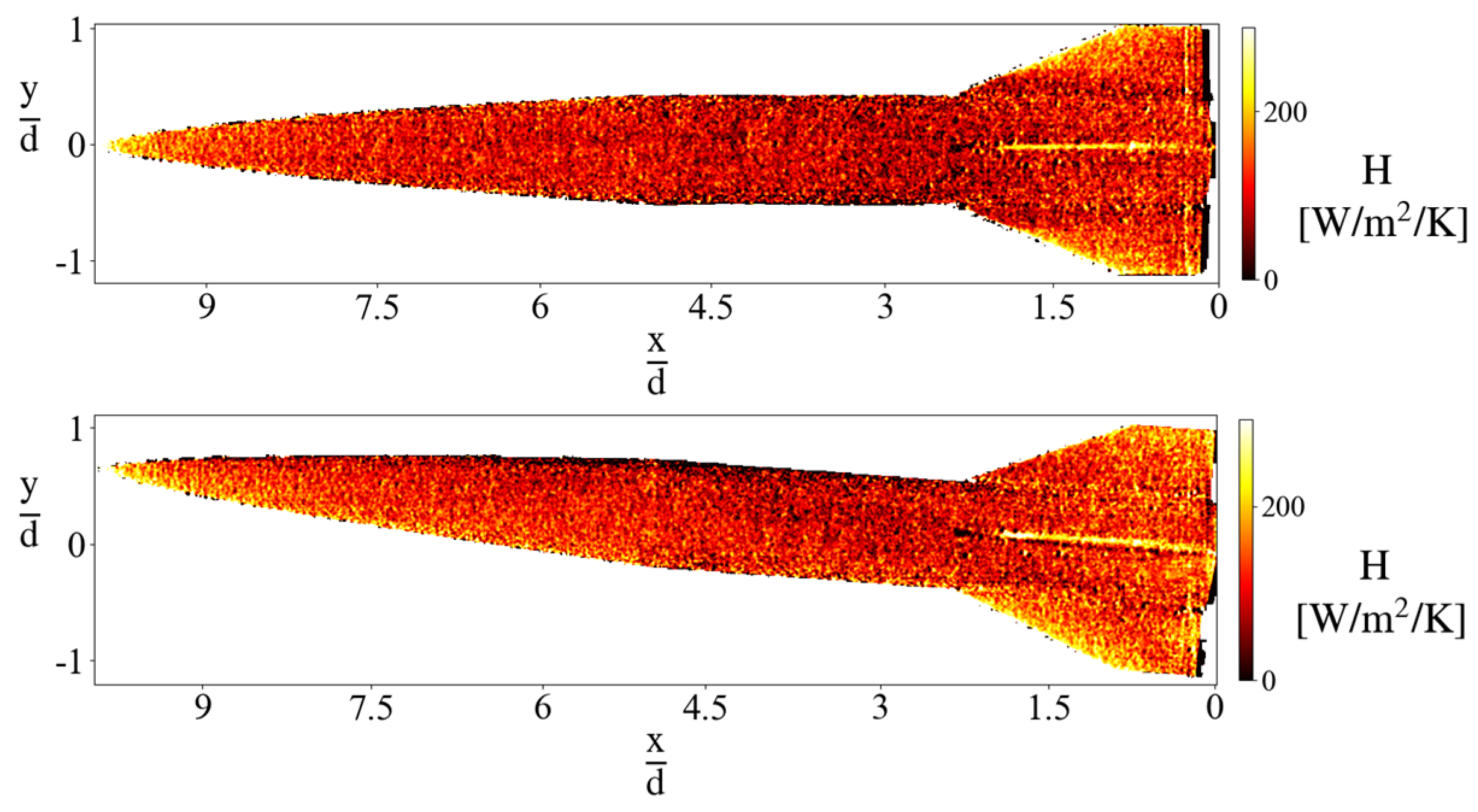
6. Average Convective Heat Transfer Coefficient
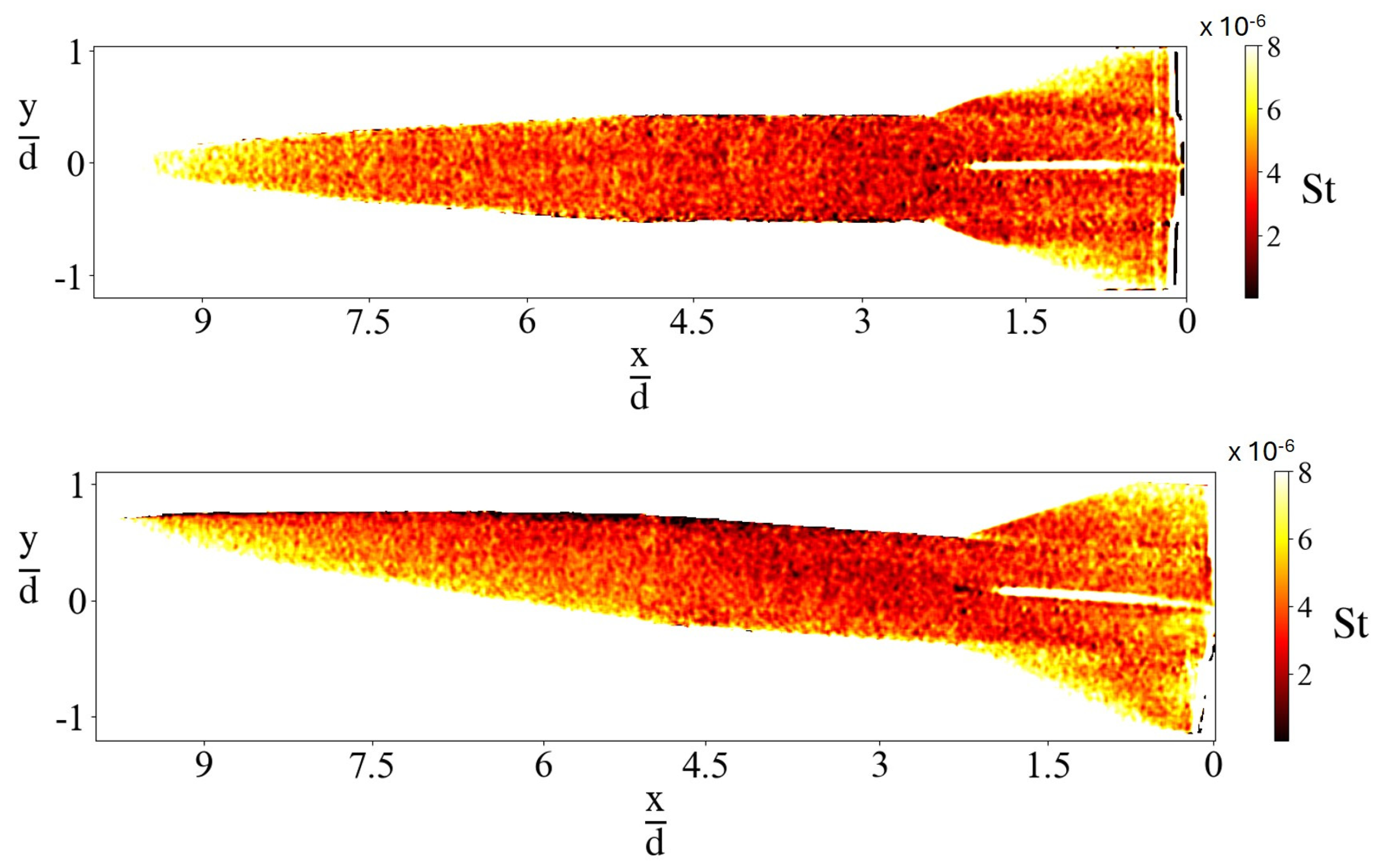
7. Modified Stanton Number
7.1. Average Profile
7.2. Spatial Distribution
8. Schlieren Visualization
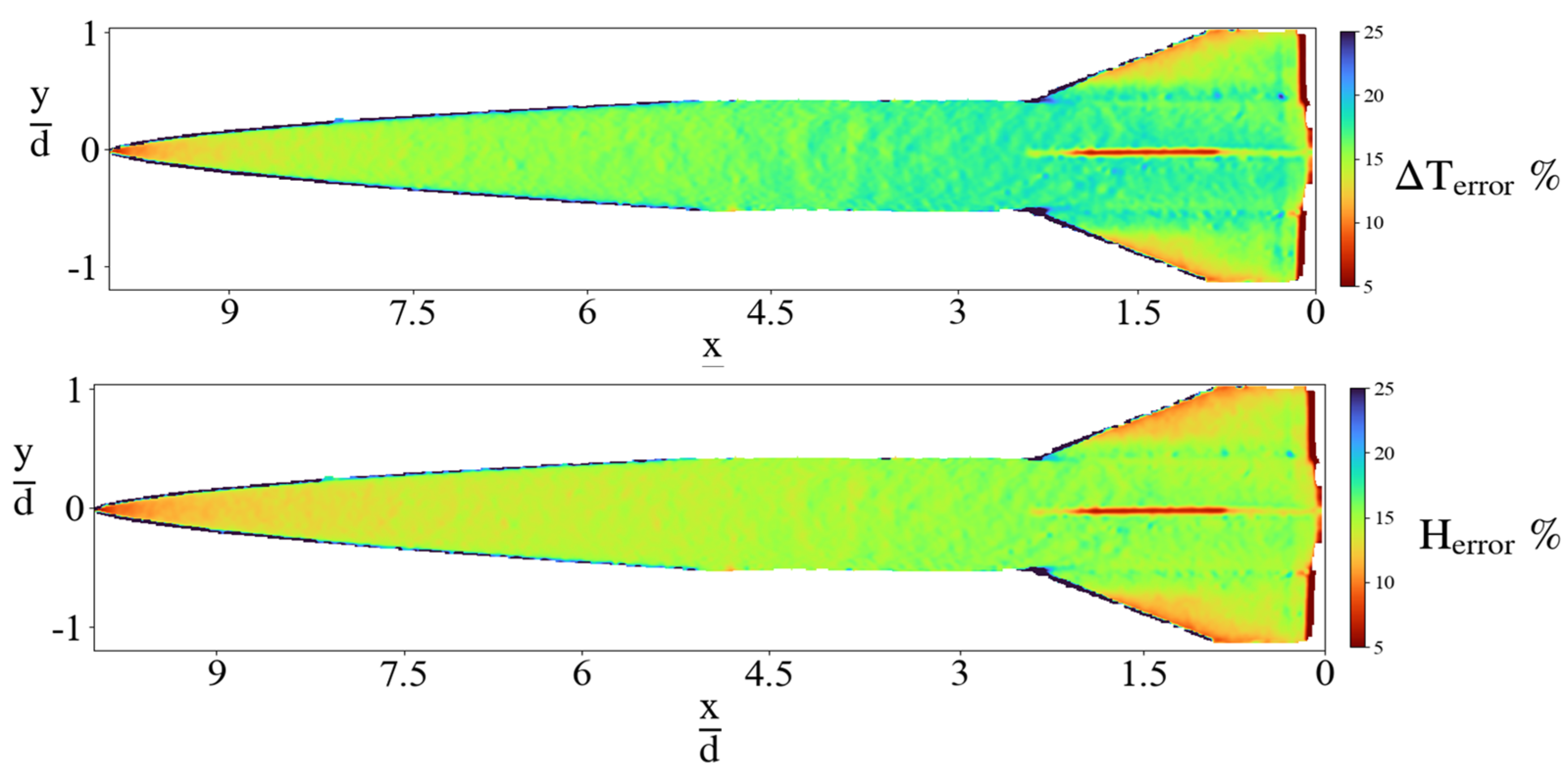
9. Uncertainty and Error Propagation
10. Summary
11. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Voland, R.T.; Huebner, L.D.; McClinton, C.R. X-43A Hypersonic Vehicle Technology Development. Acta Astronaut. 2006, 59, 181–191. [Google Scholar] [CrossRef]
- Bertin, J.J.; Cummings, R.M. Critical Hypersonic Aerothermodynamic Phenomena. Annu. Rev. Fluid Mech. 2006, 38, 129–157. [Google Scholar] [CrossRef]
- Laub, B.; Venkatapathy, E. Thermal Protection System Technology and Facility Needs for Demanding Future Planetary Missions. In Proceedings of the International Workshop Planetary Probe Atmospheric Entry and Descent Trajectory Analysis and Science, Lisbon, Portugal, 6–9 October 2003. [Google Scholar]
- Buck, G.M.; Watkins, A.N.; Danehy, P.M.; Inman, J.A.; Alderfer, D.W.; Dyakonov, A.A. Experimental Measurement of RCS Jet Interaction Effects on a Capsule Entry Vehicle. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 7–10 January 2008. [Google Scholar]
- Kurits, I.; Lewis, M.J.; Hamner, M.P.; Norris, J.D. Development of a Global Heat Transfer Measurement System at AEDC Hypervelocity Wind Tunnel 9. In Proceedings of the 2007 22nd International Congress on Instrumentation in Aerospace Simulation Facilities, Pacific Grove, CA, USA, 10–14 June 2007. [Google Scholar] [CrossRef]
- Lee, J.J.; Dutton, J.C.; Jacobi, A.M. Application of Temperature-Sensitive Paint for Surface Temperature Measurement in Heat Transfer Enhancement Applications. J. Mech. Sci. Technol. 2007, 21, 1253–1262. [Google Scholar] [CrossRef]
- Hoffman, E.N.A. Effects of Surface Roughness on Shock-Wave/Boundary-Layer Interactions at Mach 7.2. Ph.D. Thesis, The University of Texas at San Antonio, San Antonio, TX, USA, 2023. [Google Scholar]
- Liu, T.; Ward, C.A.C.; Rubal, J.; Sullivan, J.P.; Schneider, S.P. Heat-Flux Measurements with Temperature-Sensitive Paint in a Mach-6 Quiet Tunnel. J. Spacecr. Rockets 2013, 50, 282–293. [Google Scholar] [CrossRef]
- Roghelia, A.; Olivier, H.; Egorov, I.; Chuvakhov, P. Correction to: Experimental Investigation of Görtler Vortices in Hypersonic Ramp Flows. Exp. Fluids 2017, 58, 169. [Google Scholar] [CrossRef]
- Ozawa, H.; Laurence, S.J. Experimental Investigation of the Shock-Induced Flow over a Wall-Mounted Cylinder. J. Fluid Mech. 2018, 849, 1009–1042. [Google Scholar] [CrossRef]
- Ozawa, H.; Laurence, S.J.; Schramm, J.M.; Wagner, A.; Hannemann, K. Fast-Response Temperature-Sensitive-Paint Measurements on a Hypersonic Transition Cone. Exp. Fluids 2015, 56, 1853. [Google Scholar] [CrossRef]
- Smith, C.D.; Kreth, P.A.; Schmisseur, J.D.; Strickland, G. Temperature-Sensitive Paint Measurements of Cylinder-Induced Shockwave-Boundary Layer Interaction on a 6-Degree Cone with Laminar Mach 7 Flow. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar]
- Grossir, G.; Pinna, F.; Bonuccif, G.; Regert, T.; Rambaud, P.; Chazot, O. Hypersonic Boundary Layer Transition on a 7 Degree Half-Angle Cone at Mach 10. In Proceedings of the AIAA AVIATION 2014—7th AIAA Theoretical Fluid Mechanics Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Maszkiewicz, S.A.; Gillespie, G.I.; Laurence, S.J. Experimental Investigation of Transitional, Sharp-Fin-Induced Shock-Wave/Boundary-Layer Interactions at Mach 6. In Proceedings of the AIAA Science and Technology Forum and Exposition, AIAA SciTech Forum 2022, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Liu, T.; Campbell, B.T.; Burns, S.P.; Sullivan, J.P. Temperature- and Pressure-Sensitive Luminescent Paints in Aerodynamics. Appl. Mech. Rev. 1997, 50, 227–246. [Google Scholar] [CrossRef]
- Rabek, J.F. Polymer Photodegradation: Mechanisms and Experimental Methods; Springer: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Liu, T. Pressure- and Temperature-Sensitive Paints. In Encyclopedia of Aerospace Engineering; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Morawetz, H. Mechanisms of Photophysical Processes and Photochemical Reactions in Polymers-Theory and Applications, by Jan F. Rabek, John Wiley & Sons, New York, 1987, 756 Pp. Price: $204.00. J. Polym. Sci. Polym. Lett. Ed. 1988, 26, 276. [Google Scholar] [CrossRef]
- Kose, M.K. Multi-Luminophore Coatings for Pressure Sensitive Pain Applications; University of Florida: Gainesville, FL, USA, 2005. [Google Scholar]
- Liu, X.; Shao, H.; Zhou, W.; Liu, Y.; Peng, D. Apparent Temperature in Temperature-Sensitive Paint Measurement and Its Effect on Surface Heat Flux Determination for Hypersonic Flows. Meas. Sci. Technol. 2020, 31, 125302. [Google Scholar] [CrossRef]
- Schramm, J.M.; Edzards, F.; Hannemann, K. Development of Ultra-Fast Temperature Sensitive Paints for Hypersonic High Speed Flows. In Proceedings of the 21st AIAA International Space Planes and Hypersonics Technologies Conference, Hypersonics 2017, Xiamen, China, 6–9 March 2017. [Google Scholar]
- Pasiliao, C.L.; Sytsma, M.J.; Neergaard, L.J.; Witeof, Z.D.; Trolier, J.W. Preliminary Aerothermal Structural Simulation. In Proceedings of the AIAA AVIATION 2014—14th AIAA Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Klock, R.J.; Cesnik, C.E.S. Aeroelastic Stability of High-Speed Cylindrical Vehicles. In Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Blocher, B.L.; Panigrahi, A.; Eitner, M.A.; Villa, B.E.D.; Sirohi, J.; Clemens, N.T. Pressure Field and Mean Deflection Estimation of a Hypersonic Vehicle Model in Mach 5 Flow. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar] [CrossRef]
- Elizondo, V.D.; Dhanagopal, A.; Combs, C.S. Fast-Responding Pressure-Sensitive Paint Measurements of the IC3X at Mach 7.2. Aerospace 2023, 10, 890. [Google Scholar] [CrossRef]
- Willems, J.A.; McNamara, J.J.; Reasor, D.A. Coupled Fluid-Thermal Response in the Gap Region of a High-Speed Control Surface. In Proceedings of the AIAA AVIATION 2023 Forum, San Diego, CA, USA, 12–16 June 2023. [Google Scholar]
- Dhanagopal, A.; Strasser, N.S.; Andrade, A.; Hoffman, E.N.A.; Combs, C.S. Global Surface Temperature Distribution on the Initial Concept 3.X Vehicle at Mach 7. In Proceedings of the AIAA SciTech Forum and Exposition, Orlando, FL, USA, 8–12 January 2024. [Google Scholar]
- Bashor, I.P.; Hoffman, E.; Gonzalez, G.; Combs, C.S. Design and Preliminary Calibration of the Utsa Mach 7 Hypersonic Ludwieg Tube. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar]
- Hoffman, E.N.A.; Lalonde, E.J.; Garcia, M.; Valeria Delgado, E.; Chen, I.; Bilbo, H.A.; Combs, C.S. Characterization of the UTSA Mach 7 Ludwieg Tube. In Proceedings of the AIAA Science and Technology Forum and Exposition, AIAA SciTech Forum 2022, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Hoffman, E.N.A.; Valeria, D.E.; Garcia, M.; Lalonde, E.J.; Rodriguez, J.M.; Combs, C.S. Preliminary Testing of the UTSA Mach 7 Ludwieg Tube. In Proceedings of the AIAA Aviation and Aeronautics Forum and Exposition, AIAA AVIATION Forum 2021, Virtual Event, 2–6 August 2021. [Google Scholar]
- Hoffman, E.N.A.; Lalonde, E.J.; Andrade, A.; Chen, I.; Bilbo, H.A.; Combs, C.S. Flow Characterization of the UTSA Hypersonic Ludwieg Tube. Aerospace 2023, 10, 463. [Google Scholar] [CrossRef]
- Witeof, Z.D.; Neergaard, L.J. Initial Concept 3.0 Finite Elemental Model Definition; Air Force Research Laboratory: Dayton, OH, USA, 2014. [Google Scholar]
- Nakakita, K.; Osafune, T.; Asai, K. Global Heat Transfer Measurement in a Hypersonic Shock Tunnel Using Temperature-Sensitive. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 6–9 January 2003. [Google Scholar]
- Martinez Schramm, J.; Hannemann, K.; Ozawa, H.; Beck, W.; Klein, C. Development of Temperature Sensitive Paints in the High Enthalpy Shock Tunnel Göttingen, HEG. In Proceedings of the 8th European Symposium on Aerothermodynamics for Space Vehicles, Lisbon, Portugal, 2–6 March 2015. [Google Scholar]
- Nagai, H.; Nagayama, T.; Tanno, H.; Komuro, T. Boundary-Layer Transition Detection at High-Enthalpy Flow Using Temperature-Sensitive Paint. In 31st International Symposium on Shock Waves 1; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Hubner, J.P.; Carroll, B.F.; Schanze, K.S.; Ji, H.F.; Holden, M.S. Temperature- and Pressure-Sensitive Paint Measurements in Short-Duration Hypersonic Flow. AIAA J. 2001, 39, 654–659. [Google Scholar] [CrossRef]
- Dhanagopal, A.; Williamson, C.; LaLonde, E.J.; Gutierrez, S.; Andrade, A.; Delgado, V.; Combs, C.S. High-Speed Pressure Sensitive Paint Measurements of the Initial Concept 3.X Vehicle at Mach 7. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar]
- Schairer, E.T.; Mehta, R.D.; Olsen, M.E. Effects of Pressure-Sensitive Paint on Experimentally Measured Wing Forces and Pressures. AIAA J. 2002, 40, 1830–1838. [Google Scholar] [CrossRef]
- Cervantes, A.; Combs, C.S. Calibrating Fast Responsive Temperature Sensitive from 0 to 100 Degrees Celsius. In Proceedings of the AIAA AVIATION 2024 Forum, Las Vegas, NV, USA, 29 July–2 August 2024. [Google Scholar]
- Smith, C.D.; Kreth, P.A.; Schmisseur, J.D.; Strickland, G. Characterization of Temperature Sensitive Paint for Application in Hypersonic Ludwieg Tubes at the University of Tennessee. In Proceedings of the AIAA Science and Technology Forum and Exposition, AIAA SciTech Forum 2022, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Egami, Y.; Matsuda, Y.; Yamaguchi, H.; Niimi, T. Property Changes of Temperature-Sensitive Paint Immobilized in Acrylic Polymer Matrices. Sens. Actuators B Chem. 2014, 195, 677–681. [Google Scholar] [CrossRef]
- Elizondo, V.D. High-Speed Pressure-Sensitive Paint Measurements of a Hypersonic Vehicle. Ph.D. Thesis, The University of Texas at San Antonio, San Antonio, TX, USA, 2022. [Google Scholar]
- Anderson, J.D. Hypersonic and High-Temperature Gas Dynamics, 3rd ed.; American Institute of Aeronautics & Astronautics: Reston, VA, USA, 2019. [Google Scholar]
- Kleine, H.; Grönig, H. Color Schlieren Methods in Shock Wave Research. Shock Waves 1991, 1, 51–63. [Google Scholar] [CrossRef]
- Hoffman, E.N.; Kendhammer, D.M.; LaLonde, E.J.; Andrade, A.; Combs, C.S. Effects of Distributed Roughness on Shock-Wave/Boundary-Layer Interactions at Mach 7.2. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar]
- Shumway, N.M.; Laurencey, S.J. Methods for Identifying Key Features in Schlieren Images from Hypersonic Boundary-Layer Stability Experiments. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Laurence, S.J.; Wagner, A.; Hannemann, K. Schlieren-Based Techniques for Investigating Instability Development and Transition in a Hypersonic Boundary Layer. Exp. Fluids 2014, 55, 1782. [Google Scholar] [CrossRef]
- Hill, J.L.; Benitez, E.K.; Borg, M.P.; Reeder, M.F. Global Reconstruction of Hypersonic Boundary Layer Disturbance Modes. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar]











| Flow Parameter | Condition |
|---|---|
| Test Gas | Dry Air |
| Stagnation Pressure | 1.8 ± 0.02 MPa |
| Test Section Pressure | 0.34 ± 0.0002 kPa |
| Mach Number | 7.2 ± 0.2 |
| Test Time (Steady State) | 80 ms |
| Driver Tube Temperature | 582 ± 10 K |
| Initial Model Surface Temperature | 295 ± 2 K |
| Freestream Unit Reynolds Number | 7 × 106 m−1 |
| Property | SI Units |
|---|---|
| Body Length | 25.4 cm |
| Body Diameter | 2.54 cm |
| Wingspan | 5.72 cm |
| Mass | 120 g |
| Resin Flexure Strength | 28 MPa |
| Resin Extension Strength | 24 MPa |
| Component | Function | Amount |
|---|---|---|
| Ru(phen) | Luminophore | 100 mg |
| Ethanol | Solvent or thinner | 28 mL |
| Polyacrylic Acid | Binder | 13.68 mL (19.767 g) |
| Test | Model | Acquisition Rate [kHz] | Po [MPa] | To [K] | Re (×106 m−1) |
|---|---|---|---|---|---|
| 1 | Ogive 0° | 300 | 1.8 | 327 | 21 |
| 2 | Ogive 0° | 315 | 1.8 | 327 | 21 |
| 3 | Fin 0° | 315 | 1.8 | 327 | 21 |
| 4 | Fin 0° | 315 | 1.8 | 327 | 21 |
| Cause | Uncertainty |
|---|---|
| Pixel Noise | ±1.26% |
| Calibration Constant A | ±0.293 |
| Calibration Constant B | ±0.385 |
| Reference Temperature | ±2 K |
| Parameter | Avg. ΔT% | Average Flux% | Average H% | St% |
|---|---|---|---|---|
| Pixel Measurement | ±6 | 0 | ±6 | ±0.3 |
| Calibration Const A | ±3 | 0 | ±3 | ±0.2 |
| Calibration Const B | ±0.3 | ±2 | ±2 | ±2 |
| Ref Temp | ±20 | 0 | ±20 | 0 |
| Cumulative | ±22 | ±2 | ±22 | ±2 |
| Variable | Angle of Attack | Value | Uncertainty |
|---|---|---|---|
| Average Change in Surface Temperature ΔT (K) | 0° | 6–34 | ±2.15 K |
| 5° | 11–44 | ||
| Average Change in Surface Temperature at the Stagnation Point ΔT (K) | 0° | 39 | ±2.15 K |
| 5° | 43 | ||
| Stagnation Point Heat Flux q (W/m2) | 0° | 1.93 × 104 | ±100 (W/m2) |
| 5° | 4.77 × 104 | ||
| Average Heat Flux q (W/m2) | 0° | 1.26 × 103 | ±100 (W/m2) |
| 5° | 1.30 × 103 | ||
| Convective Heat Transfer Coefficient H (W/m2/K) | 0° | 84.4 | ±34.2 (W/m2/K) |
| 5° | 101.9 | ||
| Average Modified Stanton Number St (×10−6) | 0° | 0.14–46 | ±6.71 × 10−8 |
| 5° | 0.18–54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhanagopal, A.; Strasser, N.S.; Andrade, A.; Posladek, K.R.; Hoffman, E.N.A.; Combs, C.S. Thermal Evaluation of the Initial Concept 3.X Vehicle at Mach 7. Energies 2024, 17, 2916. https://doi.org/10.3390/en17122916
Dhanagopal A, Strasser NS, Andrade A, Posladek KR, Hoffman ENA, Combs CS. Thermal Evaluation of the Initial Concept 3.X Vehicle at Mach 7. Energies. 2024; 17(12):2916. https://doi.org/10.3390/en17122916
Chicago/Turabian StyleDhanagopal, Abinayaa, Nathan S. Strasser, Angelina Andrade, Kevin R. Posladek, Eugene N. A. Hoffman, and Christopher S. Combs. 2024. "Thermal Evaluation of the Initial Concept 3.X Vehicle at Mach 7" Energies 17, no. 12: 2916. https://doi.org/10.3390/en17122916
APA StyleDhanagopal, A., Strasser, N. S., Andrade, A., Posladek, K. R., Hoffman, E. N. A., & Combs, C. S. (2024). Thermal Evaluation of the Initial Concept 3.X Vehicle at Mach 7. Energies, 17(12), 2916. https://doi.org/10.3390/en17122916






