Shunt Active Power Filters in Three-Phase, Three-Wire Systems: A Topical Review
Abstract
1. Introduction
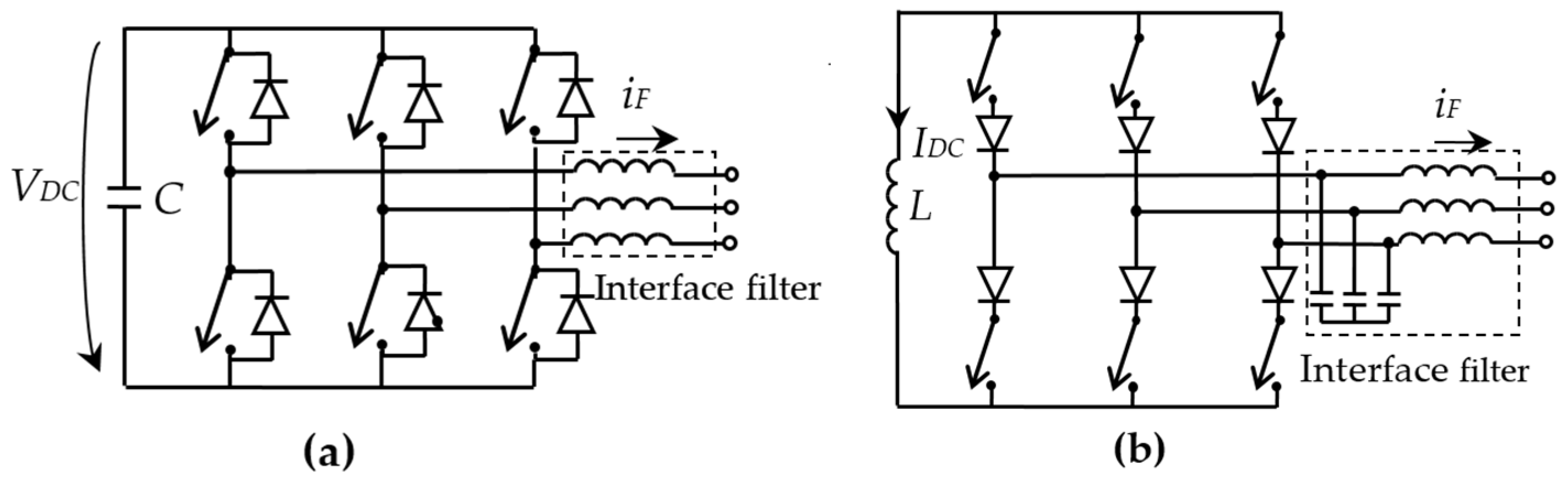
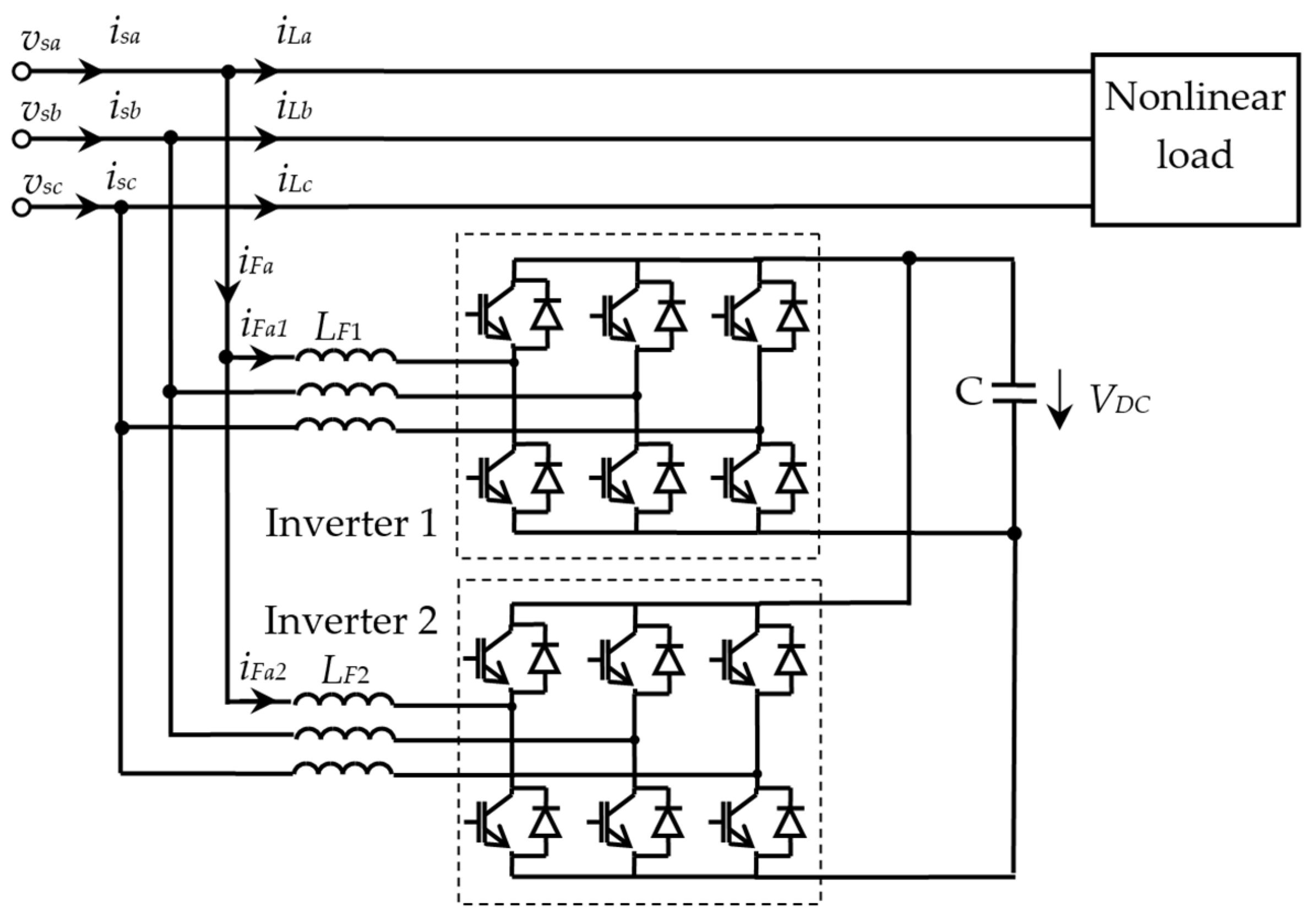
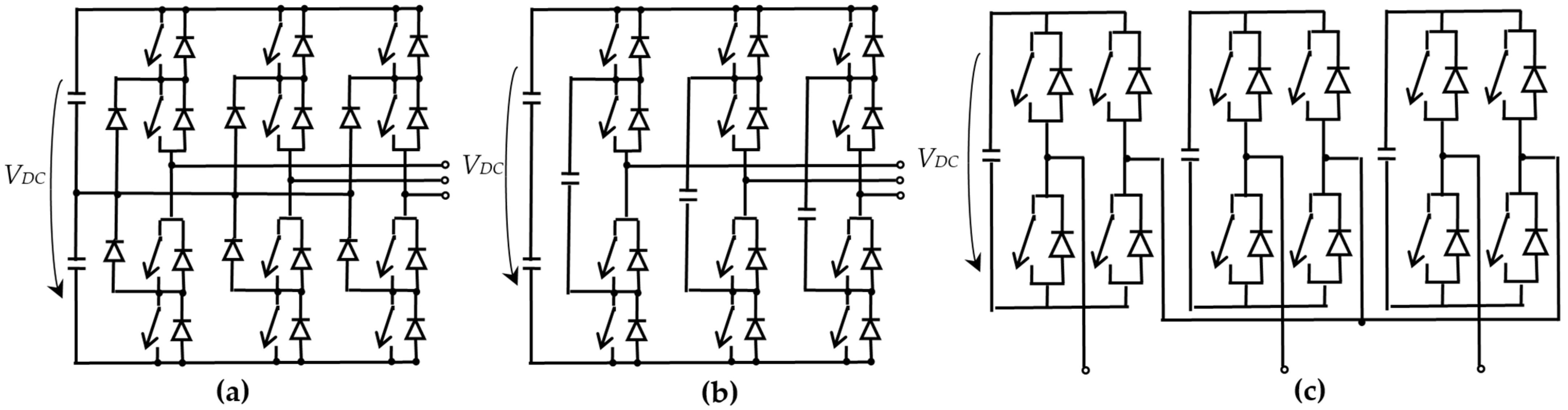
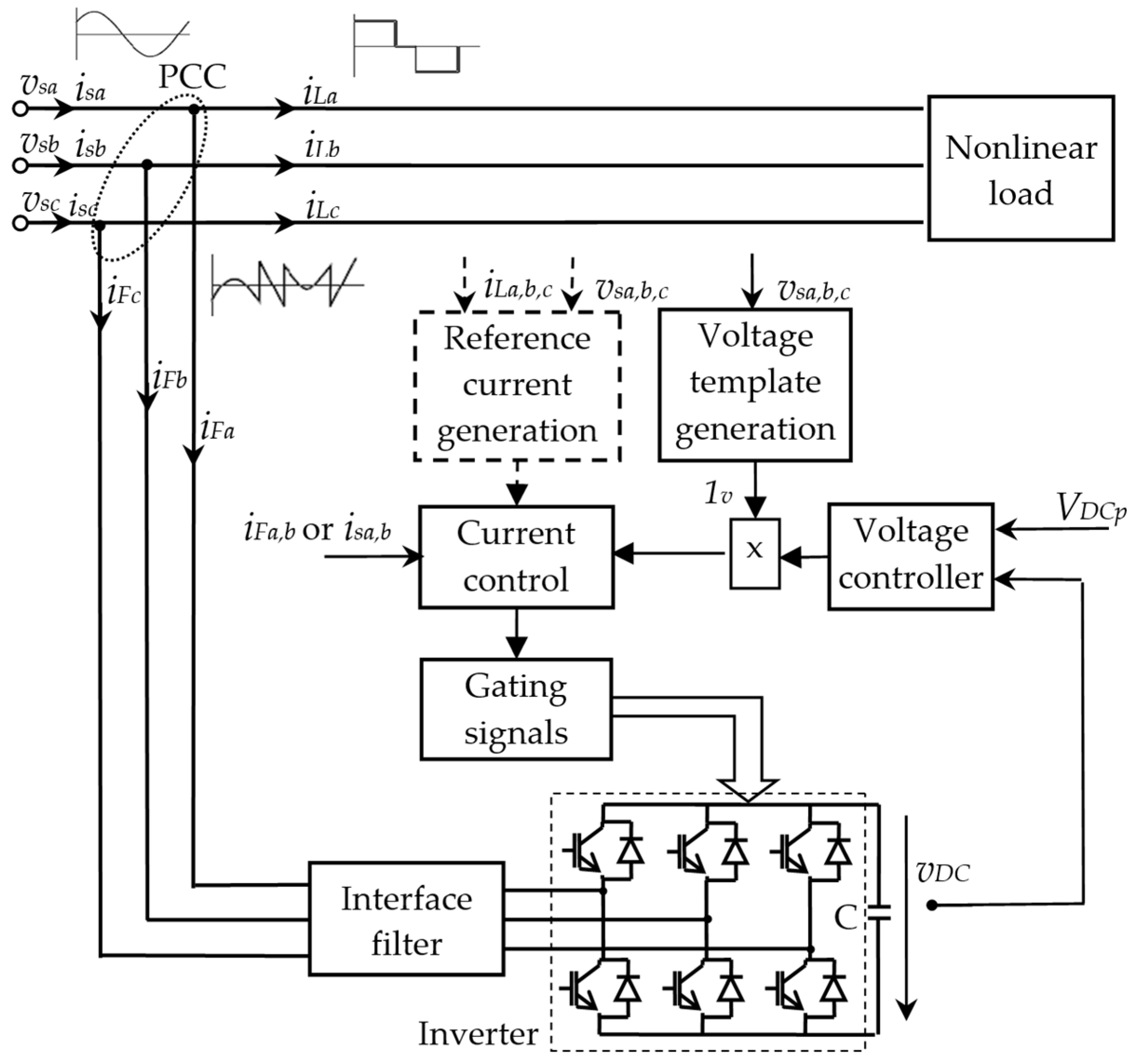
2. Power Circuit Configurations
2.1. Two-Level Topologies
2.2. Multilevel Topologies
2.3. New Power Semiconductor Devices
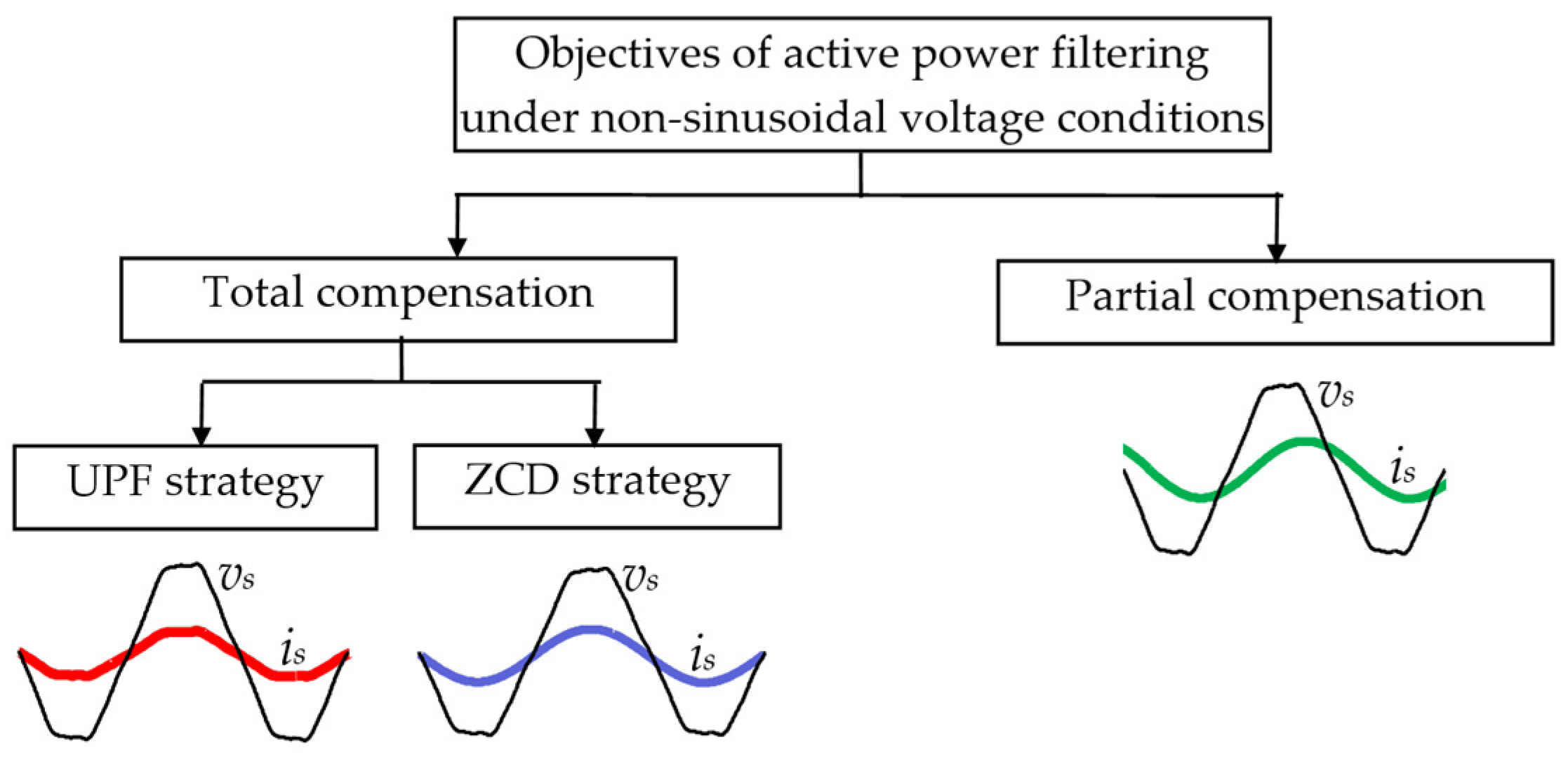
3. Objectives of Active Power Filtering
- Unity power factor (UPF):
- Zero current distortion (ZCD):
- Reactive power compensation: when the reactive component of the fundamental load current is compensated, the supply current is distorted, but its fundamental is in phase with the voltage. Unity displacement power factor is obtained.
- Compensation of current harmonics only.
- Filtering of all harmonics: when a sinusoidal supply current is obtained but out of phase with respect to the voltage.
- Selective filtering of certain harmonics: when the resulting supply current is no longer sinusoidal and its zero crossings are out of phase with respect to the voltage.
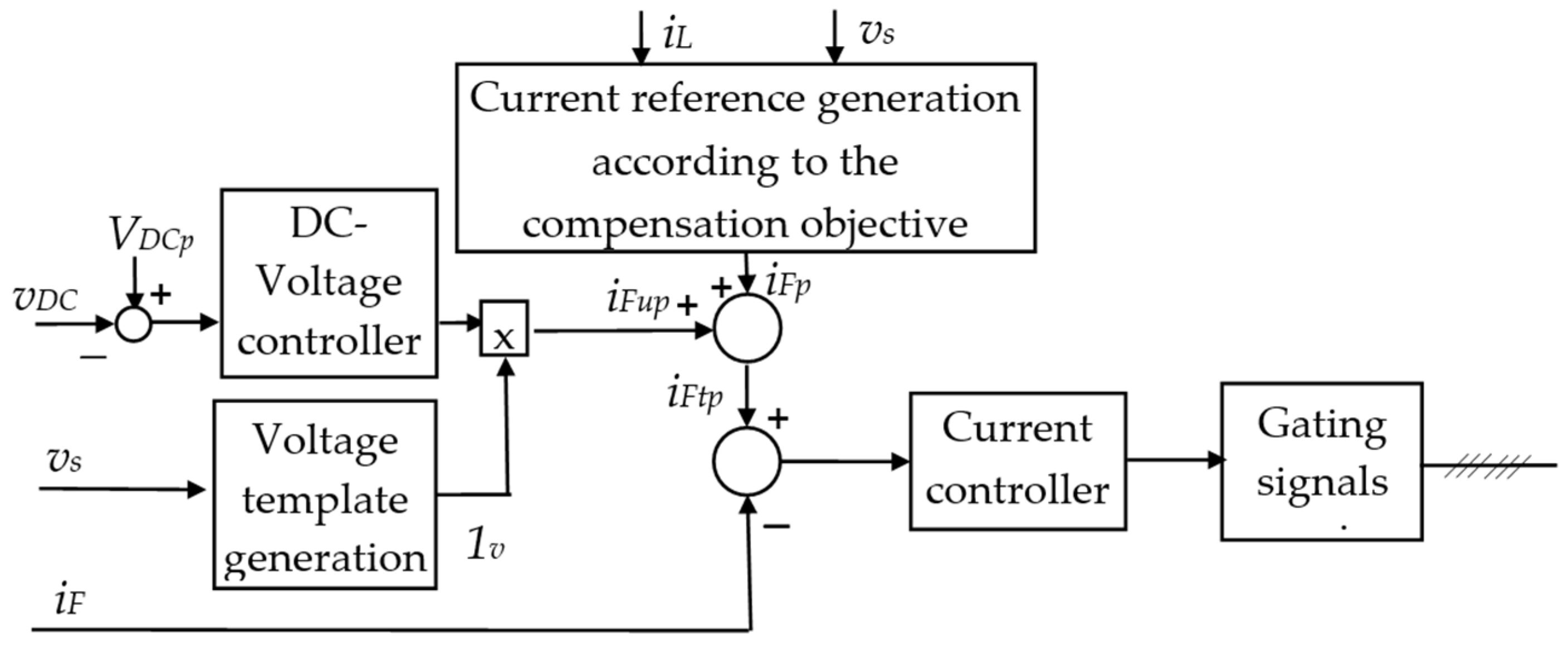
4. Reference Current Generation
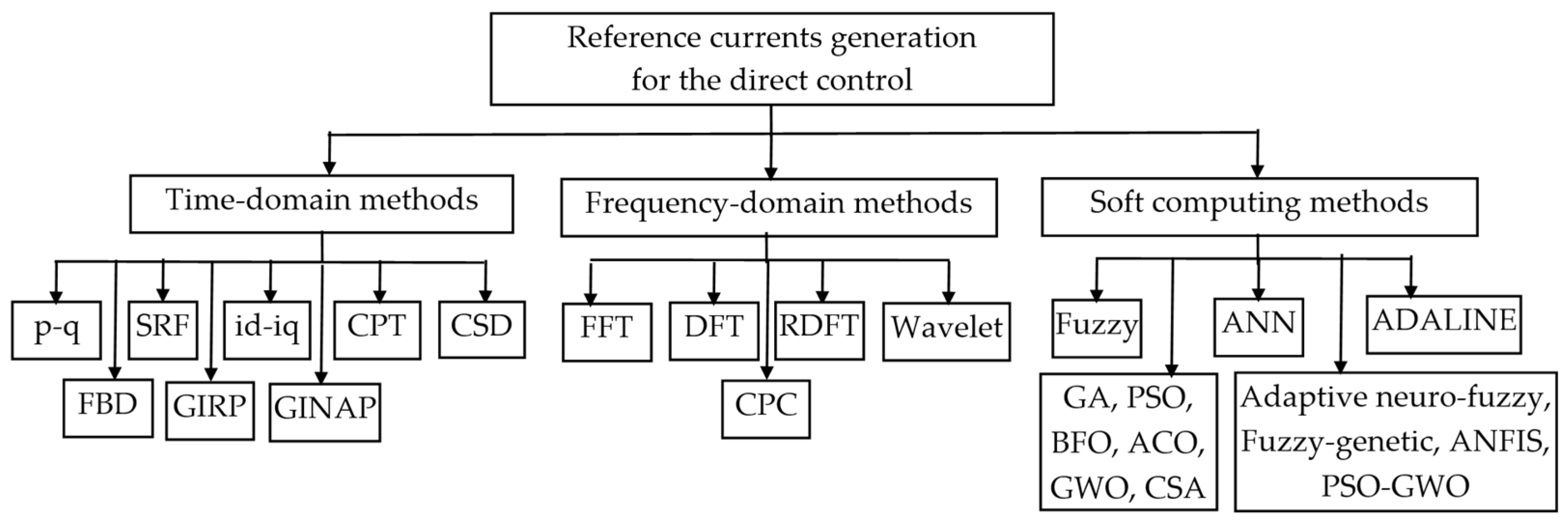
4.1. Reference Current Generation for the Direct Control
4.1.1. Time-Domain Methods
4.1.2. Frequency-Domain Methods
4.1.3. Soft-Computing Methods
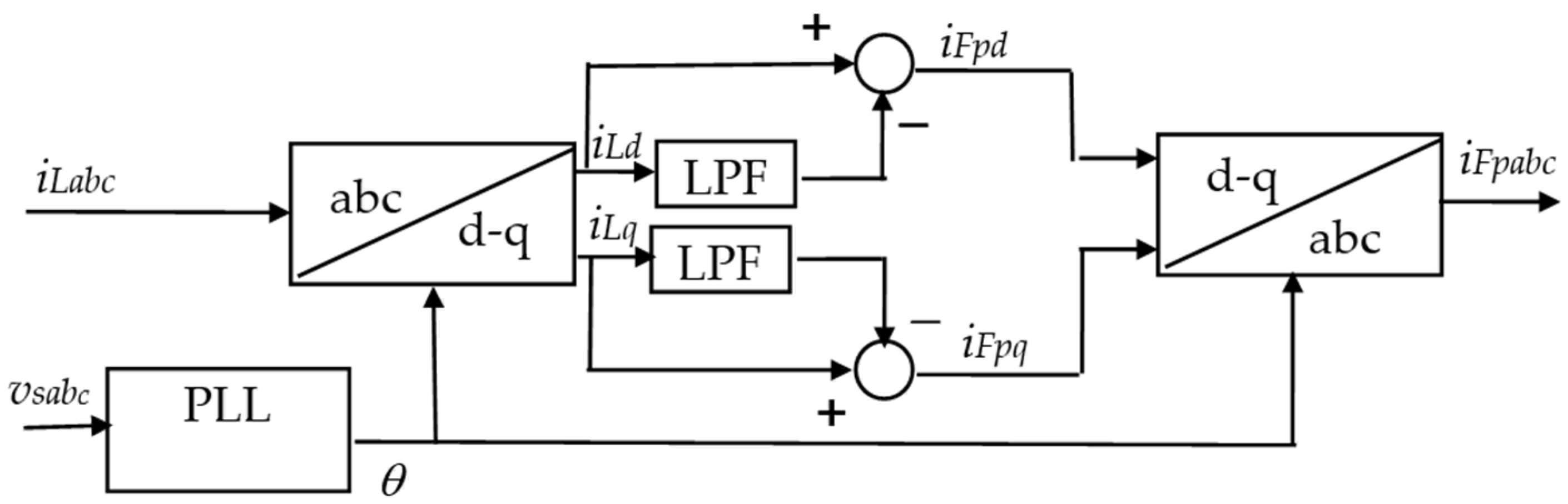
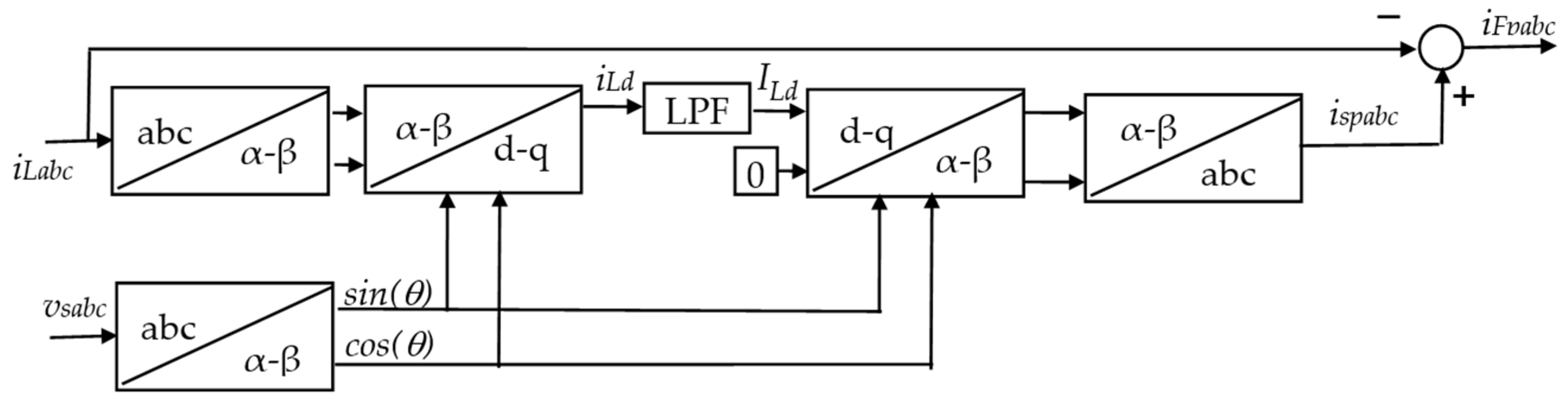
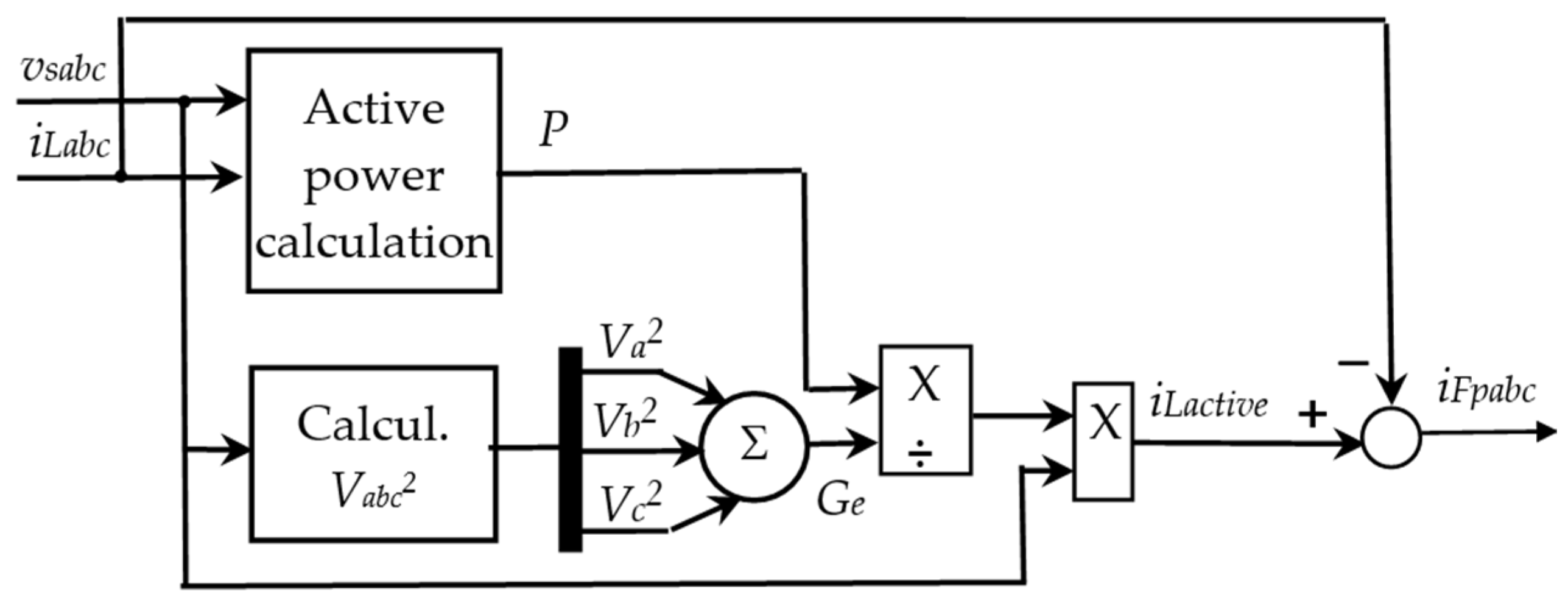
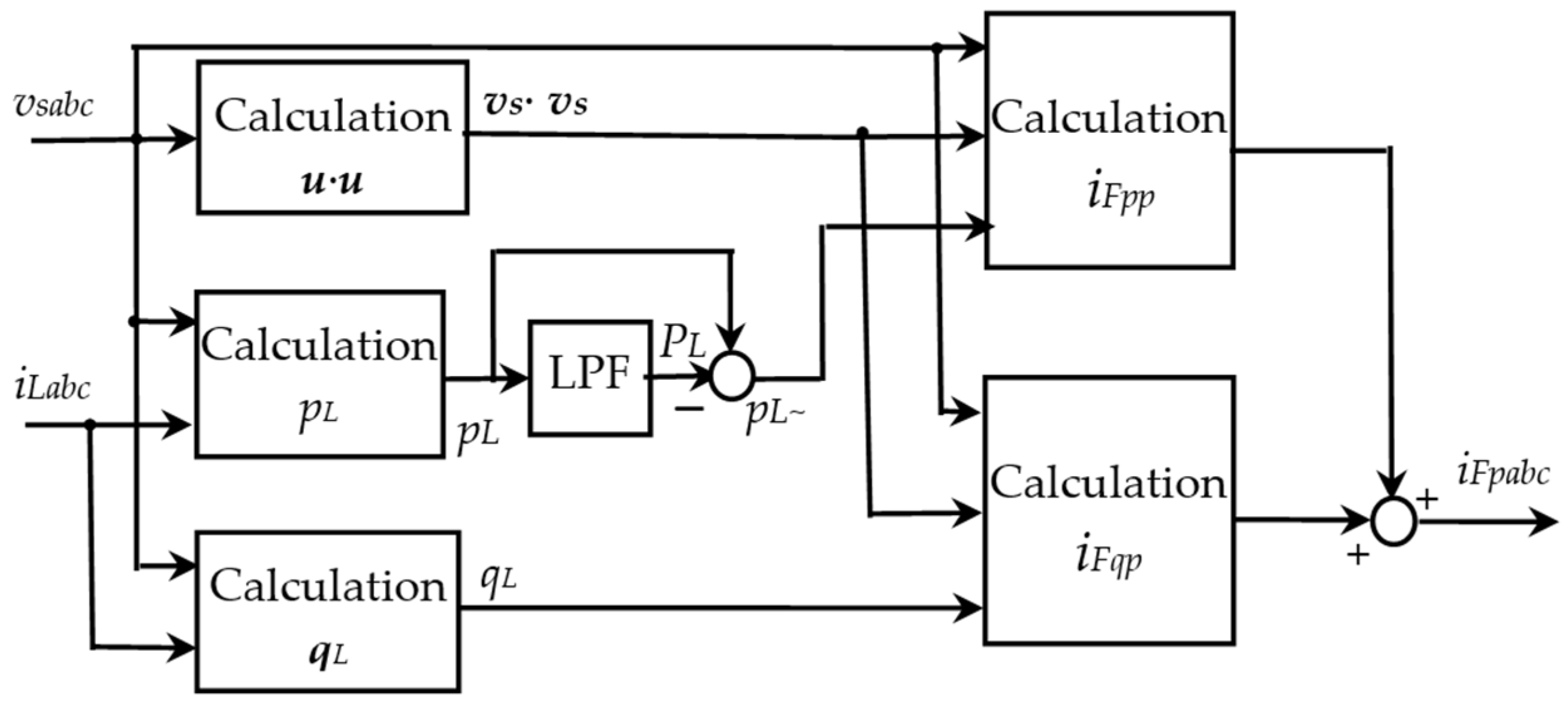
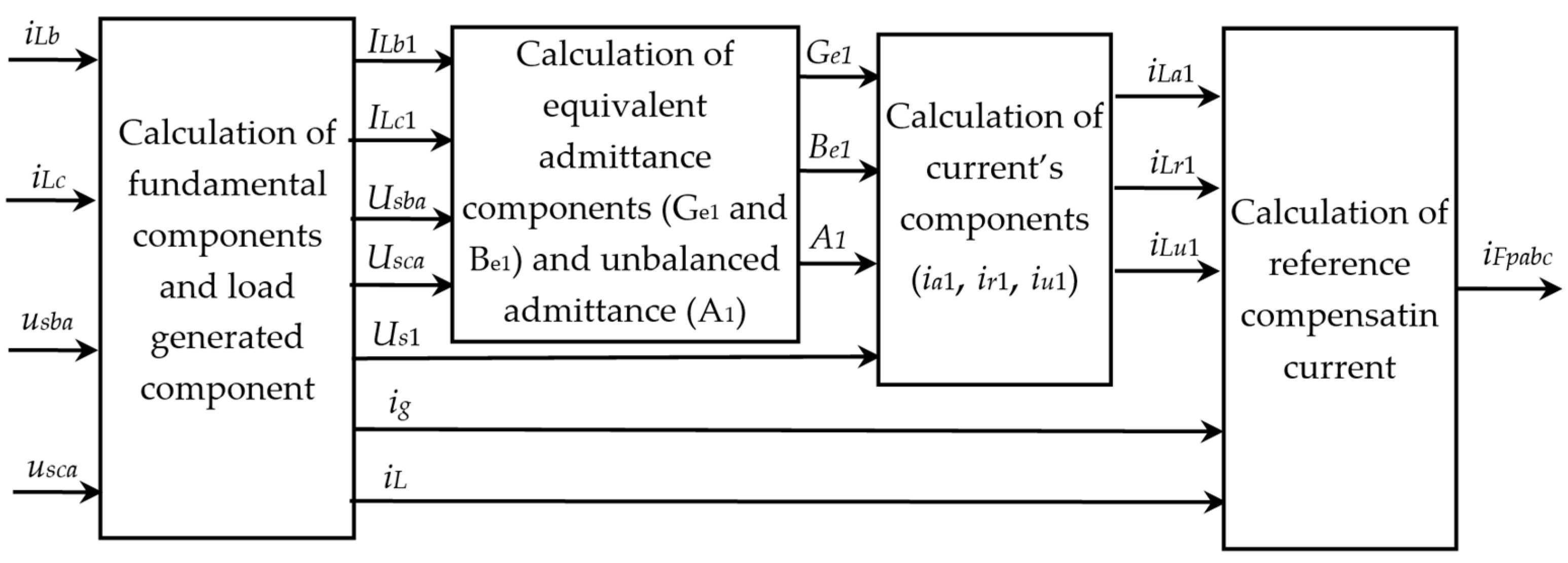
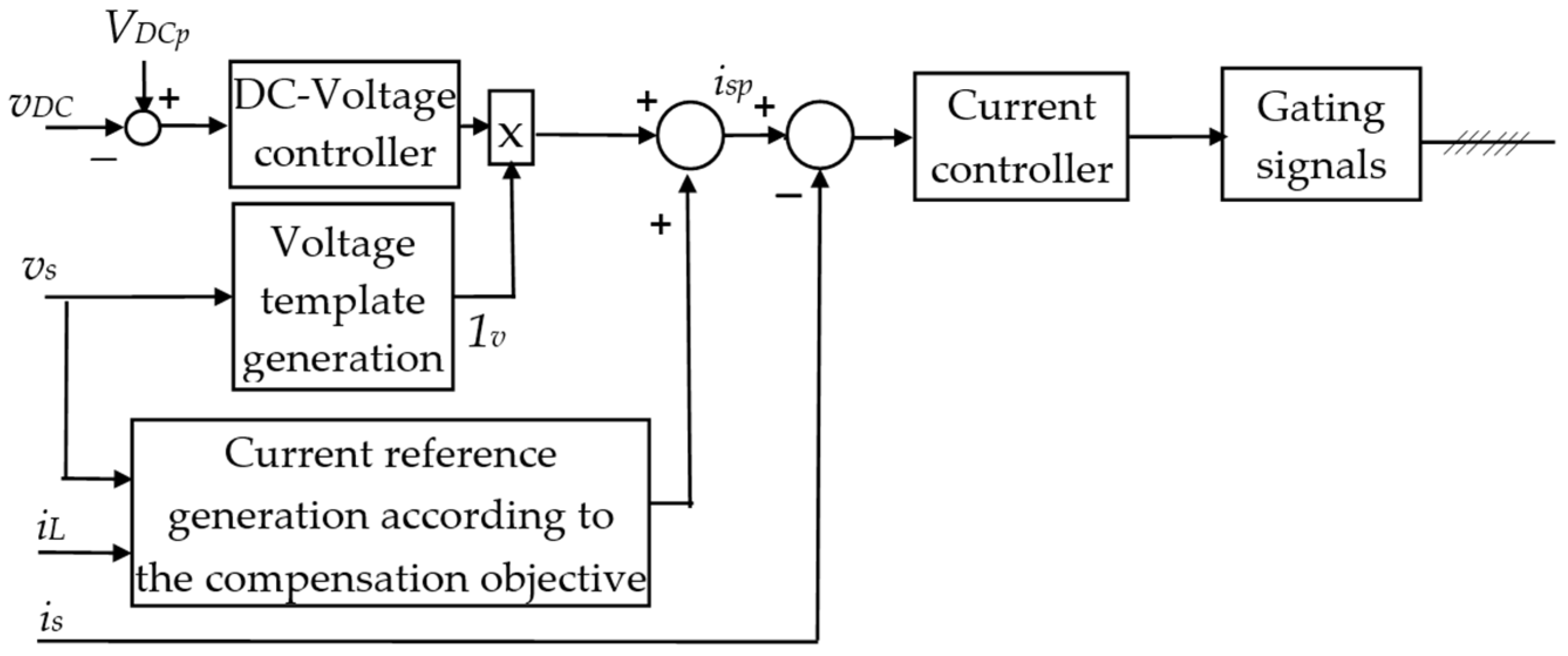
4.2. Reference Current Generation for the Indirect Control
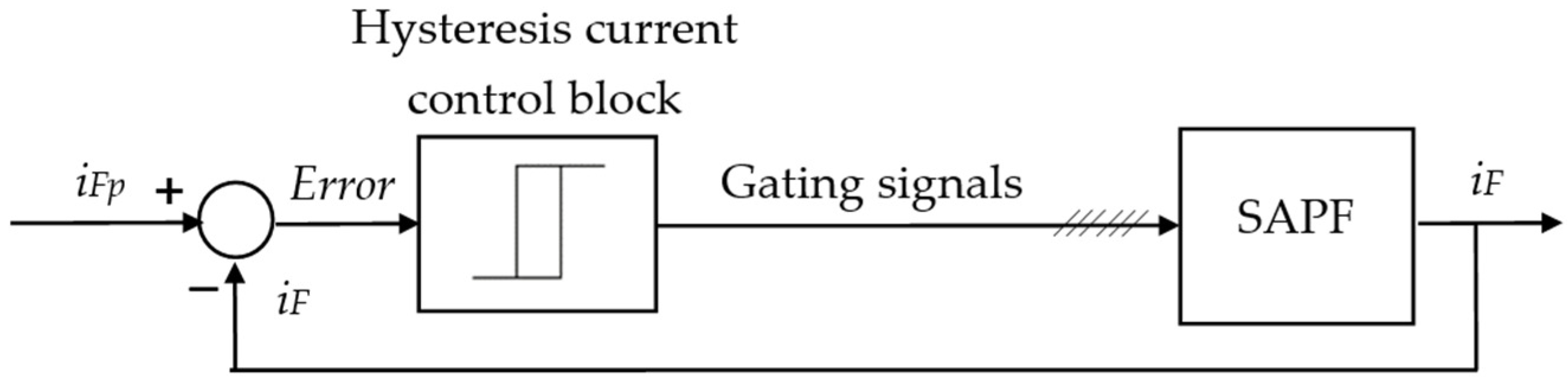
5. Current Control Techniques
6. Modulation Strategies
6.1. Sinusoidal PWM
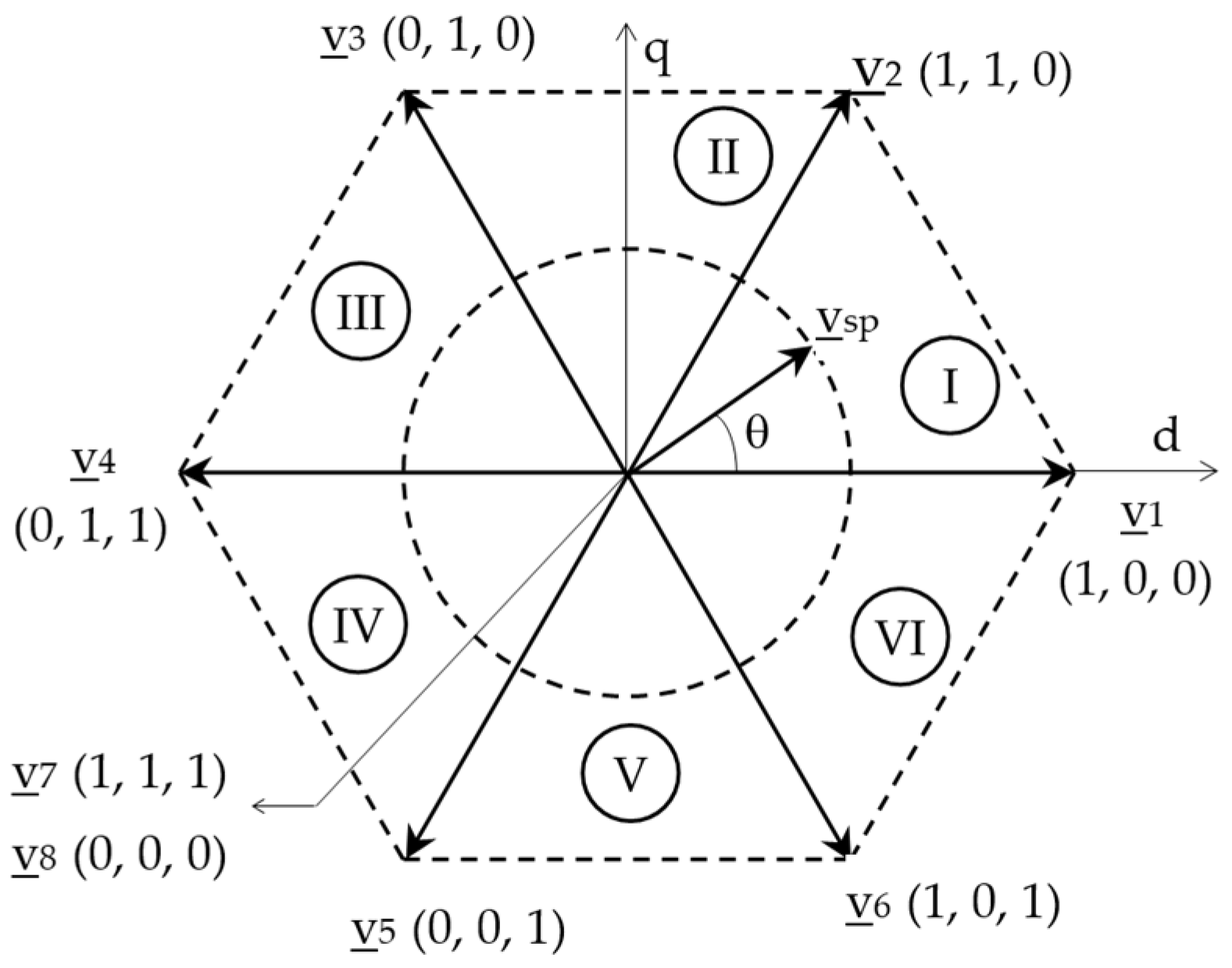
6.2. Space Vector PWM
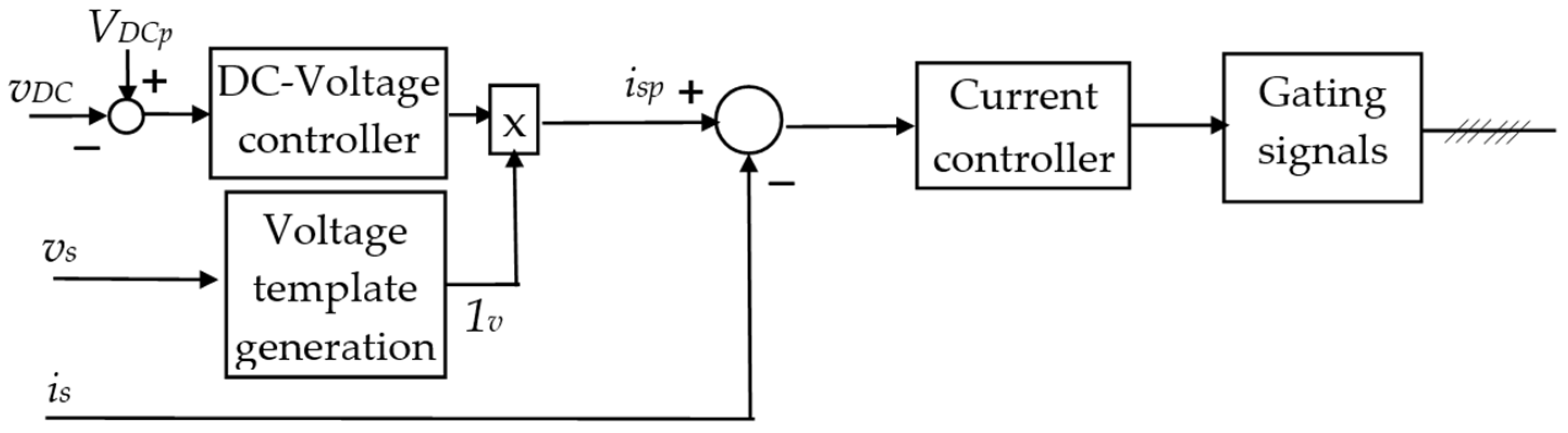
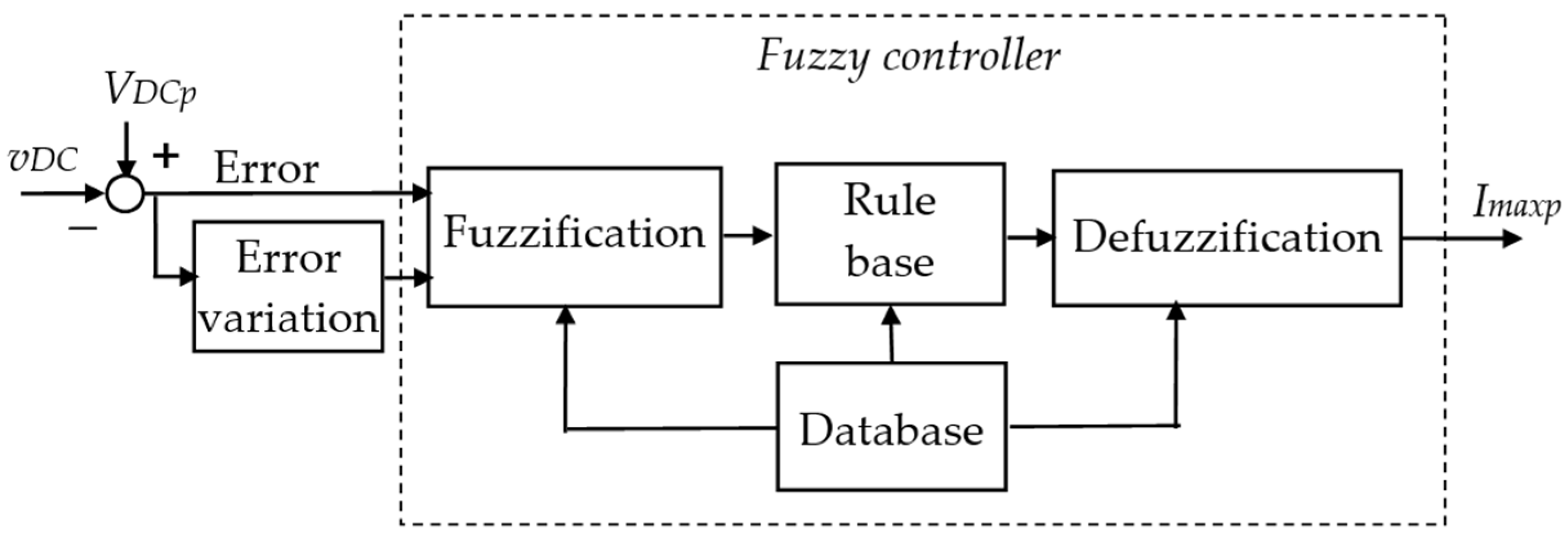
7. DC-Voltage Control
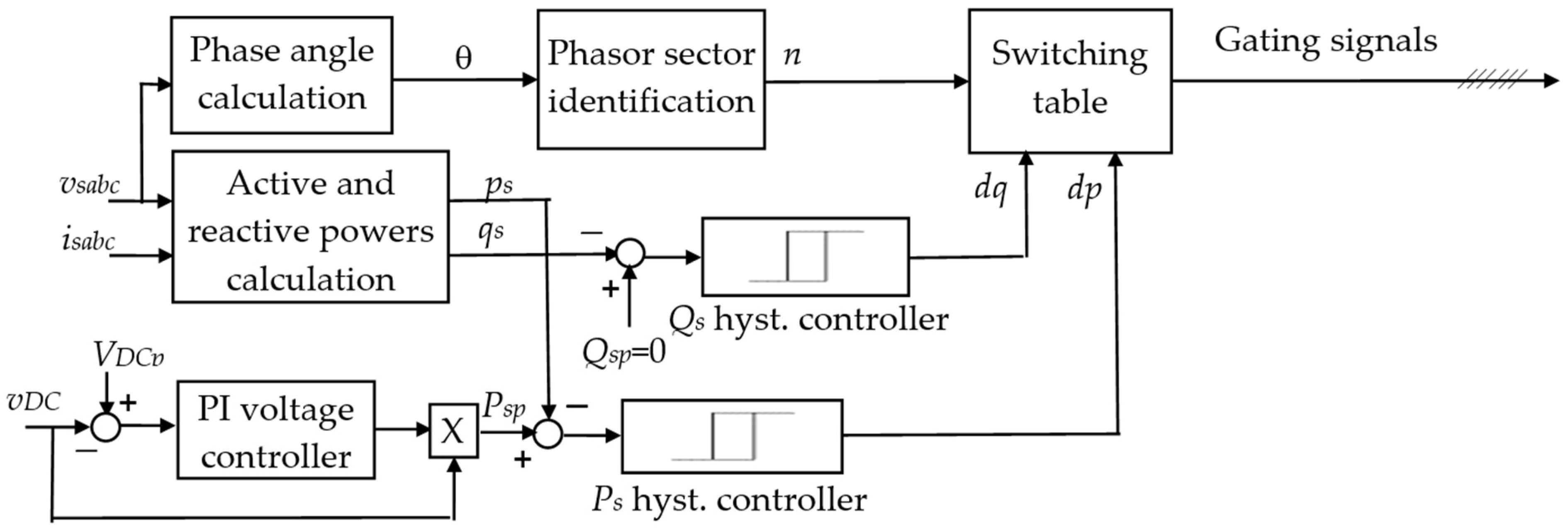
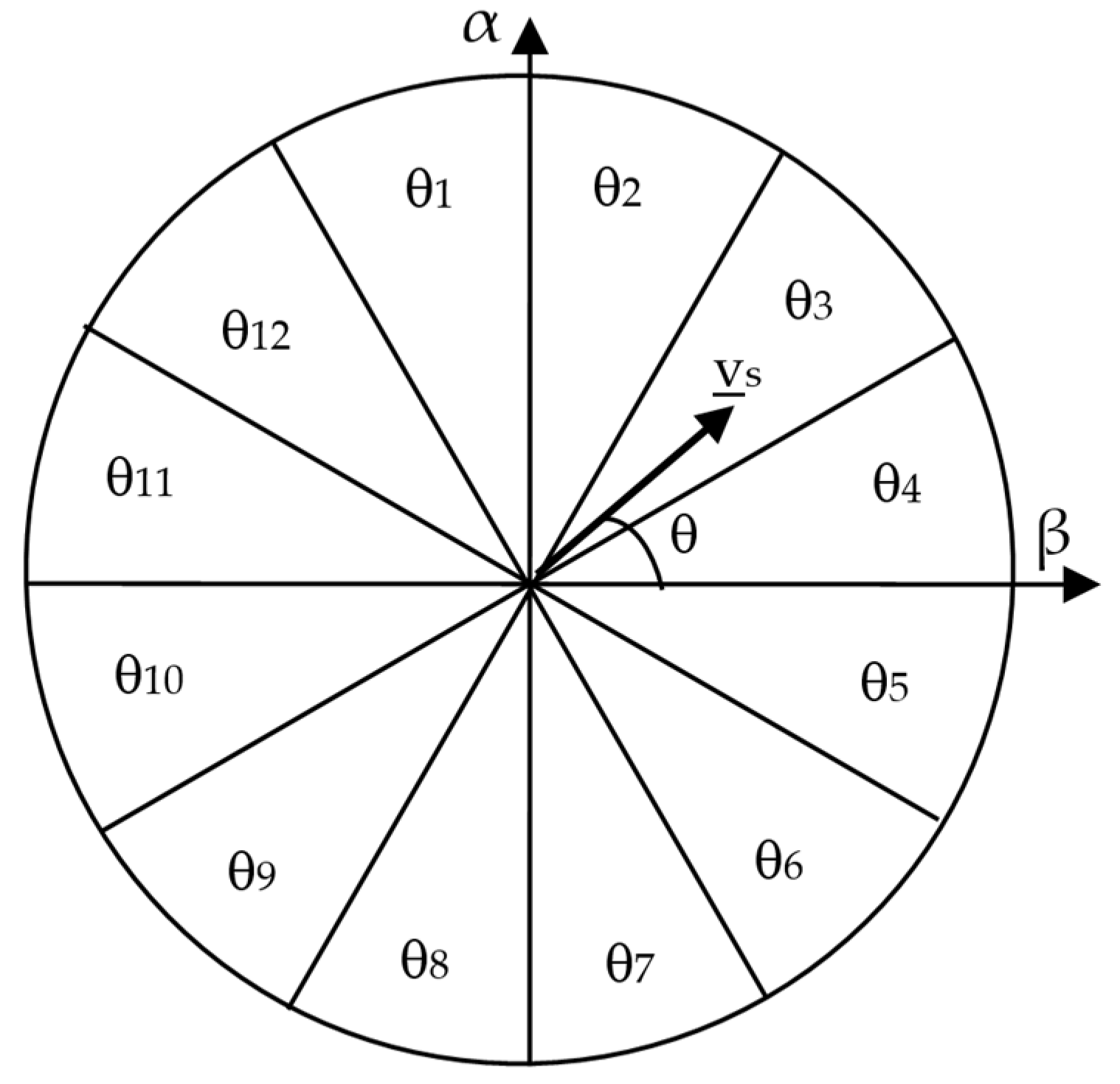
8. Direct Power Control
9. Renewable Energy Sources Integration with SAPF
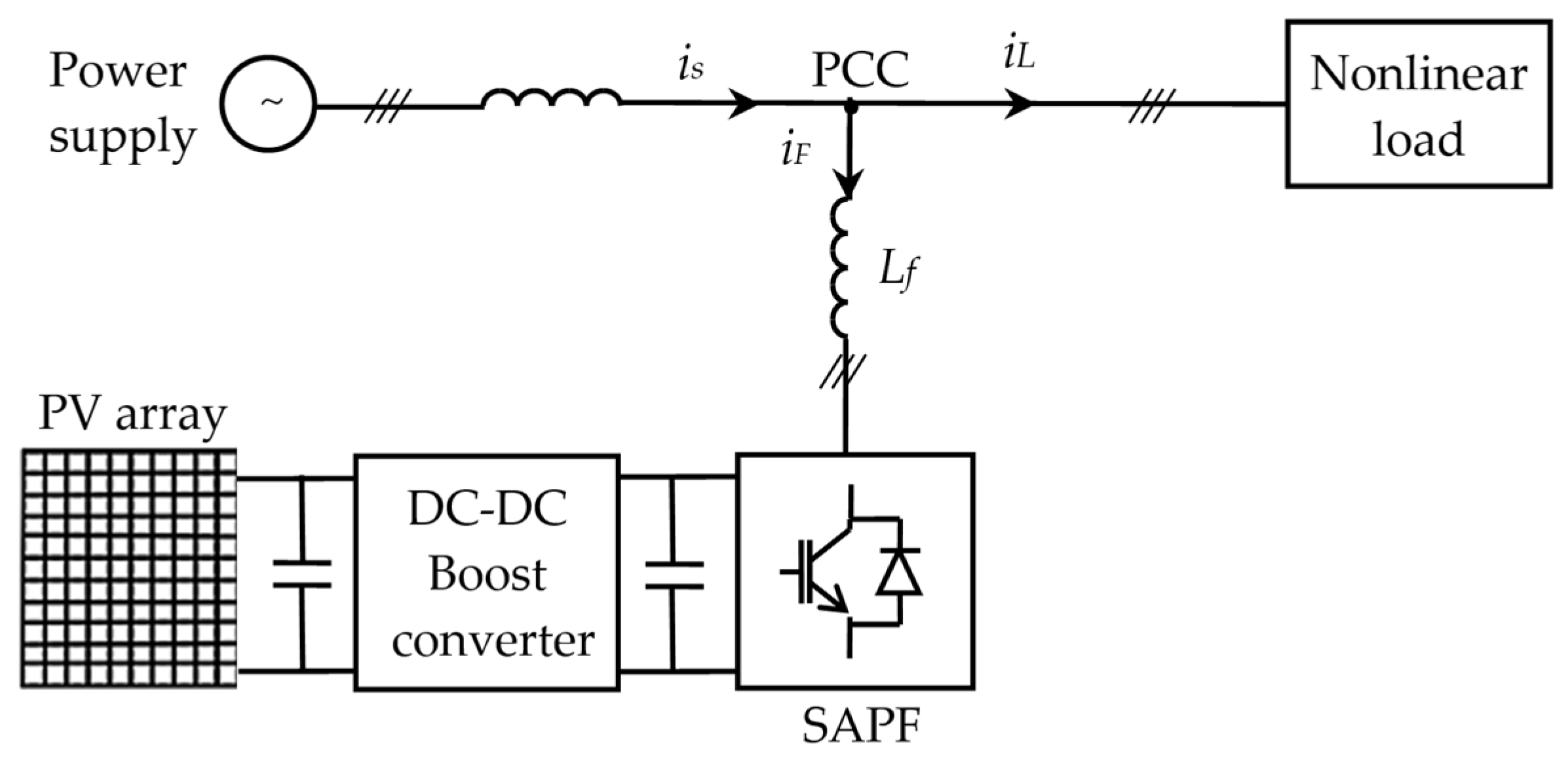
9.1. PV Integrated SAPF
9.2. Wind Energy Integrated SAPF
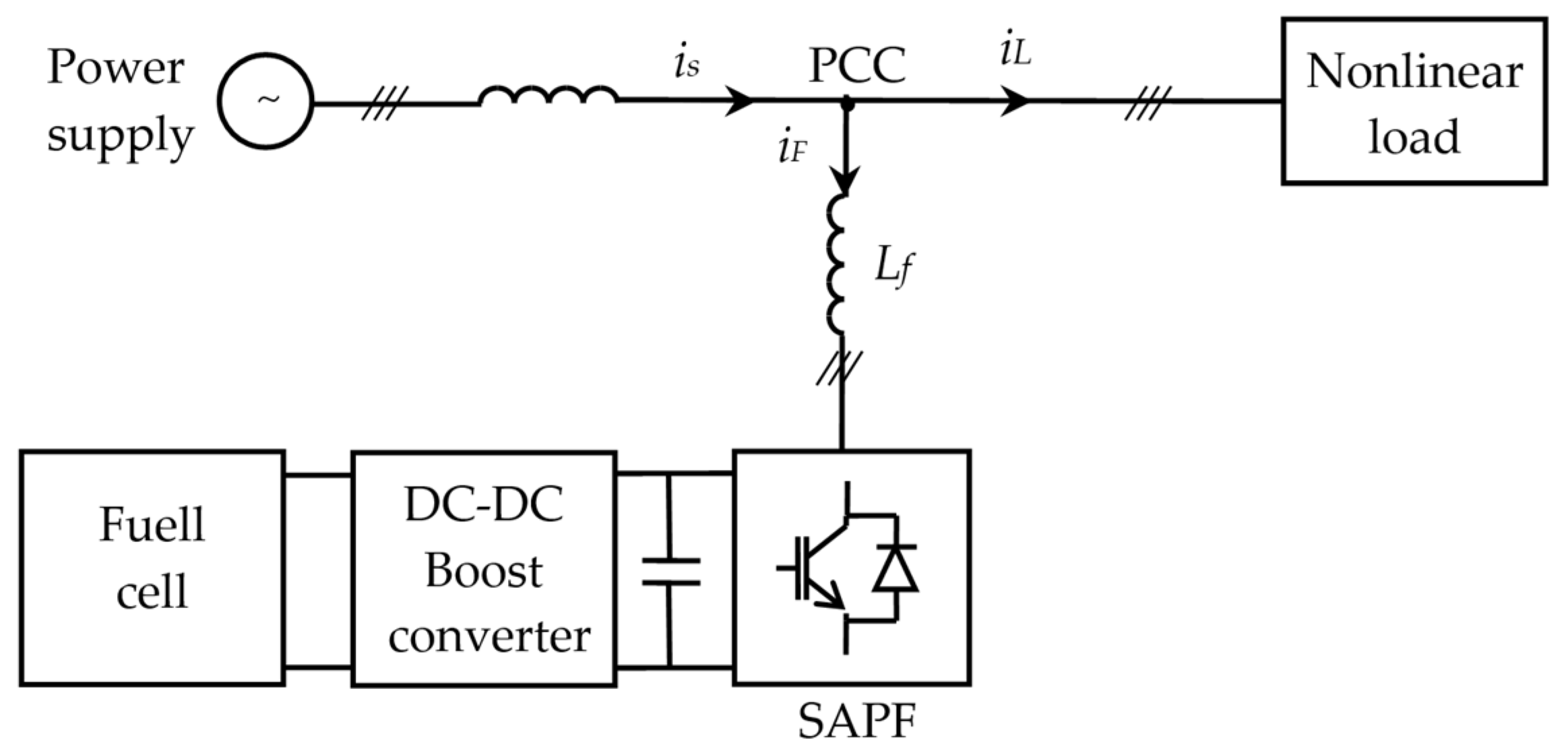
9.3. Fuel-Cell-Integrated SAPF
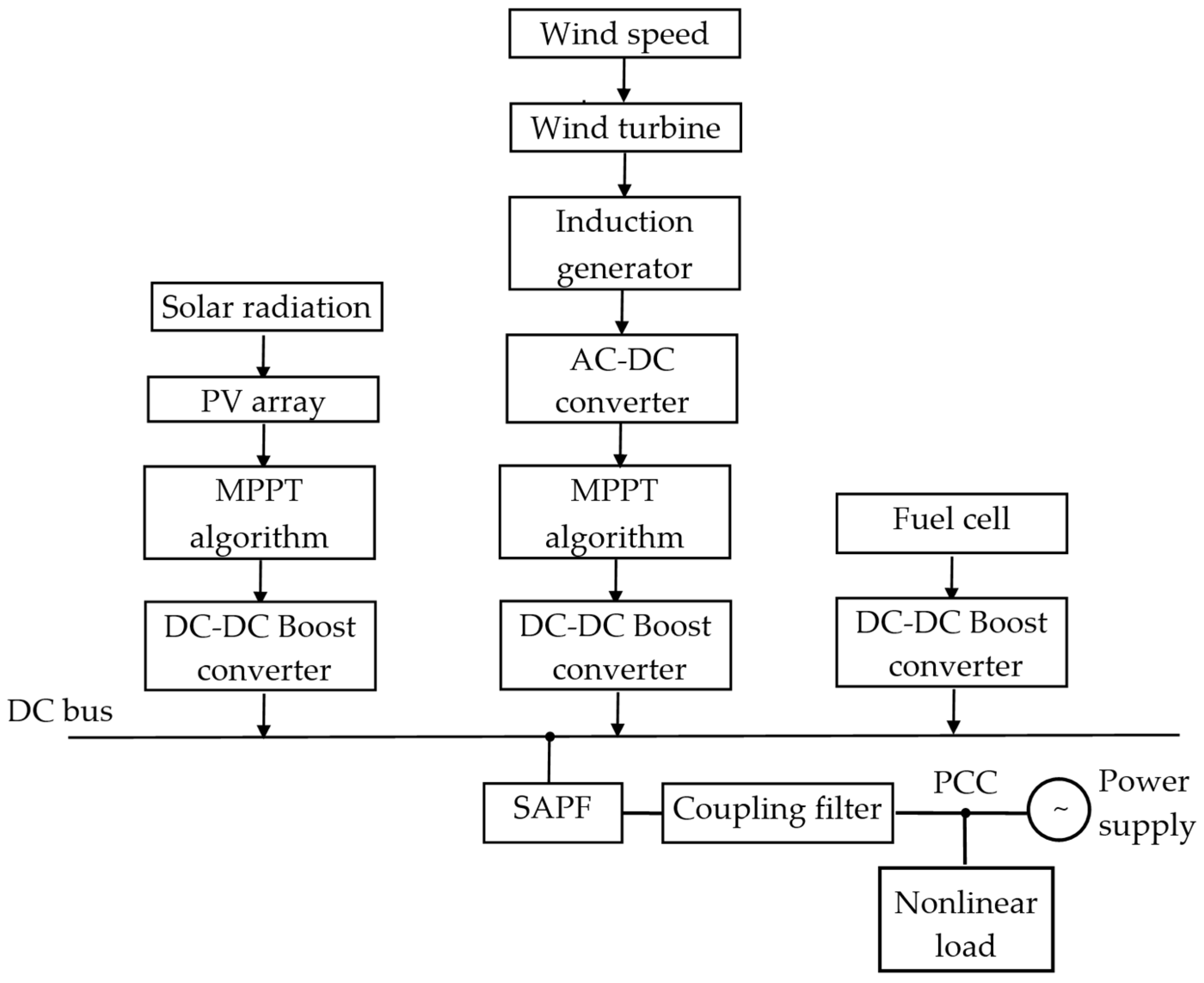
9.4. Hybrid Renewable Energy Sources Integration with SAPF
10. Optimizing the Sizing and Placement of SAPF
11. Trends and Future Developments
12. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACO | Ant Colony Optimization |
| ADALINE | Adaptive Linear Neurons |
| ANF | Adaptive Notch Filter |
| ANFIS | Adaptive Neuro Fuzzy Inference System |
| ANN | Artificial Neural Network |
| ANPC | Active Neutral Point Clamped |
| APF | Active Power Filter |
| BFO | Bacterial Foraging Optimization |
| CHB | Cascaded H-Bridge |
| CPC | Currents’ Physical Components |
| CPT | Conservative Power Theory |
| CSA | Cuckoo Search Algorithm |
| CSD | Current Synchronous Detection |
| CSI | Current Source Inverter |
| DC | Direct Current |
| DFT | Discrete Fourier Transform |
| DPC | Direct Power Control |
| DTC | Direct Torque Control |
| DWT | Discrete Wavelet Transform |
| EV | Electric Vehicle |
| FBD | Fryze–Buchholz–Depenbrock |
| FC | Flying Capacitor |
| FED | Fundamental Element Detection |
| FFT | Fast Fourier Transform |
| FIR | Finite Impulse Response |
| FRC | Fast Repetitive Control |
| GA | Genetic Algorithm |
| GaN | Gallium Nitride |
| GINAP | Generalized Instantaneous Non-Active Power |
| GIRP | Generalized Instantaneous Reactive Power |
| GTO | Gate Turn-Off Thyristor |
| GWO | Grey Wolf Optimizer |
| HPF | High-Pass Filter |
| IDWT | Inverse Discrete Wavelet Transform |
| IGBT | Insulated-Gate Bipolar Transistor |
| IFT | Inverse Discrete Fourier Transform |
| IUWPT | Inverse Undecimated Wavelet Packet Transform |
| IWPT | Inverse Wavelet Packet Transform |
| LESO | Linear Extended State Observer |
| LMS | Least Mean Square |
| LPF | Low-Pass Filter |
| LWT | Lifting Wavelet Transform |
| MOSFET | Metal Oxide Semiconductor Field-Effect Transistor |
| MPC | Model Predictive Control |
| MPM | Matrix Pencil Method |
| MPPT | Maximum Power Point Tracking |
| MRF-PLL | Multiple Reference Frame-Based PLL |
| NPC | Neutral-Point Diode Clamped |
| PCC | Point of Common Coupling |
| PI | Proportional-Integral |
| PLL | Phase-Locked Loop |
| PR | Proportional-Resonant |
| PSO | Particle Swarm Optimization |
| PSO-GWO | Particle Swarm Optimization-Grey Wolf Optimization |
| PV | Photovoltaic |
| PWM | Pulse Width Modulation |
| RB–IGBT | Reverse Blocking-Insulated Gate Bipolar Transistor |
| RDFT | Recursive Discrete Fourier Transform |
| RES | Renewable Energy Source |
| SAPF | Shunt Active Power Filter |
| SDFT | Sliding Discrete Fourier Transform |
| SGF | Savitzky–Golay Filter |
| SiC | Silicon Carbide |
| SMC | Sliding Mode Control |
| SOGI | Second Order Generalized Integrator |
| SPLL | Software Phase Lock Loop |
| SPWM | Sinusoidal Pulse Width Modulation |
| SRF | Synchronous Reference Frame |
| SVM | Support Vector Machine |
| SVPWM | Space Vector Pulse Width Modulation |
| TTA | Transformation Algorithm |
| UPF | Unity Power Factor |
| UWPT | Undecimated Wavelet Packet Transform |
| VSI | Voltage Source Inverter |
| WB-LPF | Wavelet-Based Low Pass Filter |
| ZCD | Zero Current Distortion |
| ZSI | Z-Source Inverter |
References
- Maciążek, M. Active power filters and power quality. Energies 2022, 15, 8483. [Google Scholar] [CrossRef]
- Das, S.R.; Ray, P.K.; Sahoo, A.K.; Ramasubbareddy, S.; Babu, T.S.; Kumar, N.M.; Elavarasan, R.M.; Mihet-Popa, L. A comprehensive survey on different control strategies and applications of active power filters for power quality improvement. Energies 2021, 14, 4589. [Google Scholar] [CrossRef]
- Li, D.; Wang, T.; Pan, W.; Ding, X.; Gong, J. A comprehensive review of improving power quality using active power filters. Electr. Power Syst. Res. 2021, 199, 107389. [Google Scholar] [CrossRef]
- Buła, D.; Grabowski, D.; Maciążek, M. A review on optimization of active power filter placement and sizing methods. Energies 2022, 15, 1175. [Google Scholar] [CrossRef]
- Afonso, J.L.; Tanta, M.; Pinto, J.G.O.; Monteiro, L.F.C.; Machado, L.; Sousa, T.J.C.; Monteiro, V. A review on power electronics technologies for power quality improvement. Energies 2021, 14, 8585. [Google Scholar] [CrossRef]
- Duc, M.L.; Hlavaty, L.; Bilik, P.; Martinek, R. Harmonic mitigation using meta-heuristic optimization for shunt adaptive power filters: A review. Energies 2023, 16, 3998. [Google Scholar] [CrossRef]
- Dehury, D.; Mishra, R.N.; Panda, R. Power quality enhancement by shunt active power filter employing different control strategies: A concise review. In Proceedings of the 1st International Conference on Circuits, Power and Intelligent Systems (CCPIS), Bhubaneswar, India, 1–3 September 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Smaida, E.; Saulo, M.J.; Abdellah, K.; Nyakoe, G.; Ahuna, M. Solar-powered shunt active power filter using an advanced inverter topology ZSI: A Review. In Proceedings of the 2023 IEEE Africon, Nairobi, Kenya, 20–22 September 2023; pp. 1–6. [Google Scholar] [CrossRef]
- IEEE Standard 519-2014; IEEE 519 Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. IEEE: New York, NY, USA, 2014.
- IEC Standard 61000-4-7; General Guide on Harmonics and Interharmonics Measurements, for Power Supply Systems and Equipment Connected Thereto. International Electrotechnical Commission (IEC): Geneva, Switzerland, 2010.
- IEC Standard 61000-4-30; Testing and Measurement Techniques-Power Quality Measurement Methods. International Electrotechnical Commission (IEC): Geneva, Switzerland, 2015.
- Luo, A.; Shuai, Z.; Zhu, W.; Shen, Z.J.; Tu, C. Design and application of a hybrid active power filter with injection circuit. IET Power Electron. 2010, 3, 54–64. [Google Scholar] [CrossRef]
- Shuai, Z.; Luo, A.; Shen, J.; Wang, X. Double closed-loop control method for injection-type hybrid active power filter. IEEE Trans. Power Electron. 2011, 26, 2393–2403. [Google Scholar] [CrossRef]
- Shuai, Z.; Luo, A.; Tu, C.; Liu, D. New control method of injection-type hybrid active power filter. IET Power Electron. 2011, 4, 1051–1057. [Google Scholar] [CrossRef]
- Asiminoaei, L.; Aeloiza, E.; Kim, J.H.; Enjeti, P.; Blaabjerg, F.; Moran, L.T.; Sul, S.K. Parallel interleaved inverters for reactive power and harmonic compensation. In Proceedings of the 2006 37th IEEE Power Electronics Specialists Conference, Jeju, Republic of Korea, 18–22 June 2006; pp. 1–7. [Google Scholar] [CrossRef]
- Asiminoaei, L.; Aeloiza, E.; Kim, J.H.; Enjeti, P.; Blaabjerg, F.; Moran, L.T.; Sul, S.K. An interleaved active power filter with reduced size of passive components. In Proceedings of the Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 19–23 March 2006. [Google Scholar] [CrossRef]
- Asiminoaei, L.; Aeloiza, E.; Enjeti, P.N.; Blaabjerg, F. Shunt active-power-filter topology based on parallel interleaved inverters. IEEE Trans. Ind. Electron. 2008, 55, 1175–1189. [Google Scholar] [CrossRef]
- Lin, H.; Wang, X.; Chen, D.; Guo, X.; Chen, G. A control method for the interleaved active power filter with SiC-MOSFETs. Energy Rep. 2022, 8, 400–407. [Google Scholar] [CrossRef]
- Souza, L.L.; Rocha, N.; Fernandes, D.A.; Sousa, R.P.R.; Jacobina, C.B. Grid harmonic current correction based on parallel three-phase shunt active power filter. IEEE Trans. Power Electron. 2022, 37, 1422–1434. [Google Scholar] [CrossRef]
- Hoon, Y.; Mohd Radzi, M.A.; Hassan, M.K.; Mailah, N.F. Control Algorithms of Shunt Active Power Filter for Harmonics Mitigation: A Review. Energies 2017, 10, 2038. [Google Scholar] [CrossRef]
- Vodyakho, O.; Mi, C.C. Three-level inverter-based shunt active power filter in three-phase three-wire and four-wire systems. IEEE Trans. Power Electron. 2009, 24, 1350–1363. [Google Scholar] [CrossRef]
- Mehrasa, M.; Pouresmaeil, E.; Akorede, M.F.; Jørgensen, B.N.; Catalão, J.P.S. Multilevel converter control approach of active power filter for harmonics elimination in electric grids. Energy 2015, 84, 722–731. [Google Scholar] [CrossRef]
- Kashif, M.; Hossain, M.J.; Zhuo, F.; Gautam, S. Design and implementation of a three-level active power filter for harmonic and reactive power compensation. Electr. Power Syst. Res. 2018, 165, 144–156. [Google Scholar] [CrossRef]
- Ranjan, A.; Bhaskar, D.V. Grid Resilience enhancement through TPTL NPC inverter-based shunt active power filters with dual fundamental component extraction. In Proceedings of the 2023 IEEE 2nd Industrial Electronics Society Annual On-Line Conference (ONCON), Online, 8–10 December 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, Z.; Sha, M.; Zhu, R.; Hu, S. Designing a new control method for three-level active power filter. In Proceedings of the 2023 3rd International Conference on New Energy and Power Engineering (ICNEPE), Huzhou, China, 24–26 November 2023; pp. 311–314. [Google Scholar] [CrossRef]
- Guo, X.; Lin, H.; Chen, G. SiC-MOSFET shunt active power filter based on half-cycle SDFT and repetitive control. Energy Rep. 2021, 7, 246–252. [Google Scholar] [CrossRef]
- Lin, H.; Guo, X.; Chen, D.; Wu, S.; Chen, G. A frequency adaptive repetitive control for active power filter with 380V/75A SiC-inverter. IEEE Trans. Ind. Appl. 2022, 58, 5469–5479. [Google Scholar] [CrossRef]
- Ou, M.; Zou, J.; Liu, Q.; Yang, H. A dual-loop control strategy based on PI and repetitive control for APF with CoolSiC™ MOSFET. In Proceedings of the 2023 6th International Conference on Electrical Engineering and Green Energy (CEEGE), Grimstad, Norway, 6–9 June 2023; pp. 29–34. [Google Scholar] [CrossRef]
- Buyukdegirmenci, V.T.; Sozuer, A.; Milletsever, O.C.; Kozarva, O.F.; Oz, T.; Hava, A.M. Considerations for inverter topology selection and limitations in active power filtering applications. In Proceedings of the 2022 IEEE Power and Energy Conference at Illinois (PECI), Champaign, IL, USA, 10–11 March 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Ma, C.-T.; Gu, Z.-H. Design and implementation of a GaN-based three-phase active power filter. Micromachines 2020, 11, 134. [Google Scholar] [CrossRef]
- Kumar, P.; Mahajan, A. soft computing techniques for the control of an active power filter. IEEE Trans. Power Deliver. 2009, 24, 452–461. [Google Scholar] [CrossRef]
- Kumar, R.; Bnsal, H.O. Shunt active power filter: Current status of control techniques and its integration to renewable energy sources. Sustain. Cities Soc. 2018, 42, 2210–6707. [Google Scholar] [CrossRef]
- Dubey, A.K.; Mishra, I.P.; Kumar, A. Comparative analysis of ROGI based shunt active power filter under current fed and voltage fed type non-linear loading condition. IFAC-Pap. 2022, 55, 156–161. [Google Scholar] [CrossRef]
- Tareen, W.U.K.; Aamir, M.; Mekhilef, S.; Nakaoka, M.; Seyedmahmoudian, M.; Horan, B.; Memon, M.A.; Baig, N.A. Mitigation of power quality issues due to high penetration of renewable energy sources in electric grid systems using three-phase APF/STATCOM Technologies: A Review. Energies 2018, 11, 1491. [Google Scholar] [CrossRef]
- Janpong, S.; Areerak, K.; Areerak, K. Harmonic Detection for Shunt Active Power Filter Using ADALINE Neural Network. Energies 2021, 14, 4351. [Google Scholar] [CrossRef]
- Sharma, S.; Verma, V. Modified control strategy for shunt active power filter with MRAS-based DC voltage estimation and load current sensor reduction. IEEE Trans. Ind. Appl. 2021, 57, 1652–1663. [Google Scholar] [CrossRef]
- Eslami, A.; Negnevitsky, M.; Franklin, E.; Lyden, S. An intelligent active power filter to mitigate harmonics and interharmonics. In Proceedings of the 2022 20th International Conference on Harmonics & Quality of Power (ICHQP), Naples, Italy, 29 May 2022–1 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Jai, A.A.; Ouassaid, M. Machine learning-based ADALINE neural PQ strategy for a photovoltaic integrated shunt active power filter. IEEE Access 2023, 11, 56593–56618. [Google Scholar] [CrossRef]
- Madhusudhan Reddy, M.; Srinivasa Varma, P.; Lenine, D. Improving gain of real time PI controller using particle swarm optimization in active power filter. Microprocess. Microsyst. 2023, 97, 104760. [Google Scholar] [CrossRef]
- Tao, Z.; Wang, R.; Wang, S.; Zhang, Y. Harmonic detection of active power filter based on improved gray wolf algorithm with optimized VMD. In Proceedings of the 2023 3rd International Conference on Electrical Engineering and Mechatronics Technology (ICEEMT), Nanjing, China, 21–23 July 2023; pp. 47–50. [Google Scholar] [CrossRef]
- Subash Kumar, C.S.; Rajasekar, P.; Sathiyanathan, M.; Venkatesan, M. FPGA implementation of optimum switching angle control for shunt active filter using ANNSVPWM. Int. J. Electron. 2022, 109, 1532–1549. [Google Scholar] [CrossRef]
- Zakaria, L.; Amar, B. Neural network controller for three phase shunt active power filter using self tuning filter. In Proceedings of the 2022 19th International Multi-Conference on Systems, Signals & Devices (SSD), Sétif, Algeria, 6–10 May 2022; pp. 333–338. [Google Scholar] [CrossRef]
- Rezapour, H.; Fathnia, F.; Fiuzy, M.; Falaghi, H.; Lopes, A.M. Enhancing power quality and loss optimization in distorted distribution networks utilizing capacitors and active power filters: A simultaneous approach. Int. J. Electr. Power Energy Syst. 2024, 155, 109590. [Google Scholar] [CrossRef]
- Vahedi, H.; Sheikholeslami, A.; Bina, M.T.; Vahedi, M. Review and simulation of fixed and adaptive hysteresis current control considering switching losses and high-frequency harmonics. Adv. Power Electron. 2011, 2011, 397872. [Google Scholar] [CrossRef]
- Mahanty, R. Indirect current controlled shunt active power filter for power quality improvement. Int. J. Electr. Power Energy Syst. 2014, 62, 441–449. [Google Scholar] [CrossRef]
- Palpandian, A.R.; Chaoui, H. Power Quality improvement of the grid system with advanced hysteresis controller design. In Proceedings of the 2023 IEEE 14th International Conference on Power Electronics and Drive Systems (PEDS), Montreal, QC, Canada, 7–10 August 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Guzman, R.; de Vicuña, L.G.; Morales, J.; Castilla, M.; Miret, J. Model-based control for a three-phase shunt active power filter. IEEE Trans. Ind. Electron. 2016, 63, 3998–4007. [Google Scholar] [CrossRef]
- Biswal, C.; Panigrahi, R.; Patjoshi, R. Experimental investigation of shunt active power filter for power quality enhancement. In Proceedings of the 2023 IEEE Renewable Energy and Sustainable E-Mobility Conference (RESEM), Bhopal, India, 17–18 May 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Barik, P.K.; Shankar, G.; Sahoo, P.K.; Elavarasan, R.M.; Kumar, S.; Ibanez, F.M.; Houran, M.A.; Srivastava, A.K.; Terzija, V. A novel negative feedback phase locked loop-based reference current generation technique for shunt active power filter. Int. J. Electr. Power Energy Syst. 2023, 153, 109389. [Google Scholar] [CrossRef]
- Misra, B.; Tripathy, P.; Mohanty, R.; Sahoo, S.R.; Nayak, B. Performance analysis of an adaptive hysteresis band current controller based active power filter. In Proceedings of the 2022 Second International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 21–22 April 2022 ; pp. 1–5. [Google Scholar] [CrossRef]
- Pérez-Guzmán, R.E.; Rivera, M.; Wheeler, P.W. Recent advances of predictive control in power converters. In Proceedings of the 2020 IEEE International Conference on Industrial Technology (ICIT), Buenos Aires, Argentina, 26–28 February 2020; pp. 1100–1105. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model predictive control for power converters and drives: Advances and trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef]
- Lin, J.; Yang, M. A new method of active power filter using dead beat control and repeated control. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 27–29 2022; pp. 484–488. [Google Scholar] [CrossRef]
- Chen, J.; Shao, H.C.; Liu, C. An improved deadbeat control strategy based on repetitive prediction against grid frequency fluctuation for active power filter. IEEE Access 2021, 9, 24646–24657. [Google Scholar] [CrossRef]
- Pichan, M.; Seyyedhosseini, M.; Hafezi, H. A new deadbeat-based direct power control of shunt active power filter with digital implementation delay compensation. IEEE Access 2022, 10, 72866–72878. [Google Scholar] [CrossRef]
- Zhou, L.; Zhou, Z.; Qi, J.; Han, W. Hybrid prediction-based deadbeat control for a high-performance shunt active power filter. IEEE Access 2023, 11, 11118–11131. [Google Scholar] [CrossRef]
- Ouchen, S.; Benbouzid, M.; Blaabjerg, F.; Betka, A.; Steinhart, H. Direct power control of shunt active power filter using space vector modulation based on supertwisting sliding mode control. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 3243–3253. [Google Scholar] [CrossRef]
- Elallali, A.; Abouloifa, A.; Lachkar, I.; Taghzaoui, C.; Giri, F.; Mchaouar, Y. Nonlinear control of grid-connected PV systems using active power filter with three-phase three-level NPC inverter. IFAC-Pap. 2022, 55, 61–66. [Google Scholar] [CrossRef]
- Swetha, K.V.S. Comparative analysis and performance of DSTATCOM device using PI and second-order sliding mode control. Artif. Intell. Evol. Comput. Eng. Syst. 2020, 1056, 193–203. [Google Scholar] [CrossRef]
- Chen, B.; Wu, W.; Gao, C.; Orabi, M.; Koutroulis, E.; Chung, H.; Blaabjerg, F. A new stability enhancement method using KF estimation for the PWM-SMC-based grid-tied inverter under weak grid condition. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 6950–6959. [Google Scholar] [CrossRef]
- Ullah, I.; Ashraf, M. Sliding mode control for performance improvement of shunt active power filter. SN Appl. Sci. 2019, 1, 531. [Google Scholar] [CrossRef]
- Yang, S.; Wang, P.; Tang, Y.; Zhang, L. Explicit phase lead filter design in repetitive control for voltage harmonic mitigation of VSI-based islanded microgrids. IEEE Trans. Ind. Electron. 2017, 64, 817–826. [Google Scholar] [CrossRef]
- Khajehoddin, S.A.; Karimi-Ghartemani, M.; Jain, P.K.; Bakhshai, A. A resonant controller with high structural robustness for fixed-point digital implementations. IEEE Trans. Power Electron. 2012, 27, 3352–3362. [Google Scholar] [CrossRef]
- Gao, C.; He, S.; Cui, B.; Zhang, B.; Ming, L.; Leung, K.N.; Loh, P.C. Quantization effects on digital-PR-controlled active power filter. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 5785–5797. [Google Scholar] [CrossRef]
- Puhan, P.S.; Ray, P.K.; Pottapinjara, S. Performance analysis of shunt active filter for harmonic compensation under various non-linear loads. Int. J. Emerg. Electr. Power Syst. 2021, 22, 21–29. [Google Scholar] [CrossRef]
- Santiprapan, P.; Areerak, K.; Areerak, K. An adaptive gain of proportional-resonant controller for an active power filter. IEEE Trans. Power Electron. 2024, 39, 1433–1446. [Google Scholar] [CrossRef]
- Sou, W.K.; Chao, C.W.; Gong, C.; Lam, C.S.; Wong, C.K. Analysis, design, and implementation of multi-quasi-proportional-resonant controller for thyristor-controlled LC-coupling hybrid active power filter (TCLC-HAPF). IEEE Trans. Ind. Electron. 2022, 69, 29–40. [Google Scholar] [CrossRef]
- Liu, D.; Li, B.; Huang, S.; Liu, L.; Wang, H.; Huang, Y. An Improved Frequency-Adaptive Virtual Variable Sampling-Based Repetitive Control for an Active Power Filter. Energies 2022, 15, 7227. [Google Scholar] [CrossRef]
- Xu, H.; Peng, L.; Hu, K.; Chen, M. Vector repetitive control based on harmonic sequence extraction for shunt active power filters. In Proceedings of the 2022 IEEE 13th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Kiel, Germany, 26–29 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Geng, H.; Zheng, Z.; Zou, T.; Chu, B.; Chandra, A. fast repetitive control with harmonic correction loops for shunt active power filter applied in weak grid. IEEE Trans. Ind. Appl. 2019, 55, 3198–3206. [Google Scholar] [CrossRef]
- Chen, Z.; Zha, H.; Peng, K.; Yang, J.; Yan, J. A design method of optimal PID-based repetitive control systems. IEEE Access 2020, 8, 139625–139633. [Google Scholar] [CrossRef]
- Pan, G.; Gong, F.; Jin, L.; Wu, H.; Chen, S. LCL APF based on fractional-order fast repetitive control strategy. J. Power Electron. 2021, 21, 1508–1519. [Google Scholar] [CrossRef]
- Azghandi, M.A.; Barakati, S.M.; Sahranavard, M.R. Multi-loop control of a current-source active power filter for harmonics mitigation in distribution systems. In Proceedings of the 2023 27th International Electrical Power Distribution Networks Conference (EPDC), Mashhad, Iran, Islamic Republic of Iran, 2–4 May 2023; pp. 186–190. [Google Scholar] [CrossRef]
- Yang, L.; Yang, J. A robust dual-loop current control method with a delay-compensation control link for LCL-type shunt active power filters. IEEE Trans. Ind. Electron. 2019, 34, 6183–6199. [Google Scholar] [CrossRef]
- Shen, Y.Y.; Tsai, M.J.; Zhou, J.; Cheng, P.-T. A hybrid multi-loop current control of the grid-connected converter with LCL filter. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 5409–5415. [Google Scholar] [CrossRef]
- Sivadas, D.; Vasudevan, K. Stability analysis of three-loop control for three-phase voltage source inverter interfaced to the grid based on state variable estimation. IEEE Trans. Ind. Appl. 2018, 54, 6508–6518. [Google Scholar] [CrossRef]
- Loh, P.C.; Holmes, D.G. Analysis of multiloop control strategies for LC/CL/LCL-filtered voltage-source and current-source inverters. IEEE Trans. Ind. Appl. 2005, 41, 644–654. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, N.C. Novel multiple-loop composite control strategy for active power filter. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Mishra, M.K.; Lal, V.N. An advanced proportional multiresonant controller for enhanced harmonic compensation with power ripple mitigation of grid-integrated PV systems under distorted grid voltage conditions. IEEE Trans. Ind. Appl. 2021, 57, 5318–5331. [Google Scholar] [CrossRef]
- Hans, F.; Schumacher, W.; Chou, S.F.; Wang, X. Design of multifrequency proportional–resonant current controllers for voltage-source converters. IEEE Trans. Power Electron. 2020, 35, 13573–13589. [Google Scholar] [CrossRef]
- Xie, C.; Zhao, X.; Li, K.; Zou, J.; Guerrero, J.M. Multirate resonant controllers for grid-connected inverters with harmonic compensation function. IEEE Trans. Ind. Electron. 2019, 66, 8981–8991. [Google Scholar] [CrossRef]
- Ufnalski, B.; Michalczuk, M.; Galecki, A. Robust tuning of multiresonant current controllers for grid-tied converters and erroneous use of the Naslin polynomial method. IEEE Access 2022, 10, 88211–88225. [Google Scholar] [CrossRef]
- Xie, C.; Zhao, X.; Li, K.; Zou, J.; Guerrero, J.M. A new tuning method of multiresonant current controllers for grid-connected voltage source converters. IEEE J. Emerg. Sel. Topics Power Electron. 2019, 7, 458–466. [Google Scholar] [CrossRef]
- Saad, S.; Zellouma, L. Fuzzy logic controller for three-level shunt active filter compensating harmonics and reactive power. Electr. Power Syst. Res. 2009, 79, 1337–1341. [Google Scholar] [CrossRef]
- Malvezzi, V.B.; da Silva, S.A.O.; Campanhol, L.B.G.; Angélico, B.A. A comparative analysis between the PI and fuzzy controllers for current conditioning using a shunt active power filter. In Proceedings of the 2013 Brazilian Power Electronics Conference, Gramado, Brazil, 10 April 2013; pp. 981–986. [Google Scholar] [CrossRef]
- Amoozegar, D. DSTATCOM modelling for voltage stability with fuzzy logic PI current controller. Int. J. Electr. Power Energy Syst. 2016, 76, 129–135. [Google Scholar] [CrossRef]
- Salam, A.A.; Azran Ab Hadi, N. Fuzzy logic controller for shunt active power filter. In Proceedings of the 2014 4th International Conference on Engineering Technology and Technopreneuship (ICE2T), Kuala Lumpur, Malaysia, 27–29 August 2014; pp. 256–259. [Google Scholar] [CrossRef]
- Sayahi, K.; Faouzi, B. STATCOM/APF control using two proposed DPC strategies for power quality improvement. In Proceedings of the 2021 IEEE 2nd International Conference on Signal, Control and Communication (SCC), Tunis, Tunisia, 20–22 December 2021; pp. 270–275. [Google Scholar] [CrossRef]
- Ouchen, S.; Benlaloui, I.; Khamari, D.; Boutabba, T.; Benmessaoud, F.; Betka, A. Comparative study between DPC and PDPC controls applied on shunt active power filter. In Proceedings of the 2022 5th International Conference on Power Electronics and their Applications (ICPEA), Hail, Saudi Arabia, 29–31 March 2022; pp. 1–5. [Google Scholar] [CrossRef]
- da Cruz Ferreira, R.; De Morais Martins, P.H.; Rocha, N.; Da Silva, E.R.C.; Melo, V.F.M.B. Comparison between conventional and model predictive control for direct power control applied to a shunt active power filter. In Proceedings of the 2023 IEEE 8th Southern Power Electronics Conference and 17th Brazilian Power Electronics Conference (SPEC/COBEP), Florianopolis, Brazil, 26–29 November 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Kim, J.C.; Park, J.C.; Kwak, S. Predictive direct power control technique for voltage source converter with high efficiency. IEEE Access 2018, 6, 23540–23550. [Google Scholar] [CrossRef]
- Bekakra, Y.; Zellouma, L.; Malik, O. Improved predictive direct power control of shunt active power filter using GWO and ALO –Simulation and experimental study. Ain Shams Eng. J. 2021, 12, 3859–3877. [Google Scholar] [CrossRef]
- Ouchen, S.; Betka, A.; Abdeddaim, S.; Menadi, A. Fuzzy-predictive direct power control implementation of a grid connected photovoltaic system, associated with an active power filter. Energy Convers. Manag. 2016, 122, 515–525. [Google Scholar] [CrossRef]
- Kamel, S.; Kadri, A.; Faouzi, B. Real-time implementation of a static compensator (STATCOM) / Active power filter for power quality improvement based on improved VF-DPC control strategy. In Proceedings of the 2022 8th International Conference on Control, Decision and Information Technologies (CoDIT), Istanbul, Turkey, 17–20 May 2022; pp. 1444–1449. [Google Scholar] [CrossRef]
- Ouchen, S.; Steinhart, H.; Benbouzid, M.; Blaabjerg, F. Robust DPC-SVM control strategy for shunt active power filter based on H∞ regulators. Int. J. Electr. Power Energy Syst. 2020, 117, 105699. [Google Scholar] [CrossRef]
- Belonkar, A.N.; Salodkar, M.R. Performance analysis of shunt active power filter with different switching signal generation techniques. Int. J. Sci. Res. 2015, 4, 331–336. [Google Scholar]
- Chelladurai, J.; Saravana Ilango, G.; Nagamani, C.; Senthil Kumar, S. Investigation of various PWM techniques for shunt active filter. Int. J. Elect. Eng. Elect. Syst. 2008, 1, 87–93. [Google Scholar]
- Rathnakumar, D.; LakshmanaPerumal, J.; Srinivasan, T. A new software implementation of space vector PWM. In Proceedings of the IEEE Southeastcon, Ft. Lauderdale, FL, USA, 8–10 April 2005; pp. 131–136. [Google Scholar]
- Benchouia, M.T.; Ghadbane, I.; Golea, A.; Srairi, K.; Benbouzid, M.H. Design and implementation of sliding mode and PI controllers based control for three phase shunt active power filter. Energy Procedia 2014, 50, 504–511. [Google Scholar] [CrossRef]
- Han, C.; Xinyan, Y.; Pengfei, J.; Bingyuan, Y.; Ke, D. Dynamic optimization for shunt active power filter to selectively extract harmonics with Vector Discrete Fourier Transform. In Proceedings of the 2023 IEEE 14th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Shanghai, China, 9–12 June 2023; pp. 971–977. [Google Scholar] [CrossRef]
- Majji, R.K.; Mishra, J.P.; Dongre, A.A. Extension p-q theory based MPCC strategy for shunt active power filter operation under dynamic loading scenario. In Proceedings of the 2022 IEEE Silchar Subsection Conference (SILCON), Silchar, India, 4–6 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Mikkili, S.; Padamati, A. PHC, Id-Iq and p-q control strategies for mitigation of current harmonics in three-phase three-wire shunt active filter with PI controller. Int. J. Emerg. Electr. Power Syst. 2017, 18, 20160055. [Google Scholar] [CrossRef]
- Daramukkala, P.; Mohanty, K.B.; Karthik, M.; Swain, S.D.; Behera, B.P. Normalized sigmoid function LMS adaptive filter based shunt hybrid active power filter for power quality improvement. In Proceedings of the 2023 IEEE IAS Global Conference on Renewable Energy and Hydrogen Technologies (GlobConHT), Male, Maldives, 11–12 March 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Lahiouel, Y.; Latreche, S.; Afghoul, H. Experimental realization using a dSPACE card of the PI control for an active power filter. In Proceedings of the 2022 19th International Multi-Conference on Systems, Signals & Devices (SSD), Sétif, Algeria, 6–10 May 2022; pp. 53–57. [Google Scholar] [CrossRef]
- Xiao, Z.; Xue, H.; Liu, T.; Zheng, G. Research on control strategy of shunt active power filter. In Proceedings of the 2023 8th Asia Conference on Power and Electrical Engineering (ACPEE), Tianjin, China, 14–16 April 2023; pp. 2377–2382. [Google Scholar] [CrossRef]
- El Korfolly, M.I.; Htita, I.; Elmasry, S.; Abdalla, O.H. Harmonic mitigation of variable speed drive with shunt active filter connected via LCL coupler. In Proceedings of the 2023 24th International Middle East Power System Conference (MEPCON), Mansoura, Egypt, 19–21 December 2023; pp. 1–7. [Google Scholar] [CrossRef]
- Shailly, D.; Chittora, P.; Singh, M. Comparative performance analysis of modern digital filters for power quality improvement using distributed static compensator (DSTATCOM). In Proceedings of the 2023 International Conference on Computer, Electronics & Electrical Engineering & their Applications (IC2E3), Srinagar Garhwal, India, 8–9 June 2023; pp. 1–7. [Google Scholar] [CrossRef]
- Popescu, M.; Bitoleanu, A.; Suru, V. A DSP-based implementation of the p-q theory in active power filtering under nonideal voltage conditions. IEEE Trans. Ind. Inf. 2013, 9, 880–889. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Y.; Wu, Y.; Zhang, S.; Han, X. Research on DC voltage control of APF based on improved fuzzy PI control. In Proceedings of the 2022 IEEE International Conference on Mechatronics and Automation (ICMA), Guilin, China, 7–10 August 2022; pp. 174–179. [Google Scholar] [CrossRef]
- Suru, C.V.; Popescu, M.; Linca, M.; Stanculescu, A. Fuzzy logic controller implementation for the compensating capacitor voltage of an indirect current controlled active filter. In Proceedings of the 2020 International Conference and Exposition on Electrical and Power Engineering (EPE), Iasi, Romania, 22–23 October 2020; pp. 039–044. [Google Scholar] [CrossRef]
- Deffaf, B.; Farid, H.; Benbouhenni, H.; Medjmadj, S.; Debdouche, N. Synergetic control for three-level voltage source inverter-based shunt active power filter to improve power quality. Energy Rep. 2023, 10, 1013–1027. [Google Scholar] [CrossRef]
- Li, Z.; Ren, M.; Chen, Z.; Liu, G.; Feng, D. A bi-sliding mode PI control of DC-link voltage of three-phase three-wire shunt active power filter. IEEE J. Emerg. Sel. Topics Power Electron. 2022, 10, 7581–7588. [Google Scholar] [CrossRef]
- Deffaf, B.; Hamoudi, F.; Debdouche, N. Sliding mode control of a shunt active filter-comparative analysis with conventional PI control. In Proceedings of the 2022 19th International Multi-Conference on Systems, Signals & Devices (SSD), Sétif, Algeria, 6–10 May 2022; pp. 1422–1427. [Google Scholar] [CrossRef]
- Mousavi, M.S.; Jalilian, A.; Asadi, M. A sliding mode control method of dc-link capacitor voltage used in active power filter. In Proceedings of the 2015 30th International Power System Conference (PSC), Tehran, Iran, 23–25 November 2015; pp. 123–128. [Google Scholar] [CrossRef]
- Hoang, Q.-M.; Nguyễn, B.-H.; Vo-Duy, T.; Trovão, J.P.F.; Ta, M.C. Active power filter DC voltage control based on capacitor energetic model. In Proceedings of the 2022 11th International Conference on Control, Automation and Information Sciences (ICCAIS), Hanoi, Vietnam, 21–24 November 2022; pp. 529–534. [Google Scholar] [CrossRef]
- Azghandi, M.A.; Barakati, S.M.; Yazdani, A. Impedance-based stability analysis and design of a fractional-order active damper for grid-connected current-source inverters. IEEE Trans. Sustain. Energy 2021, 12, 599–611. [Google Scholar] [CrossRef]
- Cortajarena, J.A.; Barambones, O.; Alkorta, P.; Cortajarena, J. Sliding mode control of an active power filter with photovoltaic maximum power tracking. Int. J. Electr. Power Energy Syst. 2019, 10, 747–758. [Google Scholar] [CrossRef]
- Rayudu, K.; Muni, T.V.; Mustafa, M.; Subramaniam, G.; Kishore, K.V.; Babu Lella, V.M. Design of P-Q theory controller based solar PV system with shunt active filter to improve power quality. In Proceedings of the 2022 2nd International Conference on Intelligent Technologies (CONIT), Hubli, India, 24–26 June 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Manohara, M.; Veera Reddy, V.C.; Vijaya Kumar, M. Power quality improvement of solar PV system with shunt active power filter using FS-MPC method. In Proceedings of the 2023 IEEE Renewable Energy and Sustainable E-Mobility Conference (RESEM), Bhopal, India, 17–18 May 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Sarra, M.; Belkaid, A.; Colak, I.; Boudechiche, G.; Kayisli, K. Fuzzy-MPPT controller based solar shunt active power filter. In Proceedings of the 2022 11th International Conference on Renewable Energy Research and Application (ICRERA), Istanbul, Turkey, 18–21 September 2022; pp. 436–440. [Google Scholar] [CrossRef]
- Pani, S.; Samal, S.; Nayak, B.; Panda, B.; Mohapatra, A.; Barik, P.K. Fuzzy-HCC based shunt active power filter integrated hybrid energy system for compensation of harmonics. In Proceedings of the 2022 International Conference on Intelligent Controller and Computing for Smart Power (ICICCSP), Hyderabad, India, 21–23 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Delincé, F.; Nguyen, T.; Ilves, K.; Okazaki, Y. Control of voltage source converters under varying grid impedance in active filter applications. In Proceedings of the 12th International Conference on Power Electronics, Machines and Drives (PEMD 2023), Brussels, Belgium, 23–24 October 2023; pp. 380–386. [Google Scholar] [CrossRef]
- Chaudhary, N.; Ranjan, A.; Bhaskar, D.V.; Panda, M.; Kumar, A.; Kumar, P. Harmonic reduction strategies for EV charging in power systems using shunt active power filter. In Proceedings of the 2023 3rd International Conference on Emerging Frontiers in Electrical and Electronic Technologies (ICEFEET), Patna, India, 21–22 December 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Tsvetanov, D.; Djagarov, N.; Enchev, G.; Djagarova, J.; Blaabjerg, F. Harmonic compensation in ship power system using peak detection control strategy based shunt active power filter. In Proceedings of the 2023 IEEE International Conference on Environment and Electrical Engineering and 2023 IEEE Industrial and Commercial Power Systems Europe (EEEIC / I&CPS Europe), Madrid, Spain, 6–9 June 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Tsvetanov, D.; Djagarov, N.; Grozdev, Z.; Djagarova, J. Harmonic compensation in ship power system using p-q theory control based shunt active power filter. In Proceedings of the 2022 8th International Conference on Energy Efficiency and Agricultural Engineering (EE&AE), Ruse, Bulgaria, 30 June 2022–2 July 2022; pp. 1–10. [Google Scholar] [CrossRef]
- Tsvetanov, D.; Djagarov, N.; Grozdev, Z.; Djagarova, J. Synchronous reference frame theory control for current harmonics suppression in ship power system using shunt active power filter. In Proceedings of the 2022 International Conference Automatics and Informatics (ICAI), Varna, Bulgaria, 6–8 October 2022; pp. 120–128. [Google Scholar] [CrossRef]
- Tsvetanov, D.; Djagarov, N.; Djagarova, J.; Milushev, H.; Guerrero, J.M. Reducing harmonic Distortion in Ship Power Systems: An Evaluation of Three Shunt Active Power Filter Control Strategies. In Proceedings of the 2023 25th European Conference on Power Electronics and Applications (EPE’23 ECCE Europe), Aalborg, Denmark, 4–8 September 2023; pp. 1–10. [Google Scholar] [CrossRef]
- Sattarov, R.; Ivanov, M.; Khazieva, R.; Solovev, B. Active filters in the power supply of electrified railway applications. In Proceedings of the 2022 International Ural Conference on Electrical Power Engineering (UralCon), Magnitogorsk, Russian Federation, 23–25 September 2022; pp. 26–31. [Google Scholar] [CrossRef]
- Brenna, M.; Kaleybar, H.J.; Foiadelli, F.; Zaninelli, D. Modern power quality improvement devices applied to electric railway systems. In Proceedings of the 2022 20th International Conference on Harmonics & Quality of Power (ICHQP), Naples, Italy, 29 May 2022–1 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Routimo, M.; Salo, M.; Tuusa, H. Comparison of voltage-source and current-source shunt active power filters. IEEE Trans. Power Electron. 2007, 22, 636–643. [Google Scholar] [CrossRef]
- Popescu, M.; Bitoleanu, A.; Preda, A. A new design method of an LCL Filter applied in active DC-traction substations. IEEE Trans. Ind. Appl. 2018, 54, 3497–3507. [Google Scholar] [CrossRef]
- Terciyanli, A.; Avci, T.; Yilmaz, I.; Ermis, C.; Kose, K.N.; Acik, A.; Kalaycioglu, A.S.; Akkaya, Y.; Cadirici, I. A current source converter-based active power filter for mitigation of harmonics at the interface of distribution and transmission systems. IEEE Trans. Ind. Appl. 2012, 48, 1374–1386. [Google Scholar] [CrossRef]
- Terciyanli, A.; Ermis, M.; Cadirci, I. A selective harmonic amplification method for reduction of kVA rating of current source converters in shunt active power filters. IEEE Trans. Power Deliver. 2011, 26, 65–78. [Google Scholar] [CrossRef]
- Ahmed, M.H.; Wang, M.; Hassan, M.A.S.; Ullah, I. Power loss model and efficiency analysis of three-phase inverter based on SiC MOSFETs for PV applications. IEEE Access 2019, 7, 75768–75781. [Google Scholar] [CrossRef]
- Jorge, L.; Concepcion, H.; Arjona, M.A.; Lesedi, M.; Ambrish, C. Performance evaluation of an active neutral-point-clamped multilevel converter for active filtering in G2V-V2G and V2H applications. IEEE Access 2022, 10, 41607–41621. [Google Scholar] [CrossRef]
- Alhosaini, W.; Wu, Y.; Zhao, Y. An enhanced model predictive control using virtual space vectors for grid-connected three-level neutral-point clamped inverters. IEEE Trans. Energy Convers. 2019, 34, 1963–1972. [Google Scholar] [CrossRef]
- Othman, S.; Sbita, L.; Barbot, J.-P.; Alali, M.A.E.; Ghanes, M. Shunt active power filter based on flying capacitor multilevel inverter for harmonic mitigation. In Proceedings of the 2022 IEEE 7th International Energy Conference (ENERGYCON), Riga, Latvia, 9–12 May 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Yazdani, S.; Ferdowsi, M.; Shamsi, P. Internal model based current control with embedded active damping on a three-level pv flying capacitor multilevel inverter with LCL filter. In Proceedings of the 2020 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 13–14 July 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Ray, S.; Gupta, N.; Gupta, R.A. (2018). Hardware realization of proportional-resonant regulator based advanced current control strategy for cascaded H-bridge inverter based shunt active power filter. Int. Trans. Electr. Energy Syst. 2018, 29, e2714. [Google Scholar] [CrossRef]
- Karania, N.; AlalI, M.A.; Di Gennaro, S.; Barbot, J.-P. Developed AC/DC/AC converter structure based on shunt active filter and advanced modulation approach for asymmetrical cascade H-bridge multilevel inverters. IEEE Open J. Ind. Electron. Soc. 2023, 4, 583–602. [Google Scholar] [CrossRef]
- Zhang, Y.; Dai, K.; Xu, H.; Liu, T.; Lin, H.; Dai, Z.; Kang, Y. DSP-based SiC-MOSFET SAPF with 100-khz sampling and switching frequency for wideband harmonic suppression. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 689–701. [Google Scholar] [CrossRef]
- Dai, K.; Luo, H.; Yang, H.; He, K.; Xu, Z.; Jin, P.; Cai, H.; Xu, C. PCC voltage switching harmonic mitigation by periodic carrier frequency pulse width modulation for SiC high frequency active power filter. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 23, 3040–3051. [Google Scholar] [CrossRef]
- Li, D.; Nie, C.; Huang, X.; Lin, M.; Wang, F.; Tolbert, L.M. Active power filter capability of a 10 kV SiC MOSFET-based asynchronous microgrid power conditioning system. In Proceedings of the 2023 IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 19–23 March 2023; pp. 137–143. [Google Scholar] [CrossRef]
- Mohapatra, A.; Bhawal, S.; Hatua, K. A Si IGBT and SiC MOSFET hybrid shunt active filter. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Lin, H.; Wu, L.; Guo, X.; Chen, G. Shunt active power filter using SiC-MOSFET with high accuracy compensation. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November 2020–2 December 2020; pp. 2872–2876. [Google Scholar] [CrossRef]
- Bitoleanu, A.; Popescu, M.; Suru, V.C. Active power filters. In Fundamentals and Applications; Matrix: Bucharest, Romania, 2021. (In Romanian) [Google Scholar]
- Akagi, H.; Kanazawa, Y.; Nabae, A. Instantaneous reactive power compensators comprising switching devices without energy storage components. IEEE Trans. Ind. Appl. 1984, IA-20, 625–630. [Google Scholar] [CrossRef]
- Akagi, H.; Watanabe, E.H.; Aredes, M. Instantaneous Power Theory and Applications to Power Conditioning; Wiley IEEE Press: Hoboken, NJ, USA, 2007. [Google Scholar]
- Bitoleanu, A.; Popescu, M. The p-q theory and compensating current calculation for shunt active power filters: Theoretical aspects and practical implementation. Przegląd Elektrotechniczny 2013, 6, 11–16. [Google Scholar]
- Bitoleanu, A.; Popescu, M. Shunt active power filter Overview on the reference current methods calculation and their implementation. In Proceedings of the 2013 4th International Symposium on Electrical and Electronics Engineering (ISEEE), Galati, Romania, 11–13 October 2013; pp. 1–12. [Google Scholar] [CrossRef]
- de Andrade, N.D.; Godoy, R.B.; Batista, E.A.; de Brito, M.A.G.; Soares, R.L.R. Embedded FPGA controllers for current compensation based on modern power theories. Energies 2022, 15, 6284. [Google Scholar] [CrossRef]
- Samanta, J.; Pudur, R. Comparison of p-q and d-q theory for shunt active power filter. In Proceedings of the 2022 IEEE International Power and Renewable Energy Conference (IPRECON), Kollam, India, 16–18 December 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Paredes, H.K.M.; Marafao, F.P.; da Silva, L.C.P. A comparative analysis of FBD, PQ and CPT current decompositions—Part II: Three-phase four-wire systems. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June 2009–2 July 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Barva, A.V.; Arkdev. Analysis of SAPF based on p-q and SRF theory for different supply and load conditions. In Proceedings of the 2023 International Conference on Power, Instrumentation, Energy and Control (PIECON), Aligarh, India, 10–12 February 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Bitoleanu, A.; Popescu, M. How can the IRP p-q theory be applied for active filtering under nonsinusoidal voltage operation? Przegląd Elektrotechniczny 2011, 1, 67–71. [Google Scholar]
- Popescu, M.; Bitoleanu, A.; Suru, V. Time-domain based active compensation strategies under nonsinusoidal conditions in three-phase three-wire systems. Ann. Univ. Craiova Electr. Eng. Ser. 2011, 35, 19–24. [Google Scholar]
- Popescu, M.; Bitoleanu, A.; Suru, V. Phase coordinate system and p-q theory based methods in active filtering implementation. Adv. Electr. Comp. Eng. 2013, 13, 69–74. [Google Scholar] [CrossRef]
- Popescu, M.; Dobriceanu, M.; Lincă, M.; Oprea, G. Orthogonal reference frame based methods in three-wire active power line conditioners: Practical evaluation under unbalanced load and nonideal voltage conditions. In Proceedings of the 2014 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Bran, Romania, 22–24 May 2014 2014; pp. 532–539. [Google Scholar] [CrossRef]
- Büyük, M.; Inci, M.; Tan, A.; Tümay, M. Improved instantaneous power theory based current harmonic extraction for unbalanced electrical grid conditions. Electr. Power Syst. Res. 2019, 177, 106014. [Google Scholar] [CrossRef]
- Rejil, C.; Anzari, M.; Arun Kumar, R. Design and simulation of three phase shunt active power filter using SRF theory. Adv. Electron. Electr. Eng. 2013, 3, 651–660. [Google Scholar]
- Shakerighadi, B.; Ebrahimzadeh, E.; Taul, M.G.; Blaabjerg, F.; Bak, C.L. Modeling and adaptive design of the SRF-PLL: Nonlinear time-varying framework. IEEE Access 2020, 8, 28635–28645. [Google Scholar] [CrossRef]
- Xiao, P.; Corzine, K.A.; Venayagamoorthy, G.K. Multiple reference frame-based control of three-phase PWM boost rectifiers under unbalanced and distorted input conditions. IEEE Trans. Power Electron. 2008, 23, 2006–2017. [Google Scholar] [CrossRef]
- Patjoshi, R.K.; Panigrahi, R.; Rout, S.S. A hybrid fuzzy with feedback integral phase locked loop-based control strategy for unified power quality conditioner. Trans. Inst. Meas. Control 2021, 43, 122–136. [Google Scholar] [CrossRef]
- Soares, V.; Verdelho, P.; Marques, G. Active power filter control circuit based on the instantaneous active and reactive current id-iq method. In Proceedings of the 28th Annual IEEE Power Electronics Specialists Conference, St. Louis, MO, USA, 27 June 1997; pp. 1096–1101. [Google Scholar] [CrossRef]
- Patnaik, S.S.; Panda, A.K. Performance improvement of id-iq method based active filter using particle swarm optimization. In Proceedings of the International Conference on Sustainable Energy and Intelligent Systems (SEISCON 2011), Chennai, India, 20–22 July 2011; pp. 320–325. [Google Scholar] [CrossRef]
- Mikkili, S.; Panda, A.K. SHAF for mitigation of current harmonics with p-q and Id-Iq control strategies using both PI and Fuzzy Controllers. In Proceedings of the International Conference on Sustainable Energy and Intelligent Systems (SEISCON 2011), Chennai, India, 20–22 July 2011; pp. 358–362. [Google Scholar] [CrossRef]
- Mikkili, S.; Panda, A.K. Id-Iq control strategy for mitigation of current harmonics with PI and fuzzy controllers. In Proceedings of the 2011 International Conference on Power and Energy Systems, Chennai, India, 22–24 December 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Sohagh, K.S.; Wang, L.; Han, X.; Qin, W.; Zhang, D.; Meng, R. Analysis of Id-Iq strategy for active power filter. In Proceedings of the 2020 15th IEEE Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 9–13 November 2020; pp. 722–725. [Google Scholar] [CrossRef]
- Vignesh, S.; Sebasthirani, K. An advanced current control strategy using Id-Iq controlled technique for three-phase shunt active filters. Int. J. Eng. Res. Technol. 2013, 2, 2024–2028. [Google Scholar]
- Tenti, P.; Mattavelli, P. A Time-domain approach to power term definitions under non-sinusoidal conditions. In Proceedings of the 6th International Workshop on Power Definitions and Measurements under Non-Sinusoidal Conditions, Milano, Italy, 13–15 October 2003. [Google Scholar]
- Tenti, P.; Mattavelli, P.; Tedeschi, E. Compensation techniques based on reactive power conservation. Electr. Power Qual. Util. J. 2007, XIII, 17–24. [Google Scholar]
- Haugan, T.S.; Tedeschi, E. Reactive and harmonic compensation using the conservative power theory. In Proceedings of the 2015 Tenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, Italy, 31 March 2015–2 April 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Pătrașcu, A.; Popescu, M.; Suru, V. The Conservative Power Theory and the active filtering. Bull. AGIR 2012, 4, 179–182. [Google Scholar]
- Suru, V.; Pătraşcu, A.; Popescu, M.; Bitoleanu, A. Conservative Power Theory application in shunt active power filtering under asymmetric voltage. In Proceedings of the 14th International Conference on Optimization of Electrical and Electronic Equipment (OPTIM 2014), Braşov Cheile Grădiştei, Romania, 22–24 May 2014; pp. 647–654. [Google Scholar] [CrossRef]
- Marafão, F.P.; Brandão, D.I.; Morales Paredes, H.K.; Silva, L.C.P. Possible shunt compensation strategies based on Conservative Power Theory. In Proceedings of the 2010 International School on Nonsinusoidal Currents and Compensation, Lagow, Poland, 15–18 June 2010; pp. 162–167. [Google Scholar] [CrossRef]
- Paredes, H.K.M.; Brandão, D.I.; Terrazas, T.M.; Marafão, F.P. Shunt active compensation based on the Conservative Power Theory current’s decomposition. In Proceedings of the XI Brazilian Power Electronics Conference, Natal, Brazil, 11–15 September 2011; pp. 788–794. [Google Scholar] [CrossRef]
- Mota, D.d.S.; Tedeschi, E. On adaptive moving average algorithms for the application of the conservative power theory in systems with variable frequency. Energies 2021, 14, 1201. [Google Scholar] [CrossRef]
- Syed, M.K.; Sanker Ram, B.V. Active power filtering in asymmetric power system by modified synchronous detection algorithm. In Proceedings of the TENCON 2008—2008 IEEE Region 10 Conference, Hyderabad, India, 19–21 November 2008; pp. 1–4. [Google Scholar] [CrossRef]
- Jung, Y.G.; Kim, W.Y.; Lim, Y.C.; Yang, S.H.; Harashima, F. The algorithm of expanded current synchronous detection for active power filters considering three-phase unbalanced power system. IEEE Trans. Ind. Electron. 2003, 50, 1000–1006. [Google Scholar] [CrossRef]
- Jung, Y.G. The current synchronous detection method combined with positive sequence detector for active power filters. J. Electr. Eng. Technol. 2023, 18, 431–440. [Google Scholar] [CrossRef]
- Depenbrock, M. The FBD-method, a generally applicable tool for analyzing power relations. IEEE Trans. Power Syst. 1993, 8, 381–387. [Google Scholar] [CrossRef]
- Sun, W.; Gong, Y. Research on harmonic detection method of multi-function grid-connected Inverter. In Proceedings of the 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 11–13 December 2020; pp. 1124–1129. [Google Scholar] [CrossRef]
- Popescu, M.; Bitoleanu, A.; Patrascu, C.A. MATLAB/SIMULINK library for compensating current calculation in three-phase shunt active filtering systems. Bul. AGIR 2012, 4, 246–250. [Google Scholar]
- Wang, D.; Zhang, L.; Wang, C.; Liu, S.; Liu, Q. A harmonic detection strategy based on FBD power theory. In Proceedings of the 2019 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Macao, China, 1–4 December 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Petit, J.F.; Robles, G.; Amaris, H. Current Reference control for shunt active power filters under nonsinusoidal voltage conditions. IEEE Trans. Power Deliver. 2007, 22, 2254–2261. [Google Scholar] [CrossRef]
- Yuan, C.; Yigang, H.; Zhong, L.; Jinping, W. Improved FBD reactive power and harmonic current detecting method based on voltage sequence decomposition. In Proceedings of the 2015 12th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Qingdao, China, 16–18 July 2015; pp. 567–570. [Google Scholar] [CrossRef]
- Peng, F.Z.; Lai, J.S. Generalized instantaneous reactive power theory for three-phase power systems. IEEE Trans. Instrum. Meas. 1996, 45, 293–297. [Google Scholar] [CrossRef]
- Herrera, R.S.; Salmeron, P.; Vazquez, J.R.; Litran, S.P.; Perez, A. Generalized instantaneous reactive power theory in poly-phase power systems. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–10. [Google Scholar]
- Li, E.X.; Sheng, W.-X.; Sun, J.-P.; Meng, X.-L. The study on current detecting algorithm based on generalized instantaneous reactive power theory. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Mulla, M.A.; Chudamani, R.; Chowdhury, A. Generalized instantaneous power theory and its applications to shunt active power line conditioners under balanced and unbalanced load conditions. In Proceedings of the 2012 11th International Conference on Environment and Electrical Engineering, Venice, Italy, 18–25 May 2012; pp. 413–418. [Google Scholar] [CrossRef]
- Popescu, M.; Pătraşcu, C.A.; Dobriceanu, M. Application of Generalized Instantaneous Reactive/ Non-active Power Theories in the control of shunt active power line conditioners: Practical evaluation under nonideal voltage and unbalanced load. In Proceedings of the 22nd International Conference Nonlinear Dynamics of Electronic Systems, Albena, Bulgaria, 4–6 July 2014; pp. 125–133. [Google Scholar] [CrossRef]
- Peng, F.Z.; Tolbert, L.M. Compensation of non-active current in power systems-definitions from compensation standpoint. In Proceedings of the 2000 Power Engineering Society Summer Meeting, Seattle, WA, USA, 16–20 July 2000; pp. 983–987. [Google Scholar] [CrossRef]
- Peng, F.Z.; Tolbert, L.M.; Qian, Z. Definitions and compensation of non-active current in power systems. In Proceedings of the 2002 IEEE 33rd Annual IEEE Power Electronics Specialists Conference. Proceedings, Cairns, QLD, Australia, 23–27 June 2002; pp. 1779–1784. [Google Scholar] [CrossRef]
- Xu, Y.; Tolbert, L.M.; Peng, F.Z.; Chiasson, J.N.; Chen, J. Compensation-based nonactive power definition. IEEE Power Electron. Lett. 2003, 1, 45–50. [Google Scholar] [CrossRef]
- Popescu, M.; Bitoleanu, A. Phase coordinates system versus orthogonal reference frame in control of shunt active filtering systems. In Proceedings of the 2012 International Conference on Applied and Theoretical Electricity, Craiova, Romania, 25–27 October 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Xu, Y.; Tolbert, L.M.; Chiasson, J.N.; Campbell, J.B.; Peng, F.Z. Active Filter Implementation Using a Generalized Nonactive Power Theory. In Proceedings of the 2006 IEEE Industry Applications Conference, Tampa, FL, USA, 8–12 October 2006; pp. 153–160. [Google Scholar] [CrossRef]
- Ucar, M.; Ozdemir, S.; Ozdemir, E. A combined series-parallel active filter system implementation using generalized non-active power theory. In Proceedings of the 2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, CA, USA, 21–25 February 2010; pp. 367–373. [Google Scholar] [CrossRef]
- Xu, Y.; Tolbert, L.M.; Chiasson, J.N.; Campbell, J.B.; Peng, F. Z A generalised instantaneous non-active power theory for STATCOM. IET Electr. Power Appl. 2007, 1, 853–861. [Google Scholar] [CrossRef]
- Tlusty, J.; Svec, J.; Sendra, J.B.; Valouch, V. Analysis of Generalized Non-Active Power Theory for compensation of non-periodic disturbances. In Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ’12), Santiago de Compostela, Spain, 28–30 March 2012. [Google Scholar] [CrossRef]
- Xu, Y.; Tolbert, L.M.; Xu, Y. Critical evaluation of FBD, PQ and generalized non-active power theories. In Proceedings of the 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August 2011–1 September 2011; pp. 1–10. [Google Scholar]
- Xu, Y.; Tolbert, L.M.; Chiasson, J.N.; Peng, F.Z. Dynamic response of an active filter using a generalized nonactive power theory. In Proceedings of the Fourtieth IAS Annual Meeting. Conference Record of the 2005 Industry Applications Conference, Hong Kong, China, 2–6 October 2005; pp. 1225–1231. [Google Scholar] [CrossRef]
- Valouch, V.; Muller, Z.; Svec, J.; Tlusty, J. Evaluation of IRP, FBD, SD, and generalized non-active power theories. In Proceedings of the 2012 IEEE 27th Convention of Electrical and Electronics Engineers in Israel, Eilat, Israel, 14–17 November 2012; pp. 1–5. [Google Scholar] [CrossRef]
- El Ghaly, A.; Tarnini, M.; Moubayed, N.; Chahine, K. A filter-less time-domain method for reference signal extraction in shunt active power filters. Energies 2022, 15, 5568. [Google Scholar] [CrossRef]
- Hasan, K.; Othman, M.M.; Meraj, S.T.; Mekhilef, S.; Abidin, A.F.B. Shunt active power filter based on Savitzky-Golay Filter: Pragmatic modelling and performance validation. IEEE Trans. Power Electron. 2023, 38, 8838–8850. [Google Scholar] [CrossRef]
- Hoon, Y.; Zainuri, M.A.A.M.; Al-Ogaili, A.S.; Al-Masri, A.N.; Teh, J. Active power filtering under unbalanced and distorted grid conditions using modular Fundamental Element Detection technique. IEEE Access 2021, 9, 107502–107518. [Google Scholar] [CrossRef]
- Simões, M.G.; Harirchi, F.; Babakmehr, M. Survey on time-domain power theories and their applications for renewable energy integration in smart-grids. IET Smart Grid 2019, 2, 491–503. [Google Scholar] [CrossRef]
- Sant, A.V. Shunt active power filtering with reference current generation based on dual second order generalized integrator and LMS algorithm. Energy Rep. 2022, 8, 886–893. [Google Scholar] [CrossRef]
- Badoni, M.; Singh, A.; Singh, B. Comparative performance of Wiener filter and Adaptive Least Mean Square-based control for power quality improvement. IEEE Trans. Ind. Electron. 2016, 63, 3028–3037. [Google Scholar] [CrossRef]
- Pereira, R.R.; da Silva, C.H.; da Silva, L.E.B.; Lambert-Torres, G.; Pinto, J.O.P. New strategies for application of adaptive filters in active power filters. IEEE Trans. Ind. Appl. 2011, 47, 1136–1141. [Google Scholar] [CrossRef]
- Bagheri, A.; Mardaneh, M.; Rajaei, A.; Rahideh, A. Detection of grid voltage fundamental and harmonic components using Kalman filter and generalized averaging method. IEEE Trans. Power Electron. 2016, 31, 1064–1073. [Google Scholar] [CrossRef]
- Yang, B.; Dai, K.; Yang, C.; Luo, H.; He, K.; Dai, Z. Improvement of recursive DFT for APF with higher switching frequency to suppress wideband harmonics. IEEE Access 2021, 9, 144300–144312. [Google Scholar] [CrossRef]
- Qi, H.; Zhao, C. Research and implementation of harmonic detection and current compensation technology in active power filter. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 10008–10012. [Google Scholar] [CrossRef]
- Ferrari, M. Evaluation of harmonic detection algorithms for active power filter based on voltage and current detection methods. In Proceedings of the 2018 9th IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Charlotte, NC, USA, 25–28 June 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Chen, K.F.; Mei, S.L. Composite interpolated fast Fourier transform with the Hanning window. IEEE Trans. Instrum. Meas. 2010, 59, 1571–1579. [Google Scholar] [CrossRef]
- Chen, H.; Liu, H.; Xing, Y.; Hu, H.; Sun, K. Analysis and design of enhanced DFT-based controller for selective harmonic compensation in active power filters. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 1305–1309. [Google Scholar] [CrossRef]
- Chen, H.; Liu, H.; Xing, Y.; Hu, H. Enhanced DFT-based controller for selective harmonic compensation in active power filters. IEEE Trans. Power Electron. 2019, 34, 8017–8030. [Google Scholar] [CrossRef]
- Geng, H.; Zou, T.; Chandra, A. Fast repetitive control scheme for shunt active power filter in Synchronous Rotational Frame. In Proceedings of the 2017 IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 1–5 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Barros, J.; de Apráiz, M.; Diego, R.I. A New harmonic extraction method for estimation of the reference compensation current in shunt active power filters. In Proceedings of the 2022 20th International Conference on Harmonics & Quality of Power (ICHQP), Naples, Italy, 29 May 2022–1 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, H.; Liu, G.; Shen, Y. Application of fast lifting wavelet transform to the estimation of harmonic for shunt active power filters. In Proceedings of the 2007 7th Internatonal Conference on Power Electronics, Daegu, 22–26 October 2007; pp. 96–101. [Google Scholar] [CrossRef]
- Firouzjah, K.G.; Sheikholeslami, A.; Karami-Mollaei, M.R.; Khaleghi, M. A new harmonic detection method for shunt active filter based on Wavelet transform. J. Appl. Sci. Res. 2008, 4, 1561–1568. [Google Scholar]
- Maurya, I.; Gupta, S.K.; Maurya, P. An efficient harmonic detection approach for shunt active filter based on wavelet trans-form. Ain Shams Eng. J. 2018, 9, 2833–2839. [Google Scholar] [CrossRef]
- Moradi, A.; Pichan, M. A High performance harmonic detection method based on Wavelet Transform for shunt active power filter with experimental verification. In Proceedings of the 2022 13th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tehran, Iran, 1–3 February 2022; pp. 544–548. [Google Scholar] [CrossRef]
- Modarresi, J.; Fallah, M.; Gholipour, E.; Abarzadeh, M. Performance improvement of shunt active power filter by a new wavelet-based low-pass filter: Theory and implementation. Trans. Inst. Meas. Control 2018, 40, 111–121. [Google Scholar] [CrossRef]
- Fei, J.; Zhang, L.; Zhuo, J.; Fang, Y. Wavelet fuzzy neural supertwisting sliding mode control of an active power filter. IEEE Trans. Fuzzy Syst. 2023, 31, 4051–4063. [Google Scholar] [CrossRef]
- Czarnecki, L.S. Orthogonal decomposition of the currents in a 3-phase nonlinear asymmetrical circuit with a nonsinusoidal voltage source. IEEE Trans. Instrum. Meas. 1988, 37, 30–34. [Google Scholar] [CrossRef]
- Czarnecki, L.S. Distortion power in systems with nonsinusoidal voltage. IEE Proc. B 1992, 139, 276–280. [Google Scholar] [CrossRef]
- Czarnecki, L.S.; Pearce, S.E. Compensation objectives and CPC-based generation of reference signals for shunt switching compensator control. IET Power Electron. 2009, 2, 33–41. [Google Scholar] [CrossRef]
- Czarnecki, L.S. Quasi-Instantaneous generation of reference signal for hybrid compensator control. Electr. Power Qual. Util. J. 2007, XIII, 33–38. [Google Scholar] [CrossRef]
- Popescu, M.; Bitoleanu, A.; Suru, V. Currents’ physical components theory implementation in shunt active power filtering for unbalanced loads. In Proceedings of the International School on Nonsinusoidal Currents and Compensation 2013 (ISNCC 2013), Zielona Gora, Poland, 20–21 June 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Czarnecki, L.S. Currents’ Physical Components (CPC)-based power theory A review Part II: Filters and reactive, switching and hybrid compensators. Przegląd Elektrotechniczny 2020, 96, 1–11. [Google Scholar]
- Soljan, Z.; Holdynski, G.; Zajkowski, M. Decomposition of the load’s current supplied from a sinusoidal and asymmetrical voltage source in accordance with the currents’ physical components (CPC) theory. In Proceedings of the 2019 20th International Scientific Conference on Electric Power Engineering (EPE), Kouty nad Desnou, Czech Republic, 15–17 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Soljan, Z.; Holdynski, G.; Zajkowski, M. CPC-based minimizing of balancing compensators in four-wire nonsinusoidal asymmetrical systems. Energies 2021, 14, 1815. [Google Scholar] [CrossRef]
- Patrascu, C.A.; Popescu, M.; Suru, V. CPC theory implementation for active filtering and its limits. In Proceedings of the 11th International Conference on Applied and Theoretical Electricity (ICATE), Craiova, Romania, 25–27 October 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Ginn, H.; Chen, G. Switching compensator control strategy based on CPC power theory. In Proceedings of the 2008 International School on Nonsinusoidal Currents and Compensation, Lagow, Poland, 10–13 June 2008; pp. 1–11. [Google Scholar] [CrossRef]
- Bai, Z.; Jiang, W.; Xiao, X. Analysis of reactive power compensation in hybrid active power filter based on IEEE Std. 1459-2010 and CPC theory. In Proceedings of the 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 8–21 October 2020; pp. 1550–1554. [Google Scholar] [CrossRef]
- Bitoleanu, A.; Popescu, M.; Suru, V. Optimal controllers design in indirect current control system of active DC-Traction substation. In Proceedings of the 2016 IEEE International Power Electronics and Motion Control Conference (PEMC), Varna, Bulgaria, 25–28 September 2016; pp. 912–917. [Google Scholar] [CrossRef]
- Bitoleanu, A.; Popescu, M.; Suru, C.V. Theoretical and experimental evaluation of the indirect current control in active filtering and regeneration systems. In Proceedings of the 2017 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Brasov, Romania, 25–27 May 2017; pp. 759–764. [Google Scholar] [CrossRef]
- Bouhouta, A.; Moulahoum, S.; Kabache, N.; Benyamina, A. Design and real time implementation of three phase shunt active power filter using indirect current control technique. In Proceedings of the 2019 International Conference on Advanced Electrical Engineering (ICAEE), Algiers, Algeria, 19–21 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Linca, M.; Suru, C.V.; Preda, C.A. Indirect current control algorithm implementation for an active filtering system using constant switching frequency hysteresis controllers. In Proceedings of the 2018 International Conference on Applied and Theoretical Electricity (ICATE), Craiova, Romania, 4–6 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Dubey, A.K.; Mishra, J.P.; Kumar, A. Modified CCF based shunt active power filter operation with dead-band elimination for effective harmonic and unbalance compensation in 3-phase 3-wire system. IEEE Trans. Power Deliver. 2022, 37, 2131–2142. [Google Scholar] [CrossRef]
- Preda, A.; Popescu, M.; Linca, M. Conservative Power Theory (CPT) method applied in the indirect current control for active D.C. traction substations. In Athens ATINER’S Conference Paper Series TRA2015-1561; ATINER: Athens, Greece, 2015; pp. 1–17. [Google Scholar]
- Popescu, M.; Preda, A.; Suru, V. Synchronous Reference Frame method applied in the indirect current control for active DC traction substation. In Athens ATINER’S Conference Paper Series TRA2015-1552; ATINER: Athens, Greece, 2015; pp. 1–14. [Google Scholar]
- Bose, B.K. An adaptive hysteresis-band current control technique of a voltage-fed PWM inverter for machine drive system. IEEE Trans. Ind. Electron. 1990, 37, 402–408. [Google Scholar] [CrossRef]
- Abedi, S.M.; Vahedi, H. Simplified calculation of adaptive hysteresis current control to be used in active power filter. Trends Appl. Sci. Res. 2013, 8, 46–54. [Google Scholar] [CrossRef]
- Chen, S.; Jin, C.; Shen, Y.; Zhang, Y. Current harmonic suppression method based on SVHC and improved SOGI for active power filters. In Proceedings of the 2023 8th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 22–25 September 2023; pp. 168–173. [Google Scholar] [CrossRef]
- Mohamed, Y.A.-R.I.; El-Saadany, E.F. Robust high bandwidth discrete-time predictive current control with predictive internal model—A unified approach for voltage-source PWM converters. IEEE Trans. Power Electron. 2008, 23, 12–136. [Google Scholar] [CrossRef]
- Chemidi, A.; Benhabib, M.C. A robust PWM control for a three leg shunt active power filter. In Proceedings of the 2022 19th International Multi-Conference on Systems, Signals & Devices (SSD), Sétif, Algeria, 6–10 May 2022; pp. 1434–1439. [Google Scholar] [CrossRef]
- Pariz, P.; Monfared, M. A Deadbeat controller design for single-phase active power filters based on forward-backward discretization. In Proceedings of the 2021 12th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tabriz, Iran, 2–4 February 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Da Silveira, W.B.; de Oliveira Evald, P.J.D.; Prestes, G.X.; Milbradt, D.M.C.; Tambara, R.V.; Gründling, H.A. A discrete-time robust adaptive second-order sliding mode controller for grid-connected power systems with LCL filter. In Proceedings of the 2023 15th Seminar on Power Electronics and Control (SEPOC), Santa Maria, Brazil, 22–25 October 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Fang, Y.; Fei, J.; Wang, T. Adaptive backstepping fuzzy neural controller based on fuzzy sliding mode of active power filter. IEEE Access 2020, 8, 96027–96035. [Google Scholar] [CrossRef]
- Colak, I.; Kabalci, E. Developing a novel sinusoidal pulse width modulation (SPWM) technique to eliminate side band harmonics. Int. J. Electr. Power Energy Syst. 2013, 44, 861–871. [Google Scholar] [CrossRef]
- Chen, D.; Xie, S. Review of the control strategies applied to active power filters. In Proceedings of the 2004 IEEE International Conference on Electric Utility Deregulation, Restructuring and Power Technologies, Hong Kong, China, 5–8 April 2004; pp. 666–670. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Q.; Mu, S.; Zhang, T.; Li, H.; Wang, J. A sliding mode SVPWM method for a HTS shunt active power filter. IEEE Trans. Appl. Supercond. 2021, 31, 1–2. [Google Scholar] [CrossRef]
- Arora, K.; Bhatt, H.; Tekwani, P.N.; Chauhan, S.K.; Shah, M.T. Performance investigations of adaptive ANN-SVPWM controlled shunt active power filter. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Sajjadi, M.; Majd, Y. SVPWM-based dual active filter for distribution system power quality improvement. In Proceedings of the 2021 6th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 17–20 September 2021; pp. 592–597. [Google Scholar] [CrossRef]
- Mikkili, S.; Panda, A.K. Real-time implementation of PI and fuzzy logic controllers based shunt active filter control strategies for power quality improvement. Int. J. Electr. Power Energy Syst. 2012, 43, 1114–1126. [Google Scholar] [CrossRef]
- Zhou, X.; Cui, Y.; Ma, Y. Fuzzy linear active disturbance rejection control of injection hybrid active power filter for medium and high voltage distribution network. IEEE Access 2021, 9, 8421–8432. [Google Scholar] [CrossRef]
- Deffaf, B.; Debdouche, N.; Benbouhenni, H.; Hamoudi, F.; Bizon, N. A new control for improving the power quality generated by a three-level T-type inverter. Electronics 2023, 12, 2117. [Google Scholar] [CrossRef]
- Noguchi, P.; Tomiki, H.; Kondo, S.; Takahashi, I. Direct power control of PWM converter without power-source voltage sensors. IEEE Trans. Ind. Appl. 1998, 34, 473–479. [Google Scholar] [CrossRef]
- Chen, B.S.; JoÓs, G. Direct Power Control of active filters with averaged switching frequency regulation. IEEE Trans. Power Electron. 2008, 23, 2729–2737. [Google Scholar] [CrossRef]
- Qazi, S.H.; Mustafa, M.W. Review on active filters and its performance with grid connected fixed and variable speed wind turbine generator. Renew. Sust. Energ. Rev. 2016, 57, 420–438. [Google Scholar] [CrossRef]
- Tareen, W.U.; Mekhilef, S.; Seyedmahmoudian, M.; Horan, B. Active power filter (APF) for mitigation of power quality issues in grid integration of wind and photovoltaic energy conversion system. Renew. Sust. Energ. Rev. 2017, 70, 635–655. [Google Scholar] [CrossRef]
- Colak, I.; Fulli, G.; Bayhan, S.; Chondrogiannis, S.; Demirbas, S. Critical aspects of wind energy systems in smart grid applications. Renew. Sust. Energ. Rev. 2015, 52, 155–171. [Google Scholar] [CrossRef]
- Auld, A.E.; Smedley, K.M.; Mueller, F.; Brouwer, J.; Samuelsen, G.S. Load-following active power filter for a solid oxide fuel cell supported load. J. Power Sources 2010, 195, 1905–1913. [Google Scholar] [CrossRef]
- Malik, M.; Sharma, P.R. Power quality improvement in hybrid photovoltaic and wind power system using 3 levels inverter. In Proceedings of the 2020 International Conference on Advances in Computing, Communication & Materials (ICACCM), Dehradun, India, 21–22 August 2020; pp. 253–260. [Google Scholar] [CrossRef]
- Palizban, O.; Rezaei, M.A.; Mekhilef, S. Active and reactive power control for a hybrid system with photovoltaic panel, wind turbine, fuel cells, electrolyzer and super capacitor in off-grid mode. In Proceedings of the 2011 IEEE International Conference on Control System, Computing and Engineering, Penang, Malaysia, 25–27 November 2011; pp. 404–408. [Google Scholar] [CrossRef]
- Hosseini, S.H.; Nejabatkhah, F.; Danyali, S.; Mozaffari Niapour, S.A.K. Grid-connected three-input PV/FC/Battery power system with active power filter capability. In Proceedings of the 2011 2nd IEEE PES International Conference and Exhibition on Innovative Smart Grid Technologies, Manchester, UK, 5–7 December 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Lakum, A.; Bhonsle, D.; Pandya, M. Optimal placement and sizing of active power filters in RDS using TLBO for harmonic distortion reduction. Decarbonisation Digit. Energy Syst. 2024, 1099, 289–302. [Google Scholar] [CrossRef]
- Sahoo, B.; Alhaider, M.M.; Rout, P.K. Power quality and stability improvement of microgrid through shunt active filter control application: An overview. Renew. Energy Focus. 2023, 44, 139–173. [Google Scholar] [CrossRef]




| Criterion | VSI | CSI |
|---|---|---|
| DC-energy storage | VSI uses a DC capacitor. The electrolytic capacitor is of low weight and economical but has a limited lifetime. | CSI uses a DC inductor. The inductor is heavy and bulky, high-cost, and provides more loss, but its lifetime is not limited. |
| Expanded features for multilevel structures | Yes | No |
| Power ratings | Low/medium | Medium |
| Control | Simple | Complex |
| Speed of response | Fast | Medium |
| Switching frequency | High | Low/medium |
| Switching ripple in output currents | Higher | Lower |
| Total power losses | Low | High |
| Requirements for protection | Usual | Separate clamp circuit for overvoltage |
| Efficiency when operating at light load conditions | Lower | Higher |
| Technique | Strengths | Weaknesses |
| Fixed hysteresis band control | Simple implementation; good stability; accurate current tracking; very fast transient response; and robustness to the load parameter variation | Variable switching frequency; increased switching losses; complicated filter design and selection of the DC-voltage value; and audio noises |
| Adaptive hysteresis band control | Fixed switching frequency; reduced high-frequency components of the power supply current; reduced switching losses; and better dynamic response under transient load conditions | Increased complexity of the control structure |
| Model predictive control | Easy inclusion of nonlinearities and constraints; minimizes the switching frequency in high-power inverters | Need of precise knowledge of the filter model; a lot of calculations are required |
| Deadbeat predictive control | High dynamic performance; fast response; zero steady-state error; constant switching frequency; and high compatibility for digital implementation | Performance highly depends on the accuracy of the system model; inherent delay due to the calculations |
| Sliding mode control | Strong robustness against parameter drift; system dynamics is unaffected by circuit parameters and only depend on the selected sliding surface; and reliable performance during transients | Chattering phenomenon in discrete implementation; need to choose a compromise between good transient and zero steady state performance |
| Proportional-resonant control | Periodic error elimination; periodic disturbance rejection; small steady state tracking error; and good compromise between cost and performance | Compensation effect decreases when the grid frequency fluctuates; weaker performance for dynamic loads |
| Repetitive control | Can be used to track the fundamental wave and multiple specific frequency harmonics; robust performance for periodic issues; and zero-steady-state error at all harmonic frequencies | Difficult to obtain a very fast response for fluctuating loads; difficult to guarantee system stability |
| Multi-loop control | Good performance of the LCL-type SAPFs | Controller design is complicated considering delay effect; require of a large number of sensors |
| Multiresonant control | Enable sinusoidal currents regardless of the distorted grid voltage harmonic content | The number of resulting controller gains to be tuned grows linearly with the number of frequencies to be dealt with; tuning procedures require good expert knowledge |
| Fuzzy logic control | Does not depend on a specific mathematical model; suitable for the control of unknown and uncertain systems; easy implementation for nonlinear systems; fast response; constant switching frequency; insensitive to variations in parameters and operating points | Selective harmonic elimination is not suitable; slow control method |
| dp | dq | θ1 | θ2 | θ3 | θ4 | θ5 | θ6 | θ7 | θ8 | θ9 | θ10 | θ11 | θ12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 101 | 111 | 100 | 000 | 110 | 111 | 010 | 000 | 011 | 111 | 001 | 000 |
| 1 | 1 | 111 | 111 | 000 | 000 | 111 | 111 | 000 | 000 | 111 | 111 | 000 | 000 |
| 0 | 0 | 101 | 100 | 100 | 110 | 110 | 010 | 010 | 011 | 011 | 001 | 001 | 101 |
| 0 | 1 | 100 | 110 | 110 | 010 | 010 | 011 | 011 | 001 | 001 | 101 | 101 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popescu, M.; Bitoleanu, A.; Suru, C.V.; Linca, M.; Alboteanu, L. Shunt Active Power Filters in Three-Phase, Three-Wire Systems: A Topical Review. Energies 2024, 17, 2867. https://doi.org/10.3390/en17122867
Popescu M, Bitoleanu A, Suru CV, Linca M, Alboteanu L. Shunt Active Power Filters in Three-Phase, Three-Wire Systems: A Topical Review. Energies. 2024; 17(12):2867. https://doi.org/10.3390/en17122867
Chicago/Turabian StylePopescu, Mihaela, Alexandru Bitoleanu, Constantin Vlad Suru, Mihaita Linca, and Laurentiu Alboteanu. 2024. "Shunt Active Power Filters in Three-Phase, Three-Wire Systems: A Topical Review" Energies 17, no. 12: 2867. https://doi.org/10.3390/en17122867
APA StylePopescu, M., Bitoleanu, A., Suru, C. V., Linca, M., & Alboteanu, L. (2024). Shunt Active Power Filters in Three-Phase, Three-Wire Systems: A Topical Review. Energies, 17(12), 2867. https://doi.org/10.3390/en17122867








